Abstract
Time series subject to regime shifts have attracted much interest in domains such as econometry, finance or meteorology. For discrete-valued regimes, models such as the popular Hidden Markov Chain (HMC) describe time series whose state process is unknown at all time-steps. Sometimes, time series are annotated. Thus, another category of models handles the case with regimes observed at all time-steps. We present a novel model which addresses the intermediate case: (i) state processes associated to such time series are modelled by Partially Hidden Markov Chains (PHMCs); (ii) a multivariate linear autoregressive (MLAR) model drives the dynamics of the time series, within each regime. We describe a variant of the expectation maximization (EM) algorithm devoted to PHMC-MLAR model learning. We propose a hidden state inference procedure and a forecasting function adapted to the semi-supervised framework. We first assess inference and prediction performances, and analyze EM convergence times for PHMC-MLAR, using simulated data. We show the benefits of using partially observed states as well as a fully labelled scheme with unreliable labels, to decrease EM convergence times. We highlight the robustness of PHMC-MLAR to labelling errors in inference and prediction tasks. Finally, using turbofan engine data from a NASA repository, we show that PHMC-MLAR outperforms or largely outperforms other models: PHMC and MSAR (Markov Switching AutoRegressive model) for the feature prediction task, PHMC and five out of six recent state-of-the-art methods for the prediction of machine useful remaining life.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Time series are widely present in many domains such as industry, energy, meteorology, e-commerce, social networks or health. They represent the temporal evolving of systems and help us to understand their temporal dynamics and perform short, medium or long-term predictions. A major research line has been dedicated to time series analysis. In this line, exponential smoothing models (Gardner & Everette, 2006; Bergmeir et al., 2016), Box and Jenkins models (Box et al., 2015) and nonlinear autoregressive neural networks (Yu et al., 2014; Wang et al., 2019; Noman et al., 2020) are essentially devoted to forecasting. In addition to the forecasting goal, Regime-Switching AutoRegressive models (Ubilava & Helmers, 2013; Hamilton, 1990) also allow to discover hidden behaviors of such systems.
In the cases when the studied system is stationary, that is its behavior is time-independent, the Linear AutoRegressive (LAR) model is a framework widely used to capture the autoregressive dynamics of the corresponding time series (Wold, 1954; Degtyarev and Gankevich, 2019). The LAR model is a simple linear regression model in which predictors are lagged values of the current value in the time series. However, many real-life systems are subject to changes in behaviors: for instance in econometry, we distinguish between recession and expansionary phases; in meteorology, anticyclonic conditions alternate with low pressure conditions. These systems are commonly referred to as regime-switching systems, where each regime corresponds to a specific behavior. Each time-step is associated with some state, amongst those allowed for the system. Regime-switching system modelling is achieved in two steps: (i) the state process modelling that enables to capture how states are generated, and (ii) the modelling of the autoregressive dynamics of the time series within each regime. In the latter step, a simple autoregressive framework such as the LAR model can be used. Generally, in step (i), the state process is modelled by a discrete-valued Markov process. In the current state-of-the-art literature, two categories of models can be distinguished.
In Hidden Regime-Switching AutoRegressive (HRSAR) models, the state process is hidden and is modelled by a Hidden Markov Process (HMP). This category of models has been introduced by Hamilton (1989) in the context of United States’s Gross National Product time series analysis. Several variants and extensions were subsequently designed.
In Observed Regime-Switching AutoRegressive (ORSAR) models, the state process is either observed or derived a priori. In the latter case, a clustering algorithm is used before fitting the model, to extract the regimes. The clustering may either rely on endogenous variables (i.e., the variables whose dynamics is observed through the time series) or on exogenous variables supposed to drive regime-switching. The works of Flecher et al. (2010) on the one hand, and of Bessac et al. (2016) on the other hand, illustrate the application of these models to meteorological time series.
When the state process is partially observed, which means that the system state is known at some random time-steps and unknown for the remaining time-steps, ORSAR models cannot be directly applied while HRSAR models are suboptimal in the sense that the observed states cannot be included.
Industry is a major potential supplier of such data. Many machines are monitored continuously, through multiple sensors. In parallel, technical monitoring may be carried out episodically, by humans, during expert or technician visits; these visits result in partial annotations on the state of the machine. Modelling adapted to this type of partially annotated multivariate time series is a prerequisite for predicting the evolution of the extent of wear of a machine and anticipating maintenance operations, or even avoiding accidents. The same needs have been identified for machines used in transport (trains, planes, ships). Monitoring the ageing of engineering structures (bridges, railways) can also combine the continuous collection of data from sensors and episodic assessments of the state of the structures. In a different register, manual annotation of time series data (e.g., video sequences, audio sequences) is a time-consuming task. It is very often the case that only a partial annotation is available. Automatizing the annotation of latent states, seeking to leverage the partial annotation, is therefore appealing. Thus, one can increase the amount of fully labelled data, upstream a fully supervised machine learning task such as automated speech recognition, human gesture analysis, human activity recognition, segmentation of time series. Again, the same situation can be found in software reliability modelling. For instance, time intervals between bug occurrences can be governed by a Markov chain (Bharathi & Selvarani, 2020). The latter may be considered as partially hidden, since the debugging state is an observable state. Partial annotation corresponds to a frequently encountered situation in research in biology. For instance, in de novo detection of biologically functional signals in proteins, wet-lab experiments are expected to provide guidance for annotating regions of proteins as potentially harboring such functional signals. However, experimental limitations may prevent full annotation into “signal” and “no signal” states. In this case, to avoid additional costly and time-consuming experiments, a model allowing partial annotation would be appropriate.
To overcome the ORSAR and HRSAR limitations, in this work, we propose a novel Regime-Switching AutoRegressive model that capitalizes on the observed states while the hidden states are inferred. We consider a special case of Markov process henceforth named Markov Chain. Our model is referred to as the Partially Hidden Markov Chain Multiple Linear AutoRegressive (PHMC-MLAR) model. The innovative contributions brought by this model are threefold. First, the PHMC-MLAR model is a flexible parametric model that supplies a unification of HRSAR and ORSAR models when the state process is a Markov Chain. Thus, when the state process is fully observed, PHMC-MLAR is reduced to ORSAR. Reversely, when the state process is fully hidden, PHMC-MLAR instantiates as HRSAR. Second and third, our model can be seen as both an extension of the seminal work of Scheffer and Wrobel (2001) around the Partially Hidden Markov Chain (PHMC) and an extension of the seminal work of Hamilton (1989) around the Markov-switching autoregressive (MSAR) model. On the one hand, the PHMC-MLAR model locally adds autoregressive features to a (global) PHMC framework ; this innovation clearly extends the PHMC proposal to the domain of time series modelling. Meanwhile, PHMC-MLAR adds a PHMC feature to the MSAR framework, to switch to a semi-supervised global framework. Finally, beyond the unification aspect, we contribute to the machine learning literature through designing the underlying algorithmic machinery dedicated to effective and efficient PHMC-MLAR model training. We consider multivariate time series.
The main contributions of this paper are as follows:
-
1.
We propose a new Regime-Switching AutoRegressive model that integrates the states observed at some random time-steps. This model, referred to as PHMC-MLAR, provides a unification of HRSAR and ORSAR models when the state process is modelled by a Markov Chain (MC).
-
2.
The PHMC-MLAR proposal extends two existing models of the literature, the PHMC and MSAR models. On the one hand, PHMC-MLAR incorporates local MSAR models into a global PHMC framework, to model time series. On the other hand, PHMC-MLAR replaces the Markov chain used as the global switching mechanism of the MSAR model, by a semi-supervised global framework (PHMC).
-
3.
We propose a variant of the Expectation-Maximization (EM) algorithm that allows to learn the parameters of our model.
-
4.
Inference on hidden states is carried out by a variant of the Viterbi algorithm, adapted to take into account the observed states.
-
5.
Regarding the time series forecasting task, a prediction function is proposed. We distinguish between the case where the system state is known at forecast horizons from the case where it is latent.
The Baum-Welsh algorithm is the instantiation of the EM algorithm tailored for hidden Markov models (HMMs) (Baum et al., 1970). It relies on the popular forward-backward procedure, to calculate the statistics of the Expectation step. Scheffer and Wrobel (2001) adapted this procedure to their PHMC proposal and derived a backward-forward-backward procedure. However, these authors deal with observations that are independent and categorical. Instead, we extended this PHMC framework to handle observations that are continuous time series; we therefore thoroughly revisited the backward-forward-backward procedure to incorporate the autoregressive feature.
In addition, we derived an estimation procedure to infer the unknown states in the state sequence of a discrete-valued Markov process: the introduction of partial knowledge on states, and that of the autoregressive feature, compelled us to customize the well-known Viterbi algorithm (Forney, 1973).
The ability of our model to infer the hidden states and to make accurate predictions on time series, even when the observed states are unreliable, was investigated through experiments performed on synthetic data. Our work underlines the benefits of using partially observed states to decrease EM convergence times. This performance is obtained with no or practically no impact on the quality of hidden state inference, as from labelling percentages around 20–30\(\%\); the prediction accuracy is also preserved above such percentage thresholds. For instance, for a training set of 100 sequences, with \(70\%\) labelled states, the EM algorithm converges after 22 iterations on average against 62 on average for the unsupervised case. Moreover, performing fully supervised training with a proportion of ill-labelled states is also beneficial for EM convergence. For example, given a training set of size 100 annotated with a \(70\%\)-reliable labelling function, the EM algorithm converges after a single iteration against 67 iterations for the unsupervised case. This offers promising prospects to enhance model selection for the PHMC-MLAR model. Further experimentations also show the ability of our variant of the Viterbi algorithm to infer hidden states in partially-labelled sequences. In addition, while assessing the impact on predictions generated by incorporating labelled states in the training sequences, we also compared the situations where all states are unknown at forecast horizons to the situations where all states are known. Prediction errors are subdued at all horizons in the latter case (by 44% on average), but contrasted horizons are still evidenced with low (respectively high) scores as in the former case. The constrast is kept constant whatever the percentage of observed states in the training set. Besides, we also point out the robustness of our model to labelling errors in inference task, when large training datasets and moderate labelling error rates are considered. Finally, the latter experiment highlights the remarkable robustness to error labelling in the prediction task, over the whole range of error rates.
Finally, the performance of the PHMC-MLAR model was evaluated in the context of a practical application to machine health prognostics. For this purpose, we conducted experiments on turbofan engine data from a NASA repository. Considering short, medium and long-term feature forecasting, we first show that PHMC-MLAR and MSAR models obtain comparable accuracies at the short-term horizon (\(h=5\)), whereas PHMC-MLAR presents higher forecast accuracies than MSAR at medium and long-term forecast horizons (\(h = 10, 20, 30\)). In comparison with the PHMC model, our model achieves much better performance (whatever the horizon). These results show the relevance of including an autoregressive model within each regime, as suggested in this work. Second, we evaluated the performance of PHMC-MLAR in predicting the remaining useful life (RUL) of machines. Our results show that our proposal outperforms PHMC and five of six recent state-of-the-art RUL prediction methods, including four artificial intelligence-based methods.
This paper is organized as follows. Related work is reviewed in Sect. 2. Section 3 describes the PHMC-MLAR model. Then a learning algorithm is derived in Sect. 4, to estimate the model parameters. Inference of the hidden states is addressed in Sect. 5. Section 6 presents the time series forecasting procedure. Section 7 depicts the experimental protocol that drove our experimentations on synthetic data, and discusses the results obtained. Section 8 focuses on a practical application to machine health prognostics. Therein, we depict the experimental protocol applied to realistic datasets composed of turbofan engine degradation trajectories, and we discuss the results observed. Section 9 concludes this paper and opens up future directions of research.
2 Related work
This section first highlights the links between our proposal, PHMC-MLAR, and the most closely related contributions of the literature. The PHMC-MLAR combines a variant of the Hidden Markov Model (HMM), namely the Partially Hidden Markov Chain (PHMC), with the Linear AutoRegressive (LAR) model. The rest of this section reviews the two main models that compose the hybrid model proposed.
As mentioned in the introduction, the PHMC-MLAR model unifies the HRSAR and ORSAR frameworks. However, the common thread between these latter frameworks is the implication of dependencies that drive the local dynamics within each regime. Therefore, the contributions of the literature most closely related to PHMC-MLAR are also characterized by various local dynamics.
Several models closely related to HRSAR were proposed in the literature. The MSAR model (Markov-switching AutoRegressive model) designed by Hamilton (1989) combines ARIMA (AutoRegressive Integrated Moving Average) models with an HMM, to characterize changes in the parameters of an autoregressive process. The targeted application motivating the MSAR model was economic analysis: the switch between fast growth and slow growth is governed by the outcome of the Markov process.
Further, Filardo (1994) incorporated time-varying transition probabilities between regimes in the MSAR model. For instance, the resulting model was subsequently used to reproduce the cyclic patterns existing in climatic variables (Cardenas-Gallo et al., 2016). In parallel, the Hamilton’s MSAR model was also extended into a general dynamic linear model combined with Markov-switching (Kim, 1994). Finally, Michalek and co-authors’work focused on a HRSAR model that integrates HMM with Moving Average (MA) models (Michalek et al., 2000). In the same work, the parameter estimation approximation thus derived was generalized to deal with AutoRegressive Moving Average (ARMA) hybridized with HMM. Simulations of electrophysiological recordings showed that the derived estimators allow to recover the true dynamics where standard HMM fails. The model generalized by Michalek and collaborators, to integrate HMM with ARMA, was also applied to model human activity as time signals for activity early recognition (Li & Fu, 2012).
More recently, a nonhomogeneous HRSAR model was developed to model wind time series (Ailliot et al., 2015). The aim was to acknowledge that the probability of switching from cyclonic conditions to anticyclonic conditions between time-steps t and \(t+1\) depends on the wind conditions at time-step t at some given location off the French Brittany coast. A nonhomogeneous MSAR (NHMSAR) model was thus designed for this purpose.
To our knowledge, the investigations around ORSAR models are limited to the recent work of Bessac et al. (2016) which was applied to wind time series. Therein, observed regimes are derived by running a clustering procedure on the variables under study or on extra variables. Thus are identified the states, all distinct from one other, in which the data are homogeneous. Besides comparing the ORSAR models derived from various clustering procedures, Bessac and collaborators also compare the respective merits of HRSAR and ORSAR models on real-world and simulated data.
2.1 Partially Hidden Markov Chain—PHMC(K)
Hidden Markov models (HMMs) have been successfully used in such domains as natural language processing (Morwal et al., 2012), handwriting recognition (Mouhcine et al., 2018), speech emotion recognition (Schuller et al., 2003), human action recognition (Berg et al., 2018) or renewable power prediction (Ghasvarian Jahromi et al., 2020), to name but a few.
HMM(K) is a flexible probabilistic framework able to model complex hidden-regime-switching systems. It exactly possesses K states where each state drives the specific behavior of an observed variable. This variable is itself modelled through a usual probability law such as a Gaussian law, for example. The system state process, which specifies the ongoing behavior of the latter observed variable at each time-step, is fully latent. Therefore, state inference is the main purpose of HMM models: the goal is to learn about the latent sequence of states from the observed behavior. This task is generally driven by Maximum A Posteriori (MAP) estimation implemented through the Viterbi algorithm (Forney, 1973). Importantly, the HMM framework satisfies the Markov property, which stipulates that the conditional probability distribution of the hidden state at time-step t, given the hidden states at previous time-steps \(t' < t\), only depends on the hidden state at time-step \(t-1\). Besides, the observed behavior at time-step t solely depends on the hidden variable at time-step t.
When dealing with systems in which the state process is partially observed or known, applying HMM would result in an important information loss in the sense that the observed states are ignored. To overcome this limitation, Scheffer and Wrobel (2001) have introduced the Partially Hidden Markov Chain (PHMC), which integrates partially observed states in the modelling process. The authors have proposed an active learning algorithm in which the user is asked to label difficult observations identified during model learning. More recently, Ramasso and Denoeux (2013) have proposed a model that makes use of partial knowledge on HMM states. These authors have modelled the partial knowledge by a belief function that specifies the probability of each state at each time-step. The works carried out by Ramasso and Denoeux (2013) have shown that the use of partial knowledge on states accelerates HMM model learning.
2.2 Linear AutoRegressive model—LAR(p)
An observed time series is considered to be one realization of a stochastic process. Time series analysis and forecasting thus require that the underlying stochastic process be modelled. The linear autoregressive (LAR) model is a stochastic model widely used for this purpose. A LAR model of order p is a linear model in which the regressors are the p past values of the variable, hence the term autoregression. Although the LAR model is conceptually simple and easy to learn, it can only be applied to stationary time series. When this condition is violated, model misspecification issues arise. Nonetheless, it is well known that if the autoregressive coefficients of a LAR process are all less than one in module, then the process will be stationary. This is a necessary and sufficient condition which is tested through unit root tests (Phillips & Perron, 1988; Dickey & Fuller, 1979; Kwiatkowski et al., 1992).
In the LAR(p) model, the hyper-parameter p denotes the number of past observations to include in the prediction at time-step t. Two alternative methods are generally used to fix the value of p. The first one relies on a well-known property of the partial autocorrelation function of the LAR(p) model: the autocorrelation becomes null from lag \(p+1\). The second method, more general, tests a range of candidate values for p, then selects the value that minimizes a model selection criterion such as the Bayesian information criterion (BIC) or the Akaike’s information criterion (AIC).
3 The PHMC-MLAR model
In this section, we explain how we have created a new regime-switching model called PHMC-MLAR, based on the PHMC and LAR models. The section first introduces some notations. Then Sect. 3.2 describes our proposal to model the state process by a PHMC model. Section 3.3 details how, within each regime, the dynamics of the observed variable is governed by a LAR model. Thus, the bivariate process follows a PHMC-MLAR model. A final subsection briefly discusses hyper-parameter selection in Markov-switching models.
To note, the fundamental difference between our model and the two other approaches identified in the same line (Scheffer & Wrobel, 2001; Ramasso & Denoeux, 2013) is the autoregressive dynamics of our model (see Fig. 1).
The conditional independence graphs of the Partially Hidden Markov Chain and of the Partially Hidden Markov Chain Linear Autoregressive (PHMC-MLAR) model, when the LAR order p is equal to 2. a PHMC model. b PHMC-MLAR model. Observed states are shown in dark shade whereas hidden states are colored in light shade. When a state is observed, \(\sigma _t\) is reduced to a singleton (Color figure online)
3.1 Notations
-
Symbol \(:=\) stands for the definition symbol.
-
\(\varvec{1}_A: \Omega \rightarrow \{0,1\}\) denotes the indicator function that indicates membership of an element in a subset A of \(\Omega\). As from now, \(\varvec{1}_A\) will be noted \(\varvec{1}_{\{ x \in A \}}\).
-
\(\{X_t\}_{t \in {\mathbb {Z}}}\) denotes a multidimensional stochastic process with \(X_t \in\) \({\mathbb {R}}^d\). By convention, \(X_{1-p}^0\) denotes the p initial values of the time series \(\{X_t\}\). For each \(t \ge 1\), \(X_{t-p}^{t-1}\) stands for the subseries \(\{ X_{t-p}, X_{t-p+1} \cdots X_{t-1} \}\).
-
\(\mathbf {x} = x_{1}^T\) represents an observed multivariate time series with \(\mathbf {x}_0=x_{1-p}^0\) the corresponding initial values.
-
\(\{ S_t \}_{t \in {\mathbb {N}}^*}\) denotes a state process depicting the temporal evolution of a regime-switching system where the set of states is \(\mathbf {K} = \{1, 2, \dots , K\}\). In this paper, states are instantaneous, whereas a regime is a succession of identical states. We denote \(\sigma _t\) (\(\subseteq \mathbf {K}\)) the set of possible states at time-step t with \(\sigma _t = \mathbf {K}\) when \(S_t\) is latent, and \(\sigma _t = \{k\}\) when \(S_t = k\), that is \(k^{\mathrm{th}}\) state is observed at time-step t.
-
\({\mathcal {M}}_p({\mathbb {R}})\) is the set of square matrices of order p with real coefficients.
-
Symbols in bold represent nonscalar variables (e.g., vectors).
3.2 Modelling the state process
Let \(\{ (S_t, \sigma _t) \}\) the state process which is supposed to be partially observed. Remind that if \(S_t=k\), i.e. \(k^{\mathrm{th}}\) state has been observed at time-step t, then \(\sigma _t = \{k\}\). At the extreme, \(\sigma _t = \mathbf {K}\) for a (fully) latent state \(S_t\). We draw the reader’s attention to the flexibility of the model: an intermediate case between observed (\(\{k\}\)) and latent (\(\mathbf {K}\)) would be specified by \(\sigma _t \subset \mathbf {K}\).
Let \({\mathcal {R}} = \{ k \in \mathbf {K} \,|\, \exists \, t \in {\mathbb {N}}^*, \sigma _t = \{k\} \}\), the set of states that have been observed at least once. We have \(|{\mathcal {R}}| \le K\) where K is the total number of states. Thus, \(K - |{\mathcal {R}}|\) states are undetermined and depict the hidden dynamics of the system under study. It has to be underlined that it is difficult (it not sometimes impossible) to associate a physical interpretation to the hidden dynamics. Such an interpretation requires strong knowledge upon the studied system.
In the PHMC-MLAR model, \(\{(S_t, \sigma _t)\}\) is modelled by a K-state PHMC, parametrized by transition probabilities
and stationary law \(\pi _i = P(S_1 = i), \quad \pi _i \in [0, 1], \, \sum _{i=1}^K \pi _i = 1\).
Let \(\varvec{\theta }^{(S)} = ( (\pi _i)_{i=1,...,K}, (a_{i,j})_{i,j=1,...,K})\) denote the set of parameters associated with the PHMC.
3.3 Modelling the dynamics under each state
For each state \(k \in \mathbf {K}\), \(\{X_t \in {\mathbb {R}}^d\}\) is supposed to be stationary and modelled by a p-order LAR process defined as follows:
where \(p \ge\) 1 is the number of past values of \(X_t\) to be used in modelling, k is the state at time-step t, \(\phi _{0,k} \in {\mathbb {R}}^d\) and \((\phi _{i,k} \in {\mathcal {M}}_d({\mathbb {R}}))_{i=1, \dots , p}\) are respectively the vector of intercepts and the matrices of autoregressive coefficients associated with \(k^{\mathrm{th}}\) state. The error terms \(\epsilon _{t,k} \in {\mathbb {R}}^d\) are independent and identically distributed with zero mean and covariance matrix \(h_k \in {\mathcal {M}}_d({\mathbb {R}})\).
Equation 1 defines the relationships between each dimension of \(X_t\) (a univariate time series) and both the p lagged values for the \(d - 1\) other dimensions and its own p past values. The example below illustrates this relationship in the case where \(d=3\) and \(p=2\).
It is important to underline that Eq. 1 is not defined for the p initial values denoted by \(X_{1-p}^0\). These initial values are modelled by the initial law \(g_0(x_{1-p}^0; \varvec{\psi })\) parametrized by \(\varvec{\psi }\). For instance, \(g_0\) can be a multivariate normal distribution \({\mathcal {N}}_{d \times p}(\mathbf {m}, \mathbf {V})\) where \(\mathbf {m} \in {\mathbb {R}}^{d \times p}\) is the mean and \(\mathbf {V} \in {\mathcal {M}}_{d \times p}({\mathbb {R}})\) is the variance-covariance matrix.
Note that the law of \(\{\epsilon _{t,k}\}\) and the conditional distribution \(P(X_t|X_{t-p}^{t-1}\), \(S_t=k; \, \phi _{0,k}, \, \phi _{1,k}\), \(..., \phi _{p,k}, h_k)\) belong to the same family. Usually, Gaussian white noises are used. In this case, the conditional distribution is Gaussian too, with mean and covariance matrix respectively equal to \(\phi _{0,k} + \sum _{i=1}^p \phi _{i,k} X_{t-i}\) and \(h_k\).
Let \(\varvec{\theta }^{(X,k)} = (\phi _{0,k}, \, \phi _{1,k}, ..., \phi _{p,k}, h_{k})\) the parameters of the LAR(p) process associated with \(k^{\mathrm{th}}\) state. The law of \(\{X_t\}\) is fully parametrized by \(\varvec{\theta }^{(X)} = (\varvec{\theta }^{(X,k)})_{k=1, ...,K}\) and \(\varvec{\psi }\).
To note, as in (Scheffer & Wrobel, 2001) and (Ramasso & Denoeux, 2013), the PHMC-MLAR model assumes that the same order p is shared by all \(| \mathbf {K} |\) LAR processes associated with the states in \(\mathbf {K}\).
It has also to be highlighted that the state \(S_t = k\) conditioning a LAR process of order p on \(X_t\) does not impose that the p lagged values \(X_{t-1}^{t-p}\) be observed under same state k. That is, the PHMC-MLAR model may perfectly switch from regime to regime, and even from state to state, meanwhile keeping memory of values determined by previous regimes or states.
4 Learning PHMC-MLAR models
This section first presents an instance of the Expectation-Maximization (EM) algorithm dedicated to PHMC-MLAR parameter learning. Then, we briefly discuss hyper-parameter selection in Markov-switching models.
4.1 Estimation of the PHMC-MLAR parameters
This subsection is dedicated to the presentation of an instance of the EM algorithm, to estimate the PHMC-MLAR parameters. As seen in previous subsections, the PHMC component and the LAR components of our model are respectively parametrized by \(\varvec{\theta }^{(S)}\) and \((\varvec{\theta }^{(X)}, \varvec{\psi })\). Then, the whole PHMC-MLAR model is parametrized by \((\varvec{\theta }, \varvec{\psi })\) where \(\varvec{\theta } = (\varvec{\theta }^{(S)}, \varvec{\theta }^{(X)})\). Thus, PHMC-MLAR learning consists in estimating \((\varvec{\theta }, \varvec{\psi })\) from a training dataset.
Thanks to good statistical properties such as asymptotic efficiency, a maximum likelihood estimator (MLE) is considered. However, for models with hidden variables like ours, MLE computation results in an untractable problem. To address this issue, the Expectation-Maximization (EM) algorithm is generally used, in order to approximate a set of parameters that locally maximizes the likelihood function. EM was introduced by Baum et al. (1970) to cope with Hidden Markov Model learning. This version was further extended by Dempster et al. (1977) into the versatile EM algorithm, to handle parameter estimation in a more general framework. EM has also been applied to autoregressive Markov-switching models (Hamilton, 1990) and PHMC models (Scheffer & Wrobel, 2001; Ramasso & Denoeux, 2013).
We propose to learn the PHMC-MLAR model through a dedicated instance of the EM algorithm. To fix ideas, in Sect. 4.1.1, we first consider the case where the model is trained in a single training time series context, that is considering a unique pair of data (\(\mathbf {x} = x_{t=1-p}^T, \, \Sigma =\sigma _{t=1}^T\)), with \(\mathbf {x}\) a realization of \(\{ X_t \}\) and \(\sigma _t\) the set of possible states at time-step t. Then, in Sect. 4.1.2, we briefly outline the EM algorithm in the case where N (independent) training time series \((\mathbf {x}^{(1)},\Sigma ^{(1)})\), \(\dots\), \((\mathbf {x}^{(N)},\Sigma ^{(N)})\) are used.
4.1.1 Single training time series
Let \(\mathbf {x} = x_{1-p}^T\) the observed time series with \(x_{1-p}^0\) the initial values of the autoregressive process. Let \(\Sigma = \sigma _{t=1}^T\), further simplified into \(\sigma _{1}^T\), where \(\sigma _t\) stands for the set of possible states at time-step t. Let \((S_1^T, \Sigma )\) the state process (partially observed) of \(\mathbf {x}\) with \(\sigma _t = \mathbf {K}\) if \(S_t\) is hidden, \(\sigma _t = \{k\}\) if state k is observed at time-step t, and \(\sigma _t \subset \mathbf {K}\) in the intermediate case.
MLE is implemented by maximizing the expectation (with respect to the latent variables) of the complete data likelihood. Complete data likelihood is further referred to as \({\mathcal {L}}^c\). \({\mathcal {L}}^c\) denotes the evidence/likelihood of the training data when latent/hidden variables are supposed to be known. \({\mathcal {L}}^c\) writes as follows:
with \({\mathcal {L}}_c^c\) the conditional complete data likelihood and \(g_0\) the initial law of \(X_t\).
When the expectation of \({\mathcal {L}}^c\) with respect to the partially hidden states is calculated, term \(g_0(x_{1-p}^0; \, \varvec{\psi })\) in Eq. 2 can be taken out of the expectation since it does not depend on the states:
where \(P(S_1^T \,| \,X_{1-p}^{T}=x_{1-p}^{T}, \Sigma ; \, \varvec{\varvec{\theta }})\) is the posterior probability of partially hidden states \((S_1^T, \Sigma ).\)
Then, by considering the logarithmic scale, Eq. 3 can be separately maximized with respect to \(\varvec{\theta }\) and \(\varvec{\psi }\):
It has to be noted that Eq. 4 is a simple probability observation problem. In contrast, because of the hidden states, maximization with respect to \(\varvec{\theta }\) (Eq. 5) is carried out by an instance of the EM algorithm.
EM is an iterative algorithm that alternates between E(xpectation) step and M(aximization) step. At iteration n, we obtain:
with \(P(S_1^T \,| \,X_{1-p}^{T}=x_{1-p}^{T}, \Sigma ; \, \hat{\varvec{\varvec{\kern-2pt\theta }}}_{n-1})\) the posterior probability of partially hidden states \((S_1^T, \Sigma )\) at iteration \(n-1\).
The rest of this subsection details the two EM steps.
Step E of EM
In this step, the quantity \(Q(\varvec{\theta }, \hat{\varvec{\kern-2pt\theta }}_{n-1})\) (Eq. 6) is computed. Following the conditional independence graph of the PHMC-MLAR model (see Fig. 1b), the conditional complete data likelihood writes:
with \(\varvec{\theta }^{(X,k)}\) the parameters of the LAR process associated with \(k^{\mathrm{th}}\) state and \(P(X_t=x_t \, | \, X_{t-p}^{t-1}, S_t =k; \, \varvec{\theta }^{(X,k)})\) the conditional law of \(X_t\) within k.
Notice that the terms in Eq. 8 depend on either a single state \(S_t\) or two consecutive states \(S_t, S_{t-1}\). In this same equation, products are replaced by sums when considering the logarithm scale. Then \(\ln {\mathcal {L}}_c^c (\varvec{\varvec{\theta }})\) is substituted in Eq. 6 and the expectation with respect to the posterior probability of state process is developed. After some integrations, we find that \(Q(\varvec{\theta }, \hat{\varvec{\theta }}_{n-1})\) only depends on the following probabilities:
The \(\xi _t(k, \ell )\) quantities are used to compute the \(\gamma _t(\ell )\) probabilities (\(\gamma _t(\ell ) = \sum _{j=1}^K \xi _t(j,\ell ), \text {for}\ t=2, \dots , T_i\), \(\gamma _1(\ell ) =\sum _{j=1}^K \xi _2(\ell ,j)\)). Therefore, the E-step is reduced to computing these probabilities. To this end, we have derived a backward-forward-backward procedure as an extension of the forward-backward algorithm, one of the ingredients of the Baum-Welsh algorithm (Baum et al., 1970). The backward-forward-backward algorithm was initially proposed by Scheffer and Wrobel (2001) for the purpose of PHMC model learning.
The difference with respect to the classical unsupervised framework of the MSAR model lies in that the calculus of the probabilities \(\gamma _t(\ell )\) is ruled by the \(\Sigma\) annotation. In the MSAR fully unsupervised framework, probabilities \(\gamma _t(\ell )\) always have to be computed. In the semi-supervised PHMC-MLAR framework, probability \(\gamma _t(\ell )\) reaches the minimum 0 if annotation \(\Sigma\) specifies that \(\sigma _t = \{s\}\) since \(S_t = s\) is observed and \(s \ne \ell\). In this configuration, probability \(\gamma _t(s)\) reaches the maximum 1. Thus, no calculation of probabilities \(\gamma _t(...)\) is required for the known states.
Besides, we have adapted the EM algorithm to PHMC-MLAR models by taking into consideration the autoregressive dynamics. The details about the adapted backward-forward-backward algorithm are given in Appendix A. Note that in this appendix, we have carefully indicated the conditions required to calculate the various statistics involved, in relation to the \(\Sigma\) annotation: these statistics may not be defined or they do not need to be calculated.
Step M of EM
At iteration n, this step consists in maximizing \(Q(\varvec{\theta }, \hat{\varvec{\theta }}_{n-1})\) with respect to parameters \(\varvec{\theta } = (\varvec{\theta }^{(S)}, \varvec{\theta }^{(X)})\). It is straightforward to show that \(Q(\varvec{\theta }, \hat{\varvec{\theta }}_{n-1})\) can be decomposed as follows:
where \(\varvec{\theta }^{(X,k)}\) is the set of parameters specific to regime k. Functions \(Q_S\) and \(Q_X^{(k)}\) write:
We call the reader’s attention to the fact that \(Q_S\) (respectively \(Q_X^{(k)}\)) only depends on parameters \(\varvec{\theta }^{(S)}\) (respectively \(\varvec{\theta }^{(X,k)}\)). Therefore, \(Q_S\) and \({Q_X^{(k)}}_{k=1, \dots , K}\) can be maximized apart:
Eq. 13 is an optimization problem under equality constraints which can be solved by the method of Lagrange multipliers. Thus, the re-estimation formulas of \(\varvec{\theta }^{(S)}\) write:
In contrast, it is generally difficult to derive the analytical expression for \(\hat{\varvec{\kern-2pt\theta }}_n^{(X,k)}\). That is why \(Q_X^{(k)}(\varvec{\theta }^{(X,k)}, \hat{\varvec{\kern-2pt\theta }}_{n-1})\) is maximized relying on a numerical optimization method (e.g., the quasi-Newton method).
We point out that the M-step of our algorithm is very similar to that of the unsupervised framework MSAR. The only difference relies on the fact that in our algorithm, probabilities \(\gamma _t\)’s and \(\xi _t\)’s depend on the partial annotation of states.
Finally, dealing with the multivariate case does not pose any fundamental problem with respect to the univariate case: in the M step, the number of parameters estimated per regime is simply multiplied by \(d^2\) where d is the dimension of the time series.
4.1.2 Sketch of EM algorithm: several training time series
We now consider the general case in which PHMC-MLAR model is learnt from N (independent) partially annotated time series \((\mathbf {x}^{(1)},\Sigma ^{(1)})\), \(\dots\), \((\mathbf {x}^{(N)},\Sigma ^{(N)})\), with \(\mathbf {x}_0^{(1)}, \dots , \mathbf {x}_0^{(N)}\) the associated initial values and \(\mathbf {S}^{(1)}, \dots , \mathbf {S}^{(N)}\) the corresponding state processes with partial annotations \(\Sigma ^{(1)}, \dots , \Sigma ^{(N)}\). It has to be noted that time series \(\mathbf {x}^{(i)}\)’s can have different lengths while their respective initial vectors have a common size (\(\mathbf {x}_0^{(i)} \in {\mathbb {R}}^{d \times p}\), with p the autoregressive order). The lengths of the N time series are denoted \(T_1, T_2, \dots , T_N\), respectively.
The extension from the single-training time series to the multi-training time series case does not fundamentally change the parameter estimation algorithm. Thus, at each iteration, the E-step is separatly run on each training time series, which results in quantities \((\xi _t^{(i)})_{t=1, \dots , T_i}\) for \(i = 1, \dots , N\). Then in the M-step, these probabilities are used to update model parameters \(\varvec{\theta }\). Note that when \(N=1\), the single-training time series case is recovered.
Algorithm 1 sums up the instance of EM proposed for PHMC-MLAR parameter learning.

It is well known that the EM algorithm is sensitive to the choice of the starting point \(\hat{\varvec{\theta }}^{(0)}\) as regards the risk of attraction in a local maximum. In practice, several initial values are tested and the model that provides the highest likelihood is chosen. In this work, the initialization procedure presented in Algorithm 2 is used.

4.2 Hyper-parameter selection
An important step prior to the learning of Markov-switching models is hyper-parameter selection (or model selection). Hyper-parameter selection is the problem of picking a particular structure amongst several alternatives. In the case of Markov-switching, the model structure encompasses the number of hidden states, the form of the state transition matrix and output probabilities. There exist three main frameworks to address hyper-parameter selection.
Cross-validation iteratively splits the training set in a novel training set and a validation set, to assess how the model structure under consideration generalizes to the validation set. The computational burden of this approach is prohibitive for large hyper-parameter grids.
Regularization adds a penalty term to the likelihood objective function, to favour parsimonious models. In this category, several criteria are very often used for HMMs [see the recent review by Pohle et al. (2017)]. The Bayesian Information Criterion (BIC) (Schwarz, 1978) is defined as follows:
with L the log-likelihood, \(\hat{\theta }\) the maximum likelihood estimator, \(n_{par}\) the number of parameters of the model and C a regularization term that depends on the data used to train the model. For N independent multivariate time series of dimension d and respective lengths \(T_1, T_2, \cdots , T_N\), the C penalty is \(d \times \Sigma _i T_i\).
Experiments conducted on synthetic data have shown that the BIC criterion is relevant for the selection of the number of states in MSAR models (Psaradakis & Spagnolo, 2003), and on the joint determination of the number of states and autoregressive order in Markov-switching models (Psaradakis and Spagnolo, 2006). Furthermore, works on real-world data have shown that the BIC criterion allows the selection of models that are parsimonious and relevant, (i.e., that fit the data well) (Ailliot & Monbet, 2012; Kuck & Schweikert, 2017).
It should be noted that the consistency of the BIC criterion, i.e., its ability to always choose the right number of states when an infinite sample size is used, has been established for independent mixture models (Durand, 2003). However, in the case of HMM and MSAR models, the theoretical study of the behaviour of the BIC criterion remains an open problem.
On the other hand, the Akaike Information Criterion (AIC) (Akaike, 1974) is defined as
The AIC is an asymptotically unbiased estimator of a scoring function used to rank candidate models. It is a variant of the Kullback-Leibler (KL) divergence between the true model (i.e., the process that generated the data) and the approximate candidate model. Some works about KL divergence-based selection focused on Markov-switching models have been reported in the literature (Smith et al., 2006). However, the BIC score is more documented than the AIC score as regards Markov-switching models.
In the context of probabilistic modelling, it is often enlightening to think of regularizers as expressing a prior over the parameters, and thus view the regularized maximum likelihood fitting procedure as the search for maximum a posteriori (MAP) parameters under such a prior. Dirichlet distributions are commonly used as priors for the parameter distributions in the case of variables with categorical distributions or multinomial distributions in the models. Dirichlet, normal, gamma and inverse-gamma priors are used in the case of MSARs (Pinto & Spezia, 2015; Lhuissier, 2019).
In regularized model selection for autoregressive Markov-switching models, a grid of (p, K) values is tested and the pair obtaining the minimum value for the criterion considered is retained. However, estimating such models using a grid of hyper-parameters may be computationally expensive. A Bayesian approach treats all unknown quantities as random variables, assigning priors to these quantities to infer posterior distributions. A step further, in the case of HMMs for example, when the model structure, i.e. the number of states, is part of the unknown quantities, model structures can nonetheless be compared provided one knows how to integrate over both parameters and hidden states. In practice, Bayesian integration requires approximating integrals, for example through Monte-Carlo methods, Laplace approximation or the variational Bayesian method (Ghahramani, 2001).
In a similar vein, the sticky infinite hidden Markov-switching modelling framework proposed by Fox et al. (2011) short-circuits this computation: it assumes a Markov chain with a potentially infinite number of states, thus encompassing any finite number of them. Instead, the number of states is determined during the estimation of the model, which avoids the need to fix this number using a criterion such as BIC. For instance, Bauwens et al. (2017) applied this framework to autoregressive moving average Markov-switching models. A panorama of Bayesian nonparametric methods for learning Markov-switching processes is provided in (Fox et al., 2010).
In Sect. 8.3.1, we mention that the computational resources available to us allowed us to test multiple values for the hyper-parameters, using the BIC score.
5 Hidden state inference
In HMM modelling, after a model is learnt, inference consists in finding the state sequence that maximizes the likelihood of a given observed sequence. This is equivalent to solve a Maximum A Posteriori (MAP) problem. The Greedy search method that enumerates all combinations of states requires \({\mathcal {O}}(K^T)\) operations, where K is the number of states and T is the sequence length. The Viterbi algorithm designed by Forney (1973) computes the optimal state sequence in \({\mathcal {O}}(TK^2)\) operations.
In this section, we propose a variant of the Viterbi algorithm that takes into account the observed states of the PHMC-MLAR model. Thus, the hidden states are inferred given the observed states and the given observation sequence.
Let \(\hat{\varvec{\theta }}\) the MLE parameter estimates of the PHMC-MLAR model trained on a given dataset. Let \(\mathbf {x} = x_{1}^T\) an observed time series and \(\mathbf {x}_0=x_{1-p}^0\) the corresponding initial values. Let \(\Sigma = \sigma _{t=1}^T\) the possible states at each time-step with \(\sigma _t = \{k\}\) if \(k^{\mathrm{th}}\) regime is observed at time-step t, \(\sigma _t = \mathbf {K}\) if the state process is latent at that time-step, and \(\sigma _t \subset \mathbf {K}\) in the intermediate case. Let \((\mathbf {S}, \Sigma )\) the partially hidden state process associated with this time series.
We search the optimal state sequence \(\mathbf {z}^* = (z_1^*, \dots , z_T^*)\) that maximizes the posterior probability \(P(\mathbf {S}=\mathbf {z} \,|\, \mathbf {X}=\mathbf {x}, \mathbf {X}_0=\mathbf {x}_0, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\). Thanks to Bayes’ rule, maximizing this posterior probability is equivalent to maximizing the joint probability \(P(\mathbf {S}=\mathbf {z}, \mathbf {X}=\mathbf {x} \,|\, \mathbf {X}_0=\mathbf {x}_0, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\):
where \(\mathbf {K} = \{1, 2, \dots , K\}\) is the set of possible states.
Note that the probability of a given state sequence is null if there is at least a time-step t such that \(z_t \notin \sigma _t\), that is if state \(z_t\) is not allowed at time-step t. A consequence is that \(\mathbf {z}^*\) must coincide with the observed states if there are any. This constraint entails a decrease in calculation cost, as we will see later.
Following the dynamic programming paradigm, the Viterbi algorithm makes it possible to retrieve \(\mathbf {z}^*\) by splitting the initial problem into subproblems and solving this set of smaller problems. Let \(\delta _t(\ell ; \, \hat{\varvec{\kern-2pt\theta }})\) the maximal probability of subsequence \((z_1, \dots , z_t = \ell )\) that ends within regime \(\ell\):
The information on the known states is taken into account in the \(\delta _t(\ell ; \, \hat{\varvec{\kern-2pt\theta }})\) quantities, through the \(\sigma _1^t\) terms.
The probabilities involved in these quantities are iteratively computed as follows:
At first time-step,
where
For \(t=2, \dots , T\) we have
with
Since the maximal probability of the complete state sequence, that is the maximum for the probability expressed in Eq. 16, also writes:
the optimal sequence \(\mathbf {z}^*\), defined in Eq. 17 is retrieved by backtracking as follows:
The original Viterbi algorithm runs in \({\mathcal {O}}(TK^2)\). Our variant runs in \({\mathcal {O}}((T-T_{obs})K^2 + (T_{obs}+T)K)\) where \(T_{obs}\) denotes the number of observed states and \(T-T_{obs}\) is the number of undetermined states to be inferred. To note, \({\mathcal {O}}(K^2)\) (resp. \({\mathcal {O}}(K)\)) is the computational cost of Viterbi variables \(\delta _t\)’s when the state at time-step t is undetermined (respectively observed); and \({\mathcal {O}}(TK)\) represents the backtracking computational cost. Thus, when all states are undetermined (i.e. \(T_{obs} = 0\)), our algorithm has the same complexity as the original Viterbi algorithm. Moreover, the computational cost of our algorithm decreases linearly with the number of observed states \(T_{obs}\).
6 Forecasting
Forecasting for a time series consists in predicting future values based on past values. Let us consider a PHMC-MLAR model trained on a sequence observed up to time-step T, and \(\hat{\varvec{\kern-2pt\theta }}\) the corresponding parameters. Let \(\sigma _{1}, \dots , \sigma _{T+h}\) the set of possible states from time-step 1 to time-step \(T+h\).
The optimal prediction of \(X_{T+h}\) (with respect to mean squared error) is the conditional mean \({\mathbb {E}}\left[ X_{T+h} \, | \, X_{1-p}^{T}=x_{1-p}^{T}, \, \sigma _{1}^{T+h}; \, \hat{\varvec{\kern-2pt\theta }}\right]\), which writes as follows:
with \(\mathbf {y}_{T+h} = (1, x_{T+h-1}, \dots , x_{T+h-p})\), \(\hat{\varvec{\mu }}_k = (\phi _{0,k}, \phi _{1,k}, \dots , \phi _{p,k})\) the intercept and autoregressive parameters associated with \(k^{\mathrm{th}}\) state, and \('\) denoting matrix transposition.
Equation 23 depends on smoothed probabilities \(\bar{\gamma }(i, s) = P(S_{T+i}=s \,|\, X_{1-p}^{T}=x_{1-p}^{T}, \, \sigma _{1}^{T+i}; \, \hat{\varvec{\kern-2pt\theta }})\), which are recursively computed as follows:
for \(i=1, \dots , h\), \(s \in \mathbf {K}\) and \(\gamma _{T}(l)\) defined in Eq. 10.
From Eqs. 23 and 24, we can notice that if state s is observed at time-step \(T+h\) (i.e. \(\sigma _{T+h} = \{s\}\)), then prediction \(\hat{X}_{T+h}\) equals the conditional mean of the LAR process associated with this state (since \(\bar{\gamma }(h, k) = 0\) for \(k \notin \sigma _{T+h}\)). In contrast, if state process is latent at time-step \(T+h\) (i.e., \(\sigma _{T+h} = \mathbf {K}\)), \(\hat{X}_{T+h}\) is computed as the weighted sum of the conditional means of all states, with probabilities \(\bar{\gamma }(h, k)\) as weights.
Note that for \(h=1\), the past values of the time series required in Eq. 23 are known. In contrast, for \(h > 1\), the intermediate predictions \(\hat{X}_{T+1}, \dots , \hat{X}_{T+h-1}\) are used in order to feed the autoregressive dynamics of the PHMC-MLAR framework.
It is important to underline that, the whole distribution of \(X_{T+h} | X_{1-p}^T, \, \sigma _{1}^{T+h}\) is computed as a mixture of conditional densities \(P(X_{T+h} | X_{T+h-p}^{T+h-1}, S_{T+h}; \hat{\varvec{\kern-2pt\theta }})\) (Eq. 1) weighted by probabilities \(\bar{\gamma }\)’s (Eq. 24) Thus, the point forecast in Eq. 23 is the mean of this distribution, which is called the predictive density. In practice, this predictive density can be sampled in order to build a confidence interval for the predicted values, instead of a single-point forecast.
7 Experiments
The aim of this section is two-fold: (i) assess the ability of PHMC-MLAR model to infer the hidden states, (ii) evaluate prediction accuracy. These evaluations were achieved on simulated data, following two experimental settings. On the one hand, we varied the percentage of observed states in training set, to evaluate its influence on hidden state recovery and prediction accuracy. On the other hand, we simulated unreliable observed states in training set, and evaluated the influence of uncertain labelling on hidden state inference and prediction accuracy.
This section starts with the description of the protocol used to simulate data in both experimental settings. Then, the section focuses on implementation aspects. We next present and discuss the results obtained in both experimental settings.
7.1 Simulated datasets
This subsection first focuses on the model used to generate data. Then we describe the precursor sets used to further generate the test-set and the training datasets.
7.1.1 Generative model
These experiments were achieved on simulated data from a univariate (\(d=1\)) 4-state PHMC-MLAR(2) model whose transition matrix and initial probabilities are:
Within each state \(k \in \{1, 2, 3, 4\}\), the autoregressive dynamics is a LAR(2) process defined by parameters \(\varvec{\theta }^{(X,k)} = (\phi _{0,k}, \, \phi _{1,k}, \,\phi _{2,k}, \, h_k^{\frac{1}{2}})\):
In the LAR(2) process associated with state k, stationarity is guaranteed by setting the following contraints: \(\phi _{i,k} < 1,\ i \in \{1,2\}\).
Finally, the initial law \(g_0\) is a bivariate Gaussian distribution
Figure 2 shows an example of state process (Fig. 2a) and corresponding time series (Fig. 2b) that were simulated from the previously defined PHMC-MLAR(2).
7.1.2 Precursor sets for the test-set and training datasets
The training and test sets are common to both experimental settings (influence of the percentage of observed labels, influence of labelling error).
Inference The precursor set \({\mathcal {P}}_{infer\_test}\) of the test-set is composed of \(M=100\) fully labelled observation sequences of length \(\ell = 1000\). These sequences were generated from the PHMC-MLAR(2) model described in Eqs. 25–27. A protocol repeated for each \(N \in \{1, 10, 100\}\) produced a precursor set \({\mathcal {P}}_{N\_infer\_train}\) consisting of N fully labelled observation sequences of length \(T=100\). The generative model in Eqs. 25–27 was used for this purpose.
Forecasting In this case, training sets are each reduced to a single sequence. In each such sequence, the sequence’s prefix of size \(T=100\) is used for model training, whereas the subsequence \(T+1, \cdots , T+10\) is used for testing prediction accuracy. The sequences of the unique precursor set denoted \({\mathcal {P}}_{N=1\_forecast\_train\_test}\) are generated using Eqs. 25–27.
7.2 Implementation
Our experiments required intensive computing resources from a Tier 2 data centre (Intel 2630v4, 2\(\,\times\,\)10 cores 2.2 Ghz, 20\(\,\times\,\)6 GB). We exploited data-driven parallelization to replicate our experiments on various training sets. On the other hand, code parallelization allowed us to process multiple sequences simultaneously in the step E of the EM algorithm. The software programs dedicated to model training, hidden state inference and forecasting were written in Python 3.6.9. We used the NumPy and Scipy Python libraries.
The models were learnt through the EM algorithm with precision \(\kappa = 10^{-6}\) and initialization procedure parameters \((L, N_{iter}) = (10, 5)\).
7.3 Influence of the percentage of observed states
To analyze the impact of observed states, we varied the percentage P of labelled observations (equivalently the percentage of observed states) in the training sets. P was varied from \(0\%\) (fully unsupervised case) to \(100\%\) (fully supervised case), with steps of \(10\%\). The aim is to evaluate the performance of intermediate cases for different sizes of the training datasets.
7.3.1 Hidden state inference
The test-set \({\mathcal {S}}_{infer\_test}\) was generated by unlabelling all states from the precursor set \({\mathcal {P}}_{infer\_test}\) described in Sect. 7.1.2 (\(M=100\) fully observed sequences of length \(\ell =1000\)).
To generate the training sets, the following protocol was repeated for each \(N \in \{1, 10, 100\}\) and for each percentage P: (i) considering the appropriate precursor set \({\mathcal {P}}_{N\_infer\_train}\) (N fully observed sequences of length \(T=100\)) depicted in Sect. 7.1.2, only a proportion of P observations was kept labelled while the rest was unlabelled; (ii) this process was repeated 15 times, each time varying which observations are kept labelled. Thus were produced 15 training datasets \({\mathcal {S}}_{N\_P\_infer\_train\_1}, \cdots , {\mathcal {S}}_{N\_P\_infer\_train\_15}\).
The PHMC-MLAR(2) model with 4 states was trained on each training set \({\mathcal {S}}_{N,P,infer\_train\_i}\), \(i=1, \cdots , 15\). For each trained model, state inference was achieved for the M fully hidden sequences of test-set \({\mathcal {S}}_{infer\_test}\), which yielded M sequences of predicted labels. Inference performance was evaluated by comparing the true state sequences with the inferred ones, using the Mean Percentage Error (MPE) score defined as follows:
where \(s_j\)’s and \(\hat{s}_j\)’s are respectively observed and inferred states. The MPE score varies between 0 and 1. The lower the value of the MPE score, the higher the inference performance.
Figure 3 displays \(95\%\) confidence interval for the MPE score as a function of P. As expected, the results show that inference ability increases with the number of training sequences denoted by N. Note that when the proportion of labelled observations is less than some threshold (\(P=30\%\) for \(N=1, 10\) and \(P=20\%\) for \(N=100\)), inference performance is greatly impacted by the distribution of observed states since we obtain very large confidence intervals for the MPE score.
\(95 \%\) confidence interval for mean percentage error (MPE) of hidden state inference, as a function of the percentage P of labelled observations. Models were trained on datasets of N sequences of length 100, for each of 15 replicates differing by the \(P \%\) labelled observations. For each model, inference was performed for a test-set of 100 unlabelled sequences of size 1000. The \(95 \%\) confidence interval of the MPE score was computed from the 15 replicates. The dash (red) line indicates the MPE score obtained for the unsupervised learning case (\(P = 0\%\)). Mind the differences in scales between the three subfigures (Color figure online)
For \(N = 1\), the use of labelled observations makes it possible to outperform the fully unsupervised case (\(P = 0\%\)) (which translates into small MPE scores) when at least \(30\%\) of observations are labelled (see Fig. 3a). In contrast, for \(N=10, 100\), from some threshold value of P (respectively \(30\%\) and \(20\%\)), the use of larger proportions of labelled observations sustains inference performances equal to that of the fully unsupervised case (see Fig. 3b and c). Importantly, the results show that using large proportions of labelled observations considerably speeds up model training by decreasing the number of iterations of the EM algorithm (see Fig. 4), and allows to better characterize the training data (which is reflected by a greater likelihood, see Fig. 5). Ramasso and Denoeux (2013) had already underlined the beneficial impact of partial knowledge integration on EM convergence in HPMCs. Our work confirms this advantage in the PHMC-MLAR model, with a good preservation of inference performance. Besides, the decrease in convergence time offers promising prospects to enhance model selection for the PHMC-MLAR model, by allowing examination of larger grids of hyper-parameter values.
Number of EM iterations before convergence as a function of the percentage P of labelled observations. For the description of the experimental protocol, see caption of Fig. 3. The distribution of the number of EM iterations is studied across 15 replicates. Dash (red) line and dot (green) line indicate the number of iterations for unsupervised and supersived learning cases respectively. Mind the differences in scales between the three subfigures (Color figure online)
Log-likelihood as a function of the percentage P of labelled observations. For the description of the experimental protocol, see caption of Fig. 3. The distribution of the log-likelihood is studied across 15 replicates. Dash (red) line and dot (green) line indicate the log-likelihoods for unsupervised and supervised learning cases respectively. Mind the differences in scales between the three subfigures (Color figure online)
In order to evaluate the influence of observed states in recognition phase, we considered the case \(P=10 \%\) which previously obtained the lowest inference performance. This time, we also kept labelled a proportion Q of observations within the test-set \({\mathcal {S}}_{infer\_test}\). We assessed the inference performances for the models trained on \({\mathcal {S}}_{N,P=10\%,infer\_train\_i}\), \(i=1, \cdots 15\). Figure 6 presents MPEs as a function of Q for \(N = 1, 10\) and 100. We observe that inference performances are improved by the presence of observed states. More precisely, for Q taking its values in \(25 \%\), \(50 \%\) and \(75 \%\), respectively, MPE decreases by: (i) \(19\%\), \(42\%\) and \(69\%\) for \(N=1\) (Fig. 6a); (ii) \(27\%\), \(52\%\) and \(77\%\) for \(N=10\) (Fig. 6b); and (iii) \(27\%\), \(53\%\) and \(77\%\) for \(N=100\). (Fig. 6c). These results show the ability of our variant of the Viterbi algorithm to infer partially-labelled sequences.
\(95 \%\) confidence interval for mean percentage error (MPE) of hidden state inference, as a function of the percentage Q of labelled observations within test-set, with \(P = 10\%\) labelled observations in the training sets. Models were trained on datasets of N sequences of length 100 in which \(P=10\%\) of observations have been labelled. Fifteen replicates differing by the \(P=10 \%\) labelled observations were considered. For each model, inference was performed for a test-set of 100 partially labelled (\(Q\%\)) sequences of size 1000. The \(95 \%\) confidence interval of the MPE score was computed from the 15 replicates. Mind the differences in scales between the three subfigures (Color figure online)
7.3.2 Forecasting
In this experiment, we consider models trained on a single sequence. This case corresponds to many real-world situations in which a unique time series is available (e.g., the evolution of air pollution at some geographical location). Using the precursor set \({\mathcal {P}}_{N=1\_forecast\_train\_test}\) described in Sect. 7.1.2, we generated datasets \({\mathcal {S}}_{N=1\_forecast\_train\_test\_i}\), \(i=1, \cdots , 15\) each composed of a single sequence of size 110. Again, the 15 replicates differed by the \(P\%\) labelled observations. In these sets, the sequence prefixes of length \(T=100\) were used to train the models. Out-of-sample forecasting was carried out at horizons \(T+h\), \(h=1, \dots , 10\), which means that prediction accuracy was assessed using subsequences \(T+1, \cdots , T+h\). To note, the \(P\%\) labelled observations were distributed in the sequence prefixes of length T.
Two experimental schemes were considered. First, the states at forecast horizons were supposed to be latent; that is, all states were unlabelled from \(T+1\) to \(T+h\), \(h=1, \cdots , 10\). Then, we performed the prediction evaluation when states are observed at forecast horizons. The latter situation corresponds to performing the prediction conditional on some assumption on the regime. For instance, in econometrics, assuming we know which phase will be on (growth phase versus recession) might improve the forecasting performance of the Gross National Product (GNP). In this case, all states were kept labelled from \(T+1\) to \(T+h\), \(h=1, \cdots , 10\).
Prediction performance is estimated by the Root Mean Square Error (RMSE) defined as follows:
where h is the forecast horizon and \(N_{rep}=15\) is the number of replicates. Accurate predictions are characterized by low RMSEs.
Table 1 presents the RMSEs obtained when the states at forecast horizons are supposed to be latent. Figure 7a presents the mean, median and maximum of RMSEs, computed over all forecast horizons, as a function of P, the percentage of labelled observations in the training sets. Table 1 and Fig. 7a show that as from some low P threshold (\(10\%\) or \(20\%\)), the prediction performance remains nearby constant across proportions.
Mean, median and maximum root mean square error (RMSE) of prediction at horizon h as a function of P, the percentage of labelled observations in the training datasets. The 95% confidence intervals are shown for the mean. States at forecast time-steps \(T+h\), \(h=1, \cdots 10\) are a hidden, b known. Models were trained on a single sequence, for each of 15 replicates differing by the \(P \%\) labelled observations. Model training was performed on subsequences of length 100, whereas prediction was achieved for the 10 subsequent time-steps. For each value of P, the statistics provided were computed across the 15 replicates and all horizons (Color figure online)
In addition, Table 1 also highlights that the ability to predict depends on the forecast horizon under consideration. At any given labelling percentage P, high RMSE scores (i.e., around 7) alternate with low scores (around 1) across horizons. The nonmonotonic error trend across horizons was observed empirically for MSAR models and threshold autoregressive models when they are applied to US GNP time series (Clements & Krolzig, 1998).
Finally, our experiments show that PHMC-MLAR model’s ability to better characterize the training data in presence of large proportions of labelled observations (characterized by greater likelihood, see Fig. 5a) does not translate into an improved forecast performance.
When states are known at forecast horizons, RMSEs (presented in Table 2) are reduced by \(44\%\) on average. Moreover, Fig. 7b shows that above percentage \(P = 30 \%\), prediction performances are slightly greater than that of the unsupervised case (\(P=0 \%\)). Note that as in the case when the states are unknown at forecast horizons, the prediction ability depends on the forecast horizon. Again, for a given P, the RMSE score does not systematically increase with forecast horizon h, although previously predicted values are used as inputs when predicting at next horizons.
7.4 Influence of labelling error
In this experiment, the influence of labelling error is evaluated. To simulate unreliable labels, we proceeded as follows.
At each time-step t, an error probability \(p_t\) was drawn randomly from a beta distribution with mean \(\rho\) and variance 0.2. With probability \(p_t\), the observed state \(s_t\) was replaced by a random state uniformly chosen from \(\{1, 2, 3, 4\} \setminus \{s_t\}\). So, the unreliable labels \(\tilde{s}_t\) were defined as follows:
where \({\mathcal {U}}\) is the discrete-valued uniform distribution. Thus, on average a proportion \(\rho\) of observations is assigned wrong labels.
7.4.1 Inference of hidden states
To assess inference performance in presence of labelling errors, we relied on the test-set \({\mathcal {S}}_{infer\_test}\) described in Sect. 7.3 (\(M=100\) fully hidden sequences of length \(\ell =1000\)) corresponding to the fully labelled dataset \({\mathcal {P}}_{infer\_test}\).
To generate the training sets, for each N \(\in \{1,\ 10,\ 100\}\), we considered the appropriate precursor set \({\mathcal {P}}_{N\_infer\_train}\) (N fully observed sequences of length \(T=100\)) depicted in Sect. 7.1.2.
We varied the mean labelling error probability \(\rho\) in \(\{0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7\), \(0.8, 0.9, 0.95 \}\). For \(N \in \{1,\ 10,\ 100\}\), and each value of \(\rho\), we generated 15 replicates from dataset \({\mathcal {P}}_{N\_infer\_train}\), each time varying the distribution of the wrong labels amongst the observations. The PHMC-MLAR(2) model with 4 states was trained on each of the training sets \({\mathcal {S}}_{N,\rho ,infer\_train\_1}, \cdots , {\mathcal {S}}_{N\_\rho \_infer\_train\_15}\) thus obtained.
For each trained model, state inference was achieved, which yielded \(M=100\) sequences of predicted labels of length 1000, to be compared with the label sequences within \({\mathcal {P}}_{infer\_test}\) (see Sect. 7.1.1).
Figure 8 presents \(95\%\) confidence intervals for the MPE score as a function of \(\rho\). Note that for all sizes \(N \in \{1,\ 10,\ 100\}\) of training data, the average MPE gradually increases when \(\rho\) tends to 1. Moreover, confidence intervals become more and more tight when larger training data is considered. We also observe that up to \(\rho = 0.7\), the robustness to labelling errors, translated into small MPE average and low dispersion, increases with N. However, from \(\rho \ge 0.8\), this trend is reversed and inference performance slightly decreases when N grows.
On the other hand, we underline that the fully unsupervised case outperforms supervised cases in presence of labelling errors. Up to relatively high labelling error rates (\(\rho =70\%\)), the trade-off between training time and inference performance becomes beneficial for large training datasets. For instance, for \(N=100\), with a \(70\%\)-reliable labelling function (i.e. \(\rho = 0.3\)), the EM algorithm converges after a single iteration against 67 iterations for the unsupervised case; and the resulting model has good inference abilities with an MPE score equal to \(35\%\) on average (see Fig. 8c) against \(5\%\) on average in the unsupervised case. Thus, when analyzing real-world data for which the number of states K and auto-regressive order p are unknown, model selection strategies can capitalize on such labelling functions in order to explore/prospect larger grids of values for the hyper-parameters K and p.
\(95 \%\) confidence interval for mean percentage error (MPE) of hidden state inference, as a function of the mean labelling error probability \(\rho\). Models were trained on N sequences, for each of 15 replicates differing by the \(\rho \%\) ill-labelled observations. The average MPE was computed from the 15 replicates. The dash (red) line indicates the MPE score obtained for the unsupervised learning case. Mind the differences in scales between the three subfigures (Color figure online)
7.4.2 Forecasting
As in Sect. 7.3.2, we considered models trained on a single sequence (\(N = 1\)). Again, for each value of the mean labelling error probability \(\rho\), we used precursor set \({\mathcal {P}}_{N=1\_forecast\_train\_test}\) described in Sect. 7.1.2, and we varied the distribution of wrong labels: 15 replicates (i.e., 15 sequences of length \(T=100\)) were thus generated. Out-of-sample forecasting was carried out at horizons \(T+h\), \(h = 1,\cdots ,10\).
Table 3 presents RMSE scores for different values of mean labelling error \(\rho\) when states are unknown at forecast horizons \(h = 1, \dots , 10\). The results show that at forecast horizons \(h = 1, 2, 5, 6\), the best prediction accuracies are reached when \(\rho\) is null, whereas at the remaining horizons, the highest accuracies are obtained when \(\rho = 0.8\) or 0.9. Figure 9 presents the mean, median and maximum for the prediction errors computed over the whole forecast horizons as a function of \(\rho\). We observe that the mean and median very slightly increase with \(\rho\), whereas labelling errors exert a greater impact on the maximum values of RMSEs. Therefore, this second experiment also highlights the remarkable robustness to error labelling in the prediction task, over the whole range of error rates.
Descriptive statistics for the distribution of the root mean square error (RMSE) of prediction, as a function of \(\rho\): \(\rho\) denotes the mean labelling error probability. The forecast horizons are time-steps \(T+1\) to \(T+h\), \(T=100\). The statistics are computed over all horizons. The 95% confidence intervals are shown for the mean (Color figure online)
8 Application to machine health prognostics
In this section, we report experiments on realistic machine condition data available on NASA’s CMAPSS (Commercial Modular Aero-Propulsion System Simulation) repository (https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repo-sitory/#turbofan). The application of interest is data-driven machine health prognostics. This task consists in predicting the Remaining Useful Life (RUL) of a machine: the RUL is the time period beyond which equipments will likely require repair or replacement. The aim of these experiments is two-fold: (i) assess the benefit of adding autoregressive dynamics to the PHMC model as we propose in this work; (ii) compare our model to state-of-the-art methods in the context of machine health prognostics.
The remainder of this section is organized as follows. NASA’s CMAPSS datasets are described in Sect. 8.1. Section 8.2 explains how we predicted RUL using PHMC models, with or without autoregressive dynamics. The last Sect. 8.3 is devoted to assess the performance of our model for two tasks: h-step ahead feature prediction and RUL prediction. Feature prediction performances are compared for PHMC-MLAR, PHMC and MSAR. RUL prediction performances are compared for PHMC-MLAR, PHMC, and six recent state-of-the-art RUL prediction methods.
8.1 Data description
NASA’s CMAPSS datasets are composed of realistic degradation trajectories of turbofan engines. In our experiments, we used datasets FD001 and FD003. Each dataset is divided into a training and testing subsets of 100 trajectories each. FD003 is a more complex case study than FD001 because it includes two fault modes against a single fault mode for FD001. In fact, it is known that fault occurrences are directly related to the degradation of engine operating conditions so that the number of fault modes increases the diversity of degradation trajectories.
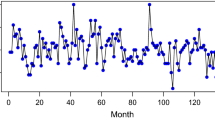
The degradation pattern of each trajectory is represented by 21 features (time series) recorded from 21 sensors. Moreover, for each trajectory, engine operational state is healthy in the early stage and begins to degrade over time until a failure occurs. At a given time-step, the RUL indicates the time period left before failure. Since the training datasets contain the whole degradation patterns, the RUL value at the last time-step of each training trajectory equals 0. In contrast, for each testing trajectory, only an incomplete (i.e. “partial”) degradation pattern and the RUL (different from 0) associated with the last time-step are available. In Fig. 10, each testing trajectory is represented by a point whose coordinates are its length and its RUL. To note, the difficult cases are caracterized by large RUL values and short partial degradation patterns (see the top left-hand side of Fig. 10).
The data-driven machine health prognostics task consists in predicting the RUL of a device, knowing its partial degradation pattern. To build such a predictive method, models are trained on training trajectories and evaluated on testing trajectories.
8.2 Machine health prognostics using PHMC-LAR models
In the literature of data-driven machine health prognostics, we distinguish between three main approaches: case-based reasoning approaches (Wang et al., 2008; Ramasso, 2014), artificial intelligence approaches (Wu et al., 2018; Zhao et al., 2019) and statistical model-based approaches (Javed et al., 2015). The method proposed in this work belongs to the family of statistical model-based approaches. The overview of our method is summed up in Fig. 11. It consists of two complementary modules: the model training module and the RUL prediction module. In the model training module, CMAPSS training datasets were annotated with operational states which were used to feed PHMC[-MLAR] (that is PHMC or PHMC-MLAR models) with partial annotations during model training (see Sect. 8.2.1). Then in the RUL prediction module, the RULs of the testing trajectories were predicted following a three-step procedure (see Sect. 8.2.2).
RUL prediction using PHMC or PHMC-MLAR models: overview of the proposed method. RUL: remaining useful life. In the training phase, we first had to assign partial state annotation to each multivariate training trajectory. We designed a synthetic health indicator, constraining it to roughly decay from 1 (healthy state) to 0 (failure state) over time, for each trajectory. By regressing HI against the features for each time-step of each training trajectory, we obtained one estimated \(\hat{HI}\) time series per trajectory [subfigure (a)]. The segmentation of this time series yielded one sequence of states per trajectory [subfigure (b)]. The four possible states are healthy (1), intermediate (2), faulty (3) and failure (4). The partial annotation \(\Sigma\) of each trajectory was obtained by setting \(\sigma _t\) to \(\{i, j\}\) in each time-step t of windows (of size 11) centered on the switch from state i to state j. Otherwise, \(\sigma _t\) was set to the state obtained through the segmentation. Only the 8 features that are sufficiently informative were retained from the 21 initial features, in the rest of the experiment. To predict a RUL for each testing trajectory, a three-step process was implemented. In step 1, the degradation pattern of each testing trajectory, known from time-step 1 to the trajectory’s length T, was completed from \(T+1\) to \(T+H\) [see subfigure (c)]. H was set at 145, the maximum RUL value observed in the testing dataset. The completion was achieved by sampling from the feature forecasting function described in Eq. 23. Iterating this sampling procedure \(R=100\) times produced R completed degradation patterns per testing trajectory. In step 2, the R patterns of each testing trajectory were each segmented into healthy, intermediate, faulty and failure states using our variant of the Viterbi algorithm. When existing, the switch from faulty to failure state allowed us to estimate the trajectory’s RUL. Otherwise, the RUL estimate was set to the maximum H. In step 3, for each testing trajectory, a final RUL estimate was aggregated from the R estimates previously obtained [see subfigure (d)] (Color figure online)
8.2.1 Engine operational states—model training
As explained in Sect. 8.1, CMAPSS training datasets contain run-to-failure trajectories, that is engines start to operate in healthy operational state and then, at some point, the state starts to degrade due to fault occurrences until the engine fails. We constructed a health indicator (HI) time series that indicates engines’ health status over time for each training trajectory. To estimate HI based on sensor measurements, we followed the approach described by Ramasso (2014), which relies on an exponential degradation model and linear regression models. In a nutshell, we first constrained the synthetic variable HI to roughly decrease from 1 (healthy state) to 0 (faulty state) over time:
with \(\sigma _1 = T_i \times 5\%\) and \(\sigma _2 = T_i \times 95\%\), as recommended in (Ramasso, 2014), t a given time-stamp and i a training trajectory of length \(T_i\). Finally, for each time-step t and trajectory i, we regressed \(HI^{(i)}_t\) against the features. We used the regression model specific to each time-step, to estimate \(\hat{HI}^{(i)}_t\).
Afterwards, operational states were obtained by segmenting the estimated HI, following the method presented in (Ramasso, 2016) and used in (Juesas & Ramasso, 2016). We considered four operational states: healthy, intermediate, faulty and failure denoted by 1, 2, 3 and 4, respectively. Figure 12 shows two examples of the estimated HI and corresponding operational states.
Since the transitions between operational states are not known precisely, there is an uncertainty about the states nearby the switching time-steps from one operational state to the next one. From this consideration, partial annotations about states were built as follows: let \(t_{i \rightarrow j}\) (\(i < j\)) the switching time-step from state i to state j; and let \(\sigma _t\) the set of possible states at time-step t. Within a time-window of size 11 centered around \(t_{i \rightarrow j}\), the doubt on the switching time-step location between states i and j was explicited. Thus, if \(t \in [t_{i \rightarrow j}-5, t_{i \rightarrow j}+5]\) then \(\sigma _t = \{i, j\}\); otherwise \(\sigma _t\) equals the state provided by the segmentation.
Thus, PHMC[-MLAR] models were trained on CMAPSS training datasets with the partial annotations obtained previously. The number of states K was fixed at 4 and Gaussian white noises were considered. Moreover, amongst the 21 features (time series) that make up each trajectory, only those features \(\{ 2 , 3 , 4 , 7 , 9 , 11 , 12 , 14 \}\) were used, that show consistent monotonic degradation trends (Wang et al., 2008) and/or present “the highest content of domain-specific information relating to the influence of fault occurrences” (Aremu et al., 2020).
Evolution of the estimated health indicator (HI) and corresponding operational states, for two training trajectories. Numbers 1, 2, 3, and 4 stand for healthy, intermediate, faulty and failure states, respectively. FD001 and FD003 are the two training datasets considered in our experiments (Color figure online)
8.2.2 RUL prediction
Once PHMC[-MLAR] model parameters had been estimated, RUL prediction for each single testing trajectory was performed using the following three-step procedure.
(i) Step 1: production of R completed partial degradation patterns, for each testing trajectory.
Let T the length of the testing trajectory under consideration, which degradation pattern is known up to time-step T. We wished to produce several evolutions of the partial degradation pattern. We could not rely on the optimal point prediction (classical method), which provides only one value (mean). Instead, we sampled from the predictive density (defined in Sect. 6, last paragraph) which characterizes each time-step \(T+h\), for h ranging from 1 to H. An iterative sampling of the predictive densities allowed us to generate one possible evolution of this degradation pattern (from time-step \(T+1\) to \(T+H\)). Besides, in order to obtain only reasonable completed patterns, the sampling was restricted to the values belonging to the interval \([Q_{25}, Q_{75}]\), where \(Q_{25}\) and \(Q_{75}\) are the predictive-density first and third quartiles. These quantiles were estimated by Monte Carlo simulations. Note that the predictive density of PHMC is similar to that of PHMC-MLAR with the difference that in PHMC model, the dependency on past observations is removed.
Performing the previous operation \(R = 100\) times, we generated R evolutions of the observed partial degradation pattern. In the sequel, the resulting completed trajectories, each of length \(T+H\), are referred to as completed degradation patterns. The maximum forecast horizon H was set at 145, which is the maximum RUL value observed within the testing datasets. An example of such completed degradation pattern is depicted in Fig. 13.
Completion of partial degradation pattern for testing trajectories. a and b Illustration with \(11{\mathrm{th}}\) testing trajectory of dataset FD001. The solid line indicates the known degradation pattern - or partial degradation pattern -, that encompasses time-steps 1 to T, the length of the testing trajectory. The dotted line denotes one simulated evolution generated by PHMC-MLAR(K=4, p = 7) model. It encompasses time-steps \(T+1\) to \(T+H\), where H is the maximum remaining useful life (RUL) value observed in the testing dataset. c and d Ilustration with \(47{\mathrm{th}}\) training trajectory of dataset FD001. In our experiments, no completion of partial degradation pattern is achieved for training trajectories. Subfigures c and d are only provided here to show how simulated evolution generated by PHMC-MLAR(K = 4, p = 7) and true (ground truth) evolution compare. For this illustration, time-step \(T'\) was set at \(T - H\) where T is the length of the training trajectory and T coincides with engine failure. The solid line indicates the true evolution encompassing time-steps 1 to \(T'\). The dashed line denotes the true evolution as from \(T'+1\) till failure at time-step T. The dotted line indicates one simulated evolution generated by PHMC-MLAR(K = 4, p = 7) model, in time interval \([T'+1,T]\) (Color figure online)
(ii) Step 2: segmentation of the R completed degradation patterns, production of R estimates of the true RUL.
For each completed degradation pattern (previously generated), we know that up to time-step T, the failure state has null probability since at time-step T, the true RUL is not null. Namely, at each time-step \(t \le T\) of a testing trajectory, the annotation \(\sigma _t\) is set to \(\{1,2,3\}\) (We remind the reader that for each time-step of a training trajectory, \(\sigma _t\) was set to \(\{i,j\}\) around each switch \(i \rightarrow j\), and was set to the unique state obtained through segmentation otherwise). We recall that such partial knowledge is taken into account by our variant of the Viterbi algorithm. Afterwards, the R patterns produced for each testing trajectory were each segmented into healthy, intermediate, faulty and failure states. Let \(\hat{t}_{3 \rightarrow 4}\) the time-step at which the engine switches from faulty state to failure state. So, \(\hat{t}_{3 \rightarrow 4} + p\) provides an estimation of engine end life time-step. To note, the term \((+ p)\) takes into account the p initial observations whose states cannot be inferred because of the autoregressive dynamics. Thus, the RUL estimate writes:
When the switching to the failure state was not achieved between the beginning and the end of the pattern, RUL estimate was set at H.
By doing so for the R patterns, we obtained R estimates of the true RUL denoted by \(\{\hat{rul}_r\}_{r=1, \dots R}\). Figure 14 presents the distribution of \(\hat{rul}_r\)’s obtained for two different testing trajectories.
(iii) Step 3: estimation of a final RUL from the R RUL estimates of a given testing trajectory.
To compute the final estimate of the RUL, the previously computed \(\hat{rul}\)’s were aggregated using a fusion rule \({\mathcal {F}}\):
The mean and median functions were first considered: the corresponding fusion rules are referred to as \({\mathcal {F}}_{mean}\) and \({\mathcal {F}}_{median}\). Then, several combinations of the minimum and maximum of the \(\hat{rul}\)’s were also considered, as suggested by Ramasso (2014):
The choice of \(a = 13/23\) will be explained in Sect. 8.2.3.
The set of final RUL estimates, considering different fusion functions, is denoted
Density of \(R=100\) estimates of the true RUL for testing trajectories. RUL: remaining useful life. a \(17{\mathrm{th}}\) trajectory from the FD001 dataset. b \(26{\mathrm{th}}\) trajectory from the FD001 dataset. Each estimate is obtained from a completed degradation pattern simulated from the PHMC-MLAR(K = 4, p = 7) model (Color figure online)
8.2.3 Performance metrics
To evaluate the performance of our model in RUL prediction, two performance metrics were used: the score function (SF) and the root mean square error (RMSE).
The score function defined by Saxena et al. (2008) has been largely used in the literature of CMAPSS datasets. This function writes:
where \(N_{test}\) is the number of testing trajectories, \(d_i=R\hat{U}L_i - RUL_i\) denotes the difference between the estimated RUL and true RUL for \(i{\mathrm{th}}\) testing trajectory.
We point out that this score function assigns higher penalties on late predictions (over-estimations of RUL). Now function SF has been defined, we return to the choice of \(a = 13/23\) in Eq. 33. This specific value was proposed by Wang et al. (2008). The motivation of these authors originates in the definition of the SF score function: this function penalizes over-estimations of RULs by 1/10 and penalizes under-estimations of RULs by 1/13. Over-estimations (late predictions) are therefore more penalized than under-estimations (early predictions). The authors transformed the 1/10 and 1/13 penalties into weights that sum to 1: 13/23 was assigned to the minimim in Eq. 33, since \(min(\hat{rul}\text {'s})\) favours RUL under-estimation, and 10/23 was assigned to the maximum in this same equation, since \(max(\hat{rul}\text {'s})\) favours over-estimation.
The RMSE of RUL prediction is computed as follows:
Both performance metrics SF and RMSE have to be minimized.
8.3 Results and analysis
This subsection first describes the best models selected for PHMC-MLAR (K = 4, p) and MSAR(p), on each of datasets FD001 and FD003. Then, we show and discuss the accuracies obtained for the feature prediction task performed with PHMC-MLAR, MSAR and PHMC, on both datasets. Third, we conduct a detailed analysis of the RUL prediction performances obtained for PHMC-MLAR and PHMC, on dataset FD001. The subsection ends with the comparison, on dataset FD001, of PHMC-MLAR against six RUL prediction methods recently reported in the literature.
8.3.1 Model selection
Remember that the number of states K was fixed at 4. In this experiment, we identified the best PHMC-MLAR and MSAR models by varying the autoregressive order p among values \(\{1, 2, \dots , 14\}\); the BIC score was used for the selection. Figure 15 displays the BIC scores of each model for both training datasets FD001 and FD003. For each model and each dataset, the value that provides the lowest BIC score was selected. Thus the best MSAR models are obtained for \(p=10\) in both datasets (see Fig. 15b and d). Regarding the PHMC-MLAR model, the BIC score allows to select \(p=13\) for FD003 dataset (see Fig. 15c). However, for FD001 dataset, models PHMC-MLAR(p = 6), PHMC-MLAR(p = 7) and PHMC-MLAR(p = 8) obtained very close BIC scores (472.509; 472.433 and 472.501, respectively), making the selection difficult (see Fig. 15a). Therefore, using the testing trajectories, a second selection has been performed among these three models based on their 30-step ahead prediction performances. This time, the model PHMC-MLAR(p = 7) was selected. We observe that this model also obtained the lowest BIC score.
8.3.2 Feature prediction performance
For each dataset, we compared the feature prediction accuracies of the previously selected PHMC-MLAR and MSAR models against that of the PHMC model. To this end, we considered short, medium and long-term forecasts: \(h=5, 10, 20, 30\). For each testing trajectory, we performed rolling h-step ahead forecasts, starting from \(t=15\) and considering increments of 5 time-steps, up to \(t+ 5 i^{*}\) with \(i^{*}\) the highest integer i such that \(t+ 5 i \le T - h\). Thus, for each trajectory, we obtained one estimate of the h-step ahead forecast RMSE. We recall that for feature prediction, the RMSE is computed as shown in Eq. 29, with \(N_{rep} = i^{*}\). To produce reliable estimates of RMSE, very short trajectories were removed (that is the ones for which less than 10 h-step ahead projections can be performed).
For the three models PHMC-MLAR, PHMC and MSAR, Table 6 (resp. Table 7) in Appendix B presents the mean and \(95\%\) confidence interval of RMSE for dataset 1 (respectively dataset 3), and for each pair (feature, prediction horizon).
The results show that PHMC-MLAR (respectively MSAR) obtains the lowest RMSE for features F9 and F14 (respectively features F2, F3, F7 and F12) on both datasets FD001 and FD003. For these two models, Table 4 displays the sum of the RMSE means computed over all features, at each forecast horizon. It can be highlighted that the two models have the same performance at short forecast horizon (that is \(h=5\)). However, our model outperforms MSAR when medium and long-term forecasts are considered (that is for \(h=10, 20, 30\)).
Compared to the PHMC model, our model obtains much better prediction performance on both datasets. Figure 16 displays the percentage of RMSE improvement (that is RMSE reduction) obtained using our model instead of the PHMC model. This figure shows that our model improves the prediction performance over PHMC for all features whatever the forecast horizon. For dataset FD001 (respectively FD003), the improvement is greater than \(40\%\) for features F9 and F14 (respectively features F7, F9, F12 and F14), whatever the forecast horizon. From these results, we can conclude that, on CMAPSS datasets, the autoregressive dynamics included in our model results in better prediction performance. Thus, for these datasets, more information is obtained from the history of past observations compared with the multivariate data point sampled at a single time-step.
Comparison of feature prediction performances for PHMC-MLAR and PHMC models. Percentages of RMSE improvement of PHMC-MLAR model over PHMC model compared along various pairs (feature, prediction horizon). a PHMC-MLAR(K = 4, p = 7) versus PHMC(K = 4), experiment with dataset FD001. b PHMC-MLAR(K = 4, p = 13) versus PHMC(K = 4), experiment with dataset FD003. An RMSE improvement corresponds to a decrease (Color figure online)
8.3.3 RUL prediction performance
We compared the RUL prediction performance of our proposal with those of the PHMC and several existing methods, on testing dataset FD001. We point out that, on this task, a comparison with MSAR would have been biased since the MSAR framework is fully unsupervised. Figure 17 depicts the performance metrics (SF, RMSE) of PHMC(K = 4) model and PHMC-MLAR(K = 4, p = 7) model, for the different fusion functions considered in this work. The results show that the fusion function \({\mathcal {F}}_{0.7\_min\_max}\) yields the best performance for PHMC-MLAR(K = 4, p = 7) model, which obtains the scores \((SF, RMSE) = (472, 17.49)\), whereas PHMC(K = 4) model shows the smallest scores \((SF, RMSE) = (17066, 34.32)\), when considering fusion function \({\mathcal {F}}_{0.9\_min\_max}\).
Overall, our model largely outperforms PHMC since its SF and RMSE values are much smaller: the RMSE was reduced by half and the SF was divided by 34, with respect to PHMC. When we go deeper into details and analyze RUL estimates, we found out that PHMC is more subject to late predictions of RUL (over-estimations), with \(70\%\) of testing trajectories for which the difference between the estimated and actual RULs is greater than 10, against only \(24\%\) for our model. This explains the very large difference between the SF of the two models (in comparison with RMSE) because the SF metric assigns higher penalties to late predictions of the RUL (see Eq. 35).
Comparison of RUL prediction performances for PHMC-MLAR and PHMC models. Mean and standard deviation of performance metrics (SF, RMSE) computed from ten executions of the methods based on PHMC-MLAR and PHMC. Performance metrics are presented for fusion functions \({\mathcal {F}}_{mean}, {\mathcal {F}}_{median}\) and \({\mathcal {F}}_{a\_min\_max}\) for \(a = \{0.5, 13/23, 0.6, 0.7, 0.8, 0.9 \}\). The scores obtained by the other fusion functions are too high; therefore they are not displayed in this figure. Mind the different scales in the two subfigures (Color figure online)
Finally, Table 5 compares the method proposed in this paper with six recent state-of-the-art methods used to predict the remaining useful life of a machine: Multi-Layer Perceptron (MLP) Switching Kalman filter ensemble (Lim et al., 2015), extreme learning machine fuzzy clustering (Javed et al., 2015), deep convolutional neural network (CNN) (Sateesh Babu et al., 2016), Vanilla long short-term memory (LSTM) (Wu et al., 2018), double LSTM (DLSTM) (Zhao et al., 2019), and complete ensemble empirical mode decomposition DLSTM (CEEMD DLSTM) (Zhao et al., 2019).
The results show that the method proposed in this work presents better performance than the first five comparison methods with a smaller RMSE and SF metrics. However, thanks to the extensive feature extraction procedure (CEEMD) used to build the input features of DLSTM, CEEMD DLSTM method presents better performance than our proposal. Note that our model is directly trained on noisy features recorded from sensors. Moreover, in contrast to CEEMD DLSTM method, our proposal provides an accurate (short, medium and long-term) prediction of features which can be used in practice to extract useful information about system operational states.
9 Conclusion
In this work, we have introduced the PHMC-MLAR model to analyze time series subject to switches in regimes. Our model is a generalization of the well-known Hidden Regime-Switching AutoRegressive (HRSAR) and Observed Regime-Switching AutoRegressive (ORSAR) models when regime-switching is modelled by a Markov Chain. Our model allows to handle the intermediate case where the state process is partially observed.
In the evaluation, we conducted experiments on simulated data and considered both inference performance and prediction accuracy. The results show that the partially observed states (when they represent a reasonable proportion) allow a better characterization of training data (reflected by greater log-likelihood), in comparison with the unsupervised case. An interesting characteristics of the PHMC-MLAR model is that the partially observed states allow faster convergence for the learning algorithm. This performance is obtained with no or practically no impact on the quality of hidden state inference, as from labelling percentages around \(20\)–\(30\%\); the prediction accuracy is also preserved above such percentage thresholds. Furthermore, faster EM convergence is also verified in a fully supervised scheme where part of the observations is ill-labelled. Model selection strategies can therefore rely on an approximate labelling function (provided by an expert or by a supervised algorithm learnt on a small subset of data for which the true labels are known), to explore larger grids of hyper-parameter values. In addition, complementary experimental studies have revealed the robustness of our model to labelling errors, particularly when large training datasets and moderate labelling error rates are considered. Finally, we showed the ability of our variant of the Viterbi algorithm to infer partially-labelled sequences.
We also conducted experiments on two realistic machine condition data (CMAPSS datasets FD001 and FD003) and considered both short/medium/long-term feature forecast accuracy and prediction accuracy for machine remaining useful life (RUL). Regarding feature prediction, we compared PHMC-MLAR with the two models it extends, MSAR and PHMC. The results show that at medium and long-term forecast horizons (\(h = 10, 20, 30\)) our model presents higher forecast accuracies than the MSAR model, whereas both models obtain comparable accuracies at short-term forecast horizon (\(h=5\)). In comparison with the PHMC model, our model achieves much better performance (whatever the horizon \(h = 5, 10, 20, 30\)). These results show the relevance of including an autoregressive model within each regime (as we suggested in this work). Regarding RUL prediction, our proposal outperforms PHMC and five out of six recent state-of-the-art RUL prediction methods, including four artificial intelligence-based methods.
A natural extension of the PHMC-MLAR model consists in putting uncertainty on partial knowledge: for instance instead of states observed with no doubt, a subset of possible states with various occurrence probabilities can be considered at each time-step. On the other hand, it is more realistic to consider time-dependent state processes, especially when large time series are analyzed. These directions will be investigated in future work.
Data availability
The CMAPSS datasets are available from https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognostic-data-repo-sitory/#turbofan.
Code availability
Not Applicable.
References
Ailliot, P., & Monbet, V. (2012). Markov-switching autoregressive models for wind time series. Environmental Modelling & Software, 30, 92–101.
Ailliot, P., Bessac, J., Monbet, V., & Pene, F. (2015). Non-homogeneous hidden Markov-switching models for wind time series. Journal of Statistical Planning and Inference, 160, 75–88.
Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723.
Aremu, O. O., Cody, R. A., Hyland-Wood, D., & McAree, P. R. (2020). A relative entropy based feature selection framework for asset data in predictive maintenance. Computers & Industrial Engineering, 145, 106536.
Baum, L. E., Petrie, T., Soules, G., & Weiss, N. (1970). A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. The Annals of Mathematical Statistics, 41(1), 164–171.
Bauwens, L., Carpantier, J. F., & Dufays, A. (2017). Autoregressive moving average infinite hidden Markov-switching models. Journal of Business and Economic Statistics, 35(2), 162–182.
Berg, J., Reckordt, T., Richter, C., & Reinhart, G. (2018). Action recognition in assembly for human-robot-cooperation using Hidden Markov models. Procedia CIRP, 76, 205–210.
Bergmeir, C., Hyndman, R. J., & Benítez, J. M. (2016). Bagging exponential smoothing methods using STL decomposition and Box-Cox transformation. International Journal of Forecasting, 32(2), 303–312.
Bessac, J., Ailliot, P., Cattiaux, J., & Monbet, V. (2016). Comparison of hidden and observed regime-switching autoregressive models for (u, v)-components of wind fields in the Northeast Atlantic. Advances in Statistical Climatology, Meteorology and Oceanography, 2(1), 1–16.
Bharathi, R., & Selvarani, R. (2020). Hidden Markov model approach for software reliability estimation with logic error. International Journal of Automation and Computing, 17, 305.
Box, G. E., Jenkins, G. M., Reinsel, G. C., & Ljung, G. M. (2015). Time series analysis: Forecasting and control (5th ed.). Wiley.
Cardenas-Gallo, I., Sanchez-Silva, M., Akhavan-Tabatabaei, R., & Bastidas-Arteaga, E. (2016). A Markov regime-switching framework application for describing El Niño Southern Oscillation (ENSO) patterns. Natural Hazards, 81(2), 829–843.
Clements, M. P., & Krolzig, H. M. (1998). A comparison of the forecast performance of Markov-switching and threshold autoregressive models of US GNP. The Econometrics Journal, 1(1), 47–75.
Degtyarev, A. B., & Gankevich, I. (2019). Evaluation of hydrodynamic pressures for autoregressive model of irregular waves. In Contemporary ideas on ship stability (pp. 37–47). Springer.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological), 39(1), 1–22.
Dickey, D. A., & Fuller, W. A. (1979). Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association, 74(366), 427–431.
Durand, J. B. (2003). Modèles à structure cachée : Inférence, sélection de modèles et applications. PhD thesis, Grenoble 1. (in French)
Filardo, A. J. (1994). Business-cycle phases and their transitional dynamics. Journal of Business & Economic Statistics, 12(3), 299–308.
Flecher, C., Naveau, P., Allard, D., & Brisson, N. (2010). A stochastic daily weather generator for skewed data. Water Resources Research, 46, W07519.
Florez-Larrahondo, G. (2020). Incremental learning of discrete hidden Markov models. PhD thesis, Mississippi State University.
Forney, G. D. (1973). The Viterbi algorithm. Proceedings of the IEEE, 61(3), 268–278.
Fox, E., Sudderth, E., Jordan, M., & Willsky, A. (2010). Bayesian nonparametric learning of Markov switching processes. IEEE Signal Processing Magazine, 27(6), 43–54.
Fox, E., Sudderth, E., Jordan, M., & Willsky, A. (2011). A sticky HDP-HMM with application to speaker diarization. Annals of Applied Statistics, 5(2A), 1020–1056.
Gardner, E., Jr., & Everette, S. (2006). Exponential smoothing: The state of the art—Part II. International Journal of Forecasting, 22(4), 637–666.
Ghahramani, Z. (2001). An introduction to hidden Markov models and Bayesian networks. International Journal of Pattern Recognition and Artificial Intelligence, 15(1), 9–42.
Ghasvarian Jahromi, K., Gharavian, D., & Mahdiani, H. (2020). A novel method for day-ahead solar power prediction based on hidden Markov model and cosine similarity. Soft Computing, 24(7), 4991–5004.
Hamilton, J. D. (1989). A new approach to the economic analysis of nonstationary time series and the business cycle. Econometrica, 57, 357–384.
Hamilton, J. D. (1990). Analysis of time series subject to changes in regime. Journal of Econometrics, 45(1–2), 39–70.
Javed, K., Gouriveau, R., & Zerhouni, N. (2015). A new multivariate approach for prognostics based on extreme learning machine and fuzzy clustering. IEEE Transactions on Cybernetics, 45(12), 2626–2639.
Juesas, P., & Ramasso, E. (2016). Ascertainment-adjusted parameter estimation approach to improve robustness against misspecification of health monitoring methods. Mechanical Systems and Signal Processing, 81, 387–401.
Kim, C. J. (1994). Dynamic linear models with Markov-switching. Journal of Econometrics, 60, 1–22.
Koenig, S., & Simmons, R. G. (1996). Unsupervised learning of probabilistic models for robot navigation. Proceedings of IEEE International Conference on Robotics and Automation, IEEE, 3, 2301–2308.
Kuck, K., & Schweikert, K. (2017). A Markov regime-switching model of crude oil market integration. Journal of Commodity Markets, 6, 16–31.
Kwiatkowski, D., Phillips, P. C., Schmidt, P., & Shin, Y. (1992). Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics, 54(1–3), 159–178.
Lhuissier, S. (2019). Bayesian inference for Markov-switching skewed autoregressive models. Banque de France working paper #726.
Li, K., & Fu, Y. (2012). ARMA-HMM: A new approach for early recognition of human activity. In 21st International Conference on Pattern Recognition (ICPR) (pp 1779–1782).
Lim, P., Goh, C. K., Tan, K. C., & Dutta, P. (2015). Multimodal degradation prognostics based on switching Kalman filter ensemble. IEEE Transactions on Neural Networks and Learning Systems, 28(1), 136–148.
Michalek, S., Wagner, M., & Timmer, J. (2000). A new approximate likelihood estimator for ARMA-filtered Hidden Markov Models. IEEE Transactions on Signal Processing, 48(6), 1537–1547.
Morwal, S., Jahan, N., & Chopra, D. (2012). Named entity recognition using hidden Markov model (HMM). International Journal on Natural Language Computing (IJNLC), 1(4), 15–23.
Mouhcine, R., Mustapha, A., & Zouhir, M. (2018). Recognition of cursive Arabic handwritten text using embedded training based on HMMs. Journal of Electrical Systems and Information Technology, 5(2), 245–251.
Noman, F., Alkawsi, G., Alkahtani, A. A., Al-Shetwi, A. Q., Tiong, S. K., Alalwan, N., et al. (2020). Multistep short-term wind speed prediction using nonlinear auto-regressive neural network with exogenous variable selection. Alexandria Engineering Journal, 60, 1221–1229.
Phillips, P. C., & Perron, P. (1988). Testing for a unit root in time series regression. Biometrika, 75(2), 335–346.
Pinto, C., & Spezia, L. (2015). Markov switching autoregressive models for interpreting vertical movement data with application to an endangered marine apex predator. Methods in Ecology and Evolution. https://doi.org/10.1111/2041-210X12494.
Pohle, J., Langrock, R., van Beest, F., & Schmidt, N. (2017). Selecting the number of states in hidden Markov models: Pragmatic solutions illustrated using animal movement. Journal of Agricultural, Biological and Environmental Statistics, 22(3), 270–293.
Psaradakis, Z., & Spagnolo, N. (2003). On the determination of the number of regimes in Markov-switching autoregressive models. Journal of Time Series Analysis, 24(2), 237–252.
Psaradakis, Z., & Spagnolo, N. (2006). Joint determination of the state dimension and autoregressive order for models with Markov regime switching. Journal of Time Series Analysis, 27(5), 753–766.
Ramasso, E. (2014). Investigating computational geometry for failure prognostics. International Journal of Prognostics and Health Management, 5(1), 005.
Ramasso, E. (2016). Segmentation of CMAPSS health indicators into discrete states for sequence-based classification and prediction purposes. Tech. rep., 6839, FEMTO-ST Institute.
Ramasso, E., & Denoeux, T. (2013). Making use of partial knowledge about hidden states in HMMs: An approach based on belief functions. IEEE Transactions on Fuzzy Systems, 22(2), 395–405.
Sateesh Babu, G., Zhao, P., & Li, X. (2016). Deep convolutional neural network based regression approach for estimation of remaining useful life. In International conference on database systems for advanced applications (pp. 214–228).
Saxena, A., Goebel, K., Simon, D., & Eklund, N. (2008). Damage propagation modeling for aircraft engine run-to-failure simulation. In International conference on prognostics and health management (pp. 1–9).
Scheffer, T., & Wrobel, S. (2001). Active learning of partially hidden Markov models. In Proceedings of the ECML/PKDD workshop on instance selection.
Schuller, B., Rigoll, G., & Lang, M. (2003). Hidden Markov model-based speech emotion recognition. In IEEE International Conference on Multimedia and Expo (ICME) (pp. 401–404).
Schwarz, G. (1978). Estimating the dimension of a model. Annals of Statistics, 6, 461–464.
Smith, A., Naik, P., & Tsai, C. L. (2006). Markov-switching model selection using Kullback-Leibler divergence. Journal of Econometrics, 134(2), 553–577.
Ubilava, D., & Helmers, C. G. (2013). Forecasting ENSO with a smooth transition autoregressive model. Environmental Modelling & Software, 40, 181–190.
Wang, P., Wang, H., & Yan, R. (2019). Bearing degradation evaluation using improved cross recurrence quantification analysis and nonlinear auto-regressive neural network. IEEE Access, 7, 38937–38946.
Wang, T., Yu, J., Siegel, D., & Lee, J. (2008). A similarity-based prognostics approach for remaining useful life estimation of engineered systems. In International Conference on Prognostics and Health Management (pp. 1–6).
Wold, H. (1954). A study in the analysis of stationary time series (2nd ed.). Almqvist and Wiksell Book Co.
Wu, Y., Yuan, M., Dong, S., Lin, L., & Liu, Y. (2018). Remaining useful life estimation of engineered systems using vanilla LSTM neural networks. Neurocomputing, 275, 167–179.
Yu, L., Zhou, L., Tan, L., Jiang, H., Wang, Y., Wei, S., & Nie, S. (2014). Application of a new hybrid model with seasonal auto-regressive integrated moving average (ARIMA) and nonlinear auto-regressive neural network (NARNN) in forecasting incidence cases of HFMD in Shenzhen, China. PLoS ONE, 9(6), e98241.
Zhao, S., Zhang, Y., Wang, S., Zhou, B., & Cheng, C. (2019). A recurrent neural network approach for remaining useful life prediction utilizing a novel trend features construction method. Measurement, 146, 279–288.
Acknowledgements
The software development and the realization of the experiments were performed at the CCIPL (Centre de Calcul Intensif des Pays de la Loire, Nantes, France).
Funding
Fatoumata Dama is supported by a PhD scholarship granted by the French Ministery for Higher Education, Research and Innovation.
Author information
Authors and Affiliations
Contributions
Not Applicable.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Consent to participate
Not Applicable.
Consent for publication
Not Applicable.
Ethical approval
Not Applicable.
Additional information
Editor: Gustavo Batista.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Appendix: backward-forward-backward algorithm
The Backward-forward-backward algorithm introduced by Scheffer and Wrobel (2001) for PHMC model learning has been adapted to the PHMC-MLAR framework. This algorithm makes it possible to compute the probabilities
in \({\mathcal {O}}(TK^2)\) operations. The analytical development for the above quantity involves three additional probabilities:
with
The algorithm operates recursively in three steps: two backward steps chained through a forward step. The first backward step computes the set of probabilities \(\tau _t(s)\) (Sect. A.1); the forward step computes probabilities \(\alpha _t(s)\) (Sect. A.2); the second backward step computes probabilities \(\beta _t(s)\). In Sect. A.4, we describe a scaling method that is necessary to prevent floating point underflow when running the algorithm, especially when large sequences are considered.
Note that the \(\xi _t(k, \ell )\) quantities can be used to compute the \(\gamma _t(\ell )\) probabilities
In practice \(\gamma _t(\ell )\) have to be normalized by dividing them by the sum \(\sum _{{\ell}=1}^K \gamma _t(\ell )\).
Proof
First, in Eq. 39, the conditional probability is transformed into a joint probability. Then, in Eq. 40, we successively maginalize \(X_{t+1}^T\), \(X_t\), \(S_t\) and \((S_{t-1}, X_1^{t-1})\). According to the conditional independence graph of the PHMC-MLAR model, the marginalization of \(X_{t+1}^T\) gives \(\beta _{t}(\ell )\), that of \(X_t\) yields \(P(X_t=x_t \, | \, S_{t}=\ell , X_{t-p}^{t-1}, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\), that of \(S_t\) gives \(P(S_{t}=\ell \, | \, S_{t-1}=k, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) and that of \((S_{t-1}, X_1^{t-1})\) provides \(\alpha _{t-1}(k)\). Finally, in Eqs. 42–44, the probability \(P(S_{t}=\ell \, | \, S_{t-1}=k, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) is developed using Bayes’ rule. Note that in Eq. 44, the probability \(P(S_t=\ell , \sigma _t \,|\, S_{t-1}=k, \sigma _{t-1}; \, \hat{\varvec{\kern-2pt\theta }})\) is null for \(\ell \notin \sigma _t\) and is not defined for \(k \notin \sigma _{t-1}\).
with
\(\square\)
1.1 A.1 First backward step
The first backward step computes probabilities \(\tau _t(s)\), the probabilities of the remaining possible states given that state \(s \in \{1, \dots , K\}\) is observed at time-step \(t \in \{1, \dots , T\}\): \(\tau _t(s) = P(\sigma _{t+1}, \dots , \sigma _{T} \,|\, S_t=s, \hat{\varvec{\kern-2pt\theta }}) = P(S_{t+1} \in \sigma _{t+1}, \dots , S_T \in \sigma _T \,|\, S_t=s, \hat{\varvec{\kern-2pt\theta }})\). This set of probabilities is computed recursively as follows:
Proof
Base case: \(t = T-1\)
By applying the definition of \(\tau _{T-1}\), we obtain:
Recursive case: \(t = T-2, \dots , 1\)
We first use the law of total probabilities (Eq. 48), followed by Bayes’ rule (Eq. 49). Note that in Eq. 49, the probability \(P(\sigma _{t+1}, \dots , \sigma _{T}\,|\, S_{t+1}=i , S_t=s, \hat{\varvec{\kern-2pt\theta }})\) is null for \(i \notin \sigma _{t+1}\) (since \(\sigma _{t+1}\) is the set of possible states at time-step \(t+1\)); otherwise it equals \(P(\sigma _{t+2}, \dots , \sigma _{T}\,|\, S_{t+1}=i, \hat{\varvec{\kern-2pt\theta }}) = \tau _{t+1}(i)\) (Eq. 50). Thus, we obtain the recursive formula presented in Eq. 45.
\(\square\)
1.2 A.2 Forward step
This step allows to compute the probabilities of being in regime s at time-step t while observing sequence \(x_1, \dots , x_t\). These probabilities, denoted by \(\alpha _t(s)\), are defined as \(\alpha _t(s) = P(S_t=s, X_1^t=x_1^t \,|\, X_{1-p}^0, \Sigma ; \,\hat{\varvec{\kern-2pt\theta }})\) for \(1 \le t \le T\), \(1 \le s \le K\). They are computed as follows:
To note, the likelihood of sequence \(x_1^T\) can be easily computed by integrating out \(S_t\) in \(\alpha _T\):
The likelihood of N independent sequences is therefore calculed by multiplying the individual likelihoods across the sequences.
Proof
Base case: \(t=1\)
In Eq. 54, using the conditional independence graph of the PHMC-MLAR model, we transform the joint probability into two conditional probabilities, \(P(X_1=x_1 \,|\, S_1=s, X_{1-p}^0; \,\hat{\varvec{\kern-2pt\theta }})\) and \(P(S_1=s \,|\, \Sigma ; \,\hat{\varvec{\kern-2pt\theta }})\). Then, in Eq. 55, Bayes’ rule is applied to the latter conditional probability. It can be easily shown that \(P(\Sigma ; \, \hat{\varvec{\kern-2pt\theta }}) = \sum _{i \in \sigma _1} \tau _1(i) \, P(S_1=i; \hat{\varvec{\kern-2pt\theta }})\). Thus we obtain Eq. 56.
Recursive case: \(t=2, \dots , T\)
As previously, the joint probability is split into two conditional probabilities (Eq. 57). We use the law of total probabilities to introduce \(S_{t-1}\) in Eq. 58. From Eqs. 58 to 59, Bayes’ rule is applied on the terms within the sum. Then, in Eq. 60, recursive terms \(\alpha _{t-1}\) weighted by probabilities \(P(S_t=s \,|\, S_{t-1}=i, \Sigma ; \,\hat{\varvec{\kern-2pt\theta }})\) appear within the sum. Finally, probabilities \(P(S_t=s \,|\, S_{t-1}=i, \Sigma ; \,\hat{\varvec{\kern-2pt\theta }})\) are computed through the calculations presented in Eqs. 61–64. Thus, by substituting Eq. 64 in Eq. 60, we obtain the recursive case (Eq. 52).
where
\(\square\)
1.3 A.3 Second backward step
In this second backward step, quantities \(\beta _t(s) =P(X_{t+1}^T=x_{t+1}^T \,|\, X_{t+1-p}^t, S_t = s, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) are computed. \(\beta _t(s)\) denotes the probability to observe sequence \(x_{t+1}, \dots , x_T\) given that state s has been observed at time-step t. These probabilities are recursively computed as follows:
Proof
Base case: \(t=T-1\)
Equation 66 is obtained by applying the law of total probabilities. In Eq. 67, Bayes’ rule is applied to \(P(S_T=i \,|\, S_{T-1} = s, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) and a quotient of probabilities appears. Then, the numerator and denominator of this quotient are transformed into products of conditional probabilities (Eq. 68). In Eq. 69, we introduce backward propagation terms \(\beta _T(i)\) and \(\tau _T(i)\), which each equal one (by definition); thanks to Markov property, probability \(P(S_T=i, \sigma _T \,|\, S_{T-1} = s, \sigma _1, \dots , \sigma _{T-1}; \, \hat{\varvec{\kern-2pt\theta }})\) is equal to \(P(S_T=i \,|\, S_{T-1} = s; \, \hat{\varvec{\kern-2pt\theta }})\) if \(i \in \sigma _T\) and \(s \in \sigma _{T-1}\), and this probability is null if \(i \notin \sigma _T\) and is undefined if \(s \notin \sigma _{T-1}\) (hence the indicator function \(\varvec{1}_{\{s \, \in \sigma _{T-1}, \, i \, \in \sigma _{T}\}}\)). Besides, in Eq. 68, a common term appears at numerator and denominator, which entails a simplification. Finally, probability \(P(\sigma _T \,|\, S_{T-1} = s, \sigma _1, \dots , \sigma _{T-1}; \, \hat{\varvec{\kern-2pt\theta }})\) appearing at denominator equals \(\tau _{T-1}(s)\) thanks to Markov property.
Recursive case: \(t=T-2, \dots , 1\)
The application of the law of total probabilities yields Eq. 70. In Eq. 71, \(X_{t+2}^T\) then \(X_{t+1}\) are marginalized, which allows to make appear the recursive term \(\beta _{t+1}\) together with the conditional probability of \(X_{t+1}\) given \(S_{t+1}\) and past values in Eq. 72. As in the base case, probability \(P(S_{t+1} = i \,|\, S_t=s, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) is computed using Bayes’ rule (Eqs. 73–76).
where
\(\square\)
1.4 A.4 Scaling of backward-forward-backward algorithm
For large sequences, i.e. large value of T, the quantities \(\tau _t(s)\), \(\alpha _t(s)\) and \(\beta _t(s)\) tend to zero as products of probabilities. Thus, the computations will require beyond the precision range of machine and PHMC-MLAR parameter estimate will be inaccurate. Generally, this problem is solved by normalizing \(\tau _t(s)\), \(\alpha _t(s)\) and \(\beta _t(s)\) by a term of same order of magnitude (Florez-Larrahondo, 2020; Koenig & Simmons, 1996). Thus, we propose the following normalization:
As previouly, \(\tilde{\tau }_t(s)\), \(\tilde{\alpha }_t(s)\) and \(\tilde{\beta }_t(s)\) can be computed recursively. The recursive formula for these quantities can be deduced from those of \(\tau _t(s)\) (Eq. 45), \(\alpha _t(s)\) (Eq. 52) and \(\beta _t(s)\) (Eq. 65). To do so, Eqs. 45, 52 and 65 are respectively divided by the normalization terms \(P(\sigma _t, \dots , \sigma _T \,|\, \sigma _{t-1}; \, \hat{\varvec{\kern-2pt\theta }})\), \(P(X_1^t=x_1^t \,|\, X_{1-p}^0, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\) and \(P(X_t^T=x_t^T \,|\, X_{1-p}^{t-1}, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }})\). After decomposing the formula obtained and after some calculations, we obtain the subsequent recurvive formulas for \(\tilde{\tau }_t\), \(\tilde{\alpha }_t\) and \(\tilde{\beta }_t\). First backward propagation
with
Forward propagation
with \(P(\sigma _{t-1} \,|\, \sigma _{t-2}; \, \hat{\varvec{\kern-2pt\theta }})\) defined in Eq. 81 and \(C_t\) the scaling term defined and computed as follows:
The proof is straightforward and is left to the reader. Note that \(P(X_1^T=x_1^T \,|\, X_{1-p}^0, \Sigma ; \, \hat{\varvec{\kern-2pt\theta }}) =\prod _{t=1}^T C_t\). Second backward propagation
where \(C_t\) and \(P(\sigma _t \,|\, \sigma _{t-1}; \, \hat{\varvec{\kern-2pt\theta }})\) are defined in Eqs. 83–84 and Eq. 81 respectively.
\(\xi _t(k, \ell )\) computation
In Eq. 37 probabilities \(\xi _t(k, \ell )\) are defined in function of quantities \(\tau _t\), \(\tau _{t-1}\), \(\alpha _{t-1}\) and \(\beta _t\). These quantities can be easily expressed in function of their normalized versions \(\tilde{\tau }_t\), \(\tilde{\tau }_{t-1}\), \(\tilde{\alpha }_{t-1}\) and \(\tilde{\beta }_t\) using Eqs. 77, 78 and 79. After substituting \(\tau _t\), \(\tau _{t-1}\), \(\alpha _{t-1}\) and \(\beta _t\) by the resulting expressions and after some simplifications, we obtain the following formula:
B Appendix: evaluation of feature prediction performance on the CMAPSS real-world data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dama, F., Sinoquet, C. Partially Hidden Markov Chain Multivariate Linear Autoregressive model: inference and forecasting—application to machine health prognostics. Mach Learn 112, 45–97 (2023). https://doi.org/10.1007/s10994-022-06209-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-022-06209-5