Model selection in reconciling hierarchical time series

Abstract

Model selection has been proven an effective strategy for improving accuracy in time series forecasting applications. However, when dealing with hierarchical time series, apart from selecting the most appropriate forecasting model, forecasters have also to select a suitable method for reconciling the base forecasts produced for each series to make sure they are coherent. Although some hierarchical forecasting methods like minimum trace are strongly supported both theoretically and empirically for reconciling the base forecasts, there are still circumstances under which they might not produce the most accurate results, being outperformed by other methods. In this paper we propose an approach for dynamically selecting the most appropriate hierarchical forecasting reconciliation method and leading to more accurate coherent forecasts. The approach, which we call conditional hierarchical forecasting, is based on machine learning classification methods that use time series features to select the reconciliation method for each hierarchy. Moreover, it allows the selection to be tailored according to the accuracy measure of preference and the hierarchical level(s) of interest. Our results suggest that conditional hierarchical forecasting can lead to significantly more accurate forecasts than standard approaches, especially at lower hierarchical levels.

1 Introduction and background

Forecasting is essential for supporting decision-making, especially in applications that involve a lot of uncertainty. For instance, accurately forecasting the future demand of stock keeping units (SKUs) can significantly improve supply chain management (Ghobbar and Friend, 2003), reduce inventory costs (Syntetos et al., 2010), and increase service levels (Pooya et al., 2019), particularly under the presence of promotions (Giir Ali et al., 2009; Abolghasemi et al., 2020). In order to obtain more accurate forecasts, forecasters typically try to identify the most appropriate forecasting model for each series from a variety of alternatives. Although this task can provide significant improvements under perfect foresight (Fildes, 2001), it is difficult to effectively perform in practice due to model, parameter, and data uncertainty (Petropoulos et al., 2018). Thus, many strategies have been proposed in the literature to effectively perform forecasting model selection (Fildes and Petropoulos, 2015), most of which are based on the in-sample and out-of-sample accuracy of the forecasting models (Tashman, 2000), their complexity (Hyndman et al., 2002), and the features that time series display (Montero-Manso et al., 2020; Petropoulos et al., 2014).

However, in business forecasting applications, data is typically grouped based on its context and characteristics, thus structuring cross-sectional hierarchies. For example, although the demand of an SKU can be reported at a store level, it can be also aggregated (summed) at a regional or national level. Similarly, demand can be aggregated for various SKUs of the same type (e.g., dairy products) or category (e.g., foods). As a result, hierarchical time series introduce additional complexity to the whole forecasting process since, apart from selecting the most appropriate forecasting model for each series, forecasters have also to account for coherence, i.e. make sure that the forecasts produced at the lower hierarchical levels will sum up to those produced at the higher ones (Athanasopoulos et al., 2020). In fact, coherence is a prerequisite in hierarchical forecasting (HF) applications as it ensures that different decisions made across different hierarchical levels will be aligned.

Naturally, the demand recorded at lower hierarchical levels will always add up to the observed demand at higher levels. However, this is rarely the case for forecasts which are usually produced for each series separately and are therefore incoherent. To achieve coherence, various HF methods can be used for reconciling the individual, base forecasts (Spiliotis et al., 2019). The most basic HF method is probably the bottom-up (BU), according to which base forecasts are produced just for the series at the lowest level of the hierarchy, and are then aggregated to provide forecasts for the series at the higher levels (Dangerfield and Morris , 1992). Top-down (TD) is another option which involves forecasting just the series at the highest level of the hierarchy and then using proportions to disaggregate these forecasts and predict the series at the lower levels Gross and Sohl 1990; Athanasopoulos et al. 2009. Middle-out (MO) mixes the above-mentioned methods, producing base forecasts for a middle level of the hierarchy and then aggregating or disaggregating them to forecast the higher and lower levels, respectively (Abolghasemi et al. , 2019). Finally, a variety of HF methods that combine (COM) the forecasts produced at all hierarchical levels have been proposed in the literature, usually resulting in coherent and more accurate forecasts (Hyndman et al., 2011; Wickramasuriya et al., 2019; Jeon et al. , 2019).

From the HF methods found in the literature, a COM method, called minimum trace (Wickramasuriya, 2019, MinT;][), has been distinguished due to the strong theory supporting it and the results of many empirical studies highlighting its merits over other alternatives (Abolghasemi et al., 2019; Burba and Chen, 2021; Spiliotis et al., 2020). However, there are still circumstances under which MinT might fail to provide the most accurate forecasts. For instance, since MinT is based on the estimation of the one-step-ahead error covariance matrix, the method might be proven inappropriate when the in-sample errors of the baseline forecasting models do not represent post-sample accuracy, the assumption that the multi-step forecast error covariance is proportional to the one-step forecast error covariance is unrealistic, or the required estimations are computationally too hard to make. Moreover, since MinT treats all levels equally, it is not optimized with respect to certain hierarchical levels of interest. Finally, given that medians are not additive, there is no reason to expect that MinT will always improve the mean absolute forecast error, or other accuracy measures that are based on absolute forecast errors.

In such cases, simpler HF methods like the BU and the TD may be useful. However, there is inadequate evidence about which of the two methods to use (Hyndman et al., 2011). For example, the BU method is typically regarded as more suitable for short-term forecasts and for hierarchies in which bottom series are not highly correlated and not dominated by noise (Kahn, 1998). On the other hand, the TD method is usually regarded as more appropriate for long-term forecasts, but less accurate for predicting the series at the lower aggregation levels due to information loss (Dangerfield and Morris, 1992; Kahn, 1998). It seems that no reconciliation method can fit all kinds of HF problems and that, similarly to forecasting model selection, the appropriateness of the different HF methods depends on various factors, including the particularities of the time series (Nenova and May, 2016) and the structure of the hierarchy (Abolghasemi et al., 2019; Fliedner, 1999; Fliedner , 2001; Gross and Sohl, 1990). The above findings reconfirm highlight the potential benefits of conditional hierarchical forecasting (CHF); i.e. the improvements in terms of forecasting accuracy that could be possibly achieved if forecasters were able to select the most appropriate HF method according to the characteristics of the series that form a hierarchy. In this paper we propose an approach for performing such a conditional selection using time series features as leading indicators (Kang et al., 2017; Spiliotis et al., 2020a) and machine learning (ML) methods for conducting the classification. Essentially, we suggest that the forecasting accuracy of the different HF methods found in the literature is closely related with the characteristics of the individual series and that, based on these relationships, “horses for courses” can be effectively identified (Petropoulos et al., 2014). In addition, CHF allows the selection to be tailored according to the accuracy measure of preference (e.g. mean absolute or squared error) and the hierarchical level(s) of interest (e.g. top or bottom level), thus adapting to the requirements of the examined forecasting task and effectively supporting decisions.

Table 1 State-of-the-art: Major studies conducted in the field of hierarchical forecasting for reconciling base forecasts using either combination or selection approaches

Table 1 summarizes major studies conducted in the field of HF, putting a particular emphasis on approaches proposed in the literature for reconciling base forecasts using either combination or selection methods. The method proposed in this paper is also included in the table to facilitate comparisons. As seen, various studies have considered ML methods for performing TD (Mancuso et al., 2020), MO (Abolghasemi et al., 2019), or BU (Burba and Chen, 2021; Spiliotis et al., 2020) reconciliation in a dynamic fashion by using base forecasts and explanatory variables as input to regression models, including neural networks (NN), regression trees (RT), and support vector machines (SVM), among others. Instead of reconciling the base forecasts directly, other studies have proposed combining the reconciled forecasts produced by standard HF methods using simple weighting schemes (Abouarghoub et al., 2018) or selecting the most appropriate one from a list of alternatives (Nenova and May, 2016). As such, the spirit of our work is similar to that of Nenova and May (2016) since both studies aim to select the most suitable reconciliation method for a hierarchy of interest. However, we take a different approach in doing so. First, in contrast to (Nenova and May, 2016), which exploits time series correlations and rank predictors (i.e., features related to the structure of the hierarchy), our selection is performed using a comprehensive set of time series features that describe the behavior of the individual series comprising the hierarchy. Time series features have been minimally considered in some other studies that evaluated the impact of the series autocorrelation (Chen and Boylan, 2009), demand type (Widiarta et al., 2007; Widiarta et al., 2008), and forecasting horizon (Burba and Chen, 2021) on the appropriateness of the BU and the TD methods, mostly using simulations and ex-post evaluations. Second, in our study we use a different set of baseline HF methods, including COM in addition to the TD and BU methods. This is done because several studies have shown that COM can outperform standard HF methods, being also significantly different in nature than BU and TD in terms of the approach used for performing the reconciliation (Hyndman et al., 2016; Hyndman et al., 2011; Abolghasemi et al., 2020). Third, we use a different set of models for conducting the classification, including more advanced decision-tree-based algorithms, such as random forests (RF) and eXtreme Gradient Boosting (XGB), that have shown promising results in various forecasting tasks and competitions (Montero-Manso et al., 2020; Chen and Guestrin, 2016). Fourth, we evaluate the performance of our method by considering diverse sets of hierarchical data and optimization criteria in terms of the hierarchical level at which the forecasts should be considered as optimal, the characteristics of time series, the measure used for assessing accuracy, and the forecasting horizon. We also conduct an empirical comparison between the method proposed in this paper and the one described in Nenova and May (2016), and show the importance of time series characteristics in selecting the most appropriate reconciliation method.

We benchmark the accuracy of the proposed approach against various HF methods, both standard and state-of-the-art, considering a variety of optimization criteria, and using three large data sets from the retail, tourism and justice sectors. Our results suggest that CHF leads to superior forecasts that outperform those of the individual HF methods examined. Thus, we conclude that selection should not be limited to forecasting models, but be expanded to HF methods as well.

The remainder of the paper is organized as follows. Section 2 describes the most popular HF methods found in the literature and Sect. 3 introduces CHF. Section 4 presents the primary data set used for the empirical evaluation of the proposed approach and describes the experimental set-up. Section 5 presents the results of the experiment and discusses our findings. Finally, Sect. 6 concludes the paper.

2 Hierarchical forecasting methods

In this section, we discuss the TD, BU, and COM as three well-established HF methods that are widely used in the literature and in practice for reconciling hierarchical base forecasts. These methods are also the ones considered in this study, both as alternatives of the conditional HF approach to be described in the next section and as benchmarks. For a more detailed discussion on the existing HF methods, their advantages, and drawbacks, please refer to the study of Athanasopoulos et al. (2020).

Before proceeding, we introduce the following notations and parameters that will facilitate the discussion of the three methods:

m::

Total number of series in the hierarchy

$m_i$::

Total number of the series for level i;

k::

Total number of the levels in hierarchy;

n::

Number of the observations in each series;

$Y_{x,t}$::

$\text {The } t^{th} \text { observation of series } Y_x$;

${\hat{Y}}_{x,n} (h)$::

h—$\text {step-ahead independent base forecast of series } Y_x \text { based on } n \text { observations}$;

${\varvec{Y}}_{i,t}$::

$\text {The vector of all observations at level } i$;

$\hat{{\varvec{Y}}}_{i,t}(h)$::

h—$\text {step-ahead forecast at level } i$;

${\varvec{Y}}_t$::

$\text {A column vector including all observations}$;

$\hat{{\varvec{Y}}}_n (h)$::

h—$\text {step-ahead independent base forecast of all series based on} n \text { observations}$;

$\tilde{{\varvec{Y}}}_n (h)$::

The final reconciled forecasts of all series

Fig. 1

A three-level hierarchical structure

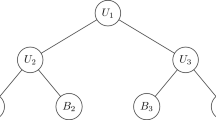
We can express a hierarchical time series as ${\varvec{Y}}_t = {\varvec{S}} {\varvec{Y}}_{k,t}$, where ${\varvec{S}}$ is a summing matrix of order $m \times m_k$. For example, we can express the three-level hierarchical time series shown in Fig. 1 as:

$$\begin{aligned} \left[ \begin{array}{c} Y_t \\ Y_{A,t} \\ Y_{B,t}\\ Y_{AA,t} \\ Y_{AB,t}\\ Y_{BA,t} \\ Y_{BB,t} \\ \end{array} \right] = \left[ \begin{array}{@{}*{4}{c}@{}} 1 &{}\quad 1 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 \\ &{}\quad &{}\quad {\varvec{I}}_4 &{}\quad \\ \end{array} \right] \times \left[ \begin{array}{c} Y_{AA,t} \\ Y_{AB,t} \\ Y_{BA,t} \\ Y_{BB,t} \\ \end{array} \right] \end{aligned}$$

Accordingly, we can express various hierarchical structures with a unified format as $\tilde{{\varvec{Y}}}_n (h)= {\varvec{S}} {\varvec{G}} \hat{{\varvec{Y}}}_n(h)$, where ${\varvec{G}}$ is a matrix of order $m \times m_k$ which elements depend on the type of the reconciliation method used, in our case the BU, TD, and COM methods Hyndman and Athanasopoulos (2021).

2.1 Bottom-up

BU is the simplest HF method according to which we forecast the series at the bottom level of the hierarchy and then aggregate these forecasts to obtain forecasts at higher levels. In this case, the matrix ${\varvec{G}}$ can be constructed as ${\varvec{G}}= [{\varvec{0}}_{m_k \times (m - m_k)}| {\varvec{I}}_{m_k}]'$, where ${\varvec{0}}_{i \times j}$ is a $i \times j$ null matrix.

2.2 Top-down

In the TD method, base forecasts are produced at the top level of the hierarchy and then disaggregated to the lower levels with appropriate factors. While there are various ways for computing such factors and disaggregating the top level forecasts, we consider the proportions of the historical averages since it is a widely used alternative that provides reasonable results (Athanasopoulos et al., 2009). These proportions are computed as follows

$$\begin{aligned} p_j = \frac{\sum _{t=1}^{n} Y_{j,t}}{\sum _{t=1}^{n} Y_t}, ~~~~~~~~ j=1, \dots , m_k \end{aligned}$$

(1)

where $p_j$ represents the average of the historical value of the bottom level series ${Y_{j,t}}$ relative to the average value of the total aggregate ${Y_t}$. We can then construct the vector ${\varvec{g}} =[p_1, p_2, p_3, \dots , p_{m_k}]$ and matrix ${\varvec{G}}= [{\varvec{g}} \mid {\varvec{0}}_{m_k \times (m - 1)}]'$.

2.3 Optimal combination

The COM method produces base forecasts for all series across all hierarchical levels and then combines them with a linear model to obtain the reconciled forecasts. Suppose

$$\begin{aligned} \tilde{{\varvec{Y}}}_n(h) = {\varvec{S}} {\varvec{G}} \hat{{\varvec{Y}}_n}(h) \end{aligned}$$

depicts the h-step-ahead reconciled forecasts. Then, the covariance matrix of the errors of these forecasts can be given by

$$\begin{aligned} {\varvec{V}}_h=\text {Var}[{\varvec{y}}_{n+h} - \tilde{{\varvec{Y}}}_n (h)]={\varvec{S}}{\varvec{G}}{\varvec{W}}_h{\varvec{G}}'{\varvec{S}}', \end{aligned}$$

where ${\varvec{W}}_h$ is the variance-covariance matrix of the h-step-ahead base forecast errors (Wickramasuriya et al., 2019; Hyndman et al., 2016). It can be shown that the matrix ${\varvec{G}}$ that minimizes the trace of ${\varvec{V}}_h$ such that it generates unbiased reconciled forecasts, i.e., ${\varvec{S}}{\varvec{G}}{\varvec{S}}={\varvec{S}}$, is given by

$$\begin{aligned} {\varvec{G}}= ({\varvec{S}}' {\varvec{W}}^{\dagger }_h{\varvec{S}})^{-1} {\varvec{S}}' {\varvec{W}}_h^{\dagger }, \end{aligned}$$

where ${\varvec{W}}^\dagger _h$ is the generalized inverse of ${\varvec{W}}_h$.

There are a few different ways to estimate ${\varvec{W}}_h$. In this study we consider the shrinkage estimation as it has been empirically shown that it yields the most accurate forecasts in many HF applications (Abolghasemi et al., 2019; Spiliotis et al., 2020; Wickramasuriya et al., 2019). Using the shrinkage method, this matrix can be estimated by ${\varvec{W}}_h=k_h\left( \lambda _D \hat{{\varvec{W}}}_{1,D} + (1-\lambda _D)\hat{{\varvec{W}}}_1\right)$. The diagonal target of the shrinkage estimator is $\hat{{\varvec{W}}}_{1,D} = \text {diag}(\hat{{\varvec{W}}}_1)$ and the shrinkage parameter is given by

$$\begin{aligned} \lambda _D = \frac{\sum _{i \ne j} \text {Var}({\hat{r}}_{ij})}{\sum _{i \ne j} {\hat{r}}^2_{ij}}, \end{aligned}$$

where ${\hat{r}}_{ij}$ is the $(i,j)^{th}$ element of the one-step-ahead in-sample correlation matrix (Schafer and Strimmer 2005).

The COM method was implemented using the MinT function of the hts package for Hyndman et al. (2020b).

3 Conditional hierarchical forecasting

Time series often depict different patterns, such as seasonality, randomness, noise, and auto-correlation (Kang et al., 2017). As a result, there is no model that can consistently forecast all types of series more accurately than other models, even relatively simple ones (Petropoulos et al., 2014; Fildes and Petropoulos, 2015). Similarly, although some models may perform better on a time series data set of particular characteristics, there is no guarantee that this will always be the case (Spiliotis et al., 2020a). For example, although exponential smoothing (Gardner, 1985) typically produces relatively accurate forecasts for seasonal series, it might be outperformed by ML methods when a large number of observations is available (Smyl , 2020). Thus, selecting the most appropriate forecasting model for each series becomes a challenging task for improving overall forecasting accuracy (Montero-Manso et al., 2020).

Model selection has been extensively studied in the forecasting literature. Although there is no unique way to determine the most appropriate forecasting model for each series, empirical studies have provided effective strategies for performing this task (Fildes and Petropoulos, 2015). From these strategies, the approaches that build on time series features are among the most promising given that the latter can effectively represent the behaviour of the series in an abstract form and match it with the relative performance of various forecasting models (Reid, 1972; Meade, 2000; Wang et al., 2009; Petropoulos et al., 2014; Kang et al., 2017; Abolghasemi et al., 2020).

Expert systems and rule-based forecasting were two of the early approaches to be suggested for forecasting model selection (Collopy and Armstrong, 1992; Mahajan and Wind, 1988). Collopy and Armstrong (1992) considered domain knowledge along with 18 time series features and proposed a framework that consisted of 99 rules to select the most appropriate forecasting model from 4 alternatives. In another study, Adya et al. (2000) considered 6 features and 64 rules to select the most accurate forecasting model from 3 alternatives. Similarly, Adya et al. (2001) proposed an approach to automatically extract time series features and choose the best forecasting model. Petropoulos et al. (2014) measured the impact of 7 time series features plus the length of the forecasting horizon on the accuracy of 14 popular forecasting models, while (Kang et al., 2017) and (Spiliotis et al., 2020a) linked the performance of standard time series forecasting models with that of various indicative features using data from well-known forecasting competitions. More recently, Montero-Manso et al. (2020) used 42 time series features to determine the weights for optimally combining 9 different forecasting models, winning the second place in the M4 forecasting competition (Makridakis et al., 2020).

Inspired by the work done in the area of forecasting model selection, we posit that HF methods can be similarly selected using time series features and, based on such a selection, improve forecasting accuracy for the case of hierarchical series, while simultaneously reducing computational cost (for more details on this topic please refer to Appendix E). In this respect, we proceed by computing various time series features across all hierarchical levels and propose using these features for selecting the HF method that best suites the hierarchy, i.e., produces on average the most accurate forecasts for all the series it comprises (Abolghasemi et al., 2020; Petropoulos et al., 2014)¹. The selection is done by employing a popular ML classification method. The proposed approach, to be called conditional HF (CHF), is summarised in Appendix A and presented in the flowchart of Fig. 2.

Fig. 2

CHF algorithm flowchart

Given that CHF builds on time series features and its accuracy is directly connected with the representatives of the features used, as well as the capacity of the algorithm employed for selecting the most appropriate HF method, it becomes evident that choosing a set of diverse, yet finite features is a prerequisite for enhancing the performance of the proposed classification approach. There are many features that can be used to describe time series patterns. For example, Fulcher et al. (2013) extracted more than 7,700 features for describing the behavior of the time series and then summarized them into 22 canonical features, losing just 7% of accuracy in a classification task (Lubba et al. 2019). Similarly, Wang et al. (2006) and Kang et al. (2017) suggested that a relatively small number of features can be used for effectively visualizing time series and performing forecasting model selection. Based on the above, we decided to consider 32 features for the CHF method so that the patterns of the hierarchical series are effectively captured without exaggerating. These features, described in Appendix B, included entropy, lumpiness, stability, hurst, seasonal-period, seasonal-strength, trend, curvature, e-acf1, e-acf10, x-acf1, x-acf10, diff1-acf1, diff1-acf10, diff2-acf1, diff2-acf10, seas-acf1, x-pacf5, diff1x-pacf5, diff2x-pacf5, seas-pacf, linearity, non-linearity, max-var-shift, max-kl-shift, fluctanal-prop-r1, unitroot-kpss, arch-acf, garch-acf, arch-r2, garch-r2, and arch-test, and were computed using the tsfeatures package for Hyndman et al. (2019). Our list of features is mostly inspired by recent studies that have successfully used time series features to develop meta-learning forecasting algorithms, e.g. for model selection and combination, (Montero-Manso et al., 2020), being tailored however for the particular requirements of the conditional hierarchical forecasting task. For more details about these features, please refer to the studies of Wang et al. (2006) and Kang et al. (2017).

Note that CHF is flexible in terms of the method that will be employed for performing the classification. That is, users can select their classification method of choice for identifying the most accurate HF method and reconciling the base forecasts produced for the examined hierarchy. In this study we considered seven methods, namely logistic regression (LR), linear discriminant analysis (LDA), regression tree (RT), RF, XGB, SVM, and neural network (NN). However, we decided to include only XGB in the main part of the paper since, in most cases, the other classification models performed worse than XGB, a powerful classification method that has been successfully applied in various forecasting and classification problems (Chatzis et al., 2018; Demolli et al., 2019; Nielsen , 2016). Appendix C summarizes the results of our experiments when classifiers other than XGB are used for implementing CHF.

Observe that CHF is also flexible in terms of the forecasting models that will be used for producing the base forecasts and the HF methods that will be considered for their reconciliation. For the latter case, we considered three HF methods (BU, TD, and COM), as described in Sect. 2. The reasoning is two-fold. First, classification methods tend to perform better when the number of classes is limited and, as a result, the key differences between the classes are easier to identify (Hastie and Tibshirani 1998). Second, we believe that the selected HF methods are diverse enough, each one focusing on different levels of the hierarchy and adopting a significantly different approach for reconciling the base forecasts. Although we could have considered more HF methods of those proposed in the literature, they are mostly variants of the examined three methods (especially the COM method) and are therefore sufficiently covered.

We should also highlight that the rolling origin evaluation of the off-line phase can be adjusted to any desirable set-up that might be more suitable to the user. For example, if computational cost is not an issue, instead of updating the forecast origin by h periods at a time, a step of one period could be considered to further increase the size of the set used for training the classification method and facilitate learning. The main motivation for considering an h-step-ahead update is that this practice suits the way the retail firms operate when forecasting their sales and making their plans, creating also a rich set on which the ML classification method can be effectively trained, without exaggerating in terms of computational cost.

Finally, although we chose to train the classification method so that the average accuracy of CHF is minimized across the entire hierarchy, this objective can be easily adjusted in order for CHF to provide more accurate forecasts for a specific level of interest, as demonstrated in Appendix C. This choice depends on the decision-makers and can vary based on their focus and objectives. However, we do believe that our choice to optimize forecasting accuracy across the entire hierarchy, weighting equally all hierarchical levels, is realistic when dealing with demand forecasting and supply chain management given that in such settings each level supports very different, yet equally important decisions. A similar weighting scheme was adopted in the latest M competition, M5 (Makridakis et al. 2020), whose objective was to produce the most accurate point forecasts for 42,840 time series that represent the hierarchical unit sales of ten Walmart stores.

4 Data and experimental setup

4.1 Data

Although HF is relevant in many applications, such as energy (Spiliotis et al., 2020b) and tourism (Kourentzes and Athanasopoulos, 2019), it is most commonly found in the retail industry where SKU demand can be grouped based on location and product-related information. Therefore, the primary data set used in this study for empirically evaluating the accuracy of the proposed HF approach involves the sales and prices recorded for 55 hierarchies, corresponding to 55 fast-moving consumer goods of a food manufacturing company sold in various locations in Australia. Although the exact labels of the products are unknown to us, the products include breakfast cereals, long-life milk, and other breakfast products.

The hierarchical structure is the same for all 55 products of the data set and is depicted in Fig. 3. The number of series at each hierarchical level is provided in Table 2. As seen, each hierarchy consists of three levels, where the top level (level 0) represents total product sales, the middle level (level 1) the product sales recorded for 2 major retailer companies, and the bottom level (level 2) the way the product sales are disaggregated across 12 distribution centers (DC), 6 per retailer company, located in different states of Australia. Thus, each hierarchy includes 15 time series, each containing 120 weeks of observations, spanning from September 2016 to December 2018.

Fig. 3

Hierarchical structure of the time series included in the examined data set, representing the sales of 55 food products sold in Australia

Table 2 Number of time series per hierarchical level in the examined data set, representing the sales of 55 food products sold in Australia

Figure 4 presents the hierarchical time series of an indicative product of the data set. Observe that sales may experience spikes at different levels of the hierarchy, i.e. different levels of the supply chain. These spikes correspond to promotional periods, and their frequency and size vary significantly for different products. Moreover, different nodes in the hierarchy may experience spikes of different extent. Finally, since each hierarchy corresponds to a different product, the series of the data set display different strengths of trend and seasonality, volume, and entropy. For example, some series depict seasonality and small volume of sales, whereas some other series report large volume of sales and entropy, making them more volatile and difficult to forecast. As such, the data set represents a diverse set of demand patterns which are affected under the presence of promotions, i.e. price changes, among others.

Fig. 4

Hierarchical sales of an indicative product of the examined data set. Level 0 represents total product sales, level 1 the product sales recorded for 2 major retailer companies, and level 2 the product sales across 12 distribution centers

In order to provide more empirical evidence regarding the effectiveness of the proposed approach over both standard and state-of-the-art HF methods on a diverse range of data, we have considered two more data sets in addition to the Sales data presented above. These data sets have different properties, thus giving a more diverse set of data for our empirical study. The first additional data set, to be called the Tourism data set, provides information on the Australian domestic tourism demand, measured as the number of overnight trips Australians spend away from home and disaggregated by state and region. The data set consists of 85 series, namely the total demand (level 0; 1 series), the demand per state (level 1; 8 series), and the demand per region (level 2; 76 series). The series are quarterly and span from q1-1998 to q4-2017 (80 periods). The second data set, to be called the Prison data set, provides information on the size of the prison population in Australia, disaggregated by state and gender. The data set consists of 25 series, namely the total prison population (level 0; 1 series), the prison population per state (level 1; 8 series), and the prison population of males and females per state (level 2; 16 series). The series are quarterly and span from q1-2005 to q4-2016 (48 periods). Each data set demonstrates a different structure, with its series being also characterized by different seasonal and trend patterns, randomness, lengths, and autocorrelation. Moreover, for each case, different forecasting horizons and optimization criteria have been used for employing CHF. The results of these experiments are summarized in Appendices 4.1 and 4.2.

4.2 Experimental setup

Considering that the examined data set involves products with sales which are highly affected by promotions, we produce base forecasts for all the series of the 55 hierarchies using a regression model with ARMA errors (Reg-ARMA), where product prices are used as a regressor variable. We choose Reg-ARMA for two reasons: First, it is a powerful method that can embody explanatory variables into the model and has been successfully implemented in various forecasting tasks (Abolghasemi et al., 2019; Abolghasemi et al., 2020). Second, it is dynamic in nature as its ARIMA component can account for unexplained variations, making it a desirable choice for forecasting sales time series that are impacted by promotions. Reg-ARMA can effectively capture sales both during promotional and non-promotional periods as price inherently carries the impact of promotions and, therefore, explains sufficiently the corresponding variations in sales. Reg-ARMA model is implemented using the forecast package for Hyndman et al. (2020a).

To evaluate the accuracy of the proposed HF approach both in terms of median and mean approximation (Kolassa, 2016), we consider two measures, namely the mean absolute scaled error (MASE) and the root mean sum of squared scaled error (RMSSE), respectively. The measures are calculated as follows:

$$\begin{aligned} \text {MASE}&= \frac{n-1}{h} \frac{ \sum \nolimits _{t=n+1}^{n+h} {|y_{t}-f_{t}|} }{\sum \nolimits _{t=2}^{n} |y_{t}-y_{t-1}|}, \\ \text {RMSSE}&= \sqrt{ \frac{n-1}{h} \frac{ \sum \nolimits _{t=n+1}^{n+h} {(y_{t}-f_{t})^2} }{\sum \nolimits _{t=2}^{n} (y_{t}-y_{t-1})^2} }, \end{aligned}$$

where $y_t$ and $f_t$ are the observation and the forecast for period t, n is the sample size (observations used for training the forecasting model), and h is the forecasting horizon. Smaller MASE and RMSSE values suggest more accurate forecasts. Note that both measures are scale-independent, thus allowing us to average the results across series.

Once the base forecasts are produced, we use the BU, TD, and COM methods to reconcile them across the three levels of the hierarchy. These baseline methods are used for benchmarking the proposed HF approach as they have been successfully applied in numerous applications and are considered standards in the area of HF (Abolghasemi et al., 2019; Hyndman et al., 2011; Hyndman et al., 2016). We also use the CHF method to select which of the three benchmarks is more suitable for forecasting each hierarchy.

Fig. 5

Time series rolling origin approach for training, evaluating, and testing forecasting models. The blue circles represent the training set and the orange circles indicate the test set on each round

In order to fit and evaluate the CHF method, we split the original data set into a training and test set. Specifically, we used the first 26 weeks of data to initially train the Reg-ARMA model and the following 58 periods to produce 4-step-ahead base forecasts on a rolling origin basis (Tashman, 2000). We considered 26 weeks of observations as the initial set to provide enough observations for training the forecasting models and then generated 4-step-ahead forecasts since this horizon (one month) is often enough in practice for operational planning on a weekly basis. Moreover, this creates a sufficient number of observations for training the classification model. We state that the initial number of observations and the number of forecast steps can be chosen differently, but one should generally consider a high enough number of observations for training both the baseline forecasting models and the classifiers.

Figure 5 depicts the rolling origin approach that we have used for training and testing the forecasting models. The blue circles represent our training set, while the orange circles indicate the test set on each round. Suppose a particular product with all 15 time series. At each iteration, and for each series, we produce 4-step-ahead forecasts and then roll the forecasting origin by four periods, i.e. we add four observations to the training data set and proceed by forecasting the following four periods. Each time that the forecast origin was updated, the set used for fitting the Reg-ARMA model was accordingly extended so that the base forecasts produced were appropriately adjusted. Moreover, on each step, the BU, TD, and COM methods were applied to reconcile the base forecasts and identify the most accurate alternative according to MASE. We consider the first 26 weeks as the initial training data set and repeat this process until the end of evaluation set, i.e. period 84, for each set of hierarchical time series. In this respect, a total of 14 accuracy measurements (average accuracy of 4-step-ahead forecasts over 58 weeks) $\times$ 55 hierarchies $\times$ 15 series $= 11,550$ evaluations were recorded. We then summarized the results across the hierarchy and constructed a data set of 14 evaluations $\times$ 55 hierarchies $= 770$ observations that was used for training the XGB classification method. The remaining 36 weeks of data were used as a test set to evaluate the actual accuracy of the proposed approach, again on a rolling origin fashion. Thus, our evaluation is based on a total of 9 accuracy measurements (average accuracy of 4-step-ahead forecasts over 36 weeks) $\times$ 55 hierarchies $\times$ 15 series $= 7,425$ observations. Note that XGB is retrained each time that we move across the window, with the values of the time series features being accordingly updated.

5 Empirical results and discussion

Table 3 displays the forecasting accuracy (MASE and RMSSE) of the three HF methods considered in this study as benchmarks as well as classes for training the CHF algorithm in the retail data set presented in Sect. 4.1. The accuracy is reported both per hierarchical level and on average (arithmetic mean of the three levels), while CHF is implemented using the XGB classifier, as described in Sect. 4.2. Note that, as explained in Sect. 3, the average accuracy of the three hierarchical levels, as measured by MASE, is used for determining the training labels of the classifiers.

Table 3 Forecasting performance of HF methods in terms of MASE and RMSSE over the test set

The results indicate that, on average, CHF is the best HF method according to both accuracy measures used. Specifically, CHF provides about 5%, 9%, and 2% more accurate forecasts than BU, TD, and COM, respectively, indicating that the XGB method has effectively managed to classify the hierarchies based on the features that their series display.

The improvements are similar if not better for the middle and bottom levels of the hierarchy. However, CHF fails to outperform TD and COM for the top hierarchical level, being about 6% and 2% less accurate, despite being still 8% better than the BU method. This finding confirms our initial claim that, depending on the hierarchical level of interest, different HF methods may be more suitable. In this study, we focused on the average accuracy of the hierarchical levels and optimized CHF with such an objective. However, as described in Sect. 3, different objectives could be considered in order to explicitly optimize the top, middle or bottom level of the hierarchy. In Appendix C we have examined such objectives and evaluated the respective performance of the CHF method. For instance, the results of Table 5 suggest that when XGB is optimized in terms of MASE and with respect to the top level, the forecast error of CHF is reduced from 0.466 (XGB-Avg) to 0.449 (XGB-L0), i.e., by 4% compared to the optimization criteria currently used.

In order to better evaluate the performance of the proposed approach, we proceed by investigating the distribution of the error ratios reported between CHF and the three benchmark methods examined in our study across all the 55 hierarchies of the data set. The results, presented per hierarchical level and accuracy measure, are visualized in Fig. 6 where box plots are used to display the minimum, 1^st quantile, median, 3^rd quantile, and maximum values of the ratios, as well as any possible outliers. Values lower than unity indicate that CHF provides more accurate forecasts and vice versa. As observed, in most of the cases, CHF outperforms the rest of the HF methods, having a median ratio value lower than unity. The only exception is when forecasting level 0 and using RMSSE for measuring forecasting accuracy, where the TD method tends to provide superior forecasts. Thus, we conclude that CHF does not only provide the most accurate forecasts on average across all the 55 hierarchies, but also the most accurate forecasts across the individual ones.

Fig. 6

The ratio of the forecasting accuracy of the CHF approach over the baseline HF methods across all 55 hierarchies included in the test set. The results are reported for each accuracy measure and hierarchical levels separately

To validate this finding, we also examine the significance of the differences reported between the various HF methods using the multiple comparisons with the best (MCB) test, as proposed by (Koning et al., 2005). According to MCB, the methods are first ranked based on the accuracy they display for each series of the hierarchy and then their average ranks are compared considering a critical difference, $r_{\alpha , K, N}$, as follows:

$$\begin{aligned} r_{\alpha , K, N}= q_a \times \sqrt{\frac{K*(K+1)}{12N}}, \end{aligned}$$

(2)

where N is the number of the time series, K is the number of the examined HF methods, and $q_a$ is the quantile of the confidence interval. In our case, where $\alpha$ is set equal to 0.05 (95% confidence), $q_a$ takes a value of 3.219. Accordingly, K is equal to 4 (TD, BU, COM, CHF) and N is equal to 7,425.

Fig. 7

MCB test conducted on the HF methods examined in this study using the test set of the sales time series data. MASE and RMSSE are used for computing the ranks and a 95% confidence level is considered. The ranks are computed considering all the series of the 55 hierarchies

The results of the MCB test are presented in Fig. 7. If the intervals of two methods do not overlap, this indicates a statistically different performance. Thus, methods that do not overlap with the gray zone of Fig. 7 are significantly worse than the best, and vice versa. As seen, our results indicate that CHF provides significantly better forecasts than the rest of the HF methods, both in terms of MASE and RMSSE. Moreover, we find that CHF is followed by COM and then by TD and BU. Interestingly, the performance of TD is not significantly different than the one of BU according to RMSSE or MASE. In this regard, we conclude that CHF performs better than the state-of-the-art HF methods found in the literature, being also significantly more accurate than the standards used for HF, such as BU and TD. As such, CHF can be effectively used for selecting the most appropriate HF method from a set of alternatives and improving the overall forecasting accuracy of various hierarchies.

We also investigate the performance of the XGB classifier in terms of precision, recall, and $\text {F}_1$ score. The precision metric measures the number of correct predictions in the total number of predictions made for each class. Recall (also known as sensitivity) informs us about the number of times that the classifier has successfully chosen the best HF method for each class. Finally, the $\text {F}_1$ score is the harmonic mean of precision and recall, computed by $F_1= 2\frac{p*r}{p+r}$, and is used to combine the information provided by the other two metrics (Sokolova and Lapalme, 2009).

Before presenting the results, we note that the TD, BU, and COM methods have been identified as the most accurate HF method in 1860, 2745, and 2820 cases, respectively. This indicates that the data set used for training the classification method was equally populated, displaying a uniform probability distribution. Having a balanced training sample is important for our experiment since it facilitates the training of the ML algorithm (enough observations from each class are available and biases can be effectively mitigated) and provides more opportunities for accuracy improvements (if no HF method is dominant, selecting between different HF methods becomes promising). The opposite is expected to be true for highly imbalanced data sets: Given a dominant HF method, even if the classifier is effectively trained, little room for improvements in terms of forecasting accuracy will be available.

The performance of the XGB classification method is presented in Table 4. According to the precision metric, XGB manages to select the COM methods more accurately but finds it difficult to make appropriate selections when the BU or TD method is preferable according to the MASE metric. This indicates that, although XGB identifies the conditions under which the COM method is preferable, the opposite is not true. We provide the details of confusion matrices in Appendix D.

Table 4 Performance of the XGB classification method

As a final step in our analysis, we investigate the significance of the time series features used by the XGB classifier, i.e. the number of times that each feature was considered by the method for making a prediction. We compute 32 features for each time series and select the top 5 of them when reconciling with different HF methods. Figure 8 presents the features that are most frequently selected by the classifier. As seen, the non-linearity at levels 1 and 2, stability at level 1, e-acf10 at level 1, and max-var-shift at level 0 are the most frequently used features and, therefore, the most critical variables for selecting a HF method. The distribution of these features vary for different selected HF methods. Non-linearity at levels 1 and 2 is among of the strongest features in our data set and stability at level 1 also plays an important role. We believe this is because promotions are frequently affecting the sales of the products strongly, thus changing the volatility of their demand both over promotional and non-promotional periods (Abolghasemi et al. 2020). Maximum variance shift at level 0 is another feature that is frequently selected. This may attribute to the sudden changes and spikes caused to sales data set by promotions. TD is selected for higher values of this metric followed by COM and BU. Finally, e-acf10, which contains the sum of squared values of the first 10 autocorrelation coefficient of the error terms of series at level 1, is also among the top selected features. One possible explanation is because sales are being affected by promotions and therefore depict high levels of variations during promotion periods. Therefore, even after fitting a forecasting model, there will still be some correlation in the remainder term.

Fig. 8

The five features most frequently used by the XGB classification method. The features are displayed for each HF method, i.e. when selected by the classifier for performing the reconciliation, separately

In order to shed more light on the importance of the time series characteristics in selecting a HF method, we investigated the performance of a LR classifier, which is a statistical and more interpretable classification model, and focused on the distributions of the estimated coefficients of the multinomial logistics. Figure 9 shows the boxplots of the estimated coefficients for the top 5 features of the series, as determined earlier by XGB. We consider the COM method as the reference group in the LR model and show two groups of boxplots including BU/COM and TD/COM coefficient ratios. Since the parameter estimates are relative to the reference group, the estimated values on the y-axis show how much the log-odds for the corresponding method is expected to change for a unit change in the time series characteristics if all the other characteristics in the model are held constant. For example, the odds of selecting BU over COM increase by less than 0.24% when maximum variance shift at level 0 (max-var-shift-L0) increases by one unit. Interestingly, when the stability at level 1 (stability.L1) increases by one unit, the odds of selecting BU over COM increase by more than 1%, on average. The results are different for selecting TD over COM. As we can see, the odds of selecting TD to COM increase the most when the sum of the first 10 auto-correlations at level 1 (e-acf-10.L1) increases by one unit.

Fig. 9

The coefficients of the top 5 features estimated by the LR classification method

We also trained a decision tree model with data for all series and hierarchies to visualise the selection process implemented by a single decision tree. We included the decision tree in Appendix D.

Note that when conducting this experiment we considered another training set-up for the classifiers where, apart from time series features, we also provided information about the correlation of the series, both across levels and within each level separately, similar to (Nenova and May, 2016). The results were similar to those reported in Table 3, and therefore we decided to exclude those features from our models for reasons of simplicity. In another experiment, we implemented the model of (Nenova and May, 2016) on our data set where we used series correlation instead of time series characteristics as input predictors. We report the details and results in Appendix E.

Another extension of the proposed approach that could be also examined in a future study is that it focuses on selecting the most appropriate hierarchical forecasting method per hierarchy. However, numerous empirical studies have shown that combining forecasts from multiple forecasting methods can improve forecasting accuracy (Makridakis et al., 2020; Lemke and Gabrys, 2010; Atiya, 2020). Thus, replacing classifiers with other methods that would combine various HF methods using appropriate weights becomes a promising alternative to CHF. Simple, equal-weighted combinations of standard HF methods have already been proven useful under some settings (Mircetic et al., 2021; Abouarghoub et al., 2018), while feature-based forecast model averaging has demonstrated its potential to generate robust and accurate forecasts (Montero-Manso et al., 2020).

6 Conclusion

This paper introduced conditional hierarchical forecasting, a dynamic approach for effectively selecting the most accurate method for reconciling incoherent hierarchical forecasts. Inspired by the work done in the area of forecasting model selection and the advances reported in the field of machine learning, the proposed approach computes various features for the time series of the examined hierarchy and relates their values to the forecasting accuracy achieved by different hierarchical forecasting methods, such as bottom-up, top-down, and combination methods, using an appropriate classification method. Based on the lessons learned, and depending on the characteristics of time series in the hierarchy, the most suitable hierarchical forecasting method can be chosen and used to enhance overall forecasting performance.

We exploited various time series features at different levels of the hierarchy that represent their behavior, and trained an extreme gradient boosting classification model to choose the most appropriate type of hierarchical forecasting method for a hierarchical time series with the selected features. The accuracy of the proposed approach was evaluated using a large data set coming from the retail industry and compared to that of three popular hierarchical forecasting methods. Our results indicate that conditional hierarchical forecasting can produce significantly more accurate forecasts than the benchmarks considered, especially at lower hierarchical levels. Thus, we suggest that, when dealing with hierarchical forecasting applications, selection should be expanded from forecasting model to reconciliation methods as well. We further validated our approach by experimenting on two additional and diverse datasets including tourism and prison datasets. These datasets have different properties and confirm our findings that the best reconciliation method can be selected as per time series characteristics and structure of the hierarchy. These factors may also impact the performance of a classifier.

Undoubtedly, our study displays some limitations that are worth investigating in future endeavors. The forecasting performance of the conditional hierarchical forecasting algorithm depends on the classification performance of the models used for its implementation and the data used for their training. For instance, if the training data set available is highly imbalanced, i.e. one hierarchical forecasting method is dominant over others, this can diminish the performance of the classification models. The class-imbalance in the training set can be more severe if we consider a larger number of hierarchical forecasting methods, thus making the multi-class classification task more challenging. Developing an algorithm that can deal with these issues within the proposed framework could help improve further the overall performance of the proposed method. Another avenue for future research that seems a natural extension to our study is to use features of the hierarchy, e.g. correlations between series, number of levels, and number of series, as alternative inputs for selecting the most appropriate reconciliation method.

Appendices

Appendix A: CHF Algorithm

The CHF algorithm, presented in detail in Sect. 3, is summarised below.

Appendix B: Time series characteristics used in this study

In this appendix, we provide a brief explanation of the time series features considered in the present study for developing the classification models used within the CHF approach. Our list is inspired by recent studies that have successfully used time series features to develop meta-learning forecasting algorithms (e.g. for model selection and combination, Montero-Manso et al., 2020), being tailored however for the particular requirements of the conditional hierarchical forecasting task.

• 1. Entropy: Measures the “forecastability” of a time series. Lower values of entropy suggest higher signal to noise ratios that make a series easier to forecast (Garland et al., 2014; Goerg , 2013; Liu et al., 2016). Entropy is calculated as shown in Eq. (3),

  $$\begin{aligned} \text {entropy}= - \int _{-\pi }^{\pi } {\hat{f}}(\lambda ) \log ({\hat{f}}(\lambda )) d\lambda , \end{aligned}$$

  (3)

  where ${\hat{f}}(\lambda )$ is the spectral density of the data, describing the strength of a time series as a function of frequency $\lambda$.

• 2. Lumpiness: Measures the variance of the variances of non-overlapping windows in a series.

• 3. Stability: Measures the variance of the mean of non-overlapping windows in a series.

• 4. Hurst: Measures the long-term memory of a time series. Hurst is equal to 0.5 plus the maximum likelihood estimate of the fractional differencing order d, where d is the degree of first differencing after fitting an autoregressive fractionally integrated moving average model to the time series.

• 5. Seasonal-period: Indicates the number of seasonal periods of a series. If a series is not seasonal, the metric takes a value of 1.

• 6. Easonal-strength: Time series depict seasonality when they exhibit a pattern that is repetitive and it is caused by seasonal factors. As such, time series with a fixed seasonality will display significant autocorrelation at fixed seasonal lags. Suppose that $S_t$, $T_t$, and $E_t$ represent the seasonality, trend, and error components of a time series Y so that $Y_t=S_t+T_t+e_t$. Based on this assumption, we can detrend $X_t=Y_t - T_t$ and deseasonlize a time series $Z_t=Y_t - S_t$. Similarly, we can subtract the trend and seasonality from the series to compute the remainder (error term) of the underlying decomposition approach, $e_t=Y_t - T_t - S_t$. The strength of seasonality can then be computed as in Eq. (4).

  $$\begin{aligned} \text {Seasonality strength}&= 1 - \frac{{\text {Var}}(e_t)}{{\text {Var}}(X_t)} \end{aligned}$$

  (4)

• 7. Trend: Trend indicates a long-term change in the mean of a time series. We measure the strength of the trend using Eq. (5).

  $$\begin{aligned} \text {Trend strength}&= 1 - \frac{{\text {Var}}(e_t)}{{\text {Var}}(Z_t)} \end{aligned}$$

  (5)

• 8. Curvature: Measures the curvature of a time series. The measure is calculated based on the coefficients of an orthogonal quadratic regression.

• 9. e-acf1: Measures the first autocorrelation coefficient after calculating the autocorrelation of the remainder of series, $e_t$.

• 10. e-acf10: It is the sum of the squares of the first ten autocorrelation coefficients after calculating the autocorrelation of the remainder of series, $e_t$.

• 11. x-acf1: Measures the first order autocorrelation of the series.

• 12. x-acf10: It is the sum of the squares of the first ten autocorrelation coefficients of the series.

• 13. diff1-acf1: Measures the first order autocorrelation of the differenced series.

• 14. diff1-acf10: It is the sum of the squares of the first ten autocorrelation coefficients of the differenced series.

• 15. diff2-acf1: Measures the first order autocorrelation of the twice differenced series.

• 16. diff2-acf10: It is the sum of the squares of the first ten autocorrelation coefficients of the twice differenced series.

• 17. seas-acf1: Measures the autocorrelation of the seasonality component of the series.

• 18. x-pacf5: It is the sum of the squares of the first five partial autocorrelation coefficients of the series.

• 19. diff1x-pacf5: It is the sum of the squares of the first five partial autocorrelation coefficients of the differenced series.

• 20. diff2x-pacf5: It is the sum of the squares of the first five partial autocorrelation coefficients of the twice differenced series.

• 21. seas-pacf: Measures the partial autocorrelation of the seasonality component of the series.

• 22. Linearity: Measures the linearity of a time series. It is calculated based on the coefficients of an orthogonal quadratic regression.

• 23. Non-linearity: Measures the non-linearity of a time series. It is calculated using a modified version of the Teräsvirta’s non-linearity test as described in (Hyndman et al. , 2019).

• 24. max-var-shift: Measures the largest variance shift between to consecutive windows in a time series.

• 25. max-kl-shift: Measures the largest Kulback-Leibler divergence between to consecutive windows in a time series.

• 26. fluctanal-prop-r1: Measures the fluctuation of a series. It fits a polynomial of order 1 and then returns the range.

• 27. unitroot-kpss: A time series is stationary if its mean, variance, and autocovariance do not depend on time. We use Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tests to check whether the time series is stationary or not. KPSS test uses a null hypothesis that an observable time series is stationary against the alternative of a unit root (Kwiatkowski et al., 1992).

• 28. arch-acf: It is the sum of squares of the first 12 autocorrelation values of a pre-whitened time series.

• 29. garch-acf: It is the sum of squares of the first 12 autocorrelation values of the residuals after fitting a GARCH(1,1) model to a pre-whitened time series.

• 30. arch-r2: It is the $R^2$ value of an AR model applied to a pre-whitened time series.

• 31. garch-r2: It is the $R^2$ value of an AR model applied to the residuals after fitting a GARCH(1,1) model to a pre-whitened time series.

• 32. arch-test: Measures autoregressive conditional heteroscedasticity (ARCH). This value is the $R^2$ value of an autoregressive model of order specified as lags applied to $x^2$.

Appendix C: Forecasting performance of CHF when additional data sets, optimization criteria, and classification methods are considered

In this appendix we summarize the forecasting performance of the three baseline HF methods (BU, TD, and COM) considered in the present study in terms of MASE and RMSSE, as well as the proposed CHF one when LR, LDA, DT, RF, SVM, XGB, or NN classification models are used for its implementation. We do so in order to provide more evidence regarding the impact of the classification method used within the proposed approach. Moreover, the results are presented for four different optimization criteria depending on the particular objective of the classification task, i.e., which forecasts should be considered as “optimal”. Specifically, we train the classifiers so that the reconciled forecasts produced by the CHF method are optimal in terms of the accuracy measured at (i) level 0, (ii) level 1, (iii) level 2, or (iv) all levels (average performance across levels 0, 1, and 2). We perform such an analysis since, depending on the decisions the forecasts opt to support, different cross-sectional levels may be more relevant, meaning that CHF should be flexible enough to be adapted accordingly.

In addition to the Sales data set presented in the main part of the paper, we consider two more data sets, namely the Prison and the Tourism ones Hyndman and Athanasopoulos (2021). By doing so we provide more empirical evidence regarding the effectiveness of the proposed method when hierarchies of different structures, series of different frequencies, lengths, and characteristics, or forecasting horizons are considered. In both cases, the base forecasts were produced using ExponenTial Smoothing (ETS, Hyndman, 2002), as implemented in the forecast package for Hyndman 2020a.

LR and LDA were implemented using the nnet and MASS packages for R, respectively [nnetR,MASSr]. DT was implemented using rpart for R [rpartR], using a complexity parameter of 0.01. RF was implemented using the randomForest package for R Liaw and Wiener (2002). We set the number of trees equal to 150 and optimized the rest of its hyper-parameters using a grid search in a 5-fold cross-validation fashion. The minimization of the error rate was used as a loss function. The optimal number of nodes was selected between 2 and 10 with an interval of 1, while the minimum size of the terminal nodes was selected between 1 and 5 with an interval of 1 Probst et al. (2019). SVM was implemented using the kernlab package for R (Karatzoglou et al., 2004). We chose the Radial Basis kernel and optimized the cost of the constraint violation, C, using a grid search between 0 and 300 with a step of 10 and a 5-fold cross-validation. The minimization of the error rate was used as a loss function. NN was implemented using the nnet package for R [nnetR]. We considered 3 fully-connected hidden layers and a logistic activation function, leaving the rest of the hyper-parameters to the default values of the package as the size of the data sets available for training do not allow for extensive cross-validation.

1.1 Sales data set

This part of the appendix presents the results of the additional experiments conducted for the case of the 55 data sets of hierarchical sales series. Six different classification models are used in addition to XGB for implementing the CHF approach, while various levels of the hierarchy are used as targets for optimizing the results. Tables 5 and 6 summarize our findings in terms of MASE and RMSSE, respectively. The significance of the results is assessed using MCB tests, as shown in Figs. 10 and 11. Our results are in line with those of Table 3, suggesting that CHF can result in superior forecasts compared to well-established HF methods when XGB is used for performing the classification. Moreover, we find that, more often than not, CHF can effectively adapt to the objective of the optimization process, thus being tailored to accurately forecast series at different hierarchical levels of interest. In addition, our results indicate that selecting an appropriate classification method that has the capacity to learn how to optimally link numerous time series features with forecasting performance, is critical for effectively implementing CHF. Interestingly, none of the additional classification methods considered performed equally well with XGB, being also outperformed by COM in most of the cases.

Table 5 Forecasting performance of the HF methods examined in this study in terms of MASE for the Sales data set

Fig. 10

MCB tests conducted on the HF methods examined in this study for the Sales data set. The results are presented for each optimization criterion separately, i.e., when the labels of the classification models are determined so that the forecasts produced are optimal in terms of level 0, level 1, level 2, or the average of all levels. In all cases, MASE is used for computing the ranks and a 95% confidence level is considered

Table 6 Forecasting performance of the HF methods examined in this study in terms of RMSSE for the Sales data set

Fig. 11

MCB tests conducted on the HF methods examined in this study for the Sales data set. The results are presented for each optimization criterion separately, i.e., when the labels of the classification models are determined so that the forecasts produced are optimal in terms of level 0, level 1, level 2, or the average of all levels. In all cases, RMSSE is used for computing the ranks and a 95% confidence level is considered

In order to better interpret our results and justify the superiority of the forecasts provided by XGB over the rest of the classification models utilized in this study for implementing CHF, we investigated the performance of the classifiers by analysing their confusion matrices. Table 7 compares the predictions made by the classification models with the true labels when the HF methods are determined so that the forecasts produced are optimal in terms of MASE for different hierarchical levels. We observe that XGB has managed to classify correctly more instances when the optimisation focused at level 1 and the average of all levels, while DT is the top-performing model when the optimisation is focused at level 0 and level 2. However, DT has misclassified more series to TD and BU when COM was the superior model, which inevitably contributed to its inferior forecast accuracy, on average. Similar conclusions can be drawn when RMSSE is used for measuring forecasting performance since, as shown in Table 8, XGB displays the highest classification accuracy in all cases, except at level 1. Again, DT has classified more series correctly at level 1 but the inferior performance in misclassifying COM has contributed to its lower accuracy, on average.

Table 7 Confusion matrices of the classification models considered for forecasting the series of the Sales data set when the HF methods (labels) are determined so that the forecasts produced are optimal in terms of MASE at level 0, level 1, level 2, or the average of all levels

Table 8 Confusion matrices of the classification models considered for forecasting the series of the Sales data set when the HF methods (labels) are determined so that the forecasts produced are optimal in terms of RMSSE at level 0, level 1, level 2, or the average of all levels

Appendix D: Variables importance

Finally, we trained a DT classifier on all 55 hierarchies of the data set to investigate the explicit conditions under which a particular HF method is more likely to be preferred over other alternatives. Figure 12 presents the structure of the DT and the rules defined by the model for performing the classification. While this model differs in terms of training from those originally considered in our study, in the sense that it is trained across all hierarchical series and not for each hierarchy separately, it sheds light on the selection process performed by decision-tree-based classifiers. For example, we observe that when the series have higher values of correlation (x-acf10.L2$\ge$ 0.75), there is a richness of information at the bottom level and the bottom series are predictable, making BU is the most preferable HF method without necessarily using information from other levels. However, when the correlation at the bottom series is low but variance at the top level is high (NonLinearity.L2<0.75 & max-var-shift-L0 $\ge$ 1.6), then COM is the selected model. For smaller values of variance shift at the top level, TD, BU, and COM have been selected over 44%,19%, and 6% of the times, respectively. This indicates that when the variance shift at the top level is smaller and correlation at the bottom level is low, proportions will be a good representative to disaggregate them and the series at the top level is helpful for predicting those at the lower levels, enabling TD to perform better on average.

Fig. 12

Decision tree of the trained DT classification model across all series and hierarchies

2.1 Prison data set

The Prison data set consists of 25 quarterly series, organized at three hierarchical levels (total, state, gender) and spanning over q1-2005 to q4-2016 (48 periods). Given that the series are relatively short but a reasonable amount of observations is required both for effectively training the baseline forecasting models and precisely computing the time series features, we start producing base forecasts after the 6^th year and use the following 16 periods for creating the labels of the classifiers in a rolling origin fashion considering one-step-ahead forecasts. We generate one-step-ahead forecasts to maximise the number of observations for training the ML classification models. Finally, the last 8 periods of data are used for evaluating the performance of the examined HF methods. Note that the set used for training the classifiers is highly imbalanced for most of the optimization criteria considered, with COM being the dominant HF method (COM is optimal at levels 1 and 2 in about 80% of the cases, while BU in the remaining 20%). The only exception is level 0 where BU and TD are the dominant HF approaches and similarly populated to each other (BU and TD are optimal at level 0 in about 40% of the cases each).

The results of the Prison data set are presented in Table 9, with their statistical significance being assessed in Fig. 13 using MCB tests. We should clarify that since the forecasts produced in this experiment refer to a single period, MASE and RMSSE results are identical. As seen, although the differences reported between the baseline HF methods and the CHF approaches are minor and, in most of the cases insignificant, the latter do manage to provide similar if not better ranks. Moreover, depending on the optimization criteria used, the CHF methods effectively select the most appropriate HF method per case, thus improving the forecasting accuracy accordingly. For instance, XGB-All displays the most accurate results on average, XGB-L0 the best performance for level 0, DT-L1, XGB-L1, SVM-L1, NN-L1 the lowest forecast error for level 1, while DT-L2, XGB-L2, and NN-L2 the top accuracy for level 2. We also find that, similar to the Sales data set, XGB is generally more effective in completing the required classification tasks, outperforming on average the rest of the CHF methods. These results are justified by the confusion matrices of Table 10. We observe that XGB is the most precise classification model at level 0 and the average of all levels (75% accuracy), performing also similar to DT and NN at levels 1 and 2 (87.5%).

Table 9 Forecasting performance of the HF methods examined in this study in terms of MASE/RMSSE for the Prison data set

Fig. 13

MCB tests conducted on the HF methods examined in this study for the Prison data set. The results are presented for each optimization criterion separately, i.e., when the labels of the classification models are determined so that the forecasts produced are optimal in terms of level 0, level 1, level 2, or the average of all levels. In all cases, MASE/RMSSE is used for computing the ranks and a 95% confidence level is considered

Table 10 Confusion matrices of the classification models considered for forecasting the series of the Prison data set when the HF methods (labels) are determined so that the forecasts produced are optimal in terms of MASE/RMSSE at level 0, level 1, level 2, or the average of all levels

2.2 Tourism data set

The Tourism data set is quarterly and spans over q1-1998 to q4-2017 (80 periods). We start producing base forecasts after the 6^th year and use the following 36 periods for creating the labels of the classifiers in a rolling origin fashion considering two-step-ahead forecasts. We considered six years of data, i.e., 24 observations as the training set to provide enough observations to train the baseline forecasting model and considered two-step-ahead rolling forecasts to generate enough observations for the ML training data set. Note that two-step-ahead forecasts is often enough in practice for short term planning in the tourism industry. Moreover, since the selected horizon is larger than the one considered in the Prison data set, this setup allows us to further evaluate the performance of the CHF approach when longer forecast periods are considered. The last 20 periods of data are used for evaluating the performance of the examined HF methods. Similar to the Prison data set, the set used for training the classifiers is imbalanced, with COM being the dominant HF method for levels 1 and 2 (COM is optimal at levels 1 and 2 in about 75% of the cases, while BU in the remaining 25%), while TD for level 0 (TD is optimal at level 0 in about 60% of the cases, while BU and COM in 20% each).

The results of the Tourism data set are presented in Tables 11 and 12, with their statistical significance being assessed in Figs. 14 and 15, respectively. As seen, the relative ranks of the HF methods examined are in agreement according to both accuracy measures used. Moreover, CHF approaches always result in significantly better average ranks than BU, being also better than TD at levels 2, 1, and the average of all levels. Therefore, we conclude that even when the differences between the proposed HF method and the baseline ones are small, CHF manages to effectively select the reconciliation method that best matches the needs of the examined forecasting task. These results can be verified by the exceptional classification performance of the classifiers considered, summarized in Tables 13 and 14. We observe that XGB and RF report an accuracy of 90% or higher across all the hierarchical levels examined, with the rest of the models achieving also comparable results in most of the cases.

Table 11 Forecasting performance of the HF methods examined in this study in terms of MASE for the Tourism data set

Fig. 14

MCB tests conducted on the HF methods examined in this study for the Tourism data set. The results are presented for each optimization criterion separately, i.e., when the labels of the classification models are determined so that the forecasts produced are optimal in terms of level 0, level 1, level 2, or the average of all levels. In all cases, MASE is used for computing the ranks and a 95% confidence level is considered

Table 12 Forecasting performance of the HF methods examined in this study in terms of RMSSE for the Tourism data set

Fig. 15

MCB tests conducted on the HF methods examined in this study for the Tourism data set. The results are presented for each optimization criterion separately, i.e., when the labels of the classification models are determined so that the forecasts produced are optimal in terms of level 0, level 1, level 2, or the average of all levels. In all cases, RMSSE is used for computing the ranks and a 95% confidence level is considered

Table 13 Confusion matrices of the classification models considered for forecasting the series of the Tourism data set when the HF methods (labels) are determined so that the forecasts produced are optimal in terms of MASE at level 0, level 1, level 2, or the average of all levels

Table 14 Confusion matrices of the classification models considered for forecasting the series of the Tourism data set when the HF methods (labels) are determined so that the forecasts produced are optimal in terms of RMSSE at level 0, level 1, level 2, or the average of all levels

Appendix E: Computational time

In order to evaluate the performance of CHF in terms of computational requirements, we recorded the computational times required to (i) execute the HF methods considered in our study for reconciling the base forecasts, (ii) execute the classification models utilized for determining the optimal HF method, and (iii) estimate the time series features exploited by the classifiers. Table 15 summarizes our findings for the case of the Sales data set as it is the largest in size from the examined ones (55 hierarchies $\times$ 9 rolling origin evaluations = 495 instances) and can therefore provide more representative results. The times reported refer to the seconds elapsed on average for forecasting a complete hierarchy and were computed using a system of the following characteristics: MacBook Pro, 2.7 GHz Dual-Core Intel Core i5 processor, and 8 GB 1867 MHz DDR3 Memory RAM.

As seen, COM is the most computationally intensive HF method (6.35 s), followed by BU (5.17 s). On the other hand, as expected, TD is much faster, requiring less than 0.2 s to run. As a result, a traditional forecasting approach that does not exploit model selection and requires computing all three HF methods before identifying the best possible, would take a total of 11.68 ss to execute, on average. Regarding the classifiers, XGB, the most accurate classification model of our study, is executed in 0.25 seconds, while simpler classification models, such as LR and LDA, are executed even faster (0.11 and 0.06 s, respectively). Given that the computation of the time series features requires 4.13 s, the complete implementation of CHF takes on average between 4.35 and 10.82 s, depending on the complexity of the classification model used and the HF method selected. Thus, the proposed method can effectively reduce computational requirements from 7 to 63% compared to an approach where all three HF methods are used to reconcile the base forecasts, while at the same time significantly improving the overall forecasting accuracy.

We should highlight that the computational cost of CHF is mostly driven by the time required for producing the base forecasts and implementing the HF method of choice (computing the features and executing the classifier accounts for less than 40% of the computational time on average). As a result, the computational savings of the proposed approach can grow further when more sophisticated methods are used for producing the base forecasts or when hierarchies that consist of more levels or series are being forecast.

Table 15 Computational time (seconds) required to run the experiment for the Sales data set

Appendix F: Benchmarking CHF against similar approaches

In order to evaluate the performance of CHF against other approaches that employ classifications models to determine the optimal HF method, we implemented the approach described in Nenova and May (2016) as, according to Table 1, it is the closest work in the literature to our study. Nenova and May (2016) (from now on called N & M) conducted an experiment on 104 two-level hierarchical series for various products. They used rank predictors, the correlation of the series of the bottom level, and a combination of them as input variables to select the most appropriate HF method from BU and three variations of TD, as implemented in the hts package for Hyndman et al. (2020b). They did so in two different paradigms, i.e., by using a four label classification model to directly select the most appropriate HF method, and by using a two-stage approach where they first determined whether BU or TD should be used and then selected the best TD variant, if needed. They used LR, LDA, DT, SVM, and C5.0 classification models to select the optimal HF method. They reported the results only for the models where they used time series correlations as predictors and found that LDA provided the most accurate forecasts. We replicated the N & M approach and implemented it on the Sales data set since it is the primary data set considered in the present study. We used correlation predictors at the bottom level and included their expectation, minimum value, maximum value, and variance as additional leading indicators. We only implemented the direct, multi-label classification approach of N & M since, in our study, we use TD, BU, and COM as the potential HF methods, meaning that the two-stage classification approach of N & M is not applicable in our settings. Although N & M did not employ the COM method, we believe it is important to include it in the evaluation as the results of several empirical studies have shown that COM is often a top-performing HF method in various settings (Hyndman et al., 2011; Abolghasemi et al., 2019; Spiliotis et al., 2020). Moreover, by doing so, we can directly compare the results of the CHF approach to that of N & M by using time series correlations as predictors rather than time series characteristics. Table 16 summarizes the performance of the N & M approach when employed for the Sales data set. Our results indicate that CHF outperforms the N & M method across all hierarchical levels regardless of the classification technique used. This finding suggests that time series features may be more useful than time series correlations for identifying the most suitable HF method.

Table 16 Forecasting performance of the Nenova and May (2016) (N & M) approach for the Sales data set over the method proposed in the present study (CHF).