Abstract
Learning from interpretation transition (LFIT) automatically constructs a model of the dynamics of a system from the observation of its state transitions. So far the systems that LFIT handled were mainly restricted to synchronous deterministic dynamics. However, other dynamics exist in the field of logical modeling, in particular the asynchronous semantics which is widely used to model biological systems. In this paper, we propose a modeling of discrete memory-less multi-valued dynamic systems as logic programs in which a rule represents what can occur rather than what will occur. This modeling allows us to represent non-determinism and to propose an extension of LFIT to learn regardless of the update schemes, allowing to capture a large range of semantics. We also propose a second algorithm which is able to learn a whole system dynamics, including its semantics, in the form of a single propositional logic program with constraints. We show through theoretical results the correctness of our approaches. Practical evaluation is performed on benchmarks from biological literature.
Similar content being viewed by others
1 Introduction
Learning the dynamics of systems with many interactive components becomes more and more important in many applications such as physics, cellular automata, biochemical systems as well as engineering and artificial intelligence systems. In artificial intelligence systems, knowledge like action rules is employed by agents and robots for planning and scheduling. In biology, learning the dynamics of biological systems corresponds to the identification of influence of genes, signals, proteins and molecules that can help biologists to understand their interactions and biological evolution.
In modeling of dynamical systems, the notion of concurrency and non-determinism is crucial. When modeling a biological regulatory network, it is necessary to represent the respective evolution of each component of the system. One of the most debated issues with regard to semantics targets the choice of a proper update mode of every component, that is, synchronous (Kauffman, 1969), asynchronous (Thomas, 1991) or more complex ones. The differences and common features of different semantics w.r.t. properties of interest (attractors, oscillators, etc.) have thus resulted in an area of research per itself (Inoue, 2011; Naldi et al., 2018; Chatain et al., 2020). But the biologists often have no idea whether a model of their system of interest should intrinsically be synchronous, asynchronous, generalized, or another semantics. It thus appears crucial to find ways to model systems from raw data without burdening the modelers with an a priori choice of the proper semantics.
For a decade, learning dynamics of systems has raised a growing interest in the field of inductive logic programming (ILP) (Muggleton et al., 2012; Cropper et al., 2020). ILP is a form of logic-based machine learning where the goal is to induce a hypothesis (a logic program) that generalises given training examples and background knowledge. Whereas most machine learning approaches learn functions, ILP frameworks learn relations.
In the specific context of learning dynamical systems, previous works proposed an ILP framework entitled learning from interpretation transition (LFIT) (Inoue et al. 2014) to automatically construct a model of the dynamics of a system from the observation of its state transitions. Figure 1 shows this learning process. Given some raw data, like time-series data of gene expression, a discretization of those data in the form of state transitions is assumed. From those state transitions, according to the semantics of the system dynamics, several inference algorithms modeling the system as a logic program have been proposed. The semantics of a system’s dynamics can indeed differ with regard to the synchronism of its variables, the determinism of its evolution and the influence of its history. The LFIT framework (Inoue et al., 2014; Ribeiro & Inoue, 2015; Ribeiro et al., 2018) proposed several modeling and learning algorithms to tackle those different semantics.
In Inoue (2011), Inoue and Sakama (2012), state transitions systems are represented with logic programs, in which the state of the world is represented by a Herbrand interpretation and the dynamics that rule the environment changes are represented by a logic program P. The rules in P specify the next state of the world as a Herbrand interpretation through the immediate consequence operator (also called the TP operator) (Van Emden & Kowalski, 1976; Apt et al., 1988) which mostly corresponds to the synchronous semantics we present in Sect. 3. In this paper, we extend upon this formalism to model multi-valued variables and any memory-less discrete dynamic semantics including synchronous, asynchronous and general semantics.
Inoue et al. (2014) proposed the LFIT framework to learn logic programs from traces of interpretation transitions. The learning setting of this framework is as follows. We are given a set of pairs of Herbrand interpretations (I, J) as positive examples such that J = TP(I), and the goal is to induce a normal logic program (NLP) P that realizes the given transition relations. As far as we know, this concept of learning from interpretation transition (LFIT) has never been considered in the ILP literature before (Inoue et al. 2014).
To date, the following systems have been tackled: memory-less deterministic systems (Inoue et al., 2014), systems with memory (Ribeiro et al., 2015a), probabilistic systems (Martínez Martínez et al., 2015) and their multi-valued extensions (Ribeiro et al. 2015b; Martınez et al., 2016). Ribeiro et al. (2018) proposes a method that allows to deal with continuous time series data, the abstraction itself being learned by the algorithm. As a summary, the systems that LFIT handled so far were restricted to synchronous deterministic dynamics.
In this paper, we extend this framework to learn systems dynamics independently of its update semantics. For this purpose, we propose a modeling of discrete memory-less multi-valued systems as logic programs in which each rule represents that a variable possibly takes some value at the next state, extending the formalism introduced in Inoue et al. (2014), Ribeiro and Inoue (2015). Research in multi-valued logic programming has proceeded along three different directions (Kifer & Subrahmanian, 1992): bilattice-based logics (Fitting, 1991; Ginsberg, 1988), quantitative rule sets (Van Emden, 1986) and annotated logics (Blair & Subrahmanian, 1989, 1988). Our representation is based on annotated logics. Here, to each variable corresponds a domain of discrete values. In a rule, a literal is an atom annotated with one of these values. It allows us to represent annotated atoms simply as classical atoms and thus to remain at a propositional level. This modeling allows us to characterize optimal programs independently of the update semantics, allowing to model the dynamics of a wide range of discrete systems. To learn such semantic-free optimal programs, we propose GULA: the General Usage LFIT Algorithm. We show from theoretical results that this algorithm can learn under a wide range of update semantics including synchronous (deterministic or not), asynchronous and generalized semantics.
Ribeiro et al. (2018) proposed a first version of GULA that we substantially extend in this manuscript. In Ribeiro et al. (2018), there was no distinction between feature and target variables, i.e., variables at time step t and \(t+1\). From this consideration, interesting properties arise and allow to characterize the kind of semantics compatible with the learning process of the algorithm (Theorem 1). It also allows to represent constraints and to propose a new algorithm (Synchronizer, Sect. 5). We show through theoretical results that this second algorithm can learn a program able to reproduce any given set of discrete state transitions and thus the behavior of any discrete memory-less dynamical semantics.
Empirical evaluation provided in Ribeiro et al. (2018) was limited to scalability in complete observability cases. With the goal to process real data, we introduce a heuristic method allowing to use GULA to learn from partial observations and predict from unobserved data. It allows us to apply the method on more realistic cases by evaluating both scalability, prediction accuracy and explanation of prediction on partial data. Evaluation is performed over the three aforementioned semantics for Boolean network benchmarks from biological literature (Klarner et al., 2016; Dubrova & Teslenko, 2011). These experiments emphasize the practical usage of the approach: our implementation reveals to be tractable on systems up to a dozen components, which is sufficient enough to capture a large variety of complex dynamic behaviors in practice.
The organization of the paper is as follows. Section 2 provides a formalization of discrete memory-less dynamics system as multi-valued logic program. Section 3 formalizes dynamical semantics under logic programs. Section 4 presents the first algorithm, GULA, which learns optimal programs regardless of the semantics. Section 5 provides extension of the formalization and a second algorithm, the Synchronizer, to represent and learn the semantics behavior itself. In Sect. 6, we propose a heuristic method allowing to use GULA to learn from partial observations and predict from unobserved data. Section 7 provides experimental evaluations regarding scalability, prediction accuracy and explanation of predictions. Section 8 discusses related work and Sect. 9 concludes the paper. All proofs of theorems and propositions are given in “Appendix”.
2 Logical modeling of dynamical systems
In this section, the concepts necessary to understand the learning algorithms we propose are formalized. In Sect. 2.1, the basic notions of multi-valued logic (\({\mathcal {M}}\mathrm {V}\mathrm {L}\)) are presented. Then, Sect. 2.2 presents a modeling of dynamics systems using this formalism.
In the following, we denote by \({\mathbb {N}}:= \{ 0, 1, 2, \ldots \}\) the set of natural numbers, and for all \(k, n \in {\mathbb {N}}\), \(\llbracket k ; n \rrbracket := \{ i \in {\mathbb {N}}\mid k \le i \le n \}\) is the set of natural numbers between k and n included. For any set S, the cardinality of S is denoted \(|S|\) and the power set of S is denoted \(\wp (S)\).
2.1 Multi-valued logic program
Let \({\mathcal {V}}=\{\mathrm {v}_1,\cdots ,\mathrm {v}_n\}\) be a finite set of \(n \in {\mathbb {N}}\) variables, \({\mathcal {V}}al\) the set in which variables take their values and \({\mathsf {dom}}: {\mathcal {V}}\rightarrow \wp ({\mathcal {V}}al)\) a function associating a domain to each variable. The atoms of \({\mathcal {M}}\mathrm {V}\mathrm {L}\) are of the form \(\mathrm {v}^{{val}}\) where \(\mathrm {v}\in {\mathcal {V}}\) and \({val}\in {\mathsf {dom}}(\mathrm {v})\). The set of such atoms is denoted by \({\mathcal {A}}^{{\mathcal {V}}}_{\mathsf{dom}} = \{\mathrm {v}^{{val}}\in {\mathcal {V}}\times {\mathcal {V}}al\mid {val}\in {\mathsf {dom}}(\mathrm {v}) \}\) for a given set of variables \({\mathcal {V}}\) and a given domain function \({\mathsf {dom}}\). In the following, we work on specific \({\mathcal {V}}\) and \({\mathsf {dom}}\) that we omit to mention when the context makes no ambiguity, thus simply writing \({\mathcal {A}}\) for \({\mathcal {A}}^{{\mathcal {V}}}_{{\mathsf {dom}}}\).
Example 1
For a system of 3 variables, the typical set of variables is \({\mathcal {V}}= \{ a, b, c \}\). In general, \({\mathcal {V}}al= {\mathbb {N}}\) so that domains are sets of natural integers, for instance: \({\mathsf {dom}}(a) = \{ 0, 1 \}\), \({\mathsf {dom}}(b) = \{ 0, 1, 2 \}\) and \({\mathsf {dom}}(c) = \{ 0, 1, 2, 3 \}\). Thus, the set of all atoms is: \({\mathcal {A}}= \{ a^0, a^1, b^0, b^1, b^2, c^0, c^1, c^2, c^3 \}\).
A \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R is defined by:
where \(\forall i \in \llbracket 0 ; m \rrbracket , \mathrm {v}_{i}^{{val}_{i}} \in {\mathcal {A}}\) are atoms in \({\mathcal {M}}\mathrm {V}\mathrm {L}\) so that every variable is mentioned at most once in the right-hand part: \(\forall j,k \in \llbracket 1 ; m \rrbracket , j \ne k \Rightarrow \mathrm {v}_j \ne \mathrm {v}_k\). If \(m = 0\), the rule is denoted: \(\mathrm {v}_{0}^{{val}_{0}} \leftarrow \top\). Intuitively, the rule R has the following meaning: the variable \(\mathrm {v}_0\) can take the value \({val}_0\) in the next dynamical step if for each \(i \in \llbracket 1 ; m \rrbracket\), variable \(\mathrm {v}_i\) has value \({val}_i\) in the current dynamical step.
The atom on the left-hand side of the arrow is called the head of R and is denoted \({\text {head}}(R) := \mathrm {v}_{0}^{{val}_{0}}\). The notation \(\mathrm {var}({{\text {head}}({R})}) := \mathrm {v}_0\) denotes the variable that occurs in \({\text {head}}(R)\). The conjunction on the right-hand side of the arrow is called the body of R, written \({\text {body}}(R)\) and can be assimilated to the set \(\{\mathrm {v}_{1}^{{val}_{1}},\cdots,\mathrm {v}_{m}^{{val}_{m}}\}\); we thus use set operations such as \(\in\) and \(\cap\) on it, and we denote it \(\emptyset\) if it is empty. The notation \(\mathrm {var}({{\text {body}}({R})}) := \{ \mathrm {v}_1, \cdots , \mathrm {v}_m \}\) denotes the set of variables that occurs in \({\text {body}}(R)\). More generally, for all sets of atoms \(X \subseteq {\mathcal {A}}\), we denote \(\mathrm {var}({X}) := \{ \mathrm {v}\in {\mathcal {V}}\mid \exists {val}\in {\mathsf {dom}}(\mathrm {v}), \mathrm {v}^{{val}}\in X \}\) the set of variables appearing in the atoms of X. A multi-valued logic program (\({\mathcal {M}}{\mathrm {VLP}}\)) is a set of \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules.
Definition 1 introduces a domination relation between rules that defines a partial anti-symmetric ordering. Intuitively, rules with more general bodies dominate other rules. In our approach, we prefer a more general rule over a more specific one.
Definition 1
(Rule Domination) Let \(R_1\), \(R_2\) be two \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules. The rule \(R_1\) dominates \(R_2\), written \({R_1}\ge {R_2}\) if \({\text {head}}(R_1) = {\text {head}}(R_2)\) and \({\text {body}}(R_1)\subseteq {\text {body}}(R_2)\).
Example 2
Let \(R_1 := a^1 \leftarrow b^1\), \(R_2 := a^1 \leftarrow b^1 \wedge c^0\). \(R_1\) dominates \(R_2\) since \({\text {head}}(R_1) = {\text {head}}(R_2) = a^1\) and \({\text {body}}(R_1) \subseteq {\text {body}}(R_2)\). Intuitively, \(R_1\) is more general than \(R_2\) on c. \(R_2\) does not dominate \(R_1\) because \({\text {body}}(R_2) \not \subseteq {\text {body}}(R_1)\). Let \(R_3 := a^1 \leftarrow a^1 \wedge b^0\), \(R_1\) (resp. \(R_2\)) does not dominate \(R_3\) (and vice versa), since \({\text {body}}(R_1) \not \subseteq {\text {body}}(R_3)\): the rules have a different condition over b. Let \(R_4 := a^1 \leftarrow a^1\), for the same reasons, \(R_1\) (resp. \(R_2\)) does not dominate \(R_4\).
Let \(R_5 := a^0 \leftarrow \emptyset\), \(R_1\) (resp. \(R_2, R_3, R_4\)) does not dominate \(R_5\) (and vice versa) since their head atoms are different (\(a^1 \ne a^0\)).
The most general body for a rule is the empty set (also denoted \(\top\)). A rule with an empty body dominates all rules with the same head atom. Furthermore, the only way two rules dominate each over is that they are the same rule, as stated by Lemma 1.
Lemma 1
(Double Domination Is Equality) Let \(R_1, R_2\) be two \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules. If \({R_1}\ge {R_2}\) and \({R_2}\ge {R_1}\) then \(R_1=R_2\).
2.2 Dynamic multi-valued logic program
We are interested in modeling non-deterministic (in a broad sense, which includes deterministic) discrete memory-less dynamical systems. In such a system, the next state is decided according to dynamics that depend on the current state of the system. From a modeling perspective, the variables of the system at time step t can be seen as target variables and the same variables at time step \(t-1\) as features variables. Furthermore, additional variables that are external to the system, like stimuli or observation variables for example, can appear only as feature or target variables.
Such a system can be represented by a \({\mathcal {M}}{\mathrm {VLP}}\) with some restrictions. First, the set of variables \({\mathcal {V}}\) is divided into two disjoint subsets: \({\mathcal {T}}\) (for targets) encoding system variables at time step t plus optional external variables like observation variables, and \({\mathcal {F}}\) (for features) encoding system variables at \(t-1\) and optional external variables like stimuli. It is thus possible that \(|{\mathcal {F}}| \ne |{\mathcal {T}}|\). Second, rules only have a conclusion at t and conditions at \(t-1\), i.e., only an atom of a variable of \({\mathcal {T}}\) can be a head and only atoms of variables in \({\mathcal {F}}\) can appear in a body. In the following, we also re-use the same notations as for the \({\mathcal {M}}\mathrm {V}\mathrm {L}\) of Sect. 2.1 such as \({\text {head}}(R)\), \({\text {body}}(R)\) and \(\mathrm {var}({{\text {head}}({R})})\).
Definition 2
(Dynamic \({\mathcal {M}}{\mathrm {VLP}}\)) Let \({\mathcal {T}}\subset {\mathcal {V}}\) and \({\mathcal {F}}\subset {\mathcal {V}}\) such that \({\mathcal {F}}= {\mathcal {V}}\setminus {\mathcal {T}}\). A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P is a \({\mathcal {M}}{\mathrm {VLP}}\) such that \(\forall R \in P, \mathrm {var}({{\text {head}}({R})}) \in {\mathcal {T}}\) and \(\forall \mathrm {v}^{{val}}\in {\text {body}}(R), \mathrm {v}\in {\mathcal {F}}\).
In the following, when there is no ambiguity, we suppose that \({\mathcal {F}}\), \({\mathcal {T}}\), \({\mathcal {V}}\) and \({\mathcal {A}}\) are already defined and we omit to define them again.
Example 3
Figure 2 gives an example of regulation network with three elements a, b and c. The information of this network is not complete; notably, the relative “force” of the components a and b on the component c is not explicit. Multiple dynamics are then possible on this network, among which four possibilities are given below by Program 1 to 4, defined on \({\mathcal {T}}:= \{a_{t}, b_{t}, c_{t}\}\), \({\mathcal {F}}:= \{a_{t-1}, b_{t-1}, c_{t-1}\}\) and \(\forall \mathrm {v}\in {\mathcal {T}}\cup {\mathcal {F}}, {\mathsf {dom}}(\mathrm {v}) := \{ 0, 1 \}\).
Example of interaction graph of a regulation network representing an incoherent feed-forward loop (Kaplan et al., 2008) where a positively influences b and c, while b (and thus, indirectly, a) negatively influences c
Program 1 is a direct translation of the relations of the regulation network. It only contains rules producing atoms with value 1 which is equivalent to a set of Boolean functions. In Program 2, a always takes value 1 while in Program 3 it always takes value 0, a having no incoming influence in the regulation network this can represent some kind of default behavior. In Program 3, the two red rules introduce potential non-determinism in the dynamics since both conditions can hold at the same time. In Program 4, the rule apply the conditions of the regulation network but it also allows each variable to keep the value 1 at t if it has it at \(t-1\) and no inhibition occurs. We insist on the fact that the index notation t or \(t-1\) is part of the variable name, not its value. This allows to distinguish variables from \({\mathcal {T}}\) (t) or \({\mathcal {F}}\) (\(t-1\)).

The dynamical system we want to learn the rules of is represented by a succession of states as formally given by Definition 3. We also define the “compatibility” of a rule with a state in Definition 4 and with a transition in Definition 5.
Definition 3
(Discrete state) A discrete state s on \({\mathcal {T}}\) (resp. \({\mathcal {F}}\)) of a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) is a function from \({\mathcal {T}}\) (resp. \({\mathcal {F}}\)) to \({\mathbb {N}}\), i.e., it associates an integer value to each variable in \({\mathcal {T}}\) (resp. \({\mathcal {F}}\)). It can be equivalently represented by the set of atoms \(\{ \mathrm {v}^{s(\mathrm {v})} \mid \mathrm {v}\in {\mathcal {T}}{ (resp.\ {\mathcal {F}})} \}\) and thus we can use classical set operations on it. We write \({\mathcal {S}}^{{\mathcal {T}}}\) (resp. \({\mathcal {S}}^{{\mathcal {F}}}\)) to denote the set of all discrete states of \({\mathcal {T}}\) (resp. \({\mathcal {F}}\)), and a couple of states \((s,s^{\prime}) \in {\mathcal {S}}^{\mathcal {F}}\times {\mathcal {S}}^{\mathcal {T}}\) is called a transition.
When there is no possible ambiguity, we sometimes (Figs. 3, 5, \(\ldots\)) denote a state only by the values of variables, without naming the variables. In this case, the variables are given in alphabetical order (a, b, \(c\ldots\)). For instance, \(\{a^0,b^1\}\) is denoted \(\fbox {01}\), \(\{a^1,b^0\}\) is denoted \(\fbox {10}\) and \(\{a^0,b^1,c^0,d^3\}\) is denoted \(\fbox {0103}\).
Example 4
Consider a dynamical system having two internal variables a and b, an external stimilus st and an observation variable ch used to trace some important events. The two sets of possible discrete states of a program defined on the two sets of variables \({\mathcal {T}}= \{a_{t}, b_{t}, ch\}\) and \({\mathcal {F}}= \{a_{t-1}, b_{t-1}, st\}\), and the set of atoms \({\mathcal {A}}= \{a^0_{t},a^1_{t},b^0_{t},b^1_{t},b^2_{t},ch^0,ch^1, a^0_{t-1},a^1_{t-1},b^0_{t-1},b^1_{t-1},b^2_{t-1},st^0,st^1\}\) are:
Here, \(a_{t-1}\) and \(a_{t}\) (resp. \(b_{t-1}\) and \(b_{t}\)) are theoretically different variables from a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) perspective. But they actually encode the same variable at different time step and thus a (resp. b) is present in both \({\mathcal {F}}\) and \({\mathcal {T}}\) in its corresponding timed form.
On the other hand, variables st and ch are respectively a stimuli and an observation variable and thus only appear in \({\mathcal {F}}, {\mathcal {S}}^{{\mathcal {F}}}\) or \({\mathcal {T}}, {\mathcal {S}}^{{\mathcal {T}}}\). Depending on the number of stimuli and observation variables, states of \({\mathcal {S}}^{{\mathcal {F}}}\) can have a different size than states in \({\mathcal {S}}^{{\mathcal {T}}}\) (see Fig. 4).
Definition 4
(Rule-state matching) Let \(s \in {\mathcal {S}}^{{\mathcal {F}}}\). The \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R matches s, written \(R\sqcap s\), if \({\text {body}}(R) \subseteq s\).
We note that this definition of matching only concerns feature variables. Target variables are never meant to be matched.
Example 5
Let \({\mathcal {F}}= \{a_{t-1},b_{t-1},st\}\), \({\mathcal {T}}= \{a_{t},b_{t},ch\}\) and \(dom(a_{t-1})\) \(=\) dom(st) \(=\) \(dom(a_{t}) = dom(ch)=\{0,1\}, dom(b_{t-1}) = dom(b_{t}) = \{0,1,2\}\). The rule \(ch^0 \leftarrow a^1_{t-1} \wedge b^1_{t-1} \wedge st^1\) only matches the state \(\{a^1_{t-1},b^1_{t-1},st^1\}\). The rule \(ch^0 \leftarrow a^0_{t-1} \wedge st^1\) matches \(\{a^0_{t-1},b^0_{t-1},st^1\}\), \(\{a^0_{t-1},b^1_{t-1},st^1\}\) and \(\{a^0_{t-1},b^2_{t-1},st^1\}\). The rule \(b^2_{t} \leftarrow a^1_{t-1}\) matches \(\{a^1_{t-1},b^0_{t-1},st^0\}\), \(\{a^1_{t-1},b^0_{t-1},st^1\}\), \(\{a^1_{t-1},b^1_{t-1},st^0\}\), \(\{a^1_{t-1},b^1_{t-1},st^1\}\), \(\{a^1_{t-1},b^2_{t-1},st^0\}\), \(\{a^1_{t-1},b^2_{t-1},st^1\}\). The rule \(a^1 \leftarrow \emptyset\) matches all states of \({\mathcal {S}}^{{\mathcal {F}}}\).
The final program we want to learn should both:
-
match the observations in a complete (all transitions are learned) and correct (no spurious transition) way;
-
represent only minimal necessary interactions (according to Occam’s razor: no overly-complex bodies of rules)
The following definitions formalize these desired properties. In Definition 5 we characterize the fact that a rule of a program is useful to describe the dynamics of one variable in a transition; this notion is then extended to a program and a set of transitions, under the condition that there exists such a rule for each variable and each transition. A conflict (Definition 6) arises when a rule describes a change that is not featured in the considered set of transitions.
Finally, Definitions 8 and 7 give the characteristics of a complete (the whole dynamics is covered) and consistent (without conflict) program.
Definition 5
(Rule and program realization) Let R be a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule and \((s,s^{\prime})\in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The rule R realizes the transition \((s,s^{\prime})\), written \(s\xrightarrow {R}s^{\prime}\), if \(R\sqcap s \wedge {\text {head}}(R) \in s^{\prime}\).
A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P realizes \((s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), written \(s\xrightarrow {P}s^{\prime}\), if \(\forall \mathrm {v}\in {\mathcal {T}}, \exists R \in P, \mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\wedge s\xrightarrow {R}s^{\prime}\). It realizes a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), written \(\mathop{\hookrightarrow}\limits^{P }{T}\), if \(\forall (s,s^{\prime}) \in T, s\xrightarrow {P}s^{\prime}\).
Example 6
The rule \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^1_{t-1}\) realizes the transition \(t = (\{a^1_{t-1},b^1_{t-1},\) \(c^0_{t-1}\}\), \(\{a^0_{t},b^1_{t},c^1_{t}\})\) since it matches the first state of t and its conclusion is in the second state. However, the rule \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\) does not realize t since it does not match the feature state of t.
Example 7
The transition \(t = (\{a^1_{t-1},b^1_{t-1}, c^0_{t-1}\}\), \(\{a^0_{t},b^1_{t},c^1_{t}\})\) is realized by Program 3 of Example 3, by using the rules \(a^0_{t} \leftarrow \emptyset\), \(b^1_{t} \leftarrow a^1_{t-1}\) and \(c^1_{t} \leftarrow a^1_{t-1}\). However, Program 2 of the same Example does not realize t since the only rule that could produce \(c^1_{t}\), that is, \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\), does not match \(\{a^1_{t-1},b^1_{t-1}, c^0_{t-1}\}\); moreover, no rule can produce \(a^0_{t}\). Programs 1 and 4 of the same Example cannot produce \(a^0_{t}\) either and thus do not realize t.
In the following, for all sets of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), we denote: \(\mathrm {first}(T) := \{ s \in {\mathcal {S}}^{{\mathcal {F}}}\mid \exists (s_1, s_2) \in T, s_1 = s \}\) the set of all initial states of these transitions. We note that \(\mathrm {first}(T) = \emptyset \iff T = \emptyset\).
Definition 6
(Conflict and Consistency) A \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R conflicts with a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) when \(\exists s \in \mathrm {first}(T), \big ( R \sqcap s \wedge \forall (s, s^{\prime}) \in T, {\text {head}}(R) \notin s^{\prime} \big )\). R is said to be consistent with T when R does not conflict with T.
A rule is consistent if for all initial states of the transitions of T (\(\mathrm {first}\)(T)) matched by the rule, there exists a transitions of T for which it verifies the conclusion.
Definition 7
(Consistent program) A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P is consistent with a set of transitions T if P does not contain any rule R conflicting with T.
Example 8
Let \(s1 = \{a^1_{t-1},b^0_{t-1},c^0_{t-1}\}, s2 = \{a^1_{t-1},b^0_{t-1}, c^1_{t-1}\}, s3 = \{a^0_{t-1},b^0_{t-1},\) \(c^0_{t-1}\}\) and
Let \(T = \{t1, t2, t3, t4, t5\}\).
Program 1 of Example 3 is consistent with T. The rule \(b^1_{t} \leftarrow a^1_{t-1}\) matches s1 and both s1 and \(b^1_{t}\) are observed in t2. The rule also matches s2 which is observed with \(b^1_{t}\) in t3. The rule \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\) matches s1 (resp. s2), which is observed with \(c^1_{t}\) in t1 (resp. t3).
Program 2 is not consistent with T since \(a^1_{t} \leftarrow \emptyset\) is not consistent with T: it matches s1, s2 and s3 but the transitions of T that include s2 (t3, t4) do not contain \(a^1_{t}\). Program 3 is not consistent with T since \(a^0_{t} \leftarrow \emptyset\) matches s1, s2, s3 but the only transition that contains s3 (t5) does not contain \(a^0_{t}\). Program 4 is not consistent with T since \(a^1_{t} \leftarrow a^1_{t-1}\) matches s2 but the transitions of T that include s2 (t3, t4) do not contain \(a^1_{t}\).
Definition 8
(Complete program) A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P is complete if \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall \mathrm {v}\in {\mathcal {T}}, \exists R \in P, R \sqcap s \wedge \mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\).
A complete \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) realizes at least one transition for each possible initial state.
Example 9
Program 1 of Example 3 is not complete since it does not have any rule over target variable \(a_t\), in fact it does not realize any transitions. Program 2 of same example is complete:
-
The rule \(a^1_{t} \leftarrow \emptyset\) will realize \(a^1_{t}\) from any feature state;
-
For \(b_t\) it has a first (resp. second) rule that matches all feature state where \(a^0_{t-1}\) (resp. \(a^1_{t-1}\)) appears and the domain of \(a_{t-1}\) being \(\{0,1\}\) all cases and thus all feature states are covered by this two rules;
-
For \(c_t\), all combinations of values of a and b are covered by the three last rules, \(\forall {val}\in {\mathsf {dom}}(c_{t-1}),\)
-
\(\{a^0_{t-1}, b^0_{t-1}, c^{{val}}_{t-1}\}\) is matched by \(c_t^{0} \leftarrow a^0_{t-1}\);
-
\(\{a^0_{t-1}, b^1_{t-1}, c^{{val}}_{t-1}\}\) is matched by \(c_t^{0} \leftarrow b^1_{t-1}\) (and \(c_t^{0} \leftarrow b^1_{t-1}\));
-
\(\{a^1_{t-1}, b^0_{t-1}, c^{{val}}_{t-1}\}\) is matched by \(c_t^{0} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\);
-
\(\{a^1_{t-1}, b^1_{t-1}, c^{{val}}_{t-1}\}\) is matched by \(c_t^{0} \leftarrow b^1_{t-1}\).
-
Program 3 is also complete, and it even realizes multiple values for \(c_t\) when both \(a^1_{t-1}\) and \(b^1_{t-1}\) are in a feature state: \(\{a^1_{t-1}, b^1_{t-1}, c^0_{t-1}\}\) is matched by both \(c_t^{0} \leftarrow b^1_{t-1}\) and \(c_t^{1} \leftarrow a^1_{t-1}\). Program 4 is not complete: no transition is realized when \(a^0_{t-1}\) is in a feature state since the only rule of \(a_t\) is \(a_t^{1} \leftarrow a^1_{t-1}\).
Definition 9 groups all the properties that we want the learned program to have: suitability and optimality, and Proposition 1 states that the optimal program of a set of transitions is unique.
Definition 9
(Suitable and optimal program) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) Pis suitable for T when:
-
P is consistent with T,
-
P realizes T,
-
P is complete,
-
For any possible \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R consistent with T, there exists \(R^{\prime}\in P\) such that \({R^{\prime}}\ge {R}\).
If in addition, for all \(R\in P\), all the \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules \(R^{\prime}\) belonging to \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for T are such that \({R^{\prime}}\ge {R}\) implies \({R}\ge {R^{\prime}}\) then P is called optimal.
Note that Definition 9 ensures local minimality regarding the ordering \(\ge\) (see Definition 1). In terms of biological models, it is more interesting to focus on local minimality, thus simple but numerous rules, modeling local influences from which the complexity of the whole system arises, than global minimality that would produce system-level rules hiding the local correlations and influences. Definition 9 also guarantees that we obtain all the minimal rules which guarantees to provide biological collaborators with the whole set of possible explanations of biological phenomena involved in the system of interest.
Proposition 1
(Uniqueness of Optimal Program) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) optimal for T is unique and denoted \(P_{{\mathcal {O}}}({T})\).
Example 10
Program 1 and 4 of Example 3 are not complete (see Example 9) and thus not suitable for T. Program 3 is complete but not consistent with T (see Example 8). Program 2 is complete, consistent and realizes T but is not suitable for T: indeed, \(c^1_{t} \leftarrow a^1_{t-1}\) is consistent with T and there is no rule in Program 2 that dominates it.
Let us consider:
P is complete, consistent, realizes T and all rules consistent with T are dominated by a rule of P. Thus, P is suitable for T. But P is not optimal since \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\) is dominated by \(c^1_{t} \leftarrow a^1_{t-1}\). By removing \(c^1_{t} \leftarrow a^1_{t-1} \wedge b^0_{t-1}\) from P, we obtain the optimal program of T.
According to Definition 9, we can obtain the optimal program by a trivial brute force enumeration algorithm: generate all rules consistent with T then remove the dominated ones as shown in Algorithm 1.

The purpose of Sect. 4 is to propose a non-trivial approach that is more efficient in practice to obtain the optimal program. This approach also respects the optimality properties of Definition 9 and thus ensures independence from the dynamical semantics, that are detailed in next Section.
3 Dynamical semantics
The aim of this section is to formalize the general notion of dynamical semantics as an update policy based on a program, and to give characterizations of several widespread existing semantics used on discrete models.
In the previous section, we supposed the existence of two distinct sets of variables \({\mathcal {F}}\) and \({\mathcal {T}}\) that represent conditions (features) and conclusions (targets) of rules. Conclusion atoms allow to create one or several new state(s) made of target variables, from conditions on the current state which is made of feature atoms.
In Definition 10, we formalize the notion of dynamical semantics which is a function that, to a program, associates a set of transitions where each state has at least one outgoing transition. Such a set of transitions can also be seen as a function that maps any state to a non-empty set of states, regarded as possible dynamical branchings. We give examples of semantics afterwards.
Definition 10
(Dynamical Semantics)
A dynamical semantics (on \({\mathcal {A}}\)) is a function that associates, to each \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P, a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) so that: \(\mathrm {first}(T) = {\mathcal {S}}^{{\mathcal {F}}}\). Equivalently, a dynamical semantics can be seen as a function of \(\big ( {\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\rightarrow ({\mathcal {S}}^{{\mathcal {F}}}\rightarrow \wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \})\big )\) where \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) is the set of \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)s.
A dynamical semantics has an infinity of possibility to produce transitions from a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\). Indeed, like \(DS_1(P)\) of Example 11, a semantics can totally ignore the \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) rules. It can also use the rule in an adversary way like \(DS_{inverse}\) that keeps only the transitions that are not permitted by the program. Such semantics can produce transitions that are not consistent with the input program, i.e., the rules which conclusions were not selected for the transition will be in conflict with the set of transitions from this feature state. The kind of semantics we are interested in are the ones that properly use the rule of the \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and ensure the properties of consistency introduced in Definition 7.
In Example 11, the dynamical semantics \(DS_{syn}\), \(DS_{asyn}\) and \(DS_{gen}\) are example of such semantics. They are trivial forms of the synchronous, asynchronous and general semantics that are widely used in bioinformatics. Indeed, \(DS_{syn}\) is trivial because it generates transitions towards an arbitrary state when the program P is not complete (if no rule matches for some target variable, the program produces an incomplete state), while \(DS_{asyn}\) and \(DS_{gen}\) are trivial because they require feature and target variables to correspond and have a specific form (labelled with \(t-1\) and t) with no additional stimuli or observation variables. We formalize those three semantics properly under our modeling in next Section with no restriction on the feature and target variables forms.
Example 11
For this example, suppose that feature and target variable are “symmetrical” (called regular variables later): \({\mathcal {T}}= \{a_{t}, b_{t}, \ldots , z_{t}\}\) and \({\mathcal {F}}= \{a_{t-1}, b_{t-1}, \ldots , z_{t-1}\}\), with: \(\forall x_t, x_{t-1} \in {\mathcal {T}}\times {\mathcal {F}}, {\mathsf {dom}}(x_t) = {\mathsf {dom}}(x_{t-1})\). Let convert be a function of \(({\mathcal {S}}^{{\mathcal {F}}}\rightarrow {\mathcal {S}}^{{\mathcal {T}}})\) such that for any \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \(P, \forall s \in {\mathcal {S}}^{{\mathcal {F}}}, convert(s) = \{\mathrm {v}^{{val}}_t \mid \mathrm {v}^{{val}}_{t-1} \in s\}\), and \(s_0 \in {\mathcal {S}}^{{\mathcal {T}}}\) an arbitrary target state that is used to ensure that each of the following semantics produces at least one target state. Let \(DS_1\), \(DS_2\), \(DS_{syn}\), \(DS_{asyn}\), \(DS_{gen}\) and \(DS_{inverse}\) be dynamical semantics defined as follows, where P is a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and \(s \in {\mathcal {S}}^{{\mathcal {F}}}\):
-
\((DS_1(P))(s) = \{ s_0 \}\)
-
\((DS_2(P))(s) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq \{{\text {head}}(R) \mid R \in P, |{\text {body}}(R)| = 3\} \} \cup \{s_0\}\)
-
\((DS_{syn}(P))(s) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq \{{\text {head}}(R) \mid R \in P, {\text {body}}(R) \subseteq s\} \} \cup \{s_0\}\)
-
\((DS_{asyn}(P))(s) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq convert(s) \cup \{{\text {head}}(R) \mid R \in P,\) \({\text {body}}(R) \subseteq s\} \wedge |\{\mathrm {v}^{{val}}_{t} \in s^{\prime} \mid \mathrm {v}^{{val}}_{t-1} \in s\}| \in \{|{\mathcal {T}}|,|{\mathcal {T}}|-1\}\}\)
-
\((DS_{gen}(P))(s) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq convert(s) \cup \{{\text {head}}(R) \mid R \in P, {\text {body}}(R) \subseteq s\}\)
-
\((DS_{inverse}(P))(s) = ({\mathcal {S}}^{{\mathcal {T}}}\setminus (DS_{syn}(P))(s)) \cup \{s_0\}\)
\(DS_1\) always outputs transitions towards \(s_0\) and totally ignores the rules of the given program and thus can produce transitions that are not consistent with the input program. \(DS_2\) uses the rules of the \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) but in an improper way, as it always considers the conclusions of rules as long as they have exactly 3 conditions, whether they match the feature state or not. \(DS_{inverse}\) uses proper rules conclusions, but in order to contradict the program: it produces transitions so that the program is not consistent, plus a transition to \(s_0\) to ensure at least a transition.
\(DS_{syn}\) use the rules in the expected way, i.e., it checks if they match the considered feature state and applies their conclusion; it is a trivial form of synchronous semantics as properly introduced later in Definition 15. \(DS_{asyn}\) also uses the rules as expected: it uses the feature state to restrict the possible target states to at most one modification compared to the feature state; this is a trivial form of asynchronous semantics, as properly introduced later in Definition 16. \(DS_{gen}\) also uses the rules as expected: it mixes the current feature state with rules conclusions to produce a partially new target state; it is a trivial form of general semantics, as properly introduced later in Definition 17.
We now aim at characterizing a set of semantics of interest for the current work, as given in Theorem 1. Beforehand, Definition 11 allows to denote as \(\mathsf {Conclusions}(s, P)\) the set of heads of rules, in a program P, matching a state s, and Definition 12 introduces a notation \({B}\vert _{X}\) to consider only atoms in a set \(B \subseteq {\mathcal {A}}\) that have their variable in a set \(X \subseteq {\mathcal {V}}\). These two notations will be used in the next theorem and afterwards. In the following, we especially use the notation of Definition 12 with \({\mathcal {A}}\) (denoted \({{\mathcal {A}}}\vert _{X}\)) and on \(\mathsf {Conclusions}\) (denoted \({\mathsf {Conclusions}}\vert _{X}(s, P)\)).
Definition 11
(Program Conclusions) Let s in \({\mathcal {S}}^{{\mathcal {F}}}\) and P a \({\mathcal {M}}{\mathrm {VLP}}\). We denote: \(\mathsf {Conclusions}(s, P) := \{ {\text {head}}(R) \in {\mathcal {A}}\mid R \in P, R \sqcap s \}\) the set of conclusion atoms in state s for the program P.
Definition 12
(Restriction of a Set of Atoms) Let \(B \subseteq {\mathcal {A}}\) be a set of atoms, and \(X \subseteq {\mathcal {V}}\) be a set of variables. We denote: \({B}\vert _{X} = \{ \mathrm {v}^{{val}}\in B \mid \mathrm {v}\in X \}\) the set of atoms of B that have their variables in X. If B is instead a function that outputs a set of atoms, we note \({B}\vert _{X}(params)\) instead of \({\big (B(params)\big )}\vert _{X}\), where params is the sequence of parameters of B.
With Definition 13, we define semantics which for any \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) produce the same behavior using the corresponding optimal program, that is, any semantics DS such that for any \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \(P, DS(P) = DS(P_{{\mathcal {O}}}({DS(P)}))\). This kind of semantics is of particular interest since they are “stable” through learning, that is, learning the optimal program from the dynamics of a system that relies on such a semantics allows to exactly reproduce the observed behavior.
Definition 13
(Pseudo-idempotent Semantics) Let DS be a dynamical semantics. DS is said pseudo-idempotent if, for all P a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\):
Theorem 1 gives another characterisation of a semantics that also ensures that it is pseudo-idempotent, and that especially applies to the semantics we are interested in this paper and formally defined later: synchronous, asynchronous and general.
Such a semantics must produce new states based on the initial state s and the heads of matching rules of the given program \(\mathsf {Conclusions}(s, P)\), as stated by point (2).
Intuitively, the semantics must be defined according to an arbitrary function \(\mathsf {pick}\) that picks target states among \({\mathcal {S}}^{{\mathcal {T}}}\) considering observed feature atoms and potential target atoms (what was and what could be). When given the atoms of the target states it outputs, this function must output the same set of target states as stated by point (1), i.e., it must produce the same states given the program conclusion or given its decision over the program conclusion.
Moreover, \(P_{{\mathcal {O}}}({DS(P)})\) being consistent with DS(P), given a state \(s \in {\mathcal {S}}^{{\mathcal {F}}}\), \(\mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})) = \mathop {\bigcup }\limits _{{s^{\prime} \in DS(P)(s)}}s^{\prime}\), i.e., all the target atoms observed in a target state of DS(P)(s) must be the head of some rule that matches s in the optimal program. In other words, it must be given to the semantics to choose from when the program \(P_{{\mathcal {O}}}({DS(P)})\) is used with semantics DS.
Thus the semantics should produce the same states, when being given the atoms of all those next states as possibilities, as stated by point (1).
Those two conditions are sufficient to ensure that DS is pseudo-idempotent and thus carries “stability” through learning.
Theorem 1
(Characterisation of Pseudo-idempotent Semantics of Interest) Let DS be a dynamical semantics.
If, for all P a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), there exists \(\mathsf {pick}\in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({{\mathcal {A}}}\vert _{{\mathcal {T}}}) \rightarrow \wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \})\) so that:
-
(1)
\(\forall D \subseteq {{\mathcal {A}}}\vert _{{\mathcal {T}}}, \mathsf {pick}(s,\mathop {\bigcup }\limits _{{s^{\prime} \in \mathsf {pick}(s,D)}}s^{\prime}) = \mathsf {pick}(s,D)\), and
-
(2)
\(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \big (DS(P)\big )(s) = \mathsf {pick}(s,\mathsf {Conclusions}(s, P))\),
then DS is pseudo-idempotent.
Example 12
Let DS be a dynamical semantics, \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) be a feature state such that \(s = \{a^0_{t-1}, b^1_{t-1}, st^0\}\), P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) such that \(\mathsf {Conclusions}(P,s) = \{a^1_t, b^1_t, ch^0, ch^2\}\). In Fig. 3, from s and \(\mathsf {Conclusions}(P,s)\), DS produces three different target states, i.e., \((DS(P))(s) = \mathsf {pick}(s,\mathsf {Conclusions}(s,P)) = \{ \{a^0_t, b^1_t, ch^2\}, \{a^0_t, b^0_t, ch^2\}, \{a^1_t, b^0_t, ch^2\}\}\). Let \(D = \mathsf {Conclusions}(P,s)\), here, the set of occurring atoms in the states produced by \(\mathsf {pick}(s,D)\) is \(D^{\prime} = \mathop {\bigcup }\limits _{{s^{\prime} \in \mathsf {pick}(s,D)}} = \{\mathbf{a}^\mathbf{0} _\mathbf{t} , a^1_t, \mathbf{b}^\mathbf{0} _\mathbf{t} , b^1_t, ch^2\}\). In this example, the function \(\mathsf {pick}\) uses all target atoms of D except \(ch^0\) and introduces two additional atoms \(\mathbf{a}^\mathbf{0} _\mathbf{t}\), \(\mathbf{b}^\mathbf{0} _\mathbf{t}\), it also only produces 3 of the 4 possible target states composed of those atoms: this semantics does not allows \(a^1_t\) and \(b^1_t\) to appear together in transition from s. If we call the function \(\mathsf {pick}\) by replacing the program conclusions by the semantics conclusions we observe the same resulting states, i.e., \(\mathsf {pick}(s,D^{\prime}) = \mathsf {pick}(s,D)\). Given the target atoms selected by the semantics, it reproduces the same set of target states in this example; if the semantics has this behavior for any feature state s and any program P, it is pseudo-idempotent.
Up to this point, no link has been made between corresponding feature (in \({\mathcal {F}}\)) and target (in \({\mathcal {T}}\)) variables or atoms. In other words, the formal link between the two atoms \(\mathrm {v}_t^{{val}}\) and \(\mathrm {v}_{t-1}^{{val}}\) with the same value has not been made yet. This link, called projection, is established in Definition 14, under the only assumption that \({\mathsf {dom}}(\mathrm {v}_t) = {\mathsf {dom}}(\mathrm {v}_{t-1})\). It has two purposes:
-
When provided with a set of transitions, for instance by using a dynamical semantics, one can describe dynamical paths, that is, successions of next states, by using each next state to generate the equivalent initial state for the next transition;
-
Some dynamical semantics (such as the asynchronous one, see Definition 16) make use of the current state to build the next state, and as such need a way to convert target variables into feature variables.
However, such a projection cannot be defined on the whole sets of target (\({\mathcal {T}}\)) and feature (\({\mathcal {F}}\)) variables, but only on two subsets \({{\overline{{\mathcal {F}}}}}\subseteq {\mathcal {F}}\) and \({{\overline{{\mathcal {T}}}}}\subseteq {\mathcal {T}}\). Note that we require the projection to be a bijection, thus: \(|{{\overline{{\mathcal {F}}}}}| = |{{\overline{{\mathcal {T}}}}}|\). These subsets \({{\overline{{\mathcal {T}}}}}\) and \({{\overline{{\mathcal {F}}}}}\) contain variables that we call afterwards regular variables: they correspond to variables that have an equivalent in both the initial states (at \(t-1\)) and the next states (at t). Variables in \({\mathcal {F}}\setminus {{\overline{{\mathcal {F}}}}}\) can be considered as stimuli variables: they can only be observed in the previous state but we do not try to explain their next value in the current state; this is typically the case of external stimuli (sun, stress, nutriment\(\ldots\)) that are unpredictable when observing only the studied system. Variables in \({\mathcal {T}}\setminus {{\overline{{\mathcal {T}}}}}\) can be considered as observation variables: they are only observed in the present state as the result of the combination of other (regular and stimuli) variables; they can be of use to assess the occurrence of a specific configuration in the previous state but cannot be used to generate the next step. For the rest of this section, we suppose that \({{\overline{{\mathcal {F}}}}}\) and \({{\overline{{\mathcal {T}}}}}\) are given and that there exists such projection functions, as given by Definition 14. Figure 4 gives a representation of these sets of variables.
It is noteworthy that projections on states are not bijective, because of stimuli variables that have no equivalent in target variables, and observation variables that have no equivalent in feature variables (see Fig. 4). Therefore, the focus is often made on regular variables (in \({{\overline{{\mathcal {F}}}}}\) and \({{\overline{{\mathcal {T}}}}}\)). Especially, for any pair of states \((s, s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), having \(\mathsf {sp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(s^{\prime}) \subseteq s\), which is equivalent to \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq s^{\prime}\), means that the regular variables in s and their projection in \(s^{\prime}\) (or conversely) hold the same value, modulo the projection.
Definition 14
(Projections) A projection on variables is a bijective function \(\mathsf {vp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}: {{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}\) so that \({{\overline{{\mathcal {T}}}}}\subseteq {\mathcal {T}}\), \({{\overline{{\mathcal {F}}}}}\subseteq {\mathcal {F}}\), and: \(\forall \mathrm {v}\in {{\overline{{\mathcal {T}}}}}, {\mathsf {dom}}(\mathsf {vp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(\mathrm {v})) = {\mathsf {dom}}(\mathrm {v}).\)
The projection on atoms (based on \(\mathsf {vp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}\)) is the bijective function:
The inverse function of \(\mathsf {vp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}\) is denoted \(\mathsf {vp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}\) and the inverse function of \(\mathsf {ap}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}\) is denoted \(\mathsf {ap}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}\).
The projections on states (based on \(\mathsf {ap}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}\) and \(\mathsf {ap}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}\)) are the functions:
Example 13
In Example 12, there are three feature variables (\(a_{t-1}\), \(b_{t-1}\), st) and three target variables (\(a_{t}\), \(b_{t}\), ch). If we consider that the regular variables are \({{\overline{{\mathcal {T}}}}}= \{a_t, b_t\}\) and \({{\overline{{\mathcal {F}}}}}= \{a_{t-1}, b_{t-1}\}\), we can define the following (bijective) projection on variables: \(\mathsf {vp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}: \left\{ \begin{array}{lll} a_t \mapsto a_{t-1} \\ b_t \mapsto b_{t-1} \end{array}\right.\). Following Definition 14, we have, for instance:
-
\(\mathsf {ap}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(a_t^1) = a_{t-1}^1\),
-
\(\mathsf {ap}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(b_{t-1}^0) = b_{t}^0\),
-
\(\mathsf {sp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(\{a_t^0, b_t^0, ch^0\}) = \{a_{t-1}^0, b_{t-1}^0\}\), and
-
\(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(\{a_{t-1}^1, b_{t-1}^0, st^1\}) = \{a_t^1, b_t^0\}\).
3.1 Synchronous, asynchronous and general semantics
In the following, we present a formal definition and a characterization of three particular semantics that are widespread in the field of complex dynamical systems: synchronous, asynchronous and general.
Note that some points in these definitions are arbitrary and could be discussed depending on the modeling paradigm. For instance, the policy about rules R so that \(\exists s \in {\mathcal {S}}^{{\mathcal {F}}}, R \sqcap s \wedge \mathsf {ap}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}({\text {head}}(R)) \in s\), which model stability in the dynamics, could be to include them (such as in the synchronous and general semantics) or exclude them (such as in the asynchronous semantics) from the possible dynamics.
The modeling method presented so far in this paper is independent to the considered semantics as long as it respects Definition 10 and the capacity of the optimal program to reproduce the observed behavior is ensured as long as the semantics respects Theorem 1.
A Boolean network with two variables inhibiting each other (top). The corresponding synchronous, asynchronous and general dynamics are given as state-transition diagrams (middle). In these state-transition diagrams, each box with a label “xy” represents both the feature state \(\{a^x_{t-1}, b^y_{t-1}\}\) and the target state \(\{a^x_t, b^y_t\}\), and each arrow represents a possible transitions between states. The corresponding optimal \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) (bottom) contain comments (in grey) that explain sub-parts of the programs
Definition 15 introduces the synchronous semantics, consisting in updating all variables at once in each step in order to compute the next state. The value of each variable in the next state is taken amongst a “pool” of atoms containing all conclusions of rules that match the current state (using \(\mathsf {Conclusions}\)) and atoms produced by a “default function” d that is explained below. However, this is taken in a loose sense: as stated above, atoms that make a variable change its value are not prioritized over atoms that don’t. Furthermore, if several atoms on the same variable are provided in the pool (as conclusions of different rules or provided by the default function), then several transitions are possible, depending on which one is chosen. Thus, for a self-transition \((s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) with \(\mathsf {sp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(s^{\prime}) \subseteq s\) to occur, there needs to be, for each atom \(\mathrm {v}^{{val}}\in s^{\prime}\) so that \(\mathrm {v}\in {{\overline{{\mathcal {T}}}}}\), either a rule that matches s and whose head is \(\mathrm {v}^{{val}}\) or that the default function gives the value \(\mathrm {v}^{{val}}\).
Note however that such a loop is not necessarily a point attractor (that is, a state for which the only possible transition is the self-transition); it is only the case if all atoms in the pool are also in \(\mathsf {sp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(s)\).
As explained above, for a given state s and a given set of variables W, the function d provides a set of “default atoms” added to the pool of atoms used to build the next state, along with rules conclusions.
This function d, however, is not explicitly given; the only constraints are that:
-
d produces atoms at least for a provided set of variables W, specifically, the set of variables having no conclusion in a given state, which is necessary in the case of an incomplete program,
-
\(d(s,\emptyset )\) is a subset of d(s, W) for all W, as it intuitively represents a set of default atoms that are always available.
Note that \(d(s,\emptyset ) = \emptyset\) always respects these constraints and is thus always a possible value. In the case of a complete program, that is, a program providing conclusions for every variables in every state, d is always called with \(W = \emptyset\) and the other cases can thus be ignored. Another typical use for d is the case of a system with Boolean variables (i.e., such that \(\forall \mathrm {v}\in {\mathcal {V}}, {\mathsf {dom}}(\mathrm {v}) = \{ 0, 1 \}\)) where a program P is built by importing only the positive rules of the system, that is, only rules with atoms \(\mathrm {v}^1_t\) as heads. This may happen when importing a model from another formalism featuring only Boolean formulas, such as Boolean networks. In this case, d can be used to provide a default atom \(\mathrm {w}^0_t\) for all variables \(\mathrm {w}\) that do not appear in \(\mathsf {Conclusions}(s, P)\), thus reproducing the dynamics of the original system.
Definition 15
(Synchronous semantics) Let \(d \in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {T}}) \rightarrow \wp ({{\mathcal {A}}}\vert _{{\mathcal {T}}}))\), so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall W \subseteq {\mathcal {T}}, W \subseteq \mathrm {var}({d(s, W)}) \wedge d(s,\emptyset ) \subseteq d(s,W)\). The synchronous semantics \({\mathcal {T}}_{syn}\) is defined by:
Example 14
It is possible to reproduce classical Boolean network dynamics using the synchronous semantics (\({\mathcal {T}}_{syn}\)) with a well-chosen default function. Indeed, Boolean models are classically defined as a set of Boolean function providing conditions in which each variable becomes active, thus implying that all the other cases make them inactive. A straightforward translation of a Boolean model into a program is thus to encode the active state of a variable with state 1 and the inactive state with 0. If the Boolean functions are represented as disjunctive normal forms, the clauses can be considered as a set of Boolean atoms of the form \(\mathrm {v}\) or \(\lnot \mathrm {v}\). Each clause c of the DNF of a variable \(\mathrm {v}\) can directly be converted into a rule R such that, \({\text {head}}(R) = \mathrm {v}^1_t\) and \(\forall v^{\prime}_{t-1} \in {\mathcal {F}}\), \(\mathrm {v}^{\prime 1}_{t-1} \in {\text {body}}(R) \iff \mathrm {v}^{\prime} \in c\) and \(\mathrm {v}^{\prime 0}_{t-1} \in {\text {body}}(R) \iff (\lnot \mathrm {v}^{\prime}) \in c\). Finally, the following default function allows to force the variables back to 0 when the original Boolean function should not be true:
In Definition 16, we formalize the asynchronous semantics that imposes that no more than one regular variable can change its value in each transition. The observation variables are not counted since they have no equivalent in feature variables to be compared to. As for the previous synchronous semantics, we use here a “pool” of atoms, made of rules conclusions and default atoms, that may be used to build the next states. The default function d used here is inspired from the previous synchronous semantics, with an additional constraint: its result always contains the atoms of the initial state. Constrains are also added on the next state to limit to at most one regular variable change. Moreover, contrary to the synchronous semantics, the asynchronous semantics prioritizes the changes. Thus, for a self-transition \((s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) with \(\mathsf {sp}_{{{\overline{{\mathcal {T}}}}}\rightarrow {{\overline{{\mathcal {F}}}}}}(s^{\prime}) \subseteq s\) to occur, it is required that all atoms of regular variables in the pool are in \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)\): \({\mathsf {Conclusions}}\vert _{{{\overline{{\mathcal {T}}}}}}(s, P) \cup {d}\vert _{{{\overline{{\mathcal {T}}}}}}(s,{{\overline{{\mathcal {T}}}}}\setminus \mathrm {var}({\mathsf {Conclusions}(s, P)})) = \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)\), which here implies: \(|\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \setminus s^{\prime}| = 0\). This only happens when \((s,s^{\prime})\) is a point attractor, in the sense that all regular variables cannot change their value.
It is different from Example 11 where the asynchronous semantics is more permissive and allows self-loops in every state. The asynchronous semantics of Definition 16, although more complex, is more widespread in the bioinformatics community (Chatain et al., 2020; Fauré et al., 2006; Klarner et al., 2014; Thieffry & Thomas, 1995); the only difference are terminal states modeled instead as (terminal) self-transitions because all states must have a successor following our definition of semantics (see Definition 10).
Definition 16
(Asynchronous semantics) Let \(d \in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {T}}) \rightarrow \wp ({{\mathcal {A}}}\vert _{{\mathcal {T}}}))\), so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall W \subseteq {\mathcal {T}}, W \subseteq \mathrm {var}({d(s, W)}) \wedge \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq d(s,\emptyset ) \subseteq d(s,W)\). The asynchronous semantics \({\mathcal {T}}_{asyn}\) is defined by:
where the notations \({{\mathcal {A}}}\vert _{{\mathcal {T}}}\), \({\mathsf {Conclusions}}\vert _{{{\overline{{\mathcal {T}}}}}}\) and \({d}\vert _{{{\overline{{\mathcal {T}}}}}}\) come from Definition 12.
A typical mapping for d is: \(d : (s, W) \mapsto \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \cup O\), where O is a set of atoms on observation variables with arbitrary values, thus conserving the previous values for regular variables and ignoring the second argument.
In Definition 17, we formalize the general semantics as a more permissive version of the synchronous one: any subset of the variables can change their value in a transition. This semantics uses the same “pool” of atoms than the synchronous semantics containing conclusions of P and default atoms provided by d, and no constraint. However, as for the asynchronous semantics, the atoms of the initial state must always be featured as default atoms. Thus, a self-transition \((s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) with \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq s^{\prime}\) occurs for each state s because, intuitively, the empty set of variables can always be selected for update. However, as for the synchronous semantics, such a self-transition is a point attractor only if all atoms of regular variables in the “pool” are in \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)\).
Finally, we note that the general semantics contains the dynamics of both the synchronous and the asynchronous semantics, but also other dynamics not featured in these two other semantics.
Definition 17
(General semantics) Let \(d \in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {T}}) \rightarrow \wp ({{\mathcal {A}}}\vert _{{\mathcal {T}}}))\), so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall W \subseteq {\mathcal {T}}, W \subseteq \mathrm {var}({d(s, W)}) \wedge \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq d(s,\emptyset ) \subseteq d(s,W)\). The general semantics \({\mathcal {T}}_{gen}\) is defined by:
Figure 5 gives an example of the transitions corresponding to these three semantics on a simple Boolean network of two variables inhibiting each other. The corresponding optimal \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) is given below each transition graph. In this example, the three programs share the rules corresponding to the inhibitions: \(a^0_{t} \leftarrow b^1_{t-1}\) and \(a^1_{t} \leftarrow b^0_{t-1}\) model the inhibition of a by b, while \(b^0_{t} \leftarrow a^1_{t-1}\) and \(b^1_{t} \leftarrow a^0_{t-1}\) model the inhibition of b by a. However, generally speaking, there may not always exist such shared rules, for instance if the interactions they represent are somehow ignored by the semantics behavior.
Furthermore, in this example, we observe additional rules (w.r.t. the synchronous case) that appear in both the asynchronous and general semantics cases. Those rules capture the default behavior of both semantics, that is, the projection of the feature state as possible target atoms. Again, such rules may not appear generally speaking, because the dynamics of the system might combine with the dynamics semantics, thus possibly merging multiple rules into more general ones (for example, conservation rules becoming rules with an empty body).
Example 15
As for the synchronous semantics, it is possible to reproduce classical Boolean network dynamics using the asynchronous (\({\mathcal {T}}_{asyn}\)) and general semantics (\({\mathcal {T}}_{gen}\)) with the same encoding of rules, and a similar default function where the projection of the current state is added:
Finally, with Theorem 2, we state that the definitions and method developed in the previous section are independent of the chosen semantics as long as it respect Theorem 1.
Theorem 2
(Semantics-Free Correctness) Let P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\).
-
\({\mathcal {T}}_{syn}(P) = {\mathcal {T}}_{syn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{syn}(P)}))\),
-
\({\mathcal {T}}_{asyn}(P) = {\mathcal {T}}_{asyn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{asyn}(P)}))\),
-
\({\mathcal {T}}_{gen}(P) = {\mathcal {T}}_{gen}(P_{{\mathcal {O}}}({{\mathcal {T}}_{gen}(P)}))\).
The next section focuses on methods and algorithm to learn the optimal program.
4 GULA
In Algorithm 1 we presented a trivial algorithm to obtain the optimal program. In this section we present a more efficient algorithm based on inductive logic programming.
Until now, the LF1T algorithm (Inoue et al., 2014; Ribeiro & Inoue, 2015; Ribeiro et al., 2015b) only tackled the learning of synchronous deterministic programs. Using the formalism introduced in the previous sections, it can now be revised to learn systems from transitions produced from any semantics respecting Theorem 1 like the three semantics defined above. Furthermore, both deterministic and non-deterministic systems can now be learned.
4.1 Learning operations
This section focuses on the manipulation of programs for the learning process. Definition 18 and Definition 19 formalize the main atomic operations performed on a rule or a program by the learning algorithm, whose objective is to make minimal modifications to a given \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) in order to be consistent with a new set of transitions.
Definition 18
(Rule least specialization) Let R be a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule and \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) such that \(R \sqcap s\). The least specialization of R by s according to \({\mathcal {F}}\) and \({\mathcal {A}}\) is:
The least specialization \(L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) produces a set of rule which matches all states that R matches except s. Thus \(L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) realizes all transitions that R realizes except the ones starting from s. Note that \(\forall R \in P, R \sqcap s \wedge |{\text {body}}(R)| = |{\mathcal {F}}| \implies L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}) = \emptyset\), i.e., a rule R matching s cannot be modified to make it not match s
if its body already contains all feature variables, because nothing can be added in its body.
Example 16
Let \({\mathcal {F}}:= \{a_{t-1},b_{t-1},c_{t-1}\}\) and \({\mathsf {dom}}(a_{t-1}) := \{0,1\}, {\mathsf {dom}}(b_{t-1}) := \{0,1,2\}, {\mathsf {dom}}(c_{t-1}) := \{0,1,2,3\}\). We give below three examples of least specialization on different initial rules and states. These situations could very well happen in the learning of a same set of transitions, at different steps of the process. The added conditions are highlighted in bold.
For \(a^0_{t} \leftarrow \emptyset\), the rule having an empty body, all possible variable values (given by \({\mathsf {dom}}\)) not appearing in the given state are candidate for a new condition. For \(b^2_{t} \leftarrow b^1_{t-1}\), there is a condition on b in the body, therefore only conditions on a and c can be added. For \(c^3_{t} \leftarrow a^1_{t-1} \wedge c^3_{t-1}\), only conditions on b can be added. Finally we can consider a case like \(L_{\mathrm {spe}}(a^1_{t} \leftarrow a^0_{t-1} \wedge b^1_{t-1} \wedge c^2_{t-1}, \{a^0_{t-1}, b^1_{t-1}, c^2_{t-1}\}, {\mathcal {A}}, {\mathcal {F}}) = \emptyset\) where a condition already exists for each variable and thus no minimal specialization of the body can be produced, thus resulting in an empty set of rules.
Definition 19
(Program least revision) Let P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) and \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) such that \(\mathrm {first}(T) = \{s\}\). Let \(R_P:=\{ R \in P \mid \hbox {} R \hbox {conflicts with} T \}\). The least revision of P by T according to \({\mathcal {A}}\) and \({\mathcal {F}}\) is \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}}):=(P \setminus R_P) \cup \mathop {\bigcup }\limits _{{R \in R_P}}L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\).
Note that according to Definition 19, \(\mathrm {first}(T) = \{s\}\) implies that all transitions for T have s as initial state.
Example 17
Let \({\mathcal {F}}:= \{a_{t-1},b_{t-1},c_{t-1}\}\) and \({\mathsf {dom}}(a_{t-1}) := \{0,1\}, {\mathsf {dom}}(b_{t-1}) := \{0,1,2\}, {\mathsf {dom}}(c_{t-1}) := \{0,1,2,3\}\). Let T be as set of transitions and P a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) as follows.
Here, we have \(\mathrm {first}(T) = \{\{a^0_{t-1},b^1_{t-1},c^2_{t-1}\}\}\) and thus the least revision of Definition 19 can be applied on P. Moreover, \(R_P = \{ b^0_{t} \leftarrow b^1_{t-1}, c^0_{t} \leftarrow a^0_{t-1} \wedge b^1_{t-1} \wedge c^2_{t-1}, c^0_{t} \leftarrow c^2_{t-1} \}\); these rules are highlighted in bold in P. The least revision of P by T over \({\mathcal {A}}\) and \({\mathcal {F}}\), \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\), is obtained by removing the rules of \(R_P\) from P and adding their least specialization, added conditions are in bold in \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) and are detailed in Example 16, except for \(a^0_t \leftarrow \emptyset\) which does not need to be revised because it is consistent with T since \(a^0_{t}\) is observed in some target states.
Theorem 3 states properties on the least revision, in order to prove it suitable to be used in the learning algorithm.
Theorem 3
(Properties of Least Revision) Let R be a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule and \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) such that \(R \sqcap s\). Let \(S_R:=\{s^{\prime} \in {\mathcal {S}}^{{\mathcal {F}}}\mid R \sqcap s^{\prime}\}\) and \(S_{\mathrm {spe}}:=\{s^{\prime} \in {\mathcal {S}}^{{\mathcal {F}}}\mid \exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s^{\prime}\}\).
Let P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and \(T, T^{\prime }\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) such that \(|\mathrm {first}(T)| = 1 \wedge \mathrm {first}(T) \cap \mathrm {first}(T^{\prime }) = \emptyset\). The following results hold:
-
1.
\(S_{\mathrm {spe}}=S_R \setminus \{s\}\),
-
2.
\(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is consistent with T,
-
3.
\(\mathop{\hookrightarrow} \limits^{P}{T^{\prime }} \implies {\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T^{\prime }}}\),
-
4.
\(\mathop{\hookrightarrow}\limits^{P }{T} \implies {\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T}}\),
-
5.
P is complete \(\implies L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is complete.
The next properties are directly used in the learning algorithm. Proposition 2 gives an explicit definition of the optimal program for an empty set of transitions, which is the starting point of the algorithm. Proposition 3 gives a method to obtain the optimal program from any suitable program by simply removing the dominated rules; this means that the \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) optimal for a set of transitions can be obtained from any \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for the same set of transitions by removing all the dominated rules. Finally, in association with these two results, Theorem 4 gives a method to iteratively compute \(P_{{\mathcal {O}}}({T})\) for any \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), starting from \(P_{{\mathcal {O}}}({\emptyset })\).
Proposition 2
(Optimal Program of Empty Set) \(P_{{\mathcal {O}}}({\emptyset })=\{\mathrm {v}^{{val}}\leftarrow \emptyset \mid \mathrm {v}\in {\mathcal {T}}\wedge \mathrm {v}^{{val}}\in {{\mathcal {A}}}\vert _{{\mathcal {T}}}\}\).
Proposition 3
(From Suitable to Optimal) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). If P is a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for T, then \(P_{{\mathcal {O}}}({T})=\{R\in P\mid \forall R^{\prime}\in P,{R^{\prime}}\ge {R} \implies R^{\prime} = R\}\).
Theorem 4
(Least Revision and Suitability) Let \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) and \(T, T^{\prime }\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) such that \(|\mathrm {first}(T^{\prime })| = 1 \wedge \mathrm {first}(T) \cap \mathrm {first}(T^{\prime }) = \emptyset\). \(L_{\mathrm {rev}}(P_{{\mathcal {O}}}({T}),T^{\prime },{\mathcal {A}},{\mathcal {F}})\) is a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for \(T \cup T^{\prime }\).
4.2 Algorithm
In this section we present GULA: the General Usage LFIT Algorithm, a revision of the LF1T algorithm (Inoue et al., 2014; Ribeiro & Inoue, 2015) to capture a set of multi-valued dynamics that especially encompass the classical synchronous, asynchronous and general semantics dynamics. For this learning algorithm to operate, there is no restriction on the semantics. GULA learns the optimal program that, under the same semantics, is able to exactly reproduce a complete set of observations, if the semantics respect Theorem 1. Section 5 will be devoted to also learning the behaviors of the semantics itself, if it is unknown.
GULA learns a logic program from the observations of its state transitions. Given as input a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), GULA iteratively constructs a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) that models the dynamics of the observed system by applying the method formalized in the previous section as shown in Algorithm 2. The algorithm can be used for both learning possibility or impossibility depending of its parameter \(learning\_mode\). When learning possibility (\(learning\_mode\) = “possibility”), the algorithm will learn the optimal logic program \(P_{{\mathcal {O}}}({T})\) and this is what will be discussed in this section. The second mode is used in a heuristical approach to obtain predictive model from partial observation and will be discussed in later sections.

From the set of transitions T, GULA learns the conditions under which each \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime} \subseteq {\mathcal {A}}, \mathrm {v}\in {\mathcal {T}}^{\prime } \subseteq {\mathcal {T}}\) may appear in the next state.
The algorithm starts by computing the set of all negative examples of the appearance of \(\mathrm {v}^{{val}}\) in next state: all states such that \(\mathrm {v}\) never takes the value \({val}\) in the next state of a transition of T (Fig. 6). Those negative examples are then used during the following learning phase to iteratively learn the set of rules \(P_{{\mathcal {O}}}({T})\). The learning phase starts by initializing a set of rules \(P_{\mathrm {v}^{{val}}}\) to \(\{R \in P_{{\mathcal {O}}}({\emptyset }) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\} = \{\mathrm {v}^{{val}}\leftarrow \emptyset \}\).
Preprocessing of the general semantics state transitions of Fig. 5 (right) into positive/negative example of the occurence of each value of variable a in next state. In blue (resp. red) are positive (resp. negatives) examples of the occurence of \(a^0_t\) (left) and \(a^1_t\) (right) in next state (Color figure online)
\(P_{\mathrm {v}^{{val}}}\) is iteratively revised against each negative example neg in \(N\!eg_{\mathrm {v}^{{val}}}\). All rules \(R_m\) of \(P_{\mathrm {v}^{{val}}}\) that match neg have to be revised. In order for \(P_{\mathrm {v}^{{val}}}\) to remain optimal, the revision of each \(R_m\) must not match neg but still matches every other state that \(R_m\) matches.
To ensure that, the least specialization (see Definition 18) is used to revise each conflicting rule \(R_m\). For each variable of \({\mathcal {F}}^{\prime}\) so that \({\text {body}}(R_m)\) has no condition over it, a condition over another value than the one observed in state neg can be added. None of those revision match neg and all states matched by \(R_m\) are still matched by at least one of its revisions.
Each revised rule can be dominated by a rule in \(P_{\mathrm {v}^{{val}}}\) or another revised rules and thus dominance must be checked from both.
The non-dominated revised rules are then added to \(P_{\mathrm {v}^{{val}}}\).
Once \(P_{\mathrm {v}^{{val}}}\) has been revised against all negatives example of \(N\!eg_{\mathrm {v}^{{val}}}\), \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\). Finally, \(P_{\mathrm {v}^{{val}}}\) is added to P and the loop restarts with another atom. Once all values of each variable have been treated, the algorithm outputs P which is then equal to \(P_{{\mathcal {O}}}({T})\). More discussion of the implementation and detailed pseudocode are given in “Appendix”. The source code of the algorithm is available at https://github.com/Tony-sama/pylfit under GPL-3.0 License.
Example 18
Execution of GULA(\({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}}\)) on the synchronous state transitions of Fig. 5 (left):
-
\({\mathcal {F}}= \{a_{t-1}, b_{t-1}\}\),
-
\({\mathcal {T}}= \{a_t, b_t\}\),
-
\({\mathcal {A}}= \{a^0_{t-1}, b^0_{t-1}, a^1_{t-1}, b^1_{t-1}, a^0_{t}, b^0_{t}, a^1_{t}, b^1_{t}\}\)
-
\(T = \{\) \((\{a^0_{t-1}, b^0_{t-1}\}, \{a^1_{t}, b^1_{t}\}),\) \((\{a^0_{t-1}, b^1_{t-1}\}, \{a^0_{t}, b^1_{t}\}),\) \((\{a^1_{t-1}, b^0_{t-1}\}, \{a^1_{t}, b^0_{t}\}),\) \((\{a^1_{t-1}, b^1_{t-1}\}, \{a^0_{t}, b^0_{t}\})\) \(\}\)
Table 1 provides each \(N\!eg_{\mathrm {v}^{{val}}}\) (first column) and shows the iterative evolution of \(P_{\mathrm {v}^{{val}}}\) (last column) over each \(neg \in N\!eg_{\mathrm {v}^{{val}}}\) during the execution of GULA(\({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}}\)). Rules in red in \(P_{\mathrm {v}^{{val}}}\) of previous step match the current negative example neg and must be revised, while rules in blue in the last column dominate rules in blue produced by the least specialization (third column).
Example 19
Execution of GULA(\({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}}\)) on the asynchronous state transitions of Fig. 5 (middle):
-
\({\mathcal {F}}= \{a_{t-1}, b_{t-1}\}\),
-
\({\mathcal {T}}= \{a_t, b_t\}\),
-
\({\mathcal {A}}= \{a^0_{t-1}, b^0_{t-1}, a^1_{t-1}, b^1_{t-1}, a^0_{t}, b^0_{t}, a^1_{t}, b^1_{t}\}\)
-
\(T = \{\) \((\{a^0_{t-1}, b^0_{t-1}\}, \{a^0_{t}, b^1_{t}\}),\) \((\{a^0_{t-1}, b^0_{t-1}\}, \{a^1_{t}, b^0_{t}\}),\) \((\{a^0_{t-1}, b^1_{t-1}\}, \{a^0_{t}, b^1_{t}\}),\) \((\{a^1_{t-1}, b^0_{t-1}\}, \{a^1_{t}, b^0_{t}\}),\) \((\{a^1_{t-1}, b^1_{t-1}\}, \{a^0_{t}, b^0_{t}\})\) \((\{a^1_{t-1}, b^1_{t-1}\}, \{a^1_{t}, b^1_{t}\})\) \(\}\)
Table 2 provides each \(N\!eg_{\mathrm {v}^{{val}}}\) (first column) and shows the iterative evolution of \(P_{\mathrm {v}^{{val}}}\) (last column) over each \(neg \in N\!eg_{\mathrm {v}^{{val}}}\) during the execution of GULA(\({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}}\)). Rules in red in the last column (\(P_{\mathrm {v}^{{val}}}\)) match the current negative example neg and must be revised, while rules in blue in the last column dominate rules in blue produced by the least specialization (third column, next line). For the general semantics transitions of Fig. 5 (right), the additional transitions that are observed compared to the asynchronous case do not alter any \(N\!eg_{\mathrm {v}^{{val}}}\), thus the learning process is the same as in Table 2 resulting in the same output program.
Theorem 5 gives the properties of the algorithm: GULA terminates and GULA is sounds, complete and optimal w.r.t. its input, i.e., all and only non-dominated consistent rules appear in its output program which is the optimal program of its input.
Finally, Theorem 6 characterizes the algorithm time and memory complexities.
Theorem 5
(GULA Termination, Soundness, Completeness, Optimality) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\).
-
(1)
Any call to GULA on finite sets terminates,
-
(2)
GULA\(({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}})=P_{{\mathcal {O}}}({T})\),
-
(3)
\(\forall {\mathcal {A}}^{\prime} \subseteq {{\mathcal {A}}}\vert _{{\mathcal {T}}}, \mathbf{GULA}({\mathcal {A}}_{{\mathcal {F}}} \cup {\mathcal {A}}^{\prime},T,{\mathcal {F}},{\mathcal {T}}) = \{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) \in {\mathcal {A}}^{\prime}\}\).
Lemma 2
(Gula can learn from any pseudo-idempotent semantics) Let DS be a pseudo-idempotent semantics, then
Lemma 2 is trivially proven from Theorem 5 since for any dynamical semantics DS and any \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P, \(\mathbf{GULA}({\mathcal {A}},DS(P),{\mathcal {F}},{\mathcal {T}}) = P_{{\mathcal {O}}}({DS(P)})\).
Lemma 3
(Gula can learn from synchronous, asynchronous and general semantics)
-
\({\mathcal {T}}_{syn}(\mathbf{GULA}({\mathcal {A}},{\mathcal {T}}_{syn}(P),{\mathcal {F}},{\mathcal {T}})) = {\mathcal {T}}_{syn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{syn}(P)})) = {\mathcal {T}}_{syn}(P)\)
-
\({\mathcal {T}}_{asyn}(\mathbf{GULA}({\mathcal {A}},{\mathcal {T}}_{asyn}(P),{\mathcal {F}},{\mathcal {T}})) = {\mathcal {T}}_{asyn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{asyn}(P)})) = {\mathcal {T}}_{asyn}(P)\)
-
\({\mathcal {T}}_{gen}(\mathbf{GULA}({\mathcal {A}},{\mathcal {T}}_{gen}(P),{\mathcal {F}},{\mathcal {T}})) = {\mathcal {T}}_{gen}(P_{{\mathcal {O}}}({{\mathcal {T}}_{gen}(P)})) = {\mathcal {T}}_{gen}(P)\)
Lemma 3 is trivially proven from Theorem 2. Thus the algorithm can be used to learn from transitions produced from both synchronous, asynchronous and general semantics.
Theorem 6
(GULA Complexity) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) be a set of transitions, Let \(n := max(|{\mathcal {F}}|,|{\mathcal {T}}|)\) and \(d := \max (\{|{\mathsf {dom}}(\mathrm {v})|) \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\}\). The worst-case time complexity of GULA when learning from T belongs to \({\mathcal {O}}(|T|^2 + |T| \times (2n^4d^{2n+2} + 2n^3d^{n+1}))\) and its worst-case memory use belongs to \({\mathcal {O}}(d^{2n} + 2nd^{n+1} + nd^{n+2})\).
The worst case complexity of GULA is higher than the brute force enumeration of Algorithm 1. The complexity of brute force enumeration is bound by the operation of removing the dominated rules (\(O(nd^{2n+2})\)), that also appear in GULA. This operation is done once in the brute force enumeration with all consistent rules and multiple time (for each negative example) in GULA, also GULA can generate several time the same rule. But, in practice, GULA is expected to manage much less rules than the whole set of possibility at each step since it removes dominated rules of previous step, thus globally dealing with less rules than all possibility and ending being more efficient in practice. Its scalability is evaluated in Sect. 7 with brute force enumeration as baseline.
To use GULA for outputting predictions, we have to assume a semantics for the model. In the next section, we will exhibit an approach to avoid such a preliminary assumption and learn a whole system dynamics, including its semantics, in the form of a single propositional logic program.
5 Learning from any dynamical semantics using constraints
Any non-deterministic (and thus deterministic) discrete memory-less dynamical system can be represented by a \({\mathcal {M}}{\mathrm {VLP}}\) with some restrictions and a dedicated dynamical semantics. For this, programs must contain two types of rules: possibility rules which have conditions on variables at \(t-1\) and conclusion on one variable at t, same as for \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\); and constraint rules which have conditions on both t and \(t-1\) but no conclusion. In the following, we also re-use the same notations as for the \({\mathcal {M}}\mathrm {V}\mathrm {L}\) of Sect. 2.1 such as \({\text {head}}(R)\), \({\text {body}}(R)\) and \(\mathrm {var}({{\text {head}}({R})})\).
5.1 Constraints \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)
Definition 20
(Constrained \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)) Let \(P^{\prime}\) be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) on \({\mathcal {A}}^{{\mathcal {F}}\cup {\mathcal {T}}}_{{\mathsf {dom}}}\), \({\mathcal {F}}\) and \({\mathcal {T}}\) two sets of variables, and \(\varepsilon\) a special variable with \({\mathsf {dom}}(\varepsilon ) = \{0, 1\}\) so that \(\varepsilon \notin {\mathcal {T}}\cup {\mathcal {F}}\). A \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P is a \({\mathcal {M}}{\mathrm {VLP}}\) such that \(P = P^{\prime} \cup \{R \in {\mathcal {M}}\mathrm {V}\mathrm {L}\mid {\text {head}}(R) = \varepsilon ^1 \wedge \forall \mathrm {v}^{{val}}\in {\text {body}}(R), \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\}\). A \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R such that \({\text {head}}(R) = \varepsilon ^1\) and \(\forall \mathrm {v}^{{val}}\in {\text {body}}(R), \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\) is called a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) constraint.
Moreover, in the following we denote \({\mathcal {V}}= {\mathcal {F}}\cup {\mathcal {T}}\cup \{\varepsilon \}\). This \({\mathcal {V}}\) is different than the one of \(P^{\prime}\) (which is \({\mathcal {F}}\cup {\mathcal {T}}\), without the special variable \(\varepsilon\)). From now, a constraint C is denoted: \(\xleftarrow []{\bot }{\text {body}}(C)\).
Example 20
\(\xleftarrow []{\bot }a^0_t \wedge a^0_{t-1}\) is a constraint that can prevent a to take the value 0 in two successive states. \(\xleftarrow []{\bot }b^1_t \wedge d^2_t \wedge c^2_{t-1}\) is a constraint that can prevent to have both \(b^1\) and \(d^2\) in the next state if \(c^2\) appears in the initial state. \(\xleftarrow []{\bot }a^0_t \wedge b^0_{t}\) is a constraint with only conditions in \({\mathcal {T}}\), it prevents a and b to take value 0 at same time. \(\xleftarrow []{\bot }a^0_{t-1} \wedge b^0_{t-1}\) is a constraint with only conditions in \({\mathcal {F}}\), it prevents any transitions from a state where a and b have value 0, thus creating final states.
Definition 21
(Constraint-transition matching) Let \((s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The constraint C matches \((s,s^{\prime})\), written \(C\sqcap (s,s^{\prime})\), iff \({\text {body}}(C) \subseteq s \cup s^{\prime}\).
Using the notion of rule and constraint matching we can use a \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) to compute the next possible states. Definition 22 provides such a method based on synchronous semantics and constraints. Given a state, the set of possible next states is the Cartesian product of the conclusion of all matching rules and default atoms. Constraints rules are then used to discard states that would generate non-valid transitions.
Definition 22
(Synchronous constrained Semantics) The synchronous constrained semantics \({\mathcal {T}}_{syn-c}\) is defined by:
Figure 7 shows the dynamics of the Boolean network of Fig. 5 under three semantics which dynamics cannot be reproduced using synchronous, asynchronous or general semantics on a program learned using GULA. In the first example (left), either all Boolean functions are applied simultaneously or nothing occurs (self-transition using projection). In the second example (center), the Boolean functions are applied synchronously but there is also always a possibility for any variable to take value 0 in the next state. In the third example (right), either the Boolean functions are applied synchronously, or each variable value is reversed (0 into 1 and 1 into 0). The original transitions of each dynamics are in black and the additional non-valid transitions in red. Using the original black transitions as input, GULA learns programs which, under the synchronous semantics (Definition 15), would realize the original black transitions plus the non-valid red ones. The idea is to learn constraints that would prevent those non-valid transitions to occur so that the observed dynamics is exactly reproduced using the synchronous constrained semantics of Definition 22. The \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)s shown below each dynamics realize all original black transitions thanks to their rules and none of the red transitions thanks to their constraints.
States transitions diagrams corresponding to three semantics that do not respect Theorem 1 (in black) applied on the Boolean network of Fig. 5. Using the synchronous semantics on the optimal program of the black transitions will produce in addition the red ones. Below each diagram, a \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) that can reproduce the same behavior using synchronous constrained semantics (Color figure online)
Definition 23
(Conflict and Consistency of constraints)
The constraint C conflicts with a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) when \(\exists (s, s^{\prime}) \in T, C \sqcap (s,s^{\prime})\). C is said to be consistent with T when C does not conflict with T.
Therefore, a constraint is consistent if it does not match any transitions of T.
Definition 24
(Complete set of constraints)
A set of constraints SC is complete with a set of transitions T if \(\forall (s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}, (s,s^{\prime}) \not \in T \implies \exists C \in SC, C \sqcap (s,s^{\prime})\).
Definition 25 groups all the properties that we want the learned set of constraints to have: suitability and optimality, and Proposition 4 states that the optimal set of constraints of a set of transitions is unique.
Definition 25
(Suitable and optimal constraints) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). A set of \({\mathcal {M}}\mathrm {V}\mathrm {L}\) constraints SC is suitable for T when:
-
SC is consistent with T,
-
SC is complete with T,
-
for all constraints C not conflicting with T, there exists \(C^{\prime}\in P\) such that \({C^{\prime}}\ge {C}\).
If in addition, for all \(C\in SC\), all the constraint rules \(C^{\prime}\) belonging to a set of constraints suitable for T are such that \({C^{\prime}}\ge {C}\) implies \({C}\ge {C^{\prime}}\), then SC is called optimal.
Proposition 4
Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The optimal set of constraints for T is unique and denoted \(C_{{\mathcal {O}}}({T})\).
The subset of constraints of \(C_{{\mathcal {O}}}({T})\) that prevent transitions permitted by \(P_{{\mathcal {O}}}({T})\) but not observed in T from happening, or, in other terms, constraints that match transitions in \({\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}))) \setminus T\), is denoted \(C^{\prime}_{{\mathcal {O}}}({T})\) and given in Definition 26.
All constraints of \(C_{{\mathcal {O}}}({T})\) that are not in this set can never match a transition produced by \(P_{{\mathcal {O}}}({T})\) with \({\mathcal {T}}_{syn-c}\) and can thus be considered useless. Finally, Theorem 7 shows that any set of transitions T can be reproduced, using the synchronous constrained semantics of Definition 22 on the \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\).
Definition 26
(Useful Constraints) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\).
\(C^{\prime}_{{\mathcal {O}}}({T}) := \{C \in C_{{\mathcal {O}}}({T}) \mid \exists (s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}, C \sqcap (s,s^{\prime}) \wedge s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime}\}\).
Theorem 7
(Optimal \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and Constraints Correctness Under Synchronous Constrained Semantics) Let \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), it holds that \(T = {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T}))\).
5.2 Algorithm
In previous sections we presented a modified version of GULA: the General Usage LFIT Algorithm from Ribeiro et al. (2018), which takes as arguments a different set of variables for conditions and conclusions of rules. This modification allows to use this modified algorithm to learn constraints and thus \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\).
Algorithm 3 show the Synchronizer algorithm, which given a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) will output \(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\) using GULA and the properties introduced in the previous section. With the new version of GULA it is possible to encode meaning in the transitions we give as input to the algorithm. The constraints we want to learn are technically rules whose head is \(\epsilon ^1\) with conditions on both \({\mathcal {F}}\) and \({\mathcal {T}}\).
It is sufficient to make the union of the two states of each transition (Fig. 8) and feed it to GULA to make it learn such rules. Constraints should match when an impossible transition is generated by the rules of the optimal program of T. GULA learns from negative examples and negative examples of impossible transitions are just the possible transitions, thus the transitions observed in T. Using the set of transitions \(T^{\prime } := \{(s \cup s^{\prime}, \{\varepsilon ^0\}) \mid (s,s^{\prime}) \in T\}\) we can use GULA to learn such constraints with \(GULA({\mathcal {A}}\cup \{\varepsilon ^1\}, T^{\prime }, {\mathcal {F}}\cup {\mathcal {T}}, \{\varepsilon \})\). Note that \(\varepsilon\), from the algorithmic viewpoint, is just a dummy variable used to make every transition of \(T^{\prime }\) a negative example of \(\varepsilon ^1\) which will be the only head of the rule we will learn here. The program produced will contain a set of rules that match none of the initial states of \(T^{\prime }\) and thus none of the transitions of T but matches all other possible transitions according to GULA properties.
Preprocessing of the state transitions of Fig. 7 (left) into negative examples of the application of constraints
Their head being \(\varepsilon ^1\), those rules are actually constraints over T. Since all and only such minimal rules are output by this second call to GULA, it corresponds to \(C_{{\mathcal {O}}}({T})\), which prevents every transitions that are not in T to be produced using the constraint synchronous semantics. Finally, the non-essential constraints can be discarded following Definition 26 and finally \(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\) is output.
The source code of the algorithm is available at https://github.com/Tony-sama/pylfit under GPL-3.0 License.

Theorem 8
(Synchronizer Correctness) Given any set of transitions T,
Synchronizer(\({\mathcal {A}}\), T, \({\mathcal {F}}\), \({\mathcal {T}}\)) outputs \(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\).
From Theorems 7 and 8, given a set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), it holds that \({\mathcal {T}}_{syn-c}(Synchronizer({\mathcal {A}}, T, {\mathcal {F}}, {\mathcal {T}})) = T\), i.e., the algorithm can be used to learn a \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) that reproduces exactly the input transitions whatever the semantics that produced them.
The complexity of the Synchronizer is basically a regular call to GULA plus a special one to learn constraints and the search for a compatible set of rules in the optimal program which could be blocked by the constraint. Since constraint can have both features and target variables in their body, the complexity of learning constraints with GULA is like considering \(|{\mathcal {F}}|+|{\mathcal {T}}|\) features but only one target value \(\epsilon ^1\). The detailed complexity of the Synchronizer is given in Theorem 9.
Theorem 9
(Synchronizer Complexity) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) be a set of transitions, let \(n := max(|{\mathcal {F}}|,|{\mathcal {T}}|)\) and \(d := \max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\})\) and \(m := |{\mathcal {F}}|+|{\mathcal {T}}|\).
The worst-case time complexity of Synchronizer when learning from T belongs to \({\mathcal {O}}( (d^{2n} + 2nd^{n+1} + nd^{n+2}) + (|T|^2 + |T| \times (2m^4d^{2m+2} + 2m^3d^{m+1})) + (d^{n^n}))\) and its worst-case memory use belongs to \({\mathcal {O}}( (d^{2n} + 2nd^{n+1} + nd^{n+2}) + (d^{2m} + 2md^{m+1} + md^{m+2}) + (nd^n))\).
The Synchronizer algorithm does not need any assumption about the semantics of the underlying model but require the full set of observations. However, when dealing with real data, we may only get access to partial observations. That is why we propose in next section a heuristic method to use GULA in such practical cases.
6 Predictions from partial observations with weighted \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)s
In this section, we present a heuristic method allowing to use GULA to learn from partial observations and predict from unobserved feature states. Previous sections were focusing on theoretical aspects of our method. The two algorithms presented in Sects. 4 and 5 are sound regarding the observations they have been provided as input. Rules of an optimal program provide minimal explanations and can reproduce what is possible over observed transitions. If observation are incomplete, the optimal program will realize a transition to every possible target state from unobserved feature state, i.e. all target atoms are always possible for unobserved feature state. In practice, when observations are partial, to get predictions and explanations from our model on unobserved feature states, we also need to model impossibilities.
Definition 27
(Rule of Impossibility) A rule of impossibility of \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) is a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R such that \(\forall (s, s^{\prime}) \in T, R \sqcap s \implies {\text {head}}(R) \notin s^{\prime}\).
A rule of impossibility is a rule that does not realise any transition of T: the conclusion of a rule of impossibility is never observed in any transition from a feature state of \(\mathrm {first}(T)\) it matches, i.e., its body is a condition so that its head is not possible. Thus, such a rule either conflicts with T (see Definition 7) for every feature states it matches or matches no feature state of T (in \(\mathrm {first}(T)\)). Note that all conflicting rules are not necessarily rules of impossibility. Indeed, a conflicting rule can still realize some transitions of T.
Definition 28
(Optimal Program of Impossibility) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). A \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) P is impossibility-suitable for T when:
-
all rules in P are rules of impossibility of T, and
-
for all rules of impossibility R of T, there exists \(R^{\prime}\in P\) such that \({R^{\prime}}\ge {R}\).
If in addition, for all \(R\in P\), all the \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules \(R^{\prime}\) belonging to \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) impossibility-suitable for T are such that \({R^{\prime}}\ge {R}\) implies \({R}\ge {R^{\prime}}\) then P is called impossibility-optimal and denoted \(\overline{P_{{\mathcal {O}}}({T})}\).
Proposition 5
(Uniqueness of Impossibility-Optimal Program) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) impossibility-optimal for T is unique and denoted \(\overline{P_{{\mathcal {O}}}({T})}\).
Rules of possibility and impossibility can be weighted according to the observations to form a Weighted \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) as given in Definition 29.
Definition 29
(Weighted \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)) A weighted program is a set of weighted rules: \(\{(w, R) \mid w \in {\mathbb {N}}\wedge R \text { is a }{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}{}\text { rule} \}\). A weighted \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), or \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), is a pair of weighted programs \((P, P^{\prime})\) on the same set of atoms \({\mathcal {A}}\), and the same feature and target variables \({\mathcal {F}}\) and \({\mathcal {T}}\).
Example 21
Let \(WP = (P,P^{\prime})\) be a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), as follows.
Let \(s := \{a^0_{t-1}, b^1_{t-1}, c^1_{t-1}\}\). The rule of possibility \(a^0_t\leftarrow b^1_{t-1}\) matches s, and the rule of impossibility \(a^0_t \leftarrow c^1_{t-1}\) also matches s. The weight of the rule of impossibility (30) being greater than that of the rule of possibility (3), we can consider that \(a^0_t\) is not likely to appear in a transition from s according to WP.
Using GULA, we can learn both rules of possibility (by using parameter \(learning\_mode\) = “possibility”) and rules of impossibility (with parameter \(learning\_mode\) = “impossibility”) from \(T \subseteq {\mathcal{S}}^{{\mathcal{F}}} \times {\mathcal{S}}^{{\mathcal{T}}}\). In Algorithm 4, GULA is used to learn two distinct \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)s: a program of possibility and a program of impossibility. The rules of both programs are then weighted by the number of observed feature states (that is, in T) they match to form a weighted \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\). This \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) can be used to make predictions from unobserved feature states (\(s \in {\mathcal {S}}^{{\mathcal {F}}}, s \notin \mathrm {first}(T)\)) by confronting the learned rules of possibility and impossibility according to their weights.

Given a feature state \(s \subseteq {\mathcal {S}}^{{\mathcal {F}}}\) we can predict and explain the likelihood of each target atom by confronting the rules of possibility and impossibility that match s. The likelihoods are computed as given in Definition 30.
Definition 30
(\({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) Prediction and Explanation)
(1) Let P be a weighted program, \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) and \(\mathrm {v}^{{val}}\in {\mathcal {A}}\) with \(\mathrm {v}\in {\mathcal {T}}\). We define the best rules of \(\mathrm {v}^{{val}}\) matching s in P as:
where: \(\left\{ \begin{array}{l} w_{\max } := \max (\{w \in {\mathbb {N}}\mid (w, R) \in P\} \cup \{0\}) \\ M := \{R \mid (w_{\max }, R) \in P \wedge {\text {head}}(R) = \mathrm {v}^{{val}}, R \sqcap s \} \end{array}\right.\).
(2) Let \(WP = (P,P^{\prime})\) be a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) and \(\mathrm {v}^{{val}}\in {\mathcal {A}}\) with \(\mathrm {v}\in {\mathcal {T}}\). We define the best rules of possibility and best rules of impossibility of \(\mathrm {v}^{{val}}\) matching s in WP as:
(3) We define the prediction of likelihood of the occurrence of \(\mathrm {v}^{{val}}\) in a transition from s according to WP as:
where: \(\left\{ \begin{array}{l} best\_rules\_of\_possibility(WP, s,\mathrm {v}^{{val}}) = (w,M) \\ best\_rules\_of\_impossibility(WP, s,\mathrm {v}^{{val}}) = (w^{\prime},M^{\prime}) \end{array}\right.\).
(4) We define the explanation of the prediction of the occurrence of \(\mathrm {v}^{{val}}\) in a transition from s according to WP as:
where: \(\left\{ \begin{array}{l} (w,R) := arbitrary(best\_rules\_of\_possibility(WP, s, \mathrm {v}^{{val}})) \\ (w^{\prime},R^{\prime}) := arbitrary(best\_rules\_of\_impossibility(WP, s, \mathrm {v}^{{val}}))) \\ arbitrary((w^{\prime \prime }, M)) = (w^{\prime \prime }, R^{\prime \prime }) \end{array}\right.\)
so that \(R^{\prime \prime }\) is taken arbitrarily in M if \(M \ne \emptyset\), or \(R^{\prime \prime } := \varnothing\) if \(M = \emptyset\).
Intuitively, \(predict(WP, s, \mathrm {v}^{{val}})\) gives a normalized score between 0 and 1 of the likelihood to observe \(\mathrm {v}^{{val}}\) after state s, where 0.5 means that we are left inconclusive. In \(predict\_and\_explain(WP, s, \mathrm {v}^{{val}})\), one of the best rules of possibility and rules of impossibility with their respective weights are given as explanation to the prediction or a weight of 0 and no rule when no rules of possibility (resp. impossibility) match s. The weights of the selected rules are used to compute the likelihood and the rules themselves are the explanation of the predictions.
Table 3 shows an example of such predictions and explanations from a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) WP from the feature state \(s=\) \(\{a_{t-1}^{0},\) \(b_{t-1}^{0},\) \(c_{t-1}^{0},\) \(d_{t-1}^{0},\) \(e_{t-1}^{1},\) \(f_{t-1}^{0},\) \(g_{t-1}^{0},\) \(h_{t-1}^{1},\) \(i_{t-1}^{1},\) \(j_{t-1}^{1}\}\) where \({\mathcal {F}}= \{a_{t-1},\ldots ,j_{t-1}\}, {\mathcal {T}}= \{a_t, \ldots , j_t\}\) and \(\forall \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}, {\mathsf {dom}}(\mathrm {v}) = \{0,1\}\). Each row of the table provides the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) prediction of the occurrence of a target atom \(\mathrm {v}^{{val}}\) and the corresponding explanation: \(predict\_and\_explain(WP, s, \mathrm {v}^{{val}})\). For example, \(i_t^1\) is very likely to be observed in a transition from s since its likelihood is almost 1 (0.90). This likelihood comes from the best possibility rule of the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\): \(i_t^{1} \leftarrow d_{t-1}^{0} \wedge j_{t-1}^{1}\), whose weight is 35, and its best impossibility rule: \(i_t^{1} \leftarrow a_{t-1}^{0} \wedge b_{t-1}^{0} \wedge g_{t-1}^{0} \wedge h_{t-1}^{1}\), which only has a weight of 4. This \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) has been learned using Algorithm 4, thus the weights correspond to the number of feature states that those rules match. Here, we can say that \(i_t^1\) is very likely to occur since \(90\%\) of the observed feature states that contain both \(d_{t-1}^{0}\) and \(j_{t-1}^{1}\) (like s) have \(i_t^1\) in a transition, according to the possibility rule R. We have the reverse case for \(a_t^1\) in this example, the best impossibility rule is much stronger than the best possibility rule leading to the likelihood of 0.05, thus \(a_t^1\) is very unlikely to be observed in a transition from s. In this example, the likelihood probability of the two atoms of each target variable (for example \(a^0\) and \(a^1\)) sums to 1.0 because the observed transitions are deterministic, but in the general case they are not related; for instance: both \(a^0\) and \(a^1\) could be very likely.
Regarding the choice of the rules for prediction, here we simply take the rules with the biggest weight from each weighted program. The intuition behind this is that rules with bigger weights are more likely to be consistent with unobserved transitions, thus the biggest weighted rule(s) is (are) the most likely to be part of the real optimal program. Note that other heuristics are possible. One could for instance combine all matching rules, for example by computing the sum or average of their weights; however, combining rules can be more noise sensitive: a lot of small-weighted incorrect rules (on unobserved states) might counter a single high-weighted rule that would happen to be optimal under all observations. This is why we chose to use a single-rule heuristics, which also happens to give a unique pair of rules as explanation (why a target atom might be possible and why it might not).
The capacity of this heuristic method to predict and explain from unobserved feature states is evaluated in Sect. 7.
7 Evaluation
In this section, both the scalability, accuracy and explanations of GULA are evaluated using Boolean network benchmarks from the biological literature. The scalability of Synchronizer is also evaluated (details are given in “Appendix”). All experimentsFootnote 1 were conducted on one core of an Intel Core i3 (6157U, 2.4 GHz) with 4 Gb of RAM.
In our experiments we use Boolean networksFootnote 2 from Boolenet (Dubrova & Teslenko, 2011) and Pyboolnet (Klarner et al., 2016). Benchmarks are performed on a wide range of networks. Some of them are small toy examples, while the biggest ones come from biological case study papers like the Boolean model for the control of the mammalian cell cycle (Fauré et al., 2006) or fission yeast (Davidich & Bornholdt, 2008). Boolean networks are converted to \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) where \(\forall v \in {\mathcal {V}}, {\mathsf {dom}}(v) = \{0,1\}\). In Dubrova and Teslenko (2011), Klarner et al. (2016) file formats, for each variable, Boolean functions are given in disjunctive normal form (DNF), a disjunction of conjunction clauses that can be considered as a set of Boolean atoms of the form \(\mathrm {v}\) or \(\lnot \mathrm {v}\). Each clause c of the DNF of a variable \(\mathrm {v}\) is directly converted into a rule R such that, \({\text {head}}(R) = \mathrm {v}^1_t\) and \(\mathrm {v}^{\prime 1}_{t-1} \in {\text {body}}(R) \iff \mathrm {v}^{\prime} \in c\) and \(\mathrm {v}^{\prime 0}_{t-1} \in {\text {body}}(R) \iff \lnot \mathrm {v}^{\prime} \in c\). For each such \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) the set T of all transitions are generated for the three considered semantics (see Sect. 3). For each generation, to simulate the cases where Boolean functions are false, each semantics uses a default function that gives \(\mathrm {v}^0, \forall \mathrm {v}\in {\mathcal {T}}\) when no rule \(R, \mathrm {v}({\text {head}}(R)) = \mathrm {v}\) matches a state. Table 4 provides the number of variables of each benchmark used in our experiments together with the number of transitions under synchronous, asynchronous and general semantics.
7.1 GULA scalability
Figure 9 shows the run time (log scale) of GULA (Algorithm 2) and brute force enumeration (Algorithm 1) when learning a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) from Boolean networks (grouped by number of variables) transitions of Table 4. Since we learn \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) the run time corresponds to the sum of two calls to GULA (resp. brute force enumeration) (possibility and impossibility mode) and the computation of each rule weight (see Algorithm 4). For the impossibility mode of the brute force enumeration (Algorithm 1), we keep impossibility rules in place of consistent rules: it suffices to replace \(P := \{R \in P \mid \forall (s,s^{\prime}) \in T, {\text {body}}(R) \subseteq s \implies \exists (s,s^{\prime \prime }) \in T, {\text {head}}(R) \in s^{\prime \prime }\}\) by \(P := \{R \in P \mid \forall (s,s^{\prime}) \in T, {\text {body}}(R) \subseteq s \implies \not \exists (s,s^{\prime \prime }) \in T, {\text {head}}(R) \in s^{\prime \prime }\}\). For each benchmark, learning is performed on 10 random subsets of \(1\%\), \(5\%\), \(10\%\), \(25\%\), \(50\%\), \(75\%\), \(100\%\) of the whole set of transitions with a time out of 1000 s.
Run time in seconds (log scale) of two calls to GULA (in blue) and brute force enumeration (in red) when learning a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) from a random set of \(1\%\), \(5\%\), \(10\%\), \(25\%\), \(50\%\), \(75\%\), \(100\%\) of the transitions of a Boolean network from Boolenet and PyBoolNet with size varying from 3 to 13 variables. Time out is set at 1000 s and 10 runs where performed for each setting (Color figure online)
For all benchmarks, we clearly see that GULA is more efficient than the trivial brute force enumeration, the difference exponentially increasing with the number of variables: about 10 times faster with 6 variables and 100 times faster with 9 variables. The brute force enumeration reaches the time out for 10 variables benchmarks and beyond.
For a given number of variables, we observe that for each benchmark the run time increases with the number of transitions until some ratio (for example \(50\%\) for 7 variables) at which point more transition can actually speed up the process. More transitions reduce the probability for a rule to be consistent, thus both methods have less rules to check for domination. This tendency is observed on the three semantics. It is important to note that the systems are deterministic with the synchronous semantics and thus the number of transitions in the synchronous case is much lower than for the two other semantics and one may expect better run time. But the quantity of transitions has little impact in fact and most of the run time goes into rule domination check (see Theorem 6). Actually, more input transitions can even imply less learning time for GULA. Having more diverse initial states can also allow the sorting of the negatives example to reduce the quantity of specialization made at each step, a freshly revised rule being revised again will not have much non-dominated candidates to generate. For example, for the benchmarks with 13 variables, for some variable values, given \(25\%\) of the transitions, the number of stored rules reached several thousands. On the other hand, when given \(100\%\) of the transitions, it rarely exceeds hundreds stored rules. Same logic can apply to the faster run time of general semantics with “low” subset of transitions: the total number of transitions being higher, more diversity appears in its subset thus higher chance for the sorting to have effect on reducing the need for least specialization. The rules are simpler for the two other semantics since rules of the form \(\mathrm {v}^{{val}}_{t} \leftarrow \mathrm {v}^{{val}}_{t-1}\) are always consistent and quickly obtained. Such simple rules have great dominance power, reducing the quantity of stored rules and thus checked for domination at each step.
GULA succeeds in learning a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) from the benchmarks with up to 10 variables for all semantics before the time-out of 1, 000 seconds for all considered sub-sets of transitions. Benchmarks from 12 variables need a substantial amount of input transitions to prevent the explosion of consistent rules and thus reaching the time out. For both semantics, the 12 variables benchmarks reached the time out several times when given less than \(100\%\) of the transitions. Even if this may seem small compared to the intrinsic complexity of biological systems, ten components are sufficient to capture the dynamic behavior of critical, yet significant, mechanisms like the cell cycle (Gibart et al., 2021).
Compared to our previous algorithm LF1T (Ribeiro & Inoue, 2015), GULA is slower in the synchronous deterministic Boolean case (even when learning only \(P_{{\mathcal {O}}}({T})\)). This was expected since it is not specifically dedicated to learning such networks: GULA learns both values (0 and 1) of each variable and pre-processes the transitions before learning rules to handle non-determinism. On the other hand, LF1T is optimized to only learn rules that make a variable take the value 1 in the next state and assume only one transition from each initial state. furthermore, LF1T only handles Boolean values and deterministic transitions while GULA can deal with multi-valued variable and any pseudo-idempotent (Theorem 1) semantics transitions.
The current implementation of the algorithm is rather naive and better performances are expected from future optimizations. In particular, the algorithm can be parallelized into as many threads as the number of different rule heads (one thread per target variable value). We are also developingFootnote 3 an approximated version of GULA that outputs a subset of \(P_{{\mathcal {O}}}({T})\) (resp. \(\overline{P_{{\mathcal {O}}}({T})}\)) sufficient to explain T (Ribeiro et al., 2020). The complexity of this new algorithm is polynomial, greatly improving the scalability of our approach but to the sacrifice of completeness. However, this algorithm is still under development and is beyond the scope of this paper.
Learning constraints is obviously more costly than learning regular rules since both feature and target variables can appear in the body, i.e., the number of features becomes \(|{\mathcal {F}}|+|{\mathcal {T}}|\). Thus by running the Synchronizer on the Boolean network benchmark it implies a call to GULA with double the number of variables to learn constraints. Under the same experimental settings, the Synchronizer reached the time-out of 1, 000 seconds on the benchmarks of 7 variables. The contribution regarding \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) being focused on theoretical results, we provided the detailed evaluation of the Synchronizer in “Appendix” to save space.
7.2 GULA predictive power
When addressing biological systems, a major challenge arises: even if the amount of produced data is increasing through the development of high-throughput RNA sequencing, it is still low with regard to all the theoretical contexts.
In this experiment, we thus evaluate the quality of the models learned by GULA in their ability to correctly predict possible values for each variable from unseen feature states, i.e., the capacity of the learned model to generalize to unobserved cases. Practically speaking, this ensures the resulting models can provide relevant information about biological experiments that were (or could) not be performed.
For each Boolean network benchmark, we first generate the set of all possible feature states. Those states are then randomly split into two sets: at least \(20\%\) will be test feature states and the remaining \(80\%\) will be potential training feature states. According to the Boolean formula of the network and a given semantics, all transitions from test feature states are generated to make the test set. All transitions are also computed from the training feature states, but only x% of the transitions are randomly chosen to form the training set with \(x \in \{1,5,10,20,30,\ldots ,100\}\). Figure 10 illustrates the construct of both training and test sets for a Boolean network of 3 variables.
The training set is used as input to learn a WDMVLP using GULA. The learned WDMVLP WP is then used to predict from each feature state s of the test set, the possibility of occurrence of each target atoms \(\mathrm {v}^{{val}}\) according to Proposition 30, i.e., \(predict(WP, s, \mathrm {v}^{{val}})\). The forecast probabilities are compared to the observed values of the test set. Let T be the set of all transitions, \(T^{\prime }\) the training set of transitions and \(T^{\prime \prime }\) the test set of transitions. For all \(\mathrm {v}^{{val}}\in {{\mathcal {A}}}\vert _{{\mathcal {T}}}\) and \(s \in \mathrm {first}(T^{\prime \prime })\), we define:
To evaluate the accuracy of prediction from the learned \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), WP, over the test set \(T^{\prime \prime }\) we consider a ratio of precision given by the complement to one of the mean absolute error between its prediction and the actual value:
Formally, if T is the whole set of transitions of the Boolean network, this experiment consists in learning the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \((P_{{\mathcal {O}}}({T^{\prime }}), \overline{P_{{\mathcal {O}}}({T^{\prime }})})\) from the training set \(T^{\prime }\subset T\) and checking both the consistency and realization of the test set \(T^{\prime \prime } \subset T\), with \(\mathrm {first}(T^{\prime }) \cap \mathrm {first}(T^{\prime \prime }) = \emptyset\). Here, we chose \(|T^{\prime }| \approx x \times 0.8 \times |T|\) and \(|T^{\prime \prime }| \approx 0.2 \times |T|\), where \(x \in \{0.01,0.05,0.1,0.2,0.3,\ldots ,1.0\}\). Intuitively, the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) learned in these experiments can be seen as an approximation of \((P_{{\mathcal {O}}}({T}),\overline{P_{{\mathcal {O}}}({T})})\) on partial observations: the learned rules can be different. These experiments aim to evaluate the discrepancies in their behaviors, i.e., we only measure the consequences of the use of the rules, not the quality of the rules themselves (which is the subject of the next experiment).
Example 22
Let \(T^{\prime \prime }\) be the test set of Fig. 10 and WP be the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) of Example 21. Let \(s := (a^1_{t-1}, b^1_{t-1}, c^1_{t-1})\) (111).
-
Expected prediction from s according to \(T^{\prime \prime }\):
\(\{(\mathrm {v}^{{val}}, actual(\mathrm {v}^{{val}}, s, T^{\prime \prime }))\} = \{(a_t^0,1), (a_t^1,0), (b_t^0,1), (b_t^1,1), (c_t^0,1), (c_t^1,1)\}\)
-
Predictions from s according to WP:
\(\{(\mathrm {v}^{{val}}, predict(WP, s, \mathrm {v}^{{val}}))\} = \{(a_t^0,0.9), (a_t^1,0.2), (b_t^0,0.8), (b_t^1,0.6), (c_t^0,1.0),\) \((c_t^1,0.0)\}\)
-
Accuracy (unique state): \(1-\frac{|1-0.9| + |0-0.2| + |1-0.8| + |1-0.6| + |1-1.0| + |1-0.0|}{|{{\mathcal {A}}}\vert _{{\mathcal {T}}}| = 6}\)\(= 0.58\)
On state s, the model prediction mean absolute error w.r.t. \(T^{\prime \prime }\) is 0.42, thus giving an accuracy of 0.58, meaning that in average, \(58\%\) of the predictions are correct.
Figure 11a–c show the accuracy of the predicted possible values w.r.t. the ratio of training data going from 1% to 100% with the three considered semantics.
Here, we also consider four trivial baselines that are random predictions and always predicting 0, 0.5 or 1.0, i.e., \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall \mathrm {v}^{{val}}\in {{\mathcal {A}}}\vert _{{\mathcal {T}}}\):
-
\(baseline\_random(s,\mathrm {v}^{{val}}) = rand(0.0,1.0)\)
-
\(baseline\_always\_0.0(s,\mathrm {v}^{{val}}) = 0.0\)
-
\(baseline\_always\_0.5(s,\mathrm {v}^{{val}}) = 0.5\)
-
\(baseline\_always\_1.0(s,\mathrm {v}^{{val}}) = 1.0\)
Accuracy score for the random baseline is expected to be around 0.5 for every semantics since the problem is equivalent to a binary classification, i.e., each atom can appear or not. Accuracy score of the three fixed baselines is exactly 0.5 in synchronous case since transitions are deterministic here: only one atom \(\mathrm {v}^{{val}}\) is possible (either \(\mathrm {v}^0\) or \(\mathrm {v}^1\)) for each target variable \(\mathrm {v}\) for each feature state of the test set, i.e., always one of the two must be predicted to 0.0 and the other one to 1.0. For asynchronous and general semantics the transitions are non-deterministic, thus always predicting 0.0 or 1.0 for each target atoms will lead to different accuracy score. Both semantics using previous value as default, it is more likely for each atom to appear in a target state, thus always predicting 1.0 is expected to perform better than 0.5 and always predicting 0.0 is expected to perform worst. That explain why, in Fig. 11b, c we can observe an accuracy score of 0.6 to 0.8 for always predicting 1.0 and 0.2 to 0.4 for always predicting 0.0.
Accuracy of the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) learned by GULA and trivial baselines when predicting possible target atoms from unseen states with different amounts of training data of transitions from Boolean network benchmarks with synchronous, asynchronous and general semantics
With synchronous semantics transitions, when given only \(5\%\) of the possible transitions, GULA starts to clearly outperform the baseline on the test set for all benchmarks size. It reaches more than \(80\%\) accuracy when given at least \(40\%\) of the transitions for benchmarks with 6 variables and only \(5\%\) of input transitions is enough to obtain same performance with 9 variables. These results show that the models learned by GULA effectively generalise some meaningful behavior from training data over test data in a deterministic context.
For the non-deterministic case of asynchronous and general semantics the performance of GULA are similar but the differences with the baselines that always predict 1.0 is smaller. As stated before, since both semantics use previous value as default, it is more likely for each atom to appear in a target state, thus predicting that all atoms are always possible is less risky. Furthermore, the transition being non-deterministic, the way we select the training set (see Fig. 10) may lead to have missing transitions from some feature state in the training set, generating false negative example for GULA equivalent to noisy data. Still, GULA start to outperforms the baseline that always predict 1.0 (and all others) for the two semantics when given more than \(50\%\) of the possible transitions as input. The performances of GULA also increase when considering more variables, with 9 variables benchmarks \(20\%\) of transition is enough to obtain \(80\%\) accuracy over unseen test data for asynchronous case and about \(2\%\) for general case. Performances are globally similar for the three semantics, showing that our method can handle a bit of noise caused by missing observations.
If one is only interested by prediction accuracy, it is certainly easier to achieve better results using statistical machine learning methods like neural networks or random forest since prediction here is basically a binary classification for each target variables values. In the cases where explainability is of interest, the rules used for the predictions and their weights may be quite simple human readable candidates for explanations (i.e., exhibit dynamic relations between biological interacting components). For a given feature state, a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) provides (using Definition 30) for each target atom the likelihood of its occurrence in a transition but also the two rules (possibility/impossibility) that explain this prediction as shown in Table 3. We consider the evaluation of explanation in the following experiment.
7.3 GULA explanation quality
In this experiment, we evaluate the quality of the models learned by GULA in their ability to correctly explain their predictions. Benchmarks and train/test sets generation is the same as in previous experiment (see Fig. 10). The learned model must predict correctly the possibility for each target atom as previously, and also provide a rule that can explain the prediction. When a target atom is possible (resp. impossible), we expect a rule of the optimal program (resp. optimal program of impossibility) to be given as explanation. By computing the Hamming distance between the rules used in the model learned from incomplete observations \((P_{{\mathcal {O}}}({T^{\prime }}), \overline{P_{{\mathcal {O}}}({T^{\prime }})})\), and the optimal rules from the full observations \((P_{{\mathcal {O}}}({T}), \overline{P_{{\mathcal {O}}}({T})})\), we can have an idea of how close we are from the theoretically optimal explanations. For that, for each experiment, we compute the optimal program and the optimal program of impossibility from the set of all transitions (T) before splitting it into train/test sets.
A \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) is then learned using GULA from the training set (\(T^{\prime }\)) as in previous experiment. The learned \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) is then used to predict from each feature state of the test set (\(T^{\prime \prime }\)), the possibility of occurrence of each target atom according to Proposition 30 as well as a rule to explain this prediction. The forecast probabilities and explanations are compared to the observed values of the test set and the rules of the optimal programs. For all \(\mathrm {v}^{{val}}\in {{\mathcal {A}}}\vert _{{\mathcal {T}}}\) and \(s \in \mathrm {first}(T^{\prime \prime })\), we define:
To compare the forecast rules and the ideal rules, we consider the Hamming distance over their bodies:
We expect both correct forecast of possibility and explanation, in the sense that an incorrect prediction yields the highest error (1.0) while a good prediction yields an error depending on the quality of the explanation (0.0 when an ideal rule is used). This is summed up in the following error function:
This allows to compute an explanation score, combining both accuracy and explanation quality from the learned \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), WP, over the test set \(T^{\prime \prime }\):
Example 23
Let \({\mathcal {F}}= \{a_{t-1}, b_{t-1}, c_{t-1}\}\), \({\mathcal {T}}= \{a_{t}, b_{t}, c_{t}\}\), a complete set of transitions \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), a train set of transitions \(T^{\prime } \subseteq T\) and a test set of transitions \(T^{\prime \prime } \subseteq T\) with \(T^{\prime } \cap T^{\prime \prime } = \emptyset\) such that:
-
Let us suppose that from the test feature state
 , the target atom \(a^1_t\) is observed in some transitions from s in \(T^{\prime \prime }\) thus we expect a probability of 1.0 and a rule from \(P_{{\mathcal {O}}}({T})\) that matches s and produce \(a^1_t\) (any of the blue rules) as explanation:
, the target atom \(a^1_t\) is observed in some transitions from s in \(T^{\prime \prime }\) thus we expect a probability of 1.0 and a rule from \(P_{{\mathcal {O}}}({T})\) that matches s and produce \(a^1_t\) (any of the blue rules) as explanation: -
-
Let WP be a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) learned from \(T^{\prime }\) and we suppose that:
-
\(predict\_and\_explain(WP, s, a^1_t) = (a^1_t, 1.0, a^1_t \leftarrow b^1_{t-1})\)
-
-
The predicted possibility is correct, thus the explanation score will depend on the explanation.
-
The explanation \(a^1_t \leftarrow b^1_{t-1}\) has a Hamming distance of 2 with \(a^1_t \leftarrow a^1_{t-1}\) (the conditions on \(a_{t-1}\) and \(b_{t-1}\) are wrong, the condition on \(c_{t-1}\) is correct), thus the error will be \(\frac{2}{|{\mathcal {F}}|} = \frac{2}{3}\).
-
The Hamming distance is only of 1 with rule \(a^1_t \leftarrow b^1_{t-1} \wedge c^1_{t-1}\) (the conditions on \(a_{t-1}\) and \(b_{t-1}\) are correct, the condition on \(c_{t-1}\) is wrong), thus the error will be \(\frac{1}{|{\mathcal {F}}|} = \frac{1}{3}\).
-
The final score for target \(a^1_t\) is \(1- min(\{\frac{2}{3},\frac{1}{3}\}) \approx 0.66\)
The prediction is correct for target \(a^1_t\) from s, but the explanation \(a^1_t \leftarrow a^1_{t-1}\) is not perfect. Still, \(66\%\) of its conditions correspond to an optimal rule  that can explain this prediction.
that can explain this prediction.
-
Now let us suppose that from the test feature state
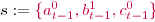 , the target atom \(a^1_t\) is never observed in any transition from s in \(T^{\prime \prime }\). Thus, we expect a predicted probability of 0.0 and, as an explanation, a rule from \(\overline{P_{{\mathcal {O}}}({T})}\) that matches s and has \(a^1_t\) as conclusion (any of the red rules):
, the target atom \(a^1_t\) is never observed in any transition from s in \(T^{\prime \prime }\). Thus, we expect a predicted probability of 0.0 and, as an explanation, a rule from \(\overline{P_{{\mathcal {O}}}({T})}\) that matches s and has \(a^1_t\) as conclusion (any of the red rules): -
-
Let WP be a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and suppose that:
-
\(predict\_and\_explain(WP, s, a^1_t) = (a^1_t, 0.0, a^1_t \leftarrow \emptyset )\)
-
-
The explanation \(a^1_t \leftarrow \emptyset\) has an Hamming distance of 1 when compared with \(a^1_t \leftarrow a^0_{t-1}\) (the condition on \(a_{t-1}\) is wrong, the conditions on \(b_{t-1}\) and \(c_{t-1}\) are correct), thus the error will be \(\frac{1}{|{\mathcal {F}}|} = \frac{1}{3}\).
-
We obtain the same Hamming distance of 1 when compared with \(a^1_t \leftarrow c^0_{t-1}\).
-
The final score for target \(a^1_t\) from s is \(1 - min(\{\frac{1}{3},\frac{1}{3}\}) \approx 0.66\).
The prediction is correct for target \(a^1_t\) from s, but the explanation \(a^1_t \leftarrow \emptyset\) is not perfect. Still, \(66\%\) of its conditions correspond to an optimal rules of impossibility ( and
and  ) that can explain this prediction.
) that can explain this prediction.
It is important to note that the metric we consider here only evaluates the quality of the explanation in the predictions, not of the entire program. Also this metrics can only be used when the actual real program is known and thus cannot be used to evaluate a model when only observations are available. Table 5 shows an example of scoring of the predictions of a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) (both accuracy and explanation score) from the feature state \(s=\) \(\{a_{t-1}^{0},\) \(b_{t-1}^{0},\) \(c_{t-1}^{0},\) \(d_{t-1}^{0},\) \(e_{t-1}^{1},\) \(f_{t-1}^{0},\) \(g_{t-1}^{0},\) \(h_{t-1}^{1},\) \(i_{t-1}^{1},\) \(j_{t-1}^{1}\}\) where \({\mathcal {F}}= \{a_{t-1},\ldots ,j_{t-1}\}, {\mathcal {T}}= \{a_t, \ldots , j_t\}\) and \(\forall \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}, {\mathsf {dom}}(\mathrm {v}) = \{0,1\}\). This example was generated using the Boolean network “faure_cellcycle” synchronous transitions (see Table 4) where we replaced variable names by letters from a to j and omitted time subscript to make the table more compact and easy to read. From the set of all transitions T are computed \(P_{{\mathcal {O}}}({T})\) and \(\overline{P_{{\mathcal {O}}}({T})}\). T is also partitioned into a training set \(T^{\prime }\) (about \(10\%\) of T) and a test set \(T^{\prime \prime }\) (about \(20\%\) of T) such that \(T^{\prime } \cap T^{\prime \prime } = \emptyset\). Here, in the test set, there is only one possible transition from s: \((s,s^{\prime}), s^{\prime} = \{a^{0}, b^{0}, c^{0}, d^{0}, e^{0}, f^{1}, g^{1}, h^{0}, i^{1}, j^{1}\}\) (deterministic transition). Thus, for atoms that appear in \(s^{\prime}\), the model is expected to predict a probability of 1.0 (\(> 0.5\)) and 0.0 (\(< 0.5\)) for the others. Furthermore, when correctly predicting the occurrence it should also provide one of the corresponding optimal rules (possibility rule if predicted possible, rule of impossibility otherwise). For instance, for \(a^0\), the model predicted a likelihood of 0.95, and since the atom was effectively observed in \(s^{\prime}\), a likelihood of 1.0 is expected, thus its accuracy is 0.95. For \(a^1\), since it is not in \(s^{\prime}\), we expect a likelihood of 0.0; because the predicted likelihood is 0.05, its accuracy is also 0.95. Regarding the explanation score, the accuracy is checked before computing the rule distance with the expected optimal rules. For \(a^0\), the likelihood prediction is above 0.5, thus the model considers \(a^0\) possible and since it is indeed observed in \(s^{\prime}\), the explanation score depends of the prediction possibility rule R; since \(R \in P_{{\mathcal {O}}}({T})\), the explanation is considered perfect and the score is 1.0. For \(a^0\), we have another perfect case of explanation but for the impossibility scenario: the atom \(a^0\) is not in \(s^{\prime}\), it is predicted unlikely, and the impossibility rule of the prediction \(R^{\prime}\) is in \(\overline{P_{{\mathcal {O}}}({T})}\). When considering instead \(h^0\) and \(h^1\), we have a wrong likelihood prediction, thus the explanation score is directly 0.0. Regarding \(c^0\), the likelihood prediction is correct, and the provided possibility rule \(R := c^0 \leftarrow d^0 \wedge h^1\) has (at most) 8 conditions out of 10 that are in common with a rule of \(P_{{\mathcal {O}}}({T})\) (that is, rule \(c_0 \leftarrow h^1 \wedge i^1\)): indeed, both rules have \(h^1\) as condition, but R misses \(i^1\) and contains a spurious \(d^0\), while the 7 remaining feature variables do not appear in both rules, leading to an explanation score of \(8/10 = 0.8\). We observe the same for the impossibility rules of \(c^1\), although the score could have been different than for \(c^0\). In this example, we see that optimal rules of the same target atoms matching the same feature state can be very different (for instance, the two actual \(\overline{P_{{\mathcal {O}}}({T})}\) rules of \(c^1\) that have no feature atom in common) that is why we consider the minimal Hamming distance in our scoring.
As a final comment, we can observe that for a given target variable, the rules for one value (for instance, \(a^0\)) in \(P_{{\mathcal {O}}}({T})\) have exactly the same body than the rules for the other value (for instance, \(a^1\)) in \(\overline{P_{{\mathcal {O}}}({T})}\). This is due to the Boolean deterministic nature of the example tackled here, but it could not be the case in general (multi-valued or non-deterministic case).
Figure 12a–c show the results of the evolution of the explanation score when learning a \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) using GULA from approximately \(1\%\) to \(80\%\) of the transitions of a Boolean network. We also use 4 trivial methods as baselines, each having a perfect value prediction, thus their score is only influenced by their explanation. The baselines explanations are trivial and take the form of a random rule, no rules, the most specific rule, the most general rule, i.e., \(\forall s \in \mathrm {first}{T^{\prime \prime }}, \forall \mathrm {v}^{{val}}\in {{\mathcal {A}}}\vert _{{\mathcal {T}}}, perfect\_prediction = actual(\mathrm {v}^{{val}}, s, T^{\prime \prime })\):
-
\(baseline\_random\_rules(s,\mathrm {v}^{{val}}) = (perfect\_prediction, \mathrm {v}^{{val}}\leftarrow body \subseteq s)\)
-
\(baseline\_no\_rules(s,\mathrm {v}^{{val}}) = (perfect\_prediction, \varnothing )\)
-
\(baseline\_most\_general\_rules(s,\mathrm {v}^{{val}}) = (perfect\_prediction, \mathrm {v}^{{val}}\leftarrow \emptyset )\)
-
\(baseline\_most\_specific\_rules(s,\mathrm {v}^{{val}}) = (perfect\_prediction, \mathrm {v}^{{val}}\leftarrow s)\)
The random baseline is expected to score around 0.5, while the no rule baseline will always have a score of 0.0. The most specific rule baseline will have all conditions of each expected rule, but also unnecessary ones. The most general rules will miss all specific conditions but avoid all unnecessary ones. Since optimal rules rarely use more than half of the total number of variable as conditions (at least for these Benchmarks), the most general rule is expected to have a better score in average compared to most specific. That’s why we observe random rule score around 0.4 to 0.5, most specific score around 0.1 to 0.4 and most general score around 0.6 to 0.8 for all semantics considered.
With synchronous semantics transitions, when given only \(50\%\) of the possible transitions, GULA start to clearly outperform the baselines on the test set for all benchmarks size. It reaches more than \(80\%\) accuracy when given at least \(25\%\) of the transitions for benchmarks with 6 variables and only \(10\%\) of input transitions is enough to obtain same performance with 9 variables. These results show that GULA, in a deterministic context, effectively learns rules that are close to the optimal ones even with a partial set of observations, showing its capacity in practice to generalize to unseen data. Such results will help to validate, using the data, models that were previously built and designed by the sole expert knowledge of the biological experts. Meanwhile we cannot rely only on deterministic semantics, as well-known models from the literature (e.g., the switch between the lytic and lysogenic cycles of the lambda phage (Thieffry and Thomas, 1995), which is composed of four components in interaction) require non-determinism to be captured efficiently.
For the non-deterministic case of asynchronous and general semantics the performance of GULA are similar but more observation are needed to obtain same performances. Like for previous experiments, in those cases we can have missing transitions for some of the observed feature states, leading to false negative examples extraction in GULA. This is more likely to happen with asynchronous semantics, since only one transition will show the change of a specific variable value from a given state while the general semantics will have several subset of change combined in a transitions. It also makes transitions less valuable in quantity of information in the asynchronous case, i.e., only one variable changes its value, starting from the second transition from the same state, all transitions only provide one positive example for the only variable that is changing its value. Still, GULA starts to outperform the most general rule baseline (and all others) for the two semantics when given more than \(50\%\) of the possible transitions as input. This shows again that our method can handle a bit of noise caused by missing observations also at the explanation level. The performances of GULA are similar when considering more variables here, the gain observed in value precision compensating the additional possibility for explanation error introduced by new variables.
It is important to recall that the baselines used here have perfect value prediction while our method also need to predict proper value to have it’s explanation evaluated. As stated before, it is certainly easier to achieve better prediction results using statistical machine learning methods. Furthermore, when good prediction model can be built from training data, it can replace our learned model to forecast the value but could be used to improve the output of GULA. Indeed, one can use such models to directly generate positive/negative examples of each atom from observed and unseen states that can be given as input to GULA in place of the raw observations. It can help to deal with noisy data and improve the diversity of initial state that can speed up and improve the quality of the rules of GULA and thus also its approximated version (Ribeiro et al., 2020). Actually, as long as feature and target variables are discrete (or can be properly discretized), GULA (or its approximated version for big systems) could be used to generate rules that could explain in a more human readable way the behavior of other less explainable models. Such a combination of predictive statistical model and \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) learning study is out of the scope of this paper but will be an interesting application part of our future works. This would not only allow to output relevant predictions w.r.t. dynamical trajectories of biological systems but also help to get a precise understanding of the underlying key interactions between components. Such an approach can also be considered for a broader range of applications. In Ortega et al. (2020), the authors investigate the promises conveys to provide declarative explanations in classical machine learning by neural networks in the context of automatic recruitment algorithms.
Explanation score of the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) learned by GULA and trivial baselines when predicting possible target atoms from unseen states with different amounts of training data of the transitions from Boolean network benchmarks with synchronous, asynchronous and general semantics
7.4 Readability of the model
So far we formalized methods and proposed algorithms in order to learn models of dynamical systems which predictions can be explained by human readable rules. Experiments and metrics of the previous sections evaluate the use of the model regarding both accuracy of predictions and quality of the explanation of the predictions. But one could also be interested about the explainability of the model itself: we could consider the readability of the program learned not only its use. In this section we do a short case study of the program learned by GULA on one of the benchmarks used in the previous experiments. Here we consider again the “faure_cellcycle” Boolean network (Fauré et al., 2006) that is composed of ten variables. Starting from the seminal contribution of Novak and Tyson, who proposed a set of ordinary differential equations (ODE) to model the mammalian cell cycle (Novák and Tyson, 2004, the authors of Fauré et al. (2006) synthesized the knowledge about the core control of mammalian cell division into a single logical model. This model, whose biological significance is high, appears as a good candidate to illustrate the impact of our contribution. As in the previous experiment, the original Boolean network is converted into its \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) equivalent as shown in Fig. 13.
Boolean functions of the “faure_cellcycle” Boolean network (Fauré et al., 2006), in .bnet file format from PyBoolNet (Klarner et al., 2016) (top) and the equivalent \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) (bottom). The rules colored in red are missing from the final learned model of Fig. 14 (Color figure online)
A training set and test set are randomly produced from all its synchronous transitions as in Fig. 10. Here we take about \(10\%\) of the transitions as the training set \(T^{\prime }\) and \(20\%\) as the test set \(T^{\prime \prime }\), with no common initial states in the two sets, as previously. The \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \((P_{{\mathcal {O}}}({T^{\prime }}),\overline{P_{{\mathcal {O}}}({T^{\prime }})})\) learned by GULA using the training set \(T^{\prime }\) as input achieves \(87.97\%\) accuracy and \(94.85\%\) explanation score. Each prediction explanation of the model is at most 40 rules: 10 Boolean variables make 20 possible atoms, and each target atom probability is explained by a rule of possibility and impossibility, thus multiplying by 2. The prediction explanation could arguably be considered readable but the program itself contains several thousands rules, in this example run: \(|P_{{\mathcal {O}}}({T^{\prime }})| = 9439\) and \(|\overline{P_{{\mathcal {O}}}({T^{\prime }})}| = 4520\).
To make the program more human readable, we can use a heuristic. What is readable or not depends of the context; for this case study, we will consider that a total of 40 rules is a reasonable number for our model and that rules with more than four conditions are not readable (thus bounding the maximal size of clauses observed in the Boolean network). As we have 10 variables in the studied Boolean network, we force to have no more than four rules per variable to achieve at most 40 rules of activation (rule with value of 1 as head) that will form our final readable model. For this, the best four rules for each possible head are selected according to their weight, the others are filtered out. We end up with at most 80 rules of possibility (resp. impossibility).
Applying this heuristic on \((P_{{\mathcal {O}}}({T^{\prime }}),\overline{P_{{\mathcal {O}}}({T^{\prime }})})\), we obtain a new \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \(WP = (WP^{\prime}, WP^{\prime \prime })\), with \(WP^{\prime} \subseteq P_{{\mathcal {O}}}({T^{\prime }})\) and \(WP^{\prime \prime } \subseteq \overline{P_{{\mathcal {O}}}({T^{\prime }})}\) (given in “Appendix” in Fig. 16). The accuracy of WP is \(97.45\%\) (+\(9.47\%\)) and explanation score is \(98.37\%\) (+\(3.52\%\)). In this example, the heuristic improved both scores but it could also reduce it; an important aspect of such a heuristic is to not lose too much prediction/explanation quality for readability. Furthermore, the rules of impossibility can now be ignored since they are only used for probabilistic predictions. Also, since we are considering only Boolean variables (and we know the system is determinist) we can also discard the rules with head atoms encoding the false value (typically: all atoms \(x^0\)). We end up with the 40 activation rules of Fig. 14 and can compare them to the original rules of the Boolean network.
The set of activation rules of the \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \((P_{{\mathcal {O}}}({T^{\prime }}), \overline{P_{{\mathcal {O}}}({T^{\prime }})})\) learned by GULA after pruning for readability. The rules that appear in the original \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) of Fig. 13 are colored in blue (Color figure online)
Here, 20 of the 22 original rules are in the final output, there are two missing rules (shown in Fig. 13) and 20 spurious rules. Most of the original program is found and the missing/spurious rules have a small impact as shown by the accuracy/explanation score. The presence of spurious rules is due to the lack of training observations, a few more negative examples could specialize them enough so that they become dominated by the original rules learned. For example, the three spurious rules of \(Cdc20_t^1\) will end up needing \(CycB_{t-1}^{1}\) as condition to remain consistent (since it is the only way to have \(Cdc20_t^1\) in the original program) with the observation and will be dominated by \(Cdc20_t^1 \leftarrow CycB_{t-1}^{1}\) and discarded. Discarding those spurious rules without the needed observation is not trivial, we could use a minimal weight of 10 for example to discard most of them but we would lose some original rules like the one of \(p27_t^1\). The weight of the rules, which is already used as a degree of confidence for the prediction of the dynamics, could also be used on the static model as a degree of confidence of the correctness of the rules. More complex analysis of the rule conditions and its relation with other rules could produce a better pruning, for example we could detect rules that will never be used for prediction, i.e., when another rule with better weight can always be applied. Developing such heuristics to ensure readability (in the sense simplicity) of the model itself would be interesting and the subject of future works.
8 Related work
8.1 Modeling dynamics
In modeling of dynamical systems, the notion of concurrency is crucial. Historically, two main dynamical semantics have been used in the field of systems biology: synchronous [Boolean networks of Stuart Kauffman (1969)] and asynchronous [René Thomas’ networks (1991)], although other semantics are sometimes proposed or used (Fages, 2020).
The choice of a given semantics has a major impact on the dynamical features of a model: attractors, trap domains, bifurcations, oscillators, etc. The links between modeling frameworks and their update semantics constitute the scope of an increasing number of papers. In Inoue (2011), the author exhibited the translation from Boolean networks into logic programs and discussed the point attractors in both synchronous and asynchronous semantics. In Noual and Sené (2018), the authors studied the synchronism-sensitivity of Boolean automata networks with regard to their dynamical behavior (more specifically their asymptotic dynamics). They demonstrate how synchronism impacts the asymptotic behavior by either modifying transient behaviors, making attractors grow or destroying complex attractors. Meanwhile, the respective merits of existing synchronous, asynchronous and generalized semantics for the study of dynamic behaviors has been discussed by Chatain and Paulevé in a series of recent papers. In Chatain et al. (2015), they introduced a new semantics for Petri nets with read arcs, called the interval semantics. Then they adapted this semantics in the context of Boolean networks (Chatain et al., 2018), and showed in Chatain et al. (2020) how the interval semantics can capture additional behaviors with regard to the already existing semantics. Their most recent work demonstrates how the most common synchronous and asynchronous semantics in Boolean networks have three major drawbacks that are to be costly for any analysis, to miss some behaviors and to predict spurious behaviors. To overcome these limits, they introduce a new paradigm, called Most Permissive Boolean Network which offers the guarantee that no realizable behavior by a qualitative model will be missed (Paulevé et al., 2020).
The choice of a relevant semantics appears clearly not only in the recent theoretical works bridging the different frameworks, but also in the features of the software provided to the persons involved in Systems Biology modeling [e.g., the GinSIM tool offers two updating modes, that are fully synchronous and fully asynchronous (Naldi et al. 2018)]. Analysis tools offer the modelers the choice of the most appropriate semantics with regard to their own problem.
8.2 Learning dynamics
In this paper, we proposed new algorithms to learn the dynamics of a system independently of its update semantics, and apply it to learn Boolean networks from the observation of their states transitions. Learning the dynamics of Boolean networks has been considered in bioinformatics in several works (Liang et al., 1998; Akutsu et al., 2003; Pal et al., 2005; Lähdesmäki et al. 2003; Fages 2020). In biological systems, the notion of concurrency is central. When modeling a biological regulatory network, it is necessary to represent the respective evolution of each component of the system. One of the most debated issues with regard to semantics targets the choice of a proper update mode of every component, that is, synchronous [Boolean networks of Stuart Kauffman (1969)], or asynchronous [René Thomas’ networks (1991)], or more complex ones. The differences and common features of different semantics w.r.t. properties of interest (attractors, oscillators, etc.) have thus resulted in an area of research per itself, especially in the field of Boolean networks (Noual & Sené, 2018; Chatain et al. 2018, 2020).
In Fages (2020), Fages discussed the differential semantics, stochastic semantics, Boolean semantics, hybrid (discrete and continuous) semantics, Petri net semantics, logic programming semantics and some learning techniques. Rather than focusing on particular semantics, our learning methods are complete algorithms that learn transition rules for any memory-less discrete dynamical systems independently of the update semantics.
As in Pal et al. (2005), we can also deal with partial transitions, but will not need to identify or enumerate all possible complete transitions. Pasula et al. (2007) learns a model as a probability distribution for the next state given the previous state and an action. Here, exactly one dynamic rule fires every time-step, which corresponds to the asynchronous semantics of Definition 16.
In Schüller and Benz (2018), action rules are learned using inductive logic programming but require as input background knowledge. In Bain and Srinivasan (2018), the authors use logic program as a meta-interpreter to explain the behaviour of a system as stepwise transitions in Petri nets. They produce new possible traces of execution, while our output is an interaction model of the system that aims to explain the observed behavior. In practice, our learned programs can also be used to predict unobserved behavior using some heuristics as shown in the experiments of Sect. 7.
Klarner et al. (2014) provide an optimization-based method for computing model reduction by exploiting the prime implicant graph of the Boolean network. This graph is similar to the rules of \(P_{{\mathcal {O}}}({T})\) that can be learned by GULA. But while Klarner et al. (2014) requires an existing model to work, we are able to learn this model from observations.
Lähdesmäki et al. (2003) propose algorithms to infer the truth table of Boolean functions of gene regulatory network from gene expression data.
Each positive (resp. negative) example represents a variable configuration that makes a Boolean function true (resp. false).
The logic programs learned by GULA are a generalization of those truth tables.
8.3 Inductive logic programming
From the inductive logic programming point of view, GULA performs a general to specific search, also called top-down approach. Algorithmically, GULA shares similarities with Progol (Muggleton, 1995, 1996) or Aleph (Srinivasan, 2001), two state-of-the-art ILP top-down approaches. Progol combines inverse entailment with general-to-specific search through a refinement graph. GULA is limited to propositional logic while those two methods handle first order predicates. Learning the equivalent of \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) rules should be possible using Progol or Aleph assuming some proper encoding. But both methods would only learn enough rules to explain the positive examples, whereas GULA outputs all optimal rules that can explain these examples. The completeness of the output program is critical when learning constraint of a \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) to guarantee the exact reproduction of the observed transitions. Thus, nor Progol or Aleph can replace GULA in the Synchronizer algorithm to learn the optimal \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\). But the completeness of the search of GULA comes with a higher complexity cost w.r.t. Progol and Aleph. The search of Progol and Aleph is guided by positives examples. Indeed, given a positive example, Progol performs an admissible A*-like search, guided by compression, over clauses which subsume the most specific clause (corresponding to the example). The search of GULA is guided by negative examples. It can also be seen as an A*-like search but for all minimal clauses that subsume none of the most specific clauses corresponding to the negative examples.
Evans et al. (2019, 2020) propose the Apperception Engine, a system able to learn programs from a sequence of state transitions. The first difference is that our approach is limited to propositional atoms while first order logic is considered in this approach. Furthermore, the Aperception Engine can predict the future, retrodict the past, and impute missing intermediate values, while we only consider rules to explain what can happen in a next state. But our input can represent transitions from multiple trajectories, while they consider a single trajectory and thus our setting can be considered as a generalized apperception task in the propositional case. Another major difference is that they only consider deterministic inputs while we also capture non-deterministic behaviors. Given the same kind of single trajectory and a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) (or \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\)), it should be possible to produce candidates past states or to try to fill in missing values. But in practice that would suppose to have many other transitions to build such \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) using GULA while the Aperception Engine can perform the task with only the given single trajectory. This system can also produce a set of constraints as well as rules. The constraints perform double duty: on the one hand, they restrict the sets of atoms that can be true at same time; on the other hand, they ensure what they call the frame axiom: each atom remains true at the next time-step unless it is overridden by a new fact which is incompatible with it. The constraints of \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) can prevent some combinations of atoms to appear, but only in next states, while in Evans et al. (2019, 2020), constraints can prevent some states to exist anywhere in the sequence, and ensure the conservation of atoms. From Theorem 7, the conservation can also be reproduced by \({\mathcal {C}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) by the right combination of optimal rules and constraints.
In Law et al. (2016) the authors propose a general framework named ILASP for learning answer set programs. ILASP is able to learn choice rules, constraints and preferences over answer sets. Our problem settings is related to what is called “context-dependant” tasks in ILASP. Our input can be straightforwardly represented using ILASP when variables are Boolean, but the learned program does not respect our notion of optimality, and thus our learning goals differ, i.e., we guarantee to miss no potential dynamical influence. Indeed, ILASP minimizes a program as a whole, i.e., the sum of the length of all rules and constraints; in contrast, we aim to minimize each rule and constraint individually and expect to find as many of them in practice and all of them in theory to ensure good properties regarding dynamical semantics.
Katzouris et al. (2015) proposes an incremental method to learn and revise event-based knowledge in the form of Event Calculus programs using XHAIL (Ray, 2009), a system that jointly abduce ground atoms and induce first-order normal logic programs. XHAIL needs to be provided with a set of mode declarations to limit the search space of possible induced rules, while our method do not require background knowledge. Still it is possible to exploit background knowledge with GULA: for example one could add heuristic inside the algorithm to discard rules with “too many” conditions; influences among variables, if known, could also be exploited to reduce possible bodies. Finally, XHAIL does not model constraints, thus is not able to prevent some combinations of atoms to appear in transitions, which can be achieve using our Synchronizer.
General research about evaluation of explainability in AI systems has been led into two major directions (Islam et al., 2020). One of them is about the evaluation of model complexity, while the second one focuses on human evaluation of explainability based on experimental studies involving a set of humans. Especially in the ILP litterature, Muggleton et al. (2018) the authors study the comprehensibility of logic programs and provide a definition of comprehensibility of hypotheses which can be estimated using human participant trials. In this work they evaluate the readability of entire programs while our explainability metric only considers the quality of the rules used for a prediction in a learned model. Furthermore, our metric evaluates a learned model against an ideal model that we consider readable at least by the experts that build it by hand, i.e., the biologists who build the Boolean network. Thus our metric cannot be used on a program alone contrary to the study of Muggleton et al. (2018) but requires the knowledge of the original program. The goal of our proposed explanation metric is to assess how the dynamics of a learned program approaches an expected one, not to provide a readability measure. This is done by considering both the choice taken (the value predicted) and the way the choice is made (the rules used).
9 Conclusions
While modeling a dynamical system, the choice of a proper semantics is critical for the relevance of the subsequent analysis of the dynamics. The works presented in this paper aim to widen the possibilities offered to a system designer in the learning phase. Until now, the systems that the LFIT framework handles were restricted to synchronous deterministic dynamics. However, many other dynamics exist in the field of logical modeling, in particular the asynchronous and generalized semantics which are of deep interest to model biological systems. In this paper, we proposed a modeling of memory-less multi-valued dynamic systems in the form of annotated logic programs and a first algorithm, GULA, that learns optimal programs for a wide range of semantics (see Theorem 1) including notably the asynchronous and generalized semantics. But the semantics need to be assumed to use the learned model, in order to produce predictions for example. Our second proposition is a new approach that makes a decisive step in the full automation of logical learning of models directly from time series, e.g., gene expression measurements along time (whose intrinsic semantics is unknown or even changeable). The Synchronizer algorithm that we proposed is able to learn a whole system dynamics, including its semantics, in the form of a single propositional logic program. This logic program explains the behavior of the system in the form of human readable propositional logic rules, as well as, be able to reproduce the behavior of the observed system without the need of knowing its semantics. Furthermore, the semantics can be explained, without any previous assumption, in the form of human readable rules inside the logic program.
This provides a precious output when dealing with real-life data coming from, e.g., biology. Typically, time series data capturing protein (i.e., gene) expressions come without any assumption on the most appropriate semantics to capture the relevant dynamical behaviors of the system. The methods introduced in this paper generate a readable view of the relationships between the different biological components at stake. GULA can be used when biological collaborators provide partial observations (as shown by our experiments), for example when addressing gene regulatory networks. Meanwhile the Synchronizer algorithm is of interest for systems with the full set of observations, e.g., when refining a model that was manually built by experts.
We took care to show the benefits of our approach on several benchmarks. While systems with ten components are able to capture the behavior of complex biological systems, we exhibit that our implementation is scalable to systems up to 10 components on a computer as simple as a single-core computer with a 1000 seconds time-out. Further work will consist in a practical use of our method on open problems coming from systems biology.
An approximate version of the method is a necessity to tackle large systems and is under development (Ribeiro et al., 2020). In addition, lack of observations and noise handling is also an issue when working with biological data. Data science methodologies and deep learning techniques can then be good candidates to tackle this challenge.
The combination of such techniques to improve our method may be of prime interest to tackle real data.
Availability of data and materials
Experiments data and sources code is available at https://github.com/Tony-sama/pylfit under GPL-3.0 License.
Code availability
Algorithms and experiments sources code is available at https://github.com/Tony-sama/pylfit under GPL-3.0 License.
Notes
Available at: https://github.com/Tony-sama/pylfit. Using command “python3 evaluations/mlj2020/mlj2020_all.py” from the repository’s tests folder, results will be in the tests/tmp folder. All experiements were run with the release version 0.2.2 https://github.com/Tony-sama/pylfit/releases/tag/v0.2.2.
Original Boolenet Boolean network files: https://people.kth.se/~dubrova/boolenet.html. Original PyBoolNet Boolean network files: https://github.com/hklarner/PyBoolNet/tree/master/PyBoolNet/Repository.
The polynomial approximation of GULA, currently named PRIDE is also available at: https://github.com/Tony-sama/pylfit
References
Akutsu, T., Kuhara, S., Maruyama, O., & Miyano, S. (2003). Identification of genetic networks by strategic gene disruptions and gene overexpressions under a boolean model. Theoretical Computer Science, 298(1), 235–251.
Apt, K. R., Blair, H. A., & Walker, A. (1988). Towards a theory of declarative knowledge. Foundations of deductive databases and logic programming p. 89
Bain, M., & Srinivasan, A. (2018). Identification of biological transition systems using meta-interpreted logic programs. Machine Learning, 107(7), 1171–1206.
Blair, H. A., & Subrahmanian, V. (1988). Paraconsistent foundations for logic programming. Journal of Non-classical Logic, 5(2), 45–73.
Blair, H. A., & Subrahmanian, V. (1989). Paraconsistent logic programming. Theoretical Computer Science, 68(2), 135–154. https://doi.org/10.1016/0304-3975(89)90126-6
Chatain, T., Haar, S., Kolčák, J., Paulevé, L., & Thakkar, A. (2020). Concurrency in boolean networks. Natural Computing, 19(1), 91–109.
Chatain, T., Haar, S., Koutny, M., & Schwoon, S. (2015). Non-atomic transition firing in contextual nets. In International conference on applications and theory of petri nets and concurrency (pp. 117–136). Springer.
Chatain, T., Haar, S., & Paulevé, L. (2018). Boolean networks: Beyond generalized asynchronicity. In AUTOMATA 2018. Springer.
Cropper, A., Dumančić, S., & Muggleton, S.H. (2020). Turning 30: New ideas in inductive logic programming. In Bessiere, C. (Ed.), Proceedings of the twenty-ninth international joint conference on artificial intelligence, IJCAI-20 (pp. 4833–4839). International Joint Conferences on Artificial Intelligence Organization. https://doi.org/10.24963/ijcai.2020/673. Survey track
Davidich, M. I., & Bornholdt, S. (2008). Boolean network model predicts cell cycle sequence of fission yeast. PLoS ONE, 3(2), e1672.
Dubrova, E., & Teslenko, M. (2011). A SAT-based algorithm for finding attractors in synchronous boolean networks. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), 8(5), 1393–1399.
Evans, R., Hernandez-Orallo, J., Welbl, J., Kohli, P., & Sergot, M. (2019). Making sense of sensory input. arXiv preprint arXiv:1910.02227
Evans, R., Hernandez-Orallo, J., Welbl, J., Kohli, P., & Sergot, M. (2020). Evaluating the apperception engine. arXiv preprint arXiv:2007.05367
Fages, F. (2020). Artificial intelligence in biological modelling. In A guided tour of artificial intelligence research (pp. 265–302). Springer.
Fauré, A., Naldi, A., Chaouiya, C., & Thieffry, D. (2006). Dynamical analysis of a generic boolean model for the control of the mammalian cell cycle. Bioinformatics, 22(14), e124–e131.
Fitting, M. (1991). Bilattices and the semantics of logic programming. The Journal of Logic Programming, 11(2), 91–116. https://doi.org/10.1016/0743-1066(91)90014-G
Gibart., L., Bernot., G., Collavizza., H., & Comet., J. (2021) Totembionet enrichment methodology: Application to the qualitative regulatory network of the cell metabolism. In Proceedings of the 14th international joint conference on biomedical engineering systems and technologies (BIOINFORMATICS) (pp. 85–92). INSTICC, SciTePress. https://doi.org/10.5220/0010186200850092.
Ginsberg, M. L. (1988). Multivalued logics: A uniform approach to reasoning in artificial intelligence. Computational Intelligence, 4(3), 265–316.
Inoue, K. (2011). Logic programming for boolean networks. In Proceedings of the twenty-second international joint conference on artificial intelligence, IJCAI’11 (Vol. 2, pp. 924–930). AAAI Press.
Inoue, K., Ribeiro, T., & Sakama, C. (2014). Learning from interpretation transition. Machine Learning, 94(1), 51–79.
Inoue, K., & Sakama, C. (2012). Oscillating behavior of logic programs. Correct Reasoning (pp. 345–362). Springer.
Islam, S. R., Eberle, W., & Ghafoor, S. K. (2020). Towards quantification of explainability in explainable artificial intelligence methods. In The thirty-third international flairs conference.
Kaplan, S., Bren, A., Dekel, E., & Alon, U. (2008). The incoherent feed-forward loop can generate non-monotonic input functions for genes. Molecular Systems Biology, 4(1), 203.
Katzouris, N., Artikis, A., & Paliouras, G. (2015). Incremental learning of event definitions with inductive logic programming. Machine Learning, 100(2–3), 555–585.
Kauffman, S. A. (1969). Metabolic stability and epigenesis in randomly constructed genetic nets. Journal of Theoretical Biology, 22(3), 437–467.
Kifer, M., & Subrahmanian, V. (1992). Theory of generalized annotated logic programming and its applications. Journal of Logic Programming, 12(4), 335–367.
Klarner, H., Bockmayr, A., & Siebert, H. (2014). Computing symbolic steady states of boolean networks. In Cellular automata (pp. 561–570). Springer.
Klarner, H., Streck, A., & Siebert, H. (2016). PyBoolNet: A python package for the generation, analysis and visualization of boolean networks. Bioinformatics, 33(5), 770–772. https://doi.org/10.1093/bioinformatics/btw682
Lähdesmäki, H., Shmulevich, I., & Yli-Harja, O. (2003). On learning gene regulatory networks under the boolean network model. Machine Learning, 52(1–2), 147–167.
Law, M., Russo, A., & Broda, K. (2016). Iterative learning of answer set programs from context dependent examples. Theory and Practice of Logic Programming, 16(5–6), 834–848. https://doi.org/10.1017/S1471068416000351
Liang, S., Fuhrman, S., & Somogyi, R. (1998). Reveal, a general reverse engineering algorithm for inference of genetic network architectures. In Proceedings of the 3rd pacific symposium on biocomputing (pp. 18–29).
Martınez, D., Alenya, G., Torras, C., Ribeiro, T., & Inoue, K. (2016). Learning relational dynamics of stochastic domains for planning. In Proceedings of the 26th international conference on automated planning and scheduling.
Martínez Martínez, D., Ribeiro, T., Inoue, K., Alenyà Ribas, G., & Torras, C. (2015). Learning probabilistic action models from interpretation transitions. In Proceedings of the technical communications of the 31st international conference on logic programming (ICLP 2015) (pp. 1–14).
Muggleton, S. (1995). Inverse entailment and progol. New Generation Computing, 13(3–4), 245–286.
Muggleton, S. (1996). Learning from positive data. In International conference on inductive logic programming (pp. 358–376). Springer.
Muggleton, S., De Raedt, L., Poole, D., Bratko, I., Flach, P., Inoue, K., & Srinivasan, A. (2012). Ilp turns 20. Machine learning, 86(1), 3–23.
Muggleton, S. H., Schmid, U., Zeller, C., Tamaddoni-Nezhad, A., & Besold, T. (2018). Ultra-strong machine learning: Comprehensibility of programs learned with ILP. Machine Learning, 107(7), 1119–1140.
Naldi, A., Hernandez, C., Abou-Jaoudé, W., Monteiro, P. T., Chaouiya, C., & Thieffry, D. (2018). Logical modeling and analysis of cellular regulatory networks with Ginsim 3.0. Frontiers in Physiology, 9, 646.
Noual, M., & Sené, S. (2018). Synchronism versus asynchronism in monotonic boolean automata networks. Natural Computing, 17(2), 393–402.
Novák, B., & Tyson, J. J. (2004). A model for restriction point control of the mammalian cell cycle. Journal of Theoretical Biology, 230(4), 563–579.
Ortega, A., Fierrez, J., Morales, A., Wang, Z., & Ribeiro, T. (2020). Symbolic AI for XAI: Evaluating LFIT inductive programming for fair and explainable automatic recruitment. Target, 1(v1), 1.
Pal, R., Ivanov, I., Datta, A., Bittner, M. L., & Dougherty, E. R. (2005). Generating boolean networks with a prescribed attractor structure. Bioinformatics, 21(21), 4021–4025.
Pasula, H. M., Zettlemoyer, L. S., & Kaelbling, L. P. (2007). Learning symbolic models of stochastic domains. Journal of Artificial Intelligence Research, 29, 309–352.
Paulevé, L., Kolčák, J., Chatain, T., & Haar, S. (2020). Reconciling qualitative, abstract, and scalable modeling of biological networks. bioRxiv.
Ray, O. (2009). Nonmonotonic abductive inductive learning. Journal of Applied Logic, 7(3), 329–340.
Ribeiro, T., Folschette, M., Magnin, M., Roux, O., & Inoue, K. (2018). Learning dynamics with synchronous, asynchronous and general semantics. In International conference on inductive logic programming (pp. 118–140). Springer.
Ribeiro, T., Folschette, M., Trilling, L., Glade, N., Inoue, K., Magnin, M., & Roux, O. (2020). Les enjeux de l’inférence de modèles dynamiques des systèmes biologiques à partir de séries temporelles. In C. Lhoussaine & E. Remy (Eds.), Approches symboliques de la modélisation et de l’analyse des systèmes biologiques. ISTE Editions. In edition.
Ribeiro, T., & Inoue, K. (2015). Learning prime implicant conditions from interpretation transition. In Inductive logic programming (pp. 108–125). Springer.
Ribeiro, T., Magnin, M., Inoue, K., & Sakama, C. (2015a). Learning delayed influences of biological systems. Frontiers in Bioengineering and Biotechnology, 2, 81.
Ribeiro, T., Magnin, M., Inoue, K., & Sakama, C. (2015b). Learning multi-valued biological models with delayed influence from time-series observations. In 2015 IEEE 14th international conference on machine learning and applications (ICMLA) (pp. 25–31). https://doi.org/10.1109/ICMLA.2015.19
Ribeiro, T., Tourret, S., Folschette, M., Magnin, M., Borzacchiello, D., Chinesta, F., Roux, O., & Inoue, K. (2018). Inductive learning from state transitions over continuous domains. In N. Lachiche & C. Vrain (Eds.), Inductive logic programming (pp. 124–139). Cham: Springer International Publishing.
Schüller, P., & Benz, M. (2018). Best-effort inductive logic programming via fine-grained cost-based hypothesis generation. Machine Learning, 107(7), 1141–1169.
Srinivasan, A. (2001). The aleph manual.
Thieffry, D., & Thomas, R. (1995). Dynamical behaviour of biological regulatory networks-II. Immunity control in bacteriophage lambda. Bulletin of Mathematical Biology, 57(2), 277–297.
Thomas, R. (1991). Regulatory networks seen as asynchronous automata: A logical description. Journal of Theoretical Biology, 153(1), 1–23.
Van Emden, M. H. (1986). Quantitative deduction and its fixpoint theory. The Journal of Logic Programming, 3(1), 37–53.
Van Emden, M. H., & Kowalski, R. A. (1976). The semantics of predicate logic as a programming language. Journal of the ACM (JACM), 23(4), 733–742.
Funding
This work was supported by JSPS KAKENHI Grant Number JP17H00763 and by the “Pays de la Loire” Region through RFI Atlanstic 2020.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Editors: Nikos Katzouris, Alexander Artikis, Luc De Raedt, Artur d’Avila Garcez, Ute Schmid, Sebastijan Dumančić, Jay Pujara.
Appendices
Appendix 1: Proofs of Sect. 2
Lemma 1
(Double Domination Is Equality) Let \(R_1, R_2\) be two \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules. If \({R_2}\ge {R_1}\) and \({R_1}\ge {R_2}\) then \(R_1=R_2\).
Proof
Let \(R_1, R_2\) be two \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules such that \({R_2}\ge {R_1}\) and \({R_1}\ge {R_2}\). Then \({\text {head}}(R_1) = {\text {head}}(R_2)\) and \({\text {body}}(R_1) \subseteq {\text {body}}(R_2)\) and \({\text {body}}(R_2) \subseteq {\text {body}}(R_1)\), hence \({\text {body}}(R_1) \subseteq {\text {body}}(R_2) \subseteq {\text {body}}(R_1)\) thus \({\text {body}}(R_1)={\text {body}}(R_2)\) and \(R_1=R_2\). \(\square\)
Proposition 1
(Uniqueness of Optimal Program) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The \({\mathcal {M}}{\mathrm {VLP}}\) optimal for T is unique and denoted \(P_{{\mathcal {O}}}({T})\).
Proof
Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). Assume the existence of two distinct \({\mathcal {M}}{\mathrm {VLP}}\)s optimal for T, denoted by \(P_{{\mathcal {O}}_1}(T)\) and \(P_{{\mathcal {O}}_2}(T)\) respectively. Then w.l.o.g. we consider that there exists a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R such that \(R\in P_{{\mathcal {O}}_1}(T)\) and \(R\not \in P_{{\mathcal {O}}_2}(T)\). By the definition of a suitable program, R is not conflicting with T and there exists a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule \(R_2\in P_{{\mathcal {O}}_2}(T)\), such that \({R_2}\ge {R}\). Using the same definition, there exists \(R_1\in P_{{\mathcal {O}}_1}(T)\) such that \({R_1}\ge {R_2}\) since \(R_2\) is not conflicting with T. Thus \({R_1}\ge {R}\) and by the definition of an optimal program \({R}\ge {R_1}\). By Lemma 1, \(R_1=R\), thus \({R_2}\ge {R}\) and \({R}\ge {R_2}\) hence \(R_2=R\), a contradiction. \(\square\)
Appendix 2: Proofs of Sect. 3
Theorem 1
(Characterisation of Pseudo-idempotent Semantics of Interest) Let DS be a dynamical semantics.
If, for all P a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), there exists \(\mathsf {pick}\in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({{\mathcal {A}}}\vert _{{\mathcal {T}}}) \rightarrow \wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \})\) so that:
-
(1)
\(\forall D \subseteq {{\mathcal {A}}}\vert _{{\mathcal {T}}}, \mathsf {pick}(s,\mathop {\bigcup }\limits _{{s^{\prime} \in \mathsf {pick}(s,D)}}s^{\prime}) = \mathsf {pick}(s,D)\), and
-
(2)
\(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \big (DS(P)\big )(s) = \mathsf {pick}(s,\mathsf {Conclusions}(s, P))\),
then DS is pseudo-idempotent.
Proof
Let DS be a dynamical semantics, P a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\), \(\mathsf {pick}\) a function from \({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {A}}_{\mathcal {T}})\) to \(\wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \}\) with the properties described in (1) and (2).
In this proof, we use the following equivalent notations, for all \((s, s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\): \((s, s^{\prime}) \in DS(P) \iff s^{\prime} \in \big (DS(P)\big )(s)\).
By Definition 10, \(\mathrm {first}(DS(P)) = {\mathcal {S}}^{{\mathcal {F}}}\) (\(*\)).
By Definition 9, \(P_{{\mathcal {O}}}({DS(P)})\) realizes DS(P). Therefore, according to Definition 5, for all \((s,s^{\prime})\) in DS(P) and \(\mathrm {v}^{{val}}\) in \(s^{\prime}\), because \(\mathrm {v}\in {\mathcal {T}}\), there exists R in \(P_{{\mathcal {O}}}({DS(P)})\) so that \(\mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\wedge R \sqcap s \wedge {\text {head}}(R) \in s^{\prime}\). Because of Definition 3, a discrete state cannot contain two different atoms on the same variable: from \(\mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\wedge \mathrm {v}^{{val}}\in s^{\prime} \wedge {\text {head}}(R) \in s^{\prime}\), it comes: \({\text {head}}(R) = \mathrm {v}^{{val}}\). Moreover, by definition of \(\mathsf {Conclusions}\), because \(R \in P \wedge R \sqcap s\), we have: \(\mathrm {v}^{{val}}\in \mathsf {Conclusions}(s,P_{{\mathcal {O}}}({DS(P)}))\). By generalizing on all \(\mathrm {v}^{{val}}\), it comes: \(s^{\prime} \subseteq \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)}))\). By generalizing on all \(s^{\prime}\), it comes: \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \mathop {\bigcup }\limits _{{s^{\prime} \in (DS(P))(s)}}s^{\prime} \subseteq \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)}))\) (\(\dagger\)).
By Definition 9, \(P_{{\mathcal {O}}}({DS(P)})\) is also consistent with DS(P). Therefore, according to Definition 7: \(\forall R \in P_{{\mathcal {O}}}({DS(P)}), \forall s \in \mathrm {first}(DS(P)), R \sqcap s \implies \exists s^{\prime} \in \big (DS(P)\big )(s), {\text {head}}(R) \in s^{\prime}\). From (\(*\)), \(\mathrm {first}(DS(P)) = {\mathcal {S}}^{{\mathcal {F}}}\), thus \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall \mathrm {v}^{{val}}\in \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})), \exists s^{\prime} \in DS(P)(s), \mathrm {v}^{{val}}\in s^{\prime}\). Thus: \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})) \subseteq \mathop {\bigcup }\limits _{{s^{\prime} \in (DS(P))(s)}}s^{\prime}\) (§).
From (\(\dagger\)) and (§): \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})) = \mathop {\bigcup }\limits _{{s^{\prime} \in (DS(P))(s)}}s^{\prime}\) (\(\star\)).
From (\(\star\)) and (2): \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})) = \mathop {\bigcup }\limits _{{s^{\prime} \in \mathsf {pick}(s, \mathsf {Conclusions}(s, P))}}s^{\prime}\) (\(\lozenge\)).
Let s in \({\mathcal {S}}^{{\mathcal {F}}}\).
-
From (2): \(\big (DS(P_{{\mathcal {O}}}({DS(P)}))\big )(s) = \mathsf {pick}(s,\mathsf {Conclusions}(s, P_{{\mathcal {O}}}({DS(P)})))\).
-
From (\(\lozenge\)): \(\big (DS(P_{{\mathcal {O}}}({DS(P)}))\big )(s) = \mathsf {pick}(s,\mathop {\bigcup }\limits _{{s^{\prime} \in \mathsf {pick}(s,\mathsf {Conclusions}(s, P))}}s^{\prime})\)
-
From (1): \(\big (DS(P_{{\mathcal {O}}}({DS(P)}))\big )(s) = \mathsf {pick}(s,\mathsf {Conclusions}(s, P))\)
-
From (2): \(\big (DS(P_{{\mathcal {O}}}({DS(P)}))\big )(s) = \big (DS(P)\big )(s)\).
Thus: \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \big (DS(P_{{\mathcal {O}}}({DS(P)}))\big )(s) = \big (DS(P)\big )(s)\), QED. \(\square\)
Theorem 2
(Semantics-Free Correctness) Let P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\).
-
\({\mathcal {T}}_{syn}(P) = {\mathcal {T}}_{syn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{syn}(P)}))\),
-
\({\mathcal {T}}_{asyn}(P) = {\mathcal {T}}_{asyn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{asyn}(P)}))\),
-
\({\mathcal {T}}_{gen}(P) = {\mathcal {T}}_{gen}(P_{{\mathcal {O}}}({{\mathcal {T}}_{gen}(P)}))\).
Proof
Let \(d \in ({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {T}}) \rightarrow \wp ({\mathcal {A}}_{{\mathcal {T}}}))\), so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall W \subseteq {\mathcal {T}}, W \subseteq \mathrm {var}({d(s, W)}) \wedge d(s,\emptyset ) \subseteq d(s,W)\).
Let p be a function from \({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {A}}_{{\mathcal {T}}})\) to \(\wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \}\) so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall D \subseteq {\mathcal {A}}_{\mathcal {T}}, p(s, D) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D})) \}\). Since \({\mathcal {T}}\setminus \mathrm {var}({D}) \subseteq \mathrm {var}({d(s, W)}), \emptyset \not \in p(s,D)\). Thus from Definition 15, \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, {\mathcal {T}}_{syn}(P)(s) = p(s,\mathsf {Conclusions}(s, P))\) (property 1).
Since \(\forall W \subseteq {\mathcal {T}}, d(s,\emptyset ) \subseteq d(s,W)\), \(\forall D \subseteq {\mathcal {A}}_{\mathcal {T}}, d(s,\emptyset ) \subseteq D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D}))\), thus \(d(s,\emptyset ) \subseteq \mathop {\bigcup }\limits _{{s^{\prime} \in p(s,D)}}s^{\prime}\) (property 2).
Moreover, \(\forall D \subseteq {\mathcal {A}}_{{\mathcal {T}}}\), let \(D^{\prime} := \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}\). Straightforwardly: \(D^{\prime} = D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D}))\) because we can always create a state with any atom in \(D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D}))\), thus all atoms of this set are in \(D^{\prime}\), and conversely (property 3). \(p(s,D^{\prime}) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq D^{\prime} \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D^{\prime}})) \}\) by definition of p. \(p(s,D^{\prime}) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq D^{\prime} \cup d(s, \emptyset ) \}\) since \(\mathrm {var}({D^{\prime}}) = {\mathcal {T}}\) by definition of \(D^{\prime}\) and p. \(p(s,D^{\prime}) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq D^{\prime} \}\) from property 2. \(p(s,D^{\prime}) = \{ s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \in D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D})) \} = p(s, D)\) from property 3. Therefore p respects (1). Since \({\mathcal {T}}_{syn}(P) = p(s,\mathsf {Conclusions}(s,P))\), p also respects (2). Thus, \({\mathcal {T}}_{syn}(P) = {\mathcal {T}}_{syn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{syn}(P)}))\) according to Theorem 1.
By definition of \({\mathcal {T}}_{gen}\): \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, ({\mathcal {T}}_{gen}(P))(s) = \{s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s^{\prime} \subseteq \mathsf {Conclusions}(s, P) \cup d(s,T\setminus \mathrm {var}({\mathsf {Conclusions}(s, P)}))\}\) with \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq d(s,\emptyset )\). Thus, the same proof gives \({\mathcal {T}}_{gen}(P) = {\mathcal {T}}_{gen}(P_{{\mathcal {O}}}({{\mathcal {T}}_{gen}(P)}))\) according to Theorem 1.
\({\mathcal {T}}_{asyn}(P) = {\mathcal {T}}_{asyn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{asyn}(P)}))\) Let p be a function from \({\mathcal {S}}^{{\mathcal {F}}}\times \wp ({\mathcal {A}}_{{\mathcal {T}}})\) to \(\wp ({\mathcal {S}}^{{\mathcal {T}}}) \setminus \{ \emptyset \}\) so that \(\forall s \in {\mathcal {S}}^{{\mathcal {F}}}, \forall D \subseteq {\mathcal {A}}_{\mathcal {T}}\):
where \({\mathcal {A}}_{\mathcal {T}}\) and \(D_{{\overline{{\mathcal {T}}}}}\) are restriction notations from Definition 12. From Definition 16, we have: \({\mathcal {T}}_{asyn}{P} = p(s,\mathsf {Conclusions}(s,P))\).
\(\forall D \subseteq {\mathcal {A}}_{\mathcal {T}}, p(s, \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}) = p(s, D)\) Let D in \({\mathcal {A}}_{\mathcal {T}}\).
-
If \((D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D})))_{{\overline{{\mathcal {T}}}}}= \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)\), then \(\mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime} = D\) and thus \(p(s, \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}) = p(s, D)\).
-
If there exists \(\mathrm {v}^{{val}}\in {\mathcal {A}}_{{\overline{{\mathcal {T}}}}}\) so that \(\mathrm {var}({D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D})) \setminus \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)}) \cap {{\overline{{\mathcal {T}}}}}= \{ \mathrm {v}\}\), then for all state \(s^{\prime} \in p(s, D)\), \(s^{\prime}\) differs from s on the regular variable \(\mathrm {v}\) and on variables in \({\mathcal {T}}\setminus {{\overline{{\mathcal {T}}}}}\). Thus, \(\mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime} = (D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D}))) \setminus \{ \mathrm {v}^{{val}^{\prime}} \mid \mathrm {v}^{{val}^{\prime}} \in s \}\). By construction of p, it comes: \(p(s, \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}) = p(s, D)\) because \(\mathrm {v}^{{val}^{\prime}} \in s^{\prime}\) would contradict the condition \(|s^{\prime} \setminus \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)| - |{\mathcal {T}}\setminus {{\overline{{\mathcal {T}}}}}| = 1\).
-
Otherwise, \(|\mathrm {var}({D \cup d(s,{\mathcal {T}}\setminus \mathrm {var}({D})) \setminus \mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)}) \cap {{\overline{{\mathcal {T}}}}}| > 1\) then there exists two states \(s^{\prime}_1, s^{\prime}_2 \in p(s, D)\), so that they differ from s on a different regular variable each. Especially, by construction of p, \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s) \subseteq s^{\prime}_1 \cup s^{\prime}_2 \subseteq D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D}))\). Therefore, \(\mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime} \subseteq D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D}))\). Finally, and by definition of p, \(D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D})) \subseteq \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}\) because for each atom in \(D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D}))\), it is possible to build a state \(s^{\prime}\) containing it: either as the projection of the initial state s or as the only variable changing its value in \(s^{\prime}\) compared to \(\mathsf {sp}_{{{\overline{{\mathcal {F}}}}}\rightarrow {{\overline{{\mathcal {T}}}}}}(s)\). In conclusion: \(D \cup d(s, {\mathcal {T}}\setminus \mathrm {var}({D})) = \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}\), which gives: \(p(s, \mathop {\bigcup }\limits _{{s^{\prime} \in p(s, D)}}s^{\prime}) = p(s, D)\).
Thus, \({\mathcal {T}}_{asyn}(P) = {\mathcal {T}}_{asyn}(P_{{\mathcal {O}}}({{\mathcal {T}}_{asyn}(P)}))\), according to Theorem 1. \(\square\)
Appendix 3: Proofs of Sect. 4
Theorem 3
(Properties of Least Revision) Let R be a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule and \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) such that \(R \sqcap s\). Let \(S_R:=\{s^{\prime} \in {\mathcal {S}}^{{\mathcal {F}}}\mid R \sqcap s^{\prime}\}\) and \(S_{\mathrm {spe}}:=\{s^{\prime} \in {\mathcal {S}}^{{\mathcal {F}}}\mid \exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s^{\prime}\}\).
Let P be a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and \(T, T^{\prime }\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) such that \(|\mathrm {first}(T)| = 1 \wedge \mathrm {first}(T) \cap \mathrm {first}(T^{\prime }) = \emptyset\). The following results hold:
-
1.
\(S_{\mathrm {spe}}=S_R \setminus \{s\}\),
-
2.
\(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is consistent with T,
-
3.
\(\mathop{\hookrightarrow} \limits^ {P}{T^{\prime }} \implies {\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T^{\prime }}}\),
-
4.
\(\mathop{\hookrightarrow}\limits^{P }{T} \implies {\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T}}\),
-
5.
P is complete \(\implies L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is complete.
Proof
-
1.
First, let us suppose that \(\exists s^{\prime \prime } \not \in S_R \setminus \{s\}\) such that \(\exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s^{\prime \prime }\). By definition of matching \(R^{\prime} \sqcap s^{\prime \prime } \implies {\text {body}}(R^{\prime}) \subseteq s^{\prime \prime }\). By definition of least specialization, \({\text {body}}(R^{\prime}) = {\text {body}}(R) \cup \{\mathrm {v}^{{val}}\}, \mathrm {v}^{{val}^{\prime}}\in s, \mathrm {v}^{{val}} \not \in {\text {body}}(R), {val}\ne {val}^{\prime}\). Let us suppose that \(s^{\prime \prime } = s\), then \({\text {body}}(R^{\prime}) \not \subseteq s^{\prime \prime }\) since \(\mathrm {v}^{{val}}\in {\text {body}}(R^{\prime})\) and \(\mathrm {v}^{{val}}\not \in s\), this is a contradiction. Let us suppose that \(s^{\prime \prime } \ne s\) then \(\lnot (R \sqcap s^{\prime \prime })\), thus \({\text {body}}(R) \not \subseteq s^{\prime \prime }\) and \({\text {body}}(R^{\prime}) \not \subseteq s^{\prime \prime }\), this is a contradiction. Second, let us assume that \(\exists s^{\prime \prime }\in S_R\setminus \{s\}\) such that \(\forall R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), \lnot (R^{\prime} \sqcap s^{\prime \prime })\). By definition of \(S_R\), \(R \sqcap s^{\prime \prime }\). By definition of matching \(\lnot (R^{\prime} \sqcap s^{\prime \prime }) \implies {\text {body}}(R^{\prime}) \not \subseteq s^{\prime \prime }\). By definition of least specialization, \({\text {body}}(R^{\prime}) = {\text {body}}(R) \cup \{\mathrm {v}^{{val}}\}, \mathrm {v}^{{val}^{\prime}}\in s, {val}\ne {val}^{\prime}\). By definition of matching \(R \sqcap s^{\prime \prime } \implies {\text {body}}(R) \subseteq s^{\prime \prime } \implies s^{\prime \prime } = {\text {body}}(R) \cup I, {\text {body}}(R) \cap I = \emptyset\) and thus \({\text {body}}(R^{\prime}) \not \subseteq s^{\prime \prime } \implies \mathrm {v}^{{val}}\not \in I\). The assumption implies that \(\forall \mathrm {v}^{{val}^{\prime}}\in I, \forall R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), \mathrm {v}^{{val}}\in {\text {body}}(R^{\prime}), {val}\ne {val}^{\prime}\). By definition of least specialization, it implies that \(\mathrm {v}^{{val}^{\prime}}\in s\) and thus \(I = s \setminus {\text {body}}(R)\) making \(s^{\prime \prime } = s\), which is a contradiction. Conclusion: \(S_{\mathrm {spe}}=S_R \setminus \{s\}\)
-
2.
By definition of a consistent program, if two sets of \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules \(SR_1, SR_2\) are consistent with T then \(SR_1 \cup SR_2\) is consistent with T. Let \(R_P=\{R\in P \mid R \sqcap s, \forall (s,s^{\prime}) \in T, {\text {head}}(R) \not \in s^{\prime}\}\) be the set of rules of P that conflict with T. By definition of least revision \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})=(P \setminus R_P) \cup \mathop {\bigcup }\limits _{{R \in R_P}}L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\). The first part of the expression \(P \setminus R_P\) is consistent with T since \(\not \exists R^{\prime} \in P \setminus R_P\) such that \(R^{\prime}\) conflicts with T. The second part of the expression \(\mathop {\bigcup }\limits _{{R \in R_P}}L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) is also consistent with T: \(\not \exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s\) thus \(\not \exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) that conflict with T and \(\mathop {\bigcup }\limits _{{R \in R_P}}L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) is consistent with T. Conclusion: \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is consistent with T.
-
3.
Let \((s_1,s_2) \in T^{\prime }\) thus \(s_1 \ne s\). From definition of realization, \(\mathrm {v}^{{val}}\in s_2 \implies \exists R \in P, {\text {head}}(R) = \mathrm {v}^{{val}}, R \sqcap s_1\). If \(\lnot R \sqcap s\) then \(R \in L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) and \(\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{{(s_1,s_2)}}\). If \(R \sqcap s\), from the first point \(\exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s_1\) and since \({\text {head}}(R^{\prime}) = {\text {head}}(R) = \mathrm {v}^{{val}}, \mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{{(s_1,s_2)}}\). Applying this reasoning on all elements of \(T^{\prime }\) implies that \(\mathop{\hookrightarrow} \limits^ {P}{T^{\prime }} \implies \mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T^{\prime }}\).
-
4.
Let \((s_1,s_2) \in T\), since \(\mathop{\hookrightarrow}\limits^{P }{T}\) by definition of realization \(\forall \mathrm {v}^{{val}}\in s_2, \exists R \in P, R \sqcap s_1, {\text {head}}(R) = \mathrm {v}^{{val}}\). By definition of conflict, R is not in conflict with T thus \(R \in L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) and \(\mathop{\hookrightarrow} \limits^ {L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})}{T}\).
-
5.
Let \((s_1,s_2) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), if P is complete, then by definition of a complete program \(\forall \mathrm {v}\in {\mathcal {V}}, \exists R \in P, R \sqcap s_1, \mathrm {var}({{\text {head}}({R})}) = v\). If \(\lnot (R \sqcap s)\) then \(R \in L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\). If \(R \sqcap s\), from the first point \(\exists R^{\prime} \in L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}}), R^{\prime} \sqcap s_1\) and thus \(R^{\prime} \in L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) and since \(\mathrm {var}({{\text {head}}({R^{\prime}})}) = \mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\), \(L_{\mathrm {rev}}(P,T,{\mathcal {A}},{\mathcal {F}})\) is complete.
\(\square\)
Proposition 2
(Optimal Program of Empty Set) \(P_{{\mathcal {O}}}({\emptyset })=\{\mathrm {v}^{{val}}\leftarrow \emptyset \mid \mathrm {v}^{{val}}\in {\mathcal {A}}_{\mathcal {T}}\}\).
Proof
Let \(P=\{\mathrm {v}^{{val}}\leftarrow \emptyset \mid \mathrm {v}^{{val}}\in {\mathcal {A}}_{\mathcal {T}}\}\). The \({\mathcal {M}}{\mathrm {VLP}}\) P is consistent and complete by construction. Like all \({\mathcal {M}}{\mathrm {VLP}}\)s, \(\mathop{\hookrightarrow} \limits^ {P}{\emptyset }\) and there is no transition in \(\emptyset\) to match with the rules in P. In addition, by construction, the rules of P dominate all \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rules. \(\square\)
Proposition 3
(From Suitable to Optimal) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). If P is a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for T, then \(P_{{\mathcal {O}}}({T})=\{R\in P\mid \forall R^{\prime}\in P,{R^{\prime}}\ge {R} \implies {R}\ge {R^{\prime}}\}\).
Proof
Since any possible \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule consistent with T is dominated, all the rules of the optimal program are dominated. Since the only rules dominating a rule of the optimal program is the rule itself, the optimal program is a subset of any suitable program. If we remove the dominated rules, only remains the optimal program. \(\square\)
Theorem 4
(Least Revision and Suitability) Let \(s \in {\mathcal {S}}^{{\mathcal {F}}}\) and \(T, T^{\prime }\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) such that \(|\mathrm {first}(T^{\prime })| = 1 \wedge \mathrm {first}(T) \cap \mathrm {first}(T^{\prime }) = \emptyset\). \(L_{\mathrm {rev}}(P_{{\mathcal {O}}}({T}),T^{\prime },{\mathcal {A}},{\mathcal {F}})\) is a \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) suitable for \(T \cup T^{\prime }\).
Proof
Let \(P=L_{\mathrm {rev}}(P_{{\mathcal {O}}}({T}),T^{\prime })\). Since \(P_{{\mathcal {O}}}({T})\) is consistent with T, by Theorem 3, P is also consistent with T and thus consistent with \(T^{\prime } \cup T\). Since \(P_{{\mathcal {O}}}({T})\) realizes T by Theorem 3, \(\mathop{\hookrightarrow}\limits^{P }{T}\). Since \(s \not \in \mathrm {first}(T)\), a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule R such that \({\text {body}}(R) = s\) does not conflict with T. By definition of suitable program \(\exists R^{\prime} \in P_{{\mathcal {O}}}({T}), {R^{\prime}}\ge {R}\), thus \(\mathop{\hookrightarrow} \limits^ {P_{{\mathcal {O}}}({T})}{T^{\prime }}\). Since \(\mathop{\hookrightarrow} \limits^ {P_{{\mathcal {O}}}({T})}{T^{\prime }}\) by Theorem 3\(\mathop{\hookrightarrow} \limits^ {P}{T^{\prime }}\) and thus \(\mathop{\hookrightarrow} \limits^ {P}{T \cup T^{\prime }}\). Since \(P_{{\mathcal {O}}}({T})\) is complete, by Theorem 3, P is also complete. To prove that P verifies the last point of the definition of a suitable \({\mathcal {M}}{\mathrm {VLP}}\), let R be a \({\mathcal {M}}\mathrm {V}\mathrm {L}\) rule not conflicting with \(T \cup T^{\prime }\). Since R is also not conflicting with T, there exists \(R^{\prime}\in P_{{\mathcal {O}}}({T})\) such that \({R^{\prime}}\ge {R}\). If \(R^{\prime}\) is not conflicting with \(T^{\prime }\), then \(R^{\prime}\) will not be revised and \(R^{\prime}\in P\), thus R is dominated by a rule of P. Otherwise, \(R^{\prime}\) is in conflict with \(T^{\prime }\), thus \(R^{\prime} \sqcap s\) and \(\forall (s,s^{\prime}) \in T^{\prime }, {\text {head}}(R^{\prime}) \not \in s^{\prime}\). Since R is not in conflict with \(T^{\prime }\) and \({\text {head}}(R) = {\text {head}}(R^{\prime})\), since \({R^{\prime}}\ge {R}\) then \({\text {body}}(R) = {\text {body}}(R^{\prime}) \cup I, \exists \mathrm {v}^{{val}}\in I, \mathrm {v}^{{val}}\not \in s\). By definition of least revision and least specialization, there is a rule \(R^{\prime \prime }\in L_{\mathrm {spe}}(R^{\prime},s)\) such that \(\mathrm {v}^{{val}}\in {\text {body}}(R^{\prime \prime })\) and since \(R^{\prime \prime } = {\text {head}}(R^{\prime}) \leftarrow {\text {body}}(R^{\prime}) \cup \mathrm {v}^{{val}}\) thus \({R^{\prime \prime }}\ge {R}\). Thus R is dominated by a rule of P. \(\square\)
Theorem 5
(GULA Termination, Soundness, Completeness, Optimality) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\).
-
(1)
Any call to GULA on finite sets terminates,
-
(2)
GULA\(({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}})=P_{{\mathcal {O}}}({T})\),
-
(3)
\(\forall {\mathcal {A}}^{\prime} \subseteq {{\mathcal {A}}}\vert _{{\mathcal {T}}}, \mathbf{GULA}({\mathcal {A}}_{{\mathcal {F}}} \cup {\mathcal {A}}^{\prime},T,{\mathcal {F}},{\mathcal {T}}) = \{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) \in {\mathcal {A}}^{\prime}\}\).
Proof
In this proof we refer to the detailed pseudo-code of GULA given in “Appendix” in Algorithm 5 and Algorithm 6.
(1) The algorithm of GULA iterates on finite sets, and thus terminates.
(3) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The algorithm iterates over each atom \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime}\), \({\mathcal {A}}^{\prime} \subseteq {\mathcal {A}}_{\mathcal {T}}\) iteratively to extract all states s such that \((s,s^{\prime}) \in T \implies \mathrm {v}^{{val}}\not \in s^{\prime}\). This is equivalent to group the transitions by initial state: generate the set \(TT = \{ T^{\prime }_s \subseteq T \mid s \in {\mathcal {S}}^{{\mathcal {F}}}, \mathrm {first}(T^{\prime }_s) = \{s\} \wedge \forall s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}, (s,s^{\prime}) \in T \implies (s,s^{\prime}) \in T^{\prime }_s \}\).
To prove that \(\forall {\mathcal {A}}^{\prime} \subseteq {\mathcal {A}}_{\mathcal {T}}, \mathbf{GULA}({\mathcal {A}}_{{\mathcal {F}}} \cup {\mathcal {A}}^{\prime},T,{\mathcal {F}},{\mathcal {T}}) = \{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) \in {\mathcal {A}}^{\prime}\}\) and thus GULA\(({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}})=P_{{\mathcal {O}}}({T})\), it suffices to prove that the main loop (Algorithm 5, lines 23-50) preserves the invariant \(P_\mathrm {v}^{{val}}=\{R \in P_{{\mathcal {O}}}({T_i}) \mid {\text {head}}(R) = \mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime}\}\) after the ith iteration where \(T_i\) is the union of all set of transitions of TT already selected line 23 after the ith iteration for all i from 0 to \(|TT|\).
Line 22 initializes \(P_{\mathrm {v}^{{val}}}\) to \(\{\mathrm {v}^{{val}}\leftarrow \emptyset \}\). Thus by Proposition 2, after line 22, \(P_{\mathrm {v}^{{val}}}= \{R \in P_{{\mathcal {O}}}({\emptyset }) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\).
Let us assume that before the \((i+1)\)th iteration of the main loop, \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({T_i})\mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\). Through the loop of lines 25-28, \(P^{\prime}=\{R\in P_{{\mathcal {O}}}({T_i})\mid R\text { does not conflict with }\) \(T_{i+1} \wedge {\text {head}}(R)=\mathrm {v}^{{val}}\}\) is computed. Then the set \(P^{\prime \prime }=\bigcup _{R\in P_{{\mathcal {O}}}({T_i})\backslash P^{\prime} \wedge {\text {head}}(R)=\mathrm {v}^{{val}}}L_{\mathrm {spe}}(R,s,{\mathcal {A}},{\mathcal {F}})\) is iteratively build through the calls to least_specialization (Algorithm 6) at line 31 and the dominated rules are pruned as they are detected by the loop of lines 32-49. Each revised rule can be dominated by a rule in \(\{R\in P_{{\mathcal {O}}}({T_i})\backslash P^{\prime}\}\) or another revised rule and thus dominance must be checked from both. But only a revised rule (\(R \in P^{\prime \prime }\)) can be dominated by a revised rule: if a rule in \(\{R\in P_{{\mathcal {O}}}({T_i})\backslash P^{\prime}\}\) is dominated by a revised rule, then it was dominated by its original rule in \(\{R\in P_{{\mathcal {O}}}({T_i})\}\) which is impossible since \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({T_i})\mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\). Thus it is safe to only check domination of the revised rules by previous rules (\(P_{{\mathcal {O}}}({T_i}) \setminus P^{\prime}\)) or by other revised rules (\(P^{\prime \prime }\)). Thus by Theorem 4 and Proposition 3, \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({T_{i+1}}) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\) after the \((i+1)\)th iteration of the main loop. By induction, at the end of all the loop lines 23-50, \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({\bigcup _{T^{\prime } \in TT} T^{\prime }})\mid {\text {head}}(R)=\mathrm {v}^{{val}}\}=\{R \in P_{{\mathcal {O}}}({T})\mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\) since it has iterated on all elements of TT. Since the same operation holds for each \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime}\), \(P=\bigcup _{\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime}}P_{\mathrm {v}^{{val}}} = \{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) = \mathrm {v}^{{val}}\wedge \mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime}\}\) after all iterations of the loop of line 6. Finally: \(\forall {\mathcal {A}}^{\prime} \subseteq {\mathcal {A}}_{\mathcal {T}}, \mathbf{GULA}({\mathcal {A}}_{{\mathcal {F}}} \cup {\mathcal {A}}^{\prime},T,{\mathcal {F}},{\mathcal {T}}) = \{ R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) \in {\mathcal {A}}^{\prime} \}\).
(2) Thus \(\mathbf{GULA}({\mathcal {A}},T,{\mathcal {F}},{\mathcal {T}})=\mathbf{GULA}({\mathcal {A}}_{\mathcal {F}}\cup {\mathcal {A}}_{\mathcal {T}},T,{\mathcal {F}},{\mathcal {T}})=\{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R) \in {\mathcal {A}}_{\mathcal {T}}\}=P_{{\mathcal {O}}}({T})\). \(\square\)
Theorem 6
(GULA Complexity) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) be a set of transitions, Let \(n := max(|{\mathcal {F}}|,|{\mathcal {T}}|)\) and \(d := \max (\{|{\mathsf {dom}}(\mathrm {v})|) \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\}\). The worst-case time complexity of GULA when learning from T belongs to \({\mathcal {O}}(|T|^2 + |T| \times (2n^4d^{2n+2} + 2n^3d^{n+1}))\) and its worst-case memory use belongs to \({\mathcal {O}}(d^{2n} + 2nd^{n+1} + nd^{n+2})\).
Proof
Let \(d_f:=\max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\})\) (resp. \(d_t :=\max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {T}}\})\)) be the maximal number of values of features (resp. target) variables.
The algorithm takes as input a set of transition \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) bounding the memory use to \(O(d_f^{|{\mathcal {F}}|}) \times d_t^{|{\mathcal {T}}|})=O(d^{2n})\). The learning is performed iteratively for each possible rule head \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime} \subseteq {\mathcal {A}}_{\mathcal {T}}\).
The extraction of negative example requires to compare each transition of T one to one and thus has a complexity of \(op_1=O(|T|^2)\). Those transitions are stored in \(N\!eg_{\mathrm {v}^{{val}}}\) which size is at most \(|{\mathcal {S}}^{{\mathcal {F}}}|\) extending the memory use to \(O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + d_f^{|{\mathcal {F}}|})\) which is bounded by \(O(d^{2n} + d^n)\).
The learning phase revises a set of rule \(P_{\mathrm {v}^{{val}}}\) where each rule has the same head \(\mathrm {v}^{{val}}\). There are at most \(d_f^{|{\mathcal {F}}|} \le d^{n}\) possible rule bodies and thus \(|P_{\mathrm {v}^{{val}}}| \le d_t^{|{\mathcal {F}}|} \le d^{n}\), the memory use of \(|P_{\mathrm {v}^{{val}}}|\) is then \(O(d_t^{|{\mathcal {F}}|})\) extending the memory bound to \(O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + d_f^{|{\mathcal {F}}|}) + d_f^{|{\mathcal {F}}|}) = O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + 2d_f^{|{\mathcal {F}}|}))\), which is bound by \(O(d^{2n} + 2d^n)\).
For each state s of \(N\!eg_{\mathrm {v}^{{val}}}\), each rule of \(P_{\mathrm {v}^{{val}}}\) that matches s are extracted into a set of rules \(R_m\). This operation has a complexity of \(op_2=O(d_f^{|{\mathcal {F}}|} \times |{\mathcal {F}}|)\) bound by \(O(nd^{n})\). Each rule of \(R_m\) are then revised using least specialization, this operation has a complexity of \(O(|{\mathcal {F}}|^2)\) bound by \(O(n^2)\). \(|R_m| \le d_f^{|{\mathcal {F}}|} \le d^{n}\) thus the revision of all matching rules is \(op_3=O(d_f^{|{\mathcal {F}}|} \times n^2)\) bounded by \(O(d^{n} \times n^2)\). All revisions are stored in LS and there are at most \(d_f \times |{\mathcal {F}}| \le dn\) revisions for each rule, thus \(|LS| \le d_f^{|{\mathcal {F}}|} \times d_f|{\mathcal {F}}| \le d^n \times dn\) extending the memory bound to \(O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + 2d_f^{|{\mathcal {F}}|}) + d_f|{\mathcal {F}}| \times d_f^{|{\mathcal {F}}|})\) bounded by \(O(d^{2n} + 2d^n + nd^{n+1})\).
Learning is performed for each \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime} \subseteq {\mathcal {T}}\), thus the memory usage of GULA is therefore \(O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + |{\mathcal {A}}^{\prime}|(2d_f^{|{\mathcal {F}}|} + d_f|{\mathcal {F}}| \times d_f^{|{\mathcal {F}}|}))\), bounded by \(O(d_f^{|{\mathcal {F}}|} \times d_t^{|{\mathcal {T}}|} + td_t(2d_f^{|{\mathcal {F}}|}) + d_f|{\mathcal {F}}| \times d_f^{|{\mathcal {F}}|}))\) wich is bounded by \(O(d^{2n} + dn(2d^n + nd^{n+1})) = O(d^{2n} + 2nd^{n+1} + nd^{n+2})\).
The worst-case memory use of GULA is thus \(O(d^{2n} + 2nd^{n+1} + nd^{n+2})\).
All rules of LS are compared to the rule of \(P_{\mathrm {v}^{{val}}}\) for domination check, this operation has a complexity of \(op_4=O(2 \times |LS| \times |P_{\mathrm {v}^{{val}}}| \times |{\mathcal {F}}|^2)=O(2 \times d_f^{|{\mathcal {F}}|} \times d_f|{\mathcal {F}}| \times d^n \times n^2)=O(2 \times |{\mathcal {F}}|^3 \times d_f^{2|{\mathcal {F}}|+1})\) which is bounded by \(O(2 \times n^3 \times d^{2n+1})\).
Learning is performed for each \(\mathrm {v}^{{val}}\in {\mathcal {A}}^{\prime} \subseteq {\mathcal {T}}\), \(|{\mathcal {A}}^{\prime}| \le |{\mathcal {T}}|d_t\), thus the complexity is bound by \(O(op_1 + |T|\times |{\mathcal {T}}| \times d_t(op_2 + op_3 + op_4))=O( |T|^2 + |T|\ times |{\mathcal {T}}| \times d_t( d_f^{|{\mathcal {F}}|} \times |{\mathcal {F}}| + d_f^{|{\mathcal {F}}|} \times n^2 + 2 \times |{\mathcal {F}}|^3 \times d_f^{2|{\mathcal {F}}|+1} ))\) which is bounded by \(O(|T|^2 + |T| \times nd(d^{n} \times n^2 + d^{n} \times n^2 + 2 \times n^3 \times d^{2n+1}))= O(|T|^2 + |T| \times nd(2n^3d^{2n+1} + 2n^2d^{n})) = O(|T|^2 + |T| \times (2n^4d^{2n+2} + 2n^3d^{n+1}))\).
The computational complexity of GULA is thus \(O(|T|^2 + |T| \times (2n^4d^{2n+2} + 2n^3d^{n+1}))\).
\(\square\)
Appendix 4: Proofs of Sect. 5
Theorem 7
(Optimal \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) and Constraints Correctness Under Synchronous Constrained Semantics) Let \(T \subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\), it holds that \(T = {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T}))\).
Proof
From Definition 9, \(\forall (s,s^{\prime}) \in T, s^{\prime} \subseteq \mathsf {Conclusions}(s,P_{{\mathcal {O}}}({T}))\) thus according to Definition 22, \(s^{\prime} \in {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}))(s)\), thus \(T \subseteq {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}))\) (property 1).
By Definition 25, \(\forall (s,s^{\prime}) \in T, \not \exists C \in C_{{\mathcal {O}}}({T}), C \sqcap (s,s^{\prime})\), thus since \(C^{\prime}_{{\mathcal {O}}}({T}) \subseteq C_{{\mathcal {O}}}({T}), \not \exists C \in C^{\prime}_{{\mathcal {O}}}({T}), C \sqcap (s,s^{\prime})\) and then \(T \subseteq {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T}))\) (property 2).
Let us suppose \(\exists (s,s^{\prime}) \in {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})), (s,s^{\prime}) \notin T\). From Definition 22, \(\forall \mathrm {v}^{{val}}\in s^{\prime}, \exists R \in P_{{\mathcal {O}}}({T}), {\text {body}}(R) \sqcap s, {\text {head}}(R) = \mathrm {v}^{{val}}\). From Definition 25, \(\exists C^{\prime} \in C_{{\mathcal {O}}}({T}), C^{\prime} \sqcap (s,s^{\prime})\) since \((s,s^{\prime}) \notin T\). But since \(\exists (s,s^{\prime}) \in {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T}))\), thus \(C^{\prime} \notin C^{\prime}_{{\mathcal {O}}}({T})\). From Definition 26, it implies that \(\exists \mathrm {v}^{{val}}\in s^{\prime}, \not \exists R \in P_{{\mathcal {O}}}({T}), {\text {head}}(R) = \mathrm {v}^{{val}}, \forall \mathrm {w}\in {\mathcal {F}}, \forall val^{\prime}, {val}^{\prime \prime } \in {\mathsf {dom}}(\mathrm {w}), \mathrm {w}^{val^{\prime}} \in {\text {body}}(R) \wedge \mathrm {w}^{val^{\prime \prime }} \in {\text {body}}(C) \implies val^{\prime} = val^{\prime \prime }\). Since \({\text {body}}(C^{\prime}) \subseteq (s \cup s^{\prime})\), \(\not \exists R \in P_{{\mathcal {O}}}({T}), {\text {head}}(R) = \mathrm {v}^{{val}}, {\text {body}}(R) \subseteq s\), thus \(s^{\prime} \not \subseteq \mathsf {Conclusions}(s,P_{{\mathcal {O}}}({T}))\) and by Definition 22, \((s,s^{\prime}) \not \in {\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T}))\), contradiction, thus \({\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})) \subseteq T\) (property 3).
From property 2 and 3: \({\mathcal {T}}_{syn-c}(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})) = T\). \(\square\)
Theorem 8
(Synchronizer Correctness) Given any set of transitions T,
Synchronizer(\({\mathcal {A}}\), T, \({\mathcal {F}}\), \({\mathcal {T}}\)) outputs \(P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\).
Proof
Let \(G1 = GULA({\mathcal {A}}, T, {\mathcal {F}}, {\mathcal {T}})\) and \(G2 = GULA({\mathcal {A}}_{{\mathcal {F}}\cup {\mathcal {T}}\cup \{\varepsilon ^1\}}, T^{\prime }, {\mathcal {F}}\cup {\mathcal {T}}, \{\varepsilon \})\). From Theorem 5, \(P = G1 = P_{{\mathcal {O}}}({T})\) (property 1).
Let \(P^{\prime} = G2\). By definition of \(T^{\prime }\): \(\forall (s,s^{\prime}) \in T^{\prime }, s^{\prime} = \{\varepsilon ^0\}\). Thus \(\forall R \in P^{\prime}\), R is consistent with \(T^{\prime }\) by Theorem 5, thus \(\not \exists (s,s^{\prime}) \in T^{\prime }, R \sqcap s\), since \({\text {head}}(R) = \varepsilon {}^1\) because \(\forall (s,s^{\prime}) \in T^{\prime }, s^{\prime} = \{\varepsilon ^0\}\) (property 2).
From Theorem 5, \(P^{\prime} = \{R \in P_{{\mathcal {O}}}({T^{\prime }}) \mid {\text {head}}(R) = \varepsilon ^1\}\). From Definition 9, \(P_{{\mathcal {O}}}({T^{\prime }})\) is complete thus \(\forall (s,s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}, ss^{\prime} := s \cup s^{\prime}, ss^{\prime} \notin \mathrm {first}(T^{\prime }), \exists R \in P^{\prime}, R \sqcap ss^{\prime}\) (property 3).
From definition of \(T^{\prime }\), \((s,s^{\prime}) \in T \implies (s \cup s^{\prime},\{\varepsilon ^0\}) \in T^{\prime }\), thus \(\forall C \in P^{\prime}, C\) is a constraint (property 4).
-
From property 2 and 4: \((s, s^{\prime}) \in T \implies (s \cup s^{\prime}, \{\varepsilon ^0\}) \in T^{\prime } \implies \not \exists C \in P^{\prime}, C \sqcap (s,s^{\prime})\), \(P^{\prime}\) consistent with T.
-
From property 3 and 4: \((s, s^{\prime}) \not \in T \implies (s \cup s^{\prime}) \not \in \mathrm {first}(T^{\prime }) \implies \exists R \in P^{\prime}, R \sqcap (s,s^{\prime})\), \(P^{\prime}\) is complete with T.
-
If there exists a constraint consistent with T that is not dominated by a constraint in \(P^{\prime}\) it implies that a rule consistent with \(T^{\prime }\) whose head is \(\varepsilon ^1\) is not dominated by a rule in G2 wich is in contradiction with Theorem 5. All constraint consistent with T are dominated by a constraint in \(P^{\prime}\).
-
From Theorem 5, the rules of G2 do not dominate eachover, thus the same hold for the constraint of \(P^{\prime}\).
-
From Definition 25, \(P^{\prime} = C_{{\mathcal {O}}}({T})\) (property 5).
Now let us prove that \(P^{\prime \prime }= C^{\prime}_{{\mathcal {O}}}({T})\). Let us suppose that \(P^{\prime \prime } \ne C^{\prime}_{{\mathcal {O}}}({T})\). Since \(P^{\prime \prime } \subseteq C_{{\mathcal {O}}}({T})\), according to Definition 26, therefore \(P^{\prime \prime }\) is missing a useful optimal constraint (\(C^{\prime}_{{\mathcal {O}}}({T}) \setminus P^{\prime \prime } \ne \emptyset\)), or contains a useless optimal constraint (\(P^{\prime \prime } \setminus C^{\prime}_{{\mathcal {O}}}({T}) \ne \emptyset\)).
1) Suppose that \(C \notin P^{\prime \prime }\) but \(C \in C^{\prime}_{{\mathcal {O}}}({T})\), meaning that \(P^{\prime \prime }\) misses a useful constraint C. Since \(C \in C^{\prime}_{{\mathcal {O}}}({T})\), \(\exists (s,s^{\prime}) s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime}\), \(C \sqcap (s,s^{\prime})\). Since \(s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime}\), according to Definition 5\(\exists S \subseteq P_{{\mathcal {O}}}({T}), s^{\prime} = \{{\text {head}}(R) \mid R \in S\} \wedge \forall R \in S, R \sqcap s\). By Definition 21, \(C \subseteq s \cup s^{\prime}\) thus \({\text {body}}(C) \cap {\mathcal {A}}_{{\mathcal {F}}} \subseteq s\) and \({\text {body}}(C) \cap {\mathcal {A}}_{{\mathcal {T}}} \subseteq s^{\prime}\). By definition of \(C_{rules}\), \(\forall \mathrm {v}^{{val}}\in {\text {body}}(C) \cap {\mathcal {A}}_{{\mathcal {T}}}, \forall R \in S, \big (\mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\wedge {\text {head}}(R) \in {\text {body}}(C) \implies R \in C_{rules}(\mathrm {v})\big )\) and since \(s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime}\), \(\forall \mathrm {v}\in C_{targets}, C_{rules}(\mathrm {v}) \ne \emptyset\). Thus there exists a combi such that \(\forall \mathrm {v}\in {\mathcal {F}}, |\{\mathrm {v}^{{val}}\in {\text {body}}(R) \mid {val}\in {\mathsf {dom}}(\mathrm {v}) \wedge R \in combi\}| \le 1\), contradiction.
2) Suppose that \(C \notin C^{\prime}_{{\mathcal {O}}}({T})\) but \(C \in P^{\prime \prime }\), meaning that \(P^{\prime \prime }\) contains a useless constraint C. Thus, \(\{(s, s^{\prime}) \in {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\mid s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime} \wedge C \sqcap (s,s^{\prime})\} = \emptyset\). Since \(C \in P^{\prime \prime }\) there is a combi such that \(|\{\mathrm {v}^{{val}}\in {\text {body}}(R) \mid {val}\in {\mathsf {dom}}(\mathrm {v}) \wedge R \in combi\}| \le 1\), thus \(\exists s \in {\mathcal {S}}^{{\mathcal {F}}}, {\text {body}}(C) \cap {\mathcal {A}}_{{\mathcal {T}}} \subseteq s \wedge \forall R \in combi, R \sqcap s\). Let \(S := \{s^{\prime} \in {\mathcal {S}}^{{\mathcal {T}}}\mid s\xrightarrow {P_{{\mathcal {O}}}({T})}s^{\prime}\}\). Because \(P_{{\mathcal {O}}}({T})\) is complete, \(S \ne \emptyset\). Since \(\forall R \in combi, R \in P_{{\mathcal {O}}}({T}), \exists s^{\prime} \in S, \forall R \in combi, {\text {head}}(R) \in s^{\prime}\). Since \({\text {body}}(C) \cap {\mathcal {A}}_{{\mathcal {T}}} = \{{\text {head}}(R) \mid R \in combi\} \subseteq s^{\prime}\), \(C \sqcap (s,s^{\prime})\).
Thus \(P^{\prime \prime }= C^{\prime}_{{\mathcal {O}}}({T})\) (property 6).
From property 1 and 6, \(Synchronizer({\mathcal {A}}, T, {\mathcal {F}}, {\mathcal {T}}) = P_{{\mathcal {O}}}({T}) \cup C^{\prime}_{{\mathcal {O}}}({T})\).
\(\square\)
Theorem 9
(Synchronizer Complexity)) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\) be a set of transitions, let \(n := max(|{\mathcal {F}}|,|{\mathcal {T}}|)\) and \(d := \max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\})\) and \(m := |{\mathcal {F}}|+|{\mathcal {T}}|\).
The worst-case time complexity of Synchronizer when learning from T belongs to \({\mathcal {O}}( (d^{2n} + 2nd^{n+1} + nd^{n+2}) + (|T|^2 + |T| \times (2m^4d^{2m+2} + 2m^3d^{m+1})) + (d^{n^n}))\) and its worst-case memory use belongs to \({\mathcal {O}}( (d^{2n} + 2nd^{n+1} + nd^{n+2}) + (d^{2m} + 2md^{m+1} + md^{m+2}) + (nd^n))\).
Proof
Let \(d_f:=\max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\})\) (resp. \(d_t :=\max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {T}}\})\)) be the maximal number of values of features (resp. target) variables. Let \(n := max(|{\mathcal {F}}|,|{\mathcal {T}}|)\) and \(d := \max (\{|{\mathsf {dom}}(\mathrm {v})| \in {\mathbb {N}}\mid \mathrm {v}\in {\mathcal {F}}\cup {\mathcal {T}}\})\) and \(m := |{\mathcal {F}}|+|{\mathcal {T}}|\).
The first call to GULA has complexity of \({\mathcal {O}}(|T|^2 + |T| \times (2n^4d^{2n+2} + 2n^3d^{n+1}))\) and the memory is bound by \({\mathcal {O}}(d^{2n} + 2nd^{n+1} + nd^{n+2})\) according to Theorem 6.
Computing \(T^{\prime } := \{(s \cup s^{\prime}, \{\varepsilon ^0\}) \mid (s,s^{\prime}) \in T\}\) has a linear complexity of \({\mathcal {O}}(|T|)\). The call \(GULA({\mathcal {A}}_{{\mathcal {F}}\cup {\mathcal {T}}\cup \{\varepsilon ^1\}}, T^{\prime }, {\mathcal {F}}\cup {\mathcal {T}}, \{\varepsilon \})\) considers target variables as features variables to learn constraints, i.e., the body of constraints can have m conditions. Thus the complexity of this call to GULA is bound by \({\mathcal {O}}(|T^{\prime }|^2 + |T^{\prime }| \times (2m^4d^{2m+2} + 2m^3d^{m+1})) = {\mathcal {O}}(|T|^2 + |T| \times (2m^4d^{2m+2} + 2m^3d^{m+1}))\) since \(|T^{\prime }| = |T|\) and the memory is bound by \({\mathcal {O}}(d^{2m} + 2md^{m+1} + md^{m+2})\) according to Theorem 6.
To discard useless constraints, Algorithm 3 searches for a set of rules that can be applied at the same time as the constraint: first it extract the constraint target variables \(C_{targets} := \{\mathrm {v}\in {\mathcal {T}}\mid \exists {val}\in {\mathsf {dom}}(\mathrm {v}), \mathrm {v}^{{val}}\in {\text {body}}(C) \}\) and search for compatible rules with the constraint \(\forall \mathrm {v}\in C_{targets}, C_{rules}(\mathrm {v}) := \{R \in P \mid \mathrm {var}({{\text {head}}({R})}) = \mathrm {v}\wedge {\text {head}}(R) \in {\text {body}}(C) \wedge \forall \mathrm {w}\in {\mathcal {F}}, \forall {val}, {val}^{\prime} \in {\mathsf {dom}}(\mathrm {w}), \big (\mathrm {w}^{{val}} \in {\text {body}}(R) \wedge \mathrm {w}^{{val}^{\prime}} \in {\text {body}}(C)\big ) \implies {val}= {val}^{\prime}\}\). The constraint contains at most \(|{\mathcal {T}}|\) target conditions. For each target variable, there is at most \(d_f^{|F|}\) rules in P. Thus, computing the Cartesian product of rules grouped by head variables has a time complexity of \({\mathcal {O}}(d_f^{|F|^{|{\mathcal {T}}|}})\) which is bound by \({\mathcal {O}}(d^{n^n})\) and a memory complexity of \({\mathcal {O}}(|P|)\) which is bound by \({\mathcal {O}}(nd^n)\).
The computational complexity of Synchronizer is thus \({\mathcal {O}}( (d^{2n} + 2nd^{n+1} + nd^{n+2}) + (|T|^2 + |T| \times (2m^4d^{2m+2} + 2m^3d^{m+1})) + (d^{n^n}))\) and its memory is bound by \({\mathcal {O}}((d^{2n} + 2nd^{n+1} + nd^{n+2}) + (d^{2m} + 2md^{m+1} + md^{m+2}) + (nd^n))\). \(\square\)
Appendix 5: Proofs of Sect. 6
Proposition 4
(Uniqueness of Impossibility-Optimal Program) Let \(T\subseteq {\mathcal {S}}^{{\mathcal {F}}}\times {\mathcal {S}}^{{\mathcal {T}}}\). The \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) impossibility-optimal for T is unique and denoted \(\overline{P_{{\mathcal {O}}}({T})}\).
Proof
Same proof than for Proposition 1 by replacing “suitable” by “impossibility-suitable”. \(\square\)
Appendix 6: Detailed pseudo-code of Sect. 4
Algorithms 5 and 6 provide the detailed pseudocode of GULA. Algorithm 5 learns from a set of transitions T the conditions under which each value \({val}\) of each variable \(\mathrm {v}\) may appear in the next state. Here, learning is performed iteratively for each value of variable to keep the pseudo-code simple. But the process can easily be parallelized by running each loop in an independent thread, bounding the run time to the variable for which the learning is the longest. In the case where we are not interested about the dynamics of some variables, the parameter \({\mathcal {A}}^{\prime}\) and \({\mathcal {T}}^{\prime }\) can be reduced accordingly.
The algorithm starts by the pre-processing of the input transitions. Lines 7-18 of Algorithm 5 correspond to the extraction of \(N\!eg_{\mathrm {v}^{{val}}}\), the set of all negative examples of the appearance of \(\mathrm {v}^{{val}}\) in next state: all states such that \(\mathrm {v}\) never takes the value \({val}\) in the next state of a transition of T. For efficiency purpose, it is important that the negatives examples are ordered in a way that reduce the difference between nearby elements, for example lexicographically. Indeed, it increase the proportion of revised rules (produced to satisfy a previous example) still consistent with the following examples, reducing the average number of rules stored and thus checked in the following processes. Those negative examples are then used during the following learning phase (lines 21-50) to iteratively learn the set of rules \(P_{{\mathcal {O}}}({T})\). The learning phase starts by initializing a set of rules \(P_{\mathrm {v}^{{val}}}\) to \(\{R \in P_{{\mathcal {O}}}({\emptyset }) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\} = \{\mathrm {v}^{{val}}\leftarrow \emptyset \}\) (see Proposition 2).
\(P_{\mathrm {v}^{{val}}}\) is iteratively revised against each negative example neg in \(N\!eg_{\mathrm {v}^{{val}}}\). All rules \(R_m\) of \(P_{\mathrm {v}^{{val}}}\) that match neg have to be revised. In order for \(P_{\mathrm {v}^{{val}}}\) to remain optimal, the revision of each \(R_m\) must not match neg but still matches every other state that \(R_m\) matches.
To ensure that, the least specialization (see Definition 18) is used to revise each conflicting rule \(R_m\). Algorithm 6 shows the pseudo code of this operation. For each variable of \({\mathcal {F}}^{\prime}\) so that \({\text {body}}(R_m)\) has no condition over it, a condition over another value than the one observed in state neg can be added (lines 3-8). None of those revision match neg and all states matched by \(R_m\) are still matched by at least one of its revisions.
Each revised rule can be dominated by a rule in \(P_{\mathrm {v}^{{val}}}\) or another revised rules and thus dominance must be checked from both. But only revised rule can be dominated by a revised rule: if a rule in \(P_{\mathrm {v}^{{val}}}\) is dominated by a revised rule, then it was dominated by its original rule and thus could not be part of \(P_{\mathrm {v}^{{val}}}\) since it would have been discard in a previous step. Thus we can safely only check the revised rules to discard the ones dominated by the new current revised rule. The non-dominated revised rules are then added to \(P_{\mathrm {v}^{{val}}}\).
Once \(P_{\mathrm {v}^{{val}}}\) has been revised against all negatives example of \(N\!eg_{\mathrm {v}^{{val}}}\), \(P_{\mathrm {v}^{{val}}}=\{R \in P_{{\mathcal {O}}}({T}) \mid {\text {head}}(R)=\mathrm {v}^{{val}}\}\), that is, \(P_{\mathrm {v}^{{val}}}\) is the subset of rules of the final optimal program having \(\mathrm {v}^{{val}}\) as head. Finally, \(P_{\mathrm {v}^{{val}}}\) is added to P and the loop restarts with another atom. Once all values of each variable have been treated, the algorithm outputs P which is then equal to \(P_{{\mathcal {O}}}({T})\).


Appendix 7: Synchronizer scalability
Figure 15 shows the run time of Synchronizer when learning from transitions of Boolean networks from Boolenet (Dubrova & Teslenko, 2011) and PyBoolnet (Klarner et al., 2016) with same settings as in the experiements of Table 4. For the synchronous and general semantics, it is only when we are given a subset of all possible transitions that the algorithm output constraints, since all combination of heads of matching rules are allowed for those two semantics. Those constraint at least prevent transitions from unseen states and also some combination of atoms that are missing in next states but that are observed individually. Even when it outputs an empty set of constraint, the learning process needs to produce and revises constraint until its no more possible, so run time of full set of transitions is also considered. In the asynchronous case, given a set of transitions T, it needs to learn the constraints ensuring at most one change per transitions, i.e., \(\{\xleftarrow []{\bot }a_{t}^{i}, b_{t}^{j}, a_{t-1}^{i^{\prime}}, b_{t-1}^{j^{\prime}} \mid a,b \in {\mathcal {A}}_{{\overline{{\mathcal {T}}}}}, i \ne i^{\prime} \wedge j \ne j^{\prime}\}\) and the ones preventing the projection when only one variable can be updated: \(\{C \mid \{a_{t}^{i}, a_{t-1}^{i} \} \in {\text {body}}(C), a \in {\mathcal {A}}_{{\overline{{\mathcal {T}}}}}, \not \exists (s,s^{\prime}) \in T, {\text {body}}(C) \subseteq s \cup s^{\prime}\}\). Those second kind of constraint will be specific to the few states this limitation occurs and show the limits of propositional representation for the explanation of the dynamics.
Learning constraints is obviously more costly than learning regular rules since both features and targets variables can appear in the body, i.e., number of features becomes \(|{\mathcal {F}}|+|{\mathcal {T}}|\). The algorithm reached the time out of 1000 s with benchmarks of 10 nodes for synchronous semantics and 7 nodes for asynchronous and general semantics. Scalability of the algorithm can be greatly improved by using the approximated version of GULA for learning both rules and constraints. If learning rules can be done in polynomial time, learning constraints remains exponential. Since we do not present this approximated algorithm in this paper we will not go into the details. In short, this approximated version needs positives examples and thus require to generate the Cartesian product of all applicable rules heads for each initial state observed which is exponential. Scalability, readability and applicability could be improved by considering first order generalization of both rule and constraints but those generalization are application dependant and thus remains as future work. Such generalization is required to perform proper prediction from unseen states, thus application of the synchronizer output for prediction from unseen states are out of the scope of this paper.
Appendix 8: Complete pruned \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) of Sect. 7.4
See Fig. 16.
Final learned \({\mathcal {W}}{\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) \(WP = (WP^{\prime}, WP^{\prime \prime })\) of Sect. 7.4 after pruning of \((P_{{\mathcal {O}}}({T^{\prime }}), \overline{P_{{\mathcal {O}}}({T^{\prime }})})\) for readability, \(|WP^{\prime}| = |WP^{\prime \prime }| = 80\). The rules that appear in the original \({\mathcal {D}}{\mathcal {M}}{\mathrm {VLP}}\) of Fig. 13 are colored in blue (Color figure online)
Appendix 9: Information about this paper
1.1 History of the paper
This paper is a substantial extension of Ribeiro et al. (2018) where a first version of GULA was introduced. In Ribeiro et al. (2018), there was no distinction between feature and target variables, i.e., variables at time step t and \(t+1\). From this consideration, interesting properties arise and allow to characterize the kind of semantics compatible with the learning process of the algorithm (Theorem 1). It also allows to represent constraints and to propose an algorithm (Synchronizer, Sect. 5) to learn programs whose dynamics can mimic any given set of transitions with optimal properties on both rules and constraints. It also allows to use GULA to learn human readable explanations in form of rules on static classification problems (as long as all variables are discrete), which will be one of the focus of our future works.
1.2 Main contributions of the paper
The main contributions of this paper are:
-
A modeling of discrete memory-less dynamics system as multi-valued propositional logic. This modeling is independent of the dynamical semantics the system relies on, as long as it respects some given properties we provided in this paper. The main contributions of this formalism is the characterization of optimality and the study of which semantics are compatible with this formalism (which includes notably synchronous, asynchronous and general semantics).
-
A first algorithm named GULA, to learn such optimal programs.
-
The formalism is also extended to represent and use constraints. This allows to reproduce any discrete memory-less dynamical semantics behaviors inside the logic program when the original semantics is unknown.
-
A second algorithm named Synchronizer, that exploits GULA to learn a logic program with constraints that can reproduce any given set of state transitions. The method we proposed is able to learn a whole system dynamics, including its semantics, in the form of a single propositional logic program. This logic program not only explains the behavior of the system in the form of human readable propositional logic rules but also is able to reproduce the behavior of the observed system without the need of knowing its semantics. Furthermore, the semantics can be explained, without any previous assumption, in the form of human readable rules inside the logic program. In other words, the approach allows to learn all the previously cited semantics, as well as new ones.
-
A heuristic method allowing to use GULA to learn a model able to predict from unseen case.
-
Evaluation of these methods on benchmarks from biological litterature regarding scalability, prediction accuracy and explanation quality.
1.3 What evidence is provided
We show through theoretical results the correctness of our approach for both modeling and algorithms (see above contribution for details). Empirical evaluation is performed on benchmarks coming from biological literature. It shows the capacity of GULA to produce correct models when all transitions are available. Also, we observe that learned models generalize to unseen data when given a partial input in those experiments.
1.4 Related work
The paper refers to relevant related work. As we discussed in the related work section, our approach is quite related to Bain and Srinivasan (2018), Evans et al. (2019, 2020), Katzouris et al. (2015), Fages (2020).
The techniques we propose in this paper are a continuation of the works on the LFIT framework from Inoue et al. (2014), Ribeiro and Inoue (2015), Ribeiro et al. (2018).
In Inoue (2011), Inoue and Sakama (2012), state transitions systems are represented with logic programs, in which the state of the world is represented by a Herbrand interpretation and the dynamics that rule the environment changes are represented by a logic program P. The rules in P specify the next state of the world as a Herbrand interpretation through the immediate consequence operator (also called the TPoperator) (Van Emden & Kowalski, 1976; Apt et al., 1988) which mostly corresponds to the synchronous semantics we present in Sect. 3. In this paper, we extend upon this formalism to model multi-valued variables and any memory-less discrete dynamic semantics including synchronous, asynchronous and general semantics.
Inoue et al. (2014) proposed the LFIT framework to learn logic programs from traces of interpretation transitions. The learning setting of this framework is as follows. We are given a set of pairs of Herbrand interpretations (I, J) as positive examples such that J = TP(I), and the goal is to induce a normal logic program (NLP) P that realizes the given transition relations. As far as we know, this concept of learning from interpretation transition (LFIT) has never been considered in the ILP literature before (Inoue et al., 2014). In this paper, we propose two algorithms that extend upon this previous work: GULA to learn the minimal rules of the dynamics from any semantics states transitions that respect Theorem 1 and Synchronizer that can capture the dynamics of any memory-less discrete dynamic semantics.
Rights and permissions
About this article
Cite this article
Ribeiro, T., Folschette, M., Magnin, M. et al. Learning any memory-less discrete semantics for dynamical systems represented by logic programs. Mach Learn 111, 3593–3670 (2022). https://doi.org/10.1007/s10994-021-06105-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-021-06105-4


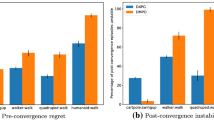
















 , the target atom
, the target atom 
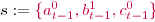 , the target atom
, the target atom 






