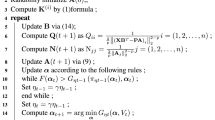Unsupervised feature selection based on kernel fisher discriminant analysis and regression learning

Abstract

In this paper, we propose a new feature selection method called kernel fisher discriminant analysis and regression learning based algorithm for unsupervised feature selection. The existing feature selection methods are based on either manifold learning or discriminative techniques, each of which has some shortcomings. Although some studies show the advantages of two-steps method benefiting from both manifold learning and discriminative techniques, a joint formulation has been shown to be more efficient. To do so, we construct a global discriminant objective term of a clustering framework based on the kernel method. We add another term of regression learning into the objective function, which can impose the optimization to select a low-dimensional representation of the original dataset. We use L_2,1-norm of the features to impose a sparse structure upon features, which can result in more discriminative features. We propose an algorithm to solve the optimization problem introduced in this paper. We further discuss convergence, parameter sensitivity, computational complexity, as well as the clustering and classification accuracy of the proposed algorithm. In order to demonstrate the effectiveness of the proposed algorithm, we perform a set of experiments with different available datasets. The results obtained by the proposed algorithm are compared against the state-of-the-art algorithms. These results show that our method outperforms the existing state-of-the-art methods in many cases on different datasets, but the improved performance comes with the cost of increased time complexity.

1 Introduction

Dimensionality reduction is a widely used preprocessing of high dimensional datasets (Yan and Xu 2007). It aims to project a high dimensional dataset into a subspace (Gu and Sheng 2016), which can wipe away noise and/or redundant and irrelevant features to obtain the new representation and keep the most important variability of the dataset (Meng et al. 2018). In addition, this projection can reduce the total computation cost, because it uses lower dimensional data than the original dataset. Therefore, the efficiency of dimensionality reduction is very important (Belkin and Niyogi 2003).

Feature selection is one of the most important dimensionality reduction methods, which can remove the redundant features in the original data and rapidly deal with massive high dimensional data (Meng et al. 2018). Feature selection (a) allows us to recognize representative features in the original dataset. Hence, the further process and computation become computationally easier, e.g. classification (Gu and Sheng 2017) in the subspace; (b) results in a subspace with less influence of noise. Thus, the further computation is robust to noise; (c) inherently resolves the problem of over fitting, which is common in many contexts (Stolkin et al. 2008), e.g. model fitting. Feature selection is widely used in text-mining (Shang et al. 2017), bio-medical treatment (Ding and Peng 2005), voice recognition (Abdulla and Kasabov 2003), commodity recommendation and security monitoring (Tian and Chen 2017). In the recent years, many feature selection methods have been developed (Gu and Sheng 2017; Stolkin et al. 2008; Mitra et al. 2002; Stolkin et al. 2007; Mao and Tsang 2013; Gu et al. 2015). Depending on the available data, e.g. labeled dataset, feature selection is divided into supervised (Sikonja and Kononenko 2003; Zhao and Liu 2007), semi-supervised (Xu et al. 2010; Shi and Ruan 2015) and unsupervised (Mitra et al. 2002; Li et al. 2014; Cai et al. 2010; Yang et al. 2011).

In supervised feature selection, a subset of original features is selected by using the relationship between labels and features. Although supervised feature selection has high accuracy, it entails high computation cost (Li et al. 2010). In some cases, there is only a fraction of label information. Hence, semi-supervised feature selection methods should make full use of these label information. By adding the label information as additional constraint on unsupervised algorithms, we can enhance the performance of the method. Thus, semi-supervised algorithms can be regarded as a special type of unsupervised feature selection method (Xu et al. 2010; Cheng et al. 2011). Apparently, unsupervised feature selection methods have been proposed to handle the unlabeled datasets. Hence, some intrinsic properties of datasets are employed for feature selection, e.g. scatter separability. Unsupervised feature selection is more difficult and more computation cost than supervised and semi-supervised feature selection due to the lack of prior information. In most of real world problem, we need to deal with unlabeled or partially labeled datasets. This may indicate the future researches must mostly solve unsupervised and semi-supervised feature selection problems. Recently, there have been already many unsupervised algorithms (Stolkin et al. 2008; Shang et al. 2017; Mitra et al. 2002; Stolkin et al. 2007; Li et al. 2014; Cai et al. 2010; Constantinopoulos et al. 2006).

Comparing to the early feature selection methods, most of the latest feature selection methods are unsupervised and many other techniques are used simultaneously to enhance their performance. Here we prefer to emphasis on the application of graph spectral theory in feature selection, which has been proved to be a strong implement for dimensionality reduction (Yan and Xu 2007; Li et al. 2014; Chen et al. 2015; Yang et al. 2010; Liu et al. 2014; Doquire and Verleysen 2013; Wei et al. 2012). A large number of other methods have been also widely used including PCA (Smith 2002), Linear Discriminant Analysis (LDA) (McLachlan 2004), Locally Linear Embedding (LLE) (Roweis and Saul 2000), Isomap (Tenenbaum et al. 2000), Locality Projection Preserving (LPP) (He and Niyogi 2004) and Laplacian Eigenmaps (LE) Meng et al. (2018), etc. Some of the graph spectral methods have better performance than traditional feature selection methods including Spectral Feature Selection (SPEC) (Zhao and Liu 2007), Laplacian Score (LapScor) (He et al. 2005), Multi-cluster Feature Selection (MCFS) (Cai et al. 2010) and Minimum Redundancy Spectral Feature Selection (MRSF) (Zhao et al. 2010). It has been found that a joint framework in some algorithms can lead to better results than the “two-step” strategy in SPEC, MCFS and MRSF. For example, JELSR unifies embedding learning and sparse regress (Hou et al. 2014), LSPE solves embedding learning and feature selection simultaneously (Fang et al. 2014) and DFSC combines self-representation with manifold learning and feature selection (Shang et al. 2016). These studies demonstrated their methods outperform other multi-stage methods.

PCA and LDA have been proposed for dimensionality reduction where PCA is able to handle linear as well as nonlinear data whereas LDA can be only applied to linear data. Sebastian Mika et al. (1999) extend LDA based on kernel methods to nonlinear fields using Kernel Fisher Discriminant Analysis (KFDA). It is proved that KFDA performs better than PCA and KPCA. Besides kernel methods, Local Discriminant Models and Global Integration (LDMGI) deals with nonlinear data by applying LDA in a small neighbor of a nominal point resembling a linear subspace (Yang et al. 2010).

The abovementioned methods show a good performance, but they only use either manifold structure or discriminative technique alone (Ma et al. 2016). Inspired by the ideas above mentioned and based on graph spectral theory, we combine the global discriminative information with manifold information and propose a joint framework for feature selection. Therefore, we propose a novel joint framework of unsupervised feature selection based on kernel fisher discriminant analysis and regression learning (KFDRL) to exploit the intrinsic characters of data and select representative features. It kernelizes LDA to be a global discriminant first, adds regression learning and L_2,1-norm regularization to construct a joint framework for feature selection. We also present update rules to compute the solution and further study the convergence and computational complexity of the proposed algorithm. The contribution of this paper is:

• (1) We propose a framework of unsupervised feature selection combining global discriminant analysis with graph spectral theory and regression learning. Therefore, our algorithm benefits all the advantages of global discriminant analysis with graph spectral theory and regression learning.

• (2) We use discriminative information to make our method superior to JELSR, which can result in a better separation of data points belonging to different classes. Our method can result in a better performance in both clustering and classification.

• (3) A mathematical model of proposed method is presented and a simple optimization strategy is applied to solve the model efficiently. We demonstrate the effectiveness of our method by a series of experiments with several datasets. We further validate our results by comparing them with the results of other feature selection algorithms.

The rest of this paper is set as follows: in Sect. 2, we introduce the formulation of the related works. In Sect. 3, the problem formulation, the algorithm and optimization process are all explained in detail. Convergence and computational complex of the algorithm are studied in Sect. 4. In Sect. 5, we present experiments and the results, which demonstrate the effectiveness of the proposed method. Final section contains conclusion and future works.

2 The related works

In this section, we will introduce some useful notations and the following two relevant works will be briefly presented (1) feature selection, MCFS, MRSF, JELSR and CGSSL (Li et al. 2014; Cai et al. 2010; Zhao et al. 2010; Hou et al. 2014) and (2) clustering algorithms, LDMGI (Yang et al. 2010), kernel method and KLDA.

2.1 Notations

We use bold capital and bold lowercase letters for matrices and vectors, for example A ∈ R^d×n is a matrix, a_i is the ith vector of A and a_ij is the jth element of a_i. Let’s tr(A) denote the trace of a square matrix A and denotes L_r,p-norm defined as follows:

$$ \left\| A \right\|_{r,p} = \left( {\sum\limits_{i = 1}^{d} {\left( {\sum\limits_{j = 1}^{n} {\left| {a_{ij} } \right|^{r} } } \right)^{{{\raise0.7ex\hbox{$p$} \!\mathord{\left/ {\vphantom {p r}}\right.\kern-0pt} \!\lower0.7ex\hbox{$r$}}}} } } \right)^{{{1 \mathord{\left/ {\vphantom {1 p}} \right. \kern-0pt} p}}} $$

(1)

The dataset represented by matrix X = [x₁, x₂, …, x_n] ∈ R^d×n has n sample vectors where each vector x_i ∈ R^d has d features. We assume samples belong to c different classes. We are interested in computing a cluster assignment matrix Y = [y₁, y₂, …, y_n]^T ∈ {0,1}^n×c, where y_i ∈ {0,1}^c×1 is a cluster assignment vector whose jth element y_ij is one when x_i belongs to jth cluster and zero otherwise. Furthermore, we define the scaled cluster assignment matrix H ∈ R^n×c, where H satisfies H^TH = I_c and I_c ∈ R^c×c is an identity matrix, as follows:

$$ \varvec{H} = \left[ {{\varvec{h}}_{1} ,{\varvec{h}}_{2} , \ldots {\varvec{h}}_{n} } \right] = {\varvec{Y}}\left( {{\varvec{Y}}^{T} {\varvec{Y}}} \right)^{{ - \frac{1}{2}}} = \left[ {\frac{{{\varvec{y}}_{1} }}{{\left\| {{\varvec{y}}_{1} } \right\|}},\frac{{{\varvec{y}}_{2} }}{{\left\| {{\varvec{y}}_{2} } \right\|}}, \ldots ,\frac{{{\varvec{y}}_{n} }}{{\left\| {{\varvec{y}}_{n} } \right\|}}} \right] $$

(2)

2.2 Feature selection

2.2.1 MCFS and MRSF

In MCFS (Cai et al. 2010) and MRSF (Zhao et al. 2010), the first step is to compute an m-D embedding representation of x_i by mapping d-D x_i into an embedding space with lower dimensions R^m where m < d. This mapping is represented by an embedding matrix P = [p₁, p₂, …,p_n] ∈ R^m×n. The embedding techniques LE and LLE proposed in Meng et al. (2018), Roweis and Saul (2000) are used and regression learning MCFS and MRSF can be defined as follows:

$$ \begin{aligned} & \arg \mathop {\hbox{min} }\limits_{{{\varvec{PP}}^{T} = {\varvec{I}}_{n \times n} }} tr({\varvec{PLP}}^{T} ) \\ & \arg \mathop {\hbox{min} }\limits_{{\varvec{W}}} \left\| {{\varvec{W}}^{T} {\varvec{X}}} \right. - \left. {\varvec{P}} \right\|_{2}^{2} + \alpha \left\| {\varvec{W}} \right\|_{1}^{1} \\ \end{aligned} $$

(3)

$$ \begin{aligned} & \arg \mathop {\hbox{min} }\limits_{{{\varvec{PP}}^{T} = {\varvec{I}}_{n \times n} }} tr({\varvec{PLP}}^{T} ) \\ & \arg \mathop {\hbox{min} }\limits_{{\varvec{W}}} \left\| {{\varvec{W}}^{T} {\varvec{X}}} \right. - \left. {\varvec{P}} \right\|_{2}^{2} + \alpha \left\| {\varvec{W}} \right\|_{2,1}^{1} \\ \end{aligned} $$

(4)

It is clear that the two methods are different in the regularization term where MCFS has L₁-norm and MRSF has L_2,1-norm. Different norms definition is used to constrain the sparse structure of the data as regression coefficient is used to rank the features. The optimization proposed in (3) is very similar to Lasso (Gu and Sheng 2016) whereas the problem formulation in (4) uses L₂-norm to rank each row of W. Although these two-step algorithms are efficient, they are still not as good as single-step algorithms, joint framework algorithms, which will be presented as follows.

2.2.2 JELSR and CGSSL

JELSR is an unsupervised algorithm, which combines embedding learning with sparse regression. It preserves local manifold structure as two variables simultaneously to get a better performance. JELSR is formulated in Eq. (5).

$$ L({\varvec{W}},{\varvec{P}}) = \arg \mathop {\hbox{min} }\limits_{{{\varvec{W}},{\varvec{PP}}^{T} = {\varvec{I}}_{m \times m} }} tr({\varvec{PLP}}^{T} ) + \beta \left( {\left\| {{\varvec{W}}^{T} {\varvec{X}} - {\varvec{P}}} \right\|_{2}^{2} + \alpha \left\| {\varvec{W}} \right\|_{2,1} } \right) $$

(5)

where W denotes the importance of each feature and P is embedding matrix. The objective formulation for CGSSL is similar to JELSR. However, CGSSL impose a low-dimensional constraint upon embedding matrix with pseudo class labels. Moreover, as a sparse structure learning technique, semantic components are used in CGSSL to match pseudo class labels with truth class labels. Hence, CGSSL can be formulated as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{S}.{\mathbf{W}},\varvec{Q,}{\mathbf{M}}}} {\varXi = }tr(\varvec{F}^{T} \varvec{LF}) + \alpha \left\| {\varvec{F} - \varvec{X}^{T} \varvec{W}} \right\|_{F}^{2} + \beta \left\| \varvec{W} \right\|_{2,1} + \gamma \left\| {\varvec{W} - \varvec{QS}} \right\|_{F}^{2} \\ & s.t.\;\;\varvec{F}^{T} \varvec{F} = \varvec{I}_{c} ,\;\varvec{F} \ge 0;\quad \varvec{Q}^{T} \varvec{Q} = \varvec{I}_{r} \\ \end{aligned} $$

(6)

where S is a matrix of weights and Q is a transformation matrix. They are used to save original features as well as embedded features. F is a scaled cluster assignment matrix to predict labels. Both JELSR and CGSSL have great performance results due to the local manifold as well as the discriminative information.

2.2.3 MDRL and RMDRL

MDRL and RMDRL (Lu et al. 2015) are proposed for image classification with a linear regression framework. A within-class graph and a between-class graph are introduced in MDRL to get an optimal subspace. Furthermore, a nuclear norm is used to learn a robust projection matrix by a developed MDRL, i.e., RMDRL. Manifold information and discriminant information are both used in a regression learning framework by MDRL and RMDRL like the proposed algorithm KFDRL. These two algorithms are respectively formulated as follows:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{{\varvec{W}},{\varvec{M}}}} \,\left\| {{\varvec{XW}} - {\varvec{Y}} - {\varvec{B}} \odot {\varvec{M}}} \right\|_{F}^{2} + \alpha Tr\left( {{\varvec{W}}^{T} {\varvec{X}}^{T} \left( {{\varvec{L}}_{w} - {\varvec{L}}_{b} } \right){\varvec{XW}}} \right) + \beta \left\| {\varvec{W}} \right\|_{2,1} + \gamma \left\| {\varvec{W}} \right\|_{1} \\ & s.t.\;\;{\varvec{M}} \ge 0 \\ \end{aligned} $$

(7)

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{{\varvec{W}},{\varvec{M}}}} \,\left\| {{\varvec{XW}} - {\varvec{Y}} - {\varvec{B}} \odot {\varvec{M}}} \right\|_{F}^{2} + \alpha Tr\left( {{\varvec{W}}^{T} {\varvec{X}}^{T} \left( {{\varvec{L}}_{w} - {\varvec{L}}_{b} } \right){\varvec{XW}}} \right) + \beta \left\| {\varvec{W}} \right\|_{*} \\ & s.t.\;\;{\varvec{M}} \ge 0 \\ \end{aligned} $$

(8)

These two algorithms first construct X, Y and B by optimal methods and then compute the W as projection matrix. In the end, they use L₁-norm and nuclear norm to select features. Note that the X is a matrix of training samples and Y is the corresponding label matrix. In other words, MDRL and RMDRL are supervised algorithms, which have different application cases with KFDRL.

2.3 Spectral clustering

Over the last few years, many studies on the graph spectral theory for clustering analysis have been published. For example, Luxburg (2007) has presented a significant spectral clustering method with graph theory. It has been shown that the spectral clustering has advantages over traditional algorithms of non-convex distribution for partitioning a complex data structure. It makes full use of geometric information in the original datasets. Hence, pseudo class labels represent a more accurate intrinsic structure information in the original datasets. In Yang et al. (2010), LDMGI computes a Laplacian matrix by using both discriminative information and manifold learning, which has a good performance in clustering images. Local discriminant model in a sufficient small local manifold area is used on spectral clustering, whose objective function can be shown as follows:

$$ \arg \mathop {\hbox{min} }\limits_{{{\varvec{G}}_{(i)} }} tr\left[ {{\varvec{G}}_{(i)}^{T} {\varvec{L}}_{i}^{{S_{i} }} {\varvec{G}}_{(i)} } \right] $$

(9)

where ${\varvec{L}}_{i} = {\varvec{H}}_{k} ({\tilde{\varvec{X}}}_{i}^{T} {\tilde{\varvec{X}}}_{i} + \lambda {\varvec{I}})^{ - 1} {\varvec{H}}_{k}$ is a local Laplacian matrix and H_i = [h_i1, h_i2, …, h_ik−1]^T ∈ R^k×c is a cluster assignment matrix. After that, a global integration method is imposed to get the global Laplacian matrix in nonlinear space:

$$ {\varvec{L}}^{S} = \sum\limits_{i = 1}^{n} {{\varvec{S}}_{i} {\varvec{L}}_{i}^{{S_{i} }} {\varvec{S}}_{i}^{T} = \left[ {{\varvec{S}}_{1} ,{\varvec{S}}_{2} , \ldots ,{\varvec{S}}_{n} } \right]} \left[ {\begin{array}{*{20}c} {{\varvec{L}}_{1}^{{s_{1} }} } & {} & {} \\ {} & \cdots & {} \\ {} & {} & {{\varvec{L}}_{n}^{{s_{n} }} } \\ \end{array} } \right]\left[ {{\varvec{S}}_{1} ,{\varvec{S}}_{2} , \ldots ,{\varvec{S}}_{n} } \right]^{T} $$

(10)

Moreover, the global discriminative model can be defined as:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{G}}} \;tr\left( {{\varvec{G}}^{T} {\varvec{L}}^{S} {\varvec{G}}} \right) \\ & s.t.\;\;{\varvec{G}}^{T} {\varvec{G}} = {\varvec{I}},\;\;{\varvec{G}} \ge 0 \\ \end{aligned} $$

(11)

where L^S contains both manifold information and discriminative information. Most of the corresponding methods employ the local-idea to handle nonlinear problems (Cai et al. 2010; Yang et al. 2010; Roweis and Saul 2000; He and Niyogi 2004; Zhao et al. 2010; Hou et al. 2014), which use (1) linear methods in each local-and-small area and (2) global integration. It has been shown to be very pragmatic in many different contexts. However, we may have some bad results due to weak robustness, low convergence rate and more complex formulism. So it is an interesting research to find a way to simplify the effectiveness and improve the robust of these algorithms.

2.4 Kernel method

The kernel method is very efficient and powerful. A group of points in a low-dimensional space can be mapped into a space with higher dimensions and become linearly separable using a proper kernel mapping. The mapping is defined by kernel function K(x, y) = < ϕ(x), ϕ(y) > , where x and y are points in low-dimensional space, ϕ(•) denotes the points in the higher dimensional space and < , > denotes the inner product. According to mercer theorem, we can transform a pair of points in low dimensional space satisfying a specific function requirement into higher dimensional space. This transformation function can be considered as a bridge between the higher and lower dimensional spaces. Kernel fisher discriminant analysis (KFDA) is one of the applications of the kernel method, which can obtain better results than LDA and PCA in the expense of more complex optimization and higher computational cost.

3 Feature selection based on kernel discriminant and sparse regression

Here, we introduce our proposed method with three terms (1) a global kernel discriminant term based on nonnegative spectral clustering (2) a regression learning term and (3) a sparse constraint regularization term. A kernel linear discriminant model is integrated into a spectral clustering model to preserve manifold information as well as discriminative information. Therefore, our method can be applied to linear and nonlinear dataset. A regression method can fit the coefficient matrix to the scaled cluster assignment matrix. Finally, a sparse regularization is performed for feature selection.

3.1 Global kernel discriminant model based on nonnegative spectral clustering

3.1.1 Nonnegative spectral clustering

In non-negative spectral clustering, Laplacian matrix L is computed by constructing a nearest neighbor graph S of data points. The spectral embedding matrix Y can be computed by Eq. (12) to retain the manifold information:

$$ \mathop {\hbox{min} }\limits_{{\varvec{Y}}} \;tr\left( {{\varvec{Y}}^{T} {\varvec{LY}}} \right) $$

(12)

In this paper, we set the embedding matrix to be cluster assignment matrix which is proposed in Li et al. (2014). Hence, Y ∈ {0,1}^n×c is discrete, which may make Eq. (12) be an NP-hard problem (Shi and Malik 2000). To address this problem, we use a well-known technique to relax the discrete variable Y to a continuous variable using Eq. (2). Therefore, Eq. (12) can be rewritten as:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{H}}} \;tr\left( {{\varvec{H}}^{T} {\varvec{LH}}} \right) \\ & s.t.\;\;{\varvec{H}}^{T} {\varvec{H}} = {\varvec{I}} \\ \end{aligned} $$

(13)

where H is nonnegative; however, it has negative elements if (13) is directly solved (Li et al. 2014) which may deteriorate the accuracy of the results. Therefore, we add a nonnegative constraint to ensure the pseudo labels are authentic and accurate:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{H}}} \;tr\left( {{\varvec{H}}^{T} {\varvec{LH}}} \right) \\ & s.t.\;\;{\varvec{H}}^{T} {\varvec{H}} = {\varvec{I}},\;\;{\varvec{H}} \ge 0 \\ \end{aligned} $$

(14)

3.1.2 Kernel discriminant model based on spectral clustering

To reveal the structure of the original datasets, we use the manifold information as well as the discriminative information. We combine the idea of LDA with spectral clustering and define between-cluster scatter matrix S_b to make the distance between different clusters the largest possible and a within-cluster scatter matrix S_w to make the distance between data points within the same clusters the smallest possible. Inspired by Mika et al. (1999), we also extend the LDA to nonlinear cases by kernel method. Let’s C_n = I_n− (1/n)1_n1 ^T _n denote a matrix used for centering the data by subtracting the mean of the data, where I_n is an identity matrix, and ${\tilde{\varvec{X}}} = {\varvec{XC}}_{n}$ denote the centered dataset. Hence, we define the total scatter matrix S_t and between-cluster scatter matrix S_b as follows:

$$ {\varvec{S}}_{t} = \tilde{\varvec{X}}{\tilde{X}^{T}} $$

(15)

$$ {\varvec{S}}_{b} = \tilde{\varvec{X}}HH^{T} {\tilde{\varvec{X}}}^{T} $$

(16)

We define mapping function ϕ(•) to map the linearly inseparable data x_i ∈ R^d to a high-dimensional Г:

$$ \varphi :\quad R^{d} \to \varGamma ,\quad {\varvec{x}} \to \varphi \left( {\varvec{x}} \right) $$

(17)

We assume the dataset in high dimensional space is linearly separable. Inspired by Shang et al. (2016), we obtain the mapping matrix ${\hat{\varvec{S}}}_{b}$ and ${\hat{\varvec{S}}}_{t}$ as follows:

$$ {\hat{\varvec{S}}}_{b} = \varphi \left( {\varvec{X}} \right){\varvec{C}}_{n} {\varvec{HH}}^{T} {\varvec{C}}_{n}^{T} \varphi \left( {\varvec{X}} \right)^{T} $$

(18)

$$ {\hat{\varvec{S}}}_{t} = \varphi \left( {\varvec{X}} \right){\varvec{C}}_{n} {\varvec{C}}_{n}^{T} \varphi \left( {\varvec{C}} \right)^{T} $$

(19)

Then the discriminant model in Г is obtained by the following formulation:

$$ \mathop {\hbox{max} }\limits_{{\varvec{H}}} \;tr\left( {\left( {{\hat{\varvec{S}}}_{t} + \mu {\varvec{I}}_{n} } \right)^{ - 1} {\hat{\varvec{S}}}_{b} } \right) $$

(20)

where μ > 0, μI_n is added to guarantee the matrix $\left( {{\hat{\varvec{S}}}_{t} + \mu {\varvec{I}}_{n} } \right)$ is always invertible. Note that tr(H^TC_nH) = tr(H^T(I_n− (1/n)1_n1 ^T _n )H) is constant and equivalent to K − 1. By subtracting this term from (20), we rewrite it as the following minimization problem:

$$ \mathop {\hbox{min} \;}\limits_{{\varvec{H}}} tr\left( {{\varvec{H}}^{T} \left( {{\varvec{C}}_{n} - {\varvec{C}}_{n}^{T} \left( {{\varvec{C}}_{n} + \mu {\varvec{K}}^{ - 1} } \right)^{ - 1} {\varvec{C}}_{n} } \right){\varvec{H}}} \right) $$

(21)

where K = ϕ(x)^T•ϕ(x) is a kernel function. We can also design and use a kernel function satisfying the mercer theorem. There are already many mature kernel function developed, such as linear kernel, Gaussian kernel, Polynomial kernel and Cosine kernel (Mika et al. 1999). In this paper, we would like to use Gaussian kernel as the kernel function defined as follows:

$$ {\varvec{K}}\left( {{\varvec{x}}_{i} ,{\varvec{x}}_{j} } \right) = \exp \left( { - \frac{{\left\| {{\varvec{x}}_{i} - {\varvec{x}}_{j} } \right\|^{2} }}{{2\sigma^{2} }}} \right) $$

(22)

where σ is the scale parameter. We put G = C_n − C ^T _n (C_n + μK⁻¹)⁻¹C_n and then rewrite (21) as follows:

$$ \mathop {\hbox{min} }\limits_{{\varvec{H}}} \;tr\left( {{\varvec{H}}^{T} {\varvec{GH}}} \right) $$

(23)

Using (15)–(23) we obtain a discriminative model in Eq. (23). Next, we will show it is inherently a spectral clustering model and G is a Laplacian matrix.

Theorem 1

The matrixGin Eq. (23) is a Laplacian matrix referring to Yang et al. (2010).

For proving the Theorem 1, it’s worth proving two lemmas.

Lemma 1

DenoteQ = I_n − (C_n + μK⁻¹)⁻¹, ∃μ leadsQas a positive semi-define matrix.

Proof

Given C_n = I_n − (1/n)1_n1 ^T _n , it’s easy clear that C_n is a symmetric positive define matrix with eigenvalues λ = 1 and (n − 1)/n. A befitting value μ in (C_n + μK⁻¹)⁻¹ results in maximum eigenvalue λ_max ≤ 1, i.e. the minimum eigenvalue of Q is bigger than zero. In this paper, we set μ = 10⁻¹². It can be calculated that ∀λ_Q ≥ 0, so Q is a positive semi-define matrix.□

Lemma 2

Given a positive semi-define matrixQ, BQB^Tmust be a positive semi-define matrix for arbitrary matrixB.

Proof

Applying Cholesky decomposition to positive semi-define matrix Q (Yang et al. 2010), we obtain Q = M^TM. Furthermore, we can pre-multiply and post-multiply it by B to get BQB^T, we can substitute Q by M^TM and get BM^TMB^T = (MB^T)^T(MB^T), so BQB^T is a positive semi-define matrix.□

We can prove the Theorem 1 on the basis of the two proved lemma above.

Proof

From Lemma 1, G can be rewritten as:

$$ {\varvec{G}} = {\varvec{C}}_{n} - {\varvec{C}}_{n}^{T} \left( {{\varvec{C}}_{n} + \mu {\varvec{K}}^{ - 1} } \right)^{ - 1} {\varvec{C}}_{n} = {\varvec{C}}_{n} \left( {{\varvec{I}}_{n} - \left( {{\varvec{C}}_{n} + \mu {\varvec{K}}^{ - 1} } \right)^{ - 1} } \right){\varvec{C}}_{n}^{T} = {\varvec{C}}_{n} {\varvec{QC}}_{n}^{T} $$

(24)

where Q is a positive semi-define matrix. So it is easy to know G is also a positive semi-define matrix by Lemma 2. Besides, it is found that C_n1_n = (I_n − (1/n)1_n1 ^T _n )1_n = 0. Hence, G1_n = 0, that is, 0 is the eigenvalue of G with corresponding eigenvector 1. Above all, we can draw a conclusion that G is a Laplacian matrix.□

From the Theorem 1 we realize that Eq. (23) represents not only a discriminative model but also a spectral clustering one. This implies the simultaneous consideration of manifold information and discriminative information (Luxburg 2007; Nie et al. 2010), which lays a solid foundation for feature selection later.

Combining Eqs. (14), (22) and (23), the first term of the proposed algorithm is obtained, i.e. the kernel discriminant model based on spectral clustering is:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{\varvec{H}}} \;tr\left( {{\varvec{H}}^{T} {\varvec{GH}}} \right) \\ & s.t.\;\;{\varvec{H}}^{T} {\varvec{H}} = {\varvec{I}},\;\;{\varvec{H}} \ge 0 \\ \end{aligned} $$

(25)

where G = C_n − C ^T _n (C_n + μK⁻¹)⁻¹C_n is a Laplacian matrix and K is a kernel function.

3.2 Regression learning

Here we are going to discuss the second term of our method. We add a regression term to the proposed formulation of our method in addition to the feature selection formulation (Zhao and Liu 2007; Cai et al. 2010). In specific, we transform the samples to the corresponding low-dimensional embedding space to fit the scaled cluster assignment matrix. Let’s W = [w₁, w₂, …, w_m] ∈ R^d×m, denotes a transformation matrix where $\left\{ {{\varvec{w}}_{i} } \right\}_{i = 1}^{m}$ is the transformation vector of each sample and m is the embedded dimension. In order to match the labels with embedded data, we set m = c, i.e. W ∈ R^d×c. Hence, the second term of the proposed algorithm can be expressed as follows:

$$ \mathop {\hbox{min} }\limits_{{\varvec{W}}} \sum\limits_{i = 1}^{n} {\left\| {{\varvec{h}}_{i} - {\varvec{X}}^{T} {\varvec{w}}_{i} } \right\|_{F}^{2} } = \left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} $$

(26)

We use the Frobenious-norm in the cost function formulation. If H is known, we can compute W by minimizing Eq. (26), whose row vector ${\hat{\mathbf{w}}}_{i}$ represents the importance of each feature. In order to guarantee the generalization of the proposed formulation in addition to a small error value, we add a regularization constraint to Eq. (26).

3.3 Feature selection

As row vectors of W have been defined above, we can rewrite the W as follows:

$$ {\varvec{W}} = \left[ {{\hat{\varvec{w}}}_{1}^{T} ,{\hat{\varvec{w}}}_{2}^{T} , \ldots ,{\hat{\varvec{w}}}_{d}^{T} } \right]^{T} $$

(27)

The third term of the purposed algorithm is to balance the fitting ability and the generalization ability. W can be considered as a representation of features whose each row represents one feature. To select features, we impose a sparse structure on W as well as a regression term to remove less important features. We use L_2,1-norm for the regularization term, which can make each row of W sparse and select more discriminative features. Hence, the formulation of the third term is defined as follows:

$$ \mathop {\hbox{min} }\limits_{{\varvec{W}}} \;\sum\limits_{i = 1}^{d} {\left( {\left\| {{\hat{\varvec{w}}}_{i} } \right\|_{2} } \right)^{1} } = \sum\limits_{i = 1}^{d} {\left( {\sum\limits_{j = 1}^{c} {\left| {{\varvec{w}}_{ij} } \right|^{2} } } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} = \left\| {\varvec{W}} \right\|_{2,1} $$

(28)

When the W is obtained, we score each row of it and rank them from large to small. The larger score the row has, the more important the feature is.

3.4 KFDRL formulations and solution

3.4.1 The framework

We use a non-negative constraint on W to satisfy its physical significance and to guarantee that the result is accurate. Using the nonnegative constraint and Eqs. (25), (26) and (28), we can now write the formulation of KFDRL as follows:

$$ \begin{aligned} & \hbox{min} \;L\left( {{\varvec{W}},{\varvec{H}}} \right) = \arg \;\hbox{min} \;tr\left( {{\varvec{H}}^{T} {\varvec{GH}}} \right) + \beta \left( {\left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} + \alpha \left\| {\varvec{W}} \right\|_{2,1} } \right) \\ & s.t.\;\;\,{\varvec{W}} \ge 0,\quad {\varvec{H}}^{T} {\varvec{H}} = {\varvec{I}},\quad {\varvec{H}} \ge 0 \\ \end{aligned} $$

(29)

where α and β are balanced parameters, α plays a role in balancing the fitting and generalization. According to Eq. (29), we would like to briefly conclude the process of KFDRL as follows. The spectral clustering model and regression learning method are used to obtain W and H in an unsupervised way, and the regularization term balances the fitting and generalization. The score of each row of W is regarded as the importance of each feature.

3.4.2 The optimization

We cannot find a closed form solution to Eq. (29) because the L_2,1-norm is non-smooth. Inspired by Lee and Seung (1999), we use alternate iteration method to find the optimal W and H. Hence, we use Lagrange relaxation and write the Lagrange multiplier form of Eq. (29) as follows:

$$ \hbox{min} \;L\left( {{\varvec{W}},{\varvec{H}}} \right) = tr\left( {{\varvec{H}}^{T} {\varvec{GH}}} \right) + \beta \left( {\left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} + \alpha \left\| {\varvec{W}} \right\|_{2,1} } \right) + \frac{\lambda }{2}\left\| {{\varvec{H}}^{T} {\varvec{H}} - {\varvec{I}}} \right\|_{F}^{2} + tr\left( {\psi {\varvec{H}}^{T} } \right) + tr\left( {\phi {\varvec{W}}^{T} } \right) $$

(30)

where λ is selected to be a large enough number, namely λ = 10⁸, to control the orthogonal constraint. Furthermore, ψ and φ are two Lagrangians for constraining W and H to be non-negative. We consider the following cases:

• (1) Considering H to be fixed, we can rewrite Eq. (30) as a function of W.

  $$ \hbox{min} \quad L_{1} \left( {\varvec{W}} \right) = \left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} + \alpha \left\| {\varvec{W}} \right\|_{2,1} + tr\left( {\phi {\varvec{W}}^{T} } \right) = \left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} + \alpha tr\left( {{\varvec{W}}^{T} {\varvec{UW}}} \right) + tr\left( {\phi {\varvec{W}}^{T} } \right) $$

  (31)

  where U ∈ R^d×d is a diagonal matrix whose diagonal elements satisfy the following formulation:

  $$ {\varvec{u}}_{ii} = \frac{1}{{2\left\| {{\hat{\varvec{w}}}_{i} } \right\|_{2} }} $$

  (32)

  If we fix U, we can conclude from $\frac{{\partial {\varvec{L}}}}{{\partial {\varvec{W}}}} = 0$ that:

  $$ 2{\varvec{XX}}^{T} {\varvec{W}} - 2{\varvec{XH}} + 2\alpha {\varvec{UW}} + \phi = 0 $$

  (33)

  Considering the KKT condition φ_ijw_ij = 0, we have:

  $$ w_{ij} \leftarrow w_{ij} \frac{{\left( {{\varvec{XH}}} \right)_{ij} }}{{\left( {{\varvec{AW}}} \right)_{ij} }} $$

  (34)

  where A = XX^T + αU.

• (2) Considering U and W are fixed, Eq. (30) can be redefined as a function of H:

  $$ \hbox{min} \quad L_{2} \left( {\varvec{H}} \right) = tr\left( {{\varvec{H}}^{T} {\varvec{GH}}} \right) + \beta \left\| {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right\|_{F}^{2} + \frac{\lambda }{2}\left\| {{\varvec{H}}^{T} {\varvec{H}} - {\varvec{I}}} \right\|_{F}^{2} + tr\left( {\psi {\varvec{H}}^{T} } \right) $$

  (35)

  The solution to Eq. (35) can be computed by $\frac{{\partial {\varvec{L}}}}{{\partial {\varvec{H}}}} = 0$, as follows:

  $$ 2{\varvec{GH}} + 2\beta \left( {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right) + 2\lambda {\varvec{H}}\left( {{\varvec{H}}^{T} {\varvec{H}} - {\varvec{I}}} \right) + \psi = 0 $$

  (36)

  Considering the KKT condition ψ_ijh_ij = 0, we have:

  $$ {\varvec{h}}_{ij} \leftarrow {\varvec{h}}_{ij} \frac{{\left( {\lambda {\varvec{H}}} \right)_{ij} }}{{\left[ {{\varvec{GH}} + \beta \left( {{\varvec{H}} - {\varvec{X}}^{T} {\varvec{W}}} \right) + \lambda \left( {{\varvec{HH}}^{T} {\varvec{H}}} \right)} \right]_{ij} }} $$

  (37)

  where G = G⁺ − G⁻, and G⁺=(|G| + G)/2, G⁻ = (|G| − G)/2.

• (3) Considering W is fixed, U can be updated by Eq. (32). Hence, at every iteration of the proposed algorithm, we compute the updated value of W and H as summarized in Table 1.

  Table 1 The procedure of KFDRL

4 Algorithm analysis

In this section, we present more analysis on KFDRL in detail, namely convergence and computational complex.

4.1 Convergence of KFDRL

Since the KFDRL is formalized as a minimization problem we need to proof that the proposed algorithm converges to an optimal solution of the objective function in Eq. (29). The convergence proof presented here is very similar to the one presented in Shang et al. (2016), Lin (2007). With U and W fixed, it is easily verified that H is convergence with an auxiliary function as in Shang et al. (2016), Lin (2007). So does the W.

Referring to Eq. (35), it is obviously that L₂(H^t+1) ≤ L₂(H^t) with the monotonically non-increased H mentioned above. That means:

$$ L\left( {{\varvec{W}}^{t} ,{\varvec{U}}^{t} ,{\varvec{H}}^{t + 1} } \right) \le L\left( {{\varvec{W}}^{t} ,{\varvec{U}}^{t} ,{\varvec{H}}^{t} } \right) $$

(38)

We firstly rewrite L₁ in Eq. (31) as follows:

$$ L_{1} \left( {\varvec{W}} \right) = \left\| {{\varvec{X}}^{T} {\varvec{W}} - {\varvec{H}}} \right\|_{F}^{2} + tr\left( {\phi {\varvec{W}}^{T} } \right) + \alpha tr\left( {{\varvec{W}}^{T} {\varvec{UW}}} \right) $$

(39)

It’s easily to know that L₁(W^t+1) ≤ L₁(W^t) with the monotonically non-increased W mentioned above when U and H fixed. Combining Eqs. (38) and (39), the following inequality could be presented:

$$ L\left( {{\mathbf{W}}^{t + 1} ,{\mathbf{U}}^{t} ,{\mathbf{H}}^{t + 1} } \right) \le L\left( {{\mathbf{W}}^{t} ,{\mathbf{U}}^{t} ,{\mathbf{H}}^{t + 1} } \right) $$

(40)

We need to present a lemma before a further convergence proof of the proposed algorithm.

Lemma 3

For arbitrary vectorsx, y ∈ Rⁿ, the following inequality holds:

$$ \left\| {\varvec{x}} \right\|_{2} - \frac{{\left\| {\varvec{x}} \right\|_{2}^{2} }}{{2\left\| {\varvec{y}} \right\|_{2} }} \le \left\| {\varvec{y}} \right\|_{2} - \frac{{\left\| {\varvec{y}} \right\|_{2}^{2} }}{{2\left\| {\varvec{y}} \right\|_{2} }} $$

(41)

The proof of this lemma can be found in Gu and Sheng (2017). We use this lemma to proof the convergence of the proposed algorithm of KFDRL in the following.

Using Lemma 3 we can show that the following inequality holds:

$$ \frac{{\left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2}^{2} }}{{2\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} }} - \left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} \ge \frac{{\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2}^{2} }}{{2\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} }} - \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} $$

(42)

which could be derived as:

$$ \begin{aligned} & \frac{{\left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2}^{2} - \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2}^{2} }}{{2\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} }} \ge \left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} - \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} \\ & \Rightarrow \quad \frac{{\left( {\left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} + \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} } \right)\left( {\left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} - \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} } \right)}}{{2\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} }} \ge \left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} - \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} \\ & \Rightarrow \quad \left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} + \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} \ge 2\left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} \\ & \Rightarrow \quad \left\| {{\hat{\varvec{w}}}_{i}^{t + 1} } \right\|_{2} \ge \left\| {{\hat{\varvec{w}}}_{i}^{t} } \right\|_{2} \\ \end{aligned} $$

(43)

Combining Eqs. (32) and (43), we have:

$$ {\varvec{U}}^{t + 1} \le {\varvec{U}}^{t} $$

(44)

Considering Eq. (39) and Eq. (40), we can obtain the following inequality formulation when W and H fixed:

$$ L\left( {{\varvec{W}}^{t + 1} ,{\varvec{U}}^{t + 1} ,{\varvec{H}}^{t + 1} } \right) \le L\left( {{\varvec{W}}^{t + 1} ,{\varvec{U}}^{t} ,{\varvec{H}}^{t + 1} } \right) $$

(45)

U is an intermediate variable function of W, it is straight forward that any reformulation of the objective function using an intermediate variable cannot affect this convergence. We can demonstrate the convergence of the algorithm proposed in Table 1 by some experimental results in the next section.

4.2 Computational complexity analysis

In this section, we analyze the computational complexity of KFDRL. It is evident that the algorithm requires the highest computation cost when it computes Laplacian matrix G, updates variables H and W, and so on. Computation of G including matrix inversion indicates the computation complexity O(n³). The update of H including both matrix inversion and multiplication indicates the computation complexity O(d³ + nd² + n²d). On the contrary, the update of W has relatively low computation complexity O(nd + d²). We neglect the influence of embedded dimension c where c ≪ d and c ≪ n. In conclusion, the total time complexity of the algorithm is O(n³ + t(d³ + nd² + n²d)) where t represents the number of iteration.

Time costs on different datasets will be shown in next section to display the computational complexity visually.

5 Experiments and analysis

In order to show the effectiveness of the method proposed in this paper, we present a number of experiments to imply the superiority of the method in different aspects. First, we introduce datasets and metrics. The parameters of KFDRL are set and a number of state-of-the-art algorithms are presented used to validate the result obtained by the algorithm proposed in this paper. Finally, we present 5 experiments.

• 1. The first experiment is to show the convergence rate of the objective function discussed before.

• 2. The second one is a toy example to intuitively show the effectiveness of KFDRL.

• 3. In the third experiment, we present feature selection and K-means clustering as a joint problem.

• 4. The forth experiment is a classification problem. We first perform feature selection and then nearest neighborhood classification. Experiments 3 and 4 are the application of dimensionality reduction in clustering and classification.

• 5. The final experiment aims to illustrate the sensitivity of the result to the parameters.

5.1 Datasets

In this paper, to validate the performance and accuracy of the result of KFDRL, we select nine UCI datasets and three samples from AT&T to perform our experiments. The detailed information about these datasets is listed in Table 2.

Table 2 Information of the experimental datasets

5.2 Evaluation metric

In order to analyze the quality of the results obtained by the algorithm, we use the clustering accuracy (ACC) and the normalized mutual information (NMI), which are two major metrics for clustering.

5.2.1 ACC

Assuming c_i and g_i represents pseudo label and true label respectively for ∀x_i. ACC clustering accuracy is defined as:

$$ ACC = \frac{{\sum\nolimits_{i = 1}^{n} {\delta (\varvec{g}_{i} ,\;map(\varvec{c}_{i} ))} }}{n} $$

(46)

where n is the total number of samples, δ(x, y) is delta function. Delta function has a value of one if x = y and zero otherwise. Map(•) computed by Hungarian algorithm (Strehl and Ghosh 2003) is a function that maps each cluster index to the best class label. Larger value of ACC means better clustering results.

5.2.2 NMI

Given two arbitrary variables P and Q, the NMI is defined as:

$$ NMI(P,Q) = \frac{MI(P,Q)}{{\sqrt {H(P)H(Q)} }} $$

(47)

where MI(P,Q) is mutual information between P and Q. H(.) denotes the information entropy (Papadimitriou and Steiglitz 1998). By definition NMI(P,Q) = 1 if P = Q and NMI(P,Q) = 0 otherwise. We can also formulate NMI in Eq. (47) using the pseudo labels t_l and true labels t_h, as follows:

$$ NMI = \frac{{\sum\nolimits_{l = 1}^{c} {\sum\nolimits_{h = 1}^{c} {t_{1,h} } \;\log \left( {\frac{{n \cdot t_{1,h} }}{{t_{1} t_{h} }}} \right)} }}{{\sqrt {\left( {\sum\nolimits_{l = 1}^{c} {t_{1} } \;\log \frac{{t_{1} }}{n}} \right)\left( {\sum\nolimits_{h = 1}^{c} {t_{h} } \;\log \frac{{t_{h} }}{n}} \right)} }} $$

(48)

where t_l,h is the number of samples identical among the two label sets. Obviously, the larger NMI is, the better clustering results have.

5.2.3 Classification accuracy

We use Euclidean distance to measure the classification accuracy. The dataset is divided in training and test sets. We use parts of dataset to train the classifier whereas the rest of the dataset is used for testing. Euclidian distance is used to measure the distance between the sample points. Hence, the samples of training and test sets belong to the same cluster if they are close.

5.3 Settings in experiments

5.3.1 Parameters settings for KFDRL

Based on the experiments in different algorithmic contexts, parameters selection affects the result of the corresponding algorithm. Therefore, it is very important to select the best parameters of KFDRL. With reference to Table 1, we can see that KFDRL has five parameters including α, β, σ, μ and λ. Some of these parameters can be set using existing method (Li et al. 2014; Hou et al. 2014; Fang et al. 2014; Shang et al. 2016). Since the algorithm shows no sensitivity to the value of λ if it has large enough value, we set λ = 10⁸, with reference to Li et al. (2014). We set the scaled parameter for Gaussian kernel function μ = 10⁻¹², based on the argument presented in Sect. 3. On the other hand, the other parameters must be set carefully as the result is sensitive to their value. Hence, we set σ = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000, 10000} based on our experience and a grid-search strategy is used to determine a small range of parameter values including the best value. Finally, the best value is computed with small enough step size tuning of the parameters in that region resulting in α = [0.1, 3.5] and β = {0.0001, 0.001, 0.01, 0.1, 1, 10, 100, 1000}.

5.3.2 The compared algorithms

We compare the results obtained by the proposed method with the ones obtained by some classical feature selection algorithms for clustering and classification problems, including LapScore, SPEC, MCFS, MRSF, JELSR, LSPE and DFSC (Zhao and Liu 2007; Cai et al. 2010; He et al. 2005; Zhao et al. 2010; Hou et al. 2014; Fang et al. 2014; Shang et al. 2016). To be fair, we use the parameters reported in the corresponding original works (Zhao and Liu 2007; Cai et al. 2010; He et al. 2005; Zhao et al. 2010; Hou et al. 2014; Fang et al. 2014; Shang et al. 2016). Hence, we use the best result of every algorithms with the parameters. We will also discuss the variable of different experiments in the later sections.

5.4 The convergence of KFDRL

This experiment is presented here to intuitively show the convergence and the rate of convergence. We apply the algorithm on four datasets including BC, Umist, Orl and Sonar. The evolutions of the objective values are shown in Fig. 1. These four pictures show the convergence of KFDRL.

Fig. 1

The convergence of objective function of KFDRL on four selected datasets. a Convergence on BC, b convergence on Orl, c convergence on Sonar, d convergence on Umist

It can be seen from Fig. 1, the value of objective function decreases very fast over the first three iterations for all four datasets. This evidences that KFDRL is very efficient in terms of convergence rate. This testifies that we can set the maximum number if iteration to five during the next experiment to decrease the computation time.

5.5 Toy example

We randomly choose three different pictures from AT&T dataset to illustrate the effectiveness of KFDRL algorithm. This shows KFDRL always trends to select more discriminative features. We draw a number of pictures from the dataset respectively with {1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9220, 10244} features selected from each sample. The pixel point is considered as black when it is not chosen. In Fig. 2, three samples are displayed in three rows. From left to right, the pictures correspond to {1024, 2048, 3072, 4096, 5120, 6144, 7168, 8192, 9220, 10244} features respectively. This figure shows how the picture drawn using different number of features approximates the original image. The more features we select, the more similar picture to the original image is drawn. As it is shown in Fig. 2, KFDRL tends to preserve more discriminative features even with small and fixed number of features. For example, the main profile of the face are recognizable in sample 1 and 3 using the picture drawn with only 1024 features, that is almost 10% of the total number of features. Nonetheless, sample 2 shows a bit less effectiveness of the method since the picture drawn by the algorithm with 1024 features does not show the nose, forehead and rim of the eye very important features for recognizing a face. In conclusion, KFDRL can automatically characterize the most important features in an image. The 4096 features (almost 40% of the total features) selected by KFDRL are necessary and sufficient to draw a picture identical to the original image while the rest of features can be regarded as redundant and irrelevant ones.

Fig. 2

Top row: an image of a face belonging to the 5th sample of class 2 of AT&T dataset; Middle row: an image of a face belonging to the 7th sample of the class 3 of AT&T dataset; Bottom row: an image of a face belonging to the 10th sample of the class 6 of AT&T dataset

5.6 Feature selection for K-means

In this section, we show the performance of K-means clustering by KFDRL where ACC and NMI are used as metrics. We set the number of selected features to be {10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120} on Coil20, Orl, Isolet and Umist, and {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22} on Ionosphere, BC and Sonar. The number of feature for each algorithm is chosen such that we obtain the best clustering result. To set the parameters of the KFDRL, namely α and β, we follow the procedure presented in Sect. 5.3.1. Nonetheless, σ is set to 1 since the result does not show any sensitivity to its value. This will be discussed and showed in detail in the later experiments.

• 1) Algorithms used for validation of the results are LapScore, SPEC, MCFS, MRSF, JELSR, LSPE and DFSC. We classify these algorithms into three categories (I) LapScore is a classical method (II) SPEC, MCFS and MRSF are two-step methods and (III) the rest of them are one-step methods.

• 2) We use the following datasets to test the algorithms: Coil20, Orl, Ionosphere, Isolet, Umist, BC and Sonar.

• 3) Procedure of the experiment: we first run all feature selection algorithms including KFDRL on each dataset. Then, the K-means clustering is applied to the datasets obtained by using feature selection algorithms. Finally, the best results of each algorithm are reported in Table 3. Since the influence from initial cases cannot be ignored for K-means clustering, we run the K-means for 100 times and then compute the average value to reduce the error.

  Table 3 The best results of ACC for each algorithm in different datasets (mean ± STD%)

Tables 3 and 4 display the best ACC and NMI obtained by different feature selection algorithms on all the datasets. The second rows in the two tables show clustering results on the original data. The best results on each dataset are marked as bold. We omit the NMI results on Sonar dataset in Table 4 because NMIs of all the algorithms including KFDRL are no larger than 10%. We can know that it lacks the mutual information and has a poor performance of the algorithm in clustering Sonar dataset.

Table 4 The best results of NMI for each algorithm in different datasets (mean ± STD %)

We can summarize the results presented in Tables 3 and 4 as follows:

• 1. ACC and NMI illustrate that KFDRL performs better than other feature selection algorithms on most of the datasets.

• 2. The traditional dimensionality reduction algorithm LapScore, which is a modified for Laplacian Eigenmaps (LE), recognizes and utilizes manifold structure embedded in high dimensional data by graph Laplacian without learning mechanism. The results reported in Tables 3 and 4 show that the joint-framework or two-step algorithms can perform better than traditional and one-step algorithms.

• 3. In comparison to other algorithms, KFDRL demonstrated superiorities. First, it simultaneously benefits from manifold and discriminative information, because the objective function proposed in KFDRL combines manifold learning and discriminative regression learning. Second, the constraints imposed on the scaled assignment cluster matrix H and on the transformation matrix W can help it to find physically meaningful features (a forced constraint imposed to the scaled assignment cluster matrix H and the transformation matrix W can fit the physical meaning). The best results obtained with feature selection for each dataset have better performance than the clustering results obtained on the original datasets. It indicates that feature selection can not only reduce the size of date to increase the computation speed, but also efficiently remove the redundant and noisy information demonstrating the great significance of data pre-processing.

• 4. KFDRL cannot show a better performance than the other algorithms in a few cases. For example, it shows that JELSR performs better than KFDRL with ACC metric on Sonar dataset. Moreover, it shows that KFDRL performs worse than all features selected and DFSC with NMI metric on the Isolet dataset, as well as JELSR and LSPE on the Umist dataset. It is noted that these methods mentioned above are all single-step methods, which describe their better performance. We explain several reasons for the worse performance of KFDRL. First, Sonar and Isolet are both voice data. The advantage of KFDRL can be identified in the task of clustering image data because the embedded dimension and the number of classes are considered to be identical (Cai et al. 2008, 2011; Liu et al. 2012), i.e. c = m. However, it cannot have better results on the Sonar and Isolet datasets. We believe the embedding learning employed in JELSR and LSPE on the Umist dataset has superiority over other techniques. As reported in Tables 3 and 4 an algorithm resulting in a better performance of clustering different datasets than others does not exist. Hence, the best algorithm still needs to be chosen based on the nature of the dataset to be clustered and finding an algorithm best for clustering all the different datasets will be an open research question for future.

• 5. In general, KFDRL performs better than JELSR on most of the datasets, which indicates that the manifold learning alone is not efficient in many cases. Nonetheless, JELSR outperforms KFDRL on the Sonar and Umist dataset, which may be a result of the inherently discriminant structure of the datasets. Hence, a discriminative based algorithm cannot perform as well as it does in the case of non-discriminant datasets. It is worth reminding that KFDRL includes discriminative and manifold learning whereas JELSR is based on manifold learning only.

5.7 Classification

In this section, we apply the dimensionality reduction algorithms to the classification problems. This will improve the classifier efficiency by reducing the corresponding feature dimensions. To study and show the performance improvement, we use the classification accuracy (AC) as the evaluation metric to show how the performance of nearest neighborhood classifier (NN) improves by using KFDRL to select the relevant features. We use the Ionosphere and Coil20 dataset because they have different sizes. From Table 2, we know that Ionosphere is a small size dataset with 34 features and 2 classes while Coil20 is a large size dataset with 1024 features and 20 classes.

We select one algorithm from each three categories (namely traditional, one-step and two-step algorithms) of algorithms recognized in this paper to ensure the representativeness of the experiment. We choose LapScore belonging to the first category, SPEC belonging to the second category, and JELSR belonging to the third category.

Similarly to the method presented in Zhao et al. (2010), we first do dimensionality reduction for original datasets by feature selection. Next, we use 50% of the dataset for training and the rest 50% for testing. NN-classifier is used to perform classification where the results are shown in Fig. 3. The vertical axis in Fig. 3 shows the AC value and the horizontal axis show the number of features selected. The black lines in two figures are both the classification results using the original dataset. We have chosen the numbers of features {2, 4, 6, 8, 10, 12, 14, 16} for classifying Ionosphere dataset and {20, 40, 60, 80, 100, 120, 140, 160} for classifying Coli20 dataset. The process is repeated 50 times resulting in 50 different partitions. Figure 3 shows some interesting results, which we discuss in the following:

Fig. 3

Classification accuracy (AC) by NN-classifier on two typical datasets. a AC with different selected features by different algorithms on Ionosphere, b AC with different selected features by different algorithms on Coil20

• 1. KFDRL results in the best performance in classifying small size dataset Ionosphere when the features selected are more than four. When the number of features larger than eight, the results obtained by almost all the algorithms are better than the original dataset for classification.

• 2. The joint-framework algorithms have a better performance than the traditional algorithm in classifying Coil20 dataset with relatively large size. However, the joint-framework algorithms result in better performance than the two-step algorithm only if the features selected are more than 60. Moreover, KFDRL shows superiority over JELSR. Although the joint-framework algorithms have better performance in most cases, the two-step algorithms show superiority over joint-framework algorithm in some cases.

• 3. SPEC and KFDRL result in 98% of classification performance using the original dataset by using only 100 selected features, almost 10% of the total number of features, which illustrates that most of the discriminative features are included in the 100 selected features. This significantly accelerates the classification rate due to the significantly fewer number of features used, as it is reported in Table 5.

  Table 5 The time cost of classification on Coil20 when selected features s = 100 (s)

• 4. Based on the results of classification of two datasets, we recognize the Ionosphere has noisy and irrelative features as such a better performance is obtained if feature selection algorithm is used. Nonetheless, it describes the fact that the more features selected the less AC value obtained. For Coil20, the best classification results obtained by using KFDRL and SPEC as the feature selection. These results are almost identical to the result obtained by classifying the original dataset. It indicates that Coil20 has many redundant features and it is less noisy. Therefore, dimensionality reduction plays an important role in cutting the computation cost and memory space usage for classifying the Coil20 dataset.

• 5. Although JELSR and KFDRL are joint-frame algorithms, the results of classification problem demonstrate that KFDRL obtains the best results of classification on most datasets by adding discriminative analysis technology. Though different methods are compared in clustering problem in many papers, we show the classification is also worth considering since it is popular application of the dimensionality reduction. We show that the discriminative analysis can improve the performance of classification problem.

• 6. For demonstrating the rationality of the classification experiment and suppressing interference from the randomly sampling, the t test is employed to test the reliability of the above AC results. The threshold of statistical significance is set to 0.05 in Table 6. “W” means KFDRL performs better than other algorithms discussed in this paper, “F” indicates KFDRL fails and “B” implies we cannot distinguish the results using statistical method. The value in brackets is p value, which indicates the probability of other methods is worse than KFDRL. The smaller the p value is, the more confidence we have on the corresponding statement.

  Table 6 t Test for AC in Fig. 3

The results reported in Table 6 illustrate that the hypothesis matches the results of AC in most cases. Hence, AC can be used as a valid metric to analyze the results of the experiments.

5.8 Parameter sensitivity

5.8.1 Sensitivity analysis of σ

We use part of Ionosphere, Sonar and Coil20 as our test datasets and use σ = {10⁻³, 10⁻², 10⁻¹, 10⁰, 10¹, 10², 10³} to test the sensitivity of the clustering algorithm with different choice of σ value whereas the other parameters are fixed. The results are shown in Fig. 4a on the BC dataset, Fig. 4b on the Ionosphere dataset, and Fig. 4c on the Coil20 dataset, where the blue and green lines show ACC and NMI, respectively.

Fig. 4

Clustering stability with different value of σ.a the sensitivity of clustering BC to σ, b the sensitivity of clustering Ionosphere to σ, c the sensitivity of clustering Coil20 to σ

It is apparent that ACC and NMI are constant for different value of σ on the BC and Ionosphere datasets because they show a slight change on the Coil20 dataset. These three datasets are different in terms of size and dimension. In Fig. 4, the result of clustering Coil20 dataset is more sensitive to changes of σ than BC and Ionosphere datasets. Considering that Coil20 is much bigger than BC and Ionosphere, we believe that the size of dataset is an important factor of the robustness of kernel function. In conclusion, the σ is almost insensitive to the datasets in this paper.

5.8.2 Sensitivity analysis of α and β

Here we focus on the sensitivity of α and β with other parameters fixed. After a grid-search we set α to in the range of 0.01 and 2.50 and β to be {0.001, 0.01, 0.1, 1, 10, 100, 1000}. We applied K-means clustering to six UCI datasets respectively with different α and β. The results shown in Fig. 5 are averaged over 15 times clustering.

Fig. 5

ACC with different α and β. Different values of α and β are selected for different datasets within the certain range. a Sensitivity on BC, b sensitivity on Sonar, c sensitivity on Ionosphere, d sensitivity on Coil20, e sensitivity on Isolet, f sensitivity on Umist

We can interpret the results shown in Fig. 5 as follows:

• 1. The ACC is constant for the Umist dataset with different values of α and β. On the other hand, for larger datasets with the number of features over 1000, such as Isolet and Coil20, the ACC changes mostly as a function of α. For the dataset whose dimension is no more than 10², such as Umist, the best ACC obtained by KFDRL can be found using α and β tuned by grid-search only. However, for the larger datasets, it is important to tune the parameters in the certain range determined by the grid-search. Similarly with most of the feature selection algorithms, it is still an open problem to find an efficient method to search a suitable value for parameters. At present, it mostly depends on experiences and test.

• 2. It is evident that α has a stronger influence on the results than β. ACC value is not sensitive to β value, as shown in Fig. 5, which indicates there is no relevance between the discriminative term and learning framework term according to Eq. (31). In fact, α is the parameter that balances fitting term and generalization term in learning process. It is why ACC is more sensitive to α value than other parameters. Improper choice of α can easily lead to the under-fitting or the over-fitting problem.

Figure 6 shows a comparison of results with the default parameters and the best parameters. This figure illustrates the importance of α and β in KFDRL algorithm. In Fig. 6, blue bars show ACC and NMI corresponding with the parameters randomly selected whereas brown bars show the ACC and NMI with the best-tuned parameters. Here we randomly select α = 1.5 and β = 10.

Fig. 6

The performance comparison between the cases with the default (i.e. α = 1.5, β = 10) and best parameters. a The performance comparison of ACC, b The performance comparison of NMI

It can be seen from Fig. 6 that a fixed α results in different performance of ACC and NMI. In other words, different α is needed for different datasets. Considering that different datasets have different intrinsic information, we believe α is impacted by a dataset itself including its size and dimension.

5.9 Time costs

Obviously, time cost is depended on the size of dataset in most cases. In this part, computational complexity in different algorithms is shown visually in the one-off running time form. Here, several representative algorithms are selected as compared algorithms, including LapScore (a classical algorithm), SPEC and MCFS (two-step algorithms), DFSC and JELSR (joint-framework algorithms). Furthermore, six medium scaled with 100 selected features and three small scaled datasets with 30 selected features are tested.

We draw the results in Fig. 7 as follows, which are obtained in seconds by MATLAB 2014a, 6 GB RAM and a 2.50 GHz CPU.

Fig. 7

Running time with different algorithms (s). a Running time on the first five datasets (s). b Running time on the last four datasets (s)

It can be seen in Fig. 7, KFDRL and DFSC are high-complexity algorithms. Thus, offline cases may be more applicable for the proposed algorithm KFDRL, especially handling big data. Here, larger scaled datasets are not chosen for their out-of-costs on the configuration. In real situation, that problem could be addressed with some developed platform, such as hadoop and spark.

6 Conclusion

A variety of feature selection algorithms have been proposed for dimensionality reduction. However, in most cases, either the manifold information or discriminative information is utilized alone. In contrast, both the manifold information and discriminative information are important for clustering, classification and other applications. Thus, in this paper, a novel unsupervised feature selection algorithm based on discriminant analysis and regression learning (KFDRL) is proposed to reduce dimensionality by better exploiting the underlying information. In particular, both manifold information and discriminative information data are used together. To achieve this goal, the kernel method is used in LDA to handle nonlinear spaces. At the same time, this LDA model is constructed and proved to be form of a spectral clustering. Thus the intrinsic information, i.e. both manifold information and discriminative information are preserved. Next, the kernel model and regression learning are unified into a joint-framework to get better performance. To select features effectively, L_2,1-norm is imposed to be a sparse constraint. A simple and efficient method, i.e. the alternative iteration update rule, is used to optimize the objective function and get a sparse representation matrix. Finally, our experiments demonstrate that KFDRL outperforms other algorithms in clustering and classification by removing noise and redundancy more effectively. In addition, the experiment demonstrates the fast convergence properties of KFDRL. The simple example problem is further used to illustrate the validity of KFDRL intuitively. The parameter sensitivity experiment implies that only one parameter in KFDRL is significantly sensitive on different datasets, and needs tuning via optimization. In conclusion, KFDRL performs highly compared to other state-of-the-art methods.

The most pressing problem is the time complexity. The experiment in terms of time costs indicates that the KFDRL has a relatively long time compared with other algorithms, especially tuning parameters. It means that if parameters in KFDRL had been decided, cost of running time can be accepted. Otherwise, the time on tuning parameters cannot be tolerant at present.

There are some remaining aspects of KFDRL which might be improved in future work, either. First, though the alternative update rule is fast and simple, a limitation is that it may converge on local optima, and is easily affected by initial values. Second, how to tune parameters efficiently is still an open problem. Third, the stability is worse when KFDRL is applied to big datasets, where the results significantly depend on parameter α. Finally, the measurement KFDRL adopts is Euclidean distance, which is not always ideal for some real problems. In future work, we will concentrate on the global optimization for feature selection and find a better way to tune parameters. Furthermore, another interesting research question is how to uncover suitable measurements for different data automatically.