Abstract
This article provides the first survey of computational models of emotion in reinforcement learning (RL) agents. The survey focuses on agent/robot emotions, and mostly ignores human user emotions. Emotions are recognized as functional in decision-making by influencing motivation and action selection. Therefore, computational emotion models are usually grounded in the agent’s decision making architecture, of which RL is an important subclass. Studying emotions in RL-based agents is useful for three research fields. For machine learning (ML) researchers, emotion models may improve learning efficiency. For the interactive ML and human–robot interaction community, emotions can communicate state and enhance user investment. Lastly, it allows affective modelling researchers to investigate their emotion theories in a successful AI agent class. This survey provides background on emotion theory and RL. It systematically addresses (1) from what underlying dimensions (e.g. homeostasis, appraisal) emotions can be derived and how these can be modelled in RL-agents, (2) what types of emotions have been derived from these dimensions, and (3) how these emotions may either influence the learning efficiency of the agent or be useful as social signals. We also systematically compare evaluation criteria, and draw connections to important RL sub-domains like (intrinsic) motivation and model-based RL. In short, this survey provides both a practical overview for engineers wanting to implement emotions in their RL agents, and identifies challenges and directions for future emotion-RL research.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This survey systematically covers the literature on computational models of emotion in reinforcement learning (RL) agents. Computational models of emotions are usually grounded in the agent decision-making architecture. In this work we focus on emotion models in a successful learning architecture: reinforcement learning, i.e. agents optimizing some reward function in a Markov Decision Process (MDP) formulation. To avoid confusion, the topic does not imply the agent should ‘learn its emotions’. Emotions are rather derived from aspects of the RL learning process (for example from the value function), and may also persist after learning has converged.
One may question why it is useful to study emotions in machines at all. The computational study of emotions is an example of bio-inspiration in computational science. Many important advancements in machine learning and optimization were based on biological principles, such as neural networks, evolutionary algorithms and swarm-based optimization (Russell et al. 1995). An example encountered in this survey is homeostasis, a concept closely related to emotions, and a biological principle that led researchers to implement goal switching in RL agents.
The study of emotions in learning agents is useful for three research fields. First, for the machine learning (ML) community, emotions may benefit learning efficiency. For example, there are important connections to the work on (intrinsically) motivated RL. Second, researchers working on interactive machine learning and human–robot interaction (HRI) may benefit from emotions to enhance both transparency (i.e. communicate agent internal state) and user empathy. Finally, from an affective modelling (AM) perspective, where emotions are mostly studied in cognitive agents, RL agents provide the general benefits of the MDP formulation: these agents require few assumptions, can be applied to a variety of tasks without much prior knowledge, and, allow for learning. This also gives AM researchers access to complex, high-dimensional test domains to evaluate emotion theories.
Emotion is an important part of human intelligence (Johnson-Laird and Oatley 1992; Damasio 1994; Baumeister et al. 2007). On the one hand, emotion has been defined as a response to a significant stimulus—characterized by brain and body arousal and a subjective feeling—that elicits a tendency towards motivated action (Calvo et al. 2015; Frijda et al. 1989). This emphasizes the relation of emotions with motivation and action. On the other hand, emotions have also been identified as complex feedback signals used to shape behaviour (Baumeister et al. 2007; Broekens et al. 2013). This view emphasizes the feedback function of emotion. The common ground in both: (1) emotions are related to action selection mechanisms and (2) emotion processing is in principle beneficial to the viability of the individual. As an illustration, Damasio (1994) showed that people with impaired emotional processing (due to brain damage) show failures in work and social life. These observations connecting emotions to action selection and adaptive decision-making sparked interest in the computer science community as well, mainly following the initial work by Cañamero (1997b) and Gadanho and Hallam (1998).
We wrote this survey for two reasons. First, while the topic of emotion in RL agents has received attention for nearly 20 years, it appears to fall in between the machine learning and affective modelling communities. In particular, there is no framework connecting the variety of models and implementations. Although Rumbell et al. (2012) compared emotion models in twelve different agents, their work does not provide a full survey of the topic, nor does it focus on agents with a learning architecture. Our main aim is to establish such a framework, hoping to bridge the communities and potentially align research agendas. As a second motivation, this survey is also useful to engineers working on social agents and robots. Emotion has an important functional role in social interaction and social robotics (Fong et al. 2003). Our survey is also a practical guideline for engineers who wish to implement emotional functionality in their RL-based agents and robots.
As a final note, the term ‘reinforcement learning’ may be misleading to readers from a cognitive AI or psychological background. RL may reminisce of ‘instrumental conditioning’, with stimulus-response experiments on short time-scales. Although indeed related, RL here refers to the computational term for a successful class of algorithms solving Markov Decision Processes by sampling and learning from data. MDPs (introduced in Sect. 2.4) provide a generic specification for short-term and long-term sequential decision-making problems with minimal assumptions. Note that many cognitive AI approaches, that usually employ a notion of ‘goal’, are also expressible in MDP formulation by defining a sparse reward function with positive reward at the goal state.
The structure of this review is as follows. First, Sect. 2 provides the necessary background on emotion and reinforcement learning from psychology, neuroscience and computer science. Section 3 discusses the survey’s methodology and proposed taxonomy. Subsequently, Sects. 4–6 contain the main results of this survey by systematically categorizing approaches to emotion elicitation, emotion types and emotion functionality. Additionally, a comparison of evaluation criteria is presented in (Sect. 7). The survey ends with a general discussion of our findings, highlights some important problems and indicates future directions in this field (Sect. 8).
2 Background
As many papers included in this survey build upon psychological (Sect. 2.1) and neuroscientific (Sect. 2.2) theories of emotion, this section provides a high-level overview of these fields. Subsequently, we position our work in the computer science and machine learning community (Sect. 2.3). We conclude these preliminaries by formally introducing computational reinforcement learning (Sect. 2.4).
2.1 Psychology
We discuss three dominant psychological emotion theories: categorical, dimensional, and componential theories (see also Lisetti and Hudlicka 2015).
Categorical emotion theory assumes there is a set of discrete emotions forming the ‘basic’ emotions. These ideas are frequently inspired by the work by Ekman et al. (1987), who identified the cross-cultural recognition of anger, fear, joy, sadness, surprise and disgust on facial expressions. In an evolutionary perspective, each basic emotion can be considered as an elementary response pattern, or action tendency (Frijda et al. 1989). For example, fear has the associated action tendency of avoidance, which helps the organism to survive a dangerous situation, accompanied by a negative feeling and prototypical facial expression. However, the concept of ‘basic’ emotions remains controversial within psychology, as is reflected in the ongoing debate about which emotions should be included. The number of emotions to be included ranges from 2 to 18, see Calvo et al. (2015).
Dimensional emotion theory (Russell 1978) assumes an underlying affective space. This space involves at least two dimensions; usually valence (i.e. positive/negative evaluation) and arousal (i.e. activation level) (Russell and Barrett 1999). For example, fear is a highly arousing and negative affective state. The theory was originally developed as a ‘Core affect’ model, i.e. describing a more long-term, underlying emotional state. Osgood et al. (1964) originally added dominance as a third dimension, resulting in the PAD (pleasure, arousal, dominance) model. Dimensional models have difficulty separating some emotion categories such as anger and disgust, which is a common critique of this theory.
Finally, componential emotion theory, best known as cognitive appraisal theory (Lazarus 1991), considers emotions as the results of evaluations (appraisals) of incoming stimuli according to personal relevance. Some examples of frequently occurring appraisal dimensions are valence, novelty, goal relevance, goal congruence and coping potential. Distinct emotions relate to specific patterns of appraisal activation. For example, anger is a result of evaluating a situation as harmful to one’s own goals with the emotion attributed to the responsible actor and at least some feeling of power. Some well-known appraisal theories that have been a basis for computational models are the OCC model (named after the authors Ortony, Clore and Collins) (Ortony et al. 1990), the component process theory of emotions (CPT) (Scherer et al. 2001), and the belief-desire theory of emotions (BDTE) (Reisenzein 2009). Although cognitive appraisal theories describe the structure of emotion well, they are limited with respect to explaining where appraisals themselves come from, what the function of emotion is in cognition and intelligence, and how they are related to evolution.
Note that the presented theories focus on different aspects of emotions. For example, appraisal theory focuses on how emotions are elicited, while categorical emotion models focus on action tendencies, i.e. the immediate function of emotions. Some consider emotions to precede action selection, while others focus on emotions as feedback signals (Baumeister et al. 2007). In this survey emotions are considered in a reward-based feedback loop, which involves both emotion elicitation and function.
2.2 Neuroscience
Affective responses and their relation to behaviour and learning have also been extensively studied in neuroscience; for a survey see Rolls and Grabenhorst (2008). We discuss theories by LeDoux, Damasio and Rolls. The work by LeDoux (2003) mainly focussed on the role of the amygdala in fear conditioning. LeDoux identified that incoming sensory stimuli can directly move from thalamus to amygdala, thereby bypassing the previously assumed intermediate step through the neo-cortex. As such, the work showed that emotional responses may also be elicited without neo-cortical reasoning.
Damasio (1994) took a different perspective on rational emotions through the ‘somatic marker hypothesis’. He proposes that emotions are the result of bodily sensations, which tell the organism that current sensations (i.e. events) are beneficial (e.g. pleasure) or harmful (e.g. pain). The somatic marker is therefore a signal that can be interpreted as feedback about the desirability of current and imagined situations. The somatic marker hypothesis has been interpreted in terms of RL as well (Dunn et al. 2006).
Later work by Rolls shifted the attention from the amygdala to the orbito-frontal cortex (OFC) (Rolls and Grabenhorst 2008) Imaging studies have implicated the OFC in both reinforcement and affect, with direct input connections of most sensory channels (taste, olfactory, visual, touch), while projecting to several brain areas involving motor behaviour (striatum) and autonomic responses (hypothalamus) (Rolls and Grabenhorst 2008). Also, single neuron studies have shown that visual and taste signals (the latter being a well-known primary reinforcer) converge on the same neurons (Rolls and Baylis 1994), coined ‘conditional reward neurons’. Earlier work already identified ‘error neurons’, which mainly respond when an expected reward is not received (Thorpe et al. 1983).
Together, these theories suggest that emotions are closely linked to reward processing. These ideas are implicitly reflected in part of the reinforcement learning-based implementations in this survey. These ideas are also reflected in Rolls’ evolutionary theory of emotion (Rolls and Grabenhorst 2008), which identifies emotions as the results of primary reinforcers (like taste, affiliative touch, pain) which specify generic goals for survival and reproductive success (like food, company and body integrity). According to Rolls, emotions exclusively emerge from these goal-related events. This view is also compatible with the cognitive appraisal view that emotions are the result of stimuli being evaluated according to their goal/need relevance. However, in cognitive appraisal theory the ‘goal’ is defined at a different level of abstraction.
2.3 Computer science
Affective modelling is a vibrant field in computer science with active subfields (Calvo et al. 2015), including work on affect detection and social signal processing (Vinciarelli et al. 2012; Calvo and D’Mello 2010), computational modelling of affect in robots and virtual agents (Marsella et al. 2010), and expression of emotion in robots and virtual agents (Ochs et al. 2015; Paiva et al. 2015; Lhommet and Marsella 2015). Since this survey focusses on affective modelling, in particular in RL-based agents, we provide some context by discussing emotions in different agent architectures, in particular symbolic and (non-RL) machine learning-based.
One of the earliest symbolic/cognitive architectures was Velasquez’ Cathexis model (Velasquez 1998). It incorporated Ekman’s six emotions in the pet robot Yuppy, which later also formed the basis for the well-known social robot Kismet (Breazeal 2003). Several well-known symbolic architectures have also incorporated emotions, either based on categorical emotions (Murphy et al. 2002), somatic marker hypothesis (Laird 2008), or appraisal theories [EMIB (Michaud 2002), EMA (Marsella and Gratch 2009) and LIDA (Franklin et al. 2014)]. Although symbolic/cognitive architecture approaches are capable of solving a variety of AI tasks, they are limited with respect to learning from exploration and feedback in unstructured tasks.
In contrast, machine learning implementations focus on learning, as the agent should gradually adapt to its environment and task. The dominant research direction in this field is reinforcement learning (RL) (Sutton and Barto 1998), which we formally introduce in the next section. There are however other machine learning implementations that incorporate emotions. Some examples include agents based on evolutionary neural networks (Parisi and Petrosino 2010), the free-energy principle (Joffily and Coricelli 2013), Bayesian models (Antos and Pfeffer 2011) or entropy (Belavkin 2004).
Finally, we want to stress that the focus of this review is on agent emotion, i.e. how it is elicited and may influence the agent’s learning loop. A related but clearly distinct topic is how human emotion may act as a teaching signal for this loop. Broekens (2007) showed human emotional feedback speeds up agent learning in a grid-world task compared to a baseline agent. There are a few other examples in this direction (Hasson et al. 2011; Moussa and Magnenat-Thalmann 2013), but in general the literature of emotion as a teaching signal is limited. Although the way in which humans actually tend to provide feedback is an active research topic (Thomaz and Breazeal 2008; Knox et al. 2012, 2013), it remains a question whether emotions would be a viable channel for human feedback. We do not further pursue this discussion here, and place our focus on agent emotions in RL agents.
2.4 Computational reinforcement learning
Computational reinforcement learning (RL) (Sutton and Barto 1998; Wiering and Van Otterlo 2012) is a successful approach that enables autonomous agents to learn from interaction with their environment. We adopt a Markov Decision Process (MDP) specified by the tuple: \(\{\mathcal {S},{\mathcal {A}},T,r,\gamma \}\), where \(\mathcal {S}\) denotes a set of states, \({\mathcal {A}} \) a set of actions, \(T: \mathcal {S} \times {\mathcal {A}} \rightarrow P(\mathcal {S})\) denotes the transition function, \(r: \mathcal {S} \times {\mathcal {A}} \times \mathcal {S} \rightarrow {\mathbb {R}}\) denotes the reward function and \(\gamma \in (0,1]\) denotes a discount parameter. The goal of the agent is to find a policy \(\pi : \mathcal {S} \rightarrow P({\mathcal {A}})\) that maximizes the expected (infinite-horizon) discounted return:
where we explicitly write out the expectation over the (possibly) stochastic policy and transition function. The optimal value function is defined as
from which we can derive the optimal policy
There are several approaches to learning the optimal policy. When the environmental dynamics \(T(s'|s,a)\) and reward function \(r(s,a,s')\) are known, we can use planning algorithms like Dynamic Programming (DP). However, in many applications the environment’s dynamics are hard to determine. As an alternative, we can use sampling-based methods to learn the policy, known as reinforcement learning.
There is a large variety of RL approaches. First, we can separate value-function methods, which try to iteratively approximate the cumulative return specified in Eq. (1), and policy search, which tries to directly optimize some parameterized policy. Policy search shows promising results in real robotic applications (Kober and Peters 2012). However, most work in RL utilizes value-function methods, on which we also focus in this survey.
Among value-function methods we should identify model-free versus model-based approaches. In model-free RL we iteratively approximate the value-function through temporal difference (TD) learning, thereby avoiding having to learn the transition function (which is usually challenging). Well-known algorithms are Q-learning (Watkins 1989), SARSA (Rummery and Niranjan 1994) and TD(\(\lambda \)) (Sutton 1988). The update equation for Q-learning is given by:
where \(\alpha \) specifies a learning rate. With additional criteria for the learning and exploration parameters we can show this estimation procedure converges to the optimal value function (Sutton and Barto 1998).
Model-based RL (Hester and Stone 2012b) is a hybrid form of planning (like DP) and sampling (like TD learning). In model-based RL, we approximate the transition and reward function from the sampled experience. After acquiring knowledge of the environment, we can mix real sample experience with planning updates. We will write \(M = \{\hat{T},{\hat{r}}\}\) to denote the estimated model. Note that a model is derived from the full agent-environment interaction history at time-point t, as given by \(g_t = \{s_0, a_0, s_1, a_1, s_2, \ldots s_{t-1}, a_{t-1}, s_t\}\).
A final aspect we have not yet discussed is the nature of the reward function. Traditional RL specifications assume an external reward signal (known as an ‘external Critic’). However, as argued by Chentanez et al. (2004), in animals the reward signal is by definition derived from neuronal activations, and the Critic therefore resides inside the organism. It therefore also incorporates information from the internal environment, making all reward ‘internal’. Singh et al. (2010) identifies two types of internal reward: extrinsic internal and intrinsic internal (we will omit ‘internal’ and simply use extrinsic and intrinsic from now on). Extrinsic reward is related to resources/stimuli/goals in the external world (e.g. food), possibly influenced by internal variables (e.g. sugar level). In RL terms, extrinsic reward explicitly depends on the content of the sensory information (i.e. the observed state). On the contrary, intrinsic reward is not dependent on external resources, but rather derived from the agent-environment history g and current model M. An example of intrinsic reward in animals is curiosity. Intrinsic reward is domain-independent, i.e. curiosity is not related to any external resource, but can happen at any state (dependent on the agent history g). In contrast, extrinsic reward for food will never occur in domains where food does not occur. Intrinsic motivation has been identified to serve a developmental role to organisms.
3 Survey structure and methodology
We intended to include all research papers in which reinforcement learning and emotion play a role. We conducted a systematic Google Scholar search for ‘Emotion’ AND ‘Reinforcement Learning’ AND ‘Computational’, and for ‘Emotion’ AND ‘Markov Decision Process’. We scanned all abstracts for the joint occurrence of emotion and learning in the proposed work. When in doubt, we assessed the full article to determine inclusion. Moreover, we investigated all papers citing several core papers in the field, for example, Gadanho and Hallam (2001), Salichs and Malfaz (2012), Broekens et al. (2007a) and Marinier and Laird (2008). This resulted in 52 papers included in this survey. A systematic overview of these papers can be found in Tables 9 and 10.
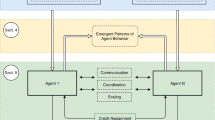
The proposed taxonomy of emotion elicitation, type and function is shown in Table 1, also stating the associated subsection where each category is discussed. The elicitation and function categories are also visually illustrated in Fig. 1, a figure that is based on the motivated RL illustration (with internal Critic) introduced in Chentanez et al. (2004). Figure 1 may be useful to refer back to during reading to integrate the different ideas. Finally, for each individual paper the reader can verify the associated category of emotion elicitation, type and function through the colour coding in the overview in Table 9.
Schematic representation of motivated reinforcement learning based on Chentanez et al. (2004). Although traditional RL assumes an external Critic (to provide the reward signal), this actually happens inside the brain of real-world organisms. Thereby the Critic also incorporates, apart from external sensations, internal motivations to determine the current reward and state. Motivations have been derived from homeostatic variables and/or internal models. The Critic then feeds the state and reward to the Agent. The Agent usually learns a value function (Adaptive Critic) and determines the next action (Actor). Note that ordinary RL, in which the reward is a fully external stimulus, is still a specific case of this scheme (with the Critic as identity function). Emotion elicitation (green) has been associated to (A) Homeostasis and extrinsic motivation (Sect. 4.1), (B) Appraisal and intrinsic motivation (Sect. 4.2), (C) Reward and value function (Sect. 4.3) and (D) Hard-wired connections from sensations (Sect. 4.4). Subsequently, the elicited emotion may also influence the learning loop. Emotion function (blue) has been linked to (I) Reward modification (Sect. 6.1), (II) State modification (Sect. 6.2), (III) Meta-learning (Sect. 6.3), (IV) Action selection (Sect. 6.4) and finally as (V) Epiphenomenon (Sect. 6.5) (Color figure online)
There is one important assumption throughout this work, which we want to emphasize here. We already introduced the distinction between extrinsic and intrinsic motivation in RL at the end of the last section. Throughout this work, we parallel extrinsic motivation with homeostasis (Sect. 4.1), and intrinsic motivation with appraisal (Sect. 4.2). The extrinsic/intrinsic distinction is clearly part of the RL literature, while homeostasis and especially appraisal belong to the affective modelling literature. We group these together, as the concept of extrinsic motivation is frequently studied in combination with homeostasis, while intrinsic motivation shows large overlap with appraisal theory. We will identify this overlap in the particular sections. However, the point we want to stress is that the concepts are not synonyms. For example, it is not clear whether some intrinsic motivation or appraisal dimensions also show homeostatic dynamics [a point at which we tend to disagree with Singh et al. (2010)]. However, a full discussion of the overlap and difference moves towards psychology, and is beyond the scope of our computational overview. We merely identify the overlap we observed in computational implementations, and therefore discuss both extrinsic/homeostasis and intrinsic/appraisal as single sections.
4 Emotion elicitation
We identify four major categories of emotion elicitation: extrinsic/homeostatic (Sect. 4.1), intrinsic/appraisal (Sect. 4.2), value function and reward-based (Sect. 4.3), and finally hard-wired (Sect. 4.4).
4.1 Homeostasis and extrinsic motivation
Several computational implementations of emotions involve homeostatic variables, drives and motivations. The notion of internal drives originates from the Drive Reduction Theory developed by Hull (1943), which identifies drive reduction as a central cause of learning. These innate drives are also known as primary reinforcers, as their rewarding nature is hard-wired in our system (due to evolutionary benefit). An example of a homeostatic variable is energy/sugar level, which has a temporal dynamic, an associated drive when in deficit (hunger) and can be satiated by an external influence (food intake). The reader might now question why machines even need something like ‘hunger’. However, for a robot the current energy level shows similarity to human sugar levels (and body integrity and pain show similarity to a robot’s mechanical integrity, etc.). Thereby, homeostasis is a useful concept to study in machines as well (see also the remark about bio-inspiration in the Introduction). There is a vast literature on motivated reinforcement learning, see e.g. Konidaris and Barto (2006) and Cos et al. (2013), mainly for its potential to naturally switch between goals. Early implementations of these ideas outside the reinforcement learning framework were by Cañamero (1997a, b).
We denote a homeostatic variable by \(h_t\), where t identifies the dependency of this variable on time. The organism’s full physiological state is captured by \(H_t = \{h_{1,t}, h_{2,t} \ldots h_{N,t}\}\), where \(h_{i,t}\) indicates the \(i{\mathrm{th}}\) homeostatic variable. Each homeostatic variable has a certain set point \(H^\star = \{h^\star _1, h^\star _2 \ldots h^\star _N \}\) (Keramati and Gutkin 2011). Furthermore, each homeostatic variable is affected by a set of external resources, associated to a particular action or state. For example, a particular homeostatic variable may increase upon resource consumption, and slightly decrease with every other action (Konidaris and Barto 2006). More formally, denoting resource consumption by \({\bar{a}}\) and the presence of a resource by \({\bar{s}}\), a simple homeostatic dynamic would be
for a resource effect of size \(\psi (s_t,a_t)\). We can also explicitly identify a drive as the difference between the current value and setpoint, i.e. \(d_{i,t} = |h^\star _i - h_{i,t}|\) (Cos et al. 2013). The overall drive of the system can then be specified by
where we introduced \(\theta _i\) to specify the weight or importance of the i-th homeostatic variable. Most examples take the absolute difference between current value and setpoint (i.e. the \(L_1\) norm) as shown above. However, we can consider the space of homeostatic variables \(H \in {\mathbb {R}}^N\) and in principle define any distance function in this space with respect to the reference point \(H^\star \) (see e.g. Fig. 2 for a Euclidean distance example).
The weight of each homeostatic variable (\(\theta _i\)) does not need to be fixed in time. For example, Konidaris makes it a non-linear function of the current homeostatic level \(h_{i,t}\) and a priority parameter \(\rho _{i,t}\): \(\theta _{i,t} = f(h_{i,t},\rho _{i,t})\). The former dependence allows priorities (i.e. rewards) to scale non-linearly with the sensory input levels [an idea reminiscent of Prospect Theory (Kahneman and Tversky 1979)]. The priority parameters \(\rho _{i,t}\) can be estimated online, for example assigning more importance to resources which are harder to obtain (i.e. that should get priority earlier). As a final note on homeostatic RL systems, note that internal variables need to be part of the state-space as well. One can either include all homeostatic variables and learn generic Q-values, or include only the dominant drive and learn drive-specific Q-values (Konidaris and Barto 2006).
Schematic illustration of homeostasis and drives. The figure shows a two-dimensional homeostatic space consisting (as an example) of energy (\(h_1\)) and water level (\(h_2\)). The set point (\(H^\star \)) indicates the desired values for the homeostatic variables. At the current time point t the agent’s homeostatic status is \(H_t\) (red). The associated drive \(D_t\) can be visualized as the distance to the set point. Note that we use the Euclidean distance for the drive here (i.e. \(D_t=||H^\star - H_t||_2\)), while the text describes the \(L_1\)-norm example (i.e. \(D_t=||H^\star - H_t||_1\), Eq. 6). We are free to choose any distance metric in homeostatic space. After taking an action the new homeostatic status becomes \(H_{t+1}\) (green), in this case bringing both homeostatic levels closer to their set point. The difference between the drives at both time points has been associated to reward and joy (see Sect. 6.1). Figure is partially based on Keramati and Gutkin (2011) (Color figure online)
The connection between drives/homeostasis and emotions is partially reflected in Damasio’s somatic marker hypothesis (Damasio 1994), stating that emotions are the result of bodily sensations. In general, we identify two ways in which homeostatic systems have been used to elicit emotions. The first elicits categorical emotions from a subset of homeostatic variables, while the second derives an overall well-being W from the sum of the homeostatic dimensions.
One of the first RL systems deriving emotions from homeostasis was by Gadanho and Hallam (1998, 2001). They describe an extensive set of internal variables (drives), including e.g. hunger (rises per timestep in lack of resources), pain (rises with collisions), restlessness (rises with non-progress) and temperature (rises with high motor usage). Emotions are related to these physiological variables, e.g. happiness is derived from the frequent motor use or decreasing hunger, sadness from low energy, fear from collisions (with less sensitivity if the agent is hungry or restless), and anger from high restlessness. Similar ideas are put forward by Coutinho et al. (2005), who specifies a more biological homeostasis: blood sugar (increases with food intake), endorphine (increases with play), energy (increases with bed rest), vascular volume (increases with water intake) and body integrity (decreases with obstacle collision). Similar examples of homeostatic emotions can be found in Von Haugwitz et al. (2012), Tanaka et al. (2004) and Goerke (2006).
A second group of implementations first defines the overall well-being (W). An example of a well-being specification is
where K denotes a reference value. Compared to the previous paragraph, now all internal variables (instead of subsets) are combined into a single emotion. Some papers leave the specification of well-being as their emotion (Gadanho 2003). Others actually identify the positive or negative difference in well-being as happy and unhappy (Salichs and Malfaz 2012) or ‘hedonic value’ (Cos et al. 2013).
In conclusion, there have been numerous approaches to homeostatic systems in emotional implementations. A summary of some of the most frequently encountered homeostatic dimensions is shown in Table 2. Although most papers use slightly different specifications for their homeostatic dimensions, it is usually a matter of labelling that does not affect the underlying principle. Homeostatic variables provide a good way to naturally implement goal and task switching. The implementation of this functionality usually involves reward modification, which is covered in Sect. 6.1.
4.2 Appraisal and intrinsic motivation
Appraisal theory is an influential psychological emotion theory (see Sect. 2). Appraisals are domain independent elements that provide (affective) meaning to a particular stimulus. As such, they are a basis for emotion elicitation, as different combinations of appraisal dimensions have different associated emotions. Examples of appraisal dimensions are novelty, recency, control and motivational relevance. These terms of course refer to abstract cognitive concepts, but in RL literature they show a large overlap with intrinsic motivation features, being independent of a specific external resource. Instead, they are functions of the agent-environment interaction history g and derived model M:
for the \(j{\mathrm{th}}\) appraisal variable. Note that the current state and action are actually included in g, but we emphasize that \(f_j(\cdot )\) is not a function of the actual content of any state s (see Sect. 2.4 for a discussion of the extrinsic/intrinsic distinction). Rather, \(f_j(\cdot )\) computes domain-independent characteristics, like ‘recency’ which may be derived from g, and ‘motivational relevance’ which can be derived by planning over M.
Intrinsic motivation is an active topic in developmental robotics (Oudeyer and Kaplan 2007). Singh et al. (2010) shows how incorporating these dimensions as extra reward provides better task achievement compared to non-intrinsically motivated agents (see Sect. 6.1). We discuss two implementations based on these ideas more extensively: Marinier and Laird (2008) and Sequeira et al. (2011). The work by Marinier and Laird (2008) takes a diverse set of appraisal dimensions based on Scherer’s appraisal theory (Scherer 1999). These include both sensory processing dimensions, like suddenness, intrinsic pleasantness and relevance, and comprehension and reasoning dimensions, like outcome probability, discrepancy from expectation, conduciveness, control and power. The implementation by Sequeira et al. (2011) uses a smaller subset of appraisal dimensions: novelty, relevance, valence and control. Note that these appraisal-based papers only elicit appraisal dimensions, without specifying categorical or dimensional emotions on top (see Table 9, i.e. appraisal papers with empty middle column).
We now highlight some appraisal implementations, both to concretize their specification in MDPs, and illustrate the differences between models. Sequeira et al. (2011) specifies ‘motivational relevance’ as inversely related to the distance to the goal. If we implement a planning procedure over our model M which returns an estimated distance \(\hat{d}(s,s^\circ )\) to the goal node \(s^\circ \) from our current node s, then the associated appraisal variable for motivational relevance could be (Sequeira et al. 2011):
Similarly, if we denote by c(s) the number of time-steps since node s was last visited, then we can specify a ‘recency’ feature as (Bratman et al. 2012):
This example intrinsic motivation vector \(\zeta = \{\zeta _{relevance}, \zeta _{recency} \}\) is used in Sect. 6.1 to show its use in reward modification.
There are several more specifications in intrinsic motivation RL literature that reflect appraisal dimensions. For example, Hester and Stone (2012a) maintain an ensemble of transition models (by stochastically adding new data to each model) and derive ‘model uncertainty’ from the KL-divergence (as a measure of the distance between two probability distributions) between the ensemble model’s predictions:
for all pairs of models i and j in the ensemble. As a second example from their paper, ‘novelty’ of a state-action pair is identified from the closest \(L_1\)-distance to a historical observation:
Recently, Houthooft et al. (2016) derive ‘curiosity/surprise’ from the KL-divergence between the old and new transition models (i.e. after updating based on the observed transition):
where \(T(\omega )\) denotes the transition model parameterized by \(\omega \). Together, Eqs. 9–13 illustrate how intrinsic motivation and appraisal theory have modelled similar notions, and gives a short illustration of the variety of concepts that are expressible in the MDP setting.
It is also important to note that appraisal theory bears similarities to many ‘domain-independent’ heuristics developed in the planning community (Russell et al. 1995). These of course include heuristics without a clear psychological or biological interpretation, but we mainly emphasize the potential for cross-breeding between different research fields. For example, some appraisal theories partition novelty into three sub-elements: familiarity, suddenness and predictability (Gratch and Marsella 2014). Each of these seem to capture different computational concepts, and such inspiration may benefit intrinsic motivation and/or planning researchers. The other way around, psychologist could seek for results from the RL or planning literature to develop and verify psychological theory as well.
There are several other implementations of appraisal dimensions, e.g. by Yu et al. (2015), Lee-Johnson et al. (2010), Williams et al. (2015), Si et al. (2010), Kim and Kwon (2010), Hasson et al. (2011) and Moussa and Magnenat-Thalmann (2013). We also encounter a few explicit social dimensions, like social fairness (Yu et al. 2015) and social accountability (Si et al. 2010), although the latter for example requires some symbolic reasoning on top of the RL paradigm. This illustrates how current RL algorithms (for now) have trouble learning complex social phenomena. Some of the appraisal systems also include homeostatic variables (Yu et al. 2015). Both Williams et al. (2015) and Lee-Johnson et al. (2010) do not mention appraisal in their paper, but their dimensions can be conceptualized as intrinsic motivation nevertheless.
In summary, some appraisal-based dimensions require cognitive reasoning, and are harder to implement. However, dimensions like novelty, motivational relevance and intrinsic pleasantness are frequently implemented (see Table 3). Table 4 provides a more systematic overview of the actual connections to the RL framework. These features usually require learned transition functions, recency features or forward planning procedures over the model space, which can all be derived from the history g. Also note that a single concept may be interpreted in very different ways (Table 4). For example, control and power have been derived from the transitions function (Kim and Kwon 2010), from the number of visits to a state (Sequeira et al. 2011), from a forward planning procedure (Si et al. 2010) and from the overall success of the agent (Williams et al. 2015). We encounter a fundamental challenge in the field here, namely how to translate abstract cognitive concepts to explicit (broadly accepted) mathematical expressions.
4.3 Value function and reward
The third branch of emotion elicitation methods in RL focusses on the value and reward functions. We can generally identify four groups: value-based, temporal difference-based, average reward-based and reward-based (Table 5).
One of the earliest approaches to sequential decision making based on emotion was by Bozinovski (1982) and Bozinovski et al. (1996), who considered emotion to be the expected cumulative reward (i.e. the state-action value) received from taking an action in that state. Thereby, Bozinovski actually developed a precursor of Q-learning grounded in emotional ideas. Other implementations have also considered emotion as the state value. For example, Matsuda et al. (2011) maintains a separate value function for fear, which is updated when the agent gets penalized. Recent work by Jacobs et al. (2014) considers the positive and negative part of the state as the hope and fear signal. Another value-based approach is by Salichs and Malfaz (2012), who model the fear for a particular state as the worst historical Q-value associated with that state. As such, their model remembers particular bad locations for which it should be afraid.
A second group of value function related implementations of emotions are based on the temporal difference error (TD). For Q-learning, the TD is given by
There has been extensive research in neuroscience on the connection between dopamine and the TD. Following these ideas, there have also been implementations connecting happiness and unhappiness to the positive and negative TD, respectively (Moerland et al. 2016; Jacobs et al. 2014; Lahnstein 2005). Models based on the temporal difference are robust against shifting the reward function by a constant (a trait that is not shared by the models of the first group of this section). More recently, Moerland et al. (2016) extended these ideas by deriving hope and fear signals from anticipated temporal differences (through explicit forward simulation from the current node).
Another branch of emotion derivations base themselves on the average reward. For example, Broekens et al. (2007a), Schweighofer and Doya (2003) and Hogewoning et al. (2007) derive a valence from the ratio between short- and long-term average reward. Shi et al. (2012) also derives emotions from the temporal change in reward function, while Blanchard and Canamero (2005) uses the average reward. Other implementations interpreted the reward itself as the emotional signal (Moren and Balkenius 2000; Balkenius and Morén 1998; Ahn and Picard 2006).
In conclusion, emotions have been related to the value function, temporal difference error or direct derivative of the reward function (Table 5). Note that some implementations try to incorporate a time dimensions as well (besides only the reward or value signal), e.g. Moerland et al. (2016), Salichs and Malfaz (2012) and Broekens et al. (2007b).
4.4 Hard-wired
While all three previous groups used internal agent/robot aspects, a final category specifies hard-wired connections from sensory input to emotions. A first group of implementations use the detected emotional state of another person to influence the emotion of the agent/robot (Hoey et al. 2013; Ficocelli et al. 2016). Hasson et al. (2011) uses facial expression recognition systems to detect human emotion, while Kubota and Wakisaka (2010) uses human speech input. Note that if these agent emotions subsequently influence agent learning, then we come very close to learning from human emotional feedback (as briefly described in Sect. 2.3).
There are several other implementations that pre-specify sensation-emotion connections. In general, these approaches are less generic compared to the earlier categories. Some use for example fuzzy logic rules to connect input to emotions (Ayesh 2004). Another example we encountered is the previous emotional state (at \(t-1\)) influencing the current emotional state (Kubota and Wakisaka 2010). An example is the Markovian transition model between emotions in Ficocelli et al. (2016), with similar ideas in Zhang and Liu (2009). This is a reasonable idea for smoother emotion dynamics, but we still categorize it as hard-wired since it does not explain how initial emotions should be generated.
Finally, there is also overlap with previously described elicitation methods. For example, Tsankova (2002) derives an emotion (frustration) directly from the collision detector. This is very similar to some homeostatic specifications, but Tsankova does not include a body integrity or pain variable (i.e. it is therefore not a homeostatic system, but the author does make the connection between pain or non-progress and frustration). In conclusion, the hard-wired emotion elicitation does not seem to provide us any deeper understanding about emotion generation in RL agents, but the papers in this category may actually implement ideas from different elicitation methods.
5 Emotion type
Having discussed the methods to elicit emotions, this section discusses which types of emotions are specified. We cover both categorical (Sect. 5.1) and dimensional (Sect. 5.2) emotion models. Note however that some appraisal theory-based papers only elicit appraisal dimensions, without specifically identifying emotions (see Table 9).
5.1 Categorical
Most papers in the emotion and RL literature elicit categorical emotions. An overview of the most occurring emotions and their associated papers is presented in Table 6. Joy (or happiness) is the most implemented emotion by a wide variety of authors. We did not include the papers that specify a valence dimension (see Sect. 5.2), but this could also be interpreted as a happy-sad dimension. A few papers Von Haugwitz et al. (2012) and Tanaka et al. (2004) specifically address Ekman’s six universal emotions (happy, sad, fear, anger, surprise, disgust), while most papers drop the latter two emotions.
In general, happy, sad, fear and anger have been implemented in all elicitation categories (homeostatic, appraisal and value-based). However, hope has mainly been connected to value function based systems. The implementations of hope try to assess anticipation (by addressing the value function (Jacobs et al. 2014), the dynamics within a decision cycle (Lahnstein 2005), or explicitly forward simulating from the current node towards expected temporal differences (Moerland et al. 2016). Hope therefore needs a time component, a notion which is not directly available from for example an extrinsic homeostasis dimension.
An overview of the most often elicited emotions (happy, sad, fear and angry) is provided in Table 7. The table shows that different elicitation methods have been associated to similar sets of categorical emotions. For example, anger (fourth column) has been associated to extrinsic homeostasis (e.g. hunger), intrinsic appraisal (e.g. non-progress) and reward-based (decreasing received reward) elicitation. Note that frustration, a closely related emotion, has been associated to obstacle detection (Tsankova 2002) and non-progress (Hasson et al. 2011) as well. The other three emotions in Table 7 have also been associated to each elicitation dimension, as is easily observed from the colour coding.
Note that Table 7 also shows how different researchers apply different elicitation methods within one paper (i.e. looking at rows instead of columns now). Moreover, a few papers even combine elicitation methods for an individual emotion. For example, Williams et al. (2015) derives fear from a combination of pain (extrinsic) and novelty (intrinsic/appraisal). It is important to realize that the elicitation methods of the previous section are clearly only a framework. These are not hard separations, and combining different approaches is clearly possible (and probably necessary), as these papers nicely illustrate.
Finally, many included papers did not fully specify the implemented connections between elicitation method and emotion type, making it difficult to replicate these studies. For example, Von Haugwitz et al. (2012) only mentions the connections between homeostatic dimensions and emotions are based on fuzzy logic, but does not indicate any principles underlying the real implementation. Similar problems occur in Tanaka et al. (2004), Ayesh (2004) and Obayashi et al. (2012), while Zhou and Coggins (2002) and Shibata et al. (1997) leave the implemented connections unspecified.
5.2 Dimensional
Relative to the number of implementations of categorical emotions, there is a much smaller corpus of work on dimensional emotions (Table 8). The most implemented dimension is valence. Not surprisingly, valence has mostly been derived from reward-based elicitation methods (Broekens et al. 2007a; Ahn and Picard 2006; Zhang and Liu 2009; Obayashi et al. 2012; Hogewoning et al. 2007). It is also connected to a few extrinsic homeostasis papers (Coutinho et al. 2005; Gadanho 2003), but then it is referred to as ‘well-being’. Although this is not completely the same concept, we group these together here for clarity.
Following the dimensional emotion models of Russell and Barrett (1999) introduced in Sect. 2.1, the second most implemented dimension is arousal. Arousal has been connected to extrinsic homeostatic dimensions [e.g. pain and overall well-being (Coutinho et al. 2005)], appraisal-like dimensions [e.g. continuation of incoming stimulus (Kuremoto et al. 2013)], and a few hard-wired implementations (Ayesh 2004; Guojiang et al. 2010). Note that some do not use the term arousal but refer to similar concepts, e.g. relaxation (Coutinho et al. 2005) and restlessness (Ayesh 2004). The only paper to extend the valence-arousal space is by Hoey et al. (2013), who also include control.
In general, the dimensional emotion models seem somewhat under-represented compared to the categorical emotion implementations. Although the implementation for valence shows some consistency among papers, there is more difficulty to specify arousal or different emotion dimensions. Nevertheless, the continuous nature of dimensional emotion models remains appealing from an engineering perspective. A possible benefit is the identification of a desirable target area in affective space, towards which the agent aims to progress (Guojiang et al. 2010).
6 Emotion function
We now discuss the ways in which emotions may influence the learning loop. It turns out emotions have been implicated with all main aspects of this loop: Reward (Sect. 6.1), State (Sect. 6.2), Adaptive Critic (Sect. 6.3) and Actor (Sect. 6.4). Finally, emotion has also been studied as an epiphenomenon, i.e. without any effect on the learning loop, but for example to communicate the learning/behavioural process to other social companions (Sect. 6.5). These categories are visualized in Fig. 1 (labels I–V). Note that this Section introduces the ways in which emotion may influence the RL loop on a conceptual level. We summarize the resulting effect, for example on learning efficiency, in Sect. 7.
6.1 Reward modification
A large group of emotional RL implementations use emotions to modify the reward function. These approaches add an additive term to the reward function that relies on emotions (we have only encountered additive specifications). The reward function is given by
where \({\tilde{r}}(t)\) denotes the external reward function and \(r^\triangle (t)\) an internal reward based on emotional mechanisms. In the RL community, Eq. 15 is known as reward shaping (Ng et al. 1999). The internal reward can be targeted at maximizing positive emotions, but is also frequently associated to homeostatic variables or appraisal dimensions (see Sects. 4.1, 4.2 for elicitation). However, the general underlying principle usually remains that agents seek to maximize positive emotions and minimize negative emotions.
Homeostasis For homeostatic systems the reward becomes dependent on the current state of the internal homeostatic variables. Some implementations use the difference in overall well-being,
where the step from well-being W to overall drive D naturally follows from Eq. (7). In this specification, the acquisition of food does not provide any reward if the associated homeostatic variable (e.g. energy/sugar level) is already satiated. Implementations of the above idea can be found in Gadanho and Hallam (2001), Salichs and Malfaz (2012) and Cos et al. (2013). Variants of this have focussed on using positive emotions [instead of well-being) as the reinforcement learning signal, e.g. in Gadanho and Hallam (1998)] and Goerke (2006)).
Appraisal-based Similar ideas are used for appraisal-based reward modifications. Some examples of appraisal dimension specifications were discussed in Sect. 4.2, with some formal examples in Eqs. 9–13. Appraisal dimensions are related to generic concepts of the agent history (novelty, recency, consistency of observations with world model) and expectations with respect to the goal (motivational relevance, intrinsic pleasantness). Several studies in the intrinsically motivated reinforcement learning literature have identified the learning and survival benefit of these dimensions (Oudeyer and Kaplan 2007; Oudeyer et al. 2007). Some authors therefore took appraisal theory as an inspiration to develop intrinsic motivation features.
Specifications in this direction therefore usually take the following form:
for J appraisal variables and \(\phi _j\) denoting the weight of the j-th appraisal dimension. We could for example use the two features in Eqs. 9–10, specifying an agent that gets rewarded for motivational relevance and recency. Note that appraisal specifications usually do not include the difference with \((t-1)\), probably because they are usually assumed not to satiate (i.e. no underlying homeostatic dynamics). We also note that a reward bonus for novelty (e.g. as in Eq. 12) is in the RL literature usually referred to as ‘optimism in the face of uncertainty’, i.e. we want to explore where we have not been yet.
Sequeira et al. (2011) actually tries to optimize the vector of weights \(\phi \) (with respect to overall goal achievement). In a more recent publication, Sequeira et al. (2014) also extends this work to actually learn the required appraisal dimensions through genetic programming. Similar ideas can be found in Marinier and Laird (2008). One of the problems with both implementations is the distance-to-goal heuristic used by both emotion-based agents, which has access to additional information compared to the baseline agent (although the heuristic does not monotonically increase with the actual distance to goal). We discuss the empirical results of these papers more systematically in Sect. 7.
6.2 State modification
Emotions have also been used as part of the state-space (learning emotion specific value functions and policies). An example is the social robot Maggie (Castro-González et al. 2013). When fear is elicited it becomes part of the state-space (replacing the dominant drive in a homeostatic system), which makes Maggie learn fear-specific action values.
Some papers explicitly write Q(s, a, e), where e denotes the emotional state, to illustrate this dependency (Ahn and Picard 2006; Ayesh 2004). More examples of such implementations can be found in Zhang and Liu (2009), Ficocelli et al. (2016), Obayashi et al. (2012) and Matsuda et al. (2011). Hoey developed a POMDP variant called Bayesian Affect Control Theory that includes the three-dimensional emotional space (valence, control, arousal) of a companion (Hoey et al. 2013) and the agent itself (Hoey and Schröder 2015). There are also implementations that use reinforcement learning to model the affective state of a human or group (Kim 2015), but note that this is a different setting (i.e. RL to steer human emotional state instead of agent emotional state).
Using emotion to modify the state can also be seen as a form of representation learning. There are not many architectures that learn the modification (most hard-code the emotion elicitation), with the exception of Williams et al. (2015). Their architecture has similarities to the bottle-neck structure frequently encountered in deep neural network research, for example in (deep) auto-encoders (Goodfellow et al. 2016). We return to the fully-learned approach in the Discussion (Sect. 8).
6.3 Meta-learning
The previous two sections showed how emotion has been implicated with determining both the reward and state, which together can be considered as the (Internal) Critic. Afterwards, the state and reward are used to learn a value function, a process that is usually referred to as the Adaptive Critic (see Fig. 1). The learning process requires appropriate (and tedious) scaling of learning parameters, most noteworthy the learning rate \(\alpha \) (see Sect. 2.4).
The connection between emotion and these learning parameters was inspired by the work of Doya (2000, 2002). He identified neuroscientific grounding for the connection between several neurotransmitters and several reinforcement learning parameters. In particular, he proposed connections between dopamine and the temporal difference error (\(\delta \)), serotonin and the discount factor (\(\gamma \)), noradrenaline and the Boltzmann action selection temperature (\(\beta \)) and acetylcholine and the learning rate (\(\alpha \)).
This work inspired both Shi et al. (2012) and Von Haugwitz et al. (2012) to implement emotional systems influencing these metaparameters. Shi identifies the connections joy \(\rightarrow \delta \), anger \( \rightarrow \beta \), fear \(\rightarrow \alpha \) and relief \(\rightarrow \gamma \), while von Haugwitz changes only the latter two to surprise \( \rightarrow (1-\alpha )\) and fear \( \rightarrow (1-\gamma )\).
Recently, Williams et al. (2015) also investigated metaparameter steering in navigation tasks. Together with Sequeira et al. (2014) they are the only ones to learn the emotional connections, and then post-characterize the emerged phenomena. Williams trains a classifier connecting a set of primary reinforcers (both appraisal and homeostasis-based) to the metaparameters of their navigation algorithm. They train two emotional nodes, and only afterwards anthropomorphized these. One node learned positive connections to progress and control and negatively to pain and uncertainty, while it caused the robot to increase its speed and reduce the local cost bias. In contrary, their second node was elicited by pain and novelty, while it caused the opposite effect of node 1. They afterwards characterized these nodes as ‘happy’ and ‘fear’, respectively.
6.4 Action selection
The final step of the RL loop involves action selection. This incorporates another crucial RL challenge, being the exploration/exploitation trade-off. Emotions have long been implicated with action readiness, and we actually already encountered two papers steering the Boltzmann action selection temperature \(\beta \) above (as it is technically also a metaparameter of the RL system). We next focus on those papers that specifically target action selection.
One branch of research focusses on directly modifying the exploration parameter. Broekens et al. (2007a, b) has done extensive investigations of the connections between valence and the exploration/exploitation trade-off. In one implementation (Broekens et al. 2007a) selection was based on internal simulation, where a valency determined the threshold for the simulation depth. In another paper (Broekens et al. 2007b) this valency directly influenced the \(\beta \) parameter in a Boltzmann action selection mechanism. Schweighofer and Doya (2003) applied small perturbations to the exploration parameters based on emotion, and subsequently kept the parameters if they performed better. Finally, Hogewoning et al. (2007) investigated a hybrid system of Broekens and Schweighofer, trying to combine their strengths.
Other papers use emotion to switch between multiple sets of value functions, thereby effectively determining which set should currently be used for action selection. For example, both Tsankova (2002) and Hasson et al. (2011) use a high frustration to switch between behaviour. Similarly, Kubota and Wakisaka (2010) use several emotions to switch between the weighting of different value functions. For example, happiness leads to exploration by selecting a value function derived from inverse recency. Note that such a recency feature was used in the appraisal section described previously, but there it modified the reward function, while now emotion is used to switch between value functions. Although this technically leads to similar behaviour, emotion intervenes at a different level.
6.5 Epiphenomenon
The final category of functions of emotions seems an empty one: Epiphenomenon. Several papers have studied emotion elicitation in RL, without the emotion influencing the learning or behavioural loop. These papers usually focus on different evaluation criteria as well (see Sect. 7). Examples of papers that only elicit emotions are Coutinho et al. (2005), Goerke (2006), Si et al. (2010), Kim and Kwon (2010), Bozinovski (1982); Bozinovski et al. (1996), Jacobs et al. (2014), Lahnstein (2005) and Moerland et al. (2016).
There can however still be a clear function of the emotion for the agent in a social communication perspective (node V in Fig. 1). Emotion may communicate the current learning and behavioural process, and also create empathy and user investment. The potential of emotions to communicate internal state and enhance empathy is infrequently evaluated in current reinforcement learning related emotion literature. This seems a fruitful direction when emotions serve to make an agent or robot more sociable and likeable.
This concludes our discussion of emotion functions in RL agents. The full overview is provided in Table 10, which mainly lists the categories per paper. The most important connections between Sects. 4–6 (i.e. column 1 to 3 in Table 9) were described in the text and tables (e.g. Tables 4, 7).
7 Evaluation
This section systematically addresses the embodiment, test scenario and main empirical results found in the different papers. A systematic overview of this section is provided in Table 10.
7.1 Embodiment
We can grossly identify 5 embodiment categories: standard single agent, multiple agents, screen agents, simulated robot and real robot. The standard agent setting usually concerns a (gridworld) navigation simulation in some environment designed by the researcher. Some agents are also designed to appear on a screen for interaction with a user (El-Nasr et al. 2000). Another group of embodiments concern simulated or real robots. Simulated robots are based on models of existing real robots, i.e. they usually incorporate more realistic physics and continuous controls.
There are also real robotic implementations in navigation and resource tasks. However, several robotic implementations (especially those involving human interaction) use the robot mainly as physical embodiment (without moving much, for example in a dialogue task). Overall, most implementations have focussed on simulated agents. It is important to note that most state-spaces stay relatively small, i.e. sensory information usually has narrow bandwidth (or is assumed to be appropriately pre-processed). Although this facilitates interpretation, a remaining question is whether the current emotion modelling methods scale to high-dimensional and complex problems.
7.2 Test scenario
Emotion implementations have been tested in different scenarios: navigation tasks with resources and/or obstacles, multiple agent interaction settings and human-agent/robot interaction tasks.
There is a wide variety of navigation tasks with additional (multiple) resources and obstacles (with associated positive and negative rewards). When resources and obstacles are non-stationary we usually see the terminology ‘prey’ and ‘predators’. Within this group we mainly see navigation tasks with a single goal and multiple obstacles [i.e. ‘mazes’ (Marinier and Laird 2008) or robot navigation (Lee-Johnson et al. 2010; Williams et al. 2015)]. A second group involves multiple resources, which are mostly connected to underlying homeostatic systems to investigate behaviour switching. A few tasks also specifically include virtual enemies (Sequeira et al. 2011) or humans with adversarial intentions (Castro-González et al. 2013; Tanaka et al. 2004).
A second, much smaller group of scenarios involves multiple agents in a social simulation scenario, either a competitive (Von Haugwitz et al. 2012; Yu et al. 2015) or co-operative one (Matsuda et al. 2011). The third category tests their implementation in interaction with humans. This can either involve a human dialogue task (Ficocelli et al. 2016; Moussa and Magnenat-Thalmann 2013) or physical interaction with a human (Blanchard and Canamero 2005; Shibata et al. 1997).
In general, most papers have constructed their own scenario. We have not seen any test scenarios being borrowed from other emotion-learning implementations, nor from the general reinforcement learning literature. This makes it hard to compare different implementations amongst each other.
7.3 Main results
Finally, we discuss what empirical results were found by the various authors. We identify three main categories in which emotions may be useful to the agent: learning efficiency, emotion dynamics and human–robot interaction (HRI) (Table 10, third column).
Learning efficiency Most authors in emotion-RL research have focussed on learning efficiency (see Table 10). Overall, emotions have been found beneficial in a variety of learning tasks. Agents with emotional functionality achieved higher average rewards (Gadanho and Hallam 2001; Sequeira et al. 2014; Yu et al. 2015) or learned faster (Marinier and Laird 2008; Ahn and Picard 2006; Zhang and Liu 2009). Others researchers focussed on the ability to avoid specific negative rewards, like the ability to avoid collisions (Gadanho and Hallam 2001; Lee-Johnson et al. 2010) and navigate away from obstacles (Shi et al. 2012). Other researchers report improved behaviour switching, where emotional agents better alternate between goals (Cos et al. 2013; Hasson et al. 2011; Goerke 2006). Finally, some authors specifically show improved exploration (Broekens et al. 2007b). Many authors that focussed on learning performance do compare to a non-emotional baseline agent, which is of course a necessary comparison. Altogether, the results show emotions may be a useful inspiration to improve learning performance of RL agents.
Emotion dynamics A second group of researchers focusses on emotion dynamics, usually comparing the emergent emotion signals to known psychological theories. For example, Jacobs et al. (2014) showed patterns of habituation and extinction, Moren and Balkenius (2000) reproduced blocking, while Blanchard and Canamero (2005) observed approach and avoidance behaviour in their emotional agent. Other researchers qualitatively interpret whether the emotion dynamics fit the (social) interaction (Tanaka et al. 2004; Moussa and Magnenat-Thalmann 2013) or occurs at appropriate states in the scenario (Moerland et al. 2016). Altogether, results in this category show that emotion in RL agents might be a viable tool to study emotion theories in computational settings.
Human–robot interaction Finally, a third group of researchers focusses on human–robot interaction evaluation. Their primary focus is to show how emotions may benefit social interaction with humans, usually by taking questionnaires with the participants after the experiment. Participants of Ficocelli et al. (2016) report more effective communication, participants of El-Nasr et al. (2000) found the agent more convincing, and participants of Shibata et al. (1997) report an increased notion of connection as well as increased perception of robot intelligence. Kim and Kwon (2010) describe an enhanced pleasant feeling of the participant after the human-agent interaction. Therefore, there is clear indication that emotion in RL agents may benefit an interactive learning setting. However, there are relatively few papers in this category compared to the other two, and this may be a direction for more research.
8 Discussion
This article surveyed the available work on emotion and reinforcement learning in agents and robots, by systematically categorizing emotion elicitation, type and function in RL agents. We first summarize the main results and identify the challenges encountered throughout the article.
Emotions have been elicited from extrinsic motivation (in combination with homeostasis), intrinsic motivation (in combination with appraisal), value and reward functions and as hard-wired implementation. We want to emphasize again that extrinsic motivation and homeostasis are not synonyms, nor are intrinsic motivations and appraisal (see Sect. 3). The hard-wired emotion elicitation seems least useful, as it does not provide any deeper understanding about emotion generation, and is by definition hand-crafted to the task. The other three elicitation methods are useful and appear to address different aspects of emotions. Homeostasis focusses on the inner resource status, appraisal on the inner model status and value/reward focusses on the learning process. They seem to cover different aspects of emotions. For example, surprise seems only elicitable from a model, joy from food requires extrinsic motivation and homeostasis, while aspects like anticipated change need value functions. Finally, note that there remains slight overlap among categories, i.e. they serve as a framework, but are not mutually exclusive. This is also illustrated by the overlap among implementations in Table 7.
Regarding emotion types we observed a relatively larger corpus of categorical implementations than dimensional models. Although dimensional models are appealing from an engineering perspective, they are usually implemented in 1D (valence) or 2D (valence-arousal) space. This makes it challenging to implement a diverse set of emotions. We do want to present a hypothesis here: dimensional and categorical emotions may fit into the same framework, but at different levels. Concepts like ‘well-being’, as encountered throughout this survey, do not appear to be categorical emotions, but could be interpreted as valence. However, an agent can have categorical emotions on top of a well-being/valence system, joining both emotion types in one system. Similarly, arousal could be related to the speed of processing of the RL loop, also entering the RL process at a different level.
Finally, emotion function could involve nearly every node in the RL loop: reward, state, value function and action selection. It seems like all approaches are useful, as each element targets a different RL challenge. The fifth emotion function category (epiphenomenon) should get more attention because it involves a different kind of usefulness (communicative). Although quite some papers are focussing on emotion dynamics, there is less work on evaluating the potential of emotions to communicate the learning process. Thomaz and Breazeal (2006) found that transparency of the learner’s internal process (in their case through the robot’s gaze direction) can improve the human’s teaching. We hypothesize emotional communication to express internal state may serve a similar role, which is a topic that could get more research attention in the future.
Advice for implementation We expect this article is useful to engineers who want to implement emotional functionality in their RL-based agent or robot. We advise to first consider what type of functionality is desired. When the goal is to have emotions visualize agent state, or have believable emotions to enhance empathy and user investment, then emotions can be implemented as an epiphenomenon (i.e. focus on Sects. 4, 5). The reader could for example first decide on the desired emotion types, and then check which available elicitation methods seem applicable (e.g. via Table 9). When one desires emotion function in their agent/robot as well, then Sect. 6 becomes relevant. We advise the reader to first consider the desired functionality, e.g. a more adaptive reward function, learning parameter tuning, or modulated exploration, and then work ‘backwards’ to emotion type and emotion elicitation. Readers may verify whether there are existing implementations of their requirements through the colour coding in Table 9.
In general, we believe researchers in the field should start focussing on integrating approaches. This survey intended to provide a framework and categorization of emotion elicitation and function, but it seems likely that these categories actually jointly occur in the behavioural loop. We look forward to systems that integrate multiple approaches. Moreover, we want to emphasize the paper by Williams et al. (2015) that took a fully learned approach. Their system contains nodes that were trained for their functional benefit, and later on characterized for the emotion patterns. We expect such an approach to both be more robust against the complexity problems encountered when developing integrated systems, and to transfer more easily between problem settings as well.
Testing and quality of the field We also systematically categorized the testing scenarios and evaluation criteria (Sect. 7; Table 10). There are several points to be noted about the current testing. First we want to stress a point already made by Cañamero (2003), who noted that ‘one should not put more emotion in the agent than what is required by the complexity of the system-environment interaction’. Many of the current implementations design their own (grid) world. While these artificial worlds are usually well-suited to assess optimization behaviour, it is frequently hard to assess which emotions should be elicited by the agent at each point in the world. On the other hand, more realistic scenarios quickly become high-dimensional, and therefore the challenge changes to a representation learning problem. Potentially, the advances in solving more complex AI scenarios with (deep) RL (Silver et al. 2016; Mnih et al. 2015) may provide more realistic test scenarios in the future as well.
There are two other important observations regarding testing and evaluation. We have not encountered any (emotional) scenario being reproduced by other researchers. This appears to us as an important problem. To enhance the standard of the field, researchers should start reproducing scenarios from other’s work to compare with, or borrow from different RL literature. The second topic we want to emphasize is the use of different evaluation criteria. Researchers should choose whether they target learning efficiency, emotion dynamics or HRI criteria. If learning performance is your criterion, then your implementation must include a baseline. When you focus on emotion dynamics, then you should try to validate by a psychological theory, or ideally compare to empirical (human) data. When you focus on human interaction criteria, then this should usually involve a questionnaire. Although questionnaires seems to be consistent practice already, we did observe authors reporting on a smaller subset of the questions (i.e. posing the risk to have a few results pop out by statistical chance).
This brings us to a final problem in the field, being the thoroughness of the papers. Frequently we were unable to fully deduce the details of each implementation. Indeed a full system description with all the details requires valuable space, but on the other hand, a well-informed colleague reading a conference paper should be able to reproduce your results. Only listing the homeostatic/appraisal variables and the emotions that were implemented does not provide deeper understanding about how the system works. This also makes it harder to compare between implementations. Differences in notational conventions and slight differences in definitions further complicate comparisons. Paying attention to these aspects of reproducibility, for example sticking to conventional RL notation (Sutton and Barto 1998), will facilitate broader uptake of the work in this field.
Future A core challenge for the future will be to integrate all aspects into one larger system, potentially taking a fully learned approach. Along the same line, it is a remaining challenge of this field (and AI in general) to translate higher-level (psychological) concepts into implementable mathematical expressions. Examples of such translations can be found in Eqs. 9–13, and we expect comparing different translations may help identify more consensus. At least the RL framework provides a common language to start comparing these translations.
With social robots increasingly positioned at our research horizon, we expect interest in emotion in functional agents to increase in the forthcoming years. However, the current implementations seldom investigate the full social interaction. Although this is a very high-level AI challenge, we believe research should focus in this direction to show empirical success. This involves all aspects of RL in a social context, i.e. robots learning from human demonstration (LfD) (Argall et al. 2009), learning from human feedback [possibly emotional (Broekens 2007)], human emotions influencing agent emotions, and agent emotions communicating internal processes back to humans.
From an affective modelling perspective, it is promising to see how a cognitive theory like appraisal theory turns out to be well-applicable to MDP settings. Apart from integrating important lines of emotion and learning research, this also illustrates how cognitive and learning theories are not mutually exclusive. We hope the affective modelling community will start to benefit from the literature on intrinsic motivation in RL as well (Bratman et al. 2012). A crucial requisite herein will be improving the types of problems that (model-based) RL can solve. Many scenarios that are interesting from an affective modelling viewpoint, for example high-dimensional social settings, are still challenging for RL. Advances in deep reinforcement learning (Mnih et al. 2015) might make more complex scenarios available soon. However, for affective modelling we especially need the transition function and model-based RL (Deisenroth and Rasmussen 2011). Recent work has also shown the feasibility of high-dimensional transition function approximation (Oh et al. 2015) in stochastic domains (Moerland et al. 2017) under uncertainty (Houthooft et al. 2016). Further progress in this direction should make the ideas covered in this survey applicable to more complicated scenarios as well.
9 Conclusion
This article surveyed emotion modelling in reinforcement learning (RL) agents. The literature has been structured according to the intrinsically motivated RL framework. We conclude by identifying the main benefits encountered in this work for the machine learning (ML), human–robot interaction (HRI), and affective modelling (AM) communities. For machine learning, emotion may benefit learning efficiency by providing inspiration for intrinsic motivation, exploration and for meta-parameter tuning. The current results should stimulate further cross-over between (intrinsic) motivation, model-based RL and emotion-RL research. For HRI research, emotions obviously are important for social interaction. More work should be done on implementing emotion models in interactive reinforcement learning algorithms, for which the survey presents a practical guideline on implementing emotions in RL agents. For affective modelling, we conclude that cognitive theories (like appraisal theory) can well be expressed in RL agents. The general benefits of RL agents (they require few assumptions, are easily applicable to all kinds of domains, and allow for learning) make them a promising test-bed for affective modelling research. This survey identifies opportunities for future work with respect to implementation and evaluation of emotion models in RL agents.
References
Ahn, H., & Picard, R. W. (2006). Affective cognitive learning and decision making: The role of emotions. In EMCSR 2006: The 18th European meeting on cybernetics and systems research.
Antos, D., & Pfeffer, A. (2011). Using emotions to enhance decision-making. In Proceedings of the international joint conference on artificial intelligence (IJCAI) (Vol. 22, p. 24).
Argall, B. D., Chernova, S., Veloso, M., & Browning, B. (2009). A survey of robot learning from demonstration. Robotics and Autonomous Systems, 57(5), 469–483.
Ayesh, A. (2004). Emotionally motivated reinforcement learning based controller. In 2004 IEEE international conference on systems, man and cybernetics (Vol. 1, pp. 874–878). IEEE.
Balkenius, C., & Morén, J. (1998). A computational model of emotional conditioning in the brain. In Proceedings of workshop on grounding emotions in adaptive systems, Zurich.
Baumeister, R. F., Vohs, K. D., DeWall, C. N., & Zhang, L. (2007). How emotion shapes behavior: Feedback, anticipation, and reflection, rather than direct causation. Personality and Social Psychology Review, 11(2), 167–203.
Belavkin, R. V. (2004). On relation between emotion and entropy. In Proceedings of the AISB’04 symposium on emotion, cognition and affective computing (pp. 1–8). AISB Press.
Blanchard, A. J., & Canamero, L. (2005). From imprinting to adaptation: Building a history of affective interaction. In Proceedings of the 5th international workshop on epigenetic robotics (pp. 23–30). Lund University Cognitive Studies.
Bozinovski, S. (1982). A self-learning system using secondary reinforcement. In E. Trappl (Ed.), Cybernetics and Systems Research (pp. 397–402). North-Holland, Amsterdam.
Bozinovski, S., Stojanov, G., & Bozinovska, L. (1996). Emotion, embodiment, and consequence driven systems. In Proc AAAI fall symposium on embodied cognition and action (pp. 12–17).
Bratman, J., Singh, S., Sorg, J., & Lewis, R. (2012). Strong mitigation: Nesting search for good policies within search for good reward. In Proceedings of the 11th international conference on autonomous agents and multiagent systems-volume 1, international foundation for autonomous agents and multiagent systems (pp. 407–414).
Breazeal, C. (2003). Emotion and sociable humanoid robots. International Journal of Human-Computer Studies, 59(1), 119–155.
Broekens, J. (2007). Emotion and reinforcement: Affective facial expressions facilitate robot learning. Artifical intelligence for human computing (pp. 113–132). Berlin: Springer.
Broekens, J., Kosters, W. A., & Verbeek, F. J. (2007a). Affect, anticipation, and adaptation: Affect-controlled selection of anticipatory simulation in artificial adaptive agents. Adaptive Behavior, 15(4), 397–422.
Broekens, J., Bosse, T., & Marsella, S. C. (2013). Challenges in computational modeling of affective processes. IEEE Transactions on Affective Computing, 4(3), 242–245.
Broekens, J., Kosters, W. A., & Verbeek, F. J. (2007b). On affect and self-adaptation: Potential benefits of valence-controlled action-selection. Bio-inspired modeling of cognitive tasks (pp. 357–366). Berlin: Springer.
Calvo, R. A., & D’Mello, S. (2010). Affect detection: An interdisciplinary review of models, methods, and their applications. IEEE Transactions on Affective Computing, 1(1), 18–37. doi:10.1109/t-affc.2010.1.
Calvo, R. A., D’Mello, S., Gratch, J., & Kappas, A. (2015). The Oxford handbook of affective computing. Oxford Library of Psychology.
Cañamero, D. (1997a). A hormonal model of emotions for behavior control. In VUB AI-Lab Memo 2006.
Cañamero, D. (1997b). Modeling motivations and emotions as a basis for intelligent behavior. In Proceedings of the first international conference on autonomous agents (pp. 148–155). ACM.
Cañamero, D. (2003). Designing emotions for activity selection in autonomous agents. Emotions in Humans and Artifacts, 115, 148.
Castro-González, Á., Malfaz, M., & Salichs, M. A. (2013). An autonomous social robot in fear. IEEE Transactions on Autonomous Mental Development, 5(2), 135–151.
Chentanez, N., Barto, A. G., & Singh, S. P. (2004). Intrinsically motivated reinforcement learning. In Advances in neural information processing systems (pp. 1281–1288).
Cos, I., Cañamero, L., Hayes, G. M., & Gillies, A. (2013). Hedonic value: Enhancing adaptation for motivated agents. Adaptive Behavior, 21(6), 465–483.
Coutinho, E., Miranda, E. R., & Cangelosi, A. (2005). Towards a model for embodied emotions. In Portuguese conference on artificial intelligence, 2005. epia 2005 (pp. 54–63). IEEE.
Damasio, A. R. (1994). Descartes’ error: Emotion, reason and the human brain. New York: Grosset/Putnam.
Deisenroth, M., & Rasmussen, C. E. (2011). PILCO: A model-based and data-efficient approach to policy search. In Proceedings of the 28th international conference on machine learning (ICML-11) (pp. 465–472).
Doshi, P., & Gmytrasiewicz, P. (2004). Towards affect-based approximations to rational planning: A decision-theoretic perspective to emotions. In Working notes of the spring symposium on architectures for modeling emotion: Cross-disciplinary foundations.
Doya, K. (2000). Metalearning, neuromodulation, and emotion. In Affective minds (p. 101).
Doya, K. (2002). Metalearning and neuromodulation. Neural Networks, 15(4), 495–506.
Dunn, B. D., Dalgleish, T., & Lawrence, A. D. (2006). The somatic marker hypothesis: A critical evaluation. Neuroscience & Biobehavioral Reviews, 30(2), 239–271.
Ekman, P., Friesen, W. V., O’Sullivan, M., Chan, A., Diacoyanni-Tarlatzis, I., Heider, K., et al. (1987). Universals and cultural differences in the judgments of facial expressions of emotion. Journal of Personality and Social Psychology, 53(4), 712.
El-Nasr, M. S., Yen, J., & Ioerger, T. R. (2000). Flame-fuzzy logic adaptive model of emotions. Autonomous Agents and Multi-agent Systems, 3(3), 219–257.
Ficocelli, M., Terao, J., & Nejat, G. (2016). Promoting interactions between humans and robots using robotic emotional behavior. IEEE Transactions on Cybernetics, 46(12), 2911–2923.
Fong, T., Nourbakhsh, I., & Dautenhahn, K. (2003). A survey of socially interactive robots. Robotics and Autonomous Systems, 42(3), 143–166.
Franklin, S., Madl, T., D’mello, S., & Snaider, J. (2014). LIDA: A systems-level architecture for cognition, emotion, and learning. IEEE Transactions on Autonomous Mental Development, 6(1), 19–41.
Frijda, N. H., Kuipers, P., & Ter Schure, E. (1989). Relations among emotion, appraisal, and emotional action readiness. Journal of Personality and Social Psychology, 57(2), 212.
Gadanho, S. C. (2003). Learning behavior-selection by emotions and cognition in a multi-goal robot task. The Journal of Machine Learning Research, 4, 385–412.
Gadanho, S. C., & Hallam, J. (1998). Emotion triggered learning for autonomous robots. DAI Research Paper.
Gadanho, S. C., & Hallam, J. (2001). Robot learning driven by emotions. Adaptive Behavior, 9(1), 42–64.
Gmytrasiewicz, P. J., & Lisetti, C. L. (2002). Emotions and personality in agent design and modeling. Game theory and decision theory in agent-based systems (pp. 81–95). Berlin: Springer.
Goerke, N. (2006). EMOBOT: A robot control architecture based on emotion-like internal values. Rijeka: INTECH Open Access Publisher.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep learning. Cambridge: MIT Press.
Gratch, J., & Marsella, S. (2014). Appraisal models. Oxford: Oxford University Press.
Guojiang, W., Xiaoxiao, W., & Kechang, F. (2010). Behavior decision model of intelligent agent based on artificial emotion. In 2010 2nd International conference on advanced computer control (ICACC) (Vol. 4, pp. 185–189). IEEE.
Hasson, C., Gaussier, P., & Boucenna, S. (2011). Emotions as a dynamical system: The interplay between the meta-control and communication function of émotions. Paladyn, 2(3), 111–125.
Hester, T., & Stone, P. (2012a). Intrinsically motivated model learning for a developing curious agent. In 2012 IEEE international conference on development and learning and epigenetic robotics (ICDL) (pp. 1–6). IEEE.
Hester, T., & Stone, P. (2012b). Learning and using models. Reinforcement learning (pp. 111–141). Berlin: Springer.
Hoey, J., & Schröder, T. (2015). Bayesian affect control theory of self. In AAAI (pp. 529–536). Citeseer.
Hoey, J., Schroder, T., & Alhothali, A. (2013). Bayesian affect control theory. In 2013 Humaine association conference on affective computing and intelligent interaction (ACII) (pp. 166–172). IEEE.
Hogewoning, E., Broekens, J., Eggermont, J., & Bovenkamp, E. G. (2007). Strategies for affect-controlled action-selection in Soar-RL. Nature inspired problem-solving methods in knowledge engineering (pp. 501–510). Berlin: Springer.
Houthooft, R., Chen, X., Duan, Y., Schulman, J., De Turck, F., & Abbeel, P. (2016). Curiosity-driven exploration in deep reinforcement learning via bayesian neural networks. arXiv preprint arXiv:1605.09674
Huang, X., Du, C., Peng, Y., Wang, X., & Liu, J. (2012). Goal-oriented action planning in partially observable stochastic domains. In: 2012 IEEE 2nd international conference on cloud computing and intelligent systems (CCIS) (Vol. 3, pp. 1381–1385). IEEE.
Hull, C. L. (1943). Principles of behavior: An introduction to behavior theory. New York: Appleton-Century.
Jacobs, E., Broekens, J., & Jonker, C. M. (2014). Emergent dynamics of joy, distress, hope and fear in reinforcement learning agents. In Adaptive learning agents workshop at AAMAS2014.
Joffily, M., & Coricelli, G. (2013). Emotional valence and the free-energy principle. PLOS Computational Biology, 9(6), e1003094. doi:10.1371/journal.pcbi.10030946.
Johnson-Laird, P. N., & Oatley, K. (1992). Basic emotions, rationality, and folk theory. Cognition and Emotion, 6(3–4), 201–223.
Kahneman, D., & Tversky, A. (1979). Prospect theory: An analysis of decision under risk. Econometrica: Journal of the Econometric Society, 47(2), 263–292.
Keramati, M., & Gutkin, B. S. (2011). A reinforcement learning theory for homeostatic regulation. In Advances in neural information processing systems (pp. 82–90).
Kim, H. R., & Kwon, D. S. (2010). Computational model of emotion generation for human-robot interaction based on the cognitive appraisal theory. Journal of Intelligent & Robotic Systems, 60(2), 263–283.
Kim, K. H., & Cho, S. B. (2015). A group emotion control system based on reinforcement learning. In SoCPaR 2015.
Knox, W. B., Glass, B., Love, B., Maddox, W. T., & Stone, P. (2012). How humans teach agents. International Journal of Social Robotics, 4(4), 409–421.
Knox, W. B., Stone, P., & Breazeal, C. (2013). Training a robot via human feedback: A case study. Lecture Notes in Computer Science, (Vol. 8239, pp. 460–470). Springer International Publishing, Book Section, 46.
Kober, J., & Peters, J. (2012). Reinforcement learning in robotics: A survey. Reinforcement learning (pp. 579–610). Berlin: Springer.
Konidaris, G., & Barto, A. (2006). An adaptive robot motivational system. In From Animals to Animats 9 (pp. 346–356). Berlin: Springer.
Kubota, N., & Wakisaka, S. (2010). Emotional model based on computational intelligence for partner robots. Modeling machine emotions for realizing intelligence (pp. 89–108). Berlin: Springer.
Kuremoto, T., Tsurusaki, T., Kobayashi, K., Mabu, S., & Obayashi, M. (2013). An improved reinforcement learning system using affective factors. Robotics, 2(3), 149–164.
Lahnstein, M. (2005). The emotive episode is a composition of anticipatory and reactive evaluations. In Proceedings of the AISB’05 symposium on agents that want and like (pp. 62–69).
Laird, J. E. (2008). Extending the Soar cognitive architecture. Frontiers in Artificial Intelligence and Applications, 171, 224.
Lazarus, R. S. (1991). Cognition and motivation in emotion. American Psychologist, 46(4), 352.
LeDoux, J. (2003). The emotional brain, fear, and the amygdala. Cellular and Molecular Neurobiology, 23(4–5), 727–738.
Lee-Johnson, C. P., & Carnegie, D., et al. (2007). Emotion-based parameter modulation for a hierarchical mobile robot planning and control architecture. In IEEE/RSJ international conference on intelligent robots and systems, 2007, IROS 2007 (pp. 2839–2844). IEEE.
Lee-Johnson, C. P., Carnegie, D., et al. (2010). Mobile robot navigation modulated by artificial emotions. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 40(2), 469–480.
Lhommet, M., & Marsella, S. C. (2015). Expressing emotion through posture and gesture (pp. 273–285). Oxford: Oxford University Press.
Lisetti, C., & Hudlicka, E. (2015). Why and how to build emotion-based agent architectures, in The Oxford Handbook of Affective Computing, Chap. 8 (Oxford Library of Psychology, 2015) p. 94.
Marinier, R., & Laird, J. E. (2008). Emotion-driven reinforcement learning. In Cognitive science (pp. 115–120).
Marsella, S., Gratch, J., & Petta, P. (2010). Computational models of emotion. In K. Scherer, T. Bänziger, & E. Roesch (Eds.), A blueprint for affective computing (pp. 21–45). Oxford: Oxford University Press.
Marsella, S. C., & Gratch, J. (2009). EMA: A process model of appraisal dynamics. Cognitive Systems Research, 10(1), 70–90.
Matsuda, A., Misawa, H., & Horio, K. (2011). Decision making based on reinforcement learning and emotion learning for social behavior. In 2011 IEEE international conference on fuzzy systems (FUZZ) (pp. 2714–2719). IEEE.
Michaud, F. (2002). EMIB–Computational architecture based on emotion and motivation for in-tentional selection and configuration of behaviour-producing modules. Cognitive Science Quarterly, 3–4, 340–361.
Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level control through deep reinforcement learning. Nature, 518(7540), 529–533.
Moerland, T. M., Broekens, J., & Jonker, C. M. (2016). Fear and hope emerge from anticipation in model-based reinforcement learning. In Proceedings of the international joint conference on artificial intelligence (IJCAI) (pp. 848–854).
Moerland, T. M., Broekens, J., & Jonker, C. M. (2017). Learning multimodal transition dynamics for model-based reinforcement learning. arXiv preprint arXiv:1705.00470.
Moren, J., & Balkenius, C. (2000). A computational model of emotional learning in the amygdala. From Animals to Animats, 6, 115–124.
Moussa, M. B., & Magnenat-Thalmann, N. (2013). Toward socially responsible agents: Integrating attachment and learning in emotional decision-making. Computer Animation and Virtual Worlds, 24(3–4), 327–334.
Murphy, R. R., Lisetti, C. L., Tardif, R., Irish, L., & Gage, A. (2002). Emotion-based control of cooperating heterogeneous mobile robots. IEEE Transactions on Robotics and Automation, 18(5), 744–757.
Ng, A. Y., Harada, D., & Russell, S. (1999). Policy invariance under reward transformations: Theory and application to reward shaping. ICML, 99, 278–287.
Obayashi, M., Takuno, T., Kuremoto, T., & Kobayashi, K. (2012). An emotional model embedded reinforcement learning system. In 2012 IEEE international conference on systems, man, and cybernetics (SMC) (pp. 1058–1063). IEEE.
Ochs, M., Niewiadomski, R., & Pelachaud, C. (2015). Facial expressions of emotions for virtual characters (pp. 261–272). Oxford: Oxford University Press.
Oh, J., Guo, X., Lee, H., Lewis, R. L., & Singh, S. (2015). Action-conditional video prediction using deep networks in atari games. In Advances in neural information processing systems (pp. 2863–2871).
Ortony, A., Clore, G. L., & Collins, A. (1990). The cognitive structure of emotions. Cambridge: Cambridge University Press.
Osgood, C. E., Suci, G. J., & Tannenbaum, P. H. (1964). The measurement of meaning. Champaign: University of Illinois Press.
Oudeyer, P. Y., & Kaplan, F. (2007). What is intrinsic motivation? A typology of computational approaches. Frontiers in Neurorobotics, 1(6).
Oudeyer, P. Y., Kaplan, F., & Hafner, V. V. (2007). Intrinsic motivation systems for autonomous mental development. IEEE Transactions on Evolutionary Computation, 11(2), 265–286.
Paiva, A., Leite, I., & Ribeiro, T. (2015). Emotion modeling for social robots (pp. 296–308). Oxford: Oxford University Press.
Parisi, D., & Petrosino, G. (2010). Robots that have emotions. Adaptive Behavior, 18(6), 453–469.
Reisenzein, R. (2009). Emotional experience in the computational belief-desire theory of emotion. Emotion Review, 1(3), 214–222.
Rolls, E. T., & Baylis, L. L. (1994). Gustatory, olfactory, and visual convergence within the primate orbitofrontal cortex. The Journal of Neuroscience, 14(9), 5437–5452.
Rolls, E. T., & Grabenhorst, F. (2008). The orbitofrontal cortex and beyond: from affect to decision-making. Progress in Neurobiology, 86(3), 216–244.
Rumbell, T., Barnden, J., Denham, S., & Wennekers, T. (2012). Emotions in autonomous agents: comparative analysis of mechanisms and functions. Autonomous Agents and Multi-Agent Systems, 25(1), 1–45.
Rummery, G. A., & Niranjan, M. (1994). On-line Q-learning using connectionist systems. Technical Report, University of Cambridge, Department of Engineering.
Russell, J. A. (1978). Evidence of convergent validity on the dimensions of affect. Journal of Personality and Social Psychology, 36(10), 1152.
Russell, J. A., & Barrett, L. F. (1999). Core affect, prototypical emotional episodes, and other things called emotion: Dissecting the elephant. Journal of Personality and Social Psychology, 76(5), 805.
Russell, S., Norvig, P., & Intelligence, A. (1995). A modern approach. Artificial Intelligence, 25, 27.
Salichs, M. A., & Malfaz, M. (2012). A new approach to modeling emotions and their use on a decision-making system for artificial agents. IEEE Transactions on Affective Computing, 3(1), 56–68.
Scherer, K. R. (1999) Appraisal theory. Handbook of cognition and emotion (pp. 637–663).
Scherer, K. R., Schorr, A., & Johnstone, T. (2001). Appraisal processes in emotion: Theory, methods, research. Oxford: Oxford University Press.
Schweighofer, N., & Doya, K. (2003). Meta-learning in reinforcement learning. Neural Networks, 16(1), 5–9.
Sequeira, P., Melo, F. S., & Paiva, A. (2011). Emotion-based intrinsic motivation for reinforcement learning agents. Affective computing and intelligent interaction (pp. 326–336). Berlin: Springer.
Sequeira, P., Melo, F. S., & Paiva, A. (2014). Learning by appraising: An emotion-based approach to intrinsic reward design. Adaptive Behavior, 22(5), 330–349.
Shi, X., Wang, Z., & Zhang, Q. (2012). Artificial emotion model based on neuromodulators and Q-learning. In W. Deng (Ed.), Future Control and Automation: Proceedings of the 2nd International Conference on Future Control and Automation (ICFCA 2012) (Vol. 1, pp. 293–299). Berlin, Heidelberg: Springer.
Shibata, T., Yoshida, M., & Yamato, J. (1997). Artificial emotional creature for human-machine interaction. In IEEE international conference on systems, man, and cybernetics, 1997. Computational cybernetics and simulation, 1997 (Vol. 3, pp. 2269–2274). IEEE.
Si, M., Marsella, S. C., & Pynadath, D. V. (2010). Modeling appraisal in theory of mind reasoning. Autonomous Agents and Multi-Agent Systems, 20(1), 14–31.
Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., et al. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484–489.
Singh, S., Lewis, R. L., Barto, A. G., & Sorg, J. (2010). Intrinsically motivated reinforcement learning: An evolutionary perspective. IEEE Transactions on Autonomous Mental Development, 2(2), 70–82.
Sutton, R. S. (1988). Learning to predict by the methods of temporal differences. Machine Learning, 3(1), 9–44.
Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: An introduction. Cambridge: MIT Press.
Tanaka, F., Noda, K., Sawada, T., & Fujita, M. (2004). Associated emotion and its expression in an entertainment robot QRIO. Entertainment computing–ICEC 2004 (pp. 499–504). Berlin: Springer.
Thomaz, A. L., & Breazeal, C. (2006). Teachable characters: User studies, design principles, and learning performance. Intelligent virtual agents (pp. 395–406). Berlin: Springer.
Thomaz, A. L., & Breazeal, C. (2008). Teachable robots: Understanding human teaching behavior to build more effective robot learners. Artificial Intelligence, 172(6), 716–737.
Thorpe, S., Rolls, E., & Maddison, S. (1983). The orbitofrontal cortex: neuronal activity in the behaving monkey. Experimental Brain Research, 49(1), 93–115.
Tsankova, D. D. (2002). Emotionally influenced coordination of behaviors for autonomous mobile robots. In 2002 First international IEEE symposium on intelligent systems, 2002, Proceedings (Vol. 1, pp. 92–97). IEEE.
Velasquez, J. (1998). Modeling emotion-based decision-making. In Emotional and intelligent: The tangled knot of cognition (pp. 164–169).
Vinciarelli, A., Pantic, M., Heylen, D., Pelachaud, C., Poggi, I., D’Errico, F., et al. (2012). Bridging the gap between social animal and unsocial machine: A survey of social signal processing. IEEE Transactions on Affective Computing, 3(1), 69–87.
Von Haugwitz, R., Kitamura, Y., & Takashima, K. (2012). Modulating reinforcement-learning parameters using agent emotions. In 2012 Joint 6th international conference on soft computing and intelligent systems (SCIS) and 13th international symposium on advanced intelligent systems (ISIS) (pp. 1281–1285). IEEE.
Watkins, C. J. C. H. (1989). Learning from delayed rewards. Ph.D. Thesis, University of Cambridge England.
Wiering, M., & Van Otterlo, M. (2012). Reinforcement learning. Adaptation, Learning, and Optimization, 12.
Williams, H., Lee-Johnson, C., Browne, W. N., & Carnegie, D. A. (2015). Emotion inspired adaptive robotic path planning. In 2015 IEEE congress on evolutionary computation (CEC) (pp. 3004–3011). IEEE
Yu, C., Zhang, M., & Ren, F. (2013). Emotional multiagent reinforcement learning in social dilemmas. PRIMA 2013: Principles and practice of multi-agent systems (pp. 372–387). Berlin: Springer.
Yu, C., Zhang, M., Ren, F., & Tan, G. (2015). Emotional multiagent reinforcement learning in spatial social dilemmas. IEEE Transactions on Neural Networks and Learning Systems, 26(12), 3083–3096.
Zhang, H., & Liu, S. (2009). Design of autonomous navigation system based on affective cognitive learning and decision-making. In 2009 IEEE international conference on robotics and biomimetics (ROBIO) (pp. 2491–2496). IEEE.
Zhou, W., & Coggins, R. (2002). Computational models of the amygdala and the orbitofrontal cortex: A hierarchical reinforcement learning system for robotic control. AI 2002: Advances in artificial intelligence (pp. 419–430). Berlin: Springer.
Author information
Authors and Affiliations
Corresponding author
Additional information
Editor: Tom Fawcett.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Moerland, T.M., Broekens, J. & Jonker, C.M. Emotion in reinforcement learning agents and robots: a survey. Mach Learn 107, 443–480 (2018). https://doi.org/10.1007/s10994-017-5666-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10994-017-5666-0