Fast learning of relational dependency networks

Abstract

A relational dependency network (RDN) is a directed graphical model widely used for multi-relational data. These networks allow cyclic dependencies, necessary to represent relational auto-correlations. We describe an approach for learning both the RDN’s structure and its parameters, given an input relational database: First learn a Bayesian network (BN), then transform the Bayesian network to an RDN. Thus fast Bayesian network learning translates into fast RDN learning. The BN-to-RDN transform comprises a simple, local adjustment of the Bayesian network structure and a closed-form transform of the Bayesian network parameters. This method can learn an RDN for a dataset with a million tuples in minutes. We empirically compare our approach to a state-of-the-art RDN learning approach that applies functional gradient boosting, using six benchmark datasets. Learning RDNs via BNs scales much better to large datasets than learning RDNs with current boosting methods.

1 Introduction

Learning graphical models is one of the main approaches to extending machine learning for relational data. Two major classes of graphical models are dependency networks (DNs) (Heckerman et al. 2000) and Bayesian networks (BNs) (Pearl 1988). While dependency networks have many attractive properties for modelling relational data (Ravkic et al. 2015; Neville and Jensen 2007), relatively few structure learning methods have been developed for relational data. We describe a new approach to learning dependency networks: first learn a Bayesian network, then convert that network to a dependency network. We utilize previously existing methods (Schulte and Khosravi 2012) to learn a parametrized Bayesian network (Poole 2003), which provides a first-order template graphical model for relational data. The structure and parameters of the Bayesian network template model are converted to a relational dependency network (RDN) (Neville and Jensen 2007), whose local distributions specify the conditional probability of a ground, or instance, random variable given the values of all other ground random variables.

This hybrid approach combines the speed of learning Bayesian networks with the advantages of dependency network inference for relational data. Our experiments show that the hybrid learning algorithm can produce dependency networks for large and complex databases, up to one million records and 19 predicates.

Motivation The problem we address in this paper is how to convert a parametrized, first-order Bayesian network to a RDN. The conversion method allows us to leverage Bayesian network learning for dependency network learning. Previous comparisons with Markov Logic Network learning methods, on several benchmark datasets, provided empirical evidence that Bayesian network learning has advantages in three broad categories (Schulte and Khosravi 2012; Khosravi et al. 2010; Friedman et al. 1999): interpretability, scalability, and discovering complex relational features along long relational pathways. Our experiments in this paper provide evidence, on several benchmark datasets, that these advantages hold also for learning RDNs, albeit to a lesser degree. The scalability advantages of Bayesian networks are due to a combination of language bias, efficient local search heuristics, closed-form parameter estimation given sufficient database statistics, and sophisticated data access methods for computing relational sufficient statistics.¹

An important advantage of RDNs over Bayesian networks is that they support inference in the presence of cyclic dependencies (Neville and Jensen 2007; Natarajan et al. 2012). Cyclic dependencies occur when a relational dataset features auto-correlations, where the value of an attribute for an individual depends on the values of the same attribute for related individuals. Figure 1 below provides an example. It is difficult for Bayesian networks to model auto-correlations because by definition, the graph structure of a Bayesian network must be acyclic (Domingos and Richardson 2007; Getoor and Taskar 2007; Taskar et al. 2002; Getoor et al. 2001). Because of the importance of relational auto-correlations, dependency networks have gained popularity since they support reasoning about cyclic dependencies using a directed graphical model.

The advantages of our hybrid approach are specific to relational data. In fact, for propositional (i.i.d.) data, which can be represented in a single table, the reverse approach has been used: use fast dependency network learning to scale up Bayesian network learning (Hulten et al. 2003). This reversal is due to two key differences between i.i.d. and relational data.

• (1) In i.i.d. data, there is no problem with cyclic dependencies. So the acyclicity constraint of Bayesian networks incurs no loss of representation power, and often makes inference more efficient (Hulten et al. 2003).

• (2) Closed-form model evaluation for Bayesian networks is relatively less important in the single-table case, because iterating over the rows of a single data table to evaluate a dependency network is relatively fast compared to iterating over ground random variables in the relational case, where they are stored across several tables.

The previous moralization method (Khosravi et al. 2010; Schulte and Khosravi 2012) also combines the learning advantages of Bayesian networks with the support undirected models offer for inference with auto-correlation: Given a relational dataset, learn a Bayesian network structure, then convert the network structure to a Markov logic structure, without parameters. The method presented also computes the dependency network parameters from the learned Bayesian network. The moralization method used only the Bayesian network structure. Our theoretical analysis shows that the learned dependency networks provide different predictions from Markov networks.

Evaluation The performance of a relational structure learning algorithm depends on a variety of factors, such as the target model class, search strategies employed, and crucially the language bias, which defines the search space of relational patterns or features for the algorithm. Common choices of language bias include whether to employ aggregate functions (e.g. average over a relational neighborhood), to allow recursive dependencies (e.g., the income of a person is predicted by the income of her friends in a social network), and to consider individuals in defining features (e.g., are actors more likely to be successful if they acted in “Brave Heart” than in a generic movie?).

Our Bayes net-to-dependency net conversion method is defined using a very general relational formalism for describing relational features [par-factors (Kimmig et al. 2014)]. Our empirical evaluation, however, utilizes previously existing structure learning algorithms whose performance depends on their specific language bias. In this paper we compare the state-of-the-art Bayesian network learning method for relational data [the Learn-and-Join (LAJ) algorithm (Schulte and Khosravi 2012)] with the state-of-the-art dependency network learning method, which uses an ensemble learning approach based on functional gradient boosting (Natarajan et al. 2012). The relational feature space searched by these two algorithms is quite similar; the key difference is that the boosting approach considers relational features that involve specific individuals, whereas the LAJ algorithm is restricted to generic features about classes of individuals only. In experiments with six benchmark datasets, we find again advantages for the Bayesian network approach with respect to interpretability, feature complexity, and scalability, albeit to a lesser degree than the Markov Logic Network methods previously considered. At the same time, the predictive accuracy of the models derived from Bayesian networks was competitive to those found by the boosting method.

Given the considerable differences in model class, search methods employed, and language bias, our evidence does not warrant a claim that dependency networks learned from Bayesian networks are superior to those learned by boosting. Instead, we conclude that the Bayesian network approach we employed is an efficient alternative that offers several advantages, especially if a user is not concerned with relational features that involve specific individuals. Section 10 below describes how the techniques we describe for Bayesian network learning can be combined with boosting techniques for dependency network learning, to take advantage of the strengths of each.

Contributions We make three main contributions:

• 1. A fast approach for learning relational dependency networks: first learn a Bayesian network, then convert it to a dependency network.

• 2. A closed-form log-linear discriminative model for computing the RDN parameters from Bayesian network structure and parameters.

• 3. Necessary and sufficient conditions for the resulting network to be consistent, defined as the existence of a single joint distribution that induces all the conditional distributions defined by the dependency network (Heckerman et al. 2000).

2 Bayesian networks and relational dependency networks

We review dependency networks and their advantages for modelling relational data. We assume familiarity with the basic concepts of Bayesian networks (Pearl 1988).

2.1 Dependency networks and Bayesian networks

The structures of both Bayesian networks and dependency networks are defined by a directed graph whose nodes are random variables. Bayesian networks must be acyclic, while dependency networks may contain cycles, including the special case of bi-directed edges. For both network types, the parameters are conditional distributions over the value of a node given its parents. The two types differ in the influence of a node’s children, however. In a Bayesian network, a node is only independent of all other nodes given an assignment of values to its parents, its children, and the co-parents of its children, whereas in a dependency network a node is independent given an assignment of values to only its parents. In graphical model terms, the Markov blanket of a node in a dependency network, the minimal set of nodes such that assigning them values will make this node independent of the rest of the network, is simply its parents.² For a Bayesian network, the Markov blanket is the node’s parents, children, and the co-parents of its children.

Consequently, a conditional probability in a dependency network effectively specifies the probability of a node value given an assignment of values to all other nodes. Following  Heckerman et al. (2000), we refer to such conditional probabilities as local probability distributions. For a single target variable, dependency network learning performs a task analogous to feature selection in discriminative learning: identifying a subset of variables that suffice for modelling the conditional distribution of the target variable.

Fig. 1

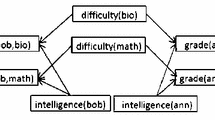
A Bayesian/dependency template network (top) and the instantiated inference graphs (bottom). By convention, predicates (Boolean functors) are capitalized. Edges from the BN template are solid blue, while edges added by the BN-to-DN transformation are dashed black. The edge set in the DN comprises both solid and dashed arrows. Note that although the template BN (top) is acyclic, its instantiation (bottom) features a bi-directed edge between gender(bob) and gender(anna) (Color figure online)

2.2 Relational dependency networks

Relational dependency networks (Neville and Jensen 2007) extend dependency networks to model distributions over multiple populations. We present the relational case using the parametrized random variable notation (Kimmig et al. 2014). A functor is a symbol denoting a function or predicate. Each functor has a set of values (constants) called the domain of the functor. Functors with Boolean ranges are called predicates and their name is capitalized. We consider only functors with finite domains. A first-order variable ranges over a domain of individuals. An expression $f(\tau _{1},\ldots ,\tau _{k})$, where $f$ is a functor and each $\tau _{i}$ is a first-order variable or a constant, is a Parametrized Random Variable (PRV). A directed acyclic graph whose nodes are PRVs is a parametrized Bayesian network structure, while a general (potentially cyclic) directed graph whose nodes are PRVs is a relational dependency network structure (RDN). A parametrized Bayesian network structure or relational dependency network structure augmented with the appropriate conditional probabilities is respectively a parametrized Bayesian network template or relational dependency network template. Note that the RDN templates that we define in this paper have the same Markov blanket as the parametrized Bayesian network templates from which they are derived but a different edge structure and probabilities. Algorithm 1, defined in Sect. 3, converts the probabilities of the parametrized Bayesian template to their counterparts in the relational dependency template.

RDNs extend dependency networks from i.i.d. to relational data via knowledge-based model construction (Neville and Jensen 2007): The first-order variables in a template RDN graph are instantiated for a specific domain of individuals to produce an instantiated or ground propositional DN graph, the inference graph. It is typically assumed that the domains of the first-order variables are finite so that the inference graph is finite. For example, each individual in a finite domain may be named by a constant, and the constants are then used to instantiate the first-order variables (Kimmig et al. 2014, Sec. 2.2.5). Figure 1 gives a dependency network template and its inference graph. Given an edge in the template RDN, instantiating both the parent and the child of the edge with the same grounding produces an edge in the inference graph. An example local probability distribution for the graph in Fig. 1 (abbreviating functors) is

$$\begin{aligned} P({g(anna)}|{g(bob)},\quad {CD(anna)},\quad {F(anna,bob)},\quad {F(bob,anna)},\quad {F(anna,anna)}). \end{aligned}$$

Language Bias The general definition of a parametrized random variable allows PRVs to contain constants as well as population variables. For instance, both ${Friend}(\mathbb {A},\mathbb {B})$ and ${Friend}({anna},\mathbb {B})$ are valid PRVs. Another language extension is to allow parametrized random variables to be formed with aggregate functions, as described by Kersting and De Raedt (2007); Getoor and Taskar 2007); see also Ravkic et al. (2015). For example, it is possible to use a functor that returns the number of friends of a generic person $\mathbb {A}$. The main contribution of this paper, our relational BN-to-DN conversion method, can be used whether the parametrized random variables contain aggregates, constants, or only first-order variables.

3 Learning relational dependency networks via Bayesian networks: overview

From now on, almost all of our discussion concerns parametrized Bayesian networks and RDNs. To shorten the discussion, we shall omit explicit mention of “parametrized” or “relational” and simply refer to Bayesian networks and dependency networks. If a particular point applies only to propositional networks, we mention this explicitly.

Fig. 2

The program flow for computing local probability distributions from a template Bayesian network. Features and weights are computed from the Bayesian network. Feature function values are computed for each query

Our algorithm for rapidly learning RDNs (Fig. 2) begins with any relational learning algorithm for Bayesian networks. Using the resulting Bayesian network as a template, we then apply a simple, fast transformation to obtain a relational dependency template. Finally we apply a closed-form computation to derive the dependency network inference graph parameters from the Bayesian structure and parameters.

BN-to-DN structure conversion Converting a Bayesian network structure to a dependency network structure is simple: for each node, add an edge pointing to the node from each member of its BN Markov blanket (Heckerman et al. 2000). The result contains bidirectional links between each node, its children, and its co-parents (nodes that share a child with this one). This is equivalent to the standard moralization method for converting a BN to an undirected model (Domingos and Lowd 2009), except that the dependency network contains bi-directed edges instead of undirected edges. Bi-directed edges permit assigning different parameters to each direction, whereas undirected edges have only one parameter.

BN-to-DN parameter conversion For propositional data, converting Bayesian network parameters to dependency network parameters is simple: using the standard BN product formula for the joint distribution, solve for the local conditional probability distributions given the Bayesian network parameters (Russell and Norvig 2010, Ch. 14.5.2). A family comprises a node and its parents. A family configuration specifies a value for a child node and each of its parents. For example, in the template of Fig. 1 (top), one family is ${gender}(\mathbb {A}), {Friend}(\mathbb {A},\mathbb {B}), {gender}(\mathbb {B})$ and one of its eight possible configurations is

$$\begin{aligned} {gender}(\mathbb {A}) = \mathrm {M}, \quad {Friend}(\mathbb {A},\mathbb {B}) = \mathrm {T},\quad {gender}(\mathbb {B}) = \mathrm {M}. \end{aligned}$$

The Markov blanket of a target node comprises multiple families, one each for the target node and each of its children, so an assignment of values to the target’s Markov blanket defines a unique configuration for each family. Hence in the propositional case the Markov blanket induces a unique log-conditional probability for each family configuration. The probability of a target node value given an assignment of values to the Markov blanket is then proportional to the exponentiated sum of these log-conditional probabilities (Russell and Norvig 2010, Ch. 14.5.2).

With relational data, however, different family configurations can be simultaneously instantiated, multiple times. For example, the configuration

$$\begin{aligned} {gender}(\mathbb {A}) = \mathrm {M},\quad {Friend}(\mathbb {A},\mathbb {B}) = \mathrm {T}, \quad {gender}(\mathbb {B}) = \mathrm {M}\end{aligned}$$

has one instance for each pair of male friends (a, b) (see also the example in Table 1). We combine these multiple instantiations in a log-linear model, which defines a conditional random field for each target node. The general form of a discriminative log-linear model (Sutton and McCallum 2007; Getoor and Taskar 2007) is that the conditional probability of a target variable value given input variable values is proportional to an exponentiated weighted sum of feature functions. A feature function maps a complete assignment of ground node values ($=$target value $+$ input variables) to a real number. We generalize the standard log-linear equation for i.i.d. data to define a relational log-linear equation following the pseudo code of Algorithm 1.

The features of the model are the family configurations (lines 3–6 of Algorithm 1) where the child node is either the target node or one of its children. The feature weights are the log-conditional BN probabilities defined for the family configuration (lines 7–9) of Algorithm 1). The feature functions are the family proportions, which is the number of times a relevant family configuration is instantiated, normalized by the total number of instantiations for that family. Without this standardization, features with more instantiations carry exponentially more weight. Ravkic et al. (2015) also use proportions for learning RDNs.

The next sections explain the details of the pipeline shown in Fig. 2. We begin at the beginning of the pipeline and review Bayesian network structure learning. Then we present the new contribution of this paper, the log-linear equation derived from the learned Bayesian network.

4 Bayesian network learning for relational data

We provide background on the previous work on learning Bayesian networks for relational data that we utilize in this paper. Readers may skip ahead to the section on the log-linear equation for local probability distributions, presented in Sect. 5, without loss of continuity. We review some of the fundamental insights and results from previous work concerning the scalability of Bayesian network learning, for both propositional and relational data.

4.1 Structure learning

For structure learning, we used the LAJ algorithm (Khosravi et al. 2010). This is a state-of-the-art parametrized Bayesian network structure learning algorithm for relational data. It employs an iterative deepening search strategy similar to that introduced by Friedman et al. (1999). We briefly review the main ideas behind the LAJ algorithm; for more details and examples please see Schulte and Khosravi (2012). The LAJ algorithm upgrades a single-table propositional BN learner for relational learning. The key idea of the algorithm can be explained in terms of the table join lattice. Recall that the (natural) join of two or more tables, written $T_{1} \bowtie T_{2} \cdots \bowtie T_{k}$ is a new table that contains the rows in the Cartesian products of the tables whose values match on common fields. A table join corresponds to a logical conjunction (Ullman 1982). Say that a join table $J$ is a subjoin of another join table $J'$ if $J' = J\bowtie J^{*}$ for some join table $J^{*}$. If $J$ is a subjoin of $J'$, then the fields (columns) of $J$ are a subset of those in $J'$. The subjoin relation defines the table join lattice. The basic idea of the LAJ algorithm is that join tables should inherit edges between descriptive attributes from their subjoins. This gives rise to the following constraints for two attributes $X_{1}$, $X_{2}$ that are both contained in some subjoin of $J$. (i) $X_{1}$ and $X_{2}$ are adjacent in a BN $B_{J}$ for $J$ if and only if they are adjacent in a BN for some subjoin of $J$. (ii) if all subjoin BNs of $J$ orient the link as $X_{1}\rightarrow X_{2}$ resp. $X_{1}\leftarrow X_{2}$, then $B_{J}$ orients the link as $X_{1}\rightarrow X_{2}$ resp. $X_{1}\leftarrow X_{2}$. The LAJ algorithm then builds a PBN for the entire database $\mathcal {D}$ by level-wise search through the table join lattice. The user chooses a single-table BN learner. The learner is applied to table joins of size 1, that is, regular data tables. Then the learner is applied to table joins of size $s,s+1,\ldots$, where the constraints (i) and (ii) are propagated from smaller joins to larger joins.

4.2 Computational cost and scalability

The computational cost of Bayesian network learning has been analyzed in previous work for both propositional and relational data. We review some of the main points as they pertain to the scalability of our overall BN-to-DN conversion approach. The complexity analysis of the LAJ algorithm (Schulte and Khosravi 2012) shows that the key computational cost is the run-time of the propositional BN learner that is used as a subroutine in the algorithm. This cost in turn depends on two key factors: (1) Model search cost, the number of candidate models generated. (2) Model evaluation cost, the cost of evaluating a candidate model. The model evaluation cost is dominated by data access (Moore and Lee 1998), especially the cost of computing sufficient statistics. In relational data, the sufficient statistics are the number of groundings that satisfy a formula in the input data (Friedman et al. 1999; Domingos and Lowd 2009; Schulte 2011). This number is well-defined if we assume that each observed individual receives a unique name or ID in the data, such as a constant (Kimmig et al. 2014). We assume throughout the paper that the number of satisfying groundings is well-defined. We discuss each factor (1) and (2) in turn.

4.2.1 Model search

While finding a Bayesian network that optimizes a model selection score is NP-hard (Chickering et al. 2004), highly efficient local search methods have been developed that provide good approximations fast. The implementation of the LAJ algorithm that we used employs Greedy Equivalence Search (GES) as its propositional BN learning method. This search strategy has the remarkable property that in the sample size limit, it is guaranteed to find an optimal Bayesian network (Chickering and Meek 2002). Thus as the sample size increases, the quality of the BN models discovered by GES increases as well, despite the NP-hardness of finding an optimal model. Given the language restriction of using only first-order variables and excluding constants, the number of models generated by relational BN model search is comparable to that generated by propositional BN model search (Schulte and Khosravi 2012). Efficient relational BN model search with both constants and variables is to our knowledge an open problem.

4.2.2 Model evaluation

Using the maximum likelihood scoring method, or other related scores, the fit of a Bayesian network to the input relational dataset can be evaluated in closed form given the sufficient statistics of the network (Friedman et al. 1999; Schulte 2011). While relational counting is not an easy problem, researchers have developed efficient solutions. These solutions find the number of instantiations of a relational feature much faster than by looping over all ground instances. Counting techniques for relational data include sorting tables on the attributes mentioned in the query (Ullman 1982; Graefe et al. 1998), and virtual join algorithms that compute counts for conjunctive queries without enumerating all tuples that satisfy the query. Examples of virtual joins are tuple ID propagation, which stores intermediate counts along a relational pathway (Yin et al. 2004), and the fast Möbius transform for queries that involve negated relationships (Qian et al. 2014). A very recent approach reduces counting instantiations to computing the partition function for a suitable Markov network (Venugopal et al. 2015). The important point for our experiments is that model evaluation by counting, which is most of what Bayes nets require, is much faster than iteratively computing model predictions for each ground fact in the input database, which is the standard model evaluation approach for other graphical model classes (Neville and Jensen 2007, Sec. 8.5.1).

5 The log-linear proportion equation

We propose a log-linear equation, the log-linear proportion equation (lower right box of Fig. 2), for computing a local probability distribution for a ground target node, $T^{*}$, given

• 1. A target value $t$ for the target node

• 2. A complete set of values $\varLambda ^{*}$ for all ground terms other than the target node

• 3. A template Bayesian network.

The template structure is represented by functions that return the set of parent nodes of $U$, $\mathrm {Pa}(U)$, and the set of child nodes of $U$, $\mathrm {Ch}(U)$. The parameters of the template are represented by the conditional probabilities of a node $U$ having a value $u$ conditional on the values of its parents,

$$\begin{aligned} \theta \left( U= u|\mathrm {Pa}(U) = \varvec{u}_{pa}\right) . \end{aligned}$$

A grounding $\gamma$ substitutes a constant for each member of a list of first-order variables, $\{\mathbb {A}_{1} = a_{1},\ldots , \mathbb {A}_{k} = a_{k}\}$. Applying a grounding to a template node defines a fully ground target node: ${gender}(\mathbb {A}) \{\mathbb {A}= sam\} = {gender}(sam)$. These are combined in the following log-linear equation to produce a local probability distribution:

Definition 1

(The log-linear proportion equation)

$$\begin{aligned}&P\left( {T}^{*} = t | \varLambda ^{*}\right) \propto \exp \nonumber \\&\sum _{U} \sum _{u,\varvec{u}_{pa}} \quad \left[ \ln \theta \left( U= u|\mathrm {Pa}(U) = \varvec{u}_{pa}\right) \right] \cdot \mathrm {p}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] \end{aligned}$$

(1)

where U  varies over $\{T\} \cup \mathrm {Ch}(T)$; the singleton value $u$ varies over the range of $U$; the vector of values $\varvec{u}_{pa}$ varies over the product of the ranges of $U's$ parents, constrained to value $t$ for occurrences of $T$; $\gamma$ grounds template node $T$; $T^{*}$ is the target ground node (i.e., $T^{*} = T\gamma$); and $\mathrm {p}^{\mathrm {r}}$ is the feature function, the family proportion.

The family proportion $\mathrm {p}^{\mathrm {r}}$ is computed as follows:

• 1. For a given family configuration $(U= u, \mathrm {Pa}(U) = \varvec{u}_{pa})$, let the family count

  $$\begin{aligned} \mathrm {n}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] \end{aligned}$$

  be the number of instantiations that (a) satisfy the family configuration and the ground node values specified by $T^{*} = t, \varLambda ^{*}$, and (b) are consistent with the equality constraint defined by the grounding $\gamma$.

• 2. The relevant family count $n^{r}$ is 0 if the family configuration contains a false relationship (other than the target node), else equals the family count. It is common in statistical–relational models to restrict predictors to existing relationships only (Getoor et al. 2007; Getoor and Taskar 2007; Russell and Norvig 2010).

• 3. The family proportion is the relevant family count, divided by the total sum of all relevant family counts for the given family:

  $$\begin{aligned}&\mathrm {p}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] \\&\quad = \frac{\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] }{\sum _{u',\varvec{u}_{pa}'}\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u', \mathrm {Pa}(U) = \varvec{u}_{pa}';T^{*} = t, \varLambda ^{*}\right] } \end{aligned}$$

In our experiments, family counts and proportions are computed using exact counting methods (see Sect. 6.2 below).

5.1 Example and pseudo code

Table 1 illustrates the computation of these quantities for predicting the gender of a new test instance (sam). Algorithm 2 shows pseudo code for computing the scores defined by the log-linear equation (1), given a list of weighted features and a target query.

Table 1 Applying the log-linear proportion equation with the Bayesian network of Fig. 1 to compute $P\left( {gender}(sam) = \mathrm {W} | \varLambda ^{*}\right)$ and $P\left( {gender}(sam) = \mathrm {M} | \varLambda ^{*}\right)$

6 Discussion and motivation

We discuss the key properties of our local distribution model, Eq. (1). We also provide a complexity analysis of the DN-to-BN conversion.

6.1 Main properties

We discuss the main properties that motivate our local distribution model. These are the following: (1) Log-linearity, (2) feature functions share a common standardized range, (3) nonrelational i.i.d. data are a special case, and (4) a random selection interpretation consistent with the probability logic of Halpern (1990), Bacchus (1990) and Schulte et al. (2014).

6.1.1 Log-linearity

The survey by Kimmig et al. (2014) shows that most statistical–relational methods define log-linear models. Khazemi et al. have shown that many relational aggregators can be represented by a log-linear model with suitable features (Kazemi et al. 2014). Equation (1) instantiates this well-established log-linear schema as follows.

• The model features are the family configurations $(U= u, \mathrm {Pa}(U) = \varvec{u}_{pa})$ where the child node is either the target node or one of its children.

• The feature weights are the log-conditional BN probabilities defined for the family configuration.

• The input variables are the values specified for the ground (non-target) nodes by the conjunction $\varLambda ^{*}$.

• The feature functions are the family proportion $\mathrm {p}^{\mathrm {r}}$.

Like other log-linear relational models, Eq. (1) enforces parameter tying, where different groundings of the same family configuration receive the same weight (Kimmig et al. 2014). In the related work Sect. 11 we compare Eq. (1) to other log-linear models such as Markov Logic networks.

6.1.2 Standardization

Using proportions as feature functions has the desirable consequence that the range of all feature functions is standardized to [0, 1] (Ravkic et al. 2015). It is well-known that the number of instantiation counts in relational data can differ for different families, depending on the population variables they contain. This ill-conditioning causes difficulties for log-linear models because families with more population variables can have an exponentially higher impact on the score prediction (Lowd and Domingos 2007). Intuitively, counts tacitly conflate the number of instantiations with the degree of information. Proportions avoid such ill-conditioning.

6.1.3 Generalizing the propositional case

An important general design principle is that relational learning should have i.i.d. learning as a special case (Van Laer and De Raedt 2001; Knobbe 2006): When we apply a relational model to a single i.i.d. data table, it should give the same result as the propositional model. Equation 1 satisfies this principle. In the propositional case, an assignment of values to all nodes other than the target node specifies a unique value for each family configuration. This means that all the family counts $n^{r}$ are either 0 or 1, hence all relevant proportions $p^{r}$ are 0 or 1, depending on whether a family configuration matches the query or not. For a simple illustration, consider the edge ${\textit{gender}}(\mathbb {A}) \rightarrow {\textit{CoffeeDr}}(\mathbb {A})$. Since this edge concerns only the Person domain associated with the single population variable $\mathbb {A}$, we may view this edge as a propositional sub-network. Suppose the query is $P({gender}(sam)= \mathrm {W}|{CoffeeDr}(sam)=\mathrm {T})$. The only family configurations with nonzero counts are ${gender}(sam)= \mathrm {W}$ (count 1) and ${CoffeeDr}(sam)=\mathrm {T}),{gender}(sam)= \mathrm {W}$ (count 1). Equation (1) gives

$$\begin{aligned}&P({g}(sam)= \mathrm {W}|{CD}(sam)=\mathrm {T}) \propto \\&\exp \{\ln P({g}(sam)= \mathrm {W}) + \ln P({CD}(sam)=\mathrm {T})|{g}(sam)= \mathrm {W})\}. \end{aligned}$$

This agrees with the i.i.d. BN formula for a local conditional probability, which is the product of the BN conditional probabilities for the target node given its children, and the target node’s children given their parents (cf. Sect. 3). In our simple two-node example, the formula can be derived immediately from Bayes’ theorem:

$$\begin{aligned}&P({g}(sam)= \mathrm {W}|{CD}(sam)=\mathrm {T}) \propto \\&P({CD}(sam)=\mathrm {T})|{g}(sam)= \mathrm {W}) \times P({g}(sam)= \mathrm {W}), \end{aligned}$$

which agrees with the solution above derived from Eq. (1). It may seem surprising that in predicting gender given coffee drinking, the model should use the conditional probability of coffee drinking given gender. However, Bayes’ theorem entails that P(X|Y) is always proportional to P(Y|X). In our example, given that the BN model specifies that women are more likely to be coffee drinkers than men, the information that Sam is a coffee drinker raises the probability that Sam is a woman.

6.1.4 Random selection interpretation

The inner sum of Eq. (1) computes the expected log-conditional probability for a family with child node $U$, when we randomly select a relevant grounding of the first-order variables in the family. The equation is therefore consistent with the random selection semantics established in classic AI research by Halpern (1990), Bacchus (1990) and Schulte et al. (2014). The expected log-conditional probability may be defined as follows. Fix a BN family with child node $U$ and parents $\mathrm {Pa}(U)$. Let $\gamma '$ be a grounding of the nodes in the family, that is consistent with the target grounding $\gamma$. The conjunction $T^{*} = t, \varLambda ^{*}$ specifies a unique value $U\gamma ' = u^{T^{*} = t, \varLambda ^{*}}$ for each ground child node $U\gamma '$. It also specifies a unique value $\mathrm {Pa}(U) \gamma '= \varvec{u}_{pa}^{T^{*} = t, \varLambda ^{*}}$ for each ground parent set $\mathrm {Pa}(U) \gamma '$. Let G be the set of all relevant groundings consistent with the target grounding, that is, the family configuration defined by the grounding is relevant.

Using this notation, the expected log-conditional probability from a randomly selected relevant grounding for the family is given by

$$\begin{aligned} \frac{1}{|G|} \sum _{\gamma ' \in G} \ln \theta \left( U\gamma ' = u^{T^{*} = t, \varLambda ^{*}}|\mathrm {Pa}(U) \gamma ' = \varvec{u}_{pa}^{T^{*} = t, \varLambda ^{*}}\right) . \end{aligned}$$

(2)

The next proposition asserts that the equivalence of random selection with the log-linear proportion equation:

Proposition 1

The expected log-conditional probability is the same as the contribution of each family in the log-linear sum of the equation in Definition 1:

$$\begin{aligned}&\frac{1}{|G|} \sum _{\gamma ' \in G} \ln \theta \left( U\gamma ' = u^{T^{*} = t, \varLambda ^{*}}|\mathrm {Pa}(U) \gamma ' = \varvec{u}_{pa}^{T^{*} = t, \varLambda ^{*}}\right) = \\&\quad \sum _{U} \sum _{u,\varvec{u}_{pa}} \quad \left[ \ln \theta \left( U= u|\mathrm {Pa}(U) = \varvec{u}_{pa}\right) \right] \cdot \mathrm {p}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] . \end{aligned}$$

A formal proof is in Sect. 13.1. Fundamentally the proposition holds because the expected value of a sum of terms is the sum of expectations of the terms.

6.2 Complexity of Algorithms 1 and 2

The loops of Algorithm 1 enumerate every family configuration in the template Bayesian network exactly once. Therefore computing features and weights takes time linear in the number of parameters of the Bayesian network.

Evaluating the log-linear equation, as shown in Algorithm 2, requires finding the number of instantiations that satisfy a conjunctive family formula, given a grounding. This is an instance of the general problem of computing the number of instantiations of a formula in a relational structure. Computing this number is a well-studied problem with highly efficient solutions, which we discussed in Sect. 4.2. To analyze the computational complexity of counting, a key parameter is the number m of first-order variables that appear in the formula (Vardi 1995). A loose upper bound on the complexity of counting instantiations is $d^{m}$, where d is the maximum size of the domain of the first-order variables. Thus counting instantiations has parametrized polynomial complexity (Flum and Grohe 2006), meaning that if m is held constant, counting instantiations requires polynomially many operations in the size of the relational structure [i.e., the size of $T^{*} = t, \varLambda ^{*}$ in Eq. (1)]. For varying m, the problem of computing the number of formula instantiations is #P-complete (Domingos and Richardson 2007, Prop.12.4).

7 Consistency of the derived dependency networks

A basic question in the theory of dependency networks is the consistency of the local probabilities. Consistent local probabilities ensure the existence of a single joint probability distribution p that induces the various local conditional probability distributions P for each node

$$\begin{aligned} P\left( T^{*} = t | \varLambda ^{*}\right) \propto p(T^{*} =t,\varLambda ^{*}) \end{aligned}$$

for all target nodes $T^{*}$ and query conjunctions $\varLambda ^{*}$ (Heckerman et al. 2000).

We present a precise condition on a template Bayesian network for its resulting dependency network to be consistent and the implications of those conditions. An template Bayesian network is edge-consistent if every edge has the same set of population variables on both nodes.

Theorem 1

A template Bayesian network is edge-consistent if and only if its derived dependency network is consistent.

The proof of this result is complex, so we present it in an appendix (Sect. 13.2). Intuitively, in a joint distribution, the correlation or potential of an edge is a single fixed quantity, whereas in Eq. (1), the correlation is adjusted by the size of the relational neighbourhood of the target node, which may be either the child or the parent of the edge. If the relational neighborhood size of the parent node is different from that of the child node, the adjustment makes the conditional distribution of the child node inconsistent with that of the parent node. The edge-consistency characterization shows that the inconsistency phenomenon is properly relational, meaning it arises when the network structure contains edges that relate parents and children from different populations.

The edge-consistency condition required by this theorem is quite restrictive: Very few template Bayesian networks will have exactly the same set of population variables on both sides of each edge.³ Therefore relational template Bayesian networks, which have multiple population variables, will most often produce inconsistent dependency networks. None of the Bayesian networks learned for our benchmark datasets (see Sect. 8) is edge-consistent, and therefore, by Theorem 1, the resulting dependency networks are inconsistent.

Inference with Inconsistent Dependency Networks Previous work has shown that dependency networks learned from data are almost always inconsistent but nonetheless provide accurate predictions using Gibbs sampling. The general idea is to apply the local probability distributions in the dependency network to update the values of each variable in turn (Heckerman et al. 2000; Neville and Jensen 2007; Lowd 2012). One approach is ordered pseudo-Gibbs sampling: fix an ordering of the random variables and update each in the fixed order. Heckerman et al. show that ordered pseudo-Gibbs sampling defines a Markov chain with a unique stationary joint distribution over the random variables (Heckerman et al. 2000, Th. 3). A recent approach was developed for Generative Stochastic Networks, where the next variable to be updated is chosen randomly, rather than according to a fixed ordering. Bengio shows that this procedure too defines a Markov chain with a unique stationary joint distribution over the random variables (Bengio et al. 2014, Sec. 3.4). Lowd discusses further methods for inference with inconsistent dependency networks (Lowd 2012).

8 Empirical evaluation: design and datasets

There is no obvious baseline method for our RDN learning method because ours is the first work that uses the approach of learning an RDN via a Bayesian network. Instead we benchmark against the performance of our method a different approach for learning RDNs, which uses an ensemble learning approach based on functional gradient boosting. Boosted functional gradient methods have been shown to outperform previous methods for learning relational dependency networks (Khot et al. 2011; Natarajan et al. 2012).

All experiments were done on a machine with 8 GB of RAM and a single Intel Core 2 QUAD Processor Q6700 with a clock speed of 2.66 GHz (there is no hyper-threading on this chip), running Linux Centos 2.6.32. Code was written in Java, JRE 1.7.0. All code and datasets are available (Khosravi et al. 2010).

8.1 Datasets

We used six benchmark real-world databases. For more details please see the references in Schulte and Khosravi (2012). Summary statistics are given in Table 2. The large datasets with over 1 M tuples are orders of magnitude larger than what has been analyzed by previous methods. The number of parametrized random variables, usually between 9 and 19, is at the upper end of what has been analyzed previously in statistical–relational learning. In the future work section we discuss scaling Bayesian network learning to even more complex relational datasets.

• UW-CSE This dataset (Kok and Domingos 2005) lists facts about the Department of Computer Science and Engineering at the University of Washington.⁴ There are two entity classes (278 Persons, 132 Courses) and two relationships (AdvisedBy, TaughtBy). There are six descriptive attributes, of average arity 3.8. The experiments reported in Natarajan et al. (2012) used the same dataset; their version is available in WILL format.⁵

• MovieLens MovieLens is a commonly-used rating dataset.⁶ We added more related attribute information about the actors, directors and movies from the Internet Movie Database (IMDb) (www.imdb.com, July 2013). It contains two entity sets, Users and Movies. The User table has 3 descriptive attributes, $age$, gender, and occupation. We discretized the attribute $age$ into three equal-frequency bins. There is one relationship table Rated corresponding to a Boolean predicate. The Rated table contains Rating as descriptive attribute. For each user and movie that appears in the database, all available ratings are included. MovieLens (1 M) contains 1 M ratings, 3883 Movies, and 6039 Users. MovieLens (0.1 M) contains about 0.1 M ratings, 1682 Movies, and 941 Users. We did not use the binary genre predicates because they are easily learned with exclusion rules.

• Mutagenesis This dataset is widely used in inductive logic programming research. It contains information on 4893 Atoms, 188 Molecules, and Bonds between them. We use the discretization of  Schulte and Khosravi (2012). Mutagenesis has two entity tables, Atom with 3 descriptive attributes of average arity 4, and Mole, with 5 descriptive attributes of average arity 5, including two attributes that are discretized into ten values each (logp and lumo). It features two relationships MoleAtom indicating which atoms are parts of which molecules, and Bond which relates two atoms and has 1 descriptive attribute of arity 5.

• Hepatitis This data is a modified version of the PKDD02 Discovery Challenge database. The database contains information on the laboratory examinations of hepatitis B and C infected patients. It contains data on the laboratory examinations of hepatitis B and C infected patients. The examinations were realized between 1982 and 2001 on 771 patients. The data are organized in 7 tables (4 entity tables, 3 relationship tables and 16 descriptive attributes). They contain basic information about the patients, results of biopsy, information on interferon therapy, results of out-hospital examinations, results of in-hospital examinations. The average arity of all descriptive attributes is 4.425.

• Mondial Data from multiple geographical Web data sources. There are two entity classes, 185 Countries and 135 Types of Economies. There are 5 descriptive attributes for each entity class, with average arity 4.4 for Country and 4.6 for Economy Type. A Borders relationship indicates which country borders which. The Economy relationship relates a country to a type of economy.

• IMDb The largest dataset in terms of number of total tuples (more than 1.3 M) and schema complexity. It combines MovieLens with data from the Internet Movie Database (IMDb)⁷ (Peralta 2007). There are 98,690 Actors, with 2 descriptive attributes of average arity 4; 2201 Directors, with 2 descriptive attributes of average arity 5.5; 3832 Movies, with 4 descriptive attributes of average arity 3.5; and 996,159 ratings.

8.2 Methods compared

Functional gradient boosting is a state-of-the-art method for applying discriminative learning to build a generative graphical model. The local discriminative models are ensembles of relational regression trees (Khot et al. 2011). Functional gradient boosting for relational data is implemented in the Boostr system (Khot et al. 2013). For functors with more than two possible values, we followed Khot et al. (2011) and converted each such functor to a set of binary predicates by introducing a predicate for each possible value. We compared the following methods:

• RDN_Bayes Our method: Learn a Bayesian network, then convert it to a RDN.

• RDN_Boost The RDN learning mode of the Boostr system (Natarajan et al. 2012).

• MLN_Boost The MLN learning mode of the Boostr system. It takes a list of target predicates for analysis. We provide each binary predicate in turn as a single target predicate, which amounts to using MLN learning to construct an RDN. This RDN uses a log-linear model for local probability distributions that is derived from Markov Logic Networks.

The measurements reported below used the default Boostr settings, with one exception: We decreased the number of regression trees in the ensemble from the default 20–10. This led to a small reduction in learning time, but did not decrease the predictive accuracy because on our datasets, Boostr does not produce more than 10 different trees. For other settings, similar changes from Boostr’s default changed neither accuracy nor learning time noticeably.

For Bayesian network structure learning, we used the implementation by the creators of the LAJ algorithm, which is available on-line (Khosravi et al. 2010). It is important to note that this implementation incorporates a language bias (cf. Sect. 8): it considers only parametrized random variables without any constants, that is, first-order variables only. This is a common restriction for statistical–relational structure learning methods [e.g. Friedman et al. (1999), Domingos and Lowd (2009) and Ravkic et al. (2015)], which trades off expressive power for faster learning. For Bayesian network parameter estimation, we used maximum likelihood estimates, computed with previous methods (Qian et al. 2014).

8.3 Prediction metrics

We follow Khot et al. (2011) and evaluate the algorithms using conditional log likelihood (CLL) and area under the precision-recall curve (AUC-PR). AUC-PR is appropriate when the target predicate features a skewed distribution as is typically the case with relationship predicates. For each fact $T^{*} = t$ in the test dataset, we evaluate the accuracy of the predicted local probability $P\left( T^{*} = t | \varLambda ^{*}\right)$, where $\varLambda ^{*}$ is a complete conjunction for all ground terms other than $T^{*}$. Thus $\varLambda ^{*}$ represents the values of the input variables as specified by the test dataset. CLL is the average of the logarithm of the local probability for each ground truth fact in the test dataset, averaged over all test predicates. For the gradient boosting method, we used the AUC-PR and likelihood scoring routines included in Boostr.

Both metrics are reported as means and standard deviations over all binary predicates.⁸ The learning methods were evaluated using 5-fold cross-validation. Each database was split into 5 folds by randomly selecting entities from each entity table, and restricting the relationship tuples in each fold to those involving only the selected entities [i.e., subgraph sampling (Schulte and Khosravi 2012)]. The models were trained on 4 of the 5 folds, then tested on the remaining one.

9 Results

We report learning times and accuracy metrics. In addition to these quantitative assessments, we inspect the learned models to compare the relational features represented in the model structures. Finally we make suggestions for combining the strengths of boosting with the strengths of Bayesian network learning.

9.1 Learning times

Table 2 shows learning times for the methods. The Bayesian network learning simultaneously learns a joint model for all parametrized random variables (PRVs). The PRVs follow the language bias of the LAJ algorithm and contain functors and population variables only (cf. Sect. 8). For the boosting method, we added together the learning times for each target PRV. On MovieLens (1 M), the boosting methods take over 2 days to learn a classifier for the relationship $B\_U2Base$, so we do not include learning time for this predicate for any boosting method. On the largest database, IMDb, the boosting methods cannot learn a local distribution model for the three relationship predicates with our system resources, so we only report learning time for descriptive attributes by the boosting methods. Likewise, our accuracy results in Tables 3 and 4 include measurements for only descriptive attributes on the datasets IMDb and MovieLens (1 M).

Table 2 Learning time

Consistent with other previous experiments on Bayesian network learning with relational data (Khosravi et al. 2010; Schulte and Khosravi 2012), Table 2 shows that RDN_Bayes scales very well with the number of data tuples: even the MovieLens dataset with 1 M records can be analyzed in seconds. RDN_Bayes scales worse with the number of PRVs, since it learns a joint model over all PRVs simultaneously, although the time remains feasible [1–3 h for 17–19 predicates; see also Schulte and Khosravi (2012)]. By contrast, the boosting methods scale well with the number of predicates, which is consistent with findings from propositional learning (Heckerman et al. 2000). Gradient boosting scales much worse with the number of data tuples.

Table 3 Conditional log-likelihood: mean (top), SD (bottom)

Table 4 Area under precision-recall curve: mean (top), SD (bottom)

9.2 Accuracy

Whereas learning times were evaluated on all PRVs, unless otherwise noted, we evaluate accuracy on the binary PRVs only (e.g., gender, Borders), because the boosting methods are based on binary classification. By the likelihood metric (Table 3), the Bayesian network method performs best on four datasets, comparably to MLN_Boost on Mutagenesis, and slightly worse than both boosting methods on the two largest datasets. By the precision-recall metric (Table 4), the Bayesian network method performs substantially better on four datasets, identically on Hepatitis, and substantially worse on Mutagenesis.

Combining these results, for most of our datasets the Bayesian network method has comparable accuracy and much faster learning. This is satisfactory because boosting is a powerful method that achieves accurate predictions by producing a tailored local model for each target predicate. By contrast, Bayesian network learning simultaneously constructs a joint model for all predicates, and uses simple maximum likelihood estimation for parameter values. Also, Boostr searches a more expressive feature space that allows constants as well as first-order variables. We conclude that Bayesian network learning with first-order variables only, scales much better to large datasets, and provides competitive accuracy in predictions.

Table 5 Difference in Markov blankets between RDN_Bayes and RDN_Boost

Fig. 3

The parents of target $gender (\mathbb {U})$ in the models discovered by RDN_Boost (left) and RDN_Bayes (right)

9.3 Comparison of model structures

Boosting is known to lead to very accurate classification models in general (Bishop 2006). For propositional data, a Bayesian network classifier with maximum likelihood estimation for parameter values is a reasonable baseline method (Grossman and Domingos 2004), but we would expect more accuracy from a boosted ensemble of regression trees. Therefore the predictive performance of our RDN models is not due to the log-linear equation (1), but due to the more powerful features that Bayesian network learning finds in relational datasets. These features involve longer chains of relationships than we observe in the boosting models. Kok and Domingos emphasize the importance of learning clauses with long relationship chains (Kok and Domingos 2010). The ability to find complex patterns involving longer relationship chains comes from the lattice search strategy, which in turn depends on the scalability of model evaluation in order to explore a complex space of relationship chains. Table 5 reports results that quantitatively confirm this analysis.

For each database, we selected the target PRV where RDN-Bayes shows the greatest predictive advantage over RDN-Boost (shown as $\varDelta$ CLL and $\varDelta$ AUC-PR). We then compute how many more PRVs the RDN-Bayes model uses to predict the target predicate than the RDN-Boost model, shown as $\varDelta$ Predicates. This number can be as high as 11 more PRVs (for Mondial). We also compare how many more population variables are contained in the Markov blanket of the RDN-Bayes model, shown as $\varDelta$ Variables. In terms of database tables, the number of population variables measures how many related tables are used for prediction in addition to the target table. This number can be as high as 2 (for IMDb and Hepatitis). To illustrate Fig. 3 shows the parents (Markov blanket) of target node ${gender}(\mathbb {U})$ from IMDb in the RDN-Boost and RDN-Bayes models. The RDN-Bayes model introduces 4 more parents and 2 more variables, Movie and Actor. These two variables correspond to a relationship chain of length 2. Thus BN learning discovers that the gender of a user can be predicted by the gender of actors that appear in movies that the user has rated.

10 Combining Bayesian network learning and gradient boosting

Gradient Boosting is a very different approach from Bayesian network conversion, in several respects: (1) Different model type: single-model Bayesian network versus ensemble of regression trees. (2) Different language bias: the LAJ structure learning algorithm considers nodes with population variables only, whereas a novel aspect of structure learning with the boosting methods is that they allow both variables and constants. (3) Different learning methods: local heuristic search to optimize a model selection score, versus boosting.

Given these fundamental differences, it is not surprising that our experiments show different strengths and limitations for each approach. Strengths of Bayes nets include: (1) Speed through fast model evaluation, which facilities exploring complex cross-table correlations that involve long chains of relationships. (2) Interpretability of the conditional probability parameters. (3) Learning easily extends to attributes with more than two possible values. Strengths of boosting include: (1) Potentially greater predictive accuracy through the use of an ensemble of regression trees. (2) Exploring a larger space of statistical–relational patterns that include both first-order variables and constants. These two approaches can be combined in several natural ways to benefit from their mutual strengths.

• Feature selection Fast Bayesian network learning methods can be used to select features. Regression tree learning should work much faster when restricted to the BN Markov blanket of a target node. The mode declaration facility of the Boostr system supports adding background knowledge about predictive predicates. For nodes whose BN Markov blankets contain disjoint features, boosting can be applied in parallel on disjoint datasets.⁹

• Initialization The Bayesian network can provide an initial dependency network for the boosting procedure. Gradient boosting can be applied to improve the estimate of the Bayesian network parameters (node conditional distribution given parents) or of the dependency network parameters (node conditional distribution given parents). It is well-known that decision trees can improve the estimation of Bayesian network parameters (Friedman and Goldszmidt 1998); a tree ensemble should provide an even more accurate model. Using boosting for local probability models would leverage its ability to learn statistical patterns with constants rather than first-order variables only.

• Proportions not Counts Functional gradient boosting can be used with proportions as feature functions rather than counts, to avoid ill-conditioned learning with feature functions of different magnitudes.

11 Related work

Dependency networks were introduced by Heckerman et al. (2000) and extended to relational data by Neville and Jensen (2007). Heckerman et al. (2000) compare Bayesian, Markov and dependency networks for nonrelational data. Neville and Jensen compare Bayesian, Markov and dependency networks for relational data, including the scalability advantages of Bayesian network learning (Neville and Jensen 2007, Sec.8.5.1). Using the parametrized random variable formalisms, Kimmig et al. compare prominent statistical–relational formalisms, for example Relational Bayesian networks, Bayes Logic Programs, and Markov Logic Networks (Kimmig et al. 2014).

Bayesian networks. There are several proposals for defining directed relational template models, based on graphs with directed edges or rules in clausal format (Getoor et al. 2007; Kersting and De Raedt 2007; Getoor and Taskar 2007). Defining the probability of a child node conditional on multiple instantiations of a parent set requires the addition of combining rules (Kersting and De Raedt 2007; Getoor and Taskar 2007) or aggregation functions (Getoor et al. 2007; Getoor and Taskar 2007). Combining rules such as the arithmetic mean (Natarajan et al. 2008) combine global parameters with a local scaling factor, as does our log-linear equation (1). In terms of combining rules, our equation uses the geometric mean rather than the arithmetic mean.¹⁰ To our knowledge, the geometric mean has not been used before as a combining rule for relational data. Another difference with template Bayesian networks is that the geometric mean is applied to the entire Markov blanket of the target node, whereas usually a combining rule applies only to the parents of the target node.

Markov Networks. Markov Logic Networks (MLNs) provide a logical template language for undirected graphical models. Richardson and Domingos propose transforming a Bayesian network to a Markov Logic network using moralization, with log-conditional probabilities as weights (Domingos and Lowd 2009). This is also the standard BN-to-MLN transformation recommended by the Alchemy system http://alchemy.cs.washington.edu/. A discriminative model can be derived from any MLN (Domingos and Lowd 2009). The structure transformation was used in previous work (Schulte and Khosravi 2012), where MLN parameters were learned, not computed in closed-form from BN parameters. The local probability distributions derived from an MLN obtained from converting a Bayesian network are the same as those defined by our log-linear Formula 1, if counts replace proportions as feature functions (Schulte 2011). Since the local probability distributions derived from an MLN are consistent, our main Theorem 1 entails that in general, there is no MLN whose log-linear local models are equivalent to our log-linear local models with proportions as feature functions. Schulte et al. report empirical evidence that using proportions instead of counts, with the Bayesian network features and parameters, substantially improves predictive accuracy (Schulte et al. 2012).

12 Conclusion and future work

Relational dependency networks offer important advantages for modelling relational data. They can be learned quickly by first learning a Bayesian network, then performing a closed-form transformation of the Bayesian network to a dependency network. The key question is how to transform BN parameters to DN parameters. We introduced a relational generalization of the standard propositional BN log-linear equation for the probability of a target node conditional on an assignment of values to its Markov blanket. The new log-linear equation uses a sum of expected values of BN log-conditional probabilities, with respect to a random instantiation of first-order variables. This is equivalent to using feature instantiation proportions as feature functions. Our main theorem provided a necessary and sufficient condition for when the local log-linear equations for different nodes are mutually consistent. On six benchmark datasets, learning RDNs via BNs scaled much better to large datasets than state-of-the-art functional gradient boosting methods, and provided competitive accuracy in predictions.

Future Work. The boosting approach to constructing a dependency network by learning a collection of discriminative models is very different from learning a Bayesian network. There are various options for hybrid approaches that combine the strengths of both. (1) Fast Bayesian network learning can be used to select features. Discriminative learning methods should work faster restricted to the BN Markov blanket of a target node. (2) The Bayesian network can provide an initial dependency network structure. Gradient boosting can then be used to fine-tune local distribution models.

One of the advanced features of the boosting system is including relational features that involve individual constants, not only first-order variables. Extending structure learning for parametrized Bayesian networks to include nodes with constants is an open problem. This would also permit an apples-to-apples comparison of the speed of Bayesian network learning vs. boosting using a compatible language bias.

Several important applications, such as large-scale information extraction from web pages (Zhang 2015), require analyzing datasets with many more parametrized random variables than the benchmarks in our experiments. One approach to modelling massive numbers of random variables is to upgrade the propositional Bayesian network learning algorithms that are designed for such datasets, for instance the Sparse Candidate algorithm (Friedman et al. 1999).

Appendix: Proofs of formal results

1.1 Equivalence between log-linear equation and random selection

This appendix proves Proposition 1. Each grounding $\gamma '$ with the same values $u= u^{T^{*} = t, \varLambda ^{*}}$ and $\varvec{u}_{pa} = \varvec{u}_{pa}^{T^{*} = t, \varLambda ^{*}}$ contributes the same log-conditional probability to the expectation. The number of such groundings is given by $\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right]$. Therefore

$$\begin{aligned}&\sum _{\gamma ' \in G} \ln \theta \left( U\gamma ' = u^{T^{*} = t, \varLambda ^{*}}|\mathrm {Pa}(U) \gamma ' = \varvec{u}_{pa}^{T^{*} = t, \varLambda ^{*}}\right) = \\&\sum _{U} \sum _{u,\varvec{u}_{pa}} \quad \left[ \ln \theta \left( U= u|\mathrm {Pa}(U) = \varvec{u}_{pa}\right) \right] \cdot \mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] . \end{aligned}$$

Also, for the total number of relevant family groundings we have

$$\begin{aligned} |G| = \sum _{u',\varvec{u}_{pa}'}\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u', \mathrm {Pa}(U) = \varvec{u}_{pa}';T^{*} = t, \varLambda ^{*}\right] . \end{aligned}$$

Therefore,

$$\begin{aligned} \mathrm {p}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] = \\ \frac{\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] }{\sum _{u',\varvec{u}_{pa}'}\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u', \mathrm {Pa}(U) = \varvec{u}_{pa}';T^{*} = t, \varLambda ^{*}\right] } =\\ \frac{\mathrm {n}^{\mathrm {r}}\left[ \gamma ;U= u, \mathrm {Pa}(U) = \varvec{u}_{pa};T^{*} = t, \varLambda ^{*}\right] }{|G|} \end{aligned}$$

These observations entail that Eq. (2) is equivalent to the contribution of each family in the log-linear sum of the equation in Definition 1.

1.2 Proof of consistency characterization

This appendix presents a proof of Theorem 1. The theorem says that a dependency network derived from a template Bayesian network is consistent if and only if the Bayesian network is edge-consistent. We begin by showing that Bayesian network edge-consistency is sufficient for dependency network consistency. This is the easy direction. That edge-consistency is also necessary requires several intermediate results.

1.2.1 Edge-consistency is sufficient for consistency

Edge consistency entails that each grounding of a node determines a unique grounding of both its parents and its children in the Bayesian network. Thus the ground dependency network is composed of disjoint dependency networks, one for each grounding. Each of the ground disjoint dependency networks is consistent, so a joint distribution over all can be defined as the product of the joint probabilities of each ground dependency network. The formal statement and proof is as follows.

Proposition 2

If a template Bayesian network is edge-consistent, then the derived dependency network is consistent.

Proof

Heckerman et al. (2000) showed that a dependency network is consistent if and only if there is a Markov network with the same graphical structure that agrees with the local conditional distributions. We argue that given edge-consistency, there is such a Markov network for the derived dependency network. This Markov network is obtained by moralizing and then grounding the Bayesian network (Domingos and Lowd 2009). Given edge-consistency, for each ground target node, each family of the ground target node has a unique grounding. Thus the relevant family counts are all either 1 or 0 (0 if the family configuration is irrelevant). The Markov network is now defined as follows: Each grounding of a family in the template Bayesian network is a clique. For an assignment of values $U^{*} = u,\mathrm {Pa}(U)^{*} = \varvec{u}_{pa}$ to a ground family, the clique potential is 1 if the assignment is irrelevant, and $\theta \left( U= u|\mathrm {Pa}(U) = \varvec{u}_{pa}\right)$ otherwise. It is easy to see that the conditional distributions induced by this Markov network agree with those defined by Eq. (1), given edge-consistency. $\square$

1.2.2 Edge-consistency is necessary for consistency

This direction requires a mild condition on the structure of the Bayesian network: it must not contain a redundant edge (Pearl 1988). An edge $T_{1}\rightarrow T_{2}$ is redundant if for every value of the parents of $T_{2}$ excluding $T_{1}$, every value of $T_{1}$ is conditionally independent of every value of $T_{2}$. Less formally, given the other parents, the node $T_{1}$ adds no probabilistic information about the child node $T_{2}$. Throughout the remainder of the proof, we assume that the template Bayesian network contains no redundant edges. Our proof is based on establishing the following theorem.

Theorem 2

Assume that a template BN contains at least one edge $e_1$ such that the parent and child do not contain the same set of population variables. Then there exists an edge $e_2$ (which may be the same as or distinct from $e_1$) from parent $T_{1}$ to child $T_{2}$, ground nodes $T_{1}^{*}$ and $T_{2}^{*}$, and a query conjunction $\varLambda ^{*}$ such that: the ground nodes $T_{1}^{*}$ and $T_{2}^{*}$ have mutually inconsistent conditional distributions $\theta \left( T_{1}^{*}|\varLambda ^{*}\right)$ and $\theta \left( T_{2}^{*}|\varLambda ^{*}\right)$ as defined by Eq. (1).

The query conjunction $\varLambda ^{*}$ here denotes a complete specification of all values for all ground nodes except for $T_{1}^{*}$ and $T_{2}^{*}$. Theorem 2 entails the necessity direction of Theorem 1 by the following argument. Suppose that there is a joint distribution p that agrees with the conditional distributions of the derived dependency network. Then for every query conjunction $\varLambda ^{*}$, and for every assignment of values $t_{1}$ resp. $t_{2}$ to the ground nodes, we have that $p(T_{1}^{*}=t_{1}|T_{2}^{*}=t_{2},\varLambda ^{*})$ and $p(T_{2}^{*}=t_{2}|T_{1}^{*}=t_{1},\varLambda ^{*})$ agree with the log-linear equation 1. Therefore, the conditional distributions $p(T_{1}^{*}|T_{2}^{*},\varLambda ^{*})$ and $p(T_{2}^{*}|T_{1}^{*},\varLambda ^{*})$ must be mutually consistent. Theorem 2 asserts that for every (non-redundant) edge-inconsistent template BN, we can find a query conjunction and two ground nodes such that the conditional distributions of the ground nodes given the query conjunction are not mutually consistent. Therefore there is no joint distribution that is consistent with all the conditional distributions defined by the log-linear equations, which establishes the necessity direction of the main Theorem 1.

1.2.3 Properties of the template BN and the input query $\varLambda ^{*}$

We begin by establishing some properties of the template BN and the query conjunction that are needed in the remainder of the proof.

The inconsistency of the BN networks arises when a parent and a child ground node have different relevant family counts. The next lemma shows that this is possible exactly when the template BN is properly relational, meaning it relates parents and children from different populations.

Lemma 1

The following conditions are equivalent for a template edge $T_{1} \rightarrow T_{2}$.

• 1. The parent and child do not contain the same population variables.

• 2. It is possible to find a grounding $\gamma$ for both parent and child, and an assignment $\varLambda ^{*}$ to all other nodes, such that the relevant family count for the $T_{2}$ family differs for $T_{1}^{*} = \gamma T_{1}$ and $T_{2}^{*} = \gamma T_{2}$.

Proof

If the parent and child contain the same population variables, then there is a 1–1 correspondence between groundings of the child and groundings of the parents. Hence the count of relevant family groundings is the same for each, no matter how parents and child are instantiated.

If the parent and child do not contain the same population variables, suppose without loss of generality that the child contains a population variable $\mathbb {A}$ not contained in the parent. Choose a common grounding $\gamma$ for the parents and child node. For the ground child node, $\gamma T_{2}$, let $\gamma$ be the only family grounding that is relevant, so the relevant count is 1. For the ground parent node, there is at least one other grounding of the child node $T_{2}'$ different from $\gamma T_{2}$ since $T_{2}$ contains another population variables. Thus it is possible to add another relevant family grounding for $\gamma T_{1}$, which means that the relevant count is at least 2. $\square$

The proof proceeds most simply if we focus on template edges that relate different populations and no common children.

Definition 2

An template edge $T_{1} \rightarrow T_{2}$ is suitable if

• 1. The parent and child do not contain the same population variables.

• 2. The parent and child have no common child.

The next lemma shows that focusing on suitable edges incurs no loss of generality.

Lemma 2

Suppose that a template BN contains an edge such that the parent and child do not contain the same population variables. Then the template BN contains a suitable edge.

Proof

Suppose that there is an edge satisfying the population variable condition. Suppose that the parent and child share a common child. Since the edge satisfies the condition, the set of population variables in the common child differs from at least one of $T_{1}, T_{2}$. Therefore there is another edge from one of $T_{1} \rightarrow T_{2}$ as parent to a new child that satisfies the population variable condition. If this edge is not suitable, there must be another shared child. Repeating this argument, we eventually arrive at an edge satisfying the population variable condition where the child node is a sink node without children. This edge is suitable. $\square$

Consider a suitable template edge $T_{1} \rightarrow T_{2}$ that produces a bi-directed ground edge $T_{1}^{*} \leftrightarrow T_{2}^{*}$. For simplicity we assume that $T_{1}$ and $T_{2}$ are binary variables with domain $\{\mathrm {T},\mathrm {F}\}$. (This incurs no loss of generality as we can choose a database $\varLambda ^{*}$ in which only two values occur.) Let $\mathrm {Pa}(T_{2})$ be the parents of $T_{2}$ other than $T_{1}$. Since the template edge is not redundant (Pearl 1988), there is a parent value setting $\mathrm {Pa}(T_{2}) = \mathbf {pa}$ such that $T_{1}$ and $T_{2}$ are conditionally dependent given $\mathrm {Pa}(T_{2}) = \mathbf {pa}$. This implies that the conditional distribution of $T_{2}$ is different for each of the two possible values of $T_{1}$:

$$\begin{aligned} \frac{\theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {F},\mathbf {pa}\right) }{\theta \left( T_{2} = \mathrm {T}|T_{1} = \mathrm {F},\mathbf {pa}\right) } \ne \frac{\theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {T},\mathbf {pa}\right) }{\theta \left( T_{2} = \mathrm {T}|T_{1} = \mathrm {T},\mathbf {pa}\right) }. \end{aligned}$$

(3)

Let $\varLambda ^{*}$ denote an assignment of values to all ground nodes other than the target nodes $T_{1}^{*}$ and $T_{2}^{*}$. We assume that the input query $\varLambda ^{*}$ assigns different relevant family counts $N_{1}$ to $T_{1}^{*}$ and $N_{2}$ to $T_{2}^{*}$. This is possible according to Lemma 1.

1.2.4 Lowd’s equation and relevant family counts

The log-linear equation 1, specifies the conditional distribution of each target node given $\varLambda ^{*}$ and a value for the other target node. We keep the assignment $\varLambda ^{*}$ fixed throughout, so for more compact notation, we abbreviate the conditional distributions as

$$\begin{aligned} p({T_{1}}^{*} = t_{1}| {T_{2}}^{*} = t_{2}) \equiv P({T_{1}}^{*} = t_{1}|{T_{2}}^{*} = t_{2},\varLambda ^{*}) \end{aligned}$$

and similarly for $P({T_{1}}^{*} = t_{1}|{T_{2}}^{*} = t_{2},\varLambda ^{*})$.

On the assumption that the dependency network is consistent, there is a joint distribution over the target nodes conditional on the assignment that agrees with the conditional distribution:

$$\begin{aligned} \frac{p({T_{1}}^{*} = t_{1}, {T_{2}}^{*} = t_{2})}{p({T_{2}}^{*} = t_{2})}= p({T_{1}}^{*} = t_{1}| {T_{2}})^{*} \end{aligned}$$

and also with the conditional $p({T_{2}}^{*} = t_{2}| {T_{1}}^{*}=t_{1}).$

Lowd (2012) pointed out that this joint distribution satisfies the equations

$$\begin{aligned} \frac{p(\mathrm {F},\mathrm {F})}{p(\mathrm {T},\mathrm {F})} \cdot \frac{p(\mathrm {T},\mathrm {F})}{p(\mathrm {T},\mathrm {T})}= \frac{p(\mathrm {F},\mathrm {F})}{p(\mathrm {T},\mathrm {T})} = \frac{p(\mathrm {F},\mathrm {F})}{p(\mathrm {F},\mathrm {T})} \cdot \frac{p(\mathrm {F},\mathrm {T})}{p(\mathrm {T},\mathrm {T})} \end{aligned}$$

(4)

Since the ratio of joint probabilities is the same as the ratio of conditional probabilities for the same conditioning event, consistency entails the following constraint on conditional probabilities via Eq. (4):

$$\begin{aligned} \frac{p({T_{2}}^{*}=\mathrm {F}|{T_{1}}^{*}=\mathrm {F})}{p({T_{2}}^{*} = \mathrm {T}| {T_{1}}^{*}=\mathrm {F})} \cdot \frac{p({T_{1}}^{*}=\mathrm {F}|{T}_{2}^{*}=\mathrm {T})}{p({T_{1}}^{*} = \mathrm {T}| {T_{2}}^{*}=\mathrm {T})} =\frac{p({T_{1}}^{*}=\mathrm {F}|{T_{2}}^{*}=\mathrm {F})}{p({T_{1}}^{*} = \mathrm {T}| {T_{2}}^{*}=\mathrm {F})} \cdot \frac{p({T_{2}}^{*}=\mathrm {F}|{T_{1}}^{*}=\mathrm {T})}{p({T_{2}}^{*} = \mathrm {T}| {T_{1}}^{*}=\mathrm {T})} \end{aligned}$$

(5)

We refer to Eq. (5) as Lowd’s equation. The idea of our proof is to show that Lowd’s equations are satisfied only if the relevant family counts for the target nodes are the same. According to the log-linear equation, each conditional probability is proportional to a product of BN parameters. The first step is to show that in Lowd’s equation, all BN parameter terms cancel out except for those that are derived from the family that comprises $T_{1}^{*}$ and their $T_{2}^{*}$ and their common grounding.

Lemma 3

The conditional probabilities for the target nodes can be written as follows:

$$\begin{aligned} P\left( {T_{2}}^{*} = t_{2} | T_{1}^{*} = t_{1},\varLambda ^{*}\right) \propto \theta \left( T_{2} = t_{2}|T_{1} = t_{1},\mathbf {pa}\right) ^{(N/N_{2}+M_{T_2=t_{2}}/N_{2})} \cdot \pi _{T_2=t_{2}} \end{aligned}$$

(6)

where $M_{T_2=t_{2}}$ and $\pi _{T_2=t_{2}}$ depend only on $t_{2}$ and not on $t_{1}$ and

$$\begin{aligned} P\left( {T_{1}}^{*} = t_{1} | T_{2}^{*} = t_{2},\varLambda ^{*}\right) \propto \theta \left( T_{2} = t_{2}|T_{1} = t_{1},\mathbf {pa}\right) ^{(N/N_{1}+M_{T_1=t_{1}}/N_{1})} \cdot \pi _{T_1=t_{1}} \end{aligned}$$

(7)

where $M_{T_1=t_{1}}$ and $\pi _{T_1=t_{1}}$ depend only on $t_{1}$ and not on $t_{2}$.

Proof Outline. This is based on analysing the different types of families that appear in the log-linear equation and their groundings. We omit this straightforward analysis to simplify the proof; the details are available from Schulte et al. (2014).

Lemma 4

Suppose that conditions (6) and (7) of Lemma 3 hold. Then Lowd’s equation (5) holds if and only if $N_{1} = N_{2}$.

Proof

Observe that in Eq. (5), each term on the left has a corresponding term with the same value for the target node assignment and the opposing conditioning assignment. For instance, the term $p({T_{2}}^{*}=\mathrm {F}|{T_{1}}^{*}=\mathrm {F})$ on the left is matched with the term $p({T_{2}}^{*}=\mathrm {F}|{T_{1}}^{*}=\mathrm {T})$ on the right. This means that the products in the log-linear expression are the same on both sides of the equation except for those factors that depend on both $t_{1}$ and $t_{2}$. Continuing the example, the factors

$$\begin{aligned} \theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {F},\mathbf {pa}\right) ^{(M_{\mathrm {F}}/N_{2})} \cdot \pi _{T_2=t_{2}} \end{aligned}$$

on the left equal the factors

$$\begin{aligned} \theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {T},\mathbf {pa}\right) ^{(M_{T_1=t_{1}}/N_{2})}\cdot \pi _{T_2=t_{2}} \end{aligned}$$

on the right side of the equation. They therefore cancel out, leaving only the term

$$\begin{aligned} \theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {F},\mathbf {pa}\right) ^{N/N_{2}} \end{aligned}$$

on the left and the term

$$\begin{aligned} \theta \left( T_{2} = \mathrm {F}|T_{1} = \mathrm {F},\mathbf {pa}\right) ^{N/N_{2}} \end{aligned}$$

on the right. Lowd’s equation can therefore be reduced to an equivalent constraint with only BN parameter terms that depend on both $t_{1}$ and $t_{2}$. For further compactness we abbreviate such terms as follows

$$\begin{aligned} \theta \left( t_{2}|t_{1}\right) \equiv \theta \left( T_{2} = t_{2}|T_{1} = t_{1},\mathbf {pa}\right) . \end{aligned}$$

With this abbreviation, the conditions of Lemma 3 entail that Lowd’s equation 5 reduces to the equivalent expressions.

$$\begin{aligned} \frac{\theta \left( \mathrm {F}|\mathrm {F}\right) ^{N/N_{2}}}{\theta \left( \mathrm {T}|\mathrm {F}\right) ^{N/N_{2}} } \cdot \frac{\theta \left( \mathrm {T}|\mathrm {F}\right) ^{N/N_{1}} }{\theta \left( \mathrm {T}|\mathrm {T}\right) ^{N/N_{1}} }= & {} \frac{\theta \left( \mathrm {F}|\mathrm {F}\right) ^{N/N_{1}} }{\theta \left( \mathrm {F}|\mathrm {T}\right) ^{N/N_{1}} } \cdot \frac{\theta \left( \mathrm {F}|\mathrm {T}\right) ^{N/N_{2}} }{\theta \left( \mathrm {T}|\mathrm {T}\right) ^{N/N_{2}} } \end{aligned}$$

(8)

$$\begin{aligned} \left( \frac{\theta \left( \mathrm {F}|\mathrm {F}\right) }{\theta \left( \mathrm {T}|\mathrm {F}\right) }\right) ^{\left( N/N_{2}-N/N_{1}\right) }= & {} \left( \frac{\theta \left( \mathrm {F}|\mathrm {T}\right) }{\theta \left( \mathrm {T}|\mathrm {T}\right) }\right) ^{\left( N/N_{2}-N/N_{1}\right) } \end{aligned}$$

(9)

By the non-redundancy assumption (3) on the BN parameters, we have

$$\begin{aligned} \frac{\theta \left( \mathrm {F}|\mathrm {F}\right) }{\theta \left( \mathrm {T}|\mathrm {F}\right) } \ne \frac{\theta \left( \mathrm {F}|\mathrm {T}\right) }{\theta \left( \mathrm {T}|\mathrm {T}\right) } \end{aligned}$$

so Eq. (9) implies that

$$\begin{aligned} N_{1} = N_{2}, \end{aligned}$$

which establishes the lemma. $\square$

Theorem 2 now follows: Lemma 1 entails that if the dependency network is consistent, the log-linear equations satisfy Lowd’s equation with the bi-directed ground edge $T_{1}^{*} \leftrightarrow T_{2}^{*}$ and the query conjunction $\varLambda ^{*}$ that satisfies the BN non-redundancy condition. Lemmas 1 and 2 show that if the template BN is relational, it must contain a suitable edge $T_{1} \rightarrow T_{2}$. Lemma 4 together with Lowd’s equation entails that the relevant counts for $T_{1}^{*}$ and $T_{2}^{*}$ must then be the same. But the query conjunction $\varLambda ^{*}$ was chosen so that the relevant counts are different. This contradiction shows that Lowd’s equation is unsatisfiable, and therefore no joint distribution exists that is consistent with the BN conditional distributions specified by the log-linear equation 1. Since Theorem 2 entails Theorem 1, our proof is complete.