Modelling relational statistics with Bayes Nets

Abstract

Class-level models capture relational statistics over object attributes and their connecting links, answering questions such as “what is the percentage of friendship pairs where both friends are women?” Class-level relationships are important in themselves, and they support applications like policy making, strategic planning, and query optimization. We represent class statistics using Parametrized Bayes Nets (PBNs), a first-order logic extension of Bayes nets. Queries about classes require a new semantics for PBNs, as the standard grounding semantics is only appropriate for answering queries about specific ground facts. We propose a novel random selection semantics for PBNs, which does not make reference to a ground model, and supports class-level queries. The parameters for this semantics can be learned using the recent pseudo-likelihood measure (Schulte in SIAM SDM, pp. 462–473, 2011) as the objective function. This objective function is maximized by taking the empirical frequencies in the relational data as the parameter settings. We render the computation of these empirical frequencies tractable in the presence of negated relations by the inverse Möbius transform. Evaluation of our method on four benchmark datasets shows that maximum pseudo-likelihood provides fast and accurate estimates at different sample sizes.

1 Introduction

Many applications store data in relational form. Relational data introduces the machine learning problem of class-level frequency estimation: building a model that can answer statistical queries about classes of individuals in the database (Getoor et al. 2001). Examples of such queries include:

• What fraction of birds fly?—referring to the class of birds.

• What fraction of the grades awarded to highly intelligent students are As?—referring to the class of (student, course-grade) pairs.

• In a social network, what is the percentage of friendship pairs where both are women?—referring to the class of friendship links.

As the examples illustrate, class-level probabilities concern the frequency, proportion, or rate of generic events and conditions, rather than the attributes and links of individual entities. Estimates of class-level frequency have several applications:

Statistical first-order patterns :

AI research into combining first-order logic and probability investigated in depth the representation of statistical patterns in relational structures (Halpern 1990; Bacchus 1990). Often such patterns can be expressed as generic statements about the average member of a class, such as “intelligent students tend to take difficult courses”.

Policy making and strategic planning :

An administrator may explore the program characteristics that attract high-ranking students in general, rather than predict the rank of a specific student in a specific program. Maier et al. (2010) describe several applications of causal-relational knowledge for decision making.

Query optimization :

A statistical model predicts a probability for given table join conditions that can be used to estimate the cardinality of a database query result (Getoor et al. 2001). Cardinality estimation is used to minimize the size of intermediate join tables (Babcock and Chaudhuri 2005).

In this paper, we apply Bayes nets to the problem of class-level frequency estimation. We define the semantics, describe a learning algorithm, and evaluate the method’s effectiveness.

Semantics

We build a Bayes net model for relational statistics, using the Parametrized Bayes nets (PBNs) of Poole (2003). The nodes in a PBN are constructed with functors and first-order variables (e.g., gender(X) may be a node). The original PBN semantics is a grounding or template semantics, where the first-order Bayes net is instantiated with all possible groundings to obtain a directed graph whose nodes are functors with constants (e.g., gender(sam)). The ground graph can be used to answer instance-level queries about individuals, such as “if user sam has 3 friends, female rozita, males ali and victor, what is the probability that sam is a woman”? However, as Getoor pointed out (Getoor 2001), the ground graph is not appropriate for answering class-level queries, which are about generic rates and percentages, not about any particular individuals.

We support class-level queries via a class-level semantics for Parametrized Bayes nets, based on Halpern’s classic random selection semantics for probabilistic first-order logic (Halpern 1990; Bacchus 1990). Halpern’s semantics views statements with first-order variables as expressing statistical information about classes of individuals. For instance, the claim “60 % is the percentage of friendship pairs where both friends are women” could be expressed by the formula

$$P\bigl(\mathit{gender}(X) = \mathit{Woman}, \mathit{gender}(Y) = \mathit{Woman}|\mathit{Friend}( X,Y) = \mathit{T}\bigr) = 60~\%. $$

Learning

A standard Bayes net parameter learning method is maximum likelihood estimation, but this method is difficult to apply for Bayes nets that represent relational data because the cyclic data dependencies in relations violate the requirements of a traditional likelihood measure. We circumvent these limitations by using a relational pseudo-likelihood measure for Bayes nets (Schulte 2011) that is well defined even in the presence of cyclic dependencies. In addition to this robustness, the relational pseudo-likelihood matches the random selection semantics because it is also based on the concept of random instantiations. The estimator that maximizes the parameters of this pseudo-likelihood function (MPLE) has a closed-form solution: the parameters are the empirical frequencies, as with classical i.i.d. maximum likelihood estimation. However, computing these empirical frequencies is nontrivial for negated relationships because enumerating the complement of a relationship table is computationally infeasible. We show that the MPLE can be made tractable for negated relationship using the Möbius transform (Kennes and Smets 1990).

Evaluation

We evaluate MPLE on four benchmark real-world datasets. On complete-population samples MPLE achieves near perfect accuracy in parameter estimates, and excellent performance on Bayes net queries. The accuracy of MPLE parameter values is high even on medium-size samples.

Paper organization

We begin with relational Bayes net models and the random selection semantics for Bayes nets (Sects. 2 and 3). Section 4 describes parameter learning and Sect. 5 presents the inverse Möbius transform for computing relational statistics. Simulation results are presented in Sect. 6, showing the run time cost of estimating parameters, together with evaluations of their accuracy. We provide deeper background on the connections between random selection semantics and probability logic in Sect. 7 and summarize related work in Sect. 8.

2 Bayes Nets for relational data

Poole introduced the Parametrized Bayes net (PBN) formalism that combines Bayes nets with logical syntax for expressing relational concepts (Poole 2003). We adopt the PBN formalism, following Poole’s presentation.

2.1 Relational concepts

We introduce here a minimum of logical terminology. In Sect. 7 we present a more complete probabilistic logic. A population is a set of individuals. Individuals are denoted by lower case expressions (e.g., bob). A population variable is capitalized. An instantiation of a population variable X selects a member x of the associated population. An instantiation corresponds to the logical concept of grounding. A functor represents a mapping $f: \mathcal{P}_{1},\ldots,\mathcal{P}_{a} \rightarrow V_{f}$ where f is the name of the functor, and V _f is the output type or range of the functor. In this paper we consider only functors with a finite range, disjoint from all populations. If V _f ={T,F}, the functor f is a (Boolean) predicate; other functors are called attributes. A predicate with more than one argument is called a relationship. We use lowercase for attribute functors and uppercase for predicates.

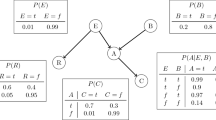
A relational structure specifies the value of a functor for any tuple of appropriate individuals (Chiang and Poole 2012). A relational structure can be visualized as a complex heterogeneous network (Russell and Norvig 2010, Chap. 8.2.1): individuals are nodes, attributes of individuals are node labels, relationships correspond to (hyper)edges, and attributes of relationships are edge labels. In relational databases, a relational structure is represented as a set of tables that list individuals and their attributes; see Fig. 1(a). The set of individual pairs or tuples that are linked by a relationship is usually much smaller than the set that are not so linked, so database tables list only the existing relationships.

Fig. 1

(a) A relational structure represented as tables. By convention, a pair not listed in the Friend table are not friends. The Friend relation is symmetric: Friend(X,Y)=Friend(Y,X). Only part of the rows are shown. (b) A Bayes net structure for this database. Friend(X,Y) is a relationship node, while the other three are attribute nodes. (c) The conditional probabilities for the Bayes net structure based upon the entries in the entire database

2.2 Bayes Nets

A Bayes Net (BN) is a directed acyclic graph (DAG) whose nodes comprise a set of random variables and conditional probability parameters. For each assignment of values to the nodes, the joint probability is specified by the product of the conditional probabilities, $P(\mathit{child}|\mathit{parent\_values})$.

A Parametrized random variable is of the form f(X ₁,…,X _a ), where the populations associated with the variables are of the appropriate type for the functor. A Parametrized Bayes Net (PBN) is a Bayes net whose nodes are parametrized random variables (Poole 2003). In the remainder of this paper we follow (Schulte and Khosravi 2012) and use the terms functor random variable and functor Bayes Net instead (FBN), for the following reasons. (1) The name “Parametrized” denotes a semantics that views the Bayes net as a template for a ground graph structure. Our random selection semantics does not refer to a ground model. (2) The usual statistical meaning of “parametrized” is that values have been assigned to the model parameters. We do not assume that such values have been assigned; learning them is a key topic of this paper.

In our view, a Functor Bayes net is a type of Bayes net whose nodes are complex objects with an internal syntax derived from the relational structure. Where the distinction between BNs in general and FBNs is not important, we simply refer to FBNs as Bayes nets and to functor random variables as functor nodes or nodes. Figure 1(b) shows an illustrative FBN. The next section presents a novel semantics of Functor Bayes nets as representing relational statistics.

3 Random selection semantics for Bayes Nets

We provide a semantics that views a functor Bayes net as a representation of a joint probability distribution over its nodes (Russell and Norvig 2010, Sect. 14.2). The semantics is for nodes that refer to population variables, rather than for ground nodes that refer to individuals as in Poole’s original paper (Poole 2003). Such a nonground node can be given a probabilistic interpretation in terms of random selections.

Consider first a node with a single population variable, e.g., gender(X). We view X as a random variable that selects a member x from its population according to a uniform population distribution P(X=x). The functor gender then represents a function of a random variable, and hence is itself a random variable. Figure 2 illustrates this interpretation.

Fig. 2

Viewing population variables as random selections from the associated population, the nodes represent functions of random variables, hence are themselves random variables. Probabilities are computed assuming the relations in Fig. 1(a) are complete (the database only describes Bob and Anna)

In the case of a functor with several population variables f(X ₁,…,X _a ), we view each population variable as representing an independent selection from its associated population (thus variables for the same population represent i.i.d. selections). This defines a distribution over a-tuples of individuals from the appropriate population. Again, any functor f(X ₁,…,X _a ) then defines a function of a random variable, and hence is itself a random variable. Figure 2 illustrates the random selection interpretation for the functor Friend(X,Y). As the random selection semantics is a key concept in this paper, we discuss two interpretations.

Random individuals

Under random selection semantics, probability formulas can be interpreted as describing the properties of random individuals. For example, the formula P(gender(X)=M)=50 % can be interpreted as “the probability is 50 % that a randomly selected person is a man”. A related interpretation that is often helpful is in terms of typical individuals (Halpern 1990); for instance, we may read the formula P(Flies(B)=T)=90 % as “the probability that a typical bird flies is 90 %”.

Class-level probabilities

Random selection formulas can also be read as describing the distribution of properties in classes of individuals. Thus we can read P(gender(X)=M)=50 % as “the percentage of persons that are men is 50 %”. Similarly, we may read the formula P(Flies(B)=T)=90 % as “the percentage of birds that fly is 90 %”. We therefore refer to probabilities defined by random selection as class-level probabilities.

Random selection semantics for Bayes Nets

Random selection semantics can be applied to view Bayes nets as representing class-level probabilities, without reference to a ground model. Via the standard product formula, a Bayes net B entails a probability value P _B for each joint assignment of values to its node. These are probability assignments that refer to population variables rather than individuals. For example, the Bayes net structure of Fig. 1(b) entails joint probabilities of the form

$$P_{B}\bigl(g(Y)=v_{1}, F(X,Y)=v_{2}, g(X) = v_{3}, CDr(X)=v_{4}\bigr), $$

where we have used the obvious abbreviations for functors, and each v _i is a constant from the appropriate range. For example, the conditional probabilities given in Fig. 1(c) entail the joint probability

$$ \textstyle P_{B}\bigl(g(X) = W, g(Y)=W, F(X, Y)=T, CDr(X)=T\bigr) = 0.028. $$

(1)

The random selection semantics for the nodes provides an interpretation of these joint probabilities. For example, the joint probability (1) can be read as “if we randomly select two persons X and Y, the chance is 2.8 % that they are both women, they are friends, and the first woman drinks coffee”.

Since the random selection semantics is not defined in terms of a ground model, it can be applied even in the presence of cyclic dependencies in the data. For instance, grounding the Bayes net of Fig. 1 shows a cyclic dependency between the genders of different users. The random selection semantics still applies, as shown in our examples, since it concerns class-level dependencies. The BN of Fig. 1 illustrates that the dependency structure among class-level random variables can be acyclic even when the dependency structure among ground instances is not.

In logic, the term “semantics” is used in a different sense than in the context of statistical models, to refer to truth conditions for logical sentences (Russell and Norvig 2010, Chap. 7.4.2). In Sect. 7, we show that the random selection semantics for Bayes nets that we have presented is in agreement with Halpern’s truth-conditional type 1 semantics for probabilistic logic. We next turn to learning and describe a method for learning Bayes net parameters that represent class-level probabilities.

4 Parameter learning for class-level probabilities

In a nonrelational learning setting, it is common to view a data table as representing information about individuals in a finite subset drawn from a large, possibly infinite population. In relational learning, we view a database $\mathcal{D}$ as representing a finite substructure of a large, possibly infinite relational structure. We make the standard assumption that the database is complete (Domingos and Lowd 2009; Khot et al. 2011): For each individual (node) observed, the database lists its attributes, and for each pair of observed individuals (nodes), the database specifies which links hold between them. Note that completeness is a statement about the information about individuals in the database. A complete database may contain only a subset of the individuals in the population about which we wish to make inferences.

A fundamental question for statistical model selection is how to measure the fit of the model. That is, we must specify a likelihood function $P_{B}(\mathcal{D})$ for a given database. The random selection semantics can be used to define a tractable pseudo-likelihood (Schulte 2011): The pseudo log-likelihood is the expected log-probability assigned by the Bayes net to the links and attributes for a random instantiation of the population variables. This is defined by the following procedure.

• 1. Randomly select a grounding for all population variables that occur in the Bayes net. The result is a ground graph with as many nodes as the original.

• 2. Look up the value assigned to each ground node in the database. Compute the log-likelihood of this joint assignment using the usual product formula; this defines a log-likelihood for this random instantiation.

• 3. The expected value of this log-likelihood—the mean over all instantiations—is the pseudo log-likelihood of the database given the Bayes net.

Table 1 shows an example computation of the pseudo likelihood. The pseudo likelihood matches the random selection semantics that we have proposed for class-level Bayes nets. It has several attractive theoretical properties (Schulte 2011). (1) Because it does not make reference to a single ground model, the measure is well defined even in the presence of cyclic dependencies in the data. For instance, grounding the Bayes net of Fig. 1 shows a cyclic dependency between the genders of different users. Nonetheless a pseudo-likelihood value can be computed as in Table 1. The pseudo-likelihood can be used to effectively learn cyclic or recursive dependencies (Schulte and Khosravi 2012). (2) It is closely related to relational pseudo-likelihood measures proposed for other graphical models (e.g., Markov random fields). (3) It is invariant under equivalence transformations of the logical predicates (database normalization). (4) For a fixed database $\mathcal{D}$ and Bayes net structure, the parameter values that maximize the pseudo-likelihood are the conditional empirical frequencies observed in the database (Schulte 2011, Proposition 3.1). We refer to these frequencies as the database probabilities. This result is exactly analogous to maximum likelihood estimation for i.i.d. data, where the empirical frequencies in an i.i.d. sample maximize the model likelihood.

Table 1 An example computation of the pseudo-likelihood for the database and the Bayes net of Fig. 1(b). Columns for functors include the grounded value and its conditional probability. The dotted row indicates entries for combinations including the other instances of Person. The pseudo log-likelihood is the mean of the lnp column

The database probability distribution $P_{\mathcal{D}}$ of a node assignment is the number of instantiations of the population variables in the functor nodes that satisfy the assignment in the database, divided by the number of all possible instantiations. The formal definition is (Chiang and Poole 2012):

• Let f ₁=v ₁,…,f _n =v _n be an assignment of appropriate values to n nodes.

• Let X ₁,…,X _ℓ be the population variables that appear in the nodes, with associated population sizes $|\mathcal{P}_{1}|, \ldots, |\mathcal{P}_{\ell}|$.

• Let $\#_{\mathcal{D}}(f_{1} = v_{1}, \ldots, f_{n} = v_{n})$ be the number of instantiations or groundings of the population variables that satisfy the assigned values in $\mathcal{D}$.

• Then the database probability of the value assignment is given by

  $$P_{\mathcal{D}}(f_{1} = v_{1}, \ldots, f_{n} = v_{n}) = \frac{\#_{\mathcal{D}}(f_{1} = v_{1}, \ldots, f_{n} = v_{n})}{|\mathcal{P}_{1}| \times\cdots\times|\mathcal{P} _{\ell}|}. $$

Example

Following Fig. 1(b), where the complete person population is {anna,bob}, we have

$$P_{\mathcal{D}}\bigl(\mathit{gender}(X) = M\bigr) = 1/2 $$

and

$$P_{\mathcal{D}}\bigl(\mathit{Friend}(X,Y) = \mathit{T}, \mathit {gender}(X) = M, \mathit{gender}(Y) = W\bigr) = 1/4. $$

In the next section we consider how to compute database probabilities.

5 Computing relational statistics

In this section we describe algorithms for computing probability estimates for the parameters $P_{\mathcal{D}}(\mathit{child}\_\mathit{value},\mathit{parent}\_ \mathit{values})$ in a functor Bayes net. The parameters can be estimated independently for each child node. We refer to a joint specification of values (child_value,parent_values) as a family state. Consider a child node specifying a relationship R ₁ whose parents comprise relationship nodes R ₂,…,R _m , and attribute nodes f ₁,…,f _j . The algorithms below can be applied in the same way in the case where the child node is an attribute node. The number of family states r is the cardinality of the Cartesian product of the ranges for every node in the family. The Bayes net parameters are r conditional probabilities of the form (we separate relationships from attributes by a semicolon)

$$ P(R_{1} = b_{1}| R_{2} = b_{2},\ldots, R_{m} = b_{m}; f_{1} = v_{1},\ldots,f_{j} = v_{j}), $$

(2)

where the b _i values are Boolean and each v _i is from the domain of f _i . Figure 3(a) provides an example with R ₁=Follows(X,Y), R ₂=Friend(X,Y), and f ₁=gender(X). In this example, all nodes are binary, so the CP-table requires the specification of r=2×2×2=8 values.¹

Fig. 3

(a) A Bayes net with two relationship nodes. (b) An illustrative trace of the inverse Möbius transform (see text)

Conditional probabilities can be easily estimated from the sufficient statistics, which are the database probabilities for a family state:

$$ P_{\mathcal{D}}(R_{1} = b_{1}, R_{2} = b_{2},\ldots, R_{m} = b_{m}; f_{1} = v_{1},\ldots,f_{j} = v_{j}). $$

(3)

For the rest of this section, we focus on computing these joint probabilities. So long as a database probability involves only positive relationships, the computation is straightforward. For example, in $P_{\mathcal{D}}(\mathit{gender}(X) = M, \mathit{Friend}(X,Y) = \mathit{T})$, the value $\#_{\mathcal{D}}(\mathit{gender}(X) = M, \mathit{Friend}(X,Y) = \mathit{T})$, the count of friendship pairs (x,y) where x is male and the Friend relationship is true, can be computed by regular table joins or optimized virtual joins (Yin et al. 2004).

Computing joint probabilities for a family containing one or more negative relationships is harder. A naive approach would explicitly construct new data tables that enumerate tuples of objects that are not related. However, the number of unrelated tuples is too large to make this scalable (think about the number of user pairs who are not friends on Facebook). In their work on learning Probabilistic Relational Models with existence uncertainty, Getoor et al. provided a “1-minus trick” for the special case of estimating a conditional probability with only a single negated relationship (Getoor et al. 2007, Sect. 5.8.4.2). They did not treat parameter learning with multiple negated relationships.

5.1 Statistics with multiple negated relationships: the fast Möbius transform

The general case of multiple negative relationships can be efficiently computed using the fast inverse Möbius transform (IMT), or Möbius transform for short. We compute the joint probabilities (3) for r family states by first computing the r Möbius parameters of the joint distribution, then using the inverse Möbius transform to transform the Möbius parameters into the desired joint probabilities. Figure 4 provides an overview of the computation steps. Because the Möbius parameters involve probabilities for events with positive relationships only, they can be estimated directly from the data. We next define the Möbius parameters, then explain the IMT.

Fig. 4

Computation of joint probabilities in a relational database. (1) Estimate Möbius parameters using standard table join operations. (2) Transform the Möbius parameters into joint probabilities. (3) Compute conditional probabilities from joint probabilities. Only the first step involves data access

Let $\mathbb{B} = B_{1},\ldots,B_{m}$ be a set of binary random variables with possible values 0 or 1, and P be the joint distribution that specifies 2^m probabilities, one for each possible assignment of values to the m binary variables. For any subset $\mathbf{B} \subseteq\mathbb{B}$ of the variables, let P(B=1) denote the probability that the variables in B are assigned the value 1, leaving the value of the other variables unspecified. The Möbius parameters of the distribution P are the values P(B=1) for all subsets $\mathbf{B} \subseteq\mathbb{B}$ (Drton and Richardson 2008, Sect. 3). There are 2^m Möbius parameters for m binary variables, with $0\leq P(\mathbb{B}=\mathbf{1})\leq P(\mathbf{B}=\mathbf{1})\leq P(\emptyset =\mathbf{1}) = 1$.

For a family state, if we fix the values v ₁,…,v _j of the attribute atoms, the sufficient statistics correspond to a joint distribution over m Boolean relationship random variables:

$$P(R_{1} = \cdot, R_{2} = \cdot,\ldots, R_{m} = \cdot; f_{1} = v_{1},\ldots,f_{j} = v_{j}). $$

We refer to the Möbius parameters of this joint distribution as the Möbius parameters for the attribute values v ₁,…,v _j .

Example

For the Bayes net of Fig. 3(a), fix the attribute condition gender(X)=W. The four Möbius parameters for this attribute condition are

5.2 The inverse Möbius transform

It is clear that the Möbius parameters can be computed from the joint probabilities by marginalization. For example, for two binary random variables, we have P(B ₁=1)=P(B ₁=1,B ₂=1)+P(B ₁=1,B ₂=0). Conversely, the Möbius inversion lemma entails that the joint probabilities can be computed from the Möbius parameters.² The Inverse Möbius Transform is an optimal algorithm for carrying out this computation, using the local update operation

$$ P(R= \mathit{F}, \mathbf{R}) = P(\mathbf{R}) - P(R= \mathit{T}, \mathbf{R}) $$

(4)

where R is a conjunction of relationship specifications, possibly with both positive and negative relationships. The equation holds for any fixed set of attribute conditions f ₁=v ₁,…,f _j =v _j . Equation (4) generalizes the 1-minus trick: the joint probabilities on the right hand side each involve exactly one less false relationship than the joint probability on the left.

As illustrated in Fig. 4, our implementation of the transform uses two data structures. Middle table: a joint probability table with r rows and k+2 columns. The first k=j+m columns are for the parent nodes, column k+1 is for the child node, and column k+2 is the joint probability for the row. The r rows enumerate all possible combinations of the child and parent node value. Thus the joint probability table is just like a conditional probability table, but with joint probabilities instead of conditional ones. Top table: the Möbius table is just like the joint probability table, but with entries T and * instead of T and F for the Boolean relationship values. The value * represents “unspecified”. The entries in the Möbius table do not involve negated relationships—all relationship nodes have the value T or ∗.

The IMT initializes the Möbius parameter values with frequency estimates from the data (top table). It then goes through the relationship nodes R ₁,…,R _m in order, at stage i replacing all occurrences of R _i =∗ with R _i =F, and applying the local update equation to obtain the probability value for the modified row. At termination, all ∗ values have been replaced by F and the table specifies all joint frequencies (middle table). In the final step, with complexity linear in r, we compute conditional probabilities (bottom table).

This algorithm is repeated for all possible assignments of values to attribute node, for every child node. Algorithm 1 gives pseudo code and Fig. 3 presents an example of the transform step.

Algorithm 1

The inverse Möbius transform for parameter estimation in a Parametrized Bayes Net

5.3 Complexity analysis

Kennes and Smets (1990) analyze the complexity of the IMT. We summarize the main points. Recall that m is the number of binary relationship nodes in a single node family.

• 1. The IMT only accesses existing links, never nonexisting links.

• 2. The inner loop of Algorithm 1 (lines 3–6) performs O(m2^m−1) updates (Kennes and Smets 1990). This is optimal (Kennes and Smets 1990, Corollary 1).

• 3. If the joint probability table for a family contains r rows, the algorithm performs O(m×r) updates in total.

In practice, the number m is small, often 4 or less.³ We may therefore treat the number of updates as proportional to the number r of Bayes net parameters.Our simulations confirm that the cost of the IMT updates is dominated by the data access cost for finding the Möbius parameter frequencies.

6 Evaluation

We evaluated the learning times (Sect. 6.2) and quality of inference (Sect. 6.3) of our approach to class-level semantics, as well as comparing the inference accuracy of our methods to Markov Logic Networks. Another set of simulations evaluates the accuracy of parameter estimates (conditional probabilities). All experiments were done on a QUAD CPU Q6700 with a 2.66 GHz CPU and 8 GB of RAM. The datasets and code are available on the Web (Khosravi et al. 2012).

6.1 Datasets

We used four benchmark real-world databases, with the modifications described by Schulte and Khosravi (2012). See that article for details.

Mondial database

A geography database, featuring one self-relationship, Borders, that indicates which countries border each other. The data are organized in 4 tables (2 entity tables, 2 relationship tables, and 10 descriptive attributes).

Hepatitis database

A modified version of the PKDD’02 Discovery Challenge database. The data are organized in 7 tables (4 entity tables, 3 relationship tables, and 16 descriptive attributes).

Financial

A dataset from the PKDD 1999 cup. The data are organized in 4 tables (2 entity tables, 2 relationship tables, and 13 descriptive attributes).

MovieLens

A dataset from the UC Irvine machine learning repository. The data are organized in 3 tables (2 entity tables, 1 relationship table, and 7 descriptive attributes).

To obtain a Bayes net structure for each dataset, we applied the learn-and-join algorithm (Schulte and Khosravi 2012) to each database with the implementation provided by the authors. This is the state-of-the-art structure learning algorithm for FBNs; for an objective function, it uses the pseudo-likelihood described in Sect. 4.

6.2 Learning times

Table 2 shows the run times for computing parameter values. The Complement method uses SQL queries that explicitly construct tables for the complement of relationships (tables representing tuples of unrelated entities), while the IMT method uses the inverse Möbius transform to compute the conditional probabilities. The IMT is faster by factors of 15–237.

Table 2 Learning times (sec) for algorithms that construct explicit complement tables or use the inverse Möbius transform

6.3 Inference

The evaluation of parameter learning for Bayes nets is based on query accuracy of the resulting nets (Allen et al. 2008) because answering probabilistic queries is the basic inference task for Bayes nets. Correct parameter values will support correct query results, so long as the given Bayes net structure matches the true distribution (i.e., is an I-map). We evaluate our algorithm by formulating random queries and comparing the results returned by our algorithm to the ground truth, the actual database frequencies.

We randomly generate queries for each dataset according to the following procedure. First, randomly choose a target node V 100 times, and go through each possible value a of V such that P(V=a) is the probability to be predicted. For each value a, choose randomly the number k of conditioning variables, ranging from 1 to 3. Make a random selection of k variables V ₁,…,V _k and corresponding values a ₁,…,a _k . The query to be answered is then P(V=a|V ₁=a ₁,…,V _k =a _k ).

As done by Getoor et al. (2001), we evaluate queries after learning parameter values on the entire database. Thus the Bayes net is viewed as a statistical summary of the data rather than as generalizing from a sample. Inference is carried out using the Approximate Updater of Tetrad (2008). Figure 5(left) shows the query performance for each database. A point (x,y) on a curve indicates a query such that the true probability value in the database is x and the probability value estimated by the model is y. The Bayes net inference is close to the ideal identity line, with an average difference of less than 1 % (inset numbers).

Fig. 5

Left: Query performance (Sect. 6.3): Estimated versus true probability, with average error and standard deviation. Number of queries/average inference time per query: Mondial, 506/0.08 sec; MovieLens, 546/0.05 sec; Hepatitis, 489/0.1 sec; Financial, 140/0.02 sec. Right: Error (Sect. 6.4): Absolute difference in estimated conditional probability parameters, averaged over 10 random subdatabases and all BN parameters. Whiskers indicate the 95th percentile. The 70 % and 90 % subsamples of the Financial database had so little variance that the whiskers are not visible

Comparison with Markov logic networks

To benchmark our results, we compare the average error of FBN inferences with frequency estimates from Markov Logic Network (MLN)s. MLNs are a good comparison point because (1) they are currently one of the most active areas of SRL research; (2) the Alchemy system provides an open-source, state-of-the-art implementation for learning and inference (Kok et al. 2009); (3) they do not require the specification of further components (e.g., a combining rule or aggregation function); and (4) their undirected model can accommodate cyclic dependencies.

Like most statistical-relational models, MLNs were designed for instance-level probabilities rather than class-level queries. We therefore need an extra step to convert instance-level probabilities into class-level probabilities. To derive class-level probability estimates from instance-level inference, the following method due to Halpern (1990, fn. 3) can be used: Introduce a new individual constant for each first-order variable in the relational model (e.g., random-student, random-course, and random-prof). Applying instance probability inference to these new individuals provides a query answer that can be interpreted as a class-level probability. To illustrate, if the only thing we know about Tweety is that Tweety is a bird, then the probability that Tweety flies should be the frequency of fliers in the bird population (Schulte 2012). That is, the class-level probability P(Flies(B)=T) can be obtained from the instance-level marginal probability P(Flies(tweety)=T) where tweety is a new constant not featured in the data used for learning. In the experiments below, we apply MLN inference to new constants as described to obtain class-level probability estimates. We compare these learning algorithms (Kok and Domingos 2010):

BN :

Bayes net parametrized with maximum pseudo likelihood estimates.

LHL :

A structure learning algorithm that produces a parametrized MLN, with Alchemy’s MC-SAT for inference.

LSM :

Another structure learning algorithm that produces a parametrized MLN, with Alchemy’s MC-SAT for inference. In experiments by Kok and Domingos, LSM outperformed previous MLN learners.

As shown in Table 3, the Bayes net models provide an order of magnitude more accurate class-level estimates than the MLN models.

Table 3 Class-level query performance of Bayes nets versus two algorithms for learning Markov Logic Networks, as indicated by average absolute error between the predicted frequency and the true database frequencies. NT denotes non-termination within the system resources

6.4 Conditional probabilities

In the previous inference results, the correct query answers are defined by the entire population, represented by the benchmark database, and the model is also trained on the entire database. To study parameter estimation at different sample sizes, we trained the model on N% of the data for varying N while continuing to define the correct value in terms of the entire population. Conceptually, we treated each benchmark database as specifying an entire population, and considered the problem of estimating the complete-population frequencies from partial-population data. The N% parameter is uniform across tables and databases. We employed standard subgraph subsampling (Frank 1977; Khosravi et al. 2010), which selects entities from each entity table uniformly at random and restricts the relationship tuples in each subdatabase to those that involve only the selected entities. Subgraph sampling provides complete link data and matches the random selection semantics. It is applicable when the observations include positive and negative link information (e.g., not listing two countries as neighbors implies that they are not neighbors). The subgraph method satisfies an ergodic law of large numbers: as the subsample size increases, the subsample relational frequencies approach the population relational frequencies.

The right side of Fig. 5 plots the difference between the true conditional probabilities and the MPLE estimates. With increasing sample size, MPLE estimates approach the true value in all cases. Even for the smaller sample sizes, the median error is close to 0, confirming that most estimates are very close to correct. As the box plots show, the 3rd quartile of estimation error is bound within 10 % on Mondial, the worst case, and within less than 5 % on the other datasets.

7 Probability logic

First-order logic was extended to incorporate statements about probabilities in Halpern and Bacchus’s classic AI papers (Halpern 1990; Bacchus 1990). Formalizing probability within logic provides a formal semantics for probability assertions and allows principles for probabilistic reasoning to be defined as logical axioms. This section provides a brief outline of probability logic. We describe how the random selection concept has been used to define a truth-conditional semantics for probability formulas (Halpern 1990; Bacchus 1990). This semantics is equivalent to our class-level interpretation of functor random variables.

7.1 Syntax

We adopt Chiang and Poole’s version of predicate logic for statistical-relational modelling (Chiang and Poole 2012). We review only the concepts that are the focus of this paper.

Individuals are represented by constants, which are written in lower case (e.g., bob). A type is associated with each individual, for instance bob is a person. The population associated with type τ, a set of individuals, is denoted by $\mathcal{P}(\tau)$. We assume that the populations are specified as part of the type description. A logical variable is capitalized and associated with a type. For example, the logical variable Person is associated with the population person. We use the definition of functor given in Sect. 2.1; we assume that the language contains functor symbols such as f,f′,g. A literal is of the form f(σ ₁,…,σ _a )=v, where v is in the range of the functor, and each σ _i is either a constant or a population variable. The types of σ ₁,…,σ _a must match the argument types of f. If all the σ ₁,…,σ _a are constants, then f(σ ₁,…,σ _a )=v is a ground literal. A ground literal is the basic unit of information. Literals can be combined to generate formulas. In this paper we consider only formulas that are conjunctions of literals, denoted by the Prolog-style comma notation $f(\sigma_{1},\ldots ,\sigma_{a}) = v, \ldots,f'(\sigma'_{1},\ldots,\sigma'_{a'}) = v'$. The work of Halpern and Bacchus shows how to extend the random selection semantics to the full syntax of first-order logic.

A probability literal is of the form

$$P(\phi) = p $$

where each p is a term that denotes a real number in the interval [0,1] and ϕ _i is a conjunctive formula as defined above. A probability formula is a conjunction of probability literals. We refer to predicate logic extended with probability formulas as probability logic.

Let {X ₁,…,X _k } be a set of logical variables of types τ ₁,…,τ _k . A grounding γ is a set γ={X ₁∖x ₁,…,X _k ∖x _k } where each x _i is a constant of the same type as X _i . A grounding γ for a formula ϕ is a grounding for the variables that appear in the formula, denoted by ϕγ.

Examples

Consider again the social network model of Fig. 1(a), with a single type, τ=person, associated with two logical variables X and Y. A conjunction of nonground literals is gender(X)=W, gender(Y)=M, Friend(X,Y)=T. Applying the grounding {X∖anna,Y∖bob} produces the conjunction of ground literals gender(anna)=W, gender(bob)=M, Friend(anna,bob)=T.

An example of a nonground probability formula is

$$P\bigl(\mathit{gender}(X) = W,\mathit{gender}(Y) = M, \mathit {Friend}(X,Y)=\mathit{T}\bigr) = 1/4, $$

while an example of a ground probability formula is

$$P\bigl(\mathit{gender}(\mathit{anna}) = W, \mathit{gender}(\mathit {bob}) = M,\mathit{Friend}( \mathit{anna},\mathit{bob})=\mathit{T}\bigr) = 1/4. $$

7.2 Semantics

Halpern defines different semantics for probability formulas depending on whether they contain only nonground probability literals (type 1), only ground probability literals (type 2), or both (type 3). Relational statistics are represented by nonground probability formulas, so we give the formal definition for the type 1 semantics only. The type 2 semantics for probability formulas with ground literals is well-known in the statistical-relational learning community (Cussens 2007; Milch et al. 2007; Russell and Norvig 2010, Chap. 14.6.1). An example of a mixed type 3 case is the connection between the class-level probabilities and individual marginal probabilities that we utilized in the Markov Logic Network experiments reported in Table 3. Schulte (2012) discusses the importance of type 3 semantics for statistical-relational learning.

A relational structure $\mathcal{S}$ specifies (1) a population for each type, and (2) for each functor f a set of tuples $\mathcal{S}_{f} = \{\langle x_{1},\ldots ,x_{a},v\rangle\}$, where the tuple 〈x ₁,…,x _a 〉 match the functor’s argument types, and the value v is in the range of f. Each tuple 〈x ₁,…,x _a 〉 appears exactly once in $\mathcal{S}_{f}$.

A relational structure defines truth conditions for ground literals, conjunctive formulas, and probability formulas as follows. If the structure $\mathcal{S}$ assigns the same value to a ground atom as a literal l, the literal is true in $\mathcal{S}$, written as $\mathcal{S}\models l$. Thus

$$\mathcal{S}\models f(x_{1},\ldots,x_{a}) = v \quad\mbox{iff}\quad \langle x_{1},\ldots,x_{a},v \rangle\in \mathcal{S}_{f}. $$

A conjunction is true if all its conjuncts are true. All ground literals listed above are true in the structure of Fig. 1(b). False literals include CoffeeDrinker(bob)=T and Friend(anna,anna)=T.

A relational structure does not determine a truth value for a nonground literal such as gender(X)=M, since a gender is not determined for a generic person X. We follow database theory and view a nonground formula as a logical query (Ullman 1982). Intuitively, the formula specifies conditions on the population variables that appear in it, and the result set lists all individuals that satisfy these conditions in a given relational structure. Formally, we denote the formula result set for a structure S as $\mathbb{R}_{\mathcal{S}}(\phi )$, defined by

$$\mathbb{R}_{\mathcal{S}}(\phi) \equiv\bigl\{\langle x_{1}, \ldots, x_{k} \rangle: \mathcal{S}\models\phi\{X_{1}\backslash x_{1},\ldots,X_{k} \backslash x_{k}\} \bigr\}. $$

To define truth conditions for nonground probability formulas, a relational structure is augmented with a distribution P _τ over each population $\mathcal{P}(\tau)$. There is no constraint on the distribution. Halpern refers to such augmented structures as type 1 relational structures; we continue to use the symbol S for type 1 structures. Given a type 1 structure, we may view a logical variable as a random selection from its population. These random selections are independent, so for a fixed set of population variables, the population distributions induce a distribution over the groundings of the variables. The random selection semantics states that the probability of a formula in a type 1 structure is the probability of the set of groundings that satisfy the formula. In other words, it is the probability that the formula is satisfied by a randomly selected grounding. The formal definitions are as follows:

• 1. $P_{\mathcal{S}}(X_{1} = x_{1},\ldots,X_{a} = x_{a}) =_{df} P_{\tau_{1}}(x_{1}) \times\cdots\times P_{\tau_{a}}(x_{a})$ where τ _i is the type of variable X _i and constant x _i .

• 2. $\mathcal{S}\models P(\phi) = p$ if and only if $p = \sum _{\langle x_{1},\ldots,x_{a} \rangle\in\mathbb{R}_{\mathcal{S} }(\phi)} P_{\mathcal{S}} (x_{1},\ldots,x_{a})$.

Each joint probability specified by a functor Bayes net is a conjunction in probability logic (like (1)). The net therefore specifies a set of nonground probability formulas. The logical meaning of these formulas according to the type 1 semantics is the same as the meaning of class-level probabilities according to the random selection semantics of Sect. 3. In the terminology of Bacchus, Grove, Koller, and Halpern, a set of nonground probability formulas is a statistical knowledge base (Bacchus et al. 1992). In this view, a functor Bayes net is a compact graphical representation of a statistical knowledge base, much as a small set of axioms can provide a compact representation of a logical knowledge base.

8 Related work and discussion

Statistical relational models

To our knowledge, the Statistical Relational Models (SRMs) of Getoor (2001), are the only prior statistical models with a class-level probability semantics. A direct empirical comparison is difficult as code has not been released, but SRMs have compared favorably with benchmark methods for estimating the cardinality of a database query result (Getoor et al. 2001) (Sect. 1).

SRMs differ from FBNs and other statistical-relational models in several respects. (1) SRMs are derived from a tuple semantics (Getoor 2001, Definition 6.3), which is different from the random selection semantics we propose for FBNs. (2) SRMs are less expressive: The queries that can be formulated using the nodes in an SRM cannot express general combinations of positive and negative relationships (Getoor 2001, Definition 6.6). This restriction stems from the fact that the SRM semantics is based on randomly selecting tuples from existing tables in the database. Complements of relationship tables are usually not stored (e.g., there is no table that lists the set of user pairs who are not friends). The expressive power of SRMs and FBNs becomes essentially equivalent if the SRM semantics is extended to include drawing random tuples from complement tables, but this entails the large increase in storage and processing described above.

Class-level vs. instance-level probabilities

Most previous work on statistical-relational learning has been concerned with instance-level probabilities for predicting the attributes and relationships of individuals (Getoor and Taskar 2007a; Russell and Norvig 2010). Examples of instance-level queries include the following.

• Given that Tweety is a bird, what is the probability that Tweety flies?

• Given that Sam and Hilary are friends, and given the genders of all their other friends, what is the probability that Sam and Hilary are both women?

• What is the probability that Jack is highly intelligent given his grades?

Probability logic represents such instance-level probabilities by formulas with ground literals (e.g., P(Flies(tweety))=p). In graphical models, instance level probabilities are defined by a template semantics (Getoor and Taskar 2007a): the functors associated with every node are grounded with every appropriate constant. Instance-level probabilities can be computed by applying inference to the resulting graph.

A key difference between class- and instance-level queries is that instance-level queries can involve an unbounded number of random variables. For instance, if m has 100 Facebook friends x ₁,…,x ₁₀₀, an instance-level query to predict the gender of m given the genders of her friends would involve 200 ground literals of the form

$$P\bigl(\mathit{gender}(\mathit{m})|\mathit{gender}(x_{1}),\mathit {Friend}(m,x_{1}), \ldots, \mathit{gender}(x_{100}),\mathit{Friend}( \mathit{m},x_{100})\bigr). $$

In contrast, class-level queries are restricted to the set of random variables in the class-level model, which is relatively small. For instance, the Bayes net of Fig. 1(b) contains four class-level random variables. This allows a query like

$$P\bigl(\mathit{gender}(X)|\mathit{gender}(Y),\mathit {Friend}(X,Y)\bigr), $$

which predicts the gender of a single generic user, given the gender of a single generic friend.

While we do not treat learning models for instance-level probabilities in this paper, we note that the Bayes net structures that we use in this paper also perform well for instance-level inference (Schulte and Khosravi 2012; Khosravi et al. 2010). The structures are learned using the random selection pseudo likelihood as the main component of the objective function. These evaluations suggest the pseudo likelihood guides learning towards models that perform well for both class-level and instance-level inferences.

Parfactors and lifted inference

Lifted inference aims to speed up instance-level inferences by computing parfactors, that is, counts of equivalent events, rather than repeating equivalent computations (Poole 2003). For instance, the inference procedure would count the number of male friends that m has, rather than repeat the same computation for each male friend. Based on the similarity with computing event counts in a database, Schulte and Khosravi refer to learning with the pseudo-likelihood as lifted learning (Schulte and Khosravi 2012). The counting algorithms in this paper can likely be applied to computing parfactors that involve negated relations. The motivation for parfactors, however, is as a means to compute instance-level predictions (e.g., predict the gender of m). In contrast, our motivation is to learn class frequencies as an end in itself. Because parfactors are used with instance-level inferences, they usually concern classes defined with reference to specific individuals, whereas the statistics we model in this paper are at the class-level only.

The complete-data and closed-world assumptions

In logic, the closed-world assumption is that “atomic sentences not known to be true are in fact false” (Russell and Norvig 2010, Chap. 8.2.8). While the closed-world assumption is used in logical reasoning rather than learning, it is relevant for learning if we view it as an assumption about how the data are generated. For instance, we have made the complete-data assumption that if a link between two individuals is not listed in a database, it does not exist. This entails that if a student registers in a course, this event is recorded in the university database, so the absence of a record implies that the student has not registered. If this assumption is not warranted for a particular data generating mechanism, the complete-data assumption fails, because for some pairs of individuals, the data does not indicate whether a link between does not actually exist or simply has not been recorded. One way to deal with missing link data is to use imputation methods (Hoff 2007; Namata et al. 2011). Another approach is downsampling existing links by adding random negative links (Khot et al. 2011; Yang et al. 2011). Many methods for dealing with missing data employ complete-data learning as a subroutine (e.g., the Expectation Maximization algorithm; cf. (Domingos and Lowd 2009, Chap. 4.3)). Given the speed and accuracy of pseudo-likelihood Bayes net learning in the complete-data case, we expect that it will be useful for learning with missing data as well.

Another important point for this paper is that our methods can be used no matter how link frequencies are estimated, whether from corrected or uncorrected observed link counts. Specifically, given estimates for the Möbius parameters, the Möbius transform finds the probabilities for negative link events that those parameters determine. This computation assumes nothing but the laws of the probability calculus.

9 Conclusion

Class-level probabilities represent relational statistics about the frequencies or rates of generic events and patterns. Representing these probabilities has been a long-standing concern of AI research. Class-level probabilities represent informative statistical dependencies in a relational structure, supporting such applications as strategic planning and query optimization. The class-level interpretation of Bayes nets is based on the classic random selection semantics for probability logic. Parameters are learned using the empirical frequencies, which are the maxima of a pseudo-likelihood function. The inverse Möbius transform makes the computation of database frequencies feasible even when the frequencies involve negated links. In evaluation on four benchmark databases, the maximum pseudo-likelihood estimates approach the true conditional probabilities as observations increase. The fit is good even for medium data sizes. Overall, our simulations show that Bayes net models derived with maximum pseudo-likelihood parameter estimates provide excellent estimates of class-level probabilities.