Efficient cross-validation for kernelized least-squares regression with sparse basis expansions

Abstract

We propose an efficient algorithm for calculating hold-out and cross-validation (CV) type of estimates for sparse regularized least-squares predictors. Holding out H data points with our method requires O(min(H ² n,Hn ²)) time provided that a predictor with n basis vectors is already trained. In addition to holding out training examples, also some of the basis vectors used to train the sparse regularized least-squares predictor with the whole training set can be removed from the basis vector set used in the hold-out computation. In our experiments, we demonstrate the speed improvements provided by our algorithm in practice, and we empirically show the benefits of removing some of the basis vectors during the CV rounds.

1 Introduction

This paper considers using the regularized least-squares (RLS) algorithm (Rifkin et al. 2003; Poggio and Smale 2003), a kernel-based learning algorithm that is also known as the kernel ridge regression (Saunders et al. 1998), the least-squares support vector machine (Suykens and Vandewalle 1999a) for regression and classification, or the Gaussian process regression (Rasmussen and Williams 2005). RLS has been shown to have a superior performance in regression and classification, has been modified to other learning problems such as ranking, and its successful practical applications are numerous (see, e.g., Pahikkala et al. 2009a, 2009c). Formally, training RLS can be considered a solving the following variational problem (for a more comprehensive introduction, see, e.g., Poggio and Smale 2003)

$$ \mathcal{A}(S)=\mathop{\mathrm {argmin}}_{f\in\mathcal{F}}\Biggl\{ \sum_{i=1}^m\bigl(f(x_i)-y_i\bigr)^2 +\lambda\| f\|_\mathcal{F}^2\Biggr\},$$

(1)

where $x_{i}\in\mathcal{X}$ are m training inputs in some input space $\mathcal{X}$ and y _i ∈ℝ their labels, λ∈ℝ₊ is a regularization parameter and ∥f∥ _k denotes the norm of f in the reproducing kernel Hilbert space (RKHS) $\mathcal{F}$.¹ The first and the second term of (1) are called the squared loss function and the regularizer, respectively. By the representer theorem (see, e.g., Schölkopf et al. 2001), the solution of (1) can be expressed as the following expansion:

$$ f(x)=\sum_{i=1}^{m}a_ik(x,x_i),$$

(2)

where a _i ∈ℝ and k is a kernel function corresponding to the RKHS $\mathcal{F}$. Accordingly, we only need to solve a regularization problem with respect to a finite number of coefficients a _i ,1≤i≤m.

The training time of RLS, that scales as O(m ³) in the worst case although one can often get closer to quadratic complexity with, for example, conjugate gradient methods (Shewchuk 1994; Suykens et al. 2002), may be too tedious if the number of training instances, m, is large. Moreover, a large number of nonzero coefficients in the expansion (2) causes slow prediction speed.² Consequently, several approaches alleviating the computational burden have been developed during the recent years. The so-called subset of regressors approach enforces sparsity on the expansion (2) meaning that only a subset of size n≪m of coefficients a _i are allowed to be nonzero, while the whole training set is still used in the training process.³ By doing this, one can immediately decrease the training time down to O(mn ²) (Poggio and Girosi 1990; Rifkin et al. 2003). One of the simplest and fastest approaches for selecting the set of basis vectors, that is, the training examples whose coefficients in the expansion (2) are nonzero, is a random selection. While, many smarter methods for selecting the basis vectors have been developed (see e.g. Smola and Bartlett 2001; Vincent and Bengio 2002), the random selection has been shown both empirically and theoretically to work as well as most of the more sophisticated methods, unless extra amount of computational resources is sacrificed for the selection process (Rifkin et al. 2003; Kumar et al. 2009). In this paper, we mainly focus on the random selection of basis vectors, since it substantially simplifies our considerations of both computational complexity of the training algorithms and estimating the prediction performance with cross-validation. In the rest of the paper, we refer to the above described approach of training RLS with randomly selected basis vectors shortly as sparse RLS.

Another approach for alleviating the computational burden is to make selection of hyperparameters and performance evaluation methods more efficient. Of them, hold-out techniques and particularly cross-validation (CV) are among the most commonly used methods, and thus, fast N-fold CV methods have also been introduced for RLS and its variations (Pelckmans et al. 2006; Pahikkala et al. 2006a; An et al. 2007; De Brabanter et al. 2010; Airola et al. 2011)). They generalize the classical leave-one-out CV (LOOCV) short-cut (Wahba 1990; Green and Silverman 1994) computable in O(m ²) time and some variations also enable the selection of the RLS regularization parameter efficiently without a separate re-training for each parameter value (Pelckmans et al. 2005, 2006; Rifkin and Lippert 2007). As a related work, we also mention fast CV approaches made for support vector machine classifiers (Cauwenberghs and Poggio 2001) and regressors (Karasuyama et al. 2009). While the CV methods for RLS usually rely on computational short-cuts based on matrix algebra, the CV methods for SVMs require solving a series of small optimization problems, whose size and number are data dependent.

One can combine the aforementioned speed improvement approaches and address the question of performing hold out efficiently with sparse RLS. In the case of RLS regression, the sparse algorithm can also be considered as the standard algorithm with a certain type of a modified kernel function (Quiñonero-Candela and Rasmussen 2005). Consequently, a straightforward way to expedite the computations is to use the sparse algorithm for training and the most efficient hold-out algorithms for standard RLS (Pahikkala et al. 2006a; An et al. 2007) for selection of hyperparameters and performance evaluation. For holding out $|\mathcal{H}|$ instances, this results in the computational complexity of $O(|\mathcal{H}|^{2}m)$. However, as mentioned above, the computational complexity of LOOCV with the previously known methods is O(m ²), which is more expensive than the training process of sparse RLS if m>n ². This motivates us in improving the efficiency by developing a sparse RLS specific method for selection of hyperparameters and performance evaluation.

Recently, Cawley and Talbot (2004) proposed this type of LOOCV algorithm. Its computational complexity of only O(mn ²) makes it much more practical than the LOOCV algorithm of standard RLS used together with the above mentioned modified kernel function, because it is as expensive as the training process of sparse RLS.

In this paper, we propose a novel hold-out method for sparse RLS that has the following merits, given that O(mn ²) floating point operations has already been spent in the training phase. We show that the method

• allows holding out several training examples simultaneously, enabling the use of CV methods other than LOOCV,

• enables the removal of basis vectors if they belong to the hold-out set, which is, for some learning tasks, a necessary property in order to avoid severely biased CV results, and

• is computationally more efficient

  • Holding out $|\mathcal{H}|$ training examples requires $O(\min(|\mathcal{H}|^{2}n,|\mathcal{H}| n^{2}))$ time.

  • Since in N-fold CV the average size of the hold-out sets is $|\mathcal{H}|=m/N$, the overall complexity of N-fold CV is $O(\min(m|\mathcal{H}| n,mn^{2}))$. That is, the required time is at most the same as the time spent for learning a sparse RLS with the whole training set.

  • As a special case, we get the complexity of LOOCV: because there are m hold-out sets of size 1, our algorithm requires only O(mn) time. The respective complexity for the previously proposed LOOCV algorithm for sparse RLS is O(mn ²) Cawley and Talbot (2004).

One may ask reasons for developing a LOOCV-algorithm with the above time complexity if one has to spend O(mn ²) time for initializing the sparse RLS predictor before computing LOOCV. We provide the two most apparent motivations for this.

First, it is well-known and straightforward to see that sparse RLS can be simultaneously trained to predict multiple outputs almost at the cost of learning to predict only one output. A typical example of this is the use of RLS for the one-versus-all type of multi-class classification (Rifkin and Klautau 2004). For other types of multi-output learning settings, see Suykens and Vandewalle (1999b), Suykens et al. (2002), for example. The complexity of training a predictor for v outputs is O(mn(n+v)), that is, the number of outputs starts to dominate the training complexity only in case there are more outputs than basis vectors. Now, we may want to compute LOOCV for each output separately. The computational cost of this is O(mnv) which is dominated by the training complexity.

As a second motivation, we consider selecting the value of the regularization parameter with CV. If our algorithm is used for LOOCV or N-fold CV with small hold-out sets, it can be combined with the simultaneous training of the sparse RLS with several values of the regularization parameter in a way that performs the parameter selection as efficiently as training only one instance of the sparse RLS (see e.g. Pahikkala et al. 2006a; Rifkin and Lippert 2007). For example, if the number of regularization parameter value candidates is c, the overall computational time of training a sparse RLS predictor with the optimal value found by LOOCV is O(mn ²+cmn)=O(mn(n+c)), where the mn ²-term is the computational cost of the initial training and cmn is the cost of running LOOCV c times. Now, if c<n, the complexity reduces to the complexity O(mn ²) of training a sparse RLS predictor once. This speed improvement is also empirically demonstrated in our experiments.

Finally, we motivate the abilities to hold out several training examples simultaneously and to remove the effect of basis vectors belonging to the hold-out set as follows. A classical motivation is that while LOOCV is known to be an almost unbiased estimator of the learning performance, it is known to suffer from larger variance than, say N-fold CV (see e.g. Kohavi 1995). Another, more practically oriented, motivation is that there exists many learning problems where the assumption of training set consisting of independently and identically distributed training examples does not hold, and this must be taken account of when designing the CV experiments in order to avoid severely biased CV results. Using large hold-out sets, in turn, raises the question of how to deal with basis vectors in the hold-out set, as it is not realistic to assume that predictions are made for data points that are at the same time among the basis vectors in training. Indeed, in our experiments, we show that not removing the basis vectors belonging to the hold-out set may also cause a serious bias in the CV results. Thus, in this types of learning tasks, our approach for efficiently removing basis vectors becomes indispensable.

The rest of the paper is organized as follows: In Sect. 2, we recall the concepts of supervised learning and discuss the issues of performance evaluation with hold-out and CV estimates. In Sect. 3, we formalize the RLS method. Section 4 considers the sparse RLS. Section 5 presents our algorithm for calculating a hold-out performance and, by that, different types of CV performance estimates for the sparse RLS. Section 6 describes the empirical part of our study and it contains both the evaluation setting and results. Section 7 concludes the paper.

2 Preliminaries

We first recall the concept of supervised learning. A supervised learner is a machine that is taught with a set of training data points with preferred output variables to perform a specific task. By a task, we mean the prediction of an output variable for an unseen data point. Formally, let $X=(x_{1},\ldots,x_{m})\in(\mathcal{X}^{m})^{\mathrm{T}}$ be a sequence of inputs and y∈ℝ^m a vector of outputs, where $\mathcal{X}$, called the input space, is the set of possible inputs. Here, $(\mathcal{X}^{m})^{\mathrm{T}}$ denotes the sets of row vectors, which contain m elements belonging to the set $\mathcal{X}$, while ℝ^m denotes the set of real valued column vectors of size m. Further, let S=(X,y) be a training set of m training instances. Unless stated otherwise, we assume that S is independently and identically distributed (i.i.d.) and drawn from an unknown probability distribution $\mathbb{D}$ over $\mathcal{X}\times\mathbb{R}$. Notice that while we call S a training set, it is actually an ordered sequence of data points.

Training a supervised learner can be seen as a process of selecting a function among a set of candidates that best performs the task in question. We assume that the algorithms under consideration may not be deterministic but randomized. That is, training a learner twice with the same training data set may result in two different learners. By following Elisseeff et al. (2005), we formalize the training algorithm as follows: An algorithm $\mathcal{A}$, which selects the function given the training set S of m instances, can be considered as a mapping

$$ \mathcal{A}{:}\quad (\mathcal{X}\times\mathbb {R})^{m}\times \mathcal{R} \rightarrow\mathcal{F},\qquad (S,r)\mapsto f,$$

(3)

where the hypothesis space $\mathcal{F}\subseteq\mathbb{R}^{\mathcal{X}}$ is a set of functions among which the algorithm selects an appropriate hypothesis $f\in\mathcal{F}$ and $\mathcal{R}$ is a space consisting of elements r modeling the randomization of the algorithm and is endowed with a probability measure ℙ. With $\mathbb{R}^{\mathcal{X}}=\{f\mid\mathcal{X}\rightarrow\mathbb{R}\}$ we denote the set of all functions from $\mathcal{X}$ to ℝ. We assume that $\mathcal{R}$ and ℙ do not depend on the training set but they may depend on m.

Let

$$p(f,z){:}\quad \mathcal{F}\times\mathcal{X}\rightarrow\mathbb{R}$$

denote the performance of a hypothesis $f:\mathcal{X}\rightarrow \mathbb{R}$ on example z=(x,y), that is, it measures how well the prediction f(x) approximates y. The performance function can be, for example, the squared loss (f(x)−y)².

Now let us consider a prediction function f returned by a randomized learning algorithm based on a fixed training set S and a fixed random seed r. We are interested in how well f will predict on unseen future data. This can be measured by the expectation of the performance p(f) on $\mathbb{D}$, that is

$$ \mathrm{E}_{z\sim\mathbb{D}}p(f,z).$$

(4)

We call this measure the expected performance of the predictor f. In the literature, this is sometimes called the true performance or conditional performance (Schiavo and Hand 2000) as it is conditioned on a fixed training set S and a fixed random seed r.

If we are interested in the performance of a learning algorithm $\mathcal{A}$ itself on the task under consideration, we need to measure the performance without tying it to a fixed training set or random seed:

$$ \mathrm{E}_{S\sim\mathbb{D}^{m},r\sim\mathbb{P},z\sim\mathbb{D}}p\bigl(\mathcal{A}(S,r),z\bigr).$$

(5)

In the literature, this is sometimes called the unconditional performance in contrast to the conditional one (Schiavo and Hand 2000). In this paper, we refer to (5) this as the expected performance of the learning algorithm $\mathcal{A}$.

As discussed for example by Dietterich (1998) and Schiavo and Hand (2000), the expected performances of predictor (4) and learning algorithm (5) correspond to two different statistical questions of interest. The former corresponds to the question of how well we expect a certain trained predictor to perform with future data points. This is of interest in majority of real world problems. The latter measures the quality of the learning algorithm itself in solving a learning task under consideration. That is, we assume a certain learning algorithm and train it with a data set of a given size. This results in a predictor and (5) indicates how well, on average, it generalizes to new data points. In addition, (5) can be useful in real world problems having a moving target, such as in the task of detecting junk mail, for example.

In practice, we can almost never directly access the probability distribution $\mathbb{D}$ to calculate (4) or (5). Rather, we are limited to their estimation instead. One such estimate is obtained from CV. Depending on the algorithm, it may be possible to access ℙ but it may still be difficult to calculate the expectation over it due to the computational reasons. Therefore, in order to measure (5), one has to rely on estimates obtained from a finite set of labeled data drawn from $\mathbb{D}$ and a finite set of random elements drawn from ℙ.

Let us first consider ways to compute estimates (5) with CV. Given a training set S of m examples, let $\mathcal{I}=\{1,\ldots,m\}$ denote an index set in which the indices refer to the instances in the training set. If the algorithm is trained with a randomly chosen r∈ℙ and with the training set of all but one example indexed by $\mathcal{I}$, and the performance is measured with the example which is not used in training, we get an estimate of (5) which is unbiased for training sets of size m−1. In addition to the unbiasedness, we would also prefer the estimate to have a small variance. This is achieved straightforwardly by averaging over several experiments of the above type. According to the central limit theorem, the average of such i.i.d. experiments approaches a normally distributed variable, whose variance decreases as the number of experiments increases.

However, in order to the experiments to be independent, we would have to sample a completely new training set, test instance, and r. This is not possible in real world situations, because of the lacking computational resources and having scarce data. Therefore, we usually have to permute our labeled data between training and testing when creating the sequence of experiments. This has the drawback that, while we can ensure the unbiasedness of the estimates of (5), the experiments are not completely independent. This complicates the theory and mathematics concerning the behavior of such estimates.

In CV or repeated hold-out, we have a sequence

$$ \bigl((\mathcal{H}_1,r_1,i_1),\ldots,(\mathcal{H}_t,r_t,i_t) \bigr)$$

(6)

of t experiments. In the jth, 1≤j≤t, experiment $(\mathcal{H}_{j},r_{j},i_{j})$, $\mathcal{H}_{j}\subset\mathcal{I}$ is the set containing the indices of examples in S that are not used for training, $r_{j}\in\mathcal{R}$, and $i_{j}\in\mathcal{H}_{j}$ is an index of an example in S used for testing. That is, in the jth experiment, the learner is trained with r _j and examples indexed by $\overline{\mathcal{H}}_{j}=\mathcal{I}\setminus\mathcal{H}_{j}$, and it is tested with example $z_{i_{j}}$. Note that the hold-out sets in (6) can overlap with each other partially or even completely. The CV performance estimate for a randomized learning algorithm can be written as

$$ \frac{1}{t} \sum_{j=1}^tp\bigl(\mathcal{A}(S_{\overline{\mathcal{H}_j}},r_j),z_{i_j}\bigr),$$

(7)

where $S_{\overline{\mathcal{H}_{j}}}$ denotes the sequence of training examples containing the ones in S indexed by $\overline{\mathcal{H}_{j}}$. If we assume that $|\mathcal{H}_{j}|=H\ \forall j\in \{1,\ldots,t\}$, then (7) is an unbiased estimator of the expected performance of the learning algorithm $\mathcal{A}$ for training sets of size m−H.

As an example, let us consider N-fold CV in which the training set is partitioned to N disjoint subsets of size H=m/N called CV folds. In N-fold CV, each example in the training set is used for testing at a time, and thus the number of experiments in the sequence (6) is t=m. Moreover, $i_{j}\in\mathcal{H}_{h}$ if and only if $\mathcal{H}_{h}=\mathcal{H}_{j}$, and $\mathcal{H}_{h}\cap \mathcal{H}_{j}=\emptyset$ if and only if $i_{j}\notin\mathcal{H}_{h}$, that is, each CV fold is used as a set $\mathcal{H}_{j}$ in H of the m experiments and each example associated to the CV fold is used once as a test example in one of the H experiments. In case of randomized algorithms, we often also require that r _h =r _j whenever $\mathcal {H}_{h}=\mathcal{H}_{j}$ in order to save training time. This is because the training has to be repeated only N times, once for each CV fold, and the same predictor can be used for several experiments in the sequence (6). Note that the notation also covers other types of CV approaches such as, say, N-fold CV repeated several times with different fold partitions (see e.g. Kohavi 1995). In repeated N-fold CV, a single data point can be used as a test example several times together with different sets $\mathcal{H}_{j}$, that is, for the jth and hth experiments, we may have i _j =i _h while $\mathcal{H}_{j}\neq\mathcal{H}_{h}$.

In addition to the unbiasedness, we would also prefer the CV estimators to have a small variance. The variance can be decreased by increasing the number of experiments we average over. However, the covariance between these experiments counters this aim. The variance of the CV estimator can be expressed via the sum of covariances between the experiments as follows:

$$ \operatorname{Var}(\mathit{CV}) =\frac{1}{t^2} \sum _{h,j=1}^t \operatorname{Cov} \bigl(p\bigl(\mathcal{A}(S_{\overline {\mathcal{H}_h}},r_h),z_{i_h}\bigr), p\bigl(\mathcal{A}(S_{\overline{\mathcal{H}_j}},r_j),z_{i_j}\bigr)\bigr),$$

(8)

where $\operatorname{Var}$ and $\operatorname{Cov}$ denote the variance and covariance, respectively. Here, the covariance between two experiments can be affected by several factors. Namely, the covariance depends on whether $z_{i_{h}}=z_{i_{j}}$, whether r _h =r _j , and how much $\overline{\mathcal {H}_{h}}$ overlaps with $\overline{\mathcal{H}_{j}}$. For a more detailed analysis of the covariance structures in case of deterministic algorithms, we refer to Nadeau and Bengio (2003).

Finally, let us briefly consider how to obtain estimates for the expected performance of the predictor f. This task is difficult without having a separate test set not used in the training phase (Dietterich 1998). We could use similar hold-out estimates as those used for estimating the expected performance of the learning algorithm $\mathcal{A}$ but they would be biased: holding out a subset of training examples means that the obtained predictor is not the same as the one, whose performance we aim to measure. Nevertheless, estimates based on hold-out are useful tools also for this purpose, since the bias is not necessarily severe, especially if the amount of training data is large. Still, care must be taken when designing the experiments as we show in Sect. 6.

3 Regularization framework

Next, we consider the hypothesis space $\mathcal{F}$. For this purpose we define so-called kernel functions. Let $\mathcal{X}$ denote the input space, which can be any set, and $\mathcal{P}$ denote the feature vector space. For any mapping $\varPhi:\mathcal{X}\rightarrow \mathcal{P}$, the inner product k(x,x′)=〈Φ(x),Φ(x′)〉 of the mapped data points is called a kernel function. We define the symmetric kernel matrix K∈ℝ^m×m, where ℝ^m×m denotes the set of real matrices of type m×m, and the entries of the kernel matrix are given by K _i,j =k(x _i ,x _j ). For simplicity, we assume that K is strictly positive definite. This can be ensured, for example, by performing a small diagonal shift.

Let a=(a ₁,…,a _m )^T∈ℝ^m be a vector determining a solution of (1) and let f _a (x) be the function determined by a. By overloading our notation, we write

$$k(x,X)=\bigl(k(x,x_1),\ldots,k(x,x_m)\bigr) \in\bigl(\mathbb{R}^m\bigr)^{\mathrm{T}},$$

where $x\in\mathcal{X}$. Using this type of matrix notation, we can write f _a (x)=k(x,X)a. Similarly, the column vector f _a (X)∈ℝ^m, that contains the label predictions of the training data points obtained with the function f _a , is f _a (X)=Ka. Further, according to the properties of the RKHS determined by the kernel k, the regularizer can be written as $\lambda\| f_{\mathbf{a}}\|_{k}^{2}=\lambda\mathbf{a}^{\mathrm{T}}\mathbf{K}\mathbf{a}$.

Using the matrix forms, we can rewrite (1) as

$$\mathcal{A}(S)=\mathop{\mathrm{argmin}}_{\mathbf{a}\in\mathbb {R}^m} \bigl\{(\mathbf{y}-\mathbf{K}\mathbf{a})^{\mathrm{T}} (\mathbf{y}-\mathbf{K}\mathbf {a}) +\lambda \mathbf{a}^{\mathrm{T}}\mathbf{K}\mathbf{a} \bigr\}.$$

The solution can be found by first taking a derivative of the objective function with respect to a, setting it to be zero, and solving with respect to a. As a solution, we obtain

$$ \mathbf{a}=(\mathbf{K}\mathbf{K}+\lambda \mathbf{K})^{-1}\mathbf{K}\mathbf{y}.$$

(9)

Due to the positive definiteness of K, the matrix KK+λ K is always invertible. Calculating the coefficient vector a from (9) involves an inversion of an m×m-matrix whose computational complexity is O(m ³) in the worst case.

4 The sparse regularized least-squares

The computational complexity of training an RLS learner, O(m ³), may be too tedious, if the number of training instances is large. However, several authors have considered sparse versions of RLS in which only a part of the training instances, often called the basis vectors, have a nonzero coefficient in (2). This means that when the training is complete, the rest of the training instances are not needed any more, when predicting the output variables of the new data points. Another advantage of the sparse RLS is that its training complexity is only O(mn ²), where n is the number of basis vectors. Further, as we will show below, there are efficient algorithms for CV and selection of the regularization parameter for sparse RLS that are analogous to the ones for the standard RLS.

As discussed above, we focus in this mainly on the random selection of basis vectors. We assume a uniform sampling of the n basis vectors among the training set of size m. That is, training sparse RLS can be considered as a randomized learning (3), where the random element r determines the set of basis vectors.

Before continuing, we introduce some notation. Let $\mathcal {M}_{\varXi \times\varPsi}$ denote the set of matrices whose rows and columns are indexed by the index sets Ξ and Ψ, respectively. With any matrix $\mathbf{M}\in\mathcal{M}_{\varXi\times\varPsi}$ and index set ϒ⊆Ξ, we use the subscript ϒ so that a matrix $\mathbf{M}_{\varUpsilon}\in\mathcal{M}_{\varUpsilon\times \varPsi}$ contains only the rows of M that are indexed by ϒ. For $\mathbf{M}\in\mathcal{M}_{\varXi\times\varPsi}$, we also use $\mathbf{M}_{\varUpsilon\varOmega} \in\mathcal{M}_{\varUpsilon \times \varOmega}$ to denote a matrix that contains only the rows and the columns that are indexed by any index sets ϒ⊆Ξ and Ω⊆Ψ, respectively.

We now follow Rifkin et al. (2003) and define the sparse RLS algorithm using the above defined notation. Recall that $\mathcal{I}=\{1,\ldots ,m\}$ denotes an index set in which the indices refer to the instances in the training set. Instead of allowing functions like in (2), we only allow

$$f(x)=\sum_{i\in\mathcal{B}} a_ik(x,x_i),$$

where the set $\mathcal{B}\subset\mathcal{I}$ indexing the basis vectors is selected in advance. In this case, the coefficient vector a can be considered as an n-dimensional vector, whose entries are indexed by $\mathcal{B}$. The label predictions for the training data points can be obtained from

$$ f_\mathbf{a}(X) =(\mathbf{K}_\mathcal {B})^{\mathrm{T}}\mathbf{a}$$

(10)

and the regularizer can be rewritten as $\lambda\mathbf{a}^{\mathrm{T}}\mathbf{K}_{\mathcal{B}\mathcal {B}}\mathbf{a}$. Therefore, with a given λ, the vector a is a minimizer of

$$ \bigl(\mathbf{y}-(\mathbf{K}_{\mathcal {B}})^{\mathrm{T}}\mathbf{a}\bigr)^{\mathrm{T}} \bigl(\mathbf{y}-(\mathbf {K}_{\mathcal{B}})^{\mathrm{T}}\mathbf{a}\bigr) +\lambda\mathbf{a}^{\mathrm{T}}\mathbf {K}_{\mathcal{B}\mathcal {B}}\mathbf{a}.$$

(11)

By setting the derivative of (11) with respect to a to zero, we get

$$ \mathbf{a}=\mathbf{P}^{-1}\mathbf {K}_{\mathcal{B}}\mathbf{y},$$

(12)

where

$$ \mathbf{P}=\mathbf{K}_{\mathcal{B}}(\mathbf {K}_{\mathcal {B}})^{\mathrm{T}}+\lambda\mathbf{K}_{\mathcal{B}\mathcal{B}} \in\mathcal {M}_{\mathcal{B}\times\mathcal{B}}.$$

(13)

The matrices $\mathbf{K}_{\mathcal{B}\mathcal{B}}$ and $\mathbf {K}_{\mathcal{B}}(\mathbf{K}_{\mathcal{B}})^{\mathrm{T}}=(\mathbf {K}\mathbf{K})_{\mathcal{B}\mathcal{B}}$ are principal submatrices of the positive definite matrices K and KK, respectively, and hence the matrix P is also positive definite and invertible (Horn and Johnson 1985, p. 397). In contrast to (9), the matrix inversion involved in (12) can be performed in O(n ³) time. Because n≪m, the overall computational complexity of (12) is dominated by the complexity of calculating $\mathbf{K}_{\mathcal{B}}(\mathbf{K}_{\mathcal{B}})^{\mathrm{T}}$ which is O(mn ²).

We now reformulate sparse RLS so that its coefficient matrix can be efficiently calculated for different values of the regularization parameter. Notice that this reformulation is already known in the machine learning community. Let

$$ \mathbf{K}_{\mathcal{B}\mathcal {B}}=\mathbf{C}\mathbf{C}^{\mathrm{T}}$$

(14)

be the Cholesky factorization of $\mathbf{K}_{\mathcal{B}\mathcal{B}}$, where $\mathbf{C}\in\mathcal{M}_{\mathcal{B}\times\mathcal{B}}$ is a lower triangular matrix with strictly positive diagonal entries. Moreover, let

$$ \mathbf{C}^{-1}\mathbf{K}_{\mathcal{B}}(\mathbf{K}_{\mathcal {B}})^{\mathrm{T}} \bigl(\mathbf{C}^{-1}\bigr)^{\mathrm{T}}=\mathbf{V}\boldsymbol{\varLambda}\mathbf {V}^{\mathrm{T}}$$

(15)

be the eigendecomposition of $\mathbf{C}^{-1}\mathbf{K}_{\mathcal{B}}(\mathbf{K}_{\mathcal {B}})^{\mathrm{T}}(\mathbf{C}^{-1})^{\mathrm{T}}$, where $\mathbf{V}\in\mathcal{M}_{\mathcal{B}\times\mathcal{B}}$ is the matrix containing the eigenvectors and $\boldsymbol{\varLambda}\in\mathcal{M}_{\mathcal{B}\times\mathcal{B}}$ is a diagonal matrix containing the eigenvalues of the decomposition. Further, we define

(16)

Then, the matrix P ⁻¹ can be expressed as

(17)

The computational complexities of calculating (14), (15) and (16), are O(n ³) (see, e.g., Golub and Van Loan 1989 for in depth discussion of the computational complexities of the decompositions).

Finally, let us first calculate $\mathbf{Q}^{\mathrm{T}}\mathbf {K}_{\mathcal{B}}\mathbf{y}$ (in O(mn) time) and store it in the memory. After this, (12) can be computed for different values of the regularization parameter from $\mathbf {a}=\mathbf{Q}\widetilde{\boldsymbol{\varLambda}}\mathbf {Q}^{\mathrm {T}}\mathbf{K}_{\mathcal{B}}\mathbf{y}$ with the complexity of O(n ²). This is because the multiplication of the shifted and inverted eigenvalues $\widetilde{\boldsymbol{\varLambda}}$ with $\mathbf{Q}^{\mathrm{T}}\mathbf{K}_{\mathcal{B}}\mathbf{y}$ can be performed in O(n) time and the multiplication of the resulting matrix from left by Q can be performed in O(n ²) time.

5 Fast computation of hold-out error

For a start, we note (see, e.g., Quiñonero-Candela and Rasmussen 2005) that the sparse approach can also be considered as performing the standard RLS regression using the modified kernel function

$$ \tilde{k}\bigl(x,x'\bigr)=k(x,X) (\mathbf{K}_{\mathcal{B}\mathcal{B}})^{-1} k(X,x).$$

(18)

Therefore, a straightforward way to construct hold-out estimates for sparse RLS would be to use the hold-out algorithms proposed by Pahikkala et al. (2006a), An et al. (2007) for the standard RLS regression with the modified kernel function (18). The computational complexity of this approach is $O(|\mathcal{H}|^{2}m)$, where m is the number of training examples and $|\mathcal{H}|$ is the size of the hold-out set. The presence of the coefficient m may make it computationally too expensive in practice and especially for CV estimates. Further, if a data point in the hold-out set is a basis vector, its effect is not completely removed from the training process, because the kernel (18) depends on it.

We now derive an algorithm for calculating a hold-out performance and, by that, a CV performance for sparse RLS. The computational complexity of computing the CV performance with our algorithm is no larger than the complexity of training sparse RLS. The algorithm presented in this section improves our previously proposed one (Pahikkala et al. 2009b). Recall that $\mathcal{I}=\{1,\ldots,m\}$ is the index set for the whole training data set and $\mathcal{B}\subset\mathcal{I}$ is the set indexing the basis vectors. Let

$$\mathcal{H}\subset\mathcal{I}$$

denote the set of indices of the hold-out data points, and let

$$\overline{\mathcal{H}}=\mathcal{I}\setminus\mathcal{H},\qquad \mathcal {E}=\mathcal{H}\cap\mathcal{B},\quad\mbox{and}\quad \mathcal{L}=\overline {\mathcal{H}}\cap\mathcal{B}.$$

Further, let $f_{\overline{\mathcal{H}}}=\mathcal{A}(S_{\overline {\mathcal{H}}})$ be the predictor obtained by training the sparse RLS algorithm with the training set $S_{\overline{\mathcal{H}}}$ from which the training instances indexed by $\mathcal{H}$ are removed. Then, $f_{\overline{\mathcal{H}}}(X_{\mathcal{H}})$ consists of the predictions for the hold-out data points $X_{\mathcal{H}}$ that are predicted by $f_{\overline{\mathcal{H}}}$. According to (12), the coefficient vector corresponding to $f_{\overline{\mathcal{H}}}$ is $\mathbf{G}^{-1}\mathbf {K}_{\mathcal{L}\overline{\mathcal{H}}}\mathbf{y}_{\overline {\mathcal{H}}}$, where $\mathbf{G}=\mathbf{K}_{\mathcal{L}\overline {\mathcal{H}}}\mathbf{K}_{\overline{\mathcal{H}}\mathcal{L}}+\lambda\mathbf{K}_{\mathcal{L}\mathcal{L}}$. The entries of this coefficient vector are indexed by $\mathcal{L}$. Therefore, according to (10), the output values corresponding to the hold-out set $\mathcal{H}$ can be obtained from

$$ f_{\overline{\mathcal{H}}}(X_\mathcal{H})=\mathbf{K}_{\mathcal{H}\mathcal{L}}\mathbf{G}^{-1} \mathbf{K}_{\mathcal{L}\overline{\mathcal{H}}}\mathbf{y}_{\overline{\mathcal{H}}}.$$

(19)

This is, of course, too cumbersome to be used in CV, but fortunately, it is possible to calculate the outputs more efficiently, if we have trained in advance the sparse RLS with the whole data set.

Proposition 1

Suppose that we have trained a sparse RLS predictor by calculating (14), (15) and (16) with the whole data set indexed by $\mathcal{I}$, and we have the following matrices stored in memory:

(20)

(21)

(22)

(23)

(24)

(25)

Let us assume that $\mathcal{E}= \mathcal{H}\cap\mathcal{B}\neq \emptyset$. Then, the hold-out predictions for a set $\mathcal{H}$ can be calculated from

$$ f_{\overline{\mathcal{H}}}(X_\mathcal{H})=-(\mathbf{J}-\mathbf{I})^{-1}\mathbf{r},$$

(26)

where

(27)

(28)

(29)

(30)

(31)

(32)

The computational complexity of this calculation is $O(\min(|\mathcal{H}|^{2}n,|\mathcal{H}| n^{2}))$.

Proof

We start by showing the tenability of (26) and continue by considering the computational complexities. Recall from (19) that the output matrix for the hold-out set can be obtained from

$$ f_{\overline{\mathcal{H}}}(X_\mathcal{H})=\mathbf{K}_{\mathcal{H}\mathcal{L}} \mathbf{G}^{-1} \mathbf {K}_{\mathcal{L}\overline{\mathcal{H}}}\mathbf{y}_{\overline{\mathcal{H}}},$$

(33)

where

and P is defined in (13). Now, due to the positive definiteness of K, both G and $\mathbf{P}_{\mathcal{L}\mathcal{L}}$ are always invertible. Let

$$\mathbf{W}=(\mathbf{P}_{\mathcal{L}\mathcal{L}})^{-1}.$$

Using the block inverse formula (see e.g. Horn and Johnson 1985) we get

$$ \mathbf{W} =\bigl(\mathbf{P}^{-1}\bigr)_{\mathcal{L}\mathcal{L}} -\bigl(\mathbf{P}^{-1}\bigr )_{\mathcal{L}\mathcal{E}}\bigl(\bigl(\mathbf{P}^{-1}\bigr)_{\mathcal{E}\mathcal{E}}\bigr)^{-1}\bigl(\mathbf{P}^{-1}\bigr)_{\mathcal{E}\mathcal{L}}.$$

(34)

Further, using the Sherman-Morrison-Woodbury (SMW) formula (see e.g. Horn and Johnson 1985), we obtain

(35)

The invertibility of the matrix $-\mathbf{I}+\mathbf{K}_{\mathcal{H}\mathcal{L}}\mathbf{W}\mathbf {K}_{\mathcal{L}\mathcal{H}}$ follows from the invertibility of G and from the Schur’s determinantal formula (see e.g. Horn and Johnson 1985, p. 21).

According to (34), (17), and (29), we get

Analogously, according to (34), (17), and (31), we get

$$\mathbf{K}_{\mathcal{H}\mathcal{L}}\mathbf{W} \mathbf{K}_{\mathcal {L}\overline{\mathcal{H}}}\mathbf {y}_{\overline{\mathcal{H}}} =\mathbf{r}.$$

Finally, we substitute (35) into (33) and we get

We now consider the computational complexity of using (26). The matrix U can be calculated from (20), (22), and (23) using (30) in $O(\min(|\mathcal{H}|^{2}n,|\mathcal{H}|n^{2}))$ time, because $|\mathcal{E}|\leq\min(|\mathcal {H}|,|\mathcal{B}|)$. Moreover, the matrix z can be calculated from (20), (22), (23), (24), and (25) using (32) in $O(|\mathcal {H}| n)$ time. The computational complexity of calculating J and r using (27) and (28) is $O(|\mathcal{H}|^{3}+|\mathcal {H}|^{2}n)$. This is because multiplication of an $|\mathcal{H}|\times n$ -matrix with a diagonal matrix $\widetilde{\boldsymbol{\varLambda}}$ can be computed in $O(|\mathcal{H}| n)$ time, the matrix inversion involved in the calculations needs $O(\min(|\mathcal{H}|^{3},n^{3}))$ time, and all the other matrix products need at most $O(\min(|\mathcal{H}|^{2}n,|\mathcal {H}| n^{2}))$ time, if performed in the optimal order. Finally, we substitute these matrices into (26). Now if $n\geq|\mathcal{H}|$, we obtain the solution by inverting the matrix I−J in $O(|\mathcal{H}|^{3})$ time. However, if $n<|\mathcal {H}|$, the inversion can still be accelerated by taking advantage of the SMW formula. Namely, we can write J=AB, where A and B are the following $|\mathcal{H}|\times n$ and $n\times |\mathcal{H}|$ matrices:

Then, we have

$$ (\mathbf{I}-\mathbf{A}\mathbf{B})^{-1} =\mathbf{I}-\mathbf{A}(-\mathbf{I}+\mathbf{B}\mathbf {A})^{-1}\mathbf{B},$$

(36)

where the identity matrices are of conformable size. The right hand side of (36) can be computed in $O(|\mathcal {H}| n^{2}+n^{3})$ time, and hence the complexity of inverting the matrix I−J becomes $O(\min(|\mathcal{H}|^{2}n,|\mathcal{H}| n^{2}))$ time, as we can choose whether to use the right or the left side of (36). □

The above proposition concerns the case in which $\mathcal{E}\neq \emptyset$, that is, the basis vectors that belong to the hold-out set are removed from the basis vector set, and hence the predictions for the hold-out examples are performed with a predictor trained with training examples indexed by $\overline{\mathcal{H}}$ and with basis vectors indexed by $\mathcal{L}$. Next, we consider an approach for the case in which $\mathcal{E}= \emptyset$. Note that, this approach can also be used if we do not intend to remove the basis vectors indexed by $\mathcal{E}$, that is, the predictions for the hold-out examples would be performed with a predictor trained with training examples indexed by $\overline{\mathcal{H}}$ and with basis vectors indexed by $\mathcal{B}$, even if $\mathcal{E}\neq\emptyset$. This is accomplished by setting the index set $\mathcal{E}$ to empty. We formulate the approach as a corollary to the above proposition.

Corollary 2

Proposition 1 also holds, if $\mathcal{E}=\emptyset$.

Proof

If $\mathcal{E}= \emptyset$, then $\mathbf{J}=\mathbf{U}\widetilde{\boldsymbol{\varLambda}}\mathbf {U}^{\mathrm{T}}$, $\mathbf{r}=\mathbf{U}\widetilde{\boldsymbol{\varLambda}}\mathbf{z}$, $\mathbf{U}=((\mathbf{K}_{\mathcal{B}})^{\mathrm{T}}\mathbf {Q})_{\mathcal{H}}$, and $\mathbf{z}=\mathbf{Q}^{\mathrm{T}}\mathbf{K}_{\mathcal{B}}\mathbf{y}-(\mathbf{Q}^{\mathrm{T}}\mathbf{K}_{\mathcal{B}})_{\mathcal{B}\mathcal{H}}\mathbf {y}_{\mathcal{H}}$. The corollary can be proved the same way as Proposition 1 except the use of the above matrices simplifies the computation of $\mathbf{K}_{\mathcal{H}\mathcal{L}}\mathbf {W}\mathbf{K}_{\mathcal{L}\mathcal{H}}$ and $\mathbf{K}_{\mathcal {H}\mathcal{L}}\mathbf{W}\mathbf{K}_{\mathcal{L}\overline{\mathcal{H}}}\mathbf {y}_{\overline{\mathcal{H}}}$. □

We further note that the calculation of matrices (20)–(25) requires O(mn ²) time, and hence the training of the sparse RLS as in Proposition 1 is computationally as efficient as the training in the ordinary way. Here it is, of course, again presupposed that the set of basis vectors used in the hold-out computation is a subset of the set of basis vectors used in computing the matrices.

We next consider different estimators for the expected performance of the learning algorithm (5) that can be constructed with our efficient hold-out algorithm. In order to minimize the variance of the performance estimator obtained by averaging over the sequence of experiments (6), we should average over as many experiments as we can afford with our computational resources, while also minimizing the covariance (8) between the experiments. Analogously to the deterministic learning algorithms, the covariance between two experiments usually increases if the overlap between the training sets increases. Similarly, the covariance is larger if the test instance is the same in the two experiments than if the test instance is different.

The randomized part of our learning algorithm is determined by the random selection of the set of the basis vectors. Intuitively, the covariance between two experiments increases if the overlap between the sets of basis vectors increases. Therefore, we should preferably have experiments, where sets of basis vectors overlap with each other as little as possible. However, this counters the efficiency requirement, because training with different sets of basis vectors requires a lot of computational resources. Nevertheless, via our efficient hold-out method, we can vary the set of basis vectors by holding out different subsets of the original basis vector set in different experiments. These effects are investigated more in detail in our experiments in Sect. 6.

Since in N-fold CV the training set is partitioned into N parts of approximately equal size, the number of training instances in each fold is $|\mathcal{H}|\approx m/N$. Then, CV is performed by using each fold as a hold-out set at a time and calculating the corresponding hold-out label predictions. According to Proposition 1, the computational complexity of each CV round is $O(\min(|\mathcal{H}|^{2}n,|\mathcal{H}|n^{2}))$, and hence we get the following corollary:

Corollary 3

The overall computational complexity of the N-fold CV is $O (\min(m|\mathcal{H}| n,\allowbreak mn^{2}) )$. Further, the computational complexity of LOOCV is O(mn) if combined with the training process of the sparse RLS predictor.

Thus, we observe that the computational complexity of N-fold CV is at most the training time of a sparse RLS predictor. The method is less complex for smaller hold-out sets (especially so for the extreme case of LOOCV) and it can be used, for example, to select the value of the regularization parameter λ efficiently from its candidate values. We formalize this in the following result:

Corollary 4

Let c be the number of candidate values for the regularization parameter λ. The computational complexity of calculating the N-fold CV output for all different candidate values is $O (c\min(m|\mathcal{H}| n,mn^{2}))$. Further, the analogous computational complexity for LOOCV is O(cmn).

Thus, if $c|\mathcal{H}|\leq n$, the selection of the regularization parameter via CV is not computationally more complex than the training process of sparse RLS.

The above considerations can be generalized for RLS that can be simultaneously trained to predict multiple outputs. This is achieved by using, instead of the label vector y, a label matrix having v columns, where v is the number of outputs. It is straightforward to see from (12) that the complexity of training a sparse RLS predictor for v outputs is O(mn(n+v)). Now, we may want to compute CV for each output separately. This gives us the following corollary:

Corollary 5

The computational complexity of calculating the N-fold CV output for all of the v outputs is $O (v\min(m|\mathcal{H}| n,mn^{2}))$. Further, the analogous computational complexity for LOOCV is O(vmn).

Again, if $v|\mathcal{H}|\leq n$, computing CV for v outputs is dominated by the training complexity.

6 Experiments

In Sect. 6.1, we measure the speed of the proposed hold-out approach in selection of hyperparameters with LOOCV. In Sect. 6.2, we compare three unbiased estimators of the expected performance of the sparse RLS learning algorithm and confirm our hypothesis of obtaining a lower variance for the performance estimate by varying the set of basis vectors in each CV round. Section 6.3 deals with experiments using artificially generated data. In Sect. 6.3.1, we repeat the experiments of Sect. 6.2 with a larger number of basis vectors. The bias on CV results caused by greedy selection of basis vectors is measured in Sect. 6.3.2. In Sect. 6.4, we consider the issues related to measuring the expected performance of a sparse RLS predictor.

6.1 Speed comparisons

To test the computational speed of the proposed CV method in practice, we make an experimental speed comparison between that and the fastest previously proposed CV approach for sparse RLS, the O(mn ²) time LOOCV algorithm proposed by Cawley and Talbot (2004). We only test LOOCV without removing the basis vectors, because the baseline method is defined only for that setting. To implement the algorithms, we use NumPy, a computationally efficient scientific computing library for Python programming language. As a test platform, we use a single core of an AMD Phenom II X6 1090T Processor. The speed comparisons are done with an artificially generated data set of 5000 examples and the number of basis vectors is varied as 500, 1000, 1500, 2000, and 2500.

We first measure the time spent for a single LOOCV run. The results are shown in Table 1. As expected, both approaches scale quadratically with respect to the number of basis vectors. The running time of the new approach is about twice as long as that of the previously proposed approach. This is due to the computation of the cache matrices required for the efficient CV computations and retraining with different regularization parameter values. Next, we measure the time spent for computing the LOOCV with the new method after the caches have already been computed. We observe that this time is negligible compared to the time required for constructing the caches. Finally, we measure the overall time required for performing a cross-validated selection of the regularization parameter λ with a set of 20 candidate values, that is, the time includes 20 LOOCV runs with different values of λ. The baseline method is run from scratch for each value of λ, while the caches used by the new method are only constructed once as the same caches can be used for each LOOCV run as shown in Sect. 5. Because of the negligible LOOCV time of the new approach, the overall hyperparameter selection time is about the same as the time spent for a single LOOCV run. For the baseline method, this is not the case and the hyperparameter selection time is 20 times longer than the time spent for a single LOOCV run as the baseline method saves only the time required for constructing the kernel matrix.

Table 1 The running times in CPU seconds of the baseline (Method 1) and the proposed algorithm (Method 2) with different amounts of basis vectors. The first two rows contain the time spent in combined training and LOOCV. The third row presents the LOOCV time of the proposed algorithm after a RLS learner has been trained. The last two rows contain the overall time spent in cross-validated selection of the regularization parameter λ for the two methods

To conclude, the proposed approach for LOOCV requires some extra computational resources for filling the caches required for computing LOOCV and performing hyperparameter selection. However, after the caches have been constructed once, the hyperparameter selection can become orders of magnitude faster that done without the caches if the regularization parameter is searched from a large grid.

6.2 Variance in estimates of expected performance of the learning algorithm

Here, we consider using N-fold CV for measuring the expected performance of the sparse RLS learning algorithm. We select the basis vectors randomly via uniform sampling from the training set. This causes some extra variance to the performance estimates in addition to the variability caused by the training set and unseen test examples. Taking the variability caused by the basis vector set into account can be accomplished, for example, by averaging over many hold-out experiments for which the set of basis vectors is randomly reselected. However, this requires the sparse RLS to be completely retrained for each CV round, which may be prohibitive in practice, especially if the number of CV rounds is large as in the case of LOOCV. With our hold-out method, taking the variability into account can still be achieved to some extent if holding out a subset of the basis vectors in each CV round.

For example, let us assume that we aim to use ten-fold CV to estimate the prediction performance of sparse RLS algorithm which randomly selects n basis vectors. We start by training sparse RLS predictor with 11n/10 randomly selected basis vectors. Then, we hold out n/10 of the basis vectors and one tenth of the non-basis vectors in each round. Consequently, this CV estimate provides an approximation of the standard CV estimate in which one tenth of the basis vectors is changed in each round instead of the whole set of basis vectors being changed. Compared to selecting the basis vectors randomly and separately for each CV round, this approach retains the computational efficiency, because we have no need to train RLS again with new basis vectors. Note also that as the original set of 11n/10 basis vectors is randomly selected from the original training set, the set of n basis vectors not belonging to a hold-out set can be considered to be randomly selected from the training examples not in the hold-out set. Thus, the hold-out experiment provides an unbiased estimate of the prediction performance of sparse RLS algorithm which randomly selects n basis vectors, and hence the average of the ten hold-out experiments also provides unbiased estimates.

We test the variability caused by the basis vector selection in four regression tasks: Ailerons, Elevators, Pole Telecomm and Pumadyn.⁴ Ailerons contains 7,154 instances and forty features per instance. The respective numbers are 8,752 and eighteen for Elevators; 5,000 and 48 for Pole Telecomm; and 4,499 and 32 for Pumadyn. In a pre-processing step, we scale the values to be regressed in the Ailerons and Elevators tasks by a factor of 1,000 because they are very small.

The kernel matrix K is formed by using a Gaussian radial basis function kernel k(x,x′)=exp(−γ|x−x′|²), where γ∈ℝ is a positive constant determining the width of the kernel. We select a suitable value for γ in a preliminary experiment for each data set (i.e., Ailerons γ=2⁻¹⁸, Elevators γ=2⁻¹⁹, Pole Telecomm γ=2⁻¹², Pumadyn γ=2⁻²¹) and use this value in the actual experiment. We ensure the positive definiteness of K by shifting it diagonally with 10⁻⁷ I, where the identity matrix I has the same order as K. In addition, we found shifting to reduce numerical errors. The tested domain for the regularization parameter λ is {2⁻¹⁵,…,2⁴} in all four tasks.

We test the following three approaches for estimating the expected performance of the sparse RLS learning algorithm in the four tasks:

• 1. Approach 1: We select thirty basis vectors randomly from the training set. Then, the training set is divided randomly into ten folds so that each fold contains three basis vectors. Finally, the sparse RLS regressor is trained and CV error is computed using the fold partition.

• 2. Approach 2: We select randomly 27 basis vectors and divide the training set randomly into ten folds so that no basis vectors are included in any fold.

• 3. Approach 3: We divide the training set randomly into ten folds. The CV estimate is obtained by selecting 27 basis vectors randomly among the examples not in the hold-out set, separately for each CV round.

Each approach is tested one hundred times with different fold partitions and different sets of basis vectors.

In all three approaches, the hold-out computations in the CV rounds correspond to the situation in which a sparse RLS regressor trained with 27 basis vectors is performing predictions for the hold-out instances. This also holds for Approach 1, where the predictor is originally trained with 30 basis vectors but three of them is held out during each CV round. The sizes of the hold-out sets are approximately m/10 in the first and third experiment and (m−27)/10 in the second one. This difference is negligible when m is large as it is in all our approaches.

The main difference between the three approaches is that three basis vectors are switched in each CV round in Approach 1, the basis vectors are the same in each CV round in Approach 2, while the sets of basis vectors may be completely different between the CV rounds in Approach 3. Thus, each of the three approaches is an unbiased estimator of the expected performance of the sparse RLS learning algorithm used with 27 randomly selected basis vectors. However, the variance of the estimates is likely to differ between the three approaches, because there are different types of dependences present between the CV rounds.

With the 100 repetitions, we estimate the variability of CV estimates caused by the selection of the basis vectors together with the fold partition in the training set. Note that these are not the whole variances of the three estimates. In order to measure the complete variability of the estimates, we should have new data sets drawn from the underlying distribution for each of the one hundred repetitions. Nevertheless, these experiments are sufficient for our purposes, since we are especially interested in the variance caused by the random selection of basis vectors.

We use the mean squared error (MSE) as a performance evaluation measure, and compute the variance estimate with the following formula: $\frac{1}{1-r}\sum_{i=1}^{r}(\mathit{MSE}^{(i)}-\mu)^{2}$, where r is the number of repetitions, $\mathit{MSE}^{(i)}$ is MSE obtained from the ith repetition, and μ is the mean CV error estimated from the sample of repetitions.

Comparing the variances in the three experiments provides supportive evidence on our hypothesis of obtaining a smaller variance for the CV estimate by varying the set of basis vectors in each round (Figs. 1, 2, 3, and 4). From the MSEs, we observe that the predictors underfit with large values of the regularization parameter, while some minor overfitting happens with the Pumadyn data set with the smallest parameter values. As expected, the estimators, where the basis vectors are separately selected in each CV round have the smallest variances caused by the basis vector selection and fold partition. In addition, the estimates in which some of the basis vectors are changed in each round have smaller variances than the estimates that have a constant set of basis vectors. Since all three approaches are unbiased estimators of the expected performance of the sparse RLS algorithm, the MSEs averaged over the one hundred repetitions are about the same, though some differences can be observed with the Pole Telecomm data set. The differences are due to the variance of the estimators and, indeed, the variances corresponding to the Pole Telecomm task are the largest among the four tasks.

Fig. 1

Mean and variance of the hundred MSEs as a function of log₂ λ in the three approaches in the Ailerons task

Fig. 2

Mean and variance of the hundred MSEs as a function of log₂ λ in the three approaches in the Elevators task

Fig. 3

Mean and variance of the hundred MSEs as a function of log₂ λ in the three approaches in the Pole Telecomm task

Fig. 4

Mean and variance of the hundred MSEs as a function of log₂ λ in the three approaches in the Pumadyn task

To conclude, in order to decrease the variance of the CV estimate of the expected performance of the sparse RLS algorithm, one can change the set of basis vectors in the CV rounds. However, changing the set completely in each round may be computationally too expensive, because it corresponds to completely retraining the predictor in each round. Nevertheless, the variance can be decreased to some extent by changing a small subset of the basis vectors per CV round as is done in Approach 1, while this does not require more computational resources than training the predictor only once.

6.3 Experiments with simulated data

6.3.1 Experiments using a larger number of basis vectors

To study the behavior of the three approaches considered in Sect. 6.2 in a task where the selection of the regularization parameter plays a more important role than in the previous experiments, we perform a similar test on a regression task in which the data is artificially generated. By generating a new data set from scratch for each repetition of the experiment, we also obtain more comprehensive view of the variance caused by sampling the training data from the underlying distribution.

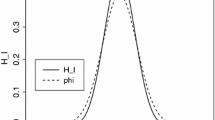
The function to be learned is a sinusoid contaminated with Gaussian noise with standard deviation 2. The data points are uniformly sampled from the interval [−20,20]. The test is done with 10-fold cross-validation, using 270 basis vectors and with overall number of training examples being 3000. Again, we used the Gaussian kernel. In this experiment, the whole data set is resampled for each repetition used in the variance estimation. Because of this, the variability of the estimates is considerably larger than in the experiments done with the real world data sets, and therefore we increased the number of repetitions to 1000. An example of a randomly sampled data and the learned function is given in Fig. 5. The mean and variance of this experiment for different values of the regularization parameter are depicted in Fig. 6.

Fig. 5

An example of a randomly sampled 3000 data points (circles), 300 basis vectors (filled circles), the target function (dashed line) and the learned function (solid line)

Fig. 6

Mean and variance of the thousand MSEs as a function of log₂ λ in the three approaches in the sinusoid task

From the behavior of the mean, one can easily observe that the learning process overfits with the small values of the regularization parameter, underfits with large values and the optimal values are in the middle, namely the values around 2⁵. However, unlike in the experiments with the real world data, Approach 3 does not seem to express smaller variance than Approach 1 for all values of the regularization parameter. The large variance of Approach 2 can be explained by the fact that since the basis vectors are never included in the hold-out sets and the ratio between the number of basis vectors and the size of the training set is about 1/10, the size of the hold-out sets are one tenth smaller than those in the other approaches. Otherwise, we can conclude that the variation of the set of basis vectors does not play as important role in the sinusoid experiment as it does with the four experiments done with real world data sets, and hence the effect is very much dependent on the application. Thus, it is possible to be able to decrease the variance of CV results by varying the set of basis vectors between CV rounds somewhat, but in most cases, a fixed set of basis vectors works well enough.

6.3.2 Bias caused by basis vector selection outside CV loop

In many cases, it makes sense to use a clever heuristic for selecting the basis vectors than the completely random selection. This can increase the prediction performance considerably or the same prediction performance can be achieved with much smaller amount of basis vectors than with random selection. The downside of the heuristic-based selection is that they are often computationally more complex than the random selection (Rifkin et al. 2003; Kumar et al. 2009).

To test the usability of the CV methods with typical basis vector selection algorithms, we implemented a randomized greedy forward selection method which is similar to the one proposed by Smola and Bartlett (2001). The pseudo code of the method is given in Algorithm 1. In short, the selection method starts from an empty set of basis vectors and iteratively adds one vector at a time until n have been selected. During each iteration, the method first draws randomly a set of 60 candidate basis vectors which have not yet been selected. From the 60 candidates, the method then selects the one which improves the training error the most. That is, for each candidate h, a sparse RLS is trained with basis vectors $\mathcal{B}\cup\{h\}$, where $\mathcal{B}$ denotes the set of basis vectors selected so far, and tested with the training data, and the candidate whose inclusion to the basis vector set provides the lowest error on the training data is selected. In the algorithm description, the function TrainingErr denotes the error on the training set made by the sparse RLS trained using the given set of basis vectors. The constant 60 is based on the idea that to find a basis vector that is with probability 0.95 among the best 0.05 ones of all possible basis vectors, it is enough to search it among a random sample of size 60. We also note that, while the RLS has to be retrained 60 times during each round of the greedy selection, the training process can take advantage of the RLS predictor trained in the previous selection round using computational short-cuts based on matrix algebra as shown by Smola and Bartlett (2001). Nevertheless, the greedy selection method is still considerably slower than the method based on completely random selection.

Algorithm 1

Randomized Greedy Selection of n Basis Vectors

We run the same three approaches as above but this time using the basis vectors selected with the randomized greedy method. With Approaches 1 and 2, respectively, 30 and 27 basis vectors are selected first on the whole training set and ten-fold CV is run afterwards. With Approach 3, 27 basis vectors are separately selected in each round of the ten-fold CV with Algorithm 1. This experiment is also repeated with a larger number of basis vectors, namely 300 and 270 depending on the approach. Since the basis vector selection is done outside the CV loop in the two first approaches, we expect the CV results to be optimistically biased, while this should not be the case with Approach 3. The three approaches are again repeated 1000 times and the sinusoid data is regenerated for each repetition. The mean and the variance of the repetitions are illustrated for different values of the regularization parameter in Fig. 7.

Fig. 7

Mean and variance of the thousand MSEs as a function of log₂ λ in the three approaches in the sinusoid task and basis vectors selected with the randomized greedy method, with 27 basis vectors (top) and 270 (bottom)

From the results, we observe that, as expected, the performances of Approaches 1 and 2 with a small number of basis vectors are optimistically biased compared to that of Approach 3. With a large number of basis vectors, Approach 1 does not seem to suffer from the bias anymore, while Approach 2 still does. Thus, removal of the basis vectors during CV rounds seems to counter the bias at least in some cases. With these experiments, the bias does not seem to be considerably serious if the CV results are used, for example, for parameter selection. Nevertheless, as observed from the results, the size of the bias can depend a lot on the experimental setting and we have no good means for predicting it in advance. To conclude, the proposed CV short-cuts should be used with basis vector selection with caution but the results may still be useful as approximate performance estimates if one needs to save the computational resources required in the re-selection of the basis vectors in each CV round, especially if LOOCV is used.

6.4 Bias caused by basis vectors in hold-out set

In order to use CV for measuring the expected performance of a fixed sparse RLS predictor learned from a certain training set and a certain set of basis vectors, the predictor learned without the hold-out set should be as close as possible to the fixed predictor under consideration. The smaller the hold-out sets are, the smaller is the change in the predictor in most of the practical cases. LOOCV is usually a good choice, because the hold-out sets are as small as possible. Moreover, the original set of basis vectors should be used during CV, since changing the set may change the predictor even more than holding out some training examples.

We address empirically the question of handling the basis vectors in the hold-out computations and consider the following three approaches:

• (i) We can remove the hold-out example from the basis vector set. This may change the predictor too much which, in turn, may increase the bias of the performance estimate.

• (ii) If the training data set is large—as it is in cases where sparse algorithms are needed—it is reasonable to skip the training examples that are also basis vectors in LOOCV in order to avoid biased results. This may cause a slight increase in the variance of the performance estimate, since the whole data set is not used in CV but the increase is usually tolerable because of the small size of the basis vector set compared to the training set size.

• (iii) The example can be kept in the basis vector set, while its effect is removed from the squared error. This may lead to a bias, because the data points for which the prediction is to be made do not usually belong to the set of basis vectors.

Since sparse RLS is usually used when the amount of training data is large, the second approach is usually preferred. However, tasks in which the training set violates the often made i.i.d. assumption are common. In such cases, one must pay careful attention on the experimental setup in order to avoid biased results caused by the dependencies.

As an example of a task, where the training set contains certain dependency structures, we consider the following regression problem. Given a sentence taken from a free text document, an automatic parser is employed to generate a set of alternative parses of the sentence. Some of the generated parses describe the syntactic structure of the sentence more correctly than the others. To reflect this correctness, a regressor is used to predict scoring for the parses. The regressor is learned from a training set, which is in turn constructed from a set of sentences and the parses extracted from the sentences. Due to the feature representation of the parses, two parses originating from a same sentence have almost always larger mutual similarity than two parses originating from different sentences. Hence, the data set consisting of the parses is heavily clustered according to the sentences the parses were generated from and this clustered structure of the data has a strong effect on the performance estimates obtained by CV. This is because the data instances that are in the same cluster as the hold-out instance have a dominant effect on the predicted output of the hold-out instance. This does not, however, model the real world use, because a regressor is usually not trained with parses originating from the sentence from which the new parse with an unknown score value is originated. The problem can be solved by performing CV on the sentence level so that all the parses generated from a sentence would always be either in the training set or in the test set.

With sparse RLS, performing CV on sentence level is still not the whole story, though. Consider the case in which the aim to use CV in order to estimate the prediction performance of the regressor trained with the available data set. Moreover, consider a hold-out set consisting of all the parses associated to a single sentence. Further, one of the examples in the hold-out set belongs to the set of basis vectors. The question still left open is whether the hold-out examples should also be removed from the set of basis vectors or not. On one hand, removing one example from the set of basis vectors in hold-out computation counters the aim of measuring the performance of the regressor trained with the whole data set, because removing a basis vector may change the regressor even more than only removing some of the training examples. On the other hand, having a basis vector that is very similar to the hold-out examples may cause a bias on the results, because it does not model the reality at the time, when the predictions are made.

To study these issues in practice, we use a data set having altogether 2,354 instances: The total number of sentences is 501 and approximately five parse candidates are generated for each sentence. The feature representation of the instances was generated using the method presented in Pahikkala et al. (2006b). This feature representation is sparse and contains tens of thousands of different features. We form the kernel matrix K by using a linear kernel and ensure its positive definiteness by a diagonal shift of 10⁻⁷ I. In addition, we have a separate test set of 600 sentences with approximately twenty parses per sentence.

Due to the sentence-wise dependencies in the data, we perform CV on the sentence level by holding out one sentence at a time. We randomly select one training instance per sentence as a basis vector, totaling n=501. This selection is intuitive and we confirmed its superiority over a complete random selection empirically in a preliminary experiment. We compare the MSE of the following CV approaches against the performance obtained with the separate test set:

• 1. The examples in the hold-out set are completely removed from the training set and from the set of basis vectors in each CV round.

• 2. The examples in the hold-out set are removed from the training set except the example that belongs to the set of basis vectors, that is, the basis vector is preserved and the square loss is evaluated on it in the training phase.

• 3. The examples in the hold-out set are removed from the training set but the set of basis vectors is preserved, that is, the basis vector in the hold-out set remains a basis vector but the square loss is not evaluated on it in the training phase.

We make a separate comparison for each λ value from 2⁻⁵ to 2¹⁴ and we perform the experiments with both an ordinary and normalized linear kernel. The kernel is normalized with the standard approach, that is, with the formula $k(x,z)/\sqrt{k(x,x)k(z,z)}$, where k(x,z) is the value of the unnormalized kernel function between data points x and z.

The results are illustrated in Fig. 8. The first approach has only a small pessimistic bias when compared to the results with a separate test set. The value of λ does not seem to have a noticeable effect on the bias, and hence this CV approach can be used to select an appropriate value. We also observe that the second approach underestimates the regression error especially with the small values of λ. This is obvious, since one of the parses associated with the hold-out sentence is left in the training set, and the prediction for the other parses is therefore much easier than it would be in reality. Hence, the second approach is not reliable due to its optimistic bias.

Fig. 8

Comparison of the MSEs of three CV approaches in the parse ranking task with a test set error as a function of log₂ λ and with unnormalized kernel (left) and normalized kernel (right)

In addition, we observe that the third approach grossly overestimates the regression error for the small values of λ. We analyze this adverse effect in the following way. First, we consider the kernel values between the basis vectors and training examples. Heat maps illustrating parts of both the original and normalized kernel matrices are shown in Fig. 9. The rows are indexed by 20 basis vectors and the columns by 100 training examples. Each of the 20 basis vectors are associated with 5 training examples. As can be easily observed from the normalized kernel matrix, the kernel values between a basis vector and the five examples associated with it are much larger than the kernel values between the basis vector and other training examples. The same phenomenon is also present in the original kernel matrix but it is more difficult to distinguish due to the excessively high values in certain entries of the matrix. The absolute value of the kernel evaluation between a basis vector and a data point associated with it is, on average over the whole training set, about three times larger than that between a basis vector and an unassociated data point, for both the normalized and unnormalized kernels (see Table 2). As discussed above, this is a property of the learning task in question and the kernel function used.

Fig. 9

Heat maps of the original (top) and normalized (bottom) kernel matrices

Table 2 The average absolute values for the kernel values, coefficients, and their products, during CV. The symbols x and v denote basis vectors inside and outside the hold-out set in a CV round, a _x and a _v denote their coefficients, and z denotes a data point in the hold-out set and associated with x. The measurements are done for both unnormalized and normalized kernels and with low and high regularization

Second, we consider the absolute values of the learned dual coefficients of the basis vectors during CV. The values are measured using small values of the regularization parameter, namely λ=2⁰ and λ=2⁻¹⁰ for the unnormalized and normalized kernels, respectively, for which the bias is large (see Table 2). On average over all CV rounds, the absolute value of the coefficient of the basis vector belonging to the hold-out set is about two or three times larger than that of a basis vector not in the hold-out set. With low regularization, RLS is close to the ordinary least-squares method that is invariant to the scaling of the kernel evaluations (Frank and Friedman 1993), and hence the basis vector gets a larger coefficient than the others as it is dissimilar with all training examples not in the hold-out set, because all the similar data points are held out. This does not cause any problems in prediction time, because the data points for which the predictions are to be made are not associated with the basis vectors. However, this is not happening in the hold-out prediction, since all the hold-out data points are associated with exactly the basis vector that is the most dissimilar with the data points used in training. Indeed, when we measure the evaluations a _x k(x,z), where x is a basis vector, a _x is its coefficient in a CV round, and z is a data point in the hold-out set of the CV round, we observe that the absolute values of the evaluations concerning the basis vector in the hold-out set are, on average, about seven times larger than the evaluations concerning the other basis vectors.

From the performance curves in Fig. 8, we see that the adverse effect disappears if the regularization is increased. To consider this in more detail, we made the same measurements also with λ=2¹⁰ and λ=2⁰ for the unnormalized and normalized kernels, respectively (see Table 2). We observe that, with more powerful regularization, RLS is not invariant to the scaling of the kernel values (Frank and Friedman 1993), and the absolute values of the coefficients of the basis vectors belonging to the hold-out set are, on average, smaller that those of the basis vectors not in the hold-out set. This, in turn, counters the effect of the kernel values in the evaluations a _x k(x,z), whose average absolute values are in this case very similar among the basis vectors inside and outside the hold-out set.

We conclude that having one of the hold-out examples in the set of basis vectors can also cause a serious bias on the regression results, because the circumstances in the hold-out computations do not correspond well enough those in the prediction time. Thus, the experiments clearly indicate that the ability to hold-out basis vectors from training is necessary in the considered task.

7 Conclusion

In this paper, we presented a hold-out algorithm for sparse RLS that improves result reliability and computational efficiency. Improvements in result reliability are achieved by a capability to hold out basis vectors. That is, some of the basis vectors used to train the sparse RLS predictor with the whole training set can be removed from the basis vector set used in the hold-out computation. In our experiments, we demonstrated that our algorithm is considerable faster in hyper parameter selection with leave-one-out cross-validation than the baseline approach without the proposed computational short-cuts. We have empirically studied the effect of holding out basis vectors in each CV round for the variance of the CV estimate and found out that it indeed lowers the variance in certain cases. We have also given empirical evidence on the necessity to hold out basis vectors in order to avoid seriously biased CV estimates. Further, we empirically measured the effect caused by greedily selecting the basis vectors outside the CV loop and, as expected, confirmed the risk of optimistic bias in the CV results.

To summarize the computational efficiency, holding out $|\mathcal{H}|$ training examples with our algorithm requires $O(\min(|\mathcal{H}|^{2}n,|\mathcal {H}| n^{2}))$ time, if a sparse RLS predictor is already trained with a set of m training instances and n basis vectors. This, in turn, enables the efficient computation of cross-validation (CV) estimates for sparse RLS. Namely, the complexity of N-fold CV estimates becomes $O(\min(m|\mathcal{H}|n,mn^{2}))$, where m, n and N are the numbers of training instances, basis vectors and CV folds, respectively. Especially, in the case of LOOCV, the algorithm has the complexity O(mn). Because the sparse RLS can be trained in O(mn ²) time for several different values of the regularization parameter in parallel, the fast CV algorithm can be used to efficiently select the optimal parameter value.