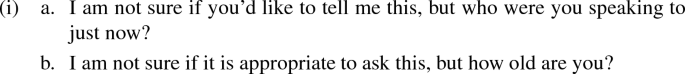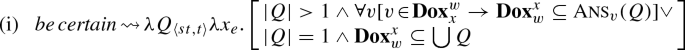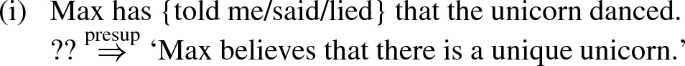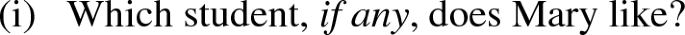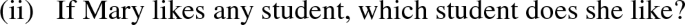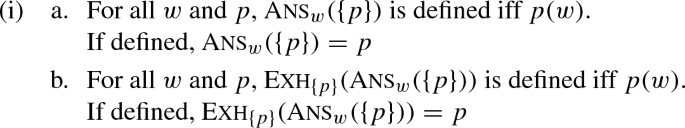Abstract
The projection pattern of the existential/uniqueness presupposition of a wh-complement varies depending on the predicate that embeds it. This variation poses problems for existing accounts that treat the presupposition as a semantic contribution of an operator merging with the wh-complement (Dayal in Locality in Wh-quantification: questions and relative clauses in Hindi. Kluwer Academic Publishers, Dordrecht, 1996) or of the embedding predicate (Uegaki in Interpreting questions under attitudes. Massachusetts Institute of Technology PhD dissertation, Cambridge, 2015). I propose that the problems can be solved if the existential/uniqueness presupposition is contributed by the propositions corresponding to the answers of the embedded question, under the Hamblin/Karttunen semantics for questions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In recent years, there has been a renewed interest in the semantic analysis of embedded questions (e.g., George 2011; Spector and Egré 2015; Uegaki 2015; Cremers 2016; Xiang 2016; Theiler et al. 2018), following earlier pioneering works (e.g., Karttunen 1977; Groenendijk and Stokhof 1984; Heim 1994; Dayal 1996; Lahiri 2002). One of the primary goals of the investigation in this domain is to provide a unified account of the interpretations of pairs of sentences of the form in (1), where Q is an interrogative and p is a declarative complement, for different predicates V:

Such a unified account would capture the interpretations of both (1a) and (1b), in terms of a general compositional mechanism that allows the predicate V to embed either a declarative or an interrogative complement (see Uegaki 2019 for a recent review).
This paper aims to further advance the investigation into the semantics of these constructions, focusing on an issue concerning their presuppositions, i.e., how the presupposition of a wh-complement is projected by different embedding predicates. At least since Katz and Postal (1964), it has been observed that wh-questions in general presuppose that at least one of its Hamblin answers (Hamblin 1973) is true. The following examples illustrate this observation (see also Keenan and Hull 1973 for early discussion):Footnote 1

In addition, it is well known that a singular-which question of the form \(\ulcorner \) Which NP \(\varphi \) ?\(\urcorner \) presupposes that exactly one NP \(\varphi \) (e.g., Dayal 1996; cf. also Groenendijk and Stokhof 1984):

I will refer to these presuppositions as the uniqueness/existential presupposition of wh-questions, or the UP/EP for short.
The UP/EP presents an additional desideratum for any unified semantic theory of the constructions in (1), as envisioned above. That is, the theory has to uniformly account for the projection behavior of the UP/EP in interrogative-embedding sentences, as in (6), as well as the presuppositions of their declarative counterparts, as in (7). (I will discuss each of these data points in detail in Sect. 2):

In the literature, Karttunen and Peters (1976) offer a pioneering analysis of the projection of the EP of interrogative complements embedded under know, wonder and matter. They treat the EP as a ‘conventional implicature’ and formulate a two-dimensional compositional analysis where both the at-issue content and the conventional implicature are calculated recursively based on the system developed in Karttunen and Peters (1979). In this system, how the EP (or the existential ‘implicature’ in their terms) is projected by each embedding predicate is stipulated in the form of meaning postulates. The goal of the current paper departs from that of Karttunen and Peters (1976) in two important respects. First, although Karttunen and Peters stipulate the projection behavior of the EP for each question-embedding verb, focusing only on interrogative-embedding sentences, my aim is to offer a unified analysis of the UP/EP of interrogative-embedding sentences, as in (6), and the presuppositions of their declarative counterparts, as in (7). Second, I aim to analyze the sentences as in (6) as semantically presupposing, rather than conventionally implicating, the relevant uniqueness/existential implications, following the current consensus on the empirical description of the phenomena (e.g., Dayal 1996; Comorovski 1996 and much subsequent literature).Footnote 2
Dayal (1996) provides a highly influential analysis of the UP/EP in terms of the maximality presupposition of the answerhood operator. However, as I will argue below, Dayal’s (1996) original account, as well as its possible extensions based on Spector and Egré (2015) and Uegaki (2015), falls short of providing a unified account of the UP/EP of interrogative-embedding sentences and the presuppositions of their declarative counterparts. The goal of this paper is thus to offer an alternative analysis that can uniformly capture both the UP/EP-projection behavior in interrogative-embedding sentences (e.g., (6)) and the presuppositions of the declarative-embedding counterparts (e.g., (7)). Specifically, assuming the Hamblin/Karttunen semantics for questions, I will argue that such a unified analysis is possible only if the UP/EP is contributed by the proposition(s) corresponding to the answer(s) of the question.Footnote 3
It should be made clear at this point that a goal of this paper is not to offer an argument for a particular compositional mechanism of question-embedding, such as the question-to-proposition reduction (e.g., Karttunen 1977; Heim 1994; Lahiri 2002; Spector and Egré 2015), the proposition-to-question reduction (Uegaki 2015), or the uniform analysis based on Inquisitive Semantics (Theiler et al. 2018). Rather, the UP/EP proves to be a general problem for existing accounts regardless of the compositional mechanism for question-embedding. Moreover, the proposed account where the answer(s) carry the UP/EP is in principle compatible with any of the three general approaches mentioned above. For the sake of simplicity, I will provide a concrete account using Spector and Egré’s (2015) question-to-proposition reduction approach, and discuss an alternative implementation within the proposition-to-question reduction approach in Appendix B.
The structure of the rest of the paper is as follows. In Sect. 2, I lay out the basic data and discuss why they pose problems for existing accounts: Dayal (1996), its possible extensions based on Spector and Egré (2015) and on Uegaki (2015). Section 3 puts forward my central proposal that the existential/uniqueness presupposition of wh-complements is contributed by the answers. It is shown that this proposal enables a proper treatment of the data presented in Sect. 2, given independently motivated assumptions about (i) the presupposition-projection properties of the embedding predicates and (ii) the general compositional mechanism for question-embedding. Section 4 discusses how the present analysis can be extended to data involving matrix questions and rogative predicates (e.g., wonder). Section 5 summarizes the proposal and discusses several open issues.
2 Data and problems for existing accounts
In this section, I present data concerning the projection of the presupposition of wh-complements, and discuss why they are problematic for the existing accounts by Dayal (1996) as well as for its possible extensions based on Spector and Egré (2015) and on Uegaki (2015). Here and in the rest of the paper, I will mostly present data involving the uniqueness presupposition (UP) of singular-which questions. However, the analyses to be discussed will be compatible with the existential presupposition (EP) of plural-which and simplex wh-questions, as they are based on Dayal’s (1996) analysis that uniformly treats both UP and EP as the maximality presupposition, as discussed at the end of Sect. 2.1.
2.1 Embedding under veridical predicates and Dayal (1996)
When a singular-which question is embedded under a veridical predicate, such as know and surprise, the uniqueness presupposition (UP) projects to the matrix level. This can be seen in the following examples:

A proper analysis of the UP/EP we are after has to be able to capture the data in (8)–(9). In addition, it also has to be able to capture the presuppositions these predicates exhibit when they embed a declarative complement, as follows:

Dayal’s (1996) analysis of the UP employing her answerhood operator straightforwardly captures this matrix projection pattern in (8)–(9). In Dayal (1996), wh-complements obligatorily merge with the answerhood operator, \(\textsc {Ans}\), defined below.Footnote 4\(^{,}\)Footnote 5

\(\textsc {Ans}\) roughly acts as a definite determiner over propositions. It carries the presupposition that there is a maximally informative true answer in the set of propositions it combines with, and picks out such a maximally informative true answer. Hereafter, I will refer to the presupposition of \(\textsc {Ans}\) as the maximality presupposition, and the proposition that the \(\textsc {Ans}\)-operator returns from a question as the Dayal-answer of the question. Given that a singular-which question denotes a set of mutually-independent ‘atomic’ answers, as in (13) (cf. Hamblin 1973),Footnote 6 this treatment captures the UP associated with it.Footnote 7\(^,\)Footnote 8

This is so because, for every w and every set Q of mutually-independent propositions, \(\textsc {Ans} _w(Q)\) is defined only if exactly one of Q’s members is true in w. Sentences like (8)–(9) have a semantic representation like (14)–(15), where \(\textsc {Ans} _w(Q)\) (with the matrix evaluation world w) serves as an argument of the embedding predicate.

The meanings in (14)–(15) are defined only if \(\textsc {Ans} _w(Q)\) is defined, which holds just in case exactly one student smokes in w, the matrix evaluation world.
The \(\textsc {Ans}\)-operator further enables a uniform treatment of the UP of singular-which questions and the EP of plural/simplex-wh questions, under the assumption that plural/simplex wh-phrases are number-neutral. This is so since the maximality presupposition is satisfied for proposition-sets that are closed under conjunction as long as there is a true answer in the set.Footnote 9
The presuppositions of the declarative cases in (10)–(11) can also be straightforwardly captured in terms of the proposition-taking lexical denotations of the predicates. Concretely, assuming that the presuppositions are encoded in the meta-language predicates know and surprise as in (16), we can capture the fact that the meanings of the declarative-embedding sentences involving these predicates in (17) have the desired presuppositions.

2.2 Embedding under non-veridical predicates
The UP/EP exhibits a different projection behavior when the wh-complement is embedded under non-veridical predicates from when it is embedded under veridical predicates. The examples in (18) illustrate that, when be certain embeds a singular-which complement, the UP does not necessarily project to the matrix level, but rather projects into the subject’s beliefs.

The contrast between know and be certain with respect to the relevant presupposition projection behavior is also clear in the following minimal pair.Footnote 10

The following is an attested example where, given the context, it is reasonable to assume that the presupposition of the which-question under be certain does not project to the matrix level, but only to the beliefs of the subject.

Footnote 11 Another non-veridical predicate, agree, exhibits a slightly different presupposition projection behavior, as illustrated in the following examples:

These examples show that the UP of the embedded question is projected not only to the belief state of the subject (Max in (21)) but also to the belief state of the individual denoted by the with-phrase (henceforth the with-argument; Kim in (21)).Footnote 12 The presupposition, however, is not necessarily projected to the matrix level. The examples in (21) can be felicitous even if there is in fact no, or more than one, student smokers.
Again, our goal is to have an analysis that accounts for the projection of the UP/EP as illustrated above, as well as the presuppositional behaviors of the relevant predicates when they embed declarative complements. The latter is illustrated in the following examples for be certain and agree:


In the following three subsections, we will consider ways to extend the basic analysis by Dayal (1996) introduced in the previous section to the non-veridical predicates.
2.3 A simple-minded account: always anchoring \(\textsc {Ans}\) to the evaluation world
The analysis in terms of Dayal’s (1996) \(\textsc {Ans}\)-operator outlined in Sect. 2.1 only considered embedding under veridical predicates. To extend this line of account to embedding under question-embedding predicates in general (including non-veridical predicates), we need to assume a general compositional mechanism for question-embedding. Let us first consider a very simple such mechanism, stated below:

According to this analysis, regardless of the semantics of the embedding predicate, embedded questions are interpreted with \(\textsc {Ans}\) evaluated with respect to the matrix evaluation world. This means that the predicted interpretation would involve the ‘actual’ answer (relative to the evaluation world) no matter what the embedding predicate is. Among other issues, such an analysis would incorrectly predict the UP to project to the matrix level even when the embedding predicate is non-veridical. For example, the embedding under be certain would be analyzed as follows:

Just as in the case with veridical predicates, the predicted meaning in (25) is defined only if \(\textsc {Ans} _w(Q)\) is defined, which in turn holds just in case exactly one student smokes in the matrix evaluation world w. Thus, this treatment fails to capture the lack of the matrix projection of the UP, as well as its projection to the subject’s beliefs observed in (18). Similarly, the projection behavior of agree would be problematic. The analysis would treat question-embedding under agree as follows:

Just as in (25), the analysis predicts the matrix projection, and no projection to the subject’s or to the with-argument’s beliefs.
In sum, the varying projection behavior of the UP/EP across veridical and non-veridical predicates cannot be captured by a simple extension of Dayal’s (1996) analysis, where embedded questions are always interpreted with \(\textsc {Ans}\) evaluated with respect to the matrix evaluation world. Such an analysis predicts the presupposition triggered by \(\textsc {Ans}\) to project to the matrix level regardless of the embedding predicate.
In order to resolve this problem, we need a mechanism that allows us to let the projection of the presupposition triggered by \(\textsc {Ans}\) vary depending on the embedding predicate. Broadly speaking, there are two approaches to this issue: an approach based on the proposition-oriented semantics and an approach based on the question-oriented semantics for the relevant embedding predicates. The former approach would encode the presuppositional behaviors of the predicates when they embed declarative complements in their proposition-taking lexical denotations, and attempt to capture the projection of the UP/EP when they embed interrogative complements, given the lexical denotations together with a compositional mechanism for question-embedding. The latter approach would directly encode how the predicates project the presupposition when they embed interrogative complements in their lexical denotations, and attempt to capture their presuppositional behavior when they take declarative complements, given the lexical denotations together with a compositional mechanism that enables question-taking predicate meanings to embed declarative complements.
In the following two subsections, we consider two extensions of the Dayal -style analysis within these two approaches: one based on the proposition-oriented semantics by Spector and Egré (2015) (Sect. 2.4) and the other based on question-oriented semantics by Uegaki (2015) (Sect. 2.5). As it turns out, both analyses fail to achieve a unified analysis of the presuppositions in declarative-embedding and interrogative-embedding sentences.
2.4 An extension based on Spector and Egré (2015)
Spector and Egré (2015) propose a proposition-oriented semantics for question-embedding that is designed to address issues surrounding non-veridical predicates, such as be certain and agree. In contrast to the naïve extension of Dayal (1996) considered in the previous section, where the embedded question is always analyzed in terms of its unique true answer in the matrix evaluation world, Spector and Egré (2015) analyze question-embedding as involving existential quantification over possible answers. Making use of Dayal’s answerhood operator, this analysis can be schematically stated as follows:

More precisely, Spector and Egré (2015) posit a lexical rule converting a proposition-taking denotation, V\(_{decl}\), of a predicate V into its question-taking counterpart. Using \(\textsc {Ans}\), their rule looks like the following:Footnote 14

According to this analysis, roughly, \(\ulcorner \)x Vs Q\(\urcorner \) asserts that there is a world \(w'\) such that ‘x Vs \(\textsc {Ans} _{w'}(Q)\)’ is true, while presupposing that the presupposition of ‘x Vs the exhaustification of \(\textsc {Ans} _{w'}(Q)\)’ can be satisfied.Footnote 15
For instance, sentences involving know/be certain and a singular-which question are analyzed as follows:

This analysis makes different predictions regarding the projection of the UP from the simple analysis sketched in the previous section. In particular, it is predicted that predicates vary with respect to how they project the UP/EP, given that their proposition-taking denotations (e.g., know, certain) have different presuppositional properties. I repeat the examples illustrating these properties for know and be certain below:

Given these presuppositional behaviors of know and be certain, we assume that the meta-language predicates know and certain have the following presuppositions:

Now, we return to (30)—the predicted meanings of know/be certain-wh sentences. To see what the predicted presuppositions underlined in (30) amount to, we have to consider both the presupposition triggered by \(\textsc {Ans}\) and that triggered by the predicates \(\mathbf{know}/\mathbf{certain}\). As a result, the predicted presuppositions in (30) can be rewritten as follows:

Let us consider (32a) and (32b) in turn. First, the predicted presupposition for Max knows which student smokes in (32a) states that ‘there is a world such that the Dayal-answer in that world is defined and the exhaustification of that answer is true in the evaluation world (w)’. This correctly predicts that the UP is satisfied in the evaluation world because the exhaustification of \(\textsc {Ans} _{w'}(Q)\) for any \(w'\) states that exactly one student smokes.
Turning to (32b), i.e., the predicted presupposition of Max is certain (about) which student smokes, we have ‘there is a world such that the Dayal-answer in that world is defined and the exhaustification of that answer is compatible with Max’s beliefs in the evaluation world (w)’. This does not predict matrix projection of the UP, unlike the simple extension of Dayal’s analysis. This is empirically correct. However, it does not predict that Max believes the UP. Crucially, the UP triggered by \(\textsc {Ans}\) does not project to Max’s belief state in (32b) since the argument of certain, i.e., \(\textsc {Ans} _{w'}(Q)\), itself is not partial when it is defined. Instead, (32b) only predicts that Max’s beliefs are compatible with some exhaustified Dayal-answer. This predicted presupposition is too weak in view of the empirical pattern we observed in the previous subsection. The predicted presupposition would be satisfied if, for example, Max considers it possible that only Ash smokes, but also considers it possible that no one smokes.Footnote 16
Essentially the same problem arises with agree. A sentence with agree embedding an interrogative complement would be analyzed as follows in the S&E-style analysis:

Again, to see what the presupposition in (33) amounts to, we have to consider the presupposition of the proposition-taking denotation of agree...with.... This is tested as in the following examples, repeated from above:

Based on these data, we can assume that \(\ulcorner \) x agrees with y that p\(\urcorner \) presupposes that y believes that p. We assume that this is encoded in agree, as follows:

With this, the underlined presupposition in (33) can be rewritten as follows:

Again, this does not amount to a matrix projection of the UP. To this extent, the prediction is correct. However, the account fails to capture the fact that the UP projects to the attitude holder Max’s beliefs, as (35) only predicts that the UP projects to Kim’s beliefs.
In sum, S&E’s analysis is designed to address some of the issues surrounding non-veridical question-embedding predicates. In particular, employing their analysis, the presupposition projection behavior of the predicates with respect to declarative complements can be used to make predictions about how the UP/EP is projected when the predicates embed wh-complements. However, it fails to completely capture the projection pattern of the UP/EP with non-veridical predicates. In particular, the analysis fails to capture the fact that the UP/EP projects to the attitude holder’s beliefs with be certain and agree.
2.5 An extension based on Uegaki (2015)
The approach considered in the previous section treated the presuppositional behaviors of the predicates when they embed declarative complements as given (i.e., something that must be encoded in their lexical semantics) and attempted to derive the projection of the UP/EP based on them. In this section, we consider an opposite approach, i.e., the approach that treats the behaviors of the predicates when they embed interrogative complements as given, and attempts to derive their presuppositional behavior when they embed declarative complements.
Uegaki (2015) offers such an approach to the presuppositional behavior of question-embedding predicates, formulated within his question-oriented semantics for question-embedding. Specifically, in Uegaki (2015), the predicates’ varying projection behavior with respect to the UP/EP is captured by letting the predicate meanings relate the subject’s attitude representation to the Dayal-answer of a question in different ways. This is done by treating \(\textsc {Ans}\) as a part of the predicate meaning. Specifically, know and be certain are analyzed as follows:

Let us consider the predictions of this analysis in turn. In (36a), know is analyzed as a question-taking predicate that relates an individual to the Dayal-answer of a question. Thus, this treatment derives the same interpretation for a sentence like Max knows which student smokes as the Dayal -style analysis does in (14) above. Thus, the analysis preserves Dayal ’s correct prediction that the UP/EP projects to the matrix level.
On the other hand, be certain in (36b) predicts something different from the simple extension of the Dayal -style analysis. According to (36b), \(\ulcorner \) x is certain (about) Q\(\urcorner \) is true iff for all worlds compatible with x’s beliefs, x believes that the Dayal-answer of Q in that world is true. The following exemplifies the treatment of the embedding of singular-which complement according to this analysis:

The interpretation given in (37) roughly states that Max believes that she has a correct belief about which student smokes. This matches the intuitive interpretation of certain-wh. In particular, it captures the obligatory strong exhaustivity of a question embedded under be certain, as Uegaki (2015) points out.Footnote 17
What is important for our purposes is the fact that the analysis captures the projection pattern of the UP/EP with be certain. Assuming universal projection out of universal quantification, (37) is defined only if \(\forall v[v\!\in \!{\mathbf{Dox}}^{\mathbf{m}}_w \rightarrow \textsc {Ans} _{v}(Q) \text{ is } \text{ defined}]\). This holds only if Max believes that exactly one student smokes. Crucially, here, the world with respect to which \(\textsc {Ans}\) is evaluated is not the matrix evaluation world, but is bound by the universal quantification over the subject’s belief worlds. This is made possible in Uegaki (2015) by letting \(\textsc {Ans}\) be part of the lexical semantics of the embedding predicate, rather than an independent operator that feeds a propositional argument to the embedding predicate, as in Dayal (1996).
Despite this welcome feature, the approach faces problems. First of all, the presupposition projection behavior of agree discussed in the previous section remains to be a problem for Uegaki (2015) since it is not straightforward to define a plausible lexical entry for agree along the lines of (36) that would derive the projection behaviors. Furthermore, as we will see in the next subsection, even if such a lexical entry were possible, the analysis would face problems when it is extended to declarative complements.
Uegaki’s (2015) analysis faces further problems when viewed as a part of the general semantic theory of question-embedding, which would encompass a unified account of the presuppositions of \(\ulcorner \) x Vs Q\(\urcorner \) and \(\ulcorner \) x Vs that p\(\urcorner \) across different predicates V, as envisioned in Sect. 1. This is so since extending the analysis to the declarative-embedding cases would make empirically incorrect predictions. To illustrate the problems, we first have to make it explicit how Uegaki’s (2015) treatment of interrogative complements embedded under know and be certain can be integrated with an analysis of declarative complements.
2.5.1 Uniform semantics for complementation
Uegaki’s (2015) analysis is based on the uniform semantics for complementation, where declarative and interrogative complements share the same semantic type, i.e., a set of propositions, which is selected by clause-embedding predicates such as know and be certain.Footnote 18 In particular, Uegaki (2015) analyzes declarative complements as denoting the singleton set consisting of the proposition it traditionally denotes. For instance, the declarative complement that Ash smokes is analyzed as follows, where A is the proposition that Ash smokes.

Given this, declarative-embedding under know is analyzed as follows:

The interpretation in (39) presupposes that Ash smokes, and asserts that Max knows that Ash smokes. Here, the presupposition of \(\textsc {Ans}\) boils down to the factivity presupposition that Ash smokes.Footnote 19 This is an empirically correct prediction.
2.5.2 Problem 1: be certain that
A problem arises when we consider declarative-embedding under be certain. The following is the interpretation predicted by Uegaki (2015) for a sentence with be certain and a declarative complement.

Assuming a universal projection of presuppositions out of universal quantification (just as in the case of (37) above), we have that (40) presupposes \(\forall v[v\!\in \!{\mathbf{Dox}}^{\mathbf{m}}_w \rightarrow \textsc {Ans} _{{v}}(\{A\}) \text{ is } \text{ defined }{]}\). Since \(\textsc {Ans} _{{v}}(\{A\})\) is defined only if A(v), this presupposition amounts to \(\forall v[v\!\in \!{\mathbf{Dox}}^{\mathbf{m}}_w \rightarrow A(v)]\), i.e., Max believes that Ash smokes. Empirically, this presupposition seems too strong for (40). Rather than presupposing Max’s belief that Ash smokes, (40) seems to presupposes that it is merely compatible with Max’s beliefs that Ash smokes.
One might attempt to remedy the situation by supposing that we have a non-universal presupposition projection in (40). Note, however, that this move runs counter to our objective, i.e., to analyze the presuppositions of certain-wh and certain-that in a unified manner, since the analysis of the projection of the UP/EP in certain-wh requires universal projection. The point here is that, as long as we are trying to achieve a unified analysis, once the presupposition of certain-wh is analyzed in terms of universal projection, one is forced to analyze the presupposition of certain-that in terms of universal projection as well, thus predicting too strong of a presupposition. Of course, one can analyze certain-wh in terms of the universal projection while claiming that we have a non-universal projection in the case of certain-that. That would be empirically adequate, but leave the question of why the projection behaviors are different between the interrogative-embedding case and the declarative-embedding case.
2.5.3 Problem 2: agree that
The second problem concerns agree. As discussed in Sect. 2.2, the presupposition of a which-question under agree projects both to the subject’s and to the with-argument’s beliefs, as illustrated below:

An analysis along the lines of Uegaki (2015) would capture this projection behavior by defining a lexical entry for agree in terms of \(\textsc {Ans}\) that derives the following:

As briefly mentioned above, it is not straightforward to define a plausible lexical entry for agree that derives these presuppositions. What is more crucial is that, regardless of whether such a lexical entry can be defined, (42) would make incorrect predictions about the presuppositions of the declarative-embedding under agree. This is so since we would have the following as the declarative-embedding case where Q is a singleton set:

This is an incorrect prediction, as an agree-that sentence does not presuppose that the subject believes the complement, as can be seen in the following example:

Taking a step back, both with be certain and with agree, we have seen that the UP projecting to the subject’s belief poses a problem for Uegaki (2015). The core of the problem is the same across the two predicates. Even if the analysis correctly predicts the projection behavior in the interrogative case, it incorrectly predicts that a similar pattern would hold for the declarative case. This is by virtue of the fact that the presupposition is encoded in the lexical semantics of the embedding predicate and that declarative complements are treated as singleton proposition-sets.Footnote 20
2.6 Diagnosing the problems
So far, I have considered three existing analyses concerning the UP/EP of wh-complements, i.e., a simple extension of Dayal (1996), an extension of Dayal (1996) based on Spector and Egré (2015) and one based on Uegaki (2015). I have argued that none of them can fully capture the data with different embedding predicates. In this section, I will state the problem in more general terms.
Abstractly, we can understand the difference between the simple extension of Dayal (1996) and its extension based on Spector and Egré (2015) on the one hand and Uegaki (2015) on the other as the difference in the locus of the presupposition carrier, i.e., which lexical item is defined as a partial function. In Dayal (1996) and in its extension following Spector and Egré (2015), the relevant presupposition is carried by the \(\textsc {Ans}\)-operator. On the other hand, in Uegaki (2015), it is carried by the embedding predicate (since the \(\textsc {Ans}\)-operator is part of the predicate’s lexical semantics). This is schematically represented in (45), where the boxes mark the items that carry the presupposition.

In (i), \(\textsc {Ans}\) is defined as a partial function that triggers the maximality presupposition. The application of \(\textsc {Ans}\) to Q is defined if this presupposition is met with respect to the matrix evaluation world and Q. Crucially, the proposition resulting from the application does not carry the presupposition. This treatment incorrectly predicts that the presupposition projects to the matrix level regardless of the embedding predicate V.
In (ii), the presupposition of \(\textsc {Ans}\) is not automatically projected to the matrix level because of the existential quantification into the world in which it is evaluated. It is projected to the matrix level in the case where V is a factive predicate like know, by virtue of the factivity presupposition. However, this is not the case with non-veridical predicates like be certain and agree. Although the lack of the matrix projection with non-veridical predicates is a correct prediction, the account fails to predict that the presupposition of \(\textsc {Ans}\) projects to the attitude holder’s beliefs. This is so because \(\textsc {Ans} _{w'}(Q)\) itself does not carry the presupposition, in the sense that it is not a partial function.
In (iii), the maximality presupposition is encoded in the lexical semantics of the predicate in ways that vary across predicates, deriving lexically-specific projection patterns. As such, this treatment overcomes the problem with the analysis in (i). Such an analysis would be adequate if our goal is just to analyze the projection pattern of the UP/EP in interrogative-embedding sentences, ignoring the presuppositions of declarative-embedding counterparts. However, given that our goal is to find an account that captures the presuppositions of both interrogative and declarative-embedding sentences, the analysis in (iii) remains problematic. This is so because it makes an incorrect prediction with respect to declarative complements, given the uniform semantics for complementation assumed in the analysis. Since the presupposition is encoded in the predicate, the analysis incorrectly predicts that the presupposition shows up with declarative complements as well, assuming that the same lexical entry is used for both interrogative and declarative complementation. The prediction with respect to the declarative complements is not a problem for the simple extension of Dayal (1996) schematized in (i) and its extension based on S&E in (ii) since \(\textsc {Ans}\) appears only in interrogative complements in these analyses.
At this point, another analytical possibility presents itself: The presupposition can in principle be carried by the complement meaning. We can schematize this possibility as follows:

Here, f is a (possibly vacuous) operator such as \(\textsc {Ans}\) that takes the question denotation as an input and passes it to the predicate meaning. What is crucial in this schema is that the semantic argument of the predicate corresponding to the interrogative complement carries the presupposition. Note that this possibility is different from that in (45-i/ii), since f(Q) as a whole in (46) carries the relevant presupposition while \(\textsc {Ans} (Q)\) in (45-i/ii) doesn’t.
It is clear at this point that the analysis schematized in (46) does not run into the same problem as the Uegaki -style analysis in (45-iii), i.e., the incorrect prediction with declarative complements, since the presupposition would not be triggered in the case of declarative complementation. The remaining questions are whether the analysis can overcome the problem for the analyses in (45-i/ii), i.e., the variation in the projection patterns across predicates, and whether it can correctly capture the projection of the UP/EP to the attitude holder’s beliefs in the case of non-veridical predicates. In the next section, I will argue that the line of analysis in (46) provides a straightforward account of the variation in the projection patterns, once we analyze the answers in the question denotation as carrying the UP/EP.
3 Proposal: presuppositional answers
I propose that it is the answer proposition that carries the UP/EP of wh-complements, rather than an operator that outputs an answer proposition (which itself is devoid of the UP/EP) (as in Dayal 1996 and its possible extensions) or a question-embedding predicate (Uegaki 2015). The gist of the proposal can be illustrated with the following examples:

In (47), it is plausible to assume that each Hamblin answer of the embedded question presupposes that there is a unique unicorn. Crucially, the projection pattern of the presupposition in (47) is exactly the same as that of the UP/EP we observed in the previous section: with know, it projects to the matrix level; with be certain, it projects to the attitude holder’s belief; with agree, it projects both to the attitude holder’s and to the with-argument’s beliefs. Thus, these examples indicate that, if the UP/EP is treated as a presupposition of an answer, just like the definiteness presupposition for the unicorn in (47), whatever analysis that accounts for the projection data in (47) should also account for the projection patterns of the UP/EP.
In this section, I will present such an analysis, and show that it captures the projection pattern of the UP/EP discussed in the previous section, once the UP/EP is treated as coming from answers. The analysis consists of two parts: (i) an existential proposition-oriented semantics for question-embedding along the lines of Spector and Egré (2015) and (ii) the lexical-semantic encoding of the presupposition projection behaviors of the embedding predicates, when they embed a presuppositional declarative complement, as in the following examples:Footnote 21

An analysis of interrogative-embedding sentences based on these independently motivated components (i-ii) captures the projection pattern of the UP/EP, once we adopt the proposal that the UP/EP comes from an answer. The analysis also naturally captures the presuppositional behavior of the predicates when they take declarative complements, as part of their lexical semantics. Thus, the analysis succeeds in capturing the presuppositions of both declarative and interrogative-embedding sentences, unlike the existing analyses considered in the previous section.
In the first two subsections below (Sect. 3.1–3.2), I will go over the two background assumptions needed for the analysis: (i) an existential semantics for question-embedding and (ii) the lexical-semantic encoding of the presupposition projection behaviors of the embedding predicates. Based on these assumptions, in Sect. 3.3, I show that my central proposal—that the answers carry the UP/EP—captures the projection pattern of the UP/EP. In Sect. 3.4, I present a particular compositional implementation of the wh-complement, which derives the UP/EP for each Hamblin answer (cf. Hirsch and Schwarz 2019).
The analysis to be presented in this section employs a proposition-oriented semantics. However, this is merely for expository purposes, and my proposal does not hinge on this. As long as my central proposal—that the answers carry the UP/EP—is adopted, the account can be formulated using either a proposition-oriented semantics or a question-oriented semantics. The formulation within a question-oriented semantics is given in Appendix B. Furthermore, the particular compositional implementation of the proposal to be discussed in Sect. 3.4 is not the only analytical option. In Appendix A, I present another implementation of the proposal, in which the \(\textsc {Ans} \)-operator is modified so that it returns a presuppositional answer as its output.
3.1 The existential semantics for question-embedding
The general compositional mechanism of question-embedding I will adopt is the existential semantics by Spector and Egré (2015). For concreteness, I will assume the general lexical rule by S&E that converts a proposition-taking denotation \(\mathbf {V}_{decl}\) to a question-taking denotation \(\mathbf {V}_{int}\), repeated from Sect. 2.4 above:

I will adopt this formulation since it is shown by Spector and Egré (2015) to be compatible with the detailed empirical considerations concerning aspects of the question-embedding phenomena other than the UP/EP.Footnote 22
One might ask what the role of the \(\textsc {Ans}\)-operator in (49) is, under the current proposal. If each answer in Q already carries the UP/EP, what function does \(\textsc {Ans}\) serve? After all, wasn’t \(\textsc {Ans}\) there to bring about the UP/EP? A short answer is that \(\textsc {Ans}\) under the current proposal would primarily be a type-shifting device. As part of the general semantics for question-embedding, we need a way to relate proposition-oriented denotations of embedding predicates with the proposition-set question denotations. \(\textsc {Ans}\) offers a way to achieve this, as it converts a proposition-set into its specific member. Unlike in Dayal (1996) and its possible extensions considered in the previous section, however, the maximality presupposition of \(\textsc {Ans}\) is not responsible for the projection of the UP/EP in sentences with wh-complements, as we will see below.
It should also be mentioned that my analysis does not rely on the presence of exhaustification in the presupposition. That is, the derivations of concrete examples presented below will go through regardless of the presence of \(\textsc {Exh}\). In fact, as long as the semantics of the question-embedding predicts an existentially quantified presupposition (over the answers in the question denotation, or the worlds with respect to which \(\textsc {Ans}\) is evaluated), the analysis makes the same predictions.
3.2 The presupposition projection properties of individual predicates
The next ingredient needed for the analysis is the presupposition projection properties of individual embedding predicates. Since the semantics for question-embedding I adopt is the Spector and Egré -style proposition-oriented semantics, these properties can be encoded in the proposition-taking denotations of the relevant predicates.
The presupposition projection properties know, be certain and agree can be tested by considering examples where these predicates embed a presuppositional declarative complement, as in the following (I will discuss the nature of the belief presupposition with know at the end of this subsection):

Schematically, we can write the presupposition-projection properties of the predicates observed in (50)–(52) as follows, where the operator \(\pi \) retrieves the presupposition from a proposition, as defined in (53).

From a theoretical perspective, the presupposition-projection properties in (54) can be understood as the combination of (a) the projection of the presupposition of the complement and (b) the presuppositions triggered by the predicates themselves. The former is constant across know, be certain and agree, and arguably universal across all attitude predicates: \(\ulcorner \) x Vs p\(\urcorner \) presupposes that x believes \(\pi (p)\) (Karttunen 1973, 1974; Heim 1992). This is stated below.Footnote 23

The latter is a lexically-dependent presupposition triggered by the embedding predicates (already touched on in Sect. 2.4). Specifically, know has the factivity presupposition that the complement is true; be certain has the presupposition that the complement is compatible with the subject’s beliefs; \(\ulcorner \) x agrees with y that p\(\urcorner \) presupposes that y believes p. These presuppositions are formally represented as follows:

The presuppositions schematized in (54) can be derived from the lexically-specific presuppositions in (56) and the general presupposition projection pattern in (55).
Before concluding this subsection, I would like to make a remark on the nature of the belief presupposition with know. In (50), the presupposition that Max believes that there is a unique unicorn seems relatively weak, compared to the status of the same belief presupposition in the case of be certain and agree. For example, (50b) may be judged true even if Max doesn’t believe in the existence of a unicorn, as long as the other presuppositions are satisfied. This is not prima facie expected under the generalization stated in (55) that all attitude predicates have the belief presupposition.
One possible explanation for why the belief presupposition is felt weak in the case of know (and other veridical predicates), compared to non-veridical predicates, stems from the pragmatics of sentence verification, especially that of truth-value-less sentences. As von Fintel (2004) and Abrusán and Szendrői (2013) show, speakers may judge a sentence as true or false even if it is semantically a presupposition failure when the sentence entails a piece of information serving as a ‘foothold’ for verification. To see this, consider the following pair of sentences:

Both of these sentences are semantically presupposition failures. However, (57a) sounds odd to most English speakers whereas (57b) tends to be felt true (Abrusán and Szendrői 2013). One way to account for the contrast is to say that, in (57b), the object DP Australia denotes an entity that serves as a foothold for verification. That is, when speakers try to verify (57b), they base the judgment on Australia, an existing entity in the actual world, and determines the sentence’s truth value depending on whether the set of its visitors include the king of France or not. Since the visitors of Australia do not include the king of France, (57b) is felt as true. On the other hand, (57a) does not mention any existing entity that can serve as the foothold for sentence verification in a similar manner.
Something similar can be said about our (50), as well as the following kind of examples:

These sentences have two presuppositions: the presupposition of the complement and the presupposition that Max—the attitude holder—believes the presupposition of the complement. In the context where the first presupposition is met but the second presupposition is violated, the sentences are presupposition failures, semantically speaking. However, it is plausible that the first presupposition serves as the foothold for verification in the following way. The presupposition of the complement represents a preliminary fact that an attitude holder must know in order for them to be considered as knowing the information represented by the complement. If they don’t know this preliminary fact, positive knowledge sentences, such as (50a), (58a), (59a), are rejected as false. Conversely, their negative counterparts, such as (50b), (58b), (59b), are judged as true. Henceforth, I will assume this pragmatic explanation for the weakness of the belief presupposition with veridical predicates. This explanation carries over to the projection behavior of the UP/EP in interrogative-embedding sentences, as we will see below.
3.3 UP/EP in each answer
Now that we have established the two background assumptions, i.e., the existential semantics for question-embedding and the presupposition-projection properties of the individual embedding predicates, we are in a position to illustrate the analysis of the projection of the UP/EP. In this section, I will present an implementation of the proposal where the UP/EP is encoded in each answer of the question denotation. To motivate the analysis, we start by observing the projection behavior of non-UP/EP presuppositions triggered within an interrogative complement, mentioned in the beginning of the section.
3.3.1 Presupposition triggers within an interrogative complement
Consider example (60), a wh-clause involving a singular definite DP inside it:

Here, it is reasonable to think that each answer in the Hamblin-denotation of this clause carries a presupposition about the unique existence of a unicorn. That is, the Hamblin-denotation of (60) would look like the following:

As suggested in the beginning of this section, what is crucial for us is that the projection of this presupposition under various embedding predicates, shown in (62), patterns exactly like the projection of the UP of singular-which questions, shown in (63):

The parallel in projection patterns in (62) and (63) is straightforwardly explained if the latter is encoded in each proposition in the Hamblin denotation, just as in (61). A Hamblin denotation for which student smokes according to this proposal would look like (64), where each proposition in the set carries the proposition that exactly one student smokes.Footnote 24

In other words, as long as the presupposition is triggered by each answer in the Hamblin denotation, the general semantics for question-embedding presented in Sect. 3.1 and the presupposition projection properties of each predicates presented in Sect. 3.2 account for the projection patterns of the UP/EP in (63). Below, I will illustrate this in the case of the three predicates, know, be certain and agree.
3.3.2 Application of the analysis to particular predicates
As stated above, my analysis takes two things as given: the existential semantics for question-embedding along the lines of Spector and Egré (2015) and the presupposition-projection properties of the proposition-oriented denotations of individual predicates. These two assumptions are repeated below for easier reference.


Also, in the illustrations to follow, I will repeatedly use the following logical fact:

More concretely, this means that, if a presupposition (e.g., the uniqueness for (62) or the UP/EP for (63)) is encoded in each proposition in Q, \(\textsc {Exh} _Q(\textsc {Ans} _w(Q))\) also presupposes the same presupposition for all w that makes \(\textsc {Ans} _w(Q)\) defined. It is easy to see why this is the case, as \(\textsc {Ans} \) is defined to pick out a certain member of Q and \(\textsc {Exh} _Q(\textsc {Ans} _w(Q))\) has the same presupposition as \(\textsc {Ans} _w(Q)\).
Know The matrix projection of the UP with know can be derived as in (67), where I use the shorthands in (66):


The derivation can be roughly paraphrased as follows. First of all, the sentence has the presupposition predicted by the lexical rule in (49). This can be rewritten as in line (i) given the projection of the presupposition of \(\textsc {Ans}\) itself and that of the know-that sentence in (54a). Line (i) can be paraphrased as ‘there is a defined Dayal-answer of Q such that its presupposition is believed by Max and it is true’. Since ‘\(\textsc {Ans} _{w'}(Q) \text{ is } \text{ defined }\)’ (i.e., ‘the Dayal-answer is defined’) is entailed by ‘\(\textsc {Exh} _Q(\textsc {Ans} _{w'}(Q))(w)\)’ (i.e., ‘the exhaustification of the Dayal-answer is true’), the former conjunct can be dropped as in line (ii). By Fact (65), this can be rewritten as in line (iii), i.e., ‘Max believes \(\mathbf{up}\) and there is a Dayal-answer of Q that is true’. Finally, since the variable \(w'\) does not appear in the first conjunct of (iii), it is equivalent to (iv).
Now, it can be proved that the second conjunct of (iv) is equivalent to \(\mathbf{up} \):

This is so because of the following reasoning: the left-hand side of (68) states that the exhaustification of some Dayal-answer is true in w. Since this Dayal-answer presupposes \(\mathbf{up}\) by assumption, this is the case only if \(\mathbf{up}\) is true in w. Conversely, if \(\mathbf{up}\) is true in w, the left-hand side is true because one can always find a Dayal-answer whose exhaustification is true in w (namely the exhaustification of the Dayal-answer in w itself).Footnote 25
All in all, the predicted presupposition of (67) can be paraphrased as follows:

The second conjunct amounts to the UP projected to the matrix level, which we have observed in the previous section. On the other hand, the belief presupposition in the first conjunct has not been mentioned in connection to the UP/EP projection with know up to this point. In fact, native speakers report that the belief presupposition seems quite weak with know, compared with be certain.

I suggest that the explanation in terms of the pragmatics of sentence verification made for the declarative counterparts in Sect. 3.2 carries over to this case. That is, the matrix UP of (67), (70) serves as a foothold for sentence verification. To see this, consider a context in which it is known that exactly one student smokes, but Max does not believe that there is a unique student smoker. In this context, the semantic analysis predicts (67), (70) to be presupposition failures, as the context violates the belief presupposition. However, once it is established that there is actually a unique student smoker, (67) can be rejected as false since Max does not know this preliminary fact. Conversely, (70)—the negation of (67)—can be judged true.
Be certain We can derive the projection of the UP with be certain in a similar fashion.

Footnote 26 Paraphrasing, (i) says that there is a defined Dayal-answer of Q the presupposition of whose exhaustification is believed by Max and whose exhaustification is compatible with Max’s beliefs. After dropping the first conjunct as it is entailed by the other conjuncts as in (ii), we can use Fact (65) to rewrite (ii) as in (iii), i.e., Max believes \(\mathbf{up}\) and there is a Dayal-answer whose exhaustification is compatible with Max’s beliefs. Since the latter conjunct is entailed by the first conjunct (see fn. 26 for a proof), we end up with the following presupposition predicted for (71).

This is exactly what we observed earlier, i.e., the projection to the subject’s beliefs.
Agree Finally, here is the derivation in the case of agree:

Again paraphrasing, (i) says that there is a defined Dayal-answer of Q such that the presupposition of its exhaustification is believed by Max and its exhaustification is believed by Kim. After dropping the first conjunct and using Fact (65), it can be rewritten as in (iii), i.e., Max believes \(\mathbf{up}\) and there is a Dayal-answer of Q whose exhaustification is believed by Kim. We end up with the following presupposition predicted for (73):

Not only does this capture the projection of the UP both to the subject’s and to the with-argument’s beliefs, but it also accounts for the asymmetry in strength between the subject’s presupposed belief and the with-argument’s presupposed belief, discussed earlier in footnote 12.Footnote 27
Summing up, once we assume that each answer in the question denotation carries the UP/EP, its projection patterns with know, be certain and agree can be accounted for, given independently motivated presupposition projection behaviors of the predicates as well as the existential semantics for question-embedding.
3.4 Internal composition of wh-complements
We now move on to the internal composition of wh-complements, i.e., how to compositionally derive the denotation of the complements where the answers carry the UP/EP. Broadly speaking, there are two approaches to this. One is to posit an additional operator that adds the Dayal-style maximality presupposition to the answers in the Hamblin denotation. The other is to treat which-NPs as a kind of definite description and derive a set of partial propositions through presupposition projection. The former approach is considered in Uegaki (2018). The latter approach has been adopted by Rullmann and Beck (1998) and Champollion et al. (2017) in their treatment of a presupposition associated with which-questions (to be detailed immediately below), and has been recently applied to the Dayal-style maximality presupposition by Hirsch and Schwarz (2019).
As stated in the introduction, my goal in this paper is to investigate the projection patterns of the UP/EP in the context of the general theory of question-embedding. Thus, the issue concerning the internal semantic composition of wh-complements is of secondary nature, as long as the composition guarantees that the individual answers in the question denotation carry the UP/EP. For this reason, I will keep my discussion of the internal composition of wh-complements minimal, and sketch a simple analysis in the latter approach mentioned above, i.e., deriving a set of partial propositions through the projection of presupposition from a definite-like semantics for which-NPs.
The analysis follows the insights of Rullmann and Beck (1998), who roughly treat the semantics of which-complements as follows:

R&B compositionally derive this using a definite-like semantics for which-NPs. As a result of the definiteness, each answer in (75) presupposes existence of a student. Note that the UP/EP we are after is stronger than the presupposition captured in (75). Rather than ‘there is a student’, we want each answer of the complement denotation to presuppose that there is a unique student smoker. To achieve this, I roughly treat the denotation of a wh-complement as follows, i.e., a set of propositions each identifying an individual with the student smoker.

Formally, this is derived by assuming an LF that looks like the following:

This structure follows the LF-based rendition of Karttunen’s (1977) analysis of questions by Heim (2016) and Dayal (2016), together with the additional assumption that the lower copy of which is realized in the LF as the operator which, defined shortly below.Footnote 28 Furthermore, following Beck and Rullmann (1999), the NP-part of a which-phrase is left downstairs to allow both the de re and de dicto readings via world-indexing on the NP. (See Hirsch and Schwarz 2019 for an analysis along the same lines.)
The translations of lexical items in (77) are given below, with the definition of the operator the in (79), akin to Link’s (1983) \(\sigma \)-operator.

Hence, the structure in (77) is translated as in (80), and each answer of the question (80) represents has the presupposition in (81) projected from the.

Since student only ranges over singular individuals, (81) effectively states that there is only one student smoker. Overall, this correctly derives the UP/EP as the presupposition of each answer. Note that this would not be possible under Rullmann and Beck’s (1998) original analysis, since it is designed to only predict existential presupposition with respect to the extension of the NP in which-NPs.
The analysis sketched above concerns which-complements, and its prediction with respect to complements involving a simplex wh-phrase (e.g., who smokes) depends on the definition of the wh-operator, who, in the lower copy position. Following Dayal’s (1996) insight, the fact that simplex wh-complements only presuppose existence (and not uniqueness) is captured by treating who as number-neutral, as follows:

3.5 Section summary
In this section, I have shown that the projection pattern of the UP/EP observed in Sect. 2 can be properly captured, once we assume that the answers to the embedded question carry the UP/EP. In addition to this central proposal, my analysis is based on two independently motivated assumptions: the existential semantics for question-embedding by Spector and Egré (2015) and the presupposition projection properties of the proposition-taking denotations of individual embedding predicates. It should also be emphasized that the analysis successfully accounts for the presuppositions of sentences involving declarative complements—something that Uegaki (2015) fails to capture—thanks to the presupposition-projection properties encoded in the proposition-taking denotations of the embedding predicates. I have also provided a compositional implementation of the central proposal, based on a definite-like semantics for the wh-item.
4 Matrix questions and rogative predicates
I have demonstrated that, once we assume that the UP/EP comes from the answers, we can correctly capture the projection patterns of the UP/EP in sentences involving wh-complements embedded under predicates such as know, be certain and agree. However, as I will discuss in detail below, the account so far does not readily explain the presence of the UP/EP in matrix questions as in (83), or the projection from under rogative predicates (those predicates that embed only interrogative complements; Lahiri 2002) as in (84).

In this section, I discuss how the current analysis can capture the data as of (83)–(84) with the help of additional assumptions.
4.1 UP/EP of matrix questions
Matrix questions, as exemplified in (85) below, seem to carry the UP/EP. (In examples involving matrix questions, I will hereafter indicate the UP/EP-like inferences with the symbol \({\mathop {\Rightarrow }\limits ^{\text{ presup }}} \), but I will refine this empirical description later and actually argue that it is an inference based on the speaker’s expectation, rather than a semantic presupposition.)

This fact cannot be immediately accounted for in the current proposal, where UP/EP comes from the answers. The reason for this is that the analysis only states that the answers carry the relevant presuppositions, and does not state that the question having such answers do.
Under the current proposal, the UP/EP-like inferences of matrix questions can be captured by assuming that information-seeking matrix questions in general come with the speaker’s expectation that at least one of their possible answers is defined. This can be stated as a pragmatic principle, following Guerzoni’s (2003) Question Bridge Principle, as follows:Footnote 29

Given the UP/EP encoded in each possible answer of a matrix wh-question, the principle in (86) is satisfied only if the speaker of such a question believes that the UP/EP is met. Hence, the data in (85) is captured as the combination of two factors: the answer-level UP/EP and the question-level speaker expectation in (86).
The account presented here can be illustrated using a matrix question involving a presupposition trigger within the clause, as follows:

We cannot capture the inference in (87) that there is a unique unicorn by the presupposition triggered by the definite DP the unicorn alone. This is so because, it is the possible answers to this question that carry the presupposition triggered by the definite, and we need a further mechanism to account for the fact that the question itself seems to imply that there is a unique unicorn. The pragmatic principle in (86) provides such a mechanism, and exactly the same explanation applies to the matrix effect of the UP/EP.
The account of the matrix EP/UP-like effect presented above is similar to the account of a matrix-level presupposition of which-questions discussed by Rullmann and Beck (1998, 226). According to R&B, the existential presupposition carried by each answer of a which-question projects to the matrix level due to the question-level presupposition, which requires that there be a true answer to a question. One crucial difference between R&B’s and my analysis (other than the content of the presupposition carried by each answer, discussed in Sect. 3.4 above) is the nature of the question-level presupposition. R&B treat the question-level presupposition as a semantic definedness condition. On the other hand, the principle above treats the question-level ‘presupposition’ as a pragmatic phenomenon. Consequently, the two accounts differ in whether the common ground or the speaker belief is required to entail the existence of a true answer (cf. also Guerzoni 2003).
I argue that the latter view—the pragmatic view based on the speaker’s expectation—is empirically more plausible, in light of the following kind of contrast between the inter-speaker and intra-speaker denial of the existence of a true answer, pointed out in Dayal (2016, 51) (cf. Karttunen and Peters 1976, 355):

As (88) shows, an interlocutor other than the questioner can overtly deny the existence of a true answer in the question denotation. In contrast, as shown in (89), it is odd for the questioner themself to overtly acknowledge the possibility that the question denotation does not contain a true answer.Footnote 30 This contrast is expected under the pragmatic view based on the speaker’s expectation while it is hard to capture under the semantic presupposition view, as far as I can see.
It is also worth noting that a pragmatic principle similar to (86) is assumed by Groenendijk and Stokhof (1984, 30–37) to account for what they call the existential ‘suggestion’ of matrix questions. However, their account is crucially different from mine in lacking the answer-level UP/EP. This has led to two empirical shortcomings in Groenendijk and Stokhof ’s treatment of the presuppositions of questions. First, since the UP/EP is treated entirely as a pragmatic phenomenon, it is not straightforward how to account for the projection patterns of UP/EP from under different embedding predicates. Second, the existential suggestion alone cannot account for the contrast between the UP triggered by singular-which questions and the EP triggered by plural-which and simplex-wh questions.
4.2 Projection from under rogative predicates
Another issue left open by the analysis presented in Sect. 3 is the treatment of cases involving rogative predicates, as exemplified in the following:

To account for this data within the current proposal, we have to state how the UP/EP carried by the answers of the embedded question is projected by the rogative predicate wonder. The analysis laid out in Sect. 3 does not automatically extend to rogative predicates. Here is why: the analysis in Sect. 3 employs the existential semantics for question-embedding by Spector and Egré (2015), which states the meaning of \(\ulcorner \) x Vs Q\(\urcorner \) in terms of the proposition-taking denotation of the predicate V. This strategy does not extend to rogative predicates since rogative predicates do not straightforwardly have proposition-taking denotations.Footnote 31
However, this simply means that the existential semantics for question-embedding employed in Sect. 3 cannot be used to analyze the presupposition-projection behavior of rogative predicates, and does not mean that the data in (90) is incompatible with the current central proposal. In fact, making a plausible assumption about the definedness condition of the question-taking denotation of rogative predicates enables us to account for their projection behavior, seen in (90). Furthermore, we will see that the structure of the additional assumption mirrors that of the pragmatic principle assumed in the account of the matrix effect above.
Under the current proposal, where each answer in the question denotation carries the UP/EP, the projection of the UP/EP in sentences involving wonder can be accounted for by assuming the following presupposition for \(\ulcorner \) x wonders Q\(\urcorner \):

When each proposition in Q carries the UP/EP, this presupposition is satisfied only if the attitude holder x believes the UP/EP. As one can easily see, the structure of this presupposition mirrors the pragmatic principle in (86) above. Above, we required that the questioner believe that the question has a defined answer. Here, we require that the wonderer believe that the question has a defined answer.
Just as in the case of the matrix effect discussed in the previous subsection, the analysis can be illustrated using an interrogative complement that involves a presupposition trigger inside the complement, such as the following:

Each possible answer of the interrogative complement in this example carries the presupposition that there is a unique unicorn. The condition in (91) predicts that this presupposition is projected by wonder to the attitude holder’s belief state, which is exactly the pattern we see in (92).
I argue that the condition along the lines of (91) is general to rogative predicates, such as investigate, be curious and inquire. This predicts the projection behavior concerning the UP/EP similar to the case of wonder for these rogative predicates. I submit that this is an empirically correct prediction.
4.3 Section summary
In this section, I have investigated how my central proposal that the UP/EP comes from the answers can be extended to the behavior of the UP/EP in matrix questions and sentences involving rogative predicates. Although the account presented in Sect. 3 cannot directly account for the data, it can do so by assuming plausible assumptions about the pragmatics of (information-seeking) matrix questions and the semantics of rogative predicates.
5 Conclusions and open issues
In this paper, I have pointed out that the projection pattern of the uniqueness/existential presupposition (UP/EP) of wh-questions under various question-embedding predicates poses problems for existing accounts of the UP/EP. Specifically, simply extending Dayal’s (1996) account based on the \(\textsc {Ans}\)-operator to question-embedding predicates in general incorrectly predicts that the UP/EP projects to the matrix level even with non-veridical predicates. Extending Dayal’s (1996) account based on Spector and Egré’s (2015) analysis of non-veridical predicates avoids the incorrect prediction that the UP/EP projects to the matrix level with non-veridical predicates. However, it fails to capture the fact that the presupposition projects to the attitude holder’s beliefs. Uegaki’s (2015) analysis, which encodes the relevant presupposition to the embedders, correctly captures the behavior of non-veridical predicates. Nevertheless, it makes incorrect predictions about the cases when the predicates embed declarative complements.
I have proposed a solution to the problems based on the idea that the UP/EP is carried by the answers in the question denotation. Once the UP/EP is encoded in the answers, the relevant projection behaviors are naturally accounted for, given two independently motivated mechanisms, i.e., existential semantics of question-embedding following Spector and Egré (2015) and the presupposition-projection behavior of individual predicates with respect to declarative complements.
Taking a step back, the current paper can be considered as contributing to the larger project that aims to construct a uniform semantics for question-embedding, currently being undertaken by a number of researchers working in the domain (e.g., George 2011; Spector and Egré 2015; Uegaki 2015; Xiang 2016; Theiler et al. 2018). Although few of the existing works specifically discuss the projection of the UP/EP, the discussion in this paper reveals that it can be properly analyzed without any significant modification to the overall semantics of question-embedding, once we assume that the answers carry the UP/EP. In the body of the paper, this is concretely shown by taking Spector and Egré’s (2015) theory of question-embedding. The current paper can be considered as providing a heretofore missing piece of the overall semantics of question-embedding.
As mentioned in Sect. 3.4, I have largely left open the issue concerning the internal composition of wh-complements, as I have focused on the analysis of the projection of the UP/EP within the context of the investigation of the semantics of question-embedding. However, it goes without saying that a more detailed investigation of the internal composition of the wh-complement provides a clearer view of the source of the UP/EP. In fact, in a recent paper, Hirsch and Schwarz (2019) argue that the UP of singular-which questions originates from the semantics of which (in a way similar to the picture I have suggested in Sect. 3.4) based on an observation that uniqueness can take scope below a position where the answerhood operator would normally take scope. It is possible that evidence from the embedding phenomena (as discussed in this paper) and that from the internal composition of wh-complements (as discussed by Hirsch and Schwarz 2019) converge to suggest that the UP/EP indeed originates from the answers, more specifically, from the semantics of the wh-element.
A related open issue is the analysis of the presupposition of non-constituent questions, such as alternative questions. If the UP/EP is attributed to the semantics of the wh-element, the presupposition of alternative questions (that exactly one of the alternatives is true) has to be accounted for in a separate fashion, possibly in terms of its intonation (e.g., Westera 2017). On the other hand, if the UP/EP is attributed to an operator that attaches to interrogative complements in general (as considered in Appendix A), a unified analysis of the presupposition of wh-complements and alternative questions would be possible. We need further empirical and theoretical investigation to properly compare the relative advantages of these two lines of analysis.
Change history
08 October 2021
A Correction to this paper has been published: https://doi.org/10.1007/s10988-021-09341-y
Notes
Note that the construction in (3) I am not sure if S, but [question] is in principle felicitous if S doesn’t violate the presupposition of the question, as can be seen in the following:
Here, I stay neutral as to whether each proposition in the question denotation contributes the UP/EP or a single answer of the question (e.g., picked out by an answerhood operator) contributes it. The first one of these two possible analyses will be presented in Sect. 3. The second possible analysis is presented in Appendix A.
The formulation using the predicate \(\textsc {Max}_{\text {inf}}\) is from Fox and Hackl (2007).
Following Heim and Kratzer (1998), I model presuppositions in terms of partial functions with the notation \(\lambda x: \pi (x).\varphi (x)\). Here, \(\pi (x)\) is the domain specification corresponding to the presupposition.
This is so since a morphologically singular NP denotes a set of atomic individuals (Sharvy 1980; Link 1983), and that a which-phrase ‘ranges over’ the denotation of the NP. This results in the set of propositions corresponding to these atomic individuals as the denotation of the whole clause. This is true both under the Karttunen -style and under the Hamblin -style compositional semantics for wh-clauses.
I assume that a linguistic expression is translated into a formula in an intermediate logical language similar to Ty2 (Gallin 1975), which then receives a model-theoretic interpretation. I notate ‘\(S \leadsto \varphi \)’ to indicate that the sentence S is translated into the formula \(\varphi \).
Here, I represent the question denotation as having the ‘de dicto’ reading, with the world index of the NP-part of the which-phrase bound by the lambda introducing the world-dependence. See Sect. 3.4 for the compositional derivation of ‘de re’ and ‘de dicto’ readings of which-questions following Beck and Rullmann (1999).
M. Erlewine (p.c.) pointed out to me that there seems to be a contrast between the projection patterns of the existential implication and the ‘less than two’ implication in (18). That is, although (18) sounds felicitous when there is in fact no student smoker (as long as Max believes that there is a student smoker), it sounds infelicitous when there are more than one student smokers. If it turns out that this judgment can be replicated systematically, the discussion in this paper should be viewed as concerning only the existential presupposition of wh-complements. At the same time, we would need an independent analysis of the ‘less than two’ implication that predicts matrix projection.
‘The Lafayette’ Vol. 114, No. 12. URL: http://digital.lafayette.edu/collections/newspaper/19871127/pdf (accessed on July 17, 2018).
More precisely, the presupposition concerning Kim’s beliefs is stronger than what is stated in (21). That is, the sentences presuppose that there is exactly one student such that Kim believes that they smoke. The same does not hold for the presupposition concerning Max’s beliefs. Since the weaker formulation of the presupposition in (21) suffices in the illustration of problems for existing analyses to be given below, I will stick to the weaker formulation in this section for the sake of simplicity. I will argue in Sect. 3.3.2 that my ultimate analysis captures the asymmetric presuppositions with respect to Max’s beliefs and Kim’s beliefs in the examples in (21).
One might have the impression that x is certain that p presupposes ‘x believes that p’. As long as we have the Hintikkan semantics for belief, i.e., truth of the proposition in all of the subject’s doxastic alternatives, the data suggest that be certain doesn’t presuppose belief. This is so because (22b) and (22c) clearly do not entail Max believes that Ash smokes in the Hintikkan sense. This still leaves open the possibility that be certain presupposes a weaker notion of belief, e.g., thinking the proposition likely (e.g. Hawthorne et al. 2016). As discussed in fn. 16 below, assuming this type of presupposition for be certain doesn’t affect my argument against the analysis of the projection of the UP/EP from under be certain considered here. Moreover, it does not affect my argument concerning agree below either.
Spector and Egré (2015) also posit a variant of this lexical rule where the answer in the assertive condition is also exhaustified, in order to capture the strongly-exhaustive reading. Also, here, I gloss over issues concerning the presuppositional monotonicity and the ‘sensitivity to false answers’ discussed in Sections 6 and 7 of Spector and Egré (2015). This simplification does not affect the argument here.
According to this rule, the answerhood in the presupposition always involves \(\textsc {Exh}\), i.e., it is ‘strongly-exhaustive’, even if the answerhood in the assertion is ‘weakly-exhaustive’. This is based on Spector and Egré ’s observation that emotive factives like surprise, which is typically associated with a weakly-exhaustive answer in their assertion involves a strongly exhaustive reading in the presupposition (Spector and Egré 2015, 1762–1764).
If \(\mathbf{certain}_w(p)(x)\) presupposes that x thinks p likely (see fn. 13 above), the predicted presupposition in (32b) would be that Max thinks some exhaustified Dayal-answer likely. This prediction still seems too weak, as it would be satisfied even if Max doesn’t rule out the possibility that no student smokes.
This is so because (37) is true iff every Dayal-answer is either incompatible with Max’s beliefs, or is entailed by it. See Theiler et al. (2018) for a similar treatment of be certain in terms of the notion of introspection.
Note that it is reasonable to assume that the predicate know in the intermediate language also presupposes the truth of the propositional argument. In such a case, the factivity is redundantly stated in (39), once by the factivity of know and once by \(\textsc {Ans}\). See Uegaki (2015) for a formulation where the attitude predicate in the intermediate language corresponding to know is non-veridical, and thus the factivity is solely contributed by \(\textsc {Ans}\).
It is in principle possible to define a lexical entry for the relevant predicates that avoids this issue, by making the entry sensitive to the cardinality of the proposition-set in the first argument. For example, the following lexical entry for be certain captures the presupposition projection behavior in the interrogative-embedding case while avoiding the problematic prediction in the declarative-embedding case:
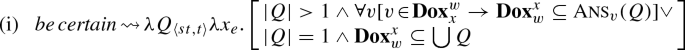
However, it is plausible to assume that there is a general constraint against a lexical entry that is sensitive to the cardinality of the proposition-set. This is so, since allowing such lexical entries leads to the danger of ruling in various empirically implausible lexical entries. One such lexical entry is *shknow discussed by Spector and Egré (2015), which would mean ‘know’ with declarative complements and ‘wonder’ with interrogative complements. See George (2011, Sect. 4.5.2), Theiler et al. (2018, Sect. 5) and Uegaki (2019, Sect. 6) for related discussion.
The parenthesized belief presupposition with know intuitively seems weaker compared with cases with the non-veridical predicates be certain and agree. I will discuss this in Sect. 3.2.
It might seem that the lexical rule in (49) is too simplistic in view of the various levels of exhaustivity involved in the readings of question-embedding sentences. Specifically, as it stands, the lexical rule only captures weak exhaustivity, but cannot capture strong exhaustivity or intermediate exhaustivity. In this paper, I will abstract away from the issue of exhaustivity, as it is orthogonal to our central concern—the projection pattern of the UP/EP. This simplification and the use of the lexical rule in (49) are warranted since the projection of the UP/EP only concerns the presuppositional part of (49), and Spector and Egré (2015) show that the presupposition of question-embedding sentences involves the one in (49), regardless of the level of exhaustivity in the assertive part. Exceptions to this statement are cases where a question is embedded by predicates that have downward-entailing presuppositions, such as realize and discover. In these cases, Spector and Egré (2015) argue that the presupposition is stronger than what would be predicted with exhaustification. Despite the difference, my analysis for other factive predicates (e.g., know) will carry over to these cases as well, as the analysis does not hinge on the presence of exhaustification in the presupposition.
Verbs of belief and conjecture (e.g., believe, think, expect, intend, suspect, assume), preferential/desiderative predicates (e.g., hope, fear, want, wish, be glad), as well as dubitative predicates (e.g., doubt) conform to this generalization (Karttunen 1973; Heim 1992). It doesn’t apply to some communication predicates, such as tell, say, and lie, as exemplified below:
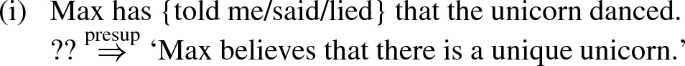
The pattern seems to be that the presupposition projection behavior in (55) is not observed for a subset of communication predicates that can be interpreted as describing an act of communication without the subject’s commitment. Although agree may be considered as a communication predicate, my sense is that it can’t describe the type of commitment-less communication that tell, say and lie can. This makes agree a predicate that is subject to the generalization in (55).
Two notes about the formula in (64). First, for the sake of simplicity, I use \(\exists \)! to indicate uniqueness here, but this is of course not intended as a general format of the logical translation of the UP/EP for wh-complements. My eventual compositional treatment of wh-complements makes use of the maximality presupposition, following Dayal (1996). This would derive the UP that is equivalent to (64) in the case of singular-which complements and an EP in the case of plural-which and simplex wh-complements. Second, I exemplify the analysis here with the de dicto reading of the NP-part of the which-phrase. In Sect. 3.4 below, I discuss how the corresponding de re reading can be derived, following Rullmann and Beck (1998).
Note that this reasoning holds regardless of the presence of the \(\textsc {Exh}\)-operator in the left-hand side. Since \(\textsc {Exh}\) makes the left-hand side stronger, we only have to prove that the left-hand side without \(\textsc {Exh}\) entails the right-hand side. The left-hand side without \(\textsc {Exh}\) holds iff some Dayal-answer is true in w. Since all Dayal-answers carry \(\mathbf{up}\) by assumption, \(\mathbf{up}\) is true in w.
This entailment holds for the following reason. If \({\mathbf{Dox}}^\mathbf{m}_w \subseteq \mathbf{up} \), there is a world in \({\mathbf{Dox}}^\mathbf{m}_w\) where only a specific student smokes. Let this world be \(w*\). Then \(w* \in {\mathbf{Dox}}^\mathbf{m}_w \wedge \textsc {Exh} _Q(\textsc {Ans} _{w*}(Q))(w*)\). Thus, the second conjunct holds. This reasoning holds even if we drop \(\textsc {Exh}\) because the 2nd conjunct of (iv) would be weaker without \(\textsc {Exh}\).
We predict the same presupposition even if \(\textsc {Exh}\) is dropped from the second conjunct of (73iv). This is so because \(\exists w'[\forall w''[w''\in {\mathbf{Dox}}_w^{\mathbf{k}} \rightarrow \textsc {Ans} _{w'}(Q)(w'')]\) holds only if \(\forall w''[w''\in {\mathbf{Dox}}_w^{\mathbf{k}} \rightarrow \mathbf{up} (w'')]\) because \(\textsc {Ans} _{w'}(Q)\) presupposes \(\mathbf{up} \) for any \(w'\) by assumption. Given that Kim believes \(\mathbf{up} \), if Kim believes a Dayal-answer, she believes its exhaustification.
In order for which to take scope over the materials in the TP, it has to be assumed that a wh-phrase internally merges to a projection below CP before internally merging to the specifier of CP.
Guerzoni’s (2003) Question Bridge Principle is different from (86) in that it is stated as a condition on the common ground, rather than on the speaker’s belief. The formulation of (86) as a condition on the speaker’s belief is crucial in view of the ease of inter-speaker cancellation of the existential/uniqueness inference of matrix questions, as will be argued below.
It is possible for the questioner to suspend the existence expectation using if any, as follows:
I argue that this construction involves a conditional question, as follows:
Following Isaacs and Rawlins (2008), I assume that conditional questions involve temporary contextual update. With respect to a temporary context in which Mary indeed likes some student, the speaker expectation that the question in the consequent contains a true answer is satisfied. Thus, (ii) does not involve any inconsistency in the speaker’s expectations. On the other hand, (89) above involves a genuine inconsistency. For, the first sentence states that the speaker considers it possible that Mary likes no student whereas the question in the second sentence invokes the speaker expectation (in the actual, non-temporary, context) that Mary likes some student.
There are attempts to analyze rogative predicates using proposition-taking semantics. For example, following suggestions in Karttunen (1977) and Guerzoni and Sharvit (2007) among others, Uegaki (2015) proposes a proposition-taking semantics for wonder, where it is decomposed into ‘want to know’. However, it is unclear if such a decompositional strategy is available for rogative predicates in general, including e.g., be curious, investigate and ask.
The operator preserves the presupposition on Q (i.e., \(\exists p\in Q[p = \textsc {Max}_{\text {inf}} (Q,w)]\)) from the original definition in order to guarantee that \(\textsc {Max}_{\text {inf}} (Q,w)\) is defined.
The equivalence between the two formulae in (98) is guaranteed by the following logical facts:
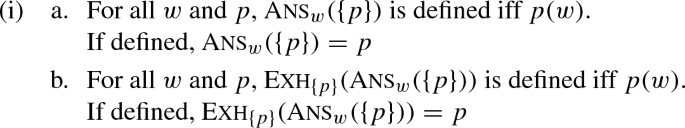
References
Abrusán, M., & Szendrői, K. (2013). Experimenting with the king of France: Topics, verifiability and definite descriptions. Semantics and Pragmatics, 6, 1–43.
Alonso-Ovalle, L., & Rouillard, V. (2019). Number inflection, Spanish bare interrogatives, and higher-order quantification. In M. Baird, & J. Pesetsky (Eds.), Proceedings of NELS 49, Vol. 1 (pp. 25–38). Amherst, MA: GLSA.
Beck, S., & Rullmann, H. (1999). A flexible approach to exhaustivity in questions. Natural Language Semantics, 7(3), 249–298.
Champollion, L., Ciardelli, I., & Roelofsen, F. (2017). On questions and presuppositions in typed inquisitive semantics. Handout for the talk given at the 2nd workshop on Inquisitiveness Below and Beyond the Sentence Boundary (InqBnB2), Amsterdam, 18–19 December 2017.
Ciardelli, I., & Roelofsen, F. (2015). Inquisitive dynamic epistemic logic. Synthese, 192(6), 1643–1687.
Comorovski, I. (1996). Interrogative Phrases and the Syntax-Semantics Interface. Dordrecht: Springer.
Cremers, A. (2016). On the semantics of embedded questions. Paris: École Normale Supérieure PhD dissertation.
Dayal, V. (1996). Locality in Wh-quantification: Questions and relative clauses in Hindi. Dordrecht: Kluwer Academic Publishers.
Dayal, V. (2016). Questions. Oxford: Oxford University Press.
Elliott, P. D., Nicolae, A. C., & Sauerland, U. (2018). Who and what do who and what range over cross-linguistically? Ms., Leibniz-Zentrum Allgemeine Sprachwissenschaft, Berlin.
Fox, D., & Hackl, M. (2007). The universal density of measurement. Linguistics and Philosophy, 29(5), 537–586.
Gallin, D. (1975). Intensional and higher-order modal logic: With applications to Montague semantics. Amsterdam: North-Holland.
George, B. R. (2011). Question embedding and the semantics of answers. Los Angeles, CA: University of California, Los Angeles PhD dissertation.
Groenendijk, J., & Stokhof, M. (1984). Studies on the semantics of questions and the pragmatics of answers. Amsterdam: University of Amsterdam PhD dissertation.
Guerzoni, E. (2003). Why even ask? On the pragmatics of questions and the semantics of answers. Cambridge, MA: MIT PhD dissertation.
Guerzoni, E., & Sharvit, Y. (2007). A question of strength: On NPIs in interrogative clauses. Linguistics and Philosophy, 30(3), 361–391.
Hamblin, C. L. (1973). Questions in Montague English. Foundations of Language, 10(1), 41–53.
Hawthorne, J., Rothschild, D., & Spectre, L. (2016). Belief is weak. Philosophical Studies, 173(5), 1393–1404.
Heim, I. (1992). Presupposition projection and the semantics of attitude verbs. Journal of Semantics, 9(3), 183.
Heim, I. (1994). Interrogative semantics and Karttunen’s semantics for know. In R. Buchalla & A. Mittwoch (Eds.), Proceedings of the ninth annual conference and the workshop on discourse of the Israel Association for Theoretical Linguistics (IATL) (pp. 128–144). Jerusalem: Academon.
Heim, I. (2016). Lecture notes on the semantics of interrogative clauses. Advanced Semantics (24.973), MIT Spring 2016. Accessible via https://stellar.mit.edu.
Heim, I., & Kratzer, A. (1998). Semantics in generative grammar. Oxford: Blackwell Publishers.
Hirsch, A., & Schwarz, B. (2019). Singular “which”, mention-some, and variable scope uniqueness. Proceedings of SALT, 29, 748–767. https://doi.org/10.3765/salt.v29i0.4637.
Isaacs, J., & Rawlins, K. (2008). Conditional questions. Journal of Semantics, 25, 269–319.
Karttunen, L. (1973). The last word. Austin, TX: University of Texas.
Karttunen, L. (1974). Presupposition and linguistic context. Theoretical Linguistics, 1(1–3), 181–194.
Karttunen, L. (1977). Syntax and semantics of questions. Linguistics and Philosophy, 1, 3–44.
Karttunen, L., & Peters, S. (1976). What indirect questions conventionally implicate. In S. Mufwene, C. Walker, & S. Steever (Eds.), CLS12: Papers from the twelfth regional meeting of the Chicago Linguistic Society (pp. 351–368). Chicago, IL: Chicago Linguistic Society.
Karttunen, L., & Peters, S. (1979). Conventional implicature. Syntax and Semantics, 11, 1–56.
Katz, J. J., & Postal, P. M. (1964). An integrated theory of linguistic descriptions. Cambridge, MA: The MIT Press.
Keenan, E., & Hull, R. (1973). The logical presuppositions of questions and answers. In J. S. Petöfi, & D. Franck (Eds.), Präsuppositionen in Philosophie und Linguistik (pp. 441–466). Frankfurt: Athenäum.
Lahiri, U. (2002). Questions and answers in embedded contexts. Oxford: Oxford University Press.
Link, G. (1983). The logical analysis of plurals and mass terms: A lattice-theoretical approach. In R. Bäuerle, C. Schwarze, & A. von Stechow (Eds.), Meaning, use, and interpretation of language (pp. 302–323). Berlin: De Gruyter.
Maldonado, M. (2020). Plural marking and d-linking in Spanish interrogatives. Journal of Semantics, 37(1), 145–170.
Rullmann, H. & Beck, S. (1998). Presupposition projection and the interpretation of which questions. Proceedings of SALT, 8, 215–232. https://doi.org/10.3765/salt.v8i0.2811.
Sharvy, R. (1980). A more general theory of definite descriptions. The Philosophical Review, 89(4), 607–624.
Spector, B., & Egré, P. (2015). A uniform semantics for embedded interrogatives: An answer, not necessarily the answer. Synthese, 192(6), 1729–1784.
Theiler, N., Roelofsen, F., & Aloni, M. (2018). A uniform semantics for declarative and interrogative complements. Journal of Semantics, 35(3), 409–466.
Theiler, N., Roelofsen, F., & Aloni, M. (2019). Picky predicates: Why believe doesn’t like interrogative complements, and other puzzles. Natural Language Semantics, 27(2), 95–134.
Uegaki, W. (2015). Interpreting questions under attitudes. Cambridge, MA: MIT PhD dissertation.
Uegaki, W. (2016). Content nouns and the semantics of question-embedding. Journal of Semantics, 33(4), 623–660.
Uegaki, W. (2018). On the projection of the presupposition of embedded questions. Proceedings of SALT, 28, 623–660. https://doi.org/10.3765/salt.v28i0.4411.
Uegaki, W. (2019). The semantics of question-embedding predicates. Language and Linguistics Compass, 13(1), 1–17.
Uegaki, W., & Sudo, Y. (2019). The \(^{*}\)hope-wh puzzle. Natural Language Semantics, 27(4), 323–356.
von Fintel, K. (2004). Would you believe it? The king of france is back! (Presuppositions and truth-value intuitions). In A. Bezuidenhout & M. Reimer (Eds.), Descriptions and beyond: An interdisciplinary collection of essays on definite and indefinite descriptions and other related phenomena (pp. 315–341). Oxford: Oxford University Press.
Westera, M. (2017). Exhaustivity and intonation: A unified theory. Amsterdam: ILLC, University of Amsterdam PhD dissertation.
Xiang, Y. (2016). Interpreting questions with non-exhaustive answers. Cambridge, MA: Harvard University PhD dissertation.
Xiang, Y. (2019). Higher-order readings of wh-questions. Ms., Rutgers University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
I would like to thank Lisa Cheng, Ivano Ciardelli, Alexandre Cremers, Danny Fox, James Griffiths, Irene Heim, Caroline Heycock, Brian Rabern, Floris Roelofsen, Bernhard Schwarz, Roger Schwarzschild, Rob Truswell, Alice Turk, as well as anonymous reviewers for Linguistics and Philosophy for helpful comments and discussion. All errors are my own. This is a substantially revised version of my 2018 paper ‘On the projection of the presupposition of embedded questions’ appeared in Proceedings of Semantics and Linguistic Theory 28.
Appendices
Appendix A: An alternative implementation
In the main text, I have provided an implementation of the analysis where each answer of the embedded question caries the UP/EP. This, however, is not the only possible implementation of the analysis. An alternative way to formulate the analysis is to redefine Dayal’s \(\textsc {Ans}\)-operator so that the relevant answer involved in the semantics of question-embedding always carries the UP/EP. A version of \(\textsc {Ans}\) redefined in such a way, which I call \(\textsc {Ans} '\), is given in (93b) below, together with the original definition of \(\textsc {Ans}\) in (93a).

The \(\textsc {Ans} '\)-operator presupposes that the ‘answer’ that it returns presupposes that the input Q contains a maximally strong true answer.Footnote 32 For example, when  (where each proposition is independent from each other) and only A is true in w, we have the following:
(where each proposition is independent from each other) and only A is true in w, we have the following:

That is, the answer A with the presupposition that the original proposition-set contains a maximally true answer.
Once we have this redefined version of the answerhood operator, the projection behavior of the UP/EP can be captured in exactly the same ways as in the analysis given in Sect. 3 of the main text. The other components of the analysis needed are the same as in the case of the analysis in the main text: the existential semantics for question-embedding (though defined in terms of \(\textsc {Ans} '\) instead of \(\textsc {Ans} \)) and the presuppositions of declarative-embedding sentences:

The projections of the UP/EP with know, be certain and agree are derived in exactly the same manners as in (67), (71), (73) in Sect. 3.3.2. This is so because every time we used Fact (65) to replace \(\pi (\textsc {Exh} _Q(\textsc {Ans} _{w'}(Q)))\) with \(\mathbf{up} \) in the derivations, we can simply use the fact that \(\textsc {Exh} _Q(\textsc {Ans} '_{w'}(Q))\) presupposes \(\mathbf{up} \) (given the redefined \(\textsc {Ans}\) ’) to replace \(\pi (\textsc {Exh} _Q(\textsc {Ans} _{w'}(Q)))\) with \(\mathbf{up} \).
More informally, the reason why the implementation in the main text and the implementation based on \(\textsc {Ans}\) ’ don’t make distinct predictions regarding the projection of the UP/EP can be stated as follows. In both implementations, the presupposition of an interrogative-embedding sentence is analyzed in terms of Spector and Egré’s (2015) lexical rule for question-embedding, which picks out a certain answer from the question denotation employing the answerhood operator. In both implementations, the answer picked out by the lexical rule caries the UP/EP, which projects to the sentential level in different ways depending on the embedding predicate. The difference between the two implementations lies in how the answer picked out by the lexical rule is guaranteed to carry the UP/EP. In analysis in Sect. 3, the answer caries the UP/EP since all answers in the question denotation do. On the other hand, in the analysis presented here, it does because of the redefined answerhood operator \(\textsc {Ans} '\).
Appendix B: An implementation within question-oriented semantics
Spector and Egré’s (2015) semantics for question-embedding assumes a proposition-oriented semantics for question-embedding predicates. That is, it assumes that the basic denotations of question-embedding predicates are proposition-taking ones, and that a lexical rule is required to convert them into question-taking counterparts. Uegaki (2015, (2016) and Theiler et al. (2018) offer a question-oriented semantics for question-embedding predicates, which goes against Spector and Egré’s (2015) assumption. According to this view, the basic denotation of a question-embedding predicate takes a question (qua a set of propositions), and a declarative complement is analyzed as providing a singleton proposition-set (or a downward-closed set of propositions with only one maximal set, in the case of Theiler et al. ). See Uegaki (2019) for a review of existing empirical arguments for preferring the question-oriented semantics over the proposition-oriented semantics for clause-embedding predicates.
Although the analysis in the main text is stated in terms of Spector and Egré’s (2015) lexical rule, the analysis is perfectly compatible with a question-oriented formulation. This is so since the question-taking denotation of a predicate resulting from the lexical rule can be considered as the basic denotation of the predicate, as exemplified below:

Given these denotations, the UP/EP carried by each answer in Q is predicted to project in the same way as in the analysis presented in Sect. 3, assuming the same presupposition-projection properties for the meta-language predicates know, certain and agree, as we have assumed in (54).
Furthermore, the analysis makes correct predictions for the declarative-embedding cases, once declarative complements are analyzed as having the singleton-set denotation, as in (97). Given the above lexical entries for the embedding predicates, the VP \(\ulcorner \) V that Ann smokes\(\urcorner \) is translated as in (98).Footnote 33

With the presuppositional properties of know, certain and agree, this results in the following empirically adequate logical translations of the VP with the concrete predicates:

In sum, although Spector and Egré’s (2015) semantics of question-embedding I will adopt in the main text assumes the proposition-oriented semantics for embedding predicates, my proposal is also compatible with the question-oriented semantics for the relevant predicates, along the lines of Uegaki (2015, (2016) and Theiler et al. (2018). Once we analyze the UP/EP as being carried by each answer of the question, the question-oriented denotations for the predicates would predict the correct projection pattern of the UP/EP. Furthermore, the analysis correctly captures the presupposition of the declarative-embedding cases as well, in terms of the presuppositional properties of the meta-language predicates.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Uegaki, W. The existential/uniqueness presupposition of wh-complements projects from the answers. Linguist and Philos 44, 911–951 (2021). https://doi.org/10.1007/s10988-020-09309-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10988-020-09309-4