Contextualizing vulnerability of ecological systems to landscape alteration

Abstract

Context

A variety of processes, such as urbanization and development projects, can degrade connectivity in habitat systems, presenting significant threats to species persistence. Effective mitigation of such threats depends in part on knowledge about where and when landscape changes may occur as well as how species may respond to changes in the landscape.

Objectives

A spatial decision support framework for informing planning efforts involving alterations to the landscape that may impact prospects for species’ inter-habitat connectivity is proposed.

Methods

As a variety of movement objectives are thought to influence species’ perception of habitat connectivity, efficient paths supporting movement among habitats in a planning period are identified by way of a multiobjective least-cost path model. This set of paths represent the best options for inter-habitat connectivity in a particular planning period. Provided this representation of inter-habitat connectivity, the worst-case scenario of landscape alteration on inter-habitat connectivity is then identified. This multi-level optimization process is repeated over a set of planning periods until inter-habitat connectivity has been completely eliminated.

Results

The results indicate that representing habitat connectivity with a limited set of paths reflecting a single objective for species movement could result in an overestimate of a habitat system’s resilience to landscape change over time. Representations of connectivity involving a more diverse set of paths reflecting tradeoffs among a set of objectives offer more robust representation of complex biological movements.

Conclusions

The application results indicate that landscape alterations occurring more proximate to habitat patches have the highest negative impact to connectivity. In addition, whereas alterations to the landscape may have no or little impact on inter-habitat connectivity in one planning period, when coupled with future alterations they can result in significant barriers to connectivity.

Introduction

Every day, decisions are made regarding the design and location of infrastructure such as roads, utility corridors, energy production facilities, housing, sound barriers, and parking lots. In many cases, those decisions translate to habitat loss and landscape fragmentation which can pose a major threat to species persistence (Brooks et al. 1999; Trombulak and Frissell 2000; Seto et al. 2012; Laurance et al. 2014). Considering the rapid pace of urbanization and infrastructure development, it is critical to understand the adverse impacts that alterations to the landscape may have on biodiversity and species persistence. One factor that is often thought to effect species persistence is the level of connectivity among habitat patches. However, quantifying the potential impact(s) that landscape alterations may have on habitat connectivity is very challenging given that the exact mixture of factors that define connectivity from the species’ perspective is often not known with a high level of certainty. Also, when assessing alternative scenarios of landscape modification, it is nearly impossible to envision what other changes to the landscape may occur in the future. For example, although a set of alterations to the landscape made today may not be viewed as detrimental to connectivity, coupled with subsequent alterations they may present significant barriers to connectivity in the future. To this end, this article describes a modeling approach for characterizing changes in inter-habitat connectivity given alterations to the landscape over time. The developed approach provides landscape planners with an effective tool for contextualizing alternative scenarios of landscape change that may be under consideration.

Habitat connectivity in landscape systems

Habitat connectivity refers to the degree to which movement among patches of habitats can be supported for a particular species (Baguette and Dyck 2007; Saura and Pascual-Hortal 2007). A variety of methods have been applied to assess habitat connectivity (McRae 2006; McRae and Beier 2007; Galpern et al. 2011; Saura et al. 2011). Network-based models of habitat connectivity represent patches of habitat in the landscape as nodes and the connections among nodes as arcs. To create a network representation of a habitat system, the region of interest can be modeled as a set of areal units of analysis (e.g., points, polygons, or grid cells). These features can be rendered as network nodes and the direct connections among them (e.g., for areas that are adjacent) can be rendered as arcs. Once the network has been defined, it can be used in numerous ways to characterize habitat connectivity and implications of changes to the system on connectivity. For example, a network representing prospects for inter-habitat connectivity at one point in time can be used to reason about its form and function in the future. That is, the change in overall connectivity before and after alterations have been made to habitats and/or connections can be tracked and used to help characterize vulnerabilities in the habitat network (Estrada and Bodin 2008).

Connectivity in this sense can be measured in a variety of ways (Hanski and Ovaskainen 2000; Jordán et al. 2003; Pascual-Hortal and Saura 2006; Estrada and Bodin 2008; Visconti and Elkin 2009; Bodin and Saura 2010). Regardless, the underlying assumption is that connectivity implies the presence of a feasible way of traversing the landscape between a pair of habitat patches. In other words, connectivity exists when there is a path or corridor that could potentially be used to facilitate inter-habitat movement (e.g., impedance or cost of traversal is not too restrictive). Likewise, connectivity between a pair of patches does not exist given the absence of a feasible path (e.g., impedance or cost of traversal is too high).

Whereas some studies have considered a single path or corridor among pairs of habitat patches, there is an increasing acknowledgement that prospects for inter-habitat connectivity might be better characterized as a set of alternative paths among each pair of habitat patches (Rayfield et al. 2010). For instance, the k-shortest and near-shortest path models are commonly used for identifying alternative paths among landscape features (Eppstein 1998; Lowe 2009). However, both the k-shortest and near-shortest path models can identify paths that are very similar, lacking diversity, a very special consideration in corridor modeling (Scaparra et al. 2014; Matisziw and Demir 2016). Another commonly applied approach is to identify sets of alternative paths between network origins and destinations that are forced to traverse specific intermediate nodes before reaching the destination, known as the gateway shortest path problem (Lombard and Church 1993; Pinto and Keitt 2009). Instead of focusing on a limited set of alternative paths, one might also consider enumeration of all potential paths connecting pairs of habitats. However, enumeration of paths is only practical for networks of relatively small size (Matisziw et al. 2007). Moreover, consideration of all paths of movement entails accounting for many paths that may be very unlikely to facilitate inter-habitat movement in practice. To help alleviate the sensitivity of least-cost paths to representations of geographic space, methods for modeling the direct connection among habitats as a broader geographic corridor have also been explored (Matisziw et al. 2015). An alternative to considering paths that are least-cost (or near least-cost) with respect to a single objective is to identify paths optimal with respect to a number of routing objectives that may factor into species’ decision-making when traversing the landscape. In this context, multiobjective least-cost path models seek to identify the set of Pareto-optimal paths, paths that represent optimal tradeoffs among the objectives. The Pareto-optimal solution set to a multiobjective least-cost path model consists of supported efficient solutions and unsupported efficient solutions (Skriver and Andersen 2000). All other feasible solutions that are not in the efficient solution set are considered inferior to or dominated by one or more efficient solution.

Modeling system change

In practice, changes to networks can be induced by a variety of phenomena such as accidents, natural disasters, and human intervention (Grubesic and Matisziw 2013). As detailed earlier, there is a need for contextualizing relative impacts to connectivity in a habitat network over time, such as those that may result from landscape alterations due to infrastructure development or landscape management projects. In such cases, a planning agency may have limited resources available for altering the landscape (e.g., road construction, landscape drainage, urban development, etc.) over a set of planning periods. Once the resources for landscape modifications available in one planning period have been used, the functionality of the landscape from the perspective of a species may change. Even though the impact to landscape connectivity for a species may not be extreme in one period, the cumulative impacts over time have the potential to compound the effects of connectivity loss. A variety of mathematical models have been proposed for identifying scenarios of change in networks (Losada et al. 2012; Matisziw et al. 2012; Li and Savachkin 2013; Starita and Scaparra 2016; Jiang and Liu 2018). In some instances, the worst-case and/or best-case scenario(s) of network change is sought (Church et al. 2004). The reason for this is that knowledge of the best and worst-case outcomes provides context for any other scenarios that could arise (e.g., proximity to best and/or worst-case scenarios). In cases where there are several entities acting upon a network in different, perhaps opposing ways, the process of network change over time can be modeled as a multi-player game (e.g., Stackelberg game) (Shen et al. 2012; Lei et al. 2018). In such approaches, one entity makes a decision to use/modify the network to optimize their planning objective(s) which is then followed by the other entity making a decision to use/modify the network to optimize their planning objective(s) in light of the actions of the other entity. For example, Acevedo et al. (2015) and Sefair et al. (2017) develop optimization models for identifying a set of sites to protect given future disturbance to some unprotected sites. In their modeling approach, the protected sites are determined by maximizing the minimum life expectancy resulting from a disturbance, while the effects of disturbance and protection on a population of interest are captured by discrete-time Markov chain.

The proposed framework in this research is a dynamic approach that considers spatial, temporal, and functional relationships among landscape features when characterizing the decision making processes underlying landscape change and species’ perception of habitat connectivity. The interplay between these two competing interests is evaluated over time. That is, in one period landscape connectivity for the species is evaluated and the set of paths that provide optimal connectivity are identified. In the next period, an entity expends resources to modify the landscape in a way that is most detrimental to habitat connectivity. Habitat connectivity from the standpoint of the species is then reassessed. This process is repeated over many periods to reason about what the worst-case scenarios of habitat system change may look like over time. Thus, any other scenario of landscape change can then be compared relative to the worst-case scenario, providing important context for planners, stakeholders, and decision-makers alike. Next, a modeling framework is described for identifying worst-case scenarios change to habitat systems. This framework involves identifying the best prospects for habitat connectivity in a period and then determining the most efficient way to degrade that connectivity via changes to the landscape. The developed methodology is then applied to a wetland system supporting amphibian populations to demonstrate its utility.

Methods

Consider a directed graph $G^{t}$ in time period $t \in T$ comprised of a set of $N^{t}$ nodes and $A^{t}$ arcs $\left( {G^{t} (N^{t} ,A^{t} )} \right)$ in which connectivity among a set of origin $o \in N^{t}$ and destination nodes $d \in N^{t}$ is of interest. A species is assumed to consider a set of objectives in reasoning about connectivity among pairs of habitats. In time $t$, a species identifies the set of efficient least-cost paths $EP_{od}^{t}$ optimizing connectivity between an origin–destination (od) pair with respect to the objectives. In other words, provided the current state of the landscape system, the suite of paths assumed to best support inter-habitat movement is known and is available to the species. The Multiobjective Habitat Connectivity Problem (MOHCP) can be used to identify these paths given the state of a habitat system at a particular point in time (Matisziw et al. 2020). Given a network $G^{t}$ in time $t$, traversal of arcs $(i,j) \in A^{t}$ is associated with a cost $c_{ijt}^{l}$ relative to each objective $l \in L$ thought to factor into movement decisions. For an origin $o \in N^{t}$ and destination node $d \in N^{t}$, the decision as to which arcs should $\left( {X_{ijt} = 1} \right)$ and should not be traversed $\left( {X_{ijt} = 0} \right)$ must be made. Therefore, the total cost of moving between an od pair relative to a particular objective is $\Phi_{l}^{t} = \sum\nolimits_{{(i,j) \in A^{t} }} {c_{ijt}^{l} } X_{ijt}$. The MOHCP for any period $t$ can be structured as follows.

$${\text{MOHCP}}:Minimize \, \left( {\Phi_{l}^{t} ,...,\Phi_{|L|}^{t} } \right)$$

(1)

s.t.

$$\sum\limits_{{j|(i,j) \in A^{t} }} {X_{ijt} - \sum\limits_{{j|(j,i) \in A^{t} }} {X_{jit} } } = \left\{ \begin{gathered} 1{\text{ for }}i = o \hfill \\ 0 \, \forall i \in N^{t} \backslash \{ o,d\} \hfill \\ {\text{ - 1 for }}i = d \hfill \\ \end{gathered} \right.$$

(2)

$$X_{ijt} = \{ 0,\;1\} \, \forall (i,\;j) \in A^{t}$$

(3)

Objective (1) minimizes inter-habitat traversal cost with respect to a set of routing objectives $l \in L$ in each time period $t \in T$. Constraints (2) ensure that if an arc on $\hat{G}^{t} (\hat{N}^{t} ,\hat{A}^{t} )$ enters node $i$ then one will exit node $i$, unless node $i$ is the origin or destination node. Constraints (3) are integer binary restrictions on arc decision variables. The model can be solved using approaches such as the Multicriteria All Non-dominated Least Cost Paths or MONISE Supported Non-dominated Least Cost Paths algorithms to identify a set of efficient solutions $EP_{od}^{t}$ for each od pair given the state of the network in time $t$ (Matisziw et al. 2020). An example describing different sets of solutions to multiobjective optimization problems as well as methods and algorithms to identify such solution sets can be found in Appendix A.

One way to characterize the worst-case scenario of connectivity loss in a planning period is to impose a practical limit on the resources available to modify the landscape in some way. For instance, consider an entity whose task is to induce changes to the landscape that maximally interfere with habitat connectivity. In any planning period, the entity has resources for making landscape changes that equate to making up to $\tau_{t}$ arcs non-traversable for the species of interest. Given the set of arcs in $\hat{G}^{t}$, the decision is then to select an arc $(i,j)$ for alteration $\left( {Q_{ijt} = 1} \right)$ or leave it unaltered $\left( {Q_{ijt} = 0} \right)$. Decisions to alter arc k in time t will impact whether a path connecting an od pair is traversable $\left( {Y_{odtk} = 1} \right)$ or not $\left( {Y_{odtk} = 0} \right)$, as well as whether connectivity between each od pair remains $\left( {Z_{od}^{t} = 0} \right)$ or been lost $\left( {Z_{od}^{t} = 1} \right)$. These decisions can be modeled in a manner similar to Matisziw et al. (2007) in the Connectivity Degradation Problem (CDP) that is described next.

Connectivity Degradation Problem (CDP)

$$Maximize \, \Gamma_{t} = \sum\limits_{o} {\sum\limits_{d} {Z_{od}^{t} } }$$

(4)

s.t.

$$\sum\limits_{{k \in EP_{od}^{t} }} {Y_{odtk} } + Z_{od}^{t} \ge 1 \, \forall o,d \in \hat{N}^{t}$$

(5)

$$Z_{od}^{t} \le \left( {1 - Y_{odtk} } \right) \, \forall o,d \in \hat{N}^{t} ,\forall k \in EP_{od}^{t}$$

(6)

$$Y_{odtk} \ge 1 - \sum\limits_{{(i,j) \in \Psi_{odtk} }} {(Q_{ijt} } + Q_{jit} {) }\forall o,d \in \hat{N}^{t} ,\forall k \in EP_{od}^{t}$$

(7)

$$Y_{odtk} \le (1 - Q_{ijt} - Q_{jit} ) \, \forall o,d \in \hat{N}^{t} ,\forall k \in EP_{od}^{t} ,\forall (i,j) \in \Psi_{odtk}$$

(8)

$$\sum\limits_{{(i,j) \in \hat{A}^{t} }} {Q_{ijt} } \le \tau_{t} + S_{t - 1} \, t \in T$$

(9)

$$Y_{odtk} = \{ 0,1\} \, \forall o,d \in \hat{N}^{t} ,\forall k \in EP_{od}^{t}$$

(10)

$$Z_{od}^{t} = \{ 0,1\} \, \forall o,d \in \hat{N}^{t}$$

(11)

$$Q_{ijt} = \{ 0,1\} \, \forall (i,j) \in \hat{A}^{t}$$

(12)

Objective (4) maximizes the connectivity loss between origin and destination habitats. Constraints (5) and (6) state that the best prospects for connectivity between an origin and destination habitat cannot be lost unless all efficient paths $k \in EP_{od}^{t}$ in that time period are lost. Constraints (7) and (8) ensure that if any arc in an efficient path $(i,j) \in \Psi_{odk}$ is selected for alteration, the path is no longer traversable $\left( {Y_{odtk} = 0} \right)$, and it is assumed that the loss of an arc in one direction $(Q_{ijt} = 1)$ or $(Q_{jit} = 1)$ disables connectivity in both directions. Constraints (9) limit the number of arcs selected for alteration to at most $\tau_{t} + s_{t - 1}$ in period t. $\tau_{t}$ is the base level of arcs that can be selected for alteration in a planning period. $s_{t - 1}$ are the number of arcs that were not selected for alteration in the prior planning period $s_{t - 1} = \tau_{t - 1} - \sum\limits_{{(i,j) \in \hat{A}^{t - 1} }} {Q_{ijt - 1} }$, reflecting unused resources that are available in the current period. Constraints (10)-(12) are binary-integer restrictions on decision variables.

Given that interdiction resources are limited in each time interval (limited to $\tau_{t} + s_{t - 1}$) and unused resources can be transferred into next time interval, it is important to assess if alternative solutions (i.e., configurations of $Q_{ijt}$) may exist that can yield the same optima for $\Gamma_{t}$. In cases where alternative optima exist, the solution maximizing connectivity loss with the lowest number of altered arcs should be found to represent the most efficient use of resources to achieve the objective. To accommodate this consideration, CDP model can first be solved to yield an optimal value of $\Gamma_{t}$. Next, a subsequent model, the Resource Minimizing CDP (RMCDP), can be structured to minimize the number of arcs selected for alteration in period $t$ required to disrupt connectivity to $\Gamma_{t}$ od pairs. Objective (13) minimizes the number of arcs to be selected for landscape alteration and Constraints (5)-(8) and (10)-(12) function as in the CDP. Constraint (14) ensures that the amount of resulting connectivity loss equals that optimized in the solution to model (4)-(12). Thus, the solution to the RMCDP is one in which the loss of connectivity is maximized and the resources (arcs) used to induce such a loss is minimized.

Resource Minimizing Connectivity Degradation Problem (RMCDP)

$$Minimize \, p_{t} = \sum\limits_{{(i,j) \in \hat{A}^{t} }} {Q_{ijt} }$$

(13)

s.t.

Equation (5)–(8) and (10)–(12)

$$\sum\limits_{o} {\sum\limits_{d} {Z_{od}^{t} } } = \Gamma_{t} \, t \in T$$

(14)

To track overall network connectivity degradation over time, the change in connectivity at time t ($\theta_{t}$) can be quantified as the ratio of the number of od pairs connected in time $t$ $(\lambda_{t} )$ with the number connected in $t - 1$ $(\lambda_{t - 1} )$ in (15) (Matisziw and Murray 2009).

$$\theta_{t} = {\raise0.7ex\hbox{${\lambda_{t} }$} \!\mathord{\left/ {\vphantom {{\lambda_{t} } {\lambda_{t - 1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\lambda_{t - 1} }$}} \, t \in T$$

(15)

Thus, $\theta_{t}$ ranges [0.0,1.0] with lower values indicating more dramatic impact to connectivity. Another measure for assessing connectivity is the total number of paths that exist in each period $t$, $\alpha_{t} = \sum\limits_{o} {\sum\limits_{d} {EP_{od}^{t} } }$. The change in objective values for efficient paths after each arc loss scenario is tracked using the measure $\beta_{t}$, defined as the proportion of efficient paths present in the current period $t$ that were identified in the prior period $t - 1$ in Eq. (16) as well. Given that efficient paths identified in earlier period are less costly than those found in subsequent periods, the higher values of $\beta_{t}$ indicate less negative impact to the quality of efficient paths for connectivity.

$$\beta_{t} = \frac{{\left| {\left\{ {EP_{od}^{t - 1} |o,d \in \hat{N}^{t - 1} } \right\} \cap \left\{ {EP_{od}^{t} |o,d \in \hat{N}^{t} } \right\}} \right|}}{{\left| {\left\{ {EP_{od}^{t} |o,d \in \hat{N}^{t} } \right\}} \right|}} \, t \in T$$

(16)

Modeling framework

The CDP and MOHCP can be used in tandem to determine the upper bound of habitat connectivity loss that can potentially occur due to landscape alterations as illustrated in Fig. 1. The initial input (Stage 1) is a network topology $\left( {G^{0} (N^{0} ,A^{0} )} \right)$, cost attributes for different movement objectives $(c_{ijt}^{l} )$, origin/destination habitats ($o \in N^{0}$ and $d \in N^{0}$), and arc loss limit $\tau_{0}$ ($s_{t - 1}$ is assumed to be zero in Period 0) which reflects the pace of landscape change. In Stage 2, a set of efficient paths optimizing multiple routing objectives reflecting species navigation decision when traversing the landscape are identified for time t using the MOHCP. Next, if any efficient paths connecting an od pair exist (Stage 3), connectivity metrics and objective values for the efficient paths are computed and reported (Stage 4). The CDP and RMCDP are then applied to identify the minimal set of arcs whose loss maximizes degradation of connectivity (Stage 5). It is assumed that arcs lost in one period are no longer viable in subsequent periods. The set $\Omega_{t}$ denotes all arcs that have been completely lost up to period $t$. The set of arcs that have been disrupted can be prevented from being used in a period through the addition of Constraint (17) to the MOHCP.

$$\sum\limits_{{(i,j) \in \Omega_{t} }} {X_{ijt} } = 0 \, t \in T$$

(17)

Fig. 1

Modeling framework for assessing habitat network degradation

Once a scenario of arc loss has been determined for time $t$, the set of efficient paths for the modified network $G^{t + 1}$ can then be re-computed (Stage 2). This re-assessment of efficient paths results in a completely or partially new set of efficient paths between each od pair, likely with higher average cost of traversal in comparison to those found in earlier iterations. The process of evaluating the system for the presence of efficient paths connecting od pairs and disrupting arcs (Stages 2—6) continues until viable paths among the od pairs no longer exist (Stage 7).

Study area and data

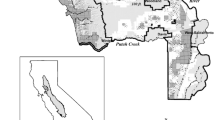
The habitat vulnerability assessment approach is applied to a wetland system (Fig. 2a) that consists of 12 wetlands that provide viable habitat for amphibian populations (Gholamialam and Matisziw 2020). Given each wetland can serve as both an origin and destination for amphibian movement, there are 132 origin–destination pairs ((12*12)-12) in the system. The network used to represent spatial variations in land use/land cover, elevation change, distance, and traversal risk for species movement between wetlands consists of 909 nodes and 1277 network arcs (Fig. 2b). In this experimental landscape network, three measures of cost are attributed to each arc: (a) traversal risk $c_{ijt}^{1}$, (b) deviation from favorable habitat $c_{ijt}^{2}$, (c) elevation change $c_{ijt}^{3}$. Using these cost attributes for each network arc, the best prospects for amphibian inter-habitat connectivity are modeled by minimizing traversal risk $\left( {Min \, \Phi_{1}^{t} = 1 - \prod\nolimits_{{(i,j) \in A^{t} }} {(1 - c_{ijt}^{1} )X_{ijt} } } \right)$, minimizing deviation from habitat with ideal soil moisture $\left( {Min \, \Phi_{2}^{t} = \sum\nolimits_{{(i,j) \in A^{t} }} {c_{ijt}^{2} } X_{ijt} } \right)$, and minimizing elevation change $\left( {Min \, \Phi_{3}^{t} = \sum\nolimits_{{(i,j) \in A^{t} }} {c_{ijt}^{3} } X_{ijt} } \right)$. In each period $t \in T$, the set of paths that optimize inter-habitat connectivity for amphibians are identified. In turn, the planning entity selects the set of arcs that degrades amphibian inter-habitat connectivity the most for landscape alteration in that period. This game continues until all inter-habitat connectivity has been lost. This process of landscape change is examined for eight different values of $\tau_{t}$ (5, 10, 15, 20, 25, 30, 35, 40), reflecting the level of resources available for landscape change in each period for three different model specifications that explore the implications of accounting for: a) all efficient paths (supported and unsupported), b) only supported efficient paths, and c) only a single least-cost path between each od pair. In total, 24 model parameterizations are examined in this respect. The algorithms used to model connectivity and landscape change are implemented using Python 3.7.9 on a Windows 10 64-bit with five 1.80 GHz processors and 16.0 GB RAM. The optimization solver Gurobi 9.0 is used to find optimal solutions to the CDP and RMCDP as well as supported efficient solutions to instances of the MOHCP.

Fig. 2

Study site: a example wetland system, b network representation of wetland system

Results

The results for 24 model parameterizations are reported in Table 1. In general, given lower levels of resources for landscape change (e.g., few arcs can be disrupted), the habitat network sustains more periods of alteration before connectivity is completely lost. For instance, given a scenario in which up to 5 arcs can be selected for alteration in each period and only a single least-cost path among each habitat pair is used to represent the best option for connectivity in each period, 62 periods of landscape alteration resulting in the loss of 122 arc are needed to eliminate connectivity. Provided the same resource base for landscape alteration in each period, when all efficient paths are used to represent connectivity among habitat pairs, connectivity can be completely disrupted in only 23 periods via the loss of 85 arcs. Likewise, when only the supported efficient paths (a subset of the efficient paths) are used to represent connectivity, 23 periods of change are also needed before all connectivity is lost. However, more resources (100 arcs) are needed to achieve the impact than was the case where all efficient paths were used to represent connectivity in each period. The network can persist through more periods when less paths are used to represent connectivity in each period not because less paths offer greater resilience, but rather because sparser representation of the system results in a greater amount of unused resource (large values of $s_{t}$) in each period.

Table 1 Computation time and total arcs rendered inoperable given different paces of landscape change $\tau_{t}$

Assessment and visualization of connectivity change

In Table 2 through Table 7, the change in inter-habitat connectivity modeled upon the three different sets of paths and two levels of arc loss, $\tau_{t} = 15$ and $\tau_{t} = 35$ for $t \in T$, is reported. In Tables, $p_{t}$ is the number of arcs lost in period $t$ $\left( {p_{t} = \sum\nolimits_{{(i,j) \in \hat{A}^{t} }} {Q_{ijt} } } \right)$, and all other variables are as previously defined. The gap between $\Gamma_{t}$ and $\lambda_{t}$ reflects the number of wetland pairs that remains connected after each landscape alteration scenario (Stage 2 of framework) and before constructing system connectivity again in the next period (Stage 4 of framework). The change in quality of paths after each landscape alteration scenario $\beta_{t}$ can then be evaluated. This metric fluctuates between 0.0 and 1.0, tending to be higher in earlier periods. Initially for $t = 0$, there are 132 least-cost paths, and 3,550 efficient paths (659 supported and 2,891 unsupported). Considering all efficient paths and given $\tau_{t} = 15$ as detailed in Table 2, connectivity among 94 wetland pairs is lost in Period $t = 0$. In Period 1, a new set of 3,871 efficient paths can be found such that connectivity is reestablished among all wetland pairs $(\theta_{1} = 1.0)$. However, in Periods 2 through 6, some wetland pairs lose connectivity which can no longer be replaced by inferior paths $(\theta_{t} < 1)$. The number of efficient paths reaches a high of 7,244 in Period 2 in which only 145 are carry overs from Period 1 $(\beta_{2} = 0.02)$. Also, out of the 3,871 paths found in Period 1,697 are carried over from those found in Period 0 $(\beta_{1} = 0.18)$. In Periods 3 and 4, there are very few paths carried over from earlier periods, but in all other subsequent periods there are no carry over paths $\beta_{t} \le 0.01$. Wetlands 9 and 10 are the only connected wetlands in the last three periods, finally losing connectivity in Period 11. Table 3 describes the model output using all efficient paths to represent connectivity scheme but with a higher level of resources for landscape change $\tau_{t} = 35$. In this case, $\beta_{t} = 0.0$ in all periods, indicating that in each period, every efficient path is rendered untraversable by the configuration of arcs selected for landscape alteration. Thus, in each subsequent period a completely new set of efficient paths need to be identified. Whereas there are 1,277 arcs in the habitat system, it should be noted that not all unaltered arcs need to be candidates for selection in each period as some may not host efficient paths. In Fig. 3, the location of arcs selected for landscape alteration for $\tau_{t} = 35$ are shown. In Period 0 (Fig. 3a), 32 arcs are selected for alteration indicating that these arcs are utilized by many efficient paths and their modification would impact inter-habitat connectivity the most. Of the 32 candidate arcs, 10 of the selected arcs were traversed by more than 356 paths (17.2%), 13 were traversed by 101 to 355 paths (4.7%), and 9 were traversed by less than 100 paths (1.4%). A similar trend can be observed in subsequent periods. As another example, in Period 1 (Fig. 3b) of the arcs selected for alteration, 13.1% were traversed by many paths, 2.9% were traversed by a moderate number of paths, and only 0.9% were traversed by a limited number of paths. Alteration of 10 arcs degrades connectivity among 56 od pairs in Period 2 (Fig. 3c) and alteration of seven arcs degrades connectivity among 42 od pairs in Period 3 (Fig. 3d). Wetlands 1, 5 and 7 remain connected in Period 4 (Fig. 3e), but only Wetlands 1 and 5 remain connected after Period 5 (Fig. 3f). Wetlands 1 and 5, sustain connectivity for two more periods, finally losing connectivity in Period 7 (Fig. 3h).

Table 2 Model output for each period $t$ considering all efficient paths and $\tau_{t} = 15$

Table 3 Model output for each period $t$ considering all efficient paths and $\tau_{t} = 35$

Fig. 3

Network utilization and worst-case set of arcs selected for alteration considering all efficient paths and $\tau_{t} = 35$ in Periods: a $t = 0$, b $t = 1$, c $t = 2$, d $t = 3$, e $t = 4$, f $t = 5$, g $t = 6$ and h) $t = 7$

As reported in Table 4, the model output for supported efficient paths where $\tau_{t} = 15$, it takes seven periods for the habitat network to completely collapse. The maximum number of supported efficient paths occurs in Period 1 in which complete connectivity among 132 wetland pairs still exists $\theta_{1} = 1$. In terms of quality of paths, there are some carry over paths in the first three periods (less than 5%) but in all later periods there are no instances where paths in one period persist in subsequent periods. When the level of resources for landscape change increases to $\tau_{t} = 35$, the habitat network can sustain nine periods of change as reported in Table 5 and Fig. 4. Of 25 arcs selected for alteration in Period 0 (Fig. 4a), 8 of them were traversed by more than 59 paths (13.5%), 11 were traversed by between 18–58 (4.6%), and 6 were traversed by less than 17 paths (1.5%). In Period 1 (Fig. 4b), of the selected arcs, 14.3% were traversed by many paths, 3.6% were traversed by a moderate number of paths, and only 0.2% were traversed by a limited number of the paths. Connectivity among 90 pairs of wetlands is lost in Period 2 through the alteration of 14 arcs (Fig. 4c). Out of these 90 pairs, connectivity among 42 of them can be reestablished in Period 3 (7 connected wetlands) through the identification of new efficient paths, whereas connectivity among the other 48 od pairs is lost indefinitely (Fig. 4d). Out of these 7 connected wetlands, connectivity among four of them can still be established in Period 4, whereas no prospects for connectivity among the other three remaining wetlands exists (Fig. 4e). Connectivity among three wetlands (1, 5 and 7) in Period 5 is impacted by the alteration of three selected arcs (Fig. 4f) and only two wetlands (1 and 5) remain connected in the last three periods. The location of arcs selected for alteration over different periods (Fig. 3 and Fig. 4) indicate that alteration of arcs located at the immediate vicinity of wetlands yields the greatest impact to connectivity. In addition, Wetlands 1, 5 and 7 exhibit greater level of resilience to landscape alteration surviving many periods of change as connectivity among them can be more readily reestablished given the large number of backup paths located in the Eastern portion of the study area.

Table 4 Model output for each period $t$ considering only supported efficient paths and $\tau_{t} = 15$

Table 5 Model output for each period $t$ considering only supported efficient paths and $\tau_{t} = 35$

Fig. 4

Network utilization and worst-case set of arcs selected for alteration considering only supported efficient paths and $\tau_{t} = 35$ in each Period: a $t = 0$, b $t = 1$, c $t = 2$, d $t = 3$, e $t = 4$, f $t = 5$, g $t = 6$, h $t = 7$ and i $t = 8$

In the case where only a single least-cost path is used to represent inter-habitat connectivity, the habitat system can persist through 16 periods of landscape alteration for $\tau_{t} = 15$ (Table 6) and 10 periods for $\tau_{t} = 35$ (Table 7). Given that only one least-cost path is used to represent connectivity among each pair of habitats in a period, the metric $\beta_{t}$ is not reported as it is not applicable. Also, the total number of paths is equal to the total number of connected wetland pairs in each period $\alpha_{t} = \lambda_{t}$, therefore, only $\lambda_{t}$ is reported. In Fig. 5, the location of least-cost paths and arcs selected for alteration given $\tau_{t} = 35$ are visualized for ten periods. Wetlands 2, 5, and 10 are the only connected wetlands in the last four periods of landscape change.

Table 6 Model output for each period $t$ considering only a single least-cost path and $\tau_{t} = 15$

Table 7 Model output for each period $t$ considering only a single least-cost path for each od pair and $\tau_{t} = 35$

Fig. 5

Network utilization and worst-case set of arcs selected for alteration considering only the least-cost path between each od pair and given $\tau_{t} = 35$ in Periods: a $t = 0$, b $t = 1$, c $t = 2$, d $t = 3$, e $t = 4$, f $t = 5$, g $t = 6$, h $t = 7$, i $t = 8$ and j $t = 9$

Distribution of path objective values

Whereas $\theta_{t}$, $\alpha_{t}$ and $\beta_{t}$ are global metrics (i.e., one measure of overall connectivity at each time period) of network connectivity, the objective values of paths identified in each period can be plotted for individual wetland pairs as a local network measure to provide direct insights into the change in inter-habitat connectivity under ongoing alteration to the landscape. As an example considering a single pair of wetlands (e.g., Wetlands 1 and 5), the objective values for paths optimizing some combination of traversal risk $\Phi_{1}$ (Fig. 6a), weighted distance $\Phi_{2}$ (Fig. 6b) and elevation change $\Phi_{3}$ (Fig. 6c) can be evaluated. Connectivity exists between Wetlands 1 and 5 for eight periods when considering all efficient paths, nine periods when considering supported efficient paths and five periods when considering only the least-cost path. In the initial period, the model considering all efficient paths and the model considering supported efficient paths have the same lower bound for the three routing objectives, and the lower bound monotonically increase in the next periods (Fig. 6a, Fig. 6b and Fig. 6c). The models considering only the least-cost path result in paths that have traversal risk (Fig. 6a) and elevation change (Fig. 6c) greater than that found for models involving efficient paths for 4 out of 5 periods. The models considering only the least-cost path did have relatively low deviation from suitable habitat (Fig. 6b) as compared to those considering the efficient paths the first three periods. However, by the fourth period, the deviation from suitable habitat associated with the least-cost path becomes relatively high as compared with the other solutions. Given that distance is optimized when considering only the least-cost path, the length of paths is also reported in Fig. 6d to compare the length of least-cost path to that of efficient paths found by solving the MOHCP. When considering the least-cost path as means of connectivity, the path length monotonically increases over the five periods (Fig. 6d). Given that the length of network arc is one of the terms in the second cost attribute when optimizing $\Phi_{2}$, the weighted distance of the least-cost path in Fig. 6b and the length of the least-cost path in Fig. 6d exhibit a similar trend over different periods.

Fig. 6

Box and Whisker diagram for path objective values: a $\Phi_{1}$, b $\Phi_{2}$, c $\Phi_{3}$ and d length from Wetland 1 to Wetland 5 considering all efficient paths, only the supported efficient paths, and only the least-cost paths providing connectivity among the od pairs given $\tau_{0} = 35$

Discussion

Species response to landscape change and connectivity loss is a complex, but critical dimension of conservation planning, one that is often neglected. Few studies have attempted to model the impact of sustained landscape alterations on inter-habitat connectivity using multi-level optimization approaches in which both the species and those altering the landscape are attempting to optimize the use of the system (Acevedo et al. 2015; Sefair et al. 2017). One problem reflects an effort to modify the landscape. The other problem reflects how habitat connectivity from the perspective of a species is changed in light of the modified landscape. However, other scenarios of landscape change such as those due to disruptive events (Ager et al. 2012), restoration efforts (Hearn et al. 2018), or random habitat loss (Yin et al. 2017) can be assessed and incorporated in the modeling framework (Fig. 1). In landscape change scenarios in which the habitat loss is known a priori, Constraint (17) can be directly updated in each period without the need to run CDP to identify the worst-case scenario in Stage 5 of the framework.

Most prior studies on habitat connectivity analysis are based on representing connectivity in a habitat system with one or a few least-cost paths connecting each od pair (Pinto and Keitt 2009; Rayfield et al. 2010; Sawyer et al. 2011; Numminen and Laine 2020). In addition to the least-cost path, a multiobjective least-cost path approach is considered to better account for more diverse paths connecting habitats, simultaneously accounting for three routing objectives. Two solution approaches are used to identify the efficient paths to the multiobjective least-cost path approach, a MONISE approach to identify the complete set of supported paths and a labeling algorithm to identify the complete set of efficient paths (supported and unsupported) (Matisziw et al. 2020).

The location at which landscape change occurs can impact the magnitude of habitat connectivity loss. Specifically, alteration of arcs traversed by many paths can result in greater connectivity loss as illustrated in Fig. 3, Fig. 4 and Fig. 5. In addition, inter-habitat connectivity persists longer when considering only one single path (least-cost path) between each od pair compared to when using many paths (efficient paths) given that a sparce representation of system leaves less arcs available for alteration in each period. Alteration of arcs directly connected to origin and destination habitat patches also appears to more quickly degrade habitat connectivity. This finding suggests that one strategy for habitat system conservation might be to limit alteration of the landscape in areas proximate to important habitat patches. The location and number of connected habitats as well as those of paths over different periods indicate that while some landscape change scenarios may initially have little impact on connectivity, when coupled with future changes present significant barriers to connectivity. For instance, all 132 wetland pairs are still connected in Period 1 after the first round of landscape change as reported in Table 2 through Table 7. Except for $\tau_{0} = 35$ when using the least-cost path (Table 7), the second round of landscape change also does not impact number of connected wetland pairs. However, some wetland pairs lose connectivity as early as in Period 3. For those wetlands that are connected for several periods before finally losing connectivity, the traversal cost increases over time. As an example, the increase in traversal cost with respect to each routing objective for paths connecting Wetland 1 to Wetland 5 can be observed in Fig. 6. Finally, if the overall quality of paths for habitat system as a whole is of interest, the global network metrics (15) and (16) can provide useful insights.

In this research, solution procedures based on NISE, MONISE and labeling algorithm are applied for solving instances of the MOHCP. A fruitful avenue for future research might be to solve this problem using other approaches (e.g., heuristics, other scalarization and labeling methods), contrasting and comparing their relative computational time and complexity. Another research direction could be to examine how network structure can be modified to reduce the computational burden. Other opportunities for future research could involve exploration of how and to what extent the Pareto-optimal representations of habitat connectivity align with actual observations of species movement. Further, given the unique nature of other study areas and applications, the modeling objectives proposed here could be extended to account for other planning goals and criteria.

Conclusion

As the landscape changes overtime, inter-habitat connectivity from the species’ perspective also likely changes. On one hand, there could be changes that facilitate/increase connectivity. On the other hand, there could be changes that degrade connectivity (e.g., loss of least-cost paths). When considering alternative scenarios for activities that can potentially impact habitat connectivity, it is therefore important to understand the relative impact they could have on connectivity. That is, what does the impact of one scenario look like with respect to others? Given there could be a myriad of planning alternatives, a more informative context is to compare the impact of a scenario with that resulting in the worst-case impact. In other words, out of all the scenarios of change to the habitat system that could be realized, which one would result in the greatest negative impact to connectivity? Identification of such a worst-case scenario is not easy though given the number of other scenarios that must be considered before a designation as worst-case can be mathematically proven. This research fills this gap in the literature and characterizes the interrelationship between habitat connectivity and landscape alteration and provides decision support for species conservation planning. The proposed framework consists of two main network optimization components, CDP and MOHCP, and identifies the worst-case scenario of landscape change given a set of viable paths for species movement. Given that the condition of the landscape is everchanging and development projects occur over time, it is essential to account for species adaption to the new environment at any given time over the planning horizon. To accomplish this goal, the best alternatives for habitat connectivity are reassessed after each landscape change scenario. Given a fixed amount of resources for landscape development in each period, the worst-case scenario of landscape change found by CDP is associated with maximal connectivity loss to habitat system.

Figure 7a depicts an example habitat network containing an origin ($o$) and destination ($d$) habitat node between which prospects for connectivity are to be assessed. There are two objectives thought to influence species movement in this case (Objectives 1 and 2) and the arc costs that are used to assess each objective are depicted respectively along each arc (e.g., for arc (a, d), cost 1 = 0.1 and cost 2 = 8). In this network, there are six feasible paths connecting the origin habitat node to destination habitat node: S1, S2, S3, S4, S5 and S6. The cost of traversing each path is the sum of the arc costs contributing to each objective. When considering the two objectives individually, Path S1 is the least costly with respect to Objective 1 whereas Path S6 is the least costly with respect to Objective 2. Path S4 represents a Pareto-optimal tradeoff between the two objectives. Paths S1, S4, and S6 constitute the set of supported, efficient solutions as they fall on the convex edge of the solution space as shown in Fig. 7b. The supported efficient paths can be identified using solution approaches such as the weighting method, NISE, and MONISE (Cohon et al. 1979; Balachandran and Gero 1985; Medrano and Church 2014; Raimundo et al. 2020). Whereas supported efficient paths are typically sought as they can be readily identified using traditional linear optimization approaches, research has found that in some instances, unsupported efficient paths can constitute a large proportion of the efficient solutions (Matisziw et al. 2020). Thus, they represent a key component of characterizing inter-habitat connectivity that is often overlooked. In the case of the example in Fig. 7, of the remaining solutions, Path S5 is an unsupported efficient solution, and it has lower cost with respect to Objective 2 and higher cost with respect to Objective 1 compared to Path S4, and lower cost with respect to Objective 1 and higher cost with respect to Objective 2 compared to Path S6. Unsupported (as well as supported) efficient paths can be found using multi-criterion labeling algorithms, dynamic programming, as well as heuristic approaches (Martins 1984; Skriver and Andersen 2000; Medrano and Church 2014; Gholamialam and Matisziw 2019). Paths S2 and S3 are inferior solutions as they are dominated by Paths S4 and S5, respectively.

Fig. 7

Illustration of inferior and efficient solutions for a biobjective least-cost path model. a network, b path objective values for supported, unsupported and inferior solutions