Abstract
Context
Connectivity assessments typically rely on resistance surfaces derived from habitat models, assuming that higher-quality habitat facilitates movement. This assumption remains largely untested though, and it is unlikely that the same environmental factors determine both animal movements and habitat selection, potentially biasing connectivity assessments.
Objectives
We evaluated how much connectivity assessments differ when based on resistance surfaces from habitat versus movement models. In addition, we tested how sensitive connectivity assessments are with respect to the parameterization of the movement models.
Methods
We parameterized maximum entropy models to predict habitat suitability, and step selection functions to derive movement models for brown bear (Ursus arctos) in the northeastern Carpathians. We compared spatial patterns and distributions of resistance values derived from those models, and locations and characteristics of potential movement corridors.
Results
Brown bears preferred areas with high forest cover, close to forest edges, high topographic complexity, and with low human pressure in both habitat and movement models. However, resistance surfaces derived from the habitat models based on predictors measured at broad and medium scales tended to underestimate connectivity, as they predicted substantially higher resistance values for most of the study area, including corridors.
Conclusions
Our findings highlighted that connectivity assessments should be based on movement information if available, rather than generic habitat models. However, the parameterization of movement models is important, because the type of movement events considered, and the sampling method of environmental covariates can greatly affect connectivity assessments, and hence the predicted corridors.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Landscapes across the globe are increasingly altered by human activities, causing substantial changes in habitat composition, configuration, and quality (Ellis et al. 2010). In fragmented landscapes, species persistence often depends on habitat connectivity and gene flow among subpopulations (Fischer and Lindenmayer 2007). Connectivity can also enhance resilience to climate change, because ranges of many species will likely shift (Bellard et al. 2012). Conservation planning thus aims to establish, maintain, and improve habitat connectivity and movement corridors (Rudnick et al. 2012).
Habitat connectivity, i.e., the degree to which landscapes facilitate or impede movement (Taylor et al. 1993), depends on both, landscape characteristics and species’ movement ability, which together determine a landscape’s permeability of movement for a species. In connectivity assessments, the landscape permeability is typically represented via a so-called resistance surface reflecting the local cost of movement for a given species through a particular environment due to behavioral and physiological factors such as aversion, energy expenditure, or mortality risk (Zeller et al. 2012). However, how resistance surfaces are defined can greatly influence the delineation of movement corridors, including their length and locations (Rayfield et al. 2011; Ziółkowska et al. 2014; Mateo Sánchez et al. 2015a). Defining ecologically meaningful resistance surfaces is thus critical (Trainor et al. 2013). Typically, resistance surfaces are derived by assigning different levels of resistance to land cover or land use categories, often based on expert opinion, resulting in resistance surface with discrete cost steps (Zeller et al. 2012), but many of the environmental factors influencing movement are continuous (Pflüger and Balkenhol 2014). Continuous resistance representations are, therefore, usually considered superior when representing how an animal experiences a landscape (Stoddard 2010).
The most common approach for deriving continuous resistance surfaces has been to parameterize a habitat suitability model (Guisan and Thuiller 2005; Elith and Leathwick 2009), and then to invert the habitat suitability index so that higher habitat suitability represents a lower cost for movement. Habitat models can be derived in a variety of ways, but are typically based on occurrence records (Elith and Leathwick 2009). This means that the underlying assumption of connectivity assessments based on habitat models is that preferred habitat also allows for easier movement (LaRue and Nielsen 2008; Ziółkowska et al. 2012; Trainor et al. 2013). This assumption remains largely untested though, and it is unlikely that the same environmental factors determine both animal movements and habitat selection, and at the same scales (Roever et al. 2014). This suggests that different input data, and potentially different modeling frameworks, should be used when modeling general habitat selection versus movement (Naves et al. 2003; Moe et al. 2007; Fernández et al. 2012; Mateo Sánchez et al. 2015a). Understanding how connectivity assessments are affected by relying on habitat models to define resistance surfaces is thus important for efficient corridor planning (Trainor et al. 2013; Elliot et al. 2014; Roever et al. 2014; Mateo Sánchez et al. 2015a, b).
To date there have been only few empirical studies that directly compare the ability of habitat suitability models to capture landscape resistance to movement against models based on actual movement data. For example, Mateo Sánchez et al. (2015a, b) compared resistance surfaces derived from habitat suitability and genetic-based models. However, while genetic data provide a synoptic measure of landscape resistance as they effectively integrate the movements of many individuals over time (Spear et al. 2010), pathway data can complement them as they provide unambiguous spatial representation of how animals move through the environment to meet their local resource needs (Zeller et al. 2012). Therefore it is important to evaluate the performance of pathway data in capturing resistance to movement against detection data.
Recent research in telemetry data analysis provides specific modeling frameworks to study animal movement based on pathway data (Kays et al. 2015). For example, step selection functions assess animals’ resource selection as they move through the landscape (Fortin et al. 2005) by comparing the characteristics of linear segments linking successive animal locations (‘steps’) with those available in the landscape (Thurfjell et al. 2014). Step selection functions have been successfully applied to investigate the effects of landscape structure on movement of large ungulates (Fortin et al. 2005; Coulon et al. 2008; Forester et al. 2009; Leblond et al. 2010; Bjørneraas et al. 2011; van Beest et al. 2012), carnivores (Dickson et al. 2005; Roever et al. 2010; Latham et al. 2011; Northrup et al. 2012; Squires et al. 2013), and forest birds (Richard and Armstrong 2010; Gillies et al. 2014). However, animals’ steps may reflect different types of behavior (Bruggeman et al. 2007), some of them active (e.g., foraging, walking), while others passive (e.g., bedding, standing; Killeen et al. 2014). Movement models should focus on steps that represent actual movement, but to our knowledge, distinction between active and passive steps has not yet been applied to parametrize resistance surfaces for corridor design.
Considering movement behavior is particularly important when assessing landscape connectivity for large mammals, because of their ability to move large distances in a relatively short amount of time. Moreover, large mammal populations require large, undisturbed habitats, which causes conflicts with people and land use in human-dominated landscapes. This makes their conservation challenging (Woodroffe 2000; Gordon 2009). This is why we focused on brown bear (Ursus arctos) as our model species to investigate habitat selection and movement behavior, and their relation to landscape connectivity. Brown bears are widely distributed across the northern hemisphere and occupy a variety of habitats, from tundra to temperate forests and even semi-deserts (Bojarska and Selva 2012). Bears are highly mobile and roam over large areas, particularly young males (Swenson et al. 2000). They are also a species of conservation concern in Europe despite the fact that their ranges have been relatively stable or even expanding in recent years, because their long-term persistence is threatened by habitat loss and fragmentation due to infrastructure and urban development (Chapron et al. 2014). Therefore it is important to understand how bears move in order to protect them and their habitat, especially in the Carpathians, one of the few places in Europe that holds a large population of bears, which, however, has been fragmented since the early twentieth century (Straka et al. 2012; Chapron et al. 2014).
Our main goal was to investigate how much resistance and connectivity estimates (including movement corridors and their characteristics) differ when based on habitat suitability models versus movement models derived from movement steps. In addition, we examined the sensitivity of those differences to models’ parameterization regarding (1) the type of movement steps (active versus all), and the method of measuring environmental covariates (averaged along steps versus measured at endpoints of steps) used in the movement models, and (2) the scale of predictor variables used in the habitat models.
Materials and methods
Study area
The Carpathian brown bear population, currently estimated at 7200 individuals, extends into Slovakia, Poland, Ukraine, Serbia, and Romania (Chapron et al. 2014). By the end of World War I, strong hunting pressure, deforestation, and agricultural expansion led to the dramatic decline and subdivision of the Carpathian population into a larger, eastern subpopulation and a smaller, isolated, western one (Fernández et al. 2012; Straka et al. 2012). Although both subpopulations increased after World War II, it remains unclear whether they are connected (Straka et al. 2012).
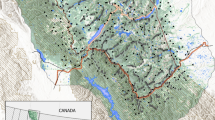
We focused on the northeastern part of the Carpathian brown bear population, including two areas where bears are permanently present (the Bieszczady Mountains in Poland, and the Poloniny Mountains in Slovakia), and a potential linkage zone to the western subpopulation (the Beskid Niski and Beskid Sądecki Mountains in Poland; Śmietana et al. 2014; Fig. 1). Both the brown bear population in Poland (<100 individuals) and Slovakia (800–1100 bears) are shared between neighboring countries (Selva et al. 2011; Chapron et al. 2014). The Bieszczady Mountains hold most of the brown bears in Poland (46–61 individuals in 2010; Selva et al. 2011), but the Poloniny Mountains are inhabited only by a small part of the brown bear population in Slovakia (at least 15 bears; Straka et al. 2013).
Study area in the northeastern Carpathians. Permanent and sporadic brown bear distribution is shown according to Chapron et al. (2014)
Brown bear telemetry data
We obtained telemetry data from nine brown bears (i.e., 15–20 % of the total brown bear population in the area according to Selva et al. 2011), including three females (two adults, one sub-adult) and six males (two adults, three sub-adults, one young individual) in 2008–2009 and 2014–2015 for a total of 57 months (Figs. 1, 2A). The tracking period for a single bear varied between 1 and 14 months. Bears were trapped in box or Aldrich traps and equipped with GPS–GSM collars (WildCell M collars, Lotek Wireless Inc., Canada; GPS-GSM PLUS collars Vectronic, Germany). Locations were recorded every 30 min or 5 h depending on the GPS device. We removed all fixes with a dilution of precision >10 (Cargnelutti et al. 2007), fixes located outside of our study area, and those for which locations were obviously erroneous (i.e., too far away from previous locations). For further analysis we used only locations with a 5-h time interval to ensure an equal sampling density for the entire tracking period (N locations = 4761, median N locations for a bear = 383, GPS-fix success rate including dilution of precision = 73 %).
Landscape variables
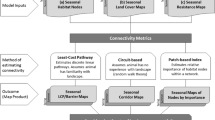
We chose potential predictor variables for the brown bear habitat and movement models based on previous studies (Güthlin et al. 2011; Koren et al. 2011; Fernández et al. 2012; Mateo Sánchez et al. 2013), and grouped them into land-cover, topography, and human-associated variables (Table 1; Fig. 2A).
We generated a land cover map with 30-m spatial resolution (with coniferous, deciduous and mixed forest, grasslands and shrubs) from five Landsat satellite images for 2011. To do so, we first segmented the image, and then conducted a supervised, hierarchical classification using a knowledge-based rule-set to extract training samples and a support vector machine classifier (Supplementary Fig. S1.1). The overall accuracy of our classification was 91.3 % evaluated based on an independent set of validation points (Supplementary Table S1.1).
In order to classify each forest pixel as either core forest or edge forest, we applied morphological spatial pattern analysis to our land-cover map (Vogt et al. 2007), using an edge width of 90 m (3 pixels). In addition, we separately delineated forest edges bordering grasslands and shrubs (Fernández et al. 2012). Topographic variables (elevation, elevation range, and slope) were calculated based on the Shuttle Radar Topography Mission (SRTM) digital elevation model, resampled to 30-m resolution, and settlements and roads were obtained from the Vector Map (VMap), level 2 (Table 1). All continuous variables were linearly rescaled to values between zero and one.
Multiscale habitat models often yield better predictions than single-scale models (Grand et al. 2004; Mateo Sánchez et al. 2013). We therefore evaluated all variables at six scales using circular moving windows with radii of 0.25, 0.5, 1, 2, 4, and 8 km (99.5 % of steps with 5-h time-interval were ≤8 km; Fig. 2A). For all binary variables (e.g., forest, forest edge), we calculated the percentage of variable occupancy in the moving window around every 30-m grid cell, and for continuous variables (e.g., elevation, distance from roads) we calculated the mean of variable values in the moving window around the cell (Table 1). For every variable we selected the scale at which it was most significant in the habitat and the movement models (see below). We evaluated all of the variables in terms of collinearity, and, if necessary, excluded one variable in pairs that had a Pearson correlation coefficient of 0.65 or greater.
Estimating movement models
To understand how landscape structure affects brown bear movement, we used step selection functions combined with case–control (conditional) logistic regression (Fortin et al. 2005; Coulon et al. 2008; Squires et al. 2013; Fig. 2B). For each observed step, we calculated its length (d) and turning angle (α) using R software (package ‘adehabitat’, v1.8.3; Calenge 2006). Steps were divided into ‘active’ and ‘passive’ based on step length, with all steps ≥1 km constituting ‘active’ steps (supplementary Fig. S2.1).
Each observed step was paired with five control steps that shared the same starting point, but differed either in length, direction, or both (Supplementary Fig. S2.2). The lengths and turning angles of control steps of a given individual were sampled from the observed ones of the other individuals in order to avoid problems of circularity (Fortin et al. 2005). To test if movement models were influenced by the random sampling of control steps, we considered five different sets of control steps. For each observed and control step we calculated (1) the average values of predictors along the step (based on all pixels which were crossed by a given step line), and (2) the exact values of predictors at the endpoints of steps (Thurfjell et al. 2014; Fig. 2B).
To select the appropriate scale for each predictor in our multiscale movement models [Fig. 2B(1)], we used univariate test of significance (Wilcoxon rank-sum/Mann–Whitney test) comparing observed and control steps, and selected the scale with the lowest p value. We further excluded all the predictors with p values higher than 0.25 as not differentiating between observed and control steps.
Spatial and-temporal autocorrelation inherent in movement data may biased standard errors of the coefficients estimated by the conditional logistic regression (Fortin et al. 2005; Craiu et al. 2008). To account for autocorrelation, we used a modified robust sandwich estimator, which required dividing observations into independent clusters. A cluster may consist of steps that are autocorrelated, as long as steps are independent among clusters (Fortin et al. 2005). Because distances among locations of all possible pairs of individual bears were on average >20 km, and pairs of bears were located within 100 m from each other in, on average, less than 1 % of cases, we considered the steps of individual bears as independent from each other. In addition, we investigated possible patterns of temporal autocorrelation in deviance residuals of our final regression models (with steps of individual bears as clusters; Fieberg et al. 2010) by following the procedure for data with uneven temporal spacing of Coulon et al. (2008). This approach involved fitting a variogram to the model residuals using the time of fixes instead of their location in geographical space. The resulting variograms showed no autocorrelation, which means that temporal autocorrelation in our input data did not affect the fit of our models.
We constructed two separate movement models, one model using all steps (movement models with all steps), and a second model using only active steps (movement models with active steps), with the ‘survival’ package (version 2.37-7; Therneau 2014) in R software. For both model types we considered predictors measured either (1) along steps (averaged), or (2) at endpoints of steps, which gave as in total four different brown bear movement models [Fig. 2B(2)].
For each of the five sets of observed and control steps we first fitted ‘full’ models using all independent variables selected with the multiscale approach, and then evaluated submodels consisting of all possible combinations of those variables using the quasilikelihood under the independence model information criterion value (QIC; Pan 2001), applicable for step selection functions (Craiu et al. 2008), with the ‘AICcmodavg’ package (version 2.0-3; Mazerolle 2015) in R software. We ranked and selected the best approximating models using delta QIC values, and calculated Akaike weights to obtain a measure of model selection uncertainty. We then averaged logistic coefficients across the five sets of observed and control steps and mapped brown bear movement surfaces by spatially applying step selection functions across the study area using the equation (Fortin et al. 2005):
where x 1 to x n were predictor variables, and β 1 to β n mean selection coefficients. We normalized brown bear movement surfaces by the sum of all grid cells in the study area to obtain relative (movement) occurrence rates, describing for each cell the relative probability that this cell was contained in a collection of movement samples (Merow et al. 2013). Finally, to remove the effect of outliers, we included only the range of relative occurrence rates contained within the 1–99th percentiles of the original movement models.
Predicting bear habitat suitability
We predicted habitat suitability using maximum entropy modeling (MaxEnt, version 3.3; Phillips et al. 2006; Fig. 2C), because it is a robust approach even for small sample sizes, and because it has higher predictive power than other modeling approaches (Elith et al. 2006; Wisz et al. 2008). The maximum entropy algorithm allows to model habitat suitability based on presence-only records, by contrasting the distribution of environmental attributes at occurrence locations with the distribution of the same attributes at a random selection of background points (Phillips et al. 2006). For all models runs, we employed a maximum of 2500 iterations, 10,000 random background points, a convergence threshold of 0.00001, and the default regularization settings. We ran ten-fold crossvalidation and calculated mean relative occurrences. To estimate variable importance, we used a jackknife procedure by measuring the test area under the receiver operating curve (AUC) for single variable models and models without the variable as well as gain changes in the MaxEnt function (Phillips et al. 2006).
In order to correct for potential sampling bias in our data, we employed a combination of spatial filtering of occurrence data and restricted background selection (Kramer-Schadt et al. 2013). First, we reduced the spatial clumping of occurrence data by randomly sampling only one record within a radius of 500 m to avoid clusters of locations (resulting from, for example, bears foraging or resting for a longer time). A radius of 500 m was a good compromise between receiving a sufficiently large number of locations for our models (~1000) while at the same time removing the majority of the spatial clumping in our occurrence data. To test if model outputs were influenced by the random sampling of occurrence records, we considered mean predictions from five different sets of presence points (mean N selected locations = 969). Second, because sampling background points from very broad areas can result in overly simplistic model predictions (Anderson and Burnham 2002; VanDerWal et al. 2009), we took background points only from the home range of our bears, estimated using minimum convex polygon (Fig. 1), and buffered by 13.2 km because this was the longest movement step in our dataset.
To select the appropriate scale for each predictor [Fig. 2C(1)], we created single-variable models and compared them using the AUC as a measure of relative variable importance (Golicher et al. 2012; Mateo Sánchez et al. 2013). For each variable, we selected the scale with the highest AUC value and excluded all other scales from further analysis (Mateo Sánchez et al. 2013). To evaluate how scale optimization affected the comparison between habitat and movement models, we also created the single-scale habitat models, i.e. with the same variables but all of them measured at a single scale. Therefore, we built six single-scale habitat models, each for one of the individual scales considered in the study [0.25, 0.5, 1, 2, 4, and 8 km; Fig. 2C(2)]. For all models, we used only quadratic and hinge features to avoid overfitting (Elith et al. 2011), and interpreted the raw output as relative occurrence rates (Merow et al. 2013). Finally, to remove outliers, we included only relative occurrence rates within the 1–99th percentiles of the original habitat models.
Resistance surfaces and connectivity assessment
To transform habitat and movement models into resistance surfaces (Zeller et al. 2012), we inverted and linearly rescaled the original values from 1 (the lowest resistance) to 100 [the highest resistance; Fig. 2B(3) and C(3)]. To compare habitat and movement models we assessed the spatial patterns and kernel density estimations of their resistance values. Lastly, we investigated the influence of different resistance surfaces on connectivity by comparing the spatial locations and characteristics of least-cost paths (i.e., paths with the minimum cumulative resistance between habitat nodes), and least-cost corridors (i.e., sets of cells for which the cumulative resistance between habitat nodes falls below a certain, user-defined threshold) delineated with the Linkage Mapper Toolkit in ArcGIS 10.2 (Fig. 2B(4), C(4); McRae and Kavanagh 2011). For each least-cost path, we calculated its (1) length, (2) ‘effective distance’, defined as the sum of cost values along the path multiplied by the grid cell dimensions (vertical/horizontal or diagonal), and (3) ‘absolute resistance’, defined as the ratio of effective distance to length. In order to compare least-cost paths and corridors among our models, we used the same set of nodes for all models. Nodes were those areas with the highest habitat suitability, calculated using an 8-km neighborhood. We further restricted this set of nodes to the area of permanent bear presence defined by Chapron et al. (2014). The least-cost paths and corridors were only constructed between a given node and its nearest neighbors (in terms of resistance), assuming that paths among more distant nodes will pass through nodes that are in-between.
Results
Movement models
We analyzed a total of 3872 movement steps, of which 36.5 % were classified as active. Our analysis revealed a substantial sensitivity of movement steps to predictors’ scale. Most land-cover variables as well as human-related variables (density of roads and settlements) were more strongly related to bear movement steps at fine scales (i.e., 0.25–0.5 km) than at medium and broad scales (i.e., 1–8 km) regardless of the type of movement steps used for the analysis. For slope and elevation range the relationship depended on the type of movement steps (fine scales for all steps, medium to broad scales for active steps), while for elevation it was strongest at the scale of 1 km regardless of the type of movement steps used for the analysis (Table 2).
Our evaluation of alternative submodels consisting of all possible combinations of independent variables resulted in several submodels that performed similarly well (i.e., delta QIC < 2). This is why we included in the final models the set of predictor variables that were most common in the five top-ranked submodels. In general, all movement models showed that brown bears preferentially traversed habitats with a high percentage of forest in the neighborhood or close to forest edges, with high topographic complexity, and with low human pressures, i.e., low density of roads and settlements, and far from settlements. Furthermore, bears selected mixed forests over forests with a high share of deciduous trees (Table 2). However, according to models based on all steps, the movement probabilities were much more driven by topographic complexity than land cover characteristics, comparing to models based on only active steps (Table 2).
Habitat models
Brown bear habitat suitability was also quite sensitive to the scale of the analysis. For most variables, the relation to bear habitat suitability was strongest (highest AUC values) for predictors measured at the scale of 8 km. Exceptions were the variables density of mixed forest, grasslands and density of settlements which were most strongly related to bear habitat suitability at the scale of 4 km. As a result, the multiscale habitat model (with a mean AUC of 0.835) did not differ significantly from the single-scale model measured at a scale of 8-km, both in terms of predictive performance (mean AUC of 0.832) and habitat suitability patterns that were predicted (Pearson correlation coefficient of 0.95; Table S3.1). The single-scale model with variables measured at a scale of 4 km was also highly correlated with the multiscale habitat model (Pearson correlation coefficient of 0.88; Table S3.1), but had much lower AUC values (mean AUC of 0.806). Single-scale models measured at fine and medium scales (0.25–2 km) showed both much lower discrimination ability (mean AUC from 0.731 to 0.785) than the multiscale habitat model, as well as considerably different patterns of habitat suitability across the study area (Supplementary Table S3.1).
Similarly to movement models, all our habitat models showed that brown bears selected forest-dominated habitats with a high density of forest edges, high elevation ranges, and low human disturbance (low density of roads and settlements, and far from roads and settlements). Bears preferred habitats dominated by mixed forests and forests with a medium share of deciduous trees, and avoided areas with a high density of grasslands. Elevation range, density of settlements and percentage of forest and mixed forest were the most important predictors, i.e., they accounted for the highest gain contributions and decreased test AUC substantially when omitted.
Comparison of resistance estimates
We found considerable differences among resistance surfaces based on movement (Supplementary Fig. S3.1) versus habitat models (Supplementary Fig. S3.2). However the magnitude and spatial pattern of these differences depended on models’ parameterization, i.e., the type of steps used (active versus all) in the movement models, and scale of predictor variables used in the habitat models. In general, the differences between habitat and movement models increased with increasing the scale of predictor variables used in habitat models, and were highest for the single-scale habitat model measured at the scale of 8 km (Pearson’s correlation coefficient from 0.31 to 0.44 depending on the movement model; supplementary Table S3.1), and the multiscale habitat model (Pearson’s correlation coefficient from 0.32 to 0.47 depending on the movement model; supplementary Table S3.1). Surprisingly, habitat models were stronger correlated with movement models with active steps than movement models with all steps, for all scales (Supplementary Table S3.1). The negative skewness of distributions of resistance values increased with increasing the scale of predictors in habitat models (from around −1.5 for models with fine-scale predictors to −2.4 for the multiscale habitat model and −2.6 for the habitat model measured at the scale of 8 km; Fig. 3).
Comparison of distribution of resistance values among habitat and movement models. As distributions of resistance values did not differ significantly between the single-scale habitat model with predictors measured at the scale of 8 km and the multiscale habitat model (Pearson’s correlation coefficient of 0.95), only density plot for the multiscale habitat model is shown in the figure
We found the highest share of high resistance values for the single-scale habitat models with predictors measured at broad scales of 4 and 8 km, and multiscale habitat model, and the lowest share of high resistance values for the movement models with active steps and movement model with all steps when predictors were measured at the endpoints of steps (Fig. 3). In general, the low resistance values were less scattered in the habitat models than in the movement models (Supplementary Fig. S3.3), with the degree of clumpiness, as measured by the contagion index, increasing with the scale at which the predictor variables used in the habitat models were measured (from 63.1 for the habitat model with predictors measured at the scale of 0.25 km, to 72.7 for the multiscale habitat model and 73.36 for the habitat model with predictors measured at the scale of 8 km), and only a few big clusters of low resistance values predicted in the single-scale habitat models with variables measured at broad scales of 4 km and 8 km, and in the multiscale habitat model [Supplementary Fig. S3.4 (E–G)]. In addition, areas with low resistance values in the habitat models were limited mainly to a narrow corridor in Poland, extending from the Bieszczady, through Beskid Niski to Beskid Sądecki Mountains (Supplementary Fig. S3.4), while they extended in the movement models to the Pogórze Przemyskie in the north-east of the study area (Supplementary Fig. S3.3), as well as to the Slovak part of the study area [in case of movement models with active steps; Supplementary Fig. S3.3 (1A, 2A)].
Comparison of least-cost corridors
We based our delineation of least-cost corridors and least-cost paths on 17 local maxima evenly distributed over the whole area permanently inhabited by the brown bears according to Chapron et al. (2014). Of these local maxima, three were located in the western part of the study area (one in the Levočské Mountains, and one in the Čergov Mountains in Slovakia; one in the Beskid Sądecki Mountains in Poland), eleven in the eastern part (three in the Poloniny Mountains in Slovakia; five in the Bieszczady Mountains, two in the Sanocko-Turczańskie Mountains, and one in the Pogórze Przemyskie in Poland), and three in the transition zone of the Beskid Niski in Poland (Figs. 4, 5).
Least-cost corridors (truncated at cumulative resistance of 200,000) delineated based on unscaled habitat models with predictors measured at a scale of (A) 250 m, (B) 500 m, (C) 1 km, (D) 2 km, (E) 4 km, (F) 8 km, and (G) multiscale habitat model in which the scale of analysis was independently optimized for each predictor variable (resulted in selection of predictors measured at broad scales of 4 and 8 km)
The predicted corridor network differed substantially among our resistance models (Figs. 4, 5). Corridors generated using resistance surfaces with higher shares of high resistance values, as in case of habitat models with predictors measured at medium and broad scales, tended to be shorter and less meandering (Fig. 5C–G). Although corridors linking nodes located in the eastern part of the study area (within and between the Bieszczady and Poloniny Mountains, and to the north to Pogórze Przemyskie) followed similar routes, major functional links connecting the western and eastern subpopulations differed strongly between movement and habitat models (Figs. 4, 5). These differences depended however on models’ parameterization, i.e., the method used to measure environmental covariates (averaged along steps versus measured at endpoints of steps) in the movement models, and scale of predictor variables used in the habitat models. In case of resistance surfaces based on movement models in which predictors were measured at endpoints of steps [Fig. 4(2A, 2B)] and single-scale habitat models with predictors measured at fine scales (Fig. 5A, B), corridors linking subpopulations converged into one main route along the Beskid Niski Mountains in Poland. In contrast, for the resistance surfaces based on movement models in which predictors were measured along steps [Fig. 4(1)], and habitat models with predictors measured at medium and broad scales (Fig. 5C–G), connections showed more extensive networks with two main routes (one along the Beskid Niski Mountains and one crossing the Slovak part of the study area) complemented by several secondary routes.
In general, least-cost paths generated based on habitat models with broad-scale predictor variables had the highest effective distances and absolute resistances (Supplementary Fig. S3.5) among all our models. Both effective distances and absolute resistances of least-cost paths increased with increasing the scale of predictor variables in the habitat models, however characteristics of least cost-paths generated based on habitat models with fine-scale predictors were more comparable to movement models (Supplementary Fig. S3.5). Among movement models, least-cost paths generated based on models with active steps were characterized by lower resistances comparing to models with all steps. The method used to measure environmental covariates also influenced least-cost paths’ characteristics, with paths based on movement models for which predictors were assessed at the endpoints of steps having lower resistances than paths based on models for which predictors were averaged along steps (Supplementary Fig. S3.5). However, those general patterns were not consistent across the study area (Fig. 6), and least-cost paths connecting nodes located within the core habitat area of the Bieszczady and Poloniny Mountains (e.g., no. 4 and 5 on Fig. 6) had much higher effective distances and absolute resistances when they were based on movement models with all steps than habitat models.
Comparison of (A) effective distances and (B) absolute resistances of connections delineated based on habitat and movement models. Characteristics of six selected strategic connections are shown only. The strategic connections were delineated between eight nodes scattered over the whole area permanently inhabited by the brown bears in our study area according to Chapron et al. (2014), and selected in such a way to characterize movement across both habitat areas (i.e., connections no. 4 and 5), sub-optimal areas (e.g., connections no. 2 and 3)
Discussion
Connectivity assessments are often based on continuous resistance surfaces that are derived from habitat suitability maps rather than movement data. However, habitat suitability may not always adequately reflect how the environment affects animal movement (Zeller et al. 2012; Elliot et al. 2014; Roever et al. 2014). Indeed, we found notable differences in the connectivity estimates derived from habitat models versus movement models, confirming that different environmental factors determined movement selection and habitat selection at different scales (Roever et al. 2014; Mateo Sánchez et al. 2015a). The magnitude and spatial patterns of these differences depended on models’ parameterization, i.e., the type of movement steps (active versus all), and the method of measuring environmental covariates (averaged along steps versus measured at endpoints of steps) used in the movement models, as well as on the scale of predictor variables used in the habitat models.
Comparing connectivity estimates based on habitat versus movement models
The resistance surface derived from the multiscale habitat model likely underestimated connectivity, because it resulted in substantially higher resistance values for most of the study area. In addition, least-cost corridors generated based on this resistance surface were, on average, shorter and less tortuous, and characterized by the highest effective distances and absolute resistances among the models that we compared. More importantly though, our results showed that the differences between multiscale habitat model and movement models differed across the study area, i.e., within optimal and sub-optimal areas. Congruent with Mateo Sánchez et al. (2015a), who analyzed movement corridors identified based on a multiscale habitat model against genetic data, we found that in areas with low habitat suitability, multiscale habitat model greatly overestimated resistance compared to models based on movement data, especially if only active steps were considered. In such sub-optimal areas, multiscale habitat model resulted in corridors with much higher effective distances and absolute resistances than movement models (Wasserman et al. 2010; Mateo Sánchez et al. 2015a). On the other hand, in core habitat areas, movement models predicted comparable (in case of movement models with active steps) or greater (in case of movement models with all steps) resistance than the multiscale habitat model, similar to findings for movement models based on genetic data (Mateo Sánchez et al. 2015a).
Influence of single versus multiscale habitat models
Interestingly, we found that major differences in resistance and connectivity estimates based on habitat versus movement models were only observed in case of the habitat models for which predictors were measured at broad spatial scales (including the multiscale habitat model). The best performing single-scale habitat models with predictors measured at scales of 4 km and 8 km resulted in similar resistance and connectivity estimates to the multiscale habitat model, while resistance surfaces based on single-scale habitat models in which predictors were measured at much finer scales were much less restrictive. As a result, networks of corridors based on fine-scale habitat models were more similar to those based on movement models. This suggests that the magnitude of discrepancies in connectivity estimates between the habitat and movement models is strongly depended on scale of predictors used to derive those models.
The difference in multiscale versus fine-scale habitat models in approximating resistance to movement is an important finding, because it suggests that habitat models can be a useful alternative to parametrize resistance to movement surfaces. While, our study confirmed that multiscale habitat models, in which the scale of the analysis is determined for each predictor variable separately, outperform single-scale habitat models (Wasserman et al. 2012; Mateo Sánchez et al. 2013), our results also showed that this increase in performance does not necessary coincide with better estimates of landscape resistance to movement. The reason for this is likely that movement through the landscape depends largely on the availability and use of local resources (Zeller et al. 2012), while habitat use may be also constrained by broad-scale patterns (Mateo Sánchez et al. 2013).
Our results have thus important implications when the goal is to protect movement corridors and plan conservation actions. We recommend, wherever possible, to conduct connectivity analyses based on actual movement data such as pathway or genetic data, and to use species distribution models based on detection data to predict probable habitat and derive patches suitable for resident populations (Squires et al. 2013; Mateo Sánchez et al. 2015a). However, if movement data are not available, habitat models with predictors measured at fine scales can be a proxy to derive resistance to movement surfaces.
Influence of movement model parameterization
In general, all of our brown bear movement models showed similar relationships to environmental heterogeneity as measured by our variables in the study area. However, the parametrization of models in terms of the type of analyzed movements steps, and the method selected to measure environmental covariates influenced the magnitude of those responses, and thus in effect also the estimates of resistance across the study area. Our results showed that movement models with all steps overestimated resistance compared to models with active steps, and that their performance in predicting effective distances of corridors was not consistent across the study area. Therefore, we suggest to, if at all possible, distinguish between different types of movement events (associated with different types of species’ behavior) when analyzing pathway telemetry data, and focus on those events that represent actual movement when parametrizing resistance to movement surfaces. Such distinction could be based not only on analysis of lengths and directions of movement steps as in our study, but also on direct measurements of activity levels by using GPS collars equipped with activity sensors recording the acceleration of the collar in two or three orthogonal directions (Gervasi et al. 2006; Löttker et al. 2009; Gottardi et al. 2010).
Resistance surfaces based on movement models where predictors were averaged along the steps predicted substantially higher resistance values than resistance surfaces based on movement models where predictors were measured at endpoints of steps. Covariates measured at endpoints of steps characterized conditions at actual animal’s relocations though, compared to the covariates measured along the steps which were based on the assumption that the animal moved in a straight line between two relocations. If the fix rate, which determines the temporal scale in step selection functions, is not optimally chosen for the studied species, averaging covariates along steps can thus lead to misleading results (Thurfjell et al. 2014). On the other hand, when only characteristics at endpoints of steps are considered, models become more prone to GPS-location errors and incidental extreme covariate values. Applying buffers to endpoints of steps and measuring covariates within those buffers can reduce this problem somewhat (Dickson et al. 2005).
Implications for brown bear conservation
In addition to our scientific findings, which are related to the resistance estimates and corridor assessment across species and landscapes, our results have important implications for the conservation of brown bear in the trans-boundary area of the northeastern Carpathians. Four main conservation messages emerge from this study. First, our study highlighted the importance of broad-scale patterns in determining habitat use of brown bears, as our best single-scale habitat model used predictors measured at the 8-km scale and the multiscale habitat model also included many predictors measured at such broad scales. Interestingly, the best-performing single-scale model tested by Mateo Sánchez et al. (2013) for brown bear in the Cantabrian Mountains also use predictors measured at a scale of 8 km, suggesting that this scale may be generally relevant for the species.
Second, our models confirmed the importance of forested areas with low human disturbance to maintain habitat suitability and connectivity (Kobler and Adamic 2000; Preatoni et al. 2005; Martin et al. 2010; Fernández et al. 2012; Martin et al. 2012; Mateo Sánchez et al. 2013, 2014). We also found high importance of topographic complexity. Preference for high topographic complexity in both habitat and movement models may be associated with better availability of heterogeneous nutritional resources, better sheltering opportunities, and less human access (Nellemann et al. 2007). Although topographic variables were not important in a previous, broad-scale habitat model of brown bear across Poland (Fernández et al. 2012), studies in other parts of Europe (Nellemann et al. 2007; Martin et al. 2010, 2012) and North America (Nielsen et al. 2006; Apps et al. 2013) also showed bear’s preference for rugged terrain.
Third, our results highlighted the need for regional planning of infrastructure and housing development and a strategic impact assessment. Currently, local spatial management plans are not obligatory in Poland, and the Carpathian Mountains have witnessed widespread unplanned housing growth, development of winter sport infrastructure, and new roads, often in remote areas (Selva et al. 2011; Fernández et al. 2012). Fourth, our movement models suggest that the linkage zone between the western and eastern Carpathian brown bear subpopulations is limited to a narrow corridor in Poland. Therefore, actions to protect, and potentially restore, the connectivity of bear habitat in the Carpathians are crucial for the conservation of brown bear (Selva et al. 2011) and likely of other large mammals.
Our results have important conservation implications beyond the Carpathians as well. Many conservation efforts for large mammals are aimed at protecting and enhancing connectivity to offset the impacts of habitat loss and fragmentation (Rudnick et al. 2012). Resistance surfaces underlie most connectivity assessments, and therefore it is important to better understand how their parameterization affects connectivity assessments (Rayfield et al. 2010; Elliot et al. 2014; Ziółkowska et al. 2014; Mateo Sánchez et al. 2015a). Our findings highlighted the importance of including movement data when parameterizing resistance surfaces, and to proceed with great caution when choosing the scale of environmental covariates, as well as their sampling methods.
References
Anderson DR, Burnham KP (2002) Avoiding pitfalls when using information-theoretic methods. J Wildl Manag 66:912–918
Apps CD, McLellan BN, Woods JG, Proctor MF (2013) Estimating grizzly bear distribution and abundance relative to habitat and human influence. J Wildl Manag 68:138–152
Bellard C, Bertelsmeier C, Leadley P, Thuiller W, Courchamp F (2012) Impacts of climate change on the future of biodiversity. Ecol Lett 15:365–377
Bjørneraas K, Solberg EJ, Herfindal I, Van Moorter B, Rolandsen CM, Tremblay J-P, Skarpe C, Sæther B-E, Eriksen R, Astrup R (2011) Moose Alces alces habitat use at multiple temporal scales in a human-altered landscape. Wildl Biol 17:44–54
Bojarska K, Selva N (2012) Spatial patterns in brown bear Ursus arctos diet: the role of geographical and environmental factors. Mamm Rev 42:120–143
Bruggeman JE, Garrott RA, White PJ, Watson FGR, Wallen R (2007) Covariates affecting spatial variability in bison travel behavior in Yellowstone National Park. Ecol Appl 17:1411–1423
Calenge C (2006) The package “adehabitat” for the R software: a tool for the analysis of space and habitat use by animals. Ecol Model 197:516–519
Cargnelutti B, Coulon A, Hewison AJM, Goulard M, Angibault JM, Morellet N (2007) Testing global positioning system performance for wildlife monitoring using mobile collars and known reference points. J Wildl Manag 71:1380–1387
Chapron G, Kaczensky P, Linnell JDC, von Arx M, Huber D, Andrén H, López-Bao JV, Adamec M, Álvares F, Anders O, Balčiauskas L, Balys V, Bedõ P, Bego F, Blanco JC, Breitenmoser U, Brøseth H, Bufka L, Bunikyte R, Ciucci P, Dutsov A, Engleder T, Fuxjäger C, Groff C, Holmala K, Hoxha B, Iliopoulos Y, Ionescu O, Jeremić J, Jerina K, Kluth G, Knauer F, Kojola I, Kos I, Krofel M, Kubala J, Kunovac S, Kusak J, Kutal M, Liberg O, Majić A, Männil P, Manz R, Marboutin E, Marucco F, Melovski D, Mersini K, Mertzanis Y, Mysłajek RW, Nowak S, Odden J, Ozolins J, Palomero G, Paunović M, Persson J, Potočnik H, Quenette P-Y, Rauer G, Reinhardt I, Rigg R, Ryser A, Salvatori V, Skrbinšek T, Stojanov A, Swenson JE, Szemethy L, Trajçe A, Tsingarska-Sedefcheva E, Váňa M, Veeroja R, Wabakken P, Wölfl M, Wölfl S, Zimmermann F, Zlatanova D, Boitani L (2014) Recovery of large carnivores in Europe’s modern human-dominated landscapes. Science 346:1517–1519
Coulon A, Morellet N, Goulard M, Cargnelutti B, Angibault J-M, Hewison AJM (2008) Inferring the effects of landscape structure on roe deer (Capreolus capreolus) movements using a step selection function. Landsc Ecol 23:603–614
Craiu RV, Duchesne T, Fortin D (2008) Inference methods for the conditional logistic regression model with longitudinal data. Biom J 50:97–109
Dickson BG, Jenness JS, Beier P (2005) Influence of vegetation, topography, and roads on cougar movement in Southern California. J Wildl Manag 69:264–276
Elith J, Leathwick JR (2009) Species distribution models: ecological explanation and prediction across space and time. Annu Rev Ecol Evol Syst 40:677–697
Elith J, Graham CH, Anderson RP, Dudík M, Ferrier S, Guisan A, Hijmans RJ, Huettmann F, Leathwick JR, Lehmann A, Li J, Lohmann LG, Loiselle BA, Manion G, Moritz C, Nakamura M, Nakazawa Y, Overton JM, Townsend Peterson A, Phillips SJ, Richardson K, Scachetti-Pereira R, Schapire RE, Soberón J, Williams S, Wisz MS, Zimmermann NE (2006) Novel methods improve prediction of species’ distributions from occurrence data. Ecography 29:129–151
Elith J, Phillips SJ, Hastie T, Dudík M, Chee YE, Yates CJ (2011) A statistical explanation of MaxEnt for ecologists. Divers Distrib 17:43–57
Elliot NB, Cushman SA, Macdonald DW, Loveridge AJ (2014) The devil is in the dispersers: predictions of landscape connectivity change with demography. J Appl Ecol 51:1169–1178
Ellis EC, Klein Goldewijk K, Siebert S, Lightman D, Ramankutty N (2010) Anthropogenic transformation of the biomes, 1700 to 2000. Glob Ecol Biogeogr 19:589–606
Fernández N, Selva N, Yuste C, Okarma H, Jakubiec Z (2012) Brown bears at the edge: modeling habitat constrains at the periphery of the Carpathian population. Biol Conserv 153:134–142
Fieberg J, Matthiopoulos J, Hebblewhite M, Boyce MS, Frair JL (2010) Correlation and studies of habitat selection: problem, red herring or opportunity? Philos Trans R Soc Lond B Biol Sci 365:2233–2244
Fischer J, Lindenmayer DB (2007) Landscape modification and habitat fragmentation: a synthesis. Glob Ecol Biogeogr 16:265–280
Forester JD, Im HK, Rathouz PJ (2009) Accounting for animal movement in estimation of resource selection functions: sampling and data analysis. Ecology 90:3554–3565
Fortin D, Hawthorne BL, Boyce MS, Smith DW, Duchesne T, Mao JS (2005) Wolves influence elk movements: behavior shapes a trophic cascade in Yellowstone National Park. Ecology 86:1320–1330
Gervasi V, Brunberg S, Swenson JE (2006) An individual-based method to measure animal activity levels: a test on brown bears. Wildl Soc Bull 34:1314–1319
Gillies CS, Beyer HL, St. Clair CC (2014) Fine-scale movement decisions of tropical forest birds in a fragmented landscape. Ecol Appl 21:944–954
Golicher D, Ford A, Cayuela L, Newton A (2012) Pseudo-absences, pseudo-models and pseudo-niches: pitfalls of model selection based on the area under the curve. Int J Geogr Inf Sci 26:2049–2063
Gordon IJ (2009) What is the future for wild, large herbivores in human-modified agricultural landscapes? Wildl Biol 15:1–9
Gottardi E, Maublanc M, De E (2010) Use of GPS activity sensors to measure active and inactive behaviours of European roe deer (Capreolus capreolus). Mammalia 74:355–362
Grand J, Buonaccorsi J, Cushman SA, Griffin CR, Neel MC (2004) A multiscale landscape approach to predicting bird and moth rarity hotspots in a threatened pitch pine-scrub oak community. Conserv Biol 18:1063–1077
Guisan A, Thuiller W (2005) Predicting species distribution: offering more than simple habitat models. Ecol Lett 8:993–1009
Güthlin D, Knauer F, Kneib T, Küchenhoff H, Kaczensky P, Rauer G, Jonozovič M, Mustoni A, Jerina K (2011) Estimating habitat suitability and potential population size for brown bears in the Eastern Alps. Biol Conserv 144:1733–1741
Kays R, Crofoot MC, Jetz W, Wikelski M (2015) Terrestrial animal tracking as an eye on life and planet. Science 348:aaa2478
Killeen J, Thurfjell H, Ciuti S, Paton D, Musiani M, Boyce MS (2014) Habitat selection during ungulate dispersal and exploratory movement at broad and fine scale with implications for conservation management. Mov Ecol 2:15
Kobler A, Adamic M (2000) Identifying brown bear habitat by a combined GIS and machine learning method. Ecol Model 135:291–300
Koren M, Find’o S, Skuban M, Kajba M (2011) Habitat suitability modelling from non-point data. The case study of brown bear habitat in Slovakia. Ecol Inf 6:296–302
Kramer-Schadt S, Niedballa J, Pilgrim JD, Schröder B, Lindenborn J, Reinfelder V, Stillfried M, Heckmann I, Scharf AK, Augeri DM, Cheyne SM, Hearn AJ, Ross J, Macdonald DW, Mathai J, Eaton J, Marshall AJ, Semiadi G, Rustam R, Bernard H, Alfred R, Samejima H, Duckworth JW, Breitenmoser-Wuersten C, Belant JL, Hofer H, Wilting A (2013) The importance of correcting for sampling bias in MaxEnt species distribution models. Divers Distrib 19:1366–1379
LaRue MA, Nielsen CK (2008) Modelling potential dispersal corridors for cougars in midwestern North America using least-cost path methods. Ecol Model 212:372–381
Latham ADM, Latham MC, Boyce MS, Boutin S (2011) Movement responses by wolves to industrial linear features and their effect on woodland caribou in northeastern Alberta. Ecol Appl 21:2854–2865
Leblond M, Dussault C, Ouellet J-P (2010) What drives fine-scale movements of large herbivores? A case study using moose. Ecography 33:1102–1112
Löttker P, Rummel A, Traube M, Stache A, Šustr P, Müller J, Heurich M (2009) New possibilities of observing animal behaviour from a distance using activity sensors in GPS-collars: an attempt to calibrate remotely collected activity data with direct behavioural observations in red deer Cervus elaphus. Wildl Biol 15:425–434
Martin J, Basille M, Van Moorter B, Kindberg J, Allainé D, Swenson JE (2010) Coping with human disturbance: spatial and temporal tactics of the brown bear (Ursus arctos). Can J Zool 88:875–883
Martin J, Revilla E, Quenette P-Y, Naves J, Allainé D, Swenson JE (2012) Brown bear habitat suitability in the Pyrenees: transferability across sites and linking scales to make the most of scarce data. J Appl Ecol 49:621–631
Mateo Sánchez MC, Cushman SA, Saura S (2013) Scale dependence in habitat selection: the case of the endangered brown bear (Ursus arctos) in the Cantabrian Range (NW Spain). Int J Geogr Inf Sci 28:1531–1546
Mateo Sánchez MC, Balkenhol N, Cushman SA, Perez T, Dominguez A, Saura S (2015a) Estimating effective landscape distances and movement corridors: comparison of habitat and genetic data. Ecosphere 6:Article 59
Mateo Sánchez MC, Balkenhol N, Cushman SA, Perez T, Dominguez A, Saura S (2015b) A comparative framework to infer landscape effects on population genetic structure: are habitat suitability models effective in explaining gene flow? Landsc Ecol 30:1405–1420
Mateo-Sánchez MC, Cushman SA, Saura S (2014) Connecting endangered brown bear subpopulations in the Cantabrian range (north-western Spain). Anim Conserv 17:430–440
May R, Van Dijk J, Wabakken P, Swenson JE, Linnell JDC, Zimmermann B, Odden J, Pedersen HC, Andersen R, Landa A (2008) Habitat differentiation within the large-carnivore community of Norway’s multiple-use landscapes. J Appl Ecol 45:1382–1391
Mazerolle MJ (2015) Package “AICcmodavg”. Model selection and multimodel inference based on (Q)AIC(c). http://cran.r-project.org/web/packages/AICcmodavg/AICcmodavg.pdf
McRae BH, Kavanagh DM (2011) Linkage mapper connectivity analysis software. The Nature Conservancy, Seattle. http://www.circuitscape.org/linkagemapper
Merow C, Smith MJ, Silander JA (2013) A practical guide to MaxEnt for modeling species’ distributions: what it does, and why inputs and settings matter. Ecography 36:1058–1069
Moe TF, Kindberg J, Jansson I, Swenson JE (2007) Importance of diel behaviour when studying habitat selection: examples from female Scandinavian brown bears (Ursus arctos). Can J Zool 85:518–525
Naves J, Wiegand T, Revilla E, Delibes M (2003) Endangered species constrained by natural and human factors: the case of brown bears in northern Spain. Conserv Biol 17:1276–1289
Naves J, Fernández-Gil A, Rodríguez C, Delibes M (2006) Brown bear food habits at the border of its range: a long-term study. J Mammal 87:899–908
Nellemann C, Støen OG, Kindberg J, Swenson JE, Vistnes I, Ericsson G, Katajisto J, Kaltenborn BP, Martin J, Ordiz A (2007) Terrain use by an expanding brown bear population in relation to age, recreational resorts and human settlements. Biol Conserv 138:157–165
Nielsen SE, Stenhouse GB, Boyce MS (2006) A habitat-based framework for grizzly bear conservation in Alberta. Biol Conserv 130:217–229
Northrup JM, Pitt J, Muhly TB, Stenhouse GB, Musiani M, Boyce MS (2012) Vehicle traffic shapes grizzly bear behaviour on a multiple-use landscape. J Appl Ecol 49:1159–1167
Ordiz A, Støen OG, Delibes M, Swenson JE (2011) Predators or prey? Spatio-temporal discrimination of human-derived risk by brown bears. Oecologia 166:59–67
Pan W (2001) Akaike’s information criterion in generalized estimating equations. Biometrics 57:120–125
Pflüger FJ, Balkenhol N (2014) A plea for simultaneously considering matrix quality and local environmental conditions when analysing landscape impacts on effective dispersal. Mol Ecol 23:2146–2156
Phillips SJ, Anderson RP, Schapire RE (2006) Maximum entropy modeling of species geographic distributions. Ecol Model 190:231–259
Posillico M, Meriggi A, Pagnin E, Lovari S, Russo L (2004) A habitat model for brown bear conservation and land use planning in the central Apennines. Biol Conserv 118:141–150
Preatoni D, Mustoni A, Martinoli A, Carlini E, Chiarenzi B, Chiozzini S, Van Dongen S, Wauters LA, Tosi G (2005) Conservation of brown bear in the Alps: space use and settlement behavior of reintroduced bears. Acta Oecol 28:189–197
Rayfield B, Fortin M-J, Fall A (2010) The sensitivity of least-cost habitat graphs to relative cost surface values. Landscape Ecol 25:519–532
Rayfield B, Fortin M-J, Fall A (2011) Connectivity for conservation: a framework to classify network measures. Ecology 92:847–858
Richard Y, Armstrong DP (2010) Cost distance modelling of landscape connectivity and gap-crossing ability using radio-tracking data. J Appl Ecol 47:603–610
Roever CL, Boyce MS, Stenhouse GB (2010) Grizzly bear movements relative to roads: application of step selection functions. Ecography 33:1113–1122
Roever CL, Beyer HL, Chase MJ, van Aarde RJ (2014) The pitfalls of ignoring behaviour when quantifying habitat selection. Divers Distrib 20:322–333
Rudnick DA, Ryan SJ, Beier P, Cushman SA, Dieffenbach F, Epps CW, Gerber LR, Hartter J, Jenness JS, Kintsch J, Merenlender AM, Perkl RM, Preziosi DV, Trombulak SC (2012) The role of landscape connectivity in planning and implementing conservation and restoration priorities. Issues Ecol 16:1–23
Selva N, Zwijacz-Kozica T, Sergiel A, Olszańska A, Zięba F (2011) Management plan for the brown bear Ursus arctos in Poland. University of Life Sciences, Warszawa
Śmietana W, Matosiuk M, Czajkowska M, Ratkiewicz M, Rutkowski R, Buś-Kicman M, Jakimiuk S (2014) An estimate of distribution and numbers of brown bear Ursus arctos(L.) in the eastern part of Polish Carpathian Mountains. Rocz Bieszczadzkie 22:289–301
Spear SF, Balkenhol N, Fortin MJ, McRae BH, Scribner K (2010) Use of resistance surfaces for landscape genetic studies: considerations for parameterization and analysis. Mol Ecol 19:3576–3591
Squires JR, DeCesare NJ, Olson LE, Kolbe JA, Hebblewhite M, Parks SA (2013) Combining resource selection and movement behavior to predict corridors for Canada lynx at their southern range periphery. Biol Conserv 157:187–195
Stoddard ST (2010) Continuous versus binary representations of landscape heterogeneity in spatially-explicit models of mobile populations. Ecol Model 221:2409–2414
Straka M, Paule L, Ionescu O, Štofík J, Adamec M (2012) Microsatellite diversity and structure of Carpathian brown bears (Ursus arctos): consequences of human caused fragmentation. Conserv Genet 13:153–164
Straka M, Stofik J, Paule L (2013) Inventory of brown bears in the Poloniny National Park (Slovakia) by combination of snow tracking and genetic identification of individuals. Rocz Bieszczadzkie 21:234–247
Swenson JE, Gerstl N, Dahle B, Zedrosser A (2000) Action plan for the conservation of the Brown bear (Ursus arctos) in Europe. In: Convention on the Conservation of European Wildlife and Natural Habitats (Bern Convention). Council of Europe Publishing, Strasbourg
Taylor PD, Fahrig L, Merriam G (1993) Connectivity is a vital element of landscape structure. Oikos 68:571–573
Therneau T (2014) Package “Survival”. Survival analysis. https://cran.r-project.org/web/packages/survival/survival.pdf
Thurfjell H, Ciuti S, Boyce MS (2014) Applications of step-selection functions in ecology and conservation. Mov Ecol 2:4
Trainor AM, Walters JR, Morris WF, Sexton J, Moody A (2013) Empirical estimation of dispersal resistance surfaces: a case study with red-cockaded woodpeckers. Landsc Ecol 28:755–767
van Beest FM, Van Moorter B, Milner JM (2012) Temperature-mediated habitat use and selection by a heat-sensitive northern ungulate. Anim Behav 84:723–735
VanDerWal J, Shoo LP, Graham C, Williams SE (2009) Selecting pseudo-absence data for presence-only distribution modeling: how far should you stray from what you know? Ecol Model 220:589–594
Vogt P, Riitters KH, Estreguil C, Kozak J, Wade TG, Wickham JD (2007) Mapping spatial patterns with morphological image processing. Landsc Ecol 22:171–177
Wasserman TN, Cushman SA, Schwartz MK, Wallin DO (2010) Spatial scaling and multi-model inference in landscape genetics: Martes americana in northern Idaho. Landscape Ecol 25:1601–1612
Wasserman TN, Cushman SA, Wallin DO, Hayden J (2012) Multi scale habitat relationships of Martes americana in northern Idaho, USA. Research Paper RMRS-RP-94. Fort Collins
Wisz MS, Hijmans RJ, Li J, Peterson AT, Graham CH, Guisan A, Elith J, Dudík M, Ferrier S, Huettmann F, Leathwick JR, Lehmann A, Lohmann L, Loiselle BA, Manion G, Moritz C, Nakamura M, Nakazawa Y, Overton JM, Phillips SJ, Richardson KS, Scachetti-Pereira R, Schapire RE, Soberón J, Williams SE, Zimmermann NE (2008) Effects of sample size on the performance of species distribution models. Divers Distrib 14:763–773
Woodroffe R (2000) Predators and people: using human densities to interpret declines of large carnivores. Anim Conserv 3:165–173
Zeller KA, McGarigal K, Whiteley AR (2012) Estimating landscape resistance to movement: a review. Landscape Ecol 27:777–797
Ziółkowska E, Ostapowicz K, Kuemmerle T, Perzanowski K, Radeloff VC, Kozak J (2012) Potential habitat connectivity of European bison (Bison bonasus) in the Carpathians. Biol Conserv 146:188–196
Ziółkowska E, Ostapowicz K, Radeloff VC, Kuemmerle T (2014) Effects of different matrix representations and connectivity measures on habitat network assessments. Landscape Ecol 29:1551–1570
Acknowledgments
We thank two reviewers for very helpful and constructive comments that improved the manuscript substantially, and J. Kozak for helpful conversations, suggestions, and assistance. We also thank K. Chrząścik, J. Ficek, D. Huber, Z. Jakubiec, M. Klimecki, A. Krzeptowski-Sabała, P. Łukaszczyk, R. Mateja, A. Olszańska, M. Pasiniewicz, B. Peek, B. Pirga, K. Zabiega and S. Zięba for their assistance in the logistics and field work in the bear projects. We gratefully acknowledge support by the National Science Centre [project 2011/03/D/ST10/05568 (EZ, KO); project 2013/08/M/NZ9/00469 (NS)], the Doctus (doctoral scholarship) program (EZ), the Einstein Foundation Berlin, Germany (TK), and the NASA Land Cover and Land Use Program (VCR). Bear data was gathered under the project N 30405532/2374 funded by the Polish Ministry of Science and Higher Education (WŚ, NS), and the project GLOBE POL-NOR/198352/85/2013 funded by the Norway Grants under the Polish-Norwegian Research Programme operated by the National Centre for Research and Development (AS, TZ-K, FZ, NS).
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ziółkowska, E., Ostapowicz, K., Radeloff, V.C. et al. Assessing differences in connectivity based on habitat versus movement models for brown bears in the Carpathians. Landscape Ecol 31, 1863–1882 (2016). https://doi.org/10.1007/s10980-016-0368-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10980-016-0368-8