Introduction

Amino-1,2,4-triazoles are a class of organic compounds that have gained considerable attention in the field of scientific research due to their versatile properties and potential applications in various domains. These compounds, featuring a 1,2,4-triazole ring with at least one amino group, have demonstrated remarkable significance in both the pharmaceutical and agrochemical sectors, driven by their distinctive chemical structure and diverse biological activities. Several of them have exhibited antifungal [1], anti-inflammatory [2], and anticancer activities [3, 4]. Thermodynamic properties would be useful to the pharmaceutical industry for the design and synthesis of this class of substances on a commercial scale. Amino-1,2,4-triazoles have also found applications in the development of agrochemicals, such as herbicides and plant growth regulators [5, 6].

Beyond their biological applications, amino-1,2,4-triazoles have been explored in materials science, including the development of polymers, catalysts, and other advanced materials, further underscoring their multifaceted significance [7]. In fact, by knowing the enthalpy of formation, chemists can predict the energy changes involved in the synthesis process and determine the most efficient conditions to obtain the desired compounds. Aminotriazoles have also gained significant attention in the field of energetic materials due to their combination of high energy content and stability. Nitrogen-rich high energy density materials differ significantly from traditional explosives, as they derive most of their energy from their high positive heats of formation, in contrast to the carbon backbone oxidation seen in the latter. These materials are also of great interest for their use in propellants, explosives, and pyrotechnics considering their heat release, combustion behavior, and overall energy storage capabilities [7,8,9]. Materials with a high nitrogen content are characterized by an abundance of N–N and C–N bonds, leading to significant positive heats of formation and can be rapidly decomposed following some external energy input. These substances often exhibit remarkable resistance to electrostatic discharge, friction, and impact. The decomposition of these compounds primarily yields dinitrogen, making them highly promising for applications requiring environmentally friendly and highly energetic materials.

In this study, we determined the standard (po = 0.1 MPa) molar enthalpies of formation for 3-amino and 3,5-diamino-1H-1,2,4-triazoles in their crystalline phase, \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{cr}})\), at T = 298.15 K, using the standard molar energies of combustion, \(\Delta_{{\text{c}}} U_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\), measured by static-bomb combustion calorimetry. For 4-amino-4H-1,2,4-triazole, only the standard molar enthalpy of sublimation, \({\Delta }_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\), was determined experimentally by Calvet microcalorimetry, as the amount of purified compound was not sufficient to carry out experiments that would enable the determination of \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{cr}})\). This technique was also used to determine \({\Delta }_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\) of 3,5-diamino-1H-1,2,4-triazole because we did not have sufficient sample for the measurements by Knudsen’s method.

Knudsen mass-loss effusion was employed to investigate the temperature-dependent vapor pressure of 3-amino-1H-1,2,4-triazole. By obtaining experimental vapor pressure values at various temperatures, the Clausius–Clapeyron equation was applied to derive \({\Delta }_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\). Additionally, the standard molar entropy, and Gibbs function of sublimation at 298.15 K were calculated.

In addition to the empirical findings, computational studies were undertaken to estimate \(\Delta_{{\text{f}}} H_{{\text{m}}}^{\text{o}} ({\text{g}})\) for all derivatives of aminotriazoles. This involved combining the enthalpies of relevant reactions, calculated at the G3(MP2) level of theory at T = 298.15 K, with the experimental \(\Delta_{{\text{f}}} H_{{\text{m}}}^{\text{o}} ({\text{g}})\) of the molecules used in the reactions.

A comparative analysis between the theoretically estimated \(\Delta_{{\text{f}}} H_{{\text{m}}}^{\text{o}} ({\text{g}})\) and experimental values reveals a good agreement, supporting the reliability of the G3(MP2) approach and allowed us to further evaluate the properties of compounds that were not experimentally studied.

Experimental

Materials

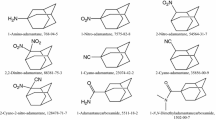
The 3-amino-, 4-amino-, and 3,5-diamino-1,2,4-triazoles obtained commercially have a certified mass fraction purity exceeding 99%. Purification of these compounds was carried out through sublimation under reduced pressure. The assessment of their purity was made by gas–liquid chromatography using an Agilent 4890D Gas Chromatography system equipped with an HP-5 column. N2, with a purity level of at least 99.98%, served as the carrier gas during chromatography. Additionally, the purity of the compounds was verified by measuring the amount of CO2 (g) produced in the combustion experiments. Detailed information can be found in Table S1 of Supporting Information. The structures of the amino-1,2,4-triazoles investigated in this study are illustrated in Fig. 1.

Fig. 1
figure 1

a 1-Amino-1H-1,2,4-triazole; b 4-Amino-4H-1,2,4-triazole; c 3-Amino-1H-1,2,4-triazole; d 5-Amino-1H-1,2,4-triazole; e 3,5-Diamino-1H-1,2,4-triazole

Full size image

Combustion calorimetry

The standard massic energies of combustion, Δcuo, were determined using a combustion isoperibol calorimeter already described in the literature [10,11,12]. The calorimeter was calibrated using Standard Reference Material (Benzoic acid NBS 39j) with Δcuo =  − 26,434 ± 3 J g−1 [13]. These calibration experiments were conducted following the procedure described [14]. The calibration result was obtained as the mean of six experiments as εcal = 15,551.2 ± 1.6 J K−1, where the uncertainty is the standard deviation of the mean.

Using this technique, Δcuo for 3-amino and 3,5-diamino-1H-1,2,4-triazoles were determined. The compounds in the pellet form, were ignited at a temperature of 298.15 K in the presence of an oxygen atmosphere with a pressure of 3.04 MPa and deionized water added to the bomb. The ignition process occurred at a precise temperature of (298.150 ± 0.001) K. The electrical energy required for ignition was determined by measuring the change in potential difference across a capacitor discharged through a platinum ignition wire. For the auxiliaries, Δcuo (CH1.686O0.843) =  − 16,240 J g−1 [14] and Δcuo (n-hexadecane) =  − 47,136.0 ± 2.3 J·g−1, with the quoted uncertainty representing the standard deviation of the mean. Nitric acid corrections were based on − 59.7 kJ mol−1.

Correction for carbon formation was based on Δcuo =  − 33 J·g−1 [14]. The pressure coefficient of massic energy, denoted as (∂u/∂p)T, for solid compounds was assumed to be − 0.2 J g−1 MPa−1 at a temperature of T = 298.15 K [15] and for cotton, the (∂u/∂p)T, =  − 0.29 J g−1 MPa−1 [16]. The amount of compound, m(cpd), used in each experiment and on which the energy of combustion was based, was calculated with reference to the total mass of CO2 (g) generated throughout the experimental procedures. This calculation considered the CO2 (g) resulting from the combustion of the cotton-thread fuse, n-hexadecane, and accounted for any losses due to carbon formation. For each compound, the change in internal energy, (Δcuo) was calculated using the procedure given by Hubbard et al. [16]. This procedure involves accounting for the contributions of all components and reactions participating in the experiments.

The specific densities of 3-amino-1H-1,2,4-triazole and 3,5-diamino-1H-1,2,4-triazole used to calculate true mass from apparent mass were ρ = 1.2695 g cm−3 and ρ = 1.3216 g cm−3, respectively [17], ρ = 1.50 g cm−3 [16] for the cotton-thread fuse and ρ = 0.773 g cm−3 for the n-hexadecane [18].

The relative atomic masses used for the elements were those recommended by the IUPAC Commission in 2013 [19].

High temperature Calvet microcalorimetry

The \(\Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\) for 4-amino-4H-1,2,4-triazole and 3,5-diamino-1H-1,2,4-triazole were assessed using a high temperature Calvet microcalorimeter (Setaram, model HT 1000). Complete information on the experimental procedures and a detailed technique description can be accessed in the literature [20, 21]. In the experimental setup, approximately 2–4 mg of the compound was used in each experiment; two identical glass capillary tubes (within ± 10 μg) were employed; the temperature of the Calvet were maintained at a predefined temperature.

The calibration constant of the calorimeter was established by averaging the results of six experiments using anthracene.

Knudsen effusion technique

The vapor pressures, the enthalpy and entropy of sublimation of 3-amino-1H-1,2,4-triazole were determined using a Knudsen effusion apparatus described in detail earlier [22]. This apparatus featured nine aluminum effusion cells operating simultaneously. To maintain precision and consistency, the apparatus included three aluminum blocks, each housing three effusion cells with orifices of varying areas. The effusion orifices were made of platinum foil with a thickness of 0.0125 mm. The specific areas and Clausing factors for each orifice are available in Table S2 of Supporting Information.

In each experiment, a temperature-controlled aluminum block was utilized, and its temperature differed from the other two blocks. Temperature dependences of absolute vapor pressures were fitted with the following Eq. (1),

$$ p = \, \left( {\Delta m/A_{{\text{o}}} w_{{\text{o}}} t} \right) \, \left( {{2}\pi RT/M} \right)^{{{1}/{2}}} , $$
(1)

where T is the temperature in the effusion experiment, Δm, the sublimed mass, t, the effusion period, M stand for the molar mass of the effusing vapor, R represent the gas constant, Ao is the area of the effusion orifice, and wo the Clausing factor (see Table S2).

Computational details

In this study, we determined absolute enthalpies for amino-1,2,4-triazole derivatives and relevant auxiliary species at a temperature of T = 298.15 K. The calculations were conducted utilizing the composite G3(MP2) methodology [23]. This theory is based on MP2(full)/6-31G(d) geometries, incorporating all electrons. The process initiated with geometry optimization at the Hartree–Fock (HF) level using the 6–31G(d) basis [24], followed by harmonic frequency determination [25, 26]. Subsequent single-point energy calculations were executed at higher levels of theory. Molar heat capacity values in the gaseous phase \({C}_{{\text{p}},{\text{m}}}^{{\text{o}}}\)(g), at diverse temperatures were obtained using statistical thermodynamic. Vibrational frequencies were determined at the HF/6-31G(d) theory level, [27]. All computations were carried out using the Gaussian 03 series of programs [28].

Results

Combustion calorimetry

Tables 1 and 2 show the results of the combustion experiments for 3-amino- and 3,5-diamino-1H-1,2,4-triazoles. The calculation of energy ΔU(IBP) for static-bomb measurements utilizes Eq. (2), as samples were ignited at T = (298.150 ± 0.001) K, [17].

$$ {\text{D}}U\left( {{\text{IBP}}} \right) \, = \, {-}\{ e_{{{\text{calor}}}} + c_{\text{p}} \left( {{\text{H}}_{{2}} {\text{O}},{\text{ l}}} \right) \, \cdot \, \Delta {\text{m}}\left( {{\text{H}}_{{2}} {\text{O}}} \right) \, + e_{{\text{f}}} \} {\text{D}}T_{{{\text{ad}}}} + {\text{D}}U\left( {{\text{ign}}} \right). $$
(2)
Table 1 Standard (pº = 0.1 MPa) massic energy of combustion of 3-amino-1H-1,2,4-triazole, at T = 298.15 K
Full size table
Table 2 Standard (pº = 0.1 MPa) massic energy of combustion of 3,5-diamino-1H-1,2,4-triazole, at T = 298.15 K
Full size table

The values of Δcuo, refer to the combustion reactions represented by Eqs. (3) and (4) for 3-amino- and 3,5-diamino-1H-1,2,4-triazoles, respectively:

$$ {\text{C}}_{{2}} {\text{H}}_{{4}} {\text{N}}_{{4}} \left( {{\text{cr}}} \right) \, + {\text{ 3O}}_{{2}} \left( {\text{g}} \right) \to {\text{2CO}}_{{2}} \left( {\text{g}} \right) \, + {\text{ 2H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \, + {\text{ 2N}}_{{2}} \left( {\text{g}} \right) $$
(3)
$$ {\text{C}}_{{2}} {\text{H}}_{{5}} {\text{N}}_{{5}} \left( {{\text{cr}}} \right) \, + { 3}.{\text{25O}}_{{2}} \left( {\text{g}} \right) \to {\text{2CO}}_{{2}} \left( {\text{g}} \right) \, + { 2}.{\text{5H}}_{{2}} {\text{O}}\left( {\text{l}} \right) \, + { 2}.{\text{5N}}_{{2}} \left( {\text{g}} \right) $$
(4)

Table 3 provides the standard molar energies, \(\Delta_{{\text{c}}} U_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\), and enthalpies, \(\Delta_{{\text{c}}} H_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\), of combustion and the standard molar enthalpies of formation in the crystalline state, \(\Delta_{{\text{f}}} H_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\) for both 3-amino- and 3,5-diamino-1H-1,2,4-triazoles, at T = 298.15 K. The determination of \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} \left( {cr} \right)\), from \(\Delta_{{\text{c}}} H_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\), involved using the standard molar enthalpies of formation for CO2(g) and H2O(l), at T = 298.15 K, which are − (393.51 ± 0.13) kJ mol−1 [29], and − (285.830 ± 0.040) kJ mol−1 [29], respectively. The uncertainties assigned to the standard molar combustion enthalpies and the standard molar enthalpies of formation are the expanded uncertainties for a confidence level of 0.95, which include the uncertainties from the calibration and the auxiliary quantities used [30, 31].

Table 3 Molar standard combustion energies and formation enthalpies of the compounds studied at T = 298.15 K and p° = 0.1 MPa
Full size table

In the literature, the reported enthalpies of combustion for 3-amino- and 3,5-diamino-1,2,4-triazole are \(\Delta_{{\text{c}}} H_{{\text{m }}}^{{\text{o}}} \left( {{\text{cr}}} \right)\) = − 1435.5 ± 3.9 kJ·mol−1 and \(\Delta_{{\text{c}}} H_{{\text{m}}}^{{\text{o}}} ({\text{cr}})\) = − 1548 kJ·mol−1, respectively [32]. These values, to the best of our knowledge, stand as the only data available for amino-1,2,4-triazoles. There is a disparity of 7.7 and 4 kJ·mol−1 between these literature values and the outcomes obtained in our study.

High temperature Calvet microcalorimetry

Table 4 shows \(\varDelta_{{{\text{cr}},298.15\;{\text{K}}}}^{{{\text{g}},{\text{T}}}} H_{{\text{m}}}^{{\text{o}}}\) obtained for 4-amino- and 3,5-diamino-1,2,4-triazoles, measured by Calvet microcalorimetry. The \(\Delta_{{{\text{cr}},298.15\;{\text{K}}}}^{{{\text{g}},{\text{T}}}} H_{{\text{m}}}^{{\text{o}}}\) was corrected to 298.15 K utilizing the following equation,

$$ \Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} (298.15\;{\text{K}}) = \Delta_{{{\text{cr}},298.15\;{\text{K}}}}^{{{\text{g}},{\text{T}}}} H_{{\text{m}}}^{{\text{o}}} - \mathop \smallint \limits_{{298.15 {\text{K}}}}^{T} C_{{\text{p,m}}}^{{\text{o}}} ({\text{g}}){\text{d}}T, $$
(5)

where T is the temperature of the hot calorimeter cells, and \(\it {\text{C}}_{\text{p,m}}^{\text{o}}\text{ (g)}\) = f(T), the temperature dependence of the molar heat capacity, evaluated by HF/6-31G(d) [27] calculations (see Eqs. (2) and (3) provided in the Supporting Information).

Table 4 Standard (po = 0.1 MPa) molar enthalpies of sublimation for 4-amino- and 3,5-diamino-1,2,4-triazoles, at T = 298.15 K evaluated by high temperature Calvet microcalorimetry
Full size table

Table 5 presents the vapor pressures of 3-amino-1H-1,2,4-triazole determined at various temperatures, using the Knudsen effusion technique. The enthalpy of sublimation, corresponding to the average temperature, \(\Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} \left( {\left\langle T \right\rangle } \right)\) was determined by assessing the slope obtained by plotting ln(p/Pa) against the reciprocal of the temperature (1/T).

Table 5 Knudsen effusion results for 3-amino-1H-1,2,4-triazole
Full size table

To obtain \({\Delta }_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} {(298}{\text{.15}}\;{\text{K}})\), Eq. (6) was used, as proposed by Chickos et al. [33]

$$ \Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} \left( {298.15\;{\text{K}}} \right) = \Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} \left( {\left\langle T \right\rangle } \right) + \Delta_{cr}^{\text{g}} C_{{{\text{p}},{\text{m}}}}^{{\text{o}}} \left( {298.15 - A\left\langle T \right\rangle } \right). $$
(6)

The value of \(\Delta_{\text{cr}}^{\text{g}} C_{\text{p,m}}^{\text{o}}\) = –15.83 J·K−1·mol−1, was calculated using Eq. (7). This equation is a rearrangement of Eq. (6) for the estimation of \(\Delta_{\text{cr}}^{\text{g}} C_{\text{p,m}}^{\text{o}}\) at T = 298.15 K, from \(C_{\text{p,m}}^{{\text{o}}} {\text{(cr)}}\) values. [34]

$$ {\Delta }_{{{\text{cr}}}}^{{\text{g}}} C_{{\text{p,m}}}^{{\text{o}}} = \, {-}\{ 0.{9 } + \, 0.{\text{176C}}_{{\text{p,m}}}^{{\text{o}}} {\text{(g)}}\} {\text{J}}\cdot{\text{K}}^{{ - {1}}} \cdot{\text{mol}}^{{ - {1}}} . $$
(7)

The gas-phase molar heat capacity, \({\text{C}}_{\text{p,m}}^{\text{o}}\text{(g)}\) = 84.82 J·K−1·mol−1 at T = 298.15 K (table S3), was obtained by statistical mechanics [27].

The values of the standard (po = 0.1 MPa) molar enthalpy, \(\Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\), entropy, \(\Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}}\), and Gibbs energy \(\Delta_{{{\text{cr}}}}^{{\text{g}}} G_{{\text{m}}}^{{\text{o}}}\), of sublimation, at T = 298.15 K, are given in Table 6. \(\Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}}\) was determined using Eq. (8). Additionally, \(\Delta_{\text{cr}}^{\text{g}} G_{\text{m}}^{\text{o}}\) was calculated using Eq. (9), with all thermodynamic parameters referenced to the temperature of 298.15 K.

$$ \Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}} (T = 298.15\;{\text{K}}) = \Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}} \left\{ {T,p\left( T \right)} \right\} + \Delta_{{{\text{cr}}}}^{{\text{g}}} C_{{\text{p,m}}}^{{\text{o}}} \ln \left( {\frac{{298.15\;{\text{K}}}}{T}} \right) - R\ln \left\{ {\frac{{p^{{\text{o}}} }}{p\left( T \right)}} \right\} $$
(8)
$$ \Delta_{{{\text{cr}}}}^{{\text{g}}} G_{{\text{m}}}^{{\text{o}}} = \Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}} - 298.15 \cdot \Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}} $$
(9)
Table 6 Values of \(\Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\), \(\Delta_{{{\text{cr}}}}^{{\text{g}}} S_{{\text{m}}}^{{\text{o}}}\), and \(\Delta_{{{\text{cr}}}}^{{\text{g}}} G_{\text{m}}^{{\text{o}}}\), at T = 298.15 K, for 3-amino-1H-1,2,4-triazole evaluated by Knudsen effusion
Full size table

Gas-phase standard molar enthalpy of formation

Hypothetical reactions were evaluated to estimate \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} (g)\) for the compounds under investigation. The enthalpy change of those reactions, \(\Delta_{{\text{r}}} H_{{\text{m}}}^{{\text{o}}} (g)\), calculated from the absolute standard enthalpies, \(H_{{{298}{\text{.15}}\;{\text{K}}}}^{{\text{o}}}\), were combined with the experimental \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} (g)\) of all molecules involved in the reactions, allowing us to estimate \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) at T = 298.15 K for the aminotriazoles. Tables, S4-S8, of the Supporting Information, present the chemical reactions used to estimate the \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) for the amino triazole derivatives as well as the calculated \(\Delta_{{\text{r}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) and the computational estimates \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) at T = 298.15 K. Table S9 in the SI provides the G3(MP2) absolute enthalpies and the experimental \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) at T = 298.15 K for all compounds included in the study, along with auxiliary molecules. To summarize, the mean values calculated from the computational estimates are collected in Table 7, together with the experimental \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{cr}})\), \(\Delta_{{{\text{cr}}}}^{{\text{g}}} H_{{\text{m}}}^{{\text{o}}}\) and \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) derived from the experimental determinations.

Table 7 Experimental and computational results for the compounds, at T = 298.15 K. Values in kJ·mol−1
Full size table
Fig. 2
figure 2

Enthalpic increments in \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) when exchanging a hydrogen atom on carbon ring by an amino group

Full size image

Discussion

Predicting enthalpies of formation

We have determined the \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) for 3-amino- and 3,5-diamino-1H-1,2,4-triazoles by computational methods using appropriate reactions. The calculated values are in excellent agreement with the experimental results, providing strong support of the estimates performed for the \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) for the compounds that have not been studied experimentally.

The standard molar enthalpy of sublimation measured at T = 298.15 K for 4-amino-4H-1,2,4-triazole together with the G3MP2 calculations for the standard molar enthalpy of formation in the gaseous state, allow us to estimate the standard molar enthalpy of formation in the condensed state as, \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{cr}})\) = (226.2 ± 1.7) kJ·mol−1.

From the experimental values of \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\), obtained for the amino-1H-1,2,4-triazoles, and the literature value for 1H-1,2,4-triazole [35], it is possible to calculate the enthalpic increments inherent to the substitution of a hydrogen atom by the amino group at positions 3- and 3,5- of 1H-1,2,4-triazole, as it is evidenced in the scheme of Fig. 2. Based on the calculated enthalpic increments, the standard molar enthalpy of formation for 5-amino-1H-1,2,4-triazole was estimated to be \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\) = (190.5 ± 3.4 kJ·mol−1). This value agrees well with the value determined computationally, within the associated uncertainty (Table 7). The agreement between these values suggests that the experimental and computational methods are reliable and consistent. This is an important validation step, as it enhances the confidence in the accuracy of the obtained thermodynamic data for amino 1,2,4-triazoles.

Structures and relative stabilities

Fully optimized structures of amino-1,2,4-triazoles reveal distinct arrangements for the amino substituent. In the case of 3-amino-, 5-amino- and 3,5-diamino- derivatives, both hydrogen atoms of the amino group project in the same direction, extending away from the planar aromatic ring. However, in 1-amino and 4-amino, they are positioned at different heights, with one above and the other below the plane of the ring, which is in line with the results obtained in previous studies [36, 37].

For the 3-amino and 5-amino isomers, the calculations have demonstrated that the 3-amino structure exhibits the lowest energy, while the 5-amino structure is only slightly higher in energy (4 kJ·mol−1). The difference in stability can be attributed to different environments of the amino group at positions 3- and 5- of the 1H-1,2,4-triazole ring.

The analysis of the results of \(\Delta_{{\text{f}}} H_{{\text{m}}}^{{\text{o}}} ({\text{g}})\), obtained by computational methods, indicates a greater stability of the 1-amino-1H-1,2,4-triazole relative to the 4-amino-4H-1,2,4-triazole. The different stability of the two isomers may be related to the energetic effects resulting from the interaction between the nitrogen atoms belonging to the ring and the amino group. In the 1-amino-1H-1,2,4-triazole isomer, the amino group is located at the 1-position, which is adjacent to the nitrogen in the ring. This can lead to the possibility of resonance stabilization through delocalization of the lone pair of electrons on the amino nitrogen into the ring. On the other hand, the 4-amino-4H-1,2,4-triazole isomer has the amino group located at position 4, which does not allow similar resonance stabilization, resulting in a different electronic distribution in the molecule.