Introduction

The backward-facing step (BFS) is a prevalent configuration in fluid dynamics studies due to its simplicity, resemblance to real-world geometries, and the fact that it provides a well-studied complex flow pattern that allows understanding fundamental flow phenomena. Its design, featuring a sudden expansion, adapts to different shapes and aspect ratios suitable for different applications. In many studies, the BFS is modelled as a rectangular channel that begins with a uniform height and then abruptly expands. This sudden expansion leads to rapid fluid deceleration, an increase in pressure and flow separation at the step, and the formation of recirculation zones downstream. These characteristics are beneficial for practical applications where heat transfer enhancement is desired. A BFS exhibits complex and nonlinear behaviour in the region immediately downstream of the step, making it a preferred test case for experimental and computational studies [1]. It significantly influences flow behaviour and characteristics, such as reattachment length and recirculation zones, making it a key research area in fluid mechanics. Historically, BFS has been a valuable platform for developing and validating models, comparing results, and attracting scientific attention to various applications, including turbulent flows [2], heat transfer [3], porous media [4], nanofluids [5] and many others [6,7,8,9,10,11].

Armaly et al. [12] performed a detailed experiment on a BFS flow, varying the Reynolds number and considering different measures to quantify the flow behaviour. Multiple recirculation zones downstream of the backward-facing step for a laminar flow were identified. Their work also presents a two-dimensional computational simulation of the same flow configuration. It was observed that, for Reynolds numbers (ReDh) above 400, two-dimensional simulations present a poor representation of the flow. By performing a three-dimensional numerical simulation and getting better agreement for ReDh > 400, Williams et al. [13] confirmed that the deviation between experimental and numerical results is due to the tridimensionality phenomena of the flow previously neglected in the simulations from Armaly et al. [12]. Erturk [14] extended Armaly et al.’s [12] 2D numerical study to Reynolds numbers up to 3,000. Biswas et al.’s [6] work investigated the effect of the expansion ratio for low and moderate Reynolds numbers in a three-dimensional BFS. This last work found that the side walls promote a jet-like flow, which is the reason for the discrepancies between the experiments and the 2D simulations, which are incapable of taking into account this behaviour [1, 15].

Following the initial studies aimed at understanding the flow phenomena in a backward-facing step channel, subsequent research has concentrated on channel design. This includes aspects such as expansion ratio, geometry of the expansion, and a variety of innovative configurations tailored for an array of applications. For example, Choi et al. [16] studied the effects on the flow of having an expansion with different inclinations for different Reynolds numbers and turbulence models (Reynolds-averaged Navier–Stokes, RANS, and large eddy simulation, LES). As anticipated, the LES model delivers superior performance compared to the RANS model, in alignment with the experimental findings of [17]. In another example, McQueen et al. [18] studied the time-dependent and dynamic flow features of a double backward-facing step, considering different separations between the equal-height steps. By identifying three distinct flow regimes, the study revealed insights into the complex dynamics of separated flow interactions, including variations in reattachment length, surface pressure, and turbulence statistics.

The work presented by Kondoh et al. [19] investigated heat transfer in a backward-facing step channel using laminar flow and an imposed temperature on the bottom wall. In that work, the following parameters are varied: the expansion ratio, the Reynolds number, and the Prandtl number [19]. It was found, against what was expected, that the peak of the Nusselt number is not necessarily located near the point of flow reattachment. Abdulrazzaq et al. [20] studied heat transfer using a double backward-facing expanding channel. Different step heights, Reynolds numbers, and fluids with different properties are compared in that work while keeping a constant heat flux on the steps of 2.0 kW m−2. It is concluded that having a second step larger or equal to the first is always preferable for all tested fluids. Furthermore, as expected, higher Reynolds numbers are also better for achieving higher Nusselt numbers. Hilo [21] conducted a comparison between a backward-facing step flow with a heated bottom wall and one with a heated, periodically corrugated bottom wall. By employing water and exploring higher Reynolds regimes (ranging from 5,000 to 20,000), Hilo [21] demonstrated, both experimentally and numerically, that the corrugated wall configuration enhances heat transfer. However, this improvement comes with an increased friction factor.

Obstacles are often introduced along channels to increase heat transfer from the bottom wall into the fluid. Nie et al. [15] employed three-dimensional simulations to illustrate the effect of positioning an obstacle in front of the entry channel of a BFS. They discovered that this setup could significantly increase the peak Nusselt number, which becomes more pronounced as the baffle-step distance decreases. However, they also noted that as this distance reduces, the friction coefficient correspondingly increases. Li et al. [22] conducted a two-dimensional numerical study featuring similar characteristics to Nie et al.’s [15] work but with the obstacle replaced by a porous baffle. They examined the variations in heat transfer and pressure drop in response to changes in baffle width and height, Darcy number, and baffle-to-step distance across different Reynolds numbers. The findings of this study have some parallels with those of Nie et al. [15], especially when the permeability of the porous baffle is low and it behaves almost like a solid wall. In these circumstances, similar patterns are observed in both studies. The Li et al.’s [22] study shows that the Nusselt number and pressure drop become less pronounced with increased baffle permeability, a phenomenon not explored in Nie et al.’s [15] work. In another numerical study, Zhao [23] investigated the impact of a porous baffle positioned after the step and adjacent to the bottom wall on the heat transfer improvement for different Reynolds numbers. His work examined how variations in the height, width, Darcy number, and thermal conductivity of the baffle affect the performance number if the bottom wall temperature was imposed. Arthur and co-workers [24, 25] investigated the inclusion of two porous baffles after the step in a BFS channel, one on the bottom wall and other on the top wall, but used a pore-level approach to model the flow through porous media (while Li et al. [22] and Zhao [23] used volume-average models). The bottom wall was kept at a constant temperature, and the dimensions and characteristics of the porous baffles were varied, similar to what was done in the works mentioned above. Building upon previous studies, Talei and Bahrami [26] explored the use of porous obstacles and/or corrugation after the step wall to enhance thermal energy exchange inside conduits with a BFS. These authors simulated five different configurations and assessed their hydrothermal characteristics, analysing for each the effects of different factors such as the Reynolds number, porous obstacle properties, location, dimension, and shape of the obstacles. On a different study, Terekhov et al. [27] investigated the number and size of solid obstacles distributed along the entry channel. It was observed that using these obstacles leads to an earlier increase in pressure drop compared to the case without obstacles. As a result, the region of maximum heat transfer on the heated lower wall moves closer to the step.

The parametric studies provided by the previous works are important for insight into the phenomena and for identifying trends. Nonetheless, they cannot answer which conditions are the best. For each of the studies presented above, optimisation would be required to find the best conditions. However, the computational effort associated is often prohibitive [28], explaining the scarce number of works in optimisation applied to heat transfer problems, especially involving multi-objective optimisation (MOO) search. As reported by Gosselin et al. [28] in their review, genetic algorithms (GA) have been applied to the optimisation of heat transfer problems, but primarily to single objective cases since they require less computational effort than MOO. In real-world problems, simplifications can often be made, but there is rarely a single optimisation target. For example, heat transfer problems aim to maximise heat transfer in a specific application. However, the solution may be trivial unless factors such as pressure drop are considered, as this variable is related to operational costs. Furthermore, cost and technological constraints on system size, material properties, and other factors could easily be overlooked in simplifications. These factors can be critical if the goal is to address real-world problems effectively. One approach to handling a multi-objective optimisation (MOO) problem is converting it into a single-objective problem through aggregation. However, this method inherently restricts achievable solutions [29]. Using more comprehensive measures such as entropy [30], entransy [31], and exergy [32] to assess system irreversibility provides a deeper understanding of the thermodynamics of the system in heat transfer optimisation literature. Entropy, for instance, is a measure of the irreversibility of a physical process, and its minimisation often leads to more efficient heat transfer systems. Entransy, another measure, represents the heat transfer potential within a system. Its dissipation often correlates with heat transfer efficiency. Lastly, exergy represents the maximum work a system can perform when it reaches equilibrium with a reference environment. Optimising exergy often leads to systems with better energy utilisation. However, these measures imply constraints. The efficiency of a heat transfer system often depends on how effectively the system navigates the trade-off between different forms of energy. For example, increasing fluid velocity might enhance heat transfer but at the expense of increased pressure. Thus, these constraints, although not explicitly stated, play a significant role in shaping the optimisation outcomes.

Optimisation of fluid characteristics, flow conditions, and geometrical parameters has already been investigated in the past in works such as [33], where the backward-facing step is used as a means to mix fuel in scramjet engines. More recently, Bagherzadeh et al. [34] performed a MOO using GA based on a trained artificial neural network (ANN) with empirical data. With the ANN, the properties of a nanofluid are modelled, and then, the pressure drop in a pipe is minimised, and the heat transfer is maximised. In both cases (Ogawa et al. [33] and Bagherzadeh et al. [34]), they used a surrogate model to avoid the computational effort of the computational fluid dynamics (CFD) model.

This work presents an optimisation study using the second version of the non-dominated sorting genetic algorithm (NSGA-II) [35] to identify a set of geometrical parameters that simultaneously optimise the heat transfer and the pressure drop on a BFS channel with two porous baffles adjacent to the top and bottom wall. All this is supported by simulations using an implementation of the finite-volume method previously validated against results from the literature. The conclusions obtained from this work will help clarify the utility of some configurations already published in previous works. Furthermore, given the commonness of the geometry analysed in different applications, this work will make a valuable contribution to the field, shedding new light on the optimal design of BFS channels with baffles and paving the way for further research.

In conclusion, while previous studies have extensively investigated various aspects of the BFS configuration, there remains a research gap in comprehensively addressing the optimisation of heat transfer and pressure drop in BFS channels with porous baffles. The novelty of this work lies in its focus on employing a multi-objective optimisation model to identify the optimal geometrical parameters and providing insights into the complex relationship between these parameters and non-isothermal fluid flow characteristics in BFS with porous baffles.

Method

Building blocks: CFD simulations for objective functions

This study uses two-dimensional CFD simulations to obtain detailed solutions for the non-isothermal fluid flow through a backward-facing step channel with two porous baffles.

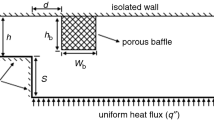
As shown in Fig. 1, there is a baffle on the top wall (at a distance of \(d_{{\text{b}}}^{{\text{t}}}\) from the step) and another on the bottom wall (at a distance of \(d_{{\text{b}}}^{{\text{b}}}\) from the step). The heights of the top and bottom porous baffles are defined as \(h_{{\text{b}}}^{{\text{t}}}\) and \(h_{{\text{b}}}^{{\text{b}}}\), respectively, while their widths are \(w_{{\text{b}}}^{{\text{t}}}\) and \(w_{{\text{b}}}^{{\text{b}}}\). A constant heat flux of \(q^{\prime\prime} = 1.0 {\text{ kW m}}^{ - 2}\) is imposed on the bottom wall immediately following the step. The step has a height of \(s = 0.01\) m, and the channel possesses an expansion ratio of \(2.0\), resulting in a total channel height of \(h = 0.02\) m. The length of the entry channel is 2 \(h\), and the total length of the wider channel is \(L = 0.5 {\text{ m}}\). The geometrical dimensions of the BFS channel and the boundary conditions were chosen to be equal to those of Li et al. [22] to enable validation of the CFD model used in this work through results comparison.

Fig. 1
figure 1

Backward-facing step configuration with top and bottom baffles

Full size image

The following nondimensional parameters were considered [22],

$$X = x/s,\quad Y = y/s$$
(1a)
$$H_{{\text{b}}}^{i} = h_{{\text{b}}}^{\text{i}} /s, \quad W_{{\text{b}}}^{\text{i}} = w_{{\text{b}}}^{\text{i}} /s, \quad D_{{\text{b}}}^{\text{i}} = d_{{\text{b}}}^{\text{i}} /h$$
(1b)
$${\text{Re}} = \frac{{\rho \overline{u}_{{{\text{in}}}} s}}{{\mu_{{\text{f}}} }}$$
(1c)
$$\text{Nu} = \frac{{q\mathrm{\prime \prime }s}}{{k_{\text{f}} \left( {T_\text{w} - T_\text{in} } \right)}}$$
(1d)

Equations (1a) and (1b) show the nondimensionalisation of the geometric variables, where in Eq. (1b), the i superscript is t or b when referring to the top or bottom porous baffle, respectively. The Reynolds number is defined in (1c) (where \(\overline{u}_{{{\text{in}}}}\) is the average velocity at the inlet, \(\rho\) is the density of the fluid, and \(\mu_{{\text{f}}}\) is the fluid dynamic viscosity) and the Nusselt number along the bottom wall is defined in (1d) (where \(k_{{\text{f}}}\) is the fluid thermal conductivity coefficient, \(T_{{\text{w}}}\) is the temperature of the wall, and \(T_{{{\text{in}}}}\) is the inlet temperature of the flow).

The flow is assumed to be laminar, permanent, and incompressible, while the porous media is considered rigid, homogeneous, isotropic, and in thermal equilibrium with the fluid. Based on those assumptions, the following conservation equations of mass (2a), linear momentum (2b), and energy (2c) are solved [22]

$$\vec{\nabla } \cdot \left( {\rho \vec{u}} \right) = 0$$
(2a)
$$\vec{\nabla } \cdot \left( {\rho \vec{u} \otimes \vec{u} - \mu_\text{f} \vec{\nabla }\vec{u}} \right) = - \vec{\nabla }\left( {p + p_{\epsilon } } \right)$$
(2b)
$$\vec{\nabla } \cdot \left( {\rho c_{\text{p}} \vec{u}T - k_{{{\text{eff}}}} \vec{\nabla }T} \right) = 0$$
(2c)

where \(c_{{\text{p}}}\) is the specific heat, \(\vec{u}\) is the velocity vector, \(p\) is the pressure, and \(\vec{\nabla }p_{\epsilon }\) stands for the pressure drop due to the presence of the porous media and is computed only within the region of the porous baffles. This pressure drop is calculated using the generalised 3D Hazen–Dupuit–Darcy equation, which is given by [36]

$$\vec{\nabla }p_{\upvarepsilon } = \vec{u}^{\text{T}} \left( {\frac{{\mu _{\text{f}} }}{K} + \frac{{F\rho }}{{\sqrt K }} \lVert\vec{u}} \rVert \right)$$
(3)

with both the inertial factor F [37] and the permeability K [22] given by

$$F = \frac{1.75}{{\sqrt {150} }}\frac{1}{{\epsilon^{3/2} }}$$
(4a)
$$K = {\text{Da}}_{{\text{b}}}^{i} s^{2}$$
(4b)

where \(\varepsilon\) is the porosity, and \({\text{Da}}_{{\text{b}}}^{i}\) is the Darcy number of baffle \(i\). In the energy Eq. (2c), \(k_\text{eff} = \varepsilon k_\text{f} + \left( {1 - \varepsilon } \right)k_\text{s}\) is the effective thermal conductivity with \(k_{{\text{s}}}\) being the conductivity of the solid phase.

The parameters assumed in this work are presented in Table 1.

Table 1 Fluid and solid properties used in the simulations [22]
Full size table

The fluid enters fully developed with a parabolic velocity profile (Re = 200) and a uniform temperature, \(T_{{{\text{in}}}} = 297.15\) K. While the bottom wall has a uniform flux of \(1.0 {\text{ kW m}}^{ - 2}\), the remaining walls are considered adiabatic. The no-slip boundary condition is also imposed on every wall. The outlet boundary condition is considered for the linear momentum and energy conservation equations.

Equations (2) are discretised using the finite volume method, and the pressure–velocity coupling is solved using the SIMPLE scheme [38]. The central difference and hybrid schemes are used to discretise the diffusion and convection terms, respectively.

Multi-objective optimisation

The application of MOO is key when multiple conflicting objectives must be considered, which is common in real-case scenarios [39, 40]. The current optimisation problem can be formulated according to

$$\min f_{\text{p}} \left( {\vec{x}} \right)\;p = 0, \, 1, \, \ldots , \, q$$
(5a)
$$x_{\text{i}}^{\min } \le x_{\text{i}} \le x_{\text{i}}^{\max } \;i = 0, \, 1, \, \ldots , \, n$$
(5b)

where \(f_{\text{p}}\) are the p objective functions being minimised, and \(x_{\text{i}}^{{{\text{min}}}}\) and \(x_{\text{i}}^{{{\text{max}}}}\) are the lower and upper bounds for the n linearly independent parameters, \(x_{\text{i}}\).

Notably, in the context of this work,

$$f_{0} = - \overline{\text{Nu}} = - \frac{1}{L}\mathop \smallint \limits_{0}^{L} {\text{Nu}} \, {\text{d}}x$$
(6)

i.e. one objective is to maximise the average Nusselt number along the bottom wall.

Another assessment of the flow behaviour is the overall pressure drop, \({\Delta }p\), which will be used as another objective function, \(f_{1} .\) Equation (7) is used in the computation of the pressure drop between the inlet at \(x = x_{{{\text{in}}}} = - 2h\) and the outlet at \(x_{{{\text{out}}}} = L\)

$$f_{1} = \Delta p = \frac{1}{h - s}\mathop \smallint \limits_{s}^{h} p\left( {x_\text{in} , y} \right) \ {\text{d}}y - \frac{1}{h}\mathop \smallint \limits_{0}^{h} p\left( {x_\text{out} , y} \right) \ {\text{d}}y$$
(7)

The decision variables considered in the present study and respective upper and lower bounds are given in Table 2.

Table 2 Parameters search range
Full size table

During optimisation, certain sets of parameters may potentially result in overlapping baffles with different permeabilities. The strategies to handle the potential conflicts are presented in Fig. 2.

Fig. 2
figure 2

Configurations with overlapping baffles and strategy followed during optimisation

Full size image

In Fig. 2a, the bottom left of the top baffle and the top right of the bottom baffle overlap. In this case, the top baffle is shifted to the end of the bottom baffle so that its distance to the step becomes \(d_{{\text{b}}}^{{\text{t}}} = d_{{\text{b}}}^{{\text{b}}} + w_{{\text{b}}}^{{\text{b}}}\). A similar strategy is applied in the situation corresponding to Fig. 2c, and the bottom baffle is pushed to the end of the top baffle. If the total extent of the top (or bottom) of a baffle falls within the other baffle, its height is shortened to fit the remaining space. This procedure is shown in Fig. 2b and Fig. 2d.

Generically, in more complex problems where the objective functions cannot be determined analytically, or their calculation is too complicated, optimisation is performed numerically by iterating over the feasible parameters [41]. This iterative process involves using optimisation algorithms to determine the parameter values to improve the objective function values until an optimal or near-optimal solution, that satisfies the problem constraints and minimises/maximises the objective functions, is found. The process continues until a termination criterion is met, such as reaching a predefined number of iterations or achieving any other measure of the quality of the solutions. Throughout this numerical optimisation process, various techniques such as gradient-based methods [42], evolutionary algorithms [43, 44], and others [45] can be employed to efficiently explore the solution space and find optimal or near-optimal solutions. The choice of the optimisation algorithm depends on the problem characteristics, such as the problem dimensionality, constraints [35], and the nature of the objective function(s). Notably, in MOO, the algorithms strive to find the set of parameters that define the Pareto-Frontier [39], i.e. a set of solutions where any further improvement in one objective would necessarily cause a degradation in at least one other objective. This set of solutions comprises the non-dominated solutions describing the Pareto-Frontier. (All other solutions are dominated.) Fig. 3 shows a generic example of how the design space (for parameters \(x_{0}\) and \(x_{1}\)) and the objective space (for the objectives f0 and f1) relate with one another.

Fig. 3
figure 3

Example of the relationship between the parameter space, the objective space, and the dominance of solutions, for two parameters and two objective functions

Full size image

During the iterative optimisation process, a set of parameters \(x_{i}\) are generated by the algorithm. Each solution is subjected to evaluation using multiple objective functions \(f_{i}\) that quantify different aspects of the problem to be optimised. In the objective space, which represents the values of the objective functions, solutions are ranked based on their domination relationships with respect to other solutions. Dominance is determined by comparing the performance of solutions across the objective space. A solution is considered to dominate another if it exhibits superior performance in at least one objective without inferior performance in any other objective. The ranking process considers the degree of domination of a solution compared to the remaining computed points. Solutions not dominated by other solutions are said to be Pareto optimal, indicating their relative desirability in the multi-objective space. Solutions that are dominated by at least one other solution are not Pareto optimal, reflecting their comparative undesirability. In addition to identifying points on the Pareto-Frontier, ensuring a well-distributed representation of this frontier is crucial. This entails capturing solutions that span the entire range of trade-offs between conflicting objectives. By achieving a diverse and evenly spread set of solutions along the Pareto-Frontier, decision-makers are provided with a comprehensive range of trade-off options. This consideration depends on their preferences and tolerance for trade-offs, enabling them to make informed choices that align with their specific requirements and desired outcomes. It is crucial to note that, in the context of this work, high heat transfer is not beneficial if it leads to an excessively large pressure drop. Furthermore, an extremely low-pressure drop is also undesirable if it results in ineffective heat transfer. These are the extremes of the Pareto-Frontier (coincident with the single objective optimisation of each of the objectives), and they highlight the importance of having a trade-off between these objectives. Therefore, there exist intermediate scenarios where both objectives could be optimised, i.e. solutions lying on the Pareto-Frontier, representing the set of optimal trade-offs between heat transfer and pressure drop.

In MOO, especially when considering evolutionary-based algorithms, the NSGA-II stands out [46]. As a derivation of GA, it is particularly effective in identifying the Pareto-Frontier [43]. While traditional single-objective GA has an easy way of sorting the population by their fitness value, the situation becomes more complex in multi-objective problems. In such problems, all individuals on the Pareto-Frontier are considered equally important, and a different ranking mechanism is required. One commonly used approach is to sort the individuals based on their distribution or capability in describing the frontier. NSGA-II addresses the challenges of multi-objective optimisation by incorporating the concept of crowding distance [43]. The crowding distance helps assess the density of solutions in the objective space, allowing NSGA-II to effectively maintain diversity and provide a well-distributed representation of the Pareto-Frontier. NSGA-II has been widely used in various domains to effectively solve complex multi-objective optimisation problems [47], so it is the algorithm selected in this work to address the optimisation process.

NSGA-II is used with a population size of 100, a crossover probability of 0.8, and a mutation rate of 0.3. Elitism is used to keep the knowledge of the first rank of the non-dominated solutions found in previous generations. Crossover is performed randomly by choosing which alleles are linearly combined according to a random weighting factor between the parents. The alleles to mutate are randomly chosen, and mutation is performed by changing the value of the allele within 20% of its current value. If the value falls outside the search limits, the allele gets the value of the search boundary limit. The stopping criteria used in this multi-objective optimisation process were simultaneously a minimum of 100 iterations and a maximum of \(1.4 \times 10^{ - 3}\) for the interquartile distance of the crowding distance.

Validation and analysis of CFD model for single baffle configuration

The computational fluid dynamics model used in this study is validated using the work of Li et al. [22]. Despite the similarity in geometry to that in Fig. 1, only one baffle, located adjacent to the top wall, is considered. Assuming incompressible laminar flow, the same fluid and solid properties (Table 1), and imposing the same boundary conditions, such as the heat flux on the bottom wall, ensures consistency with the conditions observed in the referenced study. These common conditions aim to ensure the validity and reliability of the CFD model used in our study.

This study uses a Cartesian non-uniform mesh, featuring a geometric progression that concentrates smaller volumes near the walls and gradually expands towards larger volume dimensions as it moves away from the walls. This configuration results in four vertical and two horizontal zones of progression. In all progressions, both the position of the first grid point off the wall (\(d_{0}\)) and the number of points are imposed. This way, a detailed representation of the flow characteristics near the walls and an efficient coverage of the entire domain are ensured. Different meshes were tested to ensure mesh independence for the scenario in which \({\text{Re}} = 500.0\), \(H_{{\text{b}}}^{{\text{t}}} = 1.0\), \(W_{{\text{b}}}^{{\text{t}}} = 1.0\), \(D_{{\text{b}}}^{{\text{t}}} = 1.0\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 1.0 \times 10^{ - 3}\). Table 3 shows the mesh dimension and presents the \(\overline{{{\text{Nu}}}}\) obtained for each of the meshes considered.

Table 3 Mesh independence analysis
Full size table

The Table 3 shows that increasing the mesh size from 520 × 100 to 780 × 150 only changes the \(\overline{{{\text{Nu}}}}\) by \(0.76\%\) and from 780 × 150 to 1040 × 200 by \(0.85\%\). For that reason, the mesh of 520 × 100 is assumed to be a good compromise between computational cost and the reliability of the results; therefore, it is the one used for the validation of the CFD model and for the optimisation presented in this work

A comparison between Li et al.’s [22] results and the results obtained with the CFD model used in this work is presented in Fig. 4 and Fig. 5. The normalised distance of the baffle to the step wall is varied, \(D_{{\text{b}}}^{{\text{t}}} = \left[ {1.0, 2.0, 3.0, 4.0} \right]\), while keeping the remaining parameters fixed.

Fig. 4
figure 4

Nusselt number comparison between Li et al. [22] (dashed lines) and the CFD simulation performed in this work (continuous lines), as a function of the baffle distance for \({\text{Re}} = 500\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 0.001\), \(H_{{\text{b}}}^{{\text{t}}} = 1.0\), and \(W_{{\text{b}}}^{{\text{t}}} = 1.0\)

Full size image
Fig. 5
figure 5

Normalised averaged Nusselt number comparison between Li et al. [22] and the CFD simulation performed in this work, as a function of baffle height for \({\text{Re}} = 200, {\text{Da}}_{{\text{b}}}^{{\text{t}}} = 0.001\), \(D_{{\text{b}}}^{{\text{t}}} = 1.0\), and \(W_{{\text{b}}}^{{\text{t}}} = 1.0\)

Full size image

As Fig. 4 shows, when the baffle is closer to the step \((D_{{\text{b}}}^{{\text{t}}} = 1.0)\), the peak of the Nusselt number is higher and closer to the step than when it is further away. (For the smallest distance of the baffle to the step analysed, the maximum Nusselt number is almost two times larger than for the largest distance.) With the distance decreasing, the flow deflection increases, thus increasing the impingement intensity onto the lower wall. After impingement, the flow accelerates, and the increase in velocity near the wall improves the heat transfer to the fluid. Since the Nusselt number tail, after the peak, does not change significantly with the location of the baffle, the average Nusselt number is larger when the baffle is closer to the step.

Figure 5 presents the average Nusselt number, which is computed using Eq. 6, normalised by the average Nusselt number for the case with no baffle within the channel (\(\overline{{{\text{Nu}}}}_{{\text{b}}}\)), as a function of the baffle height for \({\text{Re}} = 200\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 0.001\), \(D_{{\text{b}}}^{{\text{t}}} = 1.0\), and \(W_{{\text{b}}}^{{\text{t}}} = 1.0\).

The presence of a baffle in the channel results in an increase in velocity beneath the baffle due to the flow constriction, thereby promoting heat transfer, but leads to an increase in the pressure drop. Due to the permeability of the baffle, a portion of the flow passes through the baffle, while the remainder flows beneath it. Increasing the baffle height up to a certain point results in an increase in the heat transfer. However, there is a threshold beyond which increasing the baffle height will no longer enhance heat transfer. This is because more of the flow will bypass the constriction by moving through the baffle, limiting the increase in the velocity near the bottom wall. For the case presented in Fig. 5, this peak is found for \(H_{{\text{b}}}^{{\text{t}}} = 1.5\) resulting in \(\overline{{{\text{Nu}}}} = 2.014\).

The results depicted in Fig. 4 and Fig. 5 demonstrate a strong agreement between the results of this study and those presented by Li et al. [22]. Consequently, the validation of the CFD model has been successfully carried out.

Moreover, the results used for the validation of the CFD model and obtained for the geometry studied by Li et al. [22] reveal that there should be a trade-off between baffle height and pressure drop and suggest that the subject should be further investigated. To explore the influence of \({\text{Da}}_{{\text{b}}}^{{\text{t}}}\), \(H_{{\text{b}}}^{{\text{t}}}\) and \(D_{{\text{b}}}^{{\text{t}}}\) on the average Nusselt number, a combination of these parameters was varied for a fixed width of the baffle \(W_{{\text{b}}}^{{\text{t}}} = 8.0\) (Fig. 6).

Fig. 6
figure 6

Average Nusselt number dependency on the baffle height, distance to the step and the Darcy number of the baffle for \(W_{{\text{b}}}^{{\text{t}}} = 8.0\) and Re = 200

Full size image

Figure 6 illustrates that when the Darcy number decreases (i.e. the permeability decreases), the maximum average Nusselt number increases. Correspondingly, the optimal height of the baffle also shifts towards a higher value. This occurs because the flow encounters higher resistance when passing through the porous baffle, forcing a larger proportion of the fluid to flow between the baffle and the heated wall. Moreover, the proximity of the baffle to the step significantly impacts the average Nusselt number, which consistently increases as the distance of the baffle to the step decreases. By reducing this distance, the size of the recirculation zone near the step shrinks, forcing the flow to accelerate earlier. As a result, the heat flux is more effectively transmitted to the flow, increasing the average Nusselt value. In summary, for the flow configuration studied by Li et al. [22], a particular baffle height, Darcy number and distance that maximises the average Nusselt number exist.

Previous research by Zhao [23] explored the relationship between the Nusselt number and the pressure drop by altering the characteristics of a porous baffle placed next to the step and adjacent to the bottom wall. Zhao [23] imposed a constant temperature on the bottom wall and varied the geometrical properties of the porous baffle. The present study aims to build on previous works by considering the potential benefits of using multiple porous baffles and exploring a more extensive range of positions, dimensions, and permeabilities for the baffles. The goal is to investigate the possibility of further enhancing the combination of heat transfer and pressure drop with these modifications.

Results and discussion

The CFD model has been validated, and a general idea of the influence of the top baffle location, geometry and permeability on the average Nusselt number was obtained. The NSGA-II is now used to optimise the geometry presented in Fig. 1 and find the best compromise between both objective variables, \(\overline{{{\text{Nu}}}}\) and \({\Delta }p.\) The NSGA-II results are shown in Fig. 7 where the non-dominated solutions (blue dots) and their fit using a power regression (orange dashed line) are presented.

Fig. 7
figure 7

Non-dominated solutions for the averaged Nusselt number vs pressure drop (blue dots) and power fit of the results (orange dashed line)

Full size image

The relationship between the optimum pressure drop and the optimum average Nusselt number follows a power law according to

$${\Delta }p\left( {\overline{{{\text{Nu}}}} } \right) = 2.3 \times 10^{ - 5} \overline{{{\text{Nu}}}}^{14.0 }$$
(8)

with a R2 fitting error of 0.98. It shows, as expected, that, for the geometry presented in Fig. 1, an increase in heat transfer is obtained at the expense of an increase in pressure drop. Figure 7 shows that the relationship between the optimum pressure drop and the optimum heat transfer is nonlinear, and that the optimum pressure drop rises sharply with increasing values of the optimum Nusselt number. The function described by Eq. (7) becomes increasingly sensitive to changes in Nusselt number as the Nusselt number increases, i.e. for higher Nusselt numbers, a small increase in Nusselt number is obtained at the expense of a large increase in pressure drop. The remainder of this section explores the trade-offs between heat transfer and pressure drop, by analysing several of the optimum solutions depicted in Fig. 7.

Figure 8 presents the contour plot of the temperature and the velocity field for the non-dominated solution case where the \({\Delta }p\) is minimum (i.e. for the lower extreme of the Pareto-Frontier) — case 1.

Fig. 8
figure 8

Non-dominated solution with the lowest pressure drop (\({\Delta }p = 0.022\) Pa and \(\overline{{{\text{Nu}}}} = 1.088\)) obtained with \(D_{{\text{b}}}^{{\text{t}}} = 1.088\), \(D_{{\text{b}}}^{{\text{b}}} = 0.0\), \(W_{{\text{b}}}^{{\text{t}}} = 5.149\), \(W_{{\text{b}}}^{{\text{b}}} = 3.501\), \(H_{{\text{b}}}^{{\text{t}}} = 0.074\), \(H_{{\text{b}}}^{{\text{b}}} = 0.482\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 0.061\), and \({\text{Da}}_{{\text{b}}}^{{\text{b}}} = 0.021\) (the thick black lines indicate the baffles)

Full size image

The optimal solution with the lowest pressure drop is found when the top baffle has a small height, high Darcy numbers, and is positioned close to the step wall (Fig. 9). Additionally, the bottom baffle is located next to the step (\(D_{{\text{b}}}^{{\text{b}}} = 0\)) with about half the step height (\(H_{{\text{b}}}^{{\text{b}}} = 0.482\)) and a width of \(W_{{\text{b}}}^{{\text{b}}} = 3.501\). This solution suggests that, from a pressure drop perspective, placing a second step at the bottom wall adjacent to the first step, with half its height, and without a top baffle would be advantageous. This configuration is similar to the one presented by Abdulrazzaq et al. [20], with the difference that in the current case, the second step is permeable.

Fig. 9
figure 9

Nusselt number and x-component of the velocity at the first grid point above the bottom wall, normalised by the average velocity at the inlet, along the bottom wall for case 1

Full size image

Figure 9 shows, for case 1, the local Nusselt number and the x-component of the velocity vector at the first grid point above the bottom wall, normalised by the average velocity at the inlet. The position of the bottom porous baffle is shaded in grey for reference.

In case 1 the x-component of the velocity near the bottom wall decreases rapidly after the step, reaching a minimum (negative) value within the baffle. After this point, it increases and reaches a (positive) maximum, remaining low throughout the entire bottom wall. The Nusselt number peak occurs upstream of the maximum flow speed. The negative velocity values observed indicate that a recirculation zone behind the step exists, similarly to what happens for a backward-facing step channel with no obstacle (Fig. 10), a configuration which is not in the Pareto-Frontier depicted in Fig. 7.

Fig. 10
figure 10

Solution obtained for the unobstructed backward-facing step channel (\({\Delta }p = 0.016\) Pa and \(\overline{{{\text{Nu}}}} = 1.034\))

Full size image

When the fluid encounters the step, which is essentially a sudden expansion, it undergoes significant changes in velocity and pressure. The sudden expansion results in an adverse pressure gradient, which causes the flow to separate from the step surface, leading to the formation of a free shear layer and a recirculation zone behind the step. This zone is characterised by low velocity and high pressure compared to the inlet flow and reduced heat transfer. As the adverse pressure gradient decreases, the flow reattaches to the surface. For the case of a BFS channel with no obstacles, the reattachment point is at a distance of five step heights of the step, which is consistent with the results of other studies summarised in [25]. The reattachment point for case 1, located behind the bottom baffle, is slightly closer to the step (X = 4.7). Near the reattachment point, the heat transfer is maximum, decreasing further downstream as the thermal boundary layer thickness grows.

The inclusion of a porous obstacle within the recirculation zone behind the step introduces additional resistance to the flow because of the presence of the solid matrix. Moreover, it slightly enhances the heat transfer, since the thermal conductivity of the solid matrix is higher than that of the fluid. However, for an obstacle with the size and permeability of the one considered in case 1, there is a lack of variation in key flow characteristics from the response of a backward-facing step with no obstacle. To illustrate this, Fig. 11 presents three velocity profiles for both cases.

Fig. 11
figure 11

Velocity profiles at X equal to 0.49, 1.74 and 5.00 for an unobstructed backward-facing step channel and case 1

Full size image

In the current study, the MOO model was unable to identify non-dominated optimal solutions for the pressure drop lower than the one identified in case 1. The scenario involving an unobstructed backward-facing step (without any baffles) resulted in both a lower Nu and pressure drop. Incorporating this scenario into the objective space enriches the solution set by adding an additional point to the left of case 1. This inclusion thereby extends the range of the Pareto-Frontier, offering a broader perspective on the trade-offs between heat transfer efficiency and pressure drop. The fact that the optimisation algorithm was unable to reach such a solution can be attributed to the very low sensitivity to the pressure drop at this point with the asymptotical decrease in the non-dominated solutions.

Figure 12 presents the contour plot of the temperature and the velocity field for the non-dominated case that presents a maximum \(\overline{{{\text{Nu}}}}\) (i.e., for the upper extreme of the Pareto-Frontier) — case 2.

Fig. 12
figure 12

Non-dominated solution with the highest averaged Nusselt number (\(\overline{{{\text{Nu}}}} = 2.646\) and \({\Delta }p = 19.337\) Pa) obtained with \(D_{{\text{b}}}^{{\text{t}}} = 1.001\), \(D_{{\text{b}}}^{{\text{b}}} = 3.400\), \(W_{{\text{b}}}^{{\text{t}}} = 10.000\), \(W_{{\text{b}}}^{{\text{b}}} = 3.146\), \(H_{{\text{b}}}^{{\text{t}}} = 1.899\), \(H_{{\text{b}}}^{{\text{b}}} = 0.012\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 1.0 \times 10^{ - 5}\), and \({\text{Da}}_{{\text{b}}}^{{\text{b}}} = 0.045\) (the thick black lines indicate the baffles)

Full size image

The optimal configuration for maximising the Nusselt number redirects most of the fluid from the top of the channel to its bottom and forces it to bypass the porous baffle and flow under it, which promotes an increase in the velocity near the bottom wall and thus enhances heat transfer. (The low permeability of the baffle imposes a high pressure drop in the porous baffle and promotes an increase in the flow close to the bottom wall.) This can be clearly seen in Fig. 13, which shows four velocity profiles at \(X \approx D_{{\text{b}}}^{{\text{t}}} /2\), \(X \approx D_{{\text{b}}}^{{\text{t}}} + W_{{\text{b}}}^{{\text{t}}} /2\), \(X = 16\) and \(X = 22\). Notably, the average velocity in the middle of the channel formed by the porous baffle and the bottom wall is 1.1 m s−1. For this configuration, the width of the top baffle is the maximum allowed and the bottom baffle is almost inexistent. The height of the baffle is adjusted so the flow is distributed between the top baffle and the channel formed beneath it, ensuring efficient fluid movement and heat transfer. After the baffle, the flow behaves similarly to a flow over a backward-facing step with an expansion ratio of 19.75. This configuration eliminates the lower wall recirculation behind the step, but creates two recirculation zones, one near the top wall behind the top obstacle and another closer to the bottom wall, downstream of the first one. This second recirculation zone, characterised by smaller velocities, is responsible for a sharper decrease in the heat transfer at X≈18 (Fig. 14).

Fig. 13
figure 13

Velocity profiles at X equal to 0.5, 6.0, 16.0 and 22.0 for an unobstructed backward-facing step channel and case 2

Full size image
Fig. 14
figure 14

Nusselt number and x-component of the velocity at the first grid point above the bottom wall, normalised by the average velocity at the inlet, along the bottom wall for case 2

Full size image

Figure 14 shows the Nusselt Number and normalised velocity x-component at the first grid point above the bottom wall for case 2. The shaded grey area refers to the location of the top baffle which is the most important in this case.

The peak Nusselt number, located below the top porous baffle, is swiftly achieved as the velocity increases to its maximum value following the point of impingement. This acceleration is caused by the low Darcy number of the top baffle, which deflects most of the flow downwards. After peaking, the velocity remains almost constant until the end of the top baffle, along which the Nusselt number decreases. In the already mentioned recirculation zone on the bottom wall behind the top baffle, the Nusselt number drops more rapidly, with a subsequent Nusselt number peak downstream of this recirculation zone, because of the diversion of the flow to the heated bottom wall. The effectiveness of the configuration that corresponds to the upper extreme of the Pareto-Frontier (case 2) is significantly reduced due to the substantial increase in pressure drop caused by the porous baffle. An intermediate case of the Pareto-Frontier is shown in Fig. 15 (case 3). In this case \(\overline{{{\text{Nu}}}} = 1.976\) which is near the middle of the \(\overline{{{\text{Nu}}}}\) range of the Pareto-Frontier, but the pressure drop is significantly lower than for case 2.

Fig. 15
figure 15

Non-dominated solution for the case in which the \(\overline{{{\text{Nu}}}} = 1.976\) and \({\Delta }p = 0.386\) Pa. The results were obtained with \(D_{{\text{b}}}^{{\text{t}}} = 1.000\), \(D_{{\text{b}}}^{{\text{b}}} = 2.909\), \(W_{{\text{b}}}^{{\text{t}}} = 8.615\), \(W_{{\text{b}}}^{{\text{b}}} = 3.173\), \(H_{{\text{b}}}^{{\text{t}}} = 1.701\), \(H_{{\text{b}}}^{{\text{b}}} = 0.099\), \({\text{Da}}_{{\text{b}}}^{{\text{t}}} = 1.0 \times 10^{ - 5}\), and \({\text{Da}}_{{\text{b}}}^{{\text{b}}} = 0.042\) (the thick black lines indicate the baffles)

Full size image

The case depicted in Fig. 15 bears several similarities to the one with the maximum average Nusselt number (Fig. 12), particularly in terms of the permeability and distance of the top baffle, which fall within the lower bound values. However, a lower top baffle height and width result in a decrease in pressure drop, when compared to case 2. Furthermore, similarly to case 2, the small dimensions of the bottom baffle demonstrate that it has a negligible effect on promoting heat transfer. Despite already exhibiting a considerable average Nusselt number, the resulting pressure drop is still small. Therefore, this case represents a more practical option for real-world applications presenting a good trade-off between both objectives.

The top baffle parameters were the most critical for a broad range of solutions on the Pareto-Frontier, especially where the trade-off between \(\overline{{{\text{Nu}}}}\) and pressure drop becomes more pronounced. It was found that, by keeping the Darcy number and the distance from step constant and altering the height and width of the top baffle, it is possible to obtain many of the solutions in the Pareto-Frontier.

Conclusions

In this study, a two-dimensional backward-facing step channel with porous baffles placed after the expansion was investigated through computational fluid dynamics simulations. The CFD implementation was validated against a previously published work, which considers only one porous baffle contiguous to the top wall. Additionally, the analysis of this geometry was extended to analyse the dependence of the average Nusselt number on the height, distance from the step and permeability of the baffle.

A second porous baffle, contiguous to the bottom wall, was considered, and a multi-objective optimisation was performed. In this case, the considered design variables were the distances of the baffles to the step, their width, height, and Darcy Numbers, while the chosen objectives were the averaged Nusselt number and the pressure drop along the channel. Using non-dominated sorting genetic algorithms II, the Pareto-Frontier was identified, and it was found that, seeking the maximum average Nusselt number leads to a lower distance between the top baffle and the step and a lower permeability, while the bottom baffle effectively disappears. Conversely, if the minimum pressure drop is the goal, the top baffle becomes unnecessary, and the bottom baffle should be positioned next to the step and have approximately half its height. Therefore, the multi-objective optimisation presented in this work has offered insight into the relationship between the optimisation objectives and the different design variables of the backward-facing step channel with two porous baffles.

The current model is based on macroscopic porous media flow equations and does not include a detailed description of the flow within the porous matrices. These are semi-empirical equations that rely on closure models and lack the detailed description of nonlinear pore-scale flow features such as jets and vortices induced by the solid matrix. However, they are widely used in the context of porous media modelling, allow for the determination of volume-averaged quantities and are computationally efficient. The latter is a crucial characteristic when using the computationally intensive multiple-objective optimisation models based on GA. Another modelling choice that was made for the present study was to perform 2D simulations. Once again, this offers computational efficiency compared to 3D simulations, but may not be suitable for all scenarios, especially those with strong three-dimensional characteristics.

Future research might include three-dimensional simulations, pore-level simulations to assess the effect of pore-scale phenomena on the results, analysis of different Reynolds numbers and regimes, or adding other optimisation design parameters and objectives. In conclusion, this study has significantly contributed to the understanding of the multi-objective optimisation of porous baffles in a backward-facing step, but there is ample scope for further research to continue expanding our comprehension of this type of channel flows.