Introduction

Phase change material (PCM) based latent heat thermal energy storage (LHTES) technology continues to advance as a promising sustainable energy option. LHTES is widely used for energy savings in several applications to supplement the energy demand [1, 2]. Free cooling is one potent sustainable energy technology that facilitates substantial energy savings in a building. It can be achieved by using latent heat phase change material for thermal energy storage. The technology can be applied directly by fixing a PCM unit to ventilation apertures of a building i.e., in free cooling, integrated with air conditioning units, incorporated into building material, and as building envelopes to manage the building’s energy demand [3]. PCM-based LHTES provides for short-term thermal energy storage where the material absorbs thermal energy from hot ambient air during the day (i.e., daily high temperatures) to achieve melting and releases it during the night when a cold current is prevalent (i.e., daily low temperatures), resulting in solidification [4, 5]. Thus, during the melting, the material causes cooling of the inlet ambient air and vice versa on solidification where the excess thermal energy preheats cold ambient air inlet to the LHTES device [6]. The outlet air can be used to subsequently lower indoor temperatures during a hot day and warm it during a cold night if the system is integrated into building applications [7]. PCMS can also be integrated with renewable energy technologies such as solar or in other thermal regulating systems such as storage tanks or heat sinks [8, 9]. The major challenge in PCM-LHTES systems is poor heat transfer mainly due to the low thermal conductivity of the PCMs [10]. Research efforts have, therefore, made advancements such as design optimization of the PCM containers/heat exchanger units’ geometry or orientation, and incorporation of highly conductive nanomaterial into the PCMs to improve their thermal performance [11,12,13].

Multiple tubes and optimized shell designs for melting and solidification of PCM were theoretically investigated [14]. It was observed that there was about 27.7% improvement in the Nusselt number and improved heat transfer with varying spatial arrangement of the tubes. Other scholars [15], studied the melting of different shaped PCM; hemisphere, sphere, cube, cylinder, and frustum have constant outside hot boundary temperatures. The research found that the hemisphere had the highest melting rate. However, it was also reported that due to its bigger aspect ratio, the cylinder had increased heat capacity by 5.26% in 4200 s. The use of a cylindrical PCM-based TES unit coupled with a gas heater was investigated and it was recorded that experiments managed to store 39.6 kJ of energy against 49 kJ that had been predicted by a numerical model [16]. Enhancement of heat transfer in a PCM-TES by optimizing fins combined with the addition of conductive material led to improvement of the charge and discharge rates by about 74 and 85% respectively [17]. Other researchers asserted that increasing eccentricity in cylindrical PCM TES containers, as well as using multiwalled carbon nanotubes (MWCNT) and graphene oxide (GO), boosted the heat exchanger efficiency e.g., increasing eccentricity to 0.02 and 0.04 led to 27 and 49% improvement in heat exchange respectively [18]. Orientation of the containers was also noted to have an impact on heat transfer. It was observed that increasing Rayleigh’s number in a horizontal cylindrical capsule increased the melting rate of the PCM [19]. Furthermore, instead of cylindrical profiles, plates were investigated, and it was reported that energy savings of about 8–9% at 35 °C with different PCMs were realizable [20].

Putting the PCM in an encapsulating container promotes the heat transfer, and further prevents leakage, and retards flammability [21]. The addition of conductive nanomaterial further improves the phase change behavior of the PCM apart from just enhancing the thermal conductivity e.g., it was found that use of 1 mass% carbon nanofibers significantly boosted the thermal conductivity of PCM [22, 23]. It is asserted that the nanomaterial addition enhances the heat transfer of PCMs by enhancing their thermal conductivity [24]. A combination of both brings capital benefits to the system. Literature shows that the combination of optimizing the PCM container and the addition of 10 mass% of nano-Al2O3 caused a boost of the heat transfer performance by 34% [25]. Use of 0.5 mass% of Cu nano-additives improved heat transfer and thermal conductivity by 20% as well as reducing supercooling to 0.5 °C [26]. In another case, 0.5 mass% TiO2 enhanced the viscosity thereby reducing PCM’s leakage [22]. Use of vertical finned thermal storage with a dispersion of 5% graphene nano-plates (GNP), improved the solidification rate of a TES by 49% [27]. Some studies reported improved latent heat with nanomaterial addition e.g., by 5%, others observed a deterioration when more nanomaterial is introduced [28]. This reduction of latent heat limits the amount of nanomaterial to be added. Furthermore, to avoid sedimentation of the nanoparticles at the base of the PCM container, only a limited amount can be added. It has been observed from the literature that the amount is commonly limited to 0.1–5% nanomaterial [29] .

Fig. 1
figure 1

PCM box for direct free cooling to a room

Full size image

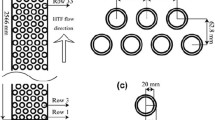
Based on the premises of this background, it observed that some studies have used the plate and cylindrical geometries over other geometries for the PCM containers and combined this with nanomaterial addition or fin arrangements. However, to the best of their knowledge, the authors noticed a shortage of studies combining the nanomaterial addition and comparison of different geometry profiles at the same time. So, in this study, an investigation is presented of the heat transfer characteristics of different shapes of PCM containers cooled and solidified during the night-time by the cold ambient air to cool the hot ambient air during the daytime for free-cooling applications (Fig. 1). The study is carried out for different PCM container shapes (cylinder, circular, rectangular, and ellipse) with an equal constant volume and cross-sectional area. The phase change material types: sp24, sp26, and sp29, and for two inlet air temperatures to the encapsulated PCM at daytime of 313 K and 318 K are used. Driven by the observed benefits of nano-additives, the study also uses nano-alumina, and copper-oxide particles to consider the nano-enhanced phase change material (NePCM) composites impact, however limiting the nanomaterial (4.0 mass%) to minimize sedimentation and latent heat deterioration. Copper-oxide and alumina are the nanoparticles of choice due to their high thermal conductivities, affordability compared to pure metal nanomaterials and because of their availability in the Egyptian market where the study was conducted. The study uses different PCMs and their corresponding nano-enhanced composites, to find the best-performing combination for free cooling applications, The impact of PCM container shapes and inclusion nanoparticles on the PCM melting and solidification, outlet air temperature, and Nusselt number is considered. To the best of their knowledge, the authors of this research declare that the manner of the comparison carried out herein using a numerical solution from Ansys Fluent 20.2 has not been done before. All the PCMs used in the study are selected in consideration of Alexandria-Egypt summer conditions and the material was supplied by Rubitherm Technologies Co., Germany [30].

Materials and methods

The PCM/NePCM will melt at set summer temperatures by absorbing energy from inlet air consequently cooling it for the purposes of lowering indoor temperatures. As the ambient temperatures drop at night, the PCM/NePCM will undergo solidification at 2 K below the lowest solidus point of the materials used. This prepares the PCM for another cycle meaning the system should manage to undergo complete melting and solidification within a day’s 24 h for practical feasibility. A 2D physical model for the setup is proposed as shown in Fig. 2. The following assumptions are considered in the computation.

  • Molten PCM is assumed an incompressible, Newtonian fluid, under transient conditions.

  • The PCM is assumed to have constant thermophysical properties except for the density which is modeled by the Boussinesq estimate to account for thermal buoyancy.

  • The NePCM composites are assumed to be continuous media in thermodynamic equilibrium,

  • There is zero velocity slip between solid nanoparticles and molten base fluid-PCM.

  • The effects of thermal radiation, viscous dissipation and volume expansion are negligible in the study.

Fig. 2
figure 2

Physical Model for the PCM box setup with numerical model

Full size image

The geometry labels are to the first letters highlighted in Fig. 2 (R-rectangular, E-ellipse, S-square, and C-circle) in the paper. Dimensions and mesh specifications for the different studied physical models are detailed in Table 1. The gap to the walls h, the cross-sectional area, and volume 1.2567 × 10–3 m3 of the geometries as well as the volume of the air region (7.5 × 10−3m3) are kept equal and constant for all geometries throughout the computations. Air-flowrate is baselined to 1.2 ms−1 [31] and calculated to ensure that the same amount of air is found in the gap h for each geometry per unit time.

Table 1 Geometry and mesh details
Full size table

Governing equations

The liquid fraction, the contact boundary Nusselt number, and the outlet temperatures are used to describe the heat transfer phenomena of the model through solving Navier–Stokes and energy equations in Ansys Fluent 20.2. The airflow and heat transfer through the physical model is governed by momentum, continuity, and energy equations as given below [31, 32]:

Momentum equation:

$$\rho \frac{\partial u}{{\partial t}} + \rho \partial_{{\text{v}}} (u_{{\text{u}}} u_{{\text{v}}} ) = \mu \partial_{{{\text{uu}}}} (u_{{\text{u}}} ) - \partial_{{\text{u}}} \left( p \right) + \rho g_{{\text{u}}} + S_{{\text{u}}}$$
(1)

Continuity equation:

$$\partial_{{\text{t}}} \left( \rho \right) + \partial_{{\text{u}}} \left( {\rho u_{{\text{u}}} } \right) = 0$$
(2)

Energy equation by the total enthalpy method:

$$\rho \frac{\partial H}{{\partial t}} = \nabla \cdot \left( {k \nabla T} \right)$$
(3)

The Darcy’s source term \({S}_{\rm u}\) is based on the liquid fraction (\(\beta\)) added to the momentum equation to turn the velocity of the PCM on during the melting and off for solidification.

Darcy’s source term is expressed as:

$$S_{{\text{u}}} = \frac{{\left( {1 - \beta } \right)^{2} }}{{\beta^{3} + \varepsilon }} A_{{\text{m }}} u_{{\text{u}}}$$
(4)

\(\varepsilon\) is usually 0.001, a small number that prevents a zero denominator and \({A}_{\rm m}\) is the mushy zone constant which is recommended to be in the orders of \({10}^{3}- {10}^{8}\), this study uses \({10}^{5}\).

The sensible heat (\({h}_{\mathrm{s}}\)) is given by [31]:

$$h_{{\text{s}}} = h_{0} + \int C_{{\text{p}}} \text{d}T$$
(5)

The enthalpy (H) becomes[33]:

$$H = h_{{\text{s}}} + \Delta H$$
(6)

\(\Delta H\) is found in the latent heat term (L) given as[34]:

$$\Delta H = \beta L$$
(7)
$$\beta = \left\{ \begin{gathered} 0\quad {\text{for }}T < T_{{{\text{solidus}}}} {\text{ solid state}} \hfill \\ \frac{{T - { }T_{{{\text{solidus}}}} }}{{T_{{{\text{liquidus}}}} - { }T_{{{\text{solidus}}}} }}\quad {\text{for }}T_{{{\text{solidus}}}} \le { }T < { }T_{{{\text{liquidus}}}} {\text{ mushy zone}} \hfill \\ {1}\quad {\text{for }}T \ge T_{{{\text{liquidus}}}} {\text{ liquid state}} \hfill \\ \end{gathered} \right.$$
(8)

Thermo-physical properties of used PCMs and nanomaterial are shown in Table 2. Properties of the nano-enhanced phase change material (NePCM) are modeled using Eqs. (9–14), where the subscripts nepcm, np and pcm denote the NePCMs, nanoparticles', and PCM properties, respectively.

Table 2 Thermal and physical properties of PCM & Nanomaterial
Full size table

The effective density of the NePCM composite is expressed by [31, 36]

$$\rho_{{{\text{nepcm}}}} = \varphi \rho_{{{\text{np}}}} + \left( {1 - \varphi } \right) \rho_{{{\text{pcm}}}}$$
(9)

The specific heat capacity for alumina nanomaterial [35]:

$$C_{{{\text{pnepcm}}}} = \frac{{A \left( {\frac{T}{{T_{\rm r} }}} \right) + B \left( {\frac{{C_{{{\text{pnp}}}} }}{{C_{{{\text{ppcm}}}} }}} \right)}}{C + \varphi } C_{{{\text{ppcm}}}}$$
(10)

Specific heat capacity for Cu and CuO nano particles [31]:

$$C_{{{\text{pnepcm}}}} = \frac{{ \varphi \rho_{{{\text{np}}}} C_{{{\text{pnp}}}} + \left( {1 - \varphi } \right) \rho_{{{\text{pcm}}}} C_{{{\text{ppcm}}}} }}{{ \rho_{{{\text{nepcm}}}} }}$$
(11)

Effective dynamic viscosity (\(\mu\)) [35]:

$$\mu_{{{\text{nepcm}}}} = A_{1} e^{{\left( {\rm A_{2} \cdot \varphi } \right)}} \mu_{{{\text{pcm}}}}$$
(12)

Thermal conductivity [35, 37]:

$$k_{{{\text{nepcm}}}} = \frac{{k_{{{\text{np}}}} + 2k_{{{\text{pcm}}}} - 2\left( {k_{{{\text{pcm}}}} - k_{{{\text{np}}}} } \right) \varphi }}{{ k_{{{\text{np}}}} + 2k_{{{\text{pcm}}}} - \left( {k_{{{\text{pcm}}}} - k_{{{\text{np}}}} } \right)\varphi }}k_{{{\text{pcm}}}} + {\varvec{k}}_{{\text{b}}}$$
(13)

where: \({{\varvec{k}}}_{{\mathbf{b}}}= 5 \times {10}^{4} \cdot \gamma .\varphi \cdot {\rho }_{\mathrm{pcm}} \cdot {{C}_{\rm p}}_{\mathrm{pcm}} \cdot \sqrt{\frac{{B}_{o} T}{{\rho }_{\mathrm{np}} \cdot {\varnothing }_{\mathrm{np}}}} \cdot f(T,\varphi )\)

Note that \(\emptyset_{{{\text{np}}}}\) is the diameter of the nanomaterial, \(\gamma\) is a coefficient given in Table 3, and \(f\left( {T,\varphi } \right)\) is usually taken as:

$$f\left( {T,\varphi } \right) = \left( {2.8217 \times { }10^{ - 2} \varphi + 3.917 \times { }10^{ - 3} } \right)\left( {\frac{T}{{T_{{\text{r}}} }}} \right) + \left( { - 3.0669 {\text{x}} 10^{ - 2} \varphi - 3.91123 \times 10^{ - 3} } \right)$$
(14)
Table 3 Curve-fit coefficients, for Eqs. (10)-(13), [35]
Full size table

\(T_{r}\) in Eqs. (10 and 14) is the reference temperature 273 K.

The latent heat L [31]:

$$L_{{{\text{nepcm}}}} = \frac{{\left( {1 - \varphi } \right) \left( {\rho_{{{\text{pcm}}}} \cdot L_{{{\text{pcm}}}} } \right)}}{{\rho_{{{\text{nepcm}}}} }}$$
(15)

Thermal expansion coefficient (\(\alpha\)) [35]:

$$\alpha_{{{\text{nepcm}}}} = \frac{{\left( {1 - \varphi } \right) \left( {\rho_{{{\text{pcm}}}} \cdot \alpha_{{{\text{pcm}}}} } \right) + \varphi \left( {\rho_{{{\text{nano}}}} \cdot \alpha_{{{\text{nano}}}} } \right) }}{{\rho_{{{\text{nepcm}}}} }}$$
(16)

The Nusselt Number calculations are done from the heat-load as shown below:

The heat load for the air region Q [38]:

$$Q = \dot{m}c_{{\text{p}}} \Delta T$$
(17)

where \(\dot{m}\), is obtained from the product of airspeed and cross-sectional area at the entrance of the PCM box. \(c_{{\text{p}}}\), is the specific heat capacity of the air and \(\Delta T\), is the temperature gradient of the inlet and outlet of the box (Tout − Tinlet).

The Nusselt Number (Nu.) for the PCM capsule [39]:

$${\text{Nu}}_{{\text{i}}} = \frac{{Q D_{{\text{i}}} }}{{k_{{{\text{air}}}} \left( {T_{{\text{s}}} - T_{\infty } } \right)}}$$
(18)

Here, \(k_{{{\text{air}}}}\), is the thermal conductivity of air, \(T_{\rm s}\) the surface temperature of the capsule and \(T_{\infty }\) the ambient temperature to the capsule.

Initial and boundary conditions

The initial, boundary and wall conditions are tabulated in Table 4. The solidus temperatures of each PCM have been given in Table 2. The simulation is run at inlet temperatures 313 K and at 318 K successively for the melting study of the materials and only at 295 K for the solidification process.

Table 4 Initial and boundary conditions
Full size table

Model solution and validation

A pressure-based solver coupled with a melting and solidification scheme is utilized for absolute velocity formulation of the 2D transient model with k-epsilon, 2nd-order realizable viscosity models. The SIMPLE algorithm is used for the pressure velocity coupling with the PRESTO mode for spatial discretization of the pressure. The energy, momentum, and dissipation rate are set to 2nd order upwind functions for a transient formulation using a first-order implicit function.

The relaxation factors are set as:

Pressure – 0.3

 

Density – 1.0

 

Momentum – 0.7

 

Liquid fraction – 0.9

 

Energy – 1.0

A time step of 1.0 s and the elements presented in Table 1 are found sufficient for the study. Figure 3 illustrates liquid fraction and outlet temperature timestep and mesh dependency study. The model is validated against the experimental results of the PCM plates study of [40]. As shown in Fig. 4, the highest error margin between the two results (present work and reference experimental work) is about 2.5%.

Fig. 3
figure 3

Time step and mesh dependency study

Full size image
Fig. 4
figure 4

Validation against the experimental work of [40]

Full size image

Results and discussion

The results presented below show the heat transfer behavior of Rubitherm’s SP24E, SP26E, and SP29Eu in summer conditions with and without nano enhancements in different container shapes. The respective nano-enhanced composites are labeled xxx_naasp.xx-A explained in Fig. 5. The base PCMs take the form xxx_spxx-A. The air domain carries heat energy by convection, passes over the PCM container transferring the energy by conduction onto the air-PCM boundary i.e., container. The graphs presented herein are curve fitted using the Avrami and sigmoidal curve fittings for the liquid fraction and the temperature profiles, respectively.

Fig. 5
figure 5

Labeling format used to discuss the results

Full size image

Impact on liquid fraction (melting)

Illustrations in Fig. 6a–f demonstrate the effect of geometry and nanomaterial addition to the different PCMs’ on the liquid fraction variation with time for the inlet temperatures 313 K and 318 K. Figure 6a-f for (sp24 at 313 K), (sp24 at 318 K), (sp26 at 313 K), (sp26 at 318 K), (sp29 at 313 K), and (sp29 at 318 K), respectively show the liquid fraction changes from zero (completely solid) to 1 (completely liquid). For the two inlet temperatures, 313 and 318 K, it is noted that the rate of melting is faster at the higher temperature for all the studied cases. This is commensurate with a higher thermal conductivity as temperature increases and higher thermal energy input per unit time. Additionally, the rate of melting is further improved by the addition of conducting nanomaterial. As the temperature difference between the PCM’s solidus and the inlet temperature increases, the studied effects consequently become pronounced such that PCMs of lower solidus temperatures (melting temperature) melt faster than higher solidus-PCMs at the same inlet temperature, i.e., sp24 and its composites melt fastest followed by sp26 and lastly sp29.

Fig. 6
figure 6

Liquid fraction vs time for PCMs & NePCMs at 313 & 318 K inlet temperatures

Full size image

Thinner profiles have faster melting. The rectangular geometry has the fastest rate of melting, followed by the elliptical, square, and circular geometries respectively. This is evident with all PCM/NePCM combinations. At inlet temperature 313 K before nanomaterial inclusion, it takes 1.64, 1.78, and 2.16 h to completely melt sp24, sp26, and sp29 respectively in rectangular containers, see Fig. 6. Whereas for the same conditions it takes 3.00, 3.22, and 4.01 h for the respective PCMs to melt in circular containers of the same cross-sectional area and volume as the rectangular capsules. The rectangular container offers the largest heat transfer improvement since the primary heat transfer fluid briefly encounters a thin blunt face then sustains contact with nearly the whole length of the capsule thereby favoring heat conduction. Large curvatures or wide blunt faces make it difficult for the fluid to maintain contact with the surface, thereby reducing the heat transfer efficiency of the profiles [41]. Thinner profiles offer lesser resistance to the flow of hot air particles in the air domain and offer a larger surface area sweep for the particles as compared to the wider geometries [42], this is also shown by the streamline diagrams in Fig. 7. Figure 7a clearly shows that there are some trailing eddies formed by the air particles at the end of the different PCM shapes. The eddies are pronounced in the case of square and circular shapes which negatively influences the heat transfer between the capsule and the air by increasing the region of no contact for the air and the capsule. It is also noted that even though the ellipse has completely laminar flow over its surface with no wake lines towards the outlet as with the other profiles (Fig. 7a), its PCM does not melt the fastest. The rectangular profile has the fastest melting PCM since its air velocity through gap h is relatively higher than that of the elliptical profile. The difference is attributed to the thin blunt edges which offer optimum resistance for just the effective heat transfer in the rectangular capsule. It therefore takes 1.78, 1.95, and 2.38 h to completely melt sp24, sp26, and sp29 respectively in elliptical profiles at 313 K.

Fig. 7
figure 7figure 7

Illustration of velocity streamlines and temperature contours for melting and solidification

Full size image

The melting performance increases as the axis ratio \({\uplambda }\), the shape width over its length approaches 0 e.g., from shape-E in Fig. 2, \({\lambda } = { }\frac{0.5b}{m}|_{{{\lambda } \to 0}}\). Within the containers themselves, the amount of PCM in direct contact with the container walls is larger in flat profiles. Remarkably therefore, the rectangular geometry has about 45% improvement in the rate of melting measured against the circular geometry. The elliptical geometry has 41% melting speed, and the least improvement is with the square profile which has 17% melting time improvement as compared to the circular profile which is the datum.

Use of thermally conductive nano-Alumina of k = 36 Wm−1 K−1 and nano-CuO of k = 40 Wm−1 K−1 enhances the heat transfer process within the PCM domain, thus increasing the rate of melting of the PCMs/NePCMs. Dispersed nanoparticles are high momentum heat carriers due to their small size, such that they improve heat transfer of the composite by Brownian motion. The thermophoretic force in the particles, however, relies on the temperature gradient such that the effect is increased for higher thermal gradients. In the case of this study, the performance is increased at 318 K as compared with 313 K, see Fig. 6d–f. Lighter Al2O3 nanocomposites have shorter melting times, such that for the same 4.0 mass% of nanomaterial, they have a slightly higher impact than the denser CuO-particles despite its higher thermal conductivity. Case in point for 313K_nalsp-C, the melting time on average is reduced by 11.56%, whereas 313K_ncuosp-C had an average 6.12% reduction of its melting time, both being measured from a case before using nano i.e., 313K_sp-C. In ascending order, the averaged-percentage improvement of the melting times due to nanomaterial enhancements; for Al2O3 NPs in the circular, square, elliptical, and finally rectangular profiles it’s 11.56, 12.29, 9.41and 9.66%, and for CuO NPs, it is 6.12, 6.32, 4.72 and 4.51% respectively at 313 K.

Nanoparticles improve the viscosity of the PCMs which results in improved velocity-uniformity. Such effects in turn promote the conduction of the NPs with layers of the PCM fluid [43]. However, wider geometries promote effective convection heat transfer efficiency. The resultant heat transfer is however influenced by all the involved heat transfer processes of the system, wherefore the favored conduction in flatter surfaces makes the combined effect of the enhancements to be superior in flatter geometries i.e., the rectangular and elliptical capsules. The combined impact of the geometry and nanomaterial enhancement ranks in the order rectangular, ellipse, square and circular, at 50.79, 46.10, 27.60, and 11.56% respectively with Al2O3 NPs and 48.00, 43.32, 22.68 and 6.12% with CuO NPs, respectively as compared to the base PCM in the cylindrical capsule.

Comparing the different types of PCMs it is found that, due to a higher thermal gradient between the Tsolidus and the Tinlet, sp24 and sp26 and their composites have the fastest rates of melting whereas sp29 has the least. It is therefore expected that the opposite is true for the solidification process which will be seen later where sp29 and its composites have the fastest solidification rates whereas sp24 trails the group.

Effect on solidification

The same mechanisms of heat transfer are expected during solidification only this time, the PCM domain is the one giving out thermal energy to the incoming air mass which is at a lower thermal gradient. The system uses Fourier’s law and Newton’s law of cooling, under the same conditions of flow characteristics, nanomaterial mass%, and geometry influence. However, solidification takes much longer time than melting as shown in Fig. 8a–c. Moreover, as discussed before concerning the PCM types, solidification is still a longer process taking approximately between 3 and 9 h compared to the melting est. 1.5–2.2 h, so the graphs are not exact inverses of each other even for the same geometry as plotted. As incoming air’s temperature goes below the Tsolidus, the PCM thickens and solidifies thereby resisting flow, reducing convection, and reducing the thermal conductivity due to the decreasing temperature resultantly diminishing the PCM’s degree of conduction. This contributes to a longer time being taken to release the energy, such that it takes ~ 17.27, 11.45, 8.39, and 7.57 h to freeze sp24 in the C, S, E, and R profiles respectively without using NPs. The percentage improvement due to the geometry change is given in Table 5. The rectangular geometry remains leading in all cases with 44–56% enhancement.

Fig. 8
figure 8

Solidification of the PCMs/NePCMs at 295 K inlet air temperature

Full size image
Table 5 Percentage increase in solidification rate due to shape change from circular as reference
Full size table

Solidification is also promoted by nanomaterial addition such that the rate of solidification is increased by 3.65, 3.87, 6.08 and 7.68% in the circular, elliptical, rectangular, and square profiles respectively when CuO NPs are added and by 10.16, 7.04, 6.08 and 11.35% for the same respective geometries when Al2O3 NPs are used. Results also indicate higher enhancement by nanomaterial addition in rectangular profiles at an average of about 7.62% since conduction becomes significantly influential with decreasing temperature which rapidly weakens convection. The nanomaterial effect is relatively pronounced for nano-alumina material from 6.08 to 17.11% improvement compared to the 3.53 to 8.02% enhancement due to nano copper oxide material addition.

Effect on outlet air temperatures

The outlet temperature accounts for the degree of cooling that can be achieved by the PCM/NePCM. This is dependent on the modes of heat transfer discussed earlier, the conduction on the PCM-container and inlet air boundary heavily influenced by geometry, then the mixed mode within the PCM-domain, influenced by geometry as well as the thermal conductivity of the PCM. At the start of melting, only conduction takes effect, then convection commences in the latter stages of the process thereby aiding the process to occur faster. Similarly, during solidification, convection is dominant at the start and diminishes with time until the process is purely conductive again. As the inlet temperature increases, the heat transferred increases and so does the degree of cooling, i.e., a larger drop in air temperature at the outlet. The container geometry and nanomaterial addition influence both these modes as discussed above and yield the following results.

From Fig. 9a–f, at time t(0), the temperature T rapidly decreases to a minimum from the initial Tin = 313/318 K in flow-time 0-200 s, then starts to increase again steadily until an inflection, a sharp increase back to Tin then the line flattens for each container shape as depicted in the plots. Generally, the circular and square PCM geometries record the lowest outlet temperatures i.e., the largest ΔT, followed by the rectangular and elliptical profiles respectively. For inlet temperature 313 K, in the order circular, square, rectangular, and elliptical profiles for sp24 & composites, the maximum temperature differences are 2.71, 2.61, 2.51, and 1.93 K. The temperature for the circular-shaped capsule rapidly dips to a minimum in the first 0–200 s then shortly rapidly increases by 0.1–0.3 K at around t = 240 s to 300 s, then steadily rises. This is noticed in the square profiles and applies in all combinations for these shapes. Sp26 shows 2.43, 2.54, 2.33 and 1.78 K temperature drops for circular, square, rectangular, and elliptical profiles respectively whereas, sp29 has the least drops of 1.80, 1.87, 1.72, and 1.33 K for the same respective shapes. The largest temperature drop is 3.56 K for 318K_ncuosp26-S. The drop increases with an increase in inlet temperature for all shapes and is highest for PCM with the least Tsolidus i.e., sp24. The circular, square, and rectangular PCM containers have comparable temperature drops which are within 0.1–0.25 K of each other whereas the ellipse has a significantly low drop. The rectangular profile showed temperature drops of 3.31, 3.1, and 2.51 K for sp24, sp26, and sp29 combinations, respectively at 318 K. It is noted that the minimum temperatures are insignificantly affected by the nanomaterial addition to the PCM in the model. Only the time to reach thermal equilibrium is reduced when nanomaterial is added. Nano alumina composites reach thermal equilibrium faster than nano-copper oxide-based composites.

Fig. 9
figure 9

Outlet temperature profiles for PCM/NePCM at different inlet temperatures during melting

Full size image

The largest temperature drop is observed in sp24 followed by sp26 the lastly sp29. This corresponds with the magnitude of variation of Tinitial from Tsolidus of each PCM. This means the degree of cooling is better for the low melting sp24 and sp26 than for the sp29.

Nanomaterial addition influences the heat transfer in the PCM domain. Literature commonly models the heat transfer to be purely conductive, however, it is needful to also consider nano-convection to sufficiently explain the heat transfer within a nanofluid. The time to reach Tin from the minimum temperature point reduces with the addition of nanomaterial, and the effect is more significant at higher inlet temperatures. The impact is also more significant with PCMs of lower melting points since there is a larger inlet temperature gradient (Tin − Tsolidus), which favors the effect of increased thermal conductivity. The effect of nanomaterial enhancement is minimum in the elliptical geometry on the outlet temperature. Similar trends are noted for the solidification process see Fig. 10a–c. From the figures, the addition of nano does not affect the degree of cooling, but rather enhances the rate of change in the air temperature.

Fig. 10
figure 10

Outlet temperature profiles during the solidification process

Full size image

Effect on the air–PCM interface Nusselt number

On the air–PCM container contact region, heat transfer can be described by Nusselt Number, a dimensonless coefficient that gives the convective to conductive heat transfer ratio. It is noted from the graphs in Fig. 11a–f, that the Nusselt number \({\text{Nu}}_{{\text{i}}}\), rapidly increases from 0 to maximum within the first 300 s, then follows a steady trend afterward until the melting is complete. The smallest is \({\text{Nu}}_{{\text{i}}}\) is found in the square geometry indicated by the blue lines in the graphs. The elliptical profile has the highest Nusselt number in all cases, owing to its hydraulic diameter which is the largest compared to the other shapes. Due to the wide blunt faces, the square profile has pronounced eddies which limit the air to capsule thereby reducing the effective heat transfer, and thus a smaller Nu. The circular and the rectangular capsules have comparable Nu numbers. The circular profile has a smoother laminar flow over a reasonable surface of the container and a big hydraulic diameter whereas the rectangular capsule has better heat transfer.

Fig. 11
figure 11

Air–PCM surface Nusselt number plots for melting PCMs/NePCMs at 313 and 318 K

Full size image

The incorporation of nanomaterial slightly amplifies the discussed patterns in the flattened geometries but has minimal effect on wider geometries. The nano-alumina particles exhibit the highest effect in this regard. Figure 11a–f shows the Nusselt for the melting cycles of each PCM at 313 and at 318 K. The results show that sp29 has the least Nusselt number and its composites also rank lowest when compared to corresponding composites of other PCMs (sp24 and sp26). Alumina-enhanced composites have the highest Nu numbers in all cases and nalsp24-R has the highest Nu.

Figure 12a–c presents Nusselt numbers for the solidification process which have similar patterns as discussed above. Peak Nusselt numbers are achieved within 0–1000 s before a steady trend is witnessed. Nanomaterial addition does not show significant enhancement of the Nusselt during the solidification process. The Nu for these processes can therefore be said to be mainly reliant on the shape of the capsule.

Fig. 12
figure 12

Nusselt number profiles during the solidification process

Full size image

Conclusions

The heat transfer behavior during melting and solidification cycles of PCM/NePCMs in 4-basic geometries (circle, rectangular, ellipse, and square) is studied for free-cooling applications. The study is performed for different inlet temperatures of 313 and 318 K for the melting phase achieved during the daylight hours and 295 K for the solidification phase to simulate the night-time.

It is noted that the rectangular profile which is of much lower axis ratio compared to the circular profile has the shortest melting times ~ 1.16–2.16 h and solidification times ~ 2.79–7.57 h.

The combined effect of the enhancements is just over 50% in the rectangular profile.

The addition of nanomaterial improves the rate of melting by at least 4.0 and 8.34% for 4.0 mass% of CuO and Al2O3 NPs respectively.

Wherefore the largest temperature drop is 3.56 K for the square capsule at 318 K, the rectangular profile achieves a competitive 3.31 K temperature drop under the same conditions.

The Nusselt number increases as the axis ratio approaches 1 and slightly increases with nano-material addition, especially with nano-alumina material.

Generally, the melting/solidification performances of sp24 and sp26 are comparable due to their similar properties.

This study does not fully account for nanomaterial sedimentation as such further experimental work is recommended.