Introduction

Studying the thermodynamic properties of soil organic matter (SOM) is a developing field that involves calculation of the enthalpy (H) of the substrate, as well as the Gibbs energy (G), or free energy, and entropy (S). These three matter-related functions are connected by the second law of thermodynamics. When applied to G, this law is mathematically written as follows:

$$ \Delta G \, = \, \Delta H \, {-} \, T\Delta S $$
(1)

H is biologically described as the energy stored in the substrates, and ΔH is the difference between the H of products and reactants involved in any reaction. ΔH is negative when the conversion from reactants to products releases heat at constant pressure, a natural assumption for living systems [1, 2].

G is the energy available to do work. ΔG is the free energy change in a system changing from an initial state (reactants) to a final state (products). The ΔG value indicates the maximum energy usable by any system changing from the initial to the final state. Depending on whether this value is positive or negative, it can indicate whether the process is spontaneous (negative ΔG) or not (positive ΔG). Although this information is useful in many research disciplines, it has been poorly explored in soil science. However, this information could provide a better understanding of the SOM lability and recalcitrance if a ΔG value could be attached to any reaction involving SOM with different chemical nature, to measure the potential of the SOM to be spontaneously decomposed or to be transformed, whether as a whole macromolecule, or as a continuum of fractions under different degree of transformation if those fractions can be determined. In general, stability is indicated by less negative ΔG values [3].

ΔS represents the change in entropy of a reaction and is a thermodynamic measure that indicates the degree of disorder in any system at the molecular level. A positive ΔS value occurs because of the decomposition of a large complex molecule into smaller products. A negative ΔS is associated with more ordered products than reactants. Cells and microorganisms can control entropy by importing or exporting products and reactants from the cell to the outside and vice versa, to guarantee that metabolic reactions will occur [4]. In general, a process with negative ∆H and positive ∆S will be spontaneous, as a positive ΔS contributes to making ΔG more negative in Eq. 1. The role of entropy in SOM decomposition, whether by combustion or microbial catabolism, remains poorly explored, uncertain and challenging due to the great complexity of calculating and interpreting this value, especially in living systems [5].

All these terms also define how far or close any system is from the equilibrium between reactants and products or between an initial and a final state. The latter would help to elucidate the state and evolution of ecosystems [5, 6]. Any system at equilibrium has the lowest possible free energy state and will spontaneously evolve until reaching a state where is not possible for the system to convert the remaining energy into work spontaneously. Any change that moves the system away from that equilibrium, i.e. by changing reactants and/or products, will make G more negative. In this respect, cells and microorganisms at equilibrium will die because there will not be enough free energy for them to sustain the metabolic reactions that are essential for living. To prevent this from occurring, cells can use energy to import reactants, as well as to export products to regulate metabolic pathways where one reaction feeds the next one [1, 7]. These processes are directly involved in SOM microbial decomposition of soils.

In Eq. 1, temperature (T) determines the impact of ΔS and ΔH on the total free energy change in the reaction as the impact of ΔS increases with T. Therefore, Eq. 1 may yield important information for predicting how the thermodynamic profile of a soil ecosystem changes with temperature, which could be applied within the context of climate change. When the ΔS associated with the decomposition of a certain organic substrate is positive, increasing temperature could make ΔG more negative, thus contributing to the potential of that SOM to be spontaneously combusted as the temperature increases. Following this line of thought and considering that the ΔH associated with soil decomposition is negative, ΔH < 0 (it is always an exothermic reaction), we can expect two possible situations that would define the sensitivity of SOM to T:

  • ΔH < 0; ΔS > 0: ΔG will be always negative and SOM decomposition will occur spontaneously at any temperature.

  • ΔH < 0; ΔS < 0: ΔG will be negative only at lower temperatures. Therefore, SOM decomposition will only occur spontaneously at those low temperatures and will consequently be more resistant to the increasing temperatures caused by global warming.

In other words, by calculating ΔH and ΔS we can determine the extent to which SOM decomposition will depend on T as a spontaneous reaction.

These thermodynamic parameters are usually calculated using Hess’s law when the stoichiometry of the reaction is known. Stoichiometric procedures using the enthalpies and free energies of formation of reactants and products have been developed for and applied to different microorganisms and specific substrates [8,9,10]. However, the chemical formulae of these reactants and products have not been established for complex organic molecules and heterogeneous microbial populations in soils, where calculation of these parameters becomes challenging. Regarding microbial metabolism and organic substrates, this problem has been solved by developing enthalpic models derived from Thorton’s rule [2] relating the energy of organic substrates to the degree of reduction. However, the applicability of these models for analysis of soil thermodynamic properties has not yet been tested. Most of the existing information about soil thermal properties only focuses on empirical interpretations of microbial metabolic rates, and different indices that do not involve thermodynamic variables [11,12,13], even though previous research has shown that the ∆H of soil microbial reactions can be estimated and that the nature of the ∆H in microbial growth reactions occurring in soils can be determined [14, 15]. There are also robust models associating the ∆H to the ∆G and ∆S of the metabolic reactions [9, 16, 17]. In addition, the necessary technology for delivering the experimental data to apply Eq. 1 to soil is already available, i.e. simultaneous thermogravimetry and differential scanning calorimetry (TG–DSC) and isothermal calorimetry.

In order to describe the thermodynamic reactions that take place in soils, it is necessary to determine the thermodynamic functions that characterize SOM and its decomposition, which are also influenced by the environmental properties of soil ecosystems [18]. Understanding the role of thermodynamics in all of these processes may be a complicated task that requires quantifying the energy content of soils. Estimating the thermodynamic functions that describe SOM constitutes a first, essential step in this process. Information about the best procedures for measuring the energy stored by soils remains scarce, with different options still under development and poorly connected.

This paper reports a method of estimating thermodynamic variables in SOM by studying the combustion reaction by TG–DSC and by applying the two thermodynamic models relating energy to the degree of reduction in organic substrates and their Gibbs energy [16, 17] to obtain the entropy of the SOM combustion from Eq. 1. These models have not yet been tested for thermodynamic characterization of organic substrates in soils and would contribute to improve the development of best procedures regarding the quantification of the soil energy budget.

Experimental

Study sites

Soil samples were collected in two types of forest: oak (Quercus petraea) and beech (Fagus sylvatica L.). Both are deciduous forests with seasonal inputs of organic matter to the soil. Oak forest soil samples were obtained in four different sites, located in Ireland (3 sites) and southern England (1 site) (Fig. 1). The three sites in Ireland are Derrycunnihy (DC samples), Glengarriff (G samples) and Uragh (K samples). These site locations can be viewed at: http://map.geohive.ie/mapviewer.html. The samples from England were collected in the Alice Holt Forest (samples Big Wood, BW; New Forest, NF; and Rogate, ROG.). Thermodynamic characterization of these samples has been reported in previous papers [19, 20]. Beech soil samples were collected from seven plots in three different sites in northern Spain (Enciso [4], Anguiano [2], and Canales [1]), all in the region of La Rioja (Spain). The sampling locations are shown in Fig. 1.

Fig. 1
figure 1

Map showing the different sampling sites

Full size image

Soil sampling

The samples represented two different soil layers: the L/F horizon (corresponding to the organic soil surface) and the underlying mineral soil. L/F horizons are highly organic, are mainly constituted by organic matter with a low degree of decomposition and are strongly influenced by the type of vegetation. The mineral soil is constituted by organic matter with a higher degree of transformation and mineralization than L/F.

Little information is available about the thermal properties of these soil layers. Comparison of the thermal properties of these different soil horizons can therefore yield information about the sensitivity of the proposed methods and the relationships between the thermodynamic parameters and different SOM properties and different forest types.

Oak forest samples

Between three and five sampling points were selected at each study site, with each point located midway between the tree stem and the maximum crown radius of an oak tree. First, all loose litter (L) and fermented (F) layers were collected within a square sampling quadrat (0.25 × 0.25 m) at each sampling point. Samples of the humic (H) layer were then collected using stainless-steel sampling rings of 100 cm3 volume and a hammering head (Eijkelkamp Soil and Water B.V., The Netherlands). After removal of the entire H layer, the same process was used to collect one sample of the top 5 cm of the mineral layer (M samples). In addition, three extra cores were obtained at each location for further chemical and thermal analysis. Within each stand, samples from the six locations were mixed and bulked samples were prepared for all laboratory analyses. In all cases, sampling produced minimal disturbance and compaction, and the depths of the different L/F, H and M layers were recorded. In some cases, the shallowness of the H layer and an abundance of stones prevented collection of samples from the H profile [20].

Beech forest samples

In each beech forest plot, four sampling points were selected in north, south, west and east directions displaced 10 m from the plot centre. First, all loose litter (L) and fermented (F) layer (H samples) were collected within a rectangular sampling quadrat (0.15 × 0.20 m) at each sampling point, using a stainless-steel rings of 100 cm3 volume and a hammering head (Eijkelkamp Soil and Water B.V., The Netherlands). After removal of the entire LF layer, the same process was used to collect samples from the top 5 cm of the mineral layer (S samples).

All soil samples obtained for the elemental and thermal analysis were manually broken up, spread on plastic trays and air-dried for 48 h at room temperature. Thereafter, coarse fractions (i.e. plant material and stones) greater than 2 mm were set aside from mineral soils and the remaining sample was sieved (2-mm) to separate fine and coarse soil fractions. LF samples were ground separately in a rotor mill. Both fractions were then oven-dried at 105 °C for 24 h (or until constant mass) and their mass (± 0.01 g) was recorded. The fine fractions from mineral soils (< 2 mm) and the grinded LF samples were used for the elemental and thermal analysis.

Elemental and thermal analysis

The total C, organic C and nitrogen (N) contents of all samples were determined in an automated LECO CHNS analyser. The thermal properties were then measured by simultaneous TG–DSC (TGA-DSC1 Mettler Toledo): the samples were placed in 100 μL open aluminium pans under a dry airflow of 50 mL min−1 with a temperature ramp from 50 to 1000 °C at 10 °C min−1 after calibration.

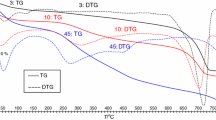
DTG curves (first derivative of TG traces) indicate the resistance of SOM to thermal oxidation in air. TG traces determine the quantity of SOM fractions with different resistance to oxidation defined by the temperatures at the maxima of the different combustion peaks in the DTG curves. In this study, DTG curves and TG traces were used to determine the quantity of the SOM, defined as the mass loss between 160 and 600 °C divided by the initial dry mass of the sample. DTG curves also yield the SOM thermal fractions, and the percentage of mineral char after combustion which is the soil mass remaining after the temperature scan.

DSC curves show the profile of the energy released by combustion of the SOM. The quantity of energy from SOM is determined by integration of the DSC curves as a function of time after baseline correction to zero from between 160 and 600 °C. The quantity of heat must be normalized to the SOM content of the samples given by the TG, to yield the total energy content of SOM, QSOM, in kilojoules per g of soil organic matter (kJ g−1 SOM). To approach the enthalpy of combustion, ΔcHSOM, at 25 °C, a value of 1.839 kJ g−1 SOM was added to QSOM to correct for the temperature difference and the heat of condensation of water [21]. The values in grams were converted to C mol using the soil C content per gram of SOM averaged for all the samples, multiplied by the atomic mass of C.

Theoretical estimation of SOM thermodynamic properties

The reaction taking place into the TG–DSC is the combustion of SOM by the dry airflow, in which oxygen is therefore the electron acceptor. It can be simplified as:

$$ {\text{SOM}}_{{({\text{S}})}} + {\text{ O}}_{{2({\text{g}})}} \to {\text{ CO}}_{{2({\text{g}})}} + {\text{ H}}_{2} {\text{O}}_{{({\text{g}})}} + {\text{heat}} $$
(2)

The heat released during SOM combustion under the TG–DSC conditions is directly obtained by integration of the DSC curve, as explained above. The heat value normalized to the amount of SOM given by the TG traces should be close to the heat of combustion of the total SOM macromolecule, since SOM can be considered as a mixture of various molecules too. Temperature correction and normalization to C mol should yield a value close to the enthalpy change associated with combustion of SOM, ΔCHSOM at 25 °C. As the enthalpy of combustion of CO2 and water in Eq. 2 is zero, ΔCHSOM represents the enthalpy of SOM. Under this assumption, the degree of reduction in SOM can be determined using the following equation [22, 23]:

$$ \Delta_{{\text{c}}} H^\circ = \, Q_{{\text{o}}} \lambda_{{\text{S}}} $$
(3)

where ∆cH° represents the enthalpy of combustion of a certain substrate under standard conditions and would be given here by the DSC for SOM normalized to the soil C content and adjusted at 25 °C, as previously explained. λS is the degree of reduction in the substrate.

Correlations between enthalpies of combustion and the degree of reduction in substrates have been reported for numerous different organic compounds, including plant material [24]. Q0, also called the oxycaloric equivalent, is the constant linking both, with previously reported values varying between 108 and 118 kJ mol−1 electron. Differences in this value for organic substrates are related to the stoichiometry and structure of the molecules [24]. However, the effect on ∆cH° calculations for SOM has not yet been tested. In this study, we used two of the reported models to determine the degree of reduction in SOM with Eq. 3. This is an essential step in estimating the Gibbs energy and entropy changes for SOM, as recently reported for enthalpic models [20].

We compared the values of these thermodynamic state variables of SOM by using the approaches and correlations reported by Roels and Sandler and Orbey [16, 17].

The relationship between enthalpies of combustion and degree of reduction is given by the following general equations:

$$ \Delta_{{\text{c}}} H^{0} = \, - 115\lambda_{{\text{i}}} $$
(4)
$$ \Delta_{{\text{c}}} H^{0} = \, - 109\lambda_{{\text{i}}} $$
(5)

Equations (4) and (5) correspond to the models proposed by Roels and Sandler and Orbey [16, 17], respectively, connecting the enthalpy of combustion, ΔcH0, and the degree of reduction in the substrate, λi, by the oxicaloric equivalents given for microbial biomass. These values are within the range previously reported for the combustion of different organic substrates, i.e. 108–118 kJ mol−1 electron [24]. Therefore, they should provide good estimates of the degree of reduction in SOM. The advantage of using these models is their connection to the Gibbs energy change in the combustion reaction, given by the following equations:

$$ \Delta_{{\text{c}}} G^{0} = \, - \, 94.4\lambda_{{\text{i}}} {-} \, 86.6 $$
(6)
$$ \Delta_{{\text{c}}} G^{0} = \, - 110.23\lambda_{{\text{i}}} $$
(7)

where ΔcG0 represents the Gibbs energy change of the combustion reaction under standard conditions, given by the models proposed by Roels (Eq. 6) and Sandler and Orbey (S&O) (Eq. 7) [16, 17]. Consequently, these models provide the thermodynamic variables required for determining the entropy change in the combustion reaction by Eq. 1.

We compared these two models (hereafter referred to as the Roels and S&O models), as options for the thermodynamic characterization of soil samples, and tested the sensitivity of the thermodynamic variables obtained in relation to different types of forest and of SOM nature.

Statistical analysis

TG–DSC measurements were made using duplicate samples from beech forests. The experimental error obtained (3%) was applied to the oak forest samples, for which only one replicate was available. This treatment was applied because of the high reproducibility of thermal analysis. Data obtained by the different models were compared by paired sample t test when the data fulfilled the normality criterion (Kolmogorov–Smirnov) for parametric statistics. When the data were not normally distributed, they were compared by Paired Sample Sign Test. These comparisons were made using the individual data (n = 43). Data for different sites and soil layers were compared by one-way ANOVA after checking the normality (Shapiro–Wilk) and homoscedasticity of the data (Levene’s test). Variable dependency in soil data was determined by Pearson correlations. The contribution of soil properties to variance among samples was studied by PCA analysis.

Results

Elemental analysis

Data on the soil elemental properties are shown in Table 1. Organic C and total C were closely and significantly correlated (n = 43; r2 = 0.98; p < 0.001) with a slope of 0.87, and it was therefore assumed that 87% of the total C of samples was organic C. N was closely correlated with total and organic C, with few differences in the slopes and intercepts, suggesting the organic nature of N in these samples (n = 43, r2 = 0.86; p < 0.001 in both cases). All L/F samples contained more N than the mineral soil samples. The C/N ratio varied among samples and sites, with no clear pattern of variation.

Table 1 Results of the elemental and thermal analysis of the samples
Full size table

Thermal analysis

The DSC plots revealed different profiles among forest ecosystems and soil layers (Fig. 2). Those corresponding to the organic litter (L/F layer) were generally more homogenous for different sites (Fig. 2a) than those corresponding to mineral soils (Fig. 2b–e). L/F layers yielded bimodal curves with two well-differentiated peaks at about 333 °C and 411 °C in the oak forest samples, and at 333 °C and 431 °C in the beech forest samples. DSC plots corresponding to the mineral soil samples (Fig. 2b–e) show remarkable differences in the curve profiles compared to those from the L/F layers, suggesting differences in the nature of the SOM. In the case of oak forests (Fig. 2b) differences in DSC profiles in the mineral samples affect the temperatures of the combustion peak and the energy content. Thus, the DSC plots showed one combustion peak at temperatures varying from 301 to 387 °C in samples DCM and GM from Ireland and BWM and NFM from England, while the DSC curves had two overlapped peaks in KM from Ireland and ROGM from England.

Fig. 2
figure 2

Averaged DSC profiles for the soil L/F layer sampled from oak and beech forests in different sites (a). Temperature of the first combustion peak is similar for samples from both forests but with higher energy in beech than oak samples. Temperature of the second combustion peak is higher in beech than in oak forests. The heat of combustion was significantly different in samples from the two forest ecosystems. b–e Represent the DSC curves for all mineral samples. The different profiles among sites and differences relative to their respective L/F layers suggest remarkable changes in the nature of the SOM

Full size image

Three different DSC profiles were obtained for the mineral samples from beech forests. Samples S7 and S2 (Fig. 2d) both from the same site (Enciso) yielded only one combustion peak at 318 °C. Samples S1 and S6 from Anguiano, and sample S3 from Canales (Fig. 2c) all yielded a first combustion peak at temperatures varying from 316 to 329 °C, followed by a shoulder at about 404–426 °C. Sample S4 from Enciso (Fig. 2e) had the most complex profile, with three combustion peaks at 326 °C, 400 °C and 499 °C. The results show high variability in the nature of the SOM among sites as mineralization proceeds.

Integration of DSC curves normalized to the SOM content given by the simultaneous TG yielded the heat of combustion, QSOM, of samples, shown (in kJ g−1 SOM) in Table 1, together with the SOM and mineral char/ash given by the TG (Table 1). L/F layers mainly differ in their char content and SOM content. The L/F layer from sites in Ireland had the highest SOM content, followed by the samples from England. The beech forest samples from Spain had the lowest SOM content and higher mineral char percentages, suggesting a higher degree of mineralization.

Conversion from kJ g−1 SOM to kJ mol−1 C

Total C and organic C were correlated with the SOM content, which was determined by thermogravimetry (n = 43; r2 = 0.96, p < 0.001; r2 = 0.90, p < 0.001, respectively). Plots of total C versus the SOM content of samples yielded a slope of 0.54 g total C per g of SOM, close to Pribyl’s correlation [25]. The plot of the organic C versus SOM yielded a slope of 0.45. This slope is closer to the glucose equivalent (0.42) corresponding to the heat of combustion value of 15.65 kJ g−1 [24]. It is also consistent with the conversion factor reported for leaves (0.455) [24]. Therefore, 0.45 was used as the conversion factor for the heat of combustion given by simultaneous TG–DSC in kJ g−1 SOM to kJ mol−1 C, to enable comparison of the QSOM values with previously reported values in the same units. The values obtained after correction of the QSOM are assumed to be close to the enthalpy change in the SOM combustion reaction in the DSC, ΔCHSOM. The enthalpy values are shown in Table 2.

Table 2 Thermodynamic variables for the soil samples used in this study
Full size table

Determining the degree of reduction, λ, Gibbs energy and entropy

The λ values obtained for all the soil samples by applying Roels (λR) and S&O (λS&O) [16, 17] correlations to the ΔCHSOM data, according to Eqs. (4) and (5), are shown in Fig. 3. The data were not normally distributed, and they were, therefore, compared using a paired sample sign test (n = 43), which revealed that the λ values were significantly different and correlated (n = 43; r2 = 1). Plotting QSOM in kJ g−1 SOM against λS&O and λR revealed the following relationships for these samples (n = 43, r2 = 1): − QSOM = 4.08 λS&O and − QSOM = 4.31 λR.

Fig. 3
figure 3

Changes in the values for the degree of reduction, λ, of all the samples obtained by correlations between Roels’, λR, and Sandler and Orbey’s, λS&O. Comparison of λR and λS&O values yielded significant differences, but the values are significantly correlated. X-axis represent the numbers for the samples. From x = 1 to x = 14 λ values for L/F samples from beech forests. From x = 15 to x = 28, λ values for mineral samples from beach forest. x = 29 to x = 34 are λ values for oak L/F samples. The remaining data are for the H and M samples from oak sites

Full size image

Based on the results, the change in Gibbs energy for the SOM combustion, ΔcGSOM, was determined from Roels (Eq. 6) and S&O (Eq. 7) [16, 17] correlations and the respective λ values (Table 2). The ΔcGSOM values obtained did not fulfil the normality test and were compared by paired sample sign test, revealing significant differences between the ΔcGSOM data obtained by both models using the individual raw data (n = 43). Differences in the ΔcGSOM obtained by the Roels and S&O [16, 17] correlations increased as the substrate turns to a more reduced state (Fig. 4), as also reported by Roels [17]. These differences are responsible for the changing entropy values determined by Eq. 1 using the ΔcGSOM obtained by each of these models (Table 2). The plot of ΔcGSOM versus ΔcHSOM revealed significant linear correlations which could serve as models for determining ΔG from the enthalpic values of soils determined by TG–DSC, as proposed for organic substrates [26].

Fig. 4
figure 4

Changes in the values of the Gibbs energy of SOM, ΔcGSOM, derived from the Roels (ΔcGR) and Sandler and Orbey (ΔcGS&O) correlations, with the enthalpy of combustion, ΔcHSOM, determined by DSC. Comparison of ΔcGR and ΔcGS&O data yielded significant differences. The differences increased as the ΔcHSOM became more negative indicating the SOM is more reduced than carbohydrates. Therefore, differences increase as substrates become more reduced

Full size image

The S&O model indicated that the entropy change increased with ΔcHSOM (Fig. 5a) and therefore, with the degree of reduction in SOM, while the Roels model showed that the entropy change followed the opposite pattern, giving negative ΔSR values at higher ΔcHSOM values (absolute values) than those for carbohydrates (− 466 kJ mol−1 C) (Fig. 5b). Entropy is expected to increase as ΔG becomes more negative and as the degree of reduction in the substrates increases [17] as data from S&O model [16] show in this work.

Fig. 5
figure 5

Variation in the entropy change, ΔS, derived from the Sandler and Orbey (ΔSS&O) (a) and the Roels (ΔSR) (b) correlations, with the enthalpy of combustion of SOM, ΔcHSOM. In each model the entropy changes vary in different ways as the SOM becomes more reduced

Full size image

For purposes of comparison, the thermodynamic properties of some of the main components of the SOM molecule are shown in Table 3. The ΔS values determined from S&O correlations ranged from 17.11 to 28.52 J mol−1 C K−1, i.e. they are lower than those reported in Table 3. The Roels model limits the entropy calculations to substrates that are more reduced than carbohydrates.

Table 3 Thermodynamic properties of substrates contributing to SOM composition, reported by different authors (Huang et al. [26](1); Reyes et al. [51](2); Goldberg et al. [37](3); Popovich [49](4); Popovich et al. [50](5); von Stockar et al. [48](6)
Full size table

Sensitivity of thermodynamic properties to SOM nature and soil ecosystems

QSOM (values obtained by direct integration of the DSC curves) and ΔcGSOM determined from S&O correlations for the soil organic L/F layer and mineral soils from both oak and beech forests ecosystems, were compared separately by one-way ANOVA. Differences were significant in all cases (two levels, L/F versus mineral samples for each of the soil ecosystems, n = 14, p < 0.05), as shown in Fig. 6.

Fig. 6
figure 6

Results of one-way ANOVA comparing the heat of combustion of samples, QSOM, obtained directly from DSC in kJ g−1 SOM and their Gibbs energy. ΔcGSOM in the y-axis represents the Gibbs energy change of SOM combustion reaction given by the S&O model in absolute values (they are negative). These thermodynamic variables differentiated the nature of SOM in different forest ecosystems

Full size image

The results show that QSOM were significantly higher in the mineral soil layer than in the L/F organic layers, indicating that the mineral soil is more reduced than the L/F layer in all samples, also reflected by more negative ΔcG values.

ΔcGSOM from beech L/F layers were also more negative than in oak L/F layers, resulting in a mineral soil with the opposite pattern, i.e. beech mineral soil has less Gibbs energy than oak mineral soil. This evolution was followed by the entropy, increasing with more negative QSOM and ΔcGSOM values, as shown in Fig. 5.

Owing to the small changes in these thermodynamic properties in some of the samples (despite being significant) the variance among different sampling sites was studied by PCA. Elemental (total C, N, and C/N ratio), thermal (SOM, QSOM) and thermodynamic properties derived from S&O correlations (λ, ΔcGSOM, and ΔSS&O) were the variables used in the analysis. PCA revealed that two principal components explained more than 95% of the variance among samples. A biplot with the distribution of samples along with principal component 1 (PC1, 68.238%) on the x-axis and principal component 2 (PC2, 27.562%) on the y-axis is shown in Fig. 7. The thermodynamic variables had the greatest weighting on PC1, while elemental properties Ctot and C/N ratios made the greatest contribution to PC2. L/F layers were more homogeneous, while the variance increased in mineral samples. The thermodynamic properties were responsible for the greatest variance in mineral soil samples from the oak forests in England and Ireland. The L/F and M samples from beech forests displayed the lowest variance among sampling sites. Therefore, thermodynamic properties were more variable as SOM evolved from the L/F litter to mineral soil and differentiated between the two types of forest ecosystem.

Fig. 7
figure 7

Biplot of PCA analysis for the variance of the elemental, thermal and thermodynamic properties of samples used in this study. The thermodynamic variables have the greatest mass on PC1. Samples H represent the LF layers from beech forests and S samples the mineral layers from beach forests. K, DC, and G are samples from Ireland. NF, Rog, and BW are the samples from UK

Full size image

Discussion

The most important step for thermodynamic characterization of soils by now, is the quantification of the QSOM, which represents the energy content of SOM. Measurements by simultaneous TG–DSC give similar QSOM values to those reported for the main components of SOM when measured directly in kJ per gram of SOM [27]. As organic matter is combusted in the TG–DSC to CO2 and water, and as the heat of combustion of these products is, by convention, zero [17], QSOM should be close to the enthalpy of oxidation of all SOM main elements in the combustion reaction in a calorimeter, as for all organic material. Therefore, QSOM must be proportional to the degree of reduction in the organic substrates forming SOM when oxygen is the electron acceptor. This has been demonstrated for a large number of organic substances [16, 17, 22, 28] as well as for plant tissues and their main components [24, 29, 30].

The relationship between the heat of combustion and the degree of reduction in organic substrates also depends on the carbon and nitrogen content and, therefore, on the elemental composition of the substrates. In the case of plant material, the relationship is linked by the glucose equivalent, which was obtained here by plotting the C content of the soil samples against the SOM content, allowing the normalization of QSOM to mol C in soil. This is a general correlation common to soil [25] together with those usually obtained between the C and N content and the heat released per gram of sample and C content of organic materials [31,32,33]. All of these correlations occur as a consequence of the relationships between energy and the degree of reduction in substrates, thus providing a way of estimating the Gibbs energy and the entropy for the thermodynamic characterization of SOM.

The QSOM values obtained were dependent on the tree species and the nature of the organic matter in the litter and mineral soil, and in all cases the SOM became more reduced, relative to the original material, as the decomposition proceeded. The difference was greater in mineral soil samples from the oak forests in Ireland and England than in the samples from beech forests in different sites in Spain, with QSOM values closer to those of their LF layers. This suggest different states of SOM decomposition at the sampling sites and forest ecosystems. In this sense, recent studies report that persistent SOM may be in a more oxidized state than carbohydrates [34]. As the data obtained here suggest QSOM is sensitive to SOM evolution, it could contribute to explain the persistence of soil organic matter [12, 35].

QSOM is dependent on SOM chemical composition and reflects the greater or lower contribution of the main components of SOM to the total molecule: lignocellulosic material, cellulose, hemicellulose, lignin, humic, and fulvic acids, etc. The average QSOM values obtained after Baraldis´correction were 18.34 ± 0.65 kJ g−1 SOM, for the beech L/F layer, and 17.34 ± 0.56 kJ g−1 SOM, for the oak L/F layer. The average QSOM value for the oak L/F layer is close to the value reported for lignocellulosic material and leaves 18 kJ g−1 [24, 36] while the average value for the beech L/F layer is close to that reported for cellulose, 17.43 kJ g−1 SOM [37, 38]. Therefore, greater or lower contributions of these compounds relative to lignin or humates (more reduced and more oxidized than carbohydrates, respectively) may explain the differing QSOM values obtained to be linked to the persistence of SOM in the future works. In this respect, in the beech forest samples, SOM varied from 18.34 ± 0.65 kJ g−1 SOM in the L/F litter to 19.15 ± 0.73 kJ g−1 SOM in the mineral soils, and in the oak forest samples, the corresponding values ranged from 17.34 ± 0.56 kJ g−1 SOM to 24.77 ± 2.25 k J g−1 SOM. These differences were found to be significant in relation to sampling sites. The SD values indicate the variance among the sites.

Average values for the oak sites indicate a higher degree of reduction than for beech sites, yielding QSOM values close to those reported for different types of lignin (22–26 kJ g−1) [24], biochar (24–29 MJ kg−1) [27] and leonardite (26 kJ g−1)[19]. Biochar contains refractory C that was not detected in the DSC and DTG curves in these samples, with the sole exception of one of the samples from Spain. Leonardite also has different DTG and DSC curve profiles than those obtained for oak mineral samples because it does not contain carbohydrates [19]. Therefore, the observed QSOM evolution can just be interpreted as the SOM of mineral soil samples from Ireland and England were little transformed, with SOM strongly influenced by a high contribution of undegraded or partially degraded lignin relative to other SOM components. By contrast, beech mineral soils may include SOM at a higher degree of decomposition with a greater contribution of substrates that are more oxidized than lignin and carbohydrates, such as fulvic and humic acids, leading to a decrease in QSOM [35, 39]. This hypothesis is supported by previous findings showing that decomposition of organic matter in oak ecosystems yields higher aromaticity at early stages, due to conversion of lignin to aromatic products, also reflected by higher QSOM values [40]. The different relation among these compounds in soils would explain why studies involving stable persistent SOM conclude that SOM evolves to a more oxidized state [12, 35].

In the present case, future studies should elucidate whether the QSOM values obtained for the mineral soils are related to the different forest ecosystems or to the different environmental factors associated with the sampling sites, such as environmental temperature and soil microbial composition [12, 39, 41].

The thermodynamic analysis showed that L/F samples from beech ecosystems have a greater potential for spontaneous combustion than the L/F oak forests, while the corresponding potential is higher in the mineral soil from the oak ecosystems than that from beech mineral soils, based on the reported ΔcGSOM data. The Gibbs energy associated with the SOM in mineral soil from beech forests would tend to increase (less negative values) if the evolution to a higher degree of SOM transformation involves a higher degree of oxidation as reported [12].

Application of the S&O model revealed that the increase in the degree of reduction in SOM raised the entropy of SOM, contributing to supply the soil organic matter with Gibbs energy and boosting the potential for spontaneous combustion as the temperature increases. This would make the mineral soils sampled in the forests in England and Ireland, more sensitive to temperature as their higher positive entropy values would decrease the Gibbs energy as temperature arises, as shown in Eq. 1. Therefore, if the entropy of SOM is a factor determining SOM sensitivity to temperature, soils with lower positive entropy change would be more resistant to temperature than soils with higher ΔS values. This would help to explain whether recalcitrant SOM is more or less sensitive to temperature than labile SOM [42,43,44]. At this stage of the research, it would only apply to the spontaneous combustion of the SOM to CO2 and water in the DSC. Although the same behaviour would not necessarily be involved when the decomposition is induced by microbial action, there is recent evidence that SOM decomposition is not ruled exclusively by microbial metabolism at extreme temperatures [45] and that at temperatures higher than 40 °C, abiotic reactions favouring SOM degradation may also be activated [45, 46]. In particular, those reactions involving direct oxidation of poorly degraded forms of lignin in soils at a low degree of decomposition [47]. In those cases, the degree of activation would depend on the ΔG and ΔS values of SOM combustion. Recent work has also shown that the oak soil samples used here were affected by extreme temperatures [46]. The findings indicated that mineral samples, with more negative ΔG values and higher entropy, were more sensitive to increasingly extreme temperatures than the L/F layer with less negative ΔG and lower entropy [46].

Here, the Roels model [17], which assumes SOM decomposition by microbial action, through microbial growth in size and number, yielded an opposite pattern for the entropy change, with entropy tending to decrease as substrates become more reduced than carbohydrates. The reasons for the differences between the two models when applied to soils are difficult to comprehend. The changes in entropy following the Roels model may be a consequence of the described capacity of microorganisms and cells to import and export entropy in the environment via metabolites [1, 7], and therefore, the model many not be compatible with a combustion reaction. In this sense, assuming that QSOM measures the potential energy that microorganisms can take from the SOM as a continuum, when the degree of reduction in the SOM is the same as that of carbohydrates, the Gibbs energy of the SOM catabolism reaction will be mainly enthalpic, and its dissipation will depend exclusively on the rate of heat dissipation of the SOM biodecomposition. If the substrates are more oxidized than carbohydrates, microorganisms will increase entropy to feed the more oxidized material with free energy, to meet the minimum energy required for heterotrophic growth (− 400 kJ mol−1 C) and maintenance (− 200 kJ mol−1 C) [1, 10, 48]. When SOM is more reduced than carbohydrates, microorganisms will apparently decrease the entropy to negative values, which may cause a decrease in Gibbs energy, which is unfavourable for living systems. These features would explain the trend in Fig. 5 for Roel’s model. The observed evolution would indicate increasing SOM recalcitrance as an unfavourable situation for the survival of the soil microbial population, reinforcing the reported evolution of SOM to a more oxidized state, as a survival tactic for the soil to preserve Gibbs energy.

For all the above reasons, the observed evolution of entropy in this work by the Roels model [17] may be an artefact caused by the reaction to which the model was applied, i.e. pure combustion rather than microbial catabolism. The correlations revealed by the S&O model [16] appear to be more consistent with the combustion reaction in the DSC, yielding ΔS values that, although lower than previously reported values, follow the expected trend of increasing with the degree of reduction in substrates [17].

Application of these models will be necessary for SOM microbial decomposition. Any method enabling monitoring of SOM catabolism (calorimetry, respirometry, etc.) [15, 19] can be used for comparison with the SOM combustion reaction. Contrast of different models for thermodynamic characterization of SOM, like those applied here, together with other methods used to compare entropy calculations [49, 50] will be essential to track the thermodynamic evolution of SOM.