Introduction

The further development of turbomachinery, aerospace and other areas of science and industry is impossible without profound knowledge and understanding of the gas dynamics and peculiarities of gas flows. Of particular interest is the control and management of the transition of supersonic to subsonic flows and vice versa, since the flow field changes significantly during such transition due to the discontinuity of the flow parameters and emergence of a shock wave, which itself has different shapes. Also, such flows are accompanied with formation of vortices, significant shear stresses, heat transfer and other peculiarities. At the time being, no single methodology exists that enables controlling a shock wave and further successful application to various geometries, where gas flow moves in a wide range of velocities.

Main aspects of the current state of knowledge about the control of a shock wave, its development, decay, as well as its impact on various elements of equipment are described in [1]. The development of gas flows with shock waves can be successfully modeled with the help of numerical methods [2, 3], methods of molecular dynamics to predict the flow structure at the molecular level [4], analytically as well as experimentally.

The CFD methodology was employed in the work [2] to analyze the flow pattern in a micro shock tube with a finite diameter at various pressure ratios and diaphragm diameters. As a result, it was shown that a relatively thicker boundary layer develops in a smaller shock tube. These results show also that the tube scale parameter (S) affects the propagation of the shock wave. Thus, for the same tube diameter, it was found that more significant shock wave decay occurred in the shock tube with a smaller value of S.

Flows of helium and argon were simulated using the Navier–Stokes equations in [5]. It was revealed via validations of simulations against experiments that the Navier–Stokes equations are more accurate in predictions of the density profile in the argon shock wave at Mach numbers ranging from 1.5 to 10. For helium, predictions using the Navier–Stokes equations agree well with the results of the bimodal model and available experimental data.

Three modes of supersonic flow were investigated using periodic supply of power pulses in the study [6]. It was revealed how shock waves arise in gas flows in channels of variable cross sections. The authors obtained relations for the parameters of such flows and the characteristic ranges of their variation in periodic modes without throttling the flow.

Among the analytical methods for modeling the shock waves, the most widely used is the one that assumes that the shock wave is a plane orthogonal to the main flow and separating the flow parameters before and after the plane [7]. One can also obtain the classical Prandtl relation and the Rankine–Hugoniot relations [8].

Using the continuum hypothesis, authors of the study [9] analyzed effects of the distributions of the flow temperature and velocity, as well as the size of the transition region, on the transformation of compression waves into shock waves. It was shown that a compression wave can turn into a shock wave when the perturbation velocities are sufficiently high. In this case, the thickness of the transition region will be comparable with the mean free path of a molecule, whereas the propagation velocity will significantly exceed the speed of sound, so that the compression wave will transform into a shock wave.

The theory of impact dynamics was applied in the work [10] to study the reflection and diffraction of a normal shock wave over a convex double wedge. As a result of the analysis, relations were obtained for prediction of the shape of the reflected and diffracted shock wave and the pressure distribution behind it. Results of calculations agree well with the experimental data. Analytical and experimental results [11] including p and v—diagrams for various types of van der Waals gases—serve as a basis for many further studies of rarefied flows in shock tubes.

The Riemann method was applied to determine the delta shock wave with Dirac delta function in the study [12]. A generalized Rankine–Hugoniot condition and a condition for the onset of entropy generation to obtain the solution for delta shock waves were proposed in the work [13]. The authors [13] also demonstrated that the modeling technique presented in their work is of a general nature and can be successfully applied to a large variety of systems.

As well known, flows with the nanoparticles in thermal engineering are becoming more and more interesting due to their ability to more intensively remove thermal loads from heat-stressed surfaces [14,15,16]. Nanofluids have also proved themselves well as lubricants [17].

After reviewing the literature on studies that dealt with shock waves in gas flows, we did not find studies related to flows with nanoparticles. But there are quite large developments in the study of shock waves in dusty flows [18,19,20,21,22]. This is the closest set of problems to this study.

In [18], an expression was obtained for the total energy carried by a weak shock wave in a dusty gas. The Lie group method was used to solve the problem of shock wave propagation in [19] and in [20] in order to analyze the effect of the mass concentration of dust particles, the ratio of the density of solid particles to the initial density of the medium, the relative specific heat and other parameters. And the influence of these parameters on the formation of the shock wave. It is shown that due to the presence of solid particles, the shock wave propagates over a smaller distance and slows down. The deceleration of the velocity of the shock wave is also shown in [21]. The velocity of solid particles in the relaxation zone was investigated using a laser Doppler velocity meter. Based on the processed data, the law of resistance was obtained, which describes the acceleration of a particle in the relaxation zone. Solutions were obtained on the basis of which unsteady changes in heat transfer parameters, the effects of an increase in the mass concentration of solid particles in a mixture and the ratio of the density of solid particles to the initial gas density on the flow variables in the region behind the shock wave were studied in [22].

To conclude, the recent decades demonstrated an increasing interest to the problems of heat transfer in flows with nanoparticles, which take place in various elements of power, biomedical, electronic, chemical and food processing equipment [23,24,25]. This trend is accompanied with the development of technologies employing effects of shock waves [26]. Therefore, in the present study, we will focus on an analytical modeling of the parameters of a gas flow with a normal shock wave in the presence of solid nanoparticles in a channel of a constant cross section. To our knowledge, such a study, as well as the analytical solutions resulting from it, has never been performed in the past, which represents the novelty of the present work.

Mathematical model

One of the most widely known cases, where shock waves emerges, is supersonic flow in the diverging part of the converging–diverging nozzles (also called Laval nozzles) [27, 28]. A fluid attains a sonic velocity at the smallest cross section of the converging part of the nozzle (a throat) and further accelerates to supersonic velocities in the diverging section of the nozzle as the pressure decreases. If the back pressure (i.e., external pressure at the outlet of the nozzle) suddenly increases, the supersonic flow must adapt to these conditions with a change in pressure within a very thin section inside the diverging nozzle between the throat and the exit cross section. This happens through a so-called normal shock wave, which induces a sudden drop in velocity to subsonic levels and an abrupt increase in pressure. After the shock, fluid flow is decelerating in the remaining part of the diverging nozzle. Flow through the shock is highly irreversible, and not isentropic anymore. The normal shock moves upstream toward the throat as the back pressure increases. Shock waves occur not only in supersonic nozzles. For instance, at the engine inlet of a supersonic aircraft the air passes through a shock and decelerates to subsonic velocities and enters the diffuser of the engine.

Thus, from the physical point of view, within the normal shock wave over a negligibly small distance (the order of a few mean free path lengths of a molecule) the values of pressure, temperature and density vary almost abruptly, whereby the velocity drops from supersonic to subsonic values. Thus, the shock wave can be modeled as a discontinuity in the flow parameters. We will consider here a normal shock wave in a nanofluid flow in a channel of a constant cross section in which the shock front and flow direction are perpendicular to each other (Fig. 1). Since a normal shock wave is negligibly thin, no heat transfer through the side boundaries can occur and the process can be regarded as adiabatic (but not isentropic). The total enthalpy of the flow before and after the shock wave is the same. The skin friction can be also neglected.

Fig. 1
figure 1

Schematic representation of the shock wave problem

Full size image

In addition, we also neglect diffusion and dissipative processes. This simplifies the conservation of momentum equation and the total enthalpy conservation equation (see below) and reduces the problem to classical Rankine–Hugoniot conditions.

The Rankine–Hugoniot conditions, also referred to as Rankine–Hugoniot jump conditions or Rankine–Hugoniot relations, describe the relationship between the states on both sides of a shock wave or a combustion wave (deflagration or detonation) in a one-dimensional flow in fluids or a one-dimensional deformation in solids. They are named in recognition of the work carried out by Scottish engineer and physicist William John Macquorn Rankine [29] and French engineer Pierre Henri Hugoniot [30,31,32].

The process of gas passage through a normal shock wave (Fig. 1) can be described by a modified system of Rankine–Hugoniot equations. This system includes the following equations:

conservation of mass

$$\rho_{1\Sigma } V_{1} = \rho_{2\Sigma } V_{2}$$
(1)

conservation of momentum

$$p_{1} + \rho_{1\Sigma } V_{1}^{2} = p_{2} + \rho_{2\Sigma } V_{2}^{2}$$
(2)

conservation of total enthalpy

$$h_{1\Sigma } + \frac{{V_{1}^{2} }}{2} = h_{2\Sigma } + \frac{{V_{2}^{2} }}{2}$$
(3)

Here and throughout the paper, the subscript “Σ” denotes physical properties of nanofluids (i.e., gases with nanoparticles) and \(h_{1\sum }\) the total enthalpy with including nanoparticles.

For flow of nanofluids, these equations must be supplemented with the condition of conservation of the concentration of nanoparticles

$$\varphi _{1} = \varphi _{2} = \varphi$$
(4)

as well as the equations for the modified density and isobaric heat capacity [33]

$$\rho _{\Sigma } = \left( {1 - \varphi } \right)\rho + \varphi \rho _{p}$$
(5)
$$\left( {c\rho } \right)_{\Sigma } = c\rho \left( {1 - \varphi } \right) + c_{p} \rho _{p} \varphi$$
(6)

which take into account the contribution of the nanoparticles to the appropriate physical properties of nanofluids.

In Eqs. (1)–(6), V is the velocity, ρ is density of a pure fluid, p is the pressure, h is the enthalpy, φ is the concentration of nanoparticles, c is the isobaric heat capacity, the subscript “1” refers to the parameters before the shock wave, the subscript “2” refers to the parameters behind the shock wave, and the subscript “p” refers to nanoparticles. We omit here the usual subscript “p” at the isobaric heat capacity of gases, because this subscript in the present study denotes the physical properties of nanoparticles.

Obviously, under the condition of zero concentration of nanoparticles φ = 0 these equations reduce to the classical Rankine–Hugoniot system [29,30,31,32].

Using the ideal gas equation of state

$$p = \rho RT$$
(7)

where \(R\) is the individual (specific) gas constant and T is the temperature, together with the Mayer’s relation

$$R = c\frac{k - 1}{k}$$
(8)

rewritten using the specific heat ratio \(k = c/c_{\nu }\) ( where \({\text{c}}_{{\upnu }}\) is the isochoric heat capacity), we represent the enthalpy in the following form.

$$h_{1\Sigma } = c_{1\Sigma } T_{1} = \frac{{c\rho_{1} \left( {1 - \varphi } \right) + c_{\rm p} \rho_{\rm p} \varphi }}{{\rho_{1} \left( {1 - \varphi } \right) + \rho_{\rm p} \varphi }}T_{1} = \frac{{\left( {1 - \varphi } \right) + \frac{{c_{\rm p} \rho_{\rm p} }}{{c\rho_{1} }}\varphi }}{{\left( {1 - \varphi } \right) + \frac{{\rho_{\rm p} }}{{\rho_{1} }}\varphi }}\frac{k}{k - 1}\frac{{p_{1} }}{{\rho_{1} }} = \frac{{c_{1\Sigma } }}{c}\frac{k}{k - 1}\frac{{p_{1} }}{{\rho_{1} }} = C_{1} \frac{k}{k - 1}\frac{{p_{1} }}{{\rho_{1} }}$$
(9)
$$\begin{gathered} h_{2\Sigma } = \hfill \\ c_{2\Sigma } T_{2} = \frac{{c\rho_{2} \left( {1 - \varphi } \right) + c_{\rm p} \rho_{\rm p} \varphi }}{{\rho_{2} \left( {1 - \varphi } \right) + \rho_{\rm p} \varphi }}T_{2} = \frac{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {1 - \varphi } \right) + \frac{{c_{\rm p} \rho_{\rm p} }}{{c\rho_{1} }}\varphi }}{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {1 - \varphi } \right) + \frac{{\rho_{\rm p} }}{{\rho_{1} }}\varphi }}\frac{k}{k - 1}\frac{{p_{2} }}{{\rho_{2} }} = \frac{{c_{2\Sigma } }}{c}\frac{k}{k - 1}\frac{{p_{2} }}{{\rho_{2} }} = C_{2} \frac{k}{k - 1}\frac{{p_{2} }}{{\rho_{2} }} \hfill \\ \end{gathered}$$
(10)

where

$$C_{1} = \frac{{\left( {1 - \varphi } \right) + \frac{{c_{p} \rho_{p} }}{{c\rho_{1} }}\varphi }}{{\left( {1 - \varphi } \right) + \frac{{\rho_{p} }}{{\rho_{1} }}\varphi }}$$
(11)
$$C_{2} = \frac{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {1 - \varphi } \right) + \frac{{c_{p} \rho_{p} }}{{c\rho_{1} }}\varphi }}{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {1 - \varphi } \right) + \frac{{\rho_{p} }}{{\rho_{1} }}\varphi }}$$
(12)

Now Eq. (3) can be written in the following form

$$C_{1} \frac{k}{k - 1}\frac{{p_{1} }}{{\rho_{1} }} + \frac{{V_{1}^{2} }}{2} = C_{2} \frac{k}{k - 1}\frac{{p_{2} }}{{\rho_{2} }} + \frac{{V_{2}^{2} }}{2}$$
(13)

Normal shock

Considering Eq. (1), one can transform Eq. (2) as

$$p_{1} - p_{2} = \rho_{1\Sigma } V_{1} \left( {V_{2} - V_{1} } \right)$$
(14)

and multiplying this equation by the factor

$$\frac{{V_{2} + V_{1} }}{{\rho_{1\Sigma } V_{1} }} = \frac{1}{{\rho_{1\Sigma } }} + \frac{1}{{\rho_{2\Sigma } }}$$
(15)

one can obtain

$$\left( {p_{1} - p_{2} } \right)\left( {\frac{1}{{\rho_{1\Sigma } }} + \frac{1}{{\rho_{2\Sigma } }}} \right) = V_{2}^{2} - V_{1}^{2}$$
(16)

It follows from Eq. (13) that

$$V_{2}^{2} - V_{1}^{2} = \frac{2k}{{k - 1}}\left( {C_{1} \frac{{p_{1} }}{{\rho_{1} }} - C_{2} \frac{{p_{2} }}{{\rho_{2} }}} \right)$$
(17)

A comparison of Eqs. (16) and (17) gives

$$\left( {p_{1} - p_{2} } \right)\left( {\frac{1}{{\rho_{1\Sigma } }} + \frac{1}{{\rho_{2\Sigma } }}} \right) = \frac{2k}{{k - 1}}\left( {C_{1} \frac{{p_{1} }}{{\rho_{1} }} - C_{2} \frac{{p_{2} }}{{\rho_{2} }}} \right)$$
(18)

or

$$\left( {1 - \frac{{p_{2} }}{{p_{1} }}} \right)\left( {1 + \frac{{\rho_{1} }}{{\rho_{2} }}\frac{{R_{1} }}{{R_{2} }}} \right)\frac{1}{{R_{1} }} = \frac{2k}{{k - 1}}\left( {C_{1} - C_{2} \frac{{p_{2} }}{{p_{1} }}\frac{{\rho_{1} }}{{\rho_{2} }}} \right)$$
(19)

where

$$R_{1} = \left( {1 - \varphi } \right) + \frac{{\rho_{p} }}{{\rho_{1} }}\varphi$$
(20)
$$R_{2} = \left( {1 - \varphi } \right) + \frac{{\rho_{p} }}{{\rho_{1} }}\frac{{\rho_{1} }}{{\rho_{2} }}\varphi$$
(21)

Solving Eq. (19) with respect to p2/p1, one can obtain

$$\frac{{p_{2} }}{{p_{1} }} = \frac{{R_{2} \left( {\left( {2C_{1} R_{1} - 1} \right)k + 1} \right)\frac{{\rho_{2} }}{{\rho_{1} }} - R_{1} \left( {k - 1} \right)}}{{R_{1} \left( {\left( {2C_{2} R_{2} - 1} \right)k + 1} \right) - R_{2} \left( {k - 1} \right)\frac{{\rho_{2} }}{{\rho_{1} }}}}$$
(22)

With account for Eqs. (11), (12), (20) and (21), one can transform Eq. (22) to

$$\frac{{p_{2} }}{{p_{1} }} = \frac{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {\frac{{\rho_{2} }}{{\rho_{1} }} + 1 + \left( {2\frac{{\rho_{p} }}{{\rho_{1} }} - \frac{{\rho_{2} }}{{\rho_{1} }} - 1} \right)\varphi + k\left( {\frac{{\rho_{2} }}{{\rho_{1} }} + 1 + \left( {1 + \left( {2\frac{{c_{p} \rho_{p} }}{{c\rho_{1} }} - 3} \right)\frac{{\rho_{2} }}{{\rho_{1} }}} \right)\varphi + 2\left( {\frac{{c_{p} \rho_{p} }}{{c\rho_{1} }} - 1} \right)\left( {\frac{{\rho_{p} }}{{\rho_{1} }} - \frac{{\rho_{2} }}{{\rho_{1} }}} \right)\varphi^{2} } \right)} \right)}}{{\frac{{\rho_{2} }}{{\rho_{1} }}\left( {k + 1 - \frac{{\rho_{2} }}{{\rho_{1} }}\left( {k - 1} \right)} \right) + \left( {2k\frac{{c_{p} \rho_{p} }}{{c\rho_{1} }} + \frac{{\rho_{2} }}{{\rho_{1} }}\left( {k\left( {\frac{{\rho_{2} }}{{\rho_{1} }} - 3} \right) + 2\frac{{\rho_{p} }}{{\rho_{1} }} - \frac{{\rho_{2} }}{{\rho_{1} }} - 1} \right)\varphi } \right) + 2k\left( {\frac{{c_{p} \rho_{p} }}{{c\rho_{1} }} - \frac{{\rho_{2} }}{{\rho_{1} }}} \right)\left( {\frac{{\rho_{p} }}{{\rho_{1} }} - 1} \right)\varphi^{2} }}$$
(23)

Equation (23) (or (22)) is the Hugoniot adiabatic. In the case of pure fluids with φ = 0, cp = 0, ρp = 0, Eqs. (22) and (23) are transformed into

$$\frac{{p_{2} }}{{p_{1} }} = \frac{{\left( {k + 1} \right)\frac{{\rho_{2} }}{{\rho_{1} }} - \left( {k - 1} \right)}}{{\left( {k + 1} \right) - \left( {k - 1} \right)\frac{{\rho_{2} }}{{\rho_{1} }}}}$$
(24)

which is the well-known Hugoniot adiabatic for ordinary (pure) gas [31, 32].

Equation (22) has the asymptote for the value of the argument ρ2/ρ1 equal to

$$\frac{{\rho_{2} }}{{\rho_{1} }} = \frac{{R_{1} \left( {\left( {2C_{2} R_{2} - 1} \right)k + 1} \right)}}{{R_{2} \left( {k - 1} \right)}}$$
(25)

Under condition (25), the pressure jump (22) goes to infinity.

The asymptote equation (i.e., argument) for Eq. (23) has the following form

$$\frac{{\rho_{2} }}{{\rho_{1} }} = \frac{{\left( {1 + \varphi \left( {2\frac{{\rho_{\rm p} }}{{\rho_{1} }} - 1} \right) + k\left( {1 - \varphi \left( {3 + 2\left( {\frac{{\rho_{\rm p} }}{{\rho_{1} }} - 1} \right)\varphi } \right)} \right) + \sqrt F } \right)}}{{\left( {k - 1} \right)\left( {1 - \varphi } \right)}}$$
(26)

where

$$F = 8\frac{{c_{\rm p} \rho_{p} }}{{c\rho_{1} }}k\left( {k - 1} \right)\varphi \left( {1 - \varphi } \right)\left( {1 + \left( {\frac{{\rho_{\rm p} }}{{\rho_{1} }} - 1} \right)\varphi } \right) + \left( {k + 1 + \left( {2\frac{{\rho_{\rm p} }}{{\rho_{1} }} - 1 - 3k} \right)\varphi - 2k\left( {\frac{{\rho_{\rm p} }}{{\rho_{1} }} - 1} \right)\varphi^{2} } \right)^{2}$$
(27)

For an ordinary (pure) fluid φ = 0, cp = 0, ρp = 0, whereas Eqs. (25) and (26) reduce to the classical solution [31, 32]

$$\frac{{\rho_{2} }}{{\rho_{1} }} = \frac{k + 1}{{k - 1}}$$
(28)

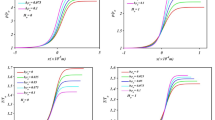
It follows from Eq. (28) that pure air (k = 1.4), when passing through the shock, cannot increase its density by more than six times [31, 32]. Figures 2 and 3 show that the asymptote of the limiting increase in density of air itself grows with increasing concentration of nanoparticles. With an increase in the concentration of nanoparticles, the asymptote shifts to the region of larger values of the argument ρ2/ρ1. This shift can be very significant. It can be attributed to the fact that an increase in the concentration of nanoparticles increases the total density of the nanofluid, which causes a reduced pressure jump in the normal shock wave (Figs. 4 and 5). In other words, a nano gas demonstrates higher compressibility than a respective pure base gas.

Fig. 2
figure 2

Asymptotic density increase in the shock wave vs. nanoparticle concentration for different densities of nanoparticles: 1 – \(\rho_{\rm p} /\rho_{1} = 2000\), 2 – \(\rho_{\rm p} /\rho_{1} = 3000\), 3 – \(\rho_{\rm p} /\rho_{1} = 4000\)

Full size image
Fig. 3
figure 3

Asymptotic density increase in the shock wave vs. nanoparticle concentration for different heat capacities of nanoparticles: 1 – \(c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 1000\), 2 – \(c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 2000\), 3 – \(c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 3000\)

Full size image
Fig. 4
figure 4

Pressure jump in the shock wave vs. density increase (Hugoniot adiabatic) for different concentrations of nanoparticles

Full size image
Fig. 5
figure 5

Pressure jump in the shock wave vs. density increase (Hugoniot adiabatic) for different densities of nanoparticles: 1- \(\begin{array}{*{20}c} {\varphi = 0} & {,\quad \rho_{\rm p} /\rho_{1} = 2000} \\ \end{array}\), 2—\(\begin{array}{*{20}c} {\varphi = 0.001} & {,\quad \rho_{\rm p} /\rho_{1} = 4000} \\ \end{array}\), 3—\(\varphi = 0.001\), \(\rho_{\rm p} /\rho_{1} = 8000\)

Full size image

Thus, due to the presence of nanoparticles, the sudden increase in pressure in a nanofluid passing through a shock wave cannot be so strong as in a respective pure fluid for the same values of ρ2/ρ1. In other words, an increase in the concentration of nanoparticles leads to a weaker pressure jump in a normal shock wave (Fig. 4). An increase in the density of nanoparticles causes qualitatively similar effect (Fig. 5). For high nanoparticle concentration (φ > 0.1), their absolute values practically cease to affect the shock adiabatic conditions (Fig. 4).

Velocity variation

Let us find the relation between the flow velocities before the shock wave and after it. We transform Eq. (14) with allowance for Eq. (1)

$$V_{1} - V_{2} = \frac{{p_{2} }}{{\rho_{2\Sigma } V_{2} }} - \frac{{p_{1} }}{{\rho_{1\Sigma } V_{1} }}$$
(29)

We will further transform the Eq. (13) for the total enthalpy. For this purpose, we will express the enthalpy through the speed of sound a

$$h_{1} = C_{1} \frac{k}{k - 1}\frac{{p_{1} }}{{\rho_{1} }} = C_{1} \frac{{a_{1}^{2} }}{k - 1}$$
(30)

The speed of sound in a pure base fluid needs to be expressed through the speed of sound in a nanofluid. Following [34], let us take derivative from Eq. (5) with respect to pressure

$$\frac{{d\rho_{\Sigma } }}{dp} = \left( {1 - \varphi } \right)\frac{d\rho }{{dp}} + \varphi \frac{{d\rho_{p} }}{dp} = \left( {1 - \varphi } \right)\frac{d\rho }{{dp}}$$
(31)

Here, the constant density of the solid phase (i.e., nanoparticles) is considered. Then one can obtain an expression for the speed of sound in a nanofluid from Eq. (31)

$$a_{\Sigma } = \frac{a}{{\sqrt {1 - \varphi } }}$$
(32)

Taking into account Eqs. (30) and (32), one can rewrite Eq. (13) in the following form

$$C_{1} \frac{{a_{1\Sigma }^{2} \left( {1 - \varphi } \right)}}{k - 1} + \frac{{V_{1}^{2} }}{2} = const$$
(33)

To find the constant in Eq. (33), we will write this equation for the critical conditions, i.e., when the flow velocity is equal to the speed of sound. Then we have from Eq. (33)

$$C_{1} \frac{{a_{1\Sigma }^{2} \left( {1 - \varphi } \right)}}{k - 1} + \frac{{V_{1}^{2} }}{2} = C_{1} \frac{{\left( {a_{\Sigma }^{*} } \right)^{2} \left( {1 - \varphi } \right)}}{k - 1} + \frac{{\left( {a_{\Sigma }^{*} } \right)^{2} }}{2} = \left( {a_{\Sigma }^{*} } \right)^{2} \left( {C_{1} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right)$$
(34)

Comparing Eqs. (30) and (34), one can obtain

$$\frac{{p_{1} }}{{\rho_{1} }} = \frac{k - 1}{{C_{1} k}}\left[ {\left( {a_{\Sigma }^{*} } \right)^{2} \left( {C_{1} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right) - \frac{{V_{1}^{2} }}{2}} \right]$$
(35)

Alternatively, one can derive

$$\frac{{p_{2} }}{{\rho_{2} }} = \frac{k - 1}{{C_{2} k}}\left[ {\left( {a_{\Sigma }^{*} } \right)^{2} \left( {C_{2} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right) - \frac{{V_{2}^{2} }}{2}} \right]$$
(36)

We will further transform Eq. (29) with allowance for Eqs. (35) and (36), which yields

$$\begin{gathered} V_{1} - V_{2} = \frac{1}{{V_{2} }}\frac{{p_{2} }}{{\rho_{2} }}\frac{1}{{R_{2} }} - \frac{1}{{V_{1} }}\frac{{p_{1} }}{{\rho_{1} }}\frac{1}{{R_{1} }} = \hfill \\ \frac{k - 1}{k}\left( {\frac{1}{{R_{2} C_{2} }}\left[ {\frac{{\left( {a_{\Sigma }^{*} } \right)^{2} }}{{V_{2} }}\left( {C_{2} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right) - \frac{{V_{2}^{{}} }}{2}} \right] - \frac{1}{{R_{1} C_{1} }}\left[ {\frac{{\left( {a_{\Sigma }^{*} } \right)^{2} }}{{V_{1} }}\left( {C_{1} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right) - \frac{{V_{1}^{{}} }}{2}} \right]} \right) \hfill \\ \end{gathered}$$
(37)

Further, introducing the concept of the velocity coefficient

$$\lambda = \frac{V}{{a_{\Sigma }^{*} }}$$
(38)

one can transform Eq. (37) as follows

$$\lambda_{1} - \lambda_{2} - \frac{k - 1}{{2k}}\left( {\frac{{\lambda_{1}^{{}} }}{{R_{1} C_{1} }} - \frac{{\lambda_{2}^{{}} }}{{R_{2} C_{2} }}} \right) = \frac{1}{{R_{2} C_{2} \lambda_{2} }}\left( {C_{2} \frac{1 - \varphi }{k} + \frac{k - 1}{{2k}}} \right) - \frac{1}{{R_{1} C_{1} \lambda_{1} }}\left( {C_{1} \frac{1 - \varphi }{k} + \frac{k - 1}{{2k}}} \right)$$
(39)

For a base pure fluid (φ = 0, C1 = 1, R1 = 1), Eq. (39) reduces to the Prandtl relation [31]

$$\lambda_{1} \lambda_{2} = 1$$
(40)

Now it is necessary to exclude the ratio of the densities ρ2/ρ1 from Eq. (39) to find the relation between the velocity coefficients as a function of the parameters of the fluid only. For this purpose, we will rewrite Eq. (1) in the following form

$$\frac{{V_{1} }}{{V_{2} }} = \frac{{\rho_{2\Sigma } }}{{\rho_{1\Sigma } }} = \frac{{\rho_{2} R_{2} }}{{\rho_{1} R_{1} }} = \frac{{\lambda_{1} }}{{\lambda_{2} }}$$
(41)

Let us express the relation ρ2/ρ1 from Eq. (41) in terms of the coefficients λ1 and λ2 and substitute the resulting relation in Eq. (39). As a result, we can obtain a quadratic equation for either λ1 or λ2. Having solved it, one can find the desired relation between the flow velocities before and after the shock wave

$$\begin{aligned} \lambda _{1} = & \left( {1 + \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right.\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right.\left( {1 + \lambda _{2}^{2} } \right)\left. { - 3} \right)\varphi - 2\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right.} \right)\varphi^{2} \\ & + k\left( {1 + } \right.\varphi\left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right. - 1 + \lambda _{2}^{2} \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} + } \right.2\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }}\left( {\varphi - 1} \right) - 2\left. {\left. {\left. {\left. {\frac{{\rho _{\rm p} }}{{\rho _{1} }}\varphi} \right)} \right)} \right)} \right) \\ & + \left( {\left( {4\lambda _{2}^{2} \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - \frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right)} \right.\left( {\varphi - 1} \right)^{2} \varphi\left( {1 + k + 2\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right)\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\frac{{\rho _{2} }}{{\rho _{1} }}} \right)} \right. \\ & \left( {1 + k\left( {1 + 2\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right)} \right) + \left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\frac{{\rho _{2} }}{{\rho _{1} }}} \right) + \left( {1 + \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right)^{2} \\ & \left( {1 + \left( {\left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right.\left( {1 + \lambda _{2}^{2} } \right) - 3} \right)} \right.\varphi - 2\left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\varphi^{2} \\ & + \left. {\left. {\left. {k\left( {1 + \left( { - 1 - 2\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }}\lambda _{2}^{2} + \frac{{\rho _{\rm p} }}{{\rho _{1} }} + \lambda _{2}^{2} \frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right)} \right.\varphi + 2\lambda _{2}^{2} \left. {\left. {\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - \frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right)\varphi^{2} } \right)} \right)^{2} } \right)} \right)} \right)^{{1/2}} / \\ & \left( {2\lambda _{2}^{2} \left( {1 - \varphi} \right)\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\varphi} \right)} \right.\left( {1 + k\left( {1 + 2\left. {\left. {\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right)} \right)} \right.} \right). \\ \end{aligned}$$
(42)

Figure 6 shows dependence (42) for different concentrations of nanoparticles. As can be seen from here, an increase in the concentration of nanoparticles up to approximately φ ≈ 0.1 reduces the ratio λ1/λ2. With a further increase in the concentration of nanoparticles, the ratio λ1/λ2 increases. That dependence of λ1/λ2 on φ has an extremum. Variation in the density and heat capacity of nanoparticles has little effect on the form of the dependence of λ1/λ2 on φ.

Fig. 6
figure 6

Velocity coefficient λ1 vs. λ2 for different concentrations of nanoparticles

Full size image

It is sometimes convenient to estimate shock wave intensity in a relative form of dependence for λ1/λ2 or λ2/λ1. To construct such dependence, we rewrite Eq. (39) such as

$$\Lambda - 1 - \frac{k - 1}{{2k}}\left( {\frac{\Lambda }{{R_{1} C_{1} }} - \frac{1}{{R_{2} C_{2} }}} \right) = \frac{1}{{R_{2} C_{2} \lambda_{2}^{2} }}\left( {C_{2} \frac{1 - \varphi }{k} + \frac{k - 1}{{2k}}} \right) - \frac{1}{{R_{1} C_{1} \Lambda_{1} \lambda_{2} }}\left( {C_{1} \frac{1 - \varphi }{k} + \frac{k - 1}{{2k}}} \right)$$
(43)

where Λ = λ1/λ2 is the relative velocity coefficient. The solution to this equation looks as

$$\begin{aligned} \Lambda = & \left( {\left( {1 + \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right)\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} + \lambda _{2}^{2} \frac{{\rho _{\rm p} }}{{\rho _{1} }} - 3} \right) - 2} \right.} \right.\left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\varphi^{2} + \\ & k\left( {1 + \varphi \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right.} \right. - 1 + \lambda _{2}^{2} \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} + } \right.2\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - \left( {\varphi - 1} \right) - 2 \\ & \left( {1 + \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi} \right.\left( {1 + \left( {\frac{{\rho _{2} }}{{\rho _{1} }}} \right. + \lambda _{2}^{2} \frac{{\rho _{2} }}{{\rho _{1} }}\left. { - 3} \right)\varphi - 2\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right.} \right)\varphi ^{2} + \left. {\left. {\left. {\frac{{\rho _{\rm p} }}{{\rho _{1} }}\varphi } \right)} \right)} \right) + \\ & \left( {\left( {4\lambda _{2}^{2} \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - \frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right)} \right.\left( {\varphi - 1} \right)^{2} \varphi \left( {1 + k + 2\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi } \right)\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\varphi } \right)} \right.\left( {1 + 2\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right) + \\ & \left( {1 + \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi ^{2} } \right)\left( {1 + } \right.\left( {\frac{{\rho _{2} }}{{\rho _{1} }}} \right. + \lambda _{2}^{2} \frac{{\rho _{2} }}{{\rho _{1} }}\left. { - 3} \right)\varphi - 2\left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)\varphi ^{2} + \\ & k\left( {1 + \left( { - 1 - 2\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }}\lambda _{2}^{2} + \frac{{\rho _{\rm p} }}{{\rho _{1} }} + 2\lambda _{2}^{2} \left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }}} \right. - \left. {\left. {\left. {\left. {\frac{{\rho _{\rm p} }}{{\rho _{1} }}} \right)\varphi ^{2} } \right)} \right)^{2} } \right)} \right)} \right.^{{1/2}} / \\ & \left( {2\lambda _{2}^{2} \left( {1 - \varphi } \right)} \right.\left( {1 + \left( {\frac{{\rho _{\rm p} }}{{\rho _{1} }} - 1} \right)} \right)\left( {1 + k\left( {1 + 2\left. {\left( {\frac{{c_{\rm p} \rho _{\rm p} }}{{c\rho _{1} }} - 1} \right)\varphi } \right)} \right)} \right). \\ \end{aligned}$$
(44)

A graphical representation of this dependence is depicted in Fig. 7.

Fig. 7
figure 7

Dependence of relative velocity coefficient vs. concentration of nanoparticles

Full size image

Figure 7 clearly indicates that with an increase in the concentration of nanoparticles, the shock wave intensity first decreases and then increases having passed a point of minimum.

Moreover, one can transform Eq. (42) to use Mach numbers instead of velocity coefficients. For this purpose, we will rewrite Eq. (34) in the dimensionless form

$$C_{1} \frac{1 - \varphi }{{k - 1}}\frac{1}{{{\text{Ma}}_{1}^{2} }} + \frac{1}{2} = \frac{1}{{\lambda_{1}^{2} }}\left( {C_{1} \frac{1 - \varphi }{{k - 1}} + \frac{1}{2}} \right)$$
(45)

From here, one can find the relation between the velocity coefficient and the Mach number

$$\lambda_{1}^{{}} = {\text{Ma}}_{1}^{{}} \sqrt {\frac{{k - 1 + 2C_{1} \left( {1 - \varphi } \right)}}{{\left( {k - 1} \right){\text{Ma}}_{1}^{2} + 2C_{1} \left( {1 - \varphi } \right)}}}$$
(46)

For a pure base gas (φ = 0, C1 = 1), Eq. (43) reduces to the classical relation [32]

$$\lambda_{1}^{{}} = {\text{Ma}}_{1}^{{}} \sqrt {\frac{k + 1}{{2 + \left( {k - 1} \right){\text{Ma}}_{1}^{2} }}}$$
(47)

Using Eq. (44) and a similar equation for the quantities λ2 and Ma2, one can rewrite Eq. (42) in the following form

$${\text{Ma}}_{1}^{{}} = A\sqrt {\frac{{2C_{1} \left( {1 - \varphi } \right)}}{{\left( {1 - A^{2} } \right)\left( {k - 1} \right) + 2C_{1} \left( {1 - \varphi } \right)}}}$$
(48)

where A is the right-hand side of Eq. (42), in which the velocity coefficient λ2 is replaced by the Mach number Ma2 in accordance with Eq. (44).

Work of dissipation and entropy generation

As said in Introduction, flow through the shock is highly irreversible, adiabatic, but not isentropic. In the flow with a shock wave, there is no generation of technical work (power). The change of the potential energy of the flow is also negligible. The first law of thermodynamics in these conditions can be written as [28]

$$w{}_{\rm Diss,12} = - \int\limits_{1}^{2} {\frac{dp}{\rho }} + \left( {\frac{{V_{1}^{2} }}{2} - \frac{{V_{2}^{2} }}{2}} \right)$$
(49)

where wDiss,12 is the dissipative work.

For adiabatic isentropic processes

$$\int\limits_{1}^{2} {\frac{dp}{\rho }} = \frac{{kR\left( {T_{2} - T_{1} } \right)}}{k - 1} = c\left( {T_{2} - T_{1} } \right)$$
(50)

Consequently, Eq. (47) can be rewritten in view of Eq. (48)

$$w{}_{Diss,12} = \left( {cT_{1} + \frac{{V_{1}^{2} }}{2}} \right) - \left( {cT_{2} + \frac{{V_{2}^{2} }}{2}} \right) = \left( {h_{1} + \frac{{V_{1}^{2} }}{2}} \right) - \left( {h_{2} + \frac{{V_{2}^{2} }}{2}} \right)$$
(51)

Then the conservation of enthalpy principle, Eq. (3), yields

$$w{}_{\rm Diss,12} = 0$$
(52)

which was expected for the adiabatic isentropic processes.

The dissipative work in a shock wave can be obtained from Eq. (47) via the integration of the Hugoniot adiabatic for ordinary (pure) gases, Eq. (24), so that

$$w{}_{Diss,12} = - \frac{{2kp_{1} }}{{\left( {k + 1} \right)^{2} \rho_{{1}} }}\left( {\frac{{\left( {k - 1} \right)\left( {\frac{{\rho_{{2}} }}{{\rho_{{1}} }} - 1} \right)}}{{1 - \frac{k - 1}{{k + 1}}\frac{{\rho_{{2}} }}{{\rho_{{1}} }}}} + 2\ln \left( {\frac{{\frac{2}{k + 1}\frac{{\rho_{{2}} }}{{\rho_{{1}} }}}}{{1 - \frac{k - 1}{{k + 1}}\frac{{\rho_{{2}} }}{{\rho_{{1}} }}}}} \right)} \right) + \left( {\frac{{V_{1}^{2} }}{2} - \frac{{V_{2}^{2} }}{2}} \right)$$
(53)

Obviously, the dissipative work in a shock wave is not equal to zero once the density jump ρ2/ρ1 is larger than unity. It is easy to ascertain that the dissipative work wDiss,12 given by Eq. (51) becomes equal to zero for adiabatic isentropic flows without the density and velocity jumps, i.e., for ρ2/ρ1 = 1 and V2 = V1. The relation for the dissipative work for nanofluids is too cumbersome, therefore we do not write is here.

It is, however, more convenient to evaluate the degree of irreversibility in a shock wave with the help of the entropy production in this thermodynamic process. The general entropy change relation for ideal gases based on the first Gibbs equation looks as [27, 28]

$$S_{2} - S_{1} = c_{v} \ln \left( {\frac{{T_{2} }}{{T_{1} }}\left( {\frac{{\rho_{1\Sigma } }}{{\rho_{2\Sigma } }}} \right)^{\text{k}} } \right) - R\ln \left( {\frac{{\rho_{1\Sigma } }}{{\rho_{2\Sigma } }}} \right)$$
(54)

Equation (52) can be rewritten in view of the Mayer’s relation [35]

$$\frac{{S_{2} - S_{1} }}{R}\left( {k - 1} \right) = \ln \left( {\frac{{p_{2} }}{{p_{1} }}\left( {\frac{{\rho_{1\Sigma } }}{{\rho_{2\Sigma } }}} \right)^{\text{k}} } \right)$$
(55)

The rates of the entropy production in a shock wave of air for different concentrations of nanoparticles, their density and heat capacity calculated based on Eq. (53) are depicted in Figs. 8–10. For pure (base) gases and gases with nanoparticles, the entropy production increases with an increase in the density jump ρ2/ρ1.

Fig. 8
figure 8

Entropy production vs. density increase (Hugoniot adiabatic) for different concentrations of nanoparticles: 1—\(\begin{array}{*{20}c} {\varphi = 0,} & {\rho_{\rm p} /\rho_{1} = 0,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 0} \\ \end{array}\); 2—\(\begin{array}{*{20}c} {\varphi = 0.0001,} & {\rho_{\rm p} /\rho_{1} = 2000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000} \\ \end{array}\), 3—\(\varphi = 0.0002\), \(\rho_{\rm p} /\rho_{1} = 2000\), \(c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000\), 4—\(\varphi = 0.01\), \(\rho_{\rm p} /\rho_{1} = 2000\), \(c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000\)

Full size image
Fig. 9
figure 9

Entropy production vs. density increase (Hugoniot adiabatic) for different densities of nanoparticles: 1—\(\begin{array}{*{20}c} {\varphi = 0,} & {\rho_{\rm p} /\rho_{1} = 0,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 0} \\ \end{array}\); 2—\(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 100,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000} \\ \end{array}\), 3—\(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 1000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000} \\ \end{array}\);

Full size image
Fig. 10
figure 10

Entropy production vs. density increase (Hugoniot adiabatic) for different heat capacities of nanoparticles: 1—\(\begin{array}{*{20}c} {\varphi = 0,} & {\rho_{\rm p} /\rho_{1} = 0,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 0} \\ \end{array}\); 2—\(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 1000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 1000} \\ \end{array}\),

Full size image

4—\(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 10000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 4000} \\ \end{array}\).

3— \(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 1000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 2000} \\ \end{array}\) ;

4—\(\begin{array}{*{20}c} {\varphi = 0.0005,} & {\rho_{\rm p} /\rho_{1} = 1000,} & {c_{\rm p} \rho_{\rm p} /\left( {c_{1} \rho_{1} } \right) = 5000} \\ \end{array}\).

As Figs. 8–10 also indicate, the higher the concentration of nanoparticles, their density and heat capacity, the more intense the entropy production. In the region of the asymptote of the limiting increase in density of air, the generation of entropy tends to infinity. With an increase in the concentration of nanoparticles, their density and heat capacity, the asymptote shifts to the right, that is, toward larger ratios of ρ2/ρ1. Therefore, in the asymptote region, the entropy generation curve for a pure gas lies above the curves with a nonzero concentration of nanoparticles.

Conclusions

In the present study, the modified Hugoniot adiabatic are used to analytically study a gas flow with nanoparticles as it passes through a normal shock wave. It is shown that the asymptote of the limiting increase in density of air itself has an extremum (a maximum) depending on the concentration of nanoparticles. At first, with an increase in the concentration of nanoparticles, the asymptote shifts to the region of large values of ρ2/ρ1. It is caused by that the increase in the nanoparticle concentration of increases the total density of the nanofluid and thus weakens the pressure jump in the shock wave. The pressure jump in a nanofluid in a shock wave cannot be so strong as in a base pure fluid for the same values of ρ2/ρ1, which means that an increase in the nanoparticle concentration causes a weaker pressure jump in a normal shock wave. An increase in the density of nanoparticles has the same effect. At relatively high concentrations (φ > 0.1), its value practically ceases affecting the Hugoniot adiabatic conditions in the shock wave. For φ > 0.5, the asymptote of the limiting increase in density of air can decrease. The studies have also demonstrated that an increase the nanoparticle concentration at first causes a decrease in the ratio of the velocity coefficients λ1/λ2 to a point of about φ ≈ 0.1. With a further increase in the concentration of nanoparticles, the ratio λ1/λ2 increases. Thus, the dependence of λ1/λ2 on φ has a point of extremum (minimum), like the dependence of the asymptote of the limiting increase in density of air. However, the points of extrema for these dependencies do not coincide, because variation in the density and heat capacity of nanoparticles has moderate effect on the dependence of the ratio λ1/λ2 on φ. For pure gases and gases with nanoparticles, the entropy production increases with an increase in the density jump ρ2/ρ1. Higher concentrations of nanoparticles, their densities and heat capacities cause more intense entropy production.