Introduction

Investigations of heat transfer augmentation and characteristics of fluid flow inside plain tubes employing a variety of inserts have gained considerable attention in recent years, as attempts are made to improve heat transfer and thermal efficiency [1, 2]. Optimising heat transfer and thermo-hydraulic performance remains a topic of interest due to its importance in numerous engineering and energy-related applications such as solar thermal power, heat exchangers, and cooling towers. Oni and Paul [3] reported that the use of twisted tape with different shapes of cuts out of the tape is a distinctive technique in enhancing thermal efficiencies. Additionally, the application of nanofluid techniques leads to an improvement in heat transfer compared to ordinary liquids [4,5,6]. Analysis of entropy generation can be utilised to optimise thermal processes [7]. Entropy generation is linked to the irreversibility of thermodynamic processes such as fluid flow and heat transfer. This study aims to analyse the combination of these methods of heat transfer improvement.

A broad-ranging study has been conducted on the augmentation of heat transmission using twisted tapes. According to the literature, the tube of a heat exchanger contains twisted tapes to boost fluid mixing between the centre and tube wall. The heat transfer rate in a pipe provided with helical tapes was examined experimentally by Eiamsa and Promvonge [8] in a range of Reynolds numbers between 2300 and 8800. Their experimental findings revealed that inserting helical tape within the tube increased heat transfer by over 10% compared to a simple tube while simultaneously raising the friction factor. Other researchers investigated the rate of heat transfer in a simple tube furnished with right–left helical inserts under turbulent flow conditions using numerical simulations [9]. Eiamsa et al. [10] examined the impact of clearance ratio (CR) on heat transmission rate as well as thermal efficiency in a hose provided with classical twisted tape with ratios (y/w = 2.5 and 5.0) and CRs (0.0, 0.1, 0.2, and 0.3). The CFD (computational fluid dynamics) simulations were performed in turbulent flows with Reynolds numbers ranging between 3000 and 10,000. The analysis indicated that the tube with solid twisted tape inserts had the highest heat transfer rate at y/w = 2.5 with CR = 0.0, at about 73.6% as compared to the ordinary tube, and the best thermal efficiency was at y/w = 2.5 and 5.0 at CR = 0.0. Cui and Tian [11] conducted numerical and experimental investigations of heat transfer and pressure drop in a pipe provided with edge-fold twisted tape (ETT) and a tube furnished with traditional spiral twisted tape (STT) with the same twist ratio and a Reynolds number domain of 2500–9500. According to their results, ETT had a greater Nusselt number and friction factor than STT. Another experiment examined the impact of preparing a circular pipe with punctured twisted tape along diverse axes (PATT), punctured twisted tape (PTT), and ordinary twisted tape (TT) at (TRs = 3, 4, and 5). The fluid flow was water, with a Reynolds number of 3000–16,000. According to their findings, PATT, PTT, and TT have greater heat transmission rates and thermal efficiencies than ordinary tubes [12]. Salman et al. [13] investigated the enhancement of heat transmission for twisted tapes with different tape-cut depths and twist ratios, evaluating both heat transfer and friction factor properties. Their findings indicated that when cut depth and twist ratio increased, pressure loss and Nusselt number decreased. The influence of increasing and decreasing amounts of TR on a helical screw insert was studied experimentally, and the authors observed that heat transfer was increased with a constant TR insert [14]. Furthermore, Sivashanmugam and Suresh [15] investigated a regularly spaced helical screw insert and observed a decrease in pressure drop as compared to a constant TR insert.

Other ideas to augment heat transfer in tubes include applying liquid–solid particle mixtures. Sohn et al. [16] observed that heat transfers increased significantly when the dynamic viscosity and thermal conductivity of fluids changed. Some researchers used different nanofluids as working fluids in pipes equipped with conventional twisted tape. Among these, Nakhchi and Esfahani [17] demonstrated that nanofluids augment thermophysical properties, heat transmission coefficient, and thermal efficiency compared to pure water. Sundar and Sharma [18] examined the effects of twisted tape inserts on nanofluid flow in circular channels. With the use of Al2O3–water nanofluid, they saw a 33.51% improvement in heat transfer coefficient. Additionally, the flow of CuO–water nanofluids in a heat exchanger using twisted tape was also studied numerically by Jafaryar et al. [19], who concluded that as the number of revolutions increases, secondary flow also increases.

Nanofluid thermal devices are increasingly important because they allow researchers to simulate heat transport with precise thermophysical property predictions [20,21,22]. Other investigators have applied nanoparticles to incrementally alter the rate of heat transfer to address different issues, such as temperature and pressure variations. Bovand et al. [23] used an Al2O3–water nanofluid to improve convective heat transport through an equilateral triangular obstacle change in the obstacle orientation. The estimated findings indicate that the side-facing flow has the highest impact of nanoparticles on heat transfer rate improvement, while the vertex-facing flow has the least. Furthermore, when the solid volume percentage increases, the needed Reynolds numbers for wake production drop. Abu-Nada and Chamkha [24] developed numerical solutions for mixed convective flow and heat transport of a nanofluid of water and Al2O3 in a lid-driven inclined square container. Their findings show that the presence of nanoparticles and the tilt of the enclosure might result in a considerable improvement in heat transfer. Dogonchi et al. [25] studied the natural convection heat transfer in a square enclosure with a wavy circular heater under a magnetic field and nanoparticles. In addition, mountainous notable investigations [26,27,28] have been carried out on heat transfer by natural convection of Fe3O4-water nanofluid. The heat transfer of copper–water nanofluid in a porous gap between a heated internal rectangular cylinder and a cold exterior circular cylinder under the influence of an inclined uniform magnetic field has been studied by Dogonchi et al. [29]. The obtained findings reveal that the heat transfer rate reduces with the Hartmann number and magnetic field inclination angle. At the same time, the average Nusselt number increases by about 16% when the nanoparticle volume fraction rises from 0 to 4% for Ra = 105, Ha = 25, and Ha = 0. Sarafraz et al. [30] examined a cooling liquid block using gallium, CuO–water nanofluid, and water. The CPU was evaluated in three modes: standby, normal, and overload. The CuO–water nanofluid showed better thermal performance than water, but a smaller pressure drop, compared to gallium. An experimental investigation into the forced convection heat transfer to multi-walled carbon nanotube nanofluids inside a chevron-type heat exchanger was performed by Sarafraz and Hormozi [31]. Ahmadi et al. [6] analysed the impact of applying elliptical-cut twisted tapes to different mass concentrations of copper oxide (CuO) nanofluid as the working fluid on the characteristics of flow and temperature within the plain tube using a computational evaluation. The results showed that the maximum thermal efficiency factor and Nusselt number for only nanofluid occurred at a mass concentration of 4%, while the state of a nanofluid combined with elliptical-cut tapes was 21% greater.

Several investigations have been carried out on entropy generation by employing heat transfer augmentation methods. Ko and Wu [32] used numerical techniques to study the generation of entropy inside a curving rectangular channel under heating. In another study, You et al. [33] studied the heat transfer increase in horizontal circuitous pipes with conical strip inserts from the view of minimal entropy production. Mwesigye et al. [34] researched the application of twisted tapes to promote heat transmission combined with generating entropy in parabolic trough receivers. Their findings indicate that the introduction of twisted tape inserts significantly reduces entropy generation rates at low Reynolds numbers.

Sheikholeslami et al. [35] evaluated entropy generation in nanofluid flow in a tube employing twisted tape turbulators. The possible impact of adjusting the pitch ratio (PR) and Reynolds number values was investigated, and the results show that raising the pitch ratio improved the Bejan number, while increasing the Reynolds number decreased this parameter. Shamsabadi et al. [36] performed a numerical investigation of nanofluid flows within a tube fitted with porous baffles. According to their results, increasing the number of baffles reduces thermal and frictional entropy generation by 14% and 32%, respectively.

According to the literature review provided above, numerous passive methods have been used in thermal systems to evaluate the rate of heat transfer and entropy generation. In other studies [3, 6], heat transfer augmentation and thermal efficiency in twisted tapes are highly dependent on the tape geometry. Moreover, in a heat exchanger system, nanofluids can be effectively applied due to their advantages in terms of thermophysical properties. As discussed previously, several attempts have been made to optimise heat transfer and entropy generation by incorporating customised twisted tapes into ordinary pipes. However, it is clear from this review that there has been no numerical or experimental examination of heat transmission as well as entropy generation in a pipe fitted with classical and elliptical-cut twisted tape inserts that use hybrid nanofluid as a working fluid. Therefore, this gap is addressed in the current work, which focuses on the application of entropy generation in the flow of hybrid nanofluid in PT, TPT, and TECT. The main objectives are to investigate the rate of heat transfer, thermal performance, and entropy generation analysis in PT, TPT, and TECT in the presence of Al2O3–Cu/water hybrid nanofluid compared with a Cu/water nanofluid.

Numerical analysis

Model geometry

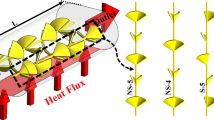
The geometries of the model are made up of plain tubes (PT), and plain tubes equipped with solid (TPT) and elliptical-cut twisted tape (TECT) inserts. As shown in Fig. 1a, the tube has a length (L) of 1 m and a 0.0195 m in inner diameter (D). The twisted tape inserts have 0.0008 m thickness (t), a 0.019 m width (W), and a 0.057 m pitch (y), as shown in Fig. 1b. The tube with elliptical-cut twisted tape has a width tape ratio of a/w = 0.7 and a long diameter-to-short diameter elliptic-cut twisted tape ratio of b/a = 2, as shown in Fig. 1c. Figure 1d illustrates the configuration of the plain twisted tape and of the elliptical-cut twisted tape. These dimensions were chosen in accordance with the experimental and numerical works in [37] and [6], which are the sources employed to verify the numerical findings of this paper.

Fig. 1
figure 1

Physical model of a PT, b TPT, c TECT, and d significant dimensions in the situation studied

Full size image

The physical model is simplified by using the following assumptions:

(1) The gravity force is neglected. (2) The numerical study of turbulent flows is performed by means of the realisable k–ε model. (3) All the simulations are performed at Reynolds numbers 7000, 9000, 11,000, 13,000, and 15,000. (4) The flow is considered incompressible and steady. (5) A constant heat flux of 600 Wm−2 and 4000 Wm−2 is applied to all tube walls, while the twisted tape has an adiabatic wall condition. Additionally, the pipe wall and classical and elliptical twisted tape are under a no-slip condition.

Properties of hybrid nanofluid

The most prevalent medium applied in receiver tubes has low thermal conductivity, and this defect has motivated various studies to address this problem. Several studies have demonstrated that incorporating nanoparticles into the base fluid improves thermal conductivity [38,39,40]. In this work, calculations were made for different mass concentrations of an Al2O3–Cu/water hybrid nanofluid. Additionally, CuO/water nanofluid was selected for comparison [6]. Table 1 summarises the thermophysical properties of Al2O3, CuO, Cu nanoparticles, and water [41]. The fluid properties are presented below:

Table 1 Flow properties at T = 300 K
Full size table

Thermophysical properties of hybrid nanofluids are expressed in terms of base fluid properties, Al2O3, Cu nanoparticles, and solid nanoparticle volume friction in the base fluid [42]. The volume fractions of the Al2O3 and Cu nanoparticles are denoted by \({\varnothing }_{1}\) and \({\varnothing }_{2}\), respectively. The determining equations for the thermophysical properties of the hybrid nanofluid of Al2O3–Cu/water are given in Eqs. (1–4). Owing to the precision of its thermophysical correlations [42], this type of hybrid nanofluid was chosen in this study. Equations for thermophysical properties of the hybrid nanofluid are represented by [42,43,44]:

Density:

$${\rho }_{\mathrm{hnf}}=\left(1- {\varnothing }_{2}\right){[(1-\varnothing }_{1}){\rho }_{\mathrm{f}}+{\varnothing }_{1}{\rho }_{\mathrm{n}1}]+{\varnothing }_{2}{\rho }_{\mathrm{n}2}$$
(1)

Specific heat:

$$(\rho {C}_{\mathrm{p}}{)}_{\mathrm{hnf}}={(1-\varnothing }_{2})[\left(1-{\varnothing }_{1}\right)(\rho {\complement }_{\mathrm{p}}{)}_{\mathrm{f}}+{\varnothing }_{1}(\rho {\complement }_{\mathrm{p}}{)}_{\mathrm{n}1}]+{\varnothing }_{2}(\rho {\complement }_{\mathrm{p}}{)}_{\mathrm{n}2}$$
(2)

Dynamic viscosity:

$${\mu }_{\mathrm{hnf}}= \frac{ {\mu }_{\mathrm{f}}}{(1-{\varnothing }_{1}{)}^{2.5}(1-{\varnothing }_{2}{)}^{2.5}}$$
(3)

Thermal conductivity:

$$\frac{{k}_{\mathrm{hnf}}}{{k}_{\mathrm{nf}}}= \frac{{k}_{\mathrm{n}2}+2{k}_{\mathrm{nf}}-2{\varnothing }_{2}({k}_{\mathrm{nf}}-{k}_{\mathrm{n}2})}{{k}_{\mathrm{n}2}+2{k}_{\mathrm{nf}}+{\varnothing }_{2}({k}_{\mathrm{nf}}-{k}_{\mathrm{n}2})}$$
(4)

where \({k}_{\mathrm{nf}}= \frac{{k}_{\mathrm{p}}+2{k}_{\mathrm{bf}} - 2\varnothing ({k}_{\mathrm{bf}}-{k}_{\mathrm{p}})}{{k}_{\mathrm{p}}+2{k}_{\mathrm{bf}} + \varnothing ({k}_{\mathrm{bf}}-{k}_{\mathrm{p}})}{k}_{\mathrm{bf}}\)

Here, \({\varnothing }_{1}\) and \({\varnothing }_{2}\) denote the volume fraction of nanoparticles, where \({\varnothing }_{1}+{\varnothing }_{2}=\varnothing\), where \(\varnothing\) is the overall volume concentration of two different types of nanoparticles dispersed in a basic fluid in the hybrid nanofluid. Further, the indices n1 and n2 refer to the Al2O3 and CuO nanoparticles, and bf, nf, and hnf represent the base fluid, nanofluid, and hybrid nanofluid, respectively.

The thermophysical parameters of the hybrid nanofluid employed are summarised in Table 2.

Table 2 Al2O3–Cu/water hybrid nanofluid properties at various concentration
Full size table

Governing equations

The Navier–Stokes equations, along with continuity and energy equations, were utilised to describe the general behaviour of the fluid. The equations for 3D, steady, and incompressible flow are as follows [45]:

The continuity equation

$$\frac{\partial }{\partial {\mathrm{x}}_{\mathrm{i}}} \left(\rho {u}_{\mathrm{i}}\right)=0$$
(5)

Transport of momentum

$$\frac{\partial }{\partial {x}_{\mathrm{j}}} \left(\rho {u}_{\mathrm{i}}{u}_{\mathrm{j}}\right)=-\frac{\partial p}{\partial {x}_{\mathrm{i}}}+ \frac{\partial }{\partial {x}_{\mathrm{j}}}\left[ {\mu }_{eff}\left(\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{j}} }+ \frac{\partial {u}_{\mathrm{j}}}{\partial {x}_{\mathrm{i}}} \right)-\frac{2}{3}{\mu }_{\mathrm{eff}}\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{i}}} {\delta }_{\mathrm{ij}} - \overline{\rho {u}_{\mathrm{i}}^{^{\prime}}{u}_{\mathrm{j} }^{^{\prime}}}\right]$$
(6)

Transport of energy

$$\frac{\partial }{\partial {x}_{\mathrm{j}}} (\rho {u}_{\mathrm{j}}{C}_{\mathrm{p}}T) = \frac{\partial }{\partial {x}_{\mathrm{j}}} \left( K \frac{\partial T}{\partial {x}_{\mathrm{j}}}+\frac{{\mu }_{\mathrm{t}}}{{\sigma }_{\mathrm{h}.\mathrm{t}}}\frac{\partial ({C}_{\mathrm{p}}T)}{\partial {x}_{\mathrm{j}}}\right)+{u}_{\mathrm{j}}\frac{\partial P}{\partial {x}_{\mathrm{i}}} +\left[ {\mu }_{\mathrm{eff}}\left(\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{j}} }+ \frac{\partial {u}_{\mathrm{j}}}{\partial {x}_{\mathrm{i}}} \right)-\frac{2}{3}{\mu }_{\mathrm{eff}}\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{i}}} {\delta }_{\mathrm{ij}} - \overline{\rho {u}_{\mathrm{i}}^{^{\prime}}{u}_{\mathrm{j} }^{^{\prime}}}\right] \frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{j}}}$$
(7)

Here \(u, \rho ,\mu ,K, \mathrm{and} T\) indicate velocity, density, dynamic viscosity, fluid thermal conductivity, and time-averaged temperature, respectively. The effective viscosity can be calculated by \({\mu }_{\mathrm{eff}}=\mu + {\mu }_{\mathrm{t}}\). The term (\(- \overline{\rho {u}_{\mathrm{i}}^{^{\prime}}{u}_{\mathrm{j} }^{^{\prime}}})\) represents the turbulence effects and Reynolds stresses.

$$- \rho {u}_{\mathrm{i}}^{^{\prime}}{u}_{\mathrm{j} }^{^{\prime}}={\mu }_{\mathrm{t}}\left(\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{j}}}+ \frac{\partial {u}_{\mathrm{j}}}{\partial {x}_{\mathrm{i}}}\right)- \frac{2}{3} (\rho {k}_{1}+ {\mu }_{\mathrm{t}}\frac{\partial {u}_{k}}{\partial {x}_{\mathrm{k}}}){\delta }_{\mathrm{ij}}$$
(8)

where k is the turbulence kinetic energy.

The realisable k−\(\varepsilon\) turbulence model can be expressed as follows.

Equation of turbulence kinetic energy (k):

$$\frac{\partial (\rho k)}{\partial \mathrm{t}}+\frac{\partial (\rho k{u}_{\mathrm{i}})}{\partial {x}_{\mathrm{i}}}= \frac{\partial }{\partial {x}_{\mathrm{j}}} \left[\left(\mu + \frac{{\mu }_{\mathrm{t}}}{{\sigma }_{\mathrm{k}}}\right)\frac{\partial k}{\partial {x}_{\mathrm{j}}}\right]+{G}_{\mathrm{k}}- \rho \varepsilon$$
(9)

Equation of turbulence dissipation rate (\(\varepsilon )\):

$$\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho \varepsilon u_{\text{i}} } \right)}}{{\partial x_{\text{i}} }} = ~\frac{\partial }{{\partial x_{\text{j}} }}~\left[ {\left( {\mu + \frac{{\mu _{\text{t}} }}{{\sigma _{\epsilon } }}} \right)\frac{{\partial \varepsilon }}{{\partial x_{\text{j}} }}} \right] + \rho C_{1} S_{\epsilon } - \rho C_{2}\frac{{\varepsilon ^{2} }}{{k + \sqrt {\mu /\rho } \varepsilon }}$$
(10)

Here \({G}_{k}\) is the production of turbulence kinetic energy and was developed in the similar manner to all the k–\(\varepsilon\) models as:

$${G}_{\mathcal{K}}=- \overline{\rho {u}_{\mathrm{i}}^{^{\prime}}{u}_{\mathrm{j} }^{^{\prime}} }\frac{\partial {u}_{\mathrm{j}}}{\partial {x}_{\mathrm{i}}}$$
(11)

From Eqs. (4) and (7)

$${G}_{\mathrm{k}}= {\mu }_{\mathrm{t}}{S}^{2}$$
(12)

The eddy viscosity is given by

$${\mu }_{\mathrm{t}}= \rho {\complement }_{\mu }\frac{{k}^{2}}{\varepsilon }$$
(13)

In the realisable k−\(\varepsilon\) model, the model coefficients \({C}_{1}\) and \({\complement }_{\mu }\) are calculated using equations [45]:

$${C}_{1}=\mathrm{max}\left[0.43,\frac{\eta }{\xi +5}\right]$$

,

$$\xi =S\frac{k}{\varepsilon},$$
$$S\stackrel{-}{=}\sqrt{2{S}_{\mathrm{ij}}{S}_{\mathrm{ij}}},$$

The remaining empirical constants are defined by [45]: \({C}_{2}=1.9,\) \({\sigma }_{\varepsilon }=1.2\).

Sij denotes the rate at which a flowing fluid deforms linearly. In 3D, there are nine elements: three linear elongation deformation elements and six shearing and deformation elements [45].

$${S}_{\mathrm{ij}}= \frac{1}{2}\left(\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{i}}}+\frac{\partial {u}_{\mathrm{i}}}{\partial {x}_{\mathrm{j}}}\right)$$
(14)

Evaluation of parameters

During the simulation, the dimensionless parameters and certain variables are presented to explain the results and describe flow and heat transmission in the circle tube and in the pipes equipped with the solid and elliptical-cut twisted tape inserts, as follows.

The flow system is represented by the Reynolds number value, Re:

$$\mathrm{Re}=\frac{\rho u D}{\mu }$$
(15)

The Nusselt number (Nu) is determined by:

$$\mathrm{Nu}=\frac{h D}{K}$$
(16)

The friction factor (f) is evaluated in the fully developed flow by measuring shear stress (τ) [46] and drop of pressure (\(\Delta p\)) [3] across the test pipe length of ordinary pipe and pipe equipped with twisted tape inserts, respectively, as:

$$f=\frac{8 * {\tau }_{w}}{\rho {u}^{2}}$$
(17)
$$f= \frac{2 \Delta p D}{\rho L{u}^{2}}$$
(18)

Also, the thermal efficiency factor for a solid and an elliptical-cut twisted tape is calculated in this research for convection heat transmission ratio and friction factor ratio.

The thermal efficiency factor is defined by

$$\eta = ~\frac{{\left( {{\raise0.7ex\hbox{${Nu}$} \!\mathord{\left/ {\vphantom {{Nu} {Nu_{\text{p}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${Nu_{\text{p}} }$}}} \right)}}{{\left( {{\raise0.7ex\hbox{$f$} \!\mathord{\left/ {\vphantom {f {f_{p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${f_{\text{p}} }$}}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} }}$$
(19)

Entropy generation

The rate of local volumetric entropy generation was determined for each single status, considering thermal and frictional effects as the only contributors:

$${S}_{\mathrm{gen},\mathrm{total}}=({S}_{\mathrm{gen}}{)}_{\mathrm{Heat transfer}}+({S}_{\mathrm{gen}}{)}_{\mathrm{Fluid friction}}$$
(20)

Usually, the volumetric entropy generation for a system is expressed as follows [47]:

$${S}_{\mathrm{H},\mathrm{T}}=\frac{k}{{T}^{2}}\left[{\left(\frac{\partial T}{\partial x}\right)}^{2}+{\left(\frac{\partial T}{\partial y}\right)}^{2}+{\left(\frac{\partial T}{\partial z}\right)}^{2}\right]$$
(21)
$${S}_{\mathrm{F},\mathrm{F}}=\frac{\mu }{T}\left\{2\left[{\left(\frac{\partial u}{\partial x}\right)}^{2}+{\left(\frac{\partial v}{\partial y}\right)}^{2}+{\left(\frac{\partial w}{\partial z}\right)}^{2}\right]\right.+{\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)}^{2}+{\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)}^{2}+\left.{\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)}^{2}\right\}$$
(22)

The total entropy generation \({(S}_{\mathrm{g},\mathrm{t}})\) is calculated by integrating the sum of the volumetric entropy production components across the volume of the tube.

$${S}_{\mathrm{g},\mathrm{t}}= \left\{\int {S}_{\mathrm{H},\mathrm{T}} + \int {S}_{\mathrm{F},\mathrm{F}}\right\} \partial V$$
(23)

The Bejan number is usually used to show the contribution of each irreversibility to the total entropy generation rate. The Bejan number can be defined as [35]

$$Be=\frac{({S}_{\mathrm{gen}}{)}_{\mathrm{Heat transfer}}}{{S}_{\mathrm{gen},\mathrm{total}}}$$
(24)

Numerical techniques

The numerical computation was performed using Star-CCM + , a commercial CFD software. The numerical computations in this investigation are performed using a pressure-based finite volume approach. For velocity–pressure coupling, the SIMPLE (Semi-Implicit Pressure-Linked Equations) method proposed by Patankar and Spalding [48] is used. The second-order upwind approach was used to discretize the momentum, turbulent kinetic energy, turbulent dissipation rate, and energy equations. A detailed estimation of the governing equations was explained by Donea and Huerta [49]. The realisable k−ε model is employed turbulence model in this work. The thermophysical properties of hybrid nanofluid with different mass concentrations are listed in Table 2. The thermal efficiency factor is calculated in Eq. 19 to understand the improvement in performance. The second-order upwind approach was used to discretize the momentum and energy equations. Additionally, MATLAB was used for solving Eqs. (20)–(23).

Grid independency

To ensure the correctness of the computations, grid independence research was conducted for the temperature for various mesh sizes to find an acceptable grid with high accuracy. At Re = 11,000, the results are obtained for water flow within a plain tube and a tube fitted with classical and elliptical-cut twisted tape. The grid independence test was done by varying the total number of cells in each tube. Here, five grids with various numbers of cells have been employed for each shape to show which number of cells is appropriate. The convergence of the computational findings with the precise answers relies on the number of cells into which the field is split. It is shown that in the PT, there is a variance of 0.24%, 0.33%, 1.2%, and 1.2% when the temperature values obtained in grids with a total of 520,000, 592,000, 624,000, and 640,000 cells are compared to those obtained in a grid with a total of 496,000 cells. For the TPT, there is a fluctuation of 0.15%, 0.35%, 0.53%, and 0.53% when the temperature values in the grids with the cell counts 1,179,769, 1,234,240, 1,526,023, and 1,611,011 are compared to those in the grid with the cell counts 1,008,117. Also, in TECT, temperature readings in grids with 2,892,319, 2,990,608, 3,359,202, and 3,413,798 cells differ by 0.17%, 0.49%, 0.73%, and 0.73% from those in grids with 2,615,663 cells. In the PT, the grids of 624,000 and 640,000 cells can be adopted, and any grid with cells from 1,526,023 to 1,611,011 would be suitable for TPT. Also, any grid with cells from 2,990,608 to 3,413,798 was found to be appropriate for TECT, because the difference in the results from such grids was negligible. Here, the grids having cell counts of 640,000, 1,611,011, and 3,413,798 are implemented to represent the domains of PT, TPT, and TECT, respectively.

Validation

The Nusselt number, friction factor, and thermal efficiency factor obtained using the realisable k–\(\varepsilon\) model for TECT were validated against the work of Ahmadi [6] for various mass concentrations of nanoparticles and a Reynolds number of 7000. A comparison of the results shows good agreement under turbulent flow conditions, as shown in Fig. 2a–c for the Nusselt number, friction factor, and thermal efficiency factor. The highest error percentages occurred at 4% concentration of nanoparticles, with values of 5.1, 3.5, and 5.5%, respectively, for the aforementioned parameters.

Fig. 2
figure 2

Variation of a Nusselt number, b friction factor, and c thermal efficiency against nanoparticle concentration Ahmadi [6]

Full size image

Results and discussion

Temperature contours

The temperature contours at the axial position of X = 0.57 m for a turbulent flow of Al2O3–Cu/water hybrid nanofluid with concentration variations are shown in Fig. 4 for the three configurations of PT, TPT, and TECT. The heat flux of the wall is 4000 Wm−2. As shown in Fig. 3a, the temperature contours in PT are similar. This might be due to the development of the flow at this location. In TPT and TECT in Fig. 3b, c, there are increased temperature distributions in the tubes due to the employment of solid and elliptical-cut twisted tape inserts. This is in agreement with Oni and Pual [3]. Namely, the temperature gradient of the TECT is higher than that of PT and TPT.

Fig. 3
figure 3

Temperature contour for a PT, b TPT and c TECT of Al2O3–Cu/water hybrid nanofluid at different mass concentrations at Re = 7000 and axial location X = 0.57 m

Full size image

Flow velocity contour

Figure 4 provides the flow velocity contours for the Al2O3–Cu/water hybrid nanofluid at different nanoparticle concentrations for PT, TPT, and TECT, at a Reynolds number of 7000. The location was selected randomly at an axial position of X = 0.57 m. As shown in Fig. 4, the difference in nanoparticle concentration does not significantly affect the velocity contour, this is in agreement with Ahmedi et al. [6]. In the PT profile in Fig. 4a, the velocity is nearly similar at this location, and the highest velocity has happened at the core, suggesting that the flow has completely developed. However, in TPT Fig. 4b, a single swirl is created around the twisted tapes. This longitudinal swirl is crucial in disrupting the boundary layer and establishing a consistent velocity throughout the flow, including the reduced gap between the tape wall and the tube wall. A good agreement between the present results and those of [37] is observed. Meanwhile, in Fig. 4c, TECT develops swirl flows at the tube walls and in the core zone. Therefore, it contributes to more fluid mixing between the core and near-wall areas. Evidently, the gap in TPT and the cut on twisted tape in TECT influence the uniformity of velocity; this is due to the swirling flow in this zone. In that zone, the distortion increases when the gap decreases in TPT and, additionally, when the cut is on twisted tape in TECT. Therefore, it increases the velocity gradient, which allows better heat transfer.

Fig. 4
figure 4

Velocity contour of a PT, b TPT and c TECT of Al2O3–Cu/water hybrid nanofluid at different mass concentrations at Re = 7000 and axial location X = 0.57 m

Full size image

Turbulent kinetic energy

Figure 5 presents the influence of different regions on the turbulent kinetic energy at location X = 0.57 m for different mass concentrations of Al2O3–Cu/water hybrid nanofluid at Re = 7000. The greatest amount of turbulent kinetic energy occurred towards the wall, as shown in PT Fig. 5a due to the low flow velocity as a result of the no-slip condition on the wall [3]. In the case of twisted tapes inserted into a circular pipe, the turbulent kinetic energy peaks at a certain distance from the tape wall when twisted tape is introduced into a tube with a steady flow, as shown in TPT in Fig. 5b. The reason for this is that the presence of the tape causes the boundary layer to become more turbulent [3]. As a consequence of the elliptical cuts on the twisted tape, the disruption of boundary layer increases in the domains as compared with TPT. This finding agrees with the work of Ahmadi et al. [6].

Fig. 5
figure 5

Turbulent kinetic energy contour of PT (a), TPT (b), and TECT (c) of Al2O3–Cu/water hybrid nanofluid at various concentrations

Full size image

Heat transfer

In this section, the Nusselt number was utilised to assess heat transfer. Figure 6 depicts the influence of various mass concentrations of nanoparticles on the Nusselt number in the TECT at a Reynolds number of 7000. In addition, as shown in Fig. 6, the Nusselt number increased as the concentration of nanoparticles was enhanced. Additionally, applying Al2O3–Cu/water hybrid nanofluid enhances heat transfer when compared to CuO/water nanofluid [6]. As shown, the Al2O3–Cu/water hybrid nanofluid has a 195 Nusselt number at ∅ = 4%, which is about 3.9% higher than that of CuO/water nanofluid [6]. According to [50], this is due to an excess in intensity, thermal conductivity, as well as dynamic viscosity. Figure 7a–d shows the influence of nanoparticle concentration in different tubes on the heat transfer for Al2O3–Cu/water hybrid nanofluid flow at various Reynolds numbers and also the effect of inserting classical and elliptical‑cut twisted tape versus ordinary tube. As noted, the heat transfer is enhanced as the Reynolds number and the concentration of nanoparticles increase. Also, it is clear that the Nusselt number in the PT is lower than that in TPT and TECT. According to [51], this is because the turbulence intensity increases with the Reynolds number, destroying the boundary layer. Additionally, as aforementioned, increasing nanoparticle concentrations augments the thermal conductivity of hybrid nanofluid flow, hence the heat transfer rate [50]. Regarding the tubes enhanced with twisted tapes, as mentioned in a previous numerical work [3, 6], the twisted tape creates quicker whirling of fluid inside tubes, resulting in the disintegration of the layer of the thermal boundaries and improved flow mixing among the fluids at the centre and the surface of the heating wall. The findings in Fig. 7d reveal that at a Reynolds number of 15,000 and ∅ = 4%, the heat transfer of TPT and TECT is 1.57 and 1.70 times that of PT, respectively. Also, TECT has the highest Nusselt number of 222.

Fig. 6
figure 6

Nusselt number variation against nanoparticle concentration in nanofluid and hybrid nanofluid at Re = 7000

Full size image
Fig. 7
figure 7

Influence of various twisted tape on Nusselt number against Reynolds number with different concentration of Al2O3–Cu hybrid nanofluid a 1%, b 2%, c 3%, and d 4%

Full size image

Friction factor

In Fig. 8, the effects of the various nanoparticle concentrations on the friction factor in TECT at Re = 11,000 are presented. As depicted, the values for the friction factor are found to remain constant over the nanoparticle concentrations tested. This is due to the friction factor being affected mostly by the Reynolds number as well as roughness [6]. Figure 9 depicts the friction factor versus the Reynolds number for Al2O3–Cu/water hybrid nanofluid at ∅ = 4% in tubes with solid and elliptical-cut twisted tape inserts. The friction factor consistently decreases as the Reynolds number increases. This occurs when the fluid’s viscous force is exceeded by the Reynolds number, causing the shear between the fluid and the pipe wall to decrease [3]. Tubes with twisted tapes have a greater friction coefficient than simple tubes because the twisted tape causes flow obstruction and swirl flow [51]. As shown, an unexpected case is found in TECT at a Reynolds number of 7000, where the friction coefficient is the same as in TPT, at about 0.208. This might be owing to the low eddy flow intensity for TECT at Re = 7000.

Fig. 8
figure 8

Variation of friction factor at different nanoparticle concentrations for PT, TPT, and TECT with Re = 11,000

Full size image
Fig. 9
figure 9

Friction factor against Reynolds number for various twisted tapes

Full size image

Thermal performance factor

Figure 10 depicts the thermal performance factor at various mass concentrations of Al2O3–Cu/water hybrid nanofluid, demonstrating that the thermal performance factor improves as the concentration of nanoparticles increases. An incremental increase in the nanoparticle concentration of hybrid nanofluid tends to enhance the thermal conductivity of water, accompanied by relatively higher viscosity [52]. Figure 11a–d compares the fluctuation in the thermal efficiency with the Reynolds number for various pipe designs and nanoparticle concentrations. The findings demonstrate a considerable enhancement in the rate of heat transmission and the performance of pressure drop for the twisted tape with a working fluid of Al2O3–Cu/water hybrid nanofluid. Furthermore, TECT has a greater thermal performance factor than TPT. Clearly, when the Reynolds number develops, the performance factor reduces proportionally. This is due to the fact that when the Reynolds number rises, the pressure decreases [3]. As shown in Fig. 11d, the highest thermal efficiency factor obtained is around 1.9 at a \(\mathrm{\varnothing }\) = 4% and Re = 7000 for TECT, which is 7.73% higher than for the same geometry with nanofluid.

Fig. 10
figure 10

Variation of thermal efficiency factor of Al2O3–Cu hybrid nanofluid versus nanoparticle concentration for TECT at different Reynolds number

Full size image
Fig. 11
figure 11

Influence of different tube designs and different mass concentrations of nanoparticles a 1%, b 2%, c 3%, and d 4% on the thermal efficiency factor against Reynolds number

Full size image

Entropy generation

The distribution of entropy generation and Bejan number was studied numerically for an ordinary liquid, a CuO/water nanofluid, and an Al2O3–Cu/water hybrid nanofluid at \(\varnothing =4\%\) inside a plain pipe and in a pipe equipped with classical and elliptical-cut twisted tape inserts. Also, entropy generation effect analyses for various configurations at Re = 7000 are shown in Figs. 12–15. In thermal systems, entropy is generated by the means of heat transfer due to a difference in temperature as well as by the irreversible dissipation of kinetic energy due to fluid friction [47]. The main goal of the current work is to assess the influence of a tube fitted with solid and elliptical-cut twisted tape inserts within the generation principles of entropy, considering fluid friction and heat transmission effects as the only contributors.

Fig. 12
figure 12

Spatial distribution of thermal entropy generation

Full size image

The local entropy generation

The development of local entropy generation is shown in Figs. 12 and 13. The local distribution of thermal entropy generation is shown in Fig. 12. The results indicate that the greatest amount of thermal entropy creation in plain tubes occurs in the zone near the wall, where the gradient of temperature is greater. However, fitting the tubes with solid and elliptical-cut twisted tape also shows a significant effect on the entropy generation rate, as noticeable with TPT and TECT, where the twisted tape generates a strong vortex flow between the pipe wall and the surface of the twisted tape, increasing thermal entropy generation. Evidently, the addition of nanoparticles leads to a lower thermal entropy generation than that in ordinary liquid, which is in keeping with the results in Ref. [53]. Another point which can be seen from Figs. 12, 14a and 15a is that the thermal entropy generation of TPT and TECT is less than that of the PT. This is owing to heat transfer improvement with TPT and TECT as compared to PT [54]. As can be discerned, the generation of thermal entropy decreases when vortex flow increases. As an example, intensification of vortical flow in the TECT leads to a reduction in the entropy generation rate of about 80% and 14.8% compared to the PT and TPT models, respectively. Figure 13 illustrates the localised generation of entropy due to fluid friction. The first observation from Fig. 13 is that in the PT, the entropy is high near the wall due to a high velocity gradient orthogonal to the wall surface. However, in TPT and TECT, frictional entropy generation shows a significant increase near the rotational axis of the classical and elliptical-cut twisted tape. The cause of this increase is the development of larger flow velocity gradients by using twisted tape in this locale. These are produced by sudden changes in vortex flow direction, and then they tend to high values. It is also observed that the generation of frictional entropy increases as the dynamic viscosity increases (see Eq. 22). Furthermore, frictional entropy generation at the entrance of the pipe is dominant across all of the tested conditions, because velocity gradients are high at the inlet of the tube, and as a result, viscous entropy generation increases [47]. An important behaviour is observed in TECT geometry, in which it is found to produce heat transfer enhancements and reduce viscous entropy generation in all cases as compared with TPT as shown in Figs. 14b, and 15b. The increase in frictional entropy generation is caused by the increase in velocity gradient and disturbances caused by the addition of the nanoparticles [55]. However, the use of twisted tapes reduces thermal entropy generation [56].

Fig. 13
figure 13

Spatial distribution of frictional entropy generation

Full size image
Fig. 14
figure 14

a Entropy production due to heat transfer, b entropy production due to fluid friction, and c total entropy production at heat flux 600 Wm−2

Full size image
Fig. 15
figure 15

a Entropy production due to heat transfer, b entropy production due to fluid friction, and c total entropy production at heat flux 4000 Wm−2

Full size image

Total entropy generation

The total amount of entropy generated is dependent on the amount of entropy generated by fluid friction and heat transfer. Figures 14 and 15 display the total entropy production for different values of three fluid flows (water, CuO/water nanofluid, and Al2O3–Cu/water hybrid nanofluid), and three different configurations (PT, TPT, and TECT). The concentration of nanoparticles is at \(\varnothing =4\%\) and the Reynolds number is 7000. In addition, the total entropy generation for different values of heat flux on the wall of the absorber pipe of 600 and 4000 Wm−2 is shown in Figs. 14 and 15, respectively. As is clear in the PT tube in Fig. 15, using nanofluid and hybrid nanofluid leads to reductions in total entropy generation. According to [53, 55, 57], increasing the volume fraction of nanoparticles reduces the generation of total entropy. Moreover, Fig. 14 shows that the total entropy generation is slightly reduced in TECT as compared with TPT. According to this study, the dimensions of the cut in the twisted tape have an intense influence on the total entropy production. A high swirl flow may contribute to a reduction in entropy generation. As a result, the elliptical-cut twisted tape could greatly reduce the total entropy generation. According to [58, 59], entropy generation reduces with a rise in swirl intensity. In other words, the increase in vortical flow results in a further reduction in the total entropy generated when the hybrid nanofluid is present. As mentioned before, twisted tape and cut twisted tape produce significant flow mixing, which, combined with the high thermal conductivity of the hybrid nanofluid, results in a greater contribution of the hybrid nanofluid to enhance heat transfer. This emanates from the fact that the classical and elliptical-cut twisted tape intensify the vortical flow. Hence, swirl flow has a greater effect on temperature gradients and, thus, on the generation of thermal entropy and, eventually, on the generation of total entropy. As shown in Fig. 15c, the addition of nanoparticles to the basis fluid leads to a drop in the generation of total entropy. Another point of Figs. 14 and 15 is that at low heat flux of 600 Wm−2, the fluid friction is dominant, and at high heat flux of 4000 Wm−2, the heat transfer is dominant. Figure 16 shows the effect of the Bejan number on PT, TPT, and TECT for water, CuO/water nanofluid, and Al2O3–Cu/water hybrid nanofluid, (a) at a heat flux of 600 Wm−2, and (b) at a heat flux of 4000 Wm−2. The Bejan number is an irreversibility distribution parameter that indicates the ratio between irreversibility thermal and total irreversibility entropy production rates. Cimpean et al. [60] define the Bejan number as a value between 0 and 1. Be = 1 denotes the point at which irreversible heat transmission prevails, Be = 0 denotes the point at which irreversibility is dominated by fluid friction effects, and Be = 0.5 denotes the point at which the rates of heat transfer and fluid friction entropy generation are equal [61]. The data gathered revealed that the Bejan number decreases rapidly with increasing vortical flow, as well as when nanoparticles are added, as shown in Fig. 16a. This is caused by low heat flux, as indicated by Magherbi et al. [62], due to the commencement of convective heat transfer. The findings indicated that the Bejan number ranges from 0 to 1, 0 \(<Be <1.\) Figure 16b for a heat flux of 4000 Wm−2, the Bejan number is close to 1 because the thermal entropy generation is prominent.

Fig. 16
figure 16

Effect of water, nanofluid, and hybrid nanofluid for PT, TPT, and TECT on Bejan number, a at heat flux 600 Wm−2, and b at heat flux 4000 Wm−2

Full size image

Conclusions

A heat transfer rate and entropy generation analysis and Bejan number were carried out for Al2O3–Cu/water hybrid turbulent nanofluid flow inside a pipe, using classical and elliptical‑cut twisted tape inserts. For heat transfer rate, parameters such as nanoparticle volume fraction, friction behaviour, and thermal efficiency factor were examined. Calculations were carried out for Reynolds numbers between 7000 and 15,000. Considering entropy generation, the impacts of parameters such as the volume fraction of nanoparticles, solid and elliptical‑cut twisted tape inserts, and various kinds of entropy generation (i.e. thermal, viscous, and total) were assessed, for which calculations were performed at Reynolds numbers of 7000. The results obtained are summarised as follows:

It has been discovered that promoting heat transfer passively using a tube with insertions of solid and elliptical-cut twisted tape results in a higher heat transfer rate than an ordinary tube.

The Nusselt number in TECT for hybrid nanofluid is found to be up to 195, which is about 3.9% greater than the Nusselt number in nanofluid at the same concentration (∅ = 4%) at Re = 7000.

TECT has a Nusselt number up to 1.7 times that of PT, while TPT has a Nusselt number up to 1.57 times that of PT. A concentration of 4% for the Al2O3–Cu/water hybrid nanofluid leads to the highest Nusselt number, which is about 222 at a Reynolds number of 15,000.

When the Reynolds number remains constant, the thermal performance factor of TECT increases as the nanoparticle concentration increases from 1 to 4%. However, as the Reynolds number increases, the thermal performance factor drops.

The results obtained show that the thermal efficiency factor for TECT at a concentration of 4% for the Al2O3–Cu/water hybrid nanofluid is about 1.9 at a Reynolds number of 7000, which is 7.73% higher than for the CuO/water nanofluid.

Through applying the hybrid nanofluid, the thermal performance factor and heat transfer rate are improved significantly.

The thermal entropy generation rate near the tube wall is much higher in comparison with that in the centre of the tube, for all geometries. Use of solid and elliptical-cut twisted tape affects the strength of the vortex flow in the zone near the wall and twisted tape surface, which causes a growth in the temperature gradient.

The rate of generation of frictional entropy increases by inserting a twisted tape into the tube, also with increasing thermal conductivity, but decreases by using elliptical-cut twisted tape.

Increasing nanoparticle concentration decreases total entropy generation.

Elliptical-cut twisted tape can generate a stronger eddy flow as compared to classical twisted tape, and as a result, total entropy generation decreases slightly.

Heat transfer dominates entropy generation at low heat flux, whereas fluid friction dominates at high heat flux.