Data-driven de-smearing of DSC signals

Abstract

In heat flux differential scanning calorimetry, a pair of identical crucibles, one empty as reference and the other filled with the sample, is heated in a furnace with a prescribed rate. The (empty) reference crucible heats faster, resulting in a temperature difference that is detected by thermocouples. Slow heating of the furnace results in weak and noisy signals; higher heating rates induce strong signals but lead to smearing if applied to materials undergoing a phase transition: The recorded peak signal is shifted toward higher temperatures. To determine the peak, the onset/endset temperatures, and the phase transition enthalpy, multiple heating rates are used to find a trade-off between noise and smearing. When plotting the melting peaks over temperature and heating rate, the visual similarity to the time evolution of a probability density under drift and diffusion catches the eye. Such a density evolution can be described by the Fokker–Planck equations. In this analogon, the de-smeared signal corresponds to the initial distribution. We propose a data-driven de-smearing approach, based on an extrapolation to a (hypothetical) zero heating rate signal. This zero rate signal is low-dimensionally parameterized and its parameters together with the drift and diffusion of the Fokker–Planck equation are fitted against the calorimetric measurements. The method is successfully tested on heat capacity data of a technical-grade high-density polyethylene (HDPE) using mid-range heating rates. The data are strongly affected by smearing, and the proposed de-smearing method ${FPEX}_{0}$ delivers reliable estimates of characteristic shape parameters of the phase transition peak effectively overcoming the problem of a deteriorating signal-to-noise ratio for heating rates approaching zero.

Introduction

One of the most common operation modes of a heat flux differential scanning calorimeter (DSC) is to increase the temperature of the furnace with a constant rate, heating both a crucible with the sample whose thermophysical properties are to be determined and an empty reference crucible. As the empty reference crucible heats faster, a temperature gradient establishes that induces a voltage in thermocouples located beneath the crucibles. Applying standard calibration procedures [1, 2], the rate of heat flow into the sample can be calculated and the sample’s heat capacity deduced.

A use case for DSC is the analysis of thermal events, which are characterized by a peak in the recorded signal in a specific temperature range. These thermal events can be, for example, thermoplastic melting or crystallization, or thermoset curing [3]. DSC heat capacity data represent overall (apparent) heat capacities. The net effect of thermal events (i.e., the phase transition enthalpy) is obtained after subtraction of the baseline from the recorded overall heat capacity [3,4,5]. For technical-grade and mixed materials, such as solid/liquid phase change materials (PCM) for thermal energy storages, the phase transition (e.g., melting) can occur over a temperature range rather than at an exact localized temperature (non-isothermal phase change) [6,7,8]. Here, the analysis of the peak shape allows to draw conclusions about the progress of the phase change, e.g., to calculate the degree of conversion as a function of temperature, see, e.g., [3, 4]. For PCM undergoing a solid/liquid phase change, the analysis yields phase fraction–temperature and enthalpy–temperature functions [7, 8].

For dynamic experiments with constant heating (or cooling) rates, the sample is not in thermal equilibrium, and therefore the measured value is not the equilibrium value [1]. Accordingly, it is often found that heat capacity data are highly sensitive to the applied heating and cooling rates and the sample mass [9, 10]. Repeated measurements with increasing heating rates and/or different sample masses deliver considerably different results. Temperature gradients within the sample increase, resulting in a shift of the recorded melting peaks toward higher temperatures. This phenomenon is known as smearing [1, 11]. Ideally, a heating rate close to zero would deliver the most informative output. But a low heating rate has, besides the prolonged experiment duration, a severe disadvantage: Small temperature differences between sample and reference lead to a poor signal-to-noise ratio in the difference of the voltage signals of the thermocouples. On the other hand, elevated heating rates induce strong but smeared signals.

Schawe and Schick [11] define smearing as “falsification [...] of the measured curve by reasons of heat conduction in sample and DSC.” Höhne et al. [1] use the term smearing in the same context to describe circumstances in which the “heat flow rate is falsified (smeared) by the thermal inertia of the measuring system (thermal lag).” Thus, de-smearing is a procedure to correct the DSC measurements for the thermal inertia of the measuring system, such that “the influence of thermal lag is eliminated” [1].

There exist several methods for de-smearing. An established set of textbook methods can be found in chapter 5.4 of [1]. Several groups investigate de-smearing approaches by various techniques for modeling the dominant heat transfer mechanisms in DSC.

Poel and Mathot [12] propose specific calibration procedures for indium (as reference material) to develop a calibration matrix and to derive correction factors for extrapolated onset and peak temperature, which are dependent on the sample mass and the heating rate (see tables 3 and 4 in [12]). Calibration matrix and correction factors are used as black box models to correct for the thermal lag of the extrapolated onset and peak temperature of a measurement at a certain mass and scanning rate.

Franquet, Gibout and co-workers [8, 10, 13] develop physical models mainly based on conductive heat transfer to account for all thermal response effects between sample and DSC apparatus. They use an a priori formulation of the enthalpy based on thermodynamical principles instead of direct extrapolation from the curve and apply a matching between experimental data and theoretical curves, giving demonstrations of their approach for pure substances and binary eutectic mixtures.

Kočí et al. [14, 15] develop a 3D computational model of a DSC sensor rod with crucibles and sample, describing the thermal phenomena in the calorimeter sample, and use it to extract pure sample data. Their approach shows good agreement with known data of aluminum and quartz samples.

A recent publication by Schawe [16] establishes a low-dimensionally parameterized nonlinear relation between measured melting onset temperature and sample mass and heating rate, by using classical models of heat transfer of DSC to describe the thermal lag. This relation is then used to correct the DSC-measured onset temperatures of pure indium.

This contribution

We propose a systematic data-driven approach for the analysis of peak signals and to recover the peak’s shape and derived characteristic quantities like peak initial and peak final temperatures of materials undergoing a phase change.

Heat capacity data are obtained from dynamic heat flux DSC with constant heating rates where the sample is not in equilibrium. To recover quasi-equilibrium values, i.e., values corresponding to a (hypothetical) zero heating rate, we propose a Fokker–Planck-based extrapolation (FPEX$_0$) of recorded peak curves. The resulting peak function, extrapolated to a (hypothetical) zero heating rate, can then be further analyzed to extract relevant thermophysical properties of material under investigation.

The approach is demonstrated on DSC measurements of a technical-grade high-density polyethylene (HDPE) recorded for different sample masses and at multiple heating rates.

Outline of the paper

Section 2 starts with a brief recapitulation of the Fokker–Planck equation (Sect. 2.1), followed by a review of a common procedure for the determination and analysis of (apparent) specific heat capacity data using heat flux DSC (Sect. 2.2). The data are affected by smearing and are the input for the proposed data-driven de-smearing FPEX$_0$ algorithm, which we explain in detail in Sect. 2.3.

Section 3 gives results for heat capacity data of a technical-grade HDPE recorded for different sample masses and at multiple heating rates (Sect. 3.1). Apparent specific heat capacity data are derived and analyzed in Sect. 3.2. The parameterization of the FPEX₀ method is concretized in Sect. 3.3, and relevant numerical algorithms are described in Sect. 3.4. Quantitative results of the FPEX$_0$ de-smearing method are presented and discussed in Sect. 3.5.

Section 4 gives concluding remarks and an outlook. An appendix with additional details on the applied and developed methods closes the paper.

Nomenclature

We consider endothermic phase transition processes, in which the heat of transition (e.g., melting) leads to a (positive) peak in the measured curves.

Throughout the paper, when referring to heat capacity data determined by heat flux DSC, the apparent specific heat capacity (see [2]) is meant, here denoted by $\tilde{c}$. Moreover, the following characteristic terms and definitions are used [1, Section 5.1]:

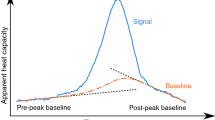
The baseline function or just baseline $f^{{\text{bl}}}$ is the line which, in the range of a peak, is constructed in such a way that it connects the measured heat capacities before and after the peak as if no heat had been exchanged, i.e., as if no heat (peak) had developed. The peak function $f^{{\text{peak}}}$ is obtained by subtracting the baseline from the recorded heat capacity. In endothermic processes as investigated in this paper, the peak begins at ${{T}^{\text{peak}}_{\text{init}}}$ (first deviation from the baseline), ascends to a peak maximum ${T^{\text{peak}}_{\text{max}}}$, and merges into the baseline again at ${T^{\text{peak}}_{\text{final}}}$. The phase transition enthalpy $\Delta h_{\text{t}}$ is calculated by integration of the endothermic peak function.

Several experiment IDs in the form ID 16-xxx are used to name the respective multiple heating rate results; see Table 2 for a list. An overview of frequently used symbols in this paper is given in Table 1.

Table 1 Selected subset of used symbols

Methods and algorithms

We start with some preliminaries, recapitulating the Fokker–Planck equations. An automated method for baseline construction is briefly presented which is used to identify a peak in an apparent specific heat capacity function $\tilde{c}$ and to recover the corresponding peak function $f^{{\text{peak}}}$. The newly proposed de-smearing algorithm FPEX$_0$ uses these peak functions from multiple heating rate DSC measurements as input. The main part of this section proposes the Fokker–Planck-based Extrapolation $(FPEX_{0})$ to a (hypothetical) zero heating rate as a data-driven de-smearing method for heat flux DSC data.

The Fokker–Planck equation: a different view on smearing

Given a probability density function $y(0,x) = y_0(x)$ for an initial time point ${t=0}$, the solution of the Fokker–Planck or Kolmogorov forward equation gives the time evolution of the scalar probability density function y(t, x) that is affected by time-dependent drift $\mu (t)$ and diffusion $D(t)$ [17]:

$$\begin{aligned} \partial _{\text{t y}}(t,x)&;= - \mu (t) \partial _{\text{x y}}(t,x) + D(t) \partial _{{\text{xx}}} y(t,x)\nonumber \\ y(0,x)&;= y_0(x) \qquad t \in [0,t_{{\text{end}}}], ~ x \in \mathbb{R}\end{aligned}$$

(1)

Figure 1 (a) depicts the time evolution of a Gaussian probability density function. The initial density at time ${t=0}$ with mean ${\mu =5}$ and variance ${\sigma ^2=0.25}$ is affected by a linearly increasing drift $\mu (t)$ and a constant diffusion $D$. The linear drift leads to a movement of the peak that is quadratically in time, as shown in Fig. 1(b). Figure 4 shows the peak signals recorded for multiple heating rates for a material undergoing an endothermic phase transition. Identifying the DSC heating rate $\beta$ with time t, and the recorded temperature T with the spatial coordinate x in Eq. 1, the similarity of Figs. 1 and 4 catches the eye. Considering the de-smearing problem for these recorded peak signals, the question rises if an initial distribution $y_0(x)$, corresponding to a hypothetical heating rate of zero, can be determined from the DSC measurement data¹. This question will be addressed in Sect. 2.3.

Fig. 1

a Time evolution of a Gaussian probability density under linear drift and constant diffusion as the solution of the Fokker–Planck Eq. 1. The red dots mark the maxima. b Positions of the drifting maxima in the (x, t)-plane with a quadratic interpolation

Fig. 2

Apparent specific heat capacity $\tilde{c}$ for geometrically graduated heating rates $\beta$ from $0.6\;\text {K}\,\text {min}^{-1}$ to $20\;\text {K}\,\text {min}^{-1}$. The sample is the HDPE RIGIDEX^® HD6070EA undergoing a solid/liquid phase transition in the probed temperature range. The dashed box is zoomed in the upper left small panel. The recorded peaks indicate a significantly extended phase transition temperature range. The effect of smearing prohibits a reasonable determination of peak location and shape parameters. For the two lowest heating rates 0.6 and $1.25\; \text {K}\,\text {min}^{-1}$ , the difference in the peak final temperature is about $1^\circ$C (see detail enlargement). Further visible is the elevated noise level in the low heating rates. The picture shows data from experiment ID 16-407 of a sample with mass 10.47 mg

Determination and analysis of heat capacity data

In a heat flux DSC, a common operating mode is to heat the furnace with a constant heating rate $\beta$ measured in ${{\text{K}\,\text {min}^{-1}}}$ [6]. The DSC signal is then preprocessed for the determination of the apparent specific heat capacity. Applying standard calibration and standard test procedures [1, 6, 18], the voltage signal from the thermocouples is transformed first into a rate of heat flow and second into apparent heat capacity data. Different DSC calibration procedures can be distinguished depending on the aim of the analysis [18]:  (a) the temperature calibration by means of (pure) materials with known melting temperature, e.g., for the determination of the melting onset temperature;  (b) the rate of heat flow calibration (this contribution) using a reference material with a known specific heat capacity for the determination of the sample’s specific heat capacity (see section A);  (c) the heat (or peak area) calibration using a material with a known enthalpy of fusion for the determination of the enthalpy of fusion (the phase transition enthalpy). A detailed review of heat flux DSC and other methods can be found in the compendium [1].

Figure 2 exemplary shows the heat capacity data determined from multiple heating rate DSC measurements. The sample is the commercial technical-grade HDPE RIGIDEX^® HD6070EA, a potential phase change material for the use in a latent heat thermal energy storage [19, 20]. The recorded peaks indicate that the phase transition takes place over an extended temperature range.

Baseline construction

There exist different approaches for baseline construction [1, 4]: formal methods without physicochemical justification, e.g., using straight lines or sigmoidal functions (this contribution), methods with a physicochemical assumption on the change of the heat capacity during transition, e.g., using exponential functions, or the area–proportional baseline method [3, 7, 21], and experimental methods. For polymers, assuming a two-phase system consisting of a crystalline phase and an amorphous phase, an enthalpy-based procedure can be used to calculate temperature-dependent mass crystallinity [22, 23], describing the progress of the phase change from amorphous to liquid state. The baseline is then calculated via the additivity of the heat capacity contributions of the amorphous and crystalline phases using the mass crystallinity as a weighting factor between both ([23], Eq. 4). This, however, requires reference curves for the enthalpies of both, the crystalline part and the amorphous part, which can be taken from databases (if available), or, in case of the liquid enthalpy, can also be obtained by extrapolation of the measured heat capacity from the melt (downwards) if an enthalpy reference value is known. Further methods are described, for example, in [24] and the references therein.

In this contribution, the baseline is constructed based on the principles described in DIN 51007 [5]. Accordingly, the baseline is assumed linear both before and after the phase transition, describing the sensible specific heat capacity. In between these linear parts, a linear interpolation is performed. Different peak shapes might be obtained depending on the selected baseline construction. It is noted that the proposed FPEX$_0$ method, however, does not depend directly on a specific baseline construction method. The algorithm for reconstructing the baseline used in this contribution is given in section B.

Determination of peak function characteristics and phase transition enthalpy

Once the baseline $f^{{\text{bl}}}$ is constructed and the peak initial and peak final temperatures ${{{T}^{\text{peak}}_{\text{init}}}}$ and ${{T^{\text{peak}}_{\text{final}}}}$ are determined, see section B, the peak function is computed by subtracting the baseline from the apparent specific heat capacity $\tilde{c}$ of the sample:

$$\begin{aligned} f^{{\text{peak}}}(T) := \tilde{c}(T) - f^{{{\text {bl}}}}(T) \; . \end{aligned}$$

(2)

The integral over the peak function is then considered² as phase transition enthalpy

$$\begin{aligned} \Delta h_{\text{t}}:= \int _{{{T}^{\text{peak}}_{\text{init}}}}^{{T^{\text{peak}}_{\text{final}}}} f^{{\text{peak}}}(T) \; \mathrm {d}T \,. \end{aligned}$$

(3)

Figures 3 and 4 show the results of the methods described in Sects. 2.2.1 and 2.2.2 applied to multiple heating rate DSC measurements from experiment ID 16-407 depicted in Fig. 5(a).

Data-driven de-smearing: Fokker–Planck-based extrapolation (FPEX$_0$) to a hypothetical zero heating rate

Comparing the time evolution of a Gaussian distribution Fig. 1 with the 3D visualization of the (smeared) heat capacity data in Fig. 4, the qualitative similarities are obvious. However, a Gaussian function is also obviously not suitable to represent the DSC signals depicted in Fig. 2.

Instead, a different initial function corresponding to a hypothetical zero heating rate has to be determined, such that, when used as initial distribution in the Fokker–Planck equation, its propagation fits the computed peak functions for all recorded heating rates.

However, the backward diffusion problem is ill-posed and not solvable without regularization. For that reason, we formulate the initial distribution $y_0(x)$ of the Fokker–Planck equation as a low-dimensionally parameterized function $y_0(x;\,\varvec{p}_{\varvec{0}})$ and try to estimate its parameters $\varvec{p}_{\varvec{0}}$ by fitting its evolution to the experimentally determined smeared peak functions, identifying time t with heating rate $\beta$ and space x with temperature T.

Drift $\mu$ and diffusion $D$ of the Fokker–Planck equation are not necessarily constant (cf. Fig. 4(b)) and are therefore parameterized, e.g., as in Eq. 6. Their parameters are combined with the parameters $\varvec{p}_{\varvec{0}}$ of the initial distribution in the vector $\varvec{p}_{\mathbf{FP }}$. We note that DSC measurements for at least two different heating rates are required to identify the parameters³.

The parameter estimation problem for determining the initial distribution $y_0$ can be written as a least-squares problem:

$$\begin{aligned} \begin{aligned} \min _{y,\,\varvec{p}_{\varvec{0}},\,\varvec{p}_{\mathbf{FP }}}&\mathop { \sum _{i,j} \left\Vert {y(t_{\text{j}},x_{\text{i}}) - f^{{\text{peak}}}(\beta _{\text{j}},T_{\text{i}})}\right\Vert _2^2 } \\ \text {s.t.}\; \partial _{\text{t}} y(t,x)&= - \mu (t;\,\varvec{p}_{\mathbf{FP }}) \partial _{\text{x}} y(t,x) + D(t;\, \varvec{p}_{\mathbf{FP }}) \partial _{\text xx} y(t,x)\\&y(0,x) = y_0(x\,; \varvec{p}_{\varvec{0}}) \qquad t \in [0,\beta _{\text{max}}], x \in \mathbb {R}\end{aligned} \end{aligned}$$

(4)

where $f^{{\text{peak}}}(\beta _{\text{j}},T_{\text{i}})$ denotes the peak function at temperature $T_{\text{i}}$, computed from heat flux DSC measurements with heating rate $\beta _{\text{j}}$.

If additional information about the reliability of the DSC measurements is available, a weighted least squares functional might be more appropriate, e.g., to include information about the signal-to-noise ratio at varying heating rates.

In addition, since many DSC programs are run to deliver data with uniform sampling (in time), the recorded measurement series for low heating rates consist of more data points than the ones with higher heating rates. As a consequence, considering all measurements simultaneously, the regression algorithm puts a stronger focus on the exact fitting of data for lower heating rates. Thus, to not implicitly add a weighting toward low heating rates measurements, it is advisable to restrict the measurement data to a common temperature grid, defined by the measurements generated at the highest heating rate. Since this common grid is solely used for calibrating the FPEX$_0$ parameters, it has no effect on baseline and peak function determination.

As an aside, we note that the Fokker–Planck equation also maintains the integral (i.e., the phase transition enthalpy) over the complete time domain (i.e., for all heating rates).

Results and discussion

The algorithms and methods from Sect. 2 are applied to DSC signals for multiple heating rates and sample masses. The original DSC measurements (voltage signals) are first transformed into heat capacity data, the baseline is constructed, and peak functions are determined (Sect. 2.2). The proposed FPEX$_0$ method is applied to compute the peak function for a (hypothetical) zero heating rate (Sect. 2.3). Shape characteristics are then determined for all peak functions, those from DSC measurements and those extrapolated by FPEX$_0$. The section closes with a discussion of the results.

Fig. 3

Detected baseline (dashed green line) by the algorithm described in Sect. 2.2.1. The dotted box is zoomed in the upper left panel. The peak function $f^{{\text{peak}}}(T)$ is computed as the difference between the apparent specific heat capacity $\tilde{c}(T)$ and the baseline $f^{{bl}}(T)$. ${T}^{{\text{peak}}_{\text{init}}}$ and ${T^{\text{peak}}_{\text{final}}}$ mark the peak initial and peak final temperatures; ${T^{\text{peak}}_{\text{max}}}$ is the peak maximum temperature. The displayed data are from experiment ID 16-407 of a sample with mass 10.47 mg, probed at a heating rate of $5\;\text {K}\,\text {min}^{-1}$

Fig. 4

(a) Computed heat capacity peak functions $f^{{\text{peak}}}$ for several heating rates, depicted in a 3D plot. The red dots mark the respective maximum values.   (b) The positions of the peak maxima in the $(T,\beta )$-plane with a quadratic fit. Note the similarity to the Fokker–Planck propagation of a probability density under drift and diffusion in Fig. 1. The picture shows data from experiment ID 16-407 of a sample with mass 10.47 mg

Heat flux DSC measurements

Heat flux DSC was used to analyze the HDPE RIGIDEX^® HD6070EA, a commercially available technical-grade material (INEOS Europe AG, Rolle, Switzerland). According to the manufacturers’ data sheet, it has a narrow molecular weight distribution. Three samples with masses of 4.08, 6.46, and 10.47 mg have been analyzed; the samples with higher masses have been probed twice. The phase transition was analyzed in a temperature range of $-10^\circ$C to $+160^\circ$C.

All data were generated by heat flux DSC using a Netzsch DSC 204 F1 Phoenix (Erich NETZSCH GmbH & Co. Holding KG, Selb, Germany). The measurement procedure for analysis of solid/liquid PCM developed in the IEA SHC Task 42/ECES Task 29 was used [6]. The samples were probed in aluminum crucibles with pierced lids, and a helium atmosphere was applied.

For each sample, an initial melting was done to eliminate the sample’s thermal history. Constant heating rates of 20, 10, 5, 2.5, 1.25, and 0.6 $\text {K}\,\text {min}^{-1}$ have been applied to the samples in that order. Each heating was followed by a cooling with a fixed rate of $-10\;\text {K}\,\text {min}^{-1}$ and a subsequent isothermal phase of 10 min duration before the next heating cycle was started.

The examined material is a semi-crystalline HDPE. As such, upon cooling from the liquid state it hardly ever reaches a fully crystalline state [23]. Crystalline and liquid/amorphous fractions coexist, the material is not in equilibrium, and phase transitions are rate-dependent [25]. This raises the question, if the studied material reaches the same state after each heating/cooling cycle. If the material is in complete liquid state after heating, and applying exactly the same procedure for all experiments upon subsequent cooling (fixed rate of $-10\;\text {K}\,\text {min}^{-1}$ and isothermal phase of 10 min duration before the next cycle, see above), it can be assumed that the material reaches the same state. The validity of this assumption is supported by the fact that all recorded curves (Figure 5) show a single peak, whose integrals (i.e., enthalpies) are almost the same (approximately 200 $\text {J}\,\text {g}^{-1}$, see Table 3), indicating that there is always the same crystal fraction that melts in the investigated temperature range. We therefore assume that the experimental design is valid for testing FPEX$_0$.

Applying the measurement procedure for the multiple heating rates mentioned above, the analysis of one sample takes approximately 11 h to complete, to which the experiment with the smallest heating rate 0.6 $\text {K}\,\text {min}^{-1}$ attributes approximately 5 h.

Figure 5 shows the recorded melting peaks in a temperature range from 100 to $160^\circ$C; the voltage signal is normalized to sample mass. Elevated heating rates lead to stronger signals; however, they result in heavy smearing.

For the highest heating rate 20 $\text {K}\,\text {min}^{-1}$, due to smearing, the upper temperature bound was not sufficient to record the complete melting process in two of the fives experiments (IDs 16-407 and 16-408); see Fig. 5. The non-identical shapes upon reprobing these samples (16-407 vs. 16-416 and 16-408 vs. 16-417) are probably a consequence of slightly different placement of the sample in the crucible (e.g., slightly more attached to a wall), resulting in an altered heat transfer from the crucible into the sample.

Fig. 5

Multiple heating rate DSC signals displayed in the temperature range from 100 to $160^\circ$C. With increasing heating rates, the phase transition peak curves become broader and their position is shifted toward higher temperatures: smearing

Peak function characteristics and phase transition enthalpy

Figure 2 shows the calculated peak functions of the sample with ID 16-407 by application of the methods described in Sect. 2.2. The original DSC signals are depicted in Fig. 5(a).

For each peak function, two characteristic quantities were determined:  (a) the peak maximum temperature ${T^{\text{peak}}_{\text{max}}}$ at which $f^{{\text{peak}}}$ takes its maximum value

and  (b) the peak final temperature ${T^{\text{peak}}_{\text{final}}}$, i.e., the temperature at which the peak function touches the baseline again. These are listed in Table 2.

In Fig. 2, it can be seen that all peak functions show a prolonged and smooth transition from the initial baseline to the ascending slope of the peak. This is because even for the lowest temperature ($-10^\circ$C) the material is in the semicrystalline state. There is no (clear) beginning of the melting/onset. Consequently, in this contribution, ${{T}^{{\text{peak}}}_{\text{init}}}$ is not considered.

It is reasonable to assume that ${T^{\text{peak}}_{\text{max}}}$ and ${T^{\text{peak}}_{\text{final}}}$ determined for the low heating rate measurements are closer to the (unknown and inaccessible) true values than the quantities computed from the smeared high heating rate signals. The peak final temperature, calculated for all conducted measurements with a heating rate of 0.6  $\text {K}\,\text {min}^{-1}$, seems to be around $133.2^\circ$C, with a standard deviation of approximately 0.3 K.

For increasing heating rates, ${T^{\text{peak}}_{\text{max}}}$ and ${T^{\text{peak}}_{\text{final}}}$ are shifted toward higher temperatures. The shift in ${T^{\text{peak}}_{\text{final}}}$ reaches up to 18 K for the high 10 $\text {K}\,\text {min}^{-1}$ heating rate and still up to 2 to 3 K at the moderate heating rate of 2.5 $\text {K}\,\text {min}^{-1}$. The shift for high and low heating rates in ${T^{\text{peak}}_{\text{max}}}$ is less pronounced, but still reaches up to 12 K; see Table 2.

In addition, Table 3 lists the results for $\Delta h_t$. For the lowest heating rate of 0.6 $\text {K}\,\text {min}^{-1}$, the phase transition enthalpy could not be reliably determined due to an elevated noise level that further complicated the identification of a peak initial temperature used as lower integration limit for peak integration; see Sect. 2.2.2. The mean value lies little below 200 $\text {J}\,\text {g}^{-1}$ with a standard deviation of approximately 5–8 %.

The variation in ${T^{\text{peak}}_{\text{max}}}$ and ${T^{\text{peak}}_{\text{final}}}$ decreases for smaller heating rates (Table 2), whereas for the phase transition enthalpy, an increasing standard deviation is observed (Table 3).

Parameterizations

In this section, we describe and discuss the parameterization choices of the initial distribution function $y_0$ and of the drift $\mu$ and diffusion $D$ functions in the Fokker–Planck Eq. 1.

Parameterization of the initial distribution $y_0(x)$

For this study, we chose as initial distribution a Fraser–Suzuki function [26] which is commonly used to describe the shape of peak signals [27, 28]:

$$\begin{aligned} y_0(x) = {\left\{ \begin{array}{ll} h \cdot \exp \left[ - \frac{\ln r}{\ln ^2 s_{\text{r}}} \cdot \ln ^2 \left( \frac{(x-z)(s_{\text{r}}^2-1)}{w_{\text{r}} s_{\text{r}}} + 1 \right) \right] &{} \text {for}\, x < z - \frac{w_{\text{r}} s_{\text{r}}}{s_{\text{r}}^2-1} \\ 0 &{} \text {for}\, x \ge z - \frac{w_{\text{r}} s_{\text{r}}}{s_r^2-1} \end{array}\right. } \end{aligned}$$

(5)

Note that in this setting, the space variable x in the Fokker–Planck equation is identified with temperature T.

With the choice $r=2$, as done in this study, Eq. 5 becomes essentially a log-normal distribution, scaled by a factor h that corresponds to $\Delta h_{\text{t}}$. The parameter z has a direct interpretation: It describes the peak maximum position (i.e., the temperature ${T^{\text{peak}}_{\text{max}}}$) at which the function $y_0(x)$ (i.e., the initial zero-heating-rate peak function) is maximal. The remaining shape parameters $w_{\text{r}}$ and $s_{\text{r}}$ characterize the narrowness of the peak and the skewness to the left. The peak final temperature ${T^{\text{peak}}_{\text{final}}}$ can be directly identified from Eq. 5 as $z - \frac{w_{\text{r}} s_{\text{r}}}{s_{\text{r}}^2-1}$.

We note that other functions may also be used as candidates for the initial distribution at zero heating rate, e.g., the Haarhoff–Van der Linde function, which has been successfully applied in peak shape modeling in chromatography [29] and capillary electrophoresis [30], a linear combination of Gaussians, low-dimensional superpositions of linear, trigonometric, or other basic functions, or also scaled and time-stretched (interpolated) measurement data, the latter requiring some special treatment if a derivative-based numerical solver for the regression problem in Eq. 4 is to be applied.

Parameterization of Fokker–Planck drift $\mu (t)$ and diffusion $D(t)$

Figure 4(b) shows the positions of the peak maxima ${T^{\text{peak}}_{\text{max}}}$ for different heating rates from experiment ID 16-407. If the drift had been constant in time, the peak maximum temperatures would have laid on a straight line, which is not the case. Indeed, the peak maximum temperatures can be approximately interpolated by a quadratic function, implying a linear drift in the Fokker–Planck equation. Similarly, the broadening of the peak functions increases with higher heating rates, suggesting also a linear parameterization of the diffusion in the Fokker–Planck Eq. 1:

$$\begin{aligned} \mu (t; \,\varvec{\varvec{p}_{\mathbf{FP }}})&= p_1^\upmu + t\cdot p_2^\upmu \nonumber \\ D(t; \,\varvec{\varvec{p}_{\mathbf{FP }}})&= p_1^{\text{D}}+ t\cdot p_2^{\text{D}}\end{aligned}$$

(6)

A drift in direction of increasing temperatures suggests $\mu (t; \,\varvec{\varvec{p}_{\mathbf{FP }}}) > 0$ for all $t \in [0,\beta _{\text{max}}]$. Negative drifts are also admissible and might be observed in cooling experiments. On the other hand, for well-posedness, a nonnegative diffusion is mandatory for all $t \in [0,\beta _{\text{max}}]$. This requirement can either be imposed by adding $D(t; \,\varvec{\varvec{p}_{\mathbf{FP }}}) \ge 0$ as constraint to the optimization problem in Eq. 4 if a suitable solver is at hand, or by choosing a slightly different parameterization; see Eq. 9. Note that putting nonnegativity constraints on $p_1^{\text{D}}$ and $p_2^{\text{D}}$ is too restrictive, as this would not allow a decreasing (but positive) diffusion.

Numerical integration and solution of the parameter estimation problem

The Fokker–Planck partial differential Eq. 1 is transformed into a system of ordinary differential equations using a method of lines discretization with central differences in the space variable.

For numerical treatment, it is necessary to restrict the space coordinate x (corresponding to temperature) to an interval $[T_{\text{min}}, T_{\text{max}}]$ and to impose adequate boundary conditions, e.g., Dirichlet conditions ${y(t,T_{\text{min}}) = y(t,T_{\text{max}}) = 0}$ or Neumann conditions of zero flux ${\frac{\partial {y}}{\partial {x}}(t,T_{\text{min}}) = \frac{\partial {y}}{\partial {x}}(t,T_{\text{max}}) = 0}$. The integration domain must be chosen sufficiently large such that the solution of the Fokker–Planck Eq. 1 is neither affected by the size of the integration domain nor by the boundary conditions. In other words, the nonzero parts of the initial and propagated densities should not touch the bounds. For initial peak functions $y_0(x)$ with local support, this can always be achieved by choosing the temperature integration domain sufficiently large.

For numerical integration, the software package SolvIND [31] was used. It includes the variable stepsize variable-order BDF integrator DAESOL-II and uses the principles of internal numerical differentiation [32], propagation of Taylor coefficients and automatic differentiation (AD) for efficient and accurate computation of first- and higher-order sensitivities that are exact up to machine precision w.r.t. the integration scheme.

We denote the discrete solution of the parameter estimation problem in Eq. 4 by $y(t_{\text{j}}, x_{\text{i}}; \,\varvec{p})$, with $\varvec{p} = ( \varvec{p}_{\varvec{0}}^{\text{T}}\!, \varvec{p}_{\mathbf{FP }}^{\text{T}}\!\,)^{\text{T}}\!$ consisting of the possibly time-dependent Fokker–Planck drift and diffusion parameters $\varvec{p}_{\mathbf{FP }}$ (Eqs. 6,9) and the parameters $\varvec{p}_{\varvec{0}}$ of the initial distribution $y_0$ (Eq. 5).

The application of efficient derivative-based solution methods to the fitting problem in Eq. 4 requires the computation of exact derivatives of the discrete solution of the Fokker–Planck model in Eq. 4 w.r.t. the regression variables, i.e., the following derivatives have to be computed:

$$\begin{aligned} \frac{{\mathrm {d}y}}{\mathrm {d}\varvec{p}_{\mathbf{FP }}} \qquad \text {and} \qquad \frac{{\mathrm {d}y}}{\mathrm {d}\varvec{p}_{\varvec{0}}} = \frac{\partial {y}}{\partial {y_0}} \frac{{\mathrm {d}y_0}}{\mathrm {d}\varvec{p}_{\varvec{0}}} \;. \end{aligned}$$

(7)

The sensitivities $\frac{\partial {y}}{\partial {y_0}}$ of the discretized Fokker–Planck solution w.r.t. the initial distribution and the sensitivities $\frac{d{y}}{d{\varvec{p}_{\mathbf{FP }}}}$ w.r.t. to the drift and diffusion parameters are computed by the numerical integrator. The derivative $\frac{d{y_0}}{d{\varvec{p}_{\varvec{0}}}}$ of the initial distribution w.r.t. to its parameterization $\varvec{p}_{\varvec{0}}$ is computed analytically for the Fraser–Suzuki parameterization that is given in Eq. 5.

The solution of the inverse (fitting) problem in Eq. 4 yields estimates for the parameters of  (a) the initial distribution $\varvec{p}_{\varvec{0}}$ and  (b) the Fokker–Planck drift and diffusion functions $\varvec{p}_{\mathbf{FP }}$.

Using Fraser–Suzuki as initial distribution Eq. 5 and the linear parameterization of drift and diffusion in Eq. 6, the parameter vector of the fitting problem reads as

$$\begin{aligned} \varvec{p} := \left( r, h, z, w_{\text{r}}, s_{\text{r}}, p_1^\upmu , p_2^\upmu , p_1^{\text{D}}, p_2^{\text{D}}\right) ^{\text{T}}\!\end{aligned}$$

(8)

The Fraser–Suzuki parameter r has been fixed to the value of $r=2$, effectively transforming Eq. 5 into a scaled log-normal density.

The nonlinear regression problem has been solved using the nonlinear least squares solver lsqnonlin of MATLAB R2017a, implementing a subspace trust region method based on an interior-reflective Newton method [33]. Since lsqnonlin can only handle bound constraints on the optimization variables, instead of the straightforward parameterization of the diffusion in Eq. 6, we use

$$\begin{aligned} D(t; \,\varvec{p}_{\mathbf{FP }}) = p_1^{\text{D}}+ t \cdot \frac{p_2^{\text{D}}-p_1^{\text{D}}}{\beta _{{\text{max}}}} \end{aligned}$$

(9)

as parametrrization. Note that, in contrast to Eq. 6, for this reformulation it is sufficient to impose nonnegativity constraints on $p_1^{\text{D}}$ and $p_2^{\text{D}}$ in order to describe (linearly) increasing and decreasing diffusion that stays nonnegative everywhere in $t \in [0, \beta _{\text{max}}]$.

The solver converged to a local minimum within a few iterations.

Data-driven de-smearing by FPEX$_0$

Fig. 6

a Data-driven de-smearing (FPEX$_0$) applied to multiple heating rate DSC signals for ID 16-407 with heating rates 0.6, 1.25, 2.5, 5, and $10\;\text {K}\,\text{{min}}^{-1}$. The peak function at a hypothetical zero heating rate is parameterized as a Fraser–Suzuki function, Eq. 5. Its propagation based on the Fokker–Planck Eq. 1 is depicted as colored “landscape.” (b) Reconstructed initial function $y_0$, i.e., the peak function $f^{{\text{peak}}}$ extrapolated to a (hypothetical) zero heating rate

The subject of the FPEX$_0$ method proposed in Sect. 2.3 is to overcome the smearing effect and reconstruct the shape of the peak function for a (hypothetical) zero heating rate, which allows to extract characteristic peak properties.

This effectively overcomes the problem of a deteriorating signal-to-noise ratio that tends to zero for heating rates approaching zero.

Figure 6 exemplary shows the results for multiple heating rate DSC measurements recorded at 0.6, 1.25, 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$ (displayed as solid lines). The surface in Fig. 6(a) shows the propagation of the extrapolated peak function by solution of the Fokker–Planck equation. The reconstructed zero rate function (black solid line at heating rate $\beta = 0$) is also displayed in Fig. 6(b).

Getting high-quality DSC signals for low heating rates poses high demands on the DSC operation. Unavoidable in any case is the prolonged time demand. Thus, in the following, we test our method using only the DSC measurements made with the intermediate heating rates 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$.

Tables 2 and 3 list the peak temperatures ${T^{\text{peak}}_{\text{max}}}$, the peak final temperatures ${T^{\text{peak}}_{\text{final}}}$, and the phase transition enthalpy $\Delta h_{\text{t}}$ of the extrapolated peak functions in the column marked with FPEX$_0$. The quantities directly computed from the DSC measurements are listed for comparison.

For the peak temperature ${T^{\text{peak}}_{\text{max}}}$, the Fokker–Planck extrapolation to a zero heating rate delivers an estimate almost identical to the result for the lowest heating rate of 0.6 $\text {K}\,\text {min}^{-1}$: $131.62^\circ$C (FPEX$_0$) vs. $131.6^\circ$C (measurements), with the same level of accuracy: a standard deviation over the five experiment series of approximately 0.2 K.

For the peak final temperature ${T^{\text{peak}}_{\text{final}}}$, however, the FPEX$_0$ de-smearing consistently delivers estimates approximately 0.5 K below the 0.6 $\text {K}\,\text {min}^{-1}$ heating rate measurements. The FPEX$_0$ method determines a mean value of $133.02^\circ$C, whereas the measurements of 0.6 $\text {K}\,\text {min}^{-1}$ heating rate lead to an estimate of $133.5^\circ$C, with the same level of accuracy as for the peak maximum temperature: a standard deviation of approximately 0.2 K.

Table 2 Characteristic temperatures determined directly from DSC measurements and estimated using FPEX$_0$. Values in the FPEX$_0$ column are obtained by extrapolation of the peak function to a zero heating rate, using only measurements for the intermediate heating rates 2.5, 5, and $10\;\text {K}\,\text {min}^{-1}$, marked by an asterisk$^*$. For heating rate $20\;\text {K}\,\text {min}^{-1}$, in the higher mass samples, the peak final temperature was not attained at the upper limit temperature due to smearing (cf. Fig. 5); estimated values are given in parentheses

The FPEX$_0$ results using the complete set of measurements of each sample with heating rates 0.6, 1.25, 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$ are listed in Table 4. For ${T^{\text{peak}}_{\text{max}}}$, a mean value of $131.65^\circ$C with a small sample standard variation of 0.17 K is estimated, lying approximately at the same value as the results for the 0.6 $\text {K}\,\text {min}^{-1}$ measurements (see Table 2). The peak final temperature ${T^{\text{peak}}_{\text{final}}}$ is estimated to be $132.6^\circ$C with a small sample standard deviation of 0.11 K, thus approximately $0.9^\circ$C below the respective values determined from the 0.6 $\text {K}\,\text {min}^{-1}$ measurements. We thus consider the FPEX$_0$ method delivering reasonable approximations of the true sample properties. An important observation is that the FPEX$_0$ peak maximum and peak final temperatures are independent from the sample mass.

For completeness, the phase transition enthalpies have been computed by integrating the respective peak functions $f^{\text{peak}}$. The values of the phase transition enthalpy estimated by FPEX$_0$ is relatively close to the value obtained directly from the DSC measurements, with the exception of the 0.6 $\text {K}\,\text {min}^{-1}$ measurements, due to the elevated noise level that prevented a reliable determination of the onset temperature. The FPEX$_0$ mean value stays close to the results computed solely from measurement data (with the mentioned exception) with approximately the same accuracy of 5%.

A visual comparison between the 0.6 $\text {K}\,\text {min}^{-1}$ measurements and the FPEX$_0$ extrapolation to a hypothetical zero heating rate is depicted in Figure 7. In the left column (I), the FPEX$_0$ extrapolation was generated using the full set of measurements, i.e., for heating rates 0.6, 1.25, 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$. In the right column (II), only data from heating rates 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$ were used. Using the limited set of measurements for calibration, (II), the extrapolated peak tends to underestimate the peak height, while for the full set (I), the extrapolated peak tends to be slightly sharper which can be explained by a small smearing effect in the 0.6 $\text {K}\,\text {min}^{-1}$ curve, compared with Figure 6 left. In both cases, the extrapolated peak maximum temperature ${T^{\text{peak}}_{\text{max}}}$ and the peak final temperature ${T^{\text{peak}}_{\text{final}}}$ are 0.1 to 0.5 K below the measured (and smeared) quantities (cf. table 2, 4 for numerical values), which is consistent with a de-smearing approach.

Fig. 7

Comparison between FPEX$_0$ extrapolation $y_0$ (black) to a hypothetical zero heating rate and measured peak curves $f^{{\text{peak}}}$ (red) for heating rate $0.6\;\text {K}\,\text {min}^{-1}$. The left column (I) shows the FPEX$_0$ extrapolations generated using DSC data with heating rates 0.6, 1.25, 2.5, 5, and $10\;\text {K}\,\text {min}^{-1}$. The right column (II) shows the FPEX$_0$ extrapolation generated using DSC data solely with heating rates 2.5, 5, and $10\;\text {K}\,\text {min}^{-1}$

Table 3 Phase transition enthalpy $\Delta h_t$, determined directly from DSC measurements and estimated using FPEX$_0$. Values in the FPEX$_0$ column are obtained by extrapolation of the peak function to a zero heating rate, using only measurements for the intermediate heating rates 2.5, 5, and $10\;\text {K}\,\text {min}^{-1}$, marked by an asterisk$^*$. For heating rate $20\;\text {K}\,\text {min}^{-1}$, in the higher mass samples, the peak final temperature was not attained at the upper limit temperature due to smearing (cf. Figure 5); estimated values are given in parentheses. The varying values at heating rate $0.6\;\text {K}\,\text {min}^{-1}$ are caused by an elevated noise level that prevented to reliably determine the peak initial temperature

Table 4 Results for FPEX$_0$ using the full set of multiple heating rate DSC measurements (0.6 to $10\;\text {K}\,\text {min}^{-1}$). The peak maximum temperature, the peak final temperature, and, for consistency, the phase transition enthalpy are given for the extrapolated zero heating rate peak functions. The values of the estimated phase transition enthalpies are significantly affected by the deteriorated signal-to-noise ratio in the $0.6\;\text {K}\,\text {min}^{-1}$ measurements

Conclusions and outlook

We have presented a data-driven de-smearing method that extrapolates peak signals collected at intermediate heating rates to a hypothetical zero heating rate. The so-called FPEX$_0$ approach uses a Fokker–Planck-based extrapolation, interpreting temperature as space and heating rate as time. Multiple heating rate DSC data are simultaneously used to estimate the parameters of an initial scaled probability distribution that is propagated in time while being affected by drift and diffusion. Effectively, the method acts as a black box model for compensating thermal lag and other (non-equilibrium) thermodynamic effects and reconstructs shape information of DSC signals from smeared measurements.

The proposed FPEX$_0$ method is applied to DSC measurements from a technical-grade HDPE, considering data recorded for three heating rates, i.e., 2.5, 5, and 10 $\text {K}\,\text {min}^{-1}$. The results indicate that FPEX$_0$ delivers reasonable approximations of the true sample properties, here the peak maximum and peak final temperatures. An important observation is that these temperatures are independent from the sample mass. Moreover, the propagated peak functions maintain the phase transition enthalpy.

From its design, the proposed data-driven de-smearing algorithm FPEX$_0$ is not limited to solid/liquid phase transitions. Its application to DSC signals containing other thermal events like glass transition, oxidation, or other reactive processes, however, has to be investigated on appropriate sample substances. The effect of heating rate-dependent changes in the (specific) heat capacity can be addressed by adding a heating rate-dependent source (or sink) term to the Fokker–Planck Eq. 1.

By visual inspection of the recovered 3D landscape, a consistency check of multiple heating rate measurement campaigns can be performed. This can also be automated by testing the residuals (i.e., the difference between the propagated FPEX$_0$ and the measurements at the respective heating rates) for extraordinary deviations.

Further studies may be interesting in the direction of automatic selection of a best fitting candidate function out of a set of existing functions (model discrimination) to parameterize the initial peak function $y_0$ for the zero heating rate in the FPEX$_0$ method, in order to yield quantitatively sound results for the data at hand. Particularly, the usage of thermophysically inspired and low-dimensionally parameterized functions, like the enthalpy functions in [10] (equation (18)), as a substitute of the heuristic Fraser–Suzuki parametrrization Eq. 5 for the extrapolated zero heating rate seem promising.

Appendices

Appendix A: Determining apparent specific heat capacity

According to DIN EN ISO 11357-4:2021-05 [34], the specific heat capacity of the sample $c_{\text{p}}^{\text{S}}$ can be computed by scaling the known specific heat capacity $c_{\text{p}}^{\text{R}}$ of a reference substance, e.g., sapphire. In our setting:

$$\begin{aligned} c_{\text{p}}^{\text{S}}(T) := c_{\text{p}}^{\text{R}}(T) \cdot \frac{m^{\text{R}}}{m^{\text{S}}} \cdot \frac{\Phi ^{\text{S}}(T) - \Phi ^0(T)}{\Phi ^{\text{R}}(T) - \Phi ^0(T)} \end{aligned}$$

(A1)

where $m^{\text{R}}$ and $m^{\text{S}}$ denote the masses of reference and sample, $\Phi^{\text{S}}$ is the rate of heat flow into the sample, $\Phi^{\text{R}}$ gives the rate of heat flow into the reference (determined by putting the reference material in the sample crucible and letting the other crucible empty), and $\Phi ^0$ is the rate of heat flow determined in a blank measurement with two empty crucibles.

Appendix B: Baseline construction

In this section, we present an automated way to reconstruct a baseline curve, following the methods in DIN 51007. The baseline is constructed by three continuous linear segments. We limit the discussion to the automatic detection of the left linear part, i.e., belonging to temperatures below the peak maximum. It is then straightforward to adapt the algorithm to detect the right linear part.

Let $T_i \in [{T_{start}}, {T^{peak}_{max}}]$ denote the temperatures at which a measurement has been taken, and let $c_{\text{p}}(T_{\text{i}})$ be the respective specific heat capacities. ${T_{\text{start}}}$ denotes the temperature to start the analysis of the data recording and ${T^{\text{peak}}_{\text{max}}}$ the temperature at which $c_{text{p}}(T)$ takes its maximum value.

As an initial guess for the (left) linear part, a linear regression is done on the first, say, $n_0$ data points⁴${c_{\text{p}}(T_{\text{i}})~(i=1,...,n_0)}$, delivering an initial left linear baseline function $f^{\text{L}}_0(T) = a_0 T + b_0$. The noise level on this initial interval $[{T_{\text{start}}}, T_{\text{n}_0}]$ can be quantified by the unbiased sample variance $\sigma ^2_0$ of the residuals:

$$\begin{aligned} \sigma ^2_0 := \frac{1}{n_0-1} \sum _{i=1}^{n_0} (r_{\text{i}} - \bar{r})^2 , \quad r_{\text{i}} := c_{\text{p}}(T_{\text{i}}) - f^{L}_0(T_{\text{i}}) , \quad \bar{r} := \frac{1}{n_0} \sum _{i=1}^{n_0} r_{\text{i}} \end{aligned}$$

(B1)

To detect how far this linear part extends, further linear regressions are repeatedly calculated by sequentially appending the respective next data point to the problem, thus solving Eq. B1 for $n_0 + k$ with $k=1,2,3,...$ . By this, a series of regression coefficients $a_{\text{k}}, b_{\text{k}}$ and unbiased sample variances $\sigma ^2_{\text{k}}$ are generated. These coefficients are monitored for a sufficient deviation⁵ from the initial estimates ${a_0, b_0, \sigma ^2_0}$. If this happens at the $\hat{k}$th linear regression, then the measurement at $T^{\text{L}}_{\text{max}}:= T_{{\text{n}}_0+\hat{\text k}}$ marks the end point of the left linear part.

The linear part of the right-hand side is detected analogously from a mirrored perspective. If we write $f^{\text L}(T)$ and $f^{\text R}\;(T)$ for the left and right linear baseline functions determined by the algorithm above and denote by $T^{\text L}_{\text{max}}$ and $T^{\text R}_{\text{min}}$ the respective stopping temperatures, then the complete baseline function $f^{{\text{bl}}}(T)$ is finally constructed as the continuous piecewise linear function

$$\begin{aligned} f^{{\text{bl}}}(T) := {\left\{ \begin{array}{ll} f^{\text L}(T)\;&{} \text {if }\; T \le T^{\text L}_{\text{max}}\\ f^{\text L}(T^{\text L}_{\text{max}}) + \frac{f^{\text R}(T^{\text R}_{\text{min}})-f^{\text L}(T^{\text L}_{\text{max}})}{T^{\text R}_{\text{min}}- T^{\text L}_{\text{max}}}\cdot (T-T^{\text L}_{\text{max}})&{} \text {if }\; T^{\text L}_{\text{max}}< T < T^{\text R}_{\text{min}}\\ f^{\text R}(T) &{} \text {if }\; T \ge T^{\text R}_{\text{min}}\end{array}\right. } \end{aligned}$$

(B2)

i.e., in the phase transition range, the baseline is linearly interpolated between left and right linear baseline.

An efficient algorithm for calculation and updating the linear regressions is found in [35]. This algorithm requires that sufficiently many measurements before and after the phase transition are available, as the calculation of the initial linear part must not contain measurements from within the phase transition temperature range.

The constructed quantities $T^{\text L}_{\text{max}}$ and $T^{\text R}_{\text{min}}$ can be interpreted as preliminary estimates for the peak initial and peak final temperatures ${{{T}^{\text{peak}}_{\text{init}}}}$ and ${{T^{\text{peak}}_{\text{final}}}}$. Especially due to noise in recorded DSC measurement, they are not necessarily identical. Once the baseline is constructed, ${{{T}^{\text{peak}}_{\text{init}}}}$ and ${{T^{\text{peak}}_{\text{final}}}}$ are determined according to the definition in [1]: ${{{T}^{\text{peak}}_{\text{init}}}}$ is the temperature at which the measured values begin to deviate from the baseline, and ${{T^{\text{peak}}_{\text{final}}}}$ is the temperature at which the measured values reach again the baseline.