Improvement of cooling performance of hybrid nanofluids in a heated pipe applying annular magnets

Abstract

In this paper, convective heat transfer of Fe₃O₄–carbon nanotubes (CNTs) hybrid nanofluid was studied in a horizontal small circular tube under influence of annular magnets. The pipe has an inner diameter of 3 mm and a length of 1.2 m. Heat transfer characteristics of the Fe₃O₄–water nanofluid were examined for many parameters, such as nanoparticle volume fraction in the range of 0.4–1.2% and Reynolds number in the range of 476–996. In order to increase the thermal conductivity of the Fe₃O₄–water nanofluid, carbon nanotubes with 0.12–0.48% volume fraction were added into the nanofluid. It was observed that for the Fe₃O₄–CNTs–water nanofluid with 1.44% volume fraction and under a magnetic field, the maximal local Nusselt number at the Reynolds number 996 increased by 61.54% compared with without a magnetic field. Results also show that compared with the deionized water, the maximal enhancements of the average Nusselt number are 67.9 and 20.89% for the Fe₃O₄–CNTs–water nanofluid with and without magnetic field, respectively.

Introduction

With increasing serious problems of global environmental pollution and energy shortages, energy conservation and environmental protection have become important themes of common concern in the world. Heat transfer efficiency in heat exchange systems is needed to be enhanced to effectively save energy. However, traditional fluids have low thermal conductivity, which is difficult to meet heat transfer requirements under some special conditions. One focus of heat transfer studies is how to find a novel heat transfer fluid to replace the traditional fluid for the improvement of the heat transfer efficiency. In the past 20 years, numerous researchers have studied heat transfer characteristics of various nanofluids. Usually, the nanofluid shows significant improvement in heat transfer performance of conventional fluids water, glycol, oil, and etc. Ali et al. [1] performed heat transfer performance of ZnO–water nanofluid in a car radiator with ranges of Reynolds numbers, volume fractions, and inlet temperatures of 7500–27,600, 0.01–0.3% and 45–55 °C, respectively. Results indicated that when the volume fraction of the nanofluid was 0.2%, the heat transfer performance of the car radiator was 46% higher than base fluid. Sajid et al. [2] studied heat transfer of a mini-channel heat sinks filled with TiO₂–water nanofluid. Results indicated that 0.012 vol.% TiO₂–water nanofluid showed a maximum enhancement of 40.57% in Nusselt number compared to water at Re = 894. Ebrahimi et al. [3] investigated heat transfer performance of Al₂O₃–water and CuO–water nanofluids in a rectangular microchannel heat sink by changing nanoparticle volume fractions, sizes and Reynolds numbers. They found that heat transfer efficiency and pressure loss of CuO–water nanofluid was higher than those of Al₂O₃–water nanofluid at the same conditions. Shanbedi et al. [4] examined the thermal conductivity of multi-walled carbon nanotubes–water nanofluid. Their results demonstrated that the thermal conductivity of the metal nanoparticles-decorated carbon nanotubes nanofluid was higher than that of gum Arabic decorated carbon nanotubes nanofluid. Zheng et al. [5] investigated effects of magnetic fields on flow characteristics and thermal performance of a plate heat exchanger filled with a magnetic nanofluid. They found that appropriate magnet arrangement resulted in good thermal performance and low flow resistance simultaneously. Kumar and Chandrasekar [6] analyzed heat transfer performance of multiwall carbon nanotube–water nanofluids in a double helically coiled tube heat exchanger, and they found that 35% heat transfer was enhancement is obtained for the 0.6 vol.% MWCNT–water nanofluid at a Dean number of 1200. Dabiri et al. [7] experimentally studied heat transfer characteristics of SiC–water and MgO–water nanofluids inside a circular tube. Results showed that an increase in heat transfer enhancement was observed by increasing volume concentration and Reynolds number. Sarafraz et al. [8] experimentally investigated convective heat transfer of carbon nanotube–water nanofluid inside a double pipe heat exchanger, and their results revealed that by adding 0.3 mass% carbon nanotubes into the base fluid, the thermal conductivity was enhanced by at most 56%. Hosseinipour et al. [9] investigated the effect of surfactants on heat transfer and pressure drop of multi-walled carbon nanotubes (MWCNT)–water nanofluids in a circular tube. They found that the MWCNT- water nanofluid with arginine showed better heat transfer performance than that with gum Arabic at the same concentrations.

Magnetic nanofluids have been widely used in different fields, such as thermal engineering [10] (heat exchanger, solar collector, air conditioning system, etc.), bioengineering and optical [11] and sealing technology. The magnetic nanofluid has remarkable potential for heat transfer applications because heat transfer process can be controlled by varying the strength and orientation of the magnetic field. Wang et al. [12] showed a large enhancement in convective heat transfer by using Fe₃O₄–water nanofluid in a stainless steel pipe under a permanent magnetic field. Fe₃O₄–water nanofluid with a magnetic cannula showed heat transfer enhancements of 26.5% and 54.5% at Re = 391 and 805, respectively. Hosseinzadeh et al. [13] analyzed heat transfer and friction factor of Fe₃O₄–water nanofluids in a horizontal circular tube under a magnetic field. It was observed that a heat transfer enhancement of 15.43% was obtained by applying a magnetic field (200 G). Goharkhah et al. [14] analyzed heat transfer and pressure drop of Fe₃O₄–water nanofluid in a parallel plate channel under an alternating magnetic field. They observed that the maximum heat transfer enhancement of 37.34% was attained by application of alternating magnetic field. Asfer et al. [15] studied heat transfer characteristics of a magnetic nanofluid in a circular pipe. They found that increasing the gradient of the magnetic field improved heat transfer. Li and Xuan [16] studied the heat transfer characteristics of magnetic nanofluids exposed to a magnetic field. They concluded that applying a uniform magnetic field opposite to the flow direction reduced the heat transfer coefficient of the magnetic nanofluid.

Hybrid nanofluids are prepared by dispersing various types of nanoparticles into a base fluid. It is found that hybrid nanofluids show enhancements of heat transfer performance and improvements of thermophysical properties compared with conventional fluids. Many scholars numerically and experimentally carried out heat transfer analysis of hybrid ferrofluids under an external magnetic field. Shahsavar et al. [17] investigated heat transfer in a heated pipe filled with a Fe₃O₄–carbon nanotubes (CNTs) hybrid nanofluid. They concluded that 0.5 vol% Fe₃O₄ and 1.35 vol% CNTs hybrid nanofluid showed a maximum enhancement of 62.7% in the local Nusselt number, compared with water at Re = 2190. Harandi et al. [18] analyzed the thermal conductivity of Fe₃O₄–carbon nanotubes–ethylene glycol (EG) hybrid nanofluid, and found that the thermal conductivity of the nanofluid was enhanced by 30% at 50 °C and 2.3% volume fraction. Askari et al. [19] investigated thermal characteristics of a Fe₃O₄-graphene nanofluid. It was observed that compared to the base fluid, the thermal conductivity of the nanofluid was enhanced up to 32% at 1% mass fraction and 50 °C. Askari et al. [20] measured the effect of hybrid Fe₃O₄-graphene nanoparticles on the thermal conductivity of water. Results revealed that a maximum increase of 31% of the thermal conductivity was achieved for 1 mass% nanoparticle concentration at 50 °C. Nadooshan et al. [21] examined the viscosity of Fe₃O₄–MWCNTs–ethylene glycol hybrid nanofluid in a temperature range of 25–50 °C and various solid volume fractions (0.1, 0.25, 0.8, 1.25 and 1.8%). Results showed that the examined hybrid nanofluid exhibited a Newtonian behavior, and higher volume fraction of the nanofluid resulted in higher viscosity. Farbod and Ahangarpour [22] investigated thermal conductivity of a MWCNTs–Ag–water nanofluid in a temperature range of 20–50 °C. It was found that compared with the MWCNTs–water nanofluid, the MWCNTs-Ag–water nanofluid with 4% Ag had a maximum enhancement of 20.4% in thermal conductivity.

The available studies on the heat transfer performance of the magnetic nanofluids have mainly focused on a single species of particles under a magnetic field. This means that the existing experimental data is insufficient for evaluation of heat transfer performance of hybrid magnetic nanofluids in a heat transfer system. This paper aims to investigate laminar convective heat transfer of Fe₃O₄–water and Fe₃O₄–CNTs–water nanofluids in a straight stainless steel pipe in presence of a magnetic field. Effects of the layout of magnets, Reynolds number and nanoparticle volume fraction on heat transfer characteristics of various nanofluids are analyzed by the experimental tests.

Experimental

Particle characterization, ferrofluid preparation and stability

In the present research, Fe₃O₄ nanoparticles were prepared by chemical coprecipitation method, and multi-wall carbon nanotubes (MWCNTs) were provided by Chengdu Organic Chemicals Co. Ltd., Chinese Academy of Sciences. These CNTs have a true density of 2.1 g cm⁻³ [21], outer diameter of 8–15 nm, with a purity of more than 99.9%. Using transmission electron microscopy (TEM) and scanning electron microscopy (SEM), micrographs of the nanoparticles Fe₃O₄ and CNTs are shown in Fig. 1. It is observed that the nanoparticle Fe₃O₄ has an average diameter of 15 ± 5 nm.

Fig. 1

Images of two nanoparticles using TEM and SEM

The photographs of Fe₃O₄–water and Fe₃O₄–CNTs–water nanofluids are provided in Fig. 2. Carbon nanotubes (CNTs) were chemically functionalized by potassium persulfate solution with pH = 13 at 85 °C. CNTs and surfactants were weighed by an electronic balance. The CNTs with surfactants were mixed into distilled water. The mixed solution was stirred by a mechanical stirrer at 1500 r min⁻¹ and dispersed by an ultrasonic cleaner for 60 min. The power and frequency of the ultrasonic cleaner were 380 W and 40 kHz, respectively. Fe₃O₄ magnetic nanoparticles and trisodium citrate dehydrate (TSC) with a ratio of 8:1 were used to synthesize a magnetic nanofluid. The CNTs and Arabic gum with a mass ratio of 5:1 were dispersed into the Fe₃O₄–water nanofluid. Zeta potentials of samples were measured using a ZS-90 zeta potential analyzer (Malvern Co., Ltd., UK). The stability of the nanofluid can be evaluated by measuring the zeta potential of the nanofluid. When the zeta potential value of the nanofluid is higher than 30 mV, it is considered that the nanofluid has a better stability. The zeta potentials of the 1.2% Fe₃O₄–water and 1.32% Fe₃O₄–CNTs–water nanofluids are − 31.6 ± 7.4 mV and − 30.8 ± 6.94 mV, respectively, which indicate that these nanofluids have good dispersion stability. Sedimentation of nanoparticles is investigated in a silicone pipe with a length of 20 cm, an outer diameter of 5 mm, and an inner diameter of 3 mm. The 1.2% Fe₃O₄–water and 1.44% Fe₃O₄–CNTs–water nanofluids are kept at experimental operation for two hours. In order to obtain high accuracy of the experimental data, the tests are repeated 5 times. For the 1.2% Fe₃O₄–water and 1.44% Fe₃O₄–CNTs–water nanofluids, the mass of the silicone tube before and after the tests increased by 0.12 and 0.13% (average value) respectively. The results reveal that a little sedimentation appears for the Fe₃O₄–CNTs–water nanofluid during the tests. Figure 3 presents the zeta potential distributions of the two nanofluids. Table 1 shows density (ρ), thermal conductivity (k), dynamic viscosity (μ) and specific heat (C_p) of the base fluid and nanoparticles.

Fig. 2

Real photographs of nanofluids

Fig. 3

Zeta potential distributions

Table 1 Physical properties of the base fluid and nanoparticles at 25 °C

Viscosities of the nanofluids are obtained using a Brookfield DV2T viscometer. According to Fig. 4, it is revealed that the viscosity is directly proportional to the volume concentration of nanoparticles. Compared with distilled water, the average viscosity of 1.68 vol% Fe₃O₄–CNTs–water nanofluid is increased by 109.6%. Figure 5 shows the viscosity of the two nanofluids as a function of shear rate at 25 °C. The viscosities of the Fe₃O₄–water nanofluid and the deionized fluid are almost constant with increasing shear rate, which indicates a Newtonian fluid behavior For the Fe₃O₄–CNTs–water nanofluid, an increase of the shear rate results in a reduction of the viscosity, showing a non-Newtonian behavior of shear thinning. Generally, it is considered that the shear thinning behavior is caused due to a reduction of suspended particle clusters under shear force.

Fig. 4

Dynamic viscosity of various nanofluids as function of temperature (shear rate of 73.38 s⁻¹)

Fig. 5

Dynamic viscosity of nanofluids as function of shear rate

Apparatus

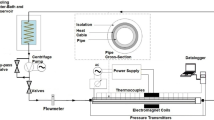
Figure 6 shows a schematic and physical diagram of the experimental system, which consists of a pump, a flow meter, a heat exchanger, a thermostatic bath, and a test section. The test section is a straight stainless steel pipe with a length of 1.2 m, an inner diameter of 3 mm, and an outer diameter of 4 mm. Wall temperature on the pipe is measured by nine T-type thermocouples with a diameter of 0.3 mm. The bulk temperatures at inlet and outlet of the test section are measured by two T-type armored thermocouples with a diameter of 1 mm. The temperature measurements of the mercury thermometer (accuracy of 0.1 °C) are used to calibrate the thermocouples. Uncertainty of temperature measurements after calibration is 0.1 °C. The thermocouple wires are directly welded on the test section to avoid any thermal resistance between thermocouples and test section. Temperature values are monitored by thermocouples connected to a 20-channel data acquisition unit. A constant heat flux for the pipe is supplied by a DC power of 0–150 W. The test section is wrapped with thermal insulation materials to minimize heat losses. A gear pump (WT3000-1JA) is used to circulate the nanofluid. In order to measure the flow rate, a turbine flowmeter of Titan 803 (Beijing Dongfang New Power Mechanical & Electrical Equipment Co., Ltd.) with a flow rate range of 0.05–0.5 L min⁻¹ is installed downstream the pump. The flowmeter is calibrated by weighing with a high-precision electronic balance. After calibration, the uncertainty of the flowmeter is 1%. A thermostatic bath maintains a constant inlet temperature of the fluid. A simple copper coil pipe cools down the outflow fluid downstream the test section.

Fig. 6

The used experimental system

Magnet arrangement

Geometry information of magnets and cannulas are presented in Fig. 7. Forced convective heat transfer in the pipe is investigated by changing the number of the magnets as in the previous research [12]. The cannulas are used to generate various magnetic fields perpendicular to the test section. Figure 8 shows three arrangements of cannulas under non-uniform permanent magnetic fields, i.e., case I, case II and case III. Data of the magnets is summarized in Table 2.

Fig. 7

Dimensions of a cannula (mm)

Fig. 8

Three magnet arrangements

Table 2 Data of permanent magnets

Analysis of experimental data

Nusselt number (Nu) is defined by:

$$ {\text{Nu}} = \frac{{hD_{{\text{i}}} }}{k} $$

(1)

where k is thermal conductivity of the fluid at 25 °C. D_i is inner diameter of a stainless steel pipe. h in Eq. (1) is the local heat transfer coefficient and calculated as:

$$ h = \frac{{q^{^{\prime\prime}} }}{{T_{{{\text{w}},{\text{i}}}} \left( x \right) - T_{{\text{b}}} \left( x \right)}} $$

(2)

where the variable x is the axial distance from the inlet of the stainless steel pipe, and q′′ is the heat flux. The fluid temperature T_b(x) is obtained by the following equation:

$$ T_{{\text{b}}} \left( x \right) = \frac{{q^{^{\prime\prime}} \pi D_{{\text{o}}} }}{{\rho QC_{{\text{p}}} }}x + T_{{{\text{in}}}} $$

(3)

where Q and ρ are volume flow rate and density of the working fluid, respectively. Due to the small inner diameter (3 mm) and a uniform heating of the pipe, the wall heat conduction along the axial direction is ignored and the heat conduction in the circumferential direction is uniform. Therefore, the heat conduction in the tube wall is approximated as a one-dimensional heat transfer problem with an internal heat source along the radial direction. The inner wall temperature T_w,i (x) is given by:

$$ T_{{{\text{w}},{\text{i}}}} \left( x \right) = T_{{{\text{w}},{\text{o}}}} \left( x \right) - \frac{\alpha VI}{{2\pi K_{{\text{w}}} L}}\left[ {\frac{{D_{{\text{o}}}^{2} }}{{D_{{\text{o}}}^{2} - D_{{\text{i}}}^{2} }}\log \left( {\frac{{D_{{\text{o}}} }}{{D_{{\text{i}}} }} - 0.5} \right)} \right] $$

(4)

where K_w and D_o are thermal conductivity and outer diameter of the stainless steel pipe, respectively.

The heat flux q′′ is calculated as:

$$ q^{^{\prime\prime}} = \frac{\alpha VI}{{\pi D_{{\text{o}}} L}} $$

(5)

where L is the length of the stainless steel pipe. I and V are the given current and voltage, respectively. Based on a series of thermal equilibrium tests using deionized water, the thermal efficiency is determined to be 0.93 ± 0.015. The thermal efficiency α of the test section is calculated by:

$$ \alpha = \frac{{Q_{{\text{m}}} c_{{\text{p}}} (T_{{{\text{in}}}} - T_{{{\text{out}}}} )}}{VI} $$

(6)

where Q_m is the mass flow rate. The density ρ_ff, specific heat C_p,_ff and thermal conductivity k_ff of the hybrid nanofluid are calculated as shown in Ref. [23]:

$$ \rho_{{{\text{ff}}}} = \varphi_{1} \rho_{1} + \varphi_{2} \rho_{2} + (1 - \varphi )\rho_{{{\text{bf}}}} $$

(7)

$$ (\rho c_{{\text{p}}} )_{{{\text{ff}}}} = \varphi_{1} (\rho c_{{\text{p}}} )_{1} + \varphi_{2} (\rho c_{{\text{p}}} )_{2} + (1 - \varphi )(\rho c_{{\text{p}}} )_{{{\text{bf}}}} $$

(8)

$$ \frac{{k_{{{\text{ff}}}} }}{{k_{{{\text{bf}}}} }} = \frac{{\varphi_{1} k_{1} + \varphi_{2} k_{2} + 2\varphi k_{{{\text{bf}}}} + 2\varphi (\varphi_{1} k_{1} + \varphi_{2} k_{2} ) - 2\varphi^{2} k_{{{\text{bf}}}} }}{{\varphi_{1} k_{1} + \varphi_{2} k_{2} + 2\varphi k_{{{\text{bf}}}} - \varphi (\varphi_{1} k_{1} + \varphi_{2} k_{2} ) + \varphi^{2} k_{{{\text{bf}}}} }} $$

(9)

The viscosity of the hybrid nanofluid (μ_ff) is obtained as follows [24]:

$$ \mu_{{{\text{ff}}}} = \mu_{{{\text{bf}}}} \left( {1 + 2.5\varphi } \right) $$

(10)

The total volume concentration (φ) of nanoparticles Fe₃O₄ and CNTs is obtained by:

$$ \varphi = \varphi_{1} + \varphi_{2} $$

(11)

where subscripts 1, 2, p and bf represent physical properties of the Fe₃O₄–water nanofluid, CNTs–water nanofluid, nanoparticles and the base fluid, respectively.

To evaluate the enhancement of heat transfer by using the hybrid nanofluid, average Nu (based on measurements of 9 thermocouples on the test section) and the increased value of the average Nu are introduced as

$$ {\text{Nu}}_{{{\text{avg}}}} = \frac{{\sum\nolimits_{{\text{i}} = 1}^{9} {{\text{Nu}}_{\text{i}} } }}{9} $$

(12)

$$ \eta = \frac{{{\text{Nu}}_{{{\text{avg}},{\text{ff}}}} - {\text{Nu}}_{{{\text{avg}},{\text{bf}}}} }}{{Nu_{{{\text{avg}},{\text{bf}}}} }} $$

(13)

Uncertainty analysis

Uncertainties of measurements are summarized in Table 3. The viscosity measurements (Brookfield DV2T viscometer) have an accuracy of 1%. The accuracy of the thermocouples after calibration is 0.1 °C. The voltage and current values used in the tests are 2.85 ± 0.1 V and 18.25 ± 0.01 A, respectively. According to the uncertainty analysis of the experimental results described in Ref. [25], the maximum uncertainty of the parameter R is calculated as

$$ {\text{Max}}.\;U_{\text{R}} = \pm \sqrt {\left( {\frac{{s_{1} }}{R}\frac{\partial R}{{\partial s_{1} }}U_{{{\text{s}}_{1} }} } \right)^{2} + \left( {\frac{{s_{2} }}{R}\frac{\partial R}{{\partial s_{2} }}U_{{{\text{x}}_{2} }} } \right)^{2} + \cdots + \left( {\frac{{s_{\text{n}} }}{R}\frac{\partial R}{{\partial s_{\text{n}} }}U_{{{\text{s}}_{\text{n}} }} } \right)^{2} } $$

(14)

where U_R is the maximum error of the parameter R. s is measurable parameter, and U_s is measured error. The maximum uncertainties of V, I, q, Re, h and Nu are determined by:

$$ U_{{\text{V}}} = \pm \frac{0.1}{{2.85}} = \pm 0.03509 $$

(15)

$$ U_{{\text{I}}} = \pm \frac{0.01}{{18.25}} = \pm 5.479 \times 10^{ - 4} $$

(16)

$$ {\text{Max}}.\;U_{{\text{q}}} = \pm \sqrt {\left( {U_{{\text{I}}} } \right)^{2} + \left( {U_{{\text{V}}} } \right)^{2} } = \pm 3.51\% $$

(17)

$$ {\text{Max}}.\;U_{{{\text{Re}}}} = \pm \sqrt {\left( {U_{\rho } } \right)^{2} + \left( {U_{Q} } \right)^{2} + \left( {U_{{D_{i} }} } \right)^{2} + \left( {U_{\mu } } \right)^{2} } = \pm 3.62\% $$

(18)

$$ {\text{Max}}{.}\;U_{{\text{h}}} = \pm \sqrt{ \left( {U_{{C_{{\text{p}}} }} } \right)^{2} + \left( {U_{\rho } } \right)^{2} + \left( {U_{{\text{Q}}} } \right)^{2} + \left( {U_{{T_{{{\text{out}}}} - T_{{{\text{in}}}} }} } \right)^{2} + \left( {U_{{D_{i} }} } \right)^{2} + \left( {U_{{\text{L}}} } \right)^{2} + \left( {U_{{T_{{\text{w}}} - T_{{\text{b}}} }} } \right)^{2}} { = } \pm 8.99\% $$

(19)

$$ {\text{Max}}{.}\;U_{{{\text{Nu}}}} = \pm \sqrt {\left( {U_{{\text{h}}} } \right)^{2} + \left( {U_{{D_{i} }} } \right)^{2} + \left( {U_{{\text{k}}} } \right)^{2} } { = } \pm 9.59\% $$

(20)

Table 3 Uncertainties of the measured variables

Therefore, the uncertainties of q, Re, h and Nu are ± 3.51, ± 3.62, ± 8.99, and ± 9.59%, respectively.

Results and discussion

Simulation analysis of Magnetic field

The software COMSOL Multiphysics 5.2 has been used to simulate the magnetic flux density and magnetic force distribution for three cases as shown in Fig. 8. The magnetic flux density and the magnetic force distribution are calculated as in https://www.comsol.com and Ref. [26]:

$$ \mathop B\limits^{ \to } = \mu_{0} \mu_{{\text{r}}} \mathop H\limits^{ \to } + \mathop {B_{{\text{r}}} }\limits^{ \to } $$

(21)

$$ \mathop {F_{{\text{M}}} }\limits^{ \to } = V_{{\text{P}}} \frac{{\chi_{\text{i}} }}{{\mu_{0} }}\mathop B\limits^{ \to } \nabla \mathop B\limits^{ \to } $$

(22)

where H is the magnetic field, and B_r is the residual magnetic flux density. B is the magnetic flux density. μ₀ is the magnetic permeability of the free space, and μ_r is the relative permeability. V_p is the nanoparticle volume, and χ_i is the magnetic susceptibility of the magnetite nanoparticles. The magnetic flux density of unsaturated ferromagnetic material lags behind the magnetic field intensity, which is called a phenomenon of hysteresis. When the magnetic field intensity drops to zero, the corresponding magnetic flux density B is called the remnant magnetic flux density (B_r).

The reliability of the present simulated results is validated by comparisons with results in Ref. [27]. In Fig. 9, it is found that the simulation results show good agreement with the results of reference [27].

Fig. 9

Comparison of simulated magnetic flux densities with results in Ref. [29]

The geometric structure in the case I is shown in Fig. 10a. The tube diameter and magnet size in the numerical simulations are consistent with the experimental structure as shown in Fig. 7. A cross section of the pipe (80 mm) near the magnets is used for simulations. The grid independence study is conducted using 0.86, 1.68 and 3.15 million grid cells as shown in Fig. 10b. By comparing the magnetic flux density along the center line of the pipe in the case with 3.15 million cells, it is found that the case with the 1.68 million cells shows almost no difference. So, the 1.68 million cells are used in this research.

Fig. 10

The details of geometry and grid

In order to investigate the effect of magnetic field strength, two magnets packaged in a cannula were placed outside the pipe. Figure 11 shows distributions of magnetic flux density (B) on cross planes (Section A–A) through the pipe centerline for case I (one cannula), case II (two adjacent cannulas) and case III (three adjacent cannulas). B between magnets for case I shows a symmetric distribution. The magnetic flux density (B) and magnetic force (F_m) along the center line of the pipe are shown in Fig. 12. The magnetic force along the centerline of the pipe has a similar periodic distribution.

Fig. 11

Magnetic flux density distribution on cross plane (A–A) through pipe centerline for three cases

Fig. 12

Magnetic flux density components (B, B_x) and magnetic force (F_mx) along the center line of the pipe for three cases

The maximum values of B exist near the edges of the magnets as shown in Figs. 11 and 12. It is also proved that large F_m exist at the edges of the magnets (dashed line in Fig. 12) based on a direct relation between magnetic flux density gradient and F_m from Eq. (22). It can be found that the peak values of B for two adjacent cannulas (case II) and three adjacent cannulas (case III) are higher than that for the one cannula (case I).

The B distributions of the magnetic flux density for one cannula, two cannulas and three cannulas show two extremum values, four extremum values and six extremum values, respectively. The maximum values of B and F_m (case II) along the centerline of the pipe are 166.9 mT and 3.68 × 10^–17 N, respectively. For case III, the maximum values of B and F_m along the centerline of the pipe are 167.8 mT and 3.63 × 10^–17 N, respectively. It is found that the maximum magnetic force hardly changed in these three cases.

Validation of test data

In order to verify the reliability of the experimental results, an experimental validation is conducted at various Re numbers (476, 663 and 996) by using DI-water as the working fluid. The reliability of the experimental data is analyzed based on the results in Fig. 13. It is found that a good agreement between the present experimental data and theoretical values (The error is less than 10%) calculated by Eq. (23) in Ref. [28]:

$$ {\text{Nu}} = \left\{ {\begin{array}{ll} {1.302\left( {\frac{{x/{\text{D}}_{\text{i}} }}{{{\text{Re}}\;{\text{Pr}}}}} \right)^{ - 1/3} - 0.5} &\quad {0.00005 \le \frac{{x/{\text{D}}_{\text{i}} }}{{{\text{Re}}\;{\text{Pr}}}} \le 0.0015} \\ {4.364 + 0.263\left( {\frac{{x/{\text{D}}_{\text{i}} }}{{{\text{Re}}\;{\text{Pr}}}}} \right)^{ - 0.506} {\text{e}}^{{ - 41\left( {\frac{{x/{\text{D}}_{\text{i}} }}{{{\text{Re}}\;{\text{Pr}}}}} \right)}} } &\quad {\frac{{x/{\text{D}}_{\text{i}} }}{{{\text{Re}}\;{\text{Pr}}}} > 0.0015} \\ \end{array} } \right. $$

(23)

Fig. 13

Nu comparison between test results and calculated values from Eq. (23)

Equation (23) is suitable for laminar convective heat transfer under constant heat flux boundary conditions. This equation is widely used to verify reliability of an experimental system [17, 27].

Magnetic nanofluid without magnetic field

Without a magnetic field, Fig. 14 presents the average Nu of Fe₃O₄–water nanofluids and Fe₃O₄–CNTs–water hybrid nanofluids at various Re numbers. It is observed that for these nanofluids, the average Nusselt number is higher than that for the base fluid. Moreover, results indicate that the average Nu of the magnetic nanofluid increases with increases both in Re and nanoparticle volume fraction. The average Nu of the Fe₃O₄–water nanofluids with volume fractions of 0.4, 0.8 and 1.2% are 1.96, 4.23 and 5.69% higher than that of the base fluid at Re = 476, respectively. When the Reynolds number is increased to 996, the average Nusselt numbers for the 0.4, 0.8 and 1.2% nanofluids are 3.65, 9.54 and 13.34% higher than that of the base fluid, respectively. For the Fe₃O₄–CNTs–water hybrid nanofluid with 1.32, 1.44 and 1.68% volume fractions, the average Nusselt number increases by 7.66–14.73%, 10.3–17.57% and 12.56–20.89% compared to the base fluid under the Reynolds number of 476–996, respectively. These data indicate that the mixture with a small amount of carbon nanotubes can improve the heat transfer performance of the Fe₃O₄–water nanofluid.

Fig. 14

Average Nusselt numbers for magnetic nanofluids with various volume concentration and Reynolds numbers

Fe₃O₄–water nanofluid with magnetic field

For the case I, case II and case III at Reynolds numbers of 476, 663 and 996, Figs. 15–17 show local Nusselt numbers of Fe₃O₄–water nanofluids with three volume fractions (0.4, 0.8 and 1.2%) along the dimensionless x axial coordinate (X/D_i). For the 0.4 vol% Fe₃O₄–water nanofluid, the local Nusselt number (Nu) reaches its maximum value nearly at the thermocouple number T7 for case I and case II. For case III, the maximum value of Nu moves from thermocouple number T7 to T8, as the Re increases. For the case III at the same position, the maximum values of local Nusselt numbers for three cases are 31.16, 34.93 and 47.04% higher than the results without magnetic field at the Reynolds numbers of 476, 663 and 996, respectively. It is found that the presence of the magnetic field results in an enhancement of the convective heat transfer coefficient for all cases at three Reynolds numbers, and three cannulas provides a nearly 50% enhancement of heat transfer. From the temperature values at the position T9, it is concluded that the heat transfer enhancement is increasing with the increase of the number of magnets, Reynolds number and nanoparticle concentration.

Fig. 15

Variation of Nusselt number vs. dimensionless distance (X/D_i) for 0.4 vol% Fe₃O₄–water nanofluid in three cases

For the 0.8 vol% Fe₃O₄–water nanofluid as shown in Fig. 16, the Nusselt number reaches its maximum value at thermocouple numbers T5–T6. It is found that with the magnetic field, the maximum values of local Nu for case I, case II and case III are 33.16, 37.36 and 42.85% higher than those without a magnetic field at the same position, respectively.

Fig. 16

Variations of Nusselt number vs. dimensionless distance (X/D_i) for 0.8 vol% Fe₃O₄–water nanofluid in three cases

Based on a similar analysis for the 1.2 vol% Fe₃O₄–water nanofluid as shown in Fig. 17, the maximal value of local Nu increases by 39.81, 53.73, and 61.13% for case I, case II and case III, respectively. This is because nanoparticle aggregation has a great effect on enhancement of convective heat transfer. The quantity of aggregated particles on the inner wall of the pipe is rising with the increase of the volume fraction and the intensity of the magnetic field. Larger local thermal conductivity exists near the position of the magnets due to the effect of the magnetic force. In addition, the aggregation of magnetic nanoparticles destroys the wall boundary layer, which enhances the heat transfer near the pipe wall.

Fig. 17

Variations of Nusselt number vs. dimensionless distance (X/D_i) for 1.2 vol% Fe₃O₄–water nanofluid in three cases

Fe₃O₄–CNTs–water nanofluid with magnetic field

For cases I-III at Reynolds number of 476, 663 and 996, Figs. 18–20 show Nusselt number distributions of Fe₃O₄–CNTs–water hybrid nanofluids with three volume fractions (1.32, 1.44 and 1.68%) along the dimensionless x axial coordinate (X/D_i). It is observed that Nusselt number for cases without magnetic field decreases along the x axial direction, whereas Nusselt number significantly increases when a magnetic field is applied to the hybrid nanofluids. For all the Reynolds numbers and with all the volume fractions, the Nusselt number reaches its maximum value at thermocouple positions T6, T6 and T7 for case I, case II and case III, respectively. Compared with the 1.32 vol% Fe₃O₄–CNTs–water nanofluid (1.2% Fe₃O₄ + 0.12% CNTs) at the same position and under no magnetic field, the maximum Nusselt number under three magnetic cannulas increases by 52.57, 56.64 and 59.86% at Reynolds numbers of 476, 663 and 996, respectively.

Fig. 18

Variations of Nusselt number vs. dimensionless distance (X/D_i) for 1.32 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.12% CNTs) nanofluid in three cases

Fig. 19

Variations of Nusselt number vs. dimensionless distance (X/D_i) for 1.44 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.24% CNTs) nanofluid in three cases

Fig. 20

Variations of Nusselt number vs. dimensionless distance (X/D_i) for 1.68 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.48% CNTs) nanofluid in three cases

For the 1.44 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.24% CNTs) nanofluid at the same position, compared with cases I-III without a magnetic field, it is found that Nusselt numbers of the hybrid nanofluids are improved by 45.57, 54.51 and 61.54%, respectively. For the 1.68 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.48% CNTs) nanofluid at the same position, it is found that Nu of the hybrid nanofluid can be improved by 32.79%, 48.74% and 56.88%, compared with cases I-III under no magnetic field, respectively. It is also revealed that Nu of hybrid nanofluid with higher volume fraction increases with increasing Re and quantity of cannulas.

As shown in Ref. [29], for the Fe₃O₄–CNTs–water hybrid nanofluids, a magnetic force changes the distribution and array of the magnetic nanoparticles and the carbon nanotubes, which results in an increased contact area between magnetic nanoparticles and nanotubes. In addition, nanoparticles CNTs and Fe₃O₄ under a magnetic field tend to migrate toward the pipe wall. The nanoparticle aggregation will intensify the disturbance of the thermal boundary layer. It is expected that local heat transfer of Fe₃O₄–CNTs–water hybrid nanofluid is higher than for the Fe₃O₄–water nanofluid due to both higher thermal conductivity and destroyed thermal boundary layer.

Table 4 shows improvements of the maximum Nusselt number for cases with various volume fractions and three Reynolds numbers, after three magnetic fields are applied. It is easily found that for the Fe₃O₄–water nanofluid, the increase in the number of cannulas results in an enhancement of heat transfer.

Table 4 Comparisons of the maximum Nusselt number for various nanofluids with and without magnetic field

For the 1.32 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.12% CNTs) nanofluid, the maximum enhancement of the local Nusselt number is higher than for 1.2 vol% Fe₃O₄–water nanofluid in most cases. This result shows that adding a small amount of multi-walled carbon nanotubes into the Fe₃O₄–water nanofluid can significantly improve the convective heat transfer in the pipe. This finding is also shown in a study about plate heat exchangers [30]. However, the enhancement in heat transfer for the 1.68 vol% Fe₃O₄–CNTs–water nanofluid is smaller than for the 1.2 vol% Fe₃O₄–water nanofluid in all cases. The reason might be that the viscosity of the 1.68 vol% Fe₃O₄–CNTs–water nanofluid under magnetic field is higher than that of 1.2 vol% Fe₃O₄–water nanofluid, which weakens heat transfer in the pipe. It is easily found that compared with cases under no magnetic field, the increase in the maximum Nusselt number is provided by the 1.44 vol% Fe₃O₄–CNTs–water (1.2% Fe₃O₄ + 0.24% CNTs) hybrid nanofluid under a magnetic field (only exception for two cannula case at Re = 996).

Improvements of the average Nusselt number for various nanofluids are plotted in Fig. 21. Enhancements for the magnetic cases, volume fractions and Reynolds numbers are shown. Results indicate that without a magnetic field the heat transfer increases with volume fractions and Re. When a magnetic field is applied to the pipe (case I, case II and case III), an optimum volume fraction (1.44 vol% Fe₃O₄–CNTs–water nanofluid) is obtained for each Reynolds number to achieve the maximum heat transfer enhancement. Heat transfer enhancements for the 1.44 vol% Fe₃O₄–CNTs–water nanofluid with a single magnetic cannula (case I) by 26.6, 31.99 and 34.85% are found at Re = 476, 663 and 996, respectively. Compared with the 1.44 vol% Fe₃O₄–CNTs–water nanofluid with double magnetic cannulas (case II), the average Nusselt number enhancement at the Reynolds number of 663 is higher than at the Reynolds number of 996. It is found that the maximum improvement of 67.9% of heat transfer is achieved by a dispersion of 1.44 vol% nanoparticles inside the DI-water at high Reynolds number with three magnetic cannulas (case III).

Fig. 21

Nu enhancement of various magnetic nanofluids vs. Reynolds number and volume concentration

Conclusions

In this study, various volume fractions of nanoparticles Fe₃O₄ and carbon nanotubes (CNTs) were used to improve the thermophysical properties of the base fluid. Heat transfer characteristics of a Fe₃O₄–CNTs–water hybrid nanofluid in a heated straight pipe were experimentally investigated and compared with Fe₃O₄–water nanofluid under magnetic field arrangement and for various Reynolds numbers.

For the 1.2 vol% Fe₃O₄–water nanofluid, the maximal values of the local Nusselt number increased by 39.81, 53.73, and 61.13% for cases with one cannula, two cannulas and three cannulas, respectively. Compared with Fe₃O₄–water nanofluid without magnetic field, the heat transfer performance can be significantly improved by increasing the number of magnetic cannulas. When 0.12% carbon nanotubes are added into 1.2% Fe₃O₄–water nanofluid, the maximum enhancement of the local Nusselt number is increased. Compared with cases under no magnetic field, a nanofluid with 1.2% Fe₃O₄ nanoparticles and 0.24% carbon nanotubes shows the maximum Nusselt number under a magnetic field in most cases.

The presence of the magnetic field improves the convective heat transfer in the pipe due to the increase in thermal conductivity, the enhancement of turbulence, and the disturbance of the thermal boundary layer. The hybrid magnetic nanofluid might be a potential cooling medium for further enhancement of the heat transfer performance.