Skip to main content
SpringerLink
Log in

Numerical study on performance enhancement of a square enclosure with multiple hot circular obstacles

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

Abstract

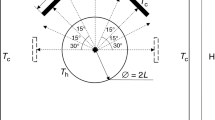
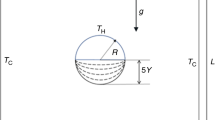
Heat dissipation from thermal enclosures is critical for their endurance and efficiency. Through geometry optimization under natural convection, we can cost-effectively obtain maximum heat dissipation. Hence, the present study numerically investigates the flow and heat transfer characteristics of two hot circular bodies in a 2D simulation. By considering and reviewing several works of literature, a modification has been done, i.e., two cylinders are considered inside an enclosure with one of them at a fixed position and the other one at three different positions (considered as three different cases). So, the fluid (air) movement around the body has been increased and helps in appreciable heat transfer from the body. Our primary concern is as to how the utilization of this geometry will impact the heat transfer rate which we have quantified in terms of Nusselt and Rayleigh numbers. The most optimum configuration is when one of the obstacles is inclined at the top of the enclosure concerning the other which is vertically symmetric, and this orientation gives an increase of 28.09% in terms of the heat transfer, and when two obstacles are considered inline is when we can witness least favorable conditions. In this orientation, a decrease of 70.08% is observed when compared to the most optimum condition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig.1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Abbreviations

T h :

Hot wall temperature (°C)

T c :

Cold wall temperature (°C)

L:

Characteristic Length (m)

g:

Gravitational Pull (m/s2)

d:

Diameter of the obstacle (m)

Nu:

Nusselt number

Ra:

Rayleigh number

C p :

Pressure Coefficient

p :

Static pressure at the point where pressure coefficient is being measured

p ∞ :

Free stream static pressure

p ○ :

Free stream stagnation pressure

ρ ∞ :

Free stream fluid density

V ∞ :

Free stream fluid velocity

Cf :

Skin Friction coefficient

τ w :

Skin shear stress on the surface

ρ :

Fluid density

v :

Free stream fluid velocity

h:

Convective heat transfer coefficient (w/k.m2)

k:

Thermal conductivity (w/k.m)

v:

Kinematic Viscosity (m2/s)

β :

Thermal expansion coefficient (k−1)

α :

Thermal diffusivity (m2/s)

T:

Surface temperature (K)

T∞ :

Bulk mean temperature (K)

U:

Average velocity magnitude (m/s)

U* :

Non-Dimensional Velocity

W:

Vorticity Magnitude (1/s)

W* :

Non-Dimensional Vorticity

BC:

Bottom Center

BL:

Bottom Left

BR:

Bottom Right

UL:

Upper Left

UR:

Upper Right

References

  1. Sarris IE, Lekakis I, Vlachos NS. Natural convection in a 2D enclosure with sinusoidal upper wall temperature. Num Heat Trans A. 2002;42:513–30.

    Article  Google Scholar 

  2. Lee JM, Ha MY, Yoon HS. Natural convection in a square enclosure with a circular cylinder at different horizontal and diagonal locations. Int J Heat Mass Trans. 2010;2010(53):5905–19.

    Article  Google Scholar 

  3. Garrpeters JM. The neutral stability of surface-tension driven cavity flows subject to buoyant forces 1. Transverse and longitudinal disturbances, Chem Eng Sci. 1992;47(5):1247–64.

    Article  CAS  Google Scholar 

  4. Sadeghipour S, Asheghi M. Free convection heat transfer from arrays of vertically separated horizontal cylinders at low Rayleigh numbers. Int J Heat Mass Trans. 1994;37(1):103–9.

    Article  CAS  Google Scholar 

  5. Marcel L, Antoine J. Coupling of wall conduction with natural convection from heated cylinders in a rectangular enclosure. Int Commun Heat Mass Trans. 1996;23(1):143–51.

    Article  Google Scholar 

  6. Bahrami T, Safikhani HR. Heat transfer enhancement inside an eccentric cylinder with an inner rotating wall using porous media: a numerical study. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09532-y.

    Article  Google Scholar 

  7. Asan H. Natural convection in an annulus between two isothermal concentric square ducts. Int Commun Heat Mass Trans. 2000;27:367–76.

    Article  Google Scholar 

  8. Kim BS, Lee DS, Kim LS, Ha MY. A numerical study of natural convection in a square enclosure with a circular cylinder at different vertical locations. Int J Heat Mass Trans. 2008;51:1888–906.

    Article  CAS  Google Scholar 

  9. Afzal A, Samee M, Abdul Razak AD. Effect of spacing on thermal performance characteristics of Li-ion battery cells. J Therm Anal Calorim. 2019;135:1797–811.

    Article  CAS  Google Scholar 

  10. Bhowmick D, Randive PR, Pati S. Natural convection heat transfer and entropy generation from a heated cylinder of different geometry in an enclosure with non-uniform temperature distribution on the walls. J Therm Anal Calorim. 2020;141:839–57.

    Article  CAS  Google Scholar 

  11. Tetsu F, Fujii M, Matsunaga T. A numerical analysis of laminar free convection around an isothermal horizontal circular cylinder. Num Heat Trans. 1979;2(3):329–44.

    Google Scholar 

  12. Bilgen E, Natural convection in enclosures with partial partitions, Renewable Energy

  13. Dutta S, Goswami N, Pati S. Natural convection heat transfer and entropy generation in a porous rhombic enclosure: influence of non-uniform heating. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09634-7.

    Article  Google Scholar 

  14. Girish N, Sankar M, Reddy K. Analysis of fully developed mixed convection in open-ended annuli with viscous dissipation. J Therm Anal Calorim. 2019. https://doi.org/10.1007/s10973-019-09120-9.

    Article  Google Scholar 

  15. Littlefield D, Desai P. Buoyant laminar convection in a vertical cylindrical annulus. J Heat Trans ASME. 1986;108(4):814–21.

    Article  CAS  Google Scholar 

  16. Lee JR, Ha MY, Balachandar S. Natural convection in a horizontal fluid layer with a periodic array of internal square cylinders-need for very large aspect ratio 2D domains. Int J Heat Fluid Flow. 2007;28(5):978–87.

    Article  CAS  Google Scholar 

  17. Pishkar I, Ghasemi B, Raisi A. Numerical study of unsteady natural convection heat transfer of Newtonian and non-Newtonian fluids in a square enclosure under oscillating heat flux. J Therm Anal Calorim. 2019;138:1697–710.

    Article  CAS  Google Scholar 

  18. Ho CJ, Wang CC. Natural convection between two horizontal cylinders inside a circular enclosure subjected to external convection. Int J Heat Flow. 1994;15(4):299–306.

    Article  CAS  Google Scholar 

  19. Basak T, Roy S, Pop I. Heat flow analysis for natural convection within trapezoidal enclosures based on heat line concept. Int J Heat Mass Trans. 2009;52(11):2471–83.

    Article  CAS  Google Scholar 

  20. Minea AA. Numerical studies on heat transfer enhancement in different closed enclosures heated symmetrically. J Therm Anal Calorim. 2015;121:711–20.

    Article  CAS  Google Scholar 

  21. Rabhi M, Bouali H, Mezrhab A. Radiation–natural convection heat transfer in inclined rectangular enclosures with multiple partitions. Ener Conver Manag. 2009;49:1228–36.

    Article  Google Scholar 

  22. Fusegi T, Hyun JM, Kuwahara K. Natural convection in a differentially heated square cavity with internal heat generation. Num Heat Trans A. 1992;21:215–29.

    Article  Google Scholar 

  23. Seyyedi SM, Ghadakpour M, Bayat M. CVFEM modeling of fluid flow induced by convective heat transfer from a hot pipe buried in soil. J Therm Anal Calorim. 2020. https://doi.org/10.1007/s10973-020-09906-2.

    Article  Google Scholar 

  24. Kim M, Doo JH, Park YG, Yoon HS, Yeong HM. Natural convection in a square enclosure with a circular cylinder according to the bottom wall temperature variation. J Mech Sci-Tech. 2014;28(12):5013–25.

    Article  Google Scholar 

  25. Corvaro F, Paroncini M, Sotte M. Experimental PIV and interferometric analysis of natural convection in a square enclosure with partially active hot and cold walls. Int J Therm Sci. 2011;50(9):1629–38.

    Article  Google Scholar 

  26. Shadlaghani A, Farzaneh M, Shahabadi M. Numerical investigation of serrated fins on natural convection from concentric and eccentric annuli with different cross-sections. J Therm Anal Calorim. 2019;135:1429–42.

    Article  CAS  Google Scholar 

  27. Paroncini M, Corvaro F, Montucchiari A, Nardini G. A numerical and experimental analysis on natural convective heat transfer in a square enclosure with partially active sidewalls. Exp Therm and Fluid Sci. 2012;36:118–25.

    Article  Google Scholar 

  28. Yuan X, Tavakkoli F, Vafai K. Analysis of natural convection in horizontal concentric annuli of varying inner shape. Num Heat Trans Part A: App. 2015;68(11):1155–74.

    Article  Google Scholar 

  29. Ramesh N, Venkateshan S. Experimental study of natural convection in a square enclosure using a differential interferometer. Int J Heat Mass Trans. 2001;44(6):1107–17.

    Article  Google Scholar 

  30. Ostrach S. Natural convection in enclosures. J Heat Trans. 1988;110:1175–90.

    Article  CAS  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the Modeling and Computing facilities made available to us by the resource Coordinators at Product Development lab at the Mechanical Engineering Department, SRMIST.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, SRM Institute of Science and Technology, Chennai, 603 203, India

    R. Siddharth, Shaik Subhani & Rajendran Senthil kumar

Authors
  1. R. Siddharth
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shaik Subhani
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Rajendran Senthil kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rajendran Senthil kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Siddharth, R., Subhani, S. & kumar, R.S. Numerical study on performance enhancement of a square enclosure with multiple hot circular obstacles. J Therm Anal Calorim 147, 3313–3330 (2022). https://doi.org/10.1007/s10973-021-10762-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-021-10762-x

Keywords

Search

Navigation