Skip to main content
SpringerLink
Log in

A study for multi-layer skin burn injuries based on DPL bioheat model

  • Published:
Journal of Thermal Analysis and Calorimetry Aims and scope Submit manuscript

A Correction to this article was published on 11 September 2020

This article has been updated

Abstract

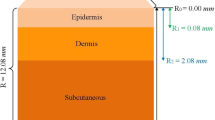
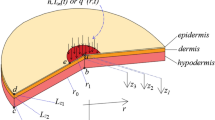
In this paper, multi-layer skin burn injuries are studied using the DPL bioheat model when skin surface is subjected to different non-Fourier boundary conditions. A skin made of three layers known as epidermis, dermis, and subcutaneous layer. These layers assumed to be homogeneous and each layer studied separately. The metabolic heat varies linearly with temperature. The diffusion and evaporation of water in the multi-layer of skin increases heat loss in the skin layer. To solve the BVP of hyperbolic PDE, the FELWG method has been used. The whole analysis presented in a non-dimensional form and the results are shown graphically. In a particular case, the result obtained is compared with the exact solution and is in good agreement. The effects of relaxation time, layer thickness, different temperature, and non-Fourier boundary condition are analyzed at the temperature of the tissue related to the burning of the skin, and the three layers are discussed in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Change history

Abbreviations

\(c_{\uprho}\) :

Specific heat/J kg\(^{-1}\,^{\circ }\)C\(^{-1}\)

k :

Thermal conductivity/W m\(^{-1}\,^{\circ }\)C\(^{-1}\)

t :

Time/s

T :

Temperature/\(^{\circ }\)C

\(D_{f}\) :

Coefficient of water diffusion in tissue/m\(^2~\text {s}^{-1}\)

\(M_{\mathrm{W}}\) :

The molar mass of water/18 g mol\(^{-1}\)

RH :

Relative humidity/%

P W :

Vapor pressure of water/Pa

r :

Space coordinate/m

ΔH vap :

Enthalpy of water vaporization/2408 J kg\(^{-1}\)

Δm :

Water vaporization rate from the skin surface/g m\(^{-2}~\text {s}^{-1}\)

\(\Delta {r}\) :

Body core distance from current tissue position/m

\(\delta c\) :

The average distance of the momentum boundary layer/m

\(\rho \) :

Density of skin/kg m\(^{-3}\)

\(R_{\mathrm{a}}\) :

Universal gas constant/8.314 J mol\(^{-1}\,^{\circ }\)C\(^{-1}\)

\(\tau _{\mathrm{q}}\) :

Phase lag of heat flux/s

\(\tau _{\mathrm{t}}\) :

Phase lag due to temperature gradient/s

\(T_{\mathrm{w}}\) :

Wall temperature at the boundary/\(^{\circ }\)C

H :

Coefficient of reference heat transfer/W m\(^{-2}\,^{\circ }\)C\(^{-1}\)

\(q_{\mathrm{w}}\) :

Reference heat flux/W m\(^{-2}\)

\(T_\mathrm{s}\) :

Ambient temperature/\(^{\circ }\)C

\(Q_\mathrm{v}\) :

Evaporation of water

\(Q_\mathrm{d}\) :

Diffusion of water

b :

Blood

c :

Core

a :

Air

f :

Diffusion of water

m :

Metabolic production

s :

Surface of skin

v :

Vaporization

W:

Water

\(F_{\mathrm{o}}\) :

Non-dimensional time

x :

Non-dimensional space coordinate

\(K_{\mathrm{i}}\) :

Kirchhoff number

\(B_{\mathrm{i}}\) :

Biot number

\(F_{\mathrm{ot}}\) :

Non-dimensional phase lag due to temperature gradient

\(F_{\mathrm{oq}}\) :

Non-dimensional phase lag of heat flux

\(P_{\mathrm{mo}}\) :

Non-dimensional coefficient of metabolic heat source

\(P_{\mathrm{f}}\) :

Non-dimensional coefficient of blood perfusion

\(\theta \) :

Non-dimensional tissue temperature

\(\theta _\mathrm{s}\) :

Non-dimensional fluid temperature

\(\theta _{\mathrm{w}}\) :

Non-dimensional wall temperature of the tissue

\(\theta _{\mathrm{b}}\) :

Non-dimensional blood temperature

References

  1. Pennes HH. Analysis of tissue and arterial blood temperature in the resting human forearm. J Appl Physiol. 1948;1:93–122.

    Article  CAS  PubMed  Google Scholar 

  2. Weinbaum S, Jiji LM. A new simplified bioheat equation for the effect of blood flow on local average tissue temperature. ASME J Biomech Eng. 1985;107:131–9.

    Article  CAS  Google Scholar 

  3. Nakayama A, Kuwahara F. A general bioheat transfer model based on the theory of porous media. Int J Heat Mass Transf. 2008;51:3190–9.

    Article  CAS  Google Scholar 

  4. Shen WS, Zhang J, Yang FQ. Skin thermal injury prediction with strain energy. Int J Nonlinear Sci Numer Simul. 2005;6:317–28.

    Article  Google Scholar 

  5. Duncan JM, David CE, Richard A. Dynamic simulations of tissue welding. Proc SPIE. 1996;2671:234–42.

    Article  Google Scholar 

  6. Ming F, Weng W, Yuan H. Numerical simulation of the effects of blood perfusion, water diffusion, and vaporization on the skin temperature and burn injuries. Numer Heat Transf Part A. 2014;65:1187–203.

    Article  Google Scholar 

  7. Ming F, Chen W, Weng W, Yuan M, Luo N, Xu X. Prediction of thermal skin burn based on the combined mathematical model of the skin and clothing. J Textile Inst. 2018;109(12):1606–12.

    Article  Google Scholar 

  8. Peng J, Tian Y. A surface heat disturbance method for measuring local tissue blood perfusion rate. J Therm Sci. 1996;5(1):28–33.

    Article  Google Scholar 

  9. Chen B, Zhang Y, Li D. Numerical investigation of the thermal response to skin tissue during laser lipolysis. J Therm Sci. 2018;27(5):470–8.

    Article  CAS  Google Scholar 

  10. Gupta PK, Singh J, Rai KN. Numerical simulation for heat transfer in tissues during thermal therapy. J Therm Biol. 2010;35(6):295–301.

    Article  Google Scholar 

  11. Gupta PK, Singh J, Rai KN. A numerical study on heat transfer in tissues during hyperthermia. Math Comput Model. 2013;57:1018–37.

    Article  Google Scholar 

  12. Cattaneo C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. C R Acad Sci. 1958;247:431–3.

    Google Scholar 

  13. Vernotte P. Les paradoxes de la theorie continue de I’equation de la chaleur. C R Acad Sci. 1958;246:3154–5.

    Google Scholar 

  14. Liu KC. Thermal propagation analysis for living tissue with surface heating. Int J Therm Sci. 2008;47:507–13.

    Article  Google Scholar 

  15. Kumar D, Kumar P, Rai KN. Numerical study on non-Fourier bio heat transfer during thermal ablation, vol. 127. Amsterdam: Elservier; 2015. p. 1300–7.

    Google Scholar 

  16. Upadhyay S, Rai KN. Finite element Legendre wavelet Galerkin approach in investigation of non-Fourier’s and non-Ficks’s effects on heat and mass transfer during drying of foods. Comput Therm Sci Int J. 2018;10:493–519.

    Article  Google Scholar 

  17. Bhattacharyya A, Seth GS, Kumar R, Chamkha AJ. Simulation Cattaneo–Christov heat flux on the flow of single and multi-walled carbon nanotubes between two stretchable coaxial rotating disks. J Therm Anal Calorim. 2020;139:1655–70.

    Article  CAS  Google Scholar 

  18. Tzou DY. A unified field approach for heat conduction from macro-to microscales. J Heat Transf. 1995;117(1):8–16.

    Article  Google Scholar 

  19. Tzou DY. Macro- to-microscale heat transfer: the lagging behavior. Washington DC: Taylor and Francis; 1996.

    Google Scholar 

  20. Zhang Y. Generalized dual-phase lag bioheat equations based on nonequilibrium heat transfer in living biological tissues. Int J Heat Mass Transf. 2009;52:4829–34.

    Article  Google Scholar 

  21. Kumar P, Kumar D, Rai KN. A numerical study on dual-phase-lag model of bioheat transfer during hyperthermia treatment. J Therm Biol. 2015;49:98–105.

    Article  PubMed  Google Scholar 

  22. Kumar P, Kumar D, Rai KN. Numerical simulation of dual-phase-lag bioheat transfer model during thermal therapy. Math Biosci. 2016;281:82–91.

    Article  CAS  PubMed  Google Scholar 

  23. Odibat Z, Kumar S. A robust computational algorithm of homotopy asymptotic method for solving systems of fractional differential equations. J Comput Nonlinear Dynam. 2019;14(8):081004.

    Article  Google Scholar 

  24. Ajou AEl, Oqielat MN, Zhour ZA, Kumar S, Momani S. Solitary solutions for time-fractional nonlinear dispersive PDEs in the sense of conformable fractional derivative. Chaos. 2019;29:093102.

    Article  PubMed  Google Scholar 

  25. Emile F, Doungmo G, Kumar S, Mugisha SB. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos Solitons Fractals. 2020;130:109467.

    Article  Google Scholar 

  26. Kumar S, Kumar A, Momani S, Aldhaifallah M, Nisar KS. Numerical solutions of nonlinear fractional model arising in the appearance of the strip patterns in two-dimensional systems. Adv Differ Equ. 2019;2019:413.

    Article  Google Scholar 

  27. Sharma B, Kumar S, Cattani C, Baleanu D. Nonlinear dynamics of Cattaneo–Christov heat flux model for third-grade power-law fluid. J Comput Nonlinear Dyn. 2019;1131.

  28. Yanying X, Chao L, Ruiqing S, Zhi W, Qingsheng W. Experimental investigation of thermal properties and fire behavior of carbon/epoxy laminate and its foam core sandwich composite. J Therm Anal Calorim. 2019;136:1237–47.

    Article  Google Scholar 

  29. Kleilton OS, Rossemberg CB, Josué SB, André GBJ, Wladymyr JBS, Sandra MCB, Rodrigo JO, Marcus VLF. Thermal, chemical, biological and mechanical properties of chitosan films with powder of eggshell membrane for biomedical applications. J Therm Anal Calorim. 2019;136:725–35.

    Article  Google Scholar 

  30. Henze M, Bogdanic L, Muehlbauer K, Schnieder M. Effect of the Biot number on metal temperature of thermal-barrier-coated turbine parts-real engine measurements. J Turbomach. 2013;135:031029.

    Article  Google Scholar 

  31. Khalid MZ, Zubair M, Ali M. An analytical method for the solution of two phase Stefan problem in cylindrical geometry. Appl Math Comput. 2019;342:295–308.

    Google Scholar 

  32. Szafer A, Zhong JH, Gore JC. Theoretical-model for water diffusion in tissues. Magn Reson Med. 1995;33:697–712.

    Article  CAS  PubMed  Google Scholar 

  33. Jiang SC, Ma N, Li HJ, Zhang XX. Effects of thermal properties and geometrical dimensions on skin burn injuries. Burns. 2002;28:713–7.

    Article  CAS  PubMed  Google Scholar 

  34. Ng EYK, Chua LT. Prediction of skin burn injury, part 2: parametric and sensitivity analysis. P I Mech Eng H. 2002;216:171–83.

    Article  CAS  Google Scholar 

  35. Johnson NN, Abraham JP, Helgeson ZI, Minkowycz WJ, Sparrow EM. An archive of skin-layer thicknesses and properties and calculations of scald burns with comparisons to experimental observations. J Therm Sci Eng Appl. 2011;3:1–9.

    Article  Google Scholar 

  36. Henriques FC, Moritz AR. Studies of thermal injuries I: the conduction of heat to and through skin and the temperatures attained therein, a theoretical and experimental investigation. Am J Pathol. 1947;23:531–49.

    Google Scholar 

  37. Stoll AM, Chianta MA. Method and rating system for evaluation of thermal protection. Aerospace Med. 1969;40:1232–7.

    CAS  PubMed  Google Scholar 

  38. Weaver JA, Stoll AM. Mathematical model of skin exposed to thermal radiation. Aerosp Med. 1969;40:24–30.

    CAS  PubMed  Google Scholar 

  39. Scheid F. Schaum’s outline of theory and problems: numerical analysis. 2nd ed. New York: McGraW-Hill; 1989.

    Google Scholar 

  40. Razzaghi M, Yousefi S. The Legendre wavelets operational matrix of integration. Int J Syst Sci. 2001;32(4):495–502.

    Article  Google Scholar 

  41. Don E. Mathematica Second edition, Schaum’s outline’s Series, ISBN: 978-0-07-160829-9.

  42. Pratap R. Getting started with matlab a quick introduction for scientists and engineers. New York: Oxford University Press; 2010.

    Google Scholar 

Download references

Acknowledgements

First author would like to thanks the CSIR, New Delhi, India, for the financial support under the JRF (09/013(0931)/2020-EMR-I) scheme and also to the Department of Mathematics (Institute of Science), Banaras Hindu University (BHU), Varanasi (U.P), India, for providing necessary facilities. We thank all anonymous reviewers for spending valuable time to give valuable comments so that our manuscript is improved in the present form.

Author information

Authors and Affiliations

  1. Department of Mathematics, Institute of Science, Banaras Hindu University, Varanasi, 221005, India

    Rajneesh Kumar Chaudhary & Jitendra Singh

  2. Department of Mathematical Sciences, IIT-BHU, Varanasi, 221005, India

    Kabindra Nath Rai

Authors
  1. Rajneesh Kumar Chaudhary
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kabindra Nath Rai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jitendra Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jitendra Singh.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

In the original publication, few equations and figure captions were published incorrectly. The original version is corrected.

Appendix

Appendix

Second kind non-Fourier boundary condition

From Eq. (23), we have found the second kind non-Fourier boundary condition, i.e.,

$$\begin{aligned} \frac{\partial }{\partial {x}}\left[ \,\theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {F_{\mathrm{o}}}}\right] \, =-K_{\mathrm{i}} \;\;\;\;at \;\;x=0. \end{aligned}$$
(63)

Taking the Laplace transform of Eq. (63), we obtained

$$\begin{aligned} \frac{\partial }{\partial {x}}\left[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} \{s \overset{\sim }{\theta }(x,s)-\theta (x,0)\}\right] \, =-\frac{K_{\mathrm{i}}}{s} \;\;\;\;at \;\;x=0. \end{aligned}$$
(64)

Using initial condition \(\theta (x,0)=0\) in Eq. (64), we get

$$\begin{aligned}&\frac{\partial }{\partial {x}}\left[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} s\overset{\sim }{\theta }(x,s)\right] \, =-\frac{K_{\mathrm{i}}}{s} \;\;\;\;at \;\;x=0, \end{aligned}$$
(65)
$$\begin{aligned}&(1+F_{\mathrm{ot}}s)\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =-\frac{K_{\mathrm{i}}}{s} \;\;\;\;at \;\;x=0, \end{aligned}$$
(66)
$$\begin{aligned}&\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =-\frac{K_{\mathrm{i}}}{s(1+F_{\mathrm{ot}}s)} \;\;\;\;at \;\;x=0. \end{aligned}$$
(67)

Inverse Laplace transform of Eq. (67) is

$$\begin{aligned} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {x}} \, =-K_{\mathrm{i}} (1-e^{-\frac{F_{\mathrm{o}}}{F_{\mathrm{ot}}}}) \;\;\;\;at \;\;x=0. \end{aligned}$$
(68)

Third kind non-Fourier boundary condition

From Eq. (23), we have found third kind non-Fourier boundary condition, i.e.,

$$\begin{aligned}&\frac{\partial }{\partial {x}}\left[ \,\theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {F_{\mathrm{o}}}}\right] \, -B_{\mathrm{i}} \theta (x,F_{\mathrm{o}})=-B_{\mathrm{i}} \theta _\mathrm{s} \;\;\;\;at \;\;x=0, \end{aligned}$$
(69)
$$\begin{aligned}&\frac{\partial }{\partial {x}}\left[ \,\theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {F_{\mathrm{o}}}}\right] \, =-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,F_{\mathrm{o}})) \;\;\;\;at \;\;x=0. \end{aligned}$$
(70)

Taking the Laplace transform of Eq. (70), we obtained

$$\begin{aligned} \frac{\partial }{\partial {x}}[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} \{s \overset{\sim }{\theta }(x,s)-\theta (x,0)\}] \, =-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,s)) \;\;\;\;at \;\;x=0. \end{aligned}$$
(71)

Using initial condition \(\theta (x,0)=0\) in Eq. (71), we get

$$\begin{aligned}&\frac{\partial }{\partial {x}}\left[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} s\overset{\sim }{\theta }(x,s)\right] \, =\frac{-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,s))}{s} \;\;\;\;at \;\;x=0, \end{aligned}$$
(72)
$$\begin{aligned}&(1+F_{\mathrm{ot}}s)\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =\frac{-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,s))}{s} \;\;\;\;at \;\;x=0, \end{aligned}$$
(73)
$$\begin{aligned}&\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =\frac{-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,s))}{s(1+F_{\mathrm{ot}}s)} \;\;\;\;at \;\;x=0. \end{aligned}$$
(74)

Inverse Laplace transform of Eq. (74) is

$$\begin{aligned} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {x}} \, =-B_{\mathrm{i}} (\theta _\mathrm{s}-\theta (x,F_{\mathrm{o}})) (1-e^{-\frac{F_{\mathrm{o}}}{F_{\mathrm{ot}}}}) \;\;\;\;at \;\;x=0. \end{aligned}$$
(75)

Non-Fourier symmetric condition

From Eq. (27), we have found non-Fourier symmetric condition, i.e.,

$$\begin{aligned} \frac{\partial }{\partial {x}}\left[ \,\theta (x,F_{\mathrm{o}})+F_{\mathrm{ot}} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {F_{\mathrm{o}}}}\right] \,= 0 \;\;\;\;at \;\;x=1. \end{aligned}$$
(76)

Taking the Laplace transform of Eq. (76), we obtained

$$\begin{aligned} \frac{\partial }{\partial {x}}[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} \{s \overset{\sim }{\theta }(x,s)-\theta (x,0)\}] \, =0 \;\;\;\;at \;\;x=1. \end{aligned}$$
(77)

Using initial condition \(\theta (x,0)=0\) in Eq. (77), we get

$$\begin{aligned}&\frac{\partial }{\partial {x}}[ \,\overset{\sim }{\theta }(x,s)+F_{\mathrm{ot}} s\overset{\sim }{\theta }(x,s)] \, =0 \;\;\;\;at \;\;x=1, \end{aligned}$$
(78)
$$\begin{aligned}&(1+F_{\mathrm{ot}}s)\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =0 \;\;\;\;at \;\;x=1,\end{aligned}$$
(79)
$$\begin{aligned}&\frac{\partial {\overset{\sim }{\theta }(x,s)}}{\partial {x}} \, =0 \;\;\;\;at \;\;x=1. \end{aligned}$$
(80)

Inverse Laplace transform of Eq. (80) is

$$\begin{aligned} \frac{\partial {\theta (x,F_{\mathrm{o}})}}{\partial {x}} \, =0 \;\;\;\;at \;\;x=1. \end{aligned}$$
(81)
Fig. 2
figure 2

Epidermis layer: Comparison of exact with approx solution

Full size image
Fig. 3
figure 3

Dermis layer:Comparison of exact with approx solution

Full size image
Fig. 4
figure 4

Subcutaneous layer: Comparison of exact with approx solution

Full size image
Fig. 5
figure 5

Epidermis layer: Effect of \(F_{\mathrm{oq}}=0.00696379\) and \(F_{\mathrm{ot}}=0\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 6
figure 6

Dermis layer: Effect of \(F_{\mathrm{oq}}=0.0140766\) and \(F_{\mathrm{ot}}=0\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 7
figure 7

Subcutaneous layer: Effect of \(F_{\mathrm{oq}}=0.00791667\) and \(F_{\mathrm{ot}}=0\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 8
figure 8

Epidermis layer: Effect of \(F_{\mathrm{oq}}=F_{\mathrm{ot}}=0.00696379\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 9
figure 9

Dermis layer: Effect of \(F_{\mathrm{oq}}=F_{\mathrm{ot}}=0.0140766\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 10
figure 10

Subcutaneous layer: Effect of \(F_{\mathrm{oq}}=F_{\mathrm{ot}}=0.00791667\) on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 11
figure 11

Epidermis layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 12
figure 12

Dermis layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 13
figure 13

Subcutaneous layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 14
figure 14

Epidermis layer: Lagging behavior on skin during different temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 15
figure 15

Dermis layer: Lagging behavior on skin during different temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 16
figure 16

Subcutaneous layer: Lagging behavior on skin during different temperature with the first kind non-Fourier boundary condition at \(F_{\mathrm{o}}=0.5\)

Full size image
Fig. 17
figure 17

Epidermis layer: The effect on skin thickness between temperature and time with the first kind non-Fourier boundary condition

Full size image
Fig. 18
figure 18

Dermis layer: The effect on skin thickness between temperature and time with the first kind non-Fourier boundary condition

Full size image
Fig. 19
figure 19

Subcutaneous layer: The effect on skin thickness between temperature and time with the first kind non-Fourier boundary condition

Full size image
Fig. 20
figure 20

Epidermis layer: Effect of lagging on skin during hot and cold temperature

Full size image
Fig. 21
figure 21

Dermis layer: Effect of lagging on skin during hot and cold temperature

Full size image
Fig. 22
figure 22

Subcutaneous layer: Effect of lagging on skin during hot and cold temperature

Full size image
Fig. 23
figure 23

Epidermis layer: Ki effect on skin

Full size image
Fig. 24
figure 24

Dermis layer: Ki effect on skin

Full size image
Fig. 25
figure 25

Subcutaneous layer: Ki effect on skin

Full size image
Fig. 26
figure 26

Epidermis layer: Bi effect on skin

Full size image
Fig. 27
figure 27

Dermis layer: Bi effect on skin

Full size image
Fig. 28
figure 28

Subcutaneous layer: Bi effect on skin

Full size image
Fig. 29
figure 29

Epidermis layer: Effect of temperature on skin during non-Fourier generalized boundary condition

Full size image
Fig. 30
figure 30

Dermis layer: Effect of temperature on skin during non-Fourier generalized boundary condition

Full size image
Fig. 31
figure 31

Subcutaneous layer: Effect of temperature on skin during non-Fourier generalized boundary condition

Full size image
Fig. 32
figure 32

Epidermis layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 33
figure 33

Dermis layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition

Full size image
Fig. 34
figure 34

Subcutaneous layer: Effect of lagging on skin temperature with the first kind non-Fourier boundary condition

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chaudhary, R.K., Rai, K.N. & Singh, J. A study for multi-layer skin burn injuries based on DPL bioheat model. J Therm Anal Calorim 146, 1171–1189 (2021). https://doi.org/10.1007/s10973-020-09967-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10973-020-09967-3

Keywords

Search

Navigation