Phase equilibria in the AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) binary systems

Abstract

Differential thermal analysis and differential scanning calorimetry were used to investigate phase equilibria in the AgCl–LnCl₃ (Ln = Ce, Sm, Gd) binary systems. It was found that systems under investigation represent typical examples of simple eutectic systems. The eutectic compositions and eutectic temperatures were found to be: x(CeCl₃) = 0.095, T_eut = 700 K (for AgCl–CeCl₃), x(SmCl₃) = 0.228, T_eut = 644 K (for AgCl–SmCl₃) and x(GdCl₃) = 0.288, T_eut = 609 K (for AgCl–GdCl₃). The thermodynamic functions of mixing in AgCl–LnCl₃ systems (Ln = Ce, Nd, Sm, Gd) were predicted on the basis of experimental data using the CALPHAD method by association model (AM) and Redlich–Kister model (RKM). The possibility of existence of the associates in the liquid phase was discussed.

Introduction

The luminescence of AgCl, AgBr and AgCl_xBr_1−x crystals and fibers doped with lanthanide ions Ln³⁺ was investigated because of the potential use as solid-state lasers that operate in the middle-infrared spectral range [1,2,3,4,5,6,7]. These materials are highly transparent in the near- and mid-IR ranges and have desirable mechanical and optical properties. Rare earth ions are characterized by complex energy level schemes, with some optical transitions of these ions being in the mid-IR range. Similar transitions or transitions between higher excited states may exist in silver halides. Incorporating rare earth in silver halide crystals and fibers may induce amplification and lasing in mid-IR. All experiments and calculations indicate that these doped crystals and fibers would be good candidates for the fabrication of mid-IR solid-state lasers or fiber lasers [1,2,3,4,5,6,7].

Therefore, the knowledge of basic thermodynamic properties for the silver halide–lanthanide halide systems is required. Unfortunately, the only data reported in the literature are four phase diagrams: AgCl-NdCl₃ [8], AgBr-PrBr₃ [9], AgBr-NdBr₃ [9, 10] and AgBr-TbBr₃ [11], and electrical conductivity of molten mixtures in whole composition range for the AgCl–NdCl₃ and AgBr-NdBr₃ binary systems [8, 10].

The present paper reports the phase diagrams of three pseudo-binary systems: AgCl–CeCl₃, AgCl–SmCl₃ and AgCl–GdCl₃, determined experimentally for the first time. Moreover, the thermochemical calculations on these systems and additional one (AgCl–NdCl₃) have been done using CALPHAD method. The functions of mixing in the liquid phase for all liquid mixtures have been calculated.

Experimental

Chemicals and sample preparation

Cerium(III) chloride and gadolinium(III) chloride were synthesized from Ce₂(CO₃)₃ and Gd₂O₃ (both 99.9% purity, Aldrich), respectively. The syntheses were carried out by dissolution of Ce₂(CO₃)₃ and Gd₂O₃ in hot concentrated HCl acid (35–38%, pure, POCH S.A.) and further evaporation and crystallization of LnCl₃·xH₂O (Ln = Ce, Gd). Ammonium chloride was then added, and these wet mixtures of hydrated LnCl₃ and NH₄Cl were slowly heated first up to 450 K and then up to 570 K to remove the water. The resulting mixtures were subsequently heated to 650 K for sublimation of unreacted NH₄Cl. Finally, the salts were melted at 1223 K (CeCl₃) and 1023 K (GdCl₃) under argon atmosphere. Crude CeCl₃ and GdCl₃ were purified by distillation under reduced pressure (~ 0.1 Pa) in a quartz ampoule at 1253 K.

Samarium(III) chloride was prepared by chlorinating the samarium(III) oxide (99.9%, Aldrich) with a current of high-purity argon (water and oxygen content less than 2 and 0.5 ppm, respectively) saturated with carbon tetrachloride CCl₄ (pure p.a., chemPUR) vapor in a quartz reactor, at 973 K for 3 h.

Purity of lanthanide chlorides was verified by complexometric and mercurimetric titration for lanthanide and chloride, respectively. The results presented in Table 1 confirm the high purity of obtained products.

Table 1 Chemical composition of synthesized lanthanide chlorides determined by titration methods

Silver chloride was POCH S.A. reagent (pure for analysis). Before use, it was dried at 450 K.

The mixtures of AgCl and LnCl₃ (Ln = Ce, Sm, Gd) were prepared in a glove box filled with argon (purity > 99.9999%, Messer). Moreover, due to silver chloride UV–Vis light sensitivity, all laboratory steps were carried out in the red light. The weighted mixtures of chlorides were melted in the vacuum-sealed quartz ampoules in an electric furnace, homogenized by shaking and solidified. Then samples were ground in an agate mortar in the glove box and placed into smaller quartz ampoules, especially for DTA/DSC measurements, and sealed under vacuum using propane–butane–oxygen burner. Ampoules for DTA measurements were about 11 mm diameter and 30 mm length, for DSC—about 6 mm and 15 mm, respectively. Mass of individual samples was 1.300–2.000 g for DTA and 0.200–0.400 g for DSC. Compositions of starting mixtures are given in Table 2.

Table 2 Eutectic and liquidus temperatures in the AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) systems derived from heating DTA or DSC curves, x is the mole fraction of respective lanthanide chloride

Measurements

Phase diagrams of the AgCl–CeCl₃ and AgCl–GdCl₃ systems were studied using differential thermal analysis (DTA) on modified Paulik–Paulik–Erdey MOM Q-1500 D derivatograph controlled by a programmer Eurotherm 2604 coupled to the PC computer equipped with i-Tools data acquisition interface. The temperature was measured with a Pt/Pt–Rh(10) thermocouple placed in the recess in the bottom of the ampoule, calibrated with high-purity metals, whose melting points were in the temperature range of our measurements. Cooling and heating were carried out at a rate of 5 K min⁻¹.

Phase equilibria measurements of the AgCl–SmCl₃ system were carried out using the 121 SETARAM differential scanning calorimeter, conducted at heating and cooling rates ranging between 1 and 5 K min⁻¹. The details of the DSC calibration and measurements procedure were described previously [12].

Results

Determination of phase diagram by DTA and DSC methods

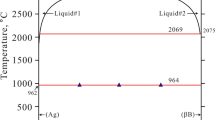
The phase diagrams of the AgCl–LnCl₃ (Ln = Ce, Sm, Gd) binary systems were determined for the first time in this work. DTA and DSC investigations were performed on samples with different compositions in the x(LnCl₃) range from 0.0 to 1.0. Due to supercooling effect observed in the samples (Fig. 1), all temperature and enthalpy values reported in this work were determined from heating curves. Solidus and liquidus temperatures were determined as T_onset and T_peak of appropriate effects, respectively. Figure 2 shows the example curves obtained for investigated systems. All experimental data are given in Table 2.

Fig. 1

DTA heating (solid lines) and cooling (dashed lines) curves for: AgCl–CeCl₃ mixtures with x(CeCl₃) = 0.011 (a); AgCl–GdCl₃ mixtures with x(GdCl₃) = 0.560 (c); and DSC heating curves for AgCl–SmCl₃ mixtures with x(SmCl₃) = 0.099 (b); heating rate: 5 K min⁻¹

Fig. 2

DTA heating curves for: AgCl–CeCl₃ mixtures with x(CeCl₃) = 0.011 (a) and x(CeCl₃) = 0.701 (b); AgCl–GdCl₃ mixtures with x(GdCl₃) = 0.075 (e) and x(GdCl₃) = 0.560 (f); and DSC heating curves for AgCl–SmCl₃ mixtures with x(SmCl₃) = 0.099 (c) and x(SmCl₃) = 0.793 (d); heating rate: 5 K min⁻¹

Almost all heating curves, for all investigated systems, showed only two peaks, which were ascribed to the eutectic and the liquidus effects, respectively. A few exceptions (one peak observed for the samples with composition close to eutectic point) resulted from overlapping of both thermal effects. It means that AgCl–LnCl₃ (Ln = Ce, Sm, Gd) phase diagrams were found to be of the simple eutectic type (points, Figs. 3, 5, 6) with no intermediate solid compounds, similarly to AgCl–NdCl₃ system (Fig. 4).

Fig. 3

Phase diagram of the AgCl–CeCl₃ binary system (top) and respective Tamman plot (bottom). Open circles—experimental data, black circles—eutectic composition determined from Tamman plot, solid lines (top)—phase equilibria calculated by CALPHAD method using association model (AM), dashed lines (top)—phase equilibria calculated by CALPHAD method using Redlich–Kister model (RKM), solid lines (bottom)—calculated Tamman plot

Fig. 4

Phase diagram of the AgCl–NdCl₃ binary system (top) and respective Tamman plot (bottom). Open circles—experimental data, black circles—eutectic composition determined from Tamman plot, solid lines (top)—phase equilibria calculated by CALPHAD method using association model (AM), dashed lines (top)—phase equilibria calculated by CALPHAD method using Redlich–Kister model (RKM), solid lines (bottom)—calculated Tamman plot

Fig. 5

Phase diagram of the AgCl–SmCl₃ binary system (top) and respective Tamman plot (bottom). Open circles—experimental data, black circles—eutectic composition determined from Tamman plot, solid lines (top)—phase equilibria calculated by CALPHAD method using association model (AM), dashed lines (top)—phase equilibria calculated by CALPHAD method using Redlich–Kister model (RKM), solid lines (bottom)—calculated Tamman plot

Fig. 6

Phase diagram of the AgCl–GdCl₃ binary system (top) and respective Tamman plot (bottom). Open circles—experimental data, black circles—eutectic composition determined from Tamman plot, solid lines (top)—phase equilibria calculated by CALPHAD method using association model (AM), dashed lines (top)—phase equilibria calculated by CALPHAD method using Redlich–Kister model (RKM), solid lines (bottom)—calculated Tamman plot

The eutectic contributions to the enthalpy of fusion are determined and plotted against composition in Figs. 3–6. These so-called Tamman constructions make it possible to evaluate accurately the eutectic compositions from the intercept of the two linear parts in Figs. 3–6. In these Tamman constructions, it was assumed that there is no solubility in the solid state. Thus, straight lines intercept the composition axis at x(LnCl₃) = 0.00 and x(LnCl₃) = 1.00. The eutectic temperatures, compositions and enthalpies of fusion for the systems under investigation are given in Table 3.

Table 3 The eutectic temperatures, compositions and enthalpies of fusion obtained experimentally (by Tamman plots) and by CALPHAD calculations using association model (AM) and Redlich–Kister model (RKM)

Phase diagram calculations by CALPHAD method

The phase diagrams of the AgCl–LnCl₃ (Ln = Ce, Sm, Gd) systems measured in this work and the phase diagram of the AgCl–NdCl₃ system investigated by Szymanska-Kolodziej et al. [8] were calculated by the CALPHAD method using the BINGSS and BINFKT program [13]. The data, used in calculations, for solid and liquid AgCl and LnCl₃ (Ln = Ce, Nd, Gd, Sm) are presented in Table 4. SGTE description was used for these compounds:

$$G^\circ \left( T \right){-}H^{\text{SER}} = A + BT + CT\ln T + DT^{2} + E/T$$

(1)

The coefficients of this equation for all of pure system components are presented in Table 5.

Table 4 The thermodynamic data for pure chlorides used in CALPHAD calculations

Table 5 The coefficients of Eq. (1) describing {G°(T) − H^SER}/J mol⁻¹ of pure system components

Interpretation by the CALPHAD method was made with using two models describing liquid phase. The first one was an association model (AM) [16], which assumes the existence of associates in the liquid phase. They are formed according to equation:

$$p{\text{AgCl}} + q{\text{LnCl}}_{3} = \left\{ {\text{Ag}}_p {\text{LnCl}}_{(p + 3q)} \right\}$$

(2)

where p and q are stoichiometry coefficients. From the mass balance in liquid phase, it has been obtained:

$$n = n_{\text{AgCl}} + n_{{{\text{LnCl}}_3}} + n_{\text{a}}$$

(3)

where n is the total number of moles, n_AgCl, $n_{{\text{LnCl}}_{3}}$ and n_a are number of mole of AgCl, LnCl₃ and associate, respectively. The mole fractions of AgCl (y_AgCl) and LnCl₃ (y_LnCl3) in this pseudoternary system have been represented by the following formulas:

$$y_{\text{AgCl}} = x_{\text{AgCl}} \cdot [1 + (p + q{-}1) \cdot y_{\text{a}} ]{-}p \cdot y_{\text{a}}$$

(4)

$$y_{{{\text{LnCl}}_3}} = x_{{{\text{LnCl}}_3}} \cdot [1 + (p + q{-}1) \cdot y_{\text{a}} ]{-}q \cdot y_{\text{a}}$$

(5)

where y_a is a mole fraction of associate.

The Gibbs energy of mixing of the liquid phase in this model has been described as:

$$\begin{aligned} G^{{^\circ {\text{MIX}}}} & = R \cdot T \cdot [(y_{\text{AgCl}} \cdot \ln (y_{\text{AgCl}} ) + y_{{{\text{LnCl}}_3}} \cdot \ln (y_{{{\text{LnCl}}_3}} ) + y_{\text{a}} \cdot \ln (y_{\text{a}} )] \cdot n \\ & \quad + C_{1} \cdot y_{\text{a}} \cdot n + (C_{2} \cdot y_{\text{AgCl}} \cdot y_{{{\text{LnCl}}_3}} ) \cdot n \\ \end{aligned}$$

(6)

where C_i is the calculated coefficients. In this work, we assume the stoichiometry (p/q ratio) of associate as an additional adjustable coefficient found by iterative method. The criterion of fitting was the standard deviation of the liquidus temperature. The dependences of coefficients C_i on temperature have been not observed. The values of mixing entropies are slightly higher than ideal ones. It means that the amount of associates in liquid phase is very small and ambiguous.

The second model used for the description of the liquid phase was the Redlich–Kister model (RKM) [17], in which Gibbs energy of mixing of the liquid phase has been described as:

$$\begin{aligned} G^{{^\circ {\text{MIX}}}} & = R \cdot T \cdot [(x_{\text{AgCl}} \cdot \ln (x_{\text{AgCl}} ) + x_{{{\text{LnCl}}_3}} \cdot \ln (x_{{{\text{LnCl}}_3}} ) \\ & \quad + x_{\text{AgCl}} \cdot x_{{{\text{LnCl}}_3}} \cdot \left[ {L_{1} + L_{2} \cdot (x_{\text{AgCl}} - x_{{{\text{LnCl}}_3}} )} \right] \\ \end{aligned}$$

(7)

where L_i is the calculated coefficients.

The results of calculations using both models are shown in Table 6.

Table 6 The coefficients of Eqs. (6) and (7) describing mixing enthalpies of liquid phases at 1100 K calculated from AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) phase diagrams, standard deviation calculated from the unbiased estimator of the population variance of liquidus (ΔT) and the entropy of mixing at mole fraction of adjusted associate stoichiometry

Taking into account that we have only liquidus data for these systems, we compared standard deviations of liquidus fitting for both models. It turned out that fitting was very similar in both cases. The consequence of this has very similar dependences of G^MIX on composition and temperature which is shown in Fig. 7.

Fig. 7

Gibbs energy of mixing of the AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) binary systems calculated by CALPHAD method using association model (a) and Redlich–Kister model (b) at 1100 K

Differences between Gibbs energies of mixing in liquid phase calculated by both models were insignificant. The main difference was the presence of small amount of configurational mixing entropy which appeared in AM interpretation. The values of p/q and correlated values of mixing entropies are shown in Table 6. All of the mixing entropies at obtained mole fraction of associate were very similar and higher about 20% than ideal mixing entropy. The RKM assumed the ideal entropy of mixing. This small difference between mixing entropies resulted in the distinctive difference in calculated values of mixing enthalpies of liquid phases, as shown in Fig. 8.

Fig. 8

Mixing enthalpies of the AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) binary systems calculated by CALPHAD method using association model (a) and Redlich–Kister model (b) at 1100 K

The presence of the configuration entropy (AM) causes a decrease in the absolute value of the calculated enthalpy of mixing by about 1000 J mol⁻¹. The result is that in the case of the AgCl–CeCl₃ system, the enthalpy of mixing achieves small positive values for the AM model.

We had expected the tendency to associate formation in AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) binary systems due to their similarity to the TlCl-SmCl₃ systems [18]. Unfortunately, the amount of associates with silver chloride turned out to be very small and may be negligible. In summary, we found that CALPHAD calculations using both (AM and RKM) models are equally good and may be usable in future interpretation.

Taking into account the shape of DTA or DSC curves, we assumed that these systems were simple eutectic ones. But the existence of incongruently melting solid compound at temperature close to eutectic point might be possible. Therefore, the CALPHAD calculations were used for the explanation of the possibility of its appearance in the above systems. We have simulated the existence of Ag₃GdCl₆ and Ag₂GdCl₅ solid compounds in AgCl–GdCl₃ binary system. It was selected because of the lowest value of Gibbs energy of mixing (Fig. 7). Both considered hypothetical compounds had Gibbs energy of formation close to zero or positive at eutectic temperature. This excludes the possibility of their existence and confirms that the systems under investigation are simple eutectics.

Conclusions

• 1. The phase diagrams of the AgCl–LnCl₃ (Ln = Ce, Sm, Gd) binary systems have been determined for the first time in this work.

• 2. All the investigated systems are simple eutectics.

• 3. The composition of eutectics was determined with the help of constructed Tamman diagrams.

• 4. Thermodynamic properties of AgCl–LnCl₃ (Ln = Ce, Nd, Sm, Gd) binary systems were calculated by CALPHAD method using association model and Redlich–Kister model. Both models gave comparable results.

• 5. An increase in the negative value of C₁ coefficient describing associate formation with the decrease in ionic radius of lanthanide (from cerium to gadolinium) and slightly positive excess entropy of mixing lead to the conclusion that existence of small amount of associate cannot be excluded [16, 19].