Introduction

Convective-radiative heat transfer in porous media is of growing importance in a wide range of technological applications [1, 2]. The increasing use of porous media in radiative energy systems such as solar collectors, solar reactors and porous burners has raised a pressing need for further understanding and modelling of this combined mode of heat transfer [3,4,5]. Further, the use of magnetic effects in advanced energy technologies (e.g. cooling of nuclear fusion reactors) necessitates inclusion of magnetohydrodynamic effects in heat transfer analyses. The current work aims to respond to these needs through conduction of a numerical analysis on a generic configuration including a vertical cylinder covered by a porous medium and subject to an impinging flow. A magnetic field is applied to the system, and nanoparticles are added to further enhance electrical and thermal conductivity. The primary objective is to understand the influences of pertinent parameters on this complex multiphysics problem.

Modelling of thermal radiation in porous media has received a sustained attention over the last few decades [6, 7]. Most of the early works was done on porous burners, chiefly because of the importance of thermal radiation in this specific application; see the reviews of the literature in Refs. [8, 9]. For conciseness, here only the studies published over the last 10 years are briefly reviewed. Using homotopy technique, Hayat et al. [10] investigated the effects of thermal radiation and magnetic fields on a flat plate covered by a porous medium and under an impinging flow. Thermal radiation was modelled through a linear version of Rosseland approximation, and an extensive parametric study was performed. Amongst other findings, Hayat et al. showed that the influences of radiation and magnetic parameters on the temperature field are quite similar [10]. Bhattacharyya and Layek [11] analysed boundary layer flow over a stretching porous flat surface by considering the effects of transpiration (fluid suction and blowing) and thermal radiation. A similarity solution was developed to investigate the effects of transpiration on the velocity and temperature fields [11]. These authors reported that by intensifying fluid suction, the wall temperature may increase in one class of their proposed solutions. In a subsequent work, the same group of authors added the effects of micropolar fluid flow to their analysis [12]. It was shown that by increasing thermal radiation, the temperature and thermal boundary layer thickness decrease and therefore the heat transfer rate from the sheet enhances [12].

Radiative-conductive thermal boundary condition was applied to a cylindrical configuration, and the entropy generation was analysed analytically by Torabi and Aziz [13]. In this analysis, the internal heat generation and thermal conductivity were assumed to be linear functions of temperature. The results reflected the strong influence of thermal radiation on the thermodynamic irreversibilities of the system [13]. Heat and mass transfer in a radiative flow of Maxwell fluid over a titled stretching surface was studied by Ashraf et al. [14]. This work included examination of a large number of parameters including Biot number, thermodiffusion parameter, Deborah number, inclined stretching angle, radiation parameter, mixed convection parameter upon the thermal and concentration boundary layers. In particular, it was shown that the thickness of thermal boundary layer decreases at higher thermal radiative powers [14]. Ashraf et al. also argued that radiation could have opposite effects upon Nusselt and Sherwood number [14]. In another theoretical work, Zhang et al. [15] considered heat and mass transfer in a nanofluid flow in porous media including magnetic and thermal radiation effects. They also added fluid transpiration to their investigation and found that this effect as well as those of magnetic field and radiation can strongly affect the velocity and temperature fields [15].

Heat transferring, radiative stagnation-point flow of a nanofluid over a flat plate was modelled by Makinde and Mishra [16]. These authors included the thermophoresis and Brownian motion of the nanoparticles in their similarity solution [16]. They reported decreasing trends of Nusselt number and increasing of Sherwood number at higher thermal radiation. An analogous study was reported by Hayat et al. [17] for non-Newtonian nanofluid flow in the presence of a magnetic field. In keeping with the previous investigations, it was shown that application of a magnetic field results in depletion of momentum and thus weakening of the hydrodynamic boundary layer [17]. Stagnation-point flow of unsteady radiative Casson fluid with chemical reactions over a stretching surface was analysed by Abbas et al. [18]. A temperature-dependent chemical reaction was considered in this work, and it was shown that through this effect radiation can significantly influence the mass transfer problem. As an important point, most of the existing studies are concerned with flat surfaces and only few investigations have been reported on the boundary layers over curved surface [19]. Carbon nanotubes were considered in a boundary layer flow of water over the axis of cylinder. It was shown that, for all investigated nanotubes, fluid temperature near the surface of cylinder was higher at larger values of curvature parameter [19].

A common point in the preceding works is the linear modelling of thermal radiation. Such simplification has been released in a few recent studies. For example, Hussian et al. [20] implemented a nonlinear model of thermal radiation in their analysis of stagnation-point flow over a vertical flat surface. This revealed that heat transfer enhancement could be more accurately predicted through incorporation of a nonlinear thermal radiation model in comparison with its linear counterpart. Mushtagh et al. [21] considered nonlinear radiation in the problem of solar absorption in a stagnation nanofluid flow in which Brownian motion of nanoparticles was considered. Hayat et al. [22] investigated the three-dimensional viscous flow on a nanofluid over stretching surface in the presence of nonlinear thermal radiation and magnetic effects. Their results showed that intensification of thermal radiation leads to increases in the gradient of temperature on the surface of the wall [22]. A similar analysis was reported by Farooq et al. [23] for a viscoelastic nanofluid flow and Hayat et al. [24] on an unsteady Oldroyd-B fluid. In the latter, it was shown that in the case of convective thermal boundary condition, increases in the radiation parameter result in the thickening of the thermal boundary layer. Other investigated configurations with nonlinear radiation include convectively heated cylinders [25], mixed convection in stretched flow of an Oldroyd-B fluid with convective condition [26], MHD Carreau fluid over stretched surface [27]. In all these works, it was asserted that implementation of nonlinear radiation improves the analysis and makes the predictions of heat transfer rates more accurate.

The preceding survey of the literature clearly shows that a wealth of stagnation-point flow configurations over flat surfaces with MHD and nonlinear radiation effects has been already investigated. However, the corresponding problem for curved surfaces has received very little attention. Further, those cases that considered the flow inside a porous medium often used local thermal equilibrium (LTE) assumption and the more accurate local thermal non-equilibrium (LTNE) approach has been rarely used together with radiation and magnetic effects. This is an important shortcoming particularly in thermochemical porous systems for which the existence of local thermal non-equilibrium is well demonstrated [28, 29]. The primary objective of the current work is to address these issues through using a semi-similarity solution technique.

Theoretical and numerical methods

Problem configuration, assumptions and governing equations

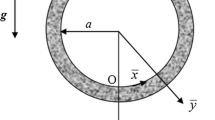
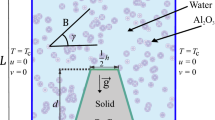
Figure 1 shows a schematic view of the problem under investigation. A heat transferring, vertical cylinder is imbedded in porous media and subject to an impinging flow of nanofluid while a magmatic field is acting on the system. The system is a simplified configuration of solar reactors and solar collectors for energy storage purposes as discussed in detail in Ref. [3]. The external surface of the cylinder can include non-uniform transpiration. The following assumptions are made throughout this work.

Fig. 1
figure 1

Schematic diagram of a stationary cylinder under radial stagnation flow and thermal radiation of nanofluid in porous media

Full size image

  • The nanofluid flow is steady and laminar.

  • The nanofluid is assumed to be Newtonian and single phase.

  • The cylinder is assumed to be infinitely long, and the porous medium is homogenous, isotropic and under local thermal non-equilibrium.

  • An external axisymmetric radial stagnation-point flow of strain rate of \(\bar{k}\) impinges on the cylinder. However, because of the non-uniformity of transpiration, the flow configuration around the cylinder can be non-axisymmetric.

  • The viscous dissipation of kinetic energy of the flow is ignored. Also, porosity, specific heat, density and thermal conductivity are assumed to be constant and thus the thermal dispersion effects are ignored.

  • A moderate range of pore-scale Reynolds number is considered in the porous medium, and hence nonlinear effects in momentum transport are negligibly small.

The details of three-dimensional governing equations and boundary conditions are provided in the followings.

The continuity of mass is expressed by

$$\frac{{\partial \left( {ru} \right)}}{\partial r} + \frac{\partial v}{\partial \varphi } + r\frac{\partial w}{\partial z} = 0.$$
(1)

The momentum equation in the radial direction [30, 31] reads

$$\frac{{\rho_{\text{nf}} }}{{\varepsilon^{2} }}\left( {u\frac{\partial u}{\partial r} + \frac{v}{r}\frac{\partial u}{\partial \varphi } - \frac{{v^{2} }}{r} + w\frac{\partial u}{\partial z}} \right) = - \frac{\partial p}{\partial r} + \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} u}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }} } \right) - \frac{{\mu_{\text{nf}} }}{{k_{1} }}u,$$
(2)

and that in angular direction and by including the magnetic forces is given by [29]

$$\frac{{\rho_{\text{nf}} }}{{\varepsilon^{2} }}\left( {u\frac{\partial v}{\partial r} + \frac{v}{r}\frac{\partial v}{\partial \varphi } + \frac{uv}{r} + w\frac{\partial u}{\partial z}} \right) = - \frac{1}{r}\frac{\partial p}{\partial \varphi } + \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{\partial r} - \frac{v}{{r^{2} }} + \frac{1}{{r^{2} }}\frac{{\partial^{2} v}}{{\partial \varphi^{2} }} + \frac{2}{{r^{2} }}\frac{\partial u}{\partial \varphi } + \frac{{\partial^{2} v}}{{\partial z^{2} }} } \right) - \frac{{\mu_{\text{nf}} }}{{k_{1} }}v - \bar{\sigma }B_{0}^{2} \cdot v.$$
(3)

The transport of momentum in the axial direction is expressed by the following equation in which buoyancy force is also included

$$\frac{{\rho_{\text{nf}} }}{{\varepsilon^{2} }}\left( {u\frac{\partial w}{\partial r} + \frac{v}{r}\frac{\partial w}{\partial \varphi } + w\frac{\partial w}{\partial z}} \right) = - \frac{\partial p}{\partial z} + \frac{{\mu_{\text{nf}} }}{\varepsilon }\left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} w}}{{\partial \varphi^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }} } \right) \pm \left( {\rho \beta } \right)_{\text{nf}} g\left( {T_{\text{nf}} - T_{\infty } } \right) - \frac{{\mu_{\text{nf}} }}{{k_{1} }} - \bar{\sigma }B_{0}^{2} \cdot w.$$
(4)

A two-equation model is used here to express the transport of thermal energy in the porous medium. The energy equation for the nanofluid phase is written as [32]

$$u\frac{{\partial T_{\text{nf}} }}{\partial r} + \frac{v}{r}\frac{{\partial T_{\text{nf}} }}{\partial \varphi } + w\frac{{\partial T_{\text{nf}} }}{\partial z} = \frac{{k_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\left( {\frac{{\partial^{2} T_{\text{nf}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{nf}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{nf}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{nf}} }}{{\partial z^{2} }} } \right) + \frac{{h_{\text{sf}} . a_{\text{sf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}\left( {T_{\text{s}} - T_{\text{nf}} } \right),$$
(5)

while the transport of thermal energy in the solid phase is expressed by

$$k_{\text{s}} \left( {\frac{{\partial^{2} T_{\text{s}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{s}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{s}} }}{{\partial z^{2} }} } \right) - h_{\text{sf}} \cdot a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{nf}} } \right) - \frac{1}{r}\frac{\partial }{\partial r}\left( {r \cdot q_{\text{r}} } \right) = 0.$$
(6)

Using Rosseland approximation [33,34,35] for thermal radiation, the radiative heat flux is simplified as follows

$$q_{\text{r}} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T_{\text{s}}^{4} }}{\partial r}.$$
(7)

Equation (6) can be now re-written in the form of

$$k_{\text{s}} \left( {\frac{{\partial^{2} T_{\text{s}} }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial r} + \frac{1}{{r^{2} }}\frac{{\partial^{2} T_{\text{s}} }}{{\partial \varphi^{2} }} + \frac{{\partial^{2} T_{\text{s}} }}{{\partial z^{2} }} } \right) - h_{\text{sf}} \cdot a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{nf}} } \right) + \frac{1}{r}\frac{\partial }{\partial r}\left( {r.\frac{{16\sigma^{*} }}{{3k^{*} }}T_{\text{s}}^{3} \frac{{\partial T_{\text{s}} }}{\partial r}} \right) = 0.$$
(8)

It should be noted that in the existing literature, \(T_{\text{s}}^{4}\) in Eq. (7) is often expanded and linearised about the ambient temperature \(T_{\infty }\) [10,11,12]. However, in the present case this simplification has been avoided and the full nonlinear form of the expression for thermal radiation is implemented.

In Eqs. (1–8) \(p\), \(\rho_{\text{nf}}\), \(\mu_{\text{nf}}\), \(T\), \(\left( {\rho C_{\text{p}} } \right)_{\text{nf}}\), \(k_{\text{nf}}\), \(\beta\), \(g\), \(T_{\infty }\), \(\sigma^{*}\), \(k^{*}\) and \(q_{\text{r}}\) are the pressure, density, kinematic viscosity of the nanofluid, temperature, the heat capacitance of the nanofluid, thermal conductivity of the nanofluid, thermal expansion coefficient, gravitational acceleration, prescribed temperature at the wall, Stefan–Boltzman constant, constant, the mean absorption coefficient and radiative heat flux, respectively. These properties are evaluated inside the boundary layer and in the vicinity of the flow impingement point.

The nanofluid properties are defined by the followings [33, 34],

$$\begin{array}{*{20}l} {\rho_{\text{nf}} = \left( {1 - \phi } \right)\rho_{\text{f}} + \phi \rho_{\text{np}} ,} \hfill & {\left( {\rho \cdot C_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho \cdot C_{\text{p}} } \right)_{\text{f}} + \phi \left( {\rho \cdot C_{\text{p}} } \right)_{\text{np}} } \hfill \\ {\mu_{\text{nf}} = \frac{{\mu_{f} }}{{\left( {1 - \phi } \right)^{2.5} }},} \hfill & {\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{k_{\text{np}} + 2k_{\text{f}} - 2\phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}}{{k_{\text{np}} + 2k_{\text{f}} + 2\phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}}} \hfill \\ \end{array}$$
(9)

in which \(\phi\) represents the nanoparticle volume fraction. In Eq. (9) the subscripts “f” and “np” denote base fluid and solid fraction properties, respectively.

The hydrodynamic boundary conditions are given by the following expressions.

$$r = a{:}\,w = 0 ,\;v = 0 ,\;u = - U_{0} \left( \varphi \right)$$
(10)
$$r = \infty{:}\,w = 2\bar{k}z , \mathop {\lim }\limits_{r \to \infty } rv = 0 , \;u = - \bar{k}\left( {r - \frac{{a^{2} }}{r}} \right)$$
(11)

Also, the followings illustrate the boundary conditions with respect to \(\varphi\) (angular coordinate)

$$\begin{aligned} u\left( {r,0} \right) = u\left( {r,2\pi } \right) , \frac{{\partial u\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial u\left( {r,2\pi } \right)}}{\partial \varphi }, \hfill \\ v\left( {r,0} \right) = v\left( {r,2\pi } \right) , \frac{{\partial v\left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial v\left( {r,2\pi } \right)}}{\partial \varphi }. \hfill \\ \end{aligned}$$
(12)

Equation (10) represents no-slip conditions on the external surface of the cylinder, and Eq. (11) shows that the viscous flow solution approaches, in an analogous way to the Hiemenz flow, the potential flow solution as \(r \to \infty\) [36,37,38,39]. This can be verified by starting from the continuity equation in the followings. \(- \frac{1}{r}\frac{{\partial \left( {ru} \right)}}{\partial r} - \frac{\partial v}{\partial \varphi } = \frac{\partial w}{\partial z}\) Constant \(= 2\bar{k}z\) and integrating in \(r\) and \(z\) directions with boundary conditions, \(w = 0\) when \(z = 0\) and \(u = - U_{0} \left( \varphi \right)\) when \(r = a\).

The boundary condition associated with the energy equations in the porous region is given by

$$\begin{array}{*{20}l} {r = a}{:}\; \hfill & \begin{aligned} T_{\text{nf}} = T_{\text{w}} = {\text{Constant,}} \hfill \\ T_{\text{s}} = T_{\text{w}} = {\text{Constant}}, \hfill \\ \end{aligned} \end{array}$$
(13)
$$\begin{array}{*{20}l} {r = \infty} {:} \hfill & \begin{aligned} T_{\text{nf}} = T_{\infty } , \hfill \\ T_{\text{s}} = T_{\infty } . \hfill \\ \end{aligned} \hfill \\ \end{array}$$

and the two boundary conditions with respect to angular coordinate, \(\varphi\) are

$$\begin{aligned} T_{\text{nf}} \left( {r,0} \right) & = T_{\text{nf}} \left( {r,2\pi } \right) , T_{\text{s}} \left( {r,0} \right) = T_{\text{s}} \left( {r,2\pi } \right) , \\ \frac{{\partial T_{\text{nf}} \left( {r,0} \right)}}{\partial \varphi } & = \frac{{\partial T_{\text{nf}} \left( {r,2\pi } \right)}}{\partial \varphi } , \frac{{\partial T_{\text{s}} \left( {r,0} \right)}}{\partial \varphi } = \frac{{\partial T_{\text{s}} \left( {r,2\pi } \right)}}{\partial \varphi }, \\ \end{aligned}$$
(14)

where \(T_{\text{w}}\) is temperature of the cylinder surface and \(T_{\infty }\) denotes the freestream temperature.

Self-similar solutions

Reducing the governing Eqs. (1–7) by applying the following similarity transformations,

$$u = - \frac{{\bar{k} \cdot a}}{\sqrt \eta }f\left( {\eta ,\varphi } \right) ,\;v = \frac{{\bar{k} \cdot a}}{\sqrt \eta }G\left( {\eta ,\varphi } \right) , \;w = \left[ {2\bar{k}f ^{\prime } \left( {\eta ,\varphi } \right) - \frac{{\bar{k}}}{\eta }\frac{\partial G}{\partial \varphi }} \right]z , \;p = \rho_{\text{f}} \bar{k}^{2} a^{2} P,$$
(15)

in which \(\eta = \left( {\frac{r}{a}} \right)^{2}\) is the dimensionless radial variable, results in the following dimensionless equations. Relations (15) automatically satisfy the continuity of mass and substitution into Eqs. (2), (3) and (4) results in:

$$\begin{aligned} & \varepsilon \left[ {\eta f^{\prime \prime \prime } + - \frac{1}{{8\eta^{2} }}\frac{{\partial^{3} G}}{{\partial \varphi^{3} }} - \frac{1}{2}\frac{{\partial G^{\prime } }}{\partial \varphi } + \frac{1}{2\eta }\frac{{\partial G ^{\prime } }}{\partial \varphi } - \frac{1}{{2\eta^{2} }}\frac{\partial G}{\partial \varphi } + \frac{1}{4\eta }\frac{{\partial^{2} f^{\prime } }}{{\partial \varphi^{2} }}} \right] \\ & \quad + Re \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {1 + ff^{\prime } - \left( {f^{\prime } } \right)^{2} - \frac{f}{2\eta }\frac{{\partial G^{\prime } }}{\partial \varphi } + \frac{f}{{2\eta^{2} }}\frac{\partial G}{\partial \varphi } - \frac{G}{2\eta }\frac{{\partial f^{\prime } }}{\partial \varphi } + \frac{G}{{4\eta^{2} }}\frac{{\partial^{2} G}}{{\partial \varphi^{2} }}} \right. \\ & \quad \left. { + \frac{{f ^{\prime } }}{2\eta }\frac{\partial G}{\partial \varphi } - \frac{1}{{4\eta^{2} }}\left( {\frac{\partial G}{\partial \varphi }} \right)^{2} } \right] + \varepsilon^{2} \cdot \lambda \left[ {1 - f^{\prime } } \right] \pm \varepsilon^{2} \cdot A_{4} \cdot \lambda_{1} \cdot \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{nf}} \\ & \quad + \varepsilon^{2} \cdot Re \cdot M\left[ {1 + \frac{1}{2\eta }\frac{\partial G}{\partial \varphi } - f^{\prime } } \right] = 0, \\ \end{aligned}$$
(16)
$$\begin{aligned} P - P_{0} & = - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) - \frac{1}{{\varepsilon \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\left[ {\left( {\frac{{f^{\prime } }}{Re} - \frac{1}{4Re}\mathop \smallint \limits_{1}^{\eta } \frac{1}{{\eta^{2} }}\frac{{\partial^{2} f}}{{\partial \varphi^{2} }}{\text{d}}\eta + \frac{1}{2Re}\mathop \smallint \limits_{1}^{\eta } \frac{1}{{\eta^{2} }}\frac{\partial G}{\partial \varphi }{\text{d}}\eta } \right)} \right. \\ & \quad \left. { + \frac{\lambda }{Re}\mathop \smallint \limits_{1}^{\eta } \frac{f}{\eta }{\text{d}}\eta } \right] - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{1}{{A_{1} \left( {1 - \phi } \right)^{2.5} }}\frac{\lambda }{Re}} \right]\left( {\frac{z}{a}} \right)^{2} + \frac{1}{{\varepsilon^{2} }}\frac{1}{{\bar{k}^{2} }}\mathop \smallint \limits_{1}^{\eta } \frac{1}{{\eta^{2} }}\left[ {G^{2} + G\frac{\partial f}{\partial \varphi }} \right]{\text{d}}\eta , \\ \end{aligned}$$
(17)

where \(Re = \frac{{\bar{k} \cdot a^{2} }}{{2\upsilon_{\text{f}} }}\) is the freestream Reynolds number, \(\lambda = \frac{{a^{2} }}{{4k_{1} }}\) is the reciprocal of Darcy number, \(Gr = \frac{{g \cdot \beta_{\text{f}} \cdot a^{3} \cdot T_{\infty } }}{{16 \cdot \upsilon_{\text{f}}^{2} }}\) is the Grashof number, \(\lambda_{1} = \frac{Gr}{{Re^{2} }} = \frac{{g \cdot \beta_{\text{f}} \cdot T_{\infty } }}{{16 \cdot \upsilon_{\text{f}}^{2} }}\) is the dimensionless mixed convection, and prime indicates differentiation with respect to \(\eta\).

Considering Eqs. (10), (11), and (12), the boundary conditions for Eqs. (16) and (17) reduce to:

$$\eta = 1:\quad f ^{\prime } \left( {1,\varphi } \right) = 0 , \quad f\left( {1,\varphi } \right) = S\left( \varphi \right)$$
(18)
$$\eta \to \infty :\quad f ^{\prime } \left( {\infty ,\varphi } \right) = 0$$
(19)
$$f\left( {\eta ,0} \right) = f\left( {\eta ,2\pi } \right) , \; \frac{{\partial f\left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial f\left( {\eta ,2\pi } \right)}}{\partial \varphi },$$
(20)

where \(S\left( \varphi \right) = \frac{{U_{0} \left( \varphi \right)}}{{\bar{k} \cdot a}}\) is the transpiration rate function. Combining Eq. (15) with Eqs. (3) and (4) yields a differential equation in terms of \(G\left( {\eta ,\varphi } \right)\) and an expression for the pressure

$$\varepsilon \cdot \left( {\eta G ^{\prime \prime } + \frac{1}{4\eta }\frac{{\partial^{2} G}}{{\partial \varphi^{2} }} - \frac{1}{2\eta }\frac{\partial f}{\partial \varphi }} \right) + Re \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {f \cdot G ^{\prime } - \frac{G}{2\eta }\frac{\partial G}{\partial \varphi }} \right] - \varepsilon^{2} \cdot G \cdot \left[ {\lambda + M} \right] = 0.$$
(21)

Considering conditions (10)–(12), the boundary and initial conditions for Eq. (21) can be written as

$$\eta = 1:\quad G\left( {1,\varphi } \right) = 0 , \;\frac{{\partial G\left( {1,\varphi } \right)}}{\partial \varphi } = 0$$
(22)
$$\eta \to \infty :\quad G\left( {\infty ,\varphi } \right) = 0$$
(23)
$$G\left( {\eta ,0} \right) = G\left( {\eta ,2\pi } \right) , \frac{{\partial G\left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial G\left( {\eta ,2\pi } \right)}}{\partial \varphi }$$
(24)

Equation (5) is non-dimensionalised by using the following transformation

$$\theta \left( {\eta ,\varphi } \right) = \frac{{T\left( {\eta ,\varphi } \right) - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},$$
(25)

and therefore

$$T\left( {\eta ,\varphi } \right) = T_{\infty } \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta } \right],$$
(26)

By substituting Eqs. (15) and (26) into Eq. (5) and neglecting the small dissipation terms, the following equation is derived.

$$\eta \theta ^{\prime \prime }_{\text{nf}} + \theta ^{\prime }_{\text{nf}} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{nf}} }}{{\partial \varphi^{2} }} + Re \cdot Pr \cdot \frac{{A_{2} }}{{A_{3} }} \cdot \left( {f \cdot \theta ^{\prime }_{\text{nf}} - \frac{G}{2\eta }\frac{{\partial \theta_{\text{nf}} }}{\partial \varphi }} \right) + \frac{Bi}{{A_{3} }}\left( {\theta_{\text{s}} - \theta_{\text{nf}} } \right) = 0,$$
(27)

in which \(\theta_{\text{w}} = \frac{{T_{\text{w}} }}{{T_{\infty } }}\) is the temperature parameter, \(Bi = \frac{{h_{\text{sf}} a_{\text{sf}} \cdot a^{2} }}{{4k_{\text{f}} }}\) is the Biot number, \(R_{\text{d}} = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3k^{*} \cdot k_{\text{s}} }}\) is the radiation parameter, and the thermal boundary conditions for the nanofluid phase reduce to

$$\eta = 1:\quad \theta_{\text{nf}} \left( {1,\varphi } \right) = 1$$
(28a)
$$\eta \to \infty :\quad \theta_{\text{nf}} \left( {\infty ,\varphi } \right) = 0$$
(28b)
$$\theta_{\text{nf}} \left( {\eta ,0} \right) = \theta_{\text{nf}} \left( {\eta ,2\pi } \right) ,\; \frac{{\partial \theta_{\text{nf}} \left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial \theta_{\text{nf}} \left( {\eta ,2\pi } \right)}}{\partial \varphi }$$
(29a,b)

Substitution of Eqs. (15) and (26) into Eq. (8) results in

$$\eta \theta ^{\prime \prime }_{\text{s}} + \theta ^{\prime }_{\text{s}} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{s}} }}{{\partial \varphi^{2} }} - Bi \cdot \gamma \cdot \left( {\theta_{\text{s}} - \theta_{\text{nf}} } \right) + R_{\text{d}} \cdot \frac{\partial }{\partial \eta }\left[ {\eta \cdot \left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{s}} } \right)^{3} \cdot \acute{\theta }_{\text{s}} } \right] = 0,$$
(30)

where \(\gamma = \frac{{k_{\text{f}} }}{{k_{\text{s}} }}\) is the modified conductivity ratio and the thermal boundary conditions for the solid phase of the porous medium are as follows

$$\eta = 1: \quad \theta_{\text{s}} \left( {1,\varphi } \right) = 1$$
(31a)
$$\eta \to \infty :\quad \theta_{\text{s}} \left( {\infty ,\varphi } \right) = 0$$
(31b)
$$\theta_{\text{s}} \left( {\eta ,0} \right) = \theta_{\text{s}} \left( {\eta ,2\pi } \right) , \;\frac{{\partial \theta_{\text{s}} \left( {\eta ,0} \right)}}{\partial \varphi } = \frac{{\partial \theta_{\text{s}} \left( {\eta ,2\pi } \right)}}{\partial \varphi }$$
(32,b)

In Eqs. (16), (17), (21) and (27), A1, A2, A3 and A4 are constants in the following forms:

$$\begin{array}{*{20}l} {A_{1} = \left( {1 - \phi } \right) + \frac{{\rho_{\text{np}} }}{{\rho_{\text{f}} }}\phi ,} \hfill & {A_{2} = \left( {1 - \phi } \right) + \frac{{\left( {\rho \cdot C_{\text{p}} } \right)_{\text{np}} }}{{\left( {\rho \cdot C_{\text{p}} } \right)_{\text{f}} }}\phi } \hfill \\ {A_{3} = \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{k_{\text{np}} + 2k_{\text{f}} - 2\phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}}{{k_{\text{np}} + 2k_{\text{f}} + 2\phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}},} \hfill & {A_{4} = \left( {1 - \phi } \right) + \frac{{\left( {\rho \cdot \beta } \right)_{\text{np}} }}{{\left( {\rho \cdot \beta } \right)_{\text{f}} }}\phi } \hfill \\ \end{array}$$
(33)

It is noted that Eq. (27) is the complete form of Eqs. (14) in Ref. [40]. Equations (16), (21), (27) and (30), and the boundary conditions (18–20), (22–24), (28–29) and (31–32), were numerically solved by employing an implicit, iterative tri-diagonal finite-difference method [41,42,43].

$$G\left( {\eta ,\varphi } \right) = 0$$
$$\begin{aligned} & \varepsilon \left[ {\eta f ^{\prime \prime \prime } + f ^{\prime \prime } + \frac{1}{4\eta }\frac{{\partial^{2} f^{\prime } }}{{\partial \varphi^{2} }}} \right] + Re \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} \left[ {1 + ff^{\prime } - \left( {f ^{\prime } } \right)^{2} } \right] \\ & \quad + \varepsilon^{2} \cdot \lambda \left[ {1 - f^{\prime } } \right] \pm \varepsilon^{2} \cdot A_{4} \cdot \lambda_{1} \cdot \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{nf}} + \varepsilon^{2} \cdot Re \cdot M\left[ {1 - f^{\prime } } \right] = 0, \\ \end{aligned}$$
(34)
$$\begin{aligned} P - P_{0} & = - \frac{1}{{2\varepsilon^{2} }}\left( {\frac{{f^{2} }}{\eta }} \right) - \frac{1}{{\varepsilon \cdot A_{1} \cdot \left( {1 - \phi } \right)^{2.5} }}\left[ {\left( {\frac{{\acute{f}}}{Re} - \frac{1}{4Re}\mathop \smallint \limits_{1}^{\eta } \frac{1}{{\eta^{2} }}\frac{{\partial^{2} f}}{{\partial \varphi^{2} }}{\text{d}}\eta } \right) + \frac{\lambda }{Re}\mathop \smallint \limits_{1}^{\eta } \frac{f}{\eta }{\text{d}}\eta } \right] \\ & \quad - 2\left[ {\frac{1}{{\varepsilon^{2} }} + \frac{1}{{A_{1} \left( {1 - \phi } \right)^{2.5} }}\frac{\lambda }{Re}} \right]\left( {\frac{z}{a}} \right)^{2} , \\ \end{aligned}$$
(35)
$$\eta \theta ^{\prime \prime }_{\text{nf}} + \theta ^{\prime }_{\text{nf}} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{nf}} }}{{\partial \varphi^{2} }} + Re \cdot Pr \cdot \frac{{A_{2} }}{{A_{3} }} \cdot \left( {f \cdot \theta^{\prime }_{\text{nf}} } \right) + \frac{Bi}{{A_{3} }}\left( {\theta_{\text{s}} - \theta_{\text{nf}} } \right) = 0,$$
(36)
$$\eta \theta ^{\prime \prime }_{\text{s}} + \theta ^{\prime }_{\text{s}} + \frac{1}{4\eta }\frac{{\partial^{2} \theta_{\text{s}} }}{{\partial \varphi^{2} }} - Bi \cdot \gamma \cdot \left( {\theta_{\text{s}} - \theta_{\text{nf}} } \right) + R_{\text{d}} \cdot \frac{\partial }{\partial \eta }\left[ {\eta \cdot \left( {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{s}} } \right)^{3} \cdot \acute{\theta }_{\text{s}} } \right] = 0.$$
(37)

Shear stress and Nusselt number

The shear stress induced by the nanofluid flow on the external surface of the cylinder is given by:

$$\sigma = \mu_{\text{nf}} \left[ {\frac{\partial w}{\partial r}} \right]_{{{\text{r}} = {\text{a}}}} ,$$
(38)

where \(\mu_{\text{nf}}\) is the nanofluid viscosity. Employing Eq. (15), a semi-similar solution for the shear stress on the surface of the cylinder can be developed. This reads

$$\sigma = \mu_{\text{nf}} \frac{2}{a}\left[ {2\bar{k}zf^{\prime \prime } \left( {1,\varphi } \right)} \right]\mathop \Rightarrow \limits^{{}} \frac{\sigma \cdot a}{{4\mu \bar{k}z}} = \left( {1 - \acute{\phi }} \right)^{ - 2.5} f^{\prime } \left( {1,\varphi } \right).$$
(39)

The local heat transfer coefficient and rate of heat transfer are defined by the following relations

$$h = \frac{{q_{\text{w}} }}{{T_{\text{w}} - T_{\infty } }} = \frac{{ - k_{\text{nf}} \left( {\frac{{\partial T_{\text{nf}} }}{\partial r}} \right)_{{{\text{r}} = {\text{a}}}} }}{{T_{\text{w}} - T_{\infty } }} = - \frac{{2k_{\text{nf}} }}{a}\frac{{\partial \theta_{\text{nf}} \left( {1,\varphi } \right)}}{\partial \eta },$$
(40)

and

$$q_{\text{w}} = - \frac{{2k_{\text{nf}} }}{a}\frac{{\partial \theta_{\text{nf}} \left( {1,\varphi } \right)}}{\partial \eta }(T_{\text{w}} - T_{\infty } ).$$
(41)

Therefore, Nusselt number is expressed as

$$Nu_{\text{nf}} = \frac{h \cdot a}{{2k_{\text{f}} }} = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\acute{\theta }_{\text{nf}} \left( {1,\varphi } \right) = - A_{3} \cdot \acute{\theta }_{\text{nf}} \left( {1,\varphi } \right).$$
(42)

Entropy generation

The volumetric rate of local entropy generation in the porous region of the problem can be expressed by the following relation [44,45,46,47,48]:

$$\begin{aligned} \dot{S}^{\prime \prime \prime }_{\text{gen}} & = \frac{{k_{\text{nf}} }}{{T_{\text{nf}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{nf}} }}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{{\partial T_{\text{nf}} }}{\partial \varphi }} \right)^{2} } \right] + \frac{{k_{\text{s}} }}{{T_{\text{s}}^{2} }}\left[ {\left( {\frac{{\partial T_{\text{s}} }}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{{\partial T_{\text{s}} }}{\partial \varphi }} \right)^{2} + \frac{{16\sigma^{*} }}{{3k^{*} }}T_{\text{s}}^{3} \left( {\frac{{\partial T_{\text{s}} }}{\partial r}} \right)^{2} } \right] \\ & \quad + h_{\text{sf}} a_{\text{sf}} \left( {T_{\text{s}} - T_{\text{nf}} } \right)\left[ {\frac{1}{{T_{\text{nf}} }} - \frac{1}{{T_{\text{s}} }}} \right] + \frac{{2\mu_{\text{nf}} }}{{T_{\infty } }}\left[ {\left( {\frac{\partial u}{\partial r}} \right)^{2} + \left( {\frac{u}{r}} \right)^{2} + \left( {\frac{\partial w}{\partial z}} \right)^{2} } \right] \\ & \quad + \frac{{\mu_{\text{nf}} }}{{T_{\infty } }}\left[ {\left( {\frac{1}{r}\frac{\partial w}{\partial \varphi }} \right)^{2} + \left( {\frac{\partial w}{\partial r}} \right)^{2} + \left( {\frac{1}{r}\frac{\partial u}{\partial \varphi }} \right)^{2} } \right] + \frac{{\mu_{\text{nf}} }}{{k_{1} T_{\infty } }}\left[ {u^{2} + w^{2} } \right] + \frac{{\bar{\sigma }B_{0}^{2} }}{{T_{\infty } }}w^{2} , \\ \end{aligned}$$
(43)

where \(N_{\text{G}} = \frac{{\dot{S} ^{\prime \prime \prime }_{\text{gen}} }}{{\dot{S} ^{\prime \prime \prime }_{0} }}\) and \(\dot{S} ^{\prime \prime \prime }_{0} = \frac{{8k_{\text{f}} \cdot \left( {T_{\text{w}} - T_{\infty } } \right)^{2} \upsilon_{\text{f}} }}{{\bar{k} \cdot a^{4} \cdot T_{\infty }^{2} }}\) are the characteristic entropy generation rate. Using the similarly variables given in Eqs. (15) and (43), the non-dimensional form of local entropy generation (NG) is given by

$$\begin{aligned} N_{\text{G}} & = \frac{{Re \cdot A_{3} \cdot \theta_{\text{w}}^{2} }}{{\left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{nf}} } \right]^{2} }}\left[ {\eta \theta _{\text{nf}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{nf}} }}{\partial \varphi }} \right)^{2} } \right] \\ & \quad + \frac{{Re \cdot \theta_{w}^{2} }}{{\gamma \cdot \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{s} } \right]^{2} }}\left[ {\eta \theta _{\text{s}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{s}} }}{\partial \varphi }} \right)^{2} } \right. \\ & \quad \left. { + \frac{{R_{\text{d}} }}{{\left( {\theta_{\text{w}} - 1} \right)^{2} }}\eta \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{s}} } \right]^{3} \cdot \left[ {\left( {\theta_{w} - 1} \right) \cdot \theta \prime_{\text{s}} } \right]^{2} } \right] \\ & \quad + Bi \cdot Re\frac{{\theta_{\text{w}}^{2} }}{{\left( {\theta_{\text{w}} - 1} \right)}}\left( {\theta_{\text{s}} - \theta_{\text{nf}} } \right) \cdot \left[ {\frac{1}{{1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{nf}} }} - \frac{1}{{1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{s}} }}} \right] \\ & \quad + \frac{{Re \cdot Br \cdot \theta_{\text{w}} }}{{\left( {\theta_{\text{w}} - 1} \right)}}\left( {1 - \phi } \right)^{ - 2.5} \left\{ {\left[ {\eta f ^{\prime \prime 2} + 4f ^{\prime 2} + \left( {\frac{f}{\eta }} \right)^{2} - 2\frac{{ff ^{\prime } }}{\eta } + \frac{1}{\eta }\left( {\frac{{\partial f ^{\prime } }}{\partial \varphi }} \right)^{2} } \right.} \right. \\ & \quad \left. {\left. { + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \lambda \left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f^{\prime 2} } \right] + 2Mf^{\prime 2} } \right\}, \\ \end{aligned}$$
(44)

in which \(Br = \frac{{\mu_{\text{f}} \left( {\bar{k} \cdot a} \right)^{2} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_{\infty } } \right)}}\) is the Brinkman number. The Bejan number, defined as the ratio of entropy generation by heat transfer to the total entropy generation, can be further expressed as

$$\begin{aligned} Be & = \left[ {\frac{{Re \cdot A_{3} \cdot \theta_{\text{w}}^{2} }}{{\left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{nf}} } \right]^{2} }}\left[ {\eta \theta _{\text{nf}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{nf}} }}{\partial \varphi }} \right)^{2} } \right] + \frac{{Re \cdot \theta_{\text{w}}^{2} }}{{\gamma \cdot \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{\text{s}} } \right]^{2} }}} \right.\left[ {\eta \theta _{\text{s}}^{\prime 2} + \frac{1}{{4\eta^{2} }}\left( {\frac{{\partial \theta_{\text{s}} }}{\partial \varphi }} \right)^{2} } \right. \\ & \quad {{\left. { + \frac{{R_{\text{d}} }}{{\left( {\theta_{\text{w}} - 1} \right)^{2} }}\eta \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{s} } \right]^{3} \cdot \left[ {\left( {\theta_{\text{w}} - 1} \right) \cdot \theta^{\prime }_{\text{s}} } \right]^{2} } \right]} \mathord{\left/ {\vphantom {{\left. { + \frac{{R_{\text{d}} }}{{\left( {\theta_{\text{w}} - 1} \right)^{2} }}\eta \left[ {1 + \left( {\theta_{\text{w}} - 1} \right)\theta_{s} } \right]^{3} \cdot \left[ {\left( {\theta_{\text{w}} - 1} \right) \cdot \theta^{\prime }_{\text{s}} } \right]^{2} } \right]} {\left[ {\frac{{Re \cdot Br \cdot \theta_{\text{w}} }}{{\left( {\theta_{\text{w}} - 1} \right)}}\left( {1 - \phi } \right)^{ - 2.5} \left\{ {\left[ {\eta f ^{\prime \prime 2} + 4f ^{\prime 2} + \left( {\frac{f}{\eta }} \right)^{2} - 2\frac{{ff ^{\prime } }}{\eta }} \right.} \right.} \right.}}} \right. \kern-0pt} {\left[ {\frac{{Re \cdot Br \cdot \theta_{\text{w}} }}{{\left( {\theta_{\text{w}} - 1} \right)}}\left( {1 - \phi } \right)^{ - 2.5} \left\{ {\left[ {\eta f ^{\prime \prime 2} + 4f ^{\prime 2} + \left( {\frac{f}{\eta }} \right)^{2} - 2\frac{{ff ^{\prime } }}{\eta }} \right.} \right.} \right.}} \\ & \quad \left. {\left. {\left. { + \frac{1}{\eta }\left( {\frac{{\partial f ^{\prime } }}{\partial \varphi }} \right)^{2} + \frac{1}{{4\eta^{2} }}\left( {\frac{\partial f}{\partial \varphi }} \right)^{2} } \right] + \lambda \left[ {\left( {\frac{f}{\eta }} \right)^{2} + 4f ^{\prime 2} } \right] + 2Mf ^{\prime 2} } \right]} \right\}. \\ \end{aligned}$$
(45)

Grid independency and validation

To verify grid independency of the numerical solution, Table 1 reports the average value of Nusselt and Bejan number as well as dimensionless shear stress with varying mesh densities of \(51 \times 18\), \(102 \times 36\), \(204 \times 72\), \(408 \times 144\) and \(816 \times 288\). It is clear from Table 1 that there are no considerable changes of \(Nu_{\text{m}}\) and \(Be_{\text{m}}\) for (\(\eta ,\varphi\)) mesh sizes of (\(204 \times 72\)), (\(408 \times 144\)) and (\(816 \times 288\)). Hence, in this work a (\(408 \times 144\)) grid in \(\eta - \varphi\) directions was used for the computational domain reported. A non-uniform grid was implemented in \(\eta\)-direction to resolve the strong gradients around the external surface of the cylinder, and a uniform mesh was applied in \(\varphi\) direction. The computational domain extends over \(\varphi_{\hbox{max} } = 360^\circ\) and \(\eta_{\hbox{max} } = 15\), where \(\eta_{\hbox{max} }\) corresponds to \(\eta \mathop \to \limits_{{}} \infty\). It is noted that, for all investigated cases, the computational domain fully contains the entire momentum and thermal boundary layers. Figure 2 shows the computational grid utilised in the current study. A convergence criterion was applied to the numerical simulations, in which when the difference between the two consecutive iterations became less than \(10^{ - 7}\). The solution was considered to have converged and therefore the iterative process was terminated. The numerical error of the implemented numerical scheme is estimated to be of \(O(\Delta \eta )^{2}\) [41,42,43]. The solutions developed in “Self-similar solutions” and “Shear stress and Nusselt number” sections were validated by comparing the average Nusselt number, shear stress and velocity parameters with those obtained from the literature for flows over cylinders with no transpiration and infinitely large permeability. Tables 2, 3 and 4 show the outcomes of this comparison. The excellent agreement between the two datasets confirms validity of the numerical simulations.

Table 1 Grid independence study at \(Re = 10,\; \lambda = 10,\;\lambda_{1} = 1.0,\; M = 1.0, \;Bi = 0.1,\;R_{\text{d}} = 1.0,\; \theta_{\text{w}} = 1.2\)
Full size table
Fig. 2
figure 2

The computational grid used in this study

Full size image
Table 2 Comparison between the current results and those of Gorla [49] on average Nusselt number and average shear stress for different values of magnetic parameter when \(Re = 100,\; \lambda = 0,\; \phi = 0,\;\lambda_{1} = 1.0,\;Bi = 1000,\; R_{\text{d}} = 0\)
Full size table
Table 3 Comparison between the present work and the results of Gorla [51] in the limit of very large porosity and permeability
Full size table
Table 4 Comparison between the present work and the results of Wang [50] in the limit of very large porosity and permeability
Full size table

Results and discussion

Two types of fluid including pure water and a CuO–water nanofluid, with varying concentration of nanoparticles, are used in the rest of this study. Table 5 summarises the thermophysical properties of the nanofluid, and Table 6 provides the default values of the pertinent parameters.

Table 5 Thermo-physical properties of the base fluid and nanoparticle [36]
Full size table
Table 6 Default values of the simulation parameters
Full size table

Temperature field, Nusselt number and friction coefficient

The hydrodynamics of nanofluids under magnetic effects are already well investigated [32], and therefore they are not further elaborated in here. Nonetheless, to illustrate the flow field, Fig. 3a depicts the distribution of f (see Eq. 15) for different values of Reynold number. Complexity of the flow field is completely evident in this figure. The radial flow field includes a stagnation and a low-velocity region that form as a result of the interactions between the impinging uniform flow and the non-uniform transpiration (see Fig. 1). This low-velocity region diminishes in size as the value of Reynold number increases. Figure 3b illustrates the variations in the temperature field of the nanofluid induced by the changes in Reynold number. As expected, at low Reynolds numbers the temperature field is nearly symmetric, and the thermal boundary layer is uniform and thick. However, increase in Reynolds number changes this significantly and results in reducing the thickness of thermal boundary layer. This is due to the well-known dependency of the thickness of velocity boundary layer upon Reynolds number and the relation between the thicknesses of thermal and velocity boundary layers through Prandtl number [52]. An exception to this general behaviour is the low-velocity region in which the thickness of the boundary layer remains large.

Fig. 3
figure 3

Effects of Reynolds number on a\(f\left( {\eta ,\varphi } \right)\), b\(\theta_{\text{nf}} \left( {\eta ,\varphi } \right)\), \(\phi = 0. 1 , \;M = 1.0 , \;R_{\text{d}} = 1.0, \;\lambda = 10 , \;\lambda_{1} = 1.0 ,\;Bi = 0.1\)

Full size image

Figure 4a shows the influences of volumetric concentration of nanoparticles on the nanofluid temperature field. Increasing the volumetric concentration of nanoparticles from 0 to 10% has resulted in a noticeable increase in the thickness of the thermal boundary layer. This can be explained by noting that thermal conductivity of the nanofluid increases by magnifying the volumetric concentration of nanoparticles. The resultant increase in the thermal diffusivity of the nanofluid is the reason for the observed thickening of the boundary layer. Figure 4b shows that variations in the mixed convection parameter do not have any noticeable influences upon most of the thermal boundary layer. Yet, increases in the value of mixed convection parameter lead to shrinkage of the high-temperature spot around the low-velocity region (see Fig. 3a), which could be due to the relative weakening of inertia forces.

Fig. 4
figure 4

\(\theta_{\text{nf}} \left( {\eta ,\varphi } \right)\) for varying values of a nanoparticle volume fraction, b mixed convection parameter \(R_{\text{d}} = 2.0, \; \phi = 0. 05, \;M = 0 , \;Re = 10 , \;Bi = 0.1 , \;\lambda = 10 , \; \lambda_{1} = 1.0\)

Full size image

Figure 5 shows the response of the nanofluid and porous solid temperature fields to the increases in radiation parameter. By introduction of thermal radiation (increasing Rd from 0 to 1), the thickness of thermal boundary layer in nanofluid and the thickness of the heated porous solid have increased noticeably. In the current modelling setting, radiation can be viewed as an added thermal diffusivity and thus introduction of thermal radiation is equivalent to making the medium more diffusive. It is well known that increases in thermal diffusivity lead to deeper thermal penetration lengths in the solid phase. This increase in thermal diffusivity thickens the thermal boundary layer in the nanofluid phase by means of heat exchanges between the porous solid and nanofluid phase. Figure 6 shows that Biot number is a key parameter affecting the temperature fields of nanofluid and porous solid phase. At low Biot numbers (Bi = 0.1), the two temperature fields can be significantly different, in which the temperature of the solid phase is much higher than that of nanofluid phase. This is because of the poor heat exchanges between solid and nanofluid phases at low Biot numbers. However, at higher Biot numbers (e.g. Bi = 10) the two temperature fields feature major similarities, as there is now a strong capability for the exchange of heat between the two phases. Theoretically, it is expected that in the limit of infinite Biot number the solid and nanofluid temperature fields become identical, and therefore a local thermal equilibrium (LTE) condition applies. However, as depicted by Fig. 6, the two temperature fields at low values of Biot numbers can be quite distinctive. This clearly reflects the importance of employing a local thermal non-equilibrium approach in the current problem.

Fig. 5
figure 5

Effects of radiation parameter on a\(\theta_{\text{nf}} \left( {\eta ,\varphi } \right)\), b\(\theta_{\text{s}} \left( {\eta ,\varphi } \right)\), \(\phi = 0. 05, \;M = 0,\;Re = 10,\;Bi = 0.1, \;\lambda = 10, \;\lambda_{1} = 1.0\)

Full size image
Fig. 6
figure 6

Effects of Biot number on a\(\theta_{\text{s}} \left( {\eta ,\varphi } \right)\), b\(Be\left( {\eta ,\varphi } \right)\), \(\phi = 0. 05, \;M = 1.0, \;Re = 10, \;R_{\text{d}} = 1.0, \;Br = 2.0, \;\lambda = 10, \;\lambda_{1} = 1.0,\;\theta_{\text{W}} = 1.2\)

Full size image

Figures 7 and 8 show the circumferential variation of Nusselt number as the pertinent parameters vary. Further information on variations of the circumferentially averaged Nusselt number with these parameters is provided in Tables 7, 8 and 9. Figure 7 shows that increases in Biot number lead to a significant drop of Nusselt number for a large fraction of the cylinder circumference. This is an important result from the modelling viewpoint, as it indicates that LTE models, which effectively assume very large Biot numbers, may highly underpredict the numerical value of Nusselt number. Hence, the use of LTNE modelling is an important necessity in the current problem. According to Fig. 7b, temperature parameter plays a key role in determining the value of Nusselt number. Increasing the temperature parameter can lead to large enhancement of heat transfer coefficient when forced and natural convection is of comparable significance. This is due to the direct dependency of energy equation (see Eq. 27) and thus natural convection upon the wall temperature. At higher values of temperature parameters, natural convection is stronger and as long as mixed convection parameter is around or below unity, the Nusselt number is enhanced. Figure 7c confirms that increases in the concentration of nanoparticles magnify the value of Nusselt number. This can be attributed to the higher thermal conductivity of nanofluid with larger concentration of nanofluid. The observed trend is consistent with that reported in other studies of nanofluid flow in porous media, see for example Refs. [33, 34].

Fig. 7
figure 7

Variation of \(Nu\) for different values of a Biot number (\(Bi\)), b temperature parameter (\(\theta_{\text{w}}\)), c nanoparticle volume fraction (\(\phi\)), d Reynolds number (\(Re\)), \(Re = 5.0,\;Bi = 0.1,\; \gamma = 1.5, \;\lambda = 10\)

Full size image
Fig. 8
figure 8

Variation of \(Nu\) for different values of a radiation parameter (\(R_{\text{d}}\)), b dimensionless mixed convection (\(\lambda_{1}\)), c permeability parameter (\(\lambda\)), d Magnetic parameter (\(M\)), \(R_{\text{d}} = 1.0,\;Re = 5.0,\;Bi = 0.1,\; \gamma = 1.5,\; \lambda = 10\)

Full size image
Table 7 Effects of Biot number, modified conductivity ratio and on average Nusselt and Bejan numbers number when \(Re = 1.0, \;\lambda = 10,\; \lambda_{1} = 1.0, \;M = 1.0,\; Bi = 0.1, \;R_{\text{d}} = 1.0, \;\theta_{\text{w}} = 1.2, \;\phi = 0.1\)
Full size table
Table 8 Effects of mixed convection, permeability and magnetic parameter on average Nusselt and Bejan number when, \(Re = 1.0, \;\lambda = 10, \;\lambda_{1} = 1.0, \;M = 1.0, \;Bi = 0.1,\; R_{\text{d}} = 1.0 , \;\theta_{\text{w}} = 1.2\)
Full size table
Table 9 Effects of Reynolds and Prandtl number and temperature parameter on average Nusselt and Bejan number when, \(Re = 1.0, \;\lambda = 10, \;\lambda_{1} = 1.0, \;M = 1.0, \;Bi = 0.1,\; R_{\text{d}} = 1.0 , \;\theta_{\text{w}} = 1.2\)
Full size table

It is well established that, in general, Reynold number dominates forced convection of heat and thus Nusselt number is strongly enhanced by increases in Reynolds number [52]. In keeping with this generic view, Fig. 7d shows that increasing Reynolds number can substantially increase the value Nusselt number. Table 9 shows that increasing the value of Reynolds number from 1 to 100 leads to an enhancement of Nusselt number by almost 15 times. Figure 8a indicates that increases in radiation parameter can result in major enhancement of Nusselt number. According to Table 7, increasing radiation parameter from 0 to 7 increases the value of circumferentially average Nusselt number by more than 80%, reflecting the strong influence of this parameter upon the heat transfer process. As discussed earlier, increases in the radiation parameter are equivalent to enhancement of the thermal conductivity of the solid phase which then leads to improvement of heat transfer in the nanofluid phase. The values of mixed convection parameter greater than one can slightly enhance Nusselt number and the inverse effect is observed for negative values of mixed convection parameter (see Fig. 7b). Figure 8c and d shows that changes in the permeability of the porous medium and intensity of the magnetic field have modest effects upon Nusselt number.

Thermodynamic irreversibilities

Figure 9 shows the distribution of Bejan number and entropy generation number in the domain with varying values of radiation parameter, while Table 7 provides the average value of Bejan number. As discussed in the previous section, increases in radiation parameter boosts Nusselt number. The resultant increase in heat transfer rate relaxes the temperature gradients in the system and thus reduces the thermal irreversibilities. This is depicted by Fig. 9a and in the reported values of average Bejan number in Table 7. The complex nature of entropy generation in the current problem is well reflected by Fig. 9b. Switching from pure water to nanofluid appears to have a strong effect upon the distribution of Bejan number (see Fig. 10a). In the absence of nanoparticles (\(\phi = 0)\) large values of Bejan number can be found in most of the domain. Addition of nanoparticles with \(\phi = 0.05\), results in a considerable reduction of Bejan number, while increasing the volumetric concentration to 0.1 eliminates all large values of Bejan number. This can be readily explained by noting the influences of nanoparticles on heat transfer coefficient. It was shown in “Temperature field, Nusselt number and friction coefficient” section that increases in the concentration of nanoparticles results in augmentation of Nusselt number and therefore enhances the heat transfer process. Consequently, the temperature gradients are partially relaxed and thus less thermal irreversibility is encountered.

Fig. 9
figure 9

Effects of radiation parameter on a\(Be\left( {\eta ,\varphi } \right)\), b\(N_{\text{G}} \left( {\eta ,\varphi } \right)\), \(Br = 2.0, \;\phi = 0. 05, \;M = 0,\;Re = 10 , \;Bi = 0.1, \;\lambda = 10,\; \lambda_{1} = 1.0\)

Full size image
Fig. 10
figure 10

Effects of nanoparticle volume fraction on a\(Be\left( {\eta ,\varphi } \right)\), b\(N_{\text{G}} \left( {\eta ,\varphi } \right)\)\(R_{\text{d}} = 2.0,\; Br = 2.0,\; M = 1.0,\;Re = 10,\; Bi = 0.1,\; \lambda = 10,\; \theta_{\text{W}} = 1.2\)

Full size image

Figure 11 depicts the effects of intensity of the magnetic field on the distribution of Bejan number and temperature of nanofluid. According to this figure, increasing the magnetic parameter by an order of magnitude does not result in any noticeable modification in Bejan number and nanofluid temperature. Nonetheless, intensification of the magnetic field by another two orders of magnitude causes a considerable reduction of Bejan number (as also confirmed by Table 8). Figure 8d shows that enhancement of Nusselt number with increases in magnetic field is rather small. Further, it can be seen from Fig. 11b that nanofluid temperature field hardly changes with variation of magnetic parameter for a few orders of magnitude. Magnetic field does not have any direct effect on the transport of thermal energy in the current problem and its indirect influences are manifested through the velocity field. Nonetheless, since low velocities are an inherent characteristic of stagnation-point flows, magnetohydrodynamic effects on the investigated heat transfer processes are not significant. Hence, the observed changes in Bejan number are induced by frictional irreversibility. It has been already demonstrated that intensifying the magnetic field increases frictional forces and hinders the nanofluid flow [31]. As a result, hydrodynamic entropy generation increases significantly, while thermal irreversibly has remained nearly unchanged. The net effect is reduction of Bejan number as shown in Fig. 11.

Fig. 11
figure 11

Effects of magnetic parameter on a\(Be\left( {\eta ,\varphi } \right)\), b\(\theta_{\text{nf}} \left( {\eta ,\varphi } \right)\), \(\phi = 0. 05,\; M = 1.0,\;Re = 100,\; R_{\text{d}} = 1.0,\;Br = 2.0,\; \lambda = 10,\; \lambda_{1} = 1.0,\;Bi = 0.1\)

Full size image

Conclusions

Transfer of heat and generation of entropy by the combined mode of radiation-convection was investigated numerically. The investigated problem included a stagnation-point flow over a cylinder embedded in a porous medium and subject to non-uniform transpiration. The three-dimensional Darcy–Brinkman model of momentum transport in porous media along with two-equation (LTNE) model of transport of thermal energy were solved in cylindrical coordinate through using a semi-similarity technique. The mathematical model considered non-thermal linear radiation, magnetohydrodynamics and mixed convection. Temperature fields of nanofluid and porous solid as well as Bejan number field were presented under varying parameters. Further, the angular distribution and the circumferentially averaged values of Nusselt number were reported. The key findings of this study can be summarised as follows.

  • Increases in the volumetric concentration of nanoparticles result in the thickening of thermal boundary layer, enhancement of Nusselt number and reduction of Bejan number.

  • Increases in radiation parameter strongly increase the value of Nusselt number, while it also reduces the average Bejan number.

  • Variation in Biot number can considerably affect the value of Nusselt and Bejan number. Hence, the use of local thermal non-equilibrium (LTNE) approach is essential for ensuring accurate prediction of heat transfer rates.

  • Magnetic effects have small influences upon Nusselt number. However, they can majorly modify Bejan number distribution by altering the frictional irreversibility of the flow.

As a closing remark, it is emphasised that the presented work was the first investigation of heat transfer and entropy generation in non-flat configurations that considered nonlinear radiation, magnetic effects and local thermal non-equilibrium in porous media.