Introduction

Human hair, together with fibres such as wool and mohair, is a member of the group of α-keratin fibres, which grow from follicles, embedded in the skin. As a consequence of cell differentiation during growth, the fibres develop a very complex structure on the cellular as well as molecular level [1,2,3].

The most important components on cellular level are the cuticle, as outer layer, and the fibre core (cortex). On the molecular level, cells contain partly α-helical intermediate filaments (IF), embedded into an amorphous matrix of IF-associated proteins (IFAPs). These two components are the basis for the standard, so-called two-phase, fibre/matrix composite model for keratin [4]. This model, where the filaments are associated on a molecular level with the helical structures in the IFs and the matrix comprises the remainder of the amorphous materials, is generally quite successful as approach to the interpretation of results derived from mechanical as well as thermal analyses [4,5,6]. For specialized analytical situations, more complex models have been developed [7,8,9,10].

To assess differences of hair types and changes to the structural components of hair by cosmetic processes, products and ingredients, both tensile testing and thermal analysis, namely, in the form of differential scanning calorimetry (DSC), are important tools [3, 11,12,13,14,15,16].

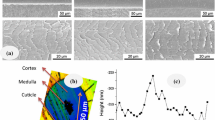
Figure 1a shows schematically the stress–strain curve of a hair fibre in water, showing three distinct regions and highlighting qualitatively the contributions from IFs and matrix [5].

Fig. 1
figure 1

a Typical stress–strain curve for hair in water up to the break (black line) (adapted from Ref. [5]), showing the components associated with the IFs (blue line) and matrix (red line). The elastic modulus wet, Ew, is indicated as the slope of the initial, quasi-elastic [32] region of the curve. The inset shows the two-phase filament matrix composite model, generally applied for data interpretation. b Typical DSC curve for Caucasian hair in water (adapted from Ref. [30]). TD, denaturation temperature. ΔHD, denaturation enthalpy. The inset shows the two-phase helix/matrix model for the fibre cortex, as basis for DSC data analysis. (Color figure online)

Full size image

For the evaluation of tensile testing results, the contribution of the cuticle is generally neglected despite its comparatively high modulus [9, 17], due to its low cross-sectional area fraction (approx. 10%) [18]. In view of the two-phase composite model, the elastic tensile modulus (Young’s modulus, E) is thus the combination of the elastic contribution by the party α-helical IFs and the viscoelastic contribution of the amorphous matrix [5, 19,20,21,22]. Tensile testing to detect changes of fibre properties is preferably done in water to enhance the analytical power of the method.

In water, keratin fibres are well above the glass transition of the amorphous matrix material [23,24,25]. The modulus of hair in water Ew is about 2 GPa, to which the matrix only makes a relatively small contribution of about 0.4 GPa [26], relaxing quickly with time to a value low enough to be generally neglected [5, 22]. The value is in good agreement with the estimates for wool [19,20,21,22], but it depends strongly on keratin type [27].

DSC of hair and other keratin fibres is preferably done in water to avoid interference from pyrolysis effects above approx. 230 °C [6, 28]. Measurements give a distinct peak around 130–150 °C, depending on material [29] and, namely, heating rate [6], which characterizes the process of protein denaturation. Figure 1b shows a typical DSC curve for Caucasian hair in water [30].

The area of the peak yields the denaturation enthalpy ΔHD, neglecting small underlying changes of heat capacity [6], which is the energy to denature the α-helical material in the intermediate filaments [29]. Denaturation enthalpies and thus helix contents show only remarkably small variations across a variety of α-keratins (25–40%) [29].

The peak location is the denaturation temperature TD, which is assumed to mainly depend on the viscosity of the matrix proteins [6, 29]. The matrix surrounds the IFs, kinetically hindering their denaturation and thus conferring heat protection. Through this stabilization effect, the denaturation temperature is well above the threshold of about 100 °C, expected for the isolated α-helix [31]. In line with this interpretation, TD increases systematically with the cross-link density of the matrix, that is, with its content of the double amino acid cystine, as was shown for a variety of keratins [29].

Since for the interpretation of tensile and, namely, Ew data as well as for DSC results variations of the same type of two-phase model are applied, it is of academic as well as commercial interest to investigate whether the plausible expectation that the parameters from both types of tests should be related is justified.

Such an investigation requires analyses by both tensile testing and DSC for the same hair material, that is in practice the same hair tresses. To broaden the data range, these hairs should also have undergone some systematic chemical and physical processes, which have induced substantial changes of the relevant fibre properties.

The authors consider it as quite a serendipitous occurrence that such a combined investigation was conducted as part of a study undertaken by the expert working group ‘Hair Care Products’ of the DGK (Deutsche Gesellschaft fuer Wissenschaftliche und Angewandte Kosmetik e.V.) on the effects of heating (thermal straightening) on untreated and bleached European hair [10, 30].

On the basis of this study, we report on a comprehensive analysis of the correlations, namely, between elastic, tensile modulus (wet) Ew as a reversible, non-destructive measure of hair properties on the one hand and denaturation temperature TD and enthalpy ΔHD on the other, as properties which can be related back to IFs and matrix through the two-phase model [29]. Additional insight is gained this way into the effects of the oxidative pre-treatment (bleaching) on the component properties.

Experimental and basic data

Hair material

As previously has been described [30], commercial, Caucasian mixed hair, untreated, medium brown (Kerling, Backnang, Germany) was used for the investigations, in what follows referred to as ‘natural’. The hair was in the form of tresses (19 cm long, 1.5 cm wide). An overall number of 12 tresses were split into two groups. The first group was left chemically untreated, while the second group was subjected to a bleaching process twice, referred to in what follows as ‘bleached’.

Chemical treatment

The bleaching process (hair oxidation) was performed by applying a commercial product (Wella, Darmstadt, Germany) based on an alkaline solution (pH 10.5) of hydrogen peroxide (9%) and ammonium persulfate, applied for 30 min and at room temperature, followed by rinsing and air-drying. The treatment was repeated after a 24-h rest period.

Thermal treatment

Prior to the thermal treatment, the hair was washed with 10% sodium lauryl ether sulphate (SLES) solution, rinsed and dried by pressing between paper towels. Such a ‘towel-dry’ tress will contain about 60% water, about 30% of which is external liquid while the other 30% are absorbed into the fibres. This is much higher than the water content of ‘dry’ hair under normal room conditions of about 10% [33]. During the thermal treatment, drying of the tress will occur. On the initially ‘towel-dry’ tresses, the thermal treatment was applied, using a commercial straightening iron set to a digital reading of 200 °C as nominal temperature [30], which is assumed to be homogeneous across the tress [34]. A tress was clamped into a tensile testing machine (Instron, UK) and drawn through the iron such that a total contact time along the tress of 1.67 s was achieved for each pass. For two tresses each, from the groups of untreated as well as bleached tresses, total contact times of 60, 300 and 800 s were realized through repetitions. After 30 repetitions, each tress was washed and brought to a towel-dry state and the thermal treatment procedure was restarted. This cumulative thermal treatment together with the intermittent ‘wet’ state of the tress was applied in order to enhance the thermal damage [35] but also to reflect realistic though bad consumer practice [36].

DSC testing

All investigations by differential scanning calorimetry (DSC) were carried out with hair snippets immersed in water [12, 29, 37]. The measurements were conducted on a power-compensated instrument (DSC-7, PerkinElmer, USA), using stainless steel, large volume pans. Tests were conducted in duplicate as standard and in triplicate, if considered as being required by lower measurement precision. The temperature range was 50–190 °C with a heating rate of 10 K min−1. From the hair tresses, small subsamples were taken (approx. 100 hairs) and completely cut into snippets, about 2 mm in length. The snippet samples were stored under standard room conditions and would thus contain about 12% of water [3, 33]. Under these conditions, hair snippets (4–7 mg) were weighed into the DSC pans and 50 μL of water added. The pans were sealed and stored overnight prior to the DSC measurement. Data obtained from the measurement (see Fig. 1b) were denaturation temperature TD (peak location) and denaturation enthalpy ΔHD, determined from the peak area on the basis of a linear baseline, neglecting small underlying changes of heat capacity [6]. In line with standard practice, no corrections were applied for the calculation of parameter values with respect to the differences of water content for standard room conditions versus the wet state of the actual measurement.

Tensile testing

Prior to tensile testing, hair fibres were mounted manually in brass crimps with a free fibre length of 30 mm (crimping press, Dia-Stron, UK). Fibre dimensions were determined by rotating the fibre under standard room conditions (20 °C, 65 %rh) in a Fibre Dimensional Analysis Unit Model 765 (FDA765, Dia-Stron, UK). This procedure yields the smallest and largest diameter at five equidistant place of the fibre and, assuming general ellipticity, the mean cross-sectional area of the fibre. Tests were conducted on 30 fibres.

For the tensile tests, all fibres were entered into a circular cassette and first immersed in water (20 °C) for 2 h for equilibration purposes. Immersion in water was furthermore maintained throughout the tests. The cassette was introduced into the Miniature Tensile Tester Model 675 (MTT675, Dia-Stron, UK) and stress–strain curves until break obtained for all fibres. Due to common experimental occurrences (such as clamp failure), tests for a number of fibres needed to be discarded for various samples. The minimum number of accepted cases was 20.

From each accepted curve, the elastic modulus in water Ew was determined in the initial elastic region of the stress–strain curve (see Fig. 1a) by the UvWin single-phase analysis tool (Dia-Stron, UK) on the basis of the cross-sectional area under standard room conditions.

All further data analyses were conducted using Excel (Version 2013, Microsoft) and Statistica (Version 13, Dell Software, 2015).

Codes for samples and basic data

According to the various steps of preparation, samples are coded as follows [30]:

  • N0 = natural hair, no thermal treatment (0 s)

  • N1 = N0 + 100 s cumulative thermal treatment

  • N2 = N0 + 300 s

  • N3 = N0 + 800 s

For oxidized, bleached hair sample coding is analogous (B0–B3).

N01 is the first and N02 the second hair tress for N0. The coding is equivalent for all other samples. Table 1 summarizes the relevant parameter values as well as their basic statistics. All further analyses will be conducted using the values in Table 1.

Table 1 Modulus and DSC parameter values for measurements in water of all hair tresses as means with the standard error (SE) and the number of values (N) for two different types of hair and treatment times with a flat straightening device at nominally 200 °C for various times
Full size table

Results and discussion

Qualitative considerations

Figure 2a, b summarizes the parameter values from Table 1 in 3D plots. For natural hair (Fig. 2a), the data follow basically a straight line through space, indicating good linear relationships between all variables. This observation thus also implies the apparent linearity within the data range for TD versus ΔHD, in line with previous observations [30].

Fig. 2
figure 2

3D plots for Ew, TD and ΔHD for natural (a) and bleached hair (b). Times of thermal treatment at 200 °C (nominally) are indicated for data pairs (see Table 1). For natural hair (2a), a straight broken line is given through the data, while the curved line for the oxidized hair (2b) is meant to reflect the expected course of the data. When comparing the graphs, the differences in scaling should be noted

Full size image

For bleached hair, apparent overall TD versus ΔHD linearity is only preserved until about 300 s of thermal treatment. Beyond that, TD and Ew approach limiting lower values in the range of ≈ 135 °C and ≈ 1 GPa, respectively (also see Table 1). The connection between the data, as indicated by the curved line in Fig. 2b, implies the expectation that upon further heating ΔHd = 0 is approached at constant values for TD and Ew [10, 30].

The stage, where TD and Ew have reached their limiting values and the α-helical material is increasingly denatured (ΔHd → 0), can be associated with properties of hair as an increasingly amorphous, cross-linked thermoset polymer [38]. The required extensive cross-linking is attributed to the thermally induced degradation of cystine to form lanthionine and, namely, the formation of new amide cross-links, such as lysinoalanine [39, 40]. Such a material would be very brittle, in line with practical observations for severely heat-treated hair, which shows a pronounced tendency for breakage, e.g. with combing and styling.

Modulus versus denaturation enthalpy

The tensile modulus of untreated hair in the wet state is largely controlled by the elastic properties of the IFs through their content of helical material of about 60% [41], which translates into about 30% for the whole fibre [29]. Since in the DSC experiment ΔHD is assumed to reflect the amount of native α-helical material in the hair [6, 29], it thus appears appropriate to first consider the correlation between wet tensile modulus and denaturation enthalpy (Ew versus ΔHD).

Figure 3 summarizes the data for Ew and ΔHD for natural and bleached hair across the whole range of treatment times (see Table 1) as a 2D projection of Fig. 2a, b along the TD axis. As expected, the values for both modulus [42, 43] and enthalpy [12, 37] are systematically lower for oxidized (bleached) compared to natural hair.

Fig. 3
figure 3

Tensile modulus (wet) Ew versus denaturation enthalpy ΔHD for natural and bleached hair for the various times (s) of heat treatment, as indicated (see Table 1). The data are in both cases well fitted by straight lines, which differ in both slopes and y-intercepts (see Table 2). The limiting value for the elastic modulus for bleached hair (0.91 GPa) is indicated by the horizontal broken line (dashed line). This intersects with the regression line for bleached hair at ΔHD = 8.6 J g−1, as indicated by the vertical broken line. To facilitate the comparison between the fits for the two types of hair, also the linear extrapolation for natural hair is indicated by the dotted line (dotted line)

Full size image

In both cases, the data in Fig. 3 are apparently reasonably well fitted by straight lines. This implies that systematic and proportional changes in the values for the parameters occur for both natural and oxidized hair within the range of the thermal treatment. For the hair types, the linear relationships are quite different, being for the oxidized hair much steeper than for the natural hair. This confirms the special sensitivity of bleached hair towards thermal treatment. The relevant parameter values for the straight line fits are given in Table 2. In view of Fig. 2b, the limiting lower modulus for bleached hair is estimated as the mean for the two values at 800 s (see Table 1) as 0.91 GPa, as graphically indicated by the horizontal broken line in Fig. 3. This line intersects with the straight line fit for bleached hair at ΔHD= 8.6 J g−1. On the basis of the initial value for the natural hair (18 J g−1, see Table 1), this would imply that ≈ 50% of the initial helical material has been denatured at the stage, when Ew and TD have achieved what are essentially their limiting lower values.

Table 2 Parameter values for the linear regressions between tensile modulus (wet) Ew and denaturation enthalpy ΔHD and denaturation temperature TD, respectively, for both natural and bleached hair
Full size table

The y-intercept for untreated hair, that is the limiting modulus when ΔHD = 0, is 1.0 ± 0.1 GPa. This would signify the condition, where all helical material would be denatured. In this case the hair would consist of amorphous, denatured IF- and matrix material. The value is in good agreement with the limiting modulus of oxidized hair (0.91 GPa, see Fig. 3), which is already reached within the experimental time range. This means that both types of hair will finally reach the same state of an amorphous thermoset polymer.

However, oxidized hair is obviously sensitized by the chemical pre-treatment and reaches this status at a very early stage of thermal treatment at which still about 50% of helical material is present. This implies that oxidized hair reaches very quickly a state where modulus is largely controlled by the thermoset properties of the matrix, so that the remaining helical material has no impact on modulus. The limiting modulus of the hair material is with 0.91 GPa about 2–3× higher than the modulus of the matrix in untreated hair (≈ 0.4 GPa, as discussed above). This highlights the amorphous, highly cross-linked nature of the final thermoset state of the material.

In view of the dominant role of the helical material in the IFs for determining ΔHD for DSC and Ew for tensile properties prior to the thermoset stage, it may be expected to also see obvious decreases in helical contents through environmental effects or cosmetic treatments by other methods, which are more directly able to assess helical content. Investigations of archaeological keratin fibres by wide-angle X-ray diffraction WAXS [44, 45] and birefringence measurements [46], which have been damaged by environmental influences over a very long time period, tend to show no change or even an unexpected increase in α-helical material. This is in contrast to parallel measurements by DSC for archaeological [46] as well as cosmetically treated hair fibres [47]. This apparent contradiction is explained by assuming breakage of helical chains without structural change of the fragments through environmental or chemical damage. The fragments are held in place through the surrounding matrix material so that no apparent damage is observed, for example, by WAXD. However, any destabilizing effect of the arrangement of helical fragments through swelling, thermal or mechanical stimuli will trigger the fragility of the structure. This initially non-obvious damage of hair is termed ‘latent damage’ [47]. In practice, latent damage will show itself through a decrease of hair quality (rough feeling, split-end formation, hair breakage) which seems to develop under practical conditions only well after the initial damaging event.

Modulus versus denaturation temperature

Figure 4 summarizes the data for wet tensile modulus versus denaturation temperature (see Table 2) for the different treatment times. The relationships can in both cases be considered as apparently linear (see Table 2). Though Ew is mainly an IF and TD a matrix property, the observation as such is not unexpected in view of the underlying linearity between ΔHD and TD, which implies equivalent changes in IFs and matrix of hair by the thermal treatment [30]. The overall relation of the straight line fits in Fig. 4 with respect to each other is, however, significantly different from Fig. 3.

Fig. 4
figure 4

Tensile modulus (wet) Ew versus denaturation temperature TD for natural and bleached hair for various times of thermal treatment (s), as indicated. Data are fitted by straight lines, where extrapolations are indicated by dotted lines (dotted line). The limiting values for Ew and TD are indicated by crossed broken lines (dashed line) similarly as in Fig. 3

Full size image

The data points for bleached hair are, compared to natural hair, strongly shifted to lower TD and Ew values, respectively. The related line exhibits a significantly steeper slope. The lines for natural and bleached hair intersect at 130.6 °C and 0.82 GPa. The cross of dotted lines marks the estimated limiting values for Ew (0.91 GPa), as discussed above and for TD as the mean for samples B3 1&2 (134.5 °C, see Table 1). This is in good agreement with the estimate by kinetic analysis [30]. The closeness of the intersection of the lines and the cross defining the limiting values for Ew and TD confirms the overall consistency of the analysis and supports the hypothesis that natural and bleached hair with heating will eventually develop towards the same state of a brittle, thermoset polymer with time. More specifically, it shows that the matrix consistently develops towards this stage with heating time, irrespective of its pre-sensitization through bleaching.

Conclusions

For thermally treated natural as well as bleached hair, changes are observed for tensile modulus (wet) as well as for the chosen DSC parameters, which in all cases show pronounced apparent linearity. The detailed analysis revealed that the linearity for bleached hair is limited to the treatment limit of 300 s, beyond which tensile modulus and denaturation temperature approach limiting values. Though bleaching imparts a specific sensitivity to hair for the thermal treatment, namely, in the matrix proteins, in all cases consistent extrapolations to the limiting state of a highly cross-linked, brittle, thermoset material are observed. The correlations between parameters hold as long as hair has not achieved the final status of a highly cross-linked, thermoset-type polymer.

This consistency of the relationships of tensile and DSC data suggests that the experimental approaches, on the one hand, come to essentially equivalent results. On the other hand, the results also imply that DSC enables to consistently further differentiate the effects of the thermal treatments with respect to their effects on IFs and matrix.

The authors are well aware that the current considerations specifically apply to modulus (wet) versus the DSC parameters. Ew was the chosen parameter because wet testing is known to have a high sensitivity for material changes and low strains (max. ≈ 1%) enable non-destructive, reversible fibre testing. Further parameters obtained by tensile testing are subject to current investigations. In view of previous observations [48], the current conclusions are expected to apply similarly and more widely for damage induced in hair by radiation (UV, visible light, IR, heat) with due considerations of the synergistic role of water content. For other treatments, similar correlations are expected, which, however, may be qualitatively and quantitatively quite different compared to the current experimental context [49].