Introduction

Nanofluids represent a new category of nanotechnology-based fluids engineered by dispersing and stably suspending nanosized particles, fibres or tubes in traditional heat transfer fluids. The employed nanoparticles can be metallic, non-metallic or carbon nanotubes and are dispersed in base fluids, such as water, ethanol, ethylene glycol and engine oil [1,2,3]. The novelty behind nanofluids is the high surface-to-volume ratio of nanoparticles that is orders of magnitude higher than that of larger particles, such as by millimetre- and micrometre-sized particles. As a consequence, the high surface area of nanoparticles was suggested to lead to an enhanced thermal conductivity in nanofluids, since more solid surface can take part in heat transfer [4]. Up to the present, nanofluids have attracted significant attention [5, 6], due to their intriguing heat transfer properties under various heat transfer modes and their potential use in a broad range of applications [7, 8].

According to an extended statistical analysis of data available in the literature, the heat transfer enhancement when nanofluids are involved is 5–9% for the conductive heat transfer, 10–14% for the mixed conductive–convective, 40–44% for pool boiling and up to 200% increase for the value of the critical heat flux [9]. Despite the reported promising heat transfer characteristics of nanofluids, the physical understanding of the underlying processes is missing [10], and a controversy remains regarding their capability and applicability in engineering applications. This controversy arises from inconsistency in the observations of reported studies, accompanied by insufficient understanding of the physical mechanisms involved in nanofluids. For example, while heat transfer enhancement is reported for forced convection [11,12,13,14], opposing results are observed for natural convection with additional puzzling discrepancy [15] between numerical [16,17,18,19] and experimental [2, 20,21,22] natural convection studies.

An attractive way to assess the heat and mass transport mechanisms in nanofluids is by experimentation under different heat transfer modes that meet extensive applicability in nature and engineering systems. One example is natural convection where only gravitational and buoyant forces are present. Given the controversy among the convection studies in nanofluids, there is an additional motivation to exploit the heat and mass transfer properties of nanofluids under natural convection that is of primary significance for numerous applications in engineering [23], atmospheric and oceanic sciences [24, 25].

Convection is in general the transport of energy due to random molecular motion (energy diffusion) and bulk, or macroscopic, motion (advection). It is the progression of conduction when the temperature variations in a fluid are large enough to overcome its resistance to motion. Convection can be classified, according to the nature of the flow, to forced convection and free or natural convection. In forced convection, the flow is caused by external means, such as a fan or a pump. In natural convection, the flow is induced by buoyant forces due to density differences, caused by temperature variations in the fluid. One of the most established models to study buoyancy-driven flows and the associated heat and mass transport mechanisms is Rayleigh–Bénard convection (RBC). This involves the use of a relatively simple apparatus, though characterised by increased controllability, known as Rayleigh–Bénard (RB) cell.

A typical RB cell is a closed system that contains a fluid, confined between two horizontal parallel plates at a distance L apart. The fluid is heated from the lower plate and cooled from the upper plate, while the insulated side walls complete the set-up. For the study of RBC, different RB cells have been employed that vary in aspect ratio Γ, shape, design and construction materials. Studies of natural convection in RB cells have been conducted for low, moderate (~ 105) and high Rayleigh numbers (> 107) over a broad range of operating conditions. Based on the resulting flow conditions, two types of natural convection are distinguished: laminar and turbulent. Turbulent natural convection has mostly attracted the scientific interest, due to the complex features associated with turbulence, and the resulting increased heat and mass transfer rates that have been reported [26].

In turbulent convection, two discrete states have been identified according to the Rayleigh number, Ra, of the flow and the aspect ratio, Γ, of the employed cell. In cells with aspect ratios close to unity, a soft turbulent state has been observed for Ra < 107 and hard turbulent state for Ra between 4 × 107 to 1012 [27,28,29], with the difference lying on the way in which the thermals and plumes develop and traverse inside. It has been widely reported that, at the hard turbulent state, a large-scale coherent flow exists [30,31,32], which is self-organised by the hot rising and cold falling plumes. This flow mode is known as mean wind or large-scale circulation (LSC). Figure 1 illustrates a two-dimensional sketch of a typical cubic RB cell, along with the LSC. Up to date, the LSC remains an attractive feature to study and further analyse, as the heat transport in turbulent natural convection takes place primarily along the periphery of the cell, in the direction of the LSC [33]. In the present study, traditional heat transfer measurements in combination with a velocimetry method are applied to study the heat transfer mechanisms in nanofluids under turbulent RBC. The study of nanofluids under RBC by focusing on the LSC is an effective way to assess the heat transfer properties of these new coolants, establish the underlying physical mechanisms and try to resolve the discrepancy among the natural convection studies. Up to the authors’ knowledge, this is the first available study, given the complexity of employing a high-spatial-resolution flow velocimetry method in nanofluids under turbulent conditions and the challenge of visualising the resulting LSC experimentally.

Fig. 1
figure 1

Schematic drawing of a cubic Rayleigh–Bénard cell, depicting the large-scale circulation

Full size image

Experimental

Experimental set-up

A classical Rayleigh–Bénard (RB) cell configuration with optical access is operated in the current study. Figure 2a shows a schematic drawing of the RB cell, including all the major components. A detailed description of this configuration is given in Ref. [2], while a brief overview of its components is included herein. The cell consists of a heating plate, A, at the bottom, a cooling plate, B, at the top and lateral walls, C. It incorporates four quartz windows, 2 square (40 mm × 40 mm) and 2 rectangular (10 mm × 40 mm), D, to allow laser-based visualisation studies. Teflon plates, E, are inserted among all the conductive components to prevent their thermal connection. Finally, insulating pans, F, and a Plexiglas cover, G, are placed outside the core of the cell to eliminate heat losses from the sides. A second set of heating elements H is placed below the heating plate to prevent any heat losses downwards. The operation of the RB cell is monitored and controlled through LabVIEW software, coupled with National Instruments hardware and an in-house electrical device that is connected to the heating plates (A, H) and thermocouples placed in the cell.

Fig. 2
figure 2

Schematic drawing of the (a) Rayleigh–Bénard cell and (b) field of view (mask) for the laser-based particle image velocimetry measurements

Full size image

Particle Image Velocimetry

Particle image velocimetry (PIV) allows instantaneous planar measurements of the temporal and spatial distribution of the flow velocity in transparent and semi-transparent fluids. PIV has been already employed to investigate flows of dilute nanofluids (semi-transparent fluids) inside various systems, such as a HyperVapotron [34] and a pool boiling apparatus [35]. The PIV technique relies on the use of a laser source to illuminate twice, with a fixed time interval, micron-sized tracer (seeding) particles dispersed in the flow, on planes defined by a thin laser sheet.

In the current study, PIV was employed for DI water and dilute Al2O3–H2O nanofluids inside the cubic RB cell, through the available optical access. A double-pulsed Nd:YAG laser (Nano T 135-15 PIV) was involved, along with a charge-coupled device (CCD) camera (Imager Intense, LaVision) that was placed perpendicular to the laser sheet. The CCD camera has a spatial resolution of 1376 × 1040 pixel, and it was used to record the displacement of the seeding particles between the two laser pulses. A Nikon AF Nikkor 50 mm f/1.4D lens with manual focus was mounted to the camera. Additionally, a bandpass filter (10 nm bandwidth, 532 nm centre wavelength) was attached to the lens to provide enhanced isolation of the Nd:YAG laser light and excellent suppression in the blocking region.

Hollow glass spheres, HGS (80A6011, Dantec Dynamics), with a nominal diameter of 10 μm and a density of 1100 kg m−3 were used as seeding particles. Specifically, a small amount of HGS φv = 0.00045 vol.% (as calculated through an optimisation study) is enough to ensure appropriate and accurate tracking of the fluid flow, while avoiding any possible change in the properties of the tested fluids. For the range of timescales of the experiments, no settling of the seeding particles was expected. The other components of the PIV apparatus included: optical components for the formulation of the thin laser sheet (< 2 mm), a desktop computer with a programmable timing unit, PTU (LaVision), for the reliable synchronisation of the external devices (laser, CCD camera) and software (DaVis 8.2.2, LaVision) for data acquisition, processing and visualisation.

Through DaVis software, 2D images of the instantaneous and temporally averaged flow fields, including velocity vectors, are generated. Each 2D velocity vector was calculated from an interrogation window of 32 × 32 pixel with a 75% overlap. The field of view (mask) for the PIV measurements was 39.2 mm × 39.2 mm, slightly smaller than the square windows, since the data close to the edges of the window, where light reflections could affect the reliability of the results, are neglected. In Fig. 2b, the field of view (blue-coloured square) and the Cartesian coordinates for the analysis of the PIV results are depicted. The applied mask provides access to the flow field established in a square area located 25.5 mm above the lower free surface of the cell and 35.5 mm below the upper free surface of the cell and 30.5 mm away from the vertical lateral walls.

Nanofluid preparation

For the study of the underlying physical mechanisms, “pure” nanofluids, without employing the electrostatic or steric stabilisation methods, were prepared. Dilute Al2O3–H2O nanofluids with a mean concentration of φv = 0.00026 vol.% were synthesised by following the two-step preparation method, reported in detail in [2]. High purity DI (deionised) water (grade 3, ISO 3696) was used with a nominal pH value of 6.9. However, the presence of CO2 in the atmosphere and the addition of nanoparticles affected the pH of the nanofluids. The selected nanoparticles were 70:30 δ:γ Al2O3 (44931, Alfa Aesar). They were spherical in shape, with an average particle size of 45 nm, as verified by transmission electron microscopy (TEM) [36], and a particle density of 3965 kg m−3.

Experimental procedure

A constant temperature gradient between the heating and cooling plates of ΔΤh,c = 63.2 °C and a constant temperature of Tc = 26.5 °C at the cooling plate were the boundary conditions in the current experimental study. The system hence had two control parameters, Rayleigh, Ra = 4.1 × 109, and Prandtl, Pr = 3.1, and two response parameters, Nusselt and Nu, and temporally averaged velocities, Vavg. PIV measurements were obtained at three different planes in the z direction of the coordinate system of Fig. 1b inside the cell to record the impact of nanoparticles on the three-dimensional flow structure and properties of the base fluid. The first plane was at the centre of the cell, z = 0 (central plane), the second was at an absolute distance z of 3 ± 1 mm behind the centre (back plane) and the third was at an absolute distance z of 4 ± 1 mm in front of the centre (front plane). The distances of the back and front planes from the central plane were deliberately asymmetric to evaluate the geometric symmetry and coherency of the LSC.

Two thousand independent pairs of images of the instantaneous flow over a long sampling time, at steady state conditions (reached after 3 h from onset of the experiment [2]), were recorded and processed, to produce the temporally averaged velocity measurements. Each laser pulse pair was emitted at a rate of 0.25 Hz, with a time interval between the pulses of 24 ms. Both water and nanofluid experiments were repeated at least four times to confirm the repeatability and reliability in the execution of the experiment. To minimise random uncertainties, the mean values of four repeated experiments per fluid and per plane are presented and compared. The fractional uncertainty in the mean of the spatially and temporally averaged absolute velocity is ≤ 2.6%. Additional error analysis is provided in “Error analysis” section.

Results and discussion

The RB cell operates under the hard turbulent state, where the existence of a large-scale circulation (LSC) that spans the height of the RB cell is expected to develop, as it has been reported in the literature. Based on the geometry of the cell (shape and aspect ratio) and the tendency of the LSC to extend along its largest spatial distance that corresponds to the most stable mode [37], the large-scale coherent flow evolves along a diagonal plane of the cell [24, 28, 38,39,40,41]. Therefore, the reported planar PIV flow measurements are projections of the diagonal flow field on the measurement plane, as seen through the square window depicted in Fig. 2.

Figures 3–5 show contours of the temporally averaged absolute velocity for DI water and dilute Al2O3–H2O nanofluids under Ra of 4.1 × 109 at the back, central and front planes, respectively. In the same figures, velocity vectors with arrow lengths proportional to the velocity magnitude (the vector length equals the pixel displacement × 10) are also depicted. Firstly, based on the direction and magnitude of the velocity vectors, a single cellular coherent structure with a preferred clockwise motion—as seen in the 2D PIV images—is observed inside the RB cell. This structure, known as large-scale circulation (LSC), is driven by hot plumes that congregate in an upwelling jet of fluid near the left-hand side and a downward jet of cold plumes that occur at the right-hand side of the field of view. Concerning the preferred orientation and direction of the LSC, no conclusive answer has been given so far, neither in cylindrical RB cells in which there is rotational symmetry, nor in cubic cells where the LSC evolves along the diagonals planes. Possible suggested reasons for the behaviour of the LSC include the effect of the earth’s Coriolis force [42], a possible tilt of the cell relative to gravity and construction imperfections of the RB cells, mainly at the heating and cooling plates [42, 43].

Fig. 3
figure 3

Contours of the temporally averaged absolute velocity, along with velocity vectors with arrow lengths proportional to the velocity magnitude for (a) DI water and (b) a dilute Al2O3–H2O nanofluid under Ra of 4.1 × 109, in the back plane

Full size image
Fig. 4
figure 4

Contours of the temporally averaged absolute velocity, along with velocity vectors with arrow lengths proportional to the velocity magnitude for (a) DI water and (b) a dilute Al2O3–H2O nanofluid under Ra of 4.1 × 109, in the central plane

Full size image
Fig. 5
figure 5

Contours of the temporally averaged absolute velocity, along with velocity vectors with arrow lengths proportional to the velocity magnitude for (a) DI water and (b) a dilute Al2O3–H2O nanofluid under Ra of 4.1 × 109, in the front plane

Full size image

By comparing the contours of the temporally averaged absolute velocity between DI water and dilute Al2O3–H2O nanofluids in all three planes, it can be clearly seen that the spatial distribution of the velocity flow field demonstrates differences between the tested fluids. Most notably, the area closer to the heating surface, where maximum velocities (in the field of view) are recorded, is notably larger for nanofluids than for water. To further evaluate the observations, the velocity characteristics for both fluids at all three planes are included and compared in Table 1.

Table 1 Velocity characteristics for DI water and dilute Al2O3–H2O nanofluids at three parallel planes in the Rayleigh–Bénard cell, in the field of view
Full size table

Following earlier findings [44], it is reconfirmed that the maximum temporally averaged absolute velocity \(\left| V \right|_{\text{avg-max}}\), the spatially and temporally averaged absolute velocity \(\overline{{\left| V \right|_{\text{avg}}}}\) and the temporally and spatially averaged standard deviation of the turbulent velocity fluctuations Stdev are consistently higher for nanofluids than for DI water in the field of view. Additionally, it is demonstrated that this trend is consistent in all three planes, with the maximum difference between the velocity characteristics for DI water and nanofluid taking place at an absolute distance z of 4 ± 1 mm (front plane) from the central plane. Starting with the central plane, the presence of nanoparticles is found to increase \(\overline{{\left| V \right|_{\text{avg}}}}\) of the base fluid by 2.7%. As far as the back plane is concerned, the increase in \(\overline{{\left| V \right|_{\text{avg}}}}\), \(\updelta\overline{{\left| V \right|_{\text{avg}}}}\), is 7.2%, while in the front plane this is 10.7%. These differences are partially attributed to the increased \(\left| V \right|_{\text{avg-max}}\) for nanofluids compared to DI water, close to the heating plate in the field of view. Due to that, it is also suggested that the range, minimum to maximum value, of the temporally averaged absolute velocity \(\left| V \right|_{\text{avg}}\) is broader for nanofluids than for water. Since the PIV measurements were performed only in the bulk region of the turbulent Rayleigh–Bénard convection (RBC), the enhanced velocity characteristics are referred specifically to this area. However, the addition of nanoparticles to the base fluid could possibly expand, shrink or slightly shift the LSC with respect to the field of view.

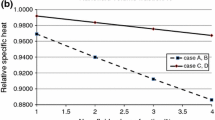
In Table 2, the experimental conditions and the heat transfer performance of DI water and dilute Al2O3–H2O nanofluids are included. It is noted that the reported data are mean values out of 12 experiments (four experiments per plane), while the methodology for the heat transfer calculations is similar with that reported in previous work by the authors [2]. By comparing the general heat transfer, as expressed with the Nu, no change is observed within the experimental uncertainty between water and nanofluids, thus verifying earlier PIV experiments conducted in a single plane close to the centre of the cubic RB cell under three different Ra [44].

Table 2 Experimental conditions and heat transfer performance of DI water and dilute Al2O3–H2O nanofluids
Full size table

Regardless of the enhanced temporally averaged flow velocity field in the bulk region of turbulent RBC, no consistent trend for the general heat transport was noted for dilute Al2O3–H2O nanofluids. At the first glance, this finding seems consistent with the literature, where it has been reported that when the LSC is either suppressed or modified, no significant variation of the heat transport across the cell is expected [45]. This is on the basis that the heat transport is determined primarily by boundary layer instabilities rather than the structure of the LSC [46]. On the other hand, due to the enhanced thermal properties of nanofluids, one would expect enhancement of heat transfer, especially since no nanoparticle sedimentation or other deteriorating mechanism was noticed. A possible explanation could be the very small concentration of nanoparticles in the base fluid—although notable heat transfer enhancement has been reported for dilute nanofluids in the literature [47,48,49]—in combination with the experimental uncertainty and the construction of the RB cell. For instance, it has been noted that the side walls of the RB cell usually carry a significant part of the heat current. Therefore, the heat exchange between the fluid and the side walls will affect the fluid flow [50] and the general heat transport calculation [51]. Another possible reason could be the modified dynamics of the thermal plumes at the boundary layer due to the addition of nanoparticles to the base fluid. Additional numerical and experimental investigations are required to assess the heat and mass transfer phenomena that occur at the whole volume of a RB cell, including the boundary layers.

Error analysis

To ensure reliability of the reported results and identify any systematic uncertainties induced by the PIV technique or the experimental methodology, all the experiments were repeated at least four times. For the uncertainties in the mean values, the methodology of Kirkup [52] was followed. Table 3 presents the four individual values of the Nusselt number and the spatially and temporally averaged absolute velocity for DI water and dilute Al2O3–H2O nanofluids in the central plane. In the same table, the mean (out of four experiments) values are included. At first, it can be seen the values for each fluid are very close to each other with the uncertainty in the mean being very small. By following the same procedure for the rest two planes, the fractional uncertainty in the mean of the Nusselt number is < 1.0%, and the fractional uncertainty in the mean of the spatially and temporally averaged absolute velocity is ≤ 2.6%. As far as the nominal uncertainty of the PIV measurements is concerned, it is related to the minimum detectable pixel shift according to the employed camera and the selected calculation parameters. For the values of the spatially and temporally averaged velocity employed in the current study, the minimum detectable shift corresponds to ≤ 0.0007 cm s−1 or ≈ 0.2%. Therefore, the results presented herein are repeatable, reliable and precise.

Table 3 Repeatability test for DI water and dilute Al2O3–H2O nanofluids at the central plane
Full size table

Conclusions

In this study, the heat and mass transfer behaviour of dilute Al2O3–H2O nanofluids under turbulent natural convection in a cubic Rayleigh–Bénard (RB) cell with optical access was experimentally investigated. A high-spatial-resolution flow velocimetry method, particle image velocimetry (PIV), was employed to measure the flow velocity at three parallel planes inside the RB cell for both DI water and nanofluids. The nanofluid results were compared with those of DI water that was used as a benchmark. Following earlier PIV experiments [44], it was confirmed that the addition of a small amount of Al2O3 nanoparticles to DI water, φv = 0.00026 vol.%, modifies the mass transfer behaviour of the base fluid in the field of view, under hard turbulence—Rayleigh number of the order of 109. It was demonstrated that the maximum temporally averaged absolute velocity \(\left| V \right|_{\text{avg-max}}\) and the spatially and temporally averaged absolute velocity \(\overline{{\left| V \right|_{\text{avg}}}}\) are higher for nanofluids compared to DI water at all three planes inside the RB cell. Despite the enhanced velocity characteristics in the bulk region of turbulent natural convection, no alteration of the heat transfer performance of the base fluid was noticed with the addition of nanoparticles. Possible reasons include the small nanoparticle loading in the base fluid and the questionable contribution of the large-scale circulation on the heat transfer rate. Finally, the altered dynamics of the thermal plumes at the boundary layer due to the presence of nanoparticles in the base fluid cannot be excluded as a counteracting mechanism. The current work assesses the heat and mass transfer behaviour of nanofluids under turbulent Rayleigh–Bénard convection in an attempt to evaluate the applicability of nanofluids to cooling applications.