Introduction

The swelling process is, by definition, an increase in the volume of a gel or solid connected with the uptake of a liquid or gas [1]. The absorption of liquids leads to changes in the mechanical properties of the swollen material and may create extra pressure when it occurs in confined spaces, which results in various deformations of the swollen material (i.e. surface creases and wrinkles) [2–4]. The discussed process may also significantly alter adsorption–desorption properties of adsorbates [5, 6]. In polymer dissolution, swelling is the first step in the interaction between liquid molecules and polymeric network, which is usually followed by solvatation of polymer chains. The immersion of cross-linked polymers in solvents does not lead to their dissolution because of their chemically bonded hydrocarbon chains; nonetheless, these links do not prevent cross-linked polymers from swelling.

The first comprehensive approach to quantitatively describing the process of swelling of nonporous materials was presented in the Flory–Rehner theory [7]. In this theory, the rate of maximum swelling is the result of the equilibrium between two major adverse effects: the entropy of mixing and the entropy of polymer chain configuration. For quantitative determination of interactions between liquid molecules and polymeric chains, the Flory–Huggins parameter was proposed; unfortunately, it cannot be applied in every case [8–10].

Historically, swelling was estimated by a weight method or by linear method with the use of the cathetometer. Both these methods require swollen particles to be in equilibrium with the solvent; neither of them is suitable for measuring the swelling of polymer particles in volatile liquids (e.g. ethanol, heptane). In the present study, for convenience and reproducibility of the presented results, instead of either of the above-mentioned methods, temperature-programmed desorption and microscopic measurements were used.

In the current research, three commercially available cross-linked porous Amberlite resins: XAD4, XAD16 and XAD7HP, immersed in ethanol and in heptane, were investigated. These materials are widely used as sorbents [11], ionites [12] and organic frameworks for composite synthesis [13]. Their insolubility and resistance to both acids and bases, along with their high sorption capacity, makes them very versatile materials. The degree of polymeric network expansion depends on the pore structure of Amberlite and on the chemical character of solvent molecules. Swelling affects their mechanical properties at the same time altering their ability to recover adsorbed substances [14]. These problems are particularly important in the case of porous polymers. Porosity is, next to the chemical character, the main feature of widely used polymer materials employed in separation sciences and adsorption. However, swelling of porous polymers is rarely investigated because of the complexity of the process. The uptake of solvent is in this case a combination of capillary action and the swelling of polymer matrix. A thermogravimetric experiment allows the evaluation of both these effects separately and provides sufficient information for better understanding of the adsorption and swelling of Amberlite resins.

Experimental

Materials

All three Amberlite resins: XAD4, XAD16 and XAD7HP referred further as XAD7, purchased from Sigma–Aldrich, were thoroughly washed with redistilled water up to the point where no chloride ions were detected in the eluent—the manufacturer provides spheres immersed in sodium chloride solution. Subsequently, polymeric material was dried in a regular dryer at 353 K for minimum 12 h and in a vacuum dryer for another 4 h at the same temperature. Anhydrous ethanol (99.8%) and n-heptane both pure p. a. were purchased from POCH, Poland, and used without any further purification.

Characterization methods

The low-temperature nitrogen adsorption–desorption experiment carried out with a volumetric adsorption analyser, ASAP 2405 (Micromeritics), provided data for calculation of the specific surface area (S BET, from BET method, p/p 0 from 0.05 to 0.25) [15], the total pore volume (V p, at p/p 0 = 0.995) and the pore size distribution (PSD, from BJH procedure) [16].

Temperature-programmed desorption was performed using Derivatograph-C (MOM, Hungary), Paulik & Paulik system. The linear mode at three heating rates (1, 5 and 10 K min−1) was employed to desorb ethanol and n-heptane from selected Amberlite resins (mass of swollen polymer was approximately 100 mg). Additionally, solvent desorption was conducted in quasistatic mode (level—0.3 mg; Q p—0.5 K min−1).

The dimensions of the swollen particles were measured with Nikon SMZ1500 optical microscope.

Results and discussion

Nitrogen adsorption

All the three Amberlite polymers selected for the study are in the form of white opaque spheres. The diameter of these particles ranges from 200 to 600 μm. Parameters characterizing the porosity of polymers were obtained with the use of low-temperature nitrogen adsorption–desorption experiment (Fig. 1; Table 1).

Fig. 1
figure 1

Low-temperature adsorption (filled figures)–desorption (open figures) of nitrogen for XAD4 (triangles), XAD16 (squares) and XAD7 (circles)

Full size image
Table 1 Porosity parameters (S BET—specific surface area, V p—pore volume, D PSD—the diameter at the peak of PSD, D = 4V p/S BET—average pore diameter), dipole momentum (ρ) [17] and density (d) of Amberlite resins
Full size table

Low-temperature adsorption–desorption of the selected Amberlite polymers reveals that N2 adsorbs reversibly on dried cross-linked polymers. Adsorption isotherms for each of them consist of a hysteresis loop whose shape for XAD4 and XAD7 may indicate that the formed pores have the ink bottle shape (plateau followed by sudden decrease on desorption curve) [17], whereas adsorption branch shows monotonous increase in the whole pressure range.

S BET, V p and D PSD in brackets are the values obtained from our previous N2 adsorption–desorption measurements [18]. The differences in values of porosity parameters may result from different batches of material and different instruments used in the studies

To examine the degree of swelling of all characterized materials in two different solvents polar (ethanol) and nonpolar (n-heptane), optical microscope measurements were used.

Microscopic studies

The dimensions of the dry and swollen polymeric spheres were measured from images obtained from an optical microscope (Fig. 2). As it may be seen, the change in the appearance of the spheres after the transition from the dry and the swollen state is noticeable. Dry particles have opaque white colour, while spheres immersed in liquid are translucent. This qualitative change is shared by all three materials, but the increase in volume in the case of XAD7 is the most noticeable of them all.

Fig. 2
figure 2

Image of dry (a, c) and swollen in ethanol (b) and in heptane (d) spheres of XAD7. Red circle marks dry bead dimension. Scale bar for (b) is the same as for (a) and (d) as for (c). (Color figure online)

Full size image

On the basis of microscope imaging, it may be seen that Amberlite polymer particles swell isotropically (wetted particles maintain the spherical shape of dry beads). From the measured diameter, radius (r) was obtained and used to calculate the volume of the bead (Vb. = 4/3πr 3). Since there is slight difference between swelling of relatively large and small particles, the sum of volumes of at least 25 spheres was taken into account and compared. From this comparison, the increase in volume, expressed as the swelling ratio (S = 100% × (V sp − V d)/V d, where V sp—the volume of swollen particles and V d—volume of dry particles), was calculated and is presented in Table 2.

Table 2 The swelling ratio (S) of the swollen Amberlites in ethanol and in n-heptane presented with the standard deviation and the confidence interval at 95% confidence level (CI)
Full size table

On the basis of the data collected in the table, as well as previous studies [18], it may be concluded that the moderately polar XAD7 matrix exhibits a much higher swelling capacity (the swelling ratio higher than 100%) in both polar and nonpolar solvents than hydrophobic polymers. What is more, polar XAD7 in n-heptane swells noticeably more than it does in ethanol. This phenomenon can be explained by the fact that the uptaken n-heptane molecules are located in the vicinity of polymeric hydrocarbon chains. Thus, n-heptane molecules, tightly packed around polymeric chains, force them to extend more. Astonishingly, the difference in swelling between XAD4 and XAD16 was observed. Despite the same chemical composition, the more porous XAD16 (with larger specific surface area and extremely large pore volume) has a greater ability to expand than the less porous XAD4.

Thermogravimetric experiment

Temperature-programmed desorption of heptane and ethanol provided TG and DTG curves (Fig. 3).

Fig. 3
figure 3

TG (black lines) and DTG (red lines) curves for XAD4, XAD16, XAD7 recorded at three different heating rates 1 K min−1 (solid line), 5 K min−1 (dashed line) and 10 K min−1 (dotted line) for desorption of ethanol (a) and n-heptane (b). (Color figure online)

Full size image

Thermogravimetric curves show that the imbibed liquid constitutes from 50 up to 70% of the swollen polymer mass. What is surprising, the material that swells the most (XAD7) has only 50% w/w of the solvent, whereas XAD16, for which the increase in volume is moderate but which has the highest specific surface area, has liquid uptake at level of 70% w/w. It is obvious that the total desorbed amount of the solvent is the sum of the solvent entrapped between the polymer chains and the solvent present inside the pores. This conclusion can be supported by weakly resolved peak on the slope of DTG curve only for XAD16. Thus, the liquid desorbed from the pores, especially wider ones, may be assumed as the part of bulk liquid which is easily desorbed.

From the peak of the desorption on DTG curves, the maximum temperature of desorption (T p) was noted. With the heat rate (β) and T p known, it is possible to estimate desorption energy of heptane and ethanol from the studied polymer using Amenomiya and Cvetanovic [19] equation:

$$\log \left( {\frac{{T_{\text{p}}^{2} }}{\beta }} \right) = \frac{{E_{\text{d}} }}{{2303RT_{\text{p}} }} + \log \left( {\frac{{E_{\text{d}} A_{0} }}{RC}} \right)$$

where E d—energy of desorption (kJ mol−1), A 0—quantity adsorbed, C—constant (related to desorption rate) and R—gas constant. Plotting linear function \(\log \left( {\frac{{T_{\text{p}}^{2} }}{\beta }} \right)\) versus \(\frac{1}{{T_{\text{p}} }}\), one can calculate the desorption energy from the coefficient of the variable by a simple mathematic transformation. In all the measured cases, the coefficient of determination of the above-mentioned function is higher than 0.9. Obtained values are presented in Table 3.

Table 3 Estimated desorption energies (E d) for ethanol and heptane
Full size table

The obtained values of desorption energy (E d) in both cases are substantially higher than those for vaporization of pure liquid (42.3 kJ mol−1 for ethanol [20], 36.3 kJ mol−1 for heptane [21]). Pore dimensions and intermolecular interactions play a crucial role in the estimation of desorption energy. These two factors may sum up or overlap and compensate themselves. The narrowing of pore diameter and establishing solvent–polymer interactions during the swelling will result in the increase in the total energy needed for solute desorption. In the case of n-heptane, which is unable to establish polar interactions with Amberlite resins, the presence of liquid meniscus curvature in the pores will be the key feature affecting the E d value. As shown in Table 3, the energy required for n-heptane desorption increases along with specific surface area and pore volume of the chosen Amberlites (XAD16 > XAD4 > XAD7). According to the Kelvin equation, the larger the liquid meniscus radius is, the less energy is needed to the occurrence of liquid–gas transition. Thus, the obtained E d values may indicate that, although pore dimensions in swollen material under study are changed, the shape of the pores is preserved. In the case of ethanol, the estimated desorption energy sequence is different than that for heptane (XAD16 > XAD7 > XAD4). XAD7, which has smaller specific surface area and pore volume than the less polar XAD4, has a noticeably higher E d value. This is probably due to the dipole–dipole interaction between ethanol and XAD7 chains. Moreover, a great ability of XAD7 matrix to swell in both ethanol and n-heptane is a crucial factor, which probably contributes to the rise of the desorption energy. Namely, during swelling, solvent molecules are located ‘inside and between’ polymer chains (occupying every sterically available inner polymer spaces), which hinders their desorption. Interestingly, XAD16, less polar than XAD7, has the highest desorption energy value. This could be caused by the extreme uptake of ethanol (70% w/w) by the highly porous XAD16 matrix. The diameter of XAD16 pores is twice as large as it is for XAD4 and three times larger than it is for XAD7. Thus, the molecules of ethanol, smaller than n-heptane, penetrates XAD16 matrix more easily, completely filling pores and establishing dipol–dipol interactions between ethanol molecules within the pores.

The thermal desorption experiment for the same systems was repeated in quasi-isothermal conditions using the heating programme incorporated into Derivatograph. Experimental curves, which may be assumed as isobars of desorption measured in this specific heating mode, are shown in Fig. 4.

Fig. 4
figure 4

TG curves gathered in isobaric mode for desorption of ethanol (a) and n-heptane (b)

Full size image

TG curves presented above have a characteristic shape. At the beginning of desorption, the temperature of the material is too low to observe mass loss (approximately horizontal line). After reaching the boiling temperature of the solvent at quasistatic desorption programme, a vertical line is registered. The mass loss on TG curve above the boiling temperature represents the liquid that evaporates from the sample, i.e. the amount of the solvent absorbed between polymer chains and inside pores. In other words, the desorbed liquid represents the total amount of the liquid present in the sample. However, for a relatively small swelling ratio (much lower than 50%) it may be assumed that the released solvent in TG experiment represents the solvent filling the pores (Fig. 5).

Fig. 5
figure 5

Comparison of pore size distribution for XAD4 (a) and XAD16 (b) obtained by low-temperature liquid nitrogen adsorption–desorption experiment (black dotted line) and derived from ethanol (blue solid line) and heptane (purple dashed line) quasistatic desorption data. (Color figure online)

Full size image

Knowing the amount of liquid evacuated above its boiling point, pore size distributions for XAD4, XAD16 (Fig. 5) and XAD7 in swollen state were estimated using the Kelvin equation and converting mass loss versus temperature to volume loss versus pore radius [22–26] and after differentiation of these curves. Taking into account the amount of the liquid adsorbate desorbed above its normal boiling point, the total pore volume of the polymers was calculated.

Because of an extremely high swelling ratio for XAD7 and a great share of solvent taking part in the swelling, it is impossible to obtain reasonable PSD values. This phenomenon can be explained by two causes. Firstly, the expanding polymeric matrix results in diminishing free inner spaces of the pore. The second cause might be related to the fact that during the TG desorption, a very small amount of the liquid is still adsorbed on pore walls and forms a surface film of some thickness. The desorption of the solvent represents the deswelling process and takes place, in this case, in the range of 1.5 °C. Any calculations in such a narrow temperature range are vitiated by errors. The sharp decrease in the solvent mass on TG curves is, in this case, registered without the characteristic inflection points, which indicates that the solvent is evacuated simultaneously from whole system. The shape of TG curves for XAD4 and XAD16 Amberlites is much more useful for pore estimation. The desorption curve is less steep and extended along the temperature axis, which facilitates the calculations of PSD. The pore size distribution estimated from n-heptane and ethanol desorption experiments is much narrower than it is for N2 adsorption, and the values of peak maximum for both used liquids are shifted towards smaller pore radius.

As it may be seen, PSD peaks maxima for n-heptane desorption for both polymers are in a reasonable correlation with the peak maximum obtained from the liquid nitrogen desorption experiment. However, for ethanol desorption, this difference is larger. This can be explained by the fact that plot of the radius (calculated from the Kelvin equation) versus temperature for alcohols (i.e. ethanol) is much steeper than it is for hydrocarbons (graph not shown). Thus, an error in estimating PSD using this method is more pronounced for ethanol than it is for n-heptane.

Model considerations

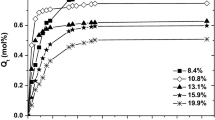
The macroscopic increase in the volume of polymer during liquid uptake is a result of both pore geometry change and the elongation of polymeric matrix. Each polymer has a certain ratio of free spaces (pores) to polymer skeleton. In other words, cross-linked polymer may be considered as a structure that consists of multiple pores with certain pore wall thickness. For porous polymers during isotropic increase in volume, the swelling ratio will affect pore wall thickness and its length. Along with the expanding, the polymer skeleton volume of free spaces between pore walls will diminish proportionally to the degree of the polymer expansion, which in turn is proportional to the amount of the polymer specimen forming the pore walls. It is very difficult to determine the thickness of pore walls in a dry and in a swollen state. For illustrative purposes and model calculations, ‘the volume ratio’ of pore volume in a dry state to the pore volume in a swollen state was taken into account (\(V_{\text{S}} /V_{{{\text{N}}_{2} }}\)). \(V_{{{\text{N}}_{2} }}\) value is known from N2 adsorption experiment and V S is determined as the pore core volume after the thickening of pore wall. Model calculations for cylindrically shaped pores at different swelling ratios are presented in Fig. 6 for ethanol (Fig. 6a) and n-heptane (Fig. 6b).

Fig. 6
figure 6

The relation of V s/\(V_{{{\text{N}}_{2} }}\) against the ratio of pore radius to pore wall thickness \(R_{{{\text{N}}_{2} }}\)/W T for different swelling ratios (S); a ethanol, b n-heptane. Curves 1, 2 and 3 correspond to Amberlite XAD4, XAD7 and XAD16. Shaded area illustrates the relation of V s/\(V_{{{\text{N}}_{2} }}\) versus \(R_{{{\text{N}}_{2} }}\)/W T in the range of S from 5 to 250%

Full size image

In calculations, the thickness of walls was assumed to fall within a wide range from 0.2 to 50 nm. The shape of these curves is independent of the pore length. For strictly geometrical reasons, these simulation calculations are valid for materials whose swelling ratio does not exceed 200%. In this model, it means that pores are completely closed and the expansion of pore walls exceeds the pore space.

In real systems, knowing the swelling ratios, one can estimate the characteristic point corresponding to the specific degree of pore filling. For the studied polymers, the location of this point is different. In the case of XAD7 swollen in ethanol, the volume ratio (V S/\(V_{{{\text{N}}_{2} }}\)) is close to zero. It means that in its swollen state, this polymer has no free volumes representing pores. For n-heptane V S/\(V_{{{\text{N}}_{2} }}\) equal to 0.3 suggests that some volumes (outside the polymer skeleton) are present even with the total saturation of XAD7 with the swelling agent. In the case of two hydrophobic polymers, XAD4 and XAD16, relatively large values of V S/\(V_{{{\text{N}}_{2} }}\) indicate that there are free volumes in the samples, which do not take part in swelling and which may be ascribed to the pores in the swollen state. It is worth mentioning that the discussed pore volumes are in wet samples filled with solvent. The results presented in Fig. 6 are numerically expressed in Table 4. Solvent volumes in column II of Table 4 are an integral part of the total particle volume being the sum of solvent, polymer and pore volumes.

Table 4 Parameters characterizing polymers under study in swollen state; V SE = V polymer × S%, where V polymer = m polymer/d polymer; V S = V TG − V SE, where V TG is a solvent volume desorbed above boiling point; R S = \(R_{{{\text{N}}_{2} }}\) × V S/\(V_{{{\text{N}}_{2} }}\)
Full size table

The swelling ratio for XAD7 and the difference in the volume of the solvent taking part in swelling, the latter of which was obtained from TG experiment (the height of the TG curve segment above the boiling point) and from a simple calculation which took into account the solvent uptake from mass of the polymer, are practically equal, and consequently, V S/\(V_{{{\text{N}}_{2} }}\) is close to zero. It means that the total volume accessible for ethanol outside the polymer matrix is in this case occupied by the swollen polymer matrix. For remaining polymers, this difference is more pronounced, as it is depicted in Table 4 (column II and V) and points in Fig. 6. V S/\(V_{{{\text{N}}_{2} }}\) values are relatively high and reach maximum for XAD4 sample.

The presented calculations are the result of TG data fitting to the model pore system characterized by low-temperature nitrogen adsorption experiment and microscopic observation of swelling expressed in swelling ratio value. The results clearly indicate that a high swelling ratio results in the elimination of pores accessible for solvent molecules. The whole internal pore system existing in a dry sample is filled with the swollen polymer skeleton. At lower swelling ratios, there remain pores which may be assumed as a free space filled with solvent. This conclusion is supported by the comparative study of pore volumes estimated from nitrogen adsorption data with those calculated from TG experiment.

If it is assumed that the total desorbed amount of solvent above the boiling point originates from pores, its volume should be equal to the pore volume derived from adsorption isotherm. Pore volumes calculated in that manner described above are listed in Table 5. Extremely high difference in pore volumes V SE and \(V_{{{\text{N}}_{2} }}\) occurs in the case of XAD7 Amberlite. Pore volumes estimated by two different methods are similar for XAD4 and XAD16 sample. This undoubtedly indicates that small swelling degree favours the existence of free space in porous polymer which may accommodate quite a large amount of the solvent.

Table 5 Pore volumes for dry and swollen material (V TG). V SE for TG data was calculated from the mass of solvent desorbed above boiling point
Full size table

Conclusions

Numerous studies of materials that have the ability to swell in polar and nonpolar liquids were conducted with the TG analysis (e.g. organic copolymers [27–32] and various hydrogels [33–39]), but to our knowledge it is the first reported approach to pore size distribution estimation in swollen cross-linked polymers with the employment of thermogravimetric analysis combined with microscopic measurements. A standard procedure based on quasi-isothermal programme of heating applied for desorption of liquid from porous solid and the Kelvin equation, along with a simple mathematic calculation, provides information concerning free spaces in the swollen material. Thermogravimetry results coupled with nitrogen adsorption data provide valuable information on the solvent uptake and make it possible to evaluate the share of polymer swelling and pore system filling in total solvent absorption. Attention has to be paid to initial porosity of the polymer and intermolecular interactions between the polymer and the solvent. Studies using TG technique facilitate investigation of polymer pores in the swollen state. Amberlite XAD7HP swells more than Amberlite XAD4 and XAD16 in both ethanol and n-heptane. Preliminary results of PSD calculations on the basis of TG data show similar pore size distributions in swollen particles as those calculated from nitrogen adsorption data but with pore radius shifted to lower values. In other words, the dimensions of pores in swollen materials are smaller than in the dry state. An increase in liquid uptake by Amberlite resins and swelling rate depends not only on the chemical composition of the polymer but also, to a great extent, on its porosity. The calculations presented here contain several simplifications; however, the correlation between macroscopic effects, thermogravimetric measurements and those predicted by model calculations is surprisingly satisfactory.