Introduction

Thermochemical heat storage using salt hydrates has attracted more and more attention, especially for long-term/seasonal solar energy storage. Compared to sensible heat storage and phase change heat storage, this technique offers considerable advantages of high energy density, low material cost and negligible heat loss during storage. In order to develop efficient heat storage systems, understanding fundamental kinetics and mechanisms of the dehydration/hydration reactions is of great importance. In this work, the thermal dehydration of lithium sulfate monohydrate (see Eq. 1) is chosen as a representative reaction for comparative investigations. This single-step reaction is relatively simple and has extensively been studied for both powders [1–5] and single crystals [5–19], which makes it suitable for comparison.

$$\begin{aligned} \hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}{\rm (s)}\,\leftrightarrows\,\hbox {Li}_2\hbox {SO}_4{\rm (s)}+\hbox {H}_2\hbox {O}\hbox {(g)} \end{aligned}$$
(1)

The interface advance is likely the most characteristic process of the dehydration reaction. The geometric models, widely used in the kinetic analysis of thermal decomposition reactions [20–25], are based upon the processes of nucleation and growth of product nuclei by interface advance. It was suggested that more reliable data can be obtained from the kinetic study of single crystals compared to powdery samples [1]. Thus, research of the reaction interface on a single crystal has been an important subject for understanding the reaction kinetics. Previous microscopic studies on single crystals [10, 11] have demonstrated that the reaction interface of the \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) dehydration reaction includes a sharp discontinuity and the product phase of reaction is composed of an open but coherent assemblage of crystallites of the dehydrated salt, without evident preferred alignment [11]. By using X-ray diffractometry in combination with the synchrotron radiation method, it was detected that the reactant–product interface is actually a reaction zone of metastable intermediate with a thickness of ca. 150 μm [7] instead of several molecular layers. It was concluded, based on various thermo-gravimetric analyses (TG) [1, 6, 10, 12, 13], that the rate of interface advance at constant temperature and water vapor pressure is constant. However, as pointed out by Modestov et al. [18], the size of samples used in those studies is comparable to the size of the reaction zone itself, which is insufficient to draw a conclusion of constant propagation rate. Therefore, experiments on the propagation of the reaction zone were designed and carried out with much larger single crystals [18]. The former conclusion was confirmed that the accumulating residual dehydrated phase has no effect on the kinetics. Nevertheless, a very different activation energy compared to previous reported values [1, 6] was obtained by fitting the constant propagation rates at various temperatures. In a subsequent study, this discrepancy was attributed to the self-cooling effect during the endothermic decomposition reaction, which can reach tens degrees celsius [26].

Despite all these contributions, the fundamental mechanisms of the elementary process of interface advance are still not clear. As stated in [18], the physics of heat and mass exchange during the interface advance of the \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) dehydration reaction is still far from being complete. The water molecules released from the reaction zone have to travel from the reaction interface to the surface of the crystal through the dehydrated part. The influence of heat and mass transfer has to be investigated in order to achieve more fundamental understanding of this reaction. To do this, in situ observations of interface propagation and mathematical models of the reaction–diffusion problem will be particularly useful in characterizing the mechanisms and kinetics of such reactions, which are almost inaccessible to direct measurement methods.

Modestov et al. [18] studied the interface propagation using an indirect measurement method, deducing the rate of interface advance from the mass loss of encapsulated crystals (TG). Here, this experiment is slightly modified which allows us to follow the interface propagation directly during the dehydration reaction. Then, a sharp interface model involving the intrinsic reaction at the interface and mass diffusion through the dehydrated crystal is developed and applied to solve the dehydration reaction problem. The mathematical framework is based on a conservative formulation within the finite difference method [27]. Instead of solving the boundary condition at the moving interface directly, an equation derived from global conservation is used. Experiments on specific prepared crystals are performed using optical microscopy, and the interface advance at various temperatures is recorded photographically. By comparing experimental results with numerical solutions, the interaction between the interfacial reaction and water vapor diffusion is discussed and elucidated.

Microscopy experiments of interface advance

In order to examine the interface advance directly, microscopy experiments with encapsulated \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) monocrystals are designed. In the previous study by Modestov et al. [18], crystals are encapsulated by metal grease on all the surfaces except one. The dehydration reaction is initiated at the open surface and restricted on the covered surfaces, which results in a one-dimensional propagation of the reaction interface in the crystal bulk. In the present study, a similar concept is used, but in addition, use is made of the fact that the structural reorganization of salt hydrates often yields small dehydrated particles with crystallite textures and cracks that scatter light [28]. This makes the reorganization visible under optical microscopy. Therefore, in this study a transparent epoxy was used such that the motion of the reaction front in the bulk can be visualized by an optical microscopy system. To this end, preparation of sample crystals is needed to prevent the surface effect from obscuring the bulk effect.

Fig. 1
figure 1

Sketch of a recrystallized single crystal of \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\)

Full size image
Fig. 2
figure 2

Example of an encapsulated crystal (the crystal will be ground at the dashed line)

Full size image

Large \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) monocrystals were grown from commercial powder (SIGMA-ALDRICH, \(\ge \)99.0 %). As shown in Fig. 1, plate-like crystals recrystallized along the crystallographic orientation [010] were collected with typical dimensions: L = 4–5 mm, W = 2–3 mm, and e = 0.5–1 mm. A liquid resin, called EpoFix, with its hardener was used to encapsulate crystals at room temperature. After solidification of the resin containing the crystal as shown in Fig. 2, samples were polished using abrasive papers of grit 600–4000 to increase their transparency and then an end surface in the direction [010] was ground to remove the resin. The crystal indicated by the dotted line was ground by a fine abrasive paper to activate an instantaneous nucleation at the entire surface, leading to the propagation of the whole reaction interface as a flat wave advancing toward the other end of the crystal.

Microscopy experiments of interface advance are carried out in the heating stage facility with a Zeiss microscope (SteREO Discovery V20). The heating stage consists of a metal base with a cavity, containing the sample holder, covered by a piece of glass. Within the heating stage, the reaction environment including temperature and water vapor pressure is well controlled. In the present study, all measurements were taken at one water vapor pressure of \(13\pm 1\) mbar, which is a practical value for application of thermochemical heat storage [29]. After the environment in the heating stage is stabilized, a crystal sample is placed in it quickly and is monitored by a camera system integrated in the microscope. Once reaction occurs, the propagation of reaction front is documented by periodic photomicrographs.

Fig. 3
figure 3

Typical sequence of the interfacial propagation in the bulk of an encapsulated \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) monocrystal during dehydration at 130 °C and 13 mbar (the crystal shape is indicated by the dashed line)

Full size image

The apparatus and experimental technique are identical to those used previously [30]. More experimental results can be found in [30]. A typical example of interface advance of an encapsulated \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) monocrystal is shown in Fig. 3. The dehydration reaction originated at the surface where the epoxy resin was removed. It is clearly seen that the reaction front is propagating in the in-depth [010] direction of the crystal, while reaction on the other faces is restricted during the early stage of the dehydration. In the post-processing, a straight line is drawn to fit the interface so that a mean distance between the reaction front and the open surface of the encapsulated crystal can be calculated. As discussed earlier, this sharp interface observed is responsible for the reorganization of crystalline structure. It has been verified that the reaction kinetics within the interface of \(\hbox {Li}_2\hbox {SO}_4{\cdot} \hbox {H}_2\hbox {O}\) crystals depend significantly on the processes of structural reorganization connected with solid product formation [8], which makes the sharp interface observed from our experiments an accurate representative of the reaction zone. The shortcoming of the optical observation so far is that the epoxy resin used cannot prevent the surface reaction completely. The reaction interface was obscured at the later stage by undesirable nuclei, and consequently only the first part of the interfacial movement during the reaction can be evaluated with acceptable accuracy.

Mathematical model of interface advance

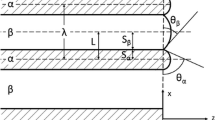
Figure 4 shows schematically a typical model for the interface advance in a planar geometry [31]. In general, the interface advance involves three processes: (1) breakdown of a reactant constituent by rupture of chemical bonds, (2) structural reorganization of this chemically changed material from the reactant structure (\(\alpha \) phase) to the more stable product structure (\(\beta \) phase) and (3) transport of dissociated water molecules through the porous product layer. In the reversible reaction presented in Eq. 1, the rate of interface advance is assumed to be determined by the forward and the reverse reaction at the interface. On the basis of previous studies [1, 6, 10, 12, 13], the forward reaction is described as a zero-order reaction. The reserve reaction is assumed to be a first-order reaction because of the product of the gaseous component. Therefore, the net mass flux of reaction at the interface is written as

$$\begin{aligned} J_{\mathrm{H}_2\mathrm{O}}=k_\mathrm{r}-k_\mathrm{r}'c_\mathrm{c} \end{aligned}$$
(2)

where \(k_\mathrm{r}\) and \(k_\mathrm{r}'\) are rate constants of the forward and the reverse reaction, respectively, and \(c_\mathrm{c}\) is the water concentration at the interface.

Fig. 4
figure 4

Schematic illustration showing the general features of the moving boundary diffusion problem considered in the present work, with concentrations and positions indicated on the axes

Full size image

In equilibrium, the net mass flux of reaction is zero:

$$\begin{aligned} k_\mathrm{r}-k_\mathrm{r}'c_\mathrm{eq}=0 \end{aligned}$$
(3)

By substituting \(k_\mathrm{r}'\) in Eq. 2, the mass flux of reaction can be rewritten as

$$\begin{aligned} J_{\mathrm{H}_2\mathrm{O}}=k_\mathrm{r}\left( 1-\frac{c_\mathrm{c}}{c_\mathrm{eq}}\right) \end{aligned}$$
(4)

where \(c_\mathrm{eq}\) is the equilibrium concentration (virtually the equilibrium water vapor pressure).

The equilibrium partial pressure of water vapor corresponding to reaction (1) is given by

$$\begin{aligned} p_\mathrm{eq}=p_0 \exp \left( \frac{-\Delta G^{\circ }}{RT}\right) \end{aligned}$$
(5)

where \(p_0\) is the standard atmospheric pressure, \(\Delta G^{\circ }\) is the standard free energy of the reaction, R is the universal gas constant, and T is temperature. Assuming that the free water vapor in the \(\beta \) phase behaves as an ideal gas, we have the equilibrium water vapor concentration as

$$\begin{aligned} c_\mathrm{eq}=\frac{p_\mathrm{eq}M}{RT}=\frac{p_{0}M}{RT}\exp \left( \frac{-\Delta G^{\circ }}{RT}\right) \end{aligned}$$
(6)

where M is the molar mass of \(\hbox {H}_2\hbox {O}\).

In terms of the propagation of reaction interface position \(\delta x_\mathrm{c}\) in a time interval \(\delta t\), the mass flux of water vapor is given by

$$\begin{aligned} J_{\mathrm{H}_2\mathrm{O}}=-c_0\frac{{\hbox{d}}x_\mathrm{c}}{\mathrm{d}t} \end{aligned}$$
(7)

where \(c_0\) is the initial water concentration in the salt hydrate and \(x_\mathrm{c}\) is the interface position (see Fig. 4). Together with Eqs. 4 and 7, the rate of interface advance is written as

$$\begin{aligned} \frac{{\hbox{d}}x_\mathrm{c}}{\mathrm{d}t}=-\frac{k_\mathrm{r}}{c_0}\left(1-\frac{c_\mathrm{c}}{c_\mathrm{eq}}\right) \end{aligned}$$
(8)

In porous materials, the water concentration distribution c(x, t) can be described by Fick’s law as

$$\begin{aligned} \frac{\partial c}{\partial t}=D_\mathrm{e}\frac{\partial ^2 c}{\partial x^2}, \quad x_\mathrm{c}\,<\,x\,<\,L \end{aligned}$$
(9)

where \(D_\mathrm{e}\) is the effective diffusivity of water through the \(\beta \) phase.

In order to preserve the mass balance at the interface, the mass flux relative to the moving interface must be considered. The amount of water generated from interfacial reaction must be equal to the amount transported away from the interface. In particular, mass flux of convection must be considered from the moving interface to a fixed frame with an absolute velocity \(-\mathrm{d}x_\mathrm{c}/\mathrm{d}t\) [32]. So the boundary condition at the moving interface is given as

$$\begin{aligned} k_\mathrm{r}\left(1-\frac{c_\mathrm{c}}{c_\mathrm{eq}}\right)=-D_\mathrm{e}\frac{\partial c(x,t)}{\partial x}\Big |_{x=x_\mathrm{c}}-\frac{\mathrm{d}x_\mathrm{c}}{\mathrm{d}t}c_\mathrm{c}, \quad x=x_\mathrm{c} \end{aligned}$$
(10)

After substitution of \(\mathrm{d}x_\mathrm{c}/\mathrm{d}t\) with Eq. 8, the boundary condition at the interface can be written as

$$\begin{aligned} \frac{\partial c(x,t)}{\partial x}\Big |_{x=x_\mathrm{c}}=-\frac{k_\mathrm{r}}{D_\mathrm{e}}\left(1-\frac{c_\mathrm{c}}{c_\mathrm{eq}}\right)\left(1-\frac{c_\mathrm{c}}{c_{0}}\right), \quad x=x_\mathrm{c} \end{aligned}$$
(11)

The other boundary condition at the outer surface is given by

$$\begin{aligned} c(x,t)=c_{{\rm g}}, \quad x=L \end{aligned}$$
(12)

where \(c_{{\rm g}}\) is the water concentration in the environment.

For the model to be as general as possible, the following nondimensional spatial and temporal variables are defined as

$$\begin{aligned} \hat{x}=\frac{x}{L}; \quad \hat{t}=\frac{D_\mathrm{e} t}{L^2}; \quad \hat{c}=\frac{c-c_{{\rm g}}}{c_\mathrm{eq}-c_{{\rm g}}};\quad s=\frac{x_\mathrm{c}}{L} \end{aligned}$$
(13)

The corresponding dimensionless forms of the above equations are

$$\begin{aligned} \frac{{\hbox{d}}s}{\mathrm{d}t}= & {} -Da\lambda (1-c_\mathrm{c}),\quad x=s \end{aligned}$$
(14)
$$\begin{aligned} \frac{\partial c}{\partial t}= & {} \frac{\partial ^2 c}{\partial x^2},\quad s < x < 1 \end{aligned}$$
(15)

with boundary conditions

$$\begin{aligned}&\frac{\partial c(x,t)}{\partial x}\Big |_{x=s}=- Da\lambda (1-c_\mathrm{c})(M-c_\mathrm{c}),\quad x=s \end{aligned}$$
(16)
$$\begin{aligned}&c(x,t)=0,\quad x=1 \end{aligned}$$
(17)

and initial conditions

$$\begin{aligned}&c(x,t)=M,\quad 0\,<\,x\,<\,1,\quad t=0 \end{aligned}$$
(18)
$$\begin{aligned}&s(t)=1,\quad t=0 \end{aligned}$$
(19)

where the hats are dropped for convenience, \(Da=k_{{\rm r}}L/(D_{{\rm e}} c_0)\) is the Damköhler number expressing the ratio of the intrinsic reaction rate to the mass diffusion rate, \(\lambda =(c_\mathrm{eq}-c_{{\rm g}})/c_\mathrm{eq}\) shows the influence of the partial pressure of the atmospheric water vapor, and \(M=(c_{0}-c_{{\rm g}})/(c_\mathrm{eq}-c_{{\rm g}})\) is the normalization factor.

The present model is solved by a numerical scheme proposed by Illingworth and Golosnoy [27]. The solution is based on the finite difference method with fully implicit formulation. The moving interface is tracked by a variable grid method using a Landau transformation so that the moving interface is fixed at a grid point. To ensure the mass conservation during the interface motion, a conservative formulation instead of Eq. 14 is derived, which considers the change of the total mass present in the system at any time-step.

$$\begin{aligned} \int _{s^{{\text t}+\Delta {\text t}}}^{1}c^{{\text t}+\Delta {\text t}}{\hbox{d}}x-\int _{s^{\text t}}^{1}c^{\text t}{\hbox{d}}x=M\Delta s+\int _{t}^{t+\Delta t}\frac{\partial c}{\partial x}\Big |_{x=1}{\hbox{d}}t \end{aligned}$$
(20)

where the terms on the left-hand side of the equation present the mass change in the dehydrated phase over a time span \(\Delta t\), the first term on the right-hand side is the mass generation from the interface advance and the second term is the mass loss at the outer surface due to diffusion.

Overall, Eqs. 15–20 completely describe the reaction–diffusion problem and can be solved in a conservative way. The set of equations are solved with implicit Euler and central difference approximations. Details of the discretization and implementation can be found in [27] where an up/down wind method was used for space discretization whereas here a central difference scheme is used.

Fig. 5
figure 5

a Relative error on the calculated interface position for different values of \(\Delta t\) (1000 nodes), b relative error for different values of \(\Delta x\) (\(\Delta t=0.01\))

Full size image

The efficiency of the numerical scheme used in the calculation is examined. Due to the lack of an analytical solution for this reaction–diffusion problem, the error regression is studied by evaluating the relative error on the interface position for different values of \(\Delta t\) and \(\Delta x\) with respect to a reference solution for 1000 regularly spaced nodes and \(\Delta t =0.01\). The relative error is given as

$$\begin{aligned} \hbox {RD}=\frac{\sum _{i=1}^n(s-s_\mathrm{ref})^2}{\sum _{i=1}^ns_\mathrm{ref}^2} \end{aligned}$$
(21)

where n is the number of time-steps and \(s_\mathrm{ref}\) is the reference solution. Results of the relative error are shown in Fig. 5 for variable \(\Delta t\) and \(\Delta x\), respectively. In both cases, the conditions are chosen the same as in the reference case except for the variable of interest. It can be seen that the influence of the time-step is linear on the relative error and the influence of the space-step is quadratic, just as expected by the applied Euler method for time integration and the central difference method for space discretization. Therefore, the numerical scheme is first-order accurate in time and second-order accurate in space.

Results and discussion

In this section, the problem of interface advance is solved for various Da values. The interaction between intrinsic reaction and mass diffusion is discussed together with the results obtained from the microscopy observations. In the definition of the Damköhler number, the reaction rate constant is generally described by an Arrhenius equation

$$\begin{aligned} k_{{\rm r}}=A\exp \left(-\frac{E_{\rm a}}{RT}\right) \end{aligned}$$
(22)

where A and \(E_{\rm a}\) are the kinetic parameters.

By substitution of \(k_{{\rm r}}\), the Damköhler number can be rewritten as a function of temperature:

$$\begin{aligned} Da=\frac{AL}{D_{{\rm e}}c_0}\exp \left( \frac{-E_{\rm a}}{RT}\right) \end{aligned}$$
(23)
Table 1 Parameters used in the calculations [17]
Full size table

At a given temperature, all parameters needed for the calculation are determined with information shown in Table 1, except the effective diffusivity for water diffusion through the dehydrated \(\mathrm{Li}_2\mathrm{SO}_4{\cdot} \mathrm{H}_2\mathrm{O}\) monocrystal. Unfortunately, a proper value is difficult to find in the literature and can vary in a wide range due to different diffusion mechanisms. In order to have different Da values, only the effective diffusivity \(D_{{\rm e}}\) is varied in the subsequent calculations.

Comparison of different numerical solutions

The water concentration profile at various Da values is calculated and shown in Fig. 6. Each profile shows the water content in the \(\beta \) phase from the moving interface (\(x=s\)) to the outer surface (\(x=1\)). The arrow indicates the direction of propagation of the sharp interface, which is between the hydrated salt crystal \(\mathrm{Li}_2\mathrm{SO}_4{\cdot} \mathrm{H}_2\mathrm{O}\) and the dehydrated phase. The time intervals between two profiles in each figure from the smallest Da value to the largest are: 33, 76, 500 and 4700 min, respectively. For small Da values, the interface moves fast and the water concentration in the \(\beta \) phase is very low. For larger Da values, the interface moves slower, and the product water accumulates in the \(\beta \) phase. The explanation is clear because the propagation of the reaction front is proportional to the deviation of water concentration at the interface (\(c_\mathrm{c}\)) from the equilibrium value (\(c_\mathrm{eq}=1\)). As mentioned above, in all calculations the intrinsic reaction rate constant is fixed at a given temperature. The Damköhler number plays a significant role in determining the nature of the reaction–diffusion dynamics. In the case of a small Da value, the effective diffusivity is relatively large compared to the interfacial reaction rate constant. Thus, water vapor has sufficient time to drain away, resulting in a low concentration at the interface. The reverse reaction rate proportional to the water concentration at the interface is small. The rate of interface advance is almost equal to the forward reaction rate, which is a constant. In contrast, for a large Da value the effective diffusivity is relatively small compared to the same reaction rate constant. Water cannot escape from the salt crystal quickly enough so that its concentration near the interface becomes higher. Thus, the rate of interface propagation decreases gradually due to the reverse reaction. In other words, a very small Da value means that the kinetics of interface advance is controlled by the intrinsic chemical reaction at the interface, while a very large Da value means that the kinetics is controlled by the diffusion of water in the \(\beta \) phase.

Fig. 6
figure 6

Profiles of water concentration distribution in the \(\beta \) phase of a plane sheet for various Da values

Full size image
Fig. 7
figure 7

a Dimensionless interface position for various Da values against the dimensional time, b normalized interface velocity for various Da values against normalized time

Full size image

To further investigate the limiting mechanism of the reaction kinetics between the intrinsic reaction and the bulk diffusion process, the dimensionless interface position and normalized interface velocity as a function of time for different values of Da are shown in Fig. 7. At \(Da=0.001\), the interface position in Fig. 7a exhibits a linear dependence on time, which is consistent with the zero-order forward reaction. In contrast, at high values of Da the process is diffusion controlled, where the plot of the interface position against time is curved because of the first-order reverse reaction.

In Fig. 7b, the normalized dimensionless interface velocity is shown on a normalized time axis. The interface velocity is defined by

$$\begin{aligned} v_\mathrm{c}=-\frac{1}{Da \lambda }\frac{\mathrm{d} s}{\mathrm{d} t}=1-c_\mathrm{c} \end{aligned}$$
(24)

As discussed above, the velocity of interface advance at a small value of Da = 0.001 shows only a small decrease during the course of the reaction. With an increasing Da value, the normalized velocity decreases gradually, which is attributed to the increasing influence of diffusion limitation. In the case of Da = 1, a rapid decrease in the interface velocity within a short period of the reaction course can be observed. The overall kinetics of interface advance is initially determined by the interfacial reaction at the outer surface. As the interface moves away from the crystal surface, water vapor cannot diffuse out of the crystal efficiently, which leads to the accumulation of water molecules. The movement of interface position is slowed down rapidly. A dynamic balance between the intrinsic reaction and the mass diffusion at the interface is reached and kept until the interface advance finishes. Together with water concentration profiles shown in Fig. 6, the transition from a reaction-controlled (Da = 0.001) to a diffusion-controlled process (Da = 0.1) can be observed. It can be concluded that both interfacial reaction and mass diffusion are important in determining the interface advance within the range of Da values between 0.001 and 0.1. Out of this range, the interface advance is completely determined by one of them.

Comparison with experimental results

The interface advance of encapsulated crystals is recorded at various temperatures and a fixed partial pressure of the atmospheric water vapor (13 mbar). The interface position as a function of time at three different temperatures is shown in Fig. 8. It is evident that temperature has a strong influence on the interface advance, particularly due to its influence on the reaction rate constant as described in Eq. 22. From the shape of the \(x_\mathrm{c}\) profile, it can be noticed that at 130 °C the slope of the line decreases gradually, while at 110 °C it is almost constant except for the first part. Regardless of the small decrease at higher temperatures, the rate of interface advance can be assumed as a constant approximately, which is in agreement with previous studies [18].

Fig. 8
figure 8

Interface position as a function of time at various temperatures from microscopy experiments

Full size image

In order to compare to the numerical solution, the effective diffusivity of water in the dehydrated \(\mathrm{Li}_2\mathrm{SO}_4{\cdot} \mathrm{H}_2\mathrm{O}\) phase is needed to determine the Da values of the reaction. Unfortunately, the value of this parameter is not precisely known. Therefore, the experimental results are fitted by the numerical solutions with a given \(D_{{\rm e}}\) value of \(3\times 10^{-8}\,{\hbox{m}}^2 \, \hbox {s}\) −1. Results are shown in Fig. 9: Symbols are experimental data and lines are numerical results. In general, the trends are predicted very well and agreement between the numerical and the experimental results is satisfactory. The relatively large difference at T = 130 °C can be attributed to the temperature influence on the effective diffusivity, which is not taken into account in the calculations.

Fig. 9
figure 9

Experimental results (symbols) fitted by numerical results (lines) with a \(D_{{\rm e}}\) value of \(3\times 10^{-8}\,\hbox {m}^2\,\hbox {s}^{-1}\)

Full size image

The found value for the effective diffusivity may be influenced by several micro-level processes: Knudsen diffusion in cracks and micropores, surface diffusion by molecules jumping from one site to a neighboring site and capillary action resulting from the balance between adhesion and cohesion forces. On the basis of the scanning electron studies from Galwey et al. [11], it was demonstrated that interface reaction results in the generation of an extensive irregular crack and pore structure. On the one hand, these pores and cracks in the dehydrated phase provide void space for the transport of water in terms of gas diffusion. On the other hand, they also create a very large surface area for surface diffusion and capillary action. It is worth noting that a diffusivity value of \(2\times 10^{-7}\,\hbox {m}^2\,\hbox {s}^{-1}\) applies for pure Knudsen diffusion. Diffusion in solid is usually more difficult than in the void space of pores and cracks. Due to the lack of information of \(\mathrm{Li}_2\mathrm{SO}_4{\cdot} \mathrm{H}_2\mathrm{O}\), the diffusivity of water diffusion in solid \(\hbox {MgSO}_4{\cdot} 7\mathrm{H}_2\mathrm{O}\) is used for comparison. It was calculated by using molecular dynamic simulations that the diffusion coefficients in the center are in the order of \(10^{-10}\,\hbox {m}^2\,\hbox {s}^{-1}\), while those near the surface are in the order of \(10^{-9}\,\hbox {m}^2\,\hbox {s}^{-1}\) [33]. Generally, it is recognized that diffusion in the solid crystal is a function of crystal structure and temperature. Compared to the regular crystal lattice used in the molecular dynamic calculations, a larger diffusivity can be expected. So, an estimation of the effective diffusivity in the order of \(10^{-8}\,\hbox {m}^2\,\hbox {s}^{-1}\) could be reasonable. Corresponding Da values from fitting can be calculated as: 0.008, 0.030 and 0.055, respectively. At these Da values, the propagation of reaction interface is a deceleratory process due to the influence of mass diffusion. The decrease in interface advance rate is also shown in the experimental results but less obvious. Water diffusion through the product phase could not be an issue in the previous studies [1, 6, 10, 12, 13] because of the small size of test crystals. However, in experiments with large crystal samples (up to 2 mm) water transport after release from the interface should be taken into consideration. Even though diffusion is enhanced due to the formation of the porous network, the impedance of water transport is still noticeable in the profile of interface advance. Therefore, it is likely to assume for the present dehydration reaction that the rate of interface advance is mainly determined by the interfacial reaction, but enhancement of mass diffusion can also increase the reaction rate to some extent.

Conclusions

In conclusion, a dynamic model is developed for investigation of interface advance during the \(\mathrm{Li}_2\mathrm{SO}_4{\cdot} \mathrm{H}_2\mathrm{O}\) dehydration reaction. For the dehydration reaction, a Damköhler number is defined to reveal the interaction between the intrinsic chemical reaction and mass diffusion. Within the range of Da values between 0.001 and 0.1, it is evident that both interfacial reaction and mass diffusion are important in determining the interface advance. In the experimental section, the interface advance of encapsulated crystals is directly tracked by microscopy experiments. By fitting the experimental results, the effective diffusivity is estimated to be in the order of \(10^{-8}\,\hbox {m}^2\,\hbox {s}^{-1}\). Corresponding Da values for various temperatures are calculated as: 0.008, 0.030 and 0.055, respectively. Based on the numerical results together with experimental observations, it can be concluded that the rate of interface advance shows a small decrease over time, instead of being constant. The present study demonstrated that our model provides an effective tool to examine the interface advance of dehydration reactions.