Validation of detection efficiency-based corrections implemented in the k0-INRIM software

Abstract

The k0-INRIM is a software implemented at the Italian Metrology Institute (INRIM) to aid users elaborating data to obtain results including uncertainty budgets for Neutron Activation Analysis (NAA). The code relies on the efficiency evaluation based on an experimental characterization of the gamma detection system to calculate efficiency-based corrections. In order to validate the models adopted for these corrections in most demanding experimental conditions, an experiment is performed to collect data from point-like and extended-sources counted far from and near to the end-cap of two gamma detectors having different relative efficiency. The results comparing the experimentally evaluated and the calculated corrections are reported with detailed uncertainty estimation.

Introduction

Gamma spectrometry represents the predominant detection technique for all the standardization methods based on Neutron Activation Analysis (NAA) where it allows to quantify γ-rays emitted from the produced radionuclides thanks to the peaks identified in the resulting γ-spectrum. Specifically, net peak counts are related to amount of emitted γ-rays from the radioactive source through the absolute full-peak efficiency (detection efficiency), which depends on source-detector geometry, energy of the emissions and intrinsic efficiency of the detector [1].

The three main standardization methods of NAA (relative, k₀, absolute) employ different approaches while dealing with gamma spectrometry: (i) the relative method compares peaks coming from the same radionuclide for standard and sample measured at the same counting distance and usually having similar shape so that the detection efficiency is modeled by a ratio approaching the unity value, (ii) the k₀-method compares peaks coming from different radionuclides for standard and sample usually having different shape and measured at different counting distance so that the detection efficiency is modeled by correction factors departing from the unity value, (iii) the absolute method is carried out with the sole acquisition of sample, thus absolute value of detection efficiency has to be carefully modeled.

For routine analysis the k₀-NAA method offers the best tradeoff between high sample throughput and suitable measurement uncertainty. However, in k₀-standardization, the detection efficiency represents a key parameter of the measurement model and is usually one of the most important contributors to the combined uncertainty of the result [2]. To date, several procedures were developed to deal with detection efficiency evaluation mainly involving a combination of experimental measurements and Monte Carlo simulations [3]; the Monte Carlo is largely appreciated for its flexibility but requires fine tuning of detector-defining parameters, through experimental characterization [4] or diagnostic tools [5], to get the best results [6]. Even when detector manufacturers provide all the necessary information, the importance of optimization and validation of the simulation in the intended counting setup cannot be overstated [7].

As an alternative to simulation procedures, we recently proposed a strategy to manage detection efficiency exclusively based on experimental determination of γ-sources in all the counting positions, which also allows to take into account correlations among input parameters [8, 9]. This strategy was adopted as a building block of the k0-INRIM software, developed at INRIM, focused on elaboration of k₀-NAA measurements [10] and will also be included in its counterpart, called Rel-INRIM software, implementing the relative standardization method, which is on its way to be completed.

The participation of k0-INRIM to an inter-comparison among well-established commercial and home-made codes, proposed by International Atomic Energy Agency (IAEA) and focused to investigate k₀-NAA software, attested the suitability of the overall implementation; interestingly, it also confirmed that the different implementations of detection efficiency approaches adopted by the various codes are the main cause of variability of results among the corresponding laboratories with discrepancies up to a few percent despite starting from identical input data [11]. Those findings reiterated the importance to not overlook the evaluation process of detection efficiency prompting the need for the study here reported.

In this work, the equation models developed for the detection efficiency and adopted in the k0-INRIM are validated in demanding experimental conditions, i.e. for close counting positions and with non-point-like samples. The outcome will point out to what extent the corrections defined in the adopted measurement model are suitable in those practical situations. The study of the estimated uncertainty of these corrections will also indicate whether the model takes into account all the significant effects.

Equation models

The monitor to analyte efficiency ratio, ${k}_{\varepsilon }$, is modelled in the k0-INRIM software as product of five correction factors:

$${k}_{\varepsilon }={k}_{\varepsilon \Delta E} \: {k}_{\varepsilon \Delta d} \: {k}_{\mathrm{pos}} \: {k}_{\mathrm{geo}} \: {k}_{\mathrm{sa}},$$

(1)

where ${k}_{\varepsilon \Delta E}$ is the energy correction factor at reference position, ${k}_{\varepsilon \Delta d}$ is the large-scale counting position correction factor (among counting positions defined in the experimental detector characterization), ${k}_{\mathrm{pos}}$ is the experimental local positioning (small deviations from the defined counting positions) correction factor, ${k}_{\mathrm{geo}}$ is the geometry correction factor (accounting for non-point sources) and ${k}_{\mathrm{sa}}$ is the γ-self-absorption correction factor. The comprehensive description of the five parameters in Eq. (1) is given in [9] while here we briefly recall the adopted formulae.

The ${k}_{\varepsilon \Delta E}$ is estimated using:

$${k}_{\varepsilon \Delta E}={e}^{\sum_{i=1}^{6}{a}_{i} \left({E}_{\mathrm{m}}^{2-i}-{E}_{\mathrm{a}}^{2-i}\right)},$$

(2)

where ${a}_{i}$ indicates fitting parameters obtained by a 6-terms expression fit performed on efficiency data calculated from acquisitions of SI traceable point-like γ-sources at reference position and $E$ is the energy of the corresponding γ-lines for monitor and analyte, here and hereafter identified with subscripts m and a, respectively. Accordingly, Eq. (2) models a ratio of two efficiencies at reference position for any pair of energies E_m and E_a. The well-known significant correlation among ${a}_{i}$ positively affects the resulting uncertainty up to making it null when the monitor and analyte energy coincide. Since both true-coincidence and true-coincidence free emissions can be used at reference position, the fitting algorithm can be fed by a large amount of data-points over an extended range of energies which makes the knowledge of ${k}_{\varepsilon \Delta E}$, to some extent, robust.

The ${k}_{\varepsilon \Delta d}$ is estimated using different formulae depending on the experimental counting scenario adopted in the analysis. In this work, the most demanding counting scenario is tested, i.e. when the standard is acquired at reference and the sample closer to the detector. The corresponding formula is:

$${k}_{\varepsilon \Delta d}={e}^{\sum_{i=1}^{6}{b}_{i} {E}_{\mathrm{a}}^{2-i}} ,$$

(3)

where ${b}_{i}$ indicates fitting parameters obtained by means of a 6-terms expression fit performed on count rate ratios calculated from acquisitions of true-coincidence free γ-emitters. The ${k}_{\varepsilon \Delta d}$ correction factor plays a significant role when the distance between reference and counting position is large. Since only true-coincidence free emissions can be used, the fitting algorithm is fed by a small amount of data-points over a limited range of energies which makes the knowledge of ${k}_{\varepsilon \Delta d}$ to some extent challenging as it strongly depends on availability and choice of γ-sources.

The ${k}_{\mathrm{pos}}$ is the ratio of two efficiency ratios at counting positions calculated via the inverse square law of distance:

$${k}_{\mathrm{pos}}={\left(\frac{{d}_{\mathrm{m}}-{d}_{0 \: \mathrm{m}}^{\prime}}{{d}_{\mathrm{m}}+\delta {d}_{\mathrm{m}}-{d}_{0 \: \mathrm{m}}^{\prime}}\right)}^{2}{\left(\frac{{d}_{\mathrm{a}}-{d}_{0 \: \mathrm{a}}^{\prime}}{{d}_{\mathrm{a}}+\delta {d}_{\mathrm{a}}-{d}_{0 \: \mathrm{a}}^{\prime}}\right)}^{-2},$$

(4)

where $d$ is the distance between the γ-reference source and the detector end-cap identifying a nominal (characterized) counting position,$\delta d$ is an offset between the nominal and the actual counting position of standard and sample and ${d}_{0}^{\prime}$ is the distance between the point-of-action within the detector crystal and the end-cap. The adopted model for ${d}_{0}^{\prime}$ is

$${d}_{0}^{\prime}={-e}^{\sum_{i=1}^{5}{l}_{i} {E}^{2-i}},$$

(5)

where ${l}_{i}$ are fitting parameters depending on nominal counting position of m and a obtained by means of a 5-terms expression fit performed on ${d}_{0}^{\prime}$ values calculated from local linearization of curves modelling normalized count rate variations versus distance [9]. The ${k}_{\mathrm{geo}}$ is the ratio of two efficiency ratios calculated via the inverse square law of distance accounting for extended cylindrical geometry of standard and sample:

$${k}_{\mathrm{geo}}={\left(1+\frac{{h}_{\mathrm{m}}}{{d}_{\mathrm{m}}+\delta {d}_{\mathrm{m}}-{d}_{0 \: \mathrm{m}}^{\prime}}\right)}^{-1}\left(1+\frac{{h}_{\mathrm{a}}}{{d}_{\mathrm{a}}+\delta {d}_{\mathrm{a}}-{d}_{0 \: \mathrm{a}}^{\prime}}\right),$$

(6)

where $h$ is the cylinder height. The adopted formula assumes that γ-emitters are homogeneously distributed in standard and sample volumes.

It is worth to note that ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ share the same parameters except $h$, thus it might be convenient to consider them as a single parameter.

The ${k}_{\mathrm{sa}}$ is the ratio of two self-absorption corrections based on the Debertin-Helmer formula [12]:

$${k}_{\mathrm{sa}}=\left(\frac{1-{e}^{-{\nu }_{\mathrm{m}}{h}_{\mathrm{m}}{\rho }_{\mathrm{m}}}}{{\nu }_{\mathrm{m}}{h}_{\mathrm{m}}{\rho }_{\mathrm{m}}}\right){\left(\frac{1-{e}^{-{\nu }_{\mathrm{a}}{h}_{\mathrm{a}}{\rho }_{\mathrm{a}}}}{{\nu }_{\mathrm{a}}{h}_{\mathrm{a}}{\rho }_{\mathrm{a}}}\right)}^{-1},$$

(7)

where, $\nu$ and $\rho$ are the mass attenuation coefficient and density, respectively.

In order to validate the novel equations developed for ${k}_{\varepsilon \Delta E}$, ${k}_{\varepsilon \Delta d},$ ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ correction factors, we carried out an experiment designed to measure ${k}_{\varepsilon }$ in specific testing conditions based on γ-spectrometry. To this aim, it is useful rearranging the measurement equation implemented in the k0-INRIM software (which in turn derives from the k₀-method original formulation [13]). The rearranged equation, short of parameters modeling blank effects, is:

$$\begin{aligned} k_{\varepsilon } = & \frac{{\left. {\lambda \frac{{\left( {n_{{\text{p}}} /COI} \right)\left( {t_{{\text{c}}} /t_{{\text{l}}} } \right) e^{{\mu \left( {1 - t_{{\text{l}}} /t_{{\text{c}}} } \right)}} }}{{\left( {1 - e^{{ - \lambda t_{{\text{i}}} }} } \right)\left( {1 - e^{{ - \lambda t_{{\text{c}}} }} } \right)}}} \right|_{{\text{m}}} }}{{\left. {\lambda \frac{{\left( {n_{{\text{p}}} /COI} \right)\left( {t_{{\text{c}}} /t_{{\text{l}}} } \right) e^{{\mu \left( {1 - t_{{\text{l}}} /t_{{\text{c}}} } \right)}} }}{{\left( {1 - e^{{ - \lambda t_{{\text{i}}} }} } \right)\left( {1 - e^{{ - \lambda t_{{\text{c}}} }} } \right)}}} \right|_{{\text{a}}} }} e^{{\left( {\lambda_{{\text{m}}} - \lambda_{{\text{a}}} } \right) t_{{\text{d m}}} - \lambda_{{\text{a}}} {\Delta }t_{{\text{d}}} }} \\ \times \left( {1 + \beta {\Delta }l_{{\text{a}}} } \right)\frac{{k_{{0 \:{\text{Au}}}} \left( {\text{a}} \right)}}{{k_{{0 \:{\text{Au}}}} \left( {\text{m}} \right)}}\frac{{G_{{\text{th a}}} + \frac{{G_{{\text{e a}}} }}{f}\left( {\frac{{Q_{{0{\text{ a}}}} - 0.429}}{{\overline{E}_{{\text{r a}}}^{\alpha } }} + \frac{0.429}{{0.55^{\alpha } \left( {1 + 2\alpha } \right)}}} \right)}}{{G_{{\text{th m}}} + \frac{{G_{{\text{e m}}} }}{f}\left( {\frac{{Q_{{0{\text{ m}}}} - 0.429}}{{\overline{E}_{{\text{r m}}}^{\alpha } }} + \frac{0.429}{{0.55^{\alpha } \left( {1 + 2\alpha } \right)}}} \right)}} \\ \times \frac{{m_{{{\text{sm}}}} \left( {1 - \eta_{{{\text{sm}}}} } \right) w_{{\text{a}}} }}{{m_{{{\text{std}}}} \left( {1 - \eta_{{{\text{std}}}} } \right) w_{{\text{m}}} }}, \\ \end{aligned}$$

(8)

where ${n}_{\mathrm{p}}$ is the net area of the full-energy peak, $COI$ is the true-coincidence correction factor, and $\frac{{k}_{0 \:\mathrm{Au}}\left(\mathrm{a}\right)}{{k}_{0 \:\mathrm{Au}}\left(\mathrm{m}\right)}=\frac{{\sigma }_{\text{a}} {\vartheta }_{\text{a}} {\gamma }_{\text{a}} {M}_{\text{m}}}{{\sigma }_{\text{m}} {\vartheta }_{\text{m}} {\gamma }_{\text{m}} {M}_{\text{a}}}$ with $\gamma$ the emission yield, $\uplambda$ is the decay constant, ${t}_{\mathrm{c}}$ and ${t}_{\mathrm{l}}$ are real and live counting times, ${\Delta t}_{\mathrm{d}}$ is the difference between the decay times at the beginning of the acquisitions of the spectra and $\mu$ is the excess counting loss constant of the detection system; subscripts std and sm refer to standard and sample, respectively. See [9] for name and detailed description of the remaining parameters.

Energy correction factor

The model adopted for the ${k}_{\varepsilon \Delta E}$ correction factor is verified by elaborating a single spectrum of a point-like γ-source containing radionuclides emitting multiple emissions acquired far from the detector end-cap. We consider two emissions at different energies of the same radionuclide, one for the monitor and one for the analyte. The proposed experimental setup allows to make negligible the effect of all other correction factors in ${k}_{\varepsilon }$ $\left({k}_{\varepsilon \Delta d}={k}_{\mathrm{pos}}={k}_{\mathrm{geo}}={k}_{\mathrm{sa}}=1\right)$. In addition, $\frac{{k}_{0 \:\mathrm{Au}}\left(\mathrm{a}\right)}{{k}_{0 \:\mathrm{Au}}\left(\mathrm{m}\right)}$ simplifies to $\frac{{\gamma }_{\text{a}}}{{\gamma }_{\text{m}}}$. Accordingly, Eq. (8) becomes:

$${k}_{\varepsilon \Delta E}^{-1}=\frac{{n}_{\mathrm{p \: a}(\mathrm{fp})} {\gamma }_{\mathrm{m}} }{{n}_{\mathrm{p \: m}(\mathrm{fp})} {\gamma }_{\mathrm{a}} }.$$

(9)

Here and hereafter, subscripts in parenthesis identify a specific sample (p for “point-source” or e for “extended”) in a specific counting position (f for “far-away” or n for “near” the detector end-cap); when a parameter refers to both samples or both positions, as it’s the case for ${k}_{\text{pos}}$ and ${k}_{\text{geo}}$ in Eq. (10,12), two couples of subscripts separated by a comma are recalled.

Equation (9) displays a ratio of γ-emission yields in place of the ratio of k₀ constants. Their values are equivalent based on the proposed experimental setup, however, the yields ratio is more suitable to evaluate uncertainties since it doesn’t take into account parameters that are fully correlated ($\sigma$, $\vartheta$ and $M$).

Large-scale counting position correction factor

The model adopted for the ${k}_{\varepsilon \Delta d}$ correction factor is verified by elaborating two spectra of an extended cylindrical γ-source, the first acquired far from the detector end-cap and the latter acquired close to the detector end-cap. We consider the same emission of a radionuclide for both the monitor and the analyte. Under this assumption, it can be demonstrated that Eq. (8) simplifies to

$${k}_{\varepsilon \Delta d}^{-1} {k}_{\text{pos(fe,ne)}}^{-1} {k}_{\text{geo(fe,ne)}}^{-1}\frac{{COI}_{(\mathrm{ne})}}{{COI}_{(\mathrm{fe})}}=\frac{{n}_{\mathrm{p}(\mathrm{ne})}}{{n}_{\mathrm{p}(\mathrm{fe})}}\frac{{t}_{\mathrm{c}(\mathrm{ne})}{ t}_{\mathrm{l}(\mathrm{fe})}}{{t}_{\mathrm{c}(\mathrm{fe})} {t}_{\mathrm{l}(\mathrm{ne})}}\frac{{e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{ne})}/{t}_{\mathrm{c}(\mathrm{ne})}\right)}}{{e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{fe})}/{t}_{\mathrm{c}(\mathrm{fe})}\right)}}\frac{\left( 1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{fe})}}\right)}{\left( 1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{ne})}}\right)} {e}^{{\mathrm{\lambda \Delta }t}_{\mathrm{d}}}.$$

(10)

In addition, the equation adopted to calculate the $COI$ value is based on De Corte's work [13]:

$$COI=\left(1-\sum_{i}{F}_{\mathrm{loss}}(i)\right)\left(1+\sum_{i}{F}_{\mathrm{sum}}(i)\right),$$

(11)

where, $i$ indicates any cascade possibly involved in a true-coincidence with the γ-emission of interest, while ${F}_{\mathrm{loss}}$ and ${F}_{\mathrm{sum}}$ represent a pool of functions depending on the investigated emission to evaluate loss and summing effects, respectively. Functions and values of relevant parameters are reported in literature [13].

Local positioning and geometry correction factors

The models adopted for the ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ correction factors are verified by elaborating two spectra of an extended cylindrical γ-source (the first acquired far from the detector end-cap and the latter acquired close to the detector end-cap) and two spectra of a point-like γ-source (the first acquired far from the detector end-cap and the latter acquired close to the detector end-cap). Both the extended cylindrical and point-like sources contain the same radionuclides. Under this assumption, the ratio of Eq. (8) evaluated on the same emission both for the monitor and the analyte acquired in the far and the closer counting position simplifies to

$${k}_{\text{pos(ne,np) }}^{-1}{k}_{\text{pos(fe,fp)}} {k}_{\text{geo(ne,np) }}^{-1}{k}_{\text{geo(fe,fp)}} =\frac{{n}_{\mathrm{p}(\mathrm{ne})} {n}_{\mathrm{p}(\mathrm{fp})}}{{n}_{\mathrm{p}(\mathrm{fe})}{ n}_{\mathrm{p}(\mathrm{np})}}\frac{{t}_{\mathrm{c}(\mathrm{ne})} {t}_{\mathrm{l}(\mathrm{fe})} {t}_{\mathrm{c}(\mathrm{fp})} {t}_{\mathrm{l}(\mathrm{np})}}{{t}_{\mathrm{c}(\mathrm{fe})} {t}_{\mathrm{l}(\mathrm{ne})}{ t}_{\mathrm{c}(\mathrm{np})} {t}_{\mathrm{l}(\mathrm{fp})} }\frac{{e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{ne})}/{t}_{\mathrm{c}(\mathrm{ne})}\right)} {e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{fp})}/{t}_{\mathrm{c}(\mathrm{fp})}\right)}}{{e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{fe})}/{t}_{\mathrm{c}(\mathrm{fe})}\right)} {e}^{\mu \left(1-{t}_{\mathrm{l}(\mathrm{np})}/{t}_{\mathrm{c}(\mathrm{np})}\right)}}\frac{\left(1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{np})}}\right)\left(1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{fe})}}\right)}{\left(1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{ne})}}\right)\left(1-{e}^{-\lambda {t}_{\mathrm{c}(\mathrm{fp})}}\right)}\frac{{e}^{{\mathrm{\lambda \Delta }t}_{\mathrm{d}(\mathrm{n})}}}{{e}^{{\mathrm{\lambda \Delta }t}_{\mathrm{d}(\mathrm{f})}}}$$

(12)

It is worth noting that in eqs. (9–10,12), all the parameters adopted to model the detection efficiency are included in the left-hand side, hereafter defined ${\mathrm{\rm K}}_{\mathrm{mod}}$, while the right hand-side, hereafter defined ${\mathrm{\rm K}}_{\mathrm{exp}}$, includes experimental data dealing with γ-spectrometry measurements; the two sides of the equation should be in agreement to validate the formulae adopted for the correction factors ${k}_{\varepsilon \Delta E}$, ${k}_{\varepsilon \Delta d}$, ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$.

Experimental

A material composed of shredded printed circuit boards (PCBs) containing Au, Cr, Sb and Zn was adopted to prepare two extended cylindrical samples, hereafter called E1 and E2, with heights at the upper limits usually reached in the real measurements; masses of 574 mg and 814 mg were pressed at 10 bar in the shape of a cylindrical tablet with 10 mm diameter resulting in heights of 3.65(3) mm and 5.45(3) mm for E1 and E2, respectively (see Fig. 1). Tablets dimensions were carefully measured with an analogic twentieth reading caliper. Numbers in parenthesis indicate the assigned standard uncertainties (k = 1) referring to the corresponding last digits of the associated values; parameters whose values are reported without uncertainty are not part of the measurement models and are only mentioned to fully describe the experimental procedure.

Fig. 1

Extended cylindrical PCB samples E1 (right) and E2 (left)

Four mono-elemental solutions were used to prepare two point-like samples (hereafter called P1 and P2); suitable volumes of Au, Se, Sb and Zn solutions (1000 mg L⁻¹ mass concentration for the first three elements and 10,000 mg L⁻¹ mass concentration for the latter) were pipetted on two filter paper disks (6 mm diameters and 0.15(5) mm thickness), evaporated with UV lamp and sealed with foils of adhesive tape (see Fig. 2).

Fig. 2

Point-like samples P1 and P2

The cylindrical extended samples E1 and E2 were then placed in polyethylene (PE) vials suitable for irradiation and piled, together with the two point-like samples P1 and P2, within a PE irradiation container (see Fig. 3).

Fig. 3

The PE irradiation container housing the cylindrical extended samples E1 and E2, and the point-like samples P1 and P2

The neutron irradiation took place for 30 min at 250 kW power in a channel of the carousel facility of TRIGA Mark II nuclear reactor of Pavia. A cooling time of 5 days was observed before retrieving the samples from the irradiation container and individually transferring them in specific counting containers: E1 and E2 were kept in their PE vials while P1 and P2 were transferred to new PE vials suitable to obtain a similar distance between the basis of support of the vial and the lower base of the samples.

The acquisitions were performed on two detection systems equipped with Hyper-pure Ge (HPGe) detectors from ORTEC: one, hereafter called OR50, providing 50% relative efficiency and 1.90 keV resolution at 1332 keV energy while the other, hereafter called OR20, providing 20% relative efficiency and 1.69 keV resolution at 1332 keV energy. The detectors were connected to their own ORTEC DSPEC 502 multi-channel analyzers and controlled by personal computers running GammaVision software for spectra acquisition. HyperLab software was used for peak elaboration.

The detector characterization on both systems was performed as described in [9, 10] adopting point-like (disks, 3 mm diameter and 0.2 mm thickness) γ-sources ¹⁵²Eu (LEA, code EU152EGMA20), ¹³³Ba (LEA, code BA133EGMA20), ²⁴¹Am (CMI, type EG1), ¹⁰⁹Cd (CMI, type EG1X), ⁵⁷Co (CMI, type EG1X), ⁶⁵Zn (homemade), ⁵¹Cr (homemade), ¹⁹⁸Au (homemade) and ¹³⁷Cs (CMI, type EG1) acquired in 10 counting positions with reference at 203.6(1) mm from detector end-cap while the two closest positions were at 43.6(1) mm and 23.6(1) mm distances, respectively. The resulting energy range containing the adopted emissions went from 53.2 keV (¹³³Ba) to 1457.6 keV (¹⁵²Eu) at the reference position and from 59.5 keV (²⁴¹Am) to 1115.5 keV (⁶⁵Zn) at the two closest counting positions. The positioning systems adopted to place γ-sources were tailored on the detectors’ diameters and composed of a series of modular plastic hollow spacers ending with platforms to place a PE container centered along the vertical axis of the detector. Spacers provide counting position slots every 20 mm from 23.6(1) mm to 203.6(1) mm; the reported counting distances consider the length from the top of the detector end-cap to the lower base of the point-like reference γ-sources and were carefully measured with the caliper.

The irradiated samples E1, E2, P1 and P2 were acquired on both detectors producing multiple spectra with acquisition times ranging from 8 to 156 h in order to reach a relative standard uncertainty due to counting below 1.5% for the least intense investigated γ-peak. Values of acquisition times (${t}_{\mathrm{c}}$ and ${t}_{\mathrm{l}}$) were computed by the γ–spectrum acquisition software with a resolution of 0.020 s; assuming the resolution value as a variability interval with uniform distribution, a standard uncertainty of 0.012 s was assigned to all counting times. Similarly, since ${\Delta t}_{\mathrm{d}}$ values were evaluated as differences of recorded dates and times, a standard uncertainty of 0.81 s was assigned to all ${\Delta t}_{\mathrm{d}}$ considering 1 s resolution as inferred from the displayed date and time format.

Two spectra of E1, E2, P1 and P2 were recorded at reference (“far-away”) position, the first to acquire γ–emissions from medium-lived activated radionuclides and the latter to acquire γ–emissions from long-lived activated radionuclides, while a single spectrum of E1, E2, P1 and P2 was recorded in both the two closest (“near”) positions from the detector end-cap. The spectra acquisition lasted 35 days. It is worth to note that the actual counting distances of the irradiated samples differed with respect to those defined during the detector characterization. The offset was calculated from dimensional measurements of counting containers and vials performed with the caliper and resulted in a value of 0.40(5) mm for E1 and E2, and 0.55(7) mm for P1 and P2.

Results and discussion

All acquired spectra were elaborated with HyperLab software to get the net peak area of the investigated emissions and convert their files to ASCII text, a format readable from the k0-INRIM software.

Aiming at pointing out possible issues affecting detection efficiency-based corrections we calculated the ratio ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ to highlight departures from 1. The uncertainty of the ratio, evaluated by applying the law of uncertainty propagation for ${\mathrm{\rm K}}_{\mathrm{exp}}$ and ${\mathrm{\rm K}}_{\mathrm{mod}}$ as non-correlated quantities, played a key role to assess whether departures from 1 are significant.

Energy correction factor

Data obtained from P1 and P2 acquired at 203.6 mm reference position on OR20 and OR50 were used to check Eq. (2) adopted as model for ${k}_{\varepsilon \Delta E}$. Emissions of ⁷⁵Se at energies 121.1 keV, 136.0 keV, 264.7 keV and 279.5 keV and emissions of ¹²⁴Sb at energies 602.7 keV, 722.8 keV and 1691.0 keV were considered to provide multiple γ-lines over a wide energy range. The 279.5 keV of ⁷⁵Se and 602.7 keV of ¹²⁴Sb were adopted as monitors to compute ${\mathrm{\rm K}}_{\mathrm{exp}}$ and ${\mathrm{\rm K}}_{\mathrm{mod}}$ according to Eq. (9) for the remaining emissions of the same radionuclide adopted as analytes. Additional emissions, like the 400.7 keV (⁷⁵Se), were not considered because their uncertainty due to counting statistics was larger than the 0.5% threshold we fixed to identify biases.

Experimental values of ${n}_{\mathrm{p}}$ and literature values of $\gamma$ [14, 15] were used to calculate ${\mathrm{\rm K}}_{\mathrm{exp}}$ whereas literature values of ${E}_{\text{m}}$ and ${E}_{\text{a}}$ and fitted values of ${a}_{i}$ were used to calculate ${\mathrm{\rm K}}_{\mathrm{mod}}$. Fitting parameters ${a}_{i}$, including their covariance matrix, were obtained by processing detector characterization data with the k0-INRIM software. The resulting ${\mathrm{\rm K}}_{\mathrm{mod}}$, ${\mathrm{\rm K}}_{\mathrm{exp}}$ and corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ ratio values obtained for each delta energy $\Delta E={E}_{\mathrm{a}}$—${E}_{\mathrm{m}}$ on both detectors OR20 and OR50 are reported in Table 1.

Table 1 ${\mathrm{\rm K}}_{\mathrm{mod}}$ and ${\mathrm{\rm K}}_{\mathrm{exp}}$ values testing the model adopted for ${k}_{\varepsilon \Delta E}$ depending on delta energy $\Delta E$

In order to graphically point out possible significant departures from 1, the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values are plotted with respect to the analyte emission energy ${E}_{\mathrm{a}}$ in Fig. 4.

Fig. 4

The ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values plotted versus the analyte energy ${E}_{\mathrm{a}}$ testing the model adopted for ${k}_{\varepsilon \Delta E}$ with both the multiple gamma emissions of ⁷⁵Se (black circles) and ¹²⁴Sb (white circles). The error bars indicate the standard uncertainty

Results plotted in Fig. 4 show departures limited within ${1}_{-0.021}^{+0.015}$. Moreover, departures are non-significant because they lie within the coverage intervals of the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values at 95% level of confidence; accordingly, ${\mathrm{\rm K}}_{\mathrm{mod}}$ is in agreement with ${\mathrm{\rm K}}_{\mathrm{exp}}$ under all test conditions. As expected, best test conditions, where the contribution to the uncertainty due to ${k}_{\varepsilon \Delta E}$ is the main one, are reached at analyte energies 121.1 keV and 1691.0 keV, i.e. at maximum delta energies.

Large-scale counting position correction factor

Data obtained from E1 and E2 acquired at 203.6 mm reference position and 43.6 mm and 23.6 mm counting positions on OR20 and OR50 were used to check Eq. (3) adopted as model for ${k}_{\varepsilon \Delta d}$. Emissions of ⁵¹Cr, ¹⁹⁸Au, ¹²²Sb and ⁶⁵Zn at energies 320.1 keV, 411.8 keV, 564.2 keV and 1115.5 keV were considered to compute ${\mathrm{\rm K}}_{\mathrm{exp}}$ and ${\mathrm{\rm K}}_{\mathrm{mod}}$ according to Eq. (10) for the two delta counting positions (43.6—203.6) mm and (23.6—203.6) mm.

Experimental values of ${t}_{\mathrm{c}}$, ${t}_{\mathrm{l}}$, ${\Delta t}_{\mathrm{d}}$ and $\mu$, and literature values of $\lambda$ were used to calculate ${\mathrm{\rm K}}_{\mathrm{exp}}$ whereas measured values of $h$, $d$ and $\delta d$, calculated values of ${d}_{0}^{\prime}$ and $COI$ and fitted values of ${b}_{i}$ were used to calculate ${\mathrm{\rm K}}_{\mathrm{mod}}$. In details, fitting parameters ${b}_{i}$, including their covariance matrix, were obtained by processing detector characterization data with the k0-INRIM software. In addition, all the considered emissions were true-coincidence free, except for the 564.2 keV of ¹²²Sb. However, the corresponding 0.9931(14) $COI$ correction at 23.6 mm counting position on the OR50 detector was small compared to the other components involved in the calculations. The COI uncertainty was evaluated by propagation of variances for all the adopted parameters and assigning a conservative 20% relative uncertainty if no value was reported in literature; the conservative choice proved acceptable since, in the framework of this experiment, COI (and its uncertainty) had negligible impact on the evaluation of ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ ratio (Table 2).

Table 2 ${\mathrm{\rm K}}_{\mathrm{mod}}$ and ${\mathrm{\rm K}}_{\mathrm{exp}}$ values testing the model adopted for ${k}_{\varepsilon \Delta d}$ depending on energy E and delta counting position $\Delta d$ on both detectors OR20 (a) and OR50 (b)

The resulting ${\mathrm{\rm K}}_{\mathrm{mod}}$, ${\mathrm{\rm K}}_{\mathrm{exp}}$ and corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ ratio values obtained for each sample, emission energy and delta counting position, $\Delta d={d}_{(\mathrm{ne})}$—${d}_{(\mathrm{fe})}$, on both detectors OR20 and OR50 are reported in Table 2a and Table 2b, respectively.

Indexes I of ${k}_{\varepsilon \Delta d}$, grouped ${k}_{\text{pos}}$ and ${k}_{\text{pos}}$, and $COI$ (related to ${\mathrm{\rm K}}_{\mathrm{mod}}$), and grouped ${n}_{\mathrm{p}}$ and grouped $t$ values (related to ${\mathrm{\rm K}}_{\mathrm{exp}}$) highlighting their contribution to the combined uncertainty of the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ ratio are given. The ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values are also displayed.

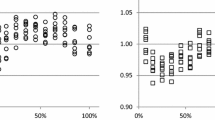
In order to graphically point out possible significant departures from 1, the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values are plotted with respect to the emission energy $E$ in Fig. 5.

Fig. 5

The ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values plotted versus the emission energy $E$ testing the model adopted for ${k}_{\varepsilon \Delta d}$ for both the counting positions 43.6 mm (black circles) and 23.6 mm (white circles). The error bars indicate the standard uncertainty

Results plotted in Fig. 5 show departures limited within ${1}_{-0.0120}^{+0.0241}$. However, departures are somewhere significant, especially at low emission energies, because they lie outside the coverage intervals of the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values at 95% level of confidence; accordingly, ${\mathrm{\rm K}}_{\mathrm{mod}}$ is not in agreement with ${\mathrm{\rm K}}_{\mathrm{exp}}$ under most test conditions. Indexes reported in Table 2 point out that the experimental setup allowed to focus exclusively on ${k}_{\varepsilon \Delta d}$ by canceling the contribution to the uncertainty due to $COI$ and $t$ and limiting the contribution due to ${k}_{\text{pos}}$ and ${k}_{\text{geo}}$. The remaining major contributor is counting statistics (grouped ${n}_{\mathrm{p}}$).

Local positioning and geometry correction factors

Data obtained from E1, E2, P1 and P2 acquired at 203.6 mm reference position and 43.6 mm and 23.6 mm counting positions on OR20 and OR50 were used to check Eq. (4) and Eq. (6) adopted as models for ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$, respectively. Emissions of ¹⁹⁸Au, ¹²²Sb, ¹²⁴Sb, ⁶⁵Zn at energies 411.8 keV, 564.2 keV, 602.7 keV, 722.8 keV, 1115.5 keV and 1691.0 keV were considered. The 203.6 mm reference position was used to compute ${\mathrm{\rm K}}_{\mathrm{exp}}$ and ${\mathrm{\rm K}}_{\mathrm{mod}}$ according to Eq. (12) for the two 43.6 mm and 23.6 mm counting positions.

The resulting ${\mathrm{\rm K}}_{\mathrm{mod}}$, ${\mathrm{\rm K}}_{\mathrm{exp}}$ and corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ ratio values obtained for each sample, emission energy and near counting position on both detectors OR20 and OR50 are reported in Table 3a and Table 3b, respectively.

Table 3 ${\mathrm{\rm K}}_{\mathrm{mod}}$ and ${\mathrm{\rm K}}_{\mathrm{exp}}$ values testing the model adopted for grouped ${k}_{\text{pos}}$ and ${k}_{\text{geo}}$ depending on energy E and near counting position ${d}_{\mathrm{n}}$ on both detectors OR20 (a) and OR50 (b)

In order to graphically point out possible significant departures from 1, the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values are plotted with respect to the emission energy $E$ in Fig. 6.

Fig. 6

The ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values plotted versus the emission energy $E$ testing the model adopted for grouped ${k}_{\text{pos}}$ and ${k}_{\text{geo}}$ for both the near counting positions 43.6 mm (black circles) and 23.6 mm (white circles). The error bars indicate the standard uncertainty

Results plotted in Fig. 6 show departures limited within ${1}_{-0.0286}^{+0.0181}$. Moreover, departures are non-significant because they lie within the coverage intervals of the ${\mathrm{\rm K}}_{\mathrm{exp}}/{\mathrm{\rm K}}_{\mathrm{mod}}$ values at 95% level of confidence; accordingly, ${\mathrm{\rm K}}_{\mathrm{mod}}$ is in agreement with ${\mathrm{\rm K}}_{\mathrm{exp}}$ under almost all test conditions. Indexes reported in Table 3 point out that the experimental setup allowed to focus exclusively on grouped ${k}_{\text{pos}}$ and ${k}_{\text{geo}}$ with counting statistics of grouped ${n}_{\mathrm{p}}$ the only other significant contributor.

The correction factors described in Eq. (1) and investigated in this study through the application of eqs. (9–10,12) have an important role within the evaluation of detection efficiency depending on the adopted standardization method of NAA: ${k}_{\varepsilon \Delta E}$ and ${k}_{\varepsilon \Delta d}$ usually represent the most impactful factors when applying the k₀-standardization, while ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ are the relevant ones when the relative-standardization is adopted, because in this case ${k}_{\varepsilon \Delta E}={k}_{\varepsilon \Delta d}=1$. Although the ${k}_{\mathrm{sa}}$ correction factor has not been investigated in this study, it affects detection efficiency to various extents regardless of the chosen standardization method since it is dependent on the sample composition.

For what concerns the suitability of the adopted models for ${k}_{\varepsilon }$ to the k₀-standardization, the data reported in Table 1 and plotted in Fig. 4 pointed out a ${\mathrm{\rm K}}_{\mathrm{mod}}$ value in agreement with corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}$ value. Thus, the analyte to monitor detection efficiency conversion due to $\Delta E$ at reference counting position is successfully modeled by ${k}_{\varepsilon \Delta E}$.

The data reported in Table 2 and plotted in Fig. 5 highlighted a ${\mathrm{\rm K}}_{\mathrm{mod}}$ value on average lower than its corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}$ value, implying an overestimation of the ${k}_{\varepsilon \Delta d}$ correction factor. The overestimation is prominent at low emission energies and for $\Delta d$ at the closest ${d}_{\mathrm{n}}$ to the detector end-cap. The reason of the bias still needs to be understood: a likely cause might be related to the dimensional measurements performed during detector characterization: in fact, distances of nominal counting positions were evaluated as the sum of the individual components (plastic spacers, ending platform, PE container, gap of the point-source itself) before assembling; if this is the case, a helpful strategy to limit the issue would be replacing the caliper with a laser measuring system in order to assess distances on the assembled counting positions and also decrease even more the overall uncertainty. In addition, the number of free-coincidence γ-sources adopted in the characterization is one of the limiting aspects of the proposed modelization and could have also played a role in this study: in fact, the 7 available experimental data represent the bare minimum amount to get a meaningful fit optimizing 6 parameters and should be carefully handled. However, considering that the overestimation resulted at a percent level, the use of ${k}_{\varepsilon \Delta d}$ is suitable to convert the analyte detection efficiency due to $\Delta d$ on applications requiring larger target relative uncertainties. Whether the highest accuracy is required, its adoption becomes questionable if the bias is not addressed, thus users should be aware of its current shortcomings.

Finally, the data reported in Table 3 and plotted in Fig. 6 pointed out a ${\mathrm{\rm K}}_{\mathrm{mod}}$ value in agreement with corresponding ${\mathrm{\rm K}}_{\mathrm{exp}}$ value. Thus, the analyte and monitor detection efficiencies conversion due to positioning and geometry are successfully modeled by ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ in case of extended cylindrical sources up to 5.4 mm height counted at the closest positions from the detector end cap. This outcome also confirms the suitability of the adopted models for ${k}_{\varepsilon }$ to the relative-standardization where only the ${k}_{\mathrm{pos}}$ and ${k}_{\mathrm{geo}}$ correction factors are relevant. In this case, no bias was noticed within the percent level uncertainty reached during the test.

Conclusion

The modeling of the detection efficiency ratio implemented in the k0-INRIM originates from an approach fully based on experimental characterization of the detection system. It provides both advantages and limitations tied to its experimental nature: while it might be of easy application since it requires no knowledge of detector dimensional parameters, it is heavily dependent on the number and energy distribution of γ-sources adopted in the characterization as well as the characterized counting positions.

Novel equation models adopted for correction factors concerning emission energy, counting position and sample geometry were investigated in challenging experimental conditions by acquisition of point-like and extended-samples both at reference and closest counting positions from the detector end-cap to highlight possible biases.

The results proved the suitability of the equation models when adopted for the relative-standardization method; on the other hand, while adopted for the k₀-standardization method, a bias at percent level of the large-scale counting position correction factor was highlighted in case of demanding experimental conditions.

The outcome of this study represents a solid endorsement towards the application of the investigated local positioning and geometry correction factors to analysis performed through the relative-standardization method and supports its scheduled implementation on a dedicated software (Rel-INRIM). Conversely, it prompts the need for further investigations of the bias affecting the large-scale counting position correction factor for its application with the k₀-standardization. Nevertheless, given the experimental simplicity and since the accounted bias is evaluated to be in the order of percent level, the use of the model could still be suitable, as it is, for routine applications of k₀-NAA where the ultimate uncertainty of the method isn’t required.