Introduction

Gamma ray spectrometry with high-purity germanium (HPGe) detectors is one of the most widely used methods for radioactivity measurements. It is virtually a non-destructive method and usually no extensive sample preparation is needed.

Measurements of environmental samples with HPGe detectors conducted in close distance to the detector will result in low detection limits with counting times compared to distant geometries. However, with decreasing distance to the detector true coincidence summing (TCS), i.e. photons being emitted from the same decay, becomes significantly larger, since the effective solid angle increases. TCS occurs when two or more gamma- or X-rays interact in the detector within the time resolution of the measurement system. The effect of TCS for low energy gamma- or X-rays in combination with another photon is particularly pronounced with an n-type or semi planar thin front contact detector that has a thin detector window and high efficiency for low energy photons. If TCS is not corrected for, the activity determination of a sample can be significantly over- or underestimated. For that reason a number of softwares have been developed over the years to address the TCS effects and the attenuation differences between the sample and the calibration source [1,2,3].

Challenges encountered when calculating TCS correction factors (hereafter only referred to as correction factors) are elucidated through comparison studies of different softwares. Some previously conducted studies were designed in order to minimize differences by only comparing the theoretical correction factors (with the same detector model and decay data). Reasonable agreement between the softwares was achieved for pure γ–γ coincidence [4, 5]. However, γ–X coincidences was found to be more difficult to correct for and large discrepancies were observed for some softwares [4,5,6]. This is highly unsatisfying and does not reveal which calculation code that can be considered as fit-for-purpose.

The calculation and comparison of correction factors for γ–γ and γ–X coincidences of 133Ba and 152Eu and different methods or softwares has been extensively investigated [4,5,6,7,8,9]. Agarwal et al. [10, 11] compares the correction factors of 125Sb with MCNP to experimental data. Whereas, to our knowledge, no previous study has compared the capability of different softwares calculating correction factors of 125Sb.

The aim with this study was to addresses the user perspective and investigate the γ–γ and γ–X TCS corrections of 133Ba, 152Eu and 125Sb with three different softwares (EFFTRAN-X, GESPECOR and VGSL) [1,2,3] and compare the results to experimental data.

Experimental

Instruments

Measurements in this work were performed using a low-background semi-planar HPGe crystal detector; S-Series PROFILE GEM Detector (Ortec, TN, USA) (S8530) (diameter 85 mm and 30 mm thickness. The detector is sensitive to energies down to 5 keV and has a relative efficiency of 50% and a FWHM of 1.64 at 1332 keV. The detector was cooled with liquid nitrogen in a Möbius recycler system (Ortec, TN, USA) and placed in a nitrogen gas flushed solid lead shield (777A, Canberra, Olen, Belgium) for low-background detectors. The pre-amplifier was placed outside the lead shield.

Electronics were analog NIM modules (linear amplifier: Ortec 572, high-voltage–power supply: Ortec 459, multichannel analyzer: Ortec 919E).

The carbon fibre window of the detector is a bit concave due to the vacuum in the detector. To ensure a placement of that can be repeated within 1% variation the detector window was covered with a flat Plexiglas screen (thickness 1 mm), same diameter as the detector. This screen does not attenuate the photon energies of interest in this study.

Softwares

Spectrum acquisition and evaluation were performed using GammaVision (Ortec, version 6.01). After evaluation, all peaks were checked manually to ensure good fits (no systematics in the residual of the fitted peaks).

In this study, three calculation codes (softwares) were used and the calculated correction factors were compared with correction factors obtained empirically. Two of the investigated codes, GESPECOR (Germanium Spectroscopy Correction factors) [1] and VGSL [2] are simulation codes and EFFTRAN-X [3] is a semi-empirical code, meaning an empirical calibration is needed in order to calculate the correction factors.

Decay data in EFFTRAN-X and GESPECOR is collected from Kordaten database, which is based mainly on the DDEP data but also contains additional radionuclides. Decay data in VGSL was based on the DDEP database.

Calibrations

To challenge the softwares a small volume source was selected for this study, due to the more pronounced TCS effects for this measurement set-up. The calibration source (5 ml) had a diameter of 21 mm and 18.3 mm height. The walls and the bottom of the source were 1 mm thick.

For protection of the endcap, a thin (1 mm) Plexiglas screen was placed on top of the detector endcap. The calibration source was placed directly on the Plexiglas screen, centered along the axis of the detector. The inclusion of this Plexiglas screen in the softwares had to be done in various ways. In EFFTRAN there is a possibility to include an absorber on the detector endcap, here the Plexiglas screen. This feature is not available in GESPECOR and VGSL. Instead a thicker container wall was selected.

A semi-empirical coincidence free calibration was established in the energy range 60–1836 keV. This followed the procedure as described in Jonsson et al. [12]. First, the detector model was optimized, based on the efficiencies of the TCS free radionuclides in the calibration source. Thereafter coincidence effects such as γ–γ (60Co and 88Y) and γ–X coincidence (139Ce) were corrected for. The corrected efficiencies were used for the fit of the final efficiency function.

Uncertainties

All measurement uncertainties in this work were evaluated according to GUM [13], and reported uncertainties are presented with a coverage factor k = 2, representing an approximate confidence interval of 95% unless otherwise stated.

An additional uncertainty component, uadd, was added (2.8%, k = 1) to the analysis settings in GammaVision. This uncertainty component was determined according to Ramebäck et al. [14].

The combined uncertainty of the activity determination was 6.0% (k = 2), not accounting for counting statistics and an uncertainty in the determination of the photon disintegration of 1% (k = 1) was assumed. For most energy lines the counting uncertainty was below 1%.

Radionuclide solutions

Three radionuclide reference solutions were purchased from Eckert & Ziegler Isotope Products, Germany, containing 133Ba, 152Eu, and 125Sb. All activities were traceable to NIST and had an uncertainty of 2.0% (133Ba and 152Eu) and 2.5% (125Sb), k = 2.

Volume sources, the same geometry as the calibration source, were prepared for each radionuclide by transferring the reference solution by mass to the volume source and it was thereafter diluted in 0.1 M HCl (37%, p.a. Merck), same as the calibration solution. The activity uncertainty in the volume sources after dilution was 3.1%, k = 2.

Coincidence summing correction factors

The dead time was below 1% for all measurements to avoid significant pile up effects and random summing [15].

For each peak energy (Ei) for the three radionuclides, an empirical correction factor Fe.corr was calculated by establishing the ratio between the certified activity (A(Ei)) of the radionuclide in the reference solution and the apparent activity (Aapp(Ei)) from the evaluation of the gamma-ray spectra.

$$F_{{{\text{e}} . {\text{corr}}}} \left( {E_{i} } \right) = A\left( {E_{i} } \right)/A_{\text{app}} \left( {E_{i} } \right)$$
(1)

An optimized detector model obtained with VGSL and GESPECOR for the given conditions was used in the calculations of theoretical correction factors with each computer program. In EFFTRAN-X the detector model derived from the optimization with GESPECOR was used.

The overall uncertainty obtained by GESPECOR was estimated to be < 2% by Novoković et al. [9]. In this study the uncertainty of the coincidence summing correction is more restrictively estimated to 1% (k = 2). The estimation is based on experiences from a previous study where the uncertainty of the summing correction factor did not significantly affect the combined uncertainty of the measurement result for volume sources [11].

Consistency tests [16] were performed for all the corrected activities in this study to determine the significance of the deviations between the calculated activity and the activity in the volume source.

Radionuclides

133Ba

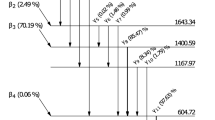
The decay of 133Ba takes place via electron capture (EC) to mainly two excited energy levels of 133Cs (437 and 383 keV; 85.4 and 14.5% respectively), followed by emissions of gamma and X-rays. There are also some highly converted gamma transitions [17]. Hence there is extensive X-ray emission in the decay of 133Ba. This will give rise to a relatively complicated spectra with many summing peaks when measured in a geometry close to the detector.

152Eu

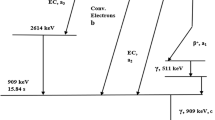
Disintegration of 152Eu to 152Sm takes place via EC (72.1%) and positron emission (0.03%), and to 152Gd via beta minus emission (27.9%). The decay scheme of 152Eu is very complicated with about 70 possible excited energy states that can be populated in the daughters [17]. This results in the emission of a large number of gamma photons (> 130) having different energies [9]. In addition, X-ray emissions of both 152Sm and 152Gd will further complicate the evaluation of a spectrum from a measurement of a 152Eu source and in measurements close to the detector, significant coincidence summing effects will occur.

125Sb

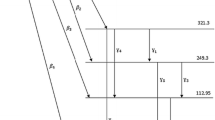
The radionuclide 125Sb decays via beta minus emission to several excited energy levels of 125Tb and 125mTb. The gamma transitions from level 2 to 1 (γ2,1, 109 keV) and from level 1 to 0 (γ1,0, 35 keV) are highly converted, giving rise to X-ray emissions from IC [17]. In addition, this causes many possible γ–X coincidence summing peaks as well.

Results and discussion

The calculated TSC factors with EFFTRAN-X, GESPECOR and VGSL were compared with the experimentally obtained correction factors for all three radionuclides, 133Ba, 152Eu and 125Sb in a volume source (Table 1). The major energy lines of each radionuclide were selected, most of them having an emission probability larger than 1%.

Table 1 Experimental and calculated coincidence correction factors for 133Ba, 152Eu and 125Sb for a 5 ml volume source geometry placed on a 1 mm Plexiglas screen at detector end cap
Full size table

It is clear that the calculated correction factors are in good agreement with each other. If the correction factors of the individual software were compared with the mean of the three softwares the result would appear to be much more concurrent (3.7% deviation at the most). This approach has been used in several intercomparison studies [4,5,6]. However, it does not reveal how accurate softwares are, only how well they agree with each other. Therefore, in this study the comparison mainly focuses on the deviation between the theoretical correction factors and the empirical values.

133Ba

Due to highly converted transition states of 133Ba, more than 30 peaks were identified in the spectrum as a result of γ–X and X–X coincidence summing peaks. Correction factors of 133Ba were calculated for all gamma emissions, within the validity of the calibration (60–1836 keV), i.e. in total eight energy lines.

A large deviation between the calculated TCS factors with the three softwares was noted for the 79.6 keV peak (between 6.3 and 12%). The uncertainty given by DDEP in the determination of the photon disintegration for this specific peak was larger than 14% (k = 2) [17]. This large uncertainty would result in a combined uncertainty of 16% (k = 2) in the activity determination at this specific energy line. It would have been difficult to draw any conclusions regarding deviations between the calculated and empirical correction factors and the 79.6 keV peak was therefore excluded from further investigations.

The highest difference between the empirical and calculated correction factors is noted for the highly converted energy line 81 keV for 133Ba (Table 1) and the 383.4 keV peak. The effect of coincidence summing is underestimated at 383.4 keV for this specific detector-geometry setup. The uncertainty caused by the deconvolution between the 79 keV and the 81 keV peak has not been included in the total uncertainty estimation for the activity determination by the 81 keV peak. The uncertainty is therefore likely underestimated. However, despite this a consistency test show that the calculated activity (using correction factors from all three softwares) and the activity in the volume source can be considered as consistent at all energy lines (k = 2) (Fig. 1).

Fig. 1
figure 1

The calculated activity in the volume source using the correction factors for 133Ba with EFFTRAN-X, GESPECOR and VGSL. The activity in the volume source is visualized by the centered horizontal dashed line. The upper and lower horizontal dashed lines are representing the uncertainty of the activity in the volume source (3.1%, k = 2). The error bars at each energy line are representing the combined uncertainty of the activity determination (k = 2)

Full size image

152Eu

The fact that 152Eu often is used in calibration sources and has many gamma photon energies (132) and possible summing combinations when measured in close geometries has most probably contributed to the large interest in studying the capability of software for TCS calculations of this radionuclide. For some softwares this has been troublesome [5].

The correction factors were generally higher than the empirical correction factors. The highest values overall were noticed for VGSL, with a maximum deviation of over 7% for two of the energy lines (444 and 564 keV), see Table 1. In Fig. 2 the error bars at each energy line are representing the combined uncertainty of the measurement (k = 2). The counting statistics varies between the different peaks due to various photon emission probabilities and background statistics in the energy range 60–1836 keV. All corrected activities were consistent with the activity in the volume source.

Fig. 2
figure 2

The calculated activity in the volume source using the correction factors for 152Eu with EFFTRAN-X, GESPECOR and VGSL. The activity in the volume source is visualized by the centered horizontal dashed line. The upper and lower horizontal dashed lines are representing the uncertainty of the activity in the volume source (3.1%, k = 2). The error bars at each energy line are representing the combined uncertainty of the activity determination (k = 2)

Full size image

125Sb

In a previous study by Agarwal et al. [10], similar to this one, the experimental correction factors are compared with correction factors obtained with MCNP for a small volume source (5 ml). The results achieved in this study agree well with the results by Agarwal et al. [10]. In this study, an accuracy within 5.0% between the experimental and calculated correction factors was reached (Table 1), compared to the maximum discrepancy of 3.3% reached by Agarwal et al. [10]. Worth noticing is that in the study by Agarwal the source was placed on a distance of 1.7 cm from the detector, whereas in this study the sample volume was measured on a 1 mm plexi screen placed on the detector endcap. Closer distance to the detector causes larger correction factors and a well optimized detector model becomes increasingly important. Hence, the small variations between the empirical and the calculated correction factors achieved in this study indicate that the detector model is well optimized.

Generally the activity was underestimated with all three calculation codes at all energy lines except one (636 keV, calculated with GESPECOR). No known systematic effects can explain this underestimation. However, the deviation between the calculated activity and the activity in the volume source is within 5%. That means the deviation is well below the combined uncertainty of the calibration and activity determination (Fig. 3).

Fig. 3
figure 3

The calculated activity in the volume source using the correction factors for 125Sb with EFFTRAN-X, GESPECOR and VGSL. The activity in the volume source is visualized by the centered horizontal dashed line. The upper and lower horizontal dashed lines are representing the uncertainty of the activity in the volume source (3.1%, k = 2). The error bars at each energy line are representing the combined uncertainty of the activity determination (k = 2)

Full size image

Comparison optimized versus unoptimized detector model

Often the manufacturer’s detector data are entered by users without any previous adjustments of the detector model. For that reason a comparison was also done between an optimized and un-optimized detector model using EFFTRAN to calculate the correction factors. During optimization in GESPECOR the distance from the active face to the entrance window was adjusted from 5 mm to 7.5 mm. Correction factors calculated with EFFTRAN for an un-optimized detector model were compared to the correction factors achieved with the optimized detector (Table 2). To calculate the deviation between the two models correction factors achieved with the optimized detector model were used as the reference values. With a shorter distance, the effect from γ–γ and γ–X summing becomes larger. In most cases, the deviations were acceptable (i.e. the activity were consistent with the activity in the volume source) but for some peaks it may affect the activity determination. The activity determination of 133Ba from the 81.0 keV peak for instance was not consistent with the activity in the volume source (Fig. 4). Hence, this clearly shows the importance of having a good knowledge of the detector model before applying any calculations.

Table 2 The deviation (in percent) between correction factors calculated with EFFTRAN for the un-optimized detector model compared with correction factors calculated for the optimized detector model
Full size table
Fig. 4
figure 4

Activtiy determination of 133Ba using correction factors calculated in EFFTRAN with an un-optimized detector model. The activity in the volume source is visualized by the centered horizontal dashed line. The upper and lower horizontal dashed lines are representing the uncertainty of the activity in the volume source (3.1%, k = 2). The error bars at each energy line are representing the combined uncertainty of the activity determination (k = 2)

Full size image

Conclusions

In previous studies, the capability of different softwares to correct for γ–X-summing effects of 133Ba and 152Eu have often been investigated and large discrepancies between calculated correction factors have been reported. Whereas γ–X-summing effects from 125Sb has only been scarcely discussed. The results in this study showed that the three investigated softwares were able to deliver correction factors for γ–X summing effects for 133Ba, 152Eu and 125Sb, which were in good agreement with the other softwares. The consistent results between the softwares shown in this study are therefore highly encouraging.

The detector model that was used in EFFTRAN was optimized in GESPECOR. This explains the similar results achieved with EFFTRAN and GESPECOR. Activities calculated with the correction factors from the softwares were for all investigated radionuclides and gamma lines consistent with the activity of the volume source, with a confidence interval of 95%.

Hence, provided that the detector model is well optimized, the investigated softwares in this study deliver correction factors that are fit-for-purpose to be used in the calculation of correction factors for small volume sources.