Introduction

Many polymer scientists used either experiments or computational models to investigate the relationships between the interactions of molecules and their morphology on macro and micro scales and their influence on various properties of the polymer [1, 2]. These relationships are linked to the molecular arrangements and interactions of the polymeric structures at an atomic level. These interactions could be between the same type of molecules or between different types of molecules within polymer mixtures (blends). The thermal and mechanical properties of polymers are strongly influenced by their morphology, degree of crystallinity and crystal structure [3]. Therefore, there is a correlation between polymer properties, molecular arrangement, and surface morphology.

Polymer morphology can be predicted by looking at the polymer relaxation dynamics when the polymer is either heated to or cooled from a melt. Instead of using expensive synthetic routes, the physical mixing of polymers to create new materials, such as blends or composites with specific properties, is used. Examples of such materials are blends prepared through melt blending of polyethylene(s) with other polymers or wax [1, 4, 5]. The properties of blends depend on the mixing method (for example, melt mixing or extrusion), their weight per cent in the total system, and how they are cooled from a melt.

The polyethylene molecular structure is controlled by the degree of crystallinity, branching and density. Therefore, different classes of polyethylenes are synthesized for use in specific applications. Semi-crystalline linear low-density polyethylene (LLDPE) copolymer, synthesized from ethylene and alpha-olefins such as 1-butene, 1-hexene and 1-octene, is of great technological importance [6]. The effects of branching (branch length and content) on the crystallinity of LLDPE have been studied with regard to crystallization and melting temperatures, crystal size and shape, and cooling rate and molar mass [6,7,8,9]. The results obtained in these studies are well explained in terms of different variables related to the crystalline structure of the LLDPE.

Although polymer scientists mixed existing polyethylenes to create new materials and characterize them in terms of their physical properties, the emerging challenge is to fully describe these properties in terms of their morphologies. This challenge is because material properties, like morphology and crystallinity, get more complex to solve when the polymers interact [10]. The morphologies of polyethylene and its blends have been well researched, especially concerning their crystallinities [11,12,13]. Blends based on polyethylenes have different morphologies, and the properties depend upon the blend composition and the crystallinities of the blend components. Different research groups studied a wide range of properties affected by the crystallization mechanism in polyethylene/polyethylene and/or polyethylene/wax blends [5, 13, 14].

For example, the role of crystallization conditions on the morphology of polyethylene blends was studied [14, 15]. Simple and sophisticated experiments under isothermal and non-isothermal conditions at cooling rates applied in industrial processes [16], were also used to study the crystallinity of polyethylene/wax blends. Different processing methods also influence the structure of the resulting new materials and their morphologies [17]. Additionally, the morphology of some polymer blends may be affected by crystallizing the prepared samples at different cooling rates (fast and slow cooling). The materials were crystallized from the melt under different conditions in previous studies. The crystallized materials were then analyzed using dynamic mechanical analysis (DMA) [5] and differential scanning calorimetry (DSC) as analytical tools to study their relaxation transitions [18].

Relaxation dynamics is often used to investigate the crystallinity of polyethylene because polyethylene molecules undergo different structural changes when they are cooled from a solution or a melt. It was reported that polyethylene undergoes three mechanical relaxations during the cooling or heating process, namely γ-, β-, and α-relaxation [19]. These relaxations describe polyethylene's structural changes during crystallization and explain various properties of the different types of polyethylene [19, 20]. For instance, to predict the deformation process of the amorphous part in polyethylene, a physical model was applied to study γ-relaxation [20]. Therefore, by analyzing both the dynamic and mechanical behaviour of the amorphous phase, it was confirmed that the crystallites act as physical ties between the amorphous chains. Thermal and dynamic mechanical properties were investigated to determine the influence of branch concentration on the γ-, β-, and α-relaxations in an ethylene/1-octene copolyethylene [21]. To summarize, there is a relationship between the structure (morphology) and the physical properties of a semicrystalline polyethylene that has been grown from solution or melt [3].

Several theoretical models have been developed to study the morphology of polymer crystals in terms of chain folding and molecular mobility [22, 23]. However, computer simulations became an important tool to complement the theoretical models due to a lack of suitable experiments to fully test the proposed theoretical models [10]. Some of these computer simulations were validated by comparison with experimental data [24, 25]. It implies that computer simulations could be sufficient when experiments are difficult to perform. For example, the study of the crystallization dynamics of polymers, which commonly occurs too far from equilibrium, is difficult through experimental analysis [11]. The crystallization dynamics of polyethylene from the melt was studied using atomistic molecular dynamic simulations. The mechanism of chain folded lamellae and the growth and cold crystallization of long polyethylene crystals at temperatures around the glass transition temperature were investigated with a united atomistic model [12]. The united atomistic model predicted small granular crystallites during cold crystallization and fast thickening of the folded chain lamellae. In another similar study, homogeneous crystal nucleation of polyethylene under supercooling was studied to characterize the crystal surface topology based on loops and tails.

However, molecular dynamics simulation can complement experimental studies to solve the crystallinity and morphology of polyethylenes and their blends [25, 26]. These simulations were successfully used to investigate melt dynamics and phase transitions of polyethylene [2]. Since polyethylene morphology is generally described in terms of crystalline and amorphous phases, molecular dynamics and experiments were able to show that molecules form entanglements in the melt and folds in the crystalline state. The degree of crystallinity is controlled by the kinds of monomers, tacticity, branching and the type of blend and blend ratios used [27]. Both experiments and computational models successfully described the polyethylene crystallinity by looking at chain movements in the molten and solid states [28].

In this study, LLDPE/wax blends were investigated. Because of its highly crystalline structure, paraffin wax is a good candidate material to be blended with polyethylene, particularly with the versatile LLDPE, to form efficient phase change materials [29]. Medium soft paraffin wax can be cocrystallized with LLDPE when the physically mixed blends are cooled from the melt or act as a plasticizer by decreasing the crystallization and melting temperatures of LLDPE [16]. The molecular mechanistic pathways in which cocrystallization and plasticization occur are difficult to determine through experiments [30]. Blend compositions and chain lengths have been used as a theoretical model to study the crystallization of the polymer blends in the context of a kinetics description of polymer crystal growth [31, 32].

A possible way to determine the molecular mechanistic pathways in which cocrystallization and plasticization of the LLDPE/wax blends occur is to use atomistic molecular dynamic simulations. According to the authors' knowledge, no reports have been published on studies done on LLDPE/wax blends using atomistic molecular dynamic simulations. The chain movements in the melt of many polymer blends were investigated by simulating the heating and cooling processes [30]. The variables such as density, specific volume and thermal expansion were used to study a blend's relaxation mechanism through molecular dynamics simulation to establish the structural, thermal or dynamic properties [33, 34].

In this study, atomistic molecular dynamic simulation was combined with DMA, DSC and XRD experiments to investigate the effect of wax content on the LLDPE relaxation dynamics. The crystallinity of the neat wax, LLDPE and their blends were investigated by studying the thermal history obtained experimentally for all the materials used. The relationship between the theoretical and computational models of systems created using short wax and long LLDPE chains were established by predicting and monitoring all the materials' glass transition temperatures.

Materials and methods

Materials

The blends were prepared using LLDPE purchased from Sasol Polymers (a division of Sasol Chemical Industries, Johannesburg, South Africa). The copolymer comprises of 2.1% hexene branches with a melt flow index (MFI) of 1.0 g/10 min (190 °C, 2.16 kg) (ASTM D1238), with an average molecular weight of 191,600 g mol−1, melting temperature of 124 °C and a density of 0.924 g cm−3. Medium soft paraffin wax (M3 wax), referred to as 'wax' in the rest of the study, was obtained from Sasol Wax (a division of Sasol Chemical Industries, Johannesburg, South Africa). It consists of 99% straight aliphatic hydrocarbons and a few branches with the formula CnH2n+2. Its carbon distribution ranges from C15 to C78. It has a density of 0.9 g cm−3, melts in a 40–60 °C temperature range, and has an average molecular weight of 440 g mol−1.

Sample preparation

A Brabender Plastograph (Brabender® GmbH & Co., Germany) with a 50 mL internal mixer was used to melt-mix all the samples. The samples were mixed at 170 °C at a speed of 30 rpm for 15 min. The blends were prepared by mixing the pure LLDPE and M3 wax according to the mass ratios shown in Table 1. The mixed samples were melt-pressed under a pressure of 50 kPa for 5 min at 170 °C using a hydraulic hot press. Two sets of samples were prepared. One set of samples was isothermally cooled at room temperature (slow-cooled) for 10–15 min. The other set of samples were quench-cooled in liquid nitrogen for about 10 min. Neat LLDPE and neat wax were treated in the same way.

Table 1 Mass ratios of both the slow- and quench-cooled samples
Full size table

Determination of thermal and mechanical properties of LLDPE/wax blends

DSC experiments were performed using a PerkinElmer DSC6000 differential scanning calorimeter (PerkinElmer, Waltham, Massachusetts, U.S.A) under a nitrogen flow of 20 ml min−1. Between 5 and 10 mg of each sample was heated from -50 to 160 °C at a rate of 10 °C min−1, cooled to -50 °C at the same rate, and again heated to 160 °C at the same rate. Three analyses were done for each sample. The enthalpies determined from the peak areas were used to indicate the crystallinity of each melting fraction.

The storage and loss moduli (E' and E") as functions of temperature were determined in a Perkin Elmer Diamond DMA dynamic mechanical analyzer (PerkinElmer, Waltham, Massachusetts, U.S.A.). The analyses were done in bending mode at a frequency of 1 Hz and a heating rate of 3 °C min−1 under a nitrogen atmosphere. LLDPE and the blend samples were heated from -130 to 130 °C. The samples were 50 mm long, 12.6 mm wide, and 1.3 mm thick.

The XRD analysis of LLDPE and the blends were done on an Empyrean X-ray diffractometer. The instrument used a crystal copper anode and Kα radiation in the angular scan range of 2θ = 5–90° with a 40 mA current and 45 kV operating voltage. The instrument applied a continuous scan to the samples. The areas under the amorphous and crystalline regions were determined in arbitrary units.

Molecular simulation methods

Materials Studio (MS) 2018 software [35] from BIOVA through the Centre for High Performance Computing (CHPC) [36] was used to do calculations. Monomers of LLDPE and wax were geometrically optimized using the density functional theory (DFT) [37] module DMol3 in MS. The Forcite molecular mechanics (MM) module, also known as the force fields, in MS was used to simulate the polymer molecules and blends.

Monomer models

As mentioned in the introduction, LLDPE is synthesized from two monomers, namely ethylene and α-olefins: 1-butene, 1-hexene, 1-octene. For this work, only 1-hexene was selected to create the LLDPE molecules. The ethylene and 1-hexene were drawn manually in MS Visualizer [35] and geometrically optimized using DMol3 in MS [37, 38]. Geometric optimization was done using the generalized gradient approximation functional of Perdew and Wang (GGA-PW91) [39, 40] with a double numeric polarized basis set with diffusion (DNP +). The DNP + basis set was chosen because the polymerization occurs according to a free radical mechanism [40, 41]. Additionally, the basis set performs well against most experimental and analytical basis sets at less simulation time [42].

The following settings were used during the geometry optimization of the monomers: quality of optimization was set to medium, the threshold for the maximum change in energy of 2.0 × 10–5 Hartree (in the Hartree wave function), a maximum force of 0.004 Hartree Å−1, number of iterations 50, maximum step size of 0.3 Å in length between any Cartesian coordinates (maximum allowed length in search of Cartesian coordinates), and 0.005 Å displacement between points. No symmetry was selected, unrestricted spin state (triplet multiplicity) and charge of zero. The following settings were used in the electronic setup: integration accuracy level set to medium, self-consistent field (SCF) tolerance was 1.0 × 10–5, 50 SCF cycles maximum, multipolar expansion (hexadecapole) with a global orbital cut-off scheme and smearing of 0.005, all electron core treatment, and a medium orbital cut-off quality was used. Monomer optimization calculations were run in the absence of a solvent.

Construction and optimization of single LLDPE chains

The optimized ethylene and 1-hexene structures were used to construct many single LLDPE polymer chains using the random copolymer build function of MS. Chains with a length from 10 to 500 (20 to 1000 backbone carbons) with branches, randomly distributed along the backbone, of different content (1-hexene) were built using forced concentrations [43]. All the LLDPE polymer chains, with varying lengths and branch content, were geometrically optimized using the Forcite module with the condensed phase optimized molecular potentials for atomistic simulation studies (COMPASS) force field [44]. COMPASS is an ab initio force field that is consistently parameterized for big molecules, such as polymers in a condensed state [44, 45]. A force field for all-atom simulations of small inorganic molecules, organic molecules, and polymers was produced by ab initio and empirical parametrization techniques [46]. A large number of valence parameters were derived from quantum mechanical calculations of small molecules, and the new Van der Waals parameters were derived by conducting MD simulations of molecular liquids and then compared to other forces like a consistent force field (CFF) if there was no data available for certain new polymers tested by COMPASS. The reliability and validity of COMPASS have been confirmed by fitting data to the experimentally determined properties of large molecules, liquids and crystals. The type II COMPASS has been extended to cover polymers and drug-like molecules without deviation from the original parameters [45]. Therefore, COMPASS is the best choice to optimize LLDPE and its blends. Geometry optimization was done with the Quasi-Newton algorithm because it minimizes structures fast and converges quickly. The convergence tolerance setup was as follows: Quality of minimization was customized with a maximum energy of 0.001 kcal mol−1 and force of 0.5 kcal mol−1 Å−1, and the different maximum iterations between points were limited to 0.005 Å. The contribution of charges in chains was energy minimized by the Gasteiger original within 50 maximum iterations for a convergence limit of 2.0 × 10–5 kcal mol−1.

Cubic simulation boxes, often called periodic systems, were created with the Amorphous Cell module in Materials Studio. All the LLDPE were added to the periodic cells through the technique described by Theodorou and Suter [58] (Fig. 1). The calculation option in the Amorphous Cell module was chosen over the construction (legacy) option because it allows for a minimum of one chain per periodic system, and the construction process was short. The torsion angles were calculated during construction while optimising the chains without relaxing the lattice parameters. A quasi-Newton algorithm was used to a convergence energy level of 0.00002 kcal mol−1 for smaller molecules and 0.001 kcal mol−1 for large molecules. The energy calculation setup for the cells was as follows: COMPASS force field, original Gasteiger (Gast_original1.0) method for calculating charges, Ewald method for electrostatic summation, and van der Waals energy calculation.

Fig. 1
figure 1

Amorphous cell of a long LLDPE (520 carbons and 70 branches) single chain after geometric and dynamics optimization at 500 K (purple atoms represent the backbone carbons, grey atoms the carbon branches and white atoms the hydrogens)

Full size image

One molecular chain per unit cell was constructed for long LLDPE chains (520 carbons in the backbone and 70 branches). This construction was followed by relaxation of the molecule inside the unit cell using an initial NVT and NPT MD ensemble to equilibrate (relax) the polymer chain in the unit cell. A similar process was followed when a unit cell contained more than one molecule, short-chains (branches per 100 carbons in the backbone) and wax molecules to investigate the effect of the number of molecules per unit cell in terms of density. All MD simulation studies were run in the bulk state, without a solvent.

The LLDPE chains in the unit cell were relaxed further by annealing the system from 150 to 450 K and back to 150 K with a heating ramp of 10 K min−1 for 20 cycles. This treatment of the unit cell was first done with NVT followed by NPT MD [48]. Torsions were calculated automatically at 0.25 radii of Van der Waals forces and loading steps of 1000 ps. The Quasi-Newton method was employed for 1000 ps with a maximum of 50 iterations within the convergence limit of 5.0 × 10–6 kcal mol−1. The partial charge of atoms was estimated using the charge equilibrium method called Gasteiger. The electrostatic energy was calculated by the Ewald summation method at an accuracy level of 0.0001 kcal mol−1. The atom-based summation was adopted for Van der Waals interaction with a cut-off distance of 15.5 Å. After the 20-circle annealing, a 1000 ps NVT MD simulation at 298 K was carried out, followed by NPT MD, first at 298 K and then at 500 K.

Construction and optimization of wax

The ethylene monomer from the database of MS was used to construct the wax chains. The constructed wax chains with different lengths (C20H22 – C44H46) were geometrically optimized using the Forcite module with the COMPASS force field [44]. Geometry optimization was done with the Quasi-Newton algorithm because the energy convergence is fast and good for short-chain polyethylenes. Periodic wax models (Fig. 2), needed for MD simulations, were created using the Amorphous Cell module in MS. The periodic systems were relaxed with the canonical constant number, volume and temperature (NVT) ensemble MD simulation, followed by an isothermal–isobaric (constant number, pressure and temperature) (NPT) ensemble MD simulation at 298 K for 1000 ps.

Fig. 2
figure 2

Amorphous cell of five wax chains after being cooled to 160 K (grey atoms represent the carbons and white atoms the hydrogens)

Full size image

Simulation of thermo-mechanical properties of LLDPE/wax blends

The LLDPE polymer and wax models were constructed based on the technique described by Theodorou and Suter [47]. For this construction, cubic simulation boxes, also called periodic systems or unit cells containing LLDPE and wax chains, were constructed using the Amorphous Cell module in MS [35]. The unit cells contained different ratios of long LLDPE chains (520 carbons in the backbone and 70 branches) or short LLDPE chains (100 carbons and 1 branch), and wax (36 carbons long with no branches), to make the desired blend systems. One such a blend system model (long 70/30 w/w LLDPE/wax) is shown in Fig. 3. In the Amorphous Cell module, two options for construction are available, namely cell calculation and construction legacy. The cell calculation was chosen over the construction legacy because it allows for a shorter construction process time (less simulation time) than the construction legacy. The setup was as follows: cubic lattice with an initial density of 0.924 g cm−3 for LLDPE and 0.900 g cm−3 for wax (which were the actual densities of the materials used in the laboratory experiments). Torsions were calculated during construction while optimizing the chains but not the lattice parameters. A Quasi-Newton algorithm was used to a convergence energy level of 0.00002 kcal mol−1 for smaller molecules and 0.001 kcal mol−1 for large molecules. The energy calculation setup was as follows: COMPASS was chosen as the force field, charges were calculated by the Gasteiger method, Ewald was used as the electrostatic summation method, and atom-based Van der Waals interactions were used.

Fig. 3
figure 3

Amorphous cell of the long 70/30 w/w LLDPE/wax after construction (in the LLDPE molecules, the purple atoms represent the backbone carbons, the grey atoms the carbon branches, and the white atoms the hydrogens; in the wax molecules, the backbone carbons are represented by grey atoms and the hydrogens by white atoms)

Full size image

Supercells with different numbers of atoms were created and minimized with NPT MD to find the density of the models. These models were then further relaxed. Supercell construction was only possible for short-chain LLDPEs and wax models. For long LLDPE chains, the computational costs were too high. Supercells (extending in all three dimensions) were constructed using the final stable unit cell after the NVT MD simulations to create the supercells with 27-unit cells. A further NPT MD equilibration was done on the created supercells by following the same settings as the single unit cell.

Molecular dynamics was repeated with the NPT ensemble at different temperatures starting from 500 to 100 K (at 25 K intervals) for 1000 ps without changing any settings in the structural equilibration. In order to compare the models with the experimental results, the blend systems had composition ratios as follows: 95/5 w/w, 90/10 w/w, 80/20 w/w, 70/30 w/w, and 60/40 w/w LLDPE/wax (Table 2). When all the MD runs for all the molecules were finished, the glass transition temperature (Tg) of all the molecules was determined from the various thermodynamic properties obtained. The two properties used to determine Tg were the change in density and volume as a function of temperature [30, 34].

Table 2 Modelled sizes of the neat materials and their respective blends
Full size table

Results and discussion

Thermal properties of LLDPE/wax blends

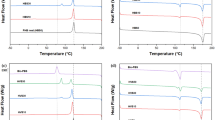
Figure 4 shows the DSC first heating curves of neat LLDPE, neat wax and their blends. Table 3 shows the observed melting enthalpies (∆Hwob−sc, ∆Hwob−qc, ∆HLob−sc, ∆HLob−qc), calculated directly from the melting peak areas in the respective DSC curves, for the wax and LLDPE fractions in the blends. It also shows the normalised melting enthalpies (∆Hwn−sc, ∆Hwn−qc, ∆HLn−sc, ∆HLn−qc), calculated by dividing the observed melting enthalpy values by the weight fractions of respectively wax and LLDPE in a particular blend. If the normalised melting enthalpy of, for example, wax is smaller than the observed melting enthalpy of neat wax, a smaller amount of wax crystallized separately in the blend, which indicates that some wax has probably cocrystallized with the LLDPE. This cocrystallization will be confirmed if the normalised melting enthalpy of the LLDPE in the same blend is larger than the observed melting enthalpy of neat LLDPE. After cooling at room temperature, the neat wax shows a melting enthalpy of 154.5 J g−1 (Table 3). If all the wax in the blends crystallized separately from the LLDPE, the ΔHwn−sc values for the melting of wax in the blends should have been very close to the melting enthalpy of neat wax. However, it is clear from Table 3 that these values are significantly smaller than 154.5 J g−1, which indicates that a significant part of the wax is probably cocrystallized with the LLDPE.

Fig. 4
figure 4

DSC first heating curves of (a) slow-cooled and (b) quench-cooled neat LLDPE, neat wax and various LLDPE/wax blends

Full size image
Table 3 Melting enthalpies of the LLDPE, wax, and the blends cooled under different conditions
Full size table

This cocrystallization is confirmed by the ΔHLn−sc values larger than the melting enthalpy of neat LLDPE, which indicates that the cocrystallized wax melted together with the LLDPE in the blends. Cocrystallization refers to the short straight wax chains crystallizing with the folded LLDPE chains in the same lamellae. The other wax chains that did not cocrystallize with the LLDPE chains, crystallized separately in the amorphous phase of the LLDPE. The cocrystallized wax will melt at the same temperature as the LLDPE, while the separately crystallized wax will melt at a lower temperature. It is further interesting that the ΔHwn−sc values generally increased with increasing wax fraction in the blend, indicating that a smaller percentage of the wax in the blend cocrystallized with the decreasing LLDPE fraction.

Another important observation was that no wax melting peak was observed at wax fractions smaller than 10 wt.% (Fig. 4). In contrast, the normalised melting enthalpy of the LLDPE fraction was observably higher than the melting enthalpy of neat LLDPE. This observation indicates that all the wax in the blend has probably cocrystallized with the LLDPE, increasing the amount of crystalline material melting at this temperature.

The difference between the melting enthalpy values of neat wax for slow and fast cooling is less than 1%, as observed in Table 3. There are also no significant differences between the melting enthalpies of the wax in the fast- and slow-cooled blends. Therefore, it is clear that supercooling of the wax and LLDPE/wax blends in liquid nitrogen did not affect the wax crystallinity. Wax chains are short compared to most polymer chains and crystallize with straight chains instead of folding to form crystalline lamellae [49]. A similar increase in the melting enthalpy of the slow- and quench-cooled samples as the wax content in the blends was increased (Table 3), shows that the wax also cocrystallized with the LLDPE when the blends were cooled in liquid nitrogen. Although the high cooling rate was reported to affect the size of the crystals, it seems not to prohibit wax crystallization or reduce the wax crystallinity [50, 51].

There was also no significant difference between the melting enthalpies of LLDPE in the blends cooled through quenching in liquid nitrogen and those cooled at room temperature. LLDPE, like other polyethylenes, crystallizes so fast that even the presence of wax or fast cooling at liquid nitrogen temperatures could not change its crystallization behaviour [15, 51]. The flexible polyethylene chains above its glass transition and the simple chemical repeat unit are responsible for this fast crystallization [52].

Thermomechanical properties of LLDPE/wax blends

Figure 5 shows the storage modulus of the slow- and quench-cooled neat LLDPE and LLDPE/wax blends as a function of temperature. In Fig. 5a, b, it is clear that an increase in wax content generally increased the modulus of the different blends. A fraction of wax crystals would have crystallized in the amorphous parts of the LLDPE or between the lamellar stacks. Van der Waals bonds between the wax crystals and the LLDPE chains would have decreased the chains' mobility and increased the sample stiffness. The presence of wax crystals also increased the total crystallinity of the blends beyond that of neat LLDPE. It is known that higher crystallinities increase sample stiffness. The increased crystallinities of these samples can be seen in the increased total enthalpy of the blends compared to that of neat LLDPE (Table 3).

Fig. 5
figure 5

Storage modulus as a function of temperature for (a) slow-cooled and (b) quench-cooled neat LLDPE and various LLDPE/wax blends

Full size image

Three relaxation peaks were observed for LLDPE and the blends (Fig. 6). The peak at about -110 °C is called the γ-transition and is regarded by some authors as the glass transition [53]. The transition is related to motions of the backbone CH2 units in the amorphous and crystalline region of LLDPE. It is also defined as crankshaft movements of the amorphous parts with higher free volume than the crystalline region. It was found that the slow-cooled samples had larger crystal lamellae and a larger crystalline fraction than the quench-cooled samples. The temperature difference was explained by the significant contribution from the crystalline fraction [54]. The peak that appears between -20 and -40 °C is called the β-transition, which is absent in a highly crystalline high-density polyethylene (HDPE) because this polymer has very few chain branches [21]. According to some authors, the β-transition is attributed to a transition at the branch points on the chains of LLDPE. However, other authors relate it to the glass transition [20, 21].

Fig. 6
figure 6

Loss modulus as a function of the temperature of (a) slow-cooled and (b) quench-cooled neat LLDPE and various LLDPE/wax blends

Full size image

The peak and peak shoulder observed in Fig. 6 between 40 and 60 °C are due to the α- and α’-transitions, respectively. These transitions are much more obvious in the slow-cooled samples, and are linked to the movement of the amorphous chains between crystals and lamellar slippage within crystals. This transition gradually disappeared with increasing wax content. Since the wax is not yet molten between 40 and 60 °C, it cannot create more free volume. However, as already mentioned, the wax crystals acted as physical crosslinks and as such, they immobilized the interlamellar amorphous material, which inhibited the transition in this temperature range [55, 56]. In the quench-cooled samples, this transition is weak for neat LLDPE and almost invisible for the blend samples. It could be that, although the faster cooling did not significantly change the total crystallinity of LLDPE, it gave rise to the formation of smaller crystals and less interlamellar amorphous material. However, as in the case of the slow-cooled blend samples, the wax crystals in the interlamellar amorphous LLDPE acted as physical crosslinks which caused the disappearance of the peak between 40 and 60 °C.

X-ray diffraction analysis

Figure 7 shows the X-ray diffraction (XRD) spectra of neat LLDPE and the blends. The spectra show that the samples were semi-crystalline, with sharp crystalline peaks and an amorphous halo visible below the two most intense peaks. The two most intense crystalline peaks around 2θ = 21° and 24° correspond to the (110) and (200) lattice planes of an orthorhombic crystal structure [9]. No new peaks are visible for the LLDPE/wax blends since the LLDPE and wax have the same crystal structure, as seen from XRD spectra obtained for a paraffin wax [57].

Fig. 7
figure 7

X-ray diffraction spectra of (a) slow-cooled and (b) quench-cooled neat LLDPE and LLDPE/wax blends

Full size image

The increasing wax content in the LLDPE/wax blends increased the peak intensity (Table 4). This increased peak intensity confirms the DSC results of an increase in the total crystallinity of the samples with increasing wax content, which confirms the cocrystallization of some of the wax with the LLDPE. As is the case with the DSC results, there are no significant differences between the XRD results of the slow-cooled and quench-cooled samples, confirming the rapid crystallization of both the LLDPE and the wax.

Table 4 The X-ray diffraction peak intensities of the LLDPE and blends cooled under different conditions
Full size table

Modeling the thermo-mechanical properties of LLDPE/wax blends

The density of short chains (100 carbons in the backbone) LLDPE mixed with the wax chains (36 carbons long) in the unit cell is plotted versus temperature in Fig. 8. All the transition temperatures determined from the curves in Fig. 8 are presented in Table 5. The transitions are labelled as either γ- or β-transitions (or relaxations), previously defined when discussing the DMA results (also see [21, 58]). When more wax (between 5 and 20%) was added to the blends, there was an increase in the γ-transition temperature. When the wax content was just above 40%, transitions were observed between -56 and -72 °C. These are known to be β-transitions for semi-crystalline polyethylene. Therefore, the results obtained from the simulations agree with those observed in the DMA analysis in terms of wax acting as a physical crosslinker in the LLDPE chains. The transition around 350 K in the neat wax models is due to the movement of the chains during melting. Some of the simulated models of the short LLDPE chains cocrystallizing with the wax are shown in Fig. 9.

Fig. 8
figure 8

Average density of short-chain LLDPE/wax blend models cooled step-wise in NPT-MD simulations as a function of temperature

Full size image
Table 5 Comparison between the modelled transition temperatures of LLDPE, wax and LLDPE/wax blends, and the real transition temperatures determined through DMA analysis
Full size table
Fig. 9
figure 9

a Amorphous cells of short LLDPE/wax (20% wax content) models at -123 °C, b short LLDPE/wax (40% wax content) models at -123 °C, and (c) short LLDPE/wax (40% wax content) models at 127 °C (in the LLDPE molecules, the purple atoms represent the backbone carbons, the grey atoms the carbon branches, and the white atoms the hydrogens; in the wax molecules, the backbone carbons are represented by grey atoms and the hydrogens by white atoms)

Full size image

The interaction of wax with long LLDPE (520 carbons in the backbone and 70 branches) chains looks different, as displayed in Fig. 10. The addition of more wax to the blends decreased the γ-transition temperature to lower values (Table 5), but a β-transition was also observed when the wax content was 20% or more (Fig. 10b) [58]. The dynamic relaxations of the LLDPE/wax blends, determined through MD simulations, correlate within 5% with the temperatures of the DMA determined γ-transitions and other published data [20, 21, 58], but the β-transition shows some fluctuations, except for the samples containing 30 and 40% wax (Table 5).

Fig. 10
figure 10

Densities of long-chain LLDPE/wax blends cooled from 450 to 100 K using NPT-MD simulations: (a) Transitions estimated by observation and (b) transitions determined by the best-fitting lines

Full size image

It is not expected that wax would show transitions (or relaxations) because of its highly crystalline molecular structure. However, the neat wax in Fig. 10b shows a γ-transition temperature at -97 °C, with a weak β-transition at 6 °C. The transition could have resulted from an amorphous zone between two adjacent layers of crystalline material or a linkage between two crystal layers [59]. They could also be related to a reorientation-translational motion of the chains in Fischer–Tropsch waxes, which was observed using spin–spin relaxation measurements in nuclear magnetic resonance (NMR) [60].

Even though the total weight percentage was kept at 100% when more wax was added, the total density of the simulated blends decreased (Fig. 10b). There was a clear increase in the total volume of the blends when the LLDPE composition ratio was reduced (Fig. 11). From basic thermodynamic state equations, volume is inversely proportional to density but directly related to enthalpy. Therefore, the simulation results presented in terms of density and volume agree that the addition of wax contributed to an increase in the total crystallinity of the blends (as described in the discussion of the DSC results).

Fig. 11
figure 11

Volume of long-chain LLDPE/wax blends cooled from 450 to 100 K using NPT-MD simulations

Full size image

Conclusions

Cocrystallization of the components in the blends was confirmed by the small normalised melting enthalpies of wax in the blends compared to the melting enthalpy of neat wax. It was further confirmed by the ΔHLn−sc values being larger than the melting enthalpy of neat LLDPE, which proved that a certain wax fraction melted with the LLDPE in the blends. Some of the short wax chains must have crystallized separately in the amorphous parts of the LLDPE chains, acting as physical crosslinkers, which was confirmed through an increase in modulus as the wax content was increased in the blends. The cooling rate did not have an observable effect on the overall crystallization of LLDPE, wax or the blends because both the wax and LLDPE cooled so fast that quenching in liquid nitrogen did not influence their respective crystallinities. Both DSC and XRD showed that the addition of wax increased the total crystallinity of the blends, which was also confirmed by molecular dynamic simulations in correlating enthalpy with the total volume of the blends. As observed from the experiment, our model confirmed that some wax chains were cocrystallized with the LLDPE lamellar stacks.