Abstract
From a macro perspective, inventor networks tend to generate remarkably stable structures over time. At the same time, we observe highly dynamic processes at the micro level, in terms of inventor entries and exits as well as formations and terminations of collaborative relationships between them. In order to explain this—at least at the first glance—contradicting pattern, we investigate processes at the intermediate network level. Our analysis draws upon co-patenting data for the entire population of West German inventors in the field of laser technology research from the onset of the technology in the early 1960s over a period of 45 years. Our findings suggest that the key factor for maintaining structural stability of networks is that directly linked partners of inventors with stabilizing properties—so-called ‘key players’—take over this function in a subsequent period. We show that processes at the intermediate network level provide new insights on the co-existence of micro fluidity and macro stability in complex adaptive systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The evident spread of R&D cooperation over the last decades (Hagedoorn 2002; Tomasello et al. 2017) indicates that innovation processes are increasingly characterized by a division of innovative labor (Wuchty et al. 2007). The reasons for this trend are straightforward. R&D cooperation enables knowledge exchange and collective learning (Grant and Baden-Fuller 2004; Buckley et al. 2009), may lead to cost saving, risk sharing, better solutions and reduced time to market (Mowery et al. 1996; Martínez-Noya and Narula 2018). Hence, the network of cooperative relationships among innovative actors constitutes an important element of the innovation system (Chaminade et al. 2019). This holds true for both interorganizational and interpersonal networks. Previous research indicates that not only a actor’s individual network position (Powell et al. 1996; Stuart 2000), but also the structural characteristics at the overall network level matter for innovation outcomes (Fleming et al. 2007). In other words, the system’s topology can be conducive to the creation of novelty in terms of innovation by providing favorable opportunities for cooperation with individual actors and to benefit from the knowledge of indirectly linked partners.
The majority of empirical network studies still neglects an in-depth analysis of the micro-foundations behind the observed macro patterns (Powell et al. 2005). Yet the findings from previous research indicate that various types of innovation networks—regardless of the respective industry or technology setting—tend to form typical and structurally stable patterns at the macro level (e.g., Powell et al. 2005; Tomasello et al. 2017). For instance, empirical evidence suggests a positive and significant relationship between ‘small-world’ characteristics (Watts and Strogatz 1998)Footnote 1 and innovative performance of firms across various industries (Schilling and Phelps 2007). Uzzi and Spiro (2005) analyzed the small-world network of creative artists in the Broadway musical industry from 1945 to 1989 and showed that ‘small-world’ patterns are positively related to creativity of the actors involved. Similarly, emergence of ‘scaling properties’ (Albert and Barabasi 2002; Barabasi and Bonabeau 2003) became evident in innovation networks. Powell et al. (2005) report for the US Life-Science industry the emergence and persistence of a power law degree distributionFootnote 2 in various sub-networks, including the interorganizational biotechnology network.
A further frequently observed network characteristic is referred to as ‘core-periphery’ structure (Borgatti and Everett 1999).Footnote 3 Rank et al. (2006) found a persistent pattern of a considerable number of companies that were only loosely connected to the network’s dense core in regional biotechnology networks. Kudic et al. (2015) report similar findings for German firms in the laser industry network based on public-funding project data. Cattani and Ferriani (2008) investigate the sources of artists’ creativity in the Hollywood motion picture industry (1992–2003) and showed that actors occupying an intermediate position between the core and the periphery of the system are in a favorable position to achieve creative results.
These observations reveal an important insight: both interorganizational and interpersonal innovation networks appear to be structurally stable in the sense that they tend to develop persistent patterns that are typically assumed to be conducive to knowledge transfer, learning and innovation. Against this backdrop, we define ‘structural stability’ as a network’s tendency to retain or regenerate typical patterns over time—i.e. non-random topologies such as those described above—in order to maintain its key functionalities, i.e. enable knowledge exchange, mutual learning, and the joint creation of novelty. This notion of stability does not mean that network structures are static but it refers to the ability of a system to repeatedly create certain structural properties despite high levels of discontinued ties and turnover of actors.
Parkhe et al. (2006) and Brenner et al. (2011) point to the insufficient consideration of processual issues—directly linked to various facets of network dynamics at the micro level—as one key limitation of network research. Over the past years only very few studies on innovation networks have been conducted to fill this gap.Footnote 4 The reasons for this are manifold. Network evolution is a complex phenomenon that is driven by various factors and appears at multiple, mutually interdependent levels. In order to draw a realistic picture of network change, entries and exits of network actor as well as formations and terminations of ties among them need to be considered simultaneously. In addition, extensive data requirements often prevent long-term investigations which are urgently needed to understand the causes, drivers and underlying mechanisms of network dynamics. Ahuja et al. (2012: 446) concludes in this context that the “paucity of empirical research likely stems from challenges such as the practical difficulties posed by obtaining longitudinal network data, the complexities of handling networks over time, and a lack of attention with the theoretical and econometric handling of endogeneity concerns”. Recent empirical studies on inventor network dynamics at the micro level show that network actors as well as their ties are in a constant state of flux (Fritsch and Kudic 2016; Fritsch and Zoellner 2018, 2020; Kudic et al. 2021).
The co-occurrence of macro stability and micro fluidity in networks may appear—at least at first glance—contradicting and incompatible. In this paper we seek to answer the question: “What explains the co-existence of macro-level stability and high levels of fluidity at the micro level of inventor networks?” This question is of key importance for a theory of network dynamics and for the understanding of innovation systems. In the following, we focus exclusively on inventor network structures, which are considered to be one specific type—among many others—of innovation networks in which nodes represent individual actors (inventors) and ties reflect joint R&D activities.Footnote 5 We base our longitudinal empirical analysis on a unique dataset encompassing all patent applications in the field of laser technology research in West Germany from the inception of the technology in the year 1961 until 2005.
The remainder of the paper is structured as follows: Sect. 2 summarizes the main contributions of previous research concerning the development and underlying relationships of network structures. Section 3 introduces the data and provides a brief overview of the development of inventor networks in the West German laser industry. Next, we corroborate the macro level stability of network structures and show the high levels of inventor-level fluidity (Sect. 4). The stability of network relationships at the intermediate group level is then analyzed in Sect. 5. Finally (Sect. 6) we discuss the main findings, draw implications and outline some fruitful avenues for further research.
2 Previous research and own research design
2.1 Knowledge, networks, and innovation
Already at the end of the nineteenth century, Alfred Marshall was among the first to acknowledge the role of knowledge in production and its transformative power within capitalist economic systems (Metcalfe 2010). He distinguished between inventions and innovations and emphasized the prominent role of entrepreneurs in his writings. Joseph Alois Schumpeter (1912) argued that innovations—‘new combinations’ of knowledge—are the major source of endogenous economic growth.
Inspired by the ideas of Schumpeter, cooperation and networks play an important role in today’s neo-Schumpeterian approach (Nelson et al. 2018) developed in the 1970s (Freeman 1974, 1991; Nelson and Winter 1974, 1982). While transaction cost theorists (Williamson 1991) describe various forms of cooperation and networks as hybrid organizational modes between the polar cases of ‘market’ and ‘hierarchy’, the highly dynamic emergence of diverse types of cooperative agreements—especially in high-tech industries such as microelectronics, telecommunication, and biotechnology—led to the insight that cooperation need to be considered an organizational form in its own (Powell 1987). The prominent role of R&D cooperation and innovation networks for explaining knowledge transfer, learning and system-inherent innovation processes is reflected in the innovation systems literature (Chaminade et al. 2019), as they are considered an integral part of regional (Asheim et al. 2019), sectoral (Malerba 2004), national or technological (Carlsson et al. 2002) systems of innovation from the very beginning.
Most innovations are not the result of linear processes but rather the outcome of repeated knowledge exchange and learning processes of various types of actors of an innovation system that are often characterized by multiple feed-back loops (Kline and Rosenberg 1986; Chaminade et al. 2019). These systems are complex and adaptive in nature. Complex, because processes and decisions of actors are path-dependent (Arthur 1989; David 1985), neither fully stochastic nor deterministic (Glueckler 2007), and they affect not only the decision maker but also the directly and indirectly connected partners. Adaptive, because each and every knowledge exchange and learning process in the system has an impact on the value and importance of an actor’s individual knowledge stock (Pyka et al. 2019).
For the purpose of this paper, we focus exclusively on one specific network layer of an innovation system, i.e. the network of inventors in the field of laser research in West Germany between 1961 and 2005. Based on the very general definition of networks “… as a set of nodes and the set of ties representing some relationship, or lack of relationship, between the nodes” (Brass et al. 2004, 795) we consider all actively operating inventors in the field of laser research in the period under investigation as potential nodes of the systems and regard co-patenting relationships as a proxy for collective knowledge exchange and learning processes with the goal of generating novelty in terms of innovations.
2.2 Linking network structure and innovation
Ahuja et al. (2012) point out that an in-depth understanding of the factors generating and shaping network structures should contribute to discovering the mechanisms and processes that drive network outcomes. There is a long and extensive debate in the innovation network literature on the role of either cohesive networks (Bourdieu 1986; Coleman 1988) or structural holes (Burt 1992, 2005) on innovativeness of actors involved. Experimental evidence (Milgram 1967) and empirical analyses (Uzzi et al. 2007) convincingly demonstrate that real-world networks often show both properties: a high level of clustering (indicating the existence of densely connected sub-groups) and short path lengths (indicating the presence of structural holes and brokers that are bridging these holes).
Proponents of the first view argue that cohesion facilitates “… the build-up of reputation, trust, social norms, and social control, for example by coalition building to constrain actions, which facilitates collaboration” (Nooteboom 2008: 619). Cohesion enables face-to-face contacts and, thus, stimulates interorganizational learning (Ejermo and Karlsson 2006; Storper and Venables 2004; Gilsing and Nooteboom 2005). However, after a certain point the positive effects of cohesiveness—or social proximity—on learning and innovation may turn into opposite because group members may become too inward looking and restrained against new influences (Boschma 2005).
Proponents of the second perspective argue that small-world networks provide brokerage opportunities. Inventors who manage to occupy such a position may gain an important advantage since they have a wider range of information and ideas broadly dispersed over the entire system. While brokers create social value for the network as a whole, it remains, however, rather unclear to what extent having a broker position also leads to benefits for the respective actor or firm in terms of better performance (Fritsch and Kauffeld-Monz 2010; Rodan and Galunic 2004).
The logical conclusion that can be drawn from the presence of a networks characterized by cohesive, densely interconnected subgroups is that some actors obviously manage to attract more partners than others. Empirical studies indicate a significantly positive relationship between actor-specific centrality measuresFootnote 6 and innovation performance (Powell et al. 1996). A high concentration of cooperation activities of a few actors together with a high number of actors with only very few links is reflected by a highly skewed degree distribution. To put it differently, while a rather limited number of ‘network hubs’ (or ‘high degree’ actors) have a dominant network position, the majority of actors has only a fairly small number of ties. A broad range of studies have observed and empirically tested such ‘scaling’ properties of networks (Powell et al. 2005; Newman et al. 2006).
Real-world networks consist only rarely of one fully connected component. A potential explanation for this observation is that formation and growth of networks is in principle possible via two distinct processes, each of which is accompanied by substantially different structural consequences (Kudic and Guenther 2017). First, isolated inventors without any tie to other actors can enter the network by attaching to an existing component. Second, new actors may form an interlinked group and enter the network as a new component. If both processes take place simultaneously, we may see at the same time growth of existing components and newly emerging small components. In other words, we observe the emergence of ‘core-periphery’ network structures that can be defined as “… a dense, cohesive core and a sparse, loosely connected periphery” (Borgatti and Everett 1999, 375). The core is typically composed of key members of the community, particularly actors who have developed dense connections to others and act as network coordinators. It has been argued that the core of sectoral innovation networks contains essential elements of the industry’s technological knowledge (Rank et al. 2006). The periphery includes actors who are only loosely connected to the core as well as to the other actors in the periphery (Cattani and Ferriani 2008, 826).
Rosenkopf and Padula (2008) confirm this pattern by showing that the likelihood of an entrant to attach to a network incumbent increases with the incumbent’s ‘prominence’ in the network as proxied, e.g., by his degree centrality or his eigenvector centrality (Bonacich 1987). Others demonstrated the emergence and solidification of a core-periphery structure in various firm and industry settings (Rank et al. 2006; Kudic et al. 2015) and showed that the occupation of an intermediate position between the core and periphery may foster creativity (Cattani and Ferriani 2008).
2.3 Network dynamics and the fluidity of actors and ties
One key insight in network research is that an in-depth study of structural phenomena requires a comprehensive understanding of the dynamics at the micro level that cause these emerging structures. Accordingly, we apply a micro-based network evolution perspective that aims at understanding how processes at the level of induvial inventors determine the development of network structures that can be observed from a macro perspective. This is very close to the structural network change approach introduced by Doreian and Stockman (2005, 3–5) according to which network evolution “… captures the idea of understanding change via some understood process …” whereas these underlying processes can be defined as a “… series of events that create, sustain and dissolve …” the network structure over time. Hence, networks change due to entries or exits of actors as well as due to formation or termination of connections among these actors, and they are affected by the intensity and quality of persistent ties (Graebner et al. 2018). These micro dynamics affect the structural configuration at higher levels of aggregation in nontrivial ways.Footnote 7
The traditional argument why cooperative agreements are formed goes back to transaction cost theory. It was argued that for a particular category of transactions—i.e. those characterized by a moderate asset specificity and frequency of disturbances—a reduction of transaction costs (as compared to the alternatives market or hierarchy) can be achieved by adopting intermediate organizational forms (Williamson 1991). Attention was drawn early to the fact that this line of reasoning neglects strategic and social influencing factors (Eisenhardt and Schoonhoven 1996). By now it is well-known that a broad variety of determinants and motives can affect the decision to form a cooperation, such as risk reduction (Sivadas and Dwyer 2000), time savings (Mowery et al. 1996), access to new national and international markets (Perlmutter and Heenan 1986; Gebrekidan and Awuah 2012), status and reputation building (Houston 2003; Arend 2009), as well as knowledge-related motives such as knowledge access (Grant and Baden-Fuller 2004; Buckley et al. 2009) and interorganizational learning (Kale et al. 2000; Nielsen and Nielsen 2009).
Once a cooperation between two or more partners is established, there are good reasons to maintain this relationship. An increasing level of trust plays a key role here, particularly in the context of mutual knowledge transfer and learning. Previous research shows that trust enhances the amount of information and knowledge that can be exchanged among partners and can decrease the related costs (Tsai and Goshal 1998; Zaheer et al. 1998). At the same time an opportunity cost argument applies. Instead of using scarce resources to identify a new suitable cooperation partner, negotiate the terms of the cooperation, and establish a well-working and trust-based relationship that may require frequent face-to-face contacts, actors could use these resources for other purposes. Since the partner-specific investments will be sunk if an R&D cooperation is abandoned, one may expect an incentive for actors to maintain a relationship over longer periods of time.
There is, however, also a number of arguments for discontinuing an existing partnership and the establishment of new ones. Termination of a cooperation may be regarded as planned in case of time-limited cooperation projects such as publicly funded R&D projects with a fixed duration. Stability of such a cooperation is often reflected in repeated projects with the same set of partners, as the above arguments for the maintenance of partnerships are typically not project-related.
An unplanned termination refers to a situation where the disadvantages outweigh the benefits. Reasons may be opportunistic behavior of project partners (Das and Teng 2000), learning races (Amburgey et al. 1996), failure of the respective project (Greve et al. 2009) and other factors that mitigate the knowledge transfer (Simonin 1999). A further reason may be that the dynamics of innovation processes lead to obsolescence or irrelevance of the present partner’s knowledge and require the continuous acquisition of new partners (Kim et al. 2006; Fritsch and Zoellner 2020). Moreover, ties are terminated in case that a cooperation partner exits the market or the technological field while newly emerging firms and actors can offer promising new opportunities for collaboration.
The above considerations suggest that fluidity of actors and links in innovation networks tends to be conducive to the performance of an innovation system while too much stability could be detrimental. This should particularly hold in a turbulent technological regime that is characteristic for the early stages of an industry life-cycle.Footnote 8 Most of the literature on the dynamics of relationships between actors is at the level of organizations, particularly the level of firms (see for example the contributions in Cropper et al. 2008). The rather few empirical studies that analyze the dynamics at the level of inventors and their ties show surprisingly high levels of entries and exits as well as newly established and terminated ties. For example, a study by Ramlogan and Consoli (2014) on collaborative research in medicine finds that the share of new cooperations in academic publications over all cooperations is above 70% in all years of the observation period.
In an analysis of regional inventor networks Fritsch and Zoellner (2020) analyzed the fluidity in regional inventor networks in successive three year periods based on patent data. They found that more than 78% of all inventors are only present in one three year period, 14.51% are active in two periods and only about 7% appear in networks for more than two successive periods. Only 9.7% of all ties between inventors can still be found in the successive period. Fritsch and Zoellner (2020) find some statistically significant relationships between the entry and exit of actors and measures of the network structure such as the share of the largest network component and the share of isolates. The results suggest that fluidity leads to some fragmentation of the networks, but that the effect is not very pronounced. Relating the levels of fluidity to the performance of networks in terms of the number of patents per R&D employee (patent productivity) suggests positive effects of new actors and ties.
2.4 What do we want to know and how can we get there?
Our analysis of the co-existence of macro-level stability and micro-level fluidity is based on a unique dataset of co-patenting relationships among inventors in the German laser industry over a period of 45 years. We employ a three-stage research design. The first step is analyzing the structural stability of the inventor network by exploring the structural features and pattern formation processes along different lines. We consult a set of standard metrics to gain an initial intuition of the system’s overall topology and related development patterns. Next, we test for the emergence of two structural phenomena—scaling properties and core-periphery structure—to check whether the system is characterized by stable pattern formation processes at the macro level. In a second step, we turn to the micro level and analyze the degree of fluidity by exploring node and tie re-occurrence rates over time. Third, in order to determine who or what keeps the system together, we identify two types of key players: those who warrant diffusion properties of the system, and those who are responsible for the structural cohesion of the system.
Our analyses clearly show that these two types of key players are anything but persistent over time. This result raises a number of questions. Who are these key players, where do they come from and why do they occupy their roles only for a short period of time? Who takes over the role of an ‘old’ key player who discontinues in the network? Are discontinuing key players and their successors typically connected? Was there an exchange of knowledge prior to the role change so that the knowledge of the ‘old’ key player remains in the system? To answer at least some of these questions, we turn our attention to the intermediate network level, specify the ego networks for each of the top key players over time and analyze to what extent these highly important roles are passed over to members of the same group.
3 Technology and data
3.1 German laser research
The acronym ‘laser’ was originally coined by Gould (1959) and stands for ‘Light Amplification by Stimulated Emission of Radiation‘Footnote 9 German laser research provides an ideal empirical setting for the purposes of this study for several reasons. First, laser technology can be characterized as knowledge-intensive and science-driven (Bertolotti 2005; Bromberg 1991; Grupp 2000). Second, the development of laser technology requires expertise from various scientific disciplines such as optics, electronic engineering and physics (Fritsch and Medrano 2015). Thus, the creation of novel products and services in this field is often a collective process characterized by a pronounced division of labor between various actors and institutions. Third, German laser research is a well-defined and documented technological field (Albrecht 2019; Buenstorf et al. 2015; Fritsch and Medrano 2015; Kudic 2015).
The roots of laser research reach back into the early twentieth century (Albrecht 2019; Bromberg 1991). However, it took until early 1960 that a research group led by Theodore H. Maiman at the Laboratories of the Hughes Aircraft Company in Malibu (California, USA) could first demonstrate the existence of a laser effect. The first laser patent application in Germany dates back to 1961 (For details, see Fritsch and Medrano 2015).
3.2 Data sources, co-patenting, and the construction of inventor networks
Our empirical study is based on patent applications in the field of laser technology in West Germany from 1961 to 2005, a period of nearly half a century. The patent data provides us with information about the applicant organizations and all of the inventors, and are the basis for identifying ties between these inventors. In order to isolate the effect of German unification in the year 1990, we exclude laser patents by inventors located in East Germany and strictly limit the analysis to inventors in West Germany.Footnote 10 The core objective of our data gathering procedure was to identify the pool of knowledge and expertise in the field of laser technology for West Germany as accurate as possible. For this purpose, the dataset includes all patenting and co-patenting activities of West German applicants and the respective inventors registered at the German Patent and Trademark Office (DPMA). Non-German applicants were only included in the data if there was at least one German co-applicant listed in the patent document. For the purpose of this paper we employed exclusively inventor data. Inventors with a foreign residence were excluded from the dataset.Footnote 11
The patent information was obtained from the database DEPATISnet (www.depatisnet.de), which is maintained by the German Patent and Trade Mark Office. From this source we selected all patent applications with priority in West Germany that were assigned to the technological field ‘devices using stimulated emission’ (IPC H01S) as either the main or secondary class. Research in this IPC class is related to laser beam sources that constitutes the basis for all kinds of applications. We account for important applications of laser technology by including those patent applications in the fields of material processing (IPC B23K), medical technology (IPC A61 without IPC A61K) and spectroscopy (IPC G01N) that mention the term ‘laser’ in the document.Footnote 12 We found an increasing number of patents in all these IPC classes over the entire observation period. In the early years of the technology, patenting activities reflect a clear dominance of research related to beam sources (IPC H01S). After the year 2000, we observe a clear trend shift from patenting in the basic technology of beam sources to its applications. Figure 4 and Table 4 in the Appendix provide further details on patenting and co-patenting activities in West German laser research.Footnote 13 In total, we identified 4381 laser-related patent applications between 1961 and 2005. A main benefit of our data is that it comprises the full population of all German inventors active in the field of laser research over the entire observation period. The data allows us to analyze R&D cooperation activities and network entry modes for the entire population of inventors from the early emergence of this technological field onwards.
A key point when using patent data for network analyses is the cleaning and standardization of the raw data based on the names of inventors. Different spellings of the names were harmonized, and a contextual plausibility check was carried out for the few cases in which different inventors with identical names appeared. A unique identification number was assigned, which allows each inventor to be accurately identified over the entire observation period. We assume that all co-inventors that are listed in a patent document were connected to each other and cooperated in the respective R&D.Footnote 14
The priority filing date of a patent application was used as timestamp. In order to investigate the development of inventor networks we divide the entire period of analysis into nine five-year windows of observation.Footnote 15 Hence, we account for the limited lifetime of cooperative ties by assuming that co-patenting relationships persist for a limited period of up to five years. This assumption is necessary since patent data provide no direct indication of tie-duration or tie-termination dates. Although the duration of projects can considerably vary, many patent applications may be based on joint research over a period of two to three years (Greve et al. 2009; Phelps 2010; Ramlogan and Consoli 2014). According to Park and Russo (1996), the average duration of a cooperative R&D project between organizations is less than five years.
For benchmarking purposes, we generate Erdős and Rényi (1959) random graph networks, comparable to their real-world counterparts in terms of size and density.Footnote 16 For analytical purposes, we employ the software package UciNet 6 (Borgatti et al. 2002, 2013). We are well aware that patents reflect only a part of the diverse types of formal and informal relationships among inventors. It is, however, plausible to assume that documented co-inventorship implies other forms of cooperation, such as co-publications and informal knowledge exchange. A comprehensive data source that accounts for the variety of relationships between innovating actors does not exist.Footnote 17
4 Macro-level stability and micro-level fluidity
4.1 Prevalence of macro-level stability
To explore the structural characteristics of the German laser industry inventor network, we draw upon basic graph-theoretical concepts and employ social network analysis (SNA) metrics (Wasserman and Faust 1994; Jackson 2008; Borgatti et al. 2013; Newman 2010). We begin by focusing on a number of measures that describe the topology of the entire system (Table 1). Network size is simply defined as the number of inventors with at least one dyadic relationship to another inventor, while the total number of actors encompasses both inventors with co-inventors as well as unconnected inventors (isolates). The share of isolated inventors, those without any ties, decreases over time (with the exception of the last period) while the total number of ties as well as the average number of ties (degree) maintained by inventors is continuously increasing. Network density, i.e. the total number of ties divided by the number of possible ties (Wasserman and Faust 1994), is decreasing. This is not surprising, since the number of potentially available network ties rises rapidly with increasing network size.
The component-based network measures provide an interesting picture of the system’s overall tendency of fragmentation. A component is defined as a connected sub-graph, while the component size simply reflects the number of inventors involved in this component. We observe an increase of the number as well of the average size of components. A closer look at the component size distribution of the three largest components reveals particular strong growth of the main component. The network diameter and the average path length follow no clear trend.Footnote 18 The same holds for the overall clustering coefficient that reflects the density of each inventor’s nearer surrounding by measuring how many of the inventor’s directly neighboring partners are interconnected. However, when using measures from our random benchmark networks (see Figs. 5 and 6 in the Appendix), a comparison of the average path length with the overall clustering coefficient reveals that German laser research networks exhibit a significantly shorter path-length and higher overall clustering coefficients.
We now turn attention to two structural properties at the overall network level that reflect structural stability of inventor networks. Figure 1 illustrates the degree distribution of the German laser research network for the entire observation period (1961–2005). The degree distribution indicates how many inventors—on average and over the entire observation period—had two, three, four or more direct cooperative relationships. It does, however, not account for the intensity of a cooperation. The graph on the left-hand side shows the degree distribution based on the total number of inventors for the entire observation period. On the right hand side, we show the normalized numbers plotted on a log–log scale. In the case of random networks, the values on the logarithmic scale should represent a curved line (towards the upper right), while the straight line (from the upper left to the lower right) that we find indicates a ‘fat-tailed’ degree distribution. Hence, the German laser research inventor network exhibits a typical ‘scale-free’ degree distribution meaning that there is a small number of inventors with an extremely high number of ties (up to 40), while the majority of the inventors have degrees far below ten.
The second structural feature we are interested in from a stability perspective is the core-periphery structure. The emergence of this macro pattern is directly linked to network entries and exits of inventors as well as formations of new partnerships or termination of existing ones.
To check whether the German laser inventor network shows a core-periphery structure we employ k-core measures.Footnote 19 A k-core measure includes all inventors that are adjacent to at least a minimum number, k, of other inventors in the component (Wasserman and Faust 1994). In a first step, we calculate k-core measures for all inventors over time. The repeated calculation of k-core measures (for k = 1, … n) enables us to plot coreness layers for different k-core intensities over time, typically referred to as k-core strata. The coreness strata allows us to check for the existence and emergence of a core-periphery structure. The larger the gap between k-core strata with high and low k values, the more pronounced is the core-periphery structure of the network.
We assign all inventors in the network into four categories based on their k-core values (c4:12 > k ≥ 10, c3: 9 ≥ k ≥ 7, c2: 6 ≥ k ≥ 4 and c1: 3 ≥ k ≥ 1) and plot the k-core strata over time. The dashed line (top of Fig. 2) provides the total number of inventors with a k-core value between one and three. These inventors can be considered to be located at the network periphery. In contrast, the solid thin line depicts the number of inventors with extremely high k-core measures in absolute terms. These inventors can be regarded as constituting the very core of the network. In addition, we calculated an average k-core level, plotted in Fig. 2 (top) as a solid fat line.
A high spread between the low-level k-core category (i.e. dashed line) and the higher-level categories (i.e. solid thin line, dashed-dotted line, and dotted line) indicates the existence of a core-periphery structure in the German laser inventor network for the entire observation period. The bottom of Fig. 2 reports the relative changes compared to the average k-core level. The k-core average is represented by 0 on the y-axis of the graph. Below average k-core values are represented by the black bar while above average k-core values are represented by the other bars in the chart. The exploration indicates a quite stable and persisting core-periphery structure over the entire observation period.
In sum, basic network metrics for the inventor networks in German laser technology indicate an increasing tendency towards a division of innovative labor. A closer look at the connectedness and cohesiveness of the network exhibits a remarkable degree of structural stability in terms of size, density and component size distribution. The network’s overall topology is characterized by a scale-free degree distribution. The exploration of k-core strata reveals a structurally stable and persistent pattern formation process. These results may be regarded as a stable segregation trend reflecting a core-periphery structure over the entire observation period. Overall, the reported patterns are largely in line with findings reported for other real-word networks (e.g., Powell et al. 2005; Kudic 2015; Tomasello et al. 2017).
4.2 The various facets of micro-level fluidity
In accordance with previous studies (Fritsch and Zoellner 2018, 2020; Phelps 2010; Ramlogan and Consoli 2014), we find rather high levels of fluidity of inventors and ties over time. The upper right part of Table 2 reports the shares of identical inventors (in percentage terms) in the networks across the different periods of analysis. For instance, the comparison between the first time period (1961–1965) and the second period (1966–1970) shows that only 8.54% of all inventors appear in both observation periods. The maximum share of identical actors in two subsequent time periods is 13.02%. With increasing time distance between the compared sub-periods this share strongly converges towards zero. This rather high fluctuation of network inventors over time indicates a low level of structural stability at the inventor level.
The numbers below the diagonal line in the lower left of Table 2 shows the shares (in percent) of reoccurring ties between pairs of inventors across different time periods. We find that discontinuation of ties tends to be even more pronounced than the fluidity of inventors. For example, only 5.85% of all ties between inventors are identical in the period 1961–1965 and 1966–1970. For more distant periods this share also strongly converges towards zero.
The very high levels of fluidity of inventors and their ties clearly demonstrate that the German laser research network exhibits a very high level of instability at the micro level. After only two observation periods, nearly the entire population of inventors is replaced by new actors. The fluidity of ties is even more pronounced. Almost no tie between inventors lasts for more than two periods. This raises the question: how is it possible that there is so much structural stability at the macro level, when the micro level exhibits such high levels of constant change?
5 The co-existence of macro stability and micro fluidity
In order to shed light on the co-existence of structural stability at the macro level and micro-level fluidity we conduct a key player analysis based on Borgatti (2003, 2006). Hence, we try to identify a set of inventors who either warrant the diffusion properties or stabilize the structural configuration of a given network. Key player metrics go way beyond typical centrality measures, such as degree centrality, betweenness centrality, or eigenvector centrality, which are typically applied to address an actor’s position within a network (Borgatti 2006).
The first identification criterion KPPNEG allows us to detect so-called (type-1) key players who, if removed from the network, would cause the most significant fragmentation of the network (Borgatti 2006). In other words, the measure allows us to identify those inventors who are most important for keeping the inventor network together. The second criterion KPPPOS identifies those key players (type-2) who are most relevant for the diffusion of knowledge in a given network structure (ibid). Hence, it enables us to determine those inventors who are most significant for the transfer of information and knowledge. The two measures follow a closely related logic, but capture two qualitatively different facets of network stability. While the KPPNEG measure addresses the physically observable tie structure, the KPPPOS measure relates directly to the functionality of the system.
We run the analyses for each of the nine observation periods and employ the results to find out whether the same or different actors are responsible for the structural stability at the overall network level.Footnote 20 Table 3 reports metrics for a diffusion based key players criterion (KPPPOS) in the period before (t − 1) and after (t + 1) a given observation period (t = 0).Footnote 21 We assign particular weight to this measure in our analysis because it directly addresses the core function of an inventor network, i.e. enabling knowledge exchange between directly and indirectly connected actors of the system. The higher the displayed key-player value, the more important the respective actor is with regard to systemic diffusion properties. For instance, in the 1961–1965 observation period, removing inventor Inv4061 would weaken the diffusion properties of the system most, followed by inventor Inv1129, etc.
Our findings show that only a very small share of inventors occupy a key player role in the network for a given observation period. Even more interesting, we find that the key player metrics for the same inventors significantly vary over time. The changing set of top key players and the highly volatile key player metrics clearly indicate that most inventors occupy this role for only one time period. Thus, contrary to our initial expectations, individual inventors are not responsible for sustaining the structural stability in terms of diffusion maintenance of the network over time. This observation underscores the high level of micro-level fluidity in inventor networks. At the same time, this raises the question of what keeps the network together and ensures its functionality.
Based on our considerations outlined above, we have good reasons to assume that the intermediate network level may provide some deeper insights into the co-existence of the characteristic macro stability and micro fluidity of inventor networks. In particular, we are curious to see whether key player positions are passed on from a prominent inventor in a given time period to members of his or her direct cooperation environment, proxied by inventor-specific ego networks.
To test this presumption, we proceed as follows. First, we explore the component size distribution for each of the nine observation windows separately and sort the components by size. Second, for each observation window we identify the largest components containing around 30%Footnote 22 of all network actors and calculate key player metrics for each component separately, based on both the diffusion and the fragmentation criterion.Footnote 23 Third, for a robustness check we define two categories of key players based on the KPPPOS criterion for each of the largest components over all time windows. Category I refers to the top 12.5% key players, and category II includes the top 25% of all identified key players. Fourth, in order to identify the direct network surrounding of the key players, we apply an ego-network approachFootnote 24 where we treat the previously identified key inventors as focal actors.
To do so, we identify the full set of directly linked partners (the ‘alters’) for each focal actor while simultaneously considering the ties between the alters. By definition, second tier ties are excluded from this group concept. Finally, we construct random ego-network benchmarks for the full set of the top 12.5% (25%) key players identified and reported above.Footnote 25 These random ego-network benchmarks are comparable in terms of size and structure to their real-world ego-network counterparts. The main difference between the empirically observed ego-networks and their corresponding random ego-networks is that all partners (‘alters’) of the key players (‘focal actors’) in a given observation period are selected randomly. Hence, step 4 and 5 allow us to assign empirically observable real-world ego-networks and a randomly generated benchmark ego-network to each key player.
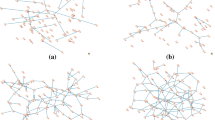
Figure 3 shows a comparison of real-world ego networks with random benchmarks for the inventors with high key-player values in the German laser research network.Footnote 26 The rationale behind our exploration is straightforward. If top key player positions are passed on from a prominent inventor to partners located in his direct cooperation environment, the top key players of a successive period should be found at a higher rate in the ego-network of the focal inventor than elsewhere. In other words, the potential overall damage caused by the removal of key players selected from the direct ego-network surrounding would be greater than in case of randomly selected partners.
The explorations on the left-hand side show comparisons between the real-world and randomly generated benchmark ego networks for the top 12.5% key players. The black dotted lines show the rate at which subsequent key player positions are filled with inventors from the key players’ direct ego networks for three selected reference periods, while the grey lines represent the random ego network benchmarks. On the right-hand side, we see the results of the same analysis for the top 25% key players. Our results clearly show that there is a much higher prospect for the successor of a top key player to be a member of the previous key player’s ego network as compared to alters from randomly generated benchmark ego networks.
6 Discussion and conclusions
6.1 Main findings
We analyzed the development of the inventor network in German laser research from the inception of the technology in 1961 until 2005, a period of 45 years. From a macro perspective, the development of this network appears to be a continuous process where each step builds on the previous one. The basic properties of the network and their development are well in accordance with other studies on innovation networks. The propensity for co-inventorship, as well as the average size of inventor teams increased considerably over time (Wuchty et al. 2007), there is a persistent tendency towards scaling, and we observe the emergence of a core-periphery structure. Overall, the results indicate a high level of structural stability at the macro level.
Investigating the development of the network at the micro level of inventors and their ties, we found high levels of fluidity. Only a rather small share of inventors in a certain five-year period reoccurs in the subsequent period. After only two periods, nearly the entire population of inventors has changed completely. According to these high levels of inventor fluidity, there is an equally pronounced degree of instability at the level of ties. Repeated and long-term ties are an exception. In sum, these findings clearly indicate rather high levels of turbulence under the surface of slowly changing macro structures.
To explore the relationship between macro level stability and micro level fluidity more deeply, and to gain a better understanding of who or what keeps the network together, we conducted a key player analysis. This analysis reveals high levels of fluidity even in key player positions in a network (based on both the diffusion and the fragmentation criterion), because these positions are only rarely occupied by the same inventors in successive periods. Our explorations show, however, a pronounced tendency for key player positions to be passed on to inventors who belong to the ego network of the previous key player. Interestingly, the passing over of key player positions via ego-network structures is not constrained by organizational boundaries. Hence, there is a tendency for continuity at the team level—regardless of whether the inventors come from same or different organizations—that may complement our understanding of the co-existence of macro stability and micro fluidity.
6.2 Implications
The simultaneous consideration of our results at the micro and the macro level has a number of interesting implications. For example, the strongly skewed and ‘fat-tailed’ degree distribution of the network cannot be explained by persistence of a small number of exceptional network actors. Network theorists frequently refer to a ‘rich-get-richer’ argument, suggesting that actors with an above-average degree in a given period attract ties at a higher rate than other actors in subsequent time periods (Albert and Barabasi 2002; Barabasi and Bonabeau 2003). Our results show continuous entry of new inventors—characterized by an above-average intensity of cooperation—who remain in the network for only a short time span. This insight challenges the logic behind the wide-spread preferential attachment mechanism, an often-implemented attachment mechanism in dynamic models of network change.
Our results also question a number of economic theories that imply longevity and persistence of partnerships. For instance, transactions-cost arguments suggest that actors typically spend considerable time and resources to identify a suitable cooperation partner and to build up trust (Das and Teng 2000) in order to counteract opportunistic behavior and reduce the risk of terminating unsuccessful partnerships (Doz 1996). In other words, a high level of micro-level fluidity caused by the frequent termination of relationships implies considerable sunk costs for the partners involved. Similarly, principle-agent theory (Spence 1976) suggests that network actors have strong incentives to remain in the networks since it allows them to continuously improve their strategic positioning and reduce information asymmetries by sending out signals to potential partners. For instance, a high and continuously increasing number of partner (reflected by an actor’s degree) signifies a high willingness and ability of cooperation that may generate valuable opportunities for future cooperation.
The findings of our key player analyses could be regarded an indication that trust may not only be relevant at the interpersonal or interorganizational level, but also at the team level. In such a case, individual investments in trust building and knowledge generation may benefit a group as a whole and are, therefore, not completely lost if a relationship between two actors is terminated. In other words, intermediate level within inventor networks seem to play an important role as intertemporal repositories where trust and knowledge may persist despite entry and exit of single members.
6.3 Limitations and further research
The high levels of fluidity at the micro level raise some fundamental questions: Why do inventors choose to establish a cooperative R&D relationship? How do they select their cooperation partners? Why is an established relationship maintained or abandoned? In a nutshell, our findings indicate that there must be forces at work that are more important than the sunk costs that occur if a relationship is abandoned.
Currently, we know very little about the dynamics of innovation networks. Particularly, the levels of discontinuing actors and of new actors in a network are largely unexplored.Footnote 27 More research in different technological fields and countries is desirable to assess the levels and patterns of network dynamics, particularly the fluidity of actors and ties in different environments. In addition, the reasons for abandoning a cooperative relationship are not very clear. To the best of our knowledge, there is still no sound empirical evidence about the drivers and structural consequences of tie terminations resulting from unsuccessful partnerships.
Similarly, knowledge and learning-related drivers of tie terminations confront us with a number of highly interesting questions. Does a new cooperation partner become more attractive primarily after the knowledge of the old partners is completely absorbed? Does the knowledge of the partner of a discontinued relationship become uninteresting or obsolete due to the general dynamics of the innovation process?Footnote 28 Do network actors follow a long-term cooperation strategy and, if so, are these decision sequences mirrored in actor-specific network trajectories or do relevant patterns only become visible at higher aggregation levels? Do these association patterns differ between established network members and newcomers?
Finally, we know nearly nothing about the role of actor fluidity in the performance of the respective innovation system. On the one hand, one might argue that a high level of fluidity indicates an effective allocation of talent and a fast diffusion of knowledge. On the other hand, fluidity of actors and ties may involve high levels of sunk costs and loss of knowledge of discontinuing actors. Hence, it is unclear if a high level of fluidity has a positive or negative effect on system performance.Footnote 29 To what extent is the knowledge of discontinuing actors lost for the respective innovation system? How do new actors impact the performance of the system? At the same time, it would be highly interesting to gain deeper insights into other layers of innovation systems, e.g. the interorganizational innovation network, and investigate co-evolutionary processes with firm level dynamics. For instance, Buenstorf and Heinisch (2020) provide empirical evidence on the long-term evolution of entries and exits of German laser technology firms. It would be interesting to analyze how different stages of industry life cycle affect network evolution and vice versa. Answers to such questions could considerably contribute to our understanding of collective innovation and the division of innovative labor.
Notes
‘Small world’ networks typically show a high level of clustering and short average path length. Thus, nodes can be reach by a small number of steps.
These types of networks are typically characterized by a small number of actors with a relatively high numbers of links (degree) while the majority of actors has one a small number of links.
A core-periphery structure in its simplest form refers to a partition of a network into a core of densely interconnected actors and peripheral actors that are sparsely connected to the core actors but not to other actors in the periphery.
For an overview, see Graebner et al. (2018).
According to Ahuja et al. (2012) any network can be conceptualized in terms of three primitives: first, the nodes that comprise the network, second the ties that connect the nodes, and third the patterns or structure that result from these connections.
The toolbox of social network analysis provides a wide range of centrality measures. Most notably, degree centrality (measures the number of direct partners of an actor) or eigenvector centrality (measures the importance of an actor based on the importance of its direct neighbor nodes).
For an in-depth discussion, see Kudic and Guenther (2017).
Buenstorf and Heinisch (2020) provide empirical evidence on science and industry evolution for the first 50 years of the German laser industry.
It describes a wide range of devices for the amplification of coherent light by stimulated photon emission generated by pumping energy through an adequate medium. A laser device emits a coherent light beam, both in a spatial and a temporal sense that can be generated based on different gain media, such as solid crystals and semiconductors, for example. The coherent light beam can be modulated and amplified.
We restrict our analysis to West Germany because of rather significant differences in patenting practices between East and West Germany before the reunification in 1990 (for details see Grupp et al. 2005).
The share of inventors with a foreign residence that were excluded was below 5% in most observation periods—for instance, 4.85% in the 1960–65 period, 4.03% in the 1966–70 period and 5.24% in the final 2001–2005 period. We also checked for the occurrence of those foreign inventors in several observation periods and found that only 2.02% of all excluded foreign inventors that were excluded in the 2001–2005 period also occurred in at least one preceding observation period.
These were the main technological fields of application during the period under inspection that could be clearly identified on the basis of IPC classification. Many of these applications were developed by diversifying producers of laser beam sources. Quite a number of producers that were already active in these fields of application and adopted the laser diversified upstream into production of beam sources (Buenstorf et al. 2015).
A closer look at the size distribution of inventor teams clearly indicates an increasing tendency towards co-patenting activities and an increasing tendency towards larger teams over time. More than 70% of all patent applications filed between 1961 and 2005, are co-patented by two or more inventors. This confirms the assessment by Wuchty et al. (2007) that innovation processes are increasingly characterized by a division of innovative labor for the German laser industry.
As an alternative to inventor networks, one could analyze cooperative patenting activities between organizations (e.g., public research institutes and firms). This assumes that researching organizations hold the relevant knowledge rather than the inventors. If the patent document names several organizations as applicants, identifying such cooperative relationships between organizations can be accomplished using the patent statistics. There is, however, no information available in such cases that identifies the partner with which an individual inventor that is listed in the patent document is affiliated. As compared to ties among inventors, co-applications of patents with several organizations are relatively rare and the construction of applicant networks is not conclusive. For example, at the onset (1961–65), we found 33 applicants while the share of isolated applicants amounts to 87%. In the middle of our observation period (1981–85), we found only 119 applicants, and again a very high share of isolates (86.3%). The low share of co-applications implies that the largest part of cooperative efforts by inventors occurs within the same organization. Analyzing inventor networks assumes that the relevant knowledge is represented by the inventors rather than by the organizations with which they are affiliated.
We conducted several robustness checks and experimented with four-year and six-year windows as well as with moving window setting, without significant differences in the reported results.
This procedure was always sufficiently often applied (n > 30) to generated representative random benchmarks. For detail see Kudic et al. (2021).
A comparison of regional innovation networks constructed with different data sources (Fritsch et al. 2020) finds that patent data tend to underestimate ties among private sector firms, while universities and other public research institutions are well-represented in patent data.
The network diameter reflects the length of the longest geodesic path, while the measure of an average path length incorporates all geodesic distances among reachable pairs of inventors, and provides an average measure at the systemic level.
For an overview of approaches for identifying core-periphery patterns, see Csermely et al. (2013).
We used specific key player software (Borgatti 2003) to identify type-1 and type-2 key players for the main component of the inventor networks in each of the 9 sub-periods.
KPPNEG identifies about the same set of key players as KPPPOS for all observation windows. This implies that the same set of inventors occupies key player roles according to both, the ‘diffusion’ and the ‘fragmentation’ criterion. Table 5 in the “Appendix” provides detailed results for the structurally-oriented key player analysis (KPPNEG metrics).
Since the size distribution is characterized by discrete size categories and varies for each observation window. The 30% value is an approximate threshold criterion. For instance, in the first time window (61–65), the three largest components contain 36.9% of all inventors. In the last time window (01–05), the largest components account for 29.6% of all inventors. Additional explorations on sized distribution of components are available upon request.
Since components can be interpreted as autarkic elements of an overall network, we run the key player analysis for the entire network and identify the most dominant key inventor for each component separately.
The random selection procedure was repeated 30 times to control for fluctuations caused by outliers.
Belderbos et al. (2015) investigate the relationship between the dynamics of R&D cooperation and innovation performance based on a panel of Spanish firms. They conclude from their analysis that it is more the persistent collaboration that has a positive effect on firm innovativeness, while the effect of discontinued cooperation was insignificant. Fritsch and Zoellner (2019) measure performance based on the number of patents per R&D employee (patent productivity), and find a positive relationship between the share of new actors and ties and the performance of the respective innovation system. While there is a positive relationship between the share of discontinued inventors and patent productivity, the relationship between the share of discontinued ties and patent productivity is positive.
References
Ahuja, G. (2000). Collaboration networks, structural hole, and innovation: A longitudinal study. Administrative Science Quarterly, 45(3), 425–455. https://doi.org/10.2307/2667105.
Ahuja, G., Soda, G., & Zaheer, A. (2012). The genesis and dynamics of organizational networks. Organization Science, 23(2), 434–448. https://doi.org/10.1287/orsc.1110.0695.
Albert, R., & Barabási, A.-L. (2002). Statistical mechanics of complex networks. Reviews of Modern Physics, 74(1), 47–97. https://doi.org/10.1103/RevModPhys.74.47.
Albrecht, H. (2019). Laserforschung in Deutschland 1960–1970. Eine vergleichende Studie zur Frühgeschichte von Laserforschung und Lasertechnik in der Bundesrepublik Deutschland und der Deutschen Demokratischen Republik. Berlin: GNT-Verlag.
Amburgey, T. L., Dacin, T., & Singh, J. V. (1996). Learning races, patent races, and capital races: strategic interaction and embeddedness within organizational fields. In J. A. Baum (Ed.), Advances in strategic management (pp. 303–322). New York: Elsevier.
Arend, R. J. (2009). Reputation for cooperation: contingent benefits in alliance activity. Strategic Management Journal, 30, 371–385. https://doi.org/10.1002/smj.740.
Arthur, B. W. (1989). Competing technologies, increasing returns, and lock-in by historical events. The Economic Journal, 99(394), 116–131. https://doi.org/10.2307/2234208.
Asheim, B. T., Isaksen, A., & Trippl, M. (2019). Regional innovation systems. Cheltenham: Elgar.
Barabási, A.-L., & Bonabeau, E. (2003). Scale-free networks. Scientific American, 288(5), 50–59. https://doi.org/10.1038/scientificamerican0503-60.
Belderbos, R., Carree, M., Lokshin, B., & Fernández, J. (2015). Inter-temporal patterns of R&D collaboration and innovative performance. Journal of Technology Transfer, 40, 123–137. https://doi.org/10.1007/s10961-014-9332-4.
Bertolotti, M. (2005). The history of the laser. Bristol: Institute of Physics Publishing.
Bonacich, P. (1987). Power and centrality: A family of measures. American Journal of Sociology, 92(5), 1170–1182. https://doi.org/10.1086/228631.
Borgatti, S. P., Everett, M. G., & Freeman, L. C. (2002). Ucinet 6 for windows. Software for social network analysis. Harvard, MA: Analytic Technologies.
Borgatti, S. P. (2003). Key player. Boston: Analytic Technologies.
Borgatti, S. P. (2006). Identifying sets of key players in a social network. Computational and Mathematical. Organization Theory, 12, 21–34. https://doi.org/10.1007/s10588-006-7084-x.
Borgatti, S. P., & Everett, M. G. (1999). Models of core/periphery structures. Social Networks, 21, 375–395. https://doi.org/10.1016/S0378-8733(99)00019-2.
Borgatti, S. P., Everett, M. G., & Johnson, J. C. (2013). Analyzing social networks. London: Sage.
Boschma, R. (2005). Proximity and innovation: A critical assessment. Regional Studies, 39(1), 61–74. https://doi.org/10.1080/0034340052000320887.
Bourdieu, P. (1986). The forms of capital. In J. Richardson (Ed.), Handbook of theory and research for the sociology of education (pp. 241–258). New York: Greenwood.
Brass, D. J., Galaskiewicz, J., Greve, H. R., & Tsai, W. (2004). Taking stock of networks and organizations: A multilevel perspective. Academy of Management Journal, 47(6), 795–817. https://doi.org/10.5465/20159624.
Brenner, T., Cantner, U., & Graf, H. (2011). Innovation networks: Measurement, performance and regional dimensions. Industry and Innovation, 18(1), 1–5. https://doi.org/10.1080/13662716.2010.528925.
Bromberg, J. L. (1991). The laser in America 1950–1970. Cambridge (MA): MIT Press.
Buckley, P. J., Glaister, K. W., Klijn, E., & Tan, H. (2009). Knowledge accession and knowledge acquisition in strategic alliances: The impact of supplementary and complementary dimensions. British Journal of Management, 20(4), 598–609. https://doi.org/10.1111/j.1467-8551.2008.00607.x.
Buenstorf, G., Fritsch, M., & Medrano, L. F. (2015). Regional knowledge and the emergence of an industry: Laser systems production in West Germany, 1975–2005. Regional Studies, 49, 59–75. https://doi.org/10.1080/00343404.2012.711947.
Burt, R. S. (1992). Structural holes: The social structure of competition. Cambridge: Harvard University Press.
Burt, R. S. (2005). Brockerage and closure—an introduction to social capital. New York: Oxford University Press.
Carlsson, B., Jacobsson, S., Holmen, M., & Rickne, A. (2002). Innovation systems: Analytical and methodological issues. Research Policy, 31(2), 233–245. https://doi.org/10.1016/S0048-7333(01)00138-X.
Cattani, G., & Ferriani, S. (2008). A core/periphery perspective on individual creative performance: Social networks and cinematic achievements in the Hollywood Film Industry. Organization Science, 19(6), 807–922. https://doi.org/10.1287/orsc.1070.0350.
Chaminade, C., Lundvall, B.-A., & Hanneef, S. (2019). Advanced introduction to national innovation systems. Cheltenham: Elgar.
Coleman, J. S. (1988). Social capital in the creation of human capital. American Journal of Sociology, 94, 95–120. https://doi.org/10.1086/228943.
Cropper, S., Ebers, M., Huxham, C., & Ring, P. S. (2008). The Oxford handbook of inter-organizational relations. Oxford: Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199282944.001.0001.
Csermely, P., London, A., Wu, L.-Y., & Uzzi, B. (2013). Structure and dynamics of core/periphery networks. Journal of Complex Networks, 1(2), 93–123. https://doi.org/10.1093/comnet/cnt016.
Das, T. K., & Teng, B.-S. (2000). Instabilities of strategic alliances: An internal tensions perspective. Organization Science, 11(1), 77–101. https://doi.org/10.1287/orsc.11.1.77.12570.
David, P. A. (1985). Clio and the economics of QWERTY. American Economic Review, 75(2), 332–337.
Doreian, P., & Stokman, F. N. (2005). The dynamics and evolution of social networks. In P. Doreian & F. N. Stokman (Eds.), Evolution of social networks (2nd ed., pp. 1–17). New York: Gordon and Breach.
Doz, Y. L. (1996). The evolution of cooperation in strategic alliances: Initial conditions or learning processes? Strategic Management Journal, 17(1), 55–83. https://doi.org/10.1002/smj.4250171006.
Eisenhardt, K. M., & Schoonhoven, C. B. (1996). Resource-based view of strategic alliance formation—strategic and social effects in entrepreneurial firms. Organization Science, 7(2), 136–150. https://doi.org/10.1287/orsc.7.2.136.
Ejermo, O., & Karlsson, C. (2006). Interregional inventor networks as studied by patent coinventorships. Research Policy, 35, 412–430. https://doi.org/10.1016/j.respol.2006.01.001.
Erdős, P., & Rényi, A. (1959). On random graphs. Publicationes Mathematicae, 6, 290–297.
Fleming, L., King, C., & Juda, A. I. (2007). Small worlds and regional innovation. Organization Science, 18, 938–954. https://doi.org/10.1287/orsc.1070.0289.
Freeman, C. (1974). The economics of industrial innovation. Harmondsworth UK: Penguin Books.
Freeman, C. (1991). Networks of innovators: A synthesis of research issues. Research Policy, 20(5), 499–514. https://doi.org/10.1016/0048-7333(91)90072-X.
Fritsch, M., & Kauffeld-Monz, M. (2010). The impact of network structure on knowledge transfer: An application of social network analysis in the context of regional innovation networks. Annals of Regional Science, 44, 21–38. https://doi.org/10.1007/s00168-008-0245-8.
Fritsch, M., & Medrano, L. F. (2015). New technology in the region—agglomeration and absorptive capacity effects on laser technology research in West Germany, 1960–2005. Economics of Innovation and New Technology, 24, 65–94. https://doi.org/10.1080/10438599.2014.897861.
Fritsch, M., & Kudic, M. (2016). Preferential attachment and pattern formation in R&D networks—plausible explanation or just a widespread myth? Jena Economic Research Papers, No. 2016-005, Friedrich Schiller University Jena. http://hdl.handle.net/10419/144901
Fritsch, M., Piontek, M., & Titze, M. (2020). Identifying cooperation for innovation- a comparison of data sources. Industry and Innovation, 27, 630–659. https://doi.org/10.1080/13662716.2019.1650253.
Fritsch, M., & Zoellner, M. (2018). Actor fluidity and knowledge persistence in regional inventor networks. Jena Economic Research Papers #2018–016, Friedrich Schiller University Jena. https://zs.thulb.uni-ena.de/servlets/MCRFileNodeServlet/jportal_derivate_00265576/wp_2018_016.pdf
Fritsch, M., & Zoellner, M. (2020). The fluidity of inventor networks. Journal of Technology Transfer, 45, 1063–1087. https://doi.org/10.1007/s10961-019-09726-z.
Gebrekidan, D. A., & Awuah, G. B. (2012). Interorganizational cooperation: A new view of strategic alliances—the case of Swedish firms in the international market. Industrial Marketing Management, 31, 679–693.
Gilsing, V., & Nooteboom, B. (2005). Density and strength of ties in innovation networks: An analysis of multimedia and biotechnology. European Management Review, 2, 179–197. https://doi.org/10.2139/ssrn.706851.
Glueckler, J. (2007). Economic geography and the evolution of networks. Journal of Economic Geography, 7, 619–634. https://doi.org/10.1093/jeg/lbm023.
Gould, G.R. (1959). The laser: light amplification by stimulated emission of radiation. In Ann Arbor Conference on Optical Pumping, Conference Proceeding, pp. 128–130.
Graebner, C., Heinrich, T., Kudic, M., & Vermeulen, B. (2018). The dynamics of and on networks: An introduction. International Journal of Economics and Econometrics, 8, 229–241.
Grant, R. M., & Baden-Fuller, C. (2004). A knowledge accessing theory of strategic alliances. Journal of Management Studies, 41(1), 61–84. https://doi.org/10.1111/j.1467-6486.2004.00421.x.
Greve, H., Brown, J. A., Mitsuhashi, H., & Rowley, T. (2009). Built to last but falling apart: Cohesion, friction, and withdrawal from interfirm alliances. Academy of Management Journal, 53, 302–322. https://doi.org/10.5465/amj.2010.49388955.
Grupp, H. (2000). Learning in a science-driven market: The case of lasers. Industrial and Corporate Change, 9, 143–172. https://doi.org/10.1093/icc/9.1.143.
Grupp, H., Dominguez Lacasa, I., Friedrich-Nishio, M., & Jungmittag, A. (2005). Innovation and growth in Germany over the past 150 years. In U. Cantner, E. Dinopoulos, & R. F. Lanzillotti (Eds.), Entrepreneurships, the new economy and public policy (pp. 267–287). Berlin: Springer.
Hagedoorn, J. (2002). Inter-firm R&D partnership: An overview of major trends and patterns since 1960. Research Policy, 31(4), 477–492. https://doi.org/10.1016/S0048-7333(01)00120-2.
Hite, J. M., & Hesterl, W. S. (2001). The evolution of firm networks: From emergence to early growth of the firm. Strategic Management Journal, 22(3), 275–286. https://doi.org/10.1002/smj.156.
Houston, M. B. (2003). Alliance partner reputation as a signal to the market: Evidence from bank loan alliances. Corporate Reputation Review, 5(4), 330–342.
Jackson, M. O. (2008). Social and economic networks. Princeton, NJ: Princeton University Press.
Kale, P., Singh, H., & Perlmutter, H. (2000). Learning and protection of proprietary assets in strategic alliances: Building relational capital. Strategic Management Journal, 21(3), 217–237. https://doi.org/10.1002/(SICI)1097-0266(200003)21:3%3c217::AID-SMJ95%3e3.0.CO;2-Y.
Kim, T.-Y., Hongseok, O., & Swaminathan, A. (2006). Framing interorganizational network change: A network inertia perspective. Academy of Management Review, 31, 704–720.
Kline, S. J., & Rosenberg, N. (1986). An overview of innovation. In R. Landau & N. Rosenberg (Eds.), The positive sum strategy (pp. 275–305). Washington, D.C.: National Academy Press.
Kudic, M. (2015). Innovation networks in the German laser industry—evolutionary change, strategic positioning, and firm innovativeness. Heidelberg: Springer.
Kudic, M., Ehrenfeld, W., & Pusch, T. (2015). On the trail of core-periphery patterns in innovation networks—measurement and new empirical findings from the German laser industry. Annals of Regional Science, 55(1), 187–220. https://doi.org/10.1007/s00168-015-0679-8.
Kudic, M., & Guenther, J. (2017). Understanding the complex nature of innovation network evolution. In A. Pyka & U. Cantner (Eds.), Foundations of economic change: A Schumpeterian view on behaviour, interaction and aggregate outcomes (pp. 501–524). Cham: Springer.
Kudic, M., Fritsch, M., & Mueller, M. (2021). Long-term evolution of inventor networks. Exploring the origins of structural change processes along different analytical levels. Germany: Mimeo, University of Siegen.
Malerba, F. (2004). Sectoral systems of innovation: basic concepts. In F. Malerba (Ed.), Sectoral systems of innovation: Concepts, issues and analyses of six major sectors in Europe (pp. 9–41). Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511493270.002.
Martínez-Noya, A., & Narula, R. (2018). What more can we learn from R&D alliances? A review and research agenda. Business Research Quarterly., 21, 195–212. https://doi.org/10.1016/j.brq.2018.04.001.
Metcalfe, S. J. (2010). The open, evolving economy: Alfred Marshall on knowledge, management and innovation. In J.-L. Gaffard & E. Salies (Eds.), Innovation, economic growth and the firm—theory and evidence of industrial dynamics (pp. 3–30). Cheltenham UK: Edward Elgar Publishing.
Milgram, S. (1967). The small-world problem. Psychology Today, 1, 60–67. https://doi.org/10.1007/978-3-658-21742-6_94.
Mowery, D. C., Oxley, J. E., & Silverman, B. S. (1996). Strategic alliances and interfirm knowledge transfer. Strategic Management Journal, 17(2), 77–92. https://doi.org/10.1002/smj.4250171108.
Nelson, R., Dosi, G., Helfat, C., Pyka, A., Saviotti, P. P., Lee, K., et al. (2018). Modern evolutionary economics—an overview. Cambridge, UK: Cambridge University Press.
Nelson, R. R., & Winter, S. G. (1974). Neoclassical vs. evolutionary theories of economic growth: Critique and prospectus. The Economic Journal, 84(336), 886–905.
Nelson, R. R., & Winter, S. G. (1982). An evolutionary theory of economic change. Cambridge: Harvard University Press.
Newman, M., Barabasi, A.-L., & Watts, D. J. (2006). The structure and dynamics of networks. Princeton, NJ: Princeton University Press.
Newman, M. E. (2010). Networks—an introduction. New York: Oxford University Press.
Nielsen, B. B., & Nielsen, S. (2009). Learning and innovation in international strategic alliances: An empirical test of the role of trust and tacitness. Journal of Management Studies, 46(6), 1031–1056. https://doi.org/10.1111/j.1467-6486.2009.00840.x.
Nooteboom, B. (2008). Learning and innovation in inter-organizational relationships. In S. Cropper, M. Ebers, C. Huxham, & P. S. Ring (Eds.), The Oxford handbook of interorganizational relations (pp. 607–634). New York: Oxford University Press.
Park, S. H., & Russo, M. V. (1996). When competition eclipses cooperation: An event history analysis of joint venture failure. Management Science, 42(6), 875–890. https://doi.org/10.1287/mnsc.42.6.875.
Perlmutter, H. V., & Heenan, D. A. (1986). Cooperate to compete globally. Harvard Business Review, 64(2), 136–152.
Parkhe, A., Wasserman, S., & Ralston, D. A. (2006). New frontiers in network theory development. Academy of Management Review, 31(3), 560–568.
Phelps, C. C. (2010). A longitudinal study of the influence of alliance network structure and composition on firm exploratory innovation. Academy of Management Journal, 53, 890–913. https://doi.org/10.5465/amj.2010.52814627.
Powell, W. W. (1987). Hybrid organizational arrangements: New form of transitional development? California Management Review, 30(1), 67–87.
Powell, W. W., Kogut, K. W., & Smith-Doerr, L. (1996). Interorganizational collaboration and the locus of innovation—networks of learning in biotechnology. Administrative Science Quarterly, 41, 116–145. https://doi.org/10.2307/2393988.
Powell, W. W., White, D. R., Kogut, K. W., & Owen-Smith, J. (2005). Network dynamics and field evolution: The growth of the interorganizational collaboration in the life sciences. American Journal of Sociology, 110, 1132–1205. https://doi.org/10.1086/421508.
Pyka, A., Kudic, M., & Müller, M. (2019). Systemic interventions in regional innovation systems: Entrepreneurship, knowledge accumulation and regional innovation. Regional Studies, 53(9), 1321–1332. https://doi.org/10.1080/00343404.2019.156670
Ramlogan, R., & Consoli, D. (2014). Dynamics of collaborative research medicine: The case of glaucoma. Journal of Technology Transfer, 39, 544–566. https://doi.org/10.1007/s10961-013-9300-4.
Rank, C., Rank, O., & Wald, A. (2006). Integrated versus core-periphery structures in regional biotechnology networks. European Management Journal, 24, 73–85. https://doi.org/10.1016/j.emj.2005.12.009.
Rodan, S., & Galunic, C. (2004). More than network structure: How knowledge heterogeneity influences managerial performance and innovativeness. Strategic Management Journal, 25(6), 541–562. https://doi.org/10.1002/smj.398.
Rosenkopf, L., & Padula, G. (2008). Investigating the microstructure of network evolution: Alliance formation in the mobile communications industry. Organization Science, 19, 669–687. https://doi.org/10.1287/orsc.1070.0339.
Schilling, M. A., & Phelps, C. C. (2007). Interfirm collaboration networks: The impact of large-scale network structure on firm innovation. Management Science, 53, 1113–1126. https://doi.org/10.1287/mnsc.1060.0624.
Schumpeter, J. A. (1912). Theorie der wirtschaftlichen Entwicklung (The theory of economic development 1934). Berlin: Duncker & Humblot.
Simonin, B. L. (1999). Ambiguity and the process of knowledge transfer in strategic alliances. Strategic Management Journal, 20(1), 595–623. https://doi.org/10.1002/(SICI)1097-0266(199907)20:7%3c595::AID-SMJ47%3e3.0.CO;2-5.
Spence, M. (1976). Informational aspects of market structure: An introduction. Quarterly Journal of Economics, 90(4), 591–597. https://doi.org/10.2307/1885323.
Storper, M., & Venables, A. J. (2004). Buzz: Face-to-face contact and the urban economy. Journal of Economic Geography, 4, 351–360. https://doi.org/10.1093/jnlecg/lbh027.
Stuart, T. E. (2000). Interorganizational alliances and the performance of firms: A study of growth and innovational rates in a high-technology industry. Strategic Management Journal, 21, 791–811. https://doi.org/10.1002/1097-0266(200008)21:8.
Sivadas, E., & Dwyer, R. F. (2000). An examination of organizational factors influencing new product success in internal and alliance-based processes. Journal of Marketing, 64(1), 31–49.
Thune, T., & Gulbrandsen, M. (2014). Dynamics of collaboration in university–industry partnerships: Do initial conditions explain development patterns? Journal of Technology Transfer, 39, 977–993. https://doi.org/10.1007/s10961-014-9331-5.
Tomasello, M. V., Napoletano, M., Garas, A., & Schweitzer, F. (2017). The rise and fall of networks. Industrial and Corporate Change, 26(4), 617–646. https://doi.org/10.1093/icc/dtw041.
Tsai, W., & Ghoshal, S. (1998). Social capital and value creation: The role of intrafirm networks. Academy of Management Journal, 41(4), 464–476. https://doi.org/10.5465/257085.
Uzzi, B., & Spiro, J. (2005). Collaboration and creativity: The small world problem. American Journal of Sociology, 111, 447–504. https://doi.org/10.1086/432782.
Uzzi, B., Amaral, L. A., & Reed-Tsochas, F. (2007). Small-world networks and management science research: A review. European Management Review, 4(2), 77–91. https://doi.org/10.1057/palgrave.emr.1500078.
Wasserman, S., & Faust, K. (1994). Social network analysis: Methods and applications. Cambridge: Cambridge University Press.
Watts, D. J., & Strogatz, S. H. (1998). Collective dynamics of ‘small-world’ networks. Nature, 393(6684), 440–442. https://doi.org/10.1038/30918.
Williamson, O. E. (1991). Comparative economic organization: The analysis of discrete structural alternatives. Administrative Science Quarterly, 36(2), 269–296. https://doi.org/10.2307/2393356.
Wuchty, S., Jones, B. F., & Uzzi, B. (2007). The increasing dominance of teams in production of knowledge. Science, 316, 1036–1039. https://doi.org/10.1126/science.1136099.
Zaheer, A., McEvily, B., & Perrone, V. (1998). Does trust matter? Exploring the effects of interorganizational and interpersonal trust on performance. Organization Science, 9(2), 141–159. https://doi.org/10.1287/orsc.9.2.141.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fritsch, M., Kudic, M. Micro dynamics and macro stability in inventor networks. J Technol Transf 47, 353–382 (2022). https://doi.org/10.1007/s10961-021-09851-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10961-021-09851-8