Skip to main content
SpringerLink
Log in

A Posteriori Error Control of Approximate Solutions to Boundary Value Problems Found by Neural Networks

  • Published:
Journal of Mathematical Sciences Aims and scope Submit manuscript

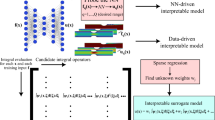
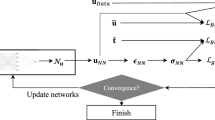
The paper discusses how to verify the quality of approximate solutions to partial differential equations constructed by deep neural networks. A posterior error estimates of the functional type, that have been developed for a wide range of boundary value problems, are used to solve this problem. It is shown, that they allow one to construct guaranteed two-sided estimates of global errors and get distribution of local errors over the domain. Results of numerical experiments are presented for elliptic boundary value problems. They show that the estimates provide much more reliable information on the quality of approximate solutions generated by networks than the loss function, which is used as a quality criterion in the Deep Galerkin method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. E. J. Han and A. Jentzen, “Deep learning-based numerical methods for highdimensional parabolic partial differential equations and backward stochastic differential equations,” Commun. Math. Stat., 5, 349–380 (2017).

    Article  MathSciNet  MATH  Google Scholar 

  2. J. He, L. Li, J. Xu, and C. Zheng, “ReLU deep neural networks and linear finite elements,” arXiv:1807.03973v2, arXiv (2018).

  3. R. Khudorozhkov, S. Tsimfer, and A. Koryagin, “PyDEns framework for solving differential equations with deep learning,” arXiv:1909.11544 [cs.LG], arXiv (2019).

  4. I. E. Lagaris, A. Likas, and D. I. Fotiadis, “Artificial neural networks for solving ordinary and partial differential equations,” IEEE Transactions on Neural Networks 9, No. 5, 987–1000 (1997).

    Article  Google Scholar 

  5. W. E and B. Yu, “The Deep Ritz Method: A deep learning-based numerical algorithm for solving variational problems,” Commun. Math. Stat., 6, 1–12 (2018).

  6. O. Pironneau, “Parameter identification of a fluid-structure system by deep-learning with an Eulerian formulation,” Methods Appl. Anal., 26, No. 3, 281–290 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  7. F. Regazzonia, L. Dede, and A. Quarteroni, “Machine learning for fast and reliable solution of time-dependent differential equations,” J. Comput. Phys., 397 , 108852 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  8. E. Samaniego, C. Anitescu, S. Goswami, V. M. Nguyen-Thanh, H. Guo, K. Hamdia, X. Zhuang, and T. Rabczuka, “An energy approach to the solution of partial differential equations in computational mechanics via machine learning: Concepts, implementation and applications,” Comput. Methods Appl. Mech. Engrg., 362, 112790 (2020).

    Article  MathSciNet  MATH  Google Scholar 

  9. S. Repin, A Posteriori Estimates for Partial Differential Equations, Walter de Gruyter GmbH & Co. KG, Berlin (2008).

    Book  MATH  Google Scholar 

  10. R. Verfürth, A Review of A Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques, Wiley-Teubner, Stuttgart (1996).

  11. S. Repin, “A posteriori error estimation for nonlinear variational problems by duality theory,” Zap. Nauchn. Semin. POMI, 243, 201–214 (1997); English transl. J. Math. Sci. 99, No. 1 (2000).

  12. S. Repin, “A posteriori error estimation for variational problems with uniformly convex functionals,” Math. Comp., 69 (230), 481–500 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  13. S. Repin, “Two-sided estimates of deviation from exact solutions of uniformly elliptic equations,” Amer. Math. Soc. Transl., 209, 143–171 (2003).

    MathSciNet  MATH  Google Scholar 

  14. S. Repin, “Estimates of deviation from exact solutions of initial-boundary value problems for the heat equation,” Rend. Mat. Acc. Lincei., 13, 121–133 (2002).

    MathSciNet  MATH  Google Scholar 

  15. S. Repin, S. Sauter, and A. Smolianski, “Two-sided a posteriori error estimates for mixed formulations of elliptic problems,” SIAM J. Num. Anal., 45, 928–945 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  16. S. Repin and M. Frolov, “A posteriori error estimates for approximate solutions of elliptic boundary value problems,” Zh. Vychisl. Mat. Mat. Fiz., 42, No. 12, 1704–1716 (2002).

    MathSciNet  Google Scholar 

  17. O. Mali, P. Nettaanmäki, and S. Repin, Accuracy Verification Methods. Theory and Algorithms, Springer, Berlin (2014).

    Book  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Peter the Great St.Petersburg Polytechnic University, St. Petersburg, Russia

    A. V. Muzalevskiy

  2. St.Petersburg Department of Steklov Institute of Mathematics, St. Petersburg, Russia

    S. I. Repin

Authors
  1. A. V. Muzalevskiy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. I. Repin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. I. Repin.

Additional information

Translated from Zapiski Nauchnykh Seminarov POMI, Vol. 499, 2021, pp. 77–104.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Muzalevskiy, A.V., Repin, S.I. A Posteriori Error Control of Approximate Solutions to Boundary Value Problems Found by Neural Networks. J Math Sci 273, 492–510 (2023). https://doi.org/10.1007/s10958-023-06516-9

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10958-023-06516-9

Search

Navigation