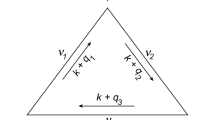
The Dynkin–Minchenko construction of enhanced Dynkin diagram is slightly modified to construct signed enhanced Dynkin diagrams of exceptional type Φ = E6, E7, E8. It is observed that these diagrams contain as subdiagrams all Carter–Stekolshchik diagrams of conjugacy classes of the Weyl groups W(Φ).
Similar content being viewed by others
References
V. I. Arnold, “Polymathematics, is Mathematics a single Science or a set of Arts,” 1–15 (2000).
J. C. Baez, “The octonions,” Bull. Amer. Math. Soc., 39, No. 2, 145–205 (2002).
P. Bala and R. W. Carter, “Classes of unipotent elements in simple algebraic groups. II,”Math. Proc. Camb. Philos. Soc., 80, 1–18 (1976).
N. Bourbaki, “Éléments de mathématique. Fasc. XXXIV. Groupes et algèbres de Lie. Chapitre IV: Groupes de Coxeter et systèmes de Tits. Chapitre V: Groupes engendrés par des réflexions. Chapitre VI: Systèmes de racines,” Actualités Scientifiques et Industrielles, No. 1337, Hermann, Paris (1968).
R. W. Carter, “Conjugacy classes in the Weyl group,” in: Seminar on Algebraic Groups and Related Finite Groups, Springer, Berlin (1970), pp. 297–318.
R. W. Carter, “Conjugacy classes in the Weyl group,” Compos. Math., 25, No. 1, 1–59 (1972).
E. B. Dynkin, “Semisimple subalgebras of semisimple Lie algebras,” Amer. Math. Soc. Transl., 6, 111–244 (1957).
E. B. Dynkin and A. N. Minchenko, “Enhanced Dynkin diagrams and Weyl orbits,” Transform. Groups, 15, No. 4, 813–841 (2010).
J. S. Frame, “The classes and representations of the groups of 27 lines and 28 bitangents,” Ann. Mat. Pura Appl., 32, No. 4, 83–119 (1951).
J. S. Frame, “The characters of the Weyl group E8,” in: J. Leech (ed.), Computational Problems in Abstract Algebra, Oxford (1967), pp. 111–130.
M. Geck and G. Pfeiffer, Characters of Finite Coxeter Groups and Iwahori–Hecke Algebras, Clarendon Press, Oxford (2000).
A. Harebov and N. Vavilov, “On the lattice of subgroups of Chevalley groups containing a split maximal torus,” Commun. Algebra, 24, No. 1, 109–133 (1996).
V. V. Kornyak, “Quantization in discrete dynamical systems,” J. Math. Sci., 168, No. 3, 390–397 (2010).
G. Lusztig, “From conjugacy classes in the Weyl group to unipotent classes,” Represent. Theory, 15, 494–530 (2011).
Yu. I. Manin, Cubic forms: algebra, geometry, arithmetic, North-Holland Mathematical Library, 4, North-Holland Publishing Co., American Elsevier Publishing Co., Amsterdam- London, New York (1974).
L. Manivel, “Configurations of lines and models of Lie algebras,” J. Algebra, 304, No. 1, 457–486 (2006).
J. McKee and C. Smyth, “Integer symmetric matrices having all their eigenvalues in the interval [−2, 2],” J. Algebra, 317, No. 1, 260–290 (2007).
J. McKee and C. Smyth, “Symmetrizable integer matrices having all their eigenvalues in the interval [−2, 2],” Algebr. Comb., 3, No. 3, 775–789 (2020).
V. Migrin and N. Vavilov, “Exceptional uniform polytopes of the E6, E7 and E8 symmetry types,” Polynomial Comput. Algebra, St.Petersburg, 1–23 (2021).
T. Oshima, “A classification of subsystems of a root system,” arXiv: math/0611904v4 [math RT] (2007).
V. Petrov, “A rational construction of Lie algebras of type E7,” J. Algebra 481, 348–361 (2017).
T. A. Springer, “Regular elements of finite reflection groups,” Invent. Math., 25, 159–198 (1974).
R. Stekolshchik, “Root systems and diagram calculus. I. Regular extensions of Carter diagrams and the uniqueness of conjugacy classes,” arXiv:1005.2769v6 [math.RT] (2012).
R. Stekolshchik, “Root systems and diagram calculus. II. Quadratic forms for the Carter diagrams,” arXiv:1010.5684v7 [math.RT] (2011).
R. Stekolshchik, “Root systems and diagram calculus. III. Semi-Coxeter orbits of linkage diagrams and the Carter theorem,” arXiv:1105.2875v3 [math.RT] (2011).
R. Stekolshchik, “Equivalence of Carter diagrams,” Algebra Discrete Math., 23, No. 1, 138–179 (2017).
N. A. Vavilov, “Do it yourself structure constants for Lie algebras of types El,” J. Math. Sci., 120, No. 4, 1513–1548 (2004).
N. A. Vavilov, “Numerology of square equations,” St. Petersburg Math. J., 20, No. 5, 687–707 (2009).
N. A. Vavilov, “Some more exceptional numerology,” J. Math. Sci., 171, No. 3, 317–321 (2010).
N. A. Vavilov and N. P. Kharchev, “Orbits of the subsystem stabilizers,” J. Math. Sci., 145, No. 1, 4751–4764 (2007).
N. A. Vavilov and A. A. Semenov, “Long root tori in Chevalley groups,” St. Petersburg Math. J., 24, No. 3, 387–430 (2013).
N. Wallach, “On maximal subsystems of root systems,” Canad. J. Math., 20, 555–574 (1968).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Zapiski Nauchnykh Seminarov POMI, Vol. 500, 2022, pp. 11–29.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Vavilov, N.A., Migrin, V.V. Enhanced Dynkin Diagrams Done Right. J Math Sci 272, 349–361 (2023). https://doi.org/10.1007/s10958-023-06429-7
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10958-023-06429-7