Introduction

A human pathogen is a microorganism such as a virus, bacterium, protozoan, or fungus that causes disease in humans. Symptoms such as sneezing, coughing, fever, and vomiting are caused by viruses and bacteria [1]. These pathogens have been a great problem since the beginning of civilization and still continue to cause disease to humans. Nowadays, in a world where modern antibiotics are designed to destroy pathogens, they continue to be a primary source of disease. For example, in 2019, human infections are approximated to cause more than 8 million deaths [2]. Despite the fact that various infectious diseases have been eliminated, new problems such as antibiotic resistance have developed [3]. In combination with investigational studies, mathematical models have importantly valuable in recognizing and analyzing host-pathogen interactions (HPI) and developing optimal treatments [4,5,6,7].

Malaria is an infectious disease caused by a pathogen called protozoa. It is a vector-borne disease caused by parasites known as Plasmodium that are transmitted to people through the bites of infected female Anopheles mosquitoes [8]. Typhoid fever is an infectious disease caused by different species of Salmonella [9]. “Most of the time, typhoid fever is caused by lack of sanitation where the disease bacteria are transmitted by ingesting contaminated food or water” World Health Organization (WHO), 2003. A mathematical model is formulated and analyzed for the dynamics of water-borne disease transmission [10]. This model is extended by introducing control intervention strategies such as vaccination, treatment, and water purification. The control model is used to determine the possible benefits of these control strategies. Furthermore, the model is proposed and analyzed for the effect of contaminated materials for the spread dynamics of COVID-19 pandemic with self-protection behavior changes [11]. It illustrates that the effects of behavioral social change towards self-protective measures are crucial to stop the transmission of the virus.

There are several mechanisms for some pathogenic organism controls, such as prevention and treatment. For example, washing your hands regularly, cleaning kitchens and bathrooms, staying home when ill, avoiding insect bites, practicing safe sex, keeping up to date with recommended vaccines, and getting medical advice. A common known preventive measure for some viral pathogens is vaccines. For instance, diseases such as measles, mumps, rubella, and influenza have vaccines, whereas diseases such as AIDS, dengue, and chikungunya do not have vaccines available [12, 13]. But, vaccination is an effective control measure against any epidemic, such as the COVID-19 pandemic [14]. According to the WHO, 133 COVID-19 vaccines were in the process during 2020 and four vaccines were approved in March 2021 by Italian and European medicine agencies [15]. Also, Anthrax and pneumococcal vaccines are the vaccines of some bacterial pathogens, but various other bacteria lack vaccines as preventive measures, but infection by such bacteria can be treated by antibiotics such as amoxicillin, ciprofloxacin, and doxycycline.

In view of the above, a nonlinear deterministic mathematical model to investigate the dynamics incorporating human pathogens in the environment and interventions with optimal control is proposed, and also their qualitative analyses using the stability theory of differential equations are established.

The paper is organized as follows. In the “Model formulation” section, we derive a mathematical model. In the “Model analysis” section, we show the details of model analysis. In the “Extension of the model into optimal control” section, we propose an optimal control problem by incorporating control variables. The obtained analytical results are shown through numerical simulations in the “Numerical simulations” section. Conclusion is presented in the “Conclusion” section.

Model formulation

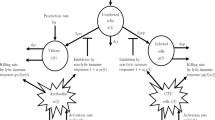
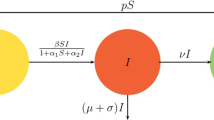
The proposed mathematical model consists of two populations: human and vector populations, with the interaction of pathogen concentration in the environmental reservoir. The total population subdivides into six compartments: susceptible human Sh(t), infected human Ih(t), recovered individuals Rh(t), susceptible vector Sv(t), infected vector Iv(t), and pathogen concentration P(t). The susceptible human is recruited into the population at rate φ. It can be infected at rate βh when it contacts with infected vector. The natural death of the human population is at a rate μh. The infected will recover to enter into the recovered compartment at a rate γ. Recovered individuals with loss of immunity at rate δ. Recruitment of vector population with rate π. The susceptible vector can be infected in two ways: through contact with pathogens from the environment at rate β1 and from infected humans at rate β2. Natural death of vector population is at rate μv. The pathogen induced by infected humans is at rate α and its death rate 𝜃. Some diseases cannot be transmitted from human to human without vectors. For instance, a vector-borne infectious disease like malaria is transmitted from human to human by a mosquito of the genus Anopheles. Based on the above assumptions, mathematical model is described by nonlinear systems of ordinary differential equations:

$$\left\{\begin{array}{l} S_{h}^{\prime} = \varphi+\delta R_{h}-\beta_{h}I_{v}S_{h}-\mu_{h} S_{h}, \\ I_{h}^{\prime} = \beta_{h}I_{v}S_{h}-(\alpha+\gamma+\mu_{h})I_{h},\\ R_{h}^{\prime} = \gamma I_{h}-(\delta+\mu_{h})R_{h} ,\\ S_{v}^{\prime} = \pi-(\beta_{1}P+\beta_{2}I_{h})S_{v}-\mu_{v}S_{v},\\ I_{v}^{\prime} = (\beta_{1}P+\beta_{2}I_{h})S_{v}-\mu_{v}I_{v},\\ P^{\prime} = \alpha I_{h}-\theta P, \end{array}\right. $$
(1)

with initial condition: Sh(0) > 0,Ih(0) ≥ 0,Rh(0) ≥ 0,Sv(0) > 0,Iv(0) ≥ 0, P(0) ≥ 0.

Model analysis

In this section, we study the invariant region, positivity of solutions, pathogen-free and coexistence equilibrium, basic reproduction number, local and global stability of equilibria, sensitivity, and bifurcation analysis of model (1).

Invariant region

Let us derive an invariant region Ω, in which the solutions of model (1) are bounded. Let N(t) = Sh(t) + Ih(t) + Rh(t) + Sv(t) + Iv(t) + P(t) be the total population. Then differentiating it both sides with respect to time t and adding the equations from the system (1), we get

$$\begin{array}{@{}rcl@{}} N^{\prime}&=&\varphi+\pi-\mu_{h} S_{h}-\mu_{h} I_{h}-\mu_{h} R_{h}-\mu_{v} S_{v}-\mu_{v} I_{v}-\theta P,\\ &\leq & \varphi+\pi-\omega N, \end{array}$$
(2)

where \(\omega =\min \left \lbrace \mu _{h}, \mu _{v}, \theta \right \rbrace\). By integrating the last inequality of Eq. (2), we obtain

$$N(t)\leq\frac{\varphi+\pi}{\omega}+ce^{-\omega t}, $$

where c is constant. As \(t\rightarrow \infty\), we obtain \(0\leq N(t)\leq \frac {\varphi +\pi }{\omega }\). Thus, the invariant region for the model (1) is given by

$${\Omega} =\left\{(S_{h}, I_{h}, S_{v}, I_{v}, R_{h}, P)\in \mathbb{R}^{6}_{+}: 0\leq S_{h}+I_{h}+S_{v}+I_{v}+R_{h}+P\leq\frac{\varphi+\pi}{\omega} \right\}$$
(3)

Therefore, the solution set is bounded and the model (1) is epidemiologically meaningful inside Ω.

Positivity of the solutions

The system (1) under study has non-negative solutions is of vital role. This will be stated as follows.

Theorem 1

Assume that the initial conditions in the model (1) holds. Then the solutions: Sh(t) > 0, Ih(t) ≥ 0, Rh(t) ≥ 0, Sv(t) > 0, Iv(t) ≥ 0 and P(t) ≥ 0 for all t ≥ 0.

Proof

From the first equation of model (1), we obtain the expression

$$S_{h}^{\prime} \geq -(\beta_{h}I_{v}(t)+\mu_{h})S_{h}(t), $$

which gives

$$S_{h}(t) \geq S_{h}(0)e^{-\int(\beta_{h}I_{v}(t)+\mu_{h})dt}. $$

By similar procedure, we show that the positivity of Ih Rh, Sv, Iv, and P so that

$$\begin{array}{@{}rcl@{}} I_{h}(t)&\geq& I_{h}(0)e^{-(\alpha+\gamma+\mu_{h})t},\\ R_{h}(t)&\geq& R_{h}(0)e^{-(\delta+\mu_{h})t},\\ S_{v}(t)&\geq& S_{v}(0)e^{-\int(\beta_{1}P(t)+\beta_{2}I_{h}(t)+\mu_{v})dt},\\ I_{v}(t)&\geq& I_{v}(0)e^{-\mu_{v} t},\\ P(t)&\geq& P(0)e^{-\theta t}. \end{array}$$

Therefore, all the solutions are non-negative for all t ≥ 0 and so the model (1) is epidemiologically meaningful and well posed in Ω.

Pathogen-free equilibrium point (PFEP)

The pathogen-free equilibrium of the model is the steady-state solution of system (1) in the absence of the pathogens. To find PFEP, \(E_{0}=\left ({S_{h}^{0}}, {I_{h}^{0}}, {R_{h}^{0}},{S_{v}^{0}}, {I_{v}^{0}}, P^{0}\right )\), we equated the left hand side of model (1) to zero, evaluating at \({I_{h}^{0}}=0, {I_{v}^{0}}=0\), P0 = 0 and solving for the non-infected state variables, we get \({S_{h}^{0}}=\varphi /\mu _{h}\) and \({S_{v}^{0}}=\pi /\mu _{v}\). Hence, PFEP is E0 = (φ/μh, 0, 0, π/μv, 0, 0).

Basic reproduction number

The basic reproduction number R0 is the average number of secondary infections caused by primary infections when all individuals are susceptible [16, 17]. To obtain the basic reproduction number, we used the next-generation matrix [18, 19]. In epidemiology, the next-generation matrix is a technique used to derive R0 for a compartmental model with multiple infectious classes discussed in [20]. The model equations are rewritten beginning with newly infective groups:

$$\left\{\begin{array}{ll} I_{h}^{\prime} &= \beta_{h}I_{v}S_{h}-(\alpha+\gamma+\mu_{h})I_{h},\\ I_{v}^{\prime}& = (\beta_{1}P+\beta_{2}I_{h})S_{v}-\mu_{v}I_{v},\\ P^{\prime} &=\alpha I_{h}-\theta P. \end{array}\right. $$
(4)

The right-hand side of Eq. (4) is decomposed as u − v with

$$u = \left[\begin{array}{cc} \beta_{h}I_{v}S_{h} \\ (\beta_{1}P+\beta_{2}I_{h})S_{v}\\ 0 \end{array}\right] , ~~~ v = \left[\begin{array}{cc} (\alpha+\gamma+\mu_{h})I_{h}\\ \mu_{v}I_{v}\\ -\alpha I_{h}+\theta P \end{array}\right]. $$

Next, by linearization approach, the associated matrices of u and v at E0 are given by

$$U = \left[\begin{array}{ccc} 0 & \frac{\beta_{h}\varphi}{\mu_{h}} &0\\ \frac{\beta_{2}\pi}{\mu_{v}} & 0 & \frac{\beta_{1}\pi}{\mu_{v}}\\ 0 & 0 & 0 \end{array}\right], ~~~ V = \left[\begin{array}{ccc} \alpha+\gamma+\mu_{h} & 0 & 0\\ 0 & \mu_{v} & 0\\ -\alpha & 0 & \theta \end{array}\right]. $$

Then V is an invertible and its inverse is given by

$$V^{-1} = \left[\begin{array}{ccc} \frac{1}{\alpha+\gamma+\mu_{h}} & 0 & 0\\ 0 & \frac{1}{\mu_{v}} & 0\\ \frac{\alpha}{(\alpha+\gamma+\mu_{h})\theta} & 0 & \frac{1}{\theta} \end{array}\right] . $$

The product of U and V− 1 can be computed as follows.

$$UV^{-1} = \left[\begin{array}{ccc} 0 & \frac{\varphi\beta_{h}}{\mu_{h}\mu_{v}}&0\\ \frac{\pi\beta_{2}}{\mu_{v}(\alpha+\gamma+\mu_{h})}+\frac{\pi\alpha\beta_{1}}{\theta\mu_{v}(\alpha+\gamma+\mu_{h})} & 0 & \frac{\pi\beta_{1}}{\theta\mu_{v}} \\ 0 & 0 &0 \end{array}\right]. $$

Since the basic reproduction number R0 is the dominant eigenvalue of the matrix UV− 1, then we obtain

$$R_{0}=\sqrt{\frac{\pi\varphi\beta_{h}(\alpha\beta_{1}+\theta\beta_{2})}{\theta\mu_{h}{\mu_{v}^{2}}(\alpha+\gamma+\mu_{h})}}. $$

Sensitivity of the basic reproduction number

In this section, we investigate sensitivity analysis of basic reproduction number R0 with respect to the main parameters. This help us to check and classify parameters which extremely affect R0 and thus determine an appropriate parameter values to minimize disease from human population. To do this, we follow similar method presented in [21,22,23].

Definition 1

The definition of normalized forward sensitivity indices of R0 with respect to g is given by

$$\begin{array}{c} {\Delta}^{R_{0}}_{g}=\frac{\partial R_{0}}{\partial g}\times \frac{g}{R_{0}}, \end{array}$$
(5)

where R0 is a given variable, g is differentiable parameter.

By applying the definition from Eq. (5), normalized forward sensitivity index of R0 is computed as follows.

$$\begin{array}{@{}rcl@{}} {\Delta}^{R_{0}}_{\varphi}&=&\frac{1}{2}>0\\ {\Delta}^{R_{0}}_{\beta_{h}}&=&\frac{1}{2}>0\\ {\Delta}^{R_{0}}_{\pi}&=&\frac{1}{2}>0\\ {\Delta}^{R_{0}}_{\beta_{1}}&=&\frac{\alpha\beta_{1}}{2\alpha\beta_{1}+2\theta\beta_{2}}>0\\ {\Delta}^{R_{0}}_{\beta_{2}}&=&\frac{\theta\beta_{2}}{2\alpha\beta_{1}+2\theta\beta_{2}}>0\\ {\Delta}^{R_{0}}_{\alpha}&=&\frac{1}{2}\alpha\left(\frac{\beta_{1}}{\alpha\beta_{1}+\theta\beta_{2}}-\frac{1}{\alpha+\gamma+\mu_{h}} \right) >0\\ {\Delta}^{R_{0}}_{\theta}&=&-\frac{\alpha\beta_{1}}{2\alpha\beta_{1}+2\theta\beta_{2}}<0\\ {\Delta}^{R_{0}}_{\mu_{h}}&=&-1+\frac{\alpha+\gamma}{2(\alpha+\gamma+\mu_{h})}<0\\ {\Delta}^{R_{0}}_{\mu_{v}}&=&-1<0\\ {\Delta}^{R_{0}}_{\gamma}&=&-\frac{\gamma}{2(\alpha+\gamma+\mu_{h})}<0 \end{array}$$

The sensitivity indices of R0 at parameter values are given in Table 1.

Table 1 Sensitivity indices and parameters
Full size table

The implication of the main parameters with positive sensitivity index is that R0 is an increasing (or decreasing) function with respect to an increase (or decrease) in these parameter values. The parameters with negative sensitivity indices, on the other hand, lead to an increase (or decrease) in R0 value when they are decreased (or increased).

From Table 1, those parameters that have positive indices (φ, βh, π, β1, β2, α) show that they have great impact on expanding the disease in the community if their values are increasing. However, those parameters in which their sensitivity indices are negative (𝜃, μh,μv, γ) have an effect of reducing pathogens from human population with values increase. Hence, we can eliminate the decrease from human population by decreasing the values of φ, βh, π, β1, and β2, the same time, by increasing the values of α, 𝜃, μh,μv, and γ. The bar diagram of the sensitivity indices in Table 1 is depicted in Fig. 1.

Fig. 1
figure 1

Normalized sensitivity indices of \(\mathcal {R}_{0}\) with respect to parameters of the model (1). Parameter values are taken from Table 2

Full size image
Table 2 Description of model parameters and their values
Full size table

Local stability of pathogen-free equilibrium

In this section, we investigate the local stability of pathogen free equilibrium E0 based on the basic reproduction number R0.

Theorem 2

If R0 < 1, then pathogen-free equilibrium E0 = (φ/μh, 0, 0, π/μv, 0, 0) of the model (1) is locally asymptotically stable, and otherwise it is unstable in Ω.

Proof

By linearizion approach, Jacobian matrix of model (1) at equilibria is given by

$$J=\left[\begin{array}{cccccc} -(\beta_{h}I_{v}+\mu_{h})& 0 & \delta & 0 &-\beta_{h}S_{h} & 0 \\ \beta_{h}I_{v}& -(\alpha+\gamma+\mu_{h}) & 0 & 0 &\beta_{h}S_{h} & 0 \\ 0 & \gamma & -(\delta+\mu_{h}) & 0 & 0 & 0\\ 0 & -\beta_{2}S_{v} & 0 & -(\beta_{1}P+\beta_{2}I_{h}+\mu_{v}) & 0 & -\beta_{1}S_{v}\\ 0 & \beta_{2}S_{v} & 0 & \beta_{1}P+\beta_{2}I_{h} & -\mu_{v} & \beta_{1}S_{v}\\ 0 & \alpha & 0 & 0 & 0 & -\theta \end{array}\right]. $$
(6)

The Jacobian matrix J at pathogen-free equilibrium E0 becomes

$$J(E_{0})=\left[\begin{array}{cccccc} -\mu_{h}& 0 & \delta & 0 &-\frac{\varphi\beta_{h}}{\mu_{h}} & 0 \\ 0& -(\alpha+\gamma+\mu_{h}) & 0 & 0 &\frac{\varphi\beta_{h}}{\mu_{h}} & 0 \\ 0 & \gamma & -(\delta+\mu_{h}) & 0 & 0 & 0\\ 0 & -\frac{\pi\beta_{2}}{\mu_{v}} & 0 & -\mu_{v} & 0 & -\frac{\pi\beta_{1}}{\mu_{v}}\\ 0 & \frac{\pi\beta_{2}}{\mu_{v}} & 0 & 0 & -\mu_{v} & \frac{\pi\beta_{1}}{\mu_{v}}\\ 0 & \alpha & 0 & 0 & 0 & -\theta \end{array}\right]. $$
(7)

It is clear by considering the first and fourth column eigenvalues are always negative (i.e., − μh < 0, − μv < 0), and so stability is controlled by the Jacobian corresponding to the Ih,Rh,Iv and P components:

$$J^{*}= \left[\begin{array}{cccc} -(\alpha+\gamma+\mu_{h}) & 0 &\frac{\varphi\beta_{h}}{\mu_{h}} & 0 \\ \gamma & -(\delta+\mu_{h}) & 0 & 0\\ \frac{\pi\beta_{2}}{\mu_{v}} & 0 & -\mu_{v} & \frac{\pi\beta_{1}}{\mu_{v}}\\ \alpha & 0 & 0 & -\theta \end{array}\right]. $$
(8)

The characteristic polynomial of Eq. (8) is given by

$$(\lambda+\delta+\mu_{h})\left(\lambda^{2}+\frac{\mu_{h}\mu_{v}(\theta+\mu_{v})(\alpha+\gamma+\mu_{h})-\pi\varphi\beta_{2}\beta_{h}}{\mu_{h}\mu_{v}(\alpha+\gamma+\mu_{h})}\lambda+\frac{\theta\mu_{h}{\mu_{v}^{2}}(\alpha+\gamma+\mu_{h})-\pi\varphi\beta_{h}}{\mu_{h}\mu_{v}(\alpha+\gamma+\mu_{h})}\right) =0$$
(9)

Next, we obtain λ = −(λ + δ) < 0, and the other characteristic equation becomes:

$$\lambda^{2}+a_{1}\lambda+a_{0}=0, $$
(10)

where

$$\begin{array}{@{}rcl@{}} a_{1}&=&\frac{\mu_{h}\mu_{v}(\theta+\mu_{v})(\alpha+\gamma+\mu_{h})-\pi\varphi\beta_{2}\beta_{h}}{\mu_{h}\mu_{v}(\alpha+\gamma+\mu_{h})},\\ a_{0}&=&\frac{\theta\mu_{h}{\mu_{v}^{2}}(\alpha+\gamma+\mu_{h})-\pi\varphi\beta_{h}}{\mu_{h}\mu_{v}(\alpha+\gamma+\mu_{h})}. \end{array}$$

The characteristic polynomial in Eq. (10) is degree n = 2, then we can find matrices:

$$M1= \left[\begin{array}{c} a_{n-1} \end{array}\right] = \left[\begin{array}{c} a_{1} \end{array}\right],\quad M2= \left[\begin{array}{cc} a_{n-1}&a_{n-3}\\ 1&a_{n-2} \end{array}\right] = \left[\begin{array}{cc} a_{1}&0\\ 1&a_{0} \end{array}\right]. $$

Applying Routh-Hurwitz criterion [24] on Eq. (10) shows that the two eigenvalues have negative real part, and so E0 is local asymptotically stable if a0 > 0,a1 and a1a0 > 0 for R0 < 1.

Global stability of pathogen-free equilibrium

Theorem 3

If R0 < 1, then the pathogen-free equilibrium E0 = (φ/μh,0,0,π/μv,0,0) of the model (1) is globally asymptotically stable in Ω.

Proof

To perform the global stability of E0, we consider Lyapunov function:

$$V=I_{h}+R_{h}+P. $$
(11)

The Lyapunov function V needs to satisfy the conditions: V (Sh,Ih,Rh,Sv,Iv,P) > 0 for all (Sh,Ih,Rh,Sv,Iv,P) / \(\left \lbrace E_{0}\right \rbrace\) and V (E0) = 0. By differentiating V with respect to t, we get

$$\begin{array}{@{}rcl@{}} V^{\prime}&=&I_{h}^{\prime}+I_{v}^{\prime}+P^{\prime}\\ &=&\left(\frac{\pi\beta_{2}}{\mu_{v}}-\gamma-\mu_{h}\right) I_{h}+\left(\frac{\varphi\beta_{h}}{\mu_{h}}-\mu_{v}\right) I_{v}+\left(\frac{\pi\beta_{1}}{\mu_{v}}-\theta\right) P\\ &=&(K-Q) \left[\begin{array}{c} I_{h} \\ I_{v} \\ P \end{array}\right] -\left[\begin{array}{ccc} \gamma& 0 & 0 \\ 0 & 0 & 0 \\ 0& 0 & 0 \end{array}\right] \left[\begin{array}{c} I_{h} \\ I_{v} \\ P \end{array}\right], \end{array}$$
(12)

where the matrices K and Q are given by

$$K = \left[\begin{array}{ccc} \frac{\pi\beta_{2}}{\mu_{v}} & 0 & 0 \\ 0 & \frac{\varphi\beta_{h}}{\mu_{h}} & 0 \\ 0 & 0 & \frac{\pi\beta_{1}}{\mu_{v}} \end{array}\right],~~ Q = \left[\begin{array}{ccc} \mu_{h} & 0 & 0 \\ 0 & \mu_{v} & 0 \\ 0 & 0 & \theta \end{array}\right]. $$

Since γ > 0, then the last inequality of Eq. (12) can be rewritten as

$$V^{\prime} \leq(K-Q) \left[\begin{array}{cc} I_{h} \\ I_{v} \\ P \end{array}\right]. $$
(13)

The eigenvalues of matrix (K − Q) all have negative real parts if πβ2/μv < μh, φβh/μh < μv and πβ1/μv < 𝜃. Equation (13) is stable only if R0 < 1. As a result, \((I_{h}, I_{v}, P) \rightarrow (0,~0,~0)\) as \(t\rightarrow \infty\). It follows by the comparison approach from [25] that \((I_{h}, I_{v}, P) \rightarrow (0,~0,~0)\). Therefore, \((S_{h}, I_{h}, R_{h}, S_{v}, I_{v}, P)\rightarrow (\varphi /\mu _{h}, 0, 0, \pi /\mu _{v}, 0, 0)\) as t approaches infinity, and E0 is globally asymptotically stable for R0 < 1 in Ω.

Coexistence equilibrium point (CEP)

We consider a situation in which pathogen persist in the human populations. A coexistence equilibrium point \(E^{*}=(S_{h}^{*}, I_{h}^{*}, R_{h}^{*},S_{v}^{*}, I_{v}^{*}, P^{*})\) can be computed as follow.

$$\begin{array}{@{}rcl@{}} \varphi+\delta R_{h}^{*}-\beta_{h}I_{v}^{*}S_{h}^{*}-\mu_{h} S_{h}^{*}&=&0, \\ \beta_{h}I_{v}^{*}S_{h}^{*}-(\alpha+\gamma+\mu_{h})I_{h}^{*}&=&0,\\ \gamma I_{h}^{*}-(\delta+\mu_{h})R_{h}^{*}&=&0,\\ \pi-(\beta_{1}P^{*}+\beta_{2}I_{h}^{*})S_{v}^{*}-\mu_{v}S_{v}^{*}&=&0,\\ (\beta_{1}P^{*}+\beta_{2}I_{h}^{*})S_{v}^{*}-\mu_{v}I_{v}^{*}&=&0,\\ \alpha I_{h}^{*}-\theta P^{*}&=&0. \end{array}$$
(14)

Solving Eq. (14), we obtain \(S_{h}^{*}, R_{h}^{*}, S_{v}^{*}, I_{v}^{*}\), and P∗ in terms of \(I_{h}^{*}\):

$$\begin{array}{@{}rcl@{}} S_{h}^{*}&=&\frac{\varphi}{\mu_{h}}-\left(\frac{\delta(\alpha+\mu_{h})+\mu_{h}(\alpha+\gamma+\mu_{h})}{\mu_{h}(\delta+\mu_{h})}\right) I_{h}^{*}, \\ R_{h}^{*}&=&\frac{\gamma}{\delta+\mu_{h}}I_{h}^{*},\\ S_{v}^{*}&=&\frac{\pi\theta\mu_{v}}{\mu_{v}(\alpha\beta_{1}+\theta\beta_{2})I_{h}^{*}+{\theta\mu_{v}^{2}}}, \\ I_{v}^{*}&=&\frac{\pi(\alpha\beta_{1}+\theta\beta_{2})I_{h}^{*}}{\mu_{v}(\alpha\beta_{1}+\theta\beta_{2})I_{h}^{*}+{\theta\mu_{v}^{2}}}, \\ P^{*}&=&\frac{\alpha}{\theta}I_{h}^{*}, \end{array}$$
(15)

where

$$I_{h}^{*}=\frac{\theta\mu_{h}{\mu_{v}^{2}}(\delta+\mu_{h})(\theta\mu_{h}{\mu_{v}^{2}}(\alpha+\gamma+\mu_{h}){R_{0}^{4}}-\pi\varphi\beta_{h}(\alpha\beta_{1}+\theta\beta_{2}))}{(\pi^{2}{\beta_{h}^{2}}\varphi(\delta+\mu_{h})(\alpha\beta_{1}+\theta\beta_{2})-\theta\mu_{h}{\mu_{v}^{2}}\pi\gamma\delta\beta_{h}{R_{0}^{2}}+\pi\varphi\beta_{h}\mu_{v}(\delta+\mu_{h})(\alpha\beta_{1}+\theta\beta_{2}))(\alpha\beta_{1}+\theta\beta_{2})}. $$

Local stability of coexistence equilibrium

Theorem 4

If R0 > 1, then the coexistence equilibrium point E∗ of model (1) is locally asymptotically stable, and otherwise it is unstable in Ω.

Proof

From Eq. (6) the Jacobian matrix J at \(E^{*}=(S_{h}^{*}, I_{h}^{*}, R_{h}^{*}, S_{v}^{*}, I_{v}^{*}, P^{*})\) is given by

$$J(E^{*})= \left[\begin{array}{cccccc} -(\beta_{h}I_{v}^{*}+\mu_{h})& 0 & \delta & 0 &-\beta_{h}S_{h}^{*} & 0 \\ \beta_{h}I_{v}^{*}& -(\alpha+\gamma+\mu_{h}) & 0 & 0 &\beta_{h}S_{h}^{*} & 0 \\ 0 & \gamma & -(\delta+\mu_{h}) & 0 & 0 & 0\\ 0 & -\beta_{2}S_{v}^{*} & 0 & -(\beta_{1}P^{*}+\beta_{2}I_{h}^{*}+\mu_{v}) & 0 & -\beta_{1}S_{v}^{*}\\ 0 & \beta_{2}S_{v}^{*} & 0 & \beta_{1}P^{*}+\beta_{2}I_{h}^{*} & -\mu_{v} & \beta_{1}S_{v}^{*}\\ 0 & \alpha & 0 & 0 & 0 & -\theta \end{array}\right]. $$
(16)

The eigenvalues of matrix (16) are computed from the following equation.

$$\begin{array}{@{}rcl@{}} \left|\begin{array}{cccccc} b_{11}-\lambda& 0 & b_{13} & 0 &b_{15} & 0 \\ b_{21}& b_{22}-\lambda & 0 & 0 &b_{25} & 0 \\ 0 & b_{32} & b_{33}-\lambda & 0 & 0 & 0\\ 0 & b_{42} & 0 & b_{44}-\lambda & 0 & b_{46}\\ 0 & b_{52} & 0 & b_{54} & b_{55}-\lambda & b_{56}\\ 0 & b_{62} & 0 & 0 & 0 & b_{66}-\lambda \end{array}\right| =0 \end{array}$$
(17)

where \(b_{11}= -(\beta _{h}I_{v}^{*}+\mu _{h}),~b_{13}=\delta ,~b_{15}=-\beta _{h}S_{h}^{*},~b_{21}=\beta _{h}I_{v}^{*},~b_{22}=-(\alpha +\gamma +\mu _{h}),~b_{25}=\beta _{h}S_{h}^{*},~b_{31}=\gamma , \) \(b_{33}=-(\delta +\mu _{h}),~b_{42}=-\beta _{2}S_{v}^{*},~b_{44}=-(\beta _{1}P^{*}+\beta _{2}I_{h}^{*}+\mu _{v}),~ b_{46}=-\beta _{1}S_{v}^{*},~b_{52}=\beta _{2}S_{v}^{*},~b_{54}=\beta _{1}P^{*}+\beta _{2}I_{h}^{*},~b_{55}=-\mu _{v},~b_{56}=\beta _{1}S_{v}^{*},~b_{62}=\alpha ,~b_{66}=\theta \).

Then the characteristic polynomial of Eq. (16) is given by

$$\lambda^{6}+B_{1}\lambda^{5}+B_{2}\lambda^{4}+B_{3}\lambda^{3}+B_{4}\lambda^{2}+B_{5}\lambda+B_{6}=0, $$
(18)

where

$$\begin{array}{@{}rcl@{}} B_{1}&=&-(b_{11}+b_{22}+b_{33}+b_{44}+b_{55}+b_{66}),\\ B_{2}&=&-b_{22}(b_{33}+b_{44}+b_{55}+b_{66})-b_{66}(b_{44}+b_{55})-b_{33}b_{66}-b_{11}(b_{22}+b_{33}+b_{44}\\&&+b_{55}+b_{66})+b_{33}b_{44}-b_{25}b_{52}+b_{46}b_{54}+b_{33}b_{55}+b_{44}b_{55},\\ B_{3}&=&b_{22}(b_{44}b_{55}-b_{46}b_{54}+b_{66}(b_{44}+b_{55}))+b_{22}b_{33}(b_{44}+b_{55}+b_{66})+b_{66}(b_{44}b_{55}\\&&-b_{25}b_{52}-b_{46}b_{54})+b_{33}b_{66}(b_{44}+b_{55})-b_{11}(b_{46}b_{54}+b_{25}b_{52}-b_{55}b_{66}\\&&-b_{44}(b_{55}+b_{66})-b_{22}b_{44}+b_{22}b_{55}+b_{22}b_{66}-b_{33}(b_{22}+b_{44}+b_{55}+b_{66}))\\&&-(b_{13}b_{21}b_{32}+b_{15}b_{21}b_{52}-b_{25}b_{33}b_{52}-b_{25}b_{44}b_{52}+b_{25}b_{42}b_{54}-b_{33}b_{46}b_{54}\\&&+b_{33}b_{44}b_{55}+b_{25}b_{56}b_{62}),\\ B_{4}&=&-(b_{22}b_{66}(b_{44}b_{55}-b_{46}b_{54})+b_{22}b_{33}(b_{44}b_{55}-b_{46}b_{54}+b_{66}(b_{44}+b_{55})))\\&&-b_{66}b_{13}b_{21}b_{32}+b_{66}(b_{15}b_{21}b_{52}-b_{44}b_{25}b_{52}+b_{25}b_{42}b_{54})+b_{33}b_{66}(b_{44}b_{55}\\&&-b_{25}b_{52}-b_{46}b_{54})+b_{11}(b_{25}b_{42}b_{54}+b_{25}b_{56}b_{62}-b_{66}(b_{25}b_{52}+b_{46}b_{54})\\&&+b_{44}(b_{25}b_{52}-b_{52}b_{66})-b_{22}b_{46}b_{54}+b_{22}b_{44}b_{55}+b_{66}(b_{22}b_{44}+b_{22}b_{55})\\&&-b_{33}(b_{46}b_{54}+b_{25}b_{52}-b_{55}b_{66}-b_{44}(b_{55}+b_{66})-b_{22}b_{44}+b_{22}b_{55}+b_{22}b_{66}))\\&&-b_{13}b_{21}b_{32}b_{44}-b_{15}b_{21}b_{33}b_{52}-b_{15}b_{21}b_{44}b_{52}-b_{25}b_{33}b_{44}b_{52}+b_{15}b_{21}b_{42}b_{54}\\&&-b_{25}b_{33}b_{42}b_{54}-b_{13}b_{21}b_{32}b_{55}+b_{15}b_{21}b_{56}b_{62}-b_{15}b_{33}b_{56}b_{62}-b_{25}b_{44}b_{56}b_{62},\\ B_{5}&=&-[b_{22}b_{33}b_{66}(b_{44}b_{55}-b_{46}b_{54})+b_{66}b_{13}b_{21}b_{32}(b_{44}+b_{55})+b_{66}(b_{15}b_{21}b_{42}b_{54}\\&&-b_{44}b_{15}b_{21}b_{52})-b_{33}b_{66}(b_{15}b_{21}b_{52}-b_{44}b_{25}b_{52}+b_{25}b_{42}b_{54})-b_{11}(b_{66}b_{25}b_{42}b_{54}\\&&+b_{44}(b_{25}b_{56}b_{62}-b_{25}b_{52}b_{66})+b_{66}(b_{22}b_{44}+b_{22}b_{55}))+b_{15}b_{21}b_{33}b_{44}b_{52}\\&&-b_{15}b_{21}b_{33}b_{42}b_{54}-b_{13}b_{21}b_{32}b_{44}b_{55}+b_{13}b_{21}b_{44}b_{55}-b_{15}b_{21}b_{33}b_{44}b_{62}\\&&+b_{25}b_{33}b_{44}b_{56}b_{62}],\\ B_{6}&=&-[b_{66}b_{13}b_{21}b_{32}(b_{46}b_{54}-b_{44}b_{55})-b_{33}b_{66}(b_{15}b_{21}b_{42}-b_{44}b_{15}b_{21}b_{52})\\&&+b_{11}b_{33}(b_{66}b_{25}b_{42}b_{54}+b_{44}(b_{25}b_{56}b_{52}-b_{25}b_{52}b_{66}))-b_{15}b_{21}b_{33}b_{44}b_{56}b_{62}]. \end{array}$$

Using the Routh-Hurwitz criterion [24], the coexistence equilibrium E∗ is locally asymptotically stable for R0 > 1 if Bi > 0, i = 1,2,⋅,6,

$$\begin{array}{@{}rcl@{}} &&B_{1}>0,~~ B_{1}B_{2}-B_{3}>0,~~ B_{1}(B_{2}B_{3}-B_{1}B_{4})-{B_{3}^{2}}+B_{5}B_{1}>0,\\ &&B_{1}B_{2}(B_{3}B_{4}-B_{2}B_{5})-{B_{1}^{2}}({B_{4}^{2}}-B_{2}B_{6})+B_{1}(B_{4}B_{5}-B_{3}B_{6})-B_{5}+B_{4}({B_{3}^{2}}-B_{1}B_{5})>0,\\&&B_{1}B_{6}B_{2}(B_{3}B_{4}-B_{1}B_{5})-B_{1}B_{6}({B_{4}^{2}}-B_{1}B_{6})-B_{1}B_{5}B_{2}(B_{3}B_{4}-B_{2}B_{5})+{B_{1}^{2}}B_{5}({B_{4}^{2}}-\\&&B_{2}B_{6})-B_{1}B_{5}(B_{4}B_{5}-B_{3}B_{6})-B_{6}B_{3}(B_{3}B_{4}-B_{1}B_{5})+B_{6}B_{1}B_{3}B_{5}+B_{5}B_{3}({B_{4}^{2}}-B_{2}B_{5})-{B_{5}^{2}}(B_{1}B_{4}-B_{5})>0,\\&&B_{1}{B_{6}^{2}}B_{2}({B_{3}^{2}}-B_{1}B_{5})-{B_{1}^{2}}{B_{6}^{2}}(B_{3}B_{4}-B_{2}B_{5})+{B_{1}^{2}}B_{5}B_{6}({B_{4}^{2}}-B_{2}B_{6})-B_{1}B_{5}B_{6}(B_{4}B_{5}-B_{3}B_{6})-\\&&{B_{6}^{2}}B_{3}({B_{3}^{2}}-B_{1}B_{5})+{B_{6}^{2}}B_{1}B_{3}B_{5}+B_{5}B_{6}B_{3}(B_{3}B_{4}-B_{2}B_{3})-B_{5}B_{6}B_{1}B_{4}B_{5}+{B_{5}^{2}}B_{6}>0. \end{array}$$

Global stability of coexistence equilibrium

Theorem 5

If R0 > 1, then the coexistence equilibrium E∗ of the model (1) is globally asymptotically stable in Ω.

Proof

To establish the global stability of the coexistence equilibrium point E∗=\((S_{h}^{*}, I_{h}^{*}, R_{h}^{*},S_{v}^{*}, I_{v}^{*}, P^{*})\), we consider Lyapunov function:

$$V=\epsilon_{1}\frac{(S_{h}-S_{h}^{*})^{2}}{2}+\epsilon_{2}\frac{(I_{h}-I_{h}^{*})^{2}}{2}+\epsilon_{3}\frac{(R_{h}-R_{h}^{*})^{2}}{2}+\epsilon_{4}\frac{(S_{v}-S_{v}^{*})^{2}}{2}+\epsilon_{5}\frac{(I_{v}-I_{v}^{*})^{2}}{2}+\epsilon_{6}\frac{(P-P^{*})^{2}}{2}, $$
(19)

where 𝜖1, 𝜖2, 𝜖3, 𝜖4, 𝜖5, 𝜖6 > 0 are to be chosen appropriately such that

$$\begin{array}{@{}rcl@{}} \epsilon_{1}&=&\frac{S_{h}}{(\beta_{h}I_{v}+\mu_{h})S_{h}-\varphi -\delta R_{h}},\\ \epsilon_{2}&=&\frac{I_{h}}{(\alpha+\gamma+\mu_{h})I_{h}-\beta_{h}I_{v}S_{h}} ,\\ \epsilon_{3}&=&\frac{R_{h}}{(\delta+\mu_{h})R_{h}-\gamma I_{h}},\\ \epsilon_{4}&=&\frac{S_{v}}{(\beta_{1}P+\beta_{2}I_{h}+\mu_{v})S_{v}-\pi},\\ \epsilon_{5}&=&\frac{I_{v}}{\mu_{v}I_{v}-(\beta_{1}P+\beta_{2}I_{h})S_{v}},\\ \epsilon_{6}&=&\frac{P}{\theta P-\alpha I_{h}}. \end{array}$$

The Lyapunov function V needs to satisfy the conditions: V (Sh,Ih,R,Sv,Iv,P) > 0 for all (Sh,Ih,R,Sv,Iv,P) / \(\left \lbrace E^{*}\right \rbrace\) and V (E∗) = 0. Applying derivative of V with respect to t, we find that

$$V^{\prime} =(S_{h}-S_{h}^{*})S_{h}^{\prime}+(I_{h}-I_{h}^{*})I_{h}^{\prime}+(R_{h}-R_{h}^{*})R_{h}^{\prime}+S_{v}-S_{v}^{*})S_{v}^{\prime}+(I_{v}-I_{v}^{*})I_{v}^{\prime}+(P-P^{*})P^{\prime}$$
(20)

By substituting corresponding equations of the model (1) into Eq. (20), we obtain that

$$\begin{array}{@{}rcl@{}} V^{\prime}&=&\epsilon_{1}(S_{h}-S_{h}^{*})[ \varphi+\delta R_{h}-\beta_{h}I_{v}S_{h}-\mu_{h} S_{h}]+\epsilon_{2}(I_{h}-I_{h}^{*})[\beta_{h}I_{v}S_{h}-(\alpha+\gamma+\mu_{h})I_{h}]\\&+&\epsilon_{3}(R_{h}-R_{h}^{*})[\gamma I_{h}-(\delta+\mu_{h})R_{h}]+\epsilon_{4}(I_{v}-I_{v}^{*})[\pi-(\beta_{1}P+\beta_{2}I_{h})S_{v}-\mu_{v}S_{v}]\\&+&\epsilon_{5}(R_{h}-R_{h}^{*})[(\beta_{1}P+\beta_{2}I_{h})S_{v}-\mu_{v}I_{v}]+\epsilon_{6}(P-P^{*})[\alpha I_{h}-\theta P]. \end{array}$$

Next, rearranging this equation, we obtain

$$\begin{array}{@{}rcl@{}} V^{\prime}&=&\epsilon_{1}(S_{h}-S_{h}^{*})\left\lbrace \frac{\varphi}{S_{h}}+\frac{\delta R_{h}}{S_{h}}-\beta_{h}I_{v}-\mu_{h}\right\rbrace \left\{S_{h}-S_{h}^{*}\right\}+\epsilon_{2}(I_{h}-I_{h}^{*})\left\{\frac{\beta_{h}I_{v}S_{h}}{I_{h}}-\alpha-\gamma-\mu_{h}\right\}\left\{I_{h}-I_{h}^{*}\right\} \\&+&\epsilon_{3}(R_{h}-R_{h}^{*})\left\{\frac{\gamma I_{h}}{R_{h}}-\delta-\mu_{h}\right\}\left\{R_{h}-R_{h}^{*} \right\}+\epsilon_{4}(S_{v}-S_{v}^{*})\left\lbrace \frac{\pi}{S_{v}}-\beta_{1}P-\beta_{2}I_{h}-\mu_{v}\right\rbrace \left\{S_{v}-S_{v}^{*}\right\}\\&+&\epsilon_{5}(I_{v}-I_{v}^{*})\left\{\frac{(\beta_{1}P+\beta_{2}I_{h})S_{v}}{I_{v}}-\mu_{v}\right\}\left\{I_{v}-I_{v}^{*}\right\}+\epsilon_{6}(P-P^{*})\left\{\frac{\alpha I_{h}}{P}-\theta\right\}\left\{P-P^{*} \right\},\\ &=&-\epsilon_{1}(S_{h}-S_{h}^{*})^{2}[ -\frac{\varphi}{S_{h}}-\frac{\delta R_{h}}{S_{h}}+\beta_{h}I_{v}+\mu_{h}] -\epsilon_{2}(I_{h}-I_{h}^{*})^{2}[-\frac{\beta_{h}I_{v}S_{h}}{I_{h}}+\alpha+\gamma+\mu_{h}] \\&-&\epsilon_{3}(R_{h}-R_{h}^{*})^{2}[-\frac{\gamma I_{h}}{R_{h}}+\delta+\mu_{h}]-\epsilon_{4}(S_{v}-S_{v}^{*})^{2}[ -\frac{\pi}{S_{v}}+\beta_{1}P+\beta_{2}I_{h}+\mu_{v}]\\&-&\epsilon_{5}(I_{v}-I_{v}^{*})^{2}[-\frac{(\beta_{1}P+\beta_{2}I_{h})S_{v}}{I_{v}}+\mu_{v}]-\epsilon_{6}(P-P^{*})^{2}[-\frac{\alpha I_{h}}{P}+\theta]. \end{array}$$

Thus, \(V^{\prime }(S_{h}, I_{h}, R, S_{v}, I_{v}, P)\leq 0\) and a coexistence equilibrium point E∗ is globally asymptotically stable with possible setting 𝜖1, 𝜖2, 𝜖3, 𝜖4, 𝜖5, 𝜖6. Hence, the maximum compact invariant set in \(\left \{(S_{h}, I_{h}, R, S_{v}, I_{v}, P)\in {\Omega }: V^{\prime }=0\right \}\) is the singleton E∗. Therefore, by LaSalle’s invariant principle [26], as \(t\rightarrow \infty\), all the solutions of the system (1) approaches E∗ in Ω for R0 > 1.

Backward bifurcation analysis

We investigated the existence of bifurcation analysis at R0 = 1 by the concept of center manifold theory [27]. Then the next theorem can be obtained.

Theorem 6

If R0 < 1, then the model (1) shows that backward bifurcation at R0 = 1.

Proof

Using center manifold theory [27], we perform back bifurcation analysis of system (1) at R0 = 1. Let us consider change of variables: Sh = x1, Ih = x2, Rh = x3, Sv = x4, Iv = x5, P = x6. Then the model (1) can be rewritten in the form \(X^{\prime }=(f_{1},~f_{2},~f_{3},~f_{4},f_{5},~f_{6})^{T}\) as:

$$\left\{\begin{array}{l} x_{1}^{\prime} = \varphi+\delta x_{3}-\beta_{h}x_{5}x_{1}-\mu_{h} x_{1}, \\ x_{2}^{\prime} = \beta_{h}x_{5}x_{1}-(\alpha+\gamma+\mu_{h})x_{2},\\ x_{3}^{\prime} = \gamma x_{2}-(\delta+\mu_{h})x_{3} ,\\ x_{4}^{\prime} = \pi-(\beta_{1}x_{6}+\beta_{2}x_{2})x_{4}-\mu_{v}x_{4},\\ x_{5}^{\prime} = (\beta_{1}x_{6}+\beta_{2}x_{2})x_{4}-\mu_{v}x_{5},\\ x_{6}^{\prime}= \alpha x_{2}-\theta x_{6}, \end{array}\right. $$
(21)

Let us use the contact rate βh as bifurcation coefficient at R0 = 1 if

$$\beta_{h}=\beta_{h}^{*}=\frac{\theta\mu_{h}{\mu_{v}^{2}}(\alpha+\gamma+\mu_{h})}{\pi\varphi(\alpha\beta_{1}+\theta\beta_{2})}. $$
(22)

By linearization method, Jacobian matrix of (21) at pathogen-free equilibrium E0 is obtained:

$$J(E_{0})= \left[\begin{array}{cccccc} -\mu_{h}& 0 & \delta & 0 &-\frac{\varphi\beta_{h}^{*}}{\mu_{h}} & 0 \\ 0& -(\alpha+\gamma+\mu_{h}) & 0 & 0 &\frac{\varphi\beta_{h}^{*}}{\mu_{h}} & 0 \\ 0 & \gamma & -(\delta+\mu_{h}) & 0 & 0 & 0\\ 0 & -\frac{\pi\beta_{2}}{\mu_{v}} & 0 & -\mu_{v} & 0 & -\frac{\pi\beta_{1}}{\mu_{v}}\\ 0 & \frac{\pi\beta_{2}}{\mu_{v}} & 0 & 0 & -\mu_{v} & \frac{\pi\beta_{1}}{\mu_{v}}\\ 0 & \alpha & 0 & 0 & 0 & -\theta \end{array}\right]. $$
(23)

The right eigenvector, u = (u1, u2, u3, u4, u5, u6)T are computed from Ju = 0 as follows.

$$Ju= \left\{\begin{array}{rrrrrr} -\mu_{h}u_{1}+\delta u_{3}-\frac{\varphi\beta_{h}^{*}}{\mu_{h}}u_{5}=0\\ -(\alpha+\gamma+\mu_{h}) u_{2}+\frac{\varphi\beta_{h}^{*}}{\mu_{h}}u_{5}=0,\\ \gamma u_{2}-(\delta+\mu_{h})u_{3}=0,\\ -\frac{\pi\beta_{2}}{\mu_{v}}u_{2}-\mu_{v}u_{4}+\frac{\pi\beta_{1}}{\mu_{v}}u_{6}=0,\\ \frac{\pi\beta_{2}}{\mu_{v}}u_{2}-\mu_{v}u_{5}+\frac{\pi\beta_{1}}{\mu_{v}}u_{6}=0,\\ \alpha u_{2}-\theta u_{6}=0. \end{array}\right. $$
(24)

Next, from Eq. (24), we get

$$\begin{array}{@{}rcl@{}} u_{1}&=&\frac{\theta}{\alpha+\mu_{h}}\left(\frac{\delta\gamma}{\delta+\mu_{h}}-\alpha-\gamma-\mu_{h}\right)u_{6},\\u_{2}&=&\frac{\theta}{\alpha}u_{6},\\u_{3}&=&\frac{\gamma\theta}{\alpha(\delta+\mu_{h})}u_{6},\\u_{4}&=&\frac{\pi}{\mu_{v}}\left(\beta_{1}-\frac{\beta_{2}\theta}{\alpha}\right) u_{6},\\u_{5}&=&\frac{\pi}{{\mu_{v}^{2}}}\left(\frac{\beta_{2}\theta}{\alpha}+\beta_{1}\right) u_{6}, \end{array}$$

where u6 = u6 > 0. Also the left eigenvector, v = (v1, v2, v3, v4, v5, v6) are computed from vJ = 0 as follows.

$$vJ= \left\{\begin{array}{rrrrrr} -\mu_{h}v_{1}=\!\!&0\\ -(\alpha+\gamma+\mu_{h}) v_{2}+\gamma v_{3}-\frac{\pi\beta_{2}}{\mu_{v}}v_{4}+\frac{\pi\beta_{2}}{\mu_{v}}v_{5}+\alpha v_{6}=&0,\\ \delta v_{1}-(\delta+\mu_{h})v_{3}=&0,\\ -\mu_{v}v_{4}=&0,\\ -\frac{\varphi\beta_{h}^{*}}{\mu_{h}}v_{1}+\frac{\varphi\beta_{h}^{*}}{\mu_{h}}v_{2}-\mu_{v}v_{5}=&0,\\ -\frac{\pi\beta_{1}}{\mu_{v}}v_{4}+\frac{\pi\beta_{1}}{\mu_{v}}v_{5}-\theta v_{6}=&0. \end{array}\right. $$
(25)

Solving (25) and then we obtain

$$v_{1}=v_{3}=v_{4}=0,~v_{2}=\frac{\mu_{h}\mu_{v}}{\varphi\beta_{h}^{*}}v_{5},~v_{6}=\frac{\pi\beta_{1}}{\theta\mu_{v}}v_{5}, $$

where v5 = v5 > 0. Based on [27], the bifurcation coefficients a and b are given by

$$\begin{array}{@{}rcl@{}} a&=&\sum\limits^{6}_{i,j,k=1}v_{k}u_{i} u_{j}\frac{\partial^{2}f_{k}}{\partial x_{i}\partial x_{j}}(E_{0}),\\ b&=&\sum\limits^{6}_{i,k=1}v_{k}u_{i}\frac{\partial^{2}f_{k}}{\partial x_{i}\partial \beta_{h}^{*}}(E_{0}). \end{array}$$
(26)

The nonzero second partial derivatives of f1, f2, f4, and f5 at E0 are given as follows:

$$\begin{array}{@{}rcl@{}} \frac{\partial^{2} f_{1}}{\partial x_{1}\partial x_{5}}&=&\frac{\partial^{2} f_{1}}{\partial x_{5}\partial x_{1}}=\;\;\;\;\; \;-\beta_{h}^{*},\\ \frac{\partial^{2} f_{2}}{\partial x_{1}\partial x_{5}}&=&\frac{\partial^{2} f_{2}}{\partial x_{5}\partial x_{1}}=\;\;\;\;\; \;\beta_{h}^{*},\\ \frac{\partial^{2} f_{4}}{\partial x_{2}\partial x_{4}}&=&\frac{\partial^{2} f_{4}}{\partial x_{4}\partial x_{2}}=\;\;\;\;\; \;-\beta_{2},\\ \frac{\partial^{2} f_{4}}{\partial x_{4}\partial x_{6}}&=&\frac{\partial^{2} f_{4}}{\partial x_{6}\partial x_{4}}=\;\;\;\;\; \;-\beta_{1},\\ \frac{\partial^{2} f_{5}}{\partial x_{2}\partial x_{4}}&=&\frac{\partial^{2} f_{5}}{\partial x_{4}\partial x_{2}}=\;\;\;\;\; \;\beta_{2},\\ \frac{\partial^{2} f_{5}}{\partial x_{4}\partial x_{6}}&=&\frac{\partial^{2} f_{5}}{\partial x_{6}\partial x_{4}}=\;\;\;\;\; \;\beta_{1},\\ \frac{\partial^{2} f_{1}}{\partial x_{5}\partial \beta_{h}^{*}}&=&\frac{\partial^{2} f_{1}}{\partial \beta_{h}^{*}\partial x_{5}}= \ x_{1}^{*}=-\frac{\varphi}{\mu_{h}},\\ \frac{\partial^{2} f_{2}}{\partial x_{5}\partial \beta_{h}^{*}}&=&\frac{\partial^{2} f_{2}}{\partial \beta_{h}^{*}\partial x_{5}}= x_{1}^{*}=\frac{\varphi}{\mu_{h}}. \end{array}$$
(27)

All the others second partial derivatives of fi, i = 1,...,6 are zero. By using Eq. (25), we get

$$\begin{array}{@{}rcl@{}} a&=&2v_{1}u_{1}u_{5}\frac{\partial^{2} f_{1}}{\partial x_{1}\partial x_{5}}+2v_{2}u_{1}u_{5}\frac{\partial^{2} f_{2}}{\partial x_{1}\partial x_{5}} +2v_{4}u_{2}u_{4}{\partial^{2} f_{4}}{\partial x_{2}\partial x_{4}}+2v_{4}u_{2}u_{6}\frac{\partial^{2} f_{4}}{\partial x_{2}\partial x_{6}}+2v_{5}u_{2}u_{4}\frac{\partial^{2} f_{5}}{\partial x_{2}\partial x_{4}} \\ &+&2v_{5}u_{4}u_{6}\frac{\partial^{2} f_{5}}{\partial x_{4}\partial x_{6}}\\ &=&\left(-\frac{\mu_{h}\mu_{v}\theta^{2}((\delta+\mu_{h})(\alpha+\mu_{h})+\gamma \mu_{h})}{\varphi\alpha(\alpha+\mu_{h})(\delta+\mu_{h})}+\frac{\pi(\alpha^{2}{\beta_{1}^{2}}-\theta^{2}{\beta_{2}^{2}})}{\mu_{v}\alpha^{2}}\right) {u_{6}^{2}}v_{5}, \end{array}$$
(28)

and

$$\begin{array}{@{}rcl@{}} b&=&2v_{1}u_{5}\frac{\partial^{2} f_{1}}{\partial x_{5}\partial \beta_{h}^{*}}+2v_{2}u_{5}\frac{\partial^{2} f_{2}}{\partial x_{5}\partial \beta_{h}^{*}}\\ &=&\frac{\pi}{\mu_{v}\beta_{h}^{*}}\left(\frac{\theta\beta_{2}}{\alpha}+\beta_{1} \right) u_{6}v_{5}. \end{array}$$
(29)

The coefficients a and b are evaluated at the parameter values so that \(a=0.1998{u_{6}^{2}}v_{5}>0\) and b = 0.1677u6v5 > 0 for u6 > 0 and v5 > 0. Therefore, the model (1) has a backward bifurcation with stable coexistence equilibrium when R0 < 1.

Extension of the model into optimal control

In this section, we extend the model (1) into optimal control problem by including control variables. This helped us to choose appropriate control strategies that used to eliminate pathogens from human populations at the end of control strategy implemented. The following three control strategies are introduced.

  1. (i)

    Prevention: personal and environmental sanitation. By this case, we aimed to separate susceptible human population from pathogens contact.

  2. (ii)

    Integrated vector management: using chemical, biological control, ...etc. to kill pathogens and their carriers.

  3. (iii)

    Diagnosis and treatment: supporting infected individuals in isolation center with medication.

At time t, u1(t), u2(t), and u3(t) denote prevention, integrated vector management, and treatment control variables, respectively. After incorporating those controls into the model (1), we obtain the corresponding state system:

$$\left\{\begin{array}{l} S_{h}^{\prime}= \varphi+\delta R_{h}-(1-u_{1})\beta_{h}I_{v}S_{h}-\mu_{h} S_{h}, \\ I_{h}^{\prime} = (1-u_{1})\beta_{h}I_{v}S_{h}-(\alpha+\gamma+\mu_{h})I_{h},\\ R_{h}^{\prime} = \gamma I_{h}-(\delta+\mu_{h})R_{h} ,\\ S_{v}^{\prime}= \pi-(\beta_{1}P+(1-u_{2})\beta_{2}I_{h})S_{v}-\mu_{v}S_{v},\\ I_{v}^{\prime} = (\beta_{1}P+(1-u_{2})\beta_{2}I_{h})S_{v}-\mu_{v}I_{v},\\ P^{\prime} = \alpha I_{h}-(1+u_{3})\theta P, \end{array}\right. $$
(30)

with initial condition: Sh(0) > 0,Ih(0) ≥ 0,Rh(0) ≥ 0,Sv(0) > 0,Iv(0) ≥ 0, P(0) ≥ 0.

The objective function J is given as similar form presented in [28] as follows.

$$J(u_{1}(.),~u_{2}(.),~u_{3}(.))=\overset{min}{u_{1}, u_{2}, u_{3}}{\int}^{t_{f}}_{0}\left(a_{1}I_{h}+a_{2}I_{v}+a_{3}P+\frac{1}{2}\sum\limits^{3}_{i=1}b_{i}{u_{i}^{2}}\right) dt, $$
(31)

where tf is the final time, while ai, bi > 0. The term \(0.5b_{1}{u_{1}^{2}}\), \(0.5b_{2}{u_{2}^{2}}\), and \(0.5b_{3}{u_{3}^{2}}\) represent cost functions which are corresponding to the control u1, u2, and u3, respectively. The objective of this study is to find the optimal control set \((u_{1}^{*},~u_{2}^{*},~u_{3}^{*})\) such that

$$J(u_{1}^{*},~u_{2}^{*},~u_{3}^{*})=min\;\left\lbrace J(u_{1},~u_{2},~u_{3}):~u_{i}\in U\right\rbrace , $$
(32)

where

$$U=\left\lbrace u(t)=(u_{1}(t),~u_{2}(t),~u_{3}(t)): 0\leq u_{i}(t)\leq 1,~0\leq t\leq t_{f},~ i=1, 2, 3 \right\rbrace . $$

Characterization of the optimal control function

Pontryagin’s minimum principle [29] helps to reduces problems (30)–(32) to a problem of minimizing the Hamiltonian H given by

$$H=J^{\prime}+\lambda_{1}S_{h}^{\prime}+\lambda_{2}I_{h}^{\prime}+\lambda_{3}R_{h}^{\prime}+\lambda_{4}S_{v}^{\prime}+\lambda_{5}I_{v}^{\prime}+\lambda_{6}P^{\prime}. $$
(33)

That is,

$$\begin{array}{@{}rcl@{}} H({\Phi}, u, \lambda)&=&a_{1}I_{h}+a_{2}I_{v}+a_{3}P+\frac{1}{2}\sum\limits^{3}_{i=1}b_{i}{u_{i}^{2}}+\lambda_{1}(\varphi+\delta R_{h}-(1-u_{1})\beta_{h}I_{v}S_{h}-\mu_{h} S_{h})\\&+&\lambda_{2}((1-u_{1})\beta_{h}I_{v}S_{h}-(\alpha+\gamma+\mu_{h})I_{h})+\lambda_{3}(\gamma I_{h}-(\delta+\mu_{h})R_{h} )\\&+&\lambda_{4}(\pi-(\beta_{1}P+(1-u_{2})\beta_{2}I_{h})S_{v}-\mu_{v}S_{v})+\lambda_{5}((\beta_{1}P+(1-u_{2})\beta_{2}I_{h})S_{v}-\mu_{v}I_{v})\\&+&\lambda_{6}(\alpha I_{h}-(1+u_{3})\theta P), \end{array}$$
(34)

where Φ = (Sh,Ih,Rh,Sv,Iv,P) which is state variables.

Based on [30], if the control u∗ and corresponding state Φ∗ are an optimal pair, there is a non-zero adjoint vector λ = (λ1, λ2, λ3, λ4, λ5, λ6) such that

$$\left\{\begin{array}{l} {\Phi}^{\prime}=\frac{\partial H({\Phi}, u, \lambda)}{\partial \lambda},\\ \lambda^{\prime}=-\frac{\partial H({\Phi}, u, \lambda)}{\partial {\Phi}},\\ \frac{\partial H({\Phi}, u, \lambda)}{\partial u}=0. \end{array}\right. $$
(35)

From the boundedness of \(u_{i}^{*}\) on [0,1] and the third equation of Eq. (35) (i.e., minimality condition), we have

$$\left\{\begin{array}{l} u_{i}^{*}=0, ~~~~~~~~\frac{\partial H}{\partial u_{i}}>0,\\ 0< u_{i}^{*}<1, ~~~\frac{\partial H}{\partial u_{i}}=0,\\ u_{i}^{*}=1, ~~~~~~~~\frac{\partial H}{\partial u_{i}}<0. \end{array}\right. $$

To obtain the adjoint variables λi, i = 1,...,6, we follow the classical result of [29]. So the following theorem can be established.

Theorem 7

Let u∗ be the solution to the optimal control problem Eqs. (30)–(32) and \((S_{h}^{*}, I_{h}^{*}, R_{h}^{*},S_{v}^{*}, I_{v}^{*}, P^{*})\) be the corresponding optimal state variables. Then there exist adjoint variables λi, i = 1,...,6 that satisfy the adjoint system:

$$\left\{\begin{array}{l} \lambda_{1}^{\prime}=\lambda_{1}((1-u_{1})\beta_{h}I_{v}+\mu_{h})-\lambda_{2}(1-u_{1})\beta_{h}I_{v},\\ \lambda_{2}^{\prime}=-a_{1}+\lambda_{2}(\alpha+\gamma+\mu_{h})-\lambda_{3}\gamma+\lambda_{4}(1-u_{2})\beta_{2}S_{v}-\lambda_{5}(1-u_{2})\beta_{2}S_{v},\\ \lambda_{3}^{\prime}=-\lambda_{1}\delta+\lambda_{3}(\delta+\mu_{h}),\\ \lambda_{4}^{\prime}=\lambda_{4}(\beta_{1}P+(1-u_{2})\beta_{2}I_{h}+\mu_{v})-\lambda_{5}(\beta_{1}P+(1-u_{2})\beta_{2}I_{h}),\\ \lambda_{5}^{\prime}=-a_{2}+\lambda_{1}(1-u_{1})\beta_{h}S_{h}-\lambda_{2}(1-u_{1})\beta_{h}S_{h}+\lambda_{5}\mu_{v},\\ \lambda_{6}^{\prime}=-a_{3}+\lambda_{4}\beta_{1}S_{v}-\lambda_{5}\beta_{1}S_{v}+\lambda_{6}(1+u_{3})\theta . \end{array}\right. $$
(36)

Together with transversality condition: λi(tf) = 0, i = 1,...,6.

Also, we get optimal controls: \(u_{1}^{*}(t),u_{2}^{*}(t)\), and \(u_{3}^{*}(t)\) which are characterized by

$$\begin{array}{@{}rcl@{}} u_{1}^{*}(t)&=&\min\left\lbrace \max\left\lbrace 0, \frac{(\lambda_{2}-\lambda_{1})\beta_{h}I_{v}S_{h}}{b_{1}}\right\rbrace, 1 \right\rbrace, \\ u_{2}^{*}(t)&=&\min\left\lbrace \max\left\lbrace 0, \frac{(\lambda_{5}-\lambda_{4})\beta_{2}I_{h}S_{v}}{b_{2}}\right\rbrace, 1 \right\rbrace,\\ u_{3}^{*}(t)&=&\min\left\lbrace \max\left\lbrace 0, \frac{\theta P\lambda_{6}}{b_{3}}\right\rbrace, 1 \right\rbrace . \end{array}$$
(37)

Proof

We find that the adjoint equations by taking the negative of ∂H/∂(Sh,Ih,Rh,Sv,Iv,P) as follows. That is,

$$\left\{\begin{array}{l} \lambda_{1}^{\prime}=-\frac{\partial H}{\partial S_{h}}=\lambda_{1}((1-u_{1})\beta_{h}I_{v}+\mu_{h})-\lambda_{2}(1-u_{1})\beta_{h}I_{v},\\ \lambda_{2}^{\prime}=-\frac{\partial H}{\partial I_{h}}=-a_{1}+\lambda_{2}(\alpha+\gamma+\mu_{h})-\lambda_{3}\gamma+\lambda_{4}(1-u_{2})\beta_{2}S_{v}-\lambda_{5}(1-u_{2})\beta_{2}S_{v},\\ \lambda_{3}^{\prime}=-\frac{\partial H}{\partial R_{h}}=-\lambda_{1}\delta+\lambda_{3}(\delta+\mu_{h}),\\ \lambda_{4}^{\prime}=-\frac{\partial H}{\partial S_{v}}=\lambda_{4}(\beta_{1}P+(1-u_{2})\beta_{2}I_{h}+\mu_{v})-\lambda_{5}(\beta_{1}P+(1-u_{2})\beta_{2}I_{h}),\\ \lambda_{5}^{\prime}=-\frac{\partial H}{\partial I_{v}}=-a_{2}+\lambda_{1}(1-u_{1})\beta_{h}S_{h}-\lambda_{2}(1-u_{1})\beta_{h}S_{h}+\lambda_{5}\mu_{v},\\ \lambda_{6}^{\prime}=-\frac{\partial H}{\partial P}=-a_{3}+\lambda_{4}\beta_{1}S_{v}-\lambda_{5}\beta_{1}S_{v}+\lambda_{6}(1+u_{3})\theta . \end{array}\right. $$

We assume that Sh(tf), Ih(tf), Rh(tf), Sv(tf), Iv(tf), and P(tf) are free, then we obtain the transversality condition: λi(tf) = 0.

We find that the optimal controls \(u_{1}^{*}(t)\), \(u_{2}^{*}(t)\), and \(u_{3}^{*}(t)\) from the third equation of (27) as follows.

$$\begin{array}{@{}rcl@{}} \frac{\partial H}{\partial u_{1}}&=&b_{1}u_{1}+(\lambda_{1}-\lambda_{2})\beta_{h}I_{v}S_{h}=0\Rightarrow u_{1}^{*}(t)=\frac{(\lambda_{2}-\lambda_{1})\beta_{h}I_{v}S_{h}}{b_{1}},\\ \frac{\partial H}{\partial u_{2}}&=&b_{2}u_{2}+(\lambda_{4}-\lambda_{5})\beta_{2}I_{h}S_{v}=0\Rightarrow u_{2}^{*}(t)=\frac{(\lambda_{5}-\lambda_{4})\beta_{2}I_{h}S_{v}}{b_{2}},\\ \frac{\partial H}{\partial u_{3}}&=&b_{3}u_{3}-\theta P\lambda_{6}=0\qquad\qquad\ \Rightarrow u_{3}^{*}(t)=\frac{\theta P\lambda_{6}}{b_{3}}. \end{array}$$

Since \(u_{i}^{*}\) is bounded on [0,1], then \(u_{i}^{*}(t)\) can be written in compact form as (37).

The second partial derivative of Hamiltonian H with respect to (u1,u2,u3) at \((u_{1}^{*}, u_{2}^{*}, u_{3}^{*})\) is positive definite. This shows that the optimal control \((u_{1}^{*}, u_{2}^{*}, u_{3}^{*})\) is a minimizer.

Numerical simulations

In this section, we provide numerical simulations obtained from the application of analytical results, as given in previous sections. The state system (30) with the impact of controls: preventive measure (u1), integrated vector management (u1), and supporting infective by medication (u3) on human population is illustrated numerically. Since the optimal system under investigation is a two point boundary value problem with separated boundary conditions at times t = 0 and t = tf, we use the forward-backward iterative scheme [31].

In order to find numerical solutions of the optimality system, first the state system (30) is computed forward with the given initial condition and controls’ initial guess in time by using a Runge-Kutta method of fourth order. Next, the adjoint system (36) is computed backward with the transversality condition in time by using Runge-Kutta algorithm of fouth order. Each control variable value is modified by averaging the new value and old value arising from the characteristic control (37). This step continues many times upto successive iterations are close enough to each other [31].

To study the behavior of the model (1), we performed numerical simulations with the set of parameter values and initial data, which are assumed for illustrative purposes. Accordingly, parameters values are given in Table 2, and with initial data: Sh(0) = 6, Ih(0) = 4, Rh(0) = 1, Sv(0) = 2, Ih(0) = 2, P(0) = 1.

To achieve optimal control strategies, the weight constants of the objective function are assumed: a1 = 600, a2 = 80, a3 = 40, b1 = 6, b2 = 100, b3 = 80 and the adjoint system with terminal condition: λi(tf) = 0, i = 1,...,6 for the final implementation time tf = 50 months. So that those strategies are given below:

  • Strategy A: u1≠ 0, u2≠ 0 and u3 = 0.

  • Strategy B: u1≠ 0, u3≠ 0 and u2 = 0.

  • Strategy C: u2≠ 0, u3≠ 0 and u1 = 0.

  • Strategy D: u1≠ 0, u2≠ 0 and u3≠ 0.

In the simulations, we present that the infected human and vector population with control and without control. The blue curve represents the uncontrolled population case while the red curve shows the controlled population.

Strategy A: Control strategy with preventive measures and integrated vector management

In Fig. 2, we present that the infected human and infected vector population with control (u1≠ 0, u2≠ 0, u3 = 0) and without control (i.e., u1 = u2 = u3 = 0). The simulation results from Fig. 2a shows that infected human goes to zero due to control u1 is at a maximum level for 50 months (Fig. 3a). Therefore, applying this control strategy is effective to eradicate disease from the population with minimum cost 1.5813 × 104 (Fig. 3).

Fig. 2
figure 2

Impact of preventive measures and integrated vector management on human (a) and vector (b) population

Full size image
Fig. 3
figure 3

Profile of control functions (u1, u2) when u3 = 0

Full size image

Strategy B: Control strategy with preventive measures and supporting infectives by medication

Figure 4a and b show that infected human and infected vector decrease. To achieve this, the control profiles u1 and u3 are implemented at a maximum rate for the whole period. The control u1 is at a maximum level for 50 months, but u2 declines after 10 months toward zero (Fig. 5).

Fig. 4
figure 4

Impact of preventive measures and supporting infectives by medication human (a) and vector (b) population

Full size image
Fig. 5
figure 5

Profile of control functions (u1, u3) when u2 = 0

Full size image

Strategy C: Control strategy with integrated vector management and supporting infectives by medication

We observe that from Fig. 6a and b, infected human and infected vector population do not approach to zero at end of strategy. The control u3 is at a maximum level for 40 months and declines afterwards to zero (Fig. 7). Hence, only the control strategy with integrated vector management and supporting infectives by medication are not enough for pathogen control.

Fig. 6
figure 6

Impact of integrated vector management and supporting infectives by medication on human (a) and vector (b) population

Full size image
Fig. 7
figure 7

Profile of control functions (u2, u3) when u1 = 0

Full size image

Strategy D: Control strategy with all controls

In this case, we discuss how all controls affect the pathogen spread in the human population. Figure 8a and b show that infected human and infected vector approach to zero at the end the period. Furthermore, Fig. 8c shows that the number of pathogen decreases at the end of the strategy. Hence, applying this control strategy is the best effective to eradicate pathogen from the system at end of 50 months.

Fig. 8
figure 8

Impact of all controls on human (a), vector (b), and pathogen (c) population

Full size image

From Fig. 9, we observe that control u1 is at a maximum level for 50 months, but u3 declines after 10 months toward zero.

Fig. 9
figure 9

Profile of control functions (u1, u2, u3) when u1≠ 0, u2≠ 0, u3≠ 0

Full size image

Conclusion

In this paper, an optimal control theory was applied to the pathogens’ impact on human disease transmission model governed by a system of nonlinear ordinary differential equations. Then it was analyzed for equilibrium points, which are locally and globally proved by Routh-Hurwitz criterion and Lyapunov function, respectively. The results of the model reveal that when the basic reproductive number, R0 is greater than unity (for instance, R0 = 4.3415), more pathogens are highly spread in the environment, as well as in human population. Thus, in order to reduce more pathogens from the systems, the proposed model is extended into optimal control problems by incorporating three control variables such as u1, u2, and u3. The Hamiltonian function and adjoint variables are investigated. The necessary optimality condition is formulated and analyzed by using Pontryagin’s minimum principle. The simulation results showed that the combined effect of prevention via personal and environmental sanitation, integrated vector management, and continuous supervision during the treatment period helps to reduce the pathogen in the community. Therefore, the results of this study show that the optimal control is sufficient to decrease pathogen from the human population at the end of the fifth month.