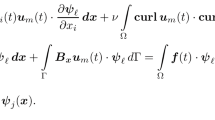A Boundary Control Problem for Stochastic 2D-Navier–Stokes Equations

Abstract

We study a stochastic velocity tracking problem for the 2D-Navier–Stokes equations perturbed by a multiplicative Gaussian noise. From a physical point of view, the control acts through a boundary injection/suction device with uncertainty, modeled by stochastic non-homogeneous Navier-slip boundary conditions. We show the existence and uniqueness of the solution to the state equation, and prove the existence of an optimal solution to the control problem.

1 Introduction

Optimization problems of evolutionary systems under uncertainty are of major relevance in technology, sciences and everyday life. The initial step in addressing the problem relies on its mathematical formulation. Once the problem has been formulated, appropriate theoretical arguments and computational methods are applied to study the existence and uniqueness of the solution, which will be ultimately determined or approximated.

In the literature, a wide range of optimization problems has been addressed.

We would like to mention the contribution [30] in applying the Multivariate Adaptive Regression Splines (MARS) model to systems of discretized stochastic differential equations (describing behavioral reactions and human sentiments), in order to estimate the relevant parameters in the equations that fit real-world historical data (see also [47]). Later [38], the authors successful apply the Robust Optimization algorithms including parametric uncertainties in MARS models, solving real market problems.

Furthermore, we must say that a strategic combination of statistical regression and optimization methods can impact knowledge in Medical Sciences with strong consequences in real life, referring to the Newroscience application, we mention [45] and references therein.

Here we focus on a so-called continuous-time stochastic optimal control problem, which is based on a dynamic law (typically a stochastic differential equation) that governs the temporal evolution of the state process y that we aim to control. Then practical control actions on the physical system are modeled by incorporating the appropriate control variable u into the dynamic law. A key step in analyzing the control problem is to show that an imput u will produce a single output $y^u$; in mathematical words this step corresponds to showing the well-posedness of the state equation. The goal or desired performance corresponds to maximizing (or minimizing) an objective (cost) functional $J=J(t, u,y^u)$.

Important applications of optimal control theory can also be found in mathematical finance [26, 36, 48]. Namely to solve investor allocation problems or Merton problems; let us mention for instance the recent work [21] (and references therein) in the context of continuous-time stochastic volatility, and [4, 40] where the authors consider adjusted to reality Hybrid Models with jumps and regime switches. We also address to the reader the paper [5] concerning the optimal management of defined contribution pension funds under the effect of inflation, mortality and uncertainty. In this framework, the investor or the manager can be seen as a player who chooses the optimal strategy to obtain the best profit. More envolved optimization problems arise when multiple players (cooperating or competing with each other) choose their own strategies to achieve their own optimal individual profits. Game theory provides the appropriate framework to tackle such complex problems (see for instance [37, 39, 41, 42]).

It is worth to mention that continuous-time optimal control problems can be classified according to the control type: feedback or not feedback. A feedback control reads $u(t)=U(t,y(t))$, where U(t, y) is a policy function defined on the state space. The theory for finding an optimal policy function relies on studying the Hamilton-Jacobi-Bellman (HJB) equation. If the state space is ${\mathbb {R}}^d$, the HJB equation is a deterministic nonlinear partial differential equation or integro-partial differential equation on ${\mathbb {R}}^d$. When the evolutionary law is a stochastic partial differential equation, the state space is infinite dimensional, and the study of a feedback control problem is a delicate issue. Even the definition of the HJB equation is far from being well understood. We refer to [10, 22, 34], where the authors proved the existence of $\epsilon$-optimal feedback controls.

We must emphasize that the difficulty of solving an optimal control problem feedback/not feedback strongly depends on the structure of the stochastic differential equation, which can be linear or nonlinear, finite or infinite dimensional. Furthermore, the noise can be of finite or infinite dimensional, continuous in time or with jumps, requiring a specific analysis accordingly.

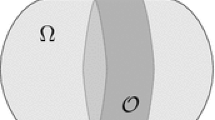
In the present article, the evolutionary law is a nonlinear stochastic partial differential equation that describes the evolution of a velocity field of a Newtonian fluid under the action of stochastic random forces and filling a two-dimensional bounded domain ${ {\mathcal {O}}}\subset {\mathbb {R}}^{2}$. The control actions are imposed on the boundary of the container and are not of feedback type. We aim to show the well-posedness of the state equation and the existence of the optimal solution. In forthcoming works we intend to apply Pontryagin’s maximum principle to deduce first-order optimality conditions and second-order sufficient optimality conditions.

More precisely, we consider the Navier–Stokes equations with non-homogeneous Navier-slip boundary conditions

$$\begin{aligned} \begin{array}{ll} \begin{array}{l} d{\textbf{y}}=(\nu \Delta {\textbf{y}}-\left( \mathbf {y\cdot }\nabla \right) {\textbf{y}}-\nabla \pi )\,dt+{\textbf{G}}(t,{\textbf{y}})\,d{{\mathcal {W}}}_{t}, \\ \\ \text{ div }\,{\textbf{y}}=0, \end{array} &{} \text{ in }{\ {\mathcal {O}}_{T}=(0,T)\times {\mathcal {O}}}, \\ {\textbf{y}}\cdot {\textbf{n}}=a,\;\quad \left[ 2D({\textbf{y}})\,{\textbf{n}} +\alpha {\textbf{y}}\right] \cdot {\varvec{\tau }}=b\;\quad &{} \text {on}\ \Gamma _{T}=(0,T)\times \Gamma , \\ {\textbf{y}}(0,{\textbf{x}})={\textbf{y}}_{0}({\textbf{x}}) &{} \text{ in }\ {{\mathcal {O}} }, \end{array} \end{aligned}$$

(1.1)

where ${\textbf{y}}={\textbf{y}}(t,{\textbf{x}})$ is the 2D-velocity random field, $\pi =\pi (t,{\textbf{x}})$ is the pressure, $\nu >0$ is the viscosity and ${\textbf{y}}_{0}$ is the initial condition that verifies

$$\begin{aligned} \text{ div }\,{\textbf{y}}_{0}=0\qquad \text{ in } \ {{\mathcal {O}}}. \end{aligned}$$

(1.2)

Here

$$\begin{aligned} D({\textbf{y}})=\frac{1}{2}\left[ \nabla {\textbf{y}}+(\nabla {\textbf{y}})^{T}\right] \end{aligned}$$

is the rate-of-strain tensor; ${\textbf{n}}$ is the external unit normal to the boundary $\Gamma \in C^{2}$ of the domain ${{\mathcal {O}}}$ and $\varvec{\tau }$ is the tangent unit vector to $\Gamma ,$ such that $({\textbf{n}},\varvec{\tau } )$ forms a standard orientation in ${\mathbb {R}}^{2}.$ The positive constant $\alpha$ is the so-called friction coefficient. The quantity a corresponds to the inflow and outflow fluid through $\Gamma$, satisfying the compatibility condition

$$\begin{aligned} \int _{\Gamma }a(t,{\textbf{x}})\,\,d\mathbf {\gamma }=0\quad \quad \text{ for } \text{ any } \;t\in [0,T]. \end{aligned}$$

(1.3)

This condition means that the quantity of inflow fluid should coincide with the quantity of outflow fluid. The boundary functions a and b will be considered as the control variables for the physical system (1.1). The term ${\textbf{G}}(t,{\textbf{y}})\,{ {\mathcal {W}}}_{t}$ is a multiplicative white noise.

The main goal of this paper is to control the solution of the system (1.1) by the boundary condition (a, b), which is a predictable stochastic process belonging to the space ${\mathcal {A}}$ of admissible controls to be defined in Sect. 4. The cost functional is given by

$$\begin{aligned} \displaystyle J(a,b,{\textbf{y}})={\mathbb {E}}\int _{{{\mathcal {O}}}_{T}}\frac{1}{2} |{\textbf{y}}-{\textbf{y}}_{d}|^{2}\,d{\textbf{x}}dt+{\mathbb {E}}\int _{\Gamma _{T}}\left( \frac{\lambda _{1}}{2}|a|^{2}+\frac{\lambda _{2}}{2} |b|^{2}\right) \,d\mathbf {\gamma }dt, \end{aligned}$$

(1.4)

where ${\textbf{y}}_{d}\in L_{2}(\Omega \times {{\mathcal {O}}}_{T})$ is a desired target field and $\lambda _{1},\lambda _{2}>0.$ We aim to control the random velocity field ${\textbf{y}}$, defined as the solution of the Stochastic Navier–Stokes equations, through minimization of the cost functional (1.4). More precisely, our goal is to solve the following problem

$$\begin{aligned} ({\mathcal {P}})\left\{ \begin{array}{l} \underset{(a,b)}{\text{ minimize }}\{J(a,b,{\textbf{y}}):~(a,b)\in {\mathcal {A}} \quad \text {and} \\ {\textbf{y}} \text{ is } \text{ the } \text{ weak } \text{ solution } \text{ of } \text{ the } \text{ system } (1.1) \text{ for } (a,b)\in {\mathcal {A}}\}. \end{array} \right. \end{aligned}$$

Let us mention that boundary control of fluid flows is of main importance in several branches of the industry, for instance, in the aviation industry. Extensive research has been carried out concerning the implementation of injection-suction devices to control the motion of the fluids (see [8, 9]). On the other hand, rotating flow is critically important across a wide range of scientific, engineering and product applications, providing design and modeling capability for diverse products such as jet engines, pumps, food production and vacuum cleaners, as well as geophysical flows. The control problem for deterministic Newtonian and non-Newtonian flows, has been widely studied in the literature (see [13,14,15, 23, 28, 29, 44]). However, it is well known that the study of turbulent flows, where small random disturbances produce strong macroscopic effects, requires a statistical approach. Recently, special attention has been devoted to stochastic optimal control problems, where control is exerted by a distributed mechanical force (see [10, 16, 22, 43]). To the best of our knowledge, this is the first paper where the boundary control problem is addressed for stochastic Navier–Stokes equations under Navier-slip boundary conditions.

The plan of the present paper is as follows. In Sect. 2, we present the general setting, by introducing the appropriate functional spaces and some necessary classical inequalities. Section 3 deals with the well-posedness of the state equations. In Sect. 4, we show the existence of an optimal solution to the control problem.

2 General Setting

Let X be a real Banach space endowed with the norm $\left\| \cdot \right\| _{X}.$ We denote $L_{p}(0,T;X)$ as the space of X-valued measurable $p-$integrable functions defined on [0, T] for $p\geqslant 1$.

For $p,r\geqslant 1$, let $L_{p}(\Omega ,L_{r}(0,T;X))$ be the space of the processes ${\textbf{v}}={\textbf{v}}(\omega ,t)$ with values in X defined on $\ \Omega \times [0,T],$ adapted to the filtration $\left\{ {\mathcal {F}} _{t}\right\} _{t\in [0,T]}$, and endowed with the norms

$$\begin{aligned} \left\| {\textbf{v}}\right\| _{L_{p}(\Omega ,L_{r}(0,T;X))}=\left( \mathbb {E(}\int _{0}^{T}\left\| {\textbf{v}}\right\| _{X}^{r}\,dt)^{\frac{ p}{r}}\right) ^{\frac{1}{p}} \end{aligned}$$

and

$$\begin{aligned} \left\| {\textbf{v}}\right\| _{L_{p}(\Omega ,L_{\infty }(0,T;X))}=\left( {\mathbb {E}}\sup _{t\in [0,T]}\left\| {\textbf{v}}\right\| _{X}^{p}\ \right) ^{\frac{1}{p}}\quad \text {if }r=\infty , \end{aligned}$$

where ${\mathbb {E}}$ is the mathematical expectation with respect to the probability measure P. As usual, in the notation for processes ${\textbf{v}}= {\textbf{v}}(\omega ,t)$, we generally omit the dependence on $\omega \in \Omega .$

We define the spaces

$$\begin{aligned} H= & {} \{{\textbf{v}}\in L_{2}({{\mathcal {O}}}):\,\text{ div } {\textbf{v}}=0\;\ \text { in}\;{\mathcal {D}}^{\prime }({{\mathcal {O}}}),\;\ {\textbf{v}}\cdot {\textbf{n}} =0\;\ \text { in}\;H^{-1/2}(\Gamma )\}, \\ V= & {} \{{\textbf{v}}\in H^{1}({{\mathcal {O}}}):\,\text{ div } {\textbf{v}}=0\;\;\text { a.e. in}\;{{\mathcal {O}}},\;\ {\textbf{v}}\cdot {\textbf{n}}=0\;\ \text { in} \;H^{1/2}(\Gamma )\}. \end{aligned}$$

We denote $(\cdot ,\cdot )$ as the inner product in $L_{2}({\mathcal {O}})$ and $\Vert \cdot \Vert _{2}$ as the associated norm. The norms in the spaces $L_{p}({\mathcal {O}})$ and $H^{p}({\mathcal {O}})$ are denoted by $\Vert \cdot \Vert _{p}$ and $\Vert \cdot \Vert _{H^{p}}$. On the space V, we consider the following inner product

$$\begin{aligned} \left( {\textbf{v}},{\textbf{z}}\right) _{V}=2\left( D{\textbf{v}},D{\textbf{z}} \right) +\alpha \int _{\Gamma }{\textbf{v}}\cdot {\textbf{z}} \end{aligned}$$

and the corresponding norm $\Vert {\textbf{v}}\Vert _{V}=\sqrt{\left( \textbf{v },{\textbf{v}}\right) _{V}}.$

Throughout the article, we often use the continuous embedding results

$$\begin{aligned} H^{1}(0,T)\subset C([0,T]),\quad H^{1}({\mathcal {O}})\subset L_{2}(\Gamma ). \end{aligned}$$

(2.1)

Let us introduce the notation

$$\begin{aligned} {\textbf{v}}_{{\mathcal {O}}}=\int _{{\mathcal {O}}}\mathbf {v\ }d\mathbf {x.} \end{aligned}$$

(2.2)

We notice that for any vector ${\textbf{v}}\in V$ we have ${\textbf{v}}_{ {\mathcal {O}}}=0,$ since

$$\begin{aligned} \int _{{\mathcal {O}}}v_{j}\mathbf {\ }d{\textbf{x}}=\int _{{\mathcal {O}}}\text{ div } ( {\textbf{v}}x_{j})\mathbf {\ }d{\textbf{x}}=\int _{\Gamma }x_{j}({\textbf{v}}\cdot \mathbf {n)\ }d\mathbf {\gamma }=0\quad \text {for }j=1,2. \end{aligned}$$

Using it and the results that can be found on the p. 62, 69 of [32], p. 125 of [35], and on the p. 16–20 of [46], we formulate the next lemma.‘

Lemma 2.1

For any ${\textbf{v}}\in H^{1}({\mathcal {O}})$ and any $q\geqslant 2$, the Gagliano-Nirenberg-Sobolev inequality

$$\begin{aligned} ||{\textbf{v}}-{\textbf{v}}_{{\mathcal {O}}}||_{q}\leqslant C||{\textbf{v}} ||_{2}^{2/q}||\nabla {\textbf{v}}||_{2}^{1-2/q} \end{aligned}$$

(2.3)

and the trace interpolation inequality

$$\begin{aligned} ||{\textbf{v}}-{\textbf{v}}_{{\mathcal {O}}}||_{L_{q}(\Gamma )}\leqslant C||\textbf{ v}||_{2}^{1/q}||\nabla {\textbf{v}}||_{2}^{1-1/q} \end{aligned}$$

(2.4)

are valid. Moreover, any ${\textbf{v}}\in V$ satisfies Korn’s inequality

$$\begin{aligned} \left\| {\textbf{v}}\right\| _{H^{1}}\leqslant C\left\| {\textbf{v}} \right\| _{V}, \end{aligned}$$

(2.5)

that is the norms $\Vert \cdot \Vert _{H^{1}}$ and $\Vert \cdot \Vert _{V}$ are equivalent.

Remark 2.2

We should mention that throughout the article, we will represent by C a generic constant that can assume different values from line to line. These constants C will depend mainly of the physical constants $\nu ,$ $\alpha ,$ the domain ${\mathcal {O}}$, a given time $T>0$.

Now, we state a formula that can be derived easily via integration by parts

$$\begin{aligned} -\int _{{\mathcal {O}}}\triangle {\textbf{v}}\cdot {\textbf{z}}\,d{\textbf{x}}=2\int _{ {\mathcal {O}}}\,D{\textbf{v}}\cdot D{\textbf{z}}-\int _{\Gamma }2({\textbf{n}}\cdot D {\textbf{v}})\cdot {\textbf{z}}, \end{aligned}$$

(2.6)

which holds for any ${\textbf{v}}\in H^{2}({\mathcal {O}})$ and ${\textbf{z}}\in V$. Let us assume that ${\textbf{v}}$ satisfies Navier-slip boundary condition (1.1), then we have

$$\begin{aligned} -\int _{{\mathcal {O}}}\triangle {\textbf{v}}\cdot {\textbf{z}}\,d{\textbf{x}}=( {\textbf{v}},{\textbf{z}}\,)_{V}-\int _{\Gamma }b({\textbf{z}}\cdot {\varvec{\tau })}\,d \mathbf {\gamma }. \end{aligned}$$

(2.7)

In what follows we will frequently use

$$\begin{aligned} uv\leqslant \varepsilon u^{2}+\frac{v^{2}}{4\varepsilon },\quad \forall \varepsilon >0, \end{aligned}$$

(2.8)

that is a particular case of Young’s inequality

$$\begin{aligned} uv\leqslant \frac{u^{p}}{p}+\frac{v^{q}}{q},\quad \frac{1}{p}+\frac{1}{q} =1,\quad \forall p,\,q>1. \end{aligned}$$

(2.9)

For a vector

$$\begin{aligned} {\textbf{h}}=({\textbf{h}}_{1},\dots ,{\textbf{h}}_{m})\in H^{m}=\overbrace{ H\times ...\times H}^{m-times} \end{aligned}$$

we introduce the norm and the absolute value of the inner product of ${\textbf{h}}$ with a fixed ${\textbf{v}}\in H$ as

$$\begin{aligned} \left\| {\textbf{h}}\right\| _{2}=\sum _{k=1}^{m}\left\| {\textbf{h}} _{k}\right\| _{2}\quad \text {and}\quad |\left( {\textbf{h}},{\textbf{v}} \right) |=\left( \sum _{k=1}^{m}\left( {\textbf{h}}_{k},{\textbf{v}}\right) ^{2}\right) ^{1/2}. \end{aligned}$$

(2.10)

Assume that the stochastic noise is represented by

$$\begin{aligned} {\textbf{G}}(t,{\textbf{y}})\,d{{\mathcal {W}}}_{t}=\sum _{k=1}^{m}G^{k}(t,{\textbf{y}} )\,d{{\mathcal {W}}}_{t}^{k}, \end{aligned}$$

where ${\textbf{G}}(t,{\textbf{y}})=(G^{1}(t,{\textbf{y}}),\dots ,G^{m}(t,\textbf{y }))$ has suitable growth assumptions, as defined in the following, and ${ {\mathcal {W}}}_{t}=({{\mathcal {W}}}_{t}^{1},\dots ,{{\mathcal {W}}}_{t}^{m})$ is a standard ${\mathbb {R}}^{m}$-valued Wiener process defined on a complete probability space $(\Omega ,{\mathcal {F}},P)$ endowed with a filtration $\left\{ {\mathcal {F}}_{t}\right\} _{t\in [0,T]}$. We assume that ${\mathcal {F}}_{0}$ contains every P-null subset of $\Omega$.

Let ${\textbf{G}}(t,{\textbf{y}}):[0,T]\times H\rightarrow H^{m}$ be Lipschitz on ${\textbf{y}}$ and satisfy the linear growth

$$\begin{aligned} \left\| {\textbf{G}}(t,{\textbf{v}})-{\textbf{G}}(t,{\textbf{z}})\right\| _{2}^{2}&\leqslant K\left\| {\textbf{v}}-{\textbf{z}}\right\| _{2}^{2}, \nonumber \\ \left\| {\textbf{G}}(t,{\textbf{v}})\right\| _{2}&\leqslant K\left( 1+\left\| {\textbf{v}}\right\| _{2}\right) ,\quad \forall {\textbf{v}}, {\textbf{z}}\in H,\;t\in [0,T] \end{aligned}$$

(2.11)

for some positive constant K.

Let us define the space of functions ${\mathcal {H}}_{p}(\Gamma )=\left\{ (a,b):||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}<+\infty \right\}$ with the norm

$$\begin{aligned} ||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}=||a||_{W_{p}^{1-\frac{1}{p}}(\Gamma )}+\,||\partial _{t}a||_{H^{\frac{1}{2}}(\Gamma )}+\Vert b\Vert _{W_{p}^{- \frac{1}{p}}(\Gamma )}+\Vert b\Vert _{L_{2}(\Gamma )}+||\partial _{t}b||_{H^{-\frac{1}{2}}(\Gamma )}. \end{aligned}$$

In this work, we consider the data a, b and ${\textbf{u}}_{0}$ belong to the following Banach spaces

$$\begin{aligned} (a,b)\in L_{2}(\Omega \times (0,T);{\mathcal {H}}_{p}(\Gamma ))\quad \text {for given}\;p\in (2,+\infty ),\quad {\textbf{u}}_{0}\in L_{2}(\Omega ;H).\nonumber \\ \end{aligned}$$

(2.12)

In addition, we assume that (a, b) is a pair of predictable stochastic processes.

3 State Equation

This section is devoted to the study of the state equation. We use the variatioal approach to show the existence and the uniqueness of solution, and deduce appropriete estimates to study the control problem.

Since, we are considering non-homogeneous boundary conditions, we first introduce a suitable change of variables based on the solution of the non-homogeneous linear Stokes equation, which allows to write the state in terms of a vector field satisfying a homogeneous Navier-slip boundary condition.

Lemma 3.1

Let (a, b) be a given pair of functions satisfying (2.12). Then there exists a unique solution

$$\begin{aligned} {\textbf{a}}\in L_{2}(\Omega ;H^{1}(\left( 0,T\right) \times {{\mathcal {O}}} ))\cap L_{2}(\Omega \times (0,T);W_{p}^{1}({{\mathcal {O}}})) \end{aligned}$$

(3.1)

of the Stokes problem with the non-homogeneous Navier-slip boundary condition

$$\begin{aligned} \begin{array}{l} -\Delta {\textbf{a}}+\nabla \pi =0,\quad \text{ div }\,{\textbf{a}}=0\quad \text { in }{{\mathcal {O}}}, \\ {\textbf{a}}\cdot {\textbf{n}}=a,\quad \left[ 2D({\textbf{a}})\,{\textbf{n}}+\alpha {\textbf{a}}\right] \cdot {\varvec{\tau }}=b\quad \text {on }\Gamma , \end{array} \end{aligned}$$

(3.2)

such that

$$\begin{aligned} ||{\textbf{a}}||_{W_{p}^{1}({{\mathcal {O}}})}+||\partial _{t}{\textbf{a}}||_{L_{2}( {{\mathcal {O}}})}\leqslant C||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )},\quad \text { a.e. in }\Omega \times (0,T). \end{aligned}$$

(3.3)

In particular, we have

$$\begin{aligned} {\textbf{a}}\in L_{2}(\Omega ;C([0,T];L_{2}({{\mathcal {O}}})))\cap L_{2}(\Omega \times (0,T);C(\overline{{{\mathcal {O}}}})\cap H^{1}({{\mathcal {O}}})). \end{aligned}$$

Proof

Let us introduce the function ${\textbf{c}}=\nabla h,$ where h is the unique solution of the system

$$\begin{aligned} \begin{array}{l} -\Delta h=0\quad \text {in }{{\mathcal {O}}}, \\ \frac{\partial h}{\partial {\textbf{n}}}=a\quad \text {on }\Gamma , \end{array} \quad \text {a.e. in }\Omega \times (0,T) \end{aligned}$$

with $\int _{\Gamma }h\,\,d\mathbf {\gamma }=0.$ Theorem 1.10, p. 15 in [27] implies that the function ${\textbf{c}}$ satisfies the estimates

$$\begin{aligned} ||{\textbf{c}}||_{W_{p}^{1}({{\mathcal {O}}})}\leqslant C_{p}||a||_{W_{p}^{1- \frac{1}{p}}(\Gamma )},\quad ||\partial _{t}{\textbf{c}}||_{H^{1}({{\mathcal {O}}} )}\leqslant C||\partial _{t}a||_{W_{2}^{\frac{1}{2}}(\Gamma )}, \end{aligned}$$

(3.4)

where the constant $C_{p}$ depends on p, $2<p<\infty$.

Let us consider the following Stokes problem

$$\begin{aligned} \begin{array}{l} -\Delta {\textbf{b}}+\nabla \pi =0,\quad \text{ div }\,{\textbf{b}}=0\quad \text { in }{{\mathcal {O}}}, \\ {\textbf{b}}\cdot {\textbf{n}}=0,\quad \left[ 2D({\textbf{b}})\,{\textbf{n}}+\alpha {\textbf{b}}\right] \cdot {\varvec{\tau }}=\widetilde{b}\quad \text {on }\Gamma , \end{array} \quad \text {a.e. in }\Omega \times (0,T) \end{aligned}$$

with $\widetilde{b}=b-\left[ 2D(\mathbf {{\textbf{c}}})\,{\textbf{n}}+\alpha \mathbf {{\textbf{c}}}\right] \cdot {\varvec{\tau }\in W_{p}^{-\frac{1}{p}}(\Gamma ) }$ by (3.4) and Lemma 2.4 in [2]. Using Theorem 2.1 in [1], we have that there exists a unique solution ${\textbf{b}}$ of this Stokes problem such that

$$\begin{aligned} ||{\textbf{b}}||_{W_{p}^{1}({{\mathcal {O}}})}\leqslant C_{p}||\widetilde{b} ||_{W_{p}^{-\frac{1}{p}}(\Gamma )},\quad ||\partial _{t}{\textbf{b}}||_{H^{1}({ {\mathcal {O}}})}\leqslant C||\partial _{t}\widetilde{b}||_{W_{2}^{-\frac{1}{2} }(\Gamma )}. \end{aligned}$$

(3.5)

Due to the regularity (2.12) and the estimates (3.4)–(3.5), we conclude that the system (3.2) has the unique solution $\mathbf { a=b+c}$, satisfying the first estimate in (3.3). The second one in (3.3) is a direct consequence of the embeedings $W_{2}^{1}(0,T) \hookrightarrow C([0,T])$ and $W_{p}^{1}({{\mathcal {O}}})\hookrightarrow C( \overline{{{\mathcal {O}}}}),$ since $2<p<+\infty .$ $\square$

With the help of the solution of the non-homogeneous Stokes equation, we introduce the notion of solution to the state system (1.1).

Definition 3.2

Let the data (a, b) and ${\textbf{u}}_{0}$ satisfy the regularity (2.12), and ${\textbf{a}}$ be the corresponding solution of (3.2). A stochastic process ${\textbf{y}}={\textbf{u}}+{\textbf{a}}$ with ${\textbf{u}}\in C([0,T];H)\cap L_{2}(0,T;V),\quad P$-a.e. in $\Omega ,$ is a strong (in the stochastic sense) solution of (1.1) with ${\textbf{y}} _{0}={\textbf{u}}_{0}+{\textbf{a}}(0)$ if P-a.e. in $\Omega$ the following equation holds

$$\begin{aligned} \left( {\textbf{y}}(t),\varvec{\varphi }\right)&=\int _{0}^{t}\left[ -\nu \left( {\textbf{y}},\varvec{\varphi }\right) _{V}+\int _{\Gamma }\nu b( \varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(({\textbf{y}} \cdot \nabla ){\textbf{y}},\varvec{\varphi })\,\right] ds \nonumber \\&\quad +\left( {\textbf{y}}_{0},\varvec{\varphi }\right) +\int _{0}^{t}\left( {\textbf{G}}(s,{\textbf{y}}(s)),\varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s},\quad \forall t\in [0,T],\quad \forall \varvec{\varphi }\in V, \end{aligned}$$

(3.6)

where the stochastic integral is defined by

$$\begin{aligned} \int _{0}^{t}\left( {\textbf{G}}(s,{\textbf{y}}(s)),\varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s}=\sum _{k=1}^{m}\int _{0}^{t}\left( G^{k}(s,{\textbf{y}}(s)), \varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s}^{k}. \end{aligned}$$

The existence of solution for the system (1.1)–(1.2) will be shown by Galerkin’s method. Since the injection operator $I:V\rightarrow H$ is a compact operator, there exists a basis $\{{\textbf{e}}_{i}\}\subset V$ of eigenfunctions verifying the property

$$\begin{aligned} \left( {\textbf{v}},{\textbf{e}}_{i}\right) _{V}=\lambda _{i}\left( {\textbf{v}}, {\textbf{e}}_{i}\right) ,\quad \forall {\textbf{v}}\in V,\;i\in {\mathbb {N}}, \end{aligned}$$

(3.7)

which is an orthonormal basis for H, and the corresponding sequence $\{\lambda _{i}\}$ of eigenvalues verifies $\lambda _{i}>0$, $\forall i\in {\mathbb {N}}$ and $\lambda _{i}\rightarrow \infty$ as $i\rightarrow \infty .$ For the details we refer to Theorem 1, p. 355, of [25]. Moreover the ellipticity of the equation (3.7) and the regularity $\Gamma \in C^{2}$ imply that $\{{\textbf{e}}_{i}\}\subset C^{2}({{\mathcal {O}}})\cap V$.

For any fixed $n\in {\mathbb {N}}$, we consider the subspace $V_{n}=\textrm{span }\,\{{\textbf{e}}_{1},\ldots ,{\textbf{e}}_{n}\}$ of V. Taking into account the relation (2.7), the approximate finite dimensional problem is: for$\ P$-a.e. in $\Omega \,$ to find ${\textbf{y}}_{n}$ in the form

$$\begin{aligned} {\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}\quad \text {with}\quad {\textbf{u}} _{n}(t)=\sum _{j=1}^{n}\beta _{j}^{n}(t){\textbf{e}}_{j},\quad t\in [0,T], \end{aligned}$$

as the solution of the following finite dimensional stochastic differential equation

$$\begin{aligned} \begin{array}{l} d\left( {\textbf{y}}_{n},\varvec{\varphi }\right) =\left[ -\nu \left( {\textbf{y}}_{n},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b( \varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(\left( \textbf{y }_{n}\cdot \nabla ){\textbf{y}}_{n},\varvec{\varphi }\right) \,\right] dt \\ \qquad \qquad \,+\left( {\textbf{G}}(t,{\textbf{y}}_{n}),\varvec{\varphi } \right) \,d{{\mathcal {W}}}_{t},\quad \forall t\in (0,T),\quad \forall \varvec{\varphi }\in V_{n}, \\ {\textbf{u}}_{n}(0)={\textbf{u}}_{n,0}, \end{array} \end{aligned}$$

(3.8)

where ${\textbf{u}}_{n,0}=\sum _{j=1}^{n}\left( {\textbf{u}}_{0},{\textbf{e}} _{j}\right) {\textbf{e}}_{j}$ is the orthogonal projection of ${\textbf{u}} _{0}\in H$ into the space $V_{n}.$ From the Parseval’s identity we infer that

$$\begin{aligned} \left\| {\textbf{u}}_{n,0}\right\| _{2}\leqslant \left\| {\textbf{u}} _{0}\right\| _{2}\quad \text {and}\quad {\textbf{u}}_{n,0}\rightarrow {\textbf{u}}_{0}\quad \text{ strongly } \text{ in } \ H. \end{aligned}$$

(3.9)

The equation (3.8) defines a system of n stochastic ordinary differential equations with locally Lipschitz nonlinearities. Hence, there exists a local-in-time adapted solution ${\textbf{u}}_{n}\in C([0,T_{n}];V_{n})$ by classical results [31]. The next lemma will establish uniform estimates, which guarantee that ${\textbf{u}}_{n}$ is a global-in-time solution.

Lemma 3.3

Let the data (a, b) and ${\textbf{u}}_{0}$ satisfy the regularity (2.12). Then the system (3.8) has a solution ${\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}$, such that

$$\begin{aligned} {\textbf{u}}_{n}\in C([0,T];H)\cap L_{2}(0,T;V),\quad P\text {-a.e. in }\Omega \text {.} \end{aligned}$$

Moreover, there exists a positive constant $C_{0}$, such that for the function

$$\begin{aligned} \xi _{0}(t)=e^{-C_{0}t-C_{0}\int _{0}^{t}||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}ds},\quad P\text {-a.e. in }\Omega \text {,} \end{aligned}$$

(3.10)

and any $t\in [0,T]$, the following estimate holds

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{0}^{2}(s)\left\| {\textbf{u}} _{n}(s)\right\| _{2}^{2}&+\nu {\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}\right\| _{V}^{2}\,ds \nonumber \\&\leqslant C\left( {\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{2}+ {\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\text {A}(s)\,ds\right) , \end{aligned}$$

(3.11)

where

$$\begin{aligned} \text {A}=||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+1\in L_{1}(\Omega \times (0,T)) \end{aligned}$$

(3.12)

and the positive constants $C_{0}$ and C are independent of the parameter n, which may depend on the regularity of the boundary $\Gamma$ and the physical constants $\nu$ and $\alpha$.

Proof

Let $\xi _{0}$ be the function defined by (3.10) with a constant $C_{0}$ to be concretized later on (see expression (3.15) below). For each $n\in {\mathbb {N}}$, let us set

$$\begin{aligned} g(t)=\xi _{0}^{2}(t)\left\| {\textbf{u}}_{n}(t)\right\| _{2}^{2}+2\nu \int _{0}^{t}\xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{V}^{2}ds,\quad t\in [0,T], \end{aligned}$$

and consider the sequence $\{\tau _{N}^{n}\}$$_{{N\in {\mathbb {N}}}}$ of the stopping times defined by

$$\begin{aligned} \tau _{N}^{n}=\inf \{t\geqslant 0:\quad g(t)\geqslant N\}\wedge T_{n}. \end{aligned}$$

(3.13)

Taking $\varvec{\varphi }={\textbf{e}}_{i}$ for each $i=1,\dots ,n$ in the equation (3.8) and using ${\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}$, we obtain

$$\begin{aligned} d\left( {\textbf{u}}_{n}\,,{\textbf{e}}_{i}\right)&=[-\nu \left( {\textbf{u}} _{n}+{\textbf{a}},{\textbf{e}}_{i}\right) _{V}+\nu \int _{\Gamma }b({\textbf{e}} _{i}\cdot {\varvec{\tau }})\,d\mathbf {\gamma }\, \\&\quad +\left( -\mathbf {\partial }_{t}{\textbf{a}}-\left( \left( {\textbf{u}}_{n}+ {\textbf{a}}\right) \mathbf {\cdot }\nabla \right) \left( {\textbf{u}}_{n}+ {\textbf{a}}\right) ,{\textbf{e}}_{i}\right) ]dt\,+\left( {\textbf{G}}(t,{\textbf{y}} _{n}),{\textbf{e}}_{i}\right) \,d{{\mathcal {W}}}_{t}. \end{aligned}$$

Step 1. Estimate in the space H up to $\tau _{N}^{n}$. The Itô formula gives

$$\begin{aligned} d\left( \left( {\textbf{u}}_{n}\,,{\textbf{e}}_{i}\right) ^{2}\right)&=2\left( {\textbf{u}}_{n},{\textbf{e}}_{i}\right) [-\nu \left( {\textbf{u}}_{n},{\textbf{e}} _{i}\right) _{V}-\nu \left( {\textbf{a}},{\textbf{e}}_{i}\right) _{V}+\nu \int _{\Gamma }b({\textbf{e}}_{i}\cdot {\varvec{\tau }})\,d\mathbf {\gamma }\, \\&\quad +\left( -\mathbf {\partial }_{t}{\textbf{a}}-\left( \left( {\textbf{u}}_{n}+ {\textbf{a}}\right) \mathbf {\cdot }\nabla \right) \left( {\textbf{u}}_{n}+ {\textbf{a}}\right) ,{\textbf{e}}_{i}\right) ]dt\, \\&\quad +2\left( {\textbf{u}}_{n},{\textbf{e}}_{i}\right) \left( {\textbf{G}}(t,\textbf{y }_{n}),{\textbf{e}}_{i}\right) \,d{{\mathcal {W}}}_{t}+|\left( {\textbf{G}}\left( t, {\textbf{y}}_{n}\right) ,{\textbf{e}}_{i}\right) |^{2}\,dt, \end{aligned}$$

where the absolute value in the last term is defined by (2.10). Summing these equalities over $i=1,\dots ,n,$ we obtain

$$\begin{aligned} d\left( \left\| {\textbf{u}}_{n}\right\| _{2}^{2}\right) +2\nu \left\| {\textbf{u}}_{n}\right\| _{V}^{2}dt&=\left[ -2\nu \left( {\textbf{a}},{\textbf{u}}_{n}\right) _{V}+\int _{\Gamma }\left\{ -a({\textbf{u}} _{n}\cdot \varvec{\tau })^{2}+2\nu b({\textbf{u}}_{n}\cdot \varvec{\tau })\right\} \,d \mathbf {\ \gamma }\,\right] dt \nonumber \\&\quad -2\left( \partial _{t}{\textbf{a}}+\left( \left( {\textbf{u}}_{n}+{\textbf{a}} \right) \mathbf {\cdot }\nabla \right) {\textbf{a}},{\textbf{u}}_{n}\right) dt\, \nonumber \\&\quad +\sum _{i=1}^{n}|\left( {\textbf{G}}\left( t,{\textbf{y}}_{n}\right) ,{\textbf{e}} _{i}\right) |^{2}\,dt+2\left( {\textbf{G}}(t,{\textbf{y}}_{n}),{\textbf{u}} _{n}\right) \,d{{\mathcal {W}}}_{t} \nonumber \\&=I_{1}dt+I_{2}dt+I_{3}dt+2\left( {\textbf{G}}(t,{\textbf{y}}_{n}),{\textbf{u}} _{n}\right) \,d{{\mathcal {W}}}_{t}. \end{aligned}$$

(3.14)

Considering Young’s inequality (2.8) for an appropriate $\varepsilon >0$, the inequalities (2.3)–(2.5) and the regularities (3.1), (3.3), we estimate the terms $I_{1},$ $I_{2}$ and $I_{3}$. Namely

$$\begin{aligned} I_{1}&\leqslant 2\nu ||{\textbf{a}}||_{V}||{\textbf{u}}_{n}||_{V}+\Vert a\Vert _{L_{\infty }(\Gamma )}\Vert {\textbf{u}}_{n}\Vert _{L_{2}(\Gamma )}^{2}+2\nu \Vert b\Vert {_{L_{2}(\Gamma )}}\Vert {\textbf{u}}_{n}\Vert {_{L_{2}(\Gamma )}} \, \\&\leqslant \frac{C}{\nu }||a||_{W_{p}^{1-\frac{1}{p}}(\Gamma )}^{2}|| {\textbf{u}}_{n}||_{2}^{2}+C\nu (||{\textbf{a}}||_{V}^{2}+\Vert b\Vert _{L_{2}(\Gamma )}^{2})+\frac{\nu }{2}||{\textbf{u}}_{n}||_{V}^{2} \\&\leqslant \frac{C}{\nu }\text {A}||{\textbf{u}}_{n}||_{2}^{2}+C\nu ||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+\frac{\nu }{2}||{\textbf{u}} _{n}||_{V}^{2}\,, \end{aligned}$$

where A is defined by (3.12). A similar reasoning gives

$$\begin{aligned} I_{2}\leqslant & {} 2\left( \Vert \partial _{t}{\textbf{a}}\Vert _{2}+\,|| {\textbf{a}}||_{C(\overline{\Omega })}\Vert \nabla {\textbf{a}}\Vert _{2}\right) \,||{\textbf{u}}_{n}||_{2}+2\Vert \nabla {\textbf{a}}\Vert _{2}\,\Vert {\textbf{u}} _{n}\Vert _{4}^{2} \\\leqslant & {} C\left( \Vert \partial _{t}{\textbf{a}}\Vert _{2}^{2}+\,||\textbf{a }||_{C(\overline{\Omega })}^{2}+\Vert \nabla {\textbf{a}}\Vert _{2}^{2}+1\right) \left( 1+||{\textbf{u}}_{n}||_{2}\right) +\frac{\nu }{2}|| {\textbf{u}}_{n}||_{V}^{2} \\\leqslant & {} C\text {A}(1+\,||{\textbf{u}}_{n}||_{2}^{2})\,+\frac{\nu }{ 2}||{\textbf{u}}_{n}||_{V}^{2} \end{aligned}$$

and

$$\begin{aligned} I_{3}= & {} \sum _{i=1}^{n}|\left( {\textbf{G}}\left( t,{\textbf{y}}_{n}\right) , {\textbf{e}}_{i}\right) |^{2}\leqslant C||{\textbf{G}}\left( t,{\textbf{y}} _{n}\right) ||_{2}^{2}\leqslant C(1+||{\textbf{y}}_{n}||_{2}^{2}) \\\leqslant & {} C(1+||{\textbf{u}}_{n}||_{2}^{2}+||{\textbf{a}}||_{2}^{2})\leqslant C(||{\textbf{u}}_{n}||_{2}^{2}+\text {A}), \end{aligned}$$

where we used the assumption (2.11). Gathering the previous estimates, we obtain the existence of a positive constant $C_{0},$ such that

$$\begin{aligned} I_{1}+I_{2}+I_{3}\leqslant 2C_{0}\text {A}(||{\textbf{u}}_{n}\Vert _{2}^{2}+1). \end{aligned}$$

(3.15)

Taking the function $\xi _{0}$ as in (3.10), thanks to (3.14)- (3.15), the application of Itô’s formula yields

$$\begin{aligned} \xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}^{2}&+2\nu \int _{0}^{s}\xi _{0}^{2}(r)\left\| {\textbf{u}}_{n}\right\| _{V}^{2}dr \\&=\left\| {\textbf{u}}_{n}(0)\right\| _{2}^{2}-2C_{0}\int _{0}^{s}\xi _{0}^{2}(r)\text {A}(r)\left\| {\textbf{u}}_{n}\right\| _{2}^{2}dr \\&\quad +\int _{0}^{s}\xi _{0}^{2}(r)(I_{1}+I_{2}+I_{3})dr+2\int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}(r,{\textbf{y}}_{n}),{\textbf{u}}_{n}\right) \,d{ {\mathcal {W}}}_{r} \\&\leqslant \left\| {\textbf{u}}_{n,0}\right\| _{2}^{2}-2C_{0}\int _{0}^{s}\xi _{0}^{2}(r)\text {A}(r)\left\| {\textbf{u}}_{n}\right\| _{2}^{2}dr \\&\quad +2C_{0}\int _{0}^{s}\xi _{0}^{2}(r)\text {A}(r)dr+2\int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}(r,{\textbf{y}}_{n}),{\textbf{u}}_{n}\right) \,d{ {\mathcal {W}}}_{r} \\&\leqslant \left\| {\textbf{u}}_{n,0}\right\| _{2}^{2}+2C_{0}\int _{0}^{s}\xi _{0}^{2}(r)\text {A} (r)dr+2\int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}(r,{\textbf{y}}_{n}), {\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{r}. \end{aligned}$$

Therefore, we can write

$$\begin{aligned} \xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}^{2}+\nu \int _{0}^{s}\xi _{0}^{2}(r)\left\| {\textbf{u}}_{n}\right\| _{V}^{2}\ dr&\leqslant \left\| {\textbf{u}}_{n,0}\right\| _{2}^{2}+C\int _{0}^{s}\xi _{0}^{2}(r)A(r)\,dr \nonumber \\&\quad +2\int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}\left( r,{\textbf{y}} _{n}\right) ,{\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{r}. \end{aligned}$$

(3.16)

Now, considering the sequence $(\tau _{N}^{n})$ of the stopping times introduced in (3.13) and using (2.11), the Burkholder-Davis-Gundy inequality gives

$$\begin{aligned}&{\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\left| \int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}\left( r,{\textbf{y}}_{n}\right) , {\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{r}\right| \leqslant {\mathbb {E}} \left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\left| \left( {\textbf{G}}\left( s,{\textbf{y}}_{n}\right) ,{\textbf{u}}_{n}\right) \right| ^{2}\,ds\right) ^{\frac{1}{2}} \\&\qquad \qquad \leqslant {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}\left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{G}}\left( s, {\textbf{y}}_{n}\right) \right\| _{2}^{2}\,ds\right) ^{\frac{1}{2}} \\&\qquad \qquad \leqslant \varepsilon \,{\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{2}(s)\Vert {\textbf{u}}_{n}(s)\Vert _{2}^{2}+C_{\varepsilon }{\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)(||{\textbf{u}}_{n}||_{2}^{2}+\text {A}(s))\,ds. \end{aligned}$$

For $t\in [0,T]$, we first take the supremun of the relation (3.16) for $s\in [0,\tau _{N}^{n}\wedge t]$, next we take the expectation and incorporate the previous estimate of the stochastic term with $\varepsilon =\frac{1}{2}$. Then considering (3.9), we deduce

$$\begin{aligned}&\frac{1}{2}{\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{2}(s)\Vert {\textbf{u}}_{n}(s)\Vert _{2}^{2}+\nu {\mathbb {E}} \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{u}} _{n}\right\| _{V}^{2}\,ds \\&\qquad \qquad \leqslant {\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{2}+C{\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\text { A}(s)\,ds+C{\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}\left\| {\textbf{u}}_{n}\right\| _{2}^{2}\,ds. \end{aligned}$$

Hence, the function

$$\begin{aligned} f(t)={\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{2}(s)\Vert {\textbf{u}}_{n}(s)\Vert _{2}^{2}+2\nu {\mathbb {E}} \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{u}} _{n}\right\| _{V}^{2}\,ds \end{aligned}$$

fulfills the Gronwall type inequality

$$\begin{aligned} \frac{1}{2}f(t)\leqslant {\mathbb {E}}\left\| {\textbf{u}}_{n}(0)\right\| _{2}^{2}+C{\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\text {A} (s)\,ds+\int _{0}^{t}f(s)ds, \end{aligned}$$

which implies

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}^{2}&+2\nu {\mathbb {E}} \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{u}} _{n}\right\| _{V}^{2}\,ds \nonumber \\&\leqslant C{\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{2}+C {\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\text {A}(s)\,ds. \end{aligned}$$

(3.17)

Step 2. The limit transition as $N\rightarrow \infty$. From (3.17) we have

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge T]}g(s)\leqslant C \end{aligned}$$

for some constant C independent of N and n. Let us fix $n\in {\mathbb {N}}$. Since ${\textbf{u}}_{n}\in C([0,T_{n}];V_{n}),$ we have $\ g(\tau _{N}^{n})\geqslant N$ and

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge T]}g(s)&\geqslant {\mathbb {E}}\left( \sup _{s\in [0,\tau _{N}^{n}\wedge T]}1_{\{\tau _{N}^{n}<T\}}g(s)\right) \nonumber \\&={\mathbb {E}}\left( 1_{\{\tau _{N}^{n}<T\}}\ g(\tau _{N}^{n})\right) \geqslant NP\left( \tau _{N}^{n}<T\right) , \end{aligned}$$

(3.18)

which implies that $P\left( \tau _{N}^{n}<T\right) \rightarrow 0$ as $N\rightarrow \infty .$ This means that $\tau _{N}^{n}\rightarrow T$ in probability as $N\rightarrow \infty$. Then, there exists a subsequence $\{\tau _{N_{k}}^{n}\}$ of $\{\tau _{N}^{n}\}$ (which may depend on n) such that

$$\begin{aligned} \tau _{N_{k}}^{n}(\omega )\rightarrow T\quad \text {for a.e. }\omega \in \Omega \quad \text {as }k\rightarrow \infty . \end{aligned}$$

Since $\tau _{N_{k}}^{n}\leqslant T_{n}\leqslant T$, we deduce that $T_{n}=T$, hence ${\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}$ is a global-in-time solution of the stochastic differential equation (3.8). In addition, for each fixed $n\in {\mathbb {N}}$, the sequence $\left\{ \tau _{N}^{n}\right\}$ is monotone on N, therefore we can apply the monotone convergence theorem in order to pass to the limit in the inequality (3.17) as $N\rightarrow \infty$, thereby deducing the estimate (3.11). $\square$

In the next lemma, by assuming a better integrability for the initial data, we improve the integrability properties for the solution ${\textbf{y}}_{n}$ of problem (3.8).

Lemma 3.4

Let the data (a, b) and ${\textbf{u}}_{0}$ satisfy the regularity (2.12). In addition we assume

$$\begin{aligned} (a,b)\in & {} L_{4}(\Omega \times (0,T);{\mathcal {H}}_{p}(\Gamma )), \nonumber \\ {\textbf{u}}_{0}\in & {} L_{4}(\Omega ;H). \end{aligned}$$

(3.19)

Then, the solution ${\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}$ of problem (3.8) has the regularity

$$\begin{aligned} {\textbf{u}}_{n}\in C([0,T];H)\cap L_{4}(0,T;V),\quad P\text {-a.e. in }\Omega \text {,} \end{aligned}$$

such that

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{0}^{4}(s)\left\| {\textbf{u}} _{n}(s)\right\| _{2}^{4}+ & {} 8\nu ^{2}{\mathbb {E}}\left( \int _{0}^{t}\xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{V}^{2}ds\right) ^{2} \nonumber \\\leqslant & {} C\left( {\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{4}+ {\mathbb {E}}\int _{0}^{t}\xi _{0}^{4}\text {B}(s)\,ds\right) ,\quad t\in [0,T],\quad \end{aligned}$$

(3.20)

where the function $\xi _{0}$ is defined in (3.10),

$$\begin{aligned} \text {B}=||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{4}+1\in L_{1}(\Omega \times (0,T)) \end{aligned}$$

(3.21)

and C is a positive constant, being independent of n.

Proof

Taking the square on both sides of the inequality (3.16) and the supremum on $s\in [0,\tau _{N}^{n}\wedge t]$ with $\tau _{N}^{n}$ defined by (3.13), we infer that

$$\begin{aligned} \begin{aligned} \sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{4}(s)\left\| {{\textbf {u}}}_{n}(s)\right\| _{2}^{4}&+\nu ^{2}\left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {{\textbf {u}}}_{n}(s)\right\| _{V}^{2}ds\right) ^{2} \\&\leqslant 8\left( \left\| {{\textbf {u}}}_{n,0}\right\| _{2}^{4}+C^{2} {\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\text{ B } (s)\,ds\right) \\&\quad +4\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\left| \int _{0}^{s}\xi _{0}^{2}(r)\left( {{\textbf {G}}}\left( r,{{\textbf {y}}}_{n}\right) ,{{\textbf {u}}} _{n}\right) \,d{{\mathcal {W}}}_{r}\right| ^{2}, \end{aligned} \end{aligned}$$

where B is defined by (3.21). Therefore taking the expectation in this inequality and applying the Burkholder-Davis-Gundy inequality

$$\begin{aligned} {\mathbb {E}}&\sup _{s\in [0,\tau _{N}^{n}\wedge t]}|\int _{0}^{s}\xi _{0}^{2}(r)\left( {\textbf{G}}\left( r,{\textbf{y}}_{n}\right) ,{\textbf{u}} _{n}\right) \,d{{\mathcal {W}}}_{r}|^{2}\leqslant {\mathbb {E}}\left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\left| \left( {\textbf{G}} \left( s,\mathbf {\ y}_{n}\right) ,{\textbf{u}}_{n}\right) \right| ^{2}\,ds\right) \\&\qquad \qquad \leqslant {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{2}\left\| {\textbf{u}}_{n}\right\| _{2}^{2}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}\left\| {\textbf{G}}\left( s,{\textbf{y}} _{n}\right) \right\| _{2}^{2}\,ds \\&\qquad \qquad \leqslant \frac{1}{2}\,{\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{4}(s)\Vert {\textbf{u}}_{n}(s)\Vert _{2}^{4}+C {\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\left( ||{\textbf{u}} _{n}||_{2}^{4}+\text {B}(s)\right) \,ds, \end{aligned}$$

we obtain

$$\begin{aligned} \frac{1}{2}{\mathbb {E}}&\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{4}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}^{4}+\nu ^{2}\mathbb {E }\left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{u}} _{n}\right\| _{V}^{2}ds\right) ^{2} \\&\qquad \leqslant C({\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{4}+\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\text {B} (s)\,ds+C{\mathbb {E}}\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)(1+|| {\textbf{u}}_{n}||_{2}^{4})\,ds. \end{aligned}$$

Using Gronwall’s inequality, we deduce that

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,\tau _{N}^{n}\wedge t]}\xi _{0}^{4}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{2}^{4}+ & {} \nu ^{2} {\mathbb {E}}\left( \int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{2}(s)\left\| {\textbf{u}}_{n}\right\| _{V}^{2}ds\right) ^{2}\leqslant C{\mathbb {E}} \left\| {\textbf{u}}_{0}\right\| _{2}^{4} \nonumber \\+ & {} C\int _{0}^{\tau _{N}^{n}\wedge t}\xi _{0}^{4}(s)\text {B} (s)\,ds,\quad \forall t\in [0,T]. \end{aligned}$$

(3.22)

Arguing as in the proof of Lemma 3.3, there exists a monotone subsequence $\{\tau _{N_{k}}^{n}\}$ of $\{\tau _{N}^{n}\}$, which converges to T a.e. $\omega \in \Omega$, as $k\rightarrow \infty$. Thus, applying the monotone convergence theorem, we can pass to the limit in (3.22) as $k\rightarrow \infty$, in order to deduce the estimate (3.20). $\square$

Theorem 3.5

Let the data (a, b) and ${\textbf{u}}_{0}$ satisfy the regularity (2.12) and (3.19). Then there exists, a unique strong solution ${\textbf{y}}={\textbf{u}}+{\textbf{a}}$ to the system (1.1)– (1.2), such that

$$\begin{aligned} {\textbf{u}}\in C([0,T];H)\cap L_{4}(0,T;V),\quad P\text {-a.e. in }\Omega , \end{aligned}$$

and for any $t\in [0,T],$ the following estimates hold

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{0}^{2}(s)\left\| {\textbf{u}} (s)\right\| _{2}^{2}&+\nu {\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\left\| {\textbf{u}}\right\| _{V}^{2}\,ds \nonumber \\&\leqslant C\left( {\mathbb {E}}\left\| {\textbf{u}}_{0}\right\| _{2}^{2}+ {\mathbb {E}}\int _{0}^{t}\xi _{0}^{2}(s)\textrm{A}(s)\,ds\right) , \end{aligned}$$

(3.23)

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{0}^{4}(s)\left\| {\textbf{u}} (s)\right\| _{2}^{4}&+\nu ^{2}{\mathbb {E}}\left( \int _{0}^{t}\xi _{0}^{2}(s)\left\| {\textbf{u}}\right\| _{V}^{2}ds\right) ^{2} \nonumber \\&\leqslant C\left( {\mathbb {E}}\left\| {\textbf{y}}_{0}\right\| _{2}^{4}+\nu ^{2}{\mathbb {E}}\int _{0}^{t}\xi _{0}^{4}(s)\textrm{B} (s)\,ds\right) , \end{aligned}$$

(3.24)

where the functions $\xi _{0}$ and A, B are defined by (3.10) and (3.12), (3.21), respectively. Here C is a positive constant that is independent of n.

Proof

The proof is splitted into three steps.

Step 1. Convergence related to the projection operator. Let $P_{n}:V\rightarrow V_{n}$ be the orthogonal projection defined by

$$\begin{aligned} P_{n}{\textbf{v}}=\sum _{j=1}^{n}\widetilde{\beta }_{j}\widetilde{{\textbf{e}}} _{j}=\sum _{j=1}^{n}\beta _{j}{\textbf{e}}_{j}\quad \text {with }\widetilde{ \beta }_{j}=\left( {\textbf{v}},\widetilde{{\textbf{e}}}_{j}\right) _{V},\quad \beta _{j}=\left( {\textbf{v}},{\textbf{e}}_{j}\right) ,\quad \forall {\textbf{v}} \in V, \end{aligned}$$

where $\{\widetilde{{\textbf{e}}}_{j}=\frac{1}{\sqrt{\lambda _{j}}}{\textbf{e}} _{j}\}_{j=1}^{\infty }$ is the orthonormal basis of V. By Parseval’s identity, for any ${\textbf{v}}\in V$ we have

$$\begin{aligned} ||P_{n}{\textbf{v}}||_{2}\leqslant & {} ||{\textbf{v}}||_{2},\quad ||P_{n}{\textbf{v}} ||_{V}\leqslant ||{\textbf{v}}||_{V}, \nonumber \\ P_{n}{\textbf{v}}\rightarrow & {} {\textbf{v}}\quad \text{ strongly } \text{ in } \text { }V. \end{aligned}$$

(3.25)

Considering an arbitrary ${\textbf{z}}\in L_{s}(\Omega \times (0,T);V)$ for some $s\geqslant 1$, we have

$$\begin{aligned} ||P_{n}{\textbf{z}}||_{V}\leqslant ||{\textbf{z}}||_{V}\quad \text{ and } \quad P_{n}{\textbf{z}}(\omega ,t)\rightarrow {\textbf{z}}(\omega ,t)\quad \text {strongly in}\ V, \end{aligned}$$

which are valid P-a.e. $\omega \in \Omega$ and a.e. $t\in (0,T).$ Hence, Lebesgue’s dominated convergence theorem implies that for any ${\textbf{z}}\in L_{s}(\Omega \times (0,T);V)$, we have

$$\begin{aligned} P_{n}{\textbf{z}}\rightarrow {\textbf{z}}\quad \text{ strongly } \text{ in } \ L_{s}(\Omega \times (0,T);V). \end{aligned}$$

(3.26)

Step 2. Passage to the limit in the weak sense.

Let us define$~f_{0}(t)=C_{0}\left( ||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+1\right)$. Since

$$\begin{aligned} \int _{0}^{T}f_{0}(s)\ ds\leqslant C(\omega )<+\infty \quad \text {for all } \omega \in \Omega \backslash A,\quad \text {where }P(A)=0 \end{aligned}$$

by (2.12), there exists a positive constant $K(\omega ),$ which depends only on $\omega \in \Omega \backslash A$ and satisfies

$$\begin{aligned} 0<K(\omega )\leqslant \xi _{0}(t)=e^{-\int _{0}^{t}f_{0}(s)\ ds}\leqslant 1\quad \text {for all }\omega \in \Omega \backslash A,\quad t\in [0,T]. \end{aligned}$$

(3.27)

The estimates (3.11) and (3.20) give that

$$\begin{aligned} {\mathbb {E}}\sup _{t\in [0,T]}\left\| \xi _{0}(t){\textbf{u}} _{n}(t)\right\| _{2}^{2}\leqslant & {} C,\quad {\mathbb {E}} \int _{0}^{T}\left\| \xi _{0}{\textbf{u}}_{n}\right\| _{V}^{2}\ dt\leqslant C, \nonumber \\ {\mathbb {E}}\sup _{t\in [0,T]}\left\| \xi _{0}(t){\textbf{u}} _{n}(t)\right\| _{2}^{4}\leqslant & {} C,\quad {\mathbb {E}}\left( \int _{0}^{T}\left\| \xi _{0}{\textbf{u}}_{n}\right\| _{V}^{2}\ dt\right) ^{2}\leqslant C \end{aligned}$$

(3.28)

for some constant C that is independent of the index n. These uniform estimates imply

$$\begin{aligned} \left\| \xi _{0}^{2}\left( {\textbf{y}}_{n}\cdot \nabla \right) {\textbf{y}} _{n}\right\| _{L_{2}(\Omega \times (0,T);V^{\prime })}\leqslant C,\quad \forall n\in {\mathbb {N}}, \end{aligned}$$

(3.29)

where $V^{\prime }$ denotes the topological dual of the space V. The uniform estimates (3.28) ensures the existence of a suitable subsequence ${\textbf{u}}_{n}$, which is indexed by the same index n to simplify the notation, and a function ${\textbf{u}},$ such that

$$\begin{aligned} \xi _{0}{\textbf{u}}_{n}&\rightharpoonup&\xi _{0}{\textbf{u}}\quad \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);V)\cap L_{4}(\Omega ,L_{2}(0,T;V)), \nonumber \\ \xi _{0}{\textbf{u}}_{n}&\rightharpoonup&\xi _{0}{\textbf{u}}\quad \text{*-weakly } \text{ in } \ L_{2}(\Omega ,L_{\infty }(0,T;H))\cap L_{4}(\Omega ,L_{\infty }(0,T;H)). \qquad \end{aligned}$$

(3.30)

Moreover, we have

$$\begin{aligned} \xi _{0}P_{n}{\textbf{u}}\rightarrow \xi _{0}{\textbf{u}}\quad \text{ strongly } \text{ in } \ L_{2}(\Omega \times (0,T);V)\cap L_{4}(\Omega ,L_{2}(0,T;V)) \end{aligned}$$

(3.31)

by (3.26). The limit function ${\textbf{u}}$ satisfies the estimates (3.23), (3.24) by the lower semicontinuity of integral in $L_{2}$ and $L_{4}$ spaces.

Considering (2.11) and (3.29), there exist some operators $B^{*}(t)$ and ${\textbf{G}}^{*}(t)$ such that

$$\begin{aligned} \xi _{0}{\textbf{G}}(t,{\textbf{y}}_{n})&\rightharpoonup&\xi _{0}{\textbf{G}} ^{*}(t)\quad \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);H^{m}), \nonumber \\ \xi _{0}^{2}\left( {\textbf{y}}_{n}\cdot \nabla \right) {\textbf{y}}_{n}&\rightharpoonup&\xi _{0}^{2}B^{*}(t)\quad \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);V^{\prime }). \end{aligned}$$

(3.32)

Since ${\textbf{y}}_{n}$ solves the equation (3.8), then using Itô’s formula, we infer that

$$\begin{aligned} d\left( \xi _{0}^{2}{\textbf{y}}_{n},\varvec{\varphi }\right)&=\xi _{0}^{2}[-\nu \left( {\textbf{y}}_{n},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(\varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma } -(\left( {\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n},\varvec{\varphi } \right) \, \\&\quad -2f_{0}(t)\left( {\textbf{y}}_{n},\varvec{\varphi }\right) ]\,dt+\xi _{0}^{2}\left( {\textbf{G}}(t,{\textbf{y}}_{n}),\varvec{\varphi }\right) \,d{ {\mathcal {W}}}_{t}, \end{aligned}$$

that is, the following integral equation holds

$$\begin{aligned} \left( \xi _{0}^{2}(t){\textbf{y}}_{n}(t),\varvec{\varphi }\right) -\left( {\textbf{y}}_{n,0},\varvec{\varphi }\right)&=\int _{0}^{t}\xi _{0}^{2}(s)[-\nu \left( {\textbf{y}}_{n}(s),\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(s)(\varvec{\varphi }\cdot {\varvec{\tau }})\,d \mathbf {\gamma } \nonumber \\&\quad -(\left( {\textbf{y}}_{n}(s)\cdot \nabla ){\textbf{y}}_{n}(s),\varvec{ \varphi }\right) \,-2f_{0}(s)\left( {\textbf{y}}_{n}(s),\varvec{\varphi } \right) ]\,ds \nonumber \\&\quad +\int _{0}^{t}\xi _{0}^{2}(s)\left( {\textbf{G}}(s,{\textbf{y}}_{n}), \varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s},\quad \forall t\in [0,T],P\text {-a.e. in }\Omega . \end{aligned}$$

(3.33)

Denoting

$$\begin{aligned} {\textbf{h}}_{n}(t)=\xi _{0}^{2}(t){\textbf{y}}_{n}(t)-\int _{0}^{t}\xi _{0}^{2}(s){\textbf{G}}(s,{\textbf{y}}_{n})\,d{{\mathcal {W}}}_{s} \end{aligned}$$

the following differential equation holds

$$\begin{aligned} \frac{\partial }{\partial t}\left( {\textbf{h}}_{n}(t),\varvec{\varphi } \right)&=\xi _{0}^{2}(t)[-\nu \left( {\textbf{y}}_{n}(t),\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(t)(\varvec{\varphi }\cdot {\varvec{\tau } })\,d\mathbf {\gamma }-(\left( {\textbf{y}}_{n}(t)\cdot \nabla ){\textbf{y}} _{n}(t),\varvec{\varphi }\right) \, \nonumber \\&\quad -2f_{0}(t)\left( {\textbf{y}}_{n}(t),\varvec{\varphi }\right) ],\quad P \text {-a.e. in }\Omega ,\quad \forall t\in [0,T]. \end{aligned}$$

(3.34)

We notice that due to the properties of the stochastic integral and the assumption (2.11), we have

$$\begin{aligned} {\textbf{h}}_{n}(t)\!\rightharpoonup \! {\textbf{h}}(t)\!=\!\xi _{0}^{2}(t){\textbf{y}} (t)\!-\!\int _{0}^{t}\xi _{0}^{2}(s){\textbf{G}}^{*}(t)\,d{{\mathcal {W}}} _{s}\, \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);H^{1}({{\mathcal {O}}})). \end{aligned}$$

Now, we pass to the limit in the equation (3.33) in the distributional sense. Namely multiplying the equation (3.34) by the test funtion $\theta (t)\eta (\omega )$, with $\theta \in C^{\infty }([0,T])$ with compact support and $\eta \in L_{2}(\Omega )$, and passing to the limit, we derive

$$\begin{aligned} {\mathbb {E}}\int _{0}^{T}\left( {\textbf{h}}(t),\varvec{\varphi }\right) \theta ^{\prime }(t)\eta&=-{\mathbb {E}}\int _{0}^{T}\xi _{0}^{2}(t)[-\nu \left( {\textbf{y}}(t),\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(t)(\varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }\, \\&\quad -\left( B^{*}(t),\varvec{\varphi }\right) -2f_{0}(t)\left( \textbf{ y}(t),\varvec{\varphi }\right) ]\theta \eta \,dt. \end{aligned}$$

Therefore $\frac{\partial {\textbf{h}}}{\partial t}\in L_{2}(\Omega \times (0,T);\left( H^{1}({\mathcal {O}})\right) ^{*})$. Since ${\textbf{h}}\in L_{2}(\Omega \times (0,T);H^{1}({\mathcal {O}}))$, we infer that ${\textbf{h}}\in L_{2}(\Omega ;C([0,T];L_{2}({\mathcal {O}}))$ by the Aubin-Lions embeeding result [3, 46]. Taking into account the continuity property of the stochastic integral, we conclude that $\xi _{0}^{2}{\textbf{y}}\in L_{2}(\Omega ;C([0,T];L_{2}({\mathcal {O}})).$ In addition

$$\begin{aligned} \xi _{0}^{2}{\textbf{y}}_{n}\rightharpoonup \xi _{0}^{2}{\textbf{y}}\quad \text { in }C_{\omega }([0,T],L_{2}(\Omega )\times L_{2}({\mathcal {O}})), \end{aligned}$$

where the index $\omega$ means that we are considering $L_{2}(\Omega )\times L_{2}({\mathcal {O}})$ endowed with the weak topology. Hence, we have

$$\begin{aligned} {\mathbb {E}}\left[ \left( \xi _{0}^{2}(t){\textbf{y}}_{n}(t),\varvec{\varphi }\right) \eta \right] \rightarrow {\mathbb {E}}\left[ \left( \xi _{0}^{2}(t) {\textbf{y}}(t),\varvec{\varphi }\right) \eta \right] ,\quad \forall t\in [0,T]. \end{aligned}$$

(3.35)

Now, we multiply the equation (3.33) by an arbitrary $\eta \in L_{2}(\Omega )$ and take the expectation, we derive

$$\begin{aligned}{} & {} \mathbb {E\ }\eta \{\left( \xi _{0}^{2}(t){\textbf{y}}_{n}(t),\varvec{ \varphi }\right) -\left( {\textbf{y}}_{n,0},\varvec{\varphi }\right) \} \\{} & {} \qquad \qquad =\mathbb {E\ }\eta \left\{ \int _{0}^{t}\xi _{0}^{2}[-\nu \left( {\textbf{y}}_{n},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(\varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(\left( {\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n},\varvec{\varphi }\right) \,\right. \\{} & {} \qquad \qquad \left. -2f_{0}\left( {\textbf{y}}_{n},\varvec{\varphi } \right) ]\,dt+\int _{0}^{t}\xi _{0}^{2}\left( {\textbf{G}}(s,{\textbf{y}}_{n}), \varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s}\right\} . \end{aligned}$$

Applying (3.30)–(3.32) and (3.35), we pass to the limit $n\rightarrow \infty$ in this equality and deduce

$$\begin{aligned}{} & {} \mathbb {E\ }\eta \left\{ \left( \xi _{0}^{2}(t){\textbf{y}}(t),\varvec{ \varphi }\right) -\left( {\textbf{y}}_{0},\varvec{\varphi }\right) \right\} =\mathbb {E\ }\eta \left\{ \int _{0}^{t}\xi _{0}^{2}[-\nu \left( {\textbf{y}},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b( \varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }\right. \\{} & {} \left. \quad \quad -\left( B^{*},\varvec{\varphi }\right) -2f_{0}\left( {\textbf{y}},\varvec{\varphi }\right) ]\,dt+\int _{0}^{t}\xi _{0}^{2}\left( {\textbf{G}}^{*}(s),\varvec{\varphi }\right) \,d{ {\mathcal {W}}}_{s}\right\} . \end{aligned}$$

Since $\eta \in L_{2}(\Omega )$ is arbitrary, the following equation holds

$$\begin{aligned}&\left( \xi _{0}^{2}(t){\textbf{y}}(t),\varvec{\varphi }\right) -\left( {\textbf{y}}_{0},\varvec{\varphi }\right) =\left\{ \int _{0}^{t}\xi _{0}^{2}[-\nu \left( {\textbf{y}},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(\varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma } \right. \nonumber \\&\left. \quad \quad -\left( B^{*},\varvec{\varphi }\right) -f_{0}\left( {\textbf{y}},\varvec{\varphi }\right) ]\,dt+\int _{0}^{t}\xi _{0}^{2}\left( {\textbf{G}}^{*},\varvec{\varphi }\right) \,d{\mathcal {W }}_{s}\right\} \end{aligned}$$

(3.36)

for any $t\in [0,T]$ and P-a.e. in $\Omega ,$ that is

$$\begin{aligned} d\left( \xi _{0}^{2}\left( {\textbf{y}},\varvec{\varphi }\right) \right)&=\xi _{0}^{2}[-\nu \left( {\textbf{y}},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b(\varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma } -\left( B^{*},\varvec{\varphi }\right) \, \\&\quad -2f_{0}\left( {\textbf{y}},\varvec{\varphi }\right) ]\,dt+\xi _{0}^{2}\left( {\textbf{G}}^{*},\varvec{\varphi }\right) \,d{\mathcal {W }}_{t}\text { and }{\textbf{y}}(0)={\textbf{y}}_{0}. \end{aligned}$$

Moreover if we use Itô’s formula

$$\begin{aligned} \ d\left( {\textbf{y}},\varvec{\varphi }\right) =d\left[ \xi _{0}^{-2}\xi _{0}^{2}\left( {\textbf{y}},\varvec{\varphi }\right) \right] =\xi _{0}^{2}\left( {\textbf{y}},\varvec{\varphi }\right) d\left( \xi _{0}^{-2}\right) +\xi _{0}^{-2}d\left[ \xi _{0}^{2}\left( {\textbf{y}}, \varvec{\varphi }\right) \right] , \end{aligned}$$

we derive that the limit function ${\textbf{y}}$ in the form ${\textbf{y}}= {\textbf{u}}+{\textbf{a}}$ with

$$\begin{aligned} \mathbf {u\in }L_{\infty }(0,T;H)\cap L_{2}(0,T;V),\quad P\text {-a.e. in } \Omega ,\quad \text {a.e. on }(0,T), \end{aligned}$$

satisfies P-a.e. in $\Omega$ the stochastic differential equation

$$\begin{aligned} d\left( {\textbf{y}},\varvec{\varphi }\right)&=[-\nu \left( {\textbf{y}}, \varvec{\varphi }\right) _{V}+\nu \int _{\Gamma }b(\varvec{\varphi } \cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(B^{*}(t),\varvec{\varphi } )\,]dt \nonumber \\&\quad +\left( {\textbf{G}}^{*}(t),\varvec{\varphi }\right) \,d{{\mathcal {W}}} _{t},\quad \forall t\in [0,T],\quad \forall \varvec{\varphi }\in V, \end{aligned}$$

(3.37)

and ${\textbf{y}}(0)={\textbf{y}}_{0}.$

Step 3. Deduction of strong convergence as $n\rightarrow \infty .$ In order to prove that the limit process ${\textbf{y}}$ satisfies the equation (3.6), we adapt the methods in [10]. Writing ${\textbf{y}}={\textbf{u}}+{\textbf{a}}$, ${\textbf{y}}_{n}={\textbf{u}}_{n}+{\textbf{a}}$ and taking the difference of the equations (3.8) and (3.37) with $\varvec{\varphi }={\textbf{e}}_{i}\in V_{n}$, $i=1,\ldots ,n$, we deduce

$$\begin{aligned} d\left( P_{n}{\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right)= & {} \left[ -\nu \left( P_{n}{\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right) _{V}+\left( ( {\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t),{\textbf{e}} _{i}\right) \right] \,dt \nonumber \\- & {} \quad \left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}} _{i}\right) \,d{{\mathcal {W}}}_{t},\quad i=1,\ldots ,n. \end{aligned}$$

(3.38)

Then the Itô’s formula yields

$$\begin{aligned} d(P_{n}{\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i})^{2}&=2\left( P_{n}\textbf{u }-{\textbf{u}}_{n},{\textbf{e}}_{i}\right) \\&\quad \times \left[ -\nu \left( P_{n}{\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}} _{i}\right) _{V}+\left( ({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t),{\textbf{e}}_{i}\right) \right] \,dt \\&\quad -2\left( P_{n}{\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right) \left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}}_{i}\right) \,d{ {\mathcal {W}}}_{t} \\&\quad +|\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}} _{i}\right) |^{2}\,dt. \end{aligned}$$

Summing over $i=1,\dots ,n,$ we derive

$$\begin{aligned} d\left( ||P_{n}{\textbf{u}}-{\textbf{u}}_{n}||_{2}^{2}\right) +2\nu ||P_{n} {\textbf{u}}-{\textbf{u}}_{n}||_{V}^{2}dt&=2(({\textbf{y}}_{n}\cdot \nabla )\textbf{ y}_{n}-B^{*}(t),P_{n}{\textbf{u}}-{\textbf{u}}_{n})\,dt \nonumber \\&\quad +\sum _{i=1}^{n}|\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t), {\textbf{e}}_{i}\right) |^{2}\,dt \nonumber \\&\quad -2\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),P_{n}{\textbf{u}} -{\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{t}. \end{aligned}$$

(3.39)

Standard computations give

$$\begin{aligned} ({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t)&=\left\{ -(( {\textbf{u}}_{n}+{\textbf{a}})\cdot \nabla )(P_{n}{\textbf{u}}-{\textbf{u}} _{n})-((P_{n}{\textbf{u}}-{\textbf{u}}_{n})\cdot \nabla )(P_{n}{\textbf{u}}+ {\textbf{a}})\right\} \\&\quad +((P_{n}{\textbf{u}}-{\textbf{u}})\cdot \nabla )(P_{n}{\textbf{u}}+{\textbf{a}})+(( {\textbf{u}}+{\textbf{a}})\cdot \nabla )(P_{n}{\textbf{u}}-{\textbf{u}}) \\&\quad +\left\{ ({\textbf{y}}\cdot \nabla ){\textbf{y}}-B^{*}(t)\right\} =\left\{ A_{0,1}+A_{0,2}\right\} +A_{1}+A_{2}+A_{3}. \end{aligned}$$

In addition, using (2.3), (2.4), (3.3) and Theorem 4.47, p. 210, of [24], we show the existence of a constant $C_{2}$, verifying the relation

$$\begin{aligned} I_{0}&:=|\left( \left\{ A_{0,1}+A_{0,2}\right\} ,P_{n}{\textbf{u}}-{\textbf{u}} _{n}\right) | \nonumber \\&\leqslant \Bigl |\int _{\Gamma }a((P_{n}{\textbf{u}}-{\textbf{u}}_{n})\cdot \varvec{\tau })^{2}\,d\mathbf {\gamma }\Bigr |+\left| \left( ((P_{n}{\textbf{u}}- {\textbf{u}}_{n})\cdot \nabla )(P_{n}{\textbf{u}}+{\textbf{a}}),P_{n}{\textbf{u}}- {\textbf{u}}_{n}\right) \right| \nonumber \\&\leqslant \Vert a\Vert _{L_{\infty }(\Gamma )}\Vert P_{n}{\textbf{u}}- {\textbf{u}}_{n}\Vert _{L_{2}(\Gamma )}^{2}+\left\| P_{n}{\textbf{u}}+\mathbf { \ a}\right\| _{V}\left\| P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right\| _{4}^{2} \nonumber \\&\leqslant (\Vert a\Vert _{L_{\infty }(\Gamma )}+\left\| {\textbf{a}} \right\| _{H^{1}}+\left\| P_{n}{\textbf{u}}\right\| _{V})\left\| P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right\| _{2}\Vert P_{n}{\textbf{u}}-\textbf{u }_{n}\Vert _{V} \nonumber \\&\leqslant C_{2}(||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+\left\| {\textbf{u}}\right\| _{V}^{2})\Vert P_{n}{\textbf{u}}-{\textbf{u}}_{n}\Vert _{2}^{2}+\nu \left\| P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right\| _{V}^{2}. \end{aligned}$$

(3.40)

On the other hand, Hölder’s inequality gives

$$\begin{aligned} I_{1}&:=|\left( A_{1},P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right) |\leqslant C||P_{n}{\textbf{u}}-{\textbf{u}}||_{4}||\nabla (P_{n}{\textbf{u}}+{\textbf{a}} )||_{2}||P_{n}{\textbf{u}}-{\textbf{u}}_{n}||_{4} \nonumber \\&\leqslant C||P_{n}{\textbf{u}}-{\textbf{u}}||_{4}(||{\textbf{u}}||_{V}+||\textbf{ a}||_{H^{1}})(||P_{n}{\textbf{u}}||_{4}+||{\textbf{u}}_{n}||_{4}) \end{aligned}$$

(3.41)

and

$$\begin{aligned} I_{2}&:=|\left( A_{2},P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right) |\leqslant C|| {\textbf{u}}+{\textbf{a}}||_{4}||\nabla (P_{n}{\textbf{u}}-{\textbf{u}})||_{2}||P_{n} {\textbf{u}}-{\textbf{u}}_{n}||_{4} \nonumber \\&\leqslant C||P_{n}{\textbf{u}}-{\textbf{u}}||_{V}(||{\textbf{u}}||_{4}+||\textbf{ a}||_{4})(||P_{n}{\textbf{u}}||_{4}\mathbf {+||u}_{n}||_{4}). \end{aligned}$$

(3.42)

The last term $A_{3}$ will be considered later on.

Denoting

$$\begin{aligned} {\textbf{G}}_{n}={\textbf{G}}(t,{\textbf{y}}_{n}),\quad {\textbf{G}}={\textbf{G}}(t, {\textbf{y}}),\quad {\textbf{G}}^{*}={\textbf{G}}^{*}(t), \end{aligned}$$

(3.43)

we have

$$\begin{aligned} \sum _{i=1}^{n}|\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t), {\textbf{e}}_{i}\right) |^{2}=\sum _{i=1}^{n}|({\textbf{G}}_{n}-{\textbf{G}}^{*},{\textbf{e}}_{i})|^{2}=\Vert P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2}. \end{aligned}$$

The standard relation $x^{2}=(x-y)^{2}-y^{2}+2xy\;$ allows to write

$$\begin{aligned} \Vert P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2}&=\Vert P_{n} {\textbf{G}}_{n}-P_{n}{\textbf{G}}\Vert _{2}^{2}-\Vert P_{n}{\textbf{G}}-P_{n} {\textbf{G}}^{*}\Vert _{2}^{2} \\&\quad -2(P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*},P_{n}{\textbf{G}}-P_{n} {\textbf{G}}^{*}). \end{aligned}$$

From (2.11) and (3.25)$_{1}$, we have

$$\begin{aligned} \Vert P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}\Vert _{2}^{2}\leqslant \Vert {\textbf{G}}_{n}-{\textbf{G}}\Vert _{2}^{2}\leqslant K\left\| {\textbf{u}}_{n}- {\textbf{u}}\right\| _{2}^{2}, \end{aligned}$$

then for the fixed constant $C_{3}=2K$ it follows that

$$\begin{aligned} \sum _{i=1}^{n}|({\textbf{G}}(t,{\textbf{y}}_{n}) -{\textbf{G}}^{*}(t),\textbf{ e}_{i})|^{2}&=\Vert P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2} \nonumber \\&\leqslant K\left\| {\textbf{u}}_{n}-{\textbf{u}}\right\| _{2}^{2}-\Vert P_{n}\mathbf {\ G}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2} \nonumber \\&\quad +2(P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*},P_{n}{\textbf{G}}-P_{n} {\textbf{G}}^{*}) \nonumber \\&\leqslant C_{3}\left\| {\textbf{u}}_{n}-P_{n}{\textbf{u}}\right\| _{2}^{2}+C\left\| P_{n}{\textbf{u}}-{\textbf{u}}\right\| _{2}^{2}-\Vert P_{n}{\textbf{G}}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2} \nonumber \\&\quad +2(P_{n}{\textbf{G}}_{n}-P_{n}{\textbf{G}}^{*},P_{n}{\textbf{G}}-P_{n} {\textbf{G}}^{*}). \end{aligned}$$

(3.44)

The positive constants $C_{2}$ and $C_{3}$ in (3.40) and (3.44) are independent of n.

We notice that with the help of the convergence results (3.26), (3.30)–(3.32), and performing a suitable limit trfansition in the equation (3.39), as $n\rightarrow \infty ,$ we can verify that all terms on the right-hand side of the equality (3.39) containing $P_{n} {\textbf{u}}-{\textbf{u}}$ will vanish; however, terms that contain $P_{n}{\textbf{u}}-{\textbf{u}}_{n}$ will remain. Fortunately, these terms can be eliminated by introducing the auxiliary function

$$\begin{aligned} \widetilde{\xi }(t)=e^{-\int _{0}^{t}\widetilde{f}(s)\ ds} \end{aligned}$$

(3.45)

with $\widetilde{f}(t)=C_{3}+\max (3C_{0},C_{2})(1+||(a,b)||_{{\mathcal {H}} _{p}(\Gamma )}^{2}+\left\| {\textbf{u}}\right\| _{V}^{2}).$

Applying Itô’s formula to the equality (3.39) and using the definition (3.45) of $\widetilde{\xi }$, we obtain

$$\begin{aligned} d(\widetilde{\xi }(t)||P_{n}{\textbf{u}}&-{\textbf{u}}_{n}||_{2}^{2})+2\nu \widetilde{\xi }(t)||P_{n}{\textbf{u}}-{\textbf{u}}_{n}||_{V}^{2}\,dt \\&\leqslant 2\widetilde{\xi }(t)(({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}} _{n}-B^{*}(t),P_{n}{\textbf{u}}-{\textbf{u}}_{n})\,dt \\&\quad +\widetilde{\xi }(t)\sum _{i=1}^{n}|\left( {\textbf{G}}(t,{\textbf{y}}_{n})- {\textbf{G}}^{*}(t),{\textbf{e}}_{i}\right) |^{2}\,dt \\&\quad -2\widetilde{\xi }(t)\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{t}-C_{3} \widetilde{\xi }(t)||P_{n}{\textbf{u}}-{\textbf{u}}_{n}||_{2}^{2}\,dt \\&\quad -C_{2}\widetilde{\xi }(t)(||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+\left\| {\textbf{u}}\right\| _{V}^{2})||P_{n}{\textbf{u}}-{\textbf{u}} _{n}||_{2}^{2}\,dt. \end{aligned}$$

Writing this equation in the integral form, taking the expectation, and applying the estimates (3.40), (3.44), we deduce that

$$\begin{aligned} {\mathbb {E}}(\widetilde{\xi }(t)||P_{n}{\textbf{u}}(t)&-{\textbf{u}} _{n}(t)||_{2}^{2})+{\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)\Vert P_{n} {\textbf{G}}-P_{n}{\textbf{G}}^{*}\Vert _{2}^{2}ds \\&+\nu \mathbb {\ E}\int _{0}^{t}\widetilde{\xi }(s)||P_{n}{\textbf{u}}-\textbf{u }_{n}||_{V}^{2}\,ds\leqslant 2{\mathbb {E}}\int _{0}^{t}\widetilde{\xi } (s)I_{1}\,ds \\&+2{\mathbb {E}}\int _{0}^{t}~\widetilde{\xi }(s)I_{2}\,ds+2{\mathbb {E}} \int _{0}^{t}\widetilde{\xi }(s)\left( A_{3},P_{n}{\textbf{u}}-{\textbf{u}} _{n}\right) \,ds \\&+C{\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)\left\| P_{n}{\textbf{u}}- \mathbf {\ u}\right\| _{2}^{2}\,ds \\&+2{\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)(P_{n}{\textbf{G}}_{n}-P_{n} {\textbf{G}}^{*},P_{n}{\textbf{G}}-P_{n}{\textbf{G}}^{*})\,ds \\&=J_{1}+J_{2}+J_{3}+J_{4}+J_{5}\quad \text {for }t\in (0,T). \end{aligned}$$

Next, we will show that the right-hand side of this inequality tends to zero as $n\rightarrow \infty$.

Considering the estimate (3.41) and using $\widetilde{\xi }\leqslant \xi _{0}^{3}$ on (0, T), then we deduce that

$$\begin{aligned} J_{1}\leqslant & {} C\left( {\mathbb {E}}\int _{0}^{T}\xi _{0}^{3}||P_{n}{\textbf{u}} -{\textbf{u}}||_{4}^{2}(||{\textbf{u}}||_{V}+||{\textbf{a}}||_{H^{1}})\ ds\right) ^{1/2} \\\times & {} \quad \left( {\mathbb {E}}\int _{0}^{T}\xi _{0}^{3}(||{\textbf{u}}||_{V}+|| {\textbf{a}}||_{H^{1}})(||P_{n}{\textbf{u}}||_{4}^{2}+||{\textbf{u}} _{n}||_{4}^{2})\ ds\right) ^{1/2}. \end{aligned}$$

Using (2.3) for $q=4$, we have

$$\begin{aligned} {\mathbb {E}}\int _{0}^{T}\xi _{0}^{3}||P_{n}{\textbf{u}}- & {} {\textbf{u}} ||_{4}^{2}(||{\textbf{u}}||_{V}+||{\textbf{a}}||_{H^{1}})\ ds \\\leqslant & {} ({\mathbb {E}}\sup _{s\in [0,t]}\xi _{0}^{2}||P_{n}{\textbf{u}}- {\textbf{u}}||_{2}^{2}\int _{0}^{T}\xi _{0}^{2}(||{\textbf{u}}||_{V}^{2}+|| {\textbf{a}}||_{H^{1}}^{2})\ ds)^{1/2} \\\times & {} \quad ({\mathbb {E}}\int _{0}^{T}\xi _{0}^{2}||P_{n}{\textbf{u}}-{\textbf{u}} ||_{V}^{2}\ ds)^{1/2}\leqslant C({\mathbb {E}}\int _{0}^{T}\xi _{0}^{2}||P_{n} {\textbf{u}}-{\textbf{u}}||_{V}^{2}\ ds)^{1/2} \end{aligned}$$

by the estimates (3.23)–(3.24). Applying similar calculations we can show that there exists a constant C, such that

$$\begin{aligned} {\mathbb {E}}\int _{0}^{T}\xi _{0}^{3}(||{\textbf{u}}||_{V}+||{\textbf{a}} ||_{H^{1}})(||P_{n}{\textbf{u}}||_{4}^{2}+||{\textbf{u}}_{n}||_{4}^{2})\ ds\leqslant C, \end{aligned}$$

that is

$$\begin{aligned} J_{1}\leqslant C\left( {\mathbb {E}}\int _{0}^{T}\xi _{0}^{2}||P_{n}{\textbf{u}}- {\textbf{u}}||_{V}^{2}\ ds\right) ^{1/4}. \end{aligned}$$

For the term $J_{2},$ using the estimate (3.42), we can show that

$$\begin{aligned} J_{2}\leqslant C\left( {\mathbb {E}}\int _{0}^{T}\xi _{0}^{2}||P_{n}{\textbf{u}}- {\textbf{u}}||_{V}^{2}\ ds\right) ^{1/2}. \end{aligned}$$

Therefore we get that the terms $J_{i},$ $i=1,2,$ converge to zero as $n\rightarrow \infty$ by (3.31).

The convergences of (3.30) and (3.31) show that

$$\begin{aligned} \xi _{0}\left( P_{n}{\textbf{u}}-{\textbf{u}}_{n}\right) \rightharpoonup 0\quad \text {weakly in }L_{2}(\Omega \times (0,T),V)\quad \text {as }n\rightarrow \infty . \end{aligned}$$

The operator $\xi _{0}^{2}A_{3}=\xi _{0}^{2}\left( ({\textbf{y}}\cdot \nabla ) {\textbf{y}}-B^{*}\right)$ belongs to $L_{2}(\Omega \times (0,T);V^{\prime })$ by (3.29) and (3.32), thus

$$\begin{aligned} J_{3}=2{\mathbb {E}}\int _{0}^{T}\widetilde{\xi }(s)(({\textbf{y}}\cdot \nabla ) {\textbf{y}})-B^{*},P_{n}{\textbf{u}}-{\textbf{u}}_{n})\,ds\rightarrow 0\quad \text {as }n\rightarrow \infty . \end{aligned}$$

Due to (3.31), we have

$$\begin{aligned} J_{4}=C{\mathbb {E}}\int _{0}^{T}\widetilde{\xi }(s)\left\| P_{n}{\textbf{u}}- {\textbf{u}}\right\| _{2}^{2}ds\rightarrow 0. \end{aligned}$$

Due to the convergence results (3.26), (3.30), (3.31), (3.32) and (3.43), we obtain

$$\begin{aligned}{} & {} \xi _{0}P_{n}\left( {\textbf{G}}_{n}-{\textbf{G}}^{*}\right) \rightharpoonup {\textbf{0}}\qquad \text { weakly in }L_{2}(\Omega \times (0,T),H^{m}), \nonumber \\{} & {} \quad \xi _{0}P_{n}({\textbf{G}}-{\textbf{G}}^{*}) \rightarrow {\textbf{G}}- {\textbf{G}}^{*}\qquad \text { strongly in }L_{2}(\Omega \times (0,T),H^{m}), \end{aligned}$$

(3.46)

that implies

$$\begin{aligned} J_{5}=2{\mathbb {E}}\int _{0}^{T}\widetilde{\xi }(s)(P_{n}{\textbf{G}}_{n}-P_{n} {\textbf{G}}^{*},P_{n}({\textbf{G}}-{\textbf{G}}^{*}))\,ds\rightarrow 0 \quad \text { as }n\rightarrow \infty . \end{aligned}$$

After combining all the convergence results, we obtain the following strong convergences

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathbb {E}}\left( \widetilde{\xi }(t)||P_{n} {\textbf{u}}(t)-{\textbf{u}}_{n}(t)||_{2}^{2}\right) =0,\qquad \lim _{n\rightarrow \infty }{\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)||P_{n} {\textbf{u}}-{\textbf{u}}_{n}||_{V}^{2}\,ds=0 \end{aligned}$$

for $t\in (0,T)$, which combined with (3.31), imply

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathbb {E}}\left( \widetilde{\xi }(t)||{\textbf{u}} _{n}(t)-{\textbf{u}}(t)||_{2}^{2}\right) =0,{\qquad }\lim _{n\rightarrow \infty }{\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)||{\textbf{u}}_{n}-{\textbf{u}} ||_{V}^{2}\,ds=0. \nonumber \\ \end{aligned}$$

(3.47)

In addition, considering (2.11), we conclude

$$\begin{aligned} {\mathbb {E}}\int _{0}^{t}\widetilde{\xi }(s)\Vert {\textbf{G}}(s,{\textbf{y}})- {\textbf{G}}^{*}(s)\Vert _{2}^{2}ds=0. \end{aligned}$$

Since $\widetilde{\xi }$ is strictly positive, we infer that

$$\begin{aligned} {\textbf{G}}(t,{\textbf{y}})={\textbf{G}}^{*}(t)\quad \text {a.e. in }\Omega \times (0,T). \end{aligned}$$

(3.48)

From (3.32) and (3.47), it follows that $\widetilde{\xi }(t)( {\textbf{y}}\cdot \nabla ){\textbf{y}}=\widetilde{\xi }(t){\textbf{B}}^{*}(t)\$ a.e. in $\Omega \times (0,T),$ that implies

$$\begin{aligned} ({\textbf{y}}\cdot \nabla ){\textbf{y}}={\textbf{B}}^{*}(t)\quad \text {a.e. in }\Omega \times (0,T). \end{aligned}$$

(3.49)

Considering the identities (3.48), ( 3.49), the equation (3.36) reads

$$\begin{aligned} \left( {\textbf{y}}(t),\varvec{\varphi }\right) -\left( {\textbf{y}}_{0}, \varvec{\varphi }\right)&=\int _{0}^{t}\left[ -\nu \left( {\textbf{y}}, \varvec{\varphi }\right) _{V}+\nu \int _{\Gamma }b(\varvec{\varphi } \cdot {\varvec{\tau }})\,d\mathbf {\gamma }-({\textbf{y}}\cdot \nabla ){\textbf{y}}, \varvec{\varphi })\right] \,ds \\&\quad +\int _{0}^{t}\left( {\textbf{G}}(s,{\textbf{y}}),\varvec{\varphi }\right) \,d{{\mathcal {W}}}_{s},\quad P\text {-a.e. in }\Omega ,\quad t\in (0,T). \end{aligned}$$

The uniqueness of the solution ${\textbf{y}}$ follows from the stability result established in the next theorem. $\square$

Let us denote by $\widehat{\mathbf {\varphi }}=\mathbf {\varphi }_{1}-\mathbf { \varphi }_{2}$ the diference of two given functions $\mathbf {\varphi }_{1}, \mathbf {\varphi }_{2}.$

Theorem 3.6

Let us consider ${\textbf{y}}_{1}={\textbf{u}}_{1}+{\textbf{a}}_{1},$${\textbf{y}}_{2}={\textbf{u}}_{2}+{\textbf{a}}_{2}$ with

$$\begin{aligned} {\textbf{u}}_{1},{\textbf{u}}_{2}\in C([0,T];H)\cap L_{4}(0,T;V),\quad P\text { -a.e. in }\Omega , \end{aligned}$$

two solutions of (1.1), satisfying the estimates (3.23), (3.24) with two corresponding boundary conditions $a_{1},\;b_{1}$, $a_{2},$ $b_{2}$ and the initial conditions

$$\begin{aligned} {\textbf{y}}_{1,0}={\textbf{u}}_{1,0}+{\textbf{a}}_{1}(0),\quad {\textbf{y}}_{2,0}= {\textbf{u}}_{2,0}+{\textbf{a}}_{2}(0). \end{aligned}$$

Then there exist a strictly positive function $f_{1}(t)\in L_{1}(0,T)\quad P$ -a.e. in $\Omega ,$ depending only on the data, such that the following estimate

$$\begin{aligned} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{1}^{2}(s)\left\| \widehat{\textbf{ y}}(s)\right\| _{2}^{2}+ & {} 2\nu \int _{0}^{t}\xi _{1}^{2}(s)\Vert \widehat{ {\textbf{y}}}(s)\Vert _{V}^{2}\,ds \nonumber \\\leqslant & {} C({\mathbb {E}}\left\| \widehat{{\textbf{y}}}_{0}\right\| _{2}^{2}+{\mathbb {E}}\int _{0}^{t}\xi _{1}^{2}||(\widehat{a},\widehat{b})||_{ {\mathcal {H}}_{p}(\Gamma )}^{2}\,ds) \end{aligned}$$

(3.50)

is valid with the function $\xi _{1}$ defined as

$$\begin{aligned} \xi _{1}(t)=e^{-\int _{0}^{t}f_{1}(s)ds}\quad \text {with }f_{1}\in L_{1}(0,T)\quad P\text {-a.e. in }\Omega . \end{aligned}$$

(3.51)

Proof

The proof follows the same reasoning as the proof of Theorem 3.5. $\square$

4 Solution to the Control Problem

This section studies the existence of an optimal solution to the optimal control problem $({\mathcal {P}}).$ We intend to control the solution of the system (1.1) by boundary values (a, b), which belongs to the space ${\mathcal {A}}$ of admissible controls defined as a compact subset of $L_{2}(\Omega \times (0,T);\mathcal {H }_{p}(\Gamma ))$ verifying an exponential integrability condition. More precisely, we assume that there exists a constant $\lambda >0$ such that

$$\begin{aligned} {\mathbb {E}}e^{4C_{0}\int _{0}^{T}||(a,b)||_{{\mathcal {H}}_{p}(\Gamma )}^{2}ds}<\lambda ,\quad \forall (a,b)\in {\mathcal {A}}. \end{aligned}$$

(4.1)

Remark 4.1

We notice that given a control pair $(a,b)\in {\mathcal {A}}$, the corresponding state ${\textbf{y}}={\textbf{u}}+{\textbf{a}}$ defined as the solution of the state equation (3.6) belongs to $L_{2}(\Omega \times (0,T)\times {\mathcal {O}})$. Namely, considering the auxiliar function $\xi _{0}$ introduced in (3.10), and the estimates (3.23), (3.24), Hölder’s inequality gives

$$\begin{aligned} \mathbb {E(}\sup _{t\in [0,T]}\Vert u(t)\Vert _{2}^{2})\leqslant ( {\mathbb {E}}\sup _{t\in [0,T]}\Vert \xi _{0}(t)u(t)\Vert _{2}^{4})^{ \frac{1}{2}}\left( {\mathbb {E}}\left( \xi _{0}^{-4}(T)\right) \right) ^{\frac{1 }{2}}<\infty . \end{aligned}$$

Therefore, the cost functional (1.4) is well defined for every $(a,b)\in {\mathcal {A}}.$

Now, we write one of the main result of the article, which establishes the existence of a solution for the optimal control problem $({\mathcal {P}})$.

Theorem 4.1

Assume that (a, b) and ${\textbf{y}}_{0}$ verify the regularity (2.12), (3.19), such that (a, b) belongs to the space ${\mathcal {A}}$. Then there exists at least one solution for the optimal control problem $({\mathcal {P}}).$

Proof

Let us consider a minimizing sequence

$$\begin{aligned} (a_{n},b_{n},{\textbf{y}}_{n})\in {\mathcal {A}}\times L_{2}(\Omega ;L_{\infty }(0,T;L_{2}({{\mathcal {O}}}))\cap L_{2}(0,T;H^{1}({{\mathcal {O}}}))) \end{aligned}$$

of the cost functional J, namely

$$\begin{aligned} J(a_{n},b_{n},{\textbf{y}}_{n})\rightarrow d=\inf ({\mathcal {P}})\quad \text {as } n\rightarrow \infty \end{aligned}$$

and ${\textbf{y}}_{n}$ is the weak solution of the system (1.1) for the sequence $(a_{n},b_{n})\in {\mathcal {A}}$.

$$\begin{aligned} d\left( {\textbf{y}}_{n}\,,\varvec{\varphi }\right)&=\left[ -\nu \left( {\textbf{y}}_{n},\varvec{\varphi }\right) _{V}\,+\nu \int _{\Gamma }b_{n}( \varvec{\varphi }\cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(\left( \textbf{y }_{n}\cdot \nabla ){\textbf{y}}_{n},\varvec{\varphi }\right) \right] dt \nonumber \\&\quad +\left( {\textbf{G}}(t,{\textbf{y}}_{n}),\varvec{\varphi }\right) \,d{ {\mathcal {W}}}_{t},\quad \forall \varvec{\varphi }\in V,\quad P\text {-a.e. in }\Omega ,\quad \forall t\in (0,T), \nonumber \\ {\textbf{u}}_{n}(0)&={\textbf{u}}_{0}\in H, \end{aligned}$$

(4.2)

Due to the compactness of ${\mathcal {A}}$, there exists a subsequence, still indexed by n, such that

$$\begin{aligned} \left( a_{n},b_{n}\right) \rightarrow (a,b)\quad {\text {strongly in }} L_{2}(\Omega \times (0,T);{\mathcal {H}}_{p}(\Gamma )). \end{aligned}$$

(4.3)

From Theorem 4.9., p. 94, of [11], there exists a subsequence of $\left( a_{n},b_{n}\right)$, still denoted by $\left( a_{n},b_{n}\right)$, and a function $h\in L_{2}(\Omega \times (0,T))$ such that

$$\begin{aligned} \Vert (a,b)\Vert _{{\mathcal {H}}_{p}(\Gamma )}\leqslant h {,\quad }\Vert (a_{n},b_{n})\Vert _{{\mathcal {H}}_{p}(\Gamma )}\leqslant h, {\quad } \forall n\in {\mathbb {N}},\text { a.e. in }\Omega \times (0,T). \end{aligned}$$

(4.4)

Considering the function $h=h(t)$, let us introduce the following weight

$$\begin{aligned} \xi _{h}(t)=e^{-C_{0}(t+\int _{0}^{t}h^{2}(s)ds)},\quad P\text {-a.e. in } \Omega \text {.} \end{aligned}$$

(4.5)

If we replace $a,b,{\textbf{a}}$ by $a_{n},b_{n},{\textbf{a}}_{n}$, respectively in the relations (3.2), (3.3), then, taking into account the estimates (3.23), (3.24), we conclude that the sequence $\textbf{ u}_{n}={\textbf{y}}_{n}-{\textbf{a}}_{n}$, $n\in {\mathbb {N}},$ satisfies the estimates

$$\begin{aligned}{} & {} {\mathbb {E}}\sup _{s\in [0,t]}\xi _{h}^{2}(s)\left\| {\textbf{u}} _{n}(s)\right\| _{2}^{2}+\nu {\mathbb {E}}\int _{0}^{t}\xi _{h}^{2}(s)\left\| {\textbf{u}}_{n}\right\| _{V}^{2}\,ds\leqslant C, \nonumber \\{} & {} \quad {\mathbb {E}}\sup _{s\in [0,t]}\xi _{h}^{4}(s)\left\| {\textbf{u}} _{n}(s)\right\| _{2}^{4}+8\nu ^{2}\mathbb {E(}\int _{0}^{t}\xi _{h}^{2}(s)\left\| {\textbf{u}}_{n}(s)\right\| _{V}^{2}ds)^{2}\leqslant C \end{aligned}$$

(4.6)

for any $t\in [0,T]$, where the constants C are independent of n. Therefore there exists a subsequence, still indexed by n, such that

$$\begin{aligned}{} & {} \xi _{h}{\textbf{u}}_{n} \rightharpoonup \xi _{h}{\textbf{u}}\quad \text{ weakly } \text{ in } L_{s}(\Omega ;L_{2}(0,T;V)), \nonumber \\{} & {} \quad \xi _{h}{\textbf{u}}_{n} \rightharpoonup \xi _{h}{\textbf{u}}\quad \text{*-weakly } \text{ in } L_{s}(\Omega ,L_{\infty }(0,T;H))\quad \text {for }s=2\text { and }4. \end{aligned}$$

(4.7)

In addition, the following uniform estimate holds

$$\begin{aligned} \left\| \xi _{h}^{2}\left( {\textbf{y}}_{n}\cdot \nabla \right) {\textbf{y}} _{n}\right\| _{L_{2}(\Omega \times (0,T);V^{\prime })}\leqslant C,\quad \forall n\in {\mathbb {N}}. \end{aligned}$$

(4.8)

Hence there exist operators $B^{*}$ and $G^{*}$ such that

$$\begin{aligned} \xi _{h}^{2}\left( {\textbf{y}}_{n}\cdot \nabla \right) {\textbf{y}}_{n}&\rightharpoonup \xi _{h}^{2}B^{*}(t)\quad \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);V^{\prime }), \nonumber \\ \xi _{h}{\textbf{G}}(t,{\textbf{y}}_{n})&\rightharpoonup \xi _{h}{\textbf{G}} ^{*}(t)\quad \text{ weakly } \text{ in } \ L_{2}(\Omega \times (0,T);H^{m}). \end{aligned}$$

(4.9)

Arguments already used in Step 2 of the proof of Theorem 3.5 allow to pass to the limit equation (4.2) in the distributional sense, as $n\rightarrow \infty$, to obtain

$$\begin{aligned} d\left( {\textbf{y}},\varvec{\varphi }\right)&=[-\nu \left( {\textbf{y}}, \varvec{\varphi }\right) _{V}+\nu \int _{\Gamma }b(\varvec{\varphi } \cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(B^{*}(t),\varvec{\varphi } )\,]dt \nonumber \\&\quad +\left( {\textbf{G}}^{*}(t),\varvec{\varphi }\right) \,d{{\mathcal {W}}} _{s},\quad P\text {-a.e. in }\Omega ,\quad \forall t\in (0,T), \nonumber \\ {\textbf{u}}(0)&={\textbf{u}}_{0}\in H,\qquad \qquad \qquad \qquad \forall \varvec{\varphi }\in V. \end{aligned}$$

(4.10)

Writing ${\textbf{y}}={\textbf{u}}+{\textbf{a}}$, ${\textbf{y}}_{n}={\textbf{u}}_{n}+ {\textbf{a}}_{n}$ and doing the difference between (4.2) and (4.10) with $\varvec{\varphi }={\textbf{e}}_{i}$, $i\in {\mathbb {N}}$, we deduce

$$\begin{aligned} d\left( {\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right)= & {} \Bigl [-\nu \left( {\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right) _{V}+\nu \int _{\Gamma }(b-b_{n})(\varvec{{\textbf{e}}_{i}}\cdot {\varvec{\tau }})\,d\mathbf {\gamma } \nonumber \\- & {} \quad \left( \partial _{t}({\textbf{a}}-{\textbf{a}}_{n}),{\textbf{e}}_{i}\right) -\nu \left( {\textbf{a}}-{\textbf{a}}_{n},{\textbf{e}}_{i}\right) _{V} \nonumber \\+ & {} \quad \left( ({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t),{\textbf{e}} _{i}\right) \Bigr ]\,dt \nonumber \\- & {} \quad \left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}} _{i}\right) \,d{{\mathcal {W}}}_{t}, \end{aligned}$$

(4.11)

which holds for any element of the basis $\left\{ {\textbf{e}}_{i}\right\} .$

By applying Itô’s formula, the equation (4.11) gives

$$\begin{aligned} d({\textbf{u}} -{\textbf{u}}_{n},{\textbf{e}}_{i})^{2}&=2\left( {\textbf{u}}-\textbf{ u}_{n},{\textbf{e}}_{i}\right) \Bigl [-\nu \left( {\textbf{u}}-{\textbf{u}}_{n}, {\textbf{e}}_{i}\right) _{V}+\nu \int _{\Gamma }(b-b_{n})(\varvec{{\textbf{e}} _{i}}\cdot {\varvec{\tau }})\,d\mathbf {\gamma } \\&\quad -\left( \partial _{t}({\textbf{a}}-{\textbf{a}}_{n}),{\textbf{e}}_{i}\right) -\nu \left( {\textbf{a}}-{\textbf{a}}_{n},{\textbf{e}}_{i}\right) _{V} \\&\quad +\left( ({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t),{\textbf{e}} _{i}\right) \Bigr ]\,dt \\&\quad -2\left( {\textbf{u}}-{\textbf{u}}_{n},{\textbf{e}}_{i}\right) \left( {\textbf{G}} (t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}}_{i}\right) \,d{\mathcal {W }}_{t}\\ {}&\quad +|\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}} _{i}\right) |^{2}\,dt. \end{aligned}$$

Summing over the index $i\in {\mathbb {N}}$, we derive

$$\begin{aligned} d(||{\textbf{u}} -{\textbf{u}}_{n}||_{2}^{2})+2\nu ||{\textbf{u}}-{\textbf{u}} _{n}||_{V}^{2}dt&=2(({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t), {\textbf{u}}-{\textbf{u}}_{n})\,dt \nonumber \\&\quad +2\nu \int _{\Gamma }(b-b_{n})(({\textbf{u}}-{\textbf{u}}_{n})\cdot {\varvec{\tau }} )\,d\mathbf {\gamma } \nonumber \\&\quad -\left( \partial _{t}({\textbf{a}}-{\textbf{a}}_{n}),{\textbf{u}}-{\textbf{u}} _{n}\right) -\nu \left( {\textbf{a}}-{\textbf{a}}_{n},{\textbf{u}}-{\textbf{u}} _{n}\right) _{V}\Bigr ]\,dt \nonumber \\&\quad +\sum _{i=1}^{\infty }|\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{e}}_{i}\right) |^{2}\,dt \nonumber \\&\quad -2\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{u}}- {\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{t}. \end{aligned}$$

(4.12)

We write

$$\begin{aligned} ({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t)&=\left\{ -(( {\textbf{u}}_{n}+{\textbf{a}}_{n})\cdot \nabla )({\textbf{u}}-{\textbf{u}}_{n})-(( {\textbf{u}}-{\textbf{u}}_{n})\cdot \nabla )({\textbf{u}}+{\textbf{a}})\right\} \\&\quad -(({\textbf{u}}_{n}+{\textbf{a}}_{n})\cdot \nabla )({\textbf{a}}_{n}-{\textbf{a}} )+(({\textbf{a}}_{n}-{\textbf{a}})\cdot \nabla )({\textbf{u}}+{\textbf{a}}) \\&\quad +\left\{ ({\textbf{y}}\cdot \nabla ){\textbf{y}}-B^{*}(t)\right\} \\&=B_{0}+B_{1}+B_{2}+B_{3}. \end{aligned}$$

With the help of (2.3), (2.4), (3.3) and (4.6), we deduce the following estimates

$$\begin{aligned} I_{0}&=|\left( B_{0},{\textbf{u}}-{\textbf{u}}_{n}\right) |\leqslant |\int _{\Gamma }a_{n}(({\textbf{u}}-{\textbf{u}}_{n})\cdot \varvec{\tau })^{2}\,d \mathbf {\gamma }| \nonumber \\&\quad +|\left( (({\textbf{u}}-{\textbf{u}}_{n})\cdot \nabla )({\textbf{u}}+{\textbf{a}}), {\textbf{u}}-{\textbf{u}}_{n}\right) |, \nonumber \\&\leqslant C(||(a_{n},b_{n})||_{{\mathcal {H}}_{p}(\Gamma )}^{2}+||(a,b)||_{ {\mathcal {H}}_{p}(\Gamma )}^{2}+\left\| {\textbf{u}}\right\| _{V}^{2})\Vert {\textbf{u}}-{\textbf{u}}_{n}\Vert _{2}^{2}+\frac{\nu }{2} \left\| {\textbf{u}}-{\textbf{u}}_{n}\right\| _{V}^{2}\, \nonumber \\&\leqslant C_{2}(h^{2}+\left\| {\textbf{u}}\right\| _{V}^{2})\Vert {\textbf{u}}-{\textbf{u}}_{n}\Vert _{2}^{2}+\frac{\nu }{2}\left\| {\textbf{u}}- {\textbf{u}}_{n}\right\| _{V}^{2}, \end{aligned}$$

(4.13)

where the function h in (4.13) is given by (4.4).

Setting

$$\begin{aligned} {\textbf{G}}_{n}={\textbf{G}}(t,{\textbf{y}}_{n}),\quad {\textbf{G}}={\textbf{G}}(t, {\textbf{y}}),\quad {\textbf{G}}^{*}={\textbf{G}}^{*}(t) \end{aligned}$$

(4.14)

and using the same arguments as in the deductions of (3.44) by taking $C_{3}=2K$, we infer that

$$\begin{aligned} \Vert {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t)\Vert _{2}^{2}&\leqslant C_{3}\left\| {\textbf{u}}_{n}-{\textbf{u}}\right\| _{2}^{2}+C\left\| {\textbf{a}}_{n}-{\textbf{a}}\right\| _{2}^{2}-\Vert {\textbf{G}}-{\textbf{G}}^{*}\Vert _{2}^{2} \nonumber \\&\quad +2({\textbf{G}}_{n}-{\textbf{G}}^{*},{\textbf{G}}-{\textbf{G}}^{*}). \end{aligned}$$

(4.15)

The positive constants $C_{2}$ and $C_{3}$ in (4.13) and (4.15) are independent of n,  and they may depend on the data.

Let us consider the function

$$\begin{aligned} \widehat{\xi }(t)=e^{-\int _{0}^{t}\widehat{f}(s)\ ds}\quad \text {with } \widehat{f}(t)=\left[ C_{3}+\max (3C_{0},C_{2})(1+h^{2})\right] . \end{aligned}$$

(4.16)

Now, by applying Itô’s formula to the equality (4.12), the definition (4.16) of $\widehat{\xi }$, we obtain

$$\begin{aligned}&d(\widehat{\xi }(t)||{\textbf{u}} -{\textbf{u}}_{n}||_{2}^{2})+\frac{3\nu }{2} \widehat{\xi }(t)||{\textbf{u}}-{\textbf{u}}_{n}||_{V}^{2}\,dt\leqslant 2 \widehat{\xi }(t)(({\textbf{y}}_{n}\cdot \nabla ){\textbf{y}}_{n}-B^{*}(t), {\textbf{u}}-{\textbf{u}}_{n})\,dt \nonumber \\&\quad +2\nu \int _{\Gamma }\widehat{\xi }(t)(b-b_{n})(({\textbf{u}}-{\textbf{u}} _{n})\cdot {\varvec{\tau }})\,d\mathbf {\gamma }+\widehat{\xi }(t)\Vert {\textbf{G}} (t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t)\Vert _{2}^{2}\,dt \nonumber \\&\quad -2\widehat{\xi }(t)\left( {\textbf{G}}(t,{\textbf{y}}_{n})-{\textbf{G}}^{*}(t),{\textbf{u}}-{\textbf{u}}_{n}\right) \,d{{\mathcal {W}}}_{t}+C\widehat{\xi } (t)\Vert (a_{n},b_{n})-(a,b)\Vert _{{\mathcal {H}}_{p}(\Gamma )} \nonumber \\&\quad -C_{3}\widehat{\xi }(t)||{\textbf{u}}-{\textbf{u}}_{n}||_{2}^{2}\,dt-C_{2} \widehat{\xi }(t)(h^{2}+\left\| {\textbf{u}}\right\| _{V}^{2})||\textbf{u }-{\textbf{u}}_{n}||_{2}^{2}\,dt. \end{aligned}$$

(4.17)

Therefore, writing the inequality (4.17) in the integral form, taking the expectation, and incorporating the estimates (4.13), (4.15 ), we infer that

$$\begin{aligned} {\mathbb {E}}(\widehat{\xi }(t)||{\textbf{u}}(t)&-{\textbf{u}}_{n}(t)||_{2}^{2})+ {\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)\Vert {\textbf{G}}-{\textbf{G}}^{*}\Vert _{2}^{2}ds+\nu \mathbb {\ E}\int _{0}^{t}\widehat{\xi }(s)||{\textbf{u}}- {\textbf{u}}_{n}||_{V}^{2}\,ds \nonumber \\&\leqslant 2\nu {\mathbb {E}}\int _{0}^{t}\int _{\Gamma }\widehat{\xi } (s)(b-b_{n})(({\textbf{u}}-{\textbf{u}}_{n})\cdot {\varvec{\tau }})\,d\mathbf {\gamma }ds \nonumber \\&\quad +2{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)|\left( B_{1},{\textbf{u}}-\textbf{u }_{n}\right) |\,ds+2{\mathbb {E}}\int _{0}^{t}~\widehat{\xi }(s)|\left( B_{2}, {\textbf{u}}-{\textbf{u}}_{n}\right) |\,ds \nonumber \\&\quad +2{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)\left( B_{3},{\textbf{u}}-{\textbf{u}} _{n}\right) \,ds+C{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)\Vert (a_{n},b_{n})-(a,b)\Vert _{{\mathcal {H}}_{p}(\Gamma )}^{2}\,ds \nonumber \\&\quad +2{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)({\textbf{G}}_{n}-{\textbf{G}}^{*},{\textbf{G}}-{\textbf{G}}^{*})\,ds \nonumber \\&=J_{0}+J_{1}+J_{2}+J_{3}+J_{4}+J_{5}\quad \text {for }t\in (0,T). \end{aligned}$$

(4.18)

In the following, we show that the right-hand side of this inequality tends to zero as $n\rightarrow \infty$. The Hölder inequality, (2.12), (3.3) and $\widehat{\xi }\leqslant \xi _{h}^{2}$ yield

$$\begin{aligned} J_{0}= & {} |2\nu \int _{\Gamma }\widehat{\xi }(s)(b-b_{n})(({\textbf{u}}-\textbf{u }_{n})\cdot {\varvec{\tau }})\,d\mathbf {\gamma }ds| \\\leqslant & {} C\Vert (a_{n},b_{n})-(a,b)\Vert _{L_{2}(\Omega \times (0,T); {\mathcal {H}}_{p}(\Gamma ))}+\frac{\nu }{2}{\mathbb {E}}\int _{0}^{t}\widehat{\xi } (s)\left\| {\textbf{u}}-{\textbf{u}}_{n}\right\| _{V}^{2}\,ds. \end{aligned}$$

Considering the estimate (4.6) and using that $\widehat{\xi } \leqslant \xi _{h}^{2}$ on (0, T), we deduce that

$$\begin{aligned} J_{1}&\leqslant {\mathbb {E}}\int _{0}^{T}\xi _{h}^{2}\left( (({\textbf{u}}_{n}+ {\textbf{a}}_{n})\cdot \nabla )({\textbf{a}}_{n}-{\textbf{a}}),{\textbf{u}}_{n}- {\textbf{u}}\right) \leqslant C({\mathbb {E}}\int _{0}^{T}\Vert {\textbf{a}}_{n}- {\textbf{a}}\Vert _{H^{1}}^{2}ds)^{1/2} \\&\quad \times [({\mathbb {E}}\int _{0}^{T}\xi _{h}^{4}\Vert {\textbf{u}} _{n}\Vert _{4}^{2}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{4}^{2}ds)^{1/2}+( {\mathbb {E}}\int _{0}^{T}\xi _{h}^{4}\Vert {\textbf{a}}_{n}\Vert _{C(\bar{ {\mathcal {O}}})}^{2}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{2}^{2}ds)^{1/2}] \\&\leqslant C\Vert (a_{n},b_{n})-(a,b)\Vert _{L_{2}(\Omega \times (0,T); {\mathcal {H}}_{p}(\Gamma ))}\rightarrow 0\quad \text {as }n\rightarrow \infty , \end{aligned}$$

where we used the following uniform estimates with respect to the parameter n

$$\begin{aligned} {\mathbb {E}}&\int _{0}^{T}\xi _{h}^{4}\Vert {\textbf{u}}\Vert _{4}^{2}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{4}^{2}ds \\&\leqslant ({\mathbb {E}}\sup _{t\in [0,T]}\xi _{h}^{4}\Vert {\textbf{u}} \Vert _{2}^{2}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{2}^{2})^{\frac{1}{2} }\times (\mathbb {E(}\int _{0}^{T}\xi _{h}^{2}\Vert {\textbf{u}}\Vert _{V}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{V}ds)^{2})^{\frac{1}{2}} \\&\leqslant C({\mathbb {E}}\sup _{t\in [0,T]}\xi _{h}^{4}\left( \Vert {\textbf{u}}\Vert _{2}^{4}+\Vert {\textbf{u}}_{n}\Vert _{2}^{4}\right) )^{\frac{1 }{2}}\times (\mathbb {E(}\int _{0}^{T}\xi _{h}^{2}\left( \Vert {\textbf{u}}\Vert _{V}^{2}+\Vert {\textbf{u}}\Vert _{V}^{2}\right) ds)^{2})^{\frac{1}{2} }\leqslant C, \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}&\int _{0}^{T}\xi _{h}^{4}\Vert {\textbf{a}}_{n}\Vert _{C(\bar{ {\mathcal {O}}})}^{2}\Vert {\textbf{u}}_{n}-{\textbf{u}}\Vert _{2}^{2}ds \\&\leqslant C({\mathbb {E}}\sup _{t\in [0,T]}\xi _{h}^{4}\left( \Vert {\textbf{u}}_{n}\Vert _{2}^{4}+\Vert {\textbf{u}}\Vert _{2}^{4}\right) )^{\frac{1 }{2}}\times (\mathbb {E(}\int _{0}^{T}\Vert (a_{n},b_{n})\Vert _{{\mathcal {H}} _{p}}^{2}ds)^{2})^{\frac{1}{2}}\leqslant C. \end{aligned}$$

For the term $J_{2},$ using Hölder’s inequality, (4.1), (4.3) and (4.6), we can show that

$$\begin{aligned} J_{2}&\leqslant {\mathbb {E}}\int _{0}^{T}\xi _{h}^{2}\left( (({\textbf{a}}_{n}- {\textbf{a}})\cdot \nabla )({\textbf{u}}+{\textbf{a}}),{\textbf{u}}_{n}-{\textbf{u}} \right) \\&\leqslant C({\mathbb {E}}\int _{0}^{T}\Vert {\textbf{a}}_{n}-{\textbf{a}}\Vert _{C( \bar{{\mathcal {O}}})}^{2}ds)^{\frac{1}{2}} \\&\quad \times ({\mathbb {E}}\sup _{t\in [0,T]}\xi _{h}^{2}\Vert {\textbf{u}}_{n}- {\textbf{u}}\Vert _{2}^{2}\int _{0}^{T}\left( \xi _{h}^{2}\Vert {\textbf{u}}\Vert _{V}^{2}+\Vert (a,b)\Vert _{{\mathcal {H}}_{p}}^{2}\right) ds)^{\frac{1}{2}} \\&\leqslant C\Vert (a_{n},b_{n})-(a,b)\Vert _{L_{2}(\Omega \times (0,T); {\mathcal {H}}_{p}(\Gamma ))}\rightarrow 0. \end{aligned}$$

Therefore, the terms $J_{1},$ $J_{2}$ converge to zero as $n\rightarrow \infty$.

The convergence (4.7) shows that

$$\begin{aligned} \xi _{h}\left( {\textbf{u}}-{\textbf{u}}_{n}\right) \rightharpoonup 0\quad \text { weakly in }L_{2}(\Omega \times (0,T),V). \end{aligned}$$

The operator $\xi _{h}^{2}B_{3}=\xi _{h}^{2}\left( ({\textbf{y}}\cdot \nabla ) {\textbf{y}}-B^{*}\right)$ belongs to $L_{2}(\Omega \times (0,T);{ V^{\prime }})$ by (4.8), thus (4.9) implies

$$\begin{aligned} J_{3}=2{\mathbb {E}}\int _{0}^{T}\widehat{\xi }(s)(({\textbf{y}}\cdot \nabla ) {\textbf{y}})-B^{*},{\textbf{u}}-{\textbf{u}}_{n})\,ds\rightarrow 0. \end{aligned}$$

The term

$$\begin{aligned} J_{4}= & {} C{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)\Vert (a_{n},b_{n})-(a,b)\Vert _{{\mathcal {H}}_{p}(\Gamma )}\,ds \\\leqslant & {} C\Vert (a_{n},b_{n})-(a,b)\Vert _{L_{2}(\Omega \times (0,T); {\mathcal {H}}_{p}(\Gamma ))}\rightarrow 0\quad \text {as }n\rightarrow \infty . \end{aligned}$$

Due to the convergence results (4.9) and (4.14), we obtain

$$\begin{aligned} \xi _{h}\left( {\textbf{G}}_{n}-{\textbf{G}}^{*}\right) \rightharpoonup {\textbf{0}}\quad \text {weakly in }L_{2}(\Omega \times (0,T),H^{m}), \end{aligned}$$

(4.19)

which implies

$$\begin{aligned} J_{5}=2{\mathbb {E}}\int _{0}^{T}\widehat{\xi }(s)({\textbf{G}}_{n}-{\textbf{G}} ^{*},{\textbf{G}}-{\textbf{G}}^{*})\,ds\rightarrow 0. \end{aligned}$$

Gathering the convergence results for $J_{i}$, $i=0,\dots ,5$, and passing to the limit in the inequality (4.18), we deduce the following strong convergences

$$\begin{aligned} \lim _{n\rightarrow \infty }{\mathbb {E}}\left( \widehat{\xi }(t)||{\textbf{u}}(t)- {\textbf{u}}_{n}(t)||_{2}^{2}\right) =0, {\quad }\lim _{n\rightarrow \infty }{\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)||{\textbf{u}}-{\textbf{u}} _{n}||_{V}^{2}\,ds=0 \nonumber \\ \end{aligned}$$

(4.20)

for $t\in (0,T).$ In addition, we obtain

$$\begin{aligned} {\mathbb {E}}\int _{0}^{t}\widehat{\xi }(s)\Vert {\textbf{G}}(s,{\textbf{y}})- {\textbf{G}}^{*}(s)\Vert ds=0, \end{aligned}$$

then

$$\begin{aligned} {\textbf{G}}(t,{\textbf{y}})={\textbf{G}}^{*}(t)\text { a.e. in }\Omega \times (0,T). \end{aligned}$$

(4.21)

On the other hand, from (4.9) and (4.20), we infer that $\widehat{\xi }(t)({\textbf{y}}\cdot \nabla ){\textbf{y}}=\widehat{\xi }(t) {\textbf{B}}^{*}(t)$ a.e. in $\Omega \times (0,T),$ that implies

$$\begin{aligned} ({\textbf{y}}\cdot \nabla ){\textbf{y}}={\textbf{B}}^{*}(t)\quad \text {a.e. in }\Omega \times (0,T). \end{aligned}$$

(4.22)

Considering the identifications (4.21)–(4.22), the equation (4.10) reads

$$\begin{aligned} \left( {\textbf{y}}(t),\varvec{\varphi }\right) -\left( {\textbf{y}}_{0}, \varvec{\varphi }\right)= & {} \int _{0}^{t}\left[ -\nu \left( {\textbf{y}}, \varvec{\varphi }\right) _{V}+\nu \int _{\Gamma }b(\varvec{\varphi } \cdot {\varvec{\tau }})\,d\mathbf {\gamma }-(B^{*}(s),\varvec{\varphi }) \right] \,ds \\{} & {} +\int _{0}^{t}\left( {\textbf{G}}^{*}(s),\varvec{\varphi }\right) \,d{ {\mathcal {W}}}_{s},\quad P\text {-a.e. in }\Omega ,\quad t\in (0,T), \end{aligned}$$

for any $\varvec{\varphi }\in V.$ Therefore ${\textbf{y}}$ is the solution of the state equation, corresponding to the control pair (a, b).

Taking into account the lower semicontinuity of the cost functional, the strong convergence (4.20) and Remark 4.1, we infer that

$$\begin{aligned} J(a,b,{\textbf{y}})\leqslant \lim _{n\rightarrow \infty }J(a_{n},b_{n},\textbf{y }_{n}), \end{aligned}$$

which implies

$$\begin{aligned} J(a,b,{\textbf{y}})=\inf ({\mathcal {P}}), \end{aligned}$$

hence the triplet $(a,b,{\textbf{y}})$ is a solution to the control problem $( {\mathcal {P}})$. $\square$

5 Conclusion and Discussion

This work adresses an optimal control problem for the evolution of a viscous incompressible Newtonian fluid filling a two-dimensional bounded domain, under the action of random forces modeled by a multiplicative Gaussian noise. We prove the existence and uniqueness of the solution to the stochastic state equation and establish the existence of an optimal control. The control is exerted at the boundary through the physical non-homogeneous Navier-slip boundary conditions.

Let us emphasise that the studies in the literature [12, 17,18,19,20] turn out that the non-homogeneous Navier-slip boundary conditions are compatible with the inviscid limit transition of the viscous state, then we expect that our approach will be relevant to control the evolution of turbulent flows typically associated with high Reynolds number (or small viscosity).

We should mention that the most results in the literature on the optimal control of fluid flows are of deterministic nature. The control of a stochastic system is much more involved and there are few results available in the literature. We refer the articles [6, 7, 10, 33], where the authors solved tracking control problems in 2D and 3D, respectively. In these works, the control variables act in the interior of the domain. Recently in [49], the authors studied a stochastic boundary control problem for the deterministic steady Navier–Stokes equations, where the stochastic control is imposed on the boundary by a stochastic non-homogeneous Dirichlet boundary condition.

In a forthcoming paper, we intend to deduce the first-order necessary optimality conditions and analyse the second-order sufficient conditions, which are important for implementing numerical methods to determine the optimal boundary control.