Robust Matching for Teams

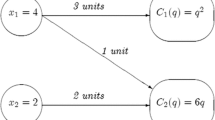
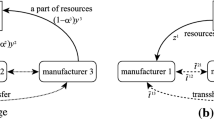
Abstract

We examine a hedonic model featuring uncertain production costs. The aim is to determine equilibrium prices and wages that facilitate the pairing of consumers with teams of producers, even when faced with the veil of uncertainty shrouding production costs. Using the framework of optimal transport theory, we identify the conditions sufficient for the existence of robust matching equilibrium. Our results show that under an additive uncertainty model for production costs, equilibrium can indeed be achieved, characterized by the expectation of the matching outcome under conditions of certainty. However, this model exhibits a twist of indeterminacy into the matching equilibrium. This departure from determinism is a distinctive feature, emphasizing the unique dynamics arising when uncertainty intersects with equilibrium-seeking mechanisms. To emphasize on this feature, we examine a special case which is related to martingale optimal transport. This case also underscores the complexity inherent in situations where uncertainty governs the equilibrium landscape. Altogether, our results offer a fresh perspective on matching scenarios marked by unpredictability in production costs.

Appendix

This section contains the proof of the results stated above.

Proof

(Proposition 2.1) Since, for every $\omega _i\in {\mathcal {W}}_i$ where $i\in \{0,\dots ,N\}$, the support of the matching between the set of types $X_i$ distributed according to $\mu _i\in {\mathcal {P}}(X_i)$ and the set of optimal goods in Z distributed according to $\nu \in {\mathcal {P}}(Z)$ satisfies (13), following from [38, Chapter 2], we have that, for every $\omega _i\in {\mathcal {W}}_i$, where $i\in \{0,1,\dots ,N\}$, $\gamma _i$ solves

$$\begin{aligned} \inf _{\gamma _i\in \varPi (\mu _i,\nu )}\int _{X_i\times Z} c_i(x_i,z)+\omega _i(x_i,z) d\gamma _i, \end{aligned}$$

where

$$\begin{aligned} \varPi (\mu _i,\nu ):=\{\gamma _i\in {\mathcal {P}}(X_i\times Z): \gamma _i\circ \pi ^{-1}_{X_i}=\mu _i \text{ and } \gamma _i\circ \pi ^{-1}_Z=\nu \}. \end{aligned}$$

From (3), since we require the optimizer to be independent of $\omega _i\in {\mathcal {W}}_i$, where $i\in \{0,\dots ,N\}$, following for instance from [11, Chapter 2], the matching $\gamma _i$ corresponding to problem (7) solves

$$\begin{aligned} \inf _{\gamma _i\in \varPi (\mu _i,\nu )}\sup _{\omega _i\in {\mathcal {W}}_i}\int _{X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z)) d\gamma _i. \end{aligned}$$

(39)

Suppose that there exists ${\tilde{\omega }}_i\in {\mathcal {W}}_i$ such that

$$\begin{aligned} \int _{X_i\times Z}{\tilde{\omega }}_i(x_i,z)d\gamma _i>0. \end{aligned}$$

Since $\omega _i=t{\tilde{\omega }}_i\in {\mathcal {W}}_i$, where $t\in {\mathbb {R}}$, by considering $t\rightarrow \infty$ we obtain

$$\begin{aligned} \sup _{\omega _i\in {\mathcal {W}}_i}\int _{X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z)) d\gamma _i=+\infty . \end{aligned}$$

Hence, to guarantee that (39) is finite, we must require that $\langle \gamma _i,{{\mathcal {W}}_i}\rangle =0$ defined in (16) holds. Therefore,

$$\begin{aligned} \inf _{\gamma _i\in \varPi (\mu _i,\nu )}\sup _{\omega _i\in {\mathcal {W}}_i}\int _{X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z)) d\gamma _i=\inf _{\gamma _i\in \varPi _{{\mathcal {W}}_i}(\mu _i,\nu )}\int _{X_i\times Z} c_i(x_i,z) d\gamma _i, \end{aligned}$$

where

$$\begin{aligned} \varPi _{{\mathcal {W}}_i}(\mu _i,\nu ):=\{\gamma _i\in {\mathcal {P}}(X_i\times Z): \\ \gamma _i\circ \pi ^{-1}_{X_i}=\mu _i \text{ and } \gamma _i\circ \pi ^{-1}_{Z}=\nu \text{ and } \langle \gamma _i,{{\mathcal {W}}_i}\rangle =0\}. \end{aligned}$$

$\square$

Proof

(Proposition 2.2) Suppose that the set $\{(\psi _i,\gamma _i,\nu )\}_{i=0}^N$ is an RME. Then, from Definition 2.2, we have that

$$\begin{aligned} \sum _{i=0}^{N}\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )= \sum _{i=0}^N\int _{X_i}\psi _i^{(c_i+\omega ^*_i)}(x_i)d\mu _i, \end{aligned}$$

for some $\omega ^*_i\in {\mathcal {W}}_i$. Since $\langle \gamma _i,{\mathcal {W}}_i\rangle =0$, we have that $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$. Therefore, by (9)-(10), for any other probability measure $\rho \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$, we have that

$$\begin{aligned} \sum _{i=0}^{N}\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\rho )\ge \sum _{i=0}^{N}\int _{X_i}\psi _i^{(c_i+\omega ^*_i)}(x_i)d\mu _i. \end{aligned}$$

Therefore, $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$ solves the primal problem (26).

Note that, for any other functions $(\varphi _0,\dots ,\varphi _N)\subset C(Z;{\mathbb {R}})$ such that

$$\begin{aligned} \sum _{i=0}^N \varphi _i(z)=0 \end{aligned}$$

holds, where $z\in Z$, we have that

$$\begin{aligned} \sum _{i=0}^N \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )\ge \sum _{i=0}^N\int _{X_i}\varphi _i^{(c_i+\omega _i)}(x_i)d\mu _i. \end{aligned}$$

Therefore, $(\psi _0,\dots ,\psi _N)$ and $(\omega ^*_0,\dots ,\omega ^*_N)$, with $\omega ^*_i\in {\mathcal {W}}_i$, solve the dual problem in (27). $\square$

The following result will be useful.

Theorem 3.1

[23, Theorem 1] Let K be a compact Hausdorff space, W an arbitrary vector space and $h:K\times W \rightarrow {\mathbb {R}}$ be lower semicontinuous in x, where $x\in K$, for each fixed $y\in W$, convex on K and concave on W. Then

$$\begin{aligned} \min _{x\in K}\sup _{y\in W}h(x,y)=\sup _{y\in W}\min _{x\in K}h(x,y). \end{aligned}$$

For the purpose of the following proof, we will denote the uniform norm by $\Vert \cdot \Vert _{\infty , X_i}$ to emphasize that the domain of the space of continuous functions of interest is $X_i$ and $\Vert \cdot \Vert$ the usual absolute value in ${\mathbb {R}}$.

Proof

(Proposition 2.3) Let $\omega _i\in {\mathcal {W}}_i$. Then, for $\psi _{i1},\psi _{i2}\in C(Z;{\mathbb {R}})$, we have that

$$\begin{aligned} \Vert \psi _{i1}^{c_i+\omega _i} - \psi _{i2}^{c_i+\omega _i}\Vert _{\infty , X_i}=&\sup _{x_i\in X_i} |\psi _{i1}^{c_i+\omega _i}(x_i)-\psi _{i2}^{c_i+\omega _i}(x_i)|\\=&\sup _{x_i\in X_i}|\sup _{z\in Z}(-c_i(x_i,z)+ \psi _{i2}(z)-\omega _i(x_i,z))\\-&\sup _{z\in Z}\big (-c_i(x_i,z)+\psi _{i1}(z)-\omega _i(x_i,z)\big ) |\\\le&\sup _{z\in Z}|\psi _{i2}(z)-\psi _{i1}(z)|\\=&\Vert \psi _{i1} - \psi _{i2}\Vert _{\infty ,Z}, \end{aligned}$$

where, in the second equality, we have used the definition of $\psi _i^{(c_i+\omega _i)}$ in (9) and in the third inequality, we have used the fact that $\Vert \sup f-\sup g\Vert \le \sup \Vert f-g\Vert$, for bounded real-valued functions f and g. Also, using a similar argument, for any $\omega _{i1},\omega _{i2}\in {\mathcal {W}}_i$, we have that

$$\begin{aligned} \Vert \psi _i^{c_i+\omega _{i1}} - \psi _i^{c_i+\omega _{i2}}\Vert _{\infty , X_i}\le \Vert \omega _{i1}-\omega _{i2}\Vert _{\infty ,X_i\times Z}. \end{aligned}$$

This shows that ${\mathcal {F}}_i(\cdot ,\cdot )$ is continuous on $C(Z;{\mathbb {R}})\times {\mathcal {W}}_i$. To show for concavity of ${\mathcal {F}}_i(\cdot ,\omega _i)$, we observe that for $\lambda \in (0,1)$ and $\psi _{i1},\psi _{i2}\in C(Z;{\mathbb {R}})$,

$$\begin{aligned} (\lambda \psi _{i1}+(1-\lambda )\psi _{i2})^{c_i+\omega _i}(x_i)=&\inf _{z\in Z}\big (c_i(x_i,z)+\omega _i(x_i,z)-(\lambda \psi _{i1}(z)\\&+(1-\lambda )\psi _{i2}(z))\big )\\=&\inf _{z\in Z}\big (\lambda (c_i(x_i,z)+\omega _i(x_i,z)-\psi _{i1}(z))\\+&(1-\lambda )(c_i(x_i,z)+\omega _i(x_i,z)-\psi _{i2}(z))\big )\\ \ge&\inf _{z\in Z}\big (\lambda ( c_i(x_i,z)+\omega _i(x_i,z)-\psi _{i1}(z))\big )\\+&\inf _{z\in Z}\big ((1-\lambda )(c_i(x_i,z)+\omega _i(x_i,z)-\psi _{i2}(z))\big )\\=&\lambda \psi _{i1}^{c_i+\omega _i}(x_i)+(1-\lambda )\psi _{i2}^{c_i+\omega _i}(x_i), \end{aligned}$$

and hence, by integrating both sides, we obtain

$$\begin{aligned} {\mathcal {F}}_i(\lambda \psi _{i1}+(1-\lambda )\psi _{i2},\omega _i)\ge \lambda {\mathcal {F}}_i(\psi _{i1},\omega _i)+(1-\lambda ){\mathcal {F}}_i(\psi _{i2},\omega _i). \end{aligned}$$

Similarly, one can show that, for $\omega _{i1},\omega _{i2}\in {\mathcal {W}}_i$,

$$\begin{aligned} \psi _i^{c_i+(\lambda \omega _{i1}+(1-\lambda )\omega _{i2})}(x_i)\ge \lambda \psi _i^{c_i+\omega _{i1}}(x_i)+(1-\lambda )\psi _i^{c_i+\omega _{i2}}(x_i), \end{aligned}$$

which proves that the functional ${\mathcal {F}}_i(\psi _i,\cdot )$ is concave in $\omega _i$, for $\psi _i\in C(Z;{\mathbb {R}})$. This concludes that $h_i$ defined in (29) is a continuous convex functional on $C(Z;{\mathbb {R}})$.

We show that the Fenchel conjugate of $h_i$ is

$$\begin{aligned} h_i^*(\nu )=\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu ), \end{aligned}$$

(40)

where $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$.

Let $h_i^*(\nu )<\infty$. If $\nu \notin {\mathscr {M}}_+(Z)$, then there exists ${\tilde{\psi }}_i\le 0$ such that

$$\begin{aligned} \int _Z {\tilde{\psi }}_i(z)d\nu \ge 0. \end{aligned}$$

Let $\omega _i\in {\mathcal {W}}_i$ and $t\ge 0$. Since $(t{\tilde{\psi }}_i)^{(c_i+\omega _i)}(x_i)\ge \min _{(x_i,z)\in X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z))$, we have

$$\begin{aligned} h_i^*(\nu )\ge \sup _{t\ge 0}\sup _{\omega _i\in {\mathcal {W}}_i} t\int _Z {\tilde{\psi }}_i(z)d\nu +\sup _{\omega _i\in {\mathcal {W}}_i}\min _{(x_i,z)\in X_i\times Z} c_i(x_i,z)+\omega _i(x_i,z)=\infty . \end{aligned}$$

Furthermore, if $\nu \notin {\mathcal {P}}(Z)$, then

$$\begin{aligned} h_i^*(\nu )\ge \sup _{t\in {\mathbb {R}}}t(\nu (Z)-\mu _i(X_i))+\sup _{\omega _i\in {\mathcal {W}}_i}\min _{(x_i,z)\in X_i\times Z} c_i(x_i,z)+\omega _i(x_i,z)=\infty . \end{aligned}$$

We proceed to show that (40) holds. If $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$, then $\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )<\infty$ and

$$\begin{aligned} \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )=\min _{\gamma _i\in \varPi (\mu _i,\nu )}\sup _{\omega _i\in {\mathcal {W}}_i}\int _{X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z))d\gamma _i. \end{aligned}$$

Let $h_{c_i}(\gamma _i,\omega _i):= \int _{X_i\times Z} (c_i(x_i,z)+\omega _i(x_i,z)) d\gamma _i$, where $(\gamma _i,\omega _i)\in \varPi (\mu _i,\nu )\times {\mathcal {W}}_i$. From [38, Chapter 1, Page 32], since $\varPi (\mu _i,\nu )$ is a compact, $h_{c_i}(\cdot ,\omega _i)$ is convex function on $\varPi (\mu _i,\nu )$ and $h_{c_i}(\gamma _i,\cdot )$ is affine functional on ${\mathcal {W}}_i$, from Theorem 3.1 and (24), we have

$$\begin{aligned} \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )=\sup _{\omega _i\in {\mathcal {W}}_i}\sup _{\psi _i\in C(Z;{\mathbb {R}})}\int _Z\psi _i(z)d\nu +\int _{X_i}^{}\psi _i^{(c_i+\omega _i)}(x_i)d\mu _i. \end{aligned}$$

Therefore, we conclude that

$$\begin{aligned} h_i^*(\nu )=\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )<\infty , \end{aligned}$$

whenever $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$. $\square$

Proof

(Proposition 2.4) Consider the map $(h_1\square h_2):C(Z,{\mathbb {R}}) \rightarrow {\mathbb {R}}$ defined as

$$\begin{aligned} (h_1\square h_2)(\psi )=\inf _{\psi _2\in C(Z;{\mathbb {R}})}h_1 (\psi -\psi _2)+h_2 (\psi _2). \end{aligned}$$

Since $h_i$ in (29) is a convex functional on $C(Z,{\mathbb {R}})$, we conclude that

$$\begin{aligned} (h_1\square h_2)(\psi )=\inf \{h_1(\psi _1)+h_2(\psi _2)\mid \sum _{i=1}^2 \psi _i(z)=\psi (z),\quad \hbox { where}\ z\in Z\} \end{aligned}$$

is a convex functional on $C(Z,{\mathbb {R}})$. Furthermore, one can check that the Fenchel conjugate of $(h_1\square h_2)$ is $(h_1\square h_2)^*(\nu )= h_1^*(\nu )+h_2^*(\nu )<\infty$, where $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$. Therefore, we conclude that ${\mathcal {L}}$ is a convex functional on $C(Z,{\mathbb {R}})$ and

$$\begin{aligned} {\mathcal {L}}^*(\nu )=\sum _{i=0}^N h_i^*(\nu ), \end{aligned}$$

where $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$. $\square$

Proof

(Proposition 2.5) From Proposition 2.4, since ${\mathcal {L}}$ is a convex functional over $C(Z;{\mathbb {R}})$, we have that ${\mathcal {L}}^{**}={\mathcal {L}}$ (see [14, Page 94]), where ${\mathcal {L}}^{**}$ is the Fenchel conjugate of ${\mathcal {L}}^{*}$. Since ${\mathcal {M}}_{{\mathcal {W}}}(\mu )\subset {\mathcal {P}}(Z)$ is a non-empty weakly compact set (as it is a closed subset of a weakly compact set ${\mathcal {P}}(Z)$), from (32), we have that

$$\begin{aligned} {\mathcal {L}}^{**}(\psi )=\max _{ \nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\langle \nu ,\psi \rangle -\sum _{i=0}^N h_i^*(\nu ). \end{aligned}$$

By setting $\psi \equiv 0$ and using Proposition 2.6, we have

$$\begin{aligned} -{\mathcal {L}}^{**}(0)=\min _{\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\sum _{i=0}^N \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu ). \end{aligned}$$

Since

$$\begin{aligned} -{\mathcal {L}}(0)=\sup _{(\psi _0,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N -h_i(\psi _i), \end{aligned}$$

(41)

where ${\mathscr {T}}$ is defined in (28), we have

$$\begin{aligned} -{\mathcal {L}}(0)=\sup _{(\omega _0,\dots ,\omega _N)\in {\mathcal {W}}}\sup _{(\psi _0,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N \int _{X_i}\psi _i^{(c_i+\omega _i)}(x_i)d\mu _i. \end{aligned}$$

Now, since $-{\mathcal {L}}^{**}(0)=-{\mathcal {L}}(0)$, we obtain that

$$\begin{aligned} \min _{\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\sum _{i=0}^N \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )= \sup _{(\omega _0,\dots ,\omega _N)\in {\mathcal {W}}}\sup _{(\psi _1,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N \int _{X_i}\psi _i^{(c_i+\omega _i)}(x_i)d\mu _i.\square \end{aligned}$$

$\square$

Proof

(Proposition 2.5) From Proposition 2.4, since ${\mathcal {L}}$ is a convex functional over $C(Z;{\mathbb {R}})$, we have that ${\mathcal {L}}^{**}={\mathcal {L}}$ (see [14, Page 94]), where ${\mathcal {L}}^{**}$ is the Fenchel conjugate of ${\mathcal {L}}^{*}$. Since ${\mathcal {M}}_{{\mathcal {W}}}(\mu )\subset {\mathcal {P}}(Z)$ is a non-empty weakly compact set (as it is a closed subset of a weakly compact set ${\mathcal {P}}(Z)$), from (32), we have that

$$\begin{aligned} {\mathcal {L}}^{**}(\psi )=\max _{ \nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\langle \nu ,\psi \rangle -\sum _{i=0}^N h_i^*(\nu ). \end{aligned}$$

By setting $\psi \equiv 0$ and using Proposition 2.6, we have

$$\begin{aligned} -{\mathcal {L}}^{**}(0)=\min _{\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\sum _{i=0}^N \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu ). \end{aligned}$$

Since

$$\begin{aligned} -{\mathcal {L}}(0)=\sup _{(\psi _0,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N -h_i(\psi _i), \end{aligned}$$

where ${\mathscr {T}}$ is defined in (28), we have

$$\begin{aligned} -{\mathcal {L}}(0)=\sup _{(\omega _0,\dots ,\omega _N)\in {\mathcal {W}}}\sup _{(\psi _0,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N \int _{X_i}\psi _i^{(c_i+\omega _i)}(x_i)d\mu _i. \end{aligned}$$

Since $-{\mathcal {L}}^{**}(0)=-{\mathcal {L}}(0)$, we obtain

$$\begin{aligned} \min _{\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )}\sum _{i=0}^N \textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu ){=} \sup _{(\omega _0,\dots ,\omega _N)\in {\mathcal {W}}}\sup _{(\psi _1,\dots ,\psi _N)\in {\mathscr {T}}}\sum _{i=0}^N \int _{X_i}\psi _i^{(c_i+\omega _i)}(x_i)d\mu _i. \end{aligned}$$

$\square$

Proof

(Proposition 2.6) Statement (i) implies that $\nu$ satisfies Definition 2.2, part 2, and Statement (ii) implies that the functions $(\psi _0,\dots ,\psi _N)$ satisfies Definition 2.2, part 1. Therefore, we are only left to show Definition 2.2, part 3.

Since $\nu \in {\mathcal {M}}_{{\mathcal {W}}}(\mu )$ solves problem $\textrm{P}$ and $(\psi _0,\dots ,\psi _N)$ and $(\omega ^*_0,\dots ,\omega ^*_N)$ solve problem $\textrm{P}^*$, using Proposition 2.5, we have that

$$\begin{aligned} \sum _{i=0}^N\textrm{K}_{c_i,{\mathcal {W}}_i}(\mu _i,\nu )= \sum _{i=0}^N\int _{X_i}\psi _i^{(c_i+\omega ^*_i)}(x_i)d\mu _i, \end{aligned}$$

where

$$\begin{aligned} \sum _{i=0}^N \psi _i(z)=0, \end{aligned}$$

and $\gamma _i\in \varPi _{{\mathcal {W}}_i}(\mu _i,\nu )$ satisfies

$$\begin{aligned} \int _{X_i\times Z}\omega _i^*(x_i,z)d\gamma _i=0. \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{i=0}^N(\int _{X_i\times Z}(c(x_i,z)-\psi _i^{(c_i+\omega ^*_i)}(x_i)-\psi _i(z)+\omega ^*_i(x_i,z))d\gamma _i)=0. \end{aligned}$$

By (9)–(10) and since

$$\begin{aligned} c_i(x_i,z)-\psi _i(z)+\omega ^*_i(x_i,z)-\psi _i^{(c_i+\omega ^*_i)}(x_i)\ge 0, \end{aligned}$$

where $(x_i,z)\in X_i\times Z$, we have that

$$\begin{aligned} c_i(x_i,z)=\psi _i^{(c_i+\omega ^*_i)}(x_i)+\psi _i(z)-\omega ^*_i(x_i,z),\quad \gamma _i\text{-a.e. } \text{ on } X_i\times Z. \end{aligned}$$

$\square$

Proof

(Theorem 2.2) Let $\omega _i^*\in {\mathcal {W}}_i$ be a maximizer for the R.H.S. of (29) and consider a minimizing sequence $\{\big (\psi _{0,n},\dots ,\psi _{N,n}\big )\}_{n\ge 1} \subset {\mathscr {T}}$. Let

$$\begin{aligned} \alpha _{i,n}:=\psi _{i,n}^{(c_i+\omega ^*_i)\overline{(c_i+\omega ^*_i)}}, \end{aligned}$$

(42)

where $\psi _{i,n}^{(c_i+\omega ^*_i)\overline{(c_i+\omega ^*_i)}}$ is defined in (25) and consider

$$\begin{aligned} \alpha _{0,n}=-\sum _{i=0}^N\alpha _{i,n}. \end{aligned}$$

Then, $\{(\alpha _{0,n},\dots ,\alpha _{N,n})\}_{n\ge 1} \subset {\mathscr {T}}$. Furthermore, for $i\in \{1,\dots ,N\}$, we have $\alpha _{i,n}\in (c_i+\omega ^*_i)-\textrm{conc}(Z;{\mathbb {R}})$, for all $n\ge 1$ and

$$\begin{aligned} \psi _{i,n}\le \alpha _{i,n}. \end{aligned}$$

(43)

Also, from (42) and (43) and since

$$\begin{aligned} h_0(\alpha _{0,n})\le h_0(\psi _{0,n})\quad \text{ and }\quad h_i(\alpha _{i,n})=h_i(\psi _{i,n}), \end{aligned}$$

for $i\in \{1,\dots ,N\}$, we have that

$$\begin{aligned} \sum _{i=0}^N h_i(\alpha _{i,n})\le \sum _{i=0}^N h_i(\psi _{i,n}), \end{aligned}$$

where $n\ge 1$. Therefore, $\{(\alpha _{0,n},\dots ,\alpha _{N,n})\}_{n\ge 1}\subset {\mathscr {T}}$ is an improved minimizing sequence. Since $c_i+\omega _i^*\in C(X_i\times Z;{\mathbb {R}})$, we have that the i-th sequence admits a minimizing subsequence $\{\alpha _{i,n}\}_{n\ge 1}$ that converges uniformly to the minimizer $\alpha _i\in (c_i+\omega ^*_i)-\textrm{conc}(Z;{\mathbb {R}})$. Therefore,

$$\begin{aligned} \sum _{i=0}^N\alpha _i(z)=0. \end{aligned}$$

$\square$