Current Limit Avoidance Algorithms for DEMO Operation

Abstract

Tokamaks are the most promising devices to prove the feasibility of energy production using nuclear fusion on Earth which is foreseen as a possible source of energy for the next centuries. In large tokamaks with superconducting poloidal field (PF) coils, the problem of avoiding saturation of the currents is of paramount importance, especially for a reactor such as the European demonstration fusion power plant DEMO. Indeed, reaching the current limits during plasma operation may cause a loss of control of the plasma shape and/or current, leading to a major disruption. Therefore, a current limit avoidance (CLA) system is essential to assure safe operation. Three different algorithms to be implemented within a CLA system are proposed in this paper: two are based on online solutions of constrained optimization problems, while the third one relies on dynamic allocation. The performance assessment for all the proposed solutions is carried out by considering challenging operation scenarios for the DEMO reactor, such as the case where more than one PF current simultaneously saturates during the discharge. An evaluation of the computational burden needed to solve the allocation problem for the various proposed alternatives is also presented, which shows the compliance of the optimization-based approaches with the envisaged deadlines for real-time implementation of the DEMO plasma magnetic control system.

1 Introduction

Nuclear fusion is foreseen as a promising source of clean and sustainable energy for the next century. A big effort is currently ongoing to develop its peaceful use toward the realization of a power plant, to support the increasing world energy demand. Tokamak [39] arose in the  50s of the last century as one of the most promising experimental devices in fusion, and this concept is still taken as a baseline for designing a power plant reactor. In this context, the demonstration power plant DEMO will represent the step before the construction of a commercial power plant in the path envisaged by the European roadmap to the realization of fusion energy [23, 24].

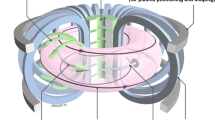
In a tokamak, a fully ionized gas of hydrogen isotopes called plasma is heated up to temperatures of tens to hundred millions degrees. At such a high temperature, the particles’ thermal agitation can overcome the Coulomb repulsive force, making it possible for the hydrogen nuclei to collide and produce fusion reactions. The confinement of such a hot plasma is achieved using external magnetic fields generated by the current that flows in both the toroidal field and poloidal field (PF) superconducting circuits (see Fig. 1). Indeed, a tokamak can be regarded as a toroidally shaped magnetic bottle, where the external magnetic field is exploited to confine the charged particles that form the plasma inside the reactor chamber.

The need for achieving increasing performance and reliability in present fusion experimental devices and future fusion reactors has leveraged plasma control importance in tokamak engineering [1, 12, 22, 28, 38]. In this context, plasma magnetic control plays a crucial role since it is needed since day one, and it is essential to successfully control high-performance plasmas, such as the ones envisaged for ITER and DEMO [10, 35].

The various sub-problems entailed by plasma magnetic control, such as the tracking of the current induced into the plasma, as well as of its shape and position [9], exploit the currents flowing in the PF circuits as actuators [17]. Therefore, the ability to reject unexpected disturbances and to cope with model uncertainties relies on the overall robustness of the control system architecture, which does not only depend on robust design techniques [7, 27, 34, 37]. Indeed, every operating plasma magnetic control algorithm requires that the currents in the PF circuits are sufficiently far from their saturation, to have enough margin to react to unexpected events. Although open-loop strategies for the optimization of the nominal PF current waveforms can be adopted [21, 32, 33], these may not be effective for scenarios at the highest values of the plasma current or when unexpected disturbances occur during plasma current ramp-up or ramp-down [19]. As a consequence, a reliable plasma magnetic control system must include a current limit avoidance (CLA) system to safely operate the machine also when disturbances and or uncertainties drive the PF currents close to their limits [4, 13, 36].

Another key factor when designing a control system for a critical infrastructure such as a nuclear power plant is to avoid as much as possible common mode failures, by adopting both different hardware and software solutions. It turns out that the availability of different algorithms represents a prerequisite to achieve the requested level of reliability. To this aim, the contribution of this paper mainly consists of three different limit avoidance algorithms, with corresponding variants, to be implemented within the a CLA system. Both approaches that require online solutions of optimization problems and input dynamic allocation [16, 20] are proposed. Although the former may resemble Model Predictive Control (MPC, [14, 34]), they trigger the solution of the corresponding optimization problem only when the PF currents are approaching their limits, whereas MPC requires solving a constrained optimization problem at each control time sample. Moreover, the solution of MPC is usually constrained also by the system dynamic, which concurs to increase the computational burden needed to solve the problem. Therefore, limit avoidance algorithms are computationally more efficient with respect to MPC. Furthermore, provided that a so-called current control scheme is adopted [17], the CLA architecture is independent of the specific control algorithm used for plasma current and shape control; therefore, it contributes to increase the flexibility and robustness of the overall plasma magnetic control system.

The effectiveness of the proposed CLA techniques is shown using numerical simulations aimed at assessing performance in challenging operation scenarios for the DEMO reactor, whose simplified pictorial view is shown in Fig. 1. In particular, scenarios where more than one PF current simultaneously saturate during the discharge are considered, as well as scenarios with relevant disturbance expected during operation. Furthermore, an evaluation of the computational burden needed to solve the limit avoidance problem for the various proposed alternatives is also presented. As it will be discussed in Sect. 5, such an analysis shows that the optimization-based approaches meet the envisaged deadlines for real-time implementation of the DEMO plasma magnetic control system.

Fig. 1

Simplified schematic view of the European DEMO (image taken from [26])

The remainder of this paper is organized as follows: the next section briefly introduces the nonlinear magnetic equilibrium code [2] used to validate the various CLA approaches. This nonlinear code also computes the control-oriented linear model exploited for the design of the proposed algorithms. The control architecture is described in Sect. 3, while Sect. 4 deals with the CLA algorithms. Performance assessment is discussed in Sect. 5, where relevant validation scenarios for the DEMO reactor are considered in simulation. Some conclusions are then drawn in Sect. 6.

2 Control Oriented Plasma Magnetic Modeling

This section introduces the modeling framework considered for both CLA design and performance assessment. The CREATE-NL nonlinear free boundary plasma equilibrium code [2] is presented first. This code will be exploited in Sect. 5 to perform a nonlinear assessment of the proposed CLA strategies. Moreover, CREATE-NL allows to generate control-oriented plasma linear models [18], which are used in Sect. 4 to design the proposed CLA algorithms.

2.1 The CREATE-NL Nonlinear Equilibrium Code

The CREATE-NL equilibrium code numerically solves the following Grad–Shafranov partial differential equation (PDE) obtained under the assumption of axial-symmetry and plasma surrounding conductive structures without inertial effects:

$$\begin{aligned} \begin{aligned}&\varDelta ^* \psi =-f \frac{df}{d\psi }-\mu _0 r^2\frac{dp}{d\psi }, \qquad \quad \; \text {in the plasma region} \\&\varDelta ^* \psi =-\mu _0 r j_{ext}(r,z,t), \qquad \quad \quad \text {in the conductors} \\&\varDelta ^* \psi =0, \qquad \qquad \qquad \qquad \quad \quad \text {elsewhere} \ \end{aligned} \end{aligned}$$

where $(r,\phi ,z)$ are the cylindrical coordinates, and the following boundary conditions are set:

$$\begin{aligned} \begin{aligned}&\psi (r,z,0)=\psi _0(r,z),\\&\psi (0,z,t)=0, \\&\lim \limits _{r^2+z^2 \rightarrow \infty } \psi (r,z,t) = 0,\quad \forall ~t, \end{aligned} \end{aligned}$$

being $\psi$ the poloidal flux per radian, $\mu _0$ the vacuum magnetic permeability, $j_{ext}$ the toroidal current density in the external conductors (both control coils and passive structures), $p = p(\psi )$ the kinetic pressure profile, and $f = f(\psi )$ the poloidal current function profile, while the $\varDelta ^*$ operator is defined as:

$$\begin{aligned} \varDelta ^*=r\frac{\partial }{\partial r}\left( \frac{1}{\mu _r r}\frac{\partial \psi }{\partial r}\right) +\frac{\partial }{\partial z}\left( \frac{1}{\mu _r}\frac{\partial \psi }{\partial z}\right) \,. \end{aligned}$$

More details about how to derive the Grad–Shafranov PDE starting from the magnetohydrodynamic theory can be found in [25, Ch. 11].

The CREATE-NL code adopts a first-order Finite Element Method (FEM), discretizing the space with a finite number $n_1$ of nodes, and assigning the plasma current density as a function of given $p(\overline{\psi })$ and $f(\overline{\psi })$, or as linear combination of basis function of the normalized flux $\overline{\psi }=\frac{(\psi -\psi _a)}{(\psi _b-\psi _a)}$, $\psi _b$ and $\psi _a$ being the flux per radian on the plasma boundary and the axis, respectively, and $n_2$ parameters $\alpha$ which can be related to integral plasma quantities poloidal beta $\beta _{pol}$ and internal inductance $l_i$. Plasma current $I_p$ evolves based on a balance of flux on the plasma boundary, given the plasma total resistance.

In a FEM approach, the solution of the Grad–Shafranov equations requires the solution of a nonlinear set of equations $F(x)=0$, $x = (\hat{\psi }^T,\pi ^T)^T$, where $\hat{\psi }$ is the vector of fluxes in the spatial discretization nodes, $\pi =(I^T,\alpha ^T)^T$. Also, currents I in the active conductors and in the passive structures become unknowns of the problem when circuits are voltage driven. In this case, circuit equations must be added to the model and the problem can then be solved with an iterative Newton-based method where the candidate solution update at the step $k+1$ is obtained as $x_{k+1}=x_k-(\frac{\partial F(x_k)}{\partial x})^T F(x_k)$.

2.2 Control-Oriented Linear Model of the Plasma Response

By solving the Grad–Shafranov PDEs, it is possible to retrieve the following nonlinear lumped parameters circuital model describing the behavior of the plasma and of the currents that flow in the surrounding conductive structures (both active and passive):

(1a)

(1b)

where:

• $x(t)=\left( I_{PF}^T(t)\ I_{VS}(t)\ I_{e}^T(t)\ I_p(t)\right) ^T\in \mathbb {R}^{n_x}$ is the vector that includes the currents in the superconducting circuits $I_{PF}(t)\in \mathbb {R}^{n_{PF}}$ (both the central solenoid and external PF coils shown in Fig. 1), the current $I_{VS}(t)$ in the in-vessel circuit which is dedicated to the plasma vertical stabilization (see the pair of in-vessel coils shown in Fig. 2, which are connected in anti series to produce a radial field exerting a vertical force on the plasma), the eddy currents in the passive structures $I_{e}(t)$ and the plasma current $I_p(t)$;

• $u(t)=\left( u_{PF}^T(t)\ u_{VS}(t)\ 0^T\ 0\right) ^T$ is the input voltages vector, where  $u_{PF}(\cdot )\in \mathbb {R}^{n_{PF}}$ is a vector that holds the voltages applied to the superconducting circuits, and $u_{vs}(\cdot )$ is the voltage applied to the in-vessel circuit used for the vertical stabilization;

• $y(t)\in \mathbb {R}^{n_y}$ is the output vector that holds all the quantities of interest, e.g.,  the plasma current and the currents in the active coils, as well as the plasma shape and position descriptors;

• $\mathcal {M}(\cdot )$ is the mutual inductance nonlinear function; this function depends on the plasma internal profiles (this dependency is taken into account using the poloidal beta $\beta _p$ and the internal inductance $l_i$), and on the plasma shape and position, whose descriptors are included in the output vector y(t);

• $R\in \mathbb {R}^{n_x\times n_x}$ is the resistance matrix;

• $\mathcal {Y}(\cdot )$ is the output nonlinear function.

Either analytically (as done by the CREATE-L code [3], embedded in the modeling suite exploited in this work) or numerically (as done by CREATE-NL), the nonlinear circuital model (1) can be linearized around a given equilibrium, specified in terms of reference plasma current $I_{p_{eq}}$ and reference values for both the poloidal beta $\beta _{p_{eq}}$ and the internal inductance $l_{i_{eq}}$. The linearized model reads as follows (time dependence is dropped for the sake of readability):

$$\begin{aligned} \begin{aligned}&L\delta \dot{x}+R\delta x=\delta u+L_E\delta \dot{w} \\&\delta y=\delta Cx\,, \end{aligned} \end{aligned}$$

(2)

where $\delta w=\left( \delta \beta _p\quad \delta l_i\right) ^T\in \mathbb {R}^2$ is the exogenous disturbance vector,¹$L\in \mathbb {R}^{n_x \times n_x}$ is the inductance matrix, $L_E\in \mathbb {R}^{n_x \times 2}$ is the flux variation-disturbance matrix, while $C\in \mathbb {R}^{n_y \times n_x}$ is the output matrix. From (2), it is straightforward to derive the following standard state-space representation of a dynamic linear system:

$$\begin{aligned} \begin{aligned}&\delta \dot{x}=A\delta x+B\delta u+F\delta \dot{w} \\&\delta y=C\delta x\,, \end{aligned} \end{aligned}$$

(3)

where $A=-L^{-1}R$, $B=L^{-1}$ and $F=L^{-1}L_E$.

When detailing the model (3) to the case of the DEMO reactor, itis $n_{PF}~=~11$, since there are 6 external PF coils (shown in cyan in Fig. 1), 5 central solenoid independent coils (shown in red in Fig. 1). Moreover, other than the plasma current and the current in the active coil, the output vector of (3) includes also the plasma-to-wall distances, the so-called gaps [11], shown in Fig. 2 and used by the proposed architecture to control the plasma shape. Finally, as far as the passive conductive structures are concerned, these have been discretized by using 100 lumped parameter circuits.

Fig. 2

DEMO reactor poloidal cross section. This figure shows the two in-vessel coils that form the VS circuit used as an actuator by the vertical stabilization system, as well as the plasma-wall gaps directions for the gaps controlled by the proposed plasma shape controller

3 Magnetic Control System Architecture

This section introduces the general architecture of the plasma magnetic control system adopted in this paper. Thanks to its flexibility, the proposed architecture allows us to easily include the CLA components. We briefly present the approaches considered to design magnetic control algorithms. For more details about axisymmetric plasma magnetic control, interested readers can refer either to [9] or [17].

Figure 3 shows a simplified block diagram of the proposed magnetic control architecture, which includes the following blocks:

• the Vertical Stabilization (VS) System, that takes care of the stabilization of the vertical elongated and unstable plasma column. At DEMO, there is a dedicated in-vessel circuit for this purpose (see Sect. 2.2). The stabilization problem is reduced to a single-input-single-output problem (SISO), by using a linear combination of the current in the in-vessel coil $I_{VS}$ and of the vertical speed of the plasma centroid $\dot{z}_c$ as controlled variable. The VS is then designed as a proportional controller, i.e.,

  $$\begin{aligned} u_{VS}(t) = k_{VS}\left( k_I\cdot I_{VS}(t)+\dot{z}_c(t)\right) , \end{aligned}$$

  where $k_{VS}$ is obtained by solving a constrained optimization problem on a finite time horizon equal to 1 s (e.g. [29]). The VS design explicitly accounts for the dynamic of the in-vessel coil power supply, which has been modeled as a first-order system in cascade with a pure delay: both the first-order time constant and the delay have been set equal to 2.5 ms.

• The PF Current Controller (PFC); this block guarantees that the currents in the superconducting PF circuits track the scenario references $I_{PF_{scen}}$, as well as the corrections $I_{PF_{I_p}}$ and $I_{PF_{SH}}$ received from the plasma current and shape controllers, respectively. For the design of the PFC, it is assumed that the eddy currents in the passive structures become negligible with a faster time scale if compared to the typical dynamical response required by the plasma current and shape controller, which are the ones that send the requests to the PFC. Therefore, to design the PFC the model (3) is purged of the $I_e(t)$ component of the state space. Furthermore, the dynamic of the PF circuits’ power supplies is also neglected when designing the PFC, since their dynamics are relatively faster if compared with the one required for the PFC. Indeed, the latter will have a settling time in the order of seconds, while, similarly to the in-vessel case, the generic PF power supply can be modeled as a first-order system with a time constant of 7.5 ms in series with a 7.5 ms pure delay. As a result, the PFC is designed as a static multi-input-multi-output (MIMO) state feedback, whose gain is obtained by exploiting the linear quadratic regulator theory and by setting the closed-loop settling time equal to $\sim 1.5~s$. Such a dynamic response permits us to consider the PF current control almost instantaneous as far as both the plasma current and shape control are concerned. Indeed, the typical settling time for these two loops is in the order of the tens of seconds in the case of the DEMO reactor.

• the Plasma Current Controller, that tracks the plasma current reference $I_{p_{ref}}$ by generating the additional request $\delta I_{PF_{I_p}}$ to be tracked by the PF coils current controller. The plasma current control problem is reduced to a SISO control problem thanks to the so-called transformer currents $I_{tr}\in \mathbb {R}^{n_{PF}}$, which are a combination of currents in the superconducting coils that are optimized with the objective of controlling $I_p$ minimizing the effect on plasma shape. In particular, a proportional-integral (PI) action has been considered in this paper, while settling time has been set equal to about 15 s.

• the Plasma Shape Controller (SC), that tracks the plasma boundary by controlling to zero the error between the reconstructed gaps $y_g$ and the corresponding reference $y_{g_{ref}}$. Similarly to the plasma current control loop, this block generates an additional request $\delta I_{PF_{SH}}$ for the PFC. As already mentioned, since the time response of the SC is slower than the one of the PFC, the former is designed by assuming a static relationship $y_g~=~C_{SH}I_{PF}$ between the currents in the superconducting coils and the controlled gaps $y_g\in \mathbb {R}^{n_{SH}}$, according to the linear model (3). By adopting an XSC-like approach [8], the proposed SC algorithm computes the currents variation $\delta I_{PF_{SH}}$ needed to compensate a plasma shape error as $\delta I_{PF_{SH}}(t)~=~C_{SH}^\dagger \delta y_g(t)$, where $C_{SH}^\dagger$ denotes the pseudo-inverse of $C_{SH}$. Such an approach allows to design the MIMO SC as $n_{PF}$ decoupled SISO loops, to each of which a PI is added. The gains of the PIs are chosen to have a settling time on each channel equal to about 10 s.

Fig. 3

Simplified block diagram of a plasma magnetic control system that includes the current limit avoidance (CLA) system

4 Current Limit Avoidance Algorithms

This section deals with the novel contribution of this paper, i.e., the proposed control algorithms to be implemented in the CLA block shown in Fig. 3.

The CLA system receives as input the total PF current request $I_{PF_{ref}}$ given by the sum of the scenario currents and the corrections computed by the outer loops, which is equal to:

$$\begin{aligned} I_{PF_{ref}}(t) = I_{PF_{scen}}(t)+\delta I_{PF_{SH}}(t)+\alpha (t)I_{tr}\,, \end{aligned}$$

(4)

where $\alpha (t)$ is the output of the SISO PI used to regulate the plasma current (see Sect. 3). If the request is in the safe region, then the CLA forwards it unmodified to the PFC, i.e., $\tilde{I}_{PF_{ref}}=I_{PF_{ref}}$, and its two additional outputs $\varDelta y_{g_{ref}}$ and $\varDelta I_{p_{ref}}$ are set equal to zero. On the other hand, if at least one component of the input vector (4) exceeds the corresponding saturation limit, then the CLA modifies the request to bring it back to the safe region while minimizing the effect on both plasma current and the plasma shape at the same time. Moreover, if this is the case, then the CLA computes the additional references $\varDelta I_{p_{ref}}$ and $\varDelta y_{g_{ref}}$ that are sent to the outer loops to hide the steady-state changes induced by $\tilde{I}_{PF_{ref}}\ne I_{PF_{ref}}$ on both the plasma current and shape; in this way, the outer loop will not react to the changes made by the CLA. As anticipated in Sect. 1, the CLA is agnostic with respect to the specific control algorithms described in Sect. 3.

The next sections are devoted to the three algorithms proposed for the implementation of the CLA, whose performance assessment is presented in Sect. 5.

4.1 CLA Based on Quadratic Programming

The first proposed approach to deal with current limits in the PF coils relies on the online solution of constrained quadratic programming (QP) problems. It is assumed that the architecture introduced in Sect. 3 is implemented as a digital control system, and we denote with $I^k_{PF_{ref}}$ and $\tilde{I}^k_{PF_{ref}}$ the k-th time sample of the CLA input and output, respectively. If, at the k-th discrete time sample, at least one component of $I^k_{PF_{ref}}$ exceeds the corresponding limit, then the CLA system computes the request $\tilde{I}^k_{PF_{ref}}$ as:

$$\begin{aligned} \tilde{I}^k_{PF_{ref}} = I^k_{PF_{scen}}+ \delta \tilde{I}^k_{PF_{SH}}+\tilde{\alpha }^k I_{tr}\,, \end{aligned}$$

where $I^k_{PF_{scen}}$ is the k-th sample of the scenario currents, while $\delta \tilde{I}^k_{PF_{SH}}$ and $\tilde{\alpha }^k I_{tr}$ are the contributions computed by the CLA to track the desired plasma shape and current, respectively, while handling the current constraints. In particular, the vector $\delta \tilde{I}^k_{PF_{SH}}~\in ~\mathbb {R}^{n_{PF}}$ and the scalar $\tilde{\alpha }^k$ are obtained by solving the following QP problem:

$$\begin{aligned} \begin{aligned} \min _{\delta \tilde{I}^k_{PF_{SH}}\,,\tilde{\alpha }^k} \left\| C_{SH}\varDelta I^k_{PF_{CLA}}\right\| _{W_{SH}}\ +\left\| c^T_{I_p}\varDelta I^k_{PF_{CLA}}\right\| _{w_{I_p}}+\left\| \tilde{I}^k_{PF_{ref}}\right\| _{W_{I_{PF}}}\\+\left\| \delta \tilde{I}^k_{PF_{SH}}-\delta \tilde{I}^{k-1}_{PF_{SH}}\right\| _{W_{V_1}}+\left\| \left( \tilde{\alpha }^k-\tilde{\alpha }^{k-1}\right) I_{tr}\right\| _{W_{V_2}}\,, \end{aligned} \end{aligned}$$

(5)

where² $\varDelta I^k_{PF_{CLA}}$ denotes the total PF currents variation computed by the CLA, i.e.,

$$\begin{aligned} \varDelta I^k_{PF_{CLA}}(\delta \tilde{I}^k_{PF_{SH}},\tilde{\alpha }^k) = \tilde{I}^k_{PF_{ref}}-I^k_{PF_{ref}}, \end{aligned}$$

where:

• the term $\left\| C_{SH}\varDelta I^k_{PF_{CLA}}\right\| _{W_{SH}}$ aims at minimizing the error on the plasma shape due to the current modification $\varDelta I^k_{PF_{CLA}}$. $C_{SH}$ is the output matrix of (3) that links the PF currents to the controlled gaps, while $W_{SH}~\in ~\mathbb {R}^{n_{SH}\times n_{SH}}$ is the corresponding weighting matrix;

• similarly to the previous term, $\left\| c^T_{I_p}\varDelta I^k_{PF_{CLA}} \right\| _{w_{I_p}}$ aims at minimizing the error on $I_p$ control, where $w_{I_p}~\in ~\mathbb {R}$ is the corresponding weighting factor and $c_{I_p}\in \mathbb {R}^{n_{PF}}$ is a vector that links $I_p$ to the PF currents; this vector can be computed by starting from the circuital model (see [9, Ch. 2.3]) and by assuming that the effect due to the relatively small plasma resistance is compensated by the plasma current controller via the transformer action;

• the term $\left\| \tilde{I}^k_{PF_{ref}}\right\| _{W_{I_{PF}}}$, with the corresponding weighting matrix $W_{I_{PF}}\in \mathbb {R}^{n_{PF}\times n_{PF}}$, aims at keeping the control effort as small as possible;

• the terms $\left\| \delta \tilde{I}^k_{PF_{SH}}-\delta \tilde{I}^{k-1}_{PF_{SH}}\right\| _{W_{V_1}}$ and $\left\| \left( \tilde{\alpha }^k-\tilde{\alpha }^{k-1}\right) I_{tr}\right\| _{W_{V_2}}$,with $W_{V_1},W_{V_2}~\in ~\mathbb {R}^{n_{PF}\times n_{PF}}$, are two further regularization terms that aim at minimizing the variation of $\tilde{I}_{PF_{ref}}$ and hence the voltages $u_{PF}$ applied by the PFC.

Once the QP problem is solved, the k-th sample of the two additional CLA outputs $\varDelta y_{ref}$ and $\varDelta I_{p_{ref}}$ are computed as:

$$\begin{aligned} \varDelta y^k_{g_{ref}}&= C_{SH}\varDelta I^k_{PF_{CLA}}\,, \end{aligned}$$

(6a)

$$\begin{aligned} \varDelta I^k_{p_{ref}}&= c_{I_p}^T\varDelta I^k_{PF_{CLA}}\,. \end{aligned}$$

(6b)

The following two possible approaches for constraints management are considered when solving the optimization problem (5):

• in the QP with hard constraints version of the proposed approach, the bounds for the PF currents are directly included in (5), i.e., the following constraint is explicitly added:

  $$\begin{aligned} \underline{I_{PF}} \le \tilde{I}^k_{PF_{ref}} \le \overline{I_{PF}}\,, \end{aligned}$$

  (7)

  where $\underline{I_{PF}},\overline{I_{PF}}\in \mathbb {R}^{n_{PF}}$ are the lower and upper bound for the PF currents, respectively;

• if the QP with soft constraints approach is adopted, the problem (5) is solved without explicit constraints, but the weights in $W_{I_{PF}}$ are assumed to vary as a function of the PF currents themselves, so to penalize current that are approaching the corresponding limits. In particular, Fig. 4 shows the behavior of a generic component of the present step weights $W_{I_{PF}}^k$ as a function of the previous step excess $\varDelta ^{out,k-1}=\tilde{I}_{PF_{ref}}^{k-1}-I_{scen}^{k-1}$, consisting in an exponential behavior in the interval [500, 600] A, (600A is considered the bound value) followed by a linear increase with respect to the excess.

Fig. 4

Behavior of the weight $W_{I_{PF}}$ used by the QP-based approach with soft constraints. This figure shows the behavior of the weight for the absolute value of the i-th PF current (the behavior is assumed symmetric with respect to 0)

The QP problem (5), either with hard or soft constraints, can be efficiently solved in real-time using the interior-point-convex algorithm. Further details about the computational burden are given in Sect. 5.5.

4.2 CLA Based on Linear Programming

Online solution of a linear programming (LP) optimization problem represents another possible approach to tackle the current limit avoidance problem.

According to the notation introduced in Sect. 4.1, the considered LP problem reads:

$$\begin{aligned} \begin{aligned} \min _{\delta \tilde{I}^k_{PF_{SH}}\,,\tilde{\alpha }^k} \sum _{i=1}^{n_{SH}} q_{i} \left| c^T_{{SH}_i}\varDelta I^k_{PF_{CLA}}\right| +m\left| c^T_{I_{p}}\varDelta I^k_{PF_{CLA}}\right| +\\ +\sum _{i=1}^{n_{PF}} r_{i} \left| \delta \tilde{I}^k_{PF_{SH_i}}-\delta I^k_{PF_{SH_i}}\right| +r_{pl} \left| \tilde{\alpha }^k- \alpha ^k\right| \end{aligned} \end{aligned}$$

(8)

subject to (7), where it assumed that $C_{SH}=\left( c_{SH_1}\ c_{SH_2}\ \cdots \ c_{SH_{n_{SH}}}\right) ^T$. Moreover, in the cost function (8):

• the term $\sum _{i=1}^{n_{y}} q_{i} \left| c^T_{SH_i}\varDelta I^k_{PF_{CLA}}\right|$ aims at minimizing the error on the plasma wall i-th gap due to the current variation $\varDelta I^k_{PF_{CLA}}$, where $q_{i}$ is the weight on the i-th gap;

• similarly to the previous term, $m\left| c^T_{I_{p}}\varDelta I^k_{PF_{CLA}}\right|$ aims at minimizing the error on $I_p$ control, where m is the corresponding weighting factor.

• the terms $\sum _{i=1}^{n_{PF}} r_{i}\left| \delta \tilde{I}^k_{PF_{SH_i}}- \delta I^k_{PF_{SH_i}}\right|$ and $r_{pl} \left| \tilde{\alpha }^k- \alpha ^k\right|$, with the corresponding weights, aim at keeping the variation made by the CLA with respect to the control effort computed by the outer loops as small as possible.

Moreover, similarly to the QP case, once the problem (8) s.t. (7) is solved, the k-th sample of the two additional CLA outputs is computed according to (6).

4.3 CLA Based on Nonlinear Dynamic System

The alternative proposed approach for CLA at DEMO computes its output as:

$$\begin{aligned} \tilde{I}_{PF_{ref}}(t) = I_{PF_{ref}}(t)+\varDelta I_{PF_{CLA}}(t)\,, \end{aligned}$$

where the correction term $\varDelta I_{PF_{CLA}}(\cdot )\in \mathbb {R}^{n_{PF}}$ is initially set equal to the null vector, and its time evolution is computed through the following nonlinear dynamic allocator:

$$\begin{aligned}&\dot{\xi }(t) =-\rho \left( \nabla J(t) \cdot \left[ I \ P^{*^T} \right] ^T \cdot B_0 \right) ^T\,,\quad \xi (0)=0\\&\varDelta I_{{PF}_{CLA}}(t) =B_0\cdot \xi (t)\,, \end{aligned}$$

where $\xi \in \mathbb {R}^{n_{d}}$ is the allocator state, columns of $B_0\in \mathbb {R}^{n_{PF}\times n_d}$ are independent allocation directions,  $P^\star$ is closed-loop dc-gain matrix between the PF currents and the gaps and $I_p$ (see [20] for more details). Moreover, $\nabla J$ is the gradient of a suitable cost function whose aim is to prevent the PF currents to saturate. In [20], it has been proved that for a sufficiently slow allocator dynamic, i.e., for a sufficiently small value of the gain $\rho >0$, the stability of the overall system is not affected and the response at constant exogenous inputs converges to a steady state value able to minimize the value of cost function J.

By taking into account that for the DEMO reactor, it is $\underline{I_{PF}}~=~-\overline{I_{PF}}$, the following choice for the cost function $J(\cdot )$ has been made:

$$\begin{aligned} \begin{aligned} J \left( \tilde{I}_{PF_{ref}}\right) =&\,\sum _{i=1}^{n_{PF}}a_i\ \left[ \max \left( 0,\frac{|\tilde{I}_{PF_{ref_i}}|-\overline{I_{PF}}_i}{\overline{I_{PF}}_i} \right) \right] ^2\\&+ \sum _{j=1}^{n_{SH}}b_j |\varDelta y_{g_{ref}\,,j}|+b_{Ip} |\varDelta I_{p_{ref}}|, \end{aligned} \end{aligned}$$

(10)

where $a_i>0$ is the weight for the i-th PF current, $b_j>=0$ is the weight for the i-th plasma-wall gap shape error due to the allocation, and $b_{Ip}>0$ is the weight for the plasma current error due the allocation. Similarly to (6), for a given value of $\varDelta I_{PF_{CLA}}$ the two additional CLA outputs are computed as

$$\begin{aligned} \varDelta y_{g_{ref}}(t)&= C_{SH}\varDelta I_{PF_{CLA}}(t)\,,\\ \varDelta I_{p_{ref}}(t)&= c^T_{I_p}\varDelta I_{PF_{CLA}}(t)\,. \end{aligned}$$

By a proper choice of the allocation directions specified by $B_0$, the following two variants of the dynamic allocator (10) are considered in Sect. 5:

• the null-based allocator, that consists in choosing $B_0={{\,\textrm{null}\,}}(P^\star$), which in turn allows to achieve $\varDelta y_{g_{ref}}=0$ and $\varDelta I_{p_{ref}}=0$ at steady state.

• The extended null allocator, in which the allocation directions are set equal to $B_0=[{{\,\textrm{null}\,}}(P^\star )\ \ d_{SVD}]$, where the added direction $d_{SVD}$ is the one that corresponds to the smallest singular value of the $P^*$ singular value decomposition (SVD).

It is worth to remark that, despite the continuous time version of the allocator has been presented in this section, its discrete-time version would be eventually deployed in the architecture presented in Sect. 4.

5 Performance Assessment

The effectiveness of the proposed CLA approaches is shown by considering two test cases for one of the DEMO reference scenarios, both consisting in a request of a plasma shape variation in presence of severe limitations on the PF currents available for control, that is when more than one PF current simultaneously reach the limits.

In what follows, we use $\varDelta I^{in}$ to denote the correction made by both the plasma shape and current controller with respect to the scenario currents, i.e.,

$$\begin{aligned} \varDelta I^{in} = I_{PF_{ref}}-I_{scen} = \delta I_{PF_{SH}}+\delta I_{PF_{I_p}}, \end{aligned}$$

and, similarly, we use $\varDelta I^{out}$ to denote $\tilde{I}_{PF_{ref}}-I_{scen}$, i.e., the difference between the CLA output and the scenario current. Moreover, $\overline{\varDelta I}$ and $\underline{\varDelta I}$ will denote the upper and lower bound on the correction computed by the CLA with respect to the scenario currents, respectively.

5.1 Reference Scenario and Test Cases

The reference scenario considered for the performance assessment refers to a flat-top equilibrium for the DEMO power plant, corresponding to the following plasma parameters: $\bar{\beta }_p~=~1.14$, $\bar{l}_i~=~0.80$ and $\bar{I}_p~=~19.0~MA$, while the equilibrium shape is the one shown in Fig. 2.

Starting from this equilibrium, Test Case I deals with a plasma shape variation request to the controller, which is aimed at reducing the plasma elongation by increasing by 10 cm with respect to its equilibrium starting value the top gap labeled as GAP2 in Fig. 2. While performing this elongation reduction, the overall objective of magnetic control includes keeping unchanged (and equal to their equilibrium values) the other five controlled gaps shown in Fig. 2, as well as the plasma current. Limits on controlled currents are assumed active. Linear simulations in the absence and presence of uncertainty are considered in Sects. 5.2 and 5.3, while the nonlinear simulation is performed in Sect. 5.4.

Test Case II deals with the same request to the plasma shape controller, but considers a more severe limitation on the current available for magnetic control. Indeed, in this case, we iteratively constrain all the PF currents by setting their limits according to Algorithm 1. In particular, at each iteration a limit on the maximum unconstrained current is added, equal to 90% of such the maximum. This assessment is run only in the linear framework.

Algorithm 1

Algorithm used for Test Case II to constrain all the DEMO PF currents with a sequential ad hoc change of the current limits. $\overline{\varDelta I}^{in}_{i}$, $\underline{\varDelta I}^{in}_{i}$ denote the upper and lower bound applied to the PF corrections at CLA input, after the i-th iteration of the algorithm. The algorithm includes $n_{PF}=11$ iterations.

Fig. 5

Time trace of the GAP2 variation for the reference scenario described in Sect. 5.1 when no limits are considered on the PF currents

Fig. 6

Time traces of the PF currents variations with respect to the nominal values for the reference scenario described in Sect. 5.1 when no limits are considered on the PF currents

Figure 5 shows the time behavior of GAP2 when the desired shape variation is requested to the plasma shape control without any limit acting on the PF currents. Figure 6 shows the corrections  $\varDelta I^{in}$ requested to the CLA for the considered test case.

To prove the effectiveness of the CLA algorithms, the following symmetric bounds have been considered for the three currents in PF1, PF3 and PF6³

$$\begin{aligned} \overline{\varDelta I_{PF_1}}=&-\underline{\varDelta I_{PF_1}} = 400~A\,,\\ \overline{\varDelta I_{PF_3}}=&-\underline{\varDelta I_{PF_3}} = 300~A\,,\\ \overline{\varDelta I_{PF_6}}=&-\underline{\varDelta I_{PF_6}} = 200~A\,. \end{aligned}$$

For the proposed approaches, the validation has been carried out by running both linear simulations with the model introduced in Sect. 2.2, and nonlinear ones by exploiting the CREATE-NL free boundary equilibrium solver [2]. It is worth to remark that all the simulations have been carried out by including the eddy current dynamic and the VS control system, i.e., the overall magnetic control architecture shown in Fig. 3 has been considered during validation. Note that the CLA techniques are referred with an abbreviated nomenclature: quadratic programming with hard constraints as $QP \ hard$, quadratic programming with soft constraints as $QP \ soft$, linear programming as LP, null-based dynamic allocator as NBDA and extended null dynamic allocator as ENDA.

5.2 Test Case I—Linear Assessment

The results for the linear simulation are reported in Figs. 7, 8, 9, 10, 11, 12, 13, 14 and 15. In particular, Fig. 7 shows the GAP behavior when the currents in PF1, PF3 and PF6 are constrained. It can be noticed that while without CLA the desired values cannot be reached at steady state, all the proposed algorithms allow us to achieve the objective. The active currents variation with respect to the initial value is reported in Figs. 8 and 9. Figure 10 shows the behavior of the plasma current variation during the transient, and it can be noticed that all CLA algorithms are able to cope with the given constraints without affecting $I_p$ at steady-state. Finally, in Figs. 11, 12, 13, 14 and 15 the reference currents behavior for the different proposed CLA approaches is reported. As expected, while with both the LP-based and the QP-based approaches with hard constraints, the limits are never exceeded, with all the other approaches the limits can be temporarily violated during the transients. Obviously, in practice, when one of the latter approaches is considered, this behavior calls for an additional margin when defining the current limits.

Fig. 7

Behavior of GAP variations for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 8

Behavior of CS currents variation for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 9

Behavior of PF currents variation for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 10

Behavior of the plasma current variation with respect to its equilibrium value for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 11

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the hard constraints QP-based algorithms is assessed using linear simulation

Fig. 12

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the soft constraints QP-based algorithms is assessed using linear simulation

Fig. 13

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the LP-based algorithms is assessed using linear simulation

Fig. 14

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the null-based dynamic allocator is assessed using linear simulation

Fig. 15

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the extended null dynamic allocator is assessed using linear simulation

5.3 Test Case I—Linear Assessment with Uncertainty

Test Case I is replicated by adding a random $+5 \%$ variation on the $C_{SH}$ and $C_{p}$ matrices used in the CLA but not on those used to simulate the plant. This test has been done to evaluate how a model uncertainty can affect CLA performance. The resulting constrained active currents time traces are reported in Fig. 16, showing similar performance to those achieved for the nominal test case. As reported in Fig 17, this kind of model uncertainty has a negligible effect on plasma shape and current error. Also, the total active current variation cost that appears to be similar to those in the nominal test case.

Fig. 16

Behavior of $\varDelta I_{PF1}$, $\varDelta I_{PF3}$ and $\varDelta I_{PF6}$ for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment, current limits are active on PF1, PF3 and PF6 and in presence of uncertainty

Fig. 17

Steady-state error on plasma shape and current and magnitude of active currents variation for the considered test case when the linear model introduced in Sect. 2.2 is used for the assessment, current limits are active on PF1, PF3 and PF6 and in presence of uncertainty

5.4 Test Case I—Nonlinear Assessment

The preliminary results obtained via fast linear simulations have been further confirmed by the nonlinear simulations carried out using the CREATE-NL equilibrium code. Figures 18 and 19 report the variation of GAP and of the plasma current, the active currents variation with respect to the initial values are reported in Figs. 20 and 21. Figures 22–26 show the reference currents behavior for the different proposed CLA algorithms.

Fig. 18

Behavior of GAP variation for the considered test case when the nonlinear solver is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 19

Behavior of the plasma current variation with respect to its equilibrium value $\varDelta I_p$ for the considered test case when the nonlinear solver is used for the assessment and current limits are active on PF1, PF3 and PF6

Fig. 20

Behavior of CS currents variation for the considered test case when the performance is assessed using nonlinear simulation

Fig. 21

Behavior of PF currents variation for the considered test case when the performance is assessed using nonlinear simulation

Fig. 22

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the hard constraints QP-based algorithms is assessed using nonlinear simulation

Fig. 23

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the soft constraints QP-based algorithms is assessed using nonlinear simulation

Fig. 24

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the LP-based algorithms is assessed using nonlinear simulation

Fig. 25

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the null-based dynamic allocator is assessed using nonlinear simulation

Fig. 26

Behavior of the three constrained reference currents PF1, PF3, and PF6 for the considered test case when the performance of the extended null dynamic allocator is assessed using nonlinear simulation

5.5 Test Case II

To further assess the capability of the proposed CLA algorithms to react to a severe limitation on the current available for plasma shape and plasma current control, we consider the case when all the PF currents are constrained and the corresponding limits are set according to Algorithm 1 to scan the effect of multiple saturations. In particular, at each iteration, a limit on the maximum unconstrained current is added and set equal to 90% of such a maximum. Tables 1 and 2 report the limits added at each iteration of Algorithm 1 when using each of the proposed CLA approaches.

Figure 27 shows the mean value of the steady-state error on controlled gaps, for the simulations derived from the application of Algorithm 1, and for the different proposed CLA approaches. The behavior of the $I_p$ variation for the last simulation, i.e., the one after which all the PF currents have been limited in turn, is reported in Fig. 29. For all the other simulations, the tracking error on $I_p$ never exceeds 100A. This further assessment confirms the capability of all the proposed CLA approaches to guarantee plasma magnetic control performance also in the presence of a severe limitation on the available control space. Indeed, the mean steady-state error is always kept below 2.5 mm, which is comparable with the expected level of noise-induced by measurement, while the plasma current variation is the same as in the unconstrained case reported in Fig. 10. From Fig. 27, it is evident that techniques based on soft constraints can perform better than those based on hard constraints. In fact from Fig. 28 the first family of techniques put more effort on currents with a slight exceeding (maximum 200A) of the limits.

All the presented results have been obtained by running the simulations on a laptop PC equipped with an Intel(R) Core(TM) i5-8250U CPU 1.60GHz with 16 GB of RAM, in the Matlab/Simulink environment, by using the MOSEK library [5] [6], version 9.3 with default settings. With this setup, the solution of the QP problem (5) requires about 5 ms. Table 3 reports the mean time required to solve the different optimization problems in Algorithm 1 and the mean number of iterations. Considering that the computational times presented include overheads due to the parsing of the optimization problem and the context switch between Simulink and Matlab, it is reasonable to conclude that, using dedicated hardware and optimized software, the proposed optimization-based CLA algorithms are suitable for the real-time control in tokamaks like DEMO in which the sampling time for magnetic control is in the order of few ms.

6 Conclusive Remarks

This paper proposed different effective solutions to tackle the problem of the PF currents saturation in tokamak devices. All the proposed techniques proved to be computationally feasible, given the complexity expected for a nuclear fusion reactor. Moreover, the availability of different solutions is a key feature to achieve the level of reliability required in a fusion power plant. Indeed, the different proposed algorithms can be deployed on a multiprocessor system on a chip (MPSoC), and hence, they can run in parallel and in isolation [15], to improve reliability using redundancy. In such an MPSoC-based architecture, the switching management among the different algorithms, for example, in the case the real-time deadline of the active algorithm is not met, should be carefully designed to guarantee overall stability [31], and it will be subject to future research. Other possible future lines of research include the evaluation of data-driven/model-free allocation approaches such as the one proposed in [30].

Table 1 Limited PF current and corresponding limit applied at each iteration of Algorithm 1, for the two different versions of the QP-based CLA, and the LP-based one

Table 2 Limited PF current and corresponding limit applied at each iteration of Algorithm 1, for the two different proposed CLA approaches based on nonlinear allocator

Table 3 Mean elapsed time and number of interior-point iterations required by the different optimization-based algorithms to find a solution to the CLA problem of Algorithm 1 considered for Test Case II

Fig. 27

Steady-state error on controlled gaps at each iteration of Algorithm 1

Fig. 28

Steady-state current exceeding at each iteration of Algorithm 1

Fig. 29

Plasma current variation at the last iteration of Algorithm 1