Plasma Magnetic Control in Tokamak Devices

Abstract

In tokamak experimental reactors, the magnetic control system is one of the main plasma control systems that is required, together with the density control, since the very beginning, even before first operations. Indeed, the magnetic control drives the current in the external poloidal circuits in order to first achieve the breakdown conditions and, after plasma formation, to track the desired plasma current, shape and position. Furthermore, when the plasma poloidal cross-section is vertically elongated, the magnetic control takes also care of the vertical stabilization of the plasma column, and therefore it is an essential system for operation. This chapter introduces a reference architecture for plasma magnetic control in tokamaks. Given the proposed architecture, the techniques to design all the required control algorithms is also presented. Experimental results obtained on the JET and EAST tokamaks and simulations for machines currently under construction are shown to prove the effectiveness of the proposed architecture and control algorithms.

Introduction

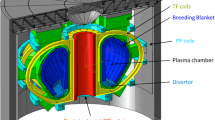
Confinement of the hot plasma in toroidal fusion devices is achieved by means of several magnetic fields. In particular, a set of coils wrapped around the vacuum vessel produce the toroidal magnetic field, as shown in the simplified tokamak schematic reported in Fig. 1. An additional external field is produced by a set of toroidal coils, called Poloidal Field (PF) coils. The produced poloidal magnetic field is needed first to achieve the conditions for plasma formation inside the vacuum chamber. Soon after plasma formation, the currents flowing in the PF coils (and hence the produced field) need to be controlled in order to induce current into the plasma and to control its value during each phase of the tokamak discharge (ramp-up, flattop and ramp-down).

Fig. 1

Simplified scheme of a tokamak

Other than controlling the plasma current, also the plasma boundary and position need to be carefully controlled, in order to achieve the desired experimental objectives. Indeed, the time evolution of PF coil currents, along with the plasma geometrical and physical parameters that define the so called scenario, is obtained as a sequence of plasma equilibria. Feedforward PF coil currents, and sometimes voltages, are then determined to obtain the desired magnetic field [25]. Being these nominal currents (and voltages) computed with numerical codes, they are affected by model uncertainty; moreover, unexpected disturbances always occur in a tokamak discharge. It follows that a plasma position and shape control system is necessary for tokamak operations. Furthermore, in the case of plasmas with a vertically elongated poloidal cross-section (see the examples reported in Fig. 2), the active control of the current in some of the PF coils is mandatory in order to generate the radial field needed to vertically stabilize the plasma column (see some examples in [7, 39, 72]).

Fig. 2

Poloidal cross-sections of two tokamaks with vertically elongated plasmas. a JET poloidal cross-section, b EAST poloidal cross section

It turns out that plasma magnetic control is one of the crucial issues to be addressed since the very beginning during the design of a tokamak. Indeed a plasma magnetic control system, although not necessarily at its full capacity, is needed since day one (examples of existing architecture can be found in [71, 83]). Furthermore, a robust and reliable plasma magnetic control system is required to successfully control high performance plasmas, such as the ones envisaged for ITER and DEMO.

The design of magnetic control systems in tokamaks relies on different design approaches, from the classic single-input single-output (SISO) ones, to more advanced multi-input multi-output (MIMO) techniques.

In early tokamaks with circular cross-section, the plasma current and position control was separated in the following two independent problems:

• horizontal position and current control by means of up-down symmetric control currents flowing into sets of poloidal field coils symmetrically placed with respect to the tokamak equatorial plane;

• vertical position control by means of updown anti-symmetric currents flowing into the poloidal field coils.

In this case a decoupled system of poloidal windings is used. This system consists of an ohmic heating winding, the so-called central solenoid, that controls the ohmic magnetic flux and thus the plasma current, as well as a vertical field circuit that controls the plasma major radius. For these tokamaks, the simplest controller structure consists of two separate SISO controllers. As an example, see the control system of the FTU tokamak [20, Ch. 6] and of ISTTOK [27]. A SISO approach is adopted also at JET to control the shape of vertically elongated plasmas; however in this case more than two plasma shape descriptors can be controlled (see [60]).

For more complex systems, or when high performance is required, MIMO decoupling controllers have been envisaged since the early eighties [42, 65], and used to solve the plasma current position and shape control problem. In general, in order to achieve better performance, model-based design approaches have been adopted.

As far as plasma boundary shape control is concerned, different solutions have been proposed either based on isoflux [41, 51, 83], or on plasma-wall gaps control [17, 19, 47, 60], whose design has been based using a wide range of techniques, including ${\mathscr {H}}_{\infty }$ and model-predictive control. Moreover, in tokamaks with vertically elongated and unstable plasmas different solutions have been proposed to solve the vertical stabilization problem: simple SISO controllers [53, 59], optimal linear-quadratic control [64], predictive control [48], nonlinear adaptive control [73], and robust control [1, 78]. In [79] a full multivariable model of the vertical instability is used to perform a matrix pencil analysis in order to provide for a rigorous demonstration of necessary conditions for stabilization of the plasma by proportional–derivative feedback of vertical displacement. In [72] an anti-windup synthesis is proposed to allow operation of the vertical controller in the presence of saturation.

This chapter introduces a reference architecture for plasma magnetic control in tokamaks, and describes the control algorithms required in each component of such architecture. In particular, the chapter is made by four main sections. “Systems and Control Basics” section introduces the systems and control jargon and backgrounds, since the reader is assumed to have some knowledge about control in order to understand the details of the proposed algorithms. Those reader who are already familiar with control theory can skip this section. “Linear Model for the Plasma and the Surrounding Conductive Structures” section presents the linearized model used to simulate the behaviour of the plasma, of PF circuits, and of the surrounding passive structures, under the axisymmetric assumption. The algorithms for plasma magnetic control, together with the overall control architecture are presented in details in “Plasma Magnetic Control” section, at the beginning of which the control magnetic problem is also stated. The effectiveness of the overall proposed magnetic control system is shown in “Experiments and Simulations” section by means of experimental results, as well as by simulations performed for machines that are currently under construction. Eventually, some conclusive remarks are given.

Those readers who want to deepen the topics discussed in this chapter, may refer to the survey [8] and to the monograph [20] for a complete overview of magnetic control in tokamaks. As far as the systems and control theory is concerned, a lot of textbooks are available for those who wants to go deeper in the subject; among the various, the author would suggest [22, 26, 43, 55, 76, 84].

Systems and Control Basics

In this section some fundamentals on systems and control theory are introduced, together with the notation the will be used in the next sections. It should be noticed. Note that, for the sake of brevity, the discussion will necessarily skip many details. The reader already familiar with this subject can move directly to “Linear Model for the Plasma and the Surrounding Conductive Structures” section.

State-Space Dynamical Systems

In the systems and control context, given a physical system, we will refer to the dynamical model in the so-called state-space form, as the following set of differential equations

$$\begin{aligned} {\dot{x}}(t)&= f\left( x(t) ,u(t) ,t\right) ,\quad x(t_0)=x_0 \end{aligned}$$

(1a)

$$\begin{aligned} y(t)&= h\left( x(t) ,u(t) ,t\right) \end{aligned}$$

(1b)

where

• $x(t)\in {\mathbb {R}}^n$ is the system state, where n is called the order of the system

• $x(t_0)\in {\mathbb {R}}^n$ is the initial condition

• $u(t)\in {\mathbb {R}}^m$ is the input vector

• $y(t)\in {\mathbb {R}}^p$ is the output vector

and where (1a) and (1b) are called state and output equation, respectively. Although it is a mathematical representation of the real physical system (see also Fig. 3), the model (1) is commonly referred to as the dynamical system in the state-space form.

Fig. 3

The physical system under consideration and the mathematical model used to described its behaviour

When the behaviour of a physical process can be assumed linear and time-invariant (LTI), the state space model (1) can be rewritten as

$$\begin{aligned} {\dot{x}}(t)&= Ax(t)+Bu(t) ,\quad x(0)=x_0 ,\end{aligned}$$

(2a)

$$\begin{aligned} y(t)&= Cx(t)+Du(t) , \end{aligned}$$

(2b)

where $A\in {\mathbb {R}}^{n\times n}$, $B\in {\mathbb {R}}^{n\times m}$, $C\in {\mathbb {R}}^{p\times n}$ and $D\in {\mathbb {R}}^{p\times m}$. A dynamical system is called SISO when $m=1$ and $p=1$, while is called MIMO otherwise. Note that, for a time-invariant system the initial time $t_0$ can be assumed to be equal to 0 without loss of generality.

Given the nonlinear and time-invariant system

$$\begin{aligned} {\dot{x}}(t)&= f\left( x(t) ,u(t)\right) ,\quad x(0)=x_0 ,\end{aligned}$$

(3a)

$$\begin{aligned} y(t)&= h\left( x(t) ,u(t)\right) \end{aligned}$$

(3b)

it is possible to describe its behaviour around equilibrium state using a LTI system. Indeed, if the input is constant, i.e. if $u(t)={\bar{u}}$, let consider the solutions $x_{e_1} ,x_{e_2} ,\ldots ,x_{e_q}$ of the homogeneous equation

$$\begin{aligned} f\bigl (x_e ,{\bar{u}})=0 . \end{aligned}$$

(4)

The solutions of (4) represent the equilibrium states of (3). Given the equilibrium state $x_{e_i}$, the correspondent output is given by

$$\begin{aligned} y_{e_i} = h\left( x_{e_i} ,{\bar{u}}\right) . \end{aligned}$$

Given an asymptotically stable equilibrium $x_e$, if $x_0=x_e+\delta x_0$ and $u(t)={\bar{u}}+\delta u(t)$, with $\delta x_0$ and $\delta u(t)$sufficiently small, then the behaviour of (3) around the considered equilibrium state is described by the LTI system

$$\begin{aligned} \delta {\dot{x}}(t)&= \frac{\partial f}{\partial x}_{\left| \begin{array}{l}x=x_e\\ u={\bar{u}}\end{array}\right. }\delta x(t)+\frac{\partial f}{\partial u}_{\left| \begin{array}{l}x=x_e\\ u={\bar{u}}\end{array}\right. }\delta u(t) ,\quad \delta {x}(0)=\delta x_0 ,\end{aligned}$$

(5a)

$$\begin{aligned} \delta y(t)&= \frac{\partial h}{\partial x}_{\left| \begin{array}{l}x=x_e\\ u={\bar{u}}\end{array}\right. }\delta x(t)+ \frac{\partial h}{\partial u}_{\left| \begin{array}{l}x=x_e\\ u={\bar{u}}\end{array}\right. }\delta u(t) . \end{aligned}$$

(5b)

The total output can be then computed as

$$\begin{aligned} y(t) = h\left( x_e ,{\bar{u}}\right) +\delta y(t) . \end{aligned}$$

When dealing with control system design it is desirable that the process to be controlled is modeled using LTI systems. This will be the case also for plasma magnetic control. In particular, the behaviour of the plasma, of the currents in the active coils and in the surrounding passive structures will be described by the LTI system that will be presented in “Linear Model for the Plasma and the Surrounding Conductive Structures” section. Although this engineering-oriented LTI models may appear too simplified with respect to the codes used to run detailed physics-oriented simulations [46, 68], it is sufficiently detailed to capture the main features of the process to be controlled, as far as magnetic control is considered. It will be the robustness of the control system that will assure both performance and stability, also in the presence of uncertainty and disturbances.

Stability of Dynamical Systems

Let $x_e\in {\mathbb {R}}^n$ be an equilibrium state for system (1), i.e. the solution of (4) for a given constant input ${\bar{u}}$. Given this input ${\bar{u}}$, according to the definition of Lyapunov stability (see [56, Ch. 4]), $x_e$ is said to be stable if, for each $\varepsilon ~>~0$, there exists a positive scalar $\delta$ (possibly depending on $t_0$ and $\varepsilon$) such that, for all $t_0\in {\mathbb {R}}^+$, if $\Vert x_0-x_e\Vert ~<~\delta (\varepsilon ,t_0)$, then¹

$$\begin{aligned} \Vert x(t)-x_e\Vert < \varepsilon , \quad t\ge t_0 . \end{aligned}$$

On the other hand, the equilibrium state $x_e$ is said to be unstable if it is not stable, while is said to be asymptotically stable if it is stable and $\delta$ can be chosen such that

$$\begin{aligned} \Vert x_0-x_e\Vert <\delta \Rightarrow \lim _{t\rightarrow +\infty }\Vert x(t)-x_e\Vert =0 . \end{aligned}$$

In the case of LTI systems (2), it can be shown that the stability property is related to the model rather than to a specific equilibrium point, as in the case of nonlinear dynamical systems. In particular, asymptotic stability of LTI systems roughly asserts that, when the input $u(t)=0$, it is

$$\begin{aligned} \lim _{t\rightarrow +\infty }x(t)=0 , \end{aligned}$$

for any initial state $x_0$. The following well known results hold for LTI systems (see also [55, Sec. 2.6.1]).

Theorem 1

System (2) isasymptotically stableif and only if Amatrix isHurwitz, that is if every eigenvalue $\lambda _i$of Ahas strictly negative real part $\left( \mathfrak {R}\left( \lambda _i\right) <0 ,\forall \ \lambda _i\right)$.

Theorem 2

System (2) isunstable if Ahas at least one eigenvalue ${\bar{\lambda }}$with strictly positive real part, that is

$$\begin{aligned} \exists \ {\bar{\lambda }}\ {\text {{s.t.}}}\ \mathfrak {R}\left( {\bar{\lambda }}\right) >0 . \end{aligned}$$

As we have already seen, for nonlinear system the stability property is related to a specific equilibrium $x_e$. However, the stability of $x_e$ can be assessed analyzing the stability property of the corresponding linearized model (5). Indeed, the following results hold (for more details about the stability of equilbria in nonlinear systems, the interested reader may refer to [56, Ch. 4]).

Theorem 3

The equilibrium state $x_e$of the nonlinear system (1) isasymptotically stable ifall the eigenvalues of the correspondent linearized system (5) have strictly negative real part.

Theorem 4

The equilibrium state $x_e$of the nonlinear system (1) isunstable ifthere exists at least one eigenvalue of the correspondent linearized model (5) with strictly positive real part.

Transfer Functions, Zeros and Poles of LTI Systems

Given a LTI system (2) the corresponding transfer matrix from the input u to the output y is defined as

$$\begin{aligned} G(s) = C\bigl (sI-A\bigr )^{-1}B+D , \end{aligned}$$

(6)

where $s\in {\mathbb {C}}$ and I denotes $n\times n$ identity matrix. If we denote with U(s) and Y(s) the Laplace transforms of u(t) and y(t), then it holds that

$$\begin{aligned} Y(s)=G(s)U(s) , \end{aligned}$$

when the initial condition of system (2) is $x(0)=0$. In the case of SISO systems, (6) is called transfer function and it can be shown that it is equal to the Laplace transform of the impulsive response of system (2) with zero initial condition. Moreover, given the transfer function G(s) and the Laplace transform of the input U(s), the time response of system (2) can be computed as inverse transform of G(s)U(s), without solving differential equations. As an example, the step response of a system can be computed as

$$\begin{aligned} y(t)={\mathscr {L}}^{-1}\left[ G(s)\frac{1}{s}\right] . \end{aligned}$$

Given a SISO LTI system, its transfer function is a rational function of s, i.e.

$$\begin{aligned} G(s) = \frac{N(s)}{D(s)}=\rho \frac{\varPi _i(s-z_i)}{\varPi _j(s-p_j)} , \end{aligned}$$

where N(s) and D(s) are polynomials in s with real coefficients and such that $deg \left( N(s)\right) ~\le ~deg \left( D(s)\right)$, while $p_j$ and $z_i$ are the poles and zeros of G(s), respectively.

From the definition of transfer function and from the definition of eigenvalue of a matrix, it readily follows that each pole of G(s) is an eigenvalue of the A matrix, while the converse is not necessary true. If all the poles of G(s) have strictly negative real part—i.e. they are located in the left half of the s-plane (LHP)—then the SISO system is said to be Bounded–Input Bounded–Output (BIBO) stable. In particular, a system is said to be BIBO stable if a bounded input to the system results in a bounded output over the time interval $[0, +\infty )$.

A transfer function can be also specified in terms of the following parameters

• time constants ($\tau$,T)

• natural frequencies ($\omega _n$,$\alpha _n$)

• damping factors ($\xi$,$\zeta$)

• gain ($\mu$)

• system type (i.e., the number g of poles/zeros in 0)

$$\begin{aligned} G(s) = \mu \frac{\varPi _i(1+T_is)\varPi _j\Bigl (1+2\frac{\zeta _j}{\alpha _{n_j}}s+\frac{s^2}{\alpha _{n_j}}\Bigr )}{s^g\varPi _k(1+\tau _ks)\varPi _l\Bigl (1+2\frac{\xi _l}{\omega _{n_l}}s+\frac{s^2}{\omega _{n_l}}\Bigr )} . \end{aligned}$$

Fig. 4

Basic interconnections in block diagrams and correspondent equivalent block. a Series connection, b parallel connection, c feedback connection. In this case it is assumed that $G_1(s)$ and $G_2(s)$ are SISO transfer functions

Moreover, when dealing with transfer functions, it is usual to resort to block diagrams which permits a graphical representation of the interconnections between systems in a convenient way. The basic interconnections between two transfer functions are shown in Fig. 4. In particular, given two asymptotically stable LTI systems whose transfer functions are $G_1(s)$ and $G_2(s)$ the following conclusions can be drawn

• the series connection $G_2(s)G_1(s)$ is asymptotically stable

• the parallel connection $G_1(s)+G_2(s)$ is asymptotically stable

• the feedback connection $\frac{G_1(s)}{1\pm G_1(s)G_2(s)}$is not necessarily stable

Indeed, since all the poles are also eigenvalues of a given LTI system, in the case of series and parallel connections, the poles remain the same as in the interconnected systems, and therefore the stability property is preserved. On the other hand, the poles of the feedback connection are not the ones of the interconnected systems, hence stability of the closed-loop system cannot be guaranteed a priori.

From this fact, it follows that the design of a feedback control loop should be carried out with care, in order not to lose stability. On the other hand, it is also true that feedback control can be used to stabilize unstable plant.

Frequency Response of LTI Systems

Given the LTI system (2), the complex function

$$\begin{aligned} G(j\omega )=C\bigl (j\omega I-A\bigr )^{-1}B+D , \end{aligned}$$

with $\omega \in {\mathbb {R}}^+$ is called frequency response of (2), and it permits to evaluate the system steady-state response to a sinusoidal input when the system is asymptotically stable. In particular if

$$\begin{aligned} u(t) = A\sin ({\bar{\omega }}t+\varphi ) , \end{aligned}$$

then the steady-state response of a LTI system is given by

$$\begin{aligned} y(t) = \left| G(j{\bar{\omega }})\right| A\sin \left( {\bar{\omega }}t+\varphi +\angle {G(j{\bar{\omega }})}\right) . \end{aligned}$$

Given a LTI system G(s) the Bode diagrams are a graphical representation of the magnitude of $G(j\omega )$ (specified in dB, that is $\left| G(j\omega )\right| _{dB}=20\log _{10}\left| G(j\omega )\right|$) and of the phase of $G(j\omega )$ (specified in degree), as a function of the frequency $\omega$ (expressed in rad/s) on a base 10 semi-log scale. Figure 5a shows an example of Bode diagram for a third order system.

Fig. 5

The different graphical representation of the frequency response of the LTI system described by the transfer function $G(s) = 10\frac{1+s}{s\left( \frac{s^2}{400}+2\frac{0.3}{20}s+1\right) } = 10\frac{1+s}{s(0.0025s^2+0.03s+1)}$. a Bode diagrams, b Nyquist plot, c Nichols plot

The Nyquist plot is a polar plot of the frequency response $G(j\omega )$ on the complex plane. This plot combines the two Bode plots—magnitude and phase—on a single graph, with the frequency $\omega$ as a parameter along the curve, ranging from $-\infty$ to $+\infty$. This alternative graphical representation of the frequency response is typically useful to check stability of closed loop systems (see “Feedback Control Systems” section). Figure 5b shows the Nyquist for the same third order system considered in Fig. 5a.

Another possible graphical representation for the frequency response of a LTI system is the Nichols plot. This plot combines the two Bode diagrams on a single plot; indeed in a Nichols plot both the magnitude and the phase of $G(j\omega )$ are plotted on a single chart, with frequency $\omega$ as a parameter along the curve.² Figure 5c shows the Nichols plot for the third order system considered in Fig. 5a. Nichols plots are useful for the design of control systems, in particular for the design of lead, lag, and lead-lag compensators; furthermore they permit to easily estimate the stability margins of a SISO closed loop system.

Feedback Control Systems

In this section we will mainly focus on the basics for the design of SISO (negative) feedback control systems. More details on the design of MIMO control systems can be found in [76, 84].

Fig. 6

Reference block diagram for a SISO (negative) feedback control system. r(t) is the reference signal, u(t) is the control input, while y(t) is the controlled output. The two exogenous signals d(t) and n(t) represent the external disturbance and the measurement noise, respectively

The objective of a control system is to make the output of a plant y(t) behave in a desired way by manipulating the plant input u(t). Referring to the scheme reported in Fig. 6, a controller should keep the output y(t) close to the reference r(t), by counteracting the effect of the disturbance d(t) and by minimizing the effect of the measurement noise n(t), even in the presence of plant unmodeled dynamics.

More in details, a controller should in principle guarantee:

• Nominal stability—The closed loop system is stable when the nominal (without uncertainty) model is considered.

• Nominal Performance—The closed loop system satisfies the performance specifications when the nominal model is considered.

• Robust stability—The closed loop system is stable for all perturbed plants (i.e., taking account uncertainty)

• Robust performance—The closed loop system satisfies the performance specifications for all perturbed plants

The main sources of difficulty in achieving the above mentioned objectives are that

• the plant model G(s) and the disturbance model $G_d(s)$ may be affected by uncertainty and/or may change with time

• the disturbance is usually not measurable

• the plant can be unstable

Feedback control represents a reliable solution to robustly guarantee the desired performance. However, the benefits of feedback come at a price: designing a feedback control system is not straightforward and instability is always around the corner.

Fig. 7

Block diagram of a one-degree-of-freedom SISO controller

With reference to the one-degree-of-freedom SISO control system shown in Fig. 7, let us introduce the following transfer functions

• K(s) is the controller transfer function

• $L(s)=G(s)K(s)$, which is the (open) loop transfer function

• $S(s)= \bigl (I+L(s)\bigr )^{-1}$, which is the sensitivity function

• $T(s)=\bigl (I+L(s)\bigr )^{-1}L(s)$, which is the complementary sensitivity function.

Note that the above definition (and many of the following introduced in this section) are written using the notation for transfer matrices, hence they hold also for MIMO control systems. For example, in the case of SISO systems, the two sensitivity functions are

$$\begin{aligned} S(s)=\frac{1}{1+L(s)} , \end{aligned}$$

and

$$\begin{aligned} T(s)=\frac{L(s)}{1+L(s)} . \end{aligned}$$

From definition of the two sensitivity transfer functions it follows that

$$\begin{aligned} T(s)+S(s) = I . \end{aligned}$$

(7)

Moreover, exploiting the linearity and applying the composition rules for block diagrams, it is possible to write the following relationships in the Laplace domain

$$\begin{aligned} Y(s)&= T(s)\cdot R(s)+S(s)\cdot G_d(s)\cdot D(s)-T(s)\cdot N(s) ,\end{aligned}$$

(8a)

$$\begin{aligned} E(s)&= -S(s)\cdot R(s)+S(s)\cdot G_d(s)\cdot D(s)-T(s)\cdot N(s) ,\end{aligned}$$

(8b)

$$\begin{aligned} U(s)&= K(s)\cdot S(s)\cdot R(s)-K(s)\cdot S(s)\cdot G_d(s)\cdot D(s)-K(s)\cdot S(s)\cdot N(s) , \end{aligned}$$

(8c)

where R(s), D(s), N(s) and E(s) are the Laplace transforms of the reference signal r(t), of the disturbance d(t), of the measurement noise n(t), and of the control error e(t). it should be noticed that, from (8a) it follows that the complementary sensitivity function T(s) correspond to the closed loop transfer function between the reference signal and the plant output.

If we now consider Eq. (8a), it can be noticed that:

• in order to reduce the effect of the disturbance d(t) on the output y(t), the sensitivity function S(s) should be kept small (particularly in the low frequency range, where the disturbance is assumed to act)

• in order to reduce the effect of the measurement noise n(t) on the output y(t), the complementary sensitivity function T(s) should be kept small (particularly in the high frequency range, where the noise should assume significant values)

However, for all frequencies the relationship (7) holds. Given this control dilemma, designing a controller K(s) is about finding a good trade-off solution between the minimization of the disturbance effect, and the minimization of the effect of the measurement noise. Moreover, since the sensitivity function describes also the relative sensitivity of the closed-loop transfer function T(s) to the relative plant model error due to model uncertainty, i.e. it is also

$$\begin{aligned} \frac{\frac{dT}{T}}{\frac{dG}{G}}=S(s) , \end{aligned}$$

it follows that keeping S(s) (especially at high frequency, where there are usually more uncertainties in the model) permits to increase the robustness of the closed-loop system.

Furthermore, when designing a feedback control system, stability of the closed-loop system may become an issue. As a simple example, Fig. 8 shows the behaviour of a SISO control system for different values of the overall gain of a proportional-integral (PI) controller.

Fig. 8

Example of controller overreaction that may cause instability of the closed-loop system. a SISO plant controlled by a proportional-integral controller, b step response of the closed-loop system for different values of the proportional gain $K_p$

Usually the frequency response $|L(j\omega )|$ of the loop transfer function has a low-pass behaviour, and the crossover frequency $\omega _c$ is defined as the frequency such that $|L(j\omega _c)|=1$ (see Fig. 9). In most of the cases the crossover frequency is a good estimation of the closed-loop bandwidth. The frequency response $L(j\omega )$ of the loop transfer function is used to define the stability margins, which are used as quantitative descriptors of the robust stability in SISO control systems.

Fig. 9

Typical frequency response $L(j\omega )$ of a loop transfer function with low-pass behaviour. The crossover frequency $\omega _c$ is also shown

With reference to the Nyquist plot of a typical $L(j\omega )$ (which is assumed to have a low-pass behaviour) shown in Fig. 10, the gain margin (GM) is defined as

$$\begin{aligned} GM = 1/|L(j\omega) _{180}| , \end{aligned}$$

where $\omega _{180}$ is the phase crossover frequency, that is the frequency such that $\angle L(j\omega) _{180}=180^{\circ }$.

Fig. 10

Nyquist plot of a typical $L(j\omega )$ with a low-pass behaviour and graphical representation of the correspondent stability margins

The phase margin (PM) is defined

$$\begin{aligned} \angle {L(j\omega _c)}+180^{\circ }. \end{aligned}$$

The Nyquist Criterion makes use of the Nyquist plot of $L(j\omega )$ (i.e., of the open loop transfer function) in order to check the stability of a closed-loop system. The readers interested to the proof of this result can refer to [76, Sec. 4.9.2]

Nyquist Stability Criterion

Consider a loop frequency response $L(j\omega )$ and let

• P be the number of poles of L(s) with strictly positive real part

• Z be the number of zeros of L(s) with strictly positive real part

The Nyquist plot of $L(j\omega )$ makes a number of encirclements N (assumed positive if clockwise) about the point $(-1 ,j0)$ equal to

$$\begin{aligned} N=Z-P . \end{aligned}$$

It follows that, the closed-loop system is asymptotically stable if and only if the Nyquist plot of $L(j\omega )$ encircles (counter clockwise) the point $(-1 ,j0)$ a number of times equal to P.

The following remarks apply to the Nyquist Stability Criterion

• If L(s) has a pole in zero whose multiplicity is equal to l, then the Nyquist plot has a discontinuity at $\omega =0$. Further analysis indicates that the poles in zero should be neglected, hence if there are no unstable poles, then the loop transfer function L(s) should be considered stable, i.e. $P=0$.

• If L(s) is stable, then the closed-loop system is unstable for any encirclement (clockwise) of the point -1.

• If L(s) is unstable, then there must be one counter clockwise encirclement of $(-1 ,j0)$ for each unstable pole of L(s).

• If the Nyquist plot of $L(j\omega )$ intersect the point $(-1 ,j0)$, then deciding upon even the marginal stability of the system becomes difficult and the only conclusion that can be drawn from the plot is that there exist poles on the imaginary axis.

From the Nyquist Stability Criterion and from the definition of the stability margins, it turns out that, given an asymptotically stable L(s)

• the GM is the factor by which the loop gain $|L(j\omega )|$ may be increased before the closed-loop system becomes unstable, and thus it is a direct safeguard against uncertainties on steady-state gain;

• the PM tells how much phase lag can added to $L(j\omega )$ at the crossover frequency $\omega _c$ before the phase at this frequency becomes $180^{\circ }$, which corresponds to closed-loop instability. Hence, the PM is a direct safeguard against uncertainty on the time delays in the closed-loop.

As conclusion of this section, we briefly introduce the root locus of the loop transfer function L(s). This alternative graphical representation of L(s) permits to evaluate how changes in L(s) affect the location of the closed-loop poles.

Indeed, the time behaviour of a closed-loop system is strictly related to the position of its poles on the complex plane. For example, for a second order closed-loop system it is possible to relate the features of the step response such as the rise and settling times and the overshoot, to the location of its poles.

The closed-loop poles are given by the roots of

$$\begin{aligned} 1+L(s) . \end{aligned}$$

(9)

Assuming that $L(s)=\rho L'(s)$, the root locus plots the locus of all possible roots of (9) as $\rho$ varies in the range $[0 ,\infty )$. Moreover, the root locus can be used to study the effect of additional poles and zeros in $L'(s)$, i.e. in the controller K(s). Hence, the root locus can be effectively used to design SISO controllers, as it will be shown in “Algorithms for Plasma Magnetic Control” section for the vertical stabilization system.

Figure 11 shows and example of root locus, when the loop transfer function is

$$\begin{aligned} L'(s) = K(s)\cdot G(s) = \frac{1+s}{s}\cdot \frac{1}{s^3+3s^2+3s+1}=\frac{1}{s(s+1)^2} . \end{aligned}$$

Fig. 11

Example of root locus for the loop transfer function $L'(s)=\frac{1}{s(s+1)^2}$

Linear Model for the Plasma and the Surrounding Conductive Structures

This section presents the linear model used to simulate the behaviour of the plasma, of the PF circuits, and of the surrounding passive structures.

In toroidal and magnetically confined fusion devices, the Grad–Shafranov equation permits to determine two-dimensions magnetic equilibria under axisymmetric assumption [74]. The Grad–Shafranov partial differential equation is solved by using numerical codes [3, 50, 54, 57], and returns the poloidal flux $\psi$, and in particular its value in the conductive structures that surrounds the plasma, both passive and active (i.e., the PF coils). This information can be used to compute the parameters of the following nonlinear lumped parameters circuital model, that can be obtained under axisymmetric assumption and describes the behaviour of the plasma and of the currents that flow in the surrounding conductive structures (more details can be found in [4, Sec. 2.2] and in [20, Ch. 2]

$$\begin{aligned} \frac{{\text{d}}}{{\text{dt}}} \left[ {\mathscr {M}} \left( y(t),\beta _p(t),l_i(t)\right) I(t)\right] + R I(t)&=U(t),\end{aligned}$$

(10a)

$$\begin{aligned} y(t)&= {\mathscr {Y}} \left( I(t),\beta _p(t),l_i(t)\right) . \end{aligned}$$

(10b)

where

• y(t) are the outputs to be controlled; other than the plasma current and the current in the active and passive structures, this vector may contain plasma shape and position descriptors, e.g. the fluxes at fixed point inside the vacuum chamber, the position of the plasma current centroid, the descriptors of the plasma boundary, such as the plasma-wall gaps (see also the examples reported in Fig. 12, where the ITER poloidal cross-section is shown).

• $I(t)=\left( I_{PF}^T(t)\ I_{e}^T(t)\ I_p(t)\right) ^T$ is the vector that includes the currents in the active coils $I_{PF}(t)$, the eddy currents in the passive structures $I_{e}(t)$, and the plasma current $I_p(t)$;

• $U(t)=\left( U_{PF}^T(t)\ 0^T\ 0\right) ^T$ is the input voltages vector;

• ${\mathscr {M}}(\cdot )$ is the mutual inductance nonlinear function; this function depends on the plasma internal profiles³ (this dependency is taken into account using the poloidal beta $\beta _p$ and the internal inductance $l_i$), and on the plasma shape and position, whose descriptors are included in the output vector y(t).

• R is the resistance matrix;

• ${\mathscr {Y}}(\cdot )$ is the output nonlinear function.

It is worth to notice that, other than on axisymmetry, the nonlinear lumped parameters model (10) relies also on the two further main assumptions, namely:

• the inertial effects are neglected at the time scale of interest, since plasma mass density is low;

• the magnetic permeability is assumed homogeneous and equal to 0 everywhere.

Fig. 12

Example of plasma-wall segments used to define gaps between the plasma boundary and the first wall for the ITER tokamak (figure taken from [14]). Along the same segments it is possible to define also points where virtual flux probes can be placed. Gaps and fluxes on these virtual probes can be added as outputs of the model presented in “Linear Model for the Plasma and the Surrounding Conductive Structures” section

Mass Versus Massless Plasma

Although a massless plasma assumption is usually made when dealing with magnetic modeling, in [49, 79] the authors proved that there are certain cases when neglecting plasma mass may lead to erroneous conclusion on plasma vertical stability.

From the magnetic control point of view, a plasma equilibrium is specified in terms of nominal values of the plasma current $I_{p_{eq}}$, of the currents in the PF circuits $I_{PF_{eq}}$, and of the disturbances, namely $\beta _{p_{eq}}$ and $l_{i_{eq}}$. Following the linearization procedure briefly described in “State-Space Dynamical Systems” section, it is possible to specify the behaviour of the plasma and of the surrounding coils around a given equilibrium by means of the following state space model

$$\begin{aligned} {\dot{x}}(t)&= A x(t)+B u(t)+ E {\dot{w}}(t)\end{aligned}$$

(11a)

$$\begin{aligned} y(t)&= C x(t)+Fw(t) , \end{aligned}$$

(11b)

where

• $x=\begin{pmatrix}\delta I^T_{PF}&\delta I_e&\delta I_p\end{pmatrix}^T$ is the vector the current variations in the PF circuits, in the passive structures, and of the plasma current;

• u is the vector of the voltage variations applied to the PF circuits;

• $w=\begin{pmatrix}\delta \beta _p&\delta l_i \end{pmatrix}^T$ is the disturbances vector, i.e. the variations of $\beta _p$ and $l_i$.

It is worth to notice that the linearization of (10) can be computed either analytically (as an example, see [4, Sec. 2.3]), or numerically as in [2].

As already mentioned in “State-Space Dynamical Systems” section, although simpler than the physics-oriented simulation codes, the availability the engineering-oriented linear model (11) is essential not only to enable model-based design of control systems. Indeed, it permits also to automate both the validation and deployment of the plasma axisymmetric magnetic control (relevant examples on existing tokamak devices can be found in [7, 24, 28, 32, 40, 52]. Furthermore, reliable linear plasma models are also used to support the design and commissioning of the magnetic diagnostic [69], as well as to run inter-shot simulations aimed at optimising the controller parameters [38].

Linear models (11) can be generated starting from nonlinear equilibrium codes, by numerically computing the derivatives in (5). For example, plasma/circuits models in the form (11) are generated by the CREATE 2D nonlinear equilibrium codes [3, 4], which are available in the Matlab/Simulink$^{\circledR }$ environment, which in turn represents the de facto standard tool for control systems design and validation. The CREATE equilibrium codes, together with the correspondent linearized models, have been extensively validated against different magnetically confined fusion devices, among which there are JET [5], TCV [17], and more recently the EAST tokamak [7, 31]. The same modeling tools have been also used to perform preliminary studies and code benchmarking for ITER [67], DEMO [81], JT-60SA [28] and DTT [6]. It shall be remarked that the CREATE-NL+ equilibrium code [70] can be integrated with transport solvers [70], in order to receive as input the plasma internal profiles, hence running coupled nonlinear simulations.

Plasma Magnetic Control

The Plasma Axisymmetric Control Problems

The plasma axisymmetric magnetic control in tokamaks includes the following control problems

• the Vertical Stabilization problem;

• the Plasma Current Control problem.

• the Plasma Shape Control problem;

• the PF Currents Control problem.

Although it may apparently seem that the PF Current Control is not directly related to the plasma magnetic control, it is important to remark that the regulation of the currents into the external active coils is usually included in the magnetic control system. Indeed, as anticipated at the beginning of “Introduction” section, plasma scenarios are defined in terms of nominal currents into the PF coils. Furthermore, in the architecture proposed in “A Flexible Architecture for Plasma Magnetic Control in Tokamaks” section the plasma current and shape controller will be designed so to compute additional references for the PF current controller. In the author’s opinion, the solution of the PF Current Control problem is a precondition to implement advanced plasma current and shape control system.

It should be also remarked that the axisymmetric control problems are not the only ones that arise during tokamak operations and which are related to the magnetic configuration. Non axisymmetric control problems, such as the control of Resistive Wall Modes or of the Neoclassical Tearing Modes are also related to magnetic instabilities. In order to tackle these problems, usually more advanced control systems are required, which integrate both plasma magnetic and kinetic control (see [16, 18, 21, 63, 80]).

A brief description of the main objectives for each of the control problems listed above is given in the next sections.

The Vertical Stabilization Problem

High performances plasmas have diverted shape with an elongated poloidal cross-section. One X-point (for single-null configurations) or even two X-points (for double-null configurations) can be active into the vacuum chamber. Such vertically elongated plasmas turn out to be vertically unstable.

In order to illustrate the plasma vertical instability, let us consider the simplified filamentary model depicted in Fig. 13, where two rings, modeling two active coils, are kept fixed and in symmetric position with respect to the r axis, while the third, which models the plasma, can freely move along the vertical direction. If the currents in the two fixed rings are equal, then the vertical position $z=0$ is an equilibrium point for the system. Given the plasma current $I_p$ and the current in the active coils I, the following two cases can be considered:

${{\mathrm{sgn}}}(I_p)\ne {{\mathrm{sgn}}}(I)\rightarrow$ :

the plasma poloidal cross-section is circular and the equilibrium is vertically stable (see Fig. 14);

${{\mathrm{sgn}}}(I_p)={{\mathrm{sgn}}}(I)\rightarrow$ :

the plasma poloidal cross-section is elongated and the equilibrium is vertically unstable (see Fig. 15).

It is important to note that the current in the two active coils of this simplified model represent differential control currents. This additional currents act on top of the equilibrium ones that counteract plasma radial expansion. Indeed, the plasma toroidal geometry generates a force that tends to expand the plasma itself outward along the major radius. An externally applied vertical field is then required to balance this force. Such a vertical field can be generated by currents in the two active coils shown in Fig. 13 that flow in the opposite direction with respect to $I_p$ (see also [44, Sec. 11.7]).

The plasma vertical instability reveals itself in the linearized model (11) by the presence of an unstable eigenvalue (i.e., real and positive) in the matrix A. Hence, it follows that an active control system is needed to vertically stabilize the plasma column. It should be recalled that, thanks to the presence of the conducting structures that surround the plasma, which slow down the growth time of the vertical instability,⁴ it is possible to use a feedback control system for the stabilization. it should be remarked that, without this passive stabilizing action, it would not be possible to actively stabilize the plasma.

Hence, it turns out that the Vertical Stabilization system is essential, since, in the case of elongated plasmas, without this system the tokamak discharge cannot be run. Other that vertically stabilize elongated plasmas, the objective of any VS system includes also the counteraction of the disturbances, such as Edge Localized Modes (ELMs), fast disturbances modeled as Vertical displacement Events (VDEs, [9]), etc.

As conclusion of this section, it is important to remark that in order to achieve plasma vertical stabilization it is not necessarily required to control the vertical position of the centroid. At least in principle, to vertically stabilize the plasma column it should be sufficient to stop the plasma, that is controlling to zero its vertical speed, as it will be shown in “The VS System” section.

Fig. 13

Simplified electromechanical model with three conductive rings (figure taken from [33]). Two rings are kept fixed and in symmetric position with respect to the r axis and model the active surrounding coils. The third ring can freely move vertically and is used to model the plasma

Fig. 14

Stable equilibrium for the simplified electromechanical model depicted in Fig. 13 (figures taken from [33]). a Force balance at the equilibrium for a circular plasma, b stable equilibrium

Fig. 15

Unstable equilibrium for the simplified electromechanical model depicted in Fig. 13 (figures taken from [33]). a Force balance at the equilibrium for an elongated plasma, b unstable equilibrium

The Plasma Current Control Problem

During a tokamak discharge, tracking the desired value for the plasma current $I_p$ is another mandatory task that must be performed by the magnetic control system (in Fig. 16 a typical time behaviour for $I_p$ is shown). To accomplish this task the current in the external PF coils should be driven by a controller so to regulate $I_p$ to the desired value. Indeed, from the $I_p$ control point of view, the plasma can be regarded as the secondary coil of a transformer. Robustness is a key requirement for the plasma current control, since it is usually required to have a single control algorithm that works for all the possible operative scenarios, independently of the desired plasma shape.

Fig. 16

The typical time behaviour of the plasma current during a tokamak discharge. The $I_p$ values and time scale shown in this figure are the ones expected for an ITER discharge. The different phases of the discharge are also reported

It should be noticed that both plasma current and shape control may use the current in the PF coils as control variables (see also “The Plasma Shape Control Problem” section). Therefore there is also a problem of actuator sharing to be taken into account when using this approach for the design of the plasma current and shape control algorithms. However, different solutions can be considered to tackle this issue, from the design of a single integrated controller (see [11, 17]), to the design of two decoupled controllers, by exploiting the possibility of generating a flux that is spatially uniform across the plasma (but with a desired temporal behavior). Such a flux will drive $I_p$ without affecting the plasma shape too much, as it will be shown in “Algorithms for Plasma Magnetic Control” section.

The Plasma Shape Control Problem

As it was already mentioned in “Introduction” section, the control of the plasma boundary is essential to achieve high performance in tokamak operations and to deal with the problem of the power exhaust. Usually, during the first phases of a discharge, when the plasma is still in the limiter configuration,⁵ the control of the plasma current centroid position (both horizontal and vertical), together with the feedforward currents in the PF coils, is typically sufficient to obtain the desired performance. Example of of the plasma centroid controllers can be found in [27, 83]. However, such a solution becomes insufficient when the plasma shape changed from limiter to divertor configuration, and when high confinement configurations are achieved, since the effect of the disturbances on the plasma shape becomes not negligible. In this phases of the discharge the control of the whole plasma boundary is required. This objective can be achieved by simultaneously regulating the position of a set of points along the plasma boundary, as it will shown in “Algorithms for Plasma Magnetic Control” section.

The PF Currents Control Problem

A tokamak scenario is usually defined as a sequence of nonlinear equilibria to be achieved during a discharge. Among the various parameters that define a single snapshot there are also the currents in the PF coils. Hence, there is the need to control in closed loop the currents that flow in the PF coils, in order to track nominal scenario currents, as well as the variations requested by the plasma current and shape controllers. In order to increase the reliability of the overall system, the PF current control problem should include also the management of the current saturation in the coils. If the nominal currents are within the plant limits, this latter problem is usually tackled when designing the plasma current and shape control system (for example see [13] and [29]).

A Flexible Architecture for Plasma Magnetic Control in Tokamaks

In this section an overview of the proposed architecture for the magnetic control system is given.

Fig. 17

The proposed architecture for the magnetic control system. The main blocks are shown. The scenario currents represent the PF nominal currents

A block diagram of the overall architecture is reported in Fig. 17, where the main components are shown. In particular, the proposed architecture envisages a dedicated block for each of the control problems introduced in “The Plasma Axisymmetric Control Problems” section, namely

• the Vertical Stabilization (VS) System, which takes care of the stabilization of the elongated and hence unstable plasmas. This system relies on a set of dedicated actuators, i.e. power supplies that are usually faster than the one used for plasma current and shape control. In the more general case, these dedicated power supplies may feed both ex-vessel and in-vessel coils. In the proposed architecture, other than the current in the actuators, the VS system receives as input the plasma vertical speed, but not the vertical position; indeed this system will only stop the plasma, leaving to the shape controller the task of bringing the plasma back to the desired position;

• the PF Current (PFC) Decoupling Controller; this block represents the inner control loop of a nested architecture that includes also the plasma current and shape controllers. This block aims at solving the PF current control problem presented in “Plasma Shape Controller” section; hence it guarantees that the currents in the PF coils track the scenario references, as well as the corrections received from the two outer loops;

• the Plasma Current Controller, which tracks the plasma current reference by generating additional requests for the PFC Decoupling Controller;

• the Plasma Shape Controller, which controls shape of the last closed flux surface within the vacuum chamber by tracking a set of plasma shape descriptors; in the proposed architecture also this block generates additional requests for the PFC Decoupling Controller.

The next sections will introduce the proposed control algorithms for each of the main blocks shown in Fig. 17.

Algorithms for Plasma Magnetic Control

We will now describe a set of possible control algorithms to be deployed in each of the main blocks reported in the architecture described in the previous section. It should be noticed that the proposed architecture can be used the implement control different control approaches with respect to the ones presented in this section.

The VS System

In all the existing machines with elongated plasmas, the vertical stabilization problem (see “The Vertical Stabilization Problem” section) is solved by designing a controller that drives the current in dedicated PF circuits that mainly generate a radial magnetic field, which in turns is needed to apply the vertical force used to stop the plasma column. One example of such dedicated circuit is the JET tokamak Radial Field Circuit [66]. At least one pair coils fed in anti-series⁶ are installed in other existing machines, and the same solution is envisaged for the tokamaks currently under construction, in order to deal with the vertical stabilization problem. A generic setup, that fits with the one existing on different machines (e.g. JET, EAST, ITER) includes both a pair of in-vessel and ex-vessel coils. For this reason in the architecture shown in Fig. 17 the VS system receives as input the vertical speed of the plasma centroid and the current flowing in the dedicated circuits, the latter possibly including both the current in dedicated in-vessel and ex-vessel circuits.

Referring to the this general case, where the VS system can use both an in-vessel and a ex-vessel circuits, the following MIMO controller can be used to vertically stabilize the plasma column

$$\begin{aligned} U_{IC}(s)&=F_{VS}(s)\cdot \left( K_v\cdot {\bar{I}}_{p_{ref}}\cdot V_p(s)+K_{ic}\cdot I_{IC}(s)\right) ,\end{aligned}$$

(12a)

$$\begin{aligned} U_{EC}(s)&=K_{ec}\cdot I_{IC}(s) , \end{aligned}$$

(12b)

where $U_{IC}$ and $U_{EC}$ are the voltages to be applied to the in-vessel and ex-vessel circuits, respectively, while $I_{IC}$ is the current flowing in the in-vessel coil, and $V_p$ is the plasma vertical speed. The controller parameters are

• $K_{ic}$ and $K_{ec}$ are the current gains;

• $K_v$ is the speed gain which, at each time sample, must be scaled by the nominal value of the plasma current ${\bar{I}}_{p_{ref}}$ (it is assumed that the plasma current controller is tracking the reference with a small steady-state error);

• $F_{VS}(s)$ is the transfer function of a dynamic compensator, which is usually a lead compensator (see [76, Section 2.6.5]).

Being not shielded by the passive structures, if available, the in-vessel circuit loop (12a) is used to achieve stabilization, while, the ex-vessel (12b) is used to reduce the current in the in-vessel circuit. Indeed, the ex-vessel circuit is used to “drain” current from the in-vessel circuit, hence reducing the root mean square value of $I_{IC}$, in order to meet the specific constraints on the power dissipation for the copper coils (see the ITER example reported in [9, 10]). It is worth to notice that, if the in-vessel coils are not installed (as in the JET case), a control law similar to (12a) can be used to determine the voltage to be applied to the ex-vessel coil in order to vertically stabilize the plasma column; i.e. the voltage $U_{EC}$ is given by

$$\begin{aligned} U_{EC}(s)=F_{VS}(s)\cdot \left( K_v\cdot {\bar{I}}_{p_{ref}}\cdot V_p(s)+K_{ec}\cdot I_{EC}(s)\right), \end{aligned}$$

where $I_{EC}$ is the current flowing in the ex-vessel circuit.

Moreover, it should be noticed once again that the proposed VS controller achieves stabilization of the plasma column without the need of controlling the vertical position. Indeed, as it was remarked in “The Vertical Stabilization Problem” section, the main objective of the VS system should be to stop the plasma, rather than to move it back to the original position. This latter task can be performed by the plasma shape controller. Moreover, the proposed controller structure is rather simple, since there are few parameters to be tuned against the operational scenario. Such a simple structure permits to envisage effective adaptive algorithms, as it is usually required during operation.

Fig. 18

Block diagram of the EAST VS system (figure taken from [31]). The plant block includes the power supply, the plasma and surrounding conductive structures, and the magnetic diagnostic

In order to better understand how the in-vessel loop achieves vertical stabilization let us consider the case of the EAST tokamak, whose block diagram is reported in Fig. 18 (more details can be found in [7, 30]). In the EAST case, two in-vessel coils (shown as red rectangles labeled as “IC” in Fig. 2b) are connected in anti-series and represent the actuator dedicated to the vertical stabilization; hence the VS system shown in Fig. 18 includes only the in-vessel loop (12a).

In order to design the controller parameters in (12a) the state space model (11) is used to derive the following input–output relationship

$$\begin{aligned} Y(s)=\begin{pmatrix}Y_1(s)\\ Y_2(s)\end{pmatrix}=W_p(s)\cdot {\widetilde{U}}_{IC}(s)=\begin{pmatrix}W_{p_1}(s)\\ W_{p_2}(s)\end{pmatrix}\cdot {\widetilde{U}}_{IC}(s) , \end{aligned}$$

(13)

where ${\widetilde{U}}_{IC}(s)$ is the actual voltage applied to the IC circuit by the power supply, while $Y_1(s)=Z_p(s)$ is the plasma vertical position, and $Y_2(s) = I_{IC}(s)$ is the current flowing in the IC circuit. The transfer matrix (13) models the behaviour of the plasma and of the surrounding conductive structures; however, when designing the VS system, the models of both the power supply and of the relevant magnetic diagnostic should be included in the plant. Indeed, these two components usually have a major impact on the performance of the closed loop system. To this aim, the power supply is modeled as a first order filter with a delay, i.e.

$$\begin{aligned} {\widetilde{U}}_{IC}(s)= \frac{e^{-\delta _{ps}s}}{1+s\tau _{ps}}\cdot U_{IC}(s) , \end{aligned}$$

(14)

where $\tau _{ps} = 100\,\upmu {\text {s}}$ and $\delta _{ps} = 550\,\upmu {\text {s}}$ are the estimated values for the power supply time constant and delay, respectively. Note that the presence of a time delay is modeled by the exponential term $e^{-\delta _{ps}s}$ in (14). Moreover, at EAST the plasma vertical speed $V_p(s)$ is estimated by means of a derivative filter applied on the measured vertical position of the centroid $Z_p(s)$, i.e.

$$\begin{aligned} V_p(s)=\frac{s}{1+s\tau _v}\cdot Z_p(s) , \end{aligned}$$

(15)

where the time derivative of the derivative filter is set equal to $\tau _v=1$ ms. As far as the current in the in-vessel circuit is concerned, it is assumed that there is no delay on its measure. The overall plant model can be obtained by computing the series of (13)–(15), which is equal to

$$\begin{aligned} W_{plant}(s)=\begin{pmatrix}1\\ \frac{s}{1+s\tau _v}\end{pmatrix}\cdot W_{p}(s)\cdot \frac{e^{-\delta _{ps}s}}{1+s\tau _{ps}} . \end{aligned}$$

(16)

In order to use a design approach for (12a) which is based on the root locus, the $550\,\upmu {\text {s}}$ time delay of the IC power supply can be replaced by its third order Padé approximation (see [76, Section 4.1.6]), that is

$$\begin{aligned} e^{-\delta _{ps}s}\cong \frac{-(s-8444)(s^2-1.34\cdot 10^4s + 8.54\cdot 10^7)}{(s+8444)(s^2+1.34\cdot 10^4s + 8.54\cdot 10^7)} . \end{aligned}$$

(17)

By exploiting the parity interlacing property (PIP, [82]), in [30] it was shown that, given the plant model (16), it is not possible to stabilize the plasma by feeding back only the vertical speed $V_p$. Indeed, given the two positive zeros introduced by the power supply delay (see (17)), the PIP requires the presence of another non negative pole in the open loop transfer function of the $U_{IC}-{\dot{V}}_p$ channel, otherwise it is not possible to move the unstable pole on the left half of the complex plane using a stable controller. In order to add such a non negative pole, either an integral action on $V_p$ or a feedback on $I_{IC}$ is needed. However, the former solution is equivalent to the feedback of the vertical position $Z_p$, hence it would add a coupling between the VS system and the plasma shape control, which is not desirable. For this reason, in (12a) it is proposed to add the feedback term on $I_{IC}$. By closing the loop on $I_{IC}$ another unstable pole is added in the $U_{IC}-V_p$ channel, as it is shown in Fig. 19a; then, by closing the proportional loop on $V_p$, it is possible to achieve closed loop stabilization, as it is shown in Fig. 19b. Note that the root locus diagrams shown in Fig. 19 are obtained considering a reduced model of order 10 for (16) (see [84, Ch. 7]).

Fig. 19

Root locus of the $U_{IC}-{\dot{V}}_p$ channel when the controller (12a) is used and the plasma model for the EAST pulse #60938 at $t=6$ s is considered (figures taken from [30]). a Root locus of the $U_{IC}-{\dot{V}}_p$ channel, when both the loops provided in (12a) are closed, b root locus of the $U_{IC}-{\dot{V}}_p$ channel, when the loop on the IC current provided in (12a) is closed

Before concluding this section, it is worth to mention that two different techniques have been proposed to robustly design the controller parameters: in [9, 10] the gains are given by the solution of an optimization problem with Bilinear Matrix Inequality constraints (BMI [77]); multi-objective optimization is used in [31] to tune the controller gains and the parameters of a lead compensator $F_{VS}(s)$.

PFC Decoupling Controller

In the proposed architecture, the Plasma Current and the Plasma Shape Controllers compute their control action as deviations with respect to the PF currents of the nominal scenario. The PFC Decoupling Controller block implements the algorithm that tracks these deviations, as well as the nominal values (see Fig. 17). In particular, it receives as input the currents in the PF circuits together with their desired values, and it generates the voltage references for the PF power supplies. When designing the control algorithm for this block, other than achieving PF decoupling, it must be taken into account that the PF currents should exhibit almost the same dynamic response, since the plasma shape controller will rely on such a behaviour (see “Plasma Shape Controller” section).

The design of the controller can be carried out starting from a plasmaless model. Such a model can be written in the following form

$$\begin{aligned} L{\dot{x}}(t)+Rx(t)=u(t) , \end{aligned}$$

(18)

where L and R are the inductance and resistance matrices, x(t) is the vector of the current in the circuits (both active and passive), and u(t) is the vector of the voltages applied to the circuits (which are equal to zero for the passive structures, see also “Linear Model for the Plasma and the Surrounding Conductive Structures” section).

The design of the PFC Decoupling Controller is based on a modified version of the inductance matrix ${\widetilde{L}}_{PF}\in {\mathbb {R}}^{n_{PF}} \times {\mathbb {R}}^{n_{PF}}$, where $n_{PF}$ is the number of PF circuits. ${\widetilde{L}}_{PF}$ is calculated by neglecting the effect of the passive structures. Furthermore, in order to minimize the control effort, in each row of ${\widetilde{L}}_{PF}$, all the mutual inductance terms which are less than the $10\%$ of the circuit self-inductance are also neglected. Thanks to this choice, the current in each circuit is controlled only by the circuits that are more coupled with it, avoiding to easily saturate the voltages without gaining any practical improvement in the control of the PF currents.

The proposed design approach aims at obtaining a first order response for all the PF circuits when the PFC Decoupling Controller is closed. Given the time constants $\tau _{PF_i}$ for the response of the ith circuit, we define:

$$\begin{aligned} \varLambda = \left( \begin{array}{llll} 1/ \tau _{PF1} &{} 0 &{} \ldots &{} 0 \\ 0 &{} 1/ \tau _{PF2} &{} \ldots &{} 0 \\ \ldots &{} \ldots &{} \ldots &{} \ldots \\ 0 &{} 0 &{} \ldots &{} 1/ \tau _{PF_n} \end{array} \right) . \end{aligned}$$

Note that, in order to have the same dynamic on all the PF circuits, the time constants $\tau _{PF_i}$ should be all equal.

The voltages to be applied to the PF circuits are then calculated as

$$\begin{aligned} U_{PF}(t) = K_{PF} \cdot \left( I_{PF_{ref}} (t)- I_{PF}(t)\right) +{\widetilde{R}}_{PF}I_{PF}(t) , \end{aligned}$$

(19)

where ${\widetilde{R}}_{PF}\in {\mathbb {R}}^{n_{PF}\times n_{PF}}$ is an estimation of the resistance matrix, while the control gain matrix $K_{PF}$ is given by

$$\begin{aligned} K_{PF} = {\widetilde{L}}_{PF} \cdot \varLambda . \end{aligned}$$

Taking into account that the estimation of the PF circuit resistances can be usually performed with good accuracy, i.e. ${\widetilde{R}}_{PF}\cong R_{PF}$, by replacing the controller output (19) in (18), it follows that the closed loop behaviour for the currents in the PF circuits is well described by the differential equation

$$\begin{aligned} {\dot{I}}_{PF}(t)=\varLambda \cdot \left( I_{PF_{ref}}(t)-I_{PF}(t)\right) . \end{aligned}$$

Since $\varLambda$ is diagonal the desired decoupling is assured by (19). Moreover, the feedback term ${\widetilde{R}}_{PF}I_{PF}(t)$ is equivalent to an integral action or, in other word, it allows to treat any coil as a supercondutive one.⁷

The Bode diagrams of the closed loop system designed for the JT-60SA tokamak are shown in Fig. 20. It can be noticed that the diagonal channels (from the ith voltage to the ith current, Fig. 20a) exhibit very similar dynamic responses, while the off-diagonal channels (whose Bode diagrams are shown in Fig. 20b) have a much lower magnitude. It follows that good decoupling is achieved.

The design approach described in this section was originally proposed for the JET tokamak in [45, 71]; the same approach was recently tested on the EAST tokamak [37].

Fig. 20

Bode diagrams for the closed loop PFC decoupling control system designed for the JT-60SA tokamak (figures taken from [28]). a Bode diagrams for the diagonal channels, b Bode diagrams for the off-diagonal channels

Plasma Current Controller

The Plasma Current Controller is one of the two feedback loops that send requests to the PFC Decoupling controller. It receives as input the plasma current together with the corresponding reference waveform, and it computes the PF current deviations needed to obtain the desired $I_p$.

Let $k_{p_{curr}}\in {\mathbb {R}}^{n_{PF}}$ be the vector of PF currents that causes a constant flux variation along a closed line containing the envisaged plasma boundary; the field generated by the linear combination of PF currents in $k_{p_{curr}}$ is called the transformer field. The elements of the $k_{p_{curr}}$ vector can be obtained via an optimization procedure based on the plasmaless model introduced in “The PF Currents Control Problem” section. Moreover, by definition, the linear combination of PF currents specified by $k_{p_{curr}}$ is such that the effect on the plasma shape is minor.

It follows that the $k_{p_{curr}}$ vector can be used to design a plasma current control algorithm that has a loose coupling with the plasma shape controller. One way to achieve this objective is to consider the following single-input–multi-output (SIMO) control law

$$\begin{aligned} \delta I_{PF}(s) = k_{p_{curr}}\cdot F_{I_p}(s) \cdot I_{p_e}(s) , \end{aligned}$$

(20)

where $I_{p_e}=I_{p_{ref}}-I_p$ is the error on $I_p$, and $F_{I_p}(s)$ is the dynamic response of the controller. This latter SISO controller is usually designed as a proportional–integral-derivative (PID) regulator, where the integral action assures zero steady-state error during the current flat-top. However, when special requirements need to be met, other structures for $F_{I_p}(s)$ can be considered. As an example, since for ITER it is important to track the reference with zero error also during the ramp-up and ramp-down phases, the transfer function $F_{I_p}(s)$ should be designed with a double integral action [14]. It should be remarked that, for tokamaks with an iron core, such as JET, the transformer field is usually obtained by driving the current in the central solenoid, hence the $k_{p_{curr}}$ becomes a scalar and the control law (20) becomes a SISO one (see [71]).

Plasma Shape Controller

The Plasma Shape Controller is the second block that generates additional reference for the PFC Decoupling Controller. In modern tokamaks, the plasma shape control problem is solved using different approaches during the different phases of the plasma discharge reported in Fig. 16. The various solutions typically deal with a different choice of the shape descriptors to be controlled, from the simple one that controls only the position of the current centroid (both horizontal and vertical, [83, Section 3.2]), to the full boundary control solution [19].

Taking into account that at low values of $I_p$, due to measurement noise, the reconstruction of the plasma-wall gaps is not reliable, the following controlled variables are typically used during the different phases of the discharge

• during the limiter phase, the controlled parameters are the limiter point position and a set of flux differences;

• during the limiter-to-divertor transition the X-point position and a set of flux differences are controlled;

• during the diverted phase the controlled variables are the plasma-wall gaps;

• after the divertor-to-limiter transition, it may be convenient to move back to the control of the limiter point position and of a set of flux differences.

It follows that the proposed architecture must be flexible enough to be able to implement both the isoflux boundary control and the gap boundary control. As an example, let us consider the ITER poloidal cross-section and the control segments shown in Fig. 12.

Let $g_i$ be the abscissa along i-th control segment, being $g_i=0$ at the first wall. Gap boundary control is achieved by imposing

$$\begin{aligned} g_{i_{ref}}-g_i=0 \end{aligned}$$

on a sufficiently large number of control segments.

Moreover, if the plasma shape intersects the i-th control segment at $g_i$, the following condition is satisfied

$$\begin{aligned} \psi (g_i)=\psi _B , \end{aligned}$$

where $\psi _B$ is the flux at the plasma boundary; hence isoflux boundary control is achieved also by controlling to 0 the difference

$$\begin{aligned} \psi (g_{i_{ref}})-\psi _B , \end{aligned}$$

where $\psi _B$ can be taken equal either to the flux at the limiter point $\psi _L$ or at the X-point $\psi _X$; the limiter-to-divertor and divetor-to-limiter transitions can be achieved by properly select the reference for $\psi _B$.

The proposed control algorithm for the Plasma Shape Controller block is based on the eXtreme Shape Controller (XSC, [19]), since this approach can be easily adapted both to gap and isoflux control. Moreover, a current limit avoidance systems that tries to avoid the saturation of the PF currents can be easily integrated within the XSC.

The main advantage of the XSC approach is the possibility of tracking a number of shape parameters larger than the number of PF circuits, by minimizing a weighted steady-state quadratic tracking error, when the references are constant signals.

The XSC control relies on the PFC Decoupling Controller presented in “The PF Currents Control Problem” section. Indeed, for the XSC design, it is assumed that each PF circuits can be treated as an independent SISO channel whose dynamic response is modeled by

$$\begin{aligned} I_{PF_i}(s) = \frac{I_{PF_{ref ,i}}(s)}{1+s\tau _{PF}} . \end{aligned}$$

It is also assumed that all the PF circuits exhibit the same bandwidth (i.e., they have the same time constant $\tau _{PF}$).

Denoting as $\delta Y(s)$ are the variations of the $n_G$ shape descriptors—which can include flux differences, position of the X-point, gaps, etc.—from the plasma linear model (11) it follows that

$$\begin{aligned} \delta Y(s) = C\frac{I_{PF_{ref}}(s)}{1+s\tau _{PF}} , \end{aligned}$$

which, at steady-state, implies

$$\begin{aligned} \delta Y(s) = C I_{PF_{ref}}(s) . \end{aligned}$$

If the number of controlled plasma shape descriptors $n_G$ is such that $n_G~>~n_{PF}$, the XSC computes the additional current references as

$$\begin{aligned} \delta I_{PF_{ref}}=C^\dag \delta Y . \end{aligned}$$

(21)

which are then sent to the PFC Decoupling Controller, in order to track the desired shape in a least-mean-square sense. In (21) the matrix $C^\dag$ denotes the pseudo-inverse of C that can be computed via the singular value decomposition (SVD). Two diagonal matrices $Q\in {\mathbb {R}}^{n_G\times n_G}$ and $N\in {\mathbb {R}}^{n_{PF}\times n_{PF}}$ can be used to weight the shape descriptors and the currents in the PF circuits, respectively. In this case the current to be sent to the PFC Decoupling Controller can be computed using the SVD of the weighted output matrix

$$\begin{aligned} {\widetilde{C}} =QCN=USV^T . \end{aligned}$$

It follows that the XSC algorithm controls to zero the error on $n_{PF}$ linear combinations of geometrical descriptors. Controlling to zero such an error is equivalent to minimizing the following steady-state performance index

$$\begin{aligned} J_{XSC} = \lim _{t\rightarrow + \infty }(\delta Y_{ref}-\delta Y(t))^TQ^TQ(\delta Y_{ref}-\delta Y(t)) . \end{aligned}$$

(22)

where $\delta Y_{ref}$ are constant references for the geometrical descriptors. When SVD of the ${\widetilde{C}}$ matrix is used to minimize (22), it may happen that some singular values (depending on the plasma configuration) are one order of magnitude smaller than the others. This fact implies that minimizing the performance index (22) retaining all the singular values results in a large control effort at the steady-state, that is a large request on some PF currents which have only a minor effect on the plasma shape. For this reason, the XSC achieves a trade-off condition, by minimizing a modified quadratic cost function that penalizes both the error on the controlled shape descriptors, and the control effort. In order to do that, only the ${\bar{n}}<n_{PF}$ linear combinations of PF currents which are related to the largest singular values are controlled. This is achieved by using only the ${\bar{n}}$ singular values when computing the pseudo-inverse $C^\dag$.

Fig. 21

Block diagram of the XSC Plasma Shape Controller. The pseudo-inverse $C^\dag$ is usually computed using the largest singular values that result from the SVD of the C matrix

The block diagram of the XSC Plasma Shape Controller is shown in Fig. 21; a set of PIDs is added in order to improve the dynamic response of the controller.

For more details on the XSC the reader is referred to [12, 19]. It worth to remark that SVD-based control approaches similar to the XSC have been used not only for magnetic control [15], but also for kinetic control (see [58, 63, 75] among the various).

Although in the XSC design the weighting matrix N can be used to reduce the use of the coils whose currents are close to saturation, the design procedure presented so far does not take explicitly into account the saturation constraints. It turns out that the PF current may saturate during the experiment, which may trigger the stop of the plasma discharge. In order to avoid current saturations it is possible to rely on a Current Limit Avoidance (CLA) system.

Fig. 22

Block diagram of the XSC Plasma Shape Controller with the Current Limit Avoidance (CLA) system (figure taken from [35]). The CLA made by the blocks in the gray shaded box, which includes the Allocator, and takes both the XSC input and output signals as inputs. In this figure the Augmented Plant represents the plant with the PFC Decoupling Controller

The CLA algorithm exploits the following idea: keep the PF currents within their limits without degrading too much the plasma shape, by finding an optimal trade-off between these two objectives.

In particular, the CLA aims at keeping the value of the plant inputs u, i.e. the PF currents, inside a desirable region, meanwhile ensuring a small tracking error $e = r-y$, i.e. a small error on the plasma shape. In order to quantify this trade-off, a continuously differentiable cost function $J_{CLA}(u^\star ,e^\star )$ is introduced, where the superscript $\star$ on a signal denotes its steady-state value.

The CLA corresponds to the gray shaded box in Fig. 22, which receives inputs from the XSC and modifies the request to the plant, i.e., the plasma controlled by the PFC Decoupling Controller (represented by the Augmented Plant block in Fig. 22). If we denote by $x_a\in {\mathbb {R}}^{n_a}$ the Allocator internal state, and by $B_0\in {\mathbb {R}}^{n_{PF}\times n_a}$ a suitable full column rank matrix, then the two allocator outputs are equal to

$$\begin{aligned} \delta u =B_0 x_a , \end{aligned}$$

(23)

and

$$\begin{aligned} \delta y =P^\star B_0 x_a , \end{aligned}$$

(24)

where $P^\star$ is the steady-state input/output gain of the plant. The output (23) modifies the PF current requests generated by the XSC, while (24) hides the resulting steady-state change in the plasma shape to the XSC. Hiding the plasma shape change to the XSC is required in order to prevent the controller to react to these changes.

The key property of the current allocator algorithm is that, under suitable assumption on the cost $J_{CLA}$, for each constant current request of the XSC, it has a unique globally asymptotically stable equilibrium $x_a^\star$ that coincides with the unique global minimizer of $J_{CLA}$.

The CLA system has been successfully deployed at JET and has made the operation with the XSC safer. More details on the CLA system and on its implementation at JET can be found in [29, 34, 36].

Experiments and Simulations

In this section both experimental and simulation results are presented in order to show the effectiveness of the control algorithms presented in “Algorithms for Plasma Magnetic Control” section.

Let us first consider the VS system described in “The VS System” section. As was already mentioned, the control law (12a) has been successfully deployed at EAST. Figure 23 compares the time traces of $I_p , r_p , z_p$, and $I_{IC}$ for the EAST pulses #69880, #70799, and #71423. During these pulses only $I_p$ and $r_p$ were controlled with the standard EAST controller described in [83], while $z_p$ was left uncontrolled. This was made on purpose in order to confirm that the proposed VS stabilizes the plasma by controlling $v_p$ and $I_{IC}$, without the need of a feedback on $z_p$.

The EAST pulse #69880 was the first one where the proposed VS was enabled for more than 1 s, from $t=2.1$ s to $t=3.3$ s. In pulse #70799 the VS controller gains were tuned with the objective of reducing the maximum absolute value of the current requested in IC. Indeed, if the absolute value of the current in IC exceeds a given threshold, the power supply is tripped and the discharge is shut down. A further fine tuning was made for pulse #71423, in order to increase the stability margins, and hence to reduce the oscillatory behaviour. Note that, during the EAST pulse #71423 a fictitious disturbance was induced on the plasma current by a bump on the correspondent control loop. The overall behaviour is equivalent to a step disturbance to be rejected by both the VS and $r_p$ control loops.

The VS system (12) has been proposed also for the ITER tokamak. In this case both the in-vessel and the ex-vessel circuits are available. A BMI optimization problem was solved to design a static and robust version of the VS system (12). Robustness was imposed by considering three different plasma equilibria when solving the optimization BMI problem. Figure 24 shows the simulated response of the closed loop system for a 20 cm VDE, for the three equilibria considered for the design, as well as for two additional ones (more details can be found in [10]).

The PFC Decoupling Controller introduced in “PFC Decoupling Control” section is routinely used at JET [62, 71]. More recently, the same algorithm has been tested at EAST, in order to improve the decoupling of the PF circuits. Indeed, according to the simulation results shown in Fig. 25, the MIMO controller (19) achieves a better decoupling when compared with the SISO PIDs used at EAST. The simulation results have been confirmed by the preliminary tests run during plasmaless discharges. In particular, Fig. 26 shows the currents in the two circuits PF1 and PF2; it is possible to note that the simulated and experimental results are in good agreement, and that the desired decoupling is achieved. Indeed, taking into account the measurement noise, the experimental current in PF2 is practically zero, when a current request is made on the PF1 circuit; the same behaviour was observed also on the other circuits.

The XSC plasma shape controller was successfully deployed at JET in 2003, and since then has been used during hundreds of pulses. Figure 27 shows the time traces of some of the controlled shape descriptors for the JET pulse #68953, while Fig. 28 shows how the XSC was used during the JET pulse #83202 to linearly change the plasma elongation while $I_p$ was ramping down.

As it was claimed in “Plasma Shape Controller” section, the XSC approach can be also adopted when isoflux control is used to track the desired shape. As an example, Fig. 29 shows a simulation of the plasma current ramp-up for JT-60SA. The simulation results reported in this figure have been obtained simulating all the controllers of the proposed architecture.

In order to made the operation with the XSC safer, the CLA system was also deployed at JET. Figures 30 and 31 shows the results of an experiment aimed at producing a severe limitation for the XSC, and hence to prove the effectiveness of the CLA system. In order to do that, up to four, out of the eight available PF circuits, have been limited, and the following strategy has been adopted to carry out the experiment. First a reference pulse was run (pulse #81710), during which the XSC without CLA successfully controlled the plasma shape between 20 s and 23 s. Afterwards, during the JET pulse #81715, the CLA system was enabled from 21 s, in order to limit the currents in the four divertor coils D1–D4 within a range smaller than the one actually available.

As expected, when a PF currents went outside their saturation limits, the CLA tried to bring them back to the permitted range while obtaining almost the same plasma shape as shown in Fig. 30. Moreover, Fig. 31 shows a comparison between the currents in the JET divertor coils for pulses #81710 and #81715. Taking into account that the limitation of more than two control currents represents already a challenging scenario at JET, the performance obtained during pulse #81715 is fully satisfactory. Furthermore, it is important to note that the CLA parameters used during this experiment included a hard constraint on the X-point position. That means that the CLA prefers to increase the shape error on the top-outer region of the plasma, rather than to change the position of the X-point, as it is shown in Fig. 30.

Fig. 23

Comparison between the EAST pulse #69880, which was the first one where the ITER-like VS was enabled for more than 1 s (from $t=2.1$ s to $t=3.3$ s), and the pulses #70799 and #74123, during which the VS controller gains were finely tuned exploiting the model. Note that during the considered time window the vertical position of the plasma current centroid was left uncontrolled in order to prove the effectiveness of the control law (12a)

Fig. 24

Closed loop response to a 20 cm VDE (figure taken from [10]). This figures reports the time traces of the in-vessel coils $I_{IC}$, of the current $I_{EX}$ in the ITER ex-vessel circuit (which is called VS1 in the ITER jargon), of the plasma vertical speed $v_p$, and of the vertical position of the plasma centroid $z_p$

Fig. 25

Simulation showing the comparison between the PFC Decoupling Controller (19) and the EAST SISO PIDs

Fig. 26

Comparison between the simulated and the experimental values for the currents in the EAST PF1 and PF2 circuits during the EAST pulse #74012. Note that, taking into account the measurement noise, the experimental current in PF2 is practically zero

Fig. 27

JET pulse #68953. During this pulse the XSC has been used to control the plasma shape using the gaps (figure taken from [33]). This figure shows the time evolution of some of the controlled plasma shape descriptors

Fig. 28

Change of the plasma elongation during the ramp-down of the JET pulse #83202) (figure taken from [36]). The elongation changes from $\sim 1.66$ to $\sim 1.54$, while $I_p$ is ramping down

Fig. 29

Closed loop simulation of the plasma current ramp-up (from 1.7 MA to 5.5 MA) of JT60-SA Scenario 2 (figures taken from [28]). Plasma shape control done using an isoflux version of the XSC. In particular, the XSC controls to zero the difference between the flux at the control points (shown as green crosses) and the flux at the X-point. Top left: plasma current versus time during the ramp-up phase. Top right: magnetic flux at the X-point and at the control points. Bottom: plasma poloidal cross-section during the plasma current ramp-up ($t = 12$ s, left) and at the flat-top ($t = 22$ s, right). The blue cross shows the desired position for the X-point (Color figure online)

Fig. 30

JET pulse #81715. Shape comparison at 22.5 s (figure taken from [35]). The black shape is the one obtained in pulse #81710 without CLA, while the red shape is the one obtained when the CLA is enabled (Color figure online)

Fig. 31

Currents in the divertor circuits (figure taken from [35]). Comparison between pulse #81710 (reference pulse without CLA) and pulse #81715 (with CLA). The shared areas correspond to regions beyond the current limits enforced by the CLA parameters

Conclusive Remarks

In this chapter the magnetic control problems in tokamak devices have been presented together with a generic architecture for the deployment of the related controllers. The proposed architecture and control algorithms result from the experience made by the members of the CREATE Consortium in the last two decades. Despite their relative simplicity if compared with other control approaches (such as model predictive control [47, 61]), the proposed control algorithms can be easily adapted to different machines, and they have been deployed, partially or completely, on various tokamaks. The same algorithms have been also proposed for ITER [14], JT-60SA [28], DEMO and DTT [6]. Finally, it is worth to remark that the design of all the proposed control algorithms are based on dynamic model of the plasma and of the surrounding coils; hence the availability of reliable plant models is a key factor for the design and deployment of plasma magnetic controllers.