Abstract
We introduce two desirable properties concerning the allocative efficiency term in the decomposition of economic efficiency. Since Farrell, economic efficiency, defined in terms of the cost, revenue, profitability, or profit functions, is decomposed into a technical efficiency measure and allocative efficiency. Resorting to duality theory, allocative efficiency is calculated as a residual. In this framework, we show that this residual is numerically inconsistent for several economic efficiency decompositions: those based on the Russell Efficiency Measures, the Slack-Based Measure and the Weighted Additive Measures. It should be expected that a technical inefficient firm, if projected to the optimal economic benchmark, e.g., that maximizing profit, should be allocative efficient, yet we show that the above decompositions may signal that it is allocative inefficient. Our first property, called ‘essential,’ demands that economic efficiency decompositions satisfy the above criterion. We also extend this property by requiring that the allocative efficiency of a technically inefficient firm, evaluated at the projected benchmark on the production frontier, coincides with the allocative efficiency of the benchmark itself. Regarding this extension of the property, we show that, besides the measures mentioned above, the Directional Distance Function and the Hölder Distance Function fail in general to comply with it. However, we also prove that, thanks to the flexibility of these two approaches in choosing a common directional vector for all the assessed firms or a specific Hölder norm, these measures may satisfy the extended essential property. We conclude that unless both properties are fulfilled, the (residual) allocative component of many previously published decompositions cannot be correctly interpreted as price inefficiency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In for-profit organizations, the measurement of economic efficiency is particularly important. Any company is interested in adjusting its level of inputs and outputs if these changes lead to economic gains. Economic efficiency measurement based on the approach initiated by Farrell (1957) has received great attention from academics and practitioners. Since Farrell, researchers have analytically decomposed cost and revenue efficiency into technical efficiency and allocative efficiency. Economic efficiency measures how close the firm is to the optimum from an economical perspective. namely cost minimization, revenue maximization, profit maximization, or profitability maximization. Technical efficiency measures how close the firm is to the production frontier of the corresponding technology. This technological gap implies economic inefficiency in the form of cost excess (cost approach) or revenue loss (revenue approach), while allocative efficiency measures the cost excess due to wrongly demanded quantities of inputs under market prices, or foregone revenue caused by wrongly supplied quantities of outputs under market prices (Aparicio et al. 2017a, b).
The measurement and decomposition of economic efficiency follows a two-step process. First, technical efficiency is estimated by projecting the assessed firm onto the production frontier (also called efficient frontier). In the case of Farrell’s approach, it is done by resorting to radial movements, relating this component to both Debreu’s (1951) coefficient of resource utilization and the inverse of Shephard’s distance functions (Shephard 1953). Secondly, allocative efficiency is derived as a ‘residual’ between economic efficiency and its corresponding technical efficiency component. That is, allocative efficiency is simply the economic loss that cannot be attributed to technical inefficiency. As a result of this residual nature, the mathematical definition and measurement of allocative efficiency have received much less attention in the literature than those associated with the formulation of technical efficiency and economic efficiency.
While Farrell unknowingly resorted to Shephard’s (radial) distance functions for his decomposition, nowadays there are many alternative ways of calculating technical efficiency and decomposing economic efficiency accordingly. Popular models are those based on the Directional Distance Function by Chambers et al. (1996, 1998) with respect to cost, revenue and profit inefficiency; the Hölder Distance Function by Briec and Lesourd (1999) for profit inefficiency; Zofio and Prieto (2006), where the Hyperbolic Graph Measure is related to the notion of profitability; Cooper et al. (2011) and Aparicio et al. (2016), who establish the duality between the profit function and the Weighted Additive Measure; Aparicio et al. (2015a), who show that cost (revenue) inefficiency can be decomposed resorting to the Russell Measure of input (output) efficiency; Aparicio et al. (2017a), who relate the Slacks-Based Measure (SBM) (Tone 2001)—previously known as Enhanced Russell Graph (ERG) by Pastor et al. (1999)—to profit inefficiency; and, finally, Halická and Trnovská (2018), who provide a decomposition of profit inefficiency in terms of the Russell Graph Measure. For a comprehensive review of these approaches, see Pastor et al. (2022).
In this study, we show that, in contrast to what is commonly assumed in the literature, the ‘residual’ allocative component cannot be correctly interpreted as price inefficiency for many of the previously published economic decompositions. If the measure used to gauge technical efficiency projects the assessed unit onto a point that is optimal from the corresponding economic perspective (e.g., maximum profit), then, there should be no room for allocative inefficiency. This means that the allocative component for the unit under evaluation should value necessarily one in the case of multiplicative approaches—those associated with economic decomposition where technical efficiency and allocative efficiency are multiplicative factors—and zero in the case of additive approaches—those where economic inefficiency is decomposed in the sum of technical inefficiency plus allocative inefficiency. We call this quality ‘the essential property’ since we understand that, otherwise, the provided decomposition is invalid because of lacking a meaningful allocative component. In particular, considering the above models proposed in the literature, we prove that the Input- and Output-oriented Radial Measures for cost and revenue efficiency, the Hyperbolic Graph Measure for profitability, and the Directional Distance Function, and the Hölder Distance Function for profit inefficiency, are among the approaches in which the allocative component can be correctly interpreted. On the contrary, the remaining additive decompositions cited in the previous paragraph fail to meet the essential property.
We also provide a refined extension of the essential property to endow the allocative component with additional internal consistency. As mentioned, technical efficiency is determined by the projection of the assessed unit onto the efficient frontier of the technology and, by definition, allocative efficiency can be determined for technically efficient firms only. In this regard, the extension that we propose means that, for any evaluated firm, its allocative component must always coincide with the value of the allocative component of the corresponding (technically efficient) projected benchmark. Regarding the list of measures that fulfill this additional property, we will prove that only the Radial Measures and the Hyperbolic Graph Measure, and the Directional Distance Function, for certain directional vectors, satisfy such extension, falling out of this group the Hölder Distance Function except for one specific norm.
Our results have relevant implications for the theory and practice of economic efficiency measurement. It shows that the range of valid approximations is smaller than initially thought, mainly confined to the cases already mentioned. Researchers should keep in mind that, in contrast to what has been commonly accepted, the definition of the allocative efficiency term as a residual in the relationship between economic efficiency and technical efficiency is not always the correct strategy for measuring actual price efficiency. The cause of this drawback plaguing many of the existing decompositions is the mechanical practice followed in the literature to decompose economic efficiency. The first authors concerned with the empirical implementation of economic efficiency never explored the properties of the decompositions, i.e., those of the allocative (in)efficiency terms, including the essential property or similar ones. Instead, they took the fulfillment of the property for granted. Formally, the allocative efficiency term is defined as the residual derived from closing the so-called Fenchel–Mahler inequality (Färe and Grosskopf 2000), previously established between an overall economic efficiency measure and an associated technical efficiency measure. Following Farrell (1957), authors like Chambers et al. (1998) resorted to the same argument for deriving an allocative inefficiency term for the decomposition of the Nerlovian efficiency, after establishing an inequality between economic inefficiency and technical inefficiency (represented by the Directional Distance Function in this case): “Finally, allocative efficiency is defined as the gap in inequality (17), namely, AE…” (Chambers et al. 1998, pp. 360–361).
The same happens, for example, in the paper by Färe et al. (2002) on the Hyperbolic Graph Measure and its relationship with economic efficiency. The authors claimed: “Following the tradition of Farrell (1957) we may define allocative efficiency AE as a residual…” (Färe et al. 2002, p. 673).
Subsequent authors followed an identical argument for decomposing overall (in)efficiency into technical and allocative (in)efficiency, without questioning whether such decomposition was sensible or not. For example, a recent contribution by Petersen (2020), exploring the definition and decomposition of ‘virtual’ profit inefficiency, also emphasizes this interpretation: “A gap between the distance function and the Nerlovian measure of profit inefficiency is a reflection of allocative inefficiency.” (Petersen 2020, p. 720).
Our contribution to the economic efficiency measurement is twofold. Following the literature, many mathematical and economical properties have been well-established for technical efficiency indices and, even, economic efficiency indices. However, so far, no author has discussed the properties that the proper decomposition of an economic efficiency index into technical and allocative components should meet. In this regard, we discuss and introduce two properties that are essential for the correct interpretation of the terms of the decomposition. These essential properties endow the decomposition of economic efficiency with a meaningful allocative component. As a second contribution of our research, we provide a taxonomy of the efficiency measures concerning the satisfaction of these two relevant properties; in particular, the lack of interpretability when they are not satisfied.
In the next section, we present some preliminary notions and well-known results regarding the decomposition of cost, revenue, and profitability efficiency, as well as profit inefficiency, into their technical and allocative components, and considering different efficiency measures. Sections 3 and 4 introduce the definitions of the essential property and its extension. We also show, contrary to current belief, that few efficiency measures satisfy these requirements, which illustrates a lack of appropriate interpretability of the allocative component as actual price efficiency. Conclusions are drawn in Sect. 5.
2 Decompositions of Economic Efficiency: Preliminary Notions, Results, and Notation
In this section, we formalize some key notions about the technology and recall how cost efficiency, revenue efficiency, profitability efficiency, and profit inefficiency have been decomposed through different approaches in the literature. Our formalization is general, both in the definitions of the technology and the technical efficiency measures. Nevertheless, certain technical efficiency measures have been exclusively calculated (empirically determined) in the literature through the nonparametric Data Envelopment Analysis (DEA) technique: the Russell measures and the Weighted Additive Measures. This is the reason why, in these cases, we also show the optimization programs that allow determining the value of the measures under DEA.
Let \(x \in {\mathbb{R}}_{ + }^{M}\) denote a column vector of inputs and \(y \in {\mathbb{R}}_{ + }^{N}\) a column vector of outputs; the production possibility set (or technology) \(T\) is given by \(T = \left\{ {\left( {x,y} \right) \in {\mathbb{R}}_{ + }^{M + N} :\,x{\text{ can produce }}y} \right\}\). In this paper, we assume that \(T\) is a subset of \({\mathbb{R}}_{ + }^{M + N}\) that satisfies the following postulates:
-
(P1)
\(T\) is nonempty;
-
(P2)
\(T\left( x \right): = \left\{ {\left( {u,y} \right) \in T:\,u \le x} \right\}\) is bounded \(\forall x \in R_{ + }^{m}\);
-
(P3)
\(T\) is a closed set;
-
(P4)
\(\left( {x,y} \right) \in T,\,\left( {x, - y} \right) \le \left( {x^{\prime}, - y^{\prime}} \right)\,\, \Rightarrow \left( {x^{\prime},y^{\prime}} \right) \in T\), i.e., inputs and outputs are freely disposable;
-
(P5)
\(T\) is a convex set.
The notion of technical inefficiency is related to the distance from the evaluated firm to the frontier of the technology. In this regard, there are in the literature two main definitions of production frontiers used as benchmarks for technical efficiency measurement. We are referring to the weakly efficient frontier and a subset of it, called the strongly efficient frontier. The weakly efficient frontier is defined as \(\partial^{W} \left( T \right) = \left\{ {\left( {x,y} \right) \in T:\left( {u, - v} \right) < \left( {x, - y} \right) \Rightarrow \left( {u,v} \right) \notin T} \right\}\), while the strongly efficient frontier is \(\partial^{S} \left( T \right) = \left\{ {\left( {x,y} \right) \in T:\left( {u, - v} \right) \le \left( {x, - y} \right),\left( {u,v} \right) \ne \left( {x,y} \right) \Rightarrow \left( {u,v} \right) \notin T} \right\}\). Depending on the efficiency measure considered, one of these two notions comes into play when characterizing the reference frontier. Whether technical efficiency is measured against the weakly or strongly efficient subset of the production technology is relevant because this determines if the efficiency measure satisfies the indication property, i.e., complies with the notion of Pareto–Koopmans efficiency. By the definitions of the strongly and the weakly efficient frontiers, the strongly efficient frontier is a subset of the weakly efficient frontier. Complying with the indication property ensures that the efficiency measure identifies projection points that belong to the strongly efficient frontier. Therefore, if the property of indication is not satisfied, the corresponding efficiency model does not necessarily project the assessed unit onto the strongly efficient frontier. If we look at the classical literature, we find that Koopmans (1951, p. 60) provides a practical definition of technical efficiency based on Pareto optimality: A producer is technically efficient if, given its actual production process, an increase in any output requires a reduction in at least one other output or an increase in at least one input, and if a reduction in any input requires an increase in at least one other input or a reduction in at least one output. Consequently, an inefficient producer could produce the same outputs with less of at least one input or could use the same inputs to produce more of at least one output. For those efficiency measures projecting the firms under evaluation to the weakly efficiency frontier \(\partial^{W} \left( T \right)\), additional input reductions or outputs expansions (slacks) in the sense of Pareto–Koopmans may exist, and therefore, they do not comply with this accepted notion of efficiency. Our results show that there exists a trade-off between the indication property and the essential properties. Among the list of popular technical efficiency measures mentioned in this paper, those that satisfy the indication property (i.e., comply with the notion of Pareto–Koopmans efficiency) do not meet our new essential properties, and vice versa.
In empirical contexts, technical efficiency measures are calculated by approximating the technology from a set of observations. Among the nonparametric methodologies that could be used, DEA stands out as one of the most applied techniques. DEA approximates the production technology from observed, cross-sectional data, relying on the Activity Analysis approach (Koopmans 1951) and mathematical programming. Based on the principle of minimum extrapolation, DEA yields the smallest subset of the input–output space as an inner approximation containing all observations and satisfying certain technological assumptions: convexity and free disposability of inputs and outputs. DEA generates convex polyhedral technologies (i.e., intersections of finite numbers of half-spaces), consisting of piecewise linear combinations of the so-called \(j = 1,\ldots,J\) Decision Making Units—i.e., firms in an economic context, thereby allowing for multiple inputs, \(x_{j} = \left( {x_{j1} ,\ldots,x_{jM} } \right) \in {\mathbb{R}}_{ + }^{M}\), and outputs, \(y_{j} = \left( {y_{j1} ,\ldots,y_{jN} } \right) \in {\mathbb{R}}_{ + }^{N}\). The DEA approximation of the production technology \(T\), under Variable Returns to Scale (VRS), is given by (Banker et al. 1984):
where \(X\) is the matrix \(\left[ {\begin{array}{*{20}l} {x_{11} } \hfill & {x_{21} } \hfill & \ldots \hfill & {x_{J1} } \hfill \\ {x_{12} } \hfill & {x_{22} } \hfill & {} \hfill & {x_{J2} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & {} \hfill \\ {x_{1M} } \hfill & {x_{2M} } \hfill & \ldots \hfill & {x_{JM} } \hfill \\ \end{array} } \right]\), \(Y\) is the matrix \(\left[ {\begin{array}{*{20}l} {y_{11} } \hfill & {y_{21} } \hfill & \ldots \hfill & {y_{J1} } \hfill \\ {y_{12} } \hfill & {y_{22} } \hfill & {} \hfill & {y_{J2} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & {} \hfill \\ {y_{1N} } \hfill & {y_{2N} } \hfill & \ldots \hfill & {y_{JN} } \hfill \\ \end{array} } \right]\), \(1_{J} \in {\mathbb{R}}_{ + }^{J}\) is the vector with all components equal to one and \(0_{J} \in {\mathbb{R}}_{ + }^{J}\) is the vector with all components equal to zero.
Within the market, firms aim at attaining the best possible economic outcome. In general, it is assumed that firms intend to maximize profit, defined as revenue minus cost. It is possible, however, that the firm faces constraints on the output or input sides that prevent the maximization of profit by choosing what would be optimal output and input quantities. In these partial cases, firms’ optimizing behavior is represented by cost and revenue functions. These three complementary perspectives, viz. cost, revenue, and profit, are also complemented in practice with the possibility of reinterpreting the economic behavior of the firm in terms of the ratio of revenue to costs, rather than their difference, corresponding to the concept of profitability, also termed return-to-dollar. Next, we summarize the definitions of cost, revenue, profitability, and profit functions, following this order.
The cost function represents the minimum cost of producing a fixed amount of outputs given input prices \(w \in {\mathbb{R}}_{ + }^{M}\). The cost function, yielding optimal input demands, defines as (e.g., Färe and Primont 1995):
where \(a \cdot b\) denotes the inner product of vectors \(a\) and \(b\).
From an output perspective, the revenue function represents the maximum revenue of selling output quantities given (fixed) amounts of output prices \(p \in {\mathbb{R}}_{ + }^{N}\). The revenue function, yielding optimal output supplies, defines in the following terms (e.g., Färe and Primont 1995):
The profitability function represents the maximum revenue to cost given the technology and input and output prices. Following Zofío and Prieto (2006), the profitability function, yielding optimal input and output quantities, defines as:
Finally, the most representative measure of economic efficiency corresponds to the profit function, defined as maximum revenue minus cost, given the technology and input and output prices. The reason is that profit maximization is the commonly accepted operating goal for firms. The profit function, yielding optimal input demands and output supplies, corresponds to (e.g., Färe and Primont 1995):
As for the profit function, Briec and Lemaire (1999) showed that the functional support of the technology is the profit function, the dual variables being the shadow prices—just like the cost and revenue functions are the functional supports of the input and output production possibility sets, respectively.
Now, we present the most usual measures of technical efficiency and their dual relationships with the above economic functions (cost, revenue, profitability, or profit), as they were established in the literature. Throughout the paper, we consider that the cost, revenue, profit and profitability functions have a finite value. The connection between the technology and functional supports can be found, for example, in Briec and Lemaire (1999) and, in a more general way, in Briec (1997a). This part of the text is organized in subsections. The first two subsections are devoted to multiplicative efficiency measures, while the last four correspond to additive inefficiency measures. As convention, we reserve the term efficiency for multiplicative measures where a value of one reflects an efficient behavior, while we reserve inefficiency for additive measures where zero reflects an efficient behavior (the larger the score the greater the inefficiency).
2.1 The Input and Output-Oriented Radial Measures
Here, we summarize the classical approach to calculate and decompose cost and revenue efficiency based on Farrell’s tradition (Farrell 1957). At the time of publishing his seminal paper, Farrell did not seem to be aware of the work by Shephard (1953), where he formalized the duality between the cost function and the input distance function, constituting the theoretical base for the decomposition of economic efficiency. Instead, Farrell cites Debreu’s (1951) ‘coefficient of resource utilization’ as a source of inspiration. Nevertheless, Shephard never introduced the concept of overall economic efficiency, nor that of allocative efficiency, being one step short of proposing the corresponding decomposition explicitly. It is worth mentioning that, regarding the technical efficiency measure, the only difference between both approaches is that Farrell’s (radial) input-oriented measure is equivalent to the inverse of Shephard’s input distance function. Although Farrell only considered a single-output technology, his ideas were later extended in a suitable way in the literature for dealing with multiple output frameworks and for two orientations (i.e., input-oriented and output-oriented), giving rise to the radial technical efficiency measures (see Charnes et al. 1978; Banker et al. 1984).
We now show the optimization model that allows calculating the input-oriented radial measure for a specific firm, o, represented by the input–output vector \(\left( {x_{o} ,y_{o} } \right)\):
Let \(\theta_{o}^{*}\) be an optimal solution of model (Eq. 6). Then, the projection point associated with the Input-oriented Radial Measure (RI) is defined as \(\left( {\hat{x}_{o}^{RI} ,y_{o} } \right) = \left( {\theta_{o}^{*} x_{o} ,y_{o} } \right)\). Note that the projection point is unique. Also, \(TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right)\) may be interpreted as the efficiency score of firm o calculated with respect to the weakly efficient frontier since slacks may exist given the inequality restrictions in (Eq. 6). Consequently, this measure does not satisfy the indication property associated with the notion of Pareto–Koopmans efficiency. This means that this efficiency model does not necessarily project the units onto the strongly efficient frontier.
Following Farrell (1957), cost efficiency is defined multiplicatively as the ratio of minimum cost to observed cost: \(CE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = \frac{{C(y_{o} ,w)}}{{w \cdot x_{o} }} \le 1\). Subsequently, enabling the decomposition of cost efficiency, the following well-known inequality holds:
Finally, the allocative efficiency (AE) component is derived from (Eq. 7) by rendering it an equality, i.e., \(AE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = {{CE_{RI} \left( {x_{o} ,y_{o} ,w} \right)} \mathord{\left/ {\vphantom {{CE_{RI} \left( {x_{o} ,y_{o} ,w} \right)} {TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right)}}} \right. \kern-0pt} {TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right)}}\). This is the reason why this component is conceptualized as a ‘residual’. Allocative efficiency corresponds to the adjustment of the projected input vector to the minimum cost input combination; i.e., from \(\left( {\theta_{o}^{*} x_{o1} ,\ldots,\theta_{o}^{*} x_{oM} } \right)\) to the optimal input demands \(x^{*} \left( {y_{o} ,w} \right)\), where \(x^{*} \left( {y_{o} ,w} \right)\)\(=\)\(\arg \min \left\{ {w \cdot x:\left( {x,y_{o} } \right) \in T} \right\}\).
Example 1
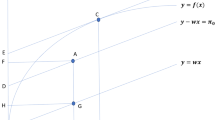
We illustrate the standard decomposition through Fig. 1 and a set of four firms (A, B, C and D) that consume two inputs to produce a common single output. Additionally, we consider that the minimum cost is achieved at point C and analyze the cost efficiency of unit A. Resorting to the standard equiproportional projection for solving technical efficiency (that is, the projection associated with a radial measure), this firm should reduce input quantities matching those used by B. Note that unit B is located onto the efficient frontier and, therefore, it is technically efficient. Afterward, the unit corrects for allocative efficiency by changing its input bundle from B to C, the production plan minimizing cost.
Illustration of the classical decomposition of economic efficiency (Farrell 1957)
From an output orientation, the radial output measure of technical efficiency can be determined by solving the following optimization program:
Let \(\phi_{o}^{*}\) be an optimal solution of model (Eq. 8). Then, the projection point associated with the Output-oriented Radial Measure (RO) is defined as \(\left( {x_{o} ,\hat{y}_{o}^{RO} } \right) = \left( {x_{o} ,\phi_{o}^{*} y_{o} } \right)\). Note that this efficient projection is unique for this type of model. Also, like its input-oriented counterpart (Eq. 6), this measure does not satisfy the indication property. This means that this efficiency model does not necessarily project the units onto the strongly efficient frontier. Additionally, revenue efficiency is usually defined as \(RE_{RO} \left( {x_{o} ,y_{o} ,p} \right) = \frac{{R\left( {x_{o} ,p} \right)}}{{p \cdot y_{o} }} \ge 1\), which is bounded by the technical efficiency score as follows (Färe and Primont 1995).
Again, following Farrell’s tradition, the residual allocative efficiency (AE) component is derived from (Eq. 9) as \(AE_{RO} \left( {x_{o} ,y_{o} ,p} \right) = {{RE_{RO} \left( {x_{o} ,y_{o} ,p} \right)} \mathord{\left/ {\vphantom {{RE_{RO} \left( {x_{o} ,y_{o} ,p} \right)} {TE_{RO}^{{}} \left( {x_{o} ,y_{o} } \right)}}} \right. \kern-0pt} {TE_{RO}^{{}} \left( {x_{o} ,y_{o} } \right)}}\).
2.2 The Hyperbolic Graph Measure
This subsection is concerned with the measurement of profitability, defined as the ratio of revenue to cost, and with the determination of profitability efficiency, comparing observed profitability to optimal profitability. From an economical perspective, the relationship between the Hyperbolic Graph Measure (Färe et al. 1985) and the profitability (or “return-to-dollar”) measure of economic performance was first suggested by Färe et al. (2002). Subsequently, Zofío and Prieto (2006) formalized it for the Generalized Distance Function (Chavas and Cox 1999), which encompasses the Hyperbolic Graph Measure as a particular case, showing that profitability efficiency can be decomposed multiplicatively into the usual technical and allocative terms.
The Hyperbolic Graph Measure for firm o is determined as the optimal value of the following optimization program, which projects the point \(\left( {x_{o} ,y_{o} } \right)\) onto the weakly efficient frontier:
Let \(\delta_{o}^{*}\) be an optimal solution of model (Eq. 10). Then, the projection point defined from the Hyperbolic (H) Graph Measure is \(\left( {\hat{x}_{o}^{H} ,\hat{y}_{o}^{H} } \right) = \left( {\delta_{o}^{*} x_{o} ,{{y_{o} } \mathord{\left/ {\vphantom {{y_{o} } {\delta_{o}^{*} }}} \right. \kern-0pt} {\delta_{o}^{*} }}} \right)\). Note that the efficient projection is unique for this measure. Additionally, the Hyperbolic Graph Measure does not meet indication. This means that this efficiency model does not necessarily project the units onto the strongly efficient frontier.
Zofío and Prieto (2006) show that the reference technology exhibits local constant returns to scale (CRS) at the profitability maximizing benchmark (Eq. 4). Accordingly, they established a relationship between profitability efficiency (\(\Gamma E\)) and the Hyperbolic measure calculated under CRS (i.e., assuming that \(T = \sigma T\), with \(\sigma \in {\mathbb{R}}_{ + + }^{{}}\)), denoted here as \(TE_{H}^{CRS} \left( {x_{o} ,y_{o} } \right) = \delta_{o}^{CRS*}\):
As usual, Zofío and Prieto (2006) determined allocative efficiency as a residual from the inequality in (11): \(AE_{H} \left( {x_{o} ,y_{o} ,w,p} \right) = {{\Gamma E_{H} \left( {x_{o} ,y_{o} ,w,p} \right)} \mathord{\left/ {\vphantom {{\Gamma E_{H} \left( {x_{o} ,y_{o} ,w,p} \right)} {\left( {\delta_{o}^{CRS*} } \right)^{2} }}} \right. \kern-0pt} {\left( {\delta_{o}^{CRS*} } \right)^{2} }}\).
2.3 The Directional Distance Function
As a measure of graph technical inefficiency, the Directional Distance Function (DDF) introduced by Chambers et al. (1998) also allows for simultaneous output expansions and input contractions through a single parameter.Footnote 1 Additionally, the DDF is related to a measure of profit inefficiency, named Nerlovian by these authors after Nerlove (1965), which is calculated as the normalized deviation between optimal and actual profit at market prices, as we show next. In particular, the DDF allows researchers to select the direction \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) \in R_{ + }^{M + N}\), with \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) \ne 0_{M + N}\), in which the firm \(\left( {x_{o} ,y_{o} } \right)\) is projected onto the frontier. The Directional Distance Function does not satisfy the indication property. This means that this efficiency model does not necessarily project the units onto the strongly efficient frontier. The associated optimization model to be solved is:
Let \(\beta_{o}^{*}\) be an optimal solution of model (Eq. 12). Then, the corresponding projection point is \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right) = \left( {x_{o} - \beta_{o}^{*} g_{o}^{ - } ,y_{o} + \beta_{o}^{*} g_{o}^{ + } } \right)\). Note that, given a directional vector \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right)\), the projection point is unique for the DDF.
Regarding the dual relationship between the DDF and a measure of profit inefficiency \(\Pi I_{DDF} \left( {x_{o} ,y_{o} ,w,p} \right)\), Chambers et al. (1998) prove that:
The numerator on the ratio above is easily recognized to be the difference between maximum attainable profit and the firm’s actual profit. In this sense, it measures profit loss due to inefficiencies. The lost profit is normalized by the factor \(w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + }\), which is related to market prices and the corresponding directional vector. The normalization resulting from duality theory has as desirable consequence that the profit inefficiency measure is units’ invariant; i.e., it is independent of the units of measurement in monetary values, since they cancel out in the numerator and denominator. The normalization of profit inefficiency prompts us to explicitly denote it by including \(\left( {\tilde{w},\tilde{p}} \right)\), since one can consider that the normalization factor is associated with prices: \(\left( {\tilde{w},\tilde{p}} \right) = \left( {w/\left( {w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + } } \right),p/\left( {w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + } } \right)} \right)\). Finally, allocative inefficiency is retrieved from (13) as an additive residual term:\(AI_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};g_{o}^{ - } ,g_{o}^{ + } } \right) = \Pi I_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};g_{o}^{ - } ,g_{o}^{ + } } \right) - TI_{DDF}^{{}} \left( {x_{o} ,y_{o} ,g_{o}^{ - } ,g_{o}^{ + } } \right)\).
2.4 The Hölder Distance Function
The Hölder distance function was first introduced to relate the notions of technical efficiency and metric distances. Briec (1999) defined the Hölder distance function for firm \(\left( {x_{o} ,y_{o} } \right)\) as follows:
where \(s_{o}^{ - } = \left( {s_{o1}^{ - } ,\ldots,s_{oM}^{ - } } \right)\) and \(s_{o}^{ + } = \left( {s_{o1}^{ + } ,\ldots,s_{oN}^{ + } } \right)\) are vectors of input and output slacks, respectively.
The Hölder norms \(\ell_{h}\) \(\left( {h \in \left[ {1,\infty } \right]} \right)\) are defined over a k-dimensional real normed space as
where \(z = \left( {z_{1} ,\ldots,z_{k} } \right) \in {\mathbb{R}}_{{}}^{k}\). From a computational perspective, the different Hölder distance functions associated with alternative norms are related to nonlinear optimization programs, which, in general, are not easily solved (see, for example, Aparicio et al. 2007, or, more recently, Aparicio et al. 2020). However, in two specific cases, it is possible to calculate these measures of technical inefficiency through one or several linear programming models. We are referring to the cases \(h = 1\) and \(h = \infty\), where the topological balls associated with these norms define polyhedral sets. In particular, \(TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;1} \right)\) can be related to the DDF and calculated as the minimum of the values \(TI_{DDF} \left( {x_{o} ,y_{o} ;\left( {0,\ldots,1_{{\left( {m^{\prime}} \right)}} ,...0} \right),0_{N} } \right),\;m^{\prime} = 1,\ldots,M,\) and the values \(TI_{DDF} \left( {x_{o} ,y_{o} ;0_{M} ,\left( {0,\ldots,1_{{\left( {n^{\prime}} \right)}} ,...0} \right)} \right),\;n^{\prime} = 1,\ldots,N.\) In the case of \(h = \infty ,\) \(TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;\infty } \right)\) \(=\)\(TI_{DDF} \left( {x_{o} ,y_{o} ;1_{M} ,1_{N} } \right)\) (see Briec 1999).
Regarding the efficient projection generated from an optimal solution \(\left( {s_{o}^{ - *} ,s_{o}^{ + *} } \right)\) of (Eq. 14), it is defined as \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right) = \left( {x_{o} - s_{o}^{ - *} ,y_{o} + s_{o}^{ + *} } \right)\). In the case of the Hölder Distance Function, in contrast to the previous measures, the projection point could not be unique. Additionally, this measure does not meet the indication property. This means that this efficiency model does not necessarily project the units onto the strongly efficient frontier.
Regarding profit inefficiency measurement, Briec and Lesourd (1999) proved that the following dual relationship holds:
where \(q\) is such as \(\frac{1}{h} + \frac{1}{q} = 1\).
By (Eq. 15), (normalized) profit inefficiency may be measured and decomposed additively into technical inefficiency and allocative inefficiency by recovering allocative inefficiency as a residual: \(AI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right) =\)\(\Pi I_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right) - TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;h} \right)\).
2.5 The Russell Measures
As previously mentioned, the measurement of technical efficiency using frontiers began with the work by Debreu (1951), Shephard (1953), and Farrell (1957). Subsequently, some of the limitations of the Farrell approach such as its lack of flexibility when adjusting inputs and outputs, resulting in the failure to satisfy the indication property, prompted further progress in this area. One of these research lines consisted in generalizing Farrell's approach to consider non-equiproportional reductions in inputs or increases in outputs; that is, resulting in the development of non-radial efficiency measures. This generalization was originally due to Färe and Lovell (1978), who proposed an axiomatic approach to the problem, suggesting that an ideal measure of efficiency should satisfy certain desirable properties. According to these ideas, they defined what they termed Russell Measure of input efficiency. Later, Färe et al. (1985) proposed an extension of the input-oriented Russell Measure to the output-oriented case, working with multiple outputs. Furthermore, Färe et al. (1985) defined a non-oriented Russell measure of technical efficiency: the so-called Russell Graph Measure. This measure extended the two oriented versions in the sense that it simultaneously considered inefficiency (radial and non-radial) in both inputs and outputs. However, its empirical application was hampered by its nonlinearity. To overcome this drawback, Pastor et al. (1999) developed a new measure, which they named Enhanced Russell Graph Measure, which has the advantage of being linear—this measure was later reintroduced by Tone (2001) as the Slacks-Based Measure. Next, we briefly present all these measures and their dual relationships with the cost, revenue, and profit functions, as established in the literature.
2.5.1 The Russell Graph Measure
Inspired by the work of Russell and Schworm (2018), we define the Russell Graph Measure of technical efficiency for the firm \(\left( {x_{o} ,y_{o} } \right)\) in a general way as follows:
where \(a \odot b\) denotes the componentwise vector product, also called Hadamard product.
Following Färe et al. (1985), under Data Envelopment Analysis, the value of the Russell Graph Measure of technical efficiency can be determined through the next nonlinear optimization program:
Recently, Halická and Trnovská (2018) have introduced a method to solve in an exact way the Russell Graph Measure in Data Envelopment Analysis. In particular, they reformulate the original nonlinear model (Eq. 17) as a semidefinite programming (SDP) model, while describing how to derive the corresponding dual program. On the one hand, the SDP reformulation of the Russell Graph Measure can be solved efficiently using standard SDP solvers. On the other hand, the dual program allows establishing, for the first time, the following relationship between profit inefficiency and the Russell Graph Measure.
Halická and Trnovská (2018) closed the inequality in (Eq. 18) including a term that was interpreted as allocative inefficiency: \(AI_{RGM} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) =\) \(\Pi I_{RGM} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) - \left[ {1 - TE_{RGM} \left( {x_{o} ,y_{o} } \right)} \right]\).
Finally, given an optimal solution \(\left( {\theta_{o}^{*} ,\phi_{o}^{*} } \right)\) of model (Eq. 16), then the corresponding projection point is defined as \(\left( {\hat{x}_{o}^{RGM} ,\hat{y}_{o}^{RGM} } \right) = \left( {\theta_{o}^{*} \odot x_{o} ,\phi_{o}^{*} \odot y_{o} } \right)\). Note that the Russell Graph Measure can yield different projection points for the same firm. Also, a relevant feature is that this measure projects observations to the strongly efficient frontier, satisfying the indication property. This means that this efficiency model always projects the units onto the strongly efficient frontier.
2.5.2 The Input- and Output-Oriented Russell Measures
In this subsection, we turn our attention to the input-oriented version of the Russell Measure of technical efficiency. The results associated with the output-oriented version will be also shown by analogy.
The Russell Measure of input efficiency can be defined in a general way through the following optimization program:
Additionally, under DEA, the Russell Measure of input efficiency can be determined by the next linear program:
Given an optimal solution \(\theta_{o}^{*}\) of model (Eq. 19), then the corresponding projection defines as \(\left( {\hat{x}_{o}^{RMI} ,y_{o}^{{}} } \right) = \left( {\theta_{o}^{*} \odot x_{o} ,y_{o} } \right)\). The Russell Measure of input efficiency can produce alternative projection points. Furthermore, it does not satisfy the indication property in the full input–output space, but it does meet the indication property in the reduced level set \(T\left( {y_{o} } \right) = \left\{ {x \in {\mathbb{R}}_{ + }^{M} :\left( {x,y_{o} } \right) \in T} \right\}\). This means that this efficiency model always projects the units onto the strongly efficient frontier of \(T\left( {y_{o} } \right)\). Additionally, Aparicio et al. (2015a) showed, under DEA, that a normalized measure of cost inefficiency can be lower bounded by the score associated with the Russell measure of input efficiency:
As usual, allocative inefficiency is defined residually as \(AI_{RMI} \left( {x_{o} ,y_{o} ,\tilde{w}} \right) =\) \(CI_{RMI} \left( {x_{o} ,y_{o} ,\tilde{w}} \right) - \left[ {1 - TE_{RMI} \left( {x_{o} ,y_{o} } \right)} \right]\).
Alternatively, relying on the Russell Measure of output efficiency, counterpart to (Eq. 20) and denoted as \(TE_{RMO} \left( {x_{o} ,y_{o} } \right)\), we attain the following relationship:
and allocative inefficiency is then residually recovered as \(AI_{RMO} \left( {x_{o} ,y_{o} ,\tilde{p}} \right) =\) \(RI_{RMO} \left( {x_{o} ,y_{o} ,\tilde{p}} \right) - \left[ {1 - TE_{RMO} \left( {x_{o} ,y_{o} } \right)} \right]\). Finally, the corresponding projection point for the Russell measure of output efficiency would be defined as \(\left( {x_{o}^{{}} ,\hat{y}_{o}^{RMO} } \right) = \left( {x_{o} ,\phi_{o}^{*} \odot y_{o} } \right)\) and may not be unique. Regarding \(TE_{RMO} \left( {x_{o} ,y_{o} } \right)\), this measure satisfies indication in the reduced level set \(T\left( {x_{o} } \right) = \left\{ {y \in {\mathbb{R}}_{ + }^{N} :\left( {x_{o} ,y} \right) \in T} \right\}\). This means that this efficiency model always projects the units onto the strongly efficient frontier of \(T\left( {x_{o} } \right)\).
2.5.3 The Enhanced Russell Graph Measure or Slacks-Based Measure
The Enhanced Russell Graph Measure (Pastor et al. 1999) is equivalent to the Slacks-Based Measure proposed by Tone (2001) and can be defined, in a general way, as follows (see Russell and Schworm 2018):
Under DEA, this measure can be computed through the following model, which may be easily linearized (Pastor et al. 1999):
Given an optimal solution \(\left( {\theta_{o}^{*} ,\phi_{o}^{*} } \right)\) of model (Eq. 23), the corresponding projection point may be defined as \(\left( {\hat{x}_{o}^{ERG} ,\hat{y}_{o}^{ERG} } \right) = \left( {\theta_{o}^{*} \odot x_{o} ,\phi_{o}^{*} \odot y_{o} } \right)\). For the firm under evaluation, the Enhanced Russell Graph Measure may yield different projection points. Additionally, this measure satisfies the property of indication. This means that this efficiency model always projects the units onto the strongly efficient frontier. Moreover, Aparicio et al. (2017a), under DEA, proved that the following inequality holds:
Applying the definition of the allocative inefficiency term as a residual, these authors derived this component from (Eq. 25) as \(AI_{ERG} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) = \Pi I_{ERG} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) - \left[ {1 - TE_{ERG} \left( {x_{o} ,y_{o} } \right)} \right]\).
2.6 The Weighted Additive Measures
After the introduction in the literature of the radial measures, other approaches for measuring the distance from a unit to the production frontier were defined, with the aim of solving certain drawbacks of the radial ones. In particular, radial measures do not satisfy the indication property, meaning that inefficiencies in the form of individual (non-radial) slacks obtained in the optimization models (Eq. 6) and (Eq. 8) are neglected. In this context, the additive model by Charnes et al. (1985) was the first graph ‘linear’ model that guaranteed that firms were compared exclusively with respect to the set of Pareto–Koopmans efficient benchmarks in the input–output space—i.e., the strongly efficient frontier \(\partial^{S} \left( T \right)\). Building upon Charnes et al. (1985), other researchers have introduced several modifications to the original additive model, weighting the slacks that appear in the objective function to make the measure independent of the units of measurement (see, for example, Lovell and Pastor 1995; Cooper et al. 1999).
In the case of the Weighted Additive Measures, following Russell and Schworm (2018), the optimization model to be solved would be as follows:
The vectors \(\rho^{ - } = \left( {\rho_{1}^{ - } ,\ldots,\rho_{M}^{ - } } \right) \in {\mathbb{R}}_{ + + }^{M}\) and \(\rho^{ + } = \left( {\rho_{1}^{ + } ,\ldots,\rho_{N}^{ + } } \right) \in {\mathbb{R}}_{ + + }^{N}\) contain, respectively, input and output weights representing the relative importance of unit inputs and unit outputs from a technical perspective.
In the case of resorting to the DEA technique, to estimate technical inefficiency for firm \(\left( {x_{o} ,y_{o} } \right),\) a possibility is to solve the following linear program (see Lovell and Pastor 1995):
If \(\left( {s_{o}^{ - *} ,s_{o}^{ + *} } \right)\) is an optimal solution of (Eq. 26), then the corresponding projection point is defined as \(\left( {\hat{x}_{o}^{WA} ,\hat{y}_{o}^{WA} } \right) = \left( {x_{o} - s_{o}^{ - *} ,y_{o} + s_{o}^{ + *} } \right)\). In the case of the Weighted Additive Measures, the projection point could be not unique. Also, this measure satisfies the property of indication. This means that this efficiency model always projects the units onto the strongly efficient frontier.
Within the Data Envelopment Analysis context, Cooper et al. (2011) proved the following dual relationship between a normalized measure of profit inefficiency and the value of the Weighted Additive Measure:
In this way, the allocative term is defined as \(AI_{WA} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};\rho^{ - } ,\rho^{ + } } \right) = \Pi I_{WA} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};\rho^{ - } ,\rho^{ + } } \right) - TI_{WA} \left( {x_{o} ,y_{o} ;\rho^{ - } ,\rho^{ + } } \right)\).
3 An Essential Property of Allocative Efficiency for Decomposing Economic Efficiency
In this section, we introduce the definition of a pair of properties related to the decomposition of economic efficiency that ensure its consistency and coherence. Invoking these properties, we show, in contrast to what has been commonly assumed until now, that the allocative component derived as a residual term in the previously published economic decompositions cannot be always correctly interpreted as actual price inefficiency, depending on the technical efficiency measure selected for decomposing overall efficiency.
The literature on efficiency measurement is plenty of contributions devoted to introducing and discussing the set of properties that a technical efficiency measure should satisfy from a technological perspective (see, for example, Färe and Lovell 1978; Pastor et al. 1999; Russell and Schworm 2018). Although it might seem otherwise, complying with these properties is also critical to the analysis of economic efficiency. To the extent that allocative efficiency is calculated as a residual, as we pointed out in the foregoing section, the measurement of technical efficiency is key to the decomposition of overall efficiency. In this regard, over the years a consensus has emerged in the literature about the properties or tests that technical efficiency measures should pass from an axiomatic perspective. Some of the most relevant properties that are identified in the literature as natural requirements for an efficiency measure are: indication, monotonicity, homogeneity, translation invariance, and units’ invariance (or commensurability). As they are well-known, we do not discuss them here, but refer to them when necessary, as we have already done with the indication property.
Regarding the desirable properties that an economic efficiency measure should satisfy, various researchers have explicitly or implicitly adopted some of them in the existing literature. Here, we summarize several of such desirable properties in relation to profit inefficiency, e.g., Kuosmanen et al. (2010) and Cooper et al. (2011), although equivalent counterparts can be stated for the cost and revenue-based efficiency measures. These properties are: indication, homogeneity of degree zero in prices and quantities, non-negativity and units’ invariance. Again, relevant to our analysis is the desired property of units’ invariance, which is satisfied by the additive economic inefficiency models as a result of the normalization process that duality theory requires for the determination of the specific Fenchel–Mahler inequalities that allow their decomposition. Multiplicative measures satisfy this property in a natural way thanks to their definition as ratios, which cancel out monetary units.
Therefore, the extant literature has clearly established the properties that technical and economic efficiency measures must satisfy. However, so far, no one has reflected on the properties that the decomposition of the economic efficiency index into technical and allocative components should meet. As previously argued, the main reason for this omission seems to be the residual nature of the allocative component. An exception is Aparicio et al. (2015b), who introduced the property that allocative efficiency should be independent of the output (input) level that is considered as reference when measuring technical inefficiency in the input (output) oriented approach. Färe et al. (2019, p. 189) named this new attribute the invariance property of allocative efficiency measure.
Next, we introduce a novel property that is essential for the correct interpretation of the efficiency terms of the decomposition, both technical and allocative. We start with the input-oriented version, which is later extended to the output-oriented case and to the graph (or non-oriented) scenario. Before introducing the definition of the essential property for the decomposition of economic efficiency, we recall the multiplicative or additive classification of the efficiency measures and their decompositions, depending on whether the measurement of the distance between the firm under evaluation, represented by \(\left( {x_{o} ,y_{o} } \right)\), and a reference benchmark on the efficient frontier, \(\left( {\hat{x}_{o} ,\hat{y}_{o} } \right)\), entails projecting the former multiplicatively by a factor expanding outputs and/or reducing inputs, or rather the addition of output quantities and/or subtraction of input quantities. Next, we introduce the formal definition of the new property.
Definition 1
(Essential property, input-oriented version). If \(\hat{x}_{o}\) is such that \(w \cdot \hat{x}_{o} = C\left( {y_{o} ,w} \right)\), then \(AE\left( {x_{o} ,y_{o} ,w} \right) = 1\) for multiplicative approaches and \(AI\left( {x_{o} ,y_{o} ,\tilde{w}} \right) = 0\) for additive approaches.
Consequently, under the multiplicative approach, if the measure used to gauge technical efficiency directly projects the assessed unit onto a benchmark that minimizes cost, there should be no room for allocative efficiency. This means that the term \(AE\left( {x_{o} ,y_{o} ,w} \right)\) must be equal to one. In parallel, when the additive approach is adopted, if the technical inefficiency measure determines a benchmark that minimizes cost, then allocative inefficiency \(AI\left( {x_{o} ,y_{o} ,\tilde{w}} \right)\) should be nil. This definition is illustrated in Fig. 2 under the multiplicative approach associated with the Input-oriented Radial Measure. When evaluating the economic inefficiency of firm D, technical efficiency is first determined by an equiproportional reduction in its inputs until the frontier is reached at benchmark C. Secondly, allocative efficiency is represented by the gap between the projected benchmark, i.e., unit C, and the firm minimizing cost. However, in this example, firm C has been chosen, so it is the cost-efficient benchmark. So, clearly, the gap must be zero and, consequently, the allocative efficiency component in the corresponding ‘multiplicative’ decomposition of cost efficiency must be one.
Once we have introduced the input-oriented version of the essential property, let us next introduce the output-oriented version and their graph (or non-oriented) variants—in this last case for profitability efficiency and profit efficiency.
Definition 2
(Essential property, output-oriented version). If \(\hat{y}_{o}\) is such that \(p \cdot \hat{y}_{o} = R\left( {x_{o} ,p} \right)\), then \(AE\left( {x_{o} ,y_{o} ,p} \right) = 1\) for multiplicative approaches and \(AI\left( {x_{o} ,y_{o} ,\tilde{p}} \right) = 0\) for additive approaches.
Definition 3
(Essential property, graph versions). (a) If \(\left( {\hat{x}_{o} ,\hat{y}_{o} } \right)\) is such that \(p \cdot \hat{y}_{o} /w \cdot \hat{x}_{o} = \Gamma \left( {w,p} \right),\) then \(AE\left( {x_{o} ,y_{o} ,w,p} \right) = 1\), and (b) if \(\left( {\hat{x}_{o} ,\hat{y}_{o} } \right)\) is such that \(p \cdot \hat{y}_{o} - w \cdot \hat{x}_{o} = \Pi \left( {w,p} \right)\), then \(AI\left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) = 0\).
In words, in the graph case, if researchers choose a multiplicative approach such as the Hyperbolic Graph Measure, then, if the measure projects the assessed firm onto a benchmark that maximizes profitability, there should be no room for allocative efficiency. This means that the term \(AE\left( {x,y,w,p} \right)\) should be necessarily one. Additionally, when the additive approach is applied, if the technical efficiency measure determines a benchmark firm that maximizes profit, then allocative inefficiency \(AI\left( {x,y,\tilde{w},\tilde{p}} \right)\) should be nil.
Next, we are going to prove that the essential property is satisfied by the Input- and Output-oriented Radial Measures concerning the cost and revenue functions, respectively, as well as by the Hyperbolic Graph Measure and the Directional Distance Function regarding the profitability function and the profit function, respectively.
Proposition 1
The following statements hold.
-
(i)
The Input-oriented Radial Measure satisfies Definition 1.
-
(ii)
The Output-oriented Radial Measure satisfies Definition 2.
-
(iii)
The Hyperbolic Graph Measure satisfies Definition 3(a).
-
(iv)
The Directional Distance Function satisfies Definition 3(b).
Proof
(i) The proof of the satisfaction of this property can be seen through the expression: \(AE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = {{CE_{RI} \left( {x_{o} ,y_{o} ,w} \right)} \mathord{\left/ {\vphantom {{CE_{RI} \left( {x_{o} ,y_{o} ,w} \right)} {TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right)}}} \right. \kern-0pt} {TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right)}} = \frac{{C\left( {y_{o} ,w} \right)}}{{TE_{RI}^{{}} \left( {x_{o} ,y_{o} } \right) \cdot \left( {w \cdot x_{o} } \right)}} = \frac{{C\left( {y_{o} ,w} \right)}}{{w \cdot \left( {\theta_{o}^{*} x_{o} } \right)}}\)\(= \frac{{C\left( {y_{o} ,w} \right)}}{{w \cdot \hat{x}_{o}^{RI} }}\). Then, if \(\hat{x}_{o}^{RI}\) is such that \(w \cdot \hat{x}_{o}^{RI} = C\left( {y_{o} ,w} \right)\), we immediately obtain that \(AE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = 1\). (ii) This statement can be proved following the same steps as in (i). (iii) Manipulating the expression \(AE_{H} \left( {x_{o} ,y_{o} ,w,p} \right) = {{\Gamma E_{H} \left( {x_{o} ,y_{o} ,w,p} \right)} \mathord{\left/ {\vphantom {{\Gamma E_{H} \left( {x_{o} ,y_{o} ,w,p} \right)} {\left( {\delta_{o}^{CRS*} } \right)^{2} }}} \right. \kern-0pt} {\left( {\delta_{o}^{CRS*} } \right)^{2} }}\), we equivalently obtain \(AE_{H} \left( {x_{o} ,y_{o} ,w,p} \right) = \frac{{p \cdot \left( {\frac{1}{{\delta_{o}^{CRS*} }}y_{o} } \right)/w \cdot \left( {\delta_{o}^{CRS*} x_{o} } \right)}}{{\Gamma \left( {w,p} \right)}} = \frac{{p \cdot \hat{y}_{o}^{H} /w \cdot \hat{x}_{o}^{H} }}{{\Gamma \left( {w,p} \right)}}\). Consequently, if \(\left( {\hat{x}_{o}^{H} ,\hat{y}_{o}^{H} } \right)\) is such that \(p \cdot \hat{y}_{o}^{H} /w \cdot \hat{x}_{o}^{H} = \Gamma \left( {w,p} \right)\), then \(AE_{H} \left( {x_{o} ,y_{o} ,w,p} \right) = 1\), which represents what we wanted to prove. (iv) Extending equation (6) in Aparicio et al. (2015b, p. 886), dealing with cost inefficiency, to profit inefficiency, we have that \(AI_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right)\)—which is by definition equal to \(\Pi I_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) -\)\(TI_{DDF}^{{}} \left( {x_{o} ,y_{o} ,g_{o}^{ - } ,g_{o}^{ + } } \right)\), can be equivalently expressed as \(\frac{{\Pi \left( {w,p} \right) - \left( {p \cdot \left( {y_{o} + \beta_{o}^{*} g_{o}^{ + } } \right) - w \cdot \left( {x_{o} - \beta_{o}^{*} g_{o}^{ - } } \right)} \right)}}{{w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + } }}\) = \(\frac{{\Pi \left( {w,p} \right) - \left( {p \cdot \hat{y}_{o}^{DDF} - w \cdot \hat{x}_{o}^{DDF} } \right)}}{{w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + } }}\). By Definition 3(b), if \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right)\) is such that \(p \cdot \hat{y}_{o}^{DDF} - w \cdot \hat{x}_{o}^{DDF} = \Pi \left( {w,p} \right)\), then \(AI_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) = 0\), thereby finishing the proof. ■
In particular, Proposition 1(i) means that the popular Input-oriented Radial Measure satisfies the essential property associated with the decomposition of cost efficiency, which allows a correct interpretation of the two terms in the decomposition: technical efficiency and allocative efficiency. Consequently, although Farrell (1957) and subsequent researchers on economic efficiency neglected the satisfaction of the so-called essential property, his definition and decomposition of cost efficiency do satisfy this necessary condition, implying the internal consistency of the decomposition. This shows that the residual allocative efficiency term rightly indicates that there cannot be any cost excess attributed to this source of inefficiency if the projected cost at the technically efficient benchmark coincides with minimum cost. Probably, Farrell did not focus his attention on this issue because the satisfaction of the property is relatively trivial in the case of radial projections measuring technical efficiency, given the multiplicative definition of allocative efficiency as the ratio of minimum cost to projected cost. However, this is not true for most of the measures introduced in the previous section, as we show next. Regarding the Output-oriented Radial Measure (ii), the Hyperbolic Graph Measure (iii), and the Directional Distance Function (iv), the property also holds.
3.1 The Essential Property in the Case of Multiple Optimal Projections
So far, we have been assuming that the projection point that is generated by the measure of technical efficiency or inefficiency is unique. However, this is not true for some of the traditional measures shown in Sect. 2, mainly those based upon slacks. In this regard, the essential property needs to be qualified to allow for this general case, which considers the existence of alternative solutions. In this way, let \(\hat{B}_{o}\) be the set of all benchmark projections yielded by the (in)efficiency model for the assessed firm \(\left( {x_{o} ,y_{o} } \right)\). Then, Definitions 1, 2 and 3 may be adapted as follows.
Definition 4
(Essential property, input-oriented version, multiple projection points). If \(\exists \hat{x}_{o} \in \hat{B}_{o}\) such that \(w \cdot \hat{x}_{o} = C\left( {y_{o} ,w} \right)\), then \(AE\left( {x_{o} ,y_{o} ,w} \right) = 1\) for multiplicative approaches and \(AI\left( {x_{o} ,y_{o} ,\tilde{w}} \right) = 0\) for additive approaches.
Definition 5
(Essential property, output-oriented version, multiple projection points). If \(\exists \hat{y}_{o} \in \hat{B}_{o}\) such that \(p \cdot \hat{y}_{o} = R\left( {x_{o} ,p} \right)\), then \(AE\left( {x_{o} ,y_{o} ,p} \right) = 1\) for multiplicative approaches and \(AI\left( {x_{o} ,y_{o} ,\tilde{p}} \right) = 0\) for additive approaches.
Definition 6
(Essential property, graph versions, multiple projection points). (a) If \(\exists \left( {\hat{x}_{o} ,\hat{y}_{o} } \right) \in \hat{B}_{o}\) such that \(p \cdot \hat{y}_{o} /w \cdot \hat{x}_{o} = \Gamma \left( {w,p} \right)\), then \(AE\left( {x_{o} ,y_{o} ,w,p} \right) = 1\), and (b) if \(\exists \left( {\hat{x}_{o} ,\hat{y}_{o} } \right) \in \hat{B}_{o}\) such that \(p \cdot \hat{y}_{o} - w \cdot \hat{x}_{o} = \Pi \left( {w,p} \right)\), then \(AI\left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) = 0\).
The above definitions state that if there is at least a projection point where optimality is achieved from an economical perspective, then the allocative inefficiency term should take value one in the multiplicative approach, and zero in the additive approach.
Regarding these new adaptations of the essential property, the Hölder Distance Function satisfies Definition 6(b), as we next prove.
Proposition 2
The Hölder Distance Function satisfies Definition 6(b).
Proof
We must prove that if \(\exists \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\) such that \(p \cdot \hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} - w \cdot \hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} = \Pi \left( {w,p} \right)\), then \(AI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right) = 0\), which is equivalent to prove that if \(\exists \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\) such that \(p \cdot \hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} - w \cdot \hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} = \Pi \left( {w,p} \right)\), then \(\Pi I_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}}\left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right) = TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;h} \right)\). First of all, note that \(\Pi I_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right)\) coincides with the distance from firm \(\left( {x_{o} ,y_{o} } \right)\) to the hyperplane \(H = \left\{ {\left( {x,y} \right) \in {\mathbb{R}}_{{}}^{M + N} :p \cdot y - w \cdot x = \Pi \left( {w,p} \right)} \right\}\) when the norm \(\left\| {\,.\,} \right\|_{h}\) is used (see Mangasarian 1999). Notice that, by hypothesis, \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right) \in H\). Additionally, \(\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\,} \right\|_{h}\) = \(TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;h} \right).\) Next, we are going to prove that \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}}} \right) \in\)\(\arg \min \left\{ {\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {x,y} \right)\,} \right\|_{h} :\left( {x,y} \right) \in H} \right\}\) and, consequently, \(\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\,} \right\|_{h}\) = \(\Pi I_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right)\) and \(\Pi I_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};h} \right)\) = \(TI_{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} \left( {x_{o} ,y_{o} ;h} \right)\), as we seek. Let us assume that \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right) \notin \arg \min \left\{ {\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {x,y} \right)\,} \right\|_{h} :\left( {x,y} \right) \in H} \right\}\) and we will arrive to a contradiction. Let \(P^{*}\) be the set of points \(\left( {x^{*} ,y^{*} } \right) \in H\) such that \(\left( {x^{*} ,y^{*} } \right) \in \arg \min \left\{ {\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {x,y} \right)\,} \right\|_{h} :\left( {x,y} \right) \in H} \right\}.\) Then, it is possible to prove that \(\left( {x^{*} ,y^{*} } \right) \in D\left( {x_{o} ,y_{o} } \right)\), with \(D\left( {x_{o} ,y_{o} } \right) = \left\{ {\left( {u,v} \right) \in {\mathbb{R}}_{{}}^{M + N} :\left( {u, - v} \right) \le \left( {x_{o} , - y_{o} } \right)} \right\}\). To see that, we invoke Theorem 2.1 in Mangasarian (1999), which states that the points \(\left( {x^{*} ,y^{*} } \right)\) have the following format: \(x^{*} = x_{0} - \frac{{\left( {p \cdot y_{o} - w \cdot x_{o} } \right) - \Pi \left( {w,p} \right)}}{{\left\| {\left( {w,p} \right)} \right\|_{q} }}z^{*}\) and \(y^{*} = y_{0} - \frac{{\left( {p \cdot y_{o} - w \cdot x_{o} } \right) - \Pi \left( {w,p} \right)}}{{\left\| {\left( {w,p} \right)} \right\|_{q} }}t^{*}\), where \(\left( {z^{*} ,t^{*} } \right) \in \arg \mathop {\max }\limits_{{}} \left\{ {p \cdot t - w \cdot z:\left\| {\left( {z,t} \right)} \right\|_{h} = 1} \right\}\). Notice that \(z^{*} \le 0_{M}\) and \(t^{*} \ge 0_{N}\). Let us suppose that \(\exists m^{\prime} = 1,\ldots,M\) such that \(z_{{m^{\prime}}}^{*} > 0\). Then, the vector \(\left( {z_{1}^{*} ,\ldots,z_{{m^{\prime} - 1}}^{*} , - z_{{m^{\prime}}}^{*} ,z_{{m^{\prime} + 1}}^{*} ,\ldots,z_{M}^{*} ,t^{*} } \right)\) satisfies \(\left\| {\left( {z_{1}^{*} ,\ldots,z_{{m^{\prime} - 1}}^{*} , - z_{{m^{\prime}}}^{*} ,z_{{m^{\prime} + 1}}^{*} ,\ldots,z_{M}^{*} ,t^{*} } \right)} \right\|_{h} = 1\) and \(p \cdot t^{*} - \sum\limits_{{m \ne m^{\prime}}}^{M} {w_{m} z_{m}^{*} } + w_{{m^{\prime}}} z_{{m^{\prime}}}^{*} > p \cdot t^{*} - \sum\limits_{{m \ne m^{\prime}}}^{M} {w_{m} z_{m}^{*} }\), which is a contradiction with the fact that \(\left( {z^{*} ,t^{*} } \right) \in \arg \mathop {\max }\limits_{{}} \left\{ {p \cdot t - w \cdot z:\left\| {\left( {z,t} \right)} \right\|_{h} = 1} \right\}\). Analogously, we can prove the same regarding the sign of \(t^{*}\). Consequently, \(\frac{{\left( {p \cdot y_{o} - w \cdot x_{o} } \right) - \Pi \left( {w,p} \right)}}{{\left\| {\left( {w,p} \right)} \right\|_{q} }}z^{*} \ge 0_{M}\) and \(\frac{{\left( {p \cdot y_{o} - w \cdot x_{o} } \right) - \Pi \left( {w,p} \right)}}{{\left\| {\left( {w,p} \right)} \right\|_{q} }}t^{*} \le 0_{N}\) since \(p \cdot y_{o} - w \cdot x_{o} \le \Pi \left( {w,p} \right)\) by the definition of the profit function. This implies that \(\left( {x^{*} , - y^{*} } \right) \le \left( {x_{o} , - y_{o} } \right)\), i.e., \(\left( {x^{*} ,y^{*} } \right) \in D\left( {x_{o} ,y_{o} } \right)\). Now, if, as we assumed, \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right) \notin P^{*}\), then \(\exists \left( {x^{\prime},y^{\prime}} \right) \in P^{*}\) such that \(\delta : = \left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {x^{\prime},y^{\prime}} \right)\,} \right\|_{h} < \left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\,} \right\|_{h}\). As Briec (1999, Lemma 1) proved, the intersection between the ball centered at \(\left( {x_{o} ,y_{o} } \right)\) with radius \(\left\| {\,\left( {x_{o} ,y_{o} } \right) - \left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\,} \right\|_{h} = \mathop {\inf }\limits_{u,v} \left\{ {\left\| {\left( {x_{o} ,y_{o} } \right) - \left( {u,v} \right)} \right\|_{h} :\left( {u,v} \right) \in \partial^{W} \left( T \right)} \right\}\) and the set \(D\left( {x_{o} ,y_{o} } \right)\) is a subset of \(T\). Then, the intersection between the ball centered at \(\left( {x_{o} ,y_{o} } \right)\) with radius \(\delta\) and the set \(D\left( {x_{o} ,y_{o} } \right)\) is a subset of the previous intersection of sets. Therefore, \(\left( {x^{\prime},y^{\prime}} \right) \in T\). Finally, we have two scenarios to be studied. (i) If \(\left( {x^{\prime},y^{\prime}} \right) \in \partial^{W} \left( T \right)\), then we achieve a contradiction with the fact that \(\left( {\hat{x}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} ,\hat{y}_{o}^{{\text{H}}{\ddot{\text{o}}} {\text{lder}}} } \right)\) is the closest point in \(\partial^{W} \left( T \right)\) to \(\left( {x_{o} ,y_{o} } \right)\). (ii) If \(\left( {x^{\prime},y^{\prime}} \right) \in T\backslash \partial^{W} \left( T \right)\), we achieve a contradiction with the fact that the hyperplane \(H\) is a supporting hyperplane of \(T\). ■
Therefore, although the Hölder distance function can yield more than one projection point, something that could a priori lead to an indetermination of the value of price inefficiency due to having the possibility of taking different valid values (each one associated with the gap between the projection point and the maximizing profit benchmark), Proposition 2 guarantees that the decomposition in (15), where the allocative term is derived as a residual, is well-defined, always producing a unique value for technical inefficiency and allocative inefficiency.
Unfortunately, as we show next through a simple numerical example, the remaining measures shown in Sect. 2 that may yield multiple projections do not satisfy the essential property. In other words, the Russell Graph Measure for profit, the input- and output-oriented versions of the Russell Measure with respect to cost and revenue, respectively, and the Enhanced Russell Graph Measure and the Weighted Additive Measure both for profit, do not yield a suitable decomposition of overall efficiency or inefficiency due to the residual nature of their corresponding allocative terms.
Example 2
Let us assume that we have observed two firms that consume two inputs for producing one output \(\left( {x_{1} ,x_{2} ,y} \right)\): A = (1, 2, 1) and B = (1, 1, 2). Additionally, we consider \(w_{1} = 1\), \(w_{2} = 2\) and \(p = 2\) as market prices. In this situation, under Data Envelopment Analysis, the strongly efficient frontier is exclusively formed by firm B, which additionally represents the point where maximum profit is achieved. Then, when one evaluates firm A resorting to the Russell Graph Measure, the Enhanced Russell Graph Measure or the Weighted Additive Measure, the only projection point is firm B, which Pareto-dominates firm A. Next, we analyze what happens with each of the above three graph measures with respect to the determination of economic efficiency and its decomposition for firm A.
-
(i)
The Russell Graph Measure: \(\Pi I_{RGM} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) = \frac{4}{3} > 1 - TE_{RGM} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} } \right) =\) \(1 - \frac{2}{3} = \frac{1}{3}\). Therefore, \(AI_{RGM} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) = 1 > 0\).
-
(ii)
The Enhanced Russell Graph Measure: \(\Pi I_{ERG} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) = 2 > 1 - TE_{ERG} \left( {x_{{{\text{1A}}}} ,x_{{{\text{2A}}}} ,y_{{\text{A}}} } \right)\) = \(1 - \frac{3}{8} = \frac{5}{8}\). Therefore, \(AI_{ERG} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) = \frac{11}{8} > 0\).
-
(iii)
The Weighted Additive Measure for input and output weights equal to one, \(\left( {\rho_{{}}^{ - } ,\rho_{{}}^{ + } } \right) = \left( {1_{M} ,1_{N} } \right){:}\) \(\Pi I_{WA} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) = 4 > TI_{WA} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} } \right) = 2\). Therefore, \(AI_{WA} \left( {x_{{{\text{A1}}}} ,x_{{{\text{A2}}}} ,y_{{\text{A}}} ,\tilde{w},\tilde{p}} \right) =\) \(2 > 0\).
Notice that all the allocative inefficiency components are strictly greater than zero, when the only projection point, firm B, is the benchmark maximizing profit. If these three approaches were associated with a consistent decomposition of economic inefficiency, the allocative inefficiency term should be zero, indicating that there is no gap associated with price inefficiency. This result implies that the essential property does not hold with respect to these three measures. Similar examples can be established for the input and output-oriented versions of the Russell measure.
We remark that, despite being overlooked until now, the essential property turns out to be very sensible from the perspective of the conceptual (and geometrical) interpretation of allocative efficiency. The main reason why this property has been neglected is that the first efficiency measures used for decomposing economic efficiency, that is, the input and output Shephard distance functions (Farrell 1957), meet this property in a natural way; although it was never explicitly proven. The subsequent developments in the literature with the objective of introducing and decomposing economic efficiency, as the Directional Distance Function, tacitly assumed the satisfaction of the essential property. Fortunately, as we showed above, the DDF satisfies the desired property. Lamentably, more modern approaches for measuring and decomposing overall efficiency do not satisfy the essential property, except the measures based upon the Hölder metrics. Consequently, some evaluated firms might exhibit an overestimation of the actual value of price (allocative) inefficiency when these approaches are used for decomposing overall inefficiency.
4 The Extended Essential Property of Allocative Efficiency
Another interesting property that, in our opinion, the components of the decomposition of economic efficiency should fulfill represents a refined extension of the essential property presented in the previous section. Before introducing its formal definition, we illustrate this notion through the simple example used in Fig. 1 above. In that example, firm A is interior to the technology and, consequently, it is not possible to directly determine its corresponding price efficiency under the traditional approach. In contrast, this value may be directly determined for firms located on the efficient frontier. So, for unit A, technical efficiency is resolved in the first stage, by projecting A onto the frontier (unit B), and, next, allocative efficiency is determined through the gap between unit B and unit C, where cost is minimized. In this regard, it seems reasonable to demand that the allocative efficiency value assigned to firm A, through firm B, coincides with the allocative efficiency value directly determined for firm B. That is, independently measuring the allocative efficiency of the firm under evaluation and that of its projection, both values should be equal. Otherwise, the projection would be assigned two or even more allocative efficiency values; that corresponding to itself plus those associated with all firms that identify it as technological benchmark. This property is related to the internal consistency of the decomposition of economic efficiency in its usual drivers.
Definition 7
(The extended essential property). (a) \(AE\left( {x_{o} ,y_{o} ,w,p} \right) = AE\left( {\hat{x}_{o} ,\hat{y}_{o} ,w,p} \right)\), \(\forall \left( {x_{o} ,y_{o} } \right) \in T\), for the multiplicative approach, and (b) \(AI\left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p}} \right) = AI\left( {\hat{x}_{o} ,\hat{y}_{o} ,\tilde{w},\tilde{p}} \right)\), \(\forall \left( {x_{o} ,y_{o} } \right) \in T\), for the additive approach.
The above property means that for any evaluated firm \(\left( {x_{o} ,y_{o} } \right)\), its allocative efficiency or inefficiency, depending on the nature of the approach (multiplicative or additive), always coincides with the allocative efficiency of its corresponding benchmark at the production frontier \(\left( {\hat{x}_{o} ,\hat{y}_{o} } \right)\). Notice that Definition 7 was established for graph measures. However, by analogy, it is easy to define oriented versions of it. This definition is especially important because, as we will prove later, only some measures (the radial measures, the hyperbolic measure, the directional distance function when the directional vector is common across firms, and the Hölder Distance Function under the norm \(\ell_{\infty }\)) satisfy it, which can be seen as an advantage in comparison with the other alternatives (the Russell Measures—graph and oriented, the Enhanced Russell Graph Measure and the Weighted Additive Measure).
A relevant relationship between the original definition of the property and its extension can be established. Specifically, if a decomposition of those presented in Sect. 2 satisfies the extended version of the essential property, then it also meets the essential property, as we prove in Proposition 3.
Proposition 3
For the approaches considered in Sect. 2, if Definition 7 holds, then the essential property is satisfied.
Proof
Seeking brevity, let us only prove the statement for the first measure presented in Sect. 2. In this regard, let us consider the Input-oriented Radial Measure of technical efficiency. In that case, if \(\left( {x_{g} ,y_{g} } \right) \in T\), that is, a generic input–output bundle belonging to the technology is such that \(w \cdot x_{g} = C\left( {y_{g} ,w} \right)\), then, by (7), \(CE_{RI} \left( {x_{g} ,y_{g} ,w} \right) = 1\). Additionally, \(TE_{RI}^{{}} \left( {x_{g} ,y_{g} } \right) = \theta_{g}^{*} \le 1\). Therefore, by (7) again, \(TE_{RI}^{{}} \left( {x_{g} ,y_{g} } \right) = 1\) and, consequently, \(AE_{RI} \left( {x_{g} ,y_{g} ,w} \right) = {{CE_{RI} \left( {x_{g} ,y_{g} ,w} \right)} \mathord{\left/ {\vphantom {{CE_{RI} \left( {x_{g} ,y_{g} ,w} \right)} {TE_{RI}^{{}} \left( {x_{g} ,y_{g} } \right)}}} \right. \kern-0pt} {TE_{RI}^{{}} \left( {x_{g} ,y_{g} } \right)}} = 1\). Let us then suppose that Definition 7(a) holds. In that case, \(AE\left( {x_{o} ,y_{o} ,w} \right) = AE\left( {\hat{x}_{o}^{RI} ,y_{o} ,w} \right)\), \(\forall \left( {x_{o} ,y_{o} } \right) \in T\). Finally, if \(\left( {\hat{x}_{o}^{RI} ,y_{o} } \right) \in T\) is such that \(w \cdot \hat{x}_{o}^{RI} = C\left( {y_{o} ,w} \right)\) (see Definition 1), then, by the reasoning shown above for the generic point \(\left( {x_{g} ,y_{g} } \right) \in T\), \(AE_{RI} \left( {\hat{x}_{o}^{RI} ,y_{o} ,w} \right) = 1\). Hence, by the hypothesis of the satisfaction of Definition 7, \(AE\left( {x_{o} ,y_{o} ,w} \right) =\) 1 as well and Definition 1 holds. ■
Because of this previous proposition, we have that if a measure on the list shown in Sect. 2 does not satisfy the essential property, then this measure results in a decomposition that cannot meet the extended variant of the property since, otherwise, it would satisfy the essential property, what would be a contradiction. This means that the Russell Graph Measure, the input and output-oriented versions of the Russell Measure, the Enhanced Russell Measure and, finally, the Weighted Additive Measure do not satisfy the extension of the proposed property (Definition 7). As for the radial measures, the Directional Distance Function and the Hölder Distance Function, we next analyze each case separately. Before doing that, it is worth mentioning that, a priori, the technical efficiency measures that can yield alternative projection benchmarks onto the efficient frontier could present a special difficulty for satisficing the extended essential property since, again, a problem of indetermination of the value of price efficiency arises. In that case, each projection point could be associated with a different value for the term \(AI\left( {\hat{x}_{o} ,\hat{y}_{o} ,w,p} \right)\).
Next, we are going to prove that the extended essential property is satisfied by the Input- and Output-oriented Radial Measures as well as by the Hyperbolic Graph Measure.
Proposition 4
The Input- and Output-oriented Radial Measures as well as the Hyperbolic Graph Measure satisfy Definition 7.
Proof
From the proof of Proposition 1(i), we have that \(AE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = \frac{{C\left( {y_{o} ,w} \right)}}{{w \cdot \hat{x}_{o}^{RI} }}\). Additionally, \(AE_{RI} \left( {\hat{x}_{o}^{RI} ,y_{o}^{{}} ,w} \right) = \frac{{C\left( {y_{o} ,w} \right)}}{{w \cdot \hat{x}_{o}^{RI} }}\) since \(\left( {\hat{x}_{o} ,\hat{y}_{o} } \right)\) is projected onto itself. Therefore, \(AE_{RI} \left( {x_{o} ,y_{o} ,w} \right) = AE_{RI} \left( {\hat{x}_{o} ,\hat{y}_{o} ,w} \right)\). Following the same steps, one can prove the property for the output-oriented measure and the Hyperbolic Graph Measure. ■
As for the Directional Distance Function, this measure does not always meet the extended essential property. We next show a simple counterexample resorting to the directional vector that is frequently chosen in empirical applications:\(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {x_{o} ,y_{o} } \right)\).
Example 3
Resorting to Example 2, let us add a new (inefficient) unit, firm C, with input–output vector \(\left( {1.5,2,1} \right)\). Assessing its technical inefficiency, we obtain that its corresponding Directional Distance Function projection, with \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {1.5,2,1} \right)\), is \(\left( {\hat{x}_{{\text{C}}}^{DDF} ,\hat{y}_{{\text{C}}}^{DDF} } \right)\) = \(\left( {1,\frac{4}{3},\frac{4}{3}} \right)\). If we compute the allocative inefficiency associated with the decomposition of profit inefficiency for firm C = \(\left( {1.5,2,1} \right)\) and its projection, \(\left( {\hat{x}_{{\text{C}}}^{DDF} ,\hat{y}_{{\text{C}}}^{DDF} } \right)\) = \(\left( {1,\frac{4}{3},\frac{4}{3}} \right)\), we obtain \(AI_{DDF} \left( {x_{{\text{C}}} ,y_{{\text{C}}} ,\tilde{w},\tilde{p};x_{{\text{C}}} ,y_{{\text{C}}} } \right) = 0.2667\) and \(AI_{DDF} \left( {\hat{x}_{{\text{C}}}^{DDF} ,\hat{y}_{{\text{C}}}^{DDF} ,\tilde{w},\tilde{p};\hat{x}_{{\text{C}}}^{DDF} ,\hat{y}_{{\text{C}}}^{DDF} } \right) = 0.3158\), respectively. This highlights that the allocative inefficiency of an interior point, once evaluated at the projected benchmark through \(TI_{DDF}^{{}} \left( {x_{o} ,y_{o} ;g_{o}^{ - } ,g_{o}^{ + } } \right)\), could not coincide with the allocative inefficiency of that reference under the DDF. The reason is that the underlying normalization factors in (13), \(w \cdot g_{o}^{ - } + p \cdot g_{o}^{ + }\), including the choice of directional vector \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {x_{o} ,y_{o} } \right)\) for the DDF technical inefficiency measure, \(TI_{DDF}^{{}} \left( {x_{o} ,y_{o} ;x_{o} ,y_{o} } \right)\), are different for firm C = \(\left( {1.5,2,1} \right)\) and its projection \(\left( {\hat{x}_{{\text{C}}}^{DDF} ,\hat{y}_{{\text{C}}}^{DDF} } \right)\) = \(\left( {1,\frac{4}{3},\frac{4}{3}} \right)\).
Fortunately, although the DDF does not satisfy the extended version of the essential property in general, we can state a condition that ensures its fulfillment.
Proposition 5
If \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {g_{{}}^{ - } ,g_{{}}^{ + } } \right)\) for all \(\left( {x_{o} ,y_{o} } \right) \in T\), then the Directional Distance Function satisfies Definition 7.
Proof
Extending equation (6) in Aparicio et al. (2015b, p. 886), dealing with cost inefficiency, to profit inefficiency, and considering the condition \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {g_{{}}^{ - } ,g_{{}}^{ + } } \right)\) for all point belonging to \(T\), we have that \(AI_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};g_{{}}^{ - } ,g_{{}}^{ + } } \right) =\)\(\frac{{\Pi \left( {w,p} \right) - \left( {p \cdot \hat{y}_{o}^{DDF} - w \cdot \hat{x}_{o}^{DDF} } \right)}}{{w \cdot g_{{}}^{ - } + p \cdot g_{{}}^{ + } }}\). Regarding the evaluation of \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right) \in T\), we have that the projection point corresponding to \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right)\) is \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right)\) in the direction of \(\left( {g_{{}}^{ - } ,g_{{}}^{ + } } \right)\). Consequently, we have \(AI_{DDF} \left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} ,\tilde{w},\tilde{p};g_{{}}^{ - } ,g_{{}}^{ + } } \right) =\) \(\frac{{\Pi \left( {w,p} \right) - \left( {p \cdot \hat{y}_{o}^{DDF} - w \cdot \hat{x}_{o}^{DDF} } \right)}}{{w \cdot g_{{}}^{ - } + p \cdot g_{{}}^{ + } }}\). The above statements are true for any \(\left( {x_{o} ,y_{o} } \right) \in T\) and its corresponding projection point \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right)\), which also satisfies that \(\left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} } \right) \in T\). Thus, we have that \(AI_{DDF} \left( {x_{o} ,y_{o} ,\tilde{w},\tilde{p};g_{o}^{ - } ,g_{o}^{ + } } \right) = AI_{DDF} \left( {\hat{x}_{o}^{DDF} ,\hat{y}_{o}^{DDF} ,\tilde{w},\tilde{p};g_{{}}^{ - } ,g_{{}}^{ + } } \right)\) for all \(\left( {x_{o} ,y_{o} } \right) \in T\). ■
In the literature, two previously used directional vectors with constant values are \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {1_{M} ,1_{N} } \right)\) and \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {\overline{x},\overline{y}} \right)\), where \(\overline{x}\) denotes the arithmetic mean of the input variables and \(\overline{y}\) denotes the arithmetic mean of the output variables. For a discussion on the available choices for directional vectors see, for example, Färe et al (2008). Juo et al. (2015) study the change of profit efficiency in the Taiwanese banking industry adopting \(\left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {\overline{x},\overline{y}} \right)\).
Finally, regarding the Hölder Distance Function, we next show through a simple counterexample that this measure fails the satisfaction of the extended version of the essential property.
Example 4
Let us consider the following data set for one input and one output: A = (4, 4), B = (5, 3), C = (3, 3), and D = (5, 5). Let us assume that \(\left( {w,p} \right) = \left( {1,4} \right)\). Under Data Envelopment Analysis, if we evaluate firm B using the Euclidean distance, we get that its allocative inefficiency equals 0.526, being A the unique technical projection point. Additionally, if we assess firm A, we get an allocative inefficiency term equal to 0.728, which does not coincide with 0.526.
5 Discussion and Conclusions
Under the traditional approach, economic efficiency is decomposed into technical efficiency and allocative efficiency. In this paper, the main conclusion is that unless a certain property, which we name essential, is fulfilled, the allocative component of all existing decompositions cannot be correctly interpreted as actual price inefficiency. The essential property states that allocative inefficiency should not exist when the corresponding technical efficiency measure directly projects the evaluated unit onto a point that is efficient from an economical perspective. Additionally, and searching for the internal consistency of the approaches, we have also introduced a refined extension of the essential property: the allocative (in)efficiency for any assessed unit must coincide with the allocative (in)efficiency measured at the corresponding projection benchmark.
Table 1 summarizes the performance of the alternative technical (in)efficiency measures considered with respect to the satisfaction of these two properties. All multiplicative economic efficiency decompositions, including those based on the Input- and Output-oriented Radial Distance functions and the Hyperbolic Graph Measure, satisfy the essential and extended properties of allocative efficiency. This is not the case for the additive decompositions of economic inefficiency. In this case, only the Directional Distance Function and the Hölder Distance Function satisfy the essential property, but they fail to meet the extended version in general. In the case of the Directional Distance Function, it is met if the directional vector \(g = \left( {g_{o}^{ - } ,g_{o}^{ + } } \right)\) is common to all firms. For the Hölder Distance Function, fulfilling the extended version requires to resort to the Chebyshev norm, i.e., \(h = \infty\), because this model is equivalent to the Directional Distance Function model with \(g = \left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {1_{M} ,1_{N} } \right)\) (see Briec 1999). On the contrary, there is no remedy for the additive decompositions of economic inefficiency based on the Russell Measures and the Weighted Additive Measures. All these measures fail to satisfy the essential properties, and no exceptions exist.
The Russell and other slack-based inefficiency measures were introduced in the literature to account for the notion of Pareto–Koopmans efficiency. Our results show that their use in the decomposition of economic efficiency could be questionable because they fail to satisfy the essential properties. However, we also stress in Table 1 that none of the decompositions complying with the essential properties, either multiplicative or the additive directional and Hölder distance functions, satisfies the indication property, which means that these efficiency models do not necessarily project the units onto the strongly efficient frontier. We have then detected a trade-off between indication and essentiality.
We believe that our results are key for current research related to the definition and measurement of economic efficiency. In general, the numerical values of profit inefficiency and its two elements can only be compared if the normalization factor is common to all firms, and this is captured by the fulfillment of the essential properties. Let us take, for example, the case of the Directional Distance Function and the most popular choice of directional vector corresponding to the individually observed quantities: \(g = \left( {g_{o}^{ - } ,g_{o}^{ + } } \right) = \left( {x_{o} ,y_{o} } \right)\) (see Briec 1997b). In this case, as we pass this choice to the measurement of economic efficiency, neither the value of profit inefficiency nor that of allocative inefficiency are comparable across observations because the normalization factor differs across observations. This unsatisfactory situation is signaled by the unfulfillment of the extended version of the essential property. In general, any research proposal that evolves the Directional Distance Function model resulting in different normalizations would run into the problems here unveiled. For example, when measuring and decomposing profit inefficiency change through (additive) Luenberger indicators as in Juo et al (2015). Briec and Kersterns (2009a) discuss this problem in relation to the determinateness property, while Briec and Kersterns (2009b, propositions 3.6 and 3.7) show that infeasibilities can be remedied by choosing a directional vector proportional to the observed output vector. Consequently, imposing minimal restrictions on the direction to guarantee feasibility is incompatible with the satisfaction of the extended version of the essential property when measuring and decomposing profit inefficiency.
Our results are even more critical for contributions that endogenize the directional vector when measuring profit inefficiency (see, for example, Zofío et al. 2013). From this perspective, these models satisfy both essential properties, although it requires the relaxation of the non-negativity constraints on the directional vector, as inputs may need to be increased and outputs decreased with respect to their observed values (i.e., the directional vector is free-valued). Petersen (2018) revisits this question and shows that the directional vector pointing in the direction that minimizes the Euclidean distance between the observed input–output vector and the efficient frontier can be considered ‘optimal’. Petersen (2020) further explores the virtual profit efficiency model under endogenous directions which fails to be units’ invariant (i.e., does not satisfy the commensurability property). In both articles, the (dual) directional vector in the volume or quantity space is different for each observation, and therefore, profit inefficiency measurement does not satisfy the extended version of the essential property.
Finally, a promising avenue of research would be the determination of additive decompositions of economic inefficiency that, based on popular definitions of technical inefficiency like the Slacks-Based Measure or the Weighted Additive Measures (see Pastor et al. 2012), satisfy the essential properties.
Notes
In Consumption Theory, Luenberger (1992a) introduced the concept of benefit function as a representation of the amount that an individual is willing to trade, in terms of a specific reference commodity bundle g, for the opportunity to move from a consumption bundle to a utility threshold. In a natural way, the notion of benefit function leads to the conceptualization of the input-oriented Directional Distance Function in Production Theory. Also, Luenberger (1992b) defined the so-called shortage function, which basically measures the distance in the direction of a vector g of a production plan to the boundary of the production possibility set. In other words, the shortage function can be seen as the precursor of the Directional Distance Function. The corresponding duality result was later completed by Chambers et al. (1998).
References
Aparicio, J., Ruiz, J.L., Sirvent, I.: Closest targets and minimum distance to the Pareto-efficient frontier in DEA. J. Prod. Anal. 28(3), 209–218 (2007). https://doi.org/10.1007/s11123-007-0039-5
Aparicio, J., Borras, F., Pastor, J.T., Vidal, F.: Measuring and decomposing firm’s revenue and cost efficiency: the Russell measures revisited. Int. J. Prod. Econ. 165, 19–28 (2015). https://doi.org/10.1016/j.ijpe.2015.03.018
Aparicio, J., Pastor, J.T., Zofio, J.L.: How to properly decompose economic efficiency using technical and allocative criteria with non-homothetic DEA technologies. Eur. J. Oper. Res. 240(3), 882–891 (2015). https://doi.org/10.1016/j.ejor.2014.08.012
Aparicio, J., Pastor, J.T., Vidal, F.: The weighted additive distance function. Eur. J. Oper. Res. 254(1), 338–346 (2016). https://doi.org/10.1016/j.ejor.2016.04.006
Aparicio, J., Ortiz, L., Pastor, J.T.: Measuring and decomposing profit inefficiency through the slacks-based measure. Eur. J. Oper. Res. 260(2), 650–654 (2017). https://doi.org/10.1016/j.ejor.2016.12.038
Aparicio, J., Pastor, J.T., Zofio, J.L.: Can Farrell’s allocative efficiency be generalized by the directional distance function approach? Eur. J. Oper. Res. 257(1), 345–351 (2017). https://doi.org/10.1016/j.ejor.2016.08.007
Aparicio, J., Kapelko, M., Monge, J.F.: A well-defined composite indicator: an application to corporate social responsibility. J. Optim. Theory Appl. 186(1), 299–323 (2020). https://doi.org/10.1007/s10957-020-01701-1
Banker, R.D., Charnes, A., Cooper, W.W.: Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 30(9), 1078–1092 (1984). https://doi.org/10.1287/mnsc.30.9.1078
Briec, W.: Minimum distance to the complement of a convex set: duality result. J. Optim. Theory Appl. 93(2), 301–319 (1997). https://doi.org/10.1023/A:1022697822407
Briec, W.: A graph type extension of Farrell technical efficiency measure. J. Prod. Anal. 8(1), 95–110 (1997). https://doi.org/10.1023/A:1007728515733
Briec, W.: Hölder distance function and measurement of technical efficiency. J. Prod. Anal. 11, 111–131 (1999). https://doi.org/10.1023/A:1007764912174
Briec, W., Kerstens, K.: Infeasibility and directional distance functions with application to the determinateness of the Luenberger productivity indicator. J. Optim. Theory Appl. 141, 55–73 (2009). https://doi.org/10.1007/s10957-008-9503-2
Briec, W., Kerstens, K.: The Luenberger productivity indicator: an economic specification leading to infeasibilities. Econ. Model. 26, 597–600 (2009). https://doi.org/10.1016/j.econmod.2009.01.007
Briec, W., Lemaire, B.: Technical efficiency and distance to a reverse convex set. Eur. J. Oper. Res. 114(1), 178–187 (1999). https://doi.org/10.1016/S0377-2217(98)00089-7
Briec, W., Lesourd, J.B.: Metric distance function and profit: some duality results. J. Optim. Theory Appl. 101(1), 15–33 (1999). https://doi.org/10.1023/A:1021762809393
Chambers, R.G., Chung, Y., Färe, R.: Benefit and distance functions. J. Econ. Theory 70, 407–419 (1996). https://doi.org/10.1006/jeth.1996.0096
Chambers, R.G., Chung, Y., Färe, R.: Profit, directional distance function, and Nerlovian efficiency. J. Optim. Theory Appl. 98(2), 351–364 (1998). https://doi.org/10.1023/A:1022637501082
Charnes, A., Cooper, W.W., Rhodes, E.: Measuring the efficiency of decision making units. Eur. J. Oper. Res. 2(6), 429–444 (1978). https://doi.org/10.1016/0377-2217(78)90138-8
Charnes, A., Cooper, W.W., Golany, B., Seiford, L., Stutz, J.: Foundations of data envelopment analysis for Pareto-Koopmans efficient empirical production functions. J. Econom. 30(1–2), 91–107 (1985). https://doi.org/10.1016/0304-4076(85)90133-2
Chavas, J.P., Cox, T.M.: A generalized distance function and the analysis of production efficiency. South. Econ. J. 66(2), 295–318 (1999). https://doi.org/10.1002/j.2325-8012.1999.tb00248.x
Cooper, W.W., Park, K.S., Pastor, J.T.: RAM: a range adjusted measure of inefficiency for use with additive models, and relations to other models and measures in DEA. J. Prod. Anal. 11(1), 5–42 (1999). https://doi.org/10.1023/A:1007701304281
Cooper, W.W., Pastor, J.T., Aparicio, J., Borras, F.: Decomposing profit inefficiency in DEA through the weighted additive model. Eur. J. Oper. Res. 212(2), 411–416 (2011). https://doi.org/10.1016/j.ejor.2011.01.054
Debreu, G.: The coefficient of resource utilization. Econometrica 19(3), 273–292 (1951). https://doi.org/10.2307/1906814
Färe, R., Grosskopf, S.: Notes on some inequalities in economics. Econ. Theory 15, 227–233 (2000). https://doi.org/10.1007/s001990050010
Färe, R., Lovell, C.A.K.: Measuring the technical efficiency of production. J. Econ. Theory 19(1), 150–162 (1978). https://doi.org/10.1016/0022-0531(78)90060-1
Färe, R., Primont, D.: Multi-Output Production and Duality: Theory and Applications. Springer Science + Business Media, New York (1995)
Färe, R., Grosskopf, S., Lovell, C.A.K.: The Measurement of Efficiency of Production. Kluwer-Nijhoff, Boston (1985)
Färe, R., Grosskopf, S., Zaim, O.: Hyperbolic efficiency and return to the dollar. Eur. J. Oper. Res. 136, 671–679 (2002). https://doi.org/10.1016/S0377-2217(01)00022-4
Färe, R., Grosskopf, S., Margaritis, D.: Efficiency and productivity: Malmquist and more. In: Fried, H., Lovell, C.A.K., Schmidt, S.S. (eds.) The Measurement of Productive Efficiency and Productivity Growth, pp. 522–622. Oxford University Press, New York (2008)
Färe, R., He, X., Li, S., Zelenyuk, V.: A unifying framework for farrell profit efficiency measurement. Oper. Res. 67(1), 183–197 (2019). https://doi.org/10.1287/opre.2018.1770
Farrell, M.J.: The measurement of productive efficiency. J. R. Stat. Soc. 120, 253–281 (1957). https://doi.org/10.2307/2343100
Halická, M., Trnovská, M.: The Russell measure model: computational aspects, duality, and profit efficiency. Eur. J. Oper. Res. 268(1), 386–397 (2018). https://doi.org/10.1016/j.ejor.2018.01.012
Halická, M., Trnovská, M.: Duality and profit efficiency for the hyperbolic measure model. Eur. J. Oper. Res. 278(2), 410–421 (2019). https://doi.org/10.1016/j.ejor.2018.12.001
Juo, J.-C., Fu, T.-T., Yu, M.-M., Lin, Y.-H.: Profit-oriented productivity change. Omega 57, 76–87 (2015). https://doi.org/10.1016/j.omega.2015.04.013
Koopmans, T.C.: Analysis of production as an efficient combination of activities. In: Koopmans, T.C. (ed.) Activity Analysis of Production and Allocation, pp. 31–97. Wiley, New York (1951)
Kuosmanen, T., Kortelainen, M., Sipiläinen, T., Cherchye, L.: Firm and industry level profit efficiency analysis using absolute and uniform shadow prices. Eur. J. Oper. Res. 202(2), 584–594 (2010). https://doi.org/10.1016/j.ejor.2009.06.002
Lovell, C.A.K., Pastor, J.T.: Units invariant and translation invariant DEA models. Oper. Res. Lett. 18(3), 147–151 (1995). https://doi.org/10.1016/0167-6377(95)00044-5
Luenberger, D.G.: Benefit function and duality. J. Math. Econ. 21(5), 461–481 (1992). https://doi.org/10.1016/0304-4068(92)90035-6
Luenberger, D.G.: New optimality principles for economic efficiency and equilibrium. J. Optim. Theory Appl. 75(2), 221–264 (1992). https://doi.org/10.1007/BF00941466
Mangasarian, O.L.: Arbitrary-norm separating plane. Oper. Res. Lett. 24(1–2), 15–23 (1999). https://doi.org/10.1016/S0167-6377(98)00049-2
Nerlove, M.: Estimation and Identification of Cobb-Douglas Production Functions. Rand McNally Company, Chicago (1965)
Pastor, J.T., Ruiz, J.L., Sirvent, I.: An enhanced DEA Russell graph efficiency measure. Eur. J. Oper. Res. 115(3), 596–607 (1999). https://doi.org/10.1016/S0377-2217(98)00098-8
Pastor, J.T., Lovell, C.A.K., Aparicio, J.: Families of linear efficiency programs based on Debreu’s loss function. J. Prod. Anal. 38, 109–120 (2012). https://doi.org/10.1007/s11123-011-0216-4
Pastor, J.T., Aparicio, J., Zofío, J.L.: Benchmarking Economic Efficiency: Technical and Allocative Fundamentals. Springer, Cham (2022)
Petersen, N.C.: Directional distance functions in DEA with optimal endogenous directions. Oper. Res. 66(4), 1068–1085 (2018). https://doi.org/10.1287/opre.2017.1711
Petersen, N.C.: Units of measurement and directional distance functions with optimal endogenous directions in data envelopment analysis. Eur. J. Oper. Res. 282(2), 712–728 (2020). https://doi.org/10.1016/j.ejor.2019.09.053
Russell, R.R., Schworm, W.: Technological inefficiency indexes: a binary taxonomy and a generic theorem J. . Prod. Anal. 49(1), 17–23 (2018). https://doi.org/10.1007/s11123-017-0518-2
Shephard, R.W.: Cost and Production Functions. Princeton Univ. Press, Princeton (1953)
Tone, K.: A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 130(3), 498–509 (2001). https://doi.org/10.1016/S0377-2217(99)00407-5
Zofio, J.L., Prieto, A.M.: Return to dollar, generalized distance function and the Fisher productivity index. Span. Econ. Rev. 8(2), 113–138 (2006). https://doi.org/10.1007/s10108-006-9004-0
Zofio, J.L., Pastor, J.T., Aparicio, J.: The directional profit efficiency measure: on why profit inefficiency is either technical or allocative. J. Prod. Anal. 40(3), 257–266 (2013). https://doi.org/10.1007/s11123-012-0292-0
Acknowledgements
We thank two anonymous reviewers for providing constructive comments and help in improving the contents and presentation of this paper. The authors also thank the grant PID2019-105952GBI00 funded by Ministerio de Ciencia e Innovación/Agencia Estatal de Investigación/https://doi.org/10.13039/501100011033. José L. Zofío also acknowledges financial support from the Grant EIN2020-112260/AEI/https://doi.org/10.13039/501100011033 and from the Comunidad de Madrid Government under Grant H2019/HUM-5761 (INNJOBMAD-CM). Additionally, J. Aparicio thanks the Grant PROMETEO/2021/063 funded by the Valencian Community (Spain).
Funding
Open Access funding provided thanks to the CRUE-CSIC agreement with Springer Nature.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Juan-Enrique Martinez Legaz.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Aparicio, J., Zofío, J.L. & Pastor, J.T. Decomposing Economic Efficiency into Technical and Allocative Components: An Essential Property. J Optim Theory Appl 197, 98–129 (2023). https://doi.org/10.1007/s10957-023-02188-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-023-02188-2