1 Introduction

Traffic congestion is a significant issue in real-life applications such as roads and communication networks. The need for measures to reduce congestion and manage traffic demand in metropolitan areas is becoming more serious as the population grows. A functioning society relies on transportation mobility to enable its members to participate in essential activities such as production, consumption, communication, and recreation. However, it is also necessary for society to introduce congestion-relief measures for the quality of life and the environment, and to protect the safety of citizens. Any well-founded transportation model recognises the individual network user’s right to decide when, where, and how to travel [30]. However, there is always a conflict of interest in the transportation system: a typical traveller expects to choose an optimal route that minimises the combined travel time and cost, given the network conditions during the travel time (Wardrop’s principle [35]). However, society’s goal often is to reduce the average travel time and environmental damage. The aggregate effect of these decisions is a network flow that does not minimise the total system costs.

In urban traffic planning, Wardrop conditions are frequently used to predict and analyse traffic flows. These equilibrium conditions, which are based on the assumption of rational route choice behaviour by individual users, define a situation in which travellers’ routes are the shortest paths between a given set of origins and destinations.

In the design and management of urban transportation systems, there is a need for efficient planning tools for analysing and predicting future scenarios. Such tools rely on the mathematical model of the transportation system, the users of the system, and their aggregate behaviour under different traffic conditions [7]. The nonlinear complementarity problem (NCP) is an important problem in mathematical programming that has many applications in different fields [19]. One of the well-known NCP functions is the Fischer-Burmeister function [16] that is used extensively in the solution of nonlinear complementarity and variational inequality problems [13]. In 1999, Qi [32] showed that the Fischer-Burmeister function and its several variants, such as the Tseng-Luo NCP function [29] and the Kanzow-Kleinmichel NCP function [22], are smooth in the areas away from the origin, strongly semi-smooth at the origin, and irrational. Moreover, Qi proposed a class of piecewise rational NCP functions with the same strongly semi-smooth property, see [32].

From the mathematical point of view, a transportation system is represented by a strongly connected network where there is at least one path connecting any origin–destination pair. This network also describes transportation options (i.e. roads, transit lines, etc.) between origin–destination pairs. In general, an optimisation problem or a mathematical programming problem refers to selecting the best (optimal) elements from a set of available alternatives. If a given set contains multiple paths between two fixed points, we may be able to consider a metric on the set and define the optimised paths as the shortest paths or geodesics of this metric. The definition and axioms of the geometry of a space basically depend on the definition of the shortest path in that space.

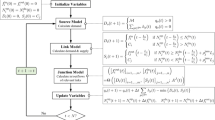
For a well-known metric, such as a Euclidean or a Riemannian metric, this is accomplished by establishing the relevant geometry to gain a better understanding of its geometric behaviour. This phenomenon may be called the geometrisation of mathematical programming. In this paper, we present some examples of geometrisation of nonlinear complementarity problem (NCP) and traffic equilibrium problem by using Finsler metrics. Finsler metrics were introduced in the first quarter of the twentieth century based on Paul Finsler’s thesis on the calculus of variations. Finsler metrics and other extensions of Euclidean and Riemannian metrics are becoming more popular in mathematical programming and optimisation theory, see for instance [2,3,4,5, 8,9,10,11, 24, 26]. The aim of this paper is to apply Finsler metrics defined on \({\mathbb {R}}^n\) to provide a geometric model for the nonlinear complementarity problem of traffic equilibrium. This work could be the first step towards using Finsler metrics in these types of mathematical programming problems. We first investigate the traffic equilibrium problem from a Finsler geometrical point of view and demonstrate that the shortest paths are solutions of a system of nonlinear equations known as the geodesics of a Randers metric. Furthermore, we show that for a dynamical transition network, optimised routes are the minimal integration of the Fischer-Burmeister function. This leads to a Finsler geometrical model for Wardrop’s dynamical user equilibrium problem.

The rest of this paper is structured as follows. In Sect. 2, we briefly define a Finsler metric on \({\mathbb {R}}^n\), the NCP and the traffic equilibrium problem. In Sect. 3, we present a Finsler geometrical model for the traffic problem and show that the optimal routes (shortest paths) of a traffic problem can be presented as geodesics of a Randers metric. In Sect. 4, first, we show that the Fischer-Burmeister function can be considered as a special Randers metric. Then, we present a dynamical model for solving NCP. Finally, we propose a mathematical model for solving the dynamical Wardrop’s user equilibrium problem.

2 Preliminaries

In this section, we briefly introduce Finsler metrics on \({\mathbb {R}}^n\), the nonlinear complementarity problem (NCP) and the traffic equilibrium problem. We assume that the reader has no background knowledge of this topic.

2.1 Finsler Metrics on \({\mathbb {R}}^n\)

Let \(M={\mathbb {R}}^n\) be the real n-dimensional space. The set of all tangent vectors at the point \(x\in M\) is called the tangent space of M and denoted by \(T_xM\). The set of all tangent spaces at \(x\in M\) is called the tangent bundle of M and denoted by TM, i.e. \(\displaystyle TM:=\bigcup _{x\in M} T_xM\). Each element of TM has the form (x, y) consisting of the point \(x\in M\) and the tangent vector \(y \in T_xM\) at the point x. Let the natural projection \(\pi :TM\rightarrow M\) be defined as \(\pi (x,y):=x\). The pair \((M,\overline{F})\) is said to be a Finsler space where \(\overline{F}:TM \rightarrow [0,\infty )\) is a function with the following properties:

  1. 1.

    \(\overline{F}\) is differentiable on \(TM \backslash \{0\} \).

  2. 2.

    \(\overline{F}\) is positively homogeneous of degree one in y, i.e. \( \overline{F}(x,\lambda y)=\lambda \overline{F}(x,y), \forall \lambda >~0\).

  3. 3.

    The Hessian matrix of \(\overline{F}^{2}\),

    $$\begin{aligned} g=(g_{ij}):=\left( {1 \over 2} \left[ \frac{\partial ^{2}}{\partial y^{i}\partial y^{j}} \overline{F}^2 \right] \right) , \end{aligned}$$
    (1)

    is positive-definite on \(TM \backslash \{0\} \) where \(i, j \in 1, \dots , n\).

The function \(\overline{F}\) is called a Finsler structure, and g is called its associated Finsler metric on manifold M. Here, we use the notation \(\overline{F}\) for the Finsler structure, rather than the usual notation F, to avoid any confusion with the function F in the nonlinear complementarity problem.

We can define a norm function on the vector space \(T_xM\) based on any Finsler metric g on M.

Let \(\{U,(x^i)\}\) or simply \((x^1,\dots , x^n)=(x^i): U \rightarrow {\mathbb {R}}^n\) be a local coordinate system on an open subset \(U\subset M\) around the point \(x \in M\). The coordinate system \(\{U,(x^i)\}\) induces a coordinate basis \(\frac{\partial }{\partial x^i}\) on \(T_xM\). Hence, we can write each tangent vector in the form \(y=y^i \frac{\partial }{\partial x^i}\,\), where we apply the Einstein summation convention or Einstein notation, that is, whenever an index variable appears twice in a single term, once in an upper (superscript) and once in a lower (subscript) position, it implies that we are summing over all of its possible values.

The local coordinate system \((x^i)\) of \(x \in M\) generates a local coordinate system \((x^i, y^i)\) on TM. The pair \((x^i, y^i)\), consisting of the position \(x\in M\) and the direction \(y\in T_xM\), is known as the line element of \((M,\overline{F})\). The Finsler structure \(\overline{F}(x,y)\) is said to be Riemannian if it is independent of the direction y and, by homogeneity of \(\overline{F}\), it is equivalent to say that \(\displaystyle \frac{\partial \overline{F}}{\partial y^i}=0\) for \(i \in 1, \dots , n\). The Finsler structure \(\overline{F}(x,y)\) is said to be Euclidean if \(g_{ij}(x,y)=\delta _{ij}\), where \(g_{ij}\) is defined by (1) and \(\delta _{ij}\) is the Kronecker delta.

If we denote by \(\Gamma (p,q)\) the collection of all piecewise \(C^\infty \) curves \(\sigma :[a,b]\subset {\mathbb {R}} \longrightarrow M\) on \((M,\overline{F})\) with \(\sigma (a)=p\) and \(\sigma (b)=q\), then the length of \(\sigma \) is defined by

$$\begin{aligned} J(\sigma ):=\int _a^b\overline{F}(\sigma ,\frac{d\sigma }{dt})dt, \end{aligned}$$

where \(\frac{d\sigma }{dt}=\frac{d\sigma ^i}{dt}\frac{\partial }{\partial x^i}\in T_{\sigma (t)}M\). For a map d defined by

$$\begin{aligned} \begin{array}{cc} d:M\times M\longrightarrow [0,\infty )\\ d(p,q):=\inf _{\Gamma (p,q)} J(\sigma ), \end{array} \end{aligned}$$

it can be shown that (M, d) satisfies the axioms of a metric space, except the symmetry property, see [4] and [33]. A geodesic, in its original sense, is a generalisation of the concept of a “straight line” in a Euclidean space. However, when the metric is not Euclidean, geodesics are not necessarily straight lines and are defined as follows. A piecewise \(C^\infty \) curve \(\sigma :[a,b]\longrightarrow M\) with \(\sigma (a)=p\) and \(\sigma (b)=q\) on the space M with the Finsler structure \(\overline{F}\) is said to be a geodesic if it is a minimal curve in \(\Gamma (p,q)\), with a constant velocity, i.e. \(J(\sigma )=d(p,q)\). Hence, geodesics are defined to be (locally) the shortest path between points in space.

For any Finsler metric g on M, we can define an inner product on the tangent space \(T_xM\) given by \(g(.,.):=<.,.>_g\) (here, for \(M={\mathbb {R}}^n\), we have \(T_xM\cong {\mathbb {R}}^n\)). In the local coordinate system \(\{U,(x^i)\}\), for all \( y,z \in T_xM\) we have \(g(y,z)=g_{ij}y^iz^j\). Each inner product defines a norm \(|| y||_g:=<y,y>_g=g_{ij} y^i y^j\) for a vector \(y\in T_xM\) with respect to g. Hence, a vector y on the tangent space \(T_xM\) can have different norms according to different Finsler metrics defined on M. For a Riemannian metric \(g_{ij}(\cdot )\), \(\overline{F}(x^i,y^i)=(g_{ij}y^iy^j)^{\frac{1}{2}} + b_i(x) y^i\), where \(\beta = b_i(x)y^i\) is a 1-form on M with \(|| \beta ||_g <1\), is a Finsler structure on M and its associated Finsler metric is called a Randers metric, see [33] for more details.

2.2 Nonlinear Complementarity Problem

Nonlinear complementarity problems (NCPs) arise from optimisation theory, engineering and economic applications. The discretisation of infinite-dimensional variational inequalities leads to linear and nonlinear complementarity problems with many degrees of freedom. The restricted NCP functions which can be used to reformulate NCPs as constrained optimisation problems were first introduced by Yamashita [36]. For a given smooth mapping \(F:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\), the NCP consists of finding a vector \(x\in {\mathbb {R}}^n\) such that

$$\begin{aligned} x\ge 0, \qquad F(x)\ge 0, \qquad F(x)^T.x=0, \end{aligned}$$
(2)

where \(F(x)^T\) is the transpose of F(x). When the NCP is reformulated as finding the zero of a self-mapping, the norm of the self-mapping naturally serves as the problem’s merit function. Luo [29] and Tseng [34] proposed a class of merit functions for NCPs and studied their several interesting properties. Kanzow, Yamashita and Fukushima [23] used a similar idea and proposed new merit functions for the NCP.

Complementarity problems can be reformulated as systems of nonlinear equations in several ways. A large number of methods have been developed based on the Newton method and its generalisations. In order to overcome some disadvantages of the class of non-smooth Newton methods and the class of the so-called smoothing methods, a third class, known as Jacobian smoothing methods, was developed in [21]. A Jacobian smoothing method is a mixture of Newton and non-smooth methods and is based on solving the mixed Newton equation: a combination of the original semi-smooth function and the Jacobian of the smooth operator of the Clarke generalised Jacobian [12]. There are also several related algorithms entitled Newtonian algorithms, see for instance [14, 20, 21, 31, 36]. Further, a solution of NCP with a neural network algorithm was presented in [28]. Among these algorithms, the modified Newton algorithm is preferred.

The modified Newton algorithm is a reformulation of system of differential Eq. (2) that converts it to a non-modal optimisation problem which is convergent under some conditions, see Sect. 8.7 of [6]. This reformulation is given by the system of equations:

$$\begin{aligned} \phi (x)=\left( \begin{array}{lcl}\phi _1(x)\\ \vdots \\ \phi _n(x)\end{array}\right) = \left( \begin{array}{lcl}\phi (x_1,F_1(x))\\ \vdots \\ \phi (x_n,F_n(x))\end{array}\right) =0, \end{aligned}$$
(3)

where the NCP function \(\phi \) is the Fischer-Burmeister NCP function [15, 16] defined as follows:

$$\begin{aligned} \begin{array}{ll} \phi :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}, \qquad \phi (a,b)=\sqrt{a^2+b^2}-(a+b),\\ where \qquad \phi (a,b)=0\, \Leftrightarrow \, a\ge 0,\, b\ge 0,\, ab=0. \end{array} \end{aligned}$$
(4)

The resulting system of nonlinear Eq. (2) is semi-smooth and the NCP has a solution x if and only if x is a solution for (3). The function \(\phi \) is locally Lipschitz and continuous at every point, hence the Clarke generalised Jacobian at every point is defined. In [17], the NCP is recast as an unconstrained minimisation problem and the natural merit function \(G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}\) given by

$$\begin{aligned} G(x)=\frac{1}{2} \sum _{i=1}^{n}\phi (x_i,F_i(x))^2=\frac{1}{2}\Vert \phi (x)\Vert ^2, \end{aligned}$$
(5)

is considered. Also, it is proved that any stationary point of the above function is a solution of the NCP if the mapping F involved in Eq. (2) is continuously differentiable and monotone. Hence, the solution of the NCP is given by solving

$$\begin{aligned} \min _{x\in {\mathbb {R}}^n} G(x). \end{aligned}$$
(6)

The NCP is mainly applied in solving the traffic equilibrium problem which is studied here, and also for the Karush–Kuhn–Tucker (KKT) optimality conditions [18].

2.3 Traffic Equilibrium Problem

Wardrop [35] Network equilibrium models have a variety of applications in urban transportation, energy distribution, game theory, spatially separated economic markets, electrical networks, and water resource planning, [1].

Assume a road network in which vehicles must travel from one location to another through a limited number of roads. Each vehicle (user) prefers shorter or wider roads to reduce their travel cost (time). However, increasing traffic on a given road will increase the cost of transportation on that road. So, some vehicles may choose a longer route to minimise their travel cost and the question that arises here is what is the minimum stability requirement for transportation strategies. Although the idea of traffic equilibrium originated as early as 1924 with Frank Knight [25], the mathematical description of equilibrium was provided for the first time in 1952 by Wardrop [35]. Wardrop’s equilibrium principles (Wardrop equilibria) are as follows:

Wardrop’s first principle: The travel times across all routes actually used are either equal to or less than those which would be experienced by a single vehicle on any unused route. Each user non-cooperatively seeks to minimise their transportation cost/time. A traffic flow that satisfies this principle is usually named user equilibrium (UE) flow.

Wardrop’s second principle At equilibrium the average journey time is minimum. This implies that each user behaves cooperatively in choosing their route to ensure the minimum cost of the whole system. A traffic flow satisfying Wardrop’s second principle is generally referred to as system optimal (SO) flow.

Wardrop equilibria are related to the idea of Nash equilibrium [27] in game theory and has been widely used since its introduction. However, analysing the transportation networks with a large number of players is more complicated than analysing games with a few numbers of players.

Wardrop equilibria can be presented mathematically as follows. Assume that \(R_{ab}\) denotes the set of simple (loop-free) routes for the origin–destination pair (a, b), \(h_r\) denotes the flow on the route \(r\in R_{ab}\), and \(c_r\) denotes the travel time on the route \(r \in R_{ab}\) as experienced by an individual user. If the flow does not depend on time, i.e. in a static model (against the dynamic model), Wardrop equilibria can be written as, see [1],

$$\begin{aligned} h_r^T(c_r(h_r)-\pi _{ab})=0,\,\, c_r(h_r)-\pi _{ab} \ge 0,\,\, h_r=d_r(\pi _{ab}), \,\, h_r \ge 0, \,\, \pi _{ab} \ge 0, \end{aligned}$$
(7)

where \(\pi _{ab}\) is the minimal rout time and \(d_r\) is the demand function of the route \(r\in R_{ab}\). In [1], an equilibrium model for predicting traffic flow on a congested transportation network is proposed based on using Wardrop’s first principle and written it as an NCP (Eq. (2)) in the following form:

$$\begin{aligned} \displaystyle \begin{array}{cc} F(x)^T \cdot x=\Big (c_r(h_r)-\pi _{ab} \quad h_r-d_r(\pi _{ab})\Big )\cdot \left( \begin{array}{cc} h_r\\ \pi _{ab} \end{array}\right) =0, \\ x=\left( \begin{array}{cc} h_r\\ \pi _{ab} \end{array}\right) \ge 0,\qquad F(x)=\left( \begin{array}{cc} c_r(h_r)-\pi _{ab}\\ h_r-d_r(\pi _{ab})\end{array}\right) \ge 0, \end{array} \end{aligned}$$
(8)

where \(F:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^n\) is a continuous function. To reduce this NCP to an unconstrained global minimisation problem, a smooth, bounded, and convex gap function G is applied, see [14]:

$$\begin{aligned} G(x)=\sum ^n_{i=1} \varphi \Big (x_i,F(x_i)\Big ), \end{aligned}$$
(9)

where \(\varphi =\frac{1}{2}\phi ^2\) and \(\phi \) is the Fischer-Burmeister function given by (4). So, solving the NCP (8) is equivalent to finding a general unconstrained solution for Eq. (6) with G given in (9).

3 A Finsler Geometric Model of Traffic Problem

In this section, we apply geometric methods to provide a mathematical model for the transportation network. Unless stated otherwise, we will assume further that

  1. (I)

    All origin–destination pairs are distinct, so we have a loop-free graph model of the transportation network.

  2. (II)

    The network is strongly connected, that is, at least one route joins each origin–destination pair. From a mathematical point of view, this condition means that we have a convex network (a subset of \({\mathbb {R}}^2\)).

  3. (III)

    The transport demand is either a constant number or a function of travel cost/time. This is typically a decreasing function of cost/time.

  4. (IV)

    All travellers have perfect information about their travel. Therefore, we have a deterministic model, unlike a stochastic model where travellers choose their paths randomly.

For any given pair of origin–destination points in the vehicle network, we usually have different route options. These routes are made by a string of streets and cross-sections and, for each route, we have an estimated travel time. This time depends on some factors such as the capacity of streets, the number of stops behind cross-sections and the travel demand of that specific route.

Now assume that we have a Riemannian metric g on \({\mathbb {R}}^2\) and its corresponding norm-squared for tangent vectors \(y\in T_x {\mathbb {R}}^2\) is given by \(\Vert y\Vert _g^2:=g(y,y)\). In traffic modelling, we can interpret this as the time it takes, using a car with fixed power, to travel from the base point of the vector y to its tip.

Let \(u\in T_x {\mathbb {R}}^2\) be a unit vector and denote the traffic congestion or any external factor that increases the traffic congestion by a vector \(\omega \in T_x {\mathbb {R}}^2\) such that \(\Vert \omega \Vert _g<1\). Before \(\omega \) sets in, a journey from the base to the tip of any unit vector u would take one unit of time. After the effect of \(\omega \), within the same one unit of time, we traverse not u but \(v=u-\omega \) instead. This is because traffic congestion is a vector in the opposite direction of flow. The measure of this new vector is not equal to 1 (\(\Vert v\Vert _g\ne 1\)). This argument for using a vector’s length is the key idea of a technique known as Okubo’s technique [4]. In fact, the geometry of movement in the former case (without considering the external factor) is the Riemannian geometry, rather than the Finslerian geometry in the latter case. Here, we consider the effect of traffic congestion (the vector field \(\omega \)) and introduce a new metric \(\overline{F}\) such that v be a unit vector with respect to the new norm corresponding to \(\overline{F}\).

Theorem 3.1

Let g be a Riemannian metric and \(\omega \) a vector field on \({\mathbb {R}}^2\) such that \(\Vert \omega \Vert _g<1\). If \(\omega \) indicates the traffic congestion, then the travel time for a car with a fixed power to pass through a vector field \(y\in T_x {\mathbb {R}}^2\) is measured by the Randers metric \(\overline{F}(x,y)=\frac{\Vert y\Vert _g}{1-\Vert \omega \Vert _g}\).

Proof

Let \(u\in T_x {\mathbb {R}}^2\) be a unit vector. After taking the effect of the vector \(\omega \) into account, we have \(v=u-\omega \), where \(\Vert v\Vert _g=1-\Vert \omega \Vert _g\). Now, a Finsler structure \(\overline{F}\) that satisfies \(\overline{F}(v)=1\) would be \(\displaystyle \overline{F}(v)=\frac{\Vert v\Vert _g}{1-\Vert \omega \Vert _g}\). For an arbitrary vector field \(y\in T_x {\mathbb {R}}^2\), the corresponding Finsler metric \(\overline{F}\) is

$$\begin{aligned} \overline{F}(x,y)=\frac{\Vert y\Vert _g}{1-\Vert \omega \Vert _g}. \end{aligned}$$

If we put \(\lambda =1-\Vert \omega \Vert _g^2\) then \(\overline{F}(x,y)\) can be written as

$$\begin{aligned} \overline{F}(x,y)=\frac{\Vert y\Vert _g}{\lambda }+\frac{\Vert \omega \Vert _g\Vert y\Vert _g}{\lambda }=\frac{\sqrt{g_{ij} y^i y^j}}{\lambda }+ \frac{g_{ij}\omega ^i y^j}{\lambda }, \end{aligned}$$
(10)

which is obviously a Randers metric. \(\square \)

Therefore, the optimal/shortest route between any arbitrary origin–destination pair (p, q) is a geodesic of the corresponding Randers metric passing through these points. Equivalently, we need to find minimums of the following integral

$$\begin{aligned} J(\sigma )=\int _0^1\overline{F}\big (x(t),y(t)\big )dt, \qquad y(t)=\frac{dx}{dt}, \end{aligned}$$
(11)

where \(\overline{F}\) is given by (10) and \(\sigma :[0,1]\rightarrow {\mathbb {R}}\) defined by \(t\rightarrow x(t)\) such that \(x(0)=p\) and \(x(1)=q\). It can be shown that, by assuming \(L=\frac{\overline{F}^2}{2}\), any minimal point x(t) of the length integral (11) is a solution of the following system of differential equations, see Chap. 5 of [33]:

$$\begin{aligned} L_{ij}\frac{d^2x^i}{dt^2}+\frac{\partial L_i}{\partial x^j}\frac{dx^j}{dt}-\frac{\partial L}{\partial x^i}=0, \end{aligned}$$
(12)

where \(L_i=\frac{\partial L}{\partial y^i}\), \(L_{ij}=\frac{\partial ^2 L}{\partial y^i\partial y^j}\). Therefore,

Corollary 3.1

If we consider traffic congestion as an external factor that affects the vehicle transition network, then the differential equation of the shortest route between any origin–destination pair is given by Eq. (12).

4 A Finslerian Model for Wardrop’s User Equilibrium Problem

In this section, we show that the Fischer-Burmeister function is a special Randers metric, and therefore, the equations of its geodesics are equations of the minimal paths. Then, we present a Finsler geometrical model for solving the dynamical Wardrop’s user equilibrium problem that may apply in solving different equilibrium problems.

4.1 Finsler Geometry and Traffic Equilibrium

Here, we illustrate that the Fischer-Burmeister function is a special Randers metric.

Proposition 4.1

The Fischer-Burmeister function is a Finsler metric of Randers type and its geodesics are the optimised paths in the NCP.

Proof

Let g be a Euclidean metric on \({\mathbb {R}}^2\) given by \(g(a,b)=\sqrt{a^1b^1+a^2b^2}\), where \(a=(a^1,a^2)\) and \(b=(b^1,b^2)\) are two arbitrary points on \({\mathbb {R}}^2\). The local coordinate system \((x^1,x^2)\) on \({\mathbb {R}}^2\) induces the local fields of frames \(\left( \frac{\partial }{\partial x^1}, \frac{\partial }{\partial x^2}\right) \) and \((dx^1,dx^2)\) on the tangent space \(T_x {\mathbb {R}}^2\) and its dual \(T^*_x {\mathbb {R}}^2\). Therefore, we have \(g\left( \frac{\partial }{\partial x^1}, \frac{\partial }{\partial x^2}\right) =\sqrt{(dx^1)^2+(dx^2)^2}\) and from Eq. (4), the Fischer-Burmeister function on \({\mathbb {R}}^2\) is given by:

$$\begin{aligned} \phi (dx^1,dx^2)=\sqrt{(dx^1)^2+(dx^2)^2}-(dx^1+dx^2 ). \end{aligned}$$
(13)

The first term in the right-hand side of (13) can be written as \(\sqrt{\delta _{ij}dx^idx^j}\), where \(\delta _{ij}\) is the Kronecker symbol and i, j run over the range 1,2. So, it is a Euclidean (or Riemannian) metric on \({\mathbb {R}}^2\). The second term in (13) is a differential 1-form \(\beta =\omega _idx^i\), where \(\forall i: \omega _i=-1\). Therefore, the Fischer-Burmeister function is a Randers metric. \(\square \)

By virtue of the above proposition, solutions of the NCP, i.e. the optimised paths of the Fischer-Burmeister function, are geodesics of a Randers metric given by Eq. (12).

4.2 The Dynamical Transition Network

The traffic congestion and transport demand in some hours of the day (peak hours) are increasing dramatically. A typical solution to address this issue, instead of building additional infrastructure, is the introduction of dynamic elements to road traffic management. This includes for instance using sensors to measure traffic flows and automatic interconnected guidance systems (for example traffic signs which open a lane in different directions depending on the time of day) to manage traffic in peak hours. Here, we generalise the method of solving the NCP, discussed in Sect.  4.1, to dynamic systems.

Theorem 4.1

If the traffic flow and the travel time are functions of time t, then the solutions of the traffic equilibrium problem are minima of the following integration

$$\begin{aligned} G(t)=\int ^{t_1}_{t_0}\varphi (h(t),c(t)) h'(t) dt, \end{aligned}$$
(14)

where \(\varphi =\frac{1}{2}\phi \) and \(\phi \) is the Fischer-Burmeister function, h(t) is the traffic flow, c(t) is the travel time, \(t_0\) is the start of travel time, and \(t_1\) is the end of travel time.

Proof

Let the traffic flow h(t) and the travel time c(t) (which is in general a function of h) be functions of time and assume that the minimal rout time \(\pi \) in (7) is zero. Then, using the Fischer-Burmeister function \(\phi \) on \({\mathbb {R}}^2\) (Eq. (13)), Eq. (5) can be written as

$$\begin{aligned} G(h)=\int ^{h_1}_{h_0}\varphi (h,c(h)) dh, \end{aligned}$$

where \(\varphi =\frac{1}{2}\phi \). Since \(dh=h'(t)dt\), this equation is equivalent to Eq. (14). Now by virtue of a well-known fact in the calculus of variation the minima of integration (14) are solutions to traffic equilibrium problem or present the shortest route (the route that requires the least amount of time to pass through it). \(\square \)

4.3 The Finsler Geometrical Model

Now, we can present a Finsler geometrical model for solving the dynamical Wardrop’s user equilibrium problem:

Lemma 4.1

Any Finsler structure \(\overline{F}(x,y)\) on \({\mathbb {R}}^2\) can be considered as a gap function in solving the NCP.

Proof

Assume that the transit network has all conditions I-IV in Sect. 3 and also traffic flow and the other ingredients in the transit network are functions of time. Further assume that \(\overline{F}(x,y):T {\mathbb {R}}^2 \backslash \{0\}\rightarrow {\mathbb {R}}^+\) is a Finsler metric on \({\mathbb {R}}^2\) and a car with a fixed power travels from point a to point b through a smooth curve r on \({\mathbb {R}}^2\). From the calculus of variation the minima of the following integral provide the shortest curve between points \(a=r(t_0)\) and \(b=r(t_1)\):

$$\begin{aligned} L(r(t))=\int _{t_0}^{t_1}\overline{F}(x(t),y(t)) dt, \qquad y(t)=\frac{dx}{dt}, \end{aligned}$$

where we assume that \(r:[t_0,t_1]\rightarrow {\mathbb {R}}\) defined by \(t\rightarrow x(t)\) such that \(x(t_0)=a\) and \(x(t_1)=b\). As a Finsler structure (see Sect. 2.1), \(\overline{F}(x,y)\) meets all the conditions of a gap function in solving the NCP. Equivalently, L(r(t)) is always a positive number that is independent of the parameter t, and \(\overline{F}\) is a differentiable function and if we put \((g_{ij}):=\left( {1 \over 2} \left[ \frac{\partial ^{2}}{\partial y^{i}\partial y^{j}}\overline{F}^2 \right] \right) \), then we have \(\det (g_{ij})\ne 0\), see Sect. 2.2 or Sect. 8.7 of [6] for more details. \(\square \)

Theorem 4.2

The optimised routes for the traffic equilibrium problem in a dynamical transition network are geodesics of a Finsler structure \(\overline{F}(x,y)\) of Randers type, where x(t) denotes the traffic flow at time t and \(y(t)=\dot{x}(t)\) is the velocity of a car with fixed power at time t.

Proof

Let x(t) be the traffic flow and \(y(t)=\dot{x}(t)\) the velocity of a car with fixed power at time t. Then, Wardrop’s user equilibrium principle can be written as

$$\begin{aligned} \overline{F}(x,y)=0\quad \Leftrightarrow \quad x\ge 0,\quad y\ge 0,\quad x.y=0. \end{aligned}$$

Here, \(\overline{F}(x,y)=0\) implies that the traffic congestion is extremely high and the car velocity is zero (\(y=0\)) or the car stops, so we have \(x.y=0\). In Sect. 3, we show that the geometrical method of solving the traffic problem leads to finding the geodesics of a Randers metric. On the other hand, Proposition 4.1 implies that the common applied mathematical method, i.e. finding the minima of the Fischer-Burmeister function, can be seen as a special case of this geometrical method. Thus, if the given Finsler metric in Lemma 4.1 be a Randers metric, it is a solution of the NCP. Therefore, from Theorem 4.1, the equations of optimised routes for the traffic equilibrium problem in a dynamical transition network are given by the geodesic equations of a Finsler metric of Randers type. \(\square \)

5 Conclusion

By analysing the nonlinear complementarity problem (NCP) of traffic equilibrium from the Finsler geometric point of view, we presented a mathematical dynamical model, based on Finsler geometry to provide the optimal paths for the dynamical Wardrop’s user equilibrium problem. Applying one of the common methods of solving NCPs, the modified Newton algorithm, we show that by assuming traffic congestion as an external factor that affects the usual vehicle transition network, the differential equation of the shortest route between any origin–destination pair is geodesic of a Finsler metric known as the Randers metric. Then, we extend this result and show that in general, the Fischer-Burmeister function is a Randers metric. Therefore, using Finsler geometry, one can solve the dynamical Wardrop’s user equilibrium problem by finding the geodesics of the corresponding Randers metric, see Eq. (12).