Equivalent Formulations of Optimal Control Problems with Maximum Cost and Applications

Abstract

We revisit the optimal control problem with maximum cost with the objective to provide different equivalent reformulations suitable to numerical methods. We propose two reformulations in terms of extended Mayer problems with state constraints, and another one in terms of a differential inclusion with upper-semi-continuous right member without state constraint. For the latter we also propose a scheme that approximates from below the optimal value. These approaches are illustrated and discussed in several examples.

1 Introduction

We consider the optimal control problem which consists in minimizing the maximum of a scalar function over a time interval

$$\begin{aligned} \inf _{u(\cdot )}{{\,\mathrm{ess\,sup}\,}}_{t \in [t_0,T]} y(t), \end{aligned}$$

where $y(t)=\theta (t,\xi (t))$ and $\xi (\cdot )$ is the solution of a controlled dynamics ${\dot{\xi }}=\phi (\xi ,u)$, $\xi (t_0)=\xi _0$. This problem is not in the usual Mayer, Lagrange or Bolza forms of the optimal control theory and therefore is not suitable to use the classical necessary optimality conditions of Pontryagin’s maximum principle or existing solving algorithms (based on direct method, shooting or Hamilton–Jacobi–Bellman equation). However, this problem falls into the class of optimal control with $L^\infty$ criterion, for which several characterizations of the value function have been proposed in the literature [3, 4, 12]. Typically, the value function is solution, in a general sense, of partial differential equation of the form

$$\begin{aligned} \min \Big (\partial _t V+ \inf _u \partial _\xi V.\phi (\xi ,u), \; V-\theta \Big )=0 \end{aligned}$$

without boundary condition. Nevertheless, although necessary optimality conditions and numerical procedures have been formulated [2, 8, 9, 11], there is no practical numerical tool to solve such problems as it exists for Mayer problems, to the best of our knowledge. The aim of the present work is to study different reformulations of this problem into Mayer form in higher dimension with possibly state or mixed constraints, for which existing numerical methods can be used. Indeed, it has already been underlined in the literature that discrete-time optimal control problems with maximum cost do not satisfy the principle of optimality but can be transformed into problems of higher dimension with additively separable objective functions [14, 15]. We pursue here this idea but in the continuous time framework, which faces the lack of differentiability of the max function.

This manuscript is organized as follows. In Sect. 2, we establish the setup and the hypotheses of this article, and define the problem. In Sect. 3, we provide equivalent formulations of the studied problem in the form of two Mayer problems with fixed initial condition, and under state or mixed constraint. In Sect. 4, we propose another formulation in terms of differential inclusion but without constraints, and then we show how the optimal value can be approximated from below by a sequence of more regular Mayer problems. Section 5 is devoted to numerical illustrations. We consider two problems for which the optimal solution can be determined explicitly (one borrowed from epidemiology), which allows to estimate and compare the numerical performances of the different formulations. These problems have been chosen linear with respect to the control variable in order to present discontinuous optimal controls, which are known to be numerically more sensitive. More precisely, the optimal solution of the first problem has pure bang–bang controls, while the second one possesses a singular arc. We discuss the issues arising in the numerical implementations of the different formulations and compare numerically with $L^p$ approximations. Finally, we discuss in Sect. 6 about the potential merits of the different formulations as practical methods to compute optimal solution of $L^\infty$ control problems.

2 Problem and Hypotheses

We shall consider autonomous dynamical systems defined on an invariant domain $\mathcal{D}$ of $\mathbb {R}^{n+1}$ of the form

$$\begin{aligned} \dot{x}= & {} f(x,y,u) ,\nonumber \\ \dot{y}= & {} g(x,y,u) , \end{aligned}$$

(1)

(where g is a scalar function) where the values of the control $u(\cdot )$ belong to a given set $U \subset \mathbb {R}^p$. More specifically, throughout the paper, we shall assume that the following properties are fulfilled.

Assumption 1

• i. U is a compact set.

• ii. The maps f and g are $C^1$ on $\mathcal{D}\times U$.

• iii. The maps f and g have linear growth, that is there exists a number $C>0$ such that

  $$\begin{aligned} ||f(x,y,u)||+|g(x,y,u)|\le C(1+||x||+|y|), \; (x,y)\in \mathcal{D}, \; u \in U . \end{aligned}$$

For instance, $y(\cdot )$ can be a smooth output of a dynamics

$$\begin{aligned} \dot{x}=f(x,u), \quad y=h(x) , \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \dot{x}= & {} f(x,u) , \\ \dot{y}= & {} g(x,u):=\nabla h(x)^T\cdot f(x,u) . \end{aligned}$$

Let $\mathcal{U}$ be the set of measurable functions $u(\cdot ): [0,T] \mapsto U$ and consider $(x_0,y_0)\in \mathcal{D}$, $T>0$. Under the usual arguments of the theory of ordinary differential equations, Assumption 1 ensures that for any $u(\cdot ) \in \mathcal{U}$ there exists a unique absolutely continuous solution $(x(\cdot ),y(\cdot ))$ of (1) on [0, T] for the initial condition $(x(0),y(0))=(x_0,y_0)$ (see, for instance, [10]). Define then the solutions set

$$\begin{aligned} \mathcal{S} :&= \{ (x(\cdot ),y(\cdot )) \in \mathcal{AC}\mathcal{}([0,T],\mathbb {R}^{n+1}), \text{ sol. } \text{ of } \text{(1) } \text{ for } u(\cdot ) \in \mathcal{U} \text{ with } (x(0),y(0))\\&=(x_0,y_0)\} . \end{aligned}$$

We consider then the optimal control problem which consists in minimizing the “peak” of the function $y(\cdot )$

$$\begin{aligned} \mathcal{P} : \quad \inf _{u(\cdot ) \in \mathcal{U}} \left( \max _{t \in [0,T]}y(t)\right) =\inf _{(x(\cdot ),y(\cdot )) \in \mathcal{S}} \left( \max _{t \in [0,T]}y(t)\right) . \end{aligned}$$

3 Formulations with Constraint

A first approach considers the family of constrained sets of solutions

$$\begin{aligned} \mathcal{S}_z := \{ (x,y) \in \mathcal{S}, \; y(t) \le z, \, t \in [0,T] \}, \quad (z \in \mathbb {R}) \end{aligned}$$

and to look for the optimization problem

$$\begin{aligned} \inf \{ z; \; \mathcal{S}_z \ne \emptyset \} . \end{aligned}$$

This problem can be reformulated as a Mayer problem

$$\begin{aligned} \mathcal{P}_0: \inf _{u(\cdot ) \in \mathcal{U}} z(T) \end{aligned}$$

for the extended dynamics in $\mathcal{D}\times \mathbb {R}$

$$\begin{aligned} \dot{x}= & {} f(x,y,u) ,\\ \dot{y}= & {} g(x,y,u) ,\\ \dot{z}= & {} 0 , \end{aligned}$$

under the state constraint

$$\begin{aligned} \mathcal{C}: \quad z(t)-y(t)\ge 0, \; t \in [0,T], \end{aligned}$$

where z(0) is free. Direct methods can be used for such a problem. However, as z(0) is free, solutions are not sought among solutions of a Cauchy problem, which prevents using other methods based on dynamic programming such as the Hamilton–Jacobi–Bellman equation.

We propose another extended dynamics in $\mathcal{D}\times \mathbb {R}$ with an additional control $v(\cdot )$ with values in [0, 1]

$$\begin{aligned} \dot{x}= & {} f(x,y,u) , \nonumber \\ \dot{y}= & {} g(x,y,u) , \nonumber \\ \dot{z}= & {} \max (g(x,y,u),0)(1-v) . \end{aligned}$$

(2)

Let $\mathcal{V}$ be the set of measurable functions $v: [0,T] \mapsto [0,1]$. Note that under Assumption 1, for any $(x_0,y_0,z_0) \in \mathcal{D}\times \mathbb {R}$ and $(u,v) \in \mathcal{U}\times \mathcal{V}$, there exists an unique absolutely solution $(x(\cdot ),y(\cdot ),z(\cdot ))$ of (2) on [0, T] for the initial condition $(x(0),y(0),z(0))=(x_0,y_0,z_0)$. Here, we fix the initial condition with $z_0=y_0$ and consider the Mayer problem

$$\begin{aligned} \mathcal{P}_1: \quad \inf _{(u(\cdot ),v(\cdot ))\in \mathcal{U}\times \mathcal{V}} z(T) \quad \text{ under } \text{ the } \text{ constraint } \mathcal{C} \end{aligned}$$

and shows its equivalence with problem $\mathcal{P}$. We first consider fixed controls $u(\cdot )$.

Proposition 3.1

For any control $u(\cdot ) \in \mathcal{U}$, the optimal control problem

$$\begin{aligned} \inf _{v \in \mathcal{V}} z(T) \text{ under } \text{ the } \text{ constraint } \mathcal{C} \end{aligned}$$

(3)

admits an optimal solution. Moreover, an optimal solution verifies

$$\begin{aligned} z(T)=\max _{t \in [0,T]}y(t) \end{aligned}$$

(4)

and is reached for a control $v(\cdot )$ that takes values in $\{0,1\}$.

Proof

From equations (2), one get that any solution $z(\cdot )$ is non-decreasing, and as z satisfies the constraint $z\ge y$, we deduce that one has

$$\begin{aligned} z(T)\ge \max _{t \in [0,T]} y(t) \end{aligned}$$

(5)

for any solution of (2), and thus

$$\begin{aligned} \max _{t \in [0,T]} y(t) \le \inf _{v \in \mathcal{V}} z(T) \text{ under } \text{ the } \text{ constraint } z(t)\ge y(t), \; t \in [0,T] . \end{aligned}$$

Let $x(\cdot )$, $y(\cdot )$ be the solution of (1) for the control $u(\cdot )$ and let I be the set of invisible points from the left of y, that is

$$\begin{aligned} I:= \left\{ t \in (0,T) , \; y(t')>y(t) \text{ for } \text{ some } t'<t \right\} . \end{aligned}$$

Consider then the control

$$\begin{aligned} v(t)={\left\{ \begin{array}{ll} 1, &{} t \in \text{ int }\,I,\\ 0, &{} t \notin \text{ int }\,I . \end{array}\right. } \end{aligned}$$

(6)

When I is empty, $y(\cdot )$ is a non-decreasing function and, when $v(t)=0$ for all $t\in [0,T]$, one has $z(t)=y(t)$ for any $t \in [0,T]$. Therefore, one has

$$\begin{aligned} z(T)=y(T)=\max _{t \in [0,T]} y(t) . \end{aligned}$$

When I is non-empty, there exists, from the sun rising Lemma [17], a countable set of disjoint non-empty intervals $I_n=(a_n,b_n)$ of [0, T] such that

• the interior of I is the union of the intervals $I_n$,

• one has $y(a_n)=y(b_n)$ if $b_n\ne T$,

• if $b_n=T$, then $y(a_n)\ge y(b_n)$.

Note that when $t \notin \text{ int }\,I$, one has $y(t)\ge y(t')$ for any $t'\le t$. Therefore, the solution z with control (6) verifies

$$\begin{aligned} z(t)={\left\{ \begin{array}{ll} y(t), &{} t \notin \text{ int }\,I , \\ y(a_n), &{} t \in I_n \text{ for } \text{ some } n , \end{array}\right. } \end{aligned}$$

(see Fig. 1 as an illustration). Let ${\bar{t}}$ be the largest time in [0, T] such that

$$\begin{aligned} y({\bar{t}})=\max _{t \in [0,T]} y(t) , \end{aligned}$$

which implies that any point $t'>{\bar{t}}$ in [0, T] is invisible from the left. Therefore, one has $z(T)=z({\bar{t}})$. As for any t z(t) is equal to $y(\tau )$ for some $\tau$, one has necessarily $z({\bar{t}})\le y({\bar{t}}$). Thus, from (5) we obtain

$$\begin{aligned} \max _{t \in [0,T]} y(t)=z(T) \end{aligned}$$

and deduce

$$\begin{aligned} \max _{t \in [0,T]} y(t)=\inf _{v(\cdot )\in \mathcal{V}} z(T) \text{ under } \text{ the } \text{ constraint } \mathcal{C} . \end{aligned}$$

$\square$

Fig. 1

Illustration of the function z (in red) corresponding to a function y (in blue) with the control given by expression (6)

Remark 3.1

The proof of Proposition 3.2 gives an optimal construction of $z(\cdot )$ which is the lower envelope of non decreasing continuous functions above the function $y(\cdot )$, as depicted in Fig. 1. However, there is no uniqueness of the optimal control $v(\cdot )$. Any admissible solution $z(\cdot )$ that is above $y(\cdot )$ and such that $z(t)={\hat{y}}$ for $t \ge {\hat{t}}=\min \{ t \in (0,T], y(t)={\hat{y}} \}$, where ${\hat{y}}:=\max _{s \in [0,T]} y(s)$, is also optimal.

We then obtain the equivalence between problems $\mathcal{P}_1$ and $\mathcal{P}$ in the following sense.

Proposition 3.2

If $(u^\star (\cdot ),v^\star (\cdot ))$ is optimal for Problem $\mathcal{P}_1$, then $u^\star (\cdot )$ is optimal for Problem $\mathcal{P}$. Conversely, if $u^\star (\cdot )$ is optimal for Problem $\mathcal{P}$, then $(u^\star (\cdot ),v^\star (\cdot ))$ is optimal for Problem $\mathcal{P}_1$ where $v^\star (\cdot )$ is optimal for the problem (3) for the fixed control $u^\star (\cdot )$.

Let us give another equivalent Mayer problem but with a mixed constraint. (This will be useful in the next section.) We consider again the extended dynamics (2), with a control $v(\cdot )$ which values belong to [0, 1] and the initial conditions $(x(0),y(0),z(0))=(x_0,y_0,y_0)$. Define then the mixed constraint

$$\begin{aligned} \mathcal{C}_m: \quad \max (y(t)-z(t),0)(1-v(t))+z(t)-y(t)\ge 0, \quad \text{ a.e. } t \in [0,T] \end{aligned}$$

and the optimal control problem

$$\begin{aligned} \mathcal{P}_2: \quad \inf _{(u(\cdot ),v(\cdot ))\in \mathcal{U}\times \mathcal{V}} z(T) \quad \text{ under } \text{ the } \text{ constraint } \mathcal{C}_m . \end{aligned}$$

Proposition 3.3

Problems $\mathcal{P}_1$ and $\mathcal{P}_2$ are equivalent.

Proof

One can immediately see that for any admissible solution that satisfies constraint $\mathcal{C}$, the constraint $\mathcal{C}_m$ is necessarily fulfilled as $\max (y-z,0)$ is identically null.

Conversely, fix an admissible control $u(\cdot )$ and consider a control $v(\cdot )$ that satisfies $\mathcal{C}_m$. We show that this implies that the solution $(y(\cdot ),z(\cdot ))$ verifies necessarily $z(t)\ge y(t)$ for any $t \in [0,T]$. If not, consider the non-empty set

$$\begin{aligned} E:=\{ t \in [0,T]; \; z(t)-y(t)<0 \} \end{aligned}$$

which is open as $z-y$ is continuous. Note that one has $\dot{z}(t)-\dot{y}(t)\ge 0$ for a.e. $t \in E$. Therefore $z-y$ is non decreasing in E and we deduce that for any $t \in E$, the interval [0, t] is necessarily included in E, which then contradicts the initial condition $z(0)=y(0)$. $\square$

4 Formulation Without State Constraint

We posit $\Pi =(x,y,z) \in \mathcal{D}\times \mathbb {R}$ and consider the differential inclusion

$$\begin{aligned} {\dot{\Pi }} \in F(\Pi ):= \bigcup _{(u,v) \in U\times [0,1]} \begin{bmatrix} f(x,y,u)\\ g(x,y,u)\\ h(x,y,z,u,v) \end{bmatrix} \end{aligned}$$

(7)

with

$$\begin{aligned} h(x,y,z,u,v)=\max (g(x,y,u),0)(1-v\mathbb {1}_{\mathbb {R}^+}(z-y)), \end{aligned}$$

where $\mathbb {1}_{\mathbb {R}^+}$ is the indicator function

$$\begin{aligned} \mathbb {1}_{\mathbb {R}^+}(\zeta )={\left\{ \begin{array}{ll} 1, &{} \zeta \ge 0 ,\\ 0, &{} \zeta <0 . \end{array}\right. } \end{aligned}$$

Let $\Pi _0=(x_0,y_0,y_0)$ and denote by $\mathcal{S}_\ell$ the set of absolutely continuous solutions of (7) with $\Pi (0)=\Pi _0 \in \mathcal{D}\times \mathbb {R}$. We consider the Mayer problem

$$\begin{aligned} \mathcal{P}_3: \quad \inf _{\Pi (\cdot ) \in \mathcal{S}_\ell } z(T) . \end{aligned}$$

Assumption 2

$$\begin{aligned} \forall (x,y) \in \mathcal{D}, \quad G(x,y):=\bigcup _ {u \in U}\begin{bmatrix} f(x,y,u)\\ g(x,y,u) \end{bmatrix} \text{ is } \text{ convex. } \end{aligned}$$

Proposition 4.1

Under Assumption 2, problem $\mathcal{P}_3$ admits an optimal solution. Moreover, any optimal solution $\Pi (\cdot )=(x(\cdot ),y(\cdot ),z(\cdot ))$ verifies

$$\begin{aligned} z(T)=\max _{t \in [0,T]} y(t) \end{aligned}$$

with $(x(\cdot ),y(\cdot ))$ solution of (1) for some control $u(\cdot ) \in \mathcal{U}$ that in turn is optimal for problem $\mathcal{P}$.

Proof

We fix the initial condition $\Pi (0)=\Pi _0$ and consider the augmented dynamics

$$\begin{aligned} {\dot{\Pi }} \in F^\dag (\Pi ):= \bigcup _{(u,v,\alpha ) \in U\times [0,1]^2} \begin{bmatrix} f(x,y,u)\\ g(x,y,u)\\ h^\dag (x,y,z,u,v,\alpha ) \end{bmatrix} \end{aligned}$$

(8)

with

$$\begin{aligned} h^\dag (x,y,z,u,v,\alpha )=(1-\alpha )h(x,y,z,u,v)+\alpha \max _{w \in U} h(x,y,z,w,0) . \end{aligned}$$

Under Assumption 2, the values of $F^\dag$ are convex compact. One can straightforwardly check that the set-valued map $F^\dag$ is upper semi-continuous¹ with linear growth. Therefore, the reachable set $\mathcal{S}_\ell ^\dag (T)$ (where $\mathcal{S}_\ell ^\dag$ denotes the set of absolutely continuous solutions of (8) with $\Pi (0)=\Pi _0$) is compact (see, for instance, [1, Proposition 3.5.5]). Then, there exists a solution $\Pi ^\star (\cdot )=(x^\star (\cdot ),y^\star (\cdot ),z^\star (\cdot ))$ of (8) which minimizes z(T).

Note that any admissible solution $(x(\cdot ),y(\cdot ),z(\cdot ))$ of system (2) that satisfies the constraint $\mathcal{C}_m$ belongs to $\mathcal{S}_\ell \subset \mathcal{S}_\ell ^\dag$. We then get the inequality

$$\begin{aligned} z^\star (T) \le \inf \{ z(T); \; (x(\cdot ),y(\cdot ),z(\cdot )) \text{ sol. } \text{ of } \text{(2) } \text{ with } \mathcal{C}_m \} . \end{aligned}$$

(9)

Let us show that any solution $\Pi (\cdot ) =(x(\cdot ),y(\cdot ),z(\cdot ))$ in $\mathcal{S}_\ell$ verifies

$$\begin{aligned} z(T)\ge \max _{t \in [0,T]} y(t) . \end{aligned}$$

(10)

We show that one has $z(t)\ge y(t)$ for any $t \in [0,T]$. We proceed by contradiction, as in the proof of Proposition 3.3. If the set $E=\{ t \in (0,T); \; z(t)-y(t)<0\}$ is non-empty, one has $\dot{z}(t)-\dot{y}(t)\ge 0$ for a.e. $t \in E$ which implies, by continuity, that one has $z(0)-y(0)<0$ which contradicts the initial condition $z(0)=y(0)$. Moreover, as the map h is nonnegative, $z(\cdot )$ is non decreasing and we conclude that (10) is verified.

On another hand, thanks to Assumptions 1 and 2, we can apply Filippov’s lemma to the set-valued map G, which asserts that $(x(\cdot ),y(\cdot ))$ is solution of (1) for a certain $u(\cdot ) \in \mathcal{U}$. With(10), we obtain

$$\begin{aligned} z^\star (T) \ge \max _{t \in [0,T]} y^\star (t) \ge \inf _{u \in \mathcal{U}} \left\{ \max _{t \in [0,T]} y(t) ; \; (x(\cdot ),y(\cdot )) \text{ sol. } \text{ of } \text{(1) } \right\} \end{aligned}$$

(11)

where $(x^\star (\cdot ),y^\star (\cdot ))$ is solution of (1) for a certain $u^\star (\cdot ) \in \mathcal{U}$.

Finally, inequalities (9) and (11) with Propositions 3.2 and 3.3 show that $z^\star (T)$ is reached by a solution of (2) under the constraint $\mathcal{C}_m$ and that $u^\star (\cdot )$ is optimal for problem $\mathcal{P}$. We also conclude that the optimal value $z^\star (T)$ is reached by a solution in $\mathcal{S}_\ell$, which is thus optimal for problem $\mathcal{P}_3$. $\square$

Remark 4.1

Let us stress that the function h is not continuous, which does not allow to use Filippov’s lemma for the set valued map F. This means that one cannot guarantee a priori that an absolutely continuous solution $\Pi (\cdot )=(x(\cdot ),y(\cdot ),z(\cdot ))$ can be synthesized by a measurable control $(u(\cdot ),v(\cdot ))$. Proposition 4.1 shows that $(x(\cdot ),y(\cdot ))$ is indeed a solution of system (1) for a measurable control $u(\cdot )$, but one cannot guarantee a priori that $z(\cdot )$ can be generated by a measurable control $v(\cdot )$, which is irrelevant for our purpose.

We end this section by exhibiting an approximation scheme from below of the optimal cost. These approaches are of major interest for minimization problems because, since upper bounds are commonly obtained via any sub-optimal control of problem $\mathcal{P}_0$, $\mathcal{P}_1$, $\mathcal{P}_2$ or $\mathcal{P}_3$ (provided typically by a numerical scheme), they are useful to frame the optimal value of the problem. This will be illustrated in Section 5.

Let us consider the family of dynamics parameterized by $\theta >0$

$$\begin{aligned} \dot{x}= & {} f(x,y,u) , \nonumber \\ \dot{y}= & {} g(x,y,u) , \nonumber \\ \dot{z}= & {} h_\theta (x,y,z,u,v) , \end{aligned}$$

(12)

with

$$\begin{aligned} h_{\theta }(x,y,z,u,v)=\max (g(x,y,u),0)(1-v\,e^{-\theta \max (y-z,0)}) . \end{aligned}$$

Here the expression $e^{-\theta \max (y-z,0)}$ plays the role of an approximation of $\mathbb {1}_{\mathbb {R}^+}(z-y)$ when $\theta$ tends to $+\infty$.

We then define the family of Mayer problems

$$\begin{aligned} \mathcal{P}^{\theta }_3: \quad \inf _{\Pi (\cdot ) \in \mathcal{S}_{\theta }} z(T), \end{aligned}$$

where $\mathcal{S}_\theta$ denotes the set of absolutely continuous solutions $\Pi (\cdot )=(x(\cdot ),y(\cdot ),z(\cdot ))$ of (12) for the initial condition $\Pi (0)=\Pi _0$. Let us underline that, for problems with Lipschitz dynamics and without state constraints, necessary conditions based on Pontryagin’s maximum principle can be derived, leading to shooting methods that are known to be very accurate. They can be initialized from numerical solutions of problems $\mathcal{P}_1$ or $\mathcal{P}_2$ that in turn can be obtained, for instance, through direct methods.

Proposition 4.2

Under Assumption 2, consider any increasing sequence of numbers $\theta _n$ $(n \in \mathbb {N})$ that tends to $+\infty$. For each $n \in \mathbb {N}$, the problem $\mathcal{P}_3^{\theta _n}$ admits an optimal solution, and for any sequence of optimal solutions $(x_n(\cdot ),y_n(\cdot ),z_n)(\cdot ))$ of $\mathcal{P}_3^{\theta _n}$, the sequence $(x_n(\cdot ),y_n(\cdot ))$ converges, up to subsequence, uniformly to an optimal solution $(x^\star (\cdot ),y^\star (\cdot ))$ of Problem $\mathcal{P}$, and its derivatives weakly to $(\dot{x}^\star (\cdot ),\dot{y}^\star (\cdot ))$ in $L^2$. Moreover, $z_n(T)$ is an increasing sequence that converges to $\max _{t \in [0,T]} y^\star (t)$.

Proof

As in the proof of Proposition 4.1, we consider for any $\theta >0$ the convexified dynamics

$$\begin{aligned} \dot{x}= & {} f(x,y,u) ,\\ \dot{y}= & {} g(x,y,u) ,\\ \dot{z}= & {} h_\theta ^\dag (x,y,z,u,v,\alpha ):=(1-\alpha )h_\theta (x,y,z,u,v)+\alpha \max _{w \in U} h_\theta (x,y,z,w,0) , \end{aligned}$$

where $\alpha \in [0,1]$. Then, there exists an absolutely continuous solution $(x^\star _\theta (\cdot ),y^\star _\theta (\cdot ),z^\star _\theta (\cdot ))$ and a measurable control $(u^\star _\theta (\cdot ),v^\star _\theta (\cdot ),\alpha ^\star _\theta (\cdot ))$ that minimize z(T). For the control $(u^\star _\theta (\cdot ),v^\star _\theta (\cdot ),0)$, the solution is given by $(x^\star _\theta (\cdot ),y^\star _\theta (\cdot ),\tilde{z}^\star _\theta (\cdot ))$ where ${\tilde{z}}^\star _\theta (\cdot )$ is solution of the Cauchy problem

$$\begin{aligned} \dot{z} = \tilde{l}_\theta (t,z):=h_\theta ^\dag (x^\star _\theta (t),y^\star _\theta (t),z;u^\star _\theta (t),v^\star _\theta (t),0), \; z(0)=y(0) \end{aligned}$$

while $z^\star _\theta (\cdot )$ is solution of

$$\begin{aligned} \dot{z} = l_\theta (t,z):=h_\theta ^\dag (x^\star _\theta (t),y^\star _\theta (t),z,u^\star _\theta (t),v^\star _\theta (t),\alpha ^\star _\theta (t)), \; z(0)=y(0) . \end{aligned}$$

One can check that the inequality

$$\begin{aligned} {\tilde{l}}_\theta (t,z) \le l_\theta (t,z), \quad t \in [0,T], \; z \in \mathbb {R}\end{aligned}$$

is fulfilled, which gives by comparison of solutions of scalar ordinary differential equations (see, for instance, [18]) the inequality

$$\begin{aligned} {\tilde{z}}^\star _\theta (t) \le z^\star _\theta (t), \quad t \in [0,T] . \end{aligned}$$

We deduce that $(x^\star _\theta (\cdot ),y^\star _\theta (\cdot ),z^\star _\theta (\cdot ))$ is necessarily a solution of (12).

Let

$$\begin{aligned} {\bar{y}}:= \inf _{u \in \mathcal{U}} \left\{ \max _{t \in [0,T]} y(t) ; \; (x(\cdot ),y(\cdot )) \text{ sol. } \text{ of } \text{(1) } \right\} . \end{aligned}$$

By Proposition 4.1, we know that there exists an optimal solution $(x(\cdot ),y(\cdot ),z(\cdot ))$ of problem $\mathcal{P}_3$ such that $z(T)={\bar{y}}$. Clearly, this solution belongs to $\mathcal{S}_\theta$ for any $\theta$, and we thus get

$$\begin{aligned} z^\star _\theta (T) \le {\bar{y}} . \end{aligned}$$

(13)

Let

$$\begin{aligned} F_{\theta }(\Pi ):= \bigcup _{(u,v) \in U\times [0,1]} \begin{bmatrix} f(x,y,u)\\ g(x,y,u)\\ h_{\theta }(x,y,z,u,v) \end{bmatrix} \end{aligned}$$

and note that one has

$$\begin{aligned} \lim _{\theta \rightarrow +\infty } d\left( F_\theta (\Pi ),F(\Pi )\right) =0, \quad \Pi \in \mathcal{D}\times \mathbb {R}. \end{aligned}$$

(14)

Consider an increasing sequence of numbers $\theta _n$ ($n \in \mathbb {N}$), and denote $\Pi _n(\cdot )=(x_n(\cdot ),y_n(\cdot ),z_n(\cdot ))$ an optimal solution of problem $\mathcal{P}_3^{\theta _n}$. Note that one has

$$\begin{aligned} \mathcal{S}_{\theta _{n+1}} \subset \mathcal{S}_{\theta _{n}} \cdots \subset \mathcal{S}_{\theta _{0}} . \end{aligned}$$

(15)

Therefore, the sequence ${\dot{\Pi }}_n(\cdot )$ is bounded, and $\Pi _n(\cdot )$ as well. As F is upper semi-continuous, we obtain that $\Pi _n(\cdot )$ converges uniformly on [0, T], up to a subsequence, to a certain $\Pi ^\star (\cdot )=(x^\star (\cdot ),y^\star (\cdot ),z^\star (\cdot ))$ which belongs to $\mathcal{S}_l$ (see, for instance, [7, Th. 3.1.7]). From property(15), we obtain that $z_n(T)$ is a non-decreasing sequence that converges to $z^\star (T)$, and from (13), we get passing at the limit

$$\begin{aligned} z^\star (T) \le {\bar{y}} . \end{aligned}$$

On another hand, $(x^\star (\cdot ),y^\star (\cdot ),z^\star (\cdot ))$ belongs to $\mathcal{S}_l$ and we get from Proposition 4.1 the inequality

$$\begin{aligned} z^\star (T) \ge {\bar{y}} . \end{aligned}$$

Therefore, one has $z^\star (T) = {\bar{y}}$ and $(x^\star (\cdot ),y^\star (\cdot ),z^\star (\cdot ))$ is then an optimal solution of problem $\mathcal{P}_3$. From Proposition 4.1, we obtain that one has necessarily

$$\begin{aligned} z^\star (T)=\max _{t \in [0,T]} y^\star (t) . \end{aligned}$$

Finally, the sequence $(\dot{x}_n(\cdot ),\dot{y}_n(\cdot ))$ being bounded, it converges, up to a subsequence, weakly to $(\dot{x}^\star (\cdot ),\dot{y}^\star (\cdot ))$ in $L^2$ thanks to Alaoglu’s theorem. $\square$

5 Numerical Illustrations

Our aim is to illustrate the different formulations on problems for which the optimal solution is known. We have considered here only direct and Hamilton–Jacobi–Bellman numerical methods, and not indirect methods. As underlined, for instance, in [6], computational schemes based on the maximum principle of Pontryagin (such as the shooting method), although usually quite accurate, require an a priori knowledge of the structure of the solution as well as a good approximation of the adjoint state. Here, our objective is to show that solving numerically problems with maximum cost considering the equivalent formulations we propose can be done straightforwardly with existing software based on direct or Hamilton–Jacobi–Bellman methods, without having to provide the structure of the optimal solution.

5.1 A Particular Class of Dynamics

We consider dynamics of the form

$$\begin{aligned} (\Sigma ): \left\{ \begin{array}{l} \dot{x}= f(x) , \\ \dot{y} = g(x,u) . \end{array}\right. \qquad x \in \mathbb {R}^n, \; u \in U , \end{aligned}$$

Proposition 5.1

A feedback control $x\mapsto \phi ^\star (x)$ such that

$$\begin{aligned} g(x,\phi ^\star (x))=\min _{u \in U} g(x,u), \quad x \in \mathbb {R}^n \end{aligned}$$

is optimal for problem $\mathcal{P}$.

Proof

For a given $x_0$ in $\mathbb {R}^n$, let $x(\cdot )$ be the solution of $\dot{x}=f(x)$, $x(0)=x_0$ independently to the control $u(\cdot )$. For any control $u(\cdot )$, the corresponding solution $y(\cdot )$ verifies

$$\begin{aligned} y(t)&= y(0)+ \int _0^t g(x(\tau ),u(\tau ))\,{\text {d}}\tau \nonumber \\&\quad \ge y(0)+ \int _0^t \min _{v \in U} g(x(\tau ),v)\,{\text {d}}\tau , \quad t \ge 0 . \end{aligned}$$

(16)

Consider the (measurable) map

$$\begin{aligned} \vartheta (t,u):= g(x(t),u), \quad (t,u) \in [0,T]\times U . \end{aligned}$$

From the existence of measurable selection of extrema of measurable maps (see, for instance, Theorem 2 in [5]), there exists a measurable control $u^\star (\cdot )$ such that

$$\begin{aligned} \vartheta (t,u^\star (t))=\min _{v \in U} \vartheta (t,v), \quad t \in [0,T] . \end{aligned}$$

Let $y^\star (\cdot )$ be defined as

$$\begin{aligned} y^\star (t):= y(0)+ \int _0^t g(x(\tau ),u^\star (t))\,{\text {d}}\tau = y(0)+ \int _0^t \min _{v \in U} g(x(\tau ),v)\,{\text {d}}\tau , \quad t \ge 0 . \end{aligned}$$

Clearly, $y^\star (\cdot )$ is solution of $\Sigma$ for the control $u^\star (\cdot )$ and one gets from (16)

$$\begin{aligned} \max _t y(t) \ge \max _t y^\star (t) . \end{aligned}$$

We conclude that $y^\star (\cdot )$ is an optimal trajectory of problem $\mathcal{P}$ for the control generated by the feedback $\phi ^\star$. $\square$

As a toy example, we have considered the system

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}=1, \; x(0)=0 , \\ \dot{y} =(1-x)(2-x)(4-x)(1+u/2), \; y(0)=0 , \end{array}\right. \qquad u \in [-1,1] \end{aligned}$$

for which

$$\begin{aligned} \phi ^\star (x)=-{{\,\mathrm{sign}\,}}\Big ( (1-x)(2-x)(4-x) \Big ) \end{aligned}$$

is an optimal control which minimizes $\max _{t \in [0,T]} y(t)$. The optimal control is thus pure bang–bang. Remark that this problem can be equivalently written with a scalar non-autonomous dynamics

$$\begin{aligned} \dot{y} = (1-t)(2-t)(4-t)(1+u/2) \end{aligned}$$

for which the open-loop control

$$\begin{aligned} u^\star (t)=-{{\,\mathrm{sign}\,}}\Big ( (1-t)(2-t)(4-t) \Big ) \end{aligned}$$

is optimal.

For $T=5$, we have first computed the exact optimal solution of problem $\mathcal{P}$ with the open-loop $u^\star (\cdot )$, by integrating the dynamics with Scipy in Python software (see Fig. 2). Effects of perturbations on the switching times on the criterion are presented in Table 1, which show a quite high sensitivity of the optimal control for this problem (as it often the case for bang–bang controls). Then, we have solved numerically problems $\mathcal{P}_0$ to $\mathcal{P}_2$ with a direct method (Bocop software using Gauss II integration scheme) for 500 time steps and an optimization relative tolerance equal to $10^{-10}$. For problem $\mathcal{P}_3$, as the dynamics is not continuous, direct methods do not work well and we have used instead a numerical scheme based on dynamic programming (BocopHJB software) with 500 time steps and a discretization of $200\times 200$ points of the state space. For the additional control v, we have considered only two possible values 0 and 1 as we know that the optimal solution is reached for $v \in \{0,1\}$ (see Proposition 3.1). The numerical results and computation times are summarized in Table 2, while Figure 3 presents the corresponding trajectories.

Fig. 2

Optimal solution: $y(\cdot )$ on the left, $u^\star (\cdot )$ on the right

Table 1 Sensitivity to the optimal switching

Table 2 Comparison of the numerical results

We note that the direct method give very accurate results, and the computation time for problem $\mathcal{P}_0$ is the lowest because it has only one control. The computation time for problem $\mathcal{P}_2$ is slightly higher than for $\mathcal{P}_1$ because the mixed constraint $\mathcal{C}_m$ is heavier to evaluate. The numerical method for problem $\mathcal{P}_3$ is of completely different nature as it computes the optimal solution for all the initial conditions on the grid, which explains a much longer computation time. The accuracy of the results is also directly related to the size of the discretization grid and can be improved by increasing this size but at the price of a longer computation time.

Fig. 3

Comparisons of the three methods on $y(\cdot )$, $u(\cdot )$, $z(\cdot )$ and $v(\cdot )$

It can be noticed in Fig. 3 some differences between the obtained trajectories. Let us underline that after the peak of $y(\cdot )$, there is no longer uniqueness of the optimal control (indeed any value of the control does not modify the value of the peak). Hence, we may think about considering an additional cost after the peak to avoid this multiplicity. However, since neither the value of the peak, nor the time when it is reached, are known, this does not seem easy to implement.

5.2 Application to an Epidemiological Model

The SIR model is one of the most basic transmission models in epidemiology for a directly transmitted infectious disease (see [19] for a complete introduction) and it retakes great importance nowadays due to Covid-19 epidemic.

Consider on a time horizon [0, T] variables S(t), I(t) and R(t) representing the fraction of susceptible, infected and recovery individuals at time $t\in [0,T]$, so that one has $S(t)+I(t)+R(t)=1$ with $S(t),I(t),R(t)\ge 0$. Let $\beta > 0$ be the rate of transmission and $\gamma >0$ the recovery rate. Interventions as lockdowns and curfew are modeled as a factor in rate transmission that we denote u and which represents our control variable taking values in $[0,u_\mathrm{max}]$ with $u_\mathrm{max} \in (0,1)$, where $u=0$ means no intervention and $u=u_\mathrm{max}$ the most restrictive one which reduces as much as possible contacts among population. The SIR dynamics including the control is then given by the following equations:

$$\begin{aligned}&\dot{S}=-(1-u)\beta SI , \end{aligned}$$

(17)

$$\begin{aligned}&\dot{I}=\,(1-u)\beta SI-\gamma I ,\end{aligned}$$

(18)

$$\begin{aligned}&\dot{R}=\gamma I . \end{aligned}$$

(19)

When the reproduction number $\mathcal{R}_0=\beta /\gamma$ is above one and the initial proportion of susceptible is above the herd immunity threshold $S_h=\mathcal{R}_0^{-1}$, it is well known that there is an epidemic outbreak. Then, the objective is to minimize the peak of the prevalence

$$\begin{aligned} \max _{t \in [0,T]} I(t) \end{aligned}$$

with respect to control $u(\cdot )$ subject to a $L^1$ budget

$$\begin{aligned} \int _{0}^{T}u(t)\le Q \end{aligned}$$

(20)

on a given time interval [0, T] where T is in chosen large enough to ensure the herd immunity of the population is reached at date T. Note that one can drop the R dynamics to study this problem. If the constraint (20) were not imposed, then the optimal solution would be the trivial control $u(t)=u_\mathrm{max}, \; t\in [0,T]$, which is in general unrealistic from an operational point of view. A similar problem has been considered in [16] but under the constraint that intervention occurs only once on a time interval of given length that we relax here. Note that the constraint (20) can be reformulated as a target condition, considering the augmented dynamics

$$\begin{aligned}&\dot{S}=-(1-u)\beta SI ,\end{aligned}$$

(21)

$$\begin{aligned}&\dot{I}=\,(1-u)\beta SI-\gamma I , \end{aligned}$$

(22)

$$\begin{aligned}&\dot{C}=-u(t) , \end{aligned}$$

(23)

with initial condition $C(0)=Q$ and target $\{ C \ge 0 \}$. Extension of the results of Sections 3 and 4 to problems with target does not present any particular difficulty and is left to the reader.

For initial conditions $I_0=I(0)>0$ and $S_0=S(0)>S_h$, the optimal solution has been determined in [13] as the feedback control

$$\begin{aligned} \psi (I,S):={\left\{ \begin{array}{ll} 1- \frac{S_{h}}{S} &{} \text{ if } I={\bar{I}} \text{ and } S> S_{h},\\ 0 &{} \text{ otherwise, } \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} {\bar{I}}:=\frac{I_0 + S_0 -S_{h}-S_{h}\log \left( \frac{S_0}{S_{h}}\right) }{Q\beta S_h+1} \end{aligned}$$

is the optimal value of the peak. The proof of the optimality of this feedback is out of the scope of the present paper and can be found in [13]. This control strategy consists in three phases:

• 1. no intervention until the prevalence I reaches ${\bar{I}}$ (null control),

• 2. maintain the prevalence I equal to ${\bar{I}}$ until S reaches $S_h$ (singular control),

• 3. no longer intervention when $S>S_h$ (null control),

as illustrated in Fig. 4 for the parameters given in Table 3. Note that differently to the previous example, this control strategy is intrinsically robust with respect to a bad choice of ${\bar{I}}$: the maximum value of I is always guaranteed to be equal to $\bar{I}$. However, a mischoice of ${\bar{I}}$ has an impact on the budget (see [13] for more details).

Fig. 4

The optimal solution for the SIR problem

Table 3 Parameters used in numerical computations and optimal value of the peak

Adding the z-variable, we end up with a dynamics in dimension four, which is numerically heavier than for the previous example. In particular, methods based on the value function are too time consuming to obtain accurate results for refined grids in a reasonable computation time. So we have considered direct methods only. We do not consider here problem $\mathcal{P}_3$, but instead its regular approximations $\mathcal{P}_3^\theta$ suitable to direct methods. For direct methods that use algebraic differentiation of the dynamics, convergence and accuracy are much better if one provides differentiable dynamics. This is why we have approximated the $\max (\cdot ,0)$ operator for problems $\mathcal{P}_1$ and $\mathcal{P}_2$ by the Laplace formula

$$\begin{aligned} \dfrac{\log \left( e^{\lambda \xi }+1\right) }{\lambda } \underset{\lambda \rightarrow +\infty }{\longrightarrow } \max (\xi ,0), \quad \xi \in \mathbb {R}\end{aligned}$$

with $\lambda =100$ for the numerical experiments. For problem $\mathcal{P}_3^\theta$, one has to be careful about the interplay between the approximations of $\max (\cdot ,0)$ and the sequence $\theta _n \rightarrow +\infty$, to provide approximations from below of the optimal value. The function $h_{\theta }$ is thus approximated by the expression

$$\begin{aligned} h_\theta (x,y,z,u,v) \simeq \dfrac{\log \left( e^{\lambda _1 g(x,y,u)}+1\right) }{\lambda _1}\left( 1-v e^{\frac{\theta }{\lambda _2} \log \left( e^{\lambda _2 (y-z)}+1\right) }\right) \end{aligned}$$

which depends on three parameters $\lambda _1$, $\lambda _2$ and $\theta$. Posit for convenience

$$\begin{aligned} \alpha :=\frac{\theta }{\lambda _2} \end{aligned}$$

and consider the function

$$\begin{aligned} \omega _{\alpha ,\lambda _2}(\xi ):=e^{-\alpha \log \left( e^{-\lambda _2 \xi }+1\right) }, \quad \xi \in \mathbb {R}\end{aligned}$$

which approximates the indicator function $\mathbb {1}_{\mathbb {R}^+}$.

Lemma 5.1

One has the following properties.

• 1. For any positive numbers $\alpha$, $\lambda _2$, the function $\omega _{\alpha ,\lambda _2}$ is increasing with

  $$\begin{aligned} \lim _{\xi \rightarrow -\infty } \omega _{\alpha ,\lambda _2}(\xi )=0, \quad \lim _{\xi \rightarrow +\infty } \omega _{\alpha ,\lambda _2}(\xi )=1 . \end{aligned}$$

• 2. For any $\varepsilon \in (0,1)$, one has $\omega _{\alpha ,\lambda _2}\left( -\varepsilon ^2\right) =\varepsilon$ and $\omega _{\alpha ,\lambda _2}(0)=1-\varepsilon$ exactly for

  $$\begin{aligned} \alpha =-\frac{\log (1-\varepsilon )}{\log (2)}, \quad \lambda _2=\frac{\log (\varepsilon ^{-\frac{1}{\alpha }}-1)}{\varepsilon ^2} . \end{aligned}$$

  (24)

Proof

One has first

$$\begin{aligned} \omega '_{\alpha ,\lambda _2}(\xi )=\lambda _2 \alpha \dfrac{e^{-\lambda _2 x}}{e^{-\lambda _2\xi }+1}\omega _{\alpha ,\lambda _2}(\xi )>0 \end{aligned}$$

and the function $\omega _{\alpha ,\lambda _2}(\cdot )$ is thus increasing. From

$$\begin{aligned} \lim _{\xi \rightarrow -\infty } -\alpha \log (e^{-\lambda _2 \xi }+1)= -\infty \end{aligned}$$

one get

$$\begin{aligned} \lim _{\xi \rightarrow -\infty } \omega _{\alpha ,\lambda _2}(\xi )=0 \end{aligned}$$

and similarly

$$\begin{aligned} \lim _{\xi \rightarrow +\infty }-\alpha \log (e^{-\lambda _2 \xi }+1)=0 \end{aligned}$$

implies

$$\begin{aligned} \lim _{\xi \rightarrow +\infty } \omega _{\alpha ,\lambda _2}(\xi )=1 . \end{aligned}$$

Finally, with simple algebraic manipulation of the conditions $\omega _{\alpha ,\lambda _2}\left( -\varepsilon ^2\right) =\varepsilon$ and $\omega _{\alpha ,\lambda _2}(0)=1-\varepsilon$, one obtains straightforwardly the expressions (24). $\square$

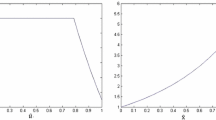
We have taken $\lambda _1=5000$ and considered a sequence of approximations of the indicator function for the values given in Table 4 according to expressions (24) of Lemma 5.1 (see Fig. 5).

Table 4 Values of parameters $\alpha$, $\lambda _2$ for different values of $\varepsilon$

Fig. 5

Approximation of the indicator function with different values of $\varepsilon$ (zoom on the abscissa axis on the right)

Computations have been performed with Bocop software on a standard laptop computer (with a Gauss II integration scheme, 600 time steps and relative tolerance $10^{-10}$). As one can see in Fig. 6 and Table 5 problems $\mathcal{P}_0$, $\mathcal{P}_1$, $\mathcal{P}_2$ give the peak values with a very good accuracy and present similar performances in terms of computation time. In Fig. 7 and Table 6, the numerical solutions of $\mathcal {P}^{\theta }_3$ are illustrated for the values of $\alpha$ and $\lambda _2$ given in Table 4. As expected, the numerical computation of the family of problems $\mathcal {P}^{\theta }_3$ provides an increasing sequence of approximation from below of the optimal value and thus complements the computation of problems $\mathcal {P}_0$, $\mathcal {P}_1$ or $\mathcal {P}_2$. From figures of Tables 5 and 6, one can safely guarantee that the optimal value belongs to the interval [0.1010, 0.1015]. However, the trajectories found for $\mathcal {P}^{\theta }_3$ are not as closed as the ones of problems $\mathcal {P}_0$, $\mathcal {P}_1$ or $\mathcal {P}_2$. This can be explained by the fact that problems $\mathcal {P}^{\theta }_3$ are not subject to the constraint $z(t) \ge y(t)$ and thus provides trajectories for which z(T) is indeed below $\max _t y(t)$.

Fig. 6

Comparisons of numerical results for the methods $\mathcal{P}_0$, $\mathcal{P}_1$, $\mathcal{P}_2$

Finally, we have compared our approximation technique with the classical approximation of the $L^{\infty }$ criterion by $L^p$ norms

$$\begin{aligned} \mathcal{P}_{L^p} : \quad \inf _{u(\cdot ) \in \mathcal{U}} ||y(t)||_{p} \end{aligned}$$

with the same direct method. To speed up the convergence, we have used the Bocop facility which allows a batch mode which consists in initializing the search from a solution found for a former value of p that have been taken $p\in \lbrace 2,5,10,15\rbrace$ (see Fig. 8). Besides, to ensure convergence it was necessary take 1200 time step instead of 600 as in previous simulations. The total time of the process is 78 s after summing computation times given in Table 7. However, one can see that the trajectory found for $p=15$ is quite far to give a peak value close from the other methods. Moreover, the same method for $p=15$ but initialized from the solution found for $p=2$ gives poor results for a computation time of 50 s (see Fig. 9). We conclude that the $L^p$ approximation is not practically reliable for this kind of problems.

Table 5 Comparison of performances for problems $\mathcal{P}_0$, $\mathcal{P}_1$, $\mathcal{P}_2$

Fig. 7

Comparison of the numerical results for problem $\mathcal {P}^{\theta }_3$

Table 6 Comparison of performances for problem $\mathcal {P}^{\theta }_3$

Fig. 8

Numerical solutions for problems $\mathcal{P}_{L^p}$

Table 7 Comparison of the numerical results with the $L^p$ approximation

Fig. 9

Numerical solution for $\mathcal{P}_{L^{15}}$ without batch iteration (computation time: 50 s)

6 Discussion and Conclusions

In this work, we have presented different reformulations of optimal control problems with maximum cost in terms of extended Mayer problems and tested them numerically on two examples whose optimal solution has bang–bang controls and singular arcs. We have proposed two kinds of formulations: one with state or mixed constraints suitable to direct methods, and another one without any constraint but less regular and suitable to dynamical programming type methods. Moreover, for the latter one, we have proposed an approximation scheme generated by a sequence of regular Mayer unconstrained problems, which performs better than approximations based on $L^p$ norms. However, although this second approach requires larger computation time, it complements the first one providing approximations of the optimal value from above.

This first work puts in perspective the study of necessary optimality conditions for the maximum cost problems with the help of these formulations, which will be the matter of a future work.

Finally, we summarize advantages and drawbacks of the different formulations for numerical computations in Table 8 that could help practitioners in the choice of the method.

Table 8 Comparison of the different formulations