Abstract
Composite optimization offers a powerful modeling tool for a variety of applications and is often numerically solved by means of proximal gradient methods. In this paper, we consider fully nonconvex composite problems under only local Lipschitz gradient continuity for the smooth part of the objective function. We investigate an adaptive scheme for PANOC-type methods (Stella et al. in Proceedings of the IEEE 56th CDC, 2017), namely accelerated linesearch algorithms requiring only the simple oracle of proximal gradient. While including the classical proximal gradient method, our theoretical results cover a broader class of algorithms and provide convergence guarantees for accelerated methods with possibly inexact computation of the proximal mapping. These findings have also significant practical impact, as they widen scope and performance of existing, and possibly future, general purpose optimization software that invoke PANOC as inner solver.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Problems involving the minimization of the sum of a smooth and a nonsmooth function are of interest for a wide variety of applications ranging from optimal and model predictive control (MPC), signal processing, compressed sensing, machine learning, and many others; see, e.g., [10, 19, 30] and references therein. Structured problems can also arise as subproblems within other numerical optimization algorithms, e.g.,the augmented Lagrangian method (ALM) [5, 7, 23]. These use cases often yield nonconvex and large-scale problems and can pose stringent requirements in terms of both computation and memory.
In the last few years, these considerations led to a renewed interest in algorithms of splitting nature [10, 19] owing to their simple operation oracles and low memory footprint, on top of their amenability to address nonsmooth, possibly nonconvex, constrained problems, making them widely applicable. The price of this flexibility is paid in terms of slow convergence and sensitivity to ill conditioning, hindering their direct employment to real-time applications, such as MPC, where optimal solutions to hard problems have to be retrieved in very limited time.
Inspired by Newton-type methods for smooth optimization, second-order information can be adopted, so as to better scale with problem size and achieve asymptotic superlinear rates. However, only local convergence guarantees can be expected without introducing a globalization strategy, such as a backtracking linesearch procedure. Unfortunately, for nonsmooth problems, even if fast search directions are available classical linesearch strategies are not applicable. In fact, lacking directional differentiability, the notion of descent directions is not relevant for possibly extended-real-valued, discontinuous functions.
In this very setting, the recently introduced PANOC [32] demonstrated how these downsides within the proximal gradient (PG) algorithm can be overcome while retaining all the favorable features. Essentially, PANOC is a linesearch method that uses the so-called forward–backward envelope (FBE) [22] as merit function to globalize the convergence of fast local methods. It offers an umbrella framework that includes the PG method as special instance; other variations are obtained by selecting virtually arbitrary update directions. A most prominent use case is the employment of directions stemming from methods of quasi-Newton type applied to the nonlinear equation \({{\text {R}}_{\gamma }}(x)=0\) that encodes first-order necessary conditions for optimality, where \({{\text {R}}_{\gamma }}\) is a (set-valued) generalization of the gradient mapping for nonsmooth problems, cf. (2.6). In accommodating arbitrary update directions, PANOC does not require differentiability properties on the merit function and waives the need of regularization terms to enforce a descent condition on the update directions. We defer a more detailed analysis to the dedicated Sect. 3.
Although the algorithm uses the same computational oracle of PG, curvature information enables asymptotic superlinear rates under mild assumptions at the limit point [32]. By employing directions of quasi-Newton type, no inner iterative procedure nor Hessian evaluations are required, making PANOC’s iterations simple, lightweight, and scalable. Because of these favorable properties, PANOC was originally meant as a nonlinear MPC solver particularly suited for embedded applications subject to limited hardware capabilities, such as land and aerial vehicles [15, 26, 28] and robotics [3, 4, 27]; see also [13, 18] for extensive surveys and comparisons with other popular methods. Its success in the field led to a reconsideration of the spectrum of problems that the solver could be applied to. On a historical note, this evolution was reflected by a swift rebranding of the acronym over the years, originally meant as Proximal Averaged Newton-type method for Optimal Control in the original publication [32], but then tacitly reproposed as the same method for Optimality Conditions in [2] (and subsequent appearances) to allude to its applicability to the much broader range of composite minimization problems. This flexibility was further exploited in [29], where PANOC is employed as inner solver for ALM minimization subproblems for the general purpose Optimization Engine (OpEn) solver.
This rapid evolution was perhaps neglectful of some aspects, primarily because PG is subject to binding assumptions to guarantee a global Lipschitz differentiability requirement. In the context of MPC, physical bounds on input variables result in optimization problems where the feasible set is bounded, in which case local Lipschitzness can be shown to suffice, making virtually no exclusion to the problems that can be addressed. In more general formulations, and especially so in a fully nonconvex setting, however, all known results are valid under a global Lipschitzness assumption, with the very recent work [14] possibly emerging as unique exception in a vast literature; see also [11, 25] for convex problems. Other alternatives are to be found in the Bregman setting [1, 8, 17], which are, however, subject to (and thus limited in applicability by) the identification of a distance-generating function enabling a so-called Lipschitz-like convexity condition and that makes induced proximal operations tractable at the same time. While this may not seem a major issue in composite minimization, it undeniably constitutes a severe drawback in ALM contexts, where constraints relaxation can produce subproblems with unbounded feasible sets, without this necessarily being the case for the original problem. Although adding large box constraints to ensure convergence may be thought of as a viable solution, unsatisfactory practical performance can persist because of poor geometry estimation, as we will show.
This paper addresses the above-mentioned shortcomings of PANOC, and of PG as a byproduct, by investigating an adaptive stepsize selection rule for its PG oracle. This criterion, in a slightly less general form, was first proposed in [20, Alg. 7], but without theoretical guarantees and driven from a different observation, namely the poor performance of PANOC if initial stepsizes are badly estimated. After confirming this claim with case study examples, we provide a complete convergence theory showing that the method, here referred to as  for clarity, can also cope with local Lipschitzness, while this is not the case for PANOC. Furthermore, we examine the robustness of the improved method with respect to suboptimal solutions of the PG subproblems. These findings will significantly impact on
for clarity, can also cope with local Lipschitzness, while this is not the case for PANOC. Furthermore, we examine the robustness of the improved method with respect to suboptimal solutions of the PG subproblems. These findings will significantly impact on  both in performance and applicability, propagating to all its dependencies, e.g.,by removing stringent assumptions of general purpose optimization solvers such as OpEn [29]. Indeed, the significance and effectiveness of
both in performance and applicability, propagating to all its dependencies, e.g.,by removing stringent assumptions of general purpose optimization solvers such as OpEn [29]. Indeed, the significance and effectiveness of  have already been demonstrated in [12, 21]. As part of the open-source Julia package ProximalAlgorithms.jl [31], our implementation PANOCplus of
have already been demonstrated in [12, 21]. As part of the open-source Julia package ProximalAlgorithms.jl [31], our implementation PANOCplus of  is publicly available.
is publicly available.
A convergence analysis of PG with a locally Lipschitz smooth term and possibly inexact inner minimizations is obtained as simple byproduct of the more general theory here developed. Indeed, a vast class of algorithms is covered by the analysis in this work, thanks to the arbitrarity of the selected update directions within the PANOC framework.
2 Problem Setting and Preliminaries
In this paper we consider structured minimization problems
where \(x\in \mathbb {R}^n\), \(n\in \mathbb {N}\), is the decision variable, under the following standing assumptions, assumed throughout.

Motivated by its efficiency and popularity, yet aware of its inability to address this general problem formulation, this paper studies a robustified variant of  algorithm with adaptive stepsize selection [32, Rem. III.4], building upon the preliminary work of [20, §6.1].
algorithm with adaptive stepsize selection [32, Rem. III.4], building upon the preliminary work of [20, §6.1].  and the proposed generalization
and the proposed generalization  will be presented and compared in Sect. 3, after the needed definitions and preliminary material are covered in this section.
will be presented and compared in Sect. 3, after the needed definitions and preliminary material are covered in this section.
2.1 Notational Conventions
With \(\mathbb {R}\) and \(\overline{\mathbb {R}}\,{:}{=}\,\mathbb {R}\cup \{ \infty \}\) we denote the real and extended real line, and by \(\mathbb {N}=\{ 0,1,\dots \}\) the set of natural numbers. The effective domain of an extended-real-valued function \(h:\mathbb {R}^n\rightarrow \overline{\mathbb {R}}\) is denoted by \({{\,\mathrm{dom}\,}}h\,{:}{=}\,\{ x\in \mathbb {R}^n\,|h(x)<\infty \}\), and we say that h is: proper if \({{\,\mathrm{dom}\,}}h\ne \emptyset \); lower semicontinuous (lsc) if \(h({{\bar{x}}})\le \liminf _{x\rightarrow {{\bar{x}}}}h(x)\) for all \({{\bar{x}}}\in \mathbb {R}^n\); coercive if \(h(x)\rightarrow \infty \) as \(\Vert x\Vert \rightarrow \infty \). For \(\alpha \in \mathbb {R}\), the \(\alpha \)-sublevel set of h is \({{\,\mathrm{lev}\,}}_{\le \alpha } h \,{:}{=}\,\{ x\in \mathbb {R}^n : h(x) \le \alpha \}\).
The notation \(T:\mathbb {R}^n\rightrightarrows \mathbb {R}^n\) indicates a set-valued mapping T that associates every \(x\in \mathbb {R}^n\) to a subset \(T(x)\subseteq \mathbb {R}^n\). The graph of T is \({{\,\mathrm{gph}\,}}T\,{:}{=}\,\{ (x,y) \}[y\in T(x)]\). Following [24, Def. 8.3], we denote by \(\hat{\partial } h:\mathbb {R}^n\rightrightarrows \mathbb {R}^n\) the regular (Fréchet) subdifferential of h, where
The (limiting) subdifferential of h is \(\partial h:\mathbb {R}^n\rightrightarrows \mathbb {R}^n\), where \(v \in \partial h({\bar{x}})\) if there exist sequences \({(x^{k},v^{k})_{k\in \mathbb {N}}}\) in \({{\,\mathrm{gph}\,}}{\hat{\partial }} f\) such that \((x^k,v^k,h(x^k))\rightarrow ({{\bar{x}}},v,h({{\bar{x}}}))\). These subdifferentials of h at \({\bar{x}}\in \mathbb {R}^n\) satisfy \({\hat{\partial }}(h+h_0)({{\bar{x}}})={\hat{\partial }} h({{\bar{x}}})+\nabla h_0({{\bar{x}}})\) and \(\partial (h+h_0)({{\bar{x}}})=\partial h({{\bar{x}}})+\nabla h_0({{\bar{x}}})\) for any \(h_0:\mathbb {R}^n\rightarrow \overline{\mathbb {R}}\) continuously differentiable around \({\bar{x}}\) [24, Ex. 8.8]. With respect to (P), we say that \(x^*\in {{\,\mathrm{dom}\,}}\varphi \) is stationary if \(0\in \partial \varphi (x^*)\), which constitutes a necessary optimality condition of \(x^*\) for the minimization of \(\varphi \) [24, Thm. 10.1].
Given a parameter value \(\gamma >0\), the Moreau envelope function \(h^\gamma \) and the proximal mapping \({{\,\mathrm{prox}\,}}_{\gamma h}\) are defined by
and we say that h is prox-bounded if it is proper and \(h + \tfrac{1}{2\gamma }\Vert \cdot \Vert ^2\) is bounded below on \(\mathbb {R}^n\) for some \(\gamma >0\). The supremum of all such \(\gamma \) is the threshold \(\gamma _h\) of prox-boundedness for h. In particular, if h is bounded below by an affine function, then \(\gamma _h = \infty \). When h is lsc, for any \(\gamma \in (0,\gamma _h)\) the proximal mapping \({{\,\mathrm{prox}\,}}_{\gamma h}\) is nonempty- and compact-valued, and the Moreau envelope \(h^\gamma \) finite and locally Lipschitz continuous [24, Thm. 1.25 and Ex. 10.32].
2.2 Proximal Gradient Iterations
Given a point \(x \in \mathbb {R}^n\), one iteration of the proximal gradient (PG) method for problem (P) consists in selecting

where \(\gamma \in (0,\gamma _g)\) is a stepsize parameter. The necessary optimality condition in the minimization problem defining the proximal mapping then reads
and in particular the fixed-point inclusion \(x\in {{\text {T}}_{\gamma }}(x)\) implies the stationarity condition \(0\in \partial \varphi (x)\). By interpreting (2.4) as a fixed-point iteration, one can also consider the associated (set-valued) fixed-point residual \({{\text {R}}_{\gamma }}\), namely
and seek fixed points of \({{\text {T}}_{\gamma }}\) as zeros of the residual \({{\text {R}}_{\gamma }}\).
2.3 Forward–Backward Envelope
At the heart of PANOC rationale is the observation that, under assumptions, the fixed-point residual \({{\text {R}}_{\gamma }}\) in (2.6) is continuous around and even differentiable at critical points [34, §4], and the inclusion problem \(0\in {{\text {R}}_{\gamma }}({}\cdot {})\) reduces to a well-behaved system of equations, when close to solutions. This motivated the adoption of Newton-type directions on \({{\text {R}}_{\gamma }}\) that enable fast convergence when close to solutions. The key tool enabling convergence regardless of whether or not the initial point happens to be sufficiently close to a solution is the so-called forward–backward envelope (FBE).
Definition 2.1
(Forward–backward envelope) Relative to (P), the FBE with stepsize \(\gamma \in (0,\gamma _g)\) is


or, equivalently, letting \(\bar{x}\) be any element of \({{\text {T}}_{\gamma }}(x)\),
Owing to its continuity properties, the FBE has been employed to generalize and improve PG-based algorithms that address the general setting of structured nonconvex optimization [9, 16, 34]. The following results are well known when f has globally Lipschitz gradient [34, Prop.s 4.2 and 4.3]. A simple proof in the more general setting addressed here is given for completeness.
Lemma 2.2
(Properties of the FBE) For any \(\gamma \in (0,\gamma _g)\) the following hold:
-
(i)
\({{\varphi }^{\mathrm{FB}}_{\gamma }}\) is real valued and strictly continuous.
-
(ii)
\({{\varphi }^{\mathrm{FB}}_{\gamma }}(x)\le \varphi (x)\) for any \(x\in \mathbb {R}^n\), with equality holding iff \(x\in {{\text {T}}_{\gamma }}(x)\).
-
(iii)
If \({{\bar{x}}}\in {{\text {T}}_{\gamma }}(x)\) and \( f({{\bar{x}}}) {}\le {} f(x) {}+{} \left\langle {\nabla f(x),{{{\bar{x}}}-x} {}}\right\rangle +{} \tfrac{L}{2}\Vert {{\bar{x}}}-x\Vert ^2 \), then
$$\begin{aligned} {{\varphi }^{\mathrm{FB}}_{\gamma }}({{\bar{x}}}) {}\le {} \varphi ({{\bar{x}}}) {}\le {} {{\varphi }^{\mathrm{FB}}_{\gamma }}(x) {}-{} \tfrac{1-\gamma L}{2\gamma }\Vert x-{{\bar{x}}}\Vert ^2. \end{aligned}$$(2.8)
Proof
Lemma 2.2(i) follows from the expression (2.7b), owing to the similar property of the Moreau envelope \(g^\gamma \), while 2.2(ii) is obtained by taking \(w=x\) in (2.7a). The first inequality in 2.2(ii) owes to item 2.2(ii) (independently of L), and the second one follows from the expression (2.7c) of \({{\varphi }^{\mathrm{FB}}_{\gamma }}\). \(\square \)
3 Good and Bad Adaptive Stepsize Selection Rules
As briefly mentioned in Sect. 2.3, the FBE is the key tool for globalizing the convergence of fast local methods, such as of quasi-Newton type, applied to the nonlinear equation \({{\text {R}}_{\gamma }}(x)=0\) encoding necessary optimality conditions for (P). Elaborating on how Newton-type directions can be selected given the nonsmooth, possibly set-valued, nature of \({{\text {R}}_{\gamma }}\) is beyond the scope of this survey, and the interested reader is referred to [32, 34]. The core idea is nevertheless the same as in the familiar context of smooth minimization: trying to enforce (supposedly fast) updates \(x\mapsto x+d\) in place of “nominal” updates \(x\mapsto {{\bar{x}}}\), where \({{\bar{x}}}\) would amount to a gradient step or, in our nonsmooth setting, a proximal gradient step \({{\bar{x}}}\in {{\text {T}}_{\gamma }}(x)\) as in (2.4). Still in complete analogy with the smooth case, accepting a candidate update \(x+d\) must be validated by a “quality check”, like an Armijo-type condition, in violation of which d is either discarded or dampened with a smaller stepsize.  is precisely a mechanism to dampen and accept update directions in a nonsmooth setting, using the FBE as validation control. Its steps are given in Algorithm 1.
is precisely a mechanism to dampen and accept update directions in a nonsmooth setting, using the FBE as validation control. Its steps are given in Algorithm 1.

A basic assumption for  is that \(\nabla f\) be globally \(L_f\)-Lipschitz, so that a well-known quadratic upper bound, see e.g., [6, Prop. A.24], ensures that \(L=L_f\) can be taken for all \(x\in \mathbb {R}^n\) in Lemma 2.2(iii). Alternatively, if g has bounded domain and the selected directions \(d^k\) are bounded, it suffices that \(\nabla f\) is locally Lipschitz-continuous; see [32, Rem. III.4]. For any \(\alpha \in (0,1)\) the choice \(\gamma _k=\nicefrac {\alpha }{L_f}\) then violates step 1.6, meaning that \(\gamma _k\equiv \gamma \) is constant. The dampening of the direction occurs at step 1.2, where starting with \(\tau _k=1\) the candidate update \(x^{k-1}+d^k\) is pushed towards \({{\bar{x}}}^{k-1}\in {{\text {T}}_{\gamma }}(x^{k-1})\) by reducing the steplength \(\tau _k\) until the value of the FBE is sufficiently reduced, cf. step 1.4. \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) is continuous (at \({{\bar{x}}}^{k-1}\)), and it is strictly smaller than \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x^{k-1}) {}-{} \beta \tfrac{1-\alpha }{2\gamma _{k-1}} \Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert ^2 \) there, cf. (2.8).
is that \(\nabla f\) be globally \(L_f\)-Lipschitz, so that a well-known quadratic upper bound, see e.g., [6, Prop. A.24], ensures that \(L=L_f\) can be taken for all \(x\in \mathbb {R}^n\) in Lemma 2.2(iii). Alternatively, if g has bounded domain and the selected directions \(d^k\) are bounded, it suffices that \(\nabla f\) is locally Lipschitz-continuous; see [32, Rem. III.4]. For any \(\alpha \in (0,1)\) the choice \(\gamma _k=\nicefrac {\alpha }{L_f}\) then violates step 1.6, meaning that \(\gamma _k\equiv \gamma \) is constant. The dampening of the direction occurs at step 1.2, where starting with \(\tau _k=1\) the candidate update \(x^{k-1}+d^k\) is pushed towards \({{\bar{x}}}^{k-1}\in {{\text {T}}_{\gamma }}(x^{k-1})\) by reducing the steplength \(\tau _k\) until the value of the FBE is sufficiently reduced, cf. step 1.4. \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) is continuous (at \({{\bar{x}}}^{k-1}\)), and it is strictly smaller than \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x^{k-1}) {}-{} \beta \tfrac{1-\alpha }{2\gamma _{k-1}} \Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert ^2 \) there, cf. (2.8).
3.1
 : the “Good” Adaptive Stepsize Rule
: the “Good” Adaptive Stepsize Rule
What is presented in Algorithm 1 is actually the “adaptive” variant of  , which still works under the assumption of global Lipschitz differentiability but waives the need of prior knowledge about \(L_f\). The \(\gamma \)-backtracking at step 1.6 decreases (i.e.,, “adapts”) \(\gamma _k\) and terminates as soon as the needed bound as in Lemma 2.2(iii) is satisfied. As first noted in [20, §6.1], however, this adaptive criterion may produce bad estimates of the local Lipschitz constant of \(\nabla f\) and overall result in poor algorithmic performance. The phenomenon can be attributed to an asynchrony between the two backtracking steps, the one dampening the update direction and the one adaptively adjusting the proximal gradient stepsize. This claim can be verified in the iteration mismatch between variable \(x^k\) and stepsize \(\gamma _{k-1}\) occurring at step 1.3 (cf. Remark 3.1).
, which still works under the assumption of global Lipschitz differentiability but waives the need of prior knowledge about \(L_f\). The \(\gamma \)-backtracking at step 1.6 decreases (i.e.,, “adapts”) \(\gamma _k\) and terminates as soon as the needed bound as in Lemma 2.2(iii) is satisfied. As first noted in [20, §6.1], however, this adaptive criterion may produce bad estimates of the local Lipschitz constant of \(\nabla f\) and overall result in poor algorithmic performance. The phenomenon can be attributed to an asynchrony between the two backtracking steps, the one dampening the update direction and the one adaptively adjusting the proximal gradient stepsize. This claim can be verified in the iteration mismatch between variable \(x^k\) and stepsize \(\gamma _{k-1}\) occurring at step 1.3 (cf. Remark 3.1).
To account for this fact, [20, Alg. 7] proposes to adapt the PG stepsize \(\gamma _k\) within the linesearch on the update direction. As recently showcased in [21], not only does this conservatism prove beneficial in preventing the acceptance of poor quality directions, but it often also reduces the overall computational cost. Although numerical simulations indicate superior performance, this refined linesearch lacks a theoretical analysis of its convergence properties.

This modification, which we allusively call the “good” adaptive variant (or  for brevity), is depicted in Algorithm 2. In fact, the method presented here presents a slight, but important generalization, namely in allowing the selection of a new direction \(d^k\) every time the stepsize \(\gamma _k\) is reduced, cf. step 2.5, which was not considered in [20, Alg. 7]. This flexibility is crucial: whenever the stepsize \(\gamma _k\) changes so does the PG residual mapping \({{\text {R}}_{\gamma }}\), and consistently so should directions using its curvature information. Moreover, we provide theoretical guarantees on the finite termination of the backtracking linesearch procedure, even without global Lipschitz gradient continuity and merely suboptimal proximal computation. These findings uphold the algorithmic framework proposed in [20, 21, 32] on two aspects: the adaptive linesearch is shown to terminate, and can cope with a merely locally Lipschitz-differentiable term f. Moreover, it will be shown that all this remains true even if the minimization problem defining the PG mapping \({{\text {T}}_{\gamma }}\) is solved inexactly and/or suboptimally.
for brevity), is depicted in Algorithm 2. In fact, the method presented here presents a slight, but important generalization, namely in allowing the selection of a new direction \(d^k\) every time the stepsize \(\gamma _k\) is reduced, cf. step 2.5, which was not considered in [20, Alg. 7]. This flexibility is crucial: whenever the stepsize \(\gamma _k\) changes so does the PG residual mapping \({{\text {R}}_{\gamma }}\), and consistently so should directions using its curvature information. Moreover, we provide theoretical guarantees on the finite termination of the backtracking linesearch procedure, even without global Lipschitz gradient continuity and merely suboptimal proximal computation. These findings uphold the algorithmic framework proposed in [20, 21, 32] on two aspects: the adaptive linesearch is shown to terminate, and can cope with a merely locally Lipschitz-differentiable term f. Moreover, it will be shown that all this remains true even if the minimization problem defining the PG mapping \({{\text {T}}_{\gamma }}\) is solved inexactly and/or suboptimally.
The peculiarity of  over the bad adaptive rule of original
over the bad adaptive rule of original  is that the two backtracking steps, the one on the direction \(\tau _k\) and the one on the PG stepsize \(\gamma _k\), are tightly intertwined. The intricate structure emerges at step 2.5 and 2.6: the direction stepsize \(\tau _k\) resets every time the proximal stepsize \(\gamma _k\) is adjusted and, conversely, the value of \(\gamma _k\) is assessed anew when \(\tau _k\) changes. This entanglement allows the evaluation of the FBE at step 2.4 with an up-to-date stepsize \(\gamma _k\), as opposed to (and eliminating) the asynchrony obstructing
is that the two backtracking steps, the one on the direction \(\tau _k\) and the one on the PG stepsize \(\gamma _k\), are tightly intertwined. The intricate structure emerges at step 2.5 and 2.6: the direction stepsize \(\tau _k\) resets every time the proximal stepsize \(\gamma _k\) is adjusted and, conversely, the value of \(\gamma _k\) is assessed anew when \(\tau _k\) changes. This entanglement allows the evaluation of the FBE at step 2.4 with an up-to-date stepsize \(\gamma _k\), as opposed to (and eliminating) the asynchrony obstructing  ’s performance. The adaptivity of
’s performance. The adaptivity of  allows the FBE \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) to better capture the (local) landscape of \(\varphi \) and, ultimately, to relax the assumption of globally Lipschitz gradient.
allows the FBE \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) to better capture the (local) landscape of \(\varphi \) and, ultimately, to relax the assumption of globally Lipschitz gradient.
To substantiate these claims, in the following Sect. 3.2 we first showcase the ineffectiveness of  applied to problem (P) where f has only locally Lipschitz-continuous gradient, and then compare the “good” and the “bad” adaptive strategies on a common ground in Sect. 3.3.
applied to problem (P) where f has only locally Lipschitz-continuous gradient, and then compare the “good” and the “bad” adaptive strategies on a common ground in Sect. 3.3.
Remark 3.1
(Algorithm notation) Algorithm 2 operates two linesearch steps within each iteration, one on the “proximal” stepsize \(\gamma _k\) at step 2.5 and one on the “direction” stepsize \(\tau _k\) at step 2.6. Whenever the respective needed conditions are violated, either \(\gamma _k\) or \(\tau _k\) is reduced and the iteration restarted from a previous step. As a consequence, variables may be overwritten within each iteration before being accepted. To avoid a heavy double-index notation, used only within proofs out of full rigor, the sub- and superscript notation is designed to differentiate temporary and permanent variables; specifically, within iteration k only variables indexed with k are updated, whereas those indexed with \(k-1\) remain untouched. Similar considerations apply to Algorithm 1.
3.2 Failure of “Bad”  Without Globally Lipschitz Gradient
Without Globally Lipschitz Gradient
Let us consider the minimization of the convex, twice continuously differentiable, coercive function \(\varphi =f+g\), where \(f(x)=\tfrac{2}{9}|x|^3\) and \(g=0\), namely
and adopt  as given in Algorithm 1. In particular, we choose directions
as given in Algorithm 1. In particular, we choose directions
As we are about to show, starting from any \(x_0>0\) this particular choice of directions complies with the bound \(\Vert d_k\Vert \le D\Vert x_{k-1}-{{\bar{x}}}_{k-1}\Vert \) for \(D=18\) and satisfies the \(\tau \)-linesearch with \(\tau _k=1\) for every k. Moreover, the choice \(\alpha =\nicefrac {16}{27}\) leads to a conveniently simple expression for the \(\gamma \)-linesearch, namely \( \gamma _k {}\le {} \tfrac{1}{2x_k} \). As a result, starting from \(x_0>0\) with \(\gamma _0>\tfrac{1}{4x_0}\), the algorithm reduces iterating the following lines
and thus produces a sequence \(x_k=x_04^k\) that is diverging, and causes the cost to increase unboundedly. We now show the claims one by one. To this end, denoting \(y_k\,{:}{=}\,\gamma _kx_k\) throughout, observe that
-
Linesearch on \(\gamma \). For \(x_k>0\) the backtracking on \(\gamma _k\) at step 1.5 (after removing a \(\frac{2}{9}x_k^3\) factor) terminates when
$$\begin{aligned} \left| 1-\tfrac{2}{3}y_k\right| ^3 {}\le {} 1-2y_k+\alpha y_k. \end{aligned}$$(3.5)To simplify the computation, observe that necessarily \(y_k\le 1\) for inequality (3.5) to hold, and in particular the argument of the absolute value is necessarily positive: in fact, since \(y_k=\gamma _kx_k>0\) and \(\alpha <1\), (3.5) implies \( \left| 1-\tfrac{2}{3}y_k\right| ^3 {}\le {} 1-y_k \), hence \(y_k\le 1\). After this simplification and by restricting the analysis to \(y_k=\gamma _kx_k>0\), it can be seen that (3.5) has solution \( 0 {}<{} \gamma _k {}\le {} \frac{9}{4x_k}\left( 1 {}-{} \sqrt{1-\tfrac{2}{3}\alpha } \right) \). For \(\alpha =\nicefrac {16}{27}\), this bound simplifies to \( 0 {}<{} \gamma _k {}\le {} \tfrac{1}{2x_k} \) as claimed. This shows the validity of the first line in (3.3). Since \(\gamma _k\) is halved (only) until it enters this range, one also has that
$$\begin{aligned} y_k\,{:}{=}\,\gamma _kx_k>\tfrac{1}{4} \quad \forall k. \end{aligned}$$(3.6) -
Bound on the directions \(\Vert d_{k+1}\Vert \le D\Vert x_k-{{\bar{x}}}_k\Vert \). Since \( d_{k+1}=\frac{9}{2\gamma _kx_k}(x_k-{{\bar{x}}}_k) \), one has \( \Vert d_{k+1}\Vert {}={} \frac{9}{2|\gamma _kx_k|}\Vert x_k-{{\bar{x}}}_k\Vert {}\le {} 18\Vert x_k-{{\bar{x}}}_k\Vert \) as it follows from (3.6).
-
Linesearch on \(\tau \). Starting with \(x_k>0\) we show that \( x_{k+1} {}={} x_k+d_{k+1} {}={} 4x_k \) satisfies the linesearch condition. Indeed, by using the expression for the FBE in (3.4), according to step 1.4 the iterate \(x_{k+1}=4x_k\) is accepted if
$$\begin{aligned} \tfrac{2}{9}(4x_k)^3 (1-4y_k) {}\le {} \tfrac{2}{9}x_k^3(1-y_k) {}-{} \beta (1-\alpha )\tfrac{2}{9}x_k^3y_k, \end{aligned}$$which is easily reduced to \( y_k {}\ge {} \frac{ 4^3 {}-{} 1 }{ 4^4 {}-{} 1 {}-{} \beta (1-\alpha ) } \). Since \(\beta (1-\alpha )<1\), one has \( \frac{ 4^3 {}-{} 1 }{ 4^4 {}-{} 1 {}-{} \beta (1-\alpha ) } {}\le {} \frac{ 4^3 {}-{} 1 }{ 4^4 {}-{} 2 } {}<{} \tfrac{1}{4} \), and (3.6) implies that the inequality always holds.
We stressed that, although we consider an exemplary problem designed to yield simple computations, similar arguments would still apply for \(C^\infty \), strongly convex formulations, e.g.,\(x^4+x^2\); see also Remark 3.2.
3.3 “Good”  Versus “Bad”
Versus “Bad” 
3.3.1 Robustness Against Poor Directions
In spite of the breakdown demonstrated in Sect. 3.2, global convergence guarantees for  can be recovered by adding a term g with bounded domain, as is the case of a possibly large but bounded box constraint, and selecting update directions \(d_k\) that are bounded, see [32, Rem. III.4]. Nonetheless, as noted in [20, §6.1], this would scarcely help in practice: early iterations would be agnostic to the large box and exhibit the same diverging behavior until the boundary is approached, at which point a drastically reduced stepsize \(\gamma \) would be the cause of a painfully slow convergence.
can be recovered by adding a term g with bounded domain, as is the case of a possibly large but bounded box constraint, and selecting update directions \(d_k\) that are bounded, see [32, Rem. III.4]. Nonetheless, as noted in [20, §6.1], this would scarcely help in practice: early iterations would be agnostic to the large box and exhibit the same diverging behavior until the boundary is approached, at which point a drastically reduced stepsize \(\gamma \) would be the cause of a painfully slow convergence.
We substantiate these claims by considering the example in Sect. 3.2 with some amendments. In particular, we let g be the indicator function of the interval \([-B,B]\), namely \(g(x)=0\) if \(|x|\le B\) and \(g(x)=\infty \) otherwise, and select directions \(d_k\) as above if \(\Vert d_k\Vert \le E\) and \(Ed_k/\Vert d_k\Vert \) otherwise, with possibly large but bounded \(B,E\ge 0\). The problem becomes
Adopting these precautions,  generates iterates that converge to a solution, starting from any initial point. We set \(B=E=100\) for the results displayed in Fig. 1 with a comparison against
generates iterates that converge to a solution, starting from any initial point. We set \(B=E=100\) for the results displayed in Fig. 1 with a comparison against  . Although the latter solves the illustrative problem in its original form (that is, with \(B=\infty \)), we stress that it would not be affected by the safeguards put in place to guarantee the convergence of “bad”
. Although the latter solves the illustrative problem in its original form (that is, with \(B=\infty \)), we stress that it would not be affected by the safeguards put in place to guarantee the convergence of “bad”  .
.
Comparison of convergence metrics versus number of evaluations of \({\text {T}}_\gamma \) for  and
and  on the illustrative problem (3.7), with directions as in (3.2) saturated in the interval \([-100,100]\). We used \(x^0 = 1\), \(\gamma _0 = 1\), \(\alpha = 0.95\), and \(\beta = 0.5\).
on the illustrative problem (3.7), with directions as in (3.2) saturated in the interval \([-100,100]\). We used \(x^0 = 1\), \(\gamma _0 = 1\), \(\alpha = 0.95\), and \(\beta = 0.5\).  ’s iterates diverge until the (safeguarding) box constraint activates, and only then, with a reduced stepsize \(\gamma \), slowly recovers
’s iterates diverge until the (safeguarding) box constraint activates, and only then, with a reduced stepsize \(\gamma \), slowly recovers
The diverging behavior of  is apparent, until the safeguards activate, as expected from Sect. 3.2. At step 1.3
is apparent, until the safeguards activate, as expected from Sect. 3.2. At step 1.3  accepts an update \(x^k\) based on the sufficient decrease of a merit function defined by the FBE with the previous stepsize \(\gamma _{k-1}\). Figure 2 illustrates this phenomenon by comparing the merit functions adopted by
accepts an update \(x^k\) based on the sufficient decrease of a merit function defined by the FBE with the previous stepsize \(\gamma _{k-1}\). Figure 2 illustrates this phenomenon by comparing the merit functions adopted by  and
and  to verify whether a tentative update is to be accepted or not. In this example,
to verify whether a tentative update is to be accepted or not. In this example,  ’s merit function are lower unbounded (see (3.4)) and full steps along the update directions \(d_k\) are accepted, in fact favored, leading to diverging iterates. In turn, this results in a temporary departure from the solution, degrading the overall efficiency of the algorithm. Conversely, at step 2.4
’s merit function are lower unbounded (see (3.4)) and full steps along the update directions \(d_k\) are accepted, in fact favored, leading to diverging iterates. In turn, this results in a temporary departure from the solution, degrading the overall efficiency of the algorithm. Conversely, at step 2.4  verifies sufficient decrease of the FBE with the current stepsize \(\gamma _k\), yielding monotone decrease of the (time varying, but lower bounded) merit function \({{\varphi }^{\mathrm{FB}}_{\gamma }}\), as depicted in Fig. 1. Note that the merit function for
verifies sufficient decrease of the FBE with the current stepsize \(\gamma _k\), yielding monotone decrease of the (time varying, but lower bounded) merit function \({{\varphi }^{\mathrm{FB}}_{\gamma }}\), as depicted in Fig. 1. Note that the merit function for  in Fig. 2 is only piecewise continuous because its evaluation is always preceded by the \(\gamma \)-stepsize backtracking, i.e.,, the stepsize \(\gamma _k=\gamma _k(x^k)\) in \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) depends on the candidate update \(x^k\) being tested. This adaptivity allows
in Fig. 2 is only piecewise continuous because its evaluation is always preceded by the \(\gamma \)-stepsize backtracking, i.e.,, the stepsize \(\gamma _k=\gamma _k(x^k)\) in \({{\varphi }^{\mathrm{FB}}_{\gamma }}\) depends on the candidate update \(x^k\) being tested. This adaptivity allows  to well estimate the geometry of the cost function \(\varphi \) and to construct a tighter merit function.
to well estimate the geometry of the cost function \(\varphi \) and to construct a tighter merit function.
Comparison of the cost function \(\varphi \) for the illustrative problem (3.1) against  ’s and
’s and  ’s merit functions with previous, or initial, estimate \(\gamma _{k-1}=1\)
’s merit functions with previous, or initial, estimate \(\gamma _{k-1}=1\)
These simulations also show that, despite the more conservative linesearch,  does not necessarily require more iterations nor function evaluations to provide a more consistent performance, nor does it lead to a smaller stepsize. Indeed, considering larger box constraints and update directions, i.e.,larger values for B, the limitations and inadequacy of “bad”
does not necessarily require more iterations nor function evaluations to provide a more consistent performance, nor does it lead to a smaller stepsize. Indeed, considering larger box constraints and update directions, i.e.,larger values for B, the limitations and inadequacy of “bad”  in this setting become apparent, while providing support in favor of the (initially) more conservative adaptive scheme of “good”
in this setting become apparent, while providing support in favor of the (initially) more conservative adaptive scheme of “good”  .
.
Remark 3.2
Noticeably, the “bad”  can exhibit this diverging behavior even when the problem admits just one feasible point. To see this, let us consider once again the illustrative example above with \(B=0\), so that \({{\,\mathrm{dom}\,}}g={{\,\mathrm{dom}\,}}\varphi =\{ 0 \}\). Then, patterning the proof in Sect. 3.2, we obtain that the algorithm produces a sequence \({x_k}_{k\in \mathbb {N}}\) that is diverging, despite the fact that \({\bar{x}}^k=0\) for every k, since \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x) {}={} x^2\bigl (\tfrac{1}{2\gamma _k} - \tfrac{4}{9}|x|\bigr ) \) is still lower unbounded for any \(\gamma _k>0\). This also confirms the necessity of imposing bounded \(\Vert d^k\Vert \) in [32, Rem. III.4], in addition to \(\Vert d^k\Vert \le D\Vert x^{k-1}-{{\bar{x}}}^{k-1}\Vert \) as in step 1.1 , not needed in the “good”
can exhibit this diverging behavior even when the problem admits just one feasible point. To see this, let us consider once again the illustrative example above with \(B=0\), so that \({{\,\mathrm{dom}\,}}g={{\,\mathrm{dom}\,}}\varphi =\{ 0 \}\). Then, patterning the proof in Sect. 3.2, we obtain that the algorithm produces a sequence \({x_k}_{k\in \mathbb {N}}\) that is diverging, despite the fact that \({\bar{x}}^k=0\) for every k, since \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x) {}={} x^2\bigl (\tfrac{1}{2\gamma _k} - \tfrac{4}{9}|x|\bigr ) \) is still lower unbounded for any \(\gamma _k>0\). This also confirms the necessity of imposing bounded \(\Vert d^k\Vert \) in [32, Rem. III.4], in addition to \(\Vert d^k\Vert \le D\Vert x^{k-1}-{{\bar{x}}}^{k-1}\Vert \) as in step 1.1 , not needed in the “good”  even with unbounded domains.
even with unbounded domains.
3.3.2 Robustness Against Poor Initial Stepsize Estimation
The poor performance of  on problem (3.7) can be attributed to the bad quality of update directions \(d^k\). We now consider a more meaningful comparison on problem (3.7), this time with directions given by a classical Newton-type approach. We extend f linearly outside of the box \([-B,B]\) so as to make it (convex and) globally Lipschitz differentiable without affecting the problem. We thus consider
on problem (3.7) can be attributed to the bad quality of update directions \(d^k\). We now consider a more meaningful comparison on problem (3.7), this time with directions given by a classical Newton-type approach. We extend f linearly outside of the box \([-B,B]\) so as to make it (convex and) globally Lipschitz differentiable without affecting the problem. We thus consider
where
Because of the constraints, the problem is nonsmooth. Nevertheless, since f is globally \(L_f\)-Lipschitz differentiable (with \(L_f=\frac{2}{3}B^2\)), the minimization of f is equivalent to that of \({{\varphi }^{\mathrm{FB}}_{\gamma }}\), when \(\gamma <\nicefrac {1}{L_f}\). As such, in the spirit of [33] we may select update directions based on a Newton method on the FBE. We simulate the scenario in which \(L_f\) is unknown, thereby selecting an initial stepsize \(\gamma _0\) larger than \(\nicefrac {1}{L_f}\). Since the cost function is coercive and has a unique stationary point, both methods are guaranteed to converge to the unique solution \(x^\star =0\).
We consider classical Newton directions
with \(\mu >0\) as regularization parameter. When not defined, \(\nabla ^2{\varphi }^{\mathrm{FB}}_{\gamma k}\) is intended in a Clarke generalized sense.
Comparison of convergence metrics versus number of evaluations of \({\text {T}}_\gamma \) for  and
and  on problem (3.8), with Newton-type directions as in (3.9) and parameters \(x^0 = 1\), \(\gamma _0 = 1\), \(\alpha = 0.95\), \(\beta = 0.5\), and \(\mu = 10^{-6}\). Similarly to the situation depicted in Fig. 2, the poor geometry estimation of
on problem (3.8), with Newton-type directions as in (3.9) and parameters \(x^0 = 1\), \(\gamma _0 = 1\), \(\alpha = 0.95\), \(\beta = 0.5\), and \(\mu = 10^{-6}\). Similarly to the situation depicted in Fig. 2, the poor geometry estimation of  is responsible for an initial divergent behavior that causes slower asymptotic convergence with a small stepsize
is responsible for an initial divergent behavior that causes slower asymptotic convergence with a small stepsize
Figure 3 shows that  ’s iterates initially diverge, even if the starting point \(x^0\) is close to the solution \(x^\star \), if the proximal stepsize \(\gamma _0\) is poorly estimated, in line with the observations above, and despite the choice of regularized Newton-type directions. Conversely,
’s iterates initially diverge, even if the starting point \(x^0\) is close to the solution \(x^\star \), if the proximal stepsize \(\gamma _0\) is poorly estimated, in line with the observations above, and despite the choice of regularized Newton-type directions. Conversely,  adaptively constructs a tighter merit function and exhibits monotone decrease of \({{\varphi }^{\mathrm{FB}}_{\gamma }}\), as depicted in Fig. 3. Once again, these simulations show that
adaptively constructs a tighter merit function and exhibits monotone decrease of \({{\varphi }^{\mathrm{FB}}_{\gamma }}\), as depicted in Fig. 3. Once again, these simulations show that  provides a more consistent performance without necessarily requiring more iterations or function evaluations; moreover, the nested linesearch procedure does not lead to a smaller stepsize nor does it hinder fast asymptotic convergence.
provides a more consistent performance without necessarily requiring more iterations or function evaluations; moreover, the nested linesearch procedure does not lead to a smaller stepsize nor does it hinder fast asymptotic convergence.
4 Algorithmic Analysis Under Inexact Proximal Oracles
In this section we analyze the properties of the iterates generated by  , starting from their well-definedness. As a substantial proof of robustness with respect to inexact prox evaluations, we will generalize the setting to an extent that the oracle of the proximal mapping is not required, and instead only a local solution of the proximal subminimization problem is needed. We will refer to this variant as the inexact
, starting from their well-definedness. As a substantial proof of robustness with respect to inexact prox evaluations, we will generalize the setting to an extent that the oracle of the proximal mapping is not required, and instead only a local solution of the proximal subminimization problem is needed. We will refer to this variant as the inexact
 and emphasize that the exact counterpart described in Algorithm 2 falls as a special case.
and emphasize that the exact counterpart described in Algorithm 2 falls as a special case.
The investigation in this section originates essentially from three observations. First, in the inexact scenario we cannot avail ourselves of the FBE, as its evaluation requires global optimality in the solution of the proximal subproblem. Second, by considering the equivalent reformulation of (P)
and defining the associated augmented Lagrangian function
we remark that
where
is the result of an exact proximal minimization. Third, in the ALM framework, algorithms can be constructed that converge in some sense to stationary points of the optimization problem, even solving the associated subproblems only approximately [7]. Therefore, we seek relaxed (sub)optimality concepts for the evaluation of the proximal mapping. This viewpoint will ultimately highlight how additionally to being used as a solver within ALMs, as in [12, 21, 29],  can operate as an ALM-type solver itself.
can operate as an ALM-type solver itself.
In the broadest possible setting, we do not require any (sub)optimality in the proximal minimization subproblem other than improvement with respect to the previous iteration. Clearly, additional conditions are needed for generating meaningful iterates, but as a proof of robustness of  we demonstrate that any choice complying with said requirement maintains the well definedness of the algorithm. We will then provide instances of such conditions that, possibly under additional assumptions on the problem, ensure optimality conditions for the limit points of the proposed inexact variant.
we demonstrate that any choice complying with said requirement maintains the well definedness of the algorithm. We will then provide instances of such conditions that, possibly under additional assumptions on the problem, ensure optimality conditions for the limit points of the proposed inexact variant.
Specifically, we consider Algorithm 2 with the following instruction replacing step 2.4 therein, remarking that “exact” \({{\bar{x}}}^k\in {{\text {T}}_{\gamma }}(x^k)\) as prescribed in Algorithm 2 comply with this relaxed requirement (any such \({{\bar{x}}}^k\) is a global minimizer of \(\mathcal {L}(x^k,{}\cdot {},-\nabla f(x^k))\), and \(\varPhi _k={{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\) in this case).

4.1 Well-Definedness and Convergence Results
A crucial complication that the stepsize adjustment in the “good”  suffers if compared with the original one in the “bad”
suffers if compared with the original one in the “bad”  , is that it gives rise to a nested dependency between \(\gamma _k\), \(\tau _k\), and \(d^k\) that could potentially give rise to infinite recursions. While this is fortunately not the case, as we are about to show, the proof is not as straightforward as in [32]. On top of this, while in the “exact” case local boundedness properties of the PG operator \({{\text {T}}_{\gamma }}\) could conveniently be exploited, in accounting also for inexactness even for a fixed \(x^k\) the set of points \({{\bar{x}}}^k\) complying with the relaxed requirement (4.4) may be unbounded. The following result will serve as surrogate of local boundedness for the suboptimal proximal operator.
, is that it gives rise to a nested dependency between \(\gamma _k\), \(\tau _k\), and \(d^k\) that could potentially give rise to infinite recursions. While this is fortunately not the case, as we are about to show, the proof is not as straightforward as in [32]. On top of this, while in the “exact” case local boundedness properties of the PG operator \({{\text {T}}_{\gamma }}\) could conveniently be exploited, in accounting also for inexactness even for a fixed \(x^k\) the set of points \({{\bar{x}}}^k\) complying with the relaxed requirement (4.4) may be unbounded. The following result will serve as surrogate of local boundedness for the suboptimal proximal operator.
Lemma 4.1
Let a constant \(c\in \mathbb {R}\), a sequence \({(\gamma _j)}_j\in \mathbb {N}\searrow 0\), and two bounded sequences \({(u^j,z^j)}_j\in \mathbb {N}\) in \(\mathbb {R}^n\) be fixed, and for every \(j\in \mathbb {N}\) let \({{\bar{z}}}^j\) be such that
Then, \({({{\bar{z}}}^j)}_j\in \mathbb {N}\) is bounded.
Proof
An application of Young’s inequality on the inner product yields
To arrive to a contradiction, up to extracting if necessary, suppose that \(0<\Vert {{\bar{z}}}^j\Vert \rightarrow \infty \). Since \(\liminf _{j\rightarrow \infty }{g({{\bar{z}}}^j)}/{\Vert {{\bar{z}}}^j\Vert ^2}>-\infty \) by [24, Ex. 1.24], dividing by \(\Vert {{\bar{z}}}^j\Vert ^2\) and passing to the limit leads to the contradiction \(0\le -1\). \(\square \)
To avoid trivialities, in what follows we assume that \(x^k\ne {{\bar{x}}}^k\) always holds. This is consistent with stopping criteria based on the PG residual \(\frac{1}{\gamma _k}\Vert x^k-{{\bar{x}}}^k\Vert \), see Sect. 4.2, in which case \(x^k={{\bar{x}}}^k\) would trigger a successful termination.
Lemma 4.2
(Well-definedness of the “good” (inexact)  ). Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). The following hold:
). Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). The following hold:
-
(i)
Well-definedness: at every iteration, the number of backtrackings at steps 2.5 and 2.6 is finite.
-
(ii)
At the end of the kth iteration (\(k\ge 1\)), one has
$$\begin{aligned} \varphi ({{\bar{x}}}^k) {}+{} \delta _k {}\le {} \varPhi _k {}\le {} \varPhi _{k-1} {}-{} \beta \delta _{k-1} \quad \text {where}\quad \delta _k {}\,{:}{=}\,{} \tfrac{1-\alpha }{2\gamma _k} \Vert {{\bar{x}}}^k-x^k\Vert ^2. \end{aligned}$$(4.5) -
(iii)
Every iterate \({{\bar{x}}}^k\) remains within \({{\,\mathrm{lev}\,}}_{\le c}\varphi \), where \(c=\varPhi _0<\infty \).
Proof
As observed in Remark 3.1, each iteration k defines or updates only variables indexed with a k sub/superscript, while those defined in previous iterations are untouched. In what follows, let us index by k, j the variables defined at the jth attempt within iteration k. Note further that \(\gamma _{k,j}L_{k,j}=\alpha \in (0,1)\) holds for every attempt j within every iteration k, since every time \(\gamma _k\) is halved the estimate \(L_k\) is doubled (cf. step 2.5).
-
4.2(i) We proceed by induction on k. If \(k=0\), there is no backtracking on \(\tau \), and from Lemma 4.1 we conclude that all the trials \({{\bar{x}}}^{0,j}\) remain confined in a bounded set \(\varOmega _0\), and therefore any stepsize \(\gamma _{0,j}<\nicefrac {1}{L_{f,\varOmega _0}}\) is accepted. Suppose now that \(k>0\) and observe that, by the definition of \(\varPhi _k\) in (4.4) and the failure of the condition at step 2.5, the inequality
$$\begin{aligned} \varphi ({{\bar{x}}}^{k-1}) {}\le {} \varPhi _{k-1} {}-{} \tfrac{1-\alpha }{2\gamma _{k-1}}\Vert x^{k-1}-{{\bar{x}}}^{k-1}\Vert ^2 \end{aligned}$$(4.6)holds. Since \(\Vert d^{k,j}\Vert \le D\Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert \) and \(\tau _{k,j}\in [0,1]\), any attempt \(x^{k,j}\) defined at step 2.3 during the kth iteration satisfies
$$\begin{aligned} \Vert x^{k,j}-{{\bar{x}}}^{k-1}\Vert {}={} \tau _{k,j}\Vert x^{k-1}-{{\bar{x}}}^{k-1} {}+{} d^{k,j} \Vert {}\le {} (1+D)\Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert \end{aligned}$$and thus remains in a bounded set, be it \(\varOmega _k\). To arrive to a contradiction, suppose that \(\gamma _{k,j}\searrow 0\) as \(j\rightarrow \infty \). Observe that condition (4.4) reads
$$\begin{aligned}&g({{\bar{x}}}^{k,j}) {}+{} \left\langle {{\nabla f(x^{k,j})}{{{\bar{x}}}^{k,j}-{{\bar{x}}}^{k-1}}}\right\rangle \quad \\&\quad {}+{} \tfrac{1}{2\gamma _{k,j}}\Vert x^{k,j}-{{\bar{x}}}^{k,j}\Vert ^2 {}\le {} g({{\bar{x}}}^{k-1}) {}+{} \tfrac{1}{2\gamma _{k,j}}\Vert x^{k,j}-{{\bar{x}}}^{k-1}\Vert ^2. \end{aligned}$$Since \({x^{k,j}}_j\in \mathbb {N}\) is bounded, an application of Lemma 4.1 reveals that \({{{\bar{x}}}^{k,j}}\) too is bounded. Up to possibly enlarging the set, both sequences remain confined in the bounded set \(\varOmega _k\), implying that the condition at step 2.5 should have terminated in finite time, whence the sought contradiction. Hence, \(\gamma _{k,j}\) is backtracked finitely many times within iteration k; up to discarding early attempts, we may denote \(\gamma _{k,j}=\gamma _k\). Condition (4.4) reads
$$\begin{aligned} \mathcal {L}(x^{k,j},{{\bar{x}}}^{k,j},-\nabla f(x^{k,j})) {}\le {}&\mathcal {L}(x^{k,j},{{\bar{x}}}^{k-1},-\nabla f(x^{k,j})) \\ {}={}&f(x^{k,j})+g({{\bar{x}}}^{k-1})+\left\langle {{\nabla f(x^{k,j})}{{{\bar{x}}}^{k-1}-x^{k,j}}}\right\rangle \\&{+{}}\tfrac{1}{2\gamma _k}\Vert x^{k,j}-{{\bar{x}}}^{k-1}\Vert ^2. \end{aligned}$$As \(\tau _{k,j}\searrow 0\), one has that \(x^{k,j}\rightarrow {{\bar{x}}}^{k-1}\). Since f and \(\nabla f\) are continuous, the right-hand side of the inequality converges to \(\varphi ({{\bar{x}}}^{k-1})\), overall resulting in
$$\begin{aligned} \limsup _{j\rightarrow \infty }\mathcal {L}(x^{k,j},{{\bar{x}}}^{k,j},-\nabla f(x^{k,j})) {}\le {} \varphi ({{\bar{x}}}^{k-1}) {}\mathop {\le }\limits ^{4.6}{} \varPhi _{k-1}-\tfrac{1-\alpha }{2\gamma _{k-1}}\Vert x^{k-1}-{{\bar{x}}}^{k-1}\Vert ^2. \end{aligned}$$Since \(\Vert x^{k-1}-{{\bar{x}}}^{k-1}\Vert >0\) and \(\beta <1\), for j large enough the condition at step 2.6 will be violated and therefore the kth iteration successfully terminated.
-
4.2(ii) Follows by combining (4.6) with the failure of the condition at step 2.6 at the end of the iteration.
-
4.2(iii) Direct consequence of Lemma 4.2(ii).\(\square \)
We next consider an asymptotic analysis of the algorithm.
Theorem 4.3
(Asymptotic analysis of the “good” (inexact)  ) Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). The following hold:
) Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). The following hold:
-
(i)
\({(\varPhi _k)}_{k\in \mathbb {N}}\) converges to a finite value \(\varphi _\star \ge \inf \varphi \) from above.
-
(ii)
\( \sum _{k\in \mathbb {N}}\frac{1}{\gamma _k}\Vert {{\bar{x}}}^k-x^k\Vert ^2 {}<{} \infty \).
-
(iii)
\( \lim _{k\rightarrow \infty }\Vert x^k-{{\bar{x}}}^k\Vert {}={} \lim _{k\rightarrow \infty }\Vert x^k-x^{k-1}\Vert {}={} \lim _{k\rightarrow \infty }\Vert {{\bar{x}}}^k-{{\bar{x}}}^{k-1}\Vert {}={} 0 \), and in particular the set of limit points of \({(x^k)}_{k\in \mathbb {N}}\) is closed and connected and coincides with that of \(({\bar{x}}^k)_{k\in \mathbb {N}}\).
-
(iv)
\(\sum _{k\in \mathbb {N}}\gamma _k=\infty \).
-
(v)
\( \liminf _{k\rightarrow \infty }\frac{1}{\gamma _k}\Vert x^k-{{\bar{x}}}^k\Vert {}={} 0 \).
-
(vi)
Consider the following assertions: (1) \(\varphi \) is level bounded; (2) \(({\bar{x}}^k)_{k\in \mathbb {N}}\) is bounded; (3) \(({x^k})_{k\in \mathbb {N}}\) is bounded; (4) \(({\gamma _k})_{k\in \mathbb {N}}\) is asymptotically constant, i.e.,, there exists \(\kappa \in \mathbb {N}\) such that \(\gamma _k=\gamma _\kappa \) for every \(k\ge \kappa \); (5) f has globally Lipschitz-continuous gradient. One has (1) \(\Rightarrow \) (2) \(\Leftrightarrow \) (3) \(\Rightarrow \) (4) \(\Leftarrow \) (5).
Proof
-
4.3(i) Follows from (4.5).
-
4.3(ii) A telescoping argument on (4.5) yields
$$\begin{aligned} \beta (1-\alpha ) \sum _{k\in \mathbb {N}}{ \tfrac{1}{2\gamma _k} \Vert {\bar{x}}^k-x^k\Vert ^2 } {}\le {} \varPhi _0 {}-{} \inf \varphi {}={} {{\varphi }^{\mathrm{FB}}_{\gamma }}(x^0)-\inf \varphi , \end{aligned}$$(4.7)whence the claimed finite sum.
-
4.3(iii) That \(\Vert x^k-{\bar{x}}^k\Vert \rightarrow 0\) follows from Theorem 4.3(ii), since \(\gamma _k\) is upper bounded. Next, by the conditions at step 2.2 and 2.2, observe that
$$\begin{aligned} \Vert x^k-x^{k-1}\Vert {}={}&\bigl \Vert (1-\tau _k)({{\bar{x}}}^{k-1}-x^{k-1}) {}+{} \tau _kd^k \bigr \Vert {}\le {} (1+D)\Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert \end{aligned}$$(4.8)and thus \(\Vert x^k-x^{k-1}\Vert \) vanishes, and in turn so does \(\Vert {{\bar{x}}}^k-{{\bar{x}}}^{k-1}\Vert \) since
$$\begin{aligned} \Vert {{\bar{x}}}^k-{{\bar{x}}}^{k-1}\Vert {}\le {}&\Vert x^k-{{\bar{x}}}^k\Vert {}+{} \Vert {{\bar{x}}}^{k-1}-x^{k-1}\Vert {}+{} \Vert x^k-x^{k-1}\Vert . \end{aligned}$$ -
4.3(vi) The first implication follows from Lemma 4.2(iii), and the second one from Theorem 4.3(ii). If \(({x^k})_{k\in \mathbb {N}}\) is bounded, and thus so is \(({\bar{x}}^k)_{k\in \mathbb {N}}\), the set \(\varOmega _k\) in the proof of Lemma 4.2(i) can be taken independent of k, and asymptotic constancy of \(\gamma _k\) follows from the same arguments therein. Finally, if \(\nabla f\) is \(L_f\)-Lipschitz continuous the condition at step 2.5 fails to hold as soon as \(\gamma _k\le \nicefrac {\alpha }{L_f}\) [6, Prop. A.24], and \(\gamma _k\) is thus asymptotically constant.
-
4.3(iv) By iteratively applying inequality (4.8), we obtain that
$$\begin{aligned} \Vert x^k-x^0\Vert {}\le {}&(1+D)\sum _{j=0}^{k-1}\Vert {{\bar{x}}}^j-x^j\Vert \\ {}={}&(1+D)\sum _{j=0}^{k-1}\gamma _j^{-\nicefrac 12}\Vert {{\bar{x}}}^j-x^j\Vert \gamma _j^{\nicefrac 12} \\ {}\le {}&\textstyle (1+D) \sqrt{ \sum _{j=0}^{k-1} \gamma _j^{-1}\Vert {{\bar{x}}}^j-x^j\Vert ^2 } \sqrt{ \sum _{j=0}^{k-1}\gamma _j } \\ {}\mathop {\le }\limits ^{4.7}{}&\textstyle (1+D) \sqrt{ 2 \frac{{{\varphi }^{\mathrm{FB}}_{\gamma }}(x^0)-\inf \varphi }{\beta (1-\alpha )} } \sqrt{ \sum _{j=0}^{k-1}\gamma _j }. \end{aligned}$$Contrary to the claim, if \({\sum _{k\in \mathbb {N}}\gamma }_k<\infty \) holds, then \(({x^k})_{k\in \mathbb {N}}\) is bounded. From Theorem 4.3(vi) proven above we then infer that \(\gamma _k\) is asymptotically constant, thus contradicting the finiteness of \(\sum _{k\in \mathbb {N}}\gamma _k\).
-
4.3(v) Immediate consequence of Theorem 4.3(ii) and 4.3(iv).\(\square \)
Remark 4.4
If the iterates remain bounded (as is the case when the objective \(\varphi \) is level bounded), owing to Lemma 4.3(vi), Algorithm 2 with exact prox evaluations as in step 2.4 eventually reduces to the original  [32] with constant stepsize, and its convergence results are then readily available, including global convergence (possibly at R-linear rates) under Kurdyka-Łojasiewicz assumptions, and superlinear when converging to a strong local minimum with directions satisfying the Dennis-Moré condition, see [32, 34].
[32] with constant stepsize, and its convergence results are then readily available, including global convergence (possibly at R-linear rates) under Kurdyka-Łojasiewicz assumptions, and superlinear when converging to a strong local minimum with directions satisfying the Dennis-Moré condition, see [32, 34].
Nevertheless, even in accounting for inexact proximal evaluations it is still possible to derive some qualitative guarantees for the limit points, provided that \({{\bar{x}}}^k\) satisfies some local suboptimality requirements. We list two such instances in the following definition and later detail a proof validating the claim.
Definition 4.5
(Prox suboptimality criteria) Relative to the minimization problem (4.3) defining the PG mapping, we say that the iterates \({{\bar{x}}}^k\) computed at step 2.4 are:
-
(i)
\(\delta \)-stationary (for some \(\delta >0\)) if \( {{\,\mathrm{dist}\,}}\bigl (0, \partial \bigl [\mathcal {L}(x^k,{}\cdot {},-\nabla f(x^k))\bigr ]({{\bar{x}}}^k) \bigr ) {}\le {} \delta \), that is, if there exists \({{\bar{v}}}^k\in \partial g({{\bar{x}}}^k)\) such that
$$\begin{aligned} \bigl \Vert {{\bar{v}}}^k+\nabla f(x^k)+\tfrac{1}{\gamma _k}({{\bar{x}}}^k-x^k) \bigr \Vert {}\le {} \delta . \end{aligned}$$(4.9) -
(ii)
Uniformly locally optimal if there exist \(r>0\) and a sequence \(\varepsilon _k\searrow 0\) such that the following local minimality condition holds:
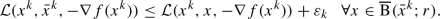 (4.10)
(4.10)
Notice that no (approximate) local minimality is required in the approximate stationarity criterion of Definition 4.5(i). Consequently, the output can be retrieved by any descent method starting at the previous iteration and terminating when \(\delta \)-stationarity is achieved. It is also worth remarking that the prox suboptimality tolerance \(\delta \) does not need to be small nor fixed for all iterations and can instead be replaced by a sequence \(\delta _k\searrow \delta \ge 0\). The uniform local optimality requirement of Definition 4.5(ii) is instead more restrictive, and is possibly subject to prior knowledge on the geometry of the augmented Lagrangian. The uniformity is dictated by the value of \(r>0\), whose role can be appreciated by considering the sequence \(z^k=\nicefrac 1k\) for \(k>0\) which consists of (isolated) local minimizers for the function
yet the limit \(z=0\) is not stationary for h. The pathology arises from the nonuniformity of the radius of local minimality of \(z^k\), which is \(r_k<\nicefrac {1}{k(k+1)}\rightarrow 0\).
Theorem 4.6
(Subsequential convergence of inexact  ) Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). Suppose that the iterates remain bounded (as is the case when \(\varphi \) is coercive), and let \(\omega \) be the set of limit points of \(({\bar{x}}^k)_{k\in \mathbb {N}}\). Then:
) Consider the iterates generated by Algorithm 2 with inexact proximal evaluation at step 2.4 as given in (4.4). Suppose that the iterates remain bounded (as is the case when \(\varphi \) is coercive), and let \(\omega \) be the set of limit points of \(({\bar{x}}^k)_{k\in \mathbb {N}}\). Then:
-
(i)
If \(({\bar{x}}^k)_{k\in \mathbb {N}}\) are \(\delta \)-stationary as in Definition 4.5(i) and \({{\,\mathrm{gph}\,}}\partial g\) is closed relative to \({{\,\mathrm{dom}\,}}g\times \mathbb {R}^n\), then \(\omega \) is made of \(\delta \)-stationary points for \(\varphi \).
-
(ii)
If the sequence \(({\bar{x}}^k)_{k\in \mathbb {N}}\) is (eventually) uniformly locally optimal as in Definition 4.5(ii) (this being true in case of exact prox evaluations, having \(r=\infty \) and \(\varepsilon _k=0\) in this case), then the set \(\omega \) is made of stationary points for \(\varphi \), and \(\varphi \) is constantly equal to \(\varphi _\star \) as in Theorem 4.3(i) there.
Proof
Up to possibly discarding early iterates, in light of the boundedness of the sequences and the consequent eventual constancy of \(\gamma _k\) by 4.3(vi), we may assume that \(\gamma _k\equiv \gamma >0\) holds for all k. Let \(x^\star \in \omega \) be fixed, and let an infinite set of indices \(K\subseteq \mathbb {N}\) be such that \(({2=k\in \mathbb {N}},{3={}})_{{{\bar{x}}}^k}^{[}k\in K]\rightarrow x^\star \), so that \(({2=k\in \mathbb {N}},{3={}})_{x^k}^{[}k\in K]\rightarrow x^\star \) too as it follows from Theorem 4.3(iii).
-
4.6 Since \(\nabla f(x^k)+\tfrac{1}{\gamma }({{\bar{x}}}^k-x^k)\rightarrow \nabla f(x^\star )\) as \(K\ni k\rightarrow \infty \), up to extracting a subsequence if necessary, it follows from (4.9) that \({{\bar{v}}}^k\rightarrow {{\bar{v}}}^\star \) with \(\Vert {{\bar{v}}}^\star +\nabla f(x^\star )\Vert \le \delta \). Since \((\varPhi _k=\mathcal {L}(x^k,{{\bar{x}}}^k,-\nabla f(x^k)))_{k\in \mathbb {N}}\) is bounded, owing to Theorem 4.3(i), and since both f and \(\nabla f\) are continuous, clearly \((g({{\bar{x}}}^k))_{k\in \mathbb {N}}\) remains bounded, and therefore, by lower semicontinuity, \(x^\star \in {{\,\mathrm{dom}\,}}g\). Since also \(({{\bar{x}}}^k)_{k\in K}\subseteq {{\,\mathrm{dom}\,}}g\), from the assumptions we conclude that \({{\bar{v}}}^\star \in \partial g(x^\star )\) and thus \({{\bar{v}}}^\star +\nabla f(x^\star )\in \partial \varphi (x^\star )\), proving \(\delta \)-stationarity of \(x^\star \) for \(\varphi \).
-
4.6 Letting \(\varphi _\star \) be as in 4.3(i) and invoking (4.5), lsc of \(\varphi \) yields \(\varphi (x^\star )\le \varphi _\star \). For k large enough so that \({{\bar{x}}}^k\) is r-close to \(x^\star \), we have
$$\begin{aligned} \varphi _\star {}={} \lim _{k\in K} \varPhi _k {}={}&\lim _{k\in K} \mathcal {L}(x^k,{{\bar{x}}}^k,-\nabla f(x^k)) \\ {}\le {}&\limsup _{k\in K} \mathcal {L}(x^k,x^\star ,-\nabla f(x^k))+\varepsilon _k \\ {}={}&\mathcal {L}(x^\star ,x^\star ,-\nabla f(x^\star )) {}={} \varphi (x^\star ) {}\le {} \varphi _\star , \end{aligned}$$owing to continuity of f and \(\nabla f\), and the fact that both \(\varepsilon _k\) and \(\Vert x^k-{{\bar{x}}}^k\Vert \) vanish (the former by assumption and the latter by 4.3(iii)). From the arbitrarity of \(x^\star \in \omega \) we conclude that \(\varphi \) is constant on \(\omega \) with value \(\varphi _\star \). Notice further this also shows that \(g({{\bar{x}}}^k)\rightarrow g(x^\star )\) as \(K\ni k\rightarrow \infty \). Ekeland’s variational principle [24, Prop. 1.43] with \(\delta _k=\sqrt{\varepsilon _k}\) ensures for every \(k\in K\) (large enough so that \(\sqrt{\varepsilon _k}\le r\)) the existence of
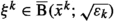 together with $$\begin{aligned} \eta ^k {}\in {} {\hat{\partial \bigl [\mathcal {L}}}(x^k,{}\cdot {},-\nabla f(x^k))\bigr ](\xi ^k) {}={} \nabla f(x^k)+{\hat{\partial }} g(\xi ^k)+\tfrac{1}{\gamma }(\xi ^k-x^k) \end{aligned}$$
together with $$\begin{aligned} \eta ^k {}\in {} {\hat{\partial \bigl [\mathcal {L}}}(x^k,{}\cdot {},-\nabla f(x^k))\bigr ](\xi ^k) {}={} \nabla f(x^k)+{\hat{\partial }} g(\xi ^k)+\tfrac{1}{\gamma }(\xi ^k-x^k) \end{aligned}$$such that \( \mathcal {L}(x^k,\xi ^k,-\nabla f(x^k)) {}\le {} \varPhi _k \) and
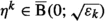 . By lsc of g and since \(\xi ^k\rightarrow x^\star \), necessarily \(g(\xi ^k)\rightarrow g(x^\star )\) and the inclusion \(-\nabla f(x^\star )\in \partial g(x^\star )\) is then readily obtained, whence the claimed stationarity of \(x^\star \) for \(\varphi \).
. By lsc of g and since \(\xi ^k\rightarrow x^\star \), necessarily \(g(\xi ^k)\rightarrow g(x^\star )\) and the inclusion \(-\nabla f(x^\star )\in \partial g(x^\star )\) is then readily obtained, whence the claimed stationarity of \(x^\star \) for \(\varphi \).
\(\square \)
Closedness of \({{\,\mathrm{gph}\,}}\partial g\) relative to \({{\,\mathrm{dom}\,}}g\times \mathbb {R}^n\) as required in Theorem4.6 is frequently encountered in applications and trivially encompasses all functions that are continuous on their domain, such as indicators of closed sets. The 0-norm is instead an example of a function which is not continuous on its domain but that nevertheless complies with the requirement in Theorem 4.6. Indeed, notice that
for \(g=\Vert {}\cdot {}\Vert _0\). Consider a sequence \(x^k\rightarrow x\) along with \(\partial g(x^k)\ni v^k\rightarrow v\); we will show that \(v\in \partial g(x)\), regardless of whether or not \(g(x^k)\) converges to g(x). Indeed, if \(x_i=0\), then trivially \(v_i\in \mathbb {R}=E_i\). Otherwise, \(x_i^k\ne 0\) holds for large enough k, thus necessarily \(v_i^k=0\), and consequently \(v_i\in \{ 0 \}=E_i\). Either way, since this holds for every component, we conclude that \(v\in \partial g(x)\).
4.2 Termination Criteria
Algorithm 2 runs indefinitely and generates an infinite sequence of iterates \((x^k)_{k\in \mathbb {N}}\) and \(({{{\bar{x}}}^k})_{k\in \mathbb {N}}\). Along its execution, we are compelled to check some suitable conditions for stopping and returning an \({{\bar{x}}}^k\) that, in some sense, satisfactorily minimizes \(\varphi \). The Theorem of 4.3(v) guarantees that the standard termination criterion on the residual
is verified in finite time. However, considering (2.5), a control on the magnitude of \(\Vert \nabla f(x^k)-\nabla f({{\bar{x}}}^k)\Vert \) must also be imposed in order to guarantee bounds on \({{\,\mathrm{dist}\,}}(0,\partial \varphi ({{\bar{x}}}^k))\). This calls for a strengthened linesearch condition at step 2.5 ensuring also the satisfaction of
so that, by a triangular inequality argument on (2.5), \(\varepsilon \)-stationarity of \({{\bar{x}}}^k\) (that is, \({{\,\mathrm{dist}\,}}(0,\partial \varphi ({{\bar{x}}}^k))\le \varepsilon \)) would be guaranteed by (4.11). On the one hand, owing to Assumption A1 the proof of Lemma 4.2(i) (and of all other results) would still verbatim apply, meaning that this criterion would not affect the well-definedness of Algorithm 2, or in fact any result presented so far. On the other hand, this would require evaluations of \(\nabla f({{\bar{x}}}^k)\), otherwise not needed, and thus affect the overall complexity. To account for this fact, a viable solution is to trigger this strengthened linesearch only after (4.11) is first satisfied, at which point the algorithm can terminate whenever (4.11) is verified again.
Note that the same conclusions can be made under suboptimal prox evaluations complying with the local uniformly of Definition 4.5(ii), as long as \(\varepsilon _k=0\) for all k. In case of \(\delta \)-stationarity as in Definition 4.5(i), instead, the same criterion would guarantee \((\delta +\varepsilon )\)-stationarity of the output.
4.3 Nonmonotone Variant
Nonmonotone linesearch procedures often prove beneficial in practice, as they can reduce conservatism in the linesearch and favor larger steps. By patterning the rationale of the ZeroFPR algorithm [34], a nonmonotone linesearch can be readily integrated in  at step 2.6 without affecting the finite termination and asymptotic properties asserted in Lemma 4.2and Theorem 4.3. This is done by changing the definition of \(\varPhi _k\) at step 2.4 into \(\varPhi _k=(1-p_k)\varPhi _{k-1}+p_k{{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\) for \(k>0\) (with \({{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\) being replaced by \(\mathcal {L}(x^k,{{\bar{x}}}^k,-\nabla f(x^k))\) in the inexact case), where \(({p_k})_{k\in \mathbb {N}}\subset (0,1]\) is any user-selected sequence bounded away from 0. The key observation enabling the possibility to replicate all the convergence results is the inequality \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\le \varPhi _k \), which follows from an elementary induction (cf. [34, Lem. 5.1]).
at step 2.6 without affecting the finite termination and asymptotic properties asserted in Lemma 4.2and Theorem 4.3. This is done by changing the definition of \(\varPhi _k\) at step 2.4 into \(\varPhi _k=(1-p_k)\varPhi _{k-1}+p_k{{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\) for \(k>0\) (with \({{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\) being replaced by \(\mathcal {L}(x^k,{{\bar{x}}}^k,-\nabla f(x^k))\) in the inexact case), where \(({p_k})_{k\in \mathbb {N}}\subset (0,1]\) is any user-selected sequence bounded away from 0. The key observation enabling the possibility to replicate all the convergence results is the inequality \( {{\varphi }^{\mathrm{FB}}_{\gamma }}(x^k)\le \varPhi _k \), which follows from an elementary induction (cf. [34, Lem. 5.1]).
4.4 Adaptive Proximal Gradient Method
By selecting \(d^k = {{\bar{x}}}^{k-1} - x^{k-1}\) at step 2.2,  reduces to the classical proximal gradient method \(x^k\in {{\text {T}}_{\gamma }}(x^{k-1})\) with an adaptive stepsize. In fact, the descent condition at step 2.6 does not need to be checked, as it is always satisfied for any \(\tau _k\), having \( x^k {}={} (1-\tau _k){{\bar{x}}}^{k-1}+\tau _k(x^k+d^k) {}={} {{\bar{x}}}^{k-1} \) independently of the value of \(\tau _k\). For this specific choice of the update direction \(d^k\), the algorithm simplifies and reduces to the proximal gradient method with adaptive stepsize selection given in Algorithm 3. Convergence results developed in the general setting of
reduces to the classical proximal gradient method \(x^k\in {{\text {T}}_{\gamma }}(x^{k-1})\) with an adaptive stepsize. In fact, the descent condition at step 2.6 does not need to be checked, as it is always satisfied for any \(\tau _k\), having \( x^k {}={} (1-\tau _k){{\bar{x}}}^{k-1}+\tau _k(x^k+d^k) {}={} {{\bar{x}}}^{k-1} \) independently of the value of \(\tau _k\). For this specific choice of the update direction \(d^k\), the algorithm simplifies and reduces to the proximal gradient method with adaptive stepsize selection given in Algorithm 3. Convergence results developed in the general setting of  can thus be readily imported, even in the inexact case.
can thus be readily imported, even in the inexact case.
Corollary 4.7
(Convergence of adaptive PG) All the assertions of Theorems 4.3 and 4.6 remain valid for the iterates generated by Algorithm 3.

We note that the exact version of Algorithm 3, that is, with \({{\bar{x}}}^k\in {{\text {T}}_{\gamma }}(x^k)\) in step 2, corresponds to a simplified version of the linesearch strategy [25, LS1], with no relaxation and in finite dimensional spaces but here analyzed for (fully) nonconvex problems. Alternatively, it can be viewed as the monotone PG method outlined in [14, Alg. 3.1] with a slightly more conservative linesearch, since
where the inequalities follow from step 3 and Lemma 2.2(ii). Remarkably, plain continuous differentiability (as opposed to locally Lipschitzian) suffices in the given reference, under a few other technical assumptions. However, the discussion therein is confined to plain PG iterations as in Algorithm 3, while our analysis is more general and captures plain PG as simple byproduct.
5 Conclusions
We investigated an adaptive scheme to appropriately select the proximal stepsize within solvers for fully nonconvex composite optimization, focusing on (and extending) the PANOC framework. Our convergence analysis demonstrates the well-definedness of the algorithm and characterizes its asymptotic properties, possibly in the absence of (global) Lipschitz gradient continuity for the smooth term. Indeed, witnessing the approach’s robustness, we considered a setting with possibly inexact proximal mapping oracle for the nonsmooth term, providing suitable conditions for its approximate computation. By means of detailed illustrative examples, we highlighted weaknesses of previous approaches and the crucial steps undertaken in this work, as well as their benefits in terms of convergence guarantees and efficiency. Our findings indicate that, by better capturing the problem’s geometry, a more conservative adaptive scheme can yield superior practical performance under weaker conditions. Comprising also arbitrary acceleration directions and nonmonotone variants, these results significantly enlarge the scope of PANOC, both as stand-alone tool for optimization and internal solver within other algorithms, e.g.,in ALM and sequential programming approaches.
Data Availability
All data generated or analyzed during this study are included in this manuscript.
References
Ahookhosh, M., Themelis, A., Patrinos, P.: A Bregman forward–backward linesearch algorithm for nonconvex composite optimization: superlinear convergence to nonisolated local minima. SIAM J. Optim. 31(1), 653–685 (2021)
Antonello, N., Stella, L., Patrinos, P., van Waterschoot, T.: Proximal gradient algorithms: applications in signal processing. arXiv:1803.01621 (2020)
Astudillo, A., Gillis, J., Decré, W., Pipeleers, G., Swevers, J.: Towards an open toolchain for fast nonlinear MPC for serial robots. IFAC-PapersOnLine 53(2), 9814–9819 (2020)
Berlin, J., Hess, G., Karlsson, A., Ljungbergh, W., Zhang, Z., Åkesson, K., Götvall, P.-L.: Trajectory generation for mobile robots in a dynamic environment using nonlinear model predictive control. In: 2021 IEEE 17th International Conference on Automation Science and Engineering (CASE), pp. 942–947 (2021)
Bertsekas, D.P.: Constrained Optimization and Lagrange Multiplier Methods. Athena Scientific, Belmont (1996)
Bertsekas, D.P.: Nonlinear Programming, 2nd edn. Athena Scientific, Belmont (1999)
Birgin, E.G., Martínez, J.M.: Practical Augmented Lagrangian Methods for Constrained Optimization. Society for Industrial and Applied Mathematics, Philadelphia (2014)
Bolte, J., Sabach, S., Teboulle, M., Vaisbourd, Y.: First order methods beyond convexity and Lipschitz gradient continuity with applications to quadratic inverse problems. SIAM J. Optim. 28(3), 2131–2151 (2018)
Bonettini, S., Prato, M., Rebegoldi, S.: Convergence of inexact forward-backward algorithms using the forward-backward envelope. SIAM J. Optim. 30(4), 3069–3097 (2020)
Combettes, P.L., Pesquet, J.-C.: Proximal splitting methods in signal processing. In: Bauschke, H.H., Burachik, R.S., Combettes, P.L., Elser, V., Luke, D.R., Wolkowicz, H. (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering, pp. 185–212. Springer, New York (2011)
Cruz, J.Y.B., Nghia, T.T.A.: On the convergence of the forwardbackward splitting method with linesearches. Optim. Methods Softw. 31(6), 1209–1238 (2016)
De Marchi, A., Jia, X., Kanzow, C., Mehlitz, P.: Constrained structured optimization and augmented Lagrangian proximal methods. arXiv:2203.05276 (2022)
Hermans, B.: Penalty and Augmented Lagrangian Methods for Model Predictive Control. Ph.D. thesis, KU Leuven (2021)
Kanzow, C., Mehlitz, P.: Convergence properties of monotone and nonmonotone proximal gradient methods revisited. arXiv:2112.01798 (2021)
Katriniok, A., Sopasakis, P., Schuurmans, M., Patrinos, P.: Nonlinear model predictive control for distributed motion planning in road intersections using PANOC. In: 2019 IEEE 58th Annual Conference on Decision and Control (CDC), pp. 5272–5278 (2019)
Liu, T., Pong, T.K.: Further properties of the forward-backward envelope with applications to difference-of-convex programming. Comput. Optim. Appl. 67(3), 489–520 (2017)
Lu, H., Freund, R.M., Nesterov, Y.: Relatively smooth convex optimization by first-order methods, and applications. SIAM J. Optim. 28(1), 333–354 (2018)
Pålsson, K., Svärling, E.: Nonlinear model predictive control for constant distance between autonomous transport robots. Master’s thesis, Chalmers University of Technology (2020)
Parikh, N., Boyd, S.: Proximal algorithms. Found. Trends Optim. 1(3), 127–239 (2014)
Pas, P.: A matrix-free nonlinear solver for embedded and large-scale optimization. Master’s thesis, KU Leuven (2021)
Pas, P., Schuurmans, M., Patrinos, P.: Alpaqa: A matrix-free solver for nonlinear MPC and large-scale nonconvex optimization. arXiv:2112.02370 (2021)
Patrinos, P., Bemporad, A.: Proximal Newton methods for convex composite optimization. In: 52nd IEEE Conference on Decision and Control (CDC), pp. 2358–2363 (2013)
Rockafellar, R.T.: Augmented Lagrangians and applications of the proximal point algorithm in convex programming. Math. Oper. Res. 1(2), 97–116 (1976)
Rockafellar, R.T., Wets, R.J.B.: Variational Analysis, vol. 317. Springer, Berlin (1998)
Salzo, S.: The variable metric forward-backward splitting algorithm under mild differentiability assumptions. SIAM J. Optim. 27(4), 2153–2181 (2017)
Sathya, A., Sopasakis, P., Van Parys, R., Themelis, A., Pipeleers, G., Patrinos, P.: Embedded nonlinear model predictive control for obstacle avoidance using PANOC. In: 2018 European Control Conference (ECC), pp. 1523–1528 (2018)
Sathya, A.S., Gillis, J., Pipeleers, G., Swevers, J.: Real-time robot arm motion planning and control with nonlinear model predictive control using augmented Lagrangian on a first-order solver. In: 2020 European Control Conference (ECC), pp. 507–512 (2020)
Small, E., Sopasakis, P., Fresk, E., Patrinos, P., Nikolakopoulos, G.: Aerial navigation in obstructed environments with embedded nonlinear model predictive control. In: 2019 18th European Control Conference (ECC), pp. 3556–3563 (2019)
Sopasakis, P., Fresk, E., Patrinos, P.: OpEn: Code generation for embedded nonconvex optimization. IFAC-PapersOnLine 53(2), 6548–6554 (2020)
Stathopoulos, G., Shukla, H., Szucs, A., Ye, P., Jones, C.N.: Operator splitting methods in control. Found. Trends Syst. Control 3(3), 249–362 (2016)
Stella, L.: ProximalAlgorithms.jl: Proximal algorithms for nonsmooth optimization in Julia. Software available at https://github.com/JuliaFirstOrder/ProximalAlgorithms.jl (2022)
Stella, L., Themelis, A., Sopasakis, P., Patrinos, P.: A simple and efficient algorithm for nonlinear model predictive control. In: 2017 IEEE 56th Annual Conference on Decision and Control (CDC), pp. 1939–1944 (2017)
Themelis, A., Ahookhosh, M., Patrinos, P.: On the acceleration of forward-backward splitting via an inexact Newton method. In: Bauschke, H.H., Burachik, R.S., Luke, D.R. (eds.) Splitting Algorithms, Modern Operator Theory, and Applications, pp. 363–412. Springer, Cham (2019)
Themelis, A., Stella, L., Patrinos, P.: Forward-backward envelope for the sum of two nonconvex functions: further properties and nonmonotone linesearch algorithms. SIAM J. Optim. 28(3), 2274–2303 (2018)
Funding
Open Access funding enabled and organized by Projekt DEAL. A. Themelis acknowledges the support of the Japan Society for the Promotion of Science (JSPS) KAKENHI Grant JP21K17710.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Communicated by Gabriele Steidl.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
De Marchi, A., Themelis, A. Proximal Gradient Algorithms Under Local Lipschitz Gradient Continuity. J Optim Theory Appl 194, 771–794 (2022). https://doi.org/10.1007/s10957-022-02048-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-022-02048-5
Keywords
- Nonsmooth nonconvex optimization
- Locally Lipschitz gradient
- Forward–backward splitting
- Linesearch methods





 : the “Good” Adaptive Stepsize Rule
: the “Good” Adaptive Stepsize Rule Without Globally Lipschitz Gradient
Without Globally Lipschitz Gradient Versus “Bad”
Versus “Bad” 



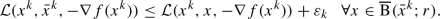
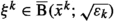 together with
together with 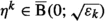 . By lsc of g and since
. By lsc of g and since