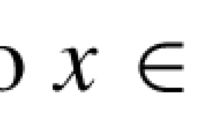1 Introduction

Set optimization problems, i.e. optimization problems with set-valued objective map, are difficult to treat because inequalities of nonconvex sets have a complex structure and they are not simple to characterize. For convex sets, the characterization of set inequalities is known (for basic results see [16]) and can be simply done using certain linear functionals. But for nonconvex sets one needs more elaborate approaches, which are sometimes named scalarization (e.g. see [13] for early results and also [5, 9, 10, 12, 21, 22] together with [20] for related results). These scalarization approaches work with appropriate \(\sup \inf \) problems.

The present paper starts with the known fact that a set inequality can be characterized by an inequality in \(\mathbb {R}\) where these \(\sup \inf \) problems play an important role. We restrict ourselves to the well-known set less order relation (introduced by Young [27] and named by Chiriaev/Walster [3]) so that the presented results also subsume the weaker l-type less and u-type less order relations (see Kuroiwa [23] for first results). The so-called minmax less order relation (introduced in [19]) is only investigated for a special result.

The results of this paper consist of conditions under which the inequalities in \(\mathbb {R}\) are well-defined, characterizations of nonoptimal sets, necessary optimality conditions for the afore-mentioned \(\sup \inf \) problems, necessary conditions for a set inequality and a necessary condition for the non-optimality of a set. The necessary conditions of the main results work with the directional derivative of a functional being used for the description of the negative order cone in the considered real linear space. For different real linear spaces, the directional derivative is calculated for various standard functionals of this type.

This paper is organized as follows: Background material and first results are summarized in Sect. 2. Investigations of non-optimal sets and optimality conditions in nonconvex set optimization are given in Sect. 3. The last section contains the main results like necessary conditions for set inequalities.

2 Basic Results

Throughout this paper we use the following standard assumption.

Assumption 2.1

Let Y be a real linear space, let \(C\subset Y\) be a convex cone, and let a functional \(\psi :Y\rightarrow \mathbb {R}\) be given with

$$\begin{aligned} \psi (y)\le 0\ \Longleftrightarrow \ y\in -C. \end{aligned}$$
(1)

Such a functional \(\psi \) (compare [7, Remark 3.3]), which characterizes the cone \(-C\), is not uniquely defined. With \(\psi \) the functional \(\alpha \psi \) also has the required properties for every \(\alpha >0\).

For convenience, known examples of these functionals are now recalled for different spaces.

Example 2.1

([7, Example 3.4] for (a)–(c))

  1. (a)

    Let the real linear space \(Y:=\mathbb {R}^{m}\) (with \(m\in \mathbb {N}\)) be given. For the polyhedral cone

    $$\begin{aligned} C:=\big \{ y\in \mathbb {R}^{m}\ \big |\ a_{i}^{T}y\le 0\text { for all } i\in \{ 1,\ldots ,k\}\big \} \end{aligned}$$

    with \(k\in \mathbb {N}\) and nonzero vectors \(a_{1},\ldots ,a_{k} \in \mathbb {R}^{m}\) the functional \(\psi :\mathbb {R}^{m}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\max _{i\in \{ 1,\ldots ,k\}}\{-a_{i}^{T}y\} \text { for all }y\in \mathbb {R}^{m} \end{aligned}$$

    fulfills the equivalence (1). In the special case \(C:=\mathbb {R}^{m}_{+}\) we get the functional \(\psi \) given by

    $$\begin{aligned} \psi (y)=\max \{y_{1},\ldots ,y_{m}\} \text { for all } y=(y_{1},\ldots ,y_{m})\in \mathbb {R}^{m}. \end{aligned}$$

    The functional \(\psi :\mathbb {R}^{m}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\Vert (y_{1},\ldots ,y_{m-1})\Vert _{2}+y_{m} \text { for all }y\in \mathbb {R}^{m} \end{aligned}$$

    (where \(m\ge 2\) and \(\Vert \cdot \Vert _{2}\) denotes the Euclidean norm in \(\mathbb {R}^{m-1}\)) is associated to the Lorentz cone

    $$\begin{aligned} C:=\big \{ y\in \mathbb {R}^{m}\ \big |\ \Vert (y_{1},\ldots ,y_{m-1})\Vert _{2} \le y_{m}\big \} . \end{aligned}$$
  2. (b)

    We now consider the real linear space \(Y:={{\mathcal {S}}}^{n}\) (with \(n\in \mathbb {N}\)) of all real symmetric (n, n) matrices. Then the functional \(\psi :\mathcal{S}^{n}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (M)=\max \{\lambda _{1},\ldots ,\lambda _{n}\} \text { for all } M\in {{\mathcal {S}}}^{n} \end{aligned}$$

    (here \(\lambda _{1},\ldots ,\lambda _{n}\) denote the n eigenvalues of the matrix M) is associated to the well-known Löwner cone

    $$\begin{aligned} C:=\big \{ M\in {{\mathcal {S}}}^{n}\ \big |\ M\text { positive semidefinite}\big \} =: {{\mathcal {S}}}^{n}_{+}. \end{aligned}$$

    And the functional \(\psi :{{\mathcal {S}}}^{n}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (M)=\max _{\begin{array}{c} {x\in \mathbb {R}^{n}_{+}}\\ {\Vert x\Vert _2=1} \end{array}} x^{T}Mx \text { for all } M\in {{\mathcal {S}}}^{n} \end{aligned}$$

    is associated to the copositive cone

    $$\begin{aligned} C:=\big \{ M\in {{\mathcal {S}}}^{n}\ \big |\ x^{T}Mx \ge 0\text { for all } x\in \mathbb {R}^{n}_{+}\big \} \end{aligned}$$

    (here \(\Vert \cdot \Vert _{2}\) denotes the Euclidean norm in \(\mathbb {R}^{n}\)).

  3. (c)

    In the infinite dimensional real linear space \(Y:=\mathcal{C}[a,b]\) of real-valued continuous functionals on [a, b] with \(-\infty< a< b < \infty \) the functional \(\psi :\mathcal{C}[a,b]\rightarrow \mathbb {R}\) given by

    $$\begin{aligned} \psi (y)=\max _{t\in [a,b]} y(t) \text { for all } y\in {{\mathcal {C}}}[a,b] \end{aligned}$$

    is associated to the natural ordering cone

    $$\begin{aligned} C:=\big \{ y\in {{\mathcal {C}}}[a,b]\ \big |\ y(t)\ge 0 \text { for all } t\in [a,b]\big \} . \end{aligned}$$
  4. (d)

    Let \((Y,\Vert \cdot \Vert )\) be a real normed space and let some continuous linear functional \(\ell \in Y^*\) be arbitrarily chosen. Then the functional \(\psi :Y\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\ell (y)+\Vert y\Vert \text { for all } y\in Y \end{aligned}$$

    is associated to the so-called Bishop-Phelps cone

    $$\begin{aligned} C(\ell ):=\{ y\in Y\ |\ \ell (y)\ge \Vert y\Vert \} \end{aligned}$$

    (compare [11, 15] for Bishop-Phelps cones).

There are various order relations, which can be used for the comparison of sets in the real linear space Y (e.g. compare [19]). In this paper we restrict ourselves to the well-known set less order relation introduced by Young [27] in 1931.

Definition 2.1

Let Assumption 2.1 be satisfied. For nonempty subsets \(A,B\subset Y\) the set less order relation \(\preccurlyeq _{s}\) is defined by

$$\begin{aligned} A\preccurlyeq _{s} B\ \ :\Longleftrightarrow \ \ B\subset A+C \text{ and } A\subset B-C. \end{aligned}$$

Next we characterize the set inclusions in Definition 2.1 by certain inequalities.

Proposition 2.1

Let Assumption 2.1 be satisfied, and let the nonempty sets \(A,B\subset Y\) be arbitrarily given. Then we assert

$$\begin{aligned} B\subset A+C\ \left\{ \begin{array}{cl} \Longrightarrow &{} \sup _{b\in B}\inf _{a\in A}\psi (a-b)\le 0\\ \Longleftarrow &{} \sup _{b\in B}\min _{a\in A}\psi (a-b)\le 0, \text {if this} \min \text {term exists}\end{array}\right. \end{aligned}$$

and

$$\begin{aligned} A\subset B-C\ \left\{ \begin{array}{cl} \Longrightarrow &{} \sup _{a\in A}\inf _{b\in B}\psi (a-b)\le 0\\ \Longleftarrow &{} \sup _{a\in A}\min _{b\in B}\psi (a-b)\le 0, \text {if this} \min \text {term exists.}\end{array}\right. \end{aligned}$$

Proof

For arbitrary nonempty sets \(A,B\subset Y\) we have

$$\begin{aligned} B\subset A+C\Longleftrightarrow & {} \forall \; b\in B\ \exists \; a\in A:\ \underbrace{b\in \{a\}+C}_{\Leftrightarrow \, a-b\in -C \,\Leftrightarrow \,\psi (a-b)\le 0}\\&\left\{ \begin{array}{c}\Longrightarrow \\ \Longleftarrow \end{array} \right.&\begin{array}{l} \sup _{b\in B}\inf _{a\in A}\psi (a-b)\le 0\\ \sup _{b\in B}\min _{a\in A}\psi (a-b)\le 0, \text { if this} \min \text {term exists.}\end{array} \end{aligned}$$

In analogy, one can prove the second part of the assertion. \(\square \)

The advantage of this simple result is that one can check the validity of the afore-mentioned set inclusions using appropriate optimization problems. Such a rewriting of these set inclusions as inequalities has been already given by Hernández and Rodríguez-Marín [13, Thm. 3.10,(iii)] in 2007 using an extension of the Tammer (formerly Gerstewitz) scalarization approach [8]. Later such a rewriting of set inclusions as inequalities was also given in [22, Thm. 3.3 and 3.8] for scalarizing functionals introduced by Tammer. Proposition 2.1 is parameter free and it subsumes these scalarization approaches.

Next, we investigate under which conditions the \(\sup \min \) problems in Proposition 2.1 are solvable.

Proposition 2.2

Let Assumption 2.1 be satisfied and, in addition, let \((Y,\Vert \cdot \Vert )\) be a real normed space. Let \(A\subset Y\) be a nonempty weakly compact set, let \(B\subset Y\) be a nonempty set, let \(\psi \) be bounded on \(A-B\), and let \(\psi (\cdot -b)\) be weakly semicontinuous for every \(b\in B\). Then the problem \(\sup _{b\in B}\min _{a\in A}\psi (a-b)\) is solvable.

Proof

First, we show the solvability of the problem \(\min _{a\in A}\psi (a-b)\) for an arbitrary \(b\in B\). Since \(\psi (\cdot -b)\) is weakly semicontinuous for every \(b\in B\) and the set A is weakly compact, there is at least one minimal solution \(a_{b}\in A\) with \(\psi (a_{b}-b)=\min _{a\in A}\psi (a-b)\) (e.g., compare [18, Thm. 2.3]). Now we consider the problem \(\sup _{b\in B}\psi (a_{b}-b)\). Because the functional \(\psi \) is assumed to be bounded on the set \(A-B\), it is evident that \(\sup _{b\in B}\psi (a_{b}-b) <\infty \), which has to be shown. \(\square \)

Remark 2.1

In a reflexive Banach space \((Y,\Vert \cdot \Vert )\) the \(\min \) subproblem in Proposition 2.2 is also solvable, if the set A is nonempty convex closed and bounded and the functional \(\psi (\cdot -b)\) is continuous and quasiconvex for all \(b\in B\) (compare [18, Thm. 2.12]).

For specific scalarizing functionals such existence results are also remarked in [22, Remark 1].

Example 2.2

Consider the function \(\psi :\mathbb {R}^{m}\rightarrow \mathbb {R}\) (with \(m\in \mathbb {N}\)) with

$$\begin{aligned} \psi (y) := \max \{y_{1},\ldots ,y_{m}\} \text { for all } y=(y_{1},\ldots ,y_{m})\in \mathbb {R}^{m} \end{aligned}$$

(compare Example 2.1,(a)). The function \(\psi \) is continuous and so, it is also weakly lower semicontinuous because weak and strong convergence coincide in \(\mathbb {R}^{m}\). If \(A,B\subset \mathbb {R}^{m}\) are nonempty sets where A is weakly compact and B is norm bounded, then the set difference \(A-B\) is norm bounded. This implies that the function \(\psi \) is bounded on the set \(A-B\). In this case the function \(\psi \) satisfies the assumptions of Proposition 2.2.

The following proposition is a direct consequence of the Propositions 2.1 and 2.2.

Proposition 2.3

Let Assumption 2.1 be satisfied and, in addition, let \((Y,\Vert \cdot \Vert )\) be a real normed space. Let \(A,B\subset Y\) be nonempty weakly compact sets, let \(\psi \) be bounded on \(A-B\), and let the functionals \(\psi (a-\cdot )\) and \(\psi (\cdot -b)\) be weakly lower semicontinuous for every \(a\in A\) and \(b\in B\), respectively. Then

$$\begin{aligned} \max \left\{ \sup _{b\in B}\mathop {\mathrm {min}}_{a\in A}\psi (a-b), \ \sup _{a\in A}\mathop {\mathrm {min}}_{b\in B}\psi (a-b)\right\} \le 0 \ \ \Longrightarrow \ \ A\preccurlyeq _{s} B. \end{aligned}$$

This proposition gives a sufficient condition for the set less order relation, which may be helpful in practice (see also [22, Corollary 3.11] for specific scalarizing functionals).

3 Optimality

We now turn our attention to problems of set optimization. Based on the set less order relation in a real linear space Y, we consider a family \({\mathcal {F}}\) of nonempty subsets of Y and we investigate optimal sets of \({\mathcal {F}}\).

Definition 3.1

Let Assumption 2.1 be satisfied, and let \({\mathcal {F}}\) be a family of nonempty subsets of Y. A set \({\bar{A}}\in {{\mathcal {F}}}\) is called an optimal set of \({\mathcal {F}}\), iff

$$\begin{aligned} A\preccurlyeq _{s}{\bar{A}},\ \ A\in {{\mathcal {F}}} \ \ \Longrightarrow \ \ {\bar{A}}\preccurlyeq _{s}A. \end{aligned}$$

Under Assumption 2.1 recall for any nonempty subset A of Y that the set

$$\begin{aligned} \min A := \{ a\in A\ |\ (\{a\}-C)\cap A\subset \{a\}+C\} \end{aligned}$$

denotes the set of all minimal elements of A, and the set

$$\begin{aligned} \max A := \{ a\in A\ |\ (\{a\}+C)\cap A\subset \{a\}-C\} \end{aligned}$$

is called the set of maximal elements of A. Of course, if the convex cone C is pointed (i.e. \(C\cap (-C)=\{0_{Y}\}\)), then \(\min A = \{ a\in A\ |\ (\{a\}-C)\cap A = \{a\}\}\) and \(\max A = \{ a\in A\ |\ (\{a\}+C)\cap A = \{a\}\}\).

With the following proposition we investigate the question: What does it mean, if for some set \(A\in {{\mathcal {F}}}\) the two inequalities \(A\preccurlyeq _{s}{\bar{A}}\) and \({\bar{A}}\preccurlyeq _{s}A\) given in Definition 3.1 hold?

Proposition 3.1

Let Assumption 2.1 be satisfied and, in addition, let the convex cone C be pointed. Let \({\mathcal {F}}\) be a family of nonempty subsets of Y, for which the set of minimal elements and the set of maximal elements are nonempty. For every \(A\in {{\mathcal {F}}}\) let the set equalities

$$\begin{aligned} A+C=(\min A)+C\text { and }A-C=(\max A)-C \end{aligned}$$
(2)

be satisfied. For some \({\bar{A}}\in {{\mathcal {F}}}\), we then have

$$\begin{aligned} {\bar{A}}\text { optimal}\Longleftrightarrow & {} \text {for every } A\in {{\mathcal {F}}} \text { with } A\preccurlyeq _{s}{\bar{A}} :\\&\min A = \min {\bar{A}}\text { and }\max A = \max {\bar{A}} . \end{aligned}$$

Proof

For some \({\bar{A}}\in {{\mathcal {F}}}\) and an arbitrary \(A\in {{\mathcal {F}}}\) it holds by definition

$$\begin{aligned} A\preccurlyeq _{s}{\bar{A}}\text { and } {\bar{A}}\preccurlyeq _{s}A \ \ \Longleftrightarrow \ \ {\bar{A}}\subset A+C,\ A\subset {\bar{A}}-C, \ A\subset {\bar{A}}+C,\ {\bar{A}}\subset A-C. \end{aligned}$$

By [17, Lemma 2.4] this is equivalent to the inclusions

$$\begin{aligned} {\bar{A}}+C\subset A+C,\ A-C\subset {\bar{A}}-C, \ A+C\subset {\bar{A}}+C,\ {\bar{A}}-C\subset A-C \end{aligned}$$

again being equivalent to

$$\begin{aligned} {\bar{A}}+C=A+C,\ {\bar{A}}-C=A-C. \end{aligned}$$

By the equalities (2) this can be written as

$$\begin{aligned} (\min {\bar{A}})+C=(\min A)+C,\ (\max {\bar{A}})-C=(\max A)-C. \end{aligned}$$
(3)

The first equality implies \(\min {\bar{A}}\subset (\min A)+C\), which means

$$\begin{aligned} \forall \ {\bar{a}}\in \min {\bar{A}}\ \exists \ a\in \min A,\, c\in C: {\bar{a}}=a+c. \end{aligned}$$

Since the first equality in (3) also implies \(\min A\subset (\min {\bar{A}})+C\), there are \({\hat{a}}\in \min {\bar{A}}\) and \({\hat{c}}\in C\) with \(a={\hat{a}}+{\hat{c}}\). Hence, we get \({\bar{a}}=a+c={\hat{a}}+{\hat{c}}+c\). Because of \({\bar{a}}, {\hat{a}}\in \min {\bar{A}}\) we obtain \({\hat{c}}+c=0_Y\), i.e. \(c=-{\hat{c}}\). Since C is pointed, we conclude \(c\in C\cap (-C)=\{0_{Y}\}\). Consequently, we have \({\bar{a}}=a\) and thereby \(\min {\bar{A}}\subset \min A\). By renaming we also get \(\min A \subset \min {\bar{A}}\), an so we have \(\min A = \min {\bar{A}}\). The equality \(\max A = \max {\bar{A}}\) can be proven in analogy. The assertion then follows with the definition of optimality. \(\square \)

Figure 1 illustrates that the set equalities (2) may also be satisfied for nonconvex sets. For \(Y:=\mathbb {R}^{2}\), \(C:=\mathbb {R}^{2}_{+}\) and A given in Fig. 1 we have \(A+C=(\min A)+C\) and \(A-C=(\max A)-C\).

Fig. 1
figure 1

Illustration of the set equalities (2)

Full size image

But the set inequalities (2) do not hold in general; for instance, if we choose \(Y:=\mathbb {R}^{2}\), \(C:=\mathbb {R}^{2}_{+}\) and \(A:=\{(y_1,y_2)\in \mathbb {R}^2\ |\ y_1^2+y_2^2 < 1\}\cup \{(-1,0)\}\) we have \(\min A=\{(-1,0)\}\) and we get \((\min A)+C= \{(y_1,y_2)\in \mathbb {R}^2\ |\ y_1\ge -1,\; y_2\ge 0\}\ne A+C\), i.e. the first set inequality in (2) is not satisfied.

Remark 3.1

Under the assumptions of Proposition 3.1 we have

For instance, if one works with a descent method for the calculation of an optimal set, one can use this result in order to decide whether a set \({\bar{A}}\) is not optimal. Let \({\bar{A}}\in {{\mathcal {F}}}\) be given and let some set \(A\in {{\mathcal {F}}}\) with \(A\preccurlyeq _{s}{\bar{A}}\) be calculated. If one can check that \(\min A \ne \min {\bar{A}}\) or \(\max A \ne \max {\bar{A}}\), one knows that the set \({\bar{A}}\) cannot be optimal.

The assumption in Proposition 3.1 that the set equalities (2) are fulfilled for all \(A\in {{\mathcal {F}}}\) can be avoided, if one works with a more strict order relation introduced in [19, Def. 3.5].

Definition 3.2

Let Assumption 2.1 be satisfied.

  1. (a)

    For subsets \(A,B\subset Y\), for which the set of minimal elements \(\min (\cdot )\) and the set of maximal elements \(\max (\cdot )\) are nonempty, the minmax less order relation \(\preccurlyeq _{m}\) is defined by

    $$\begin{aligned} A\preccurlyeq _{m} B\ \ :\Longleftrightarrow \ \ \min A \preccurlyeq _{s}\min B \text{ and } \max A \preccurlyeq _{s}\max B. \end{aligned}$$
  2. (b)

    Let \({\mathcal {F}}\) be a family of subsets of Y, for which the set of minimal elements and the set of maximal elements are nonempty. A set \({\bar{A}}\in {{\mathcal {F}}}\) is called a minmax optimal set of \({\mathcal {F}}\), iff

    $$\begin{aligned} A\preccurlyeq _{m}{\bar{A}},\ \ A\in {{\mathcal {F}}} \ \ \Longrightarrow \ \ {\bar{A}}\preccurlyeq _{m}A. \end{aligned}$$

Proposition 3.2

Let Assumption 2.1 be satisfied and, in addition, let the convex cone C be pointed. Let \({\mathcal {F}}\) be a family of nonempty subsets of Y, for which the set of minimal elements and the set of maximal elements are nonempty. For some \({\bar{A}}\in \mathcal{F}\), we then have

$$\begin{aligned} {\bar{A}}\text { minmax optimal}\Longleftrightarrow & {} \text {for every } A\in {{\mathcal {F}}} \text { with } A\preccurlyeq _{m}{\bar{A}} :\\&\min A = \min {\bar{A}}\text { and }\max A = \max {\bar{A}} . \end{aligned}$$

Proof

In analogy to the proof of Proposition 3.1 we obtain for some \({\bar{A}}\in {{\mathcal {F}}}\) and an arbitrary \(A\in {{\mathcal {F}}}\)

$$\begin{aligned}&A\preccurlyeq _{m}{\bar{A}}\text { and } {\bar{A}}\preccurlyeq _{m}A\\&\quad \Longleftrightarrow \min A \preccurlyeq _{s}\min {\bar{A}}, \ \max A \preccurlyeq _{s}\max {\bar{A}}, \ \min {\bar{A}} \preccurlyeq _{s}\min A, \ \max {\bar{A}} \preccurlyeq _{s}\max A\\&\quad \Longleftrightarrow (\min {\bar{A}})+C\subset (\min A)+C, \ (\min A)-C\subset (\min {\bar{A}})-C,\\&\qquad (\max {\bar{A}})+C\subset (\max A)+C, \ (\max A)-C\subset (\max {\bar{A}})-C,\\&\qquad (\min A)+C\subset (\min {\bar{A}})+C, \ (\min {\bar{A}})-C\subset (\min A)-C,\\&\qquad (\max A)+C\subset (\max {\bar{A}})+C, \ (\max {\bar{A}})-C\subset (\max A)-C\\&\quad \Longleftrightarrow (\min A)+C=(\min {\bar{A}})+C,\ (\min A)-C=(\min {\bar{A}})-C,\\&\qquad (\max A)+C=(\max {\bar{A}})+C,\ (\max A)-C=(\max {\bar{A}})-C\\&\quad \Longleftrightarrow \min A=\min {\bar{A}},\ \max A=\max {\bar{A}}. \end{aligned}$$

This leads to the assertion. \(\square \)

The proof of this proposition follows the lines in [17, Lemma 2.8,(a)].

Remark 3.2

Notice that Proposition 3.2 does not require the assumption (2) because \((\min A)+C=\big (\!\min (\min A)\big )+C\) and the other set equalities follow similarly.

4 Necessary Conditions for Set Inequalities

The set less order relation is defined by certain set inclusions; by Proposition 2.1 these set inclusions are characterized by appropriate inequalities. And now we investigate necessary conditions for these inequalities.

Under Assumption 2.1 we consider two arbitrary nonempty subsets \(A,B\subset Y\). For an arbitrarily chosen \({\bar{b}}\in B\) we use the abbreviation

$$\begin{aligned} {\hat{A}}_{{\bar{b}}}:=\Big \{{\hat{a}}\in A\ \Big |\ \psi ({\hat{a}}-{\bar{b}})=\min _{a\in A} \psi (a-{\bar{b}})\Big \} . \end{aligned}$$

\({\hat{A}}_{{\bar{b}}}\) denotes the set of all minimal solutions of the optimization problem \(\min _{a\in A} \psi (a-{\bar{b}})\).

For the first result we need a technical lemma.

Lemma 4.1

Let Assumption 2.1 be satisfied, and let \(h\in Y\) be arbitrarily chosen. For nonempty subsets \(A,B\subset Y\) let \({\bar{b}}\in B\) and \({\hat{a}}\in {\hat{A}}_{{\bar{b}}}\) be arbitrarily given. Let \({\hat{A}}_{{\bar{b}}}\ne A\). Suppose that

$$\begin{aligned} \exists \;{\bar{\lambda }}>0,\,\alpha \in \mathbb {R}:&\psi (a-{\bar{b}}+\lambda h)>\alpha >\psi ({\hat{a}}-{\bar{b}}) \text { for all } \lambda \in [0,{\bar{\lambda }}],\ a\in A\backslash {\hat{A}}_{{\bar{b}}}\nonumber \\&\text {and}\nonumber \\&\psi ({\hat{a}}-{\bar{b}}+\cdot h):[0,{\bar{\lambda }}]\rightarrow \mathbb {R}\text { is continuous at }\lambda =0. \end{aligned}$$
(4)

Then there exists some \({\tilde{\lambda }}>0\) so that

$$\begin{aligned} \min _{a\in A}\psi (a-{\bar{b}}+\lambda h) = \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi (a-{\bar{b}}+\lambda h) \text { for all }\lambda \in [0,{\tilde{\lambda }}] \end{aligned}$$

provided that these min terms exist.

Proof

Let \(h\in Y\), \({\bar{b}}\in B\) and \({\hat{a}}\in {\hat{A}}_{{\bar{b}}}\) be arbitrarily chosen. By the definition of the set \({\hat{A}}_{{\bar{b}}}\) we obtain \(\psi ({\hat{a}}-{\bar{b}})=\min _{a\in A}\psi (a-{\bar{b}})\). By the assumptions there is a sufficiently small \(\varepsilon >0\) and some \({\tilde{\lambda }}\in [0,{\bar{\lambda }}]\) with

$$\begin{aligned} \psi (a-{\bar{b}}+\lambda h)>\alpha >\alpha -\varepsilon \ge \psi ({\hat{a}}-{\bar{b}}+\lambda h) \text { for all } \lambda \in [0,{\tilde{\lambda }}] \text { and all }a\in A\backslash {\hat{A}}_{{\bar{b}}}. \end{aligned}$$

Consequently, we obtain

$$\begin{aligned} \inf _{a\in A\backslash {\hat{A}}_{{\bar{b}}}}\psi (a-{\bar{b}}+\lambda h) \ge \alpha >\psi ({\hat{a}}-{\bar{b}}+\lambda h)\ge \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi (a-{\bar{b}}+\lambda h)\text { for all } \lambda \in [0,{\tilde{\lambda }}]. \end{aligned}$$

These inequalities imply

$$\begin{aligned} \min _{a\in A}\psi (a-{\bar{b}}+\lambda h) = \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi (a-{\bar{b}}+\lambda h) \text { for all }\lambda \in [0,{\tilde{\lambda }}], \end{aligned}$$

which has to be shown. \(\square \)

Under the condition (4) Lemma 4.1 states that the minimal value \(\min _{a\in {\hat{A}}_{{\bar{b}}}} [0] \psi (a-{\bar{b}}+\lambda h)\) remains unchanged for sufficiently small \(\lambda \ge 0\), if the set \({\hat{A}}_{{\bar{b}}}\) is replaced by its superset A. The continuity requirement in the second part of the condition (4) is fulfilled for many functionals \(\psi \) used in practice (compare Example 2.1). The inequalities in the first part of the condition (4) are decisive for Lemma 4.1. By the definition of the set \({\hat{A}}_{{\bar{b}}}\) it obviously holds

$$\begin{aligned} \psi (a-{\bar{b}}) > \psi ({\hat{a}}-{\bar{b}})\text { for all }a\in A\backslash {\hat{A}}_{{\bar{b}}}. \end{aligned}$$

But in (4) we replace the argument \(a-{\bar{b}}\) by \(a-{\bar{b}}+\lambda h\), i.e. we consider elements with respect to the direction of h, and we require a stronger inequality. Besides the functional \(\psi \) the special choice of the set A plays a central role for this condition.

For simplicity we use the following notation for the next result. Under Assumption 2.1 we consider nonempty subsets \(A,B\in Y\) and define the functional \(\varphi :B\rightarrow \mathbb {R}\) with

$$\begin{aligned} \varphi (b)=\min _{a\in A}\psi (a-b)\text { for all } b\in B \end{aligned}$$

provided that the \(\min \) term exists. Next, we investigate the question under which conditions the functional \(\varphi \) has a directional derivative.

Theorem 4.1

Let Assumption 2.1 be satisfied, and let \(A,B\subset Y\) be arbitrarily chosen. Let \({\bar{b}}\in B\) be a solution of the optimization problem \(\max _{b\in B}\min _{a\in A}\psi (a-b)\), and let \({\hat{A}}_{{\bar{b}}}\ne A\). Let \(\varphi \) be directionally differentiable at \({\bar{b}}\) in every direction \({\bar{b}}-b\) with arbitrary \(b\in B\). For an arbitrary \(b\in B\) and an arbitrary \({\hat{a}}\in {\hat{A}}_{{\bar{b}}}\) suppose that

$$\begin{aligned} \exists \;{\bar{\lambda }}>0,\,\alpha \in \mathbb {R}:&\!\!\psi (a-{\bar{b}}+\lambda ({\bar{b}}-b))\!>\!\alpha \! >\!\psi ({\hat{a}}-{\bar{b}}) \text { for all } \lambda \in [0,{\bar{\lambda }}], a\in A\backslash {\hat{A}}_{{\bar{b}}}\\&\!\!\text {and}\\&\!\!\psi ({\hat{a}}-{\bar{b}}+\cdot ({\bar{b}}-b)):[0,{\bar{\lambda }}]\rightarrow \mathbb {R}\text { is continuous at } \lambda =0. \end{aligned}$$

In addition, suppose that for all \(b\in B\)

$$\begin{aligned}&\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}}\min _{a\in {\hat{A}}_{{\bar{b}}} \frac{1}{\lambda }\Big (\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\psi \big ( a-{\bar{b}}\big )\Big )}\\&\quad =\min _{a\in {\hat{A}}_{{\bar{b}}}}\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big (\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\psi \big ( a-{\bar{b}}\big )\Big ) . \end{aligned}$$

Then it follows

$$\begin{aligned} \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b) \le 0\text { for all }b\in B \end{aligned}$$

provided that the arising \(\min \) terms exist (\(\psi ' (a-{\bar{b}})({\bar{b}}-b)\) denotes the directional derivative of \(\psi \) at \(a-{\bar{b}}\) in the direction \({\bar{b}}-b\)).

Proof

First, we determine the directional derivative of \(\varphi \) at \({\bar{b}}\) in every direction \(b-{\bar{b}}\) with arbitrary \(b\in B\). With Lemma 4.1 and the assumptions of this theorem, we then get for all \(b\in B\)

$$\begin{aligned} \varphi '({\bar{b}})(b-{\bar{b}})= & {} \mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big (\varphi \big ({\bar{b}}+\lambda (b-{\bar{b}})\big )-\varphi \big ({\bar{b}}\big )\Big )\\= & {} \mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big ( \min _{a\in A}\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\underbrace{\min _{a\in A}\psi \big (a-{\bar{b}}\big )}_{=\min _{a\in {\hat{A}}_{{\bar{b}}}}\psi (a-{\bar{b}})}\Big )\\= & {} \mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big ( \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\min _{a\in {\hat{A}}_{{\bar{b}}}}\underbrace{\psi \big (a-{\bar{b}}\big )}_{=\text {const.}\forall a\in {\hat{A}}_{{\bar{b}}}}\Big )\\= & {} \mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda } \min _{a\in {\hat{A}}_{{\bar{b}}}}\Big ( \psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) - \psi \big (a-{\bar{b}}\big )\Big )\\= & {} \mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}}\min _{a\in {\hat{A}}_{{\bar{b}}}} \frac{1}{\lambda }\Big ( \psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) - \psi \big (a-{\bar{b}}\big )\Big )\\= & {} \min _{a\in {\hat{A}}_{{\bar{b}}}}\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big ( \psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) - \psi \big (a-{\bar{b}}\big )\Big )\\= & {} \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b). \end{aligned}$$

Since \({\bar{b}}\in B\) is a maximal solution of the problem \(\max _{b\in B}\varphi (b) = -\min _{b\in B} -\varphi (b)\) and \(\varphi \) has a directional derivative at \({\bar{b}}\) in every direction \(b-{\bar{b}}\) with arbitrary \(b\in B\), by [18, Thm. 3.8,(a)] we obtain

$$\begin{aligned} 0 \le -\varphi ' ({\bar{b}})(b-{\bar{b}}) = -\min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b) \text { for all }b\in B, \end{aligned}$$

which leads to the assertion. \(\square \)

Early investigations on directional derivatives of \(\sup \inf \) functions can be found in [4] (compare also [2]).

With this necessary condition for certain \(\min \max \) problems, we then obtain necessary conditions for set inequalities as well.

Corollary 4.1

Let Assumption 2.1 be satisfied, and let \(A,B\subset Y\) be arbitrarily chosen. Let \({\bar{a}}\in A\) be a solution of the optimization problem \(\max _{a\in A}\min _{b\in B}\psi (a-b)\) and let \({\bar{b}}\in B\) be a solution of the optimization problem \(\max _{b\in B}\min _{a\in A}\psi (a-b)\). Let \({\hat{A}}_{{\bar{b}}}\ne A\) and \({\hat{B}}_{{\bar{a}}}\ne B\). Let \(\min _{b\in B}\psi (\cdot -b)\) be directionally differentiable at \({\bar{a}}\) in every direction \(a-{\bar{a}}\) with arbitrary \(a\in A\), and let \(\min _{a\in A}\psi (a-\cdot )\) be directionally differentiable at \({\bar{b}}\) in every direction \({\bar{b}}-b\) with arbitrary \(b\in B\). For an arbitrary \(a\in A\) and an arbitrary \({\hat{b}}\in {\hat{B}}_{{\bar{a}}}\) suppose that

$$\begin{aligned} \exists \;{\bar{\lambda }}_{1}>0,\,\alpha _{1}\in \mathbb {R}:&\psi ({\bar{a}}-b+\lambda (a-{\bar{a}}))>\alpha _{1} >\psi ({\bar{a}}-{\hat{b}})\\& \text {for all } \lambda \in [0,{\bar{\lambda }}_{1}],\, b\in B\backslash {\hat{B}}_{{\bar{a}}}\\&\text {and}\\&\psi ({\bar{a}}-{\hat{b}}+\cdot (a-{\bar{a}})):[0,{\bar{\lambda }}_{1}]\rightarrow \mathbb {R}\text { is continuous at }\lambda =0. \end{aligned}$$

Moreover, for an arbitrary \(b\in B\) and an arbitrary \({\hat{a}}\in {\hat{A}}_{{\bar{b}}}\) suppose that

$$\begin{aligned} \exists \;{\bar{\lambda }}_{2}>0,\,\alpha _{2}\in \mathbb {R}:&\psi (a-{\bar{b}}+\lambda ({\bar{b}}-b))>\alpha _{2} >\psi ({\hat{a}}-{\bar{b}})\\&\text {for all } \lambda \in [0,{\bar{\lambda }}_{2}],\, a\in A\backslash {\hat{A}}_{{\bar{b}}}\\&\text {and}\\&\psi ({\hat{a}}-{\bar{b}}+\cdot ({\bar{b}}-b)):[0,{\bar{\lambda }}_{2}]\rightarrow \mathbb {R}\text { is continuous at }\lambda =0. \end{aligned}$$

In addition, suppose that for all \(a\in A\)

$$\begin{aligned}&\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}}\min _{b\in {\hat{B}}_{\bar{a}}} \frac{1}{\lambda }\Big (\psi \big ({\bar{a}}-b+\lambda (a-{\bar{a}})\big ) -\psi \big ( {\bar{a}}-b\big )\Big )\\&\quad =\min _{b\in {\hat{B}}_{{\bar{a}}}}\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big (\psi \big ({\bar{a}}-b+\lambda (a-{\bar{a}})\big ) -\psi \big ( {\bar{a}}-b\big )\Big ) \end{aligned}$$

and for all \(b\in B\)

$$\begin{aligned}&\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}}\min _{a\in {\hat{A}}_{\bar{b}}} \frac{1}{\lambda }\Big (\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\psi \big ( a-{\bar{b}}\big )\Big )\\&\quad =\min _{a\in {\hat{A}}_{{\bar{b}}}}\mathop {\mathrm {lim}}_{\lambda \rightarrow 0_{+}} \frac{1}{\lambda }\Big (\psi \big (a-{\bar{b}}+\lambda ({\bar{b}}-b)\big ) -\psi \big ( a-{\bar{b}}\big )\Big ) . \end{aligned}$$

If the inequality \(A\preccurlyeq _{s} B\) is satisfied, then we have

$$\begin{aligned}&\min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b) \le 0\text { for all }b\in B\end{aligned}$$
(5)
$$\begin{aligned}&\min _{b\in {\hat{B}}_{{\bar{a}}}}\psi ' ({\bar{a}}-b)(a-{\bar{a}}) \le 0\text { for all }a\in A \end{aligned}$$
(6)

provided that the arising \(\min \) terms exist.

Proof

Let the set inequality \(A\preccurlyeq _{s} B\) hold for arbitrary \(\emptyset \ne A,B\subset Y\). By Proposition 2.1 and the assumptions, we then have

$$\begin{aligned} 0 \ge \sup _{b\in B}\mathop {\mathrm {inf}}_{a\in A}\psi (a-b) = \max _{b\in B}\min _{a\in A}\psi (a-b) = \min _{a\in A}\psi (a-{\bar{b}}) \end{aligned}$$

and

$$\begin{aligned} 0 \ge \sup _{a\in A}\mathop {\mathrm {inf}}_{b\in B}\psi (a-b) = \max _{a\in A}\min _{b\in B}\psi (a-b) = \min _{b\in B}\psi ({\bar{a}}-b). \end{aligned}$$

Hence, the inequalities (5) and (6) follow from Theorem 4.1. \(\square \)

Remark 4.1

The inequalities (5) and (6) are necessary conditions for the set inequality \(A\preccurlyeq _{s} B\) but in general, they are not sufficient. Even if these inequalities imply \(\max _{b\in B}\min _{a\in A}\psi (a-b) = \min _{a\in A}\psi (a-{\bar{b}})\) and \(\max _{a\in A}\min _{b\in B}\psi (a-b) = \min _{b\in B}\psi ({\bar{a}}-b)\), one has to assume that \(\psi ({\bar{a}}-{\bar{b}})\le 0\) because in this case we have

$$\begin{aligned} \max _{b\in B}\min _{a\in A}\psi (a-b) = \min _{a\in A}\psi (a-{\bar{b}}) \le \psi ({\bar{a}}-{\bar{b}})\le 0 \end{aligned}$$

and

$$\begin{aligned} \max _{a\in A}\min _{b\in B}\psi (a-b) = \min _{b\in B}\psi ({\bar{a}}-b)\le \psi ({\bar{a}}-{\bar{b}})\le 0. \end{aligned}$$

An application of Proposition 2.1 then gives \(A\preccurlyeq _{s} B\).

By Corollary 4.2 we now present a necessary condition for sets to be non-optimal.

Corollary 4.2

Let Assumption 2.1 be satisfied, and let the convex cone C be pointed. Let \({\mathcal {F}}\) be a family of nonempty subsets of the real linear space Y, for which the set of minimal elements and the set of maximal elements are nonempty and the set equalities (2) are satisfied (for every \(A\in {{\mathcal {F}}}\)). In addition, let some set \(B\in {{\mathcal {F}}}\) and every set \(A'\in {{\mathcal {F}}}\) with \(\min A'\ne \min B\) or \(\max A'\ne \max B\) satisfy the assumptions of Corollary 4.1. If the set B is not an optimal set of \({\mathcal {F}}\), then there exists some set \(A\in {{\mathcal {F}}}\) so that the inequalities (5) and (6) hold and \(\min A\ne \min B\) or \(\max A\ne \max B\).

Proof

The assertion is a simple consequence of Remark 3.1 and Corollary 4.1. \(\square \)

The assumptions of Corollaries 4.1 and 4.2 concerning the considered sets and the functional \(\psi \) are very strong. For the two sets it seems to be helpful, if they consist of finitely many elements. But for the functional \(\psi \) we need the directional derivative, which depends on the order cone C. In the following proposition the directional derivative of \(\psi \) is investigated for various special real linear spaces and order cones.

Proposition 4.1

Let Assumption 2.1 be satisfied.

  1. (a)

    [18, Exercise 8.3] Let \(Y:=\mathbb {R}^m\) and \(C:=\mathbb {R}^{m}_{+}\) be chosen. Then the functional \(\psi :\mathbb {R}^m\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\max \{y_{1},\ldots ,y_{m}\} \text { for all }y=(y_{1},\ldots ,y_{m})\in \mathbb {R}^m \end{aligned}$$

    has the directional derivative at an arbitrary \({\bar{y}}\in \mathbb {R}^m\) given by

    $$\begin{aligned} \psi '({\bar{y}})(h)=\max _{i\in I({\bar{y}})}\{ h_i\} \text { for all }h\in \mathbb {R}^m \end{aligned}$$

    with

    $$\begin{aligned} I({\bar{y}}):=\{ i\in \{ 1,\ldots ,m\}\ |\ {\bar{y}}_{i}=\psi ({\bar{y}})\} . \end{aligned}$$
  2. (b)

    Let the real linear space \(Y:={{\mathcal {C}}}[0,1]\) of continuous real-valued functionals on [0, 1] and the natural order cone \(C:=\{ y\in {{\mathcal {C}}}[0,1]\ |\ y(t)\ge 0\text { for all }t\in [0,1] \}\) be chosen. Then the functional \(\psi :{{\mathcal {C}}}[0,1]\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\max _{t\in [0,1]} y(t) \text { for all }y\in {{\mathcal {C}}}[0,1] \end{aligned}$$

    has the directional derivative at an arbitrary \({\bar{y}}\in \mathcal{C}[0,1]\) given by

    $$\begin{aligned} \psi '({\bar{y}})(h)=\max _{t\in M({\bar{y}})} h(t) \text { for all }h\in {{\mathcal {C}}}[0,1] \end{aligned}$$

    with

    $$\begin{aligned} M({\bar{y}}):=\{ t\in [0,1]\ |\ {\bar{y}}(t)=\psi ({\bar{y}})\} . \end{aligned}$$
  3. (c)

    [14, page 275] Let the real Hilbert space \(Y:={{\mathcal {S}}}^n\) of real symmetric (n, n) matrices (with \(n\!\in \!\mathbb {N}\)) and the Löwner cone \(C:={{\mathcal {S}}}^{n}_{+}:=\{ A\in {{\mathcal {S}}}^{n}\ |\ \)A\(\text { positive semidefinite} \}\) be chosen. Then the functional \(\psi :{{\mathcal {S}}}^{n}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (A)=\max _{\Vert x\Vert _{2}=1} x^{T}Ax\ \Big (\! =\text {maximal eigenvalue of }A\Big ) \text { for all }A\in {{\mathcal {S}}}^{n} \end{aligned}$$

    (\(\,\Vert \cdot \Vert _{2}\) denotes the Euclidean norm in \(\mathbb {R}^n\)) has the directional derivative at an arbitrary \({\bar{A}}\in {{\mathcal {S}}}^{n}\) given by

    $$\begin{aligned} \psi '({\bar{A}})(H)=\max _{x\in X({\bar{A}})} x^{T}Hx \text { for all }H\in {{\mathcal {S}}}^{n} \end{aligned}$$

    with

    $$\begin{aligned} X({\bar{A}}):=\{ x\in \mathbb {R}^{n}\ |\ \Vert x\Vert _{2}=1\text { and }{\bar{A}}x=\psi ({\bar{A}})x\} \end{aligned}$$

    (\(X({\bar{A}})\) denotes the set of all normed eigenvalues associated to the maximal eigenvalue of \({\bar{A}}\)).

  4. (d)

    Let the real Hilbert space \(Y:={{\mathcal {S}}}^n\) of real symmetric (n, n) matrices (with \(n\!\in \!\mathbb {N}\)) and the copositive cone

    $$\begin{aligned} C:=\big \{ M\in {{\mathcal {S}}}^{n}\ \big |\ x^{T}Mx \ge 0\text { for all } x\in \mathbb {R}^{n}_{+}\big \} \end{aligned}$$

    be chosen. Then the functional \(\psi :{{\mathcal {S}}}^{n}\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (M)=\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}} x^{T}Mx \text { for all } M\in {{\mathcal {S}}}^{n} \end{aligned}$$

    (\(\,\Vert \cdot \Vert _{2}\) denotes the Euclidean norm in \(\mathbb {R}^n\)) has the directional derivative at an arbitrary \({\bar{A}}\in {{\mathcal {S}}}^{n}\) given by

    $$\begin{aligned} \psi '({\bar{A}})(H)=\max _{x\in X({\bar{A}})} x^{T}Hx \text { for all }H\in {{\mathcal {S}}}^{n} \end{aligned}$$

    with

    $$\begin{aligned} X({\bar{A}}):=\{ x\in \mathbb {R}^{n}_{+}\ |\ \Vert x\Vert _{2}=1\text { and }\psi ({\bar{A}})=x^{T}{\bar{A}}x\} . \end{aligned}$$
  5. (e)

    Let a real normed space \((Y,\Vert \cdot \Vert )\) and the Bishop-Phelps cone

    $$\begin{aligned} C(\ell ):=\{ y\in Y\ |\ \ell (y)\ge \Vert y\Vert \}\} \end{aligned}$$

    for an arbitrary continuous linear functional \(\ell \in Y^*\) be chosen. Then the functional \(\psi :Y\rightarrow \mathbb {R}\) with

    $$\begin{aligned} \psi (y)=\ell (y)+\Vert y\Vert \text { for all } y\in Y \end{aligned}$$

    has the directional derivative at an arbitrary \({\bar{y}}\in Y\) given by

    $$\begin{aligned} \psi '({\bar{y}})(h)=\ell (h) +\max _{{\tilde{\ell }}\in \partial \Vert {\bar{y}}\Vert } {\tilde{\ell }}(h) \text { for all }h\in Y \end{aligned}$$

    with the subdifferential

    $$\begin{aligned} \partial \Vert {\bar{y}}\Vert = \left\{ \begin{array}{ll} \{{\tilde{\ell }}\in Y^*\ |\ {\tilde{\ell }}({\bar{y}})=\Vert {\bar{y}}\Vert \text { and } \Vert {\tilde{\ell }}\Vert _{Y^*}=1\} &{} \text {if }{\bar{y}}\ne 0_{Y}\\ \{{\tilde{\ell }}\in Y^*\ |\ \Vert {\tilde{\ell }}\Vert _{Y^*}\le 1\} &{} \text {if }{\bar{y}}= 0_{Y}\end{array}\right\} \end{aligned}$$

    of the norm \(\Vert \cdot \Vert \) at \({\bar{y}}\).

Proof

  1. (b)

    For arbitrarily chosen \({\bar{y}},h\in {{\mathcal {C}}}[0,1]\) we obtain

    $$\begin{aligned} \psi '({\bar{y}})(h)= & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda }\Big ( \psi ({\bar{y}}+\lambda h)-\psi ({\bar{y}})\Big )\nonumber \\= & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda }\Big ( \underbrace{\max _{t\in [0,1]}{\bar{y}}(t)+\lambda h(t)}_{\ge \max \limits _{t\in M({\bar{y}})}{\bar{y}}(t)+\lambda h(t)}- \underbrace{\max _{t\in [0,1]}{\bar{y}}(t)}_{=\max \limits _{t\in M({\bar{y}})}{\bar{y}}(t)}\Big )\nonumber \\\ge & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda }\Big ( \max _{t\in M({\bar{y}})}\big ({\bar{y}}(t)+\lambda h(t)\big )- \max _{t\in M({\bar{y}})}\underbrace{{\bar{y}}(t)}_{=\text {const.}}\Big )\nonumber \\= & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda } \max _{t\in M({\bar{y}})}{\bar{y}}(t)+\lambda h(t)- {\bar{y}}(t)\nonumber \\= & {} \max _{t\in M({\bar{y}})} h(t). \end{aligned}$$
    (7)

    Next, we prove the converse inequality. For every \(\lambda >0\) there is some \(t_{\lambda }\in [0,1]\) with

    $$\begin{aligned} {\bar{y}}(t_{\lambda })+\lambda h(t_{\lambda })=\max _{t\in [0,1]}{\bar{y}}(t)+\lambda h(t). \end{aligned}$$
    (8)

    For some \({\tilde{t}}\in M({\bar{y}})\) we obtain for all \(\lambda >0\)

    $$\begin{aligned} \max _{t\in [0,1]}\big ({\bar{y}}(t)+\lambda h(t)\big ) -\max _{t\in [0,1]}{\bar{y}}(t) \ge {\bar{y}}({\tilde{t}})+\lambda h({\tilde{t}})-{\bar{y}}({\tilde{t}}) =\lambda h({\tilde{t}}) \end{aligned}$$

    and

    $$\begin{aligned} \max _{t\in [0,1]}\big ({\bar{y}}(t)+\lambda h(t)\big ) -\max _{t\in [0,1]}{\bar{y}}(t)\le & {} \max _{t\in [0,1]}{\bar{y}}(t)+\lambda \max _{t\in [0,1]}h(t)- \max _{t\in [0,1]}{\bar{y}}(t)\\= & {} \lambda \max _{t\in [0,1]}h(t). \end{aligned}$$

    So, we conclude for some \(\alpha >0\)

    $$\begin{aligned} \Big |\max _{t\in [0,1]}\big ({\bar{y}}(t)+\lambda h(t)\big ) -\max _{t\in [0,1]}{\bar{y}}(t)\Big |\le \lambda \alpha \text { for all }\lambda >0, \end{aligned}$$

    and with the equality (8) we get

    $$\begin{aligned} \lim _{\lambda \rightarrow 0_{+}} {\bar{y}}(t_{\lambda })+\lambda h(t_{\lambda }) = \lim _{\lambda \rightarrow 0_{+}}\max _{t\in [0,1]}{\bar{y}}(t)+\lambda h(t)=\max _{t\in [0,1]}{\bar{y}}(t). \end{aligned}$$

    Then there is a sequence \((\lambda _{k})_{k\in \mathbb {N}}\) of positive real numbers converging to 0 with \(\lim _{k\rightarrow \infty } t_{\lambda _{k}} =: {\hat{t}}\in [0,1]\), and it is evident that \({\hat{t}}\in M({\bar{y}})\). Hence, we conclude

    $$\begin{aligned} \psi '({\bar{y}})(h)= & {} \lim _{k\rightarrow \infty }\frac{1}{\lambda _{k}} \Big (\underbrace{\max _{t\in [0,1]} \big ({\bar{y}}(t) +\lambda _{k} h(t)\big )}_{ ={\bar{y}}(t_{\lambda _{k}})+\lambda _{k}h(t_{\lambda _{k}})} - \underbrace{\max _{t\in [0,1]}{\bar{y}}(t)}_{ \ge {\bar{y}}(t_{\lambda _{k}})}\Big )\nonumber \\\le & {} \lim _{k\rightarrow \infty }\frac{1}{\lambda _{k}} \Big ({\bar{y}}(t_{\lambda _{k}})+\lambda _{k}h(t_{\lambda _{k}}) - {\bar{y}}(t_{\lambda _{k}})\Big )\nonumber \\= & {} \lim _{k\rightarrow \infty }h(t_{\lambda _{k}})\nonumber \\= & {} h({\hat{t}})\nonumber \\\le & {} \max _{t\in M({\bar{y}})} h(t). \end{aligned}$$
    (9)

    The inequalities (7) and (9) lead to the assertion.

  2. (d)

    For arbitrarily chosen \({\bar{A}},H\in {{\mathcal {S}}}^n\) we have

    $$\begin{aligned} \psi '({\bar{A}})(H)= & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda }\Big ( \psi ({\bar{A}}+\lambda H)-\psi ({\bar{A}})\Big )\nonumber \\= & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda }\Big ( \underbrace{\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x}_{\ge \max \limits _{x\in X({\bar{A}})}x^{T}({\bar{A}}+\lambda H)x} - \underbrace{\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x}_{ =\max \limits _{x\in X({\bar{A}})}\underbrace{\scriptstyle x^{T}{\bar{A}}x}_{\scriptscriptstyle \overset{=\text {const.}}{\text {on } X({\bar{A}})}}} \Big )\nonumber \\\ge & {} \lim _{\lambda \rightarrow 0_{+}}\frac{1}{\lambda } \max _{x\in X({\bar{A}})} x^{T}{\bar{A}}x+\lambda x^{T}Hx-x^{T}{\bar{A}}x\nonumber \\= & {} \max _{x\in X({\bar{A}})}x^{T}Hx. \end{aligned}$$
    (10)

    For the proof of the converse inequality choose an arbitrary \(\lambda >0\). Then there exists some \(x_{\lambda }\in \mathbb {R}^{n}_{+}\) with \(\Vert x_{\lambda }\Vert _{2}=1\) so that

    $$\begin{aligned} x_{\lambda }^{T}({\bar{A}}+\lambda H)x_{\lambda } = \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x. \end{aligned}$$

    For an arbitrary \({\tilde{x}}\in X({\bar{A}})\) we obtain

    $$\begin{aligned} \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x - \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x\ge & {} {\tilde{x}}^{T}({\bar{A}}+\lambda H){\tilde{x}} - {\tilde{x}}^{T}{\bar{A}}{\tilde{x}}\\= & {} \lambda {\tilde{x}}^{T}H{\tilde{x}}\text { for all }\lambda >0 \end{aligned}$$

    and with

    $$\begin{aligned}&\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x - \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x\\&\quad \le \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x + \lambda \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}Hx - \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x\\&\quad = \lambda \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}Hx \text { for all }\lambda >0 \end{aligned}$$

    we conclude for some \(\alpha \ge 0\)

    $$\begin{aligned} \Bigg |\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x - \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x\Bigg | \le \lambda \alpha \text { for all } \lambda > 0. \end{aligned}$$

    Hence, we have

    $$\begin{aligned} \lim _{\lambda \rightarrow 0_{+}} x_{\lambda }^{T}({\bar{A}}+\lambda H)x_{\lambda } = \max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x. \end{aligned}$$

    So, there is a sequence \((\lambda _{k})_{k\in \mathbb {N}}\) of positive real numbers converging to 0 with \(\lim _{k\rightarrow \infty } x_{\lambda _{k}} =: {\hat{x}}\in X({\bar{A}})\). And we conclude

    $$\begin{aligned} \psi '({\bar{A}})(H)= & {} \lim _{k\rightarrow \infty }\frac{1}{\lambda _{k}}\Big ( \underbrace{\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}({\bar{A}}+\lambda H)x}_{ =x_{\lambda _{k}}^{T}({\bar{A}}+\lambda _{k}H)x_{\lambda _{k}}} - \underbrace{\max _{\overset{\scriptstyle x\in \mathbb {R}^{n}_{+}}{\scriptstyle \Vert x\Vert _2=1}}x^{T}{\bar{A}}x}_{ \ge x_{\lambda _{k}}^{T}{\bar{A}}x_{\lambda _{k}}} \Big )\nonumber \\\le & {} \lim _{k\rightarrow \infty }\frac{1}{\lambda _{k}}\Big ( x_{\lambda _{k}}^{T}{\bar{A}}x_{\lambda _{k}} + \lambda _{k}x_{\lambda _{k}}^{T}Hx_{\lambda _{k}} - x_{\lambda _{k}}^{T}{\bar{A}}x_{\lambda _{k}}\Big )\nonumber \\= & {} \lim _{k\rightarrow \infty } x_{\lambda _{k}}^{T}Hx_{\lambda _{k}}\nonumber \\= & {} {\hat{x}}^{T}H{\hat{x}}\nonumber \\\le & {} \max _{x\in X({\bar{A}})}x^{T}Hx. \end{aligned}$$
    (11)

    The inequalities (10) and (11) imply the assertion.

  3. (e)

    Since the norm \(\Vert \cdot \Vert \) is continuous and convex, its directional derivative is given by [18, Theorem 3.28]. Then for arbitrarily chosen \({\bar{y}},h\in Y\) we obtain

    $$\begin{aligned} \psi '({\bar{y}})(h)=\ell (h) +\max _{{\tilde{\ell }}\in \partial \Vert {\bar{y}}\Vert } {\tilde{\ell }}(h) \end{aligned}$$

    where the subdifferential \(\partial \Vert {\bar{y}}\Vert \) is calculated in [18, Example 3.24,(b)].

\(\square \)

The proof of part (b) follows the lines of the proof of the directional derivative of the maximum norm (compare [18, Exercise 3.2]). Investigations of the directional derivative of the maximal eigenvalue of a symmetric matrix have been already given in [25] (compare also [1, 6, 24, 26, 28]).

Remark 4.2

If in Proposition 4.1,(c) the maximal eigenvalue of a matrix \({\bar{A}}\in {{\mathcal {S}}}^{n}\) is simple, then the associated normed eigenvector \({\bar{x}}\) is unique and the set \(X({\bar{A}})\) consists only of this vector. In this special case the directional derivative is simply given as

$$\begin{aligned} \psi '({\bar{A}})(H)={\bar{x}}^{T}H{\bar{x}} \text { for all } H\in \mathcal{S}^{n}. \end{aligned}$$

If the maximal eigenvalue of \({\bar{A}}\) is a double eigenvalue, then the set \(X({\bar{A}})\) is a circle in a two dimensional subspace of \(\mathbb {R}^{n}\) spanned by the associated eigenvectors. Let \({\bar{x}}^{1}\) and \({\bar{x}}^{2}\) be orthogonal normed eigenvectors associated to the maximal eigenvalue of \({\bar{A}}\). Then this subspace is spanned by \({\bar{x}}^{1}\) and \({\bar{x}}^{2}\), and we have

$$\begin{aligned} X({\bar{A}})=\{\alpha {\bar{x}}^{1}+\beta {\bar{x}}^{2}\ |\ \alpha ,\beta \in \mathbb {R}\text { and } \Vert \alpha {\bar{x}}^{1}+\beta {\bar{x}}^{2}\Vert _{2}=1\} . \end{aligned}$$

In this special case we obtain the directional derivative

$$\begin{aligned} \psi '({\bar{A}})(H) =\max _{\overset{\alpha ,\beta \in \mathbb {R}}{\scriptscriptstyle \Vert \alpha {\bar{x}}^{1}+\beta {\bar{x}}^{2}\Vert _{2}=1}} \big (\alpha {\bar{x}}^{1}+\beta {\bar{x}}^{2}\big )^{T}H \big (\alpha {\bar{x}}^{1}+\beta {\bar{x}}^{2}\big ) \text { for all } H\in {{\mathcal {S}}}^{n}. \end{aligned}$$

This maximization problem with only two real variables is very simple to solve.

Fig. 2
figure 2

Illustration of the closed balls A, B and D defined in Example 4.1

Full size image

Example 4.1

We now apply the necessary conditions of Corollary 4.1 and Proposition 2.1 to the very simple case \(Y:=\mathbb {R}^{2}\) and \(C:=\mathbb {R}_{+}^{2}\), and we choose the functional \(\psi :\mathbb {R}^{2}\rightarrow \mathbb {R}\) with

$$\begin{aligned} \psi (y)=\max \{y_{1},y_{2}\} \text { for all } y=(y_{1},y_{2})\in \mathbb {R}^{2} \end{aligned}$$

(compare Example 2.1,(a)). For convenience only we consider the closed balls \(A:=\mathcal {B}\big ( (2,2),2\big )\), \(B:=\mathcal {B}\big ( (5.5,3.5),1\big )\) and \(D:=\mathcal {B}\big ( (3,5),0.5\big )\) illustrated in Fig. 2. Then we investigate two cases.

  1. (a)

    It is geometrically obvious from the definition of the set less order relation that \(A\preccurlyeq _{s}B\). We investigate the necessary conditions (5) and (6) for this order relation. The optimization problem \(\max _{a\in A}\min _{b\in B}\psi (a-b)\) equals \(\max _{a\in A}\min _{b\in B}\max \{a_{1}-b_{1},a_{2}-b_{2}\}\), and \({\bar{a}}:=(2,4)\in A\) is a maximal solution of this problem. Moreover, we obtain \({\bar{b}}:=(5.5,2.5)\in B\) as maximal solution of the problem \(\max _{b\in B}\min _{a\in A}\max \{a_{1}-b_{1},a_{2}-b_{2}\}\). By Proposition 4.1,(a) we can write for all \(b\in B\)

    $$\begin{aligned} \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b) =\min _{a\in {\hat{A}}_{{\bar{b}}}}\max _{i\in I(a-{\bar{b}})} \{{\bar{b}}_{i}-b_{i}\} \end{aligned}$$
    (12)

    with

    $$\begin{aligned} {\hat{A}}_{{\bar{b}}}= & {} \Big \{{\hat{a}}\in A\ \Big |\ \psi ({\hat{a}}-{\bar{b}})=\min _{a\in A}\psi (a-{\bar{b}})\Big \}\\= & {} \Big \{{\hat{a}}\in A\ \Big |\ \max \{{\hat{a}}_{1}-5.5,{\hat{a}}_{2}-2.5\} =\min _{a\in A}\max \{a_{1}-5.5,a_{2}-2.5\}\Big \}\\= & {} \{(2,0)\} \end{aligned}$$

    and

    $$\begin{aligned} I(a-{\bar{b}})= & {} \{ i\in \{ 1,2\}\ |\ a_{i}-{\bar{b}}_{i}=\psi (a-{\bar{b}})\}\\= & {} \{ i\in \{ 1,2\}\ |\ a_{i}-{\bar{b}}_{i}=\max \{a_{1}-5.5,a_{2}-2.5\}\} . \end{aligned}$$

    For \(a:=(2,0)\) it follows

    $$\begin{aligned} I(a-{\bar{b}}) = I((-3.5,-2.5))=\{2\} , \end{aligned}$$

    and then we get with (12)

    $$\begin{aligned} \min _{a\in {\hat{A}}_{{\bar{b}}}}\psi ' (a-{\bar{b}})({\bar{b}}-b) = 2.5-b_{2} \le 0\text { for all } b\in B. \end{aligned}$$

    So, the necessary condition (5) is shown. With \({\hat{B}}_{{\bar{a}}}=\{(5.5,4.5)\}\) and \(I({\bar{a}}-b)=\{2\}\) for \(b:=(5.5,4.5)\) we get

    $$\begin{aligned} \min _{b\in {\hat{B}}_{{\bar{a}}}}\psi ' ({\bar{a}}-b)(a-{\bar{a}}) =\min _{b\in {\hat{B}}_{{\bar{a}}}}\max _{i\in I({\bar{a}}-b)} \{a_{1}-2,a_{2}-4\} =a_{2}-4 \le 0\,\forall \, a\in A, \end{aligned}$$

    and the necessary condition (6) is satisfied as well.

  2. (b)

    It is evident from Fig. 2 that \(A\not \preccurlyeq _{s}D\). For these two sets we obtain \({\bar{a}}:=(4,2)\) as maximal solution of the problem

    $$\begin{aligned} \max _{a\in A}\min _{d\in D}\max \{ a_{1}-d_{1},a_{2}-d_{2}\} =\min _{d\in D}\max \{ 4-d_{1},2-d_{2}\} =0.5 > 0. \end{aligned}$$

    By Proposition 2.1, we then conclude \(A\not \subset D-C\).

5 Conclusions

The investigation of set inequalities generally leads to nontrivial necessary or sufficient conditions. Starting from known \(\sup \inf \) problems characterizations are given for set inequalities and optimal and non-optimal sets. The decisive key for the main results is the use of directional derivatives. For various standard cones the directional derivative of the functionals describing the negative cone is recalled or calculated. It seems to be that the presented technique of proof can also be applied to additional functionals used in practice. A simple example shows the usefulness of this theory but it also demonstrates that the decision, whether a set inequality holds or not, is a difficult task.