Revisiting a Three-Player Pursuit-Evasion Game

Abstract

We consider the game of a holonomic evader passing between two holonomic pursuers. The optimal trajectories of this game are known. We give a detailed explanation of the game of kind’s solution and present a computationally efficient way to obtain trajectories numerically by integrating the retrograde path equations. Additionally, we propose a method for calculating the partial derivatives of the Value function in the game of degree. This latter result applies to differential games with homogeneous Value.

1 Introduction

Pursuit-evasion (PE) games began to be investigated intensively in the middle of the twentieth century, primarily for military purposes. In this period, Rufus Isaacs’ defining work, differential games [8], was born, in which he lays the theoretical foundations of PE games and, more generally, Differential Games. Today, there is a growing interest in the topic due to the proliferation of self-driving vehicles and drones, as PE game theory can also be used effectively for collision avoidance [6] and other applications of unmanned vehicles such as protecting a region from intruders [10, 11].

Isaacs’ method of solving two-player differential games is based on the idea of semipermeable surfaces. These are surfaces in the state space which both players strive to penetrate in the opposite direction, but both are prevented from doing so by the opponent. Hence, optimal trajectories are running on such surfaces. Optimal trajectories can be obtained by integrating path equations in retrograde time, from an endstate. In some cases, this can be done analytically. In the simplest cases, even feedback strategies can be given analytically [3, 12], which means that in any state, each player’s best control decision is obtainable.

Isaacs’ work has been the starting point for many researchers. For a precise and more general formulation of its base ideas, refer to [1]. The many types of singular surfaces introduced by Isaacs have been further investigated in [2], which will be of use in this paper.

With the advancement of computational techniques, previously impossible problems became solvable. Instead of analytically solving the integration and then giving strategies, one can numerically evaluate each (relevant) state in a discretized state space using the Hamilton–Jacobi–Isaacs equation [14]. This solution concept suffers from the curse of dimensionality, and we often settle for a suboptimal solution, especially when the number of agents—and therefore, the dimensionality of the state space—is high [5].

The game we are analyzing in this paper has three agents and simple dynamics. It is a relatively simple pursuit-evasion game example; in fact, Hagedorn and Breakwell have been able to give an analytical solution in 1976[7]. However, the analytic form of the optimal trajectories includes elliptic integrals; thus, the agents’ feedback strategies could not be given. We take a different route: we give the path equations in a simple form and integrate numerically. Doing so allows us to efficiently compute the agents’ optimal strategies, which we will present in a subsequent paper. Kumkov et al. write on Hagedorn and Breakwell’s work: "Computations (...) are very complicated. It would be reasonable to check them and, possibly, to rewrite in an easier way" [9], which we also hope to have accomplished.

In the next section, we formulate the game. In Sects. 3 and 4, we present the path equations inside the playable state space and at the boundary. The complete solution of the game of kind, where the outcome is binary, is given in Sect. 5. In Sect. 6, we give the game of degree - continuous outcome - counterpart of the game based on the game of kind. This logic was also followed by Hagedorn and Breakwell [7], but we also provide the derivatives of the Value. Results are summarized, and future work is inspected in Sect. 7.

2 The Game of Kind

In the game considered, there are three players: two cooperating pursuers and a faster evader. The game is played in the plane without borders or obstacles. Each agent is omnidirectional—it can change direction instantaneously—and has fixed velocity. The joint six-dimensional state of the system is governed by

$$\begin{aligned} f\left( \phi _1,\phi _2,\psi \right) = \dot{x} = \begin{bmatrix} \dot{x}_{p_1} \\ \dot{x}_{p_2} \\ \dot{x}_{e} \end{bmatrix} = \begin{bmatrix} v_p \phi _1 \\ v_p \phi _2 \\ v_e \psi \end{bmatrix} \end{aligned}$$

(1)

where $x_{p_1}$, $x_{p_2}$ and $x_e$ are two-dimensional column vectors that correspond to the planar coordinates of pursuer 1 ($P_1$), pursuer 2 ($P_2$) and the evader (E), respectively. The constant scalar velocities are denoted by $v_p$ and $v_e$ for the pursuers and evader, with $v_e>v_p$. The control variables of the agents are $\phi _1$, $\phi _2$ and $\psi$ two-dimensional unit vectors.

The goal of the evader is to pass between the two pursuers—in either direction—without getting captured. The objective of the pursuers is the opposite. They win either by approaching each other and thus preventing the evader from passing between or by capture. Capture means approaching E closer than a given $d_c$ capture distance as formalized by

$$\begin{aligned} d_i = ||x_e-x_{p_i}|| < d_c \qquad \text {for any}\ i \in \{1,2\} \end{aligned}$$

(2)

Note that capture may occur after the evader has crossed the line segment between the pursuers.

A very similar setting is examined in [15]. The problem also has some similarities with region protection like in [11], with the evader being the intruder. However, a significant difference is that the pursuers (defenders) are not constrained to the boundary of a region, allowing for much more complex optimal solutions even with just a few agents. Let us point out that the source of the complexity of the game under study is the superiority of the evader, as opposed to similar situations, e.g., in [3, 12] where a slower evader (target) enables closed-form solutions.

2.1 Terminal Surfaces

To make the following analysis more transparent, we visualize the playing area. This requires the reduction of the six-dimensional state space, which is possible without loss of information because the game is inherently invariant to translation and rotation of the agents’ joint configuration. Let us introduce the "XYZ" reduced space. We relocate the base of the coordinate system such that the pursuers are always located on the x axis, with the origin halfway between them. Then, the X and Y refer to the relative coordinates of the evader and Z to the distance between the pursuers. This way, we can transform any state unambiguously to the three-dimensional reduced space.

Since the evader is allowed to cross between the pursuers in any direction, without loss of generality, we will consider states with reduced coordinate $Y<0$ as prior to crossing. States where $Y>0$ are considered such that E has already passed between and may yet have to escape.

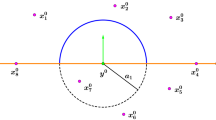
Based on the previous description, the game can terminate in one of the following three ways: the evader is captured, the pursuers close the gap by coming within a distance of $2d_c$ of each other (before the evader has crossed, i.e., $Y<0$¹), or the evader gets through and reaches a safe state. The first two cases will correspond to terminal surfaces—penetration of which leads to an immediate win for the pursuers. The third is not well defined, but later we will see that a precise formalization is not necessary. In fact, we will only need the surfaces corresponding to capture, depicted in Fig. 1 in the "XYZ" space. They form oblique cylinders with radius $d_c$: these are states where the inequality in (2) becomes an equation. Neglecting the other two possibilities for termination will be justified in Sect. 5.

Fig. 1

Regions of the terminal surfaces related to capture, in the reduced space with $v_e/v_p=1.1$

The critical attribute of a region on a terminal surface is its usability. A region is usable if the player who prefers penetration of the surface can apply such control that the opponent is unable to prevent it. The condition of usability can be given generally as

$$\begin{aligned} \min _{\phi _1,\phi _2} \max _\psi \nu ^T f\left( \phi _1,\phi _2,\psi \right) < 0 \end{aligned}$$

where $\nu$ is the normal to the surface, directed to the playing space².

To follow the traditional way, we would have to either obtain the surfaces in six dimensions, or the state equations in the reduced space. Instead, we will determine usability of capture surfaces by noting that capture occurs if and only if $d_i=d_c$ and $\dot{d}_i<0$ for any $i\in \{1,2\}$.

When $d_i=d_c$ holds for only one pursuer, the usability criterion is written as

$$\begin{aligned} \min _{\phi _i}\max _\psi \dot{d}_i < 0 \end{aligned}$$

(3)

Let us introduce

$$\begin{aligned} \begin{aligned} p_i&= x_e - x_{p_i} \\ \dot{p}_i&= \dot{x}_e - \dot{x}_{p_i} = v_e \psi - v_p \phi _i \end{aligned} \end{aligned}$$

(4)

Then, writing the derivative of the length of a two-dimensional vector:

$$\begin{aligned} \dot{d}_i = \frac{d||p_i||}{dt} = \frac{\dot{p}_i^T p_i }{||p_i||} \end{aligned}$$

(5)

and (3) can be written as

$$\begin{aligned} \min _{\phi _i}\max _\psi \frac{\left( v_e \psi - v_p \phi _i\right) ^T p_i}{||p_i||} < 0 \end{aligned}$$

(6)

Note that $\psi$ and $\phi _i$ are unit vectors and $v_e>v_p$, therefore the direction of the vector $(v_e \psi - v_p \phi _i)$ is decided by the evader. Hence, E can always make $\dot{d}_i$ positive. The surface is nonusable, except in the following case.

Fig. 2

Configuration at the usable part

On the section of the two nonusable cylindrical surfaces, the configuration of the agents is similar to that in Fig. 2: both pursuers are at distance $d_c$ from the evader, with the parameter $\gamma$ being the angle difference between $P_1E$ and the symmetry axis (the bisector of $P_1P_2$). Now the usability criterion is inspected regarding to both pursuers simultaneously; thus, (3) modifies to

$$\begin{aligned} \min _{\phi _1,\phi _2}\max _\psi \min _i \dot{d}_i < 0,\qquad i\in \{1,2\} \end{aligned}$$

(7)

and (6) modifies to

$$\begin{aligned} \min _{\phi _1,\phi _2}\max _\psi \min _i \frac{\left( v_e \psi - v_p \phi _i\right) ^T p_i}{||p_i||} < 0 \end{aligned}$$

(8)

Optimal (minimizing) control of the pursuers is still heading along $p_i$, toward the evader. In contrast to the single pursuer case, because of symmetry, the evader can, at best, move on the perpendicular bisector of the pursuers’ points, as shown in Fig. 2. The condition (8) then further reduces to

$$\begin{aligned} v_e \cos \gamma - v_p < 0 \end{aligned}$$

We conclude that the section is usable for $\gamma >\cos ^{-1}(v_p/v_e)$ and nonusable for $\gamma <\cos ^{-1}(v_p/v_e)$. The boundary of the usable part (BUP) is the point where $\gamma =\overline{\gamma }=\cos ^{-1}(v_p/v_e)$. Configuration in this point is as in Fig. 2, with $\gamma =\overline{\gamma }$; corresponding to the relative coordinates shown in Fig. 1. Importance of this point is stated in the next section.

3 Solution in the Open Space

According to Isaac’s principle, [8], the state space can be split into two parts, from one of which capture can be guaranteed through optimal play of the pursuers (capture zone, CZ). For states in the other part, the evader can ensure escape if it plays optimally (escape zone, EZ). In this case, closing the gap is treated similarly to capture. The two parts are separated by a barrier. Optimal play of both players on the barrier leads to an edge case between capture and escape, with trajectories staying on the barrier.

The payoff of the game can be defined at terminal states, which is positive if the evader wins and negative if the pursuers win. The payoff of the edge case, which terminates in the BUP, is zero. We now define the Value (V) of the game as a function over the playable space that equals the eventual payoff assuming optimal play on both sides³; hence it is positive for states in EZ, negative for states in CZ, and zero on the barrier. By definition, it is evident that through optimal play, the game’s state follows a trajectory along which the Value is constant. As a consequence, the gradient of the Value is normal to any optimal trajectory and thus normal to the barrier.

Following Isaac’s protocol, we try to create a family of optimal paths with $V=0$ that generate the barrier. On one side of the barrier, the Value will be negative and positive on the other. We generate the barrier by integrating paths in retrograde time, starting from the terminal state with zero Value, the BUP. To obtain these paths, we need to simultaneously integrate states and the partial derivatives of V (but not V itself). Hence, we need the differential equations in time for x and the gradient of V. We will also need the state and derivatives at the endpoint, the BUP.

Let us make a remark on dimensionality. In general differential games, the $n-1$-dimensional barrier separating an n dimensional state space is integrated starting from an $n-2$-dimensional manifold. In this case, however, we only found an $n-3$-dimensional boundary of the usable part—a point in the reduced space. Still, we will see that it is sufficient: trajectories ending in this point form a surface in the reduced space, which will indeed be the barrier.

3.1 Optimality Condition

The Value function is assumed to be twice differentiable in x. For clarity, let us define the gradient of V as a six-dimensional row vector in the form

$$\begin{aligned} \nabla V = \begin{bmatrix} \frac{\partial V}{\partial x_{p_1}}&\frac{\partial V}{\partial x_{p_2}}&\frac{\partial V}{\partial x_e} \end{bmatrix}= \begin{bmatrix} V_{p_1}&V_{p_2}&V_e \end{bmatrix} \end{aligned}$$

The instantaneous goal of the agents is to minimize (maximize) the current Value. This is expressed by the first main equation, also including the fact that optimality results in constant V,

$$\begin{aligned} \min _{\phi _1,\phi _2} \max _\psi \dot{V}=\min _{\phi _1,\phi _2} \max _\psi H\left( \nabla V,\phi _1,\phi _2,\psi \right) = 0 \end{aligned}$$

(9)

where

$$\begin{aligned} H\left( \nabla V,\phi _1,\phi _2,\psi \right) = \nabla V f\left( \phi _1,\phi _2,\psi \right) = v_p V_{p_1} \phi _1 + v_p V_{p_2} \phi _2 + v_e V_e \psi \end{aligned}$$

(10)

Optimal controls will be the unit vectors aligning with the corresponding Value derivatives:

$$\begin{aligned} \begin{aligned} \psi ^*&=\frac{V_e^T}{||V_e||} \\ \phi _1^*&=-\frac{V_{p1}^T}{||V_{p1}||} \\ \phi _2^*&=-\frac{V_{p2}^T}{||V_{p2}||} \end{aligned} \end{aligned}$$

(11)

Substituting (11) into (9) gives the second main equation

$$\begin{aligned} \nabla V f\left( \phi _1^*,\phi _2^*,\psi ^*\right) = - v_p V_{p_1} \frac{V_{p1}^T}{||V_{p1}||} - v_p V_{p_2} \frac{V_{p2}^T}{||V_{p2}||} + v_e V_e \frac{V_e^T}{||V_e||} =0 \end{aligned}$$

or

$$\begin{aligned} v_e ||V_e|| - v_p (||V_{p1}|| + ||V_{p2}||) = 0 \end{aligned}$$

(12)

Differentiating the left side by any agent’s coordinates—$\xi \in \{p_1,p_2,e\}$—gives

$$\begin{aligned} \begin{aligned} v_e \frac{ \frac{\partial V_e}{\partial x_\xi } V_e^T}{||V_e||} - v_p \frac{ \frac{\partial V_{p1}}{\partial x_\xi } V_{p1}^T}{||V_{p1}||} -v_p \frac{ \frac{\partial V_{p2}}{\partial x_\xi } V_{p2}^T}{||V_{p2}||}&= v_e \frac{\partial V_e}{\partial x_\xi }\psi ^* + v_p \frac{\partial V_{p1}}{\partial x_\xi }\phi _1^* +v_p \frac{\partial V_{p2}}{\partial x_\xi }\phi _2^* \\&= v_e \frac{\partial V_\xi }{\partial x_e}\psi ^* + v_p\frac{\partial V_\xi }{\partial x_{p1}} \phi _1^* +v_p \frac{\partial V_\xi }{\partial x_{p2}} \phi _2^* \\&= \frac{\partial V_\xi }{\partial x_e}\dot{x}_e + \frac{\partial V_\xi }{\partial x_{p1}} \dot{x}_{p1} + \frac{\partial V_\xi }{\partial x_{p2}} \dot{x}_{p2} \\&= \dot{V}_\xi \end{aligned} \end{aligned}$$

(13)

using (11), (1) and the interchangeability of the second derivatives of V. Differentiating by the time is considered along the optimal path.

The right side of (12) is zero everywhere, therefore

$$\begin{aligned} \dot{V}_\xi =0 \end{aligned}$$

(14)

This means that the derivatives of the Value are constant. Considering (11), the optimal controls are thus also constant, which causes all agents to move along straight lines.

3.2 Boundary of the Usable Part

We already determined the configuration of the agents at the BUP. Again referring to invariance to translation and rotation, we can choose the state to match the XYZ-transformation by placing the pursuers on the x axis. Considering Fig. 2, this gives us

$$\begin{aligned} x = \begin{bmatrix} - dc \sin \overline{\gamma } \\ 0 \\ dc \sin \overline{\gamma } \\ 0 \\ 0 \\ dc \cos \overline{\gamma } \end{bmatrix} \end{aligned}$$

Now we need to determine $\nabla V$. In the game of kind, the Value—and therefore its derivatives—is only defined up to a scalar multiplier. Hence, we can choose $||V_{p1}||=1$. From (12)

$$\begin{aligned} v_e ||V_e|| = v_p \left( ||V_{p1}|| + ||V_{p2}||\right) \end{aligned}$$

and because of symmetry $||V_{p1}|| = ||V_{p2}||$, so

$$\begin{aligned} ||V_e|| = \frac{2 v_p}{v_e} = 2 \cos \overline{\gamma } \end{aligned}$$

since $\overline{\gamma }=\cos ^{-1}(v_p/v_e)$.

Now, we know the lengths of vectors $V_\xi$. Their directions can be deduced based on (11): they are aligned with the control unit vectors of the agents shown in Fig. 2, oppositely directed for the pursuers. Hence, the Value derivatives at the BUP are

$$\begin{aligned} \nabla V = \begin{bmatrix} V_{p_1}&V_{p_2}&V_e \end{bmatrix}= \begin{bmatrix} - \sin \overline{\gamma }&- \cos \overline{\gamma }&\sin \overline{\gamma }&- \cos \overline{\gamma }&0&2 \cos \overline{\gamma } \end{bmatrix} \end{aligned}$$

Using these initial values and the differential Eqs. (11) and (14), we can integrate a single optimal path on the barrier, which runs in the interior of the playable space. To obtain a family of optimal trajectories, we need additional considerations.

4 Solution on the Nonusable Part

In the previous section, we assumed twice continuous differentiability of V. However, this is not true along the nonusable parts (NUP, refer to Fig. 1): they are surfaces that separate an immediate capture zone from a space of states with various Values. Therefore, the deduction of (13) and so (14) are not valid on the surface. In this section, we will give the path equations of possible paths along the nonusable surfaces.

Before expounding on the curved paths, let us describe how curved and straight parts form optimal trajectories. In reversed time, every optimal trajectory starts from the boundary of the usable part. Applying the previous results at this point, a straight trajectory is acquired, which runs in the interior of the playing space, where V is differentiable; thus (13) and (14) remain valid, and the controls remain constant. On the other hand, the BUP is on both nonusable surfaces (corresponding to capture); hence, the trajectory may start (in reverse time) along such a surface. After an arbitrary⁴ time, the trajectory diverges from the surface and, being in the interior, obeys the equations derived previously. We state without proof that both $d_i$ distances strictly increase (still in retrograde time) after such a junction point; therefore, the trajectory will never meet a nonusable surface again. Hence, we can summarize in forward time: every optimal trajectory starts with a straight phase lasting until the state reaches a nonusable surface. Then, the state evolves along that surface up until the BUP. The duration of the straight and curved phases is denoted by $t_2$ and $t_1$, respectively. An example trajectory is shown in Fig. 3.

Fig. 3

An optimal trajectory with parameters: $v_e=1.1$, $v_p=1$, $d_c=1$, $t_1=10$, $t_2=10$

We will consider $P_1$ to be the pursuer threatening E from here on. For $P_2$, a symmetrical solution applies.

When moving along the capture surface of a pursuer, the game may have no saddle point. If the evader’s optimal strategy in a given time instant is such that $P_1$ has a control decision that results in immediate capture, it will apply it and win. But if E knows this beforehand, it can take countermeasures, and this way, V might increase. Optimality is retained by defining the upper saddle point[2] as a solution where E has instantaneous informational advantage, i.e., its control is defined as function of $P_1$’s control: $\psi (\phi _1)$. This solves the ambiguity of the optimal controls, but we have to modify the first main equation.

Let us introduce $\theta = \angle (x_e-x_1)$ and

$$\begin{aligned} \mathrm{e}(\theta ) = \begin{bmatrix} \cos \theta \\ \sin \theta \end{bmatrix} \end{aligned}$$

Now the surface where $d_1 = ||x_e-x_{p_1}|| = d_c$ can be parameterized by

$$\begin{aligned} s = \begin{bmatrix} x_{p_1} \\ x_{p_2} \\ \theta \end{bmatrix} \end{aligned}$$

five-dimensional vector, with

$$\begin{aligned} x = \sigma (s) = \begin{bmatrix} x_{p_1} \\ x_{p_2} \\ x_{p_1}+d_c \mathrm{e}(\theta ) \end{bmatrix} \end{aligned}$$

As $\nabla V$ generally does not exist on the NUP, the normal to the barrier can instead be given as its limit at the straight and curved paths’ junction

$$\begin{aligned} \lambda = \lim _{\tau \rightarrow 0}\frac{\partial V(\sigma (s) - \tau f^*)}{\partial x} = \begin{bmatrix} \lambda _{p1}&\lambda _{p2}&\lambda _e \end{bmatrix} \end{aligned}$$

where $f^*$, being constant in the open space along the trajectory, has no arguments.

We can write the main equation as

$$\begin{aligned}&\min _{\phi _1,\phi _2} \max _{\psi \in \tilde{\psi }(\phi _1)} \left( v_p \lambda _{p_1} \phi _1 + v_p \lambda _{p_2} \phi _2 + v_e \lambda _e \psi (\phi _1) \right) \nonumber \\&= \min _{\phi _1,\phi _2} \max _{\psi \in \tilde{\psi }(\phi _1)} H\left( \lambda , \phi _1 , \phi _2, \psi (\phi _1)\right) =0 \end{aligned}$$

(15)

where $\tilde{\psi }(\phi _1)$ is the set of the reactive strategies of E that ensure its safety:

$$\begin{aligned} \tilde{\psi }(\phi _1) = \{\psi : v_e \psi ^T\mathrm{e}(\theta ) \ge v_p \phi _1^T \mathrm{e}(\theta ) \} \end{aligned}$$

(16)

where $v_e \psi ^T\mathrm{e}(\theta )$ is the speed at which the evader moves away from the pursuer, and $v_p \phi _1^T \mathrm{e}(\theta )$ is the speed at which $P_1$ moves toward E.

4.1 Controls at the Junction

We will now derive the optimal controls of the agents at the junction between the straight and curved part of an optimal trajectory. Notice that in (15), $P_2$ minimizes independently, therefore its optimal control is (with some abuse of notation), similarly to (11),

$$\begin{aligned} \phi _2^*=-\frac{\lambda _{p2}}{||\lambda _{p2}||} \end{aligned}$$

The optimal reactive strategy of the evader is given by

$$\begin{aligned} \psi ^*(\phi _1)= {\left\{ \begin{array}{ll} \psi ^*=\frac{\lambda _e}{||\lambda _e||}, &{}\text {if } \frac{\lambda _e}{||\lambda _e||} \in \tilde{\psi }(\phi _1) \\ \text {some } \tilde{\psi }^* \in \tilde{\psi }(\phi _1)&{} \text {otherwise} \end{array}\right. } \end{aligned}$$

Let us also define

$$\begin{aligned} \phi _1^*=-\frac{\lambda _{p1}}{||\lambda _{p1}||} \end{aligned}$$

which minimizes H without considering the constraint on $\psi$. We will indirectly prove that this is the optimal control also when applying the constraint on $\psi$. We will also see that the second branch of $\psi ^*(\phi _1)$ can be neglected.

Let us assume that $P_1$ can exploit the nonusable surface, i.e., there exists a $\phi _1$ such that

$$\begin{aligned} H\left( \lambda ,\phi _1,\phi _2^*,\psi ^*(\phi _1)\right) < H\left( \lambda ,\phi _1^*,\phi _2^*,\psi ^*(\phi _1^*)\right) \end{aligned}$$

The presence of a capture surface can only benefit the pursuer, thus

$$\begin{aligned} H\left( \lambda ,\phi _1^*,\phi _2^*,\psi ^*(\phi _1^*)\right) \le H\left( \lambda ,\phi _1^*,\phi _2^*,\psi ^*\right) \end{aligned}$$

where the right-hand side replicates the open-space solution: at the state $x\rightarrow \sigma (s)$, $\nabla V = \lambda$ based on the similarity between (11) and the previously redefined controls we can write the results of the open space as

$$\begin{aligned} H\left( \lambda ,\phi _1^*,\phi _2^*,\psi ^*\right) = 0 \end{aligned}$$

Summarizing the inequalities, we get

$$\begin{aligned} H\left( \lambda ,\phi _1,\phi _2^*,\psi ^*(\phi _1)\right) < 0 \end{aligned}$$

which contradicts the definition of the barrier. Therefore, both inequalities have to be equalities, $\phi _1^*$ is the optimal control in the junction for $P_1$, and $\psi ^*(\phi _1^*)=\psi ^*$. However, $\phi _1^*$ may not be unique. We will not prove that no other $\phi _1$ values exist for which $H(\lambda ,\phi _1,\phi _2^*,\psi ^*(\phi _1))=0$, but it is simple to check numerically and is also suggested by the fact that we can construct the full barrier using only this straightforward solution.

In backward time, the optimal trajectory can leave the nonusable surface at any time $t_1$. Hence, any point on the curved path can be a junction, for which the optimal solution is as derived. This means that the agents’ controls will be $\phi _1^*$, $\phi _2^*$, and $\psi ^*$ throughout the optimal trajectory. To integrate, we now need the differential equations for $\lambda$.

4.2 Obtaining Path Equations

In the next part, we will follow the methods of [2].

Let us define the Value on the nonusable surface as a twice continuously differentiable function of the parametrization s

$$\begin{aligned} U(s)=V(\sigma (s)) = \lim _{\tau \rightarrow 0} V\left( \sigma (s) - \tau f^*\right) \end{aligned}$$

where the limit is only needed to obtain the derivatives

$$\begin{aligned} \frac{\partial U(s)}{\partial s} = \lim _{\tau \rightarrow 0} \frac{\partial V\left( \sigma (s) - \tau f^*\right) }{\partial s} = \lim _{\tau \rightarrow 0} \frac{\partial V\left( \sigma (s) - \tau f^*\right) }{\partial x} \frac{\partial \sigma (s)}{\partial s} \end{aligned}$$

Thus,

$$\begin{aligned} \frac{\partial U(s)}{\partial s} = \lambda \frac{\partial \sigma (s)}{\partial s} \end{aligned}$$

with

$$\begin{aligned} \frac{\partial \sigma (s)}{\partial s}=\begin{bmatrix} I &{} 0 &{} 0 \\ 0 &{} I &{} 0 \\ I &{} 0 &{} d_c \mathrm{e}(\theta + \pi /2) \end{bmatrix} \end{aligned}$$

(17)

being a six-by-five matrix. The second derivative of $\sigma$ is zero except for $\frac{\partial ^2 \sigma (s)}{\partial \theta ^2}$ which means that

$$\begin{aligned} \frac{\partial ^2 U(s)}{\partial s_i \partial s_j} = \frac{\partial \lambda }{\partial s_i} \frac{\partial \sigma (s)}{\partial s_j} = \frac{\partial \lambda }{\partial s_j} \frac{\partial \sigma (s)}{\partial s_i} \end{aligned}$$

(18)

for any $i\ne j$. Since $\lambda$ is the normal to the barrier, along an optimal path we can write

$$\begin{aligned} \lambda f^* = 0 \end{aligned}$$

(19)

Then, for any element of s

$$\begin{aligned} \lambda \frac{\partial f^*}{\partial s_i} = \lambda \sum _{u\in \{\phi _1,\phi _2,\psi \}} \frac{\partial f^*}{\partial u}\frac{\partial u}{\partial s_i}= \sum _{u\in \{ \phi _1,\phi _2,\psi \}} \frac{\partial H}{\partial u}\frac{\partial u}{\partial s_i}= 0 \end{aligned}$$

because f is only a function of the controls, and—as shown in the previous section—$\phi _1^*,\phi _2^*,\psi ^*(\phi _1^*)$ supply the unconstrained minimum for H. Hence, differentiating (19) gives

$$\begin{aligned} \frac{\partial \lambda }{\partial s_i} f^* = 0 \end{aligned}$$

Using that $f^*$ can be written on the surface as

$$\begin{aligned} f^* = \frac{\partial \sigma (s)}{\partial s} \frac{ds}{dt} = \sum _{j=1}^5 \frac{\partial \sigma (s)}{\partial s_j} \frac{ds_j}{dt} \end{aligned}$$

and using (18),

$$\begin{aligned} \begin{aligned} \frac{\partial \lambda }{\partial s_i} f^*&= \frac{\partial \lambda }{\partial s_i} \sum _{j=1}^5 \frac{\partial \sigma (s)}{\partial s_j} \frac{ds_j}{dt} \\&= \sum _{j=1}^5 \frac{\partial \lambda }{\partial s_i} \frac{\partial \sigma (s)}{\partial s_j} \frac{ds_j}{dt} \\&= \sum _{j=1}^5 \frac{\partial \lambda }{\partial s_j} \frac{\partial \sigma (s)}{\partial s_i} \frac{ds_j}{dt} \\&= \left( \sum _{j=1}^5 \frac{\partial \lambda }{\partial s_j} \frac{ds_j}{dt} \right) \frac{\partial \sigma (s)}{\partial s_i} \\&= \dot{\lambda } \frac{\partial \sigma (s)}{\partial s_i} = 0 \end{aligned} \end{aligned}$$

This gives us for $i=\{1,2\}$, $i=\{3,4\}$ and $i=5$—the columns of the block matrix in (17)

$$\begin{aligned} \begin{aligned} \dot{\lambda }_1 + \dot{\lambda }_e&= 0 \\ \dot{\lambda }_2&= 0 \\ \dot{\lambda }_e d_c \mathrm{e}(\theta + \pi /2)&= 0 \end{aligned} \end{aligned}$$

(20)

From (20), we can deduce that both $\dot{\lambda }_1$ and $\dot{\lambda }_e$ are parallel to $\mathrm{e}(\theta )$, and all derivatives of $\lambda$ are defined up to a scalar multiplier. We will express this as

$$\begin{aligned} \dot{\lambda }_1= \alpha p \end{aligned}$$

(21)

where—and later on—p refers to $p_1$ from (4).

To obtain $\alpha$, first let us write—refer to (5) for the derivative of vector length

$$\begin{aligned} \frac{d\psi ^*}{dt}= \frac{d\frac{\lambda _e}{||\lambda _e||}}{dt}=\frac{\dot{\lambda }_e ||\lambda _e|| - \lambda _e \frac{\lambda _e^T \dot{\lambda }_e}{||\lambda _e||}}{||\lambda _e||^2} = \frac{\dot{\lambda }_e}{||\lambda _e||} \left( I - \psi ^* \circ \psi ^{*T}\right) \end{aligned}$$

(22)

and

$$\begin{aligned} \frac{d\phi _1^*}{dt}= \frac{d \left( - \frac{\lambda _1}{||\lambda _1||}\right) }{dt}= - \frac{\dot{\lambda }_1 ||\lambda _1|| - \lambda _1 \frac{\lambda _1^T \dot{\lambda }_1}{||\lambda _1||}}{||\lambda _1||^2} = - \frac{\dot{\lambda }_1}{||\lambda _1||} \left( I - \phi _1^* \circ \phi _1^{*T}\right) \end{aligned}$$

(23)

Next, let us reformulate the condition of staying on the surface—see (8) and (16)

$$\begin{aligned} v_e \psi ^T p = v_p \phi _1^T p \end{aligned}$$

(24)

then, using $\dot{p}_1$ from (4) as $\dot{p}$,

$$\begin{aligned} \left( v_e \psi - v_p \phi _1\right) ^T p = \dot{p}^T p = 0 \end{aligned}$$

which we derivate as

$$\begin{aligned} \begin{aligned} \frac{d \left( \left( v_e \psi ^T - v_p \phi _1^T \right) p \right) }{dt}&= \left( v_e \frac{\dot{\lambda }_e^T}{||\lambda _e||} \left( I - \psi \circ \psi ^T\right) \right. \\&\quad \left. + v_p \frac{\dot{\lambda }_{p1}^T}{||\lambda _{p1}||} \left( I - \phi _1 \circ \phi _1^T\right) \right) p+ \left( v_e \psi ^T - v_p \phi _1^T \right) \dot{p} \\&= \dot{\lambda }_{p1}^T \left( - \frac{v_e}{||\lambda _e||} \left( I - \psi \circ \psi ^T\right) \right. \\&\quad \left. + \frac{v_p}{||\lambda _{p1}||} \left( I - \phi _1 \circ \phi _1^T\right) \right) p+ \dot{p}^T \dot{p} = 0 \end{aligned} \end{aligned}$$

using (20), (22) and (23).

Now substituting (21) and solving for $\alpha$:

$$\begin{aligned} \alpha = \frac{\dot{p}^T \dot{p}}{ p^T \left( \frac{v_e}{||\lambda _e||} \left( I - \psi \circ \psi ^T\right) - \frac{v_p}{||\lambda _{p1}||} \left( I - \phi _1 \circ \phi _1^T\right) \right) p } \end{aligned}$$

which we can calculate at any point. Now (21) and (20) are sufficient to calculate the derivatives of $\lambda$. Using the controls from the previous subsection, we can numerically integrate optimal trajectories along the nonusable surface.

4.3 Brief Analysis

Integrating backward from the BUP, maintaining Isaacs’ main equations gives us optimal trajectories of the game. In Fig. 4, an optimal trajectory with no straight phase ($t_2=0$) is shown. This trajectory may seem suboptimal for the pursuers because $P_1$ implements a swerve maneuver instead of simply heading toward $P_2$ to close the gap. However, it can be shown that greedily closing the gap would benefit the evader by allowing for significantly earlier crossing.

Fig. 4

Curved part with parameters: $v_e=1.5$, $v_p=1$, $d_c=1$

Two conditions constrain the duration of the curved phase. First, at some point during the integration of the curved path, we arrive at a state where the first pursuer’s movement direction is aligned with $EP_1$; it moves away from the evader. This configuration is shown in Fig. 4 as initial state x(0). If we integrate beyond this point, the curvature of $P_1$’s path changes sign, and, depending on the parameters, we may arrive at a singularity where the numerical integration fails. Second, according to Sect. 2.1, in states where the reduced coordinate Y is positive, the evader is assumed to have already crossed the line between the pursuers. The sign of Y changes at $Y=0$, when all three agents are located on a straight line. Hence, configurations prior to the edge configuration—marked in Fig. 4 with dashed lines—are not part of the optimal trajectory⁵. Even without our condition on Y, such configurations would not be part of the optimal trajectory because the evader would choose to cross between the pursuers in the other direction.

We need to show that the second condition is more strict, i.e., to obtain paths that are optimal given our problem statement, integration beyond the singularity is never needed—regardless of parameters.

In Fig. 4, we see that for $v_e/v_p=1.5$, the singular point appears beyond the edge configuration. We will give intuitive proof for general velocity ratios. Let us consider the limit case where $v_e/v_p\rightarrow \infty$, shown in Fig. 5. In the limit, the evader compasses the pursuer, which is moving toward the final position of E. The singular state—where $P_1$ is moving away from E—is exactly when the agents form a line. We argue that for any other velocity ratio $1<v_e/v_p<\infty$, the structure is more similar to that in Fig. 4, and we never have to integrate up to the singular point regardless of parameters $v_e$, $v_p$.

Fig. 5

Curved trajectory in the limit case: $v_e/v_p\rightarrow \infty$, $d_c=1$

Changing parameter $d_c$ would proportionally scale all coordinates but not change the structure of the solution; therefore, the optimal trajectories can be integrated for any parameters.

Note that in [7], Hagedorn and Breakwell give the optimal solution as a function of the first pursuer’s control. Therefore, their solution is inherently constrained by the singular point.

5 The Barrier

From the boundary of the usable part, with given $d_c$, we can integrate in retrograde time any optimal trajectory that runs for $t_1$ time along one of the nonusable surfaces and then for $t_2$ time in the open space. We may use any ordinary differential equation solver. An example is shown in Fig. 6. The numerical results agree with those of [7].

Fig. 6

An optimal trajectory with parameters: $v_e=1.1$, $v_p=1$, $d_c=1$, $t_1=10$, $t_2=10$

Calculating such paths with $t_1\in [0,t_{1,max}]$ gives us the barrier, shown in Fig. 7. Here, the $t_1$ value which corresponds to the edge configuration introduced earlier is denoted $t_{1,max}$. For states above and in front (in positive Y direction) of the barrier, escape can be guaranteed. Although optimal strategies are only defined on the barrier, agents following those specified optimal strategies sufficiently near the barrier will cause the state to evolve parallel to it. In the CZ, the state will either end up on the UP of the section or arrive at the terminal surface where the pursuers meet. In the EZ, after passing the BUP, the evader has some trivial escape strategies, moving away from the pursuers.

Fig. 7

The barrier for parameters: $v_e=1.5$, $v_p=1$, $d_c=1$

Figure 8 shows sections of the barrier to visualize escape and capture zones better. Here, blue circles correspond to states where the evader has already been captured. From the definition, crossing has already occurred in states with $Y>0$; hence, the black lines separating EZ and CZ. In the section with $Z=2.2$, there are states where even though the evader has already crossed, the pursuers can capture it. In the last subfigure, the barrier wraps around the pursuers; however, the $Y>0$ part is neglected due to the problem definition.

Fig. 8

Sections of the barrier

Now let us justify neglecting the two termination possibilities besides capture, mentioned in Sect. 2.1. First, note that the entire $Y<0$, $Z=2*d_c$ surface—winning condition for the pursuers—lies on the CZ side of the barrier. Therefore, trajectories in the escape zone will never end on this surface; the outcome is not influenced by it. On the other hand, the evader’s safe region still does not have to be defined precisely. Let it be some $Y=\tilde{Y}$ plane where $\tilde{Y}>d_c$. This is valid because on the EZ side, following the barrier, the evader can reach a state with $Y>0$ and $\gamma <\overline{\gamma }$, meaning that neither closing the gap or capture poses a threat to its escape. Then, simply moving away from the pursuers eventually gets the state to $Y=\tilde{Y}$. When starting from the CZ, the evader would have to either illegally cross $Y=0$ outside the pursuers’ gap or cross the barrier to get to the $Y=\tilde{Y}$ surface, which is also impossible. Hence neither this type of terminal surface influences the capture and escape regions of the game.

6 The Game of Degree

We will now define the continuous-payoff counterpart (GoD) of the previously analyzed game. The agents’ dynamics are the same, but in this game, there is no capture. The evader tries to pass between the pursuers while maintaining the highest possible distance from both of them. The pursuers try to approach the evader as close as possible. Formally, we can define the payoff as

$$\begin{aligned} J = \min _t \min _i d_i(t) = \min _t \min _i ||x_e(t)-x_{p_i}(t)|| \end{aligned}$$

for $t\in [0,\infty ]$ and $i\in \{1,2\}$. The Value of the game can be interpreted as the eventual payoff with optimal play on both sides. As opposed to previously, it will be written as a function of the state, with GoD in the lower index.

The game of degree can be informally defined as the following question: for a state x, what is the longest $d_c$ distance such that escape occurs in the game of kind? Thus, $V_{GoD}(x)=d_c$ if and only if the state x is on the barrier of the game of kind with $d_c$ capture distance. Note that the Value in the GoK is zero in such states; hence, V and $V_{GoD}(x)$ are not interchangeable. The GoD can be treated as the family of games of kind with all possible —positive—$d_c$ values.

In the GoD, optimal trajectories run along semipermeable surfaces according to Isaacs’ theory. $V_{GoD}$ is constant along these trajectories. The semipermeable surface with $V_{GoD}\equiv d_c$ corresponds to the barrier of the game of kind with $d_c$ capture distance, with the same optimal trajectories. Using the previous results, we can integrate such trajectories: both the state and the normal to the surface previously denoted as $\lambda$.

In the game of degree, as opposed to the GoK, the exact Value has significance, and we may want to calculate its gradient. We know that this gradient is aligned with the normal to the semipermeable surface, $\lambda$, but it may have to be scaled. This can be done by recognizing that the Value is a homogeneous function of the state. Namely, if we shrink or enlarge the game by multiplying the state by a scalar value, we will obtain the same optimal solution on a different timescale, with proportionally modified Value. Formally,

$$\begin{aligned} V_{GoD}(ax)=aV_{GoD}(x) \end{aligned}$$

for any $a>0$ scalar. Applying Euler’s homogeneous function theorem gives us

$$\begin{aligned} \nabla V_{GoD}(x) x = V_{GoD}(x) \end{aligned}$$

which can be used to obtain $\nabla V_{GoD}(x)$ when knowing its direction. Therefore, for given $d_c=V_{GoD}(x)$, $t_1$ and $t_2$ parameters, we can integrate the optimal trajectories and then obtain $\nabla V_{GoD}(x)$ values by rescaling the $\lambda$ resulting from the integration. Note that homogeneity also applies to other games with holonomic dynamics and without obstacles.

The analogy of the two games allows us the calculate the optimal trajectories in the game of degree for states that have a counterpart on the barrier. Not all states do so, however. In Fig. 9, the contour plot of $V_{GoD}$ is shown on a Z-section in the XYZ space. The lowest contour is that of $V_{GoD}(x)=0$, which means that in the terminating state, all three agents meet at one point—game of kind with point capture. Initial states below result in the pursuers meeting before the evader could pass through, for which the $V_{GoD}$ is negative but not defined. On the sides, two curved lines of states are marked for which the optimal trajectory has no straight part. Outside of the inner region are the nonoptimal states: the evader is already too close to one of the evaders, making the payoff lower even though the other pursuer poses no threat. In these states, there is no optimal strategy.

Fig. 9

Contour plot of the Value in a Z-section. The stars mark the positions of the pursuers

7 Conclusions

In this work, we have provided an efficient way of obtaining optimal trajectories in the game of passing between two pursuers. We can calculate optimal paths for states in a region in the six-dimensional state space from six parameters: translation and rotation of the endstate, the capture distance (the Value in the GoD), and the lengths of the straight and curved parts. In this process, we also get the derivatives of the Value of the game, scaled in the game of degree. This scaling is based on a general concept and applies to a variety of similar games.

The next step in our research is to provide optimal feedback strategies. For this, we will reverse the connection: calculate the path parameters from the initial state. In the future, we aim to use these results in solving a game where the superior evader has been encircled by three (or more) pursuers and has to escape[4, 13].