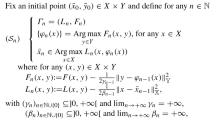On the Generic Structure and Stability of Stackelberg Equilibria

Abstract

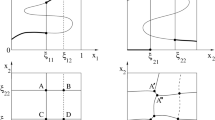
We consider a noncooperative Stackelberg game, where the two players choose their strategies within domains $X\subseteq {{\mathbb {R}}}^m$ and $Y\subseteq {{\mathbb {R}}}^n$. Assuming that the cost functions F, G for the two players are sufficiently smooth, we study the structure of the best reply map for the follower and the optimal strategy for the leader. Two main cases are considered: either $X=Y=[0,1]$, or $X={{\mathbb {R}}}, Y={{\mathbb {R}}}^n$ with $n\ge 1$. Using techniques from differential geometry, including a multi-jet version of Thom’s transversality theorem, we prove that, for an open dense set of cost functions $F\in {{\mathcal {C}}}^2$ and $G\in {{\mathcal {C}}}^3$, the Stackelberg equilibrium is unique and is stable w.r.t. small perturbations of the two cost functions.

Appendix

Assume $f:{{\mathbb {R}}}^m\mapsto {{\mathbb {R}}}^n$

• $x\in {{\mathbb {R}}}^m$ is a critical point of f if the Jacobian matrix Df(x) has rank $<n$.    Equivalently: if the differential Df(x) is not surjective.

• $y\in {{\mathbb {R}}}^n$ is a critical value of f  if $y=f(x)$ for some critical point x.

Lemma A.1

(Sard’s Lemma [18]) For any $f\in {{\mathcal {C}}}^\infty ({{\mathbb {R}}}^m;\,{{\mathbb {R}}}^n)$, the set of critical values has n-dimensional measure zero.

1.1 Transversality

Let $f : X \mapsto Y$ be a smooth map of manifolds and let W be a submanifold of Y.

We say that f is transverse to W at a point p, and write $f \cap \!\!\!\!|~ _p W$, if

• either $f ( p ) \notin W$,

• or else $f(p) \in W$ and   $(df)_p(T_pX) + T_{f(p)}W~= ~T_{f(p)}Y$.

We say that f is transverse to W, and write $f \cap \!\!\!\!|~ W$, if $f \cap \!\!\!\!|~ _p W$ for every $p\in X$.

Example A.1

Take $X={{\mathbb {R}}}^m$,   $Y={{\mathbb {R}}}^n$ with $m<n$. Assume $W=\{y_0\}$ for some $y_0\in {{\mathbb {R}}}^n$. In this case, transversality implies

• either $f (x) \not = y_0$,

• or else $f(x) = y_0$ and   rank $(Df(x)) = n$.

Since the second alternative is impossible, one has

$$\begin{aligned} f \cap \!\!\!\!|~ W\qquad \iff \qquad f(x)\not = y_0\qquad \hbox {for all}~x\in {{\mathbb {R}}}^2. \end{aligned}$$

Lemma A.2

(Transversality Lemma) Let $X, \Theta$, and Y be smooth manifolds, W a submanifold of Y. Let $\theta \mapsto \phi ^\theta$ be a smooth map which to each $\theta \in \Theta$ associates a function $\phi ^\theta \in {{\mathcal {C}}}^\infty (X,Y)$, and define $\varPhi :X\times \Theta \mapsto Y$ by setting $\varPhi (x,\theta )=\phi ^\theta (x)$.

If $\varPhi \cap \!\!\!\!|~ W$ then the set $\{\theta \in \Theta :~~\phi ^\theta \cap \!\!\!\!|~ W\}$ is dense in $\Theta$.

1.2 A Multi-jet Transversality Theorem

We state here a version of the multi-jet transversality theorem which is used several times in the paper. In the following, for given integers $m,n\ge 1$ we consider maps $f:{{\mathbb {R}}}^{m+n}\mapsto {{\mathbb {R}}}$. Let ${{\mathcal {P}}}^k$ be the space of polynomials of degree $\le k$ in the $m+n$ variables $(x,y)\in {{\mathbb {R}}}^m\times {{\mathbb {R}}}^n$. Identifying a polynomial with its coefficients, clearly, ${{\mathcal {P}}}^k$ is a finite-dimensional vector space. The product space

$$\begin{aligned} J^k({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})~:=~{{\mathbb {R}}}^{m+n}\times {{\mathcal {P}}}^k \end{aligned}$$

is a jet bundle over the space $R^{m+n}$. Any function $f:{{\mathbb {R}}}^{m+n}\mapsto {{\mathbb {R}}}$ determines a section of this bundle, defined as $j^kf(x,y)~=~P^{(x,y)}$, where the polynomial $P^{(x,y)}(\cdot )$ is the kth-order Taylor approximation of the function f at the point (x, y).

Next, for $s\ge 1$ we call

$$\begin{aligned} Z^{(s)}:= \Big \{(x,y_1,\ldots , y_s)\in {{\mathbb {R}}}^m\times {{\mathbb {R}}}^n\times \cdots \times {{\mathbb {R}}}^n\,:~ y_i\not = y_j~\hbox {for all}~~1\le i<j\le s\Big \}.\nonumber \\ \end{aligned}$$

(105)

Notice that $Z^{(s)}$ is an open subset of a vector space of dimension $m+sn$; hence it is a manifold. The set

$$\begin{aligned} \begin{array}{rl}J^k_s({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})&{}=~\Big \{(x,y_1,\ldots , y_s, P_1,\ldots ,P_s)~\in ~ {{\mathbb {R}}}^m\times {{\mathbb {R}}}^n\times \cdots \times {{\mathbb {R}}}^n\times {{\mathcal {P}}}^k \times \cdots \times {{\mathcal {P}}}^k:\\ &{}\qquad y_i\not = y_j~~\hbox {for all}~~1\le i<j\le s\Big \} \end{array} \end{aligned}$$

(106)

is a kth-order jet bundle over $Z^{(s)}$. Any smooth function $f:{{\mathbb {R}}}^{m+n}\mapsto {{\mathbb {R}}}$ determines a section of this bundle defined as

$$\begin{aligned} j^k_s f(x, y_1,\ldots , y_s)~=~(Q^{(x, y_1)},~\ldots ~, Q^{(x, y_s)}), \end{aligned}$$

(107)

where $Q^{(x, y_i)}$ is the polynomial of degree $\le k$ determined by the kth-order Taylor approximation to f at the point $(x, y_i)$. We can now state a version of the multi-jet transversality theorem which is used in our paper. The proof is similar to the one on p. 57–59 of [12], with some simplifications due to the fact that our maps are defined on Euclidean spaces, rather than on general manifolds.

Theorem A.1

Let W be a smooth submanifold of $J^k_s({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})$. Then the set of functions $f\in {{\mathcal {C}}}^\infty ({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})$ which are transversal to W is dense, in the ${{\mathcal {C}}}^\infty$ topology.

Proof

1. Cover the open set $Z^{(s)}$ with countably many open sets $V_\nu , \nu \ge 1$, such that

• If $(x, y_1,\ldots , y_s)\in V_\nu$ and $({\tilde{x}}, {\tilde{y}}_1,\ldots , {\tilde{y}}_s)\in V_\nu$, then $y_i\not = {\tilde{y}}_j$ for all $1\le i<j\le s$.

Construct ${{\mathcal {C}}}^\infty$ functions $\phi _\nu :{{\mathbb {R}}}^{m+n}\mapsto [0,1]$, $\nu \ge 1$, with the following properties.

• Supp$(\phi _\nu )\subset V_\nu$.

• For each $\nu \ge 1$, call $V_\nu ' \subset V_\nu$ the interior of the set where $\phi _\nu =1$. Then $\bigcup _{\nu \ge 1} V_\nu '=Z^{(s)}$.

2. For each $\nu \ge 1$, and any polynomials $P_1,\ldots , P_s$ of degree $\le k$, define the function

$$\begin{aligned} f^{(P)}(x,y)~=~f(x,y)+ \sum _{\ell =1}^s \phi _k(x,y) P_\ell (x,y_\ell ). \end{aligned}$$

(108)

We now consider the map

$$\begin{aligned} (x,y_1,\ldots , y_s, P_1,\ldots , P_s)~\mapsto ~\Big (j^k f^{(P)} (x, y_1),~ \ldots ~j^k f^{(P)} (x, y_s)\Big ). \end{aligned}$$

(109)

The right-hand sides are the coefficients of the kth-order Taylor approximations to the maps $(x,y)\mapsto f^{(P)}(x,y)$ at the points $(x, y_\ell )$. Since $\phi _\nu \equiv 1$ on $V'_\nu$, clearly, the differential of the map (109) has full rank. Hence this map is transversal to any manifold W, restricted to $V_\nu '$. By the transversality theorem, there is a residual set ${{\mathcal {S}}}_\nu \subset {{\mathcal {C}}}^\infty ({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})$ such that, for every $f\in {{\mathcal {S}}}_\nu$, the map $j^k_sf$ in (107) is transversal to W at every point $(x, y_1,\ldots ,y_s, P_1,\ldots , P_s )\in W$ such that $(x, y_1,\ldots ,y_s)\in V_\nu '$.

3. Repeating the same argument for every $\nu \ge 1$, we obtain a sequence of residual subsets ${{\mathcal {S}}}_\nu$. The intersection ${{\mathcal {S}}}:=\bigcap _{\nu \ge 1}{{\mathcal {S}}}_\nu$ is still residual in ${{\mathcal {C}}}^\infty ({{\mathbb {R}}}^{m+n};\,{{\mathbb {R}}})$. By construction, for every $f\in {{\mathcal {S}}}$ the map $j^k_sf$ is transversal to W. $\square$