Diameters of Symmetric and Lifted Simple Exclusion Models

Abstract

We determine diameters of Markov chains describing one-dimensional N-particle models with an exclusion interaction, namely the symmetric simple exclusion process (Ssep) and one of its non-reversible liftings, the lifted totally asymmetric simple exclusion process (Tasep). The diameters provide lower bounds for the mixing times, and we discuss the implications of our findings for the analysis of these models.

1 Exclusion Models

Arguably the simplest models for gases of interacting particles are the lattice exclusion models [1, 2]. One-dimensional exclusion models describe N hard-sphere particles moving on a one-dimensional lattice with L sites. The original model is the symmetric simple exclusion process (Ssep) [3], which implements a discrete Markov chain based on the Metropolis algorithm. A configuration $x=\{ x_1, x_2, \dots , x_N \}$ in the sample space $\Omega ^{\textsc {Ssep}}$ is an ordered N-tuple with $x_1< x_2< \dots < x_N$ of the positions of the N particles, which are indistinguishable. In the Ssep, a single move, from time t to time $t+1$, first samples uniformly at random an active particle i that attempts to move, and then proposes, with equal probability, a forward or a backward move. If this move would violate the exclusion condition, it is rejected:

(1)

The Ssep is well-defined both for periodic and hard-wall boundary conditions:

• In hard-wall boundary conditions, if a particle at time t attempts to hop beyond the boundary of the lattice, its move is rejected so that $x^{(t+1)} = x^{(t)}$.

• In periodic boundary conditions, the lattice is treated as if it wraps around, meaning that particles leaving the lattice from one end re-enter from the opposite end. This creates a toroidal geometry.

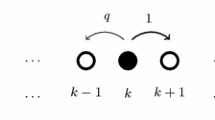
The much studied Tasep (totally asymmetric simple exclusion process) [4] differs from the Ssep in that, at each time step, a forward move is proposed:

(2)

Here, we require periodic boundary conditions because of the fixed direction of moves. The Tasep can be interpreted as one half of a lifting [5] of the Ssep  [6]. In this paper, we consider the lifted Tasep  [7, 8]. A configuration x in $\Omega ^{\textsc {l-T}}$ again consists of an ordered N-tuple $\{ x_1, x_2, \dots , x_N \}$ with $x_1< x_2\dots < x_N$, and in addition the position $x_i \in x$ of the active particle i, which is the only one that can move:

(3)

(4)

where $\overline{\alpha }= 1 - \alpha$. As sketched in Eqs. (3) and (4), from a sample $x^{(t)}$, the active particle i first advances deterministically, but if it is blocked ($x_{i+1} = x_i + 1$, with periodic boundary conditions in i and x), it passes the pointer on to the blocking particle $i+1$. Then, the move from $x^{(t)}$ to $x^{(t+1)}$ is completed by transferring the pointer with probability $\alpha$ to the preceeding particle (pullback move from $x^{(t)}$ to $x^{(t+1)}$) or otherwise with probability $\overline{\alpha }$, by taking no further action (forward move from $x^{(t)}$ to $x^{(t+1)}$) (see the right-hand sides of Eqs. (3) and (4)). The transition matrix of this Markov chain is doubly stochastic, so that in the stationary state, all configurations $x \in \Omega ^{\textsc {l-T}}$ are equally probable [7].

The lifted Tasep is a one-dimensional lattice reduction for the hard-sphere event-chain Monte Carlo algorithm [9]. Its parameter $\alpha$ corresponds to a factor field [8]. The model is integrable by Bethe ansatz [7], although many questions remain. Compared to the Ssep, the lifted Tasep can also be seen as a kinetically constrained lattice gas [10], as each of its configurations is connected only to two other configurations, whereas in the Ssep, the connectivity is 2N. Nevertheless, we will find that the diameter of the lifted Tasep is only roughly double that of the Ssep. Non-rigorous exact enumerations for small system sizes indicate that for a critical value $\alpha _\text {crit}$ of the pullback, the mixing time (the time it takes to be close to the uniform distribution in total variation distance, starting from a worst-case configuration) scales as $\mathcal {O}\left( N^2 \right)$ (for $N \propto L$), the same scaling as we derive here rigorously for the diameter. In Eqs. (1) and (2), configurations are represented by the positions of the particles and in Eqs. (3) and (4), an additional pointer is introduced.

2 Diameters of Exclusion Models

Let P be a Markov chain with sample space $\Omega$ and stationary distribution $\pi$. We use $P^t(x,\cdot )$ to denote the distribution of the chain at time t, assuming x as the starting configuration. Then we refer to

$$\begin{aligned} t_{\text {mix}}(P):=\min _t \left\{ t\ge 0, \max _{x\in \Omega } \Vert P^t(x,\cdot ) - \pi \Vert _{TV} \le \frac{1}{4} \right\} \end{aligned}$$

(5)

as the mixing time of P, where $\Vert \cdot \Vert _{TV}$ denotes the total variation distance. The diameter of a discrete-time Markov chain P in $\Omega$ is defined as

$$\begin{aligned} d = \max _{X,Y\in \Omega } d(X,Y), \end{aligned}$$

(6)

where d(X, Y) is the smallest number of moves of P needed to reach Y from X. For non-reversible Markov chains, d(X, Y) may differ from d(Y, X). The diameter bounds the mixing time from below by d/2 [11]. The diameter of a lifted Markov chain cannot be smaller than that of its collapsed chain (the chain of which it is a lifting). Although we are interested in the diameter of the lifted Tasep, we therefore first compute that of the Ssep. On the other hand, the diameter of a lifted Markov chain can be much larger than that of its collapsed chain. As an example, the lifted Tasep for $\alpha =0$ is not irreducible, so that its diameter is infinite for finite N and L. Naturally, the diameter of the lifted Tasep is independent of $\alpha$, for $0< \alpha < 1$.

2.1 Diameter of the SSEP

We establish the diameter $d^{|\textsc {Ssep}|}_{N, P}$ of the Ssep with hard-wall boundary conditions and, analogously, the diameter $d^{\textsc {Ssep}}_{N, P}$ for the periodic Ssep (see Table 1 for examples)

Table 1 Diameter $d^{\textsc {Ssep}}_{N, L}$ of the Ssep with periodic boundary conditions, obtained by exact enumeration. Data are compatible with Eq. (8)

Theorem 1

Let $N \le L$. For hard-wall boundary conditions, we have

(7)

(8)

Before proving Theorem 1, we provide an upper bound for the diameter which is independent of boundary conditions (Lemma 1), as well as a tool to reduce the periodic Ssep to the hard-wall Ssep (Lemma 2).

Lemma 1

Let $x=\{x_1, x_2, \dots , x_N\}$ and $y=\{y_1, y_2, \dots , y_N\}$ be two configurations in $\Omega ^{\textsc {Ssep}}$. Then, for both periodic and hard-wall boundary conditions, we have

$$\begin{aligned} d^{\textsc {Ssep}} (x,y) \le \sum _{i=1}^N |y_i - x_i|. \end{aligned}$$

(9)

Consequently, $d^{\textsc {Ssep}}_{N, L}, d^{|\textsc {Ssep}|}_{N, L}\le N(L-N)$.

Proof

For fixed L, we prove by induction on $N\le L$ that x can reach y in at most $\sum _{i=1}^N |y_i - x_i|$ moves; these moves do not invoke periodic boundary conditions, and for each particle i, the direction of moves taken from $x_i$ to $y_i$ are monotone, that is, either all forward or all backward. The case $N=1$ is obvious. Suppose the induction holds for $N\le k$. Now consider $N = k+1$. We claim that there exists a flexible particle at $x_i\in x$ such that there are no particles in x within the interval $[x_i, y_i]$ or $[y_i, x_i]$ (whichever is a valid interval), except the flexible particle itself. Before displacing any other particle, we can move the flexible particle from $x_i$ to $y_i$ using monotone Ssep moves only, without invoking periodic boundary conditions. After this movement, we apply the induction hypothesis to two smaller instances whose number of particles is at most k: we can move particles in $\{ x_1, \dots , x_{i-1} \}$ to $\{ y_1, \dots , y_{i-1} \}$ in $\sum _{j=1}^{i-1} |y_j- x_j|$ monotone moves without invoking periodic boundary conditions; similarly, we can move particles in $\{ x_{i+1}, \dots , x_{N} \}$ to $\{ y_{i+1}, \dots , y_{N} \}$ in $\sum _{j=i+1}^{N} |y_j- x_j|$ monotone moves without invoking periodic boundary conditions. These two instances are independent of each other because $y_i$ divides the [1, L] into halves. More precisely, if $x_i < y_i$ then $x_{i-1}, y_{i-1}< y_i < y_{i+1}$ and by the property of flexible particle, $x_{i+1} > y_i$; if $x_i > y_i$ then $x_{i+1}, y_{i+1}> y_i > y_{i-1}$ and by the property of flexible particle, $x_{i-1} < y_{i}$. Hence, we establish the induction.

It remains to show the existence of a flexible particle. For the sake of contradiction, we assume that there is no flexible particle. If $y_1 \le x_1$, then the particle $i=1$, at $x_1$, is flexible. If the particle $i=1$, at $x_1$, is not flexible, then we must have $x_1 < x_2 \le y_1$. This also implies $x_2 < y_2$. Moreover, if $x_2$ is not flexible, then we have $x_2 < x_3 \le y_2$. We continue in this fashion and obtain for each $i=1,2,\dots , N-1$ that $x_i < x_{i+1} \le y_i$. At the end, we know $x_N \le y_{N-1} < y_N$. Since, by definition, particle N is the most forward, it must be flexible, so there is a contradiction. $\square$

With the following lemma, we reduce the Ssep with periodic boundary conditions to the one with hard-wall boundary conditions. We denote by [a, b] the periodic interval of a and b, in other words the interval from a to b if $a\le b$ and, using this definition, $[a,L] \cup [1,b]$ if $a>b$.

Lemma 2

Let $x=\{ x_1, x_2, \dots , x_N \}$ and $y=\{ y_1, y_2, \dots , y_N \}$ be configurations in $\Omega ^{\textsc {Ssep}}$. There then exists a periodic interval [a, b] of length $\lfloor L/2 \rfloor$ or $\lfloor L/2 \rfloor + 1$ that contains the same number of particles in x and in y.

Proof of Lemma 2

With periodic boundary conditions, there are L distinct periodic intervals of length $m:= \lfloor L/2 \rfloor + 1$. Let $S_0 = [a_0, b_0]$ be one of the intervals such that $|x\cap S_0| - |y\cap S_0|$ achieves its maximum among these L intervals. Let $S_i:= [a_i, b_i]$ be the translation of $S_0$ by i, where $a_i:=(a_0 + i) \mod L$ and $b_i:=(b_0 +i) \mod L$. Let $g(i):= |x \cap S_i| - |y \cap S_i|$. By definition, $g(0)\ge 0$. If $g(0) = 0$, then we are done, so we assume $g(0)>0$.

Since both x and y have N particles, if $|x \cap S_0| > |y \cap S_0|$, then there must be some $S_j$ for which $|x\cap S_j| < |y\cap S_j|$, that is, $g(j) < 0$. For every $i\ge 1$,

$$\begin{aligned} g(i) - g(i-1) = \mathbb {1}[b_{i} \in x] - \mathbb {1}[b_{i} \in y] - \mathbb {1}[a_{i-1} \in x] + \mathbb {1}[a_{i-1} \in y] \in [-2, 2]. \end{aligned}$$

(10)

Among $i=1,\dots , j$, there is the first $j^*$ such that $g(j^*) < 0$. Since $g(j^*) - g(j^*-1) \ge -2$ and $g(j^*-1)\ge 0$, $g(j^* - 1) \in \{1,0\}$. If $g(j^* - 1) = 0$, then $S_{j^*-1}$ is the desired interval of length m. Otherwise, $g(j^* - 1) = 1$, and $g(j^*) = -1$, which is only possible when

$$\begin{aligned} b_{j^*} \notin x, b_{j^*} \in y, a_{{j^*}-1}\in x, \text { and } a_{{j^*}-1}\notin y. \end{aligned}$$

(11)

Then we check that $S^*:=[a_{j^*}, b_{{j^*}-1}]$ is a desired interval. Indeed,

$$\begin{aligned} |S^* \cap x|&= |S_{{j^*}-1} \cap x| - 1 = g(j^*-1) + |S_{j^*-1} \cap y| - 1 \end{aligned}$$

(12)

$$\begin{aligned}&= 1 + |S_{j^*-1} \cap y| - 1 = |S_{j^*-1} \cap y| = |S^* \cap y|, \end{aligned}$$

(13)

and $S^*$ is of length $m-1$. $\square$

Proof of Theorem 1

The diameter of the Ssep is at most $N(L-N)$ for both boundary conditions, as follows from Lemma 1.

For hard-wall boundary conditions, moving between $\widetilde{A}$ and $\widetilde{B}$,

(14)

requires $N(L-N)$ moves, because every particle in $\widetilde{A}$ has to be translated by $L-N$ moves to yield its corresponding particle in $\widetilde{B}$. Therefore, Eq. (7) is established, that is, the first claim of the theorem.

For the periodic Ssep, we first consider the case of even L. Lemma 2 implies that there exists a periodic interval $[a,b] \subseteq [1,L]$ of length L/2 or $L/2 + 1$ with k particles both in x and in y. By the periodic boundary conditions, $[1,L] \setminus [a,b]$ is also a periodic interval [c, d] of length L/2 or $L/2-1$. In both configurations x and y, there are $N-k$ particles in [c, d]. Then we obtain two smaller instances of the Ssep with hard-wall boundary conditions: on [a, b], $N_1 = k$ and $L_1 = L/2$ (or $L/2 + 1$), and on [c, d], $N_2 = N-k$ and $L_2 = L - L_1 = L/2$ (or $L/2 - 1$). Moreover,

$$\begin{aligned} d^{\textsc {Ssep}}_{N, L} \le d^{|\textsc {Ssep}|}_{N_1, L_1} + d^{|\textsc {Ssep}|}_{N_2, L_2}. \end{aligned}$$

(15)

Two cases must be considered for the length $L_1$.

In the case $L_1 = L_2 = L/2$, we may apply Lemma 1 to both instances and obtain:

(16)

(17)

(18)

(19)

where the last inequality follows from the fact that $(x+y)^2 / 2 \le x^2 + y^2$ for any $x,y\in \mathbb {R}$.

Alternatively, in the case $L_1 = L/2 + 1$ and $L_2 = L/2 - 1$, a similar computation yields for the hard-wall diameters:

$$\begin{aligned} d^{|\textsc {Ssep}|}_{N_1, L_1} + d^{|\textsc {Ssep}|}_{N_2, L_2}&\le N_1 (L_1 - N_1) + N_2(L_2 - N_2) \end{aligned}$$

(20)

$$\begin{aligned}&= k \left( \frac{L}{2} + 1 - k\right) + (N-k) \left[ \frac{L}{2}- 1 - (N-k)\right] \end{aligned}$$

(21)

$$\begin{aligned}&= \left[ k \cdot \frac{L}{2}+ (N-k) \cdot \frac{L}{2}\right] - \underbrace{ \left[ k^2 + (N-k)^2 - k + (N-k)\right] }_{f_1(k)}, \end{aligned}$$

(22)

where $f_1(k):\mathbb {R} \rightarrow \mathbb {R}$ given by $f_1(k)=k^2 + (N-k)^2 - k + (N-k)$. By checking the derivative of $f_1$, we see that for any $k \ge 0$,

$$\begin{aligned} f_1(k) \ge f_1\left( \frac{N-1}{2}\right) = \frac{N^2-1}{2}. \end{aligned}$$

(23)

Thus,

$$\begin{aligned} d^{\textsc {Ssep}}_{N, L} \le d^{|\textsc {Ssep}|}_{N_1, L_1} + d^{|\textsc {Ssep}|}_{N_2, L_2} \le \frac{NL}{2} - f_1(k) \le \frac{NL}{2} - \frac{N^2-1}{2} = \frac{N(L-N)}{2} + \frac{1}{2}. \end{aligned}$$

(24)

If N is odd, then

(25)

If N is even, then

(26)

Since $d^{\textsc {Ssep}}_{N, L}$ is an integer and in this case is the largest integer satisfying the above inequality, we have

(27)

When L is odd, Lemma 2 in turn implies the existence of a periodic interval $[a,b] \subseteq [1,L]$ of length $\lfloor L/2 \rfloor$ or $\lceil L/2 \rceil$ with the same number of particles in x and in y. In either case, we can choose to set $L_1 = \lfloor L/2 \rfloor , N_1 = k,L_2 = \lceil L/2 \rceil$ and $N_2 = N - k$ for some $k\in [0,N]$. By an analogous computation, we have

$$\begin{aligned} d^{\textsc {Ssep}}_{N, L} \le d^{|\textsc {Ssep}|}_{N_1, L_1} + d^{|\textsc {Ssep}|}_{N_2, L_2} \le \frac{NL}{2} - \underbrace{\left[ \left( k+\frac{1}{2}\right) k + (N-k)\left( N-k + \frac{1}{2}\right) \right] }_{f_2(k)}, \end{aligned}$$

(28)

with $f_2(k) = \left( k+\frac{1}{2}\right) k + (N-k)\left( N-k-\frac{1}{2}\right)$. Again, by checking the derivative of $f_2$, we obtain that for any $k\ge 0$,

$$\begin{aligned} f_2(k) \ge f_2\left( \frac{2N-1}{4}\right) = \frac{N^2}{2} -\frac{1}{8}. \end{aligned}$$

(29)

Thus,

$$\begin{aligned} d^{\textsc {Ssep}}_{N, L} \le \frac{NL}{2} -f_2(k) = \frac{N(L-N)}{2} + \frac{1}{8}. \end{aligned}$$

(30)

Since $N(L-N)$ is even, $\frac{N(L-N)}{2}$ is the largest integer below $\frac{N(L-N)}{2} + \frac{1}{8}$. Since any diameter is an integer, we have effectively

(31)

establishing the upper bound of Eq. (8) for the periodic Ssep.

Finally we show the lower bound of Eq. (8) by providing two configurations that achieve this diameter. For simplicity, we suppose N and L to be even (but the following argument generalizes to arbitrary integers N and $L> N$). We show that for the periodic Ssep, moving from configuration $\widetilde{A}$ to configuration $\widetilde{A}_L$, which are shown below, takes at least $\lceil \frac{N(L-N)}{2} \rceil$ steps.

(32)

For a sequence $\mathcal {S}$ of periodic Ssep moves that lead $\widetilde{A}$ to $\widetilde{A}_L$ and for a particle at poition $L/2 + i$ in $\widetilde{A}_L$, we can trace back its location in $\widetilde{A}$, denoted by $\mathcal {S}_i$. Crucially, for any $\mathcal {S}$ between $\widetilde{A}$ and $\widetilde{A}_L$, there exists an integer $k\in [0,N]$ such that if $k>0$ then

$$\begin{aligned} \mathcal {S}_1 + (k-1) = \mathcal {S}_2 + (k-2) = \mathcal {S}_3+ (k-3) = \dots = \mathcal {S}_{k}= N, \end{aligned}$$

(33)

and moreover if $k < N$ then

$$\begin{aligned} 1 = \mathcal {S}_{k+1} = \mathcal {S}_{k+2} - 1 = \dots = \mathcal {S}_{N} - (N - k - 1). \end{aligned}$$

(34)

Accounting for Eqs. (33) and (34), the number of moves required for $\mathcal {S}$ is at least

$$\begin{aligned}&\sum _{i=1}^{k} \left[ \left( \frac{L}{2} + i\right) - \mathcal {S}_i \right] + \sum _{i=k+1}^{N} \left[ \mathcal {S}_i + L - \left( \frac{L}{2} +i\right) \right] \end{aligned}$$

(35)

$$\begin{aligned}&= \sum _{i=1}^{k} \left[ \left( \frac{L}{2} + i\right) - (N -k + i) \right] +\sum _{i=k+1}^{N} \left[ i - k + L - \left( \frac{L}{2} + i\right) \right] \end{aligned}$$

(36)

$$\begin{aligned}&= \sum _{i=1}^{k} \left[ \frac{L}{2} - (N-k) \right] + \sum _{i=k+1}^{N} \left[ \frac{L}{2} -k \right] \end{aligned}$$

(37)

$$\begin{aligned}&= \frac{NL}{2} - 2k(N-k). \end{aligned}$$

(38)

Note that $k(N-k)$ as a function of k takes its maximum when $k = \frac{N}{2}$. Thus, we obtain a lower bound of Eq. (38)

(39)

Therefore, $d^{\textsc {Ssep}}_{N, L}(\widetilde{A}, \widetilde{A}_L) \ge \lceil \frac{N(L-N)}{2} \rceil$, and we complete the lower bound of Eq. (8). $\square$

Remark 1

The proof of Theorem 1 is constructive. It thus provides an algorithm for transforming any configuration x of the SSEP with periodic boundary conditions into a configuration y in at most $d^{\textsc {Ssep}}_{N, L}$ Ssep moves, that first identifies a periodic interval of appropriate length.

2.2 Upper Bounds for the Diameter of the Lifted TASEP

With the diameter defined as in Eq. (6) and applied to the lifted Tasep and its sample space $\Omega ^{\textsc {l-T}}$, the following Conjecture 1 is obtained from exact enumeration for small N and L (see Table 2). This conjecture suggests that for large N and L with $N/L = \text {const}$, the diameter of the lifted Tasep (which is inherently periodic) is roughly double that of the Ssep with periodic boundary conditions. This is remarkable because the lifted Tasep has only two possible moves per (lifted) configuration, whereas the Ssep has 2N moves at its disposal, at each time step.

Conjecture 1

For $N<L$, the diameter $d^{\textsc {l-T}}_{N, L}$ of the lifted Tasep of N particles on L sites satisfies

$$\begin{aligned} d^{\textsc {l-T}}_{N, L} = N (L-N) + 2 N - 3. \end{aligned}$$

(40)

Furthermore, the configurations A and B,

(41)

uniquely realize, up to translations, the diameter, so that $d^{\textsc {l-T}}_{N, L} = d(A, B)$.

Table 2 Diameter of the lifted Tasep, obtained by exact enumeration. Data are compatible with Eq. (40)

We show that the configurations A and B from Eq. (41) actually saturate the bound of Eq. (40):

Lemma 3

For A and B in Eq. (41), we have $d^{\textsc {l-T}}(A,B) = N(L-N) + 2N - 3$.

Finally, we establish an upper bound of the diameter for the lifted Tasep that is tight up to a term of linear order:

Theorem 2

The diameter of the lifted Tasep with N particles on $L > N$ sites satisfies

$$\begin{aligned} d^{\textsc {l-T}}_{N,L} = N(L-N) + \mathcal {O}\left( L \right) . \end{aligned}$$

(42)

We provide the proofs of Lemma 3 and Theorem 2.

Proof of Lemma 3

First, we use $N-1$ forward moves, so that $x_N = N$ becomes active:

(43)

Next we forward particle N to the position $L-1$, followed by a pullback move, to make particle $N-1$ active.

(44)

We repeat these moves until any particle i is at position $L-N+i$. For this, we have used $N(L-N)$ moves:

(45)

Finally, we need $N-2$ additional forward moves to render particle $N-1$ active without moving particles:

(46)

In total, $(N-1) + N(L-N) + (N-2) = N(L-N) + 2N - 3$ moves have led from A to B without invoking periodic boundary conditions.

We have shown that $d^{\textsc {l-T}}(A,B) \le N(L-N) + 2N - 3$ with A and B from Eq. (41). To establish the equality in this formula, we now argue that each of the above-mentioned moves is necessary. First, since each move can change at most one particle by one unit in position, the required mass transport demands at least $N(L-N)$ moves from A to B. This justifies the moves in Eq. (45). Moreover, starting from A, the only way one can allow any particle to be moved is following the moves as in Eq. (43), which takes $N-1$ moves. Similarly, the only way that a state can transition to B is through the $N-2$ moves as used in Eq. (46). As Eqs. (43) and (46) happen respectively before and after the mass transport, they contain no overlapping moves. Also, moves in both Eqs. (43) and (46) are independent of the mass transport since they change no particle positions. Hence, it takes at least $N(L-N) + (N-1) + (N-2) = N(L-N) + 2N - 3$ moves to reach B from A. $\square$

We introduce several notions useful for the proof of Theorem thm:LT2. We say that a configuration $y'$ is an ancestor of a configuration y if $y'$ can reach y by forward moves that do not cross the periodic boundary conditions at position L. As a forward move advances the pointer by one unit, a configuration with the pointer at i has $i-1 \le L-1$ ancestors. Let $C_y$ be an ancestor of y such that the backmost particle in $C_y$ is active:

(47)

As a symmetric definition, we say that a configuration $x'$ is a successor of x if x is an ancestor of $x'$. Let $\widehat{C}_x$ be a (not necessarity uniquely defined) successor of x such that the foremost particle in $\widehat{C}_x$ is active:

(48)

Lastly, for two integers $a,b\in [1,L]$, we denote by D(a, b) the periodic distance from a to b, that is, if $b\ge a$, then $D(a,b) = b-a$, and if $a>b$ then $D(a,b) = L-a + b$.

Proof of Theorem 2

The theorem is obvious if $N\le 2$ or $L=N$. In what follows, we assume $L>N\ge 3$.

For any pair of configurations x and y, there is a sequence of lifted-Tasep moves from x to y in three stages:

$$\begin{aligned} \underbrace{x \rightarrow \widehat{C}_x}_{\text {stage 1}} \quad \underbrace{\widehat{C}_x \rightarrow C_y}_{\text {stage 2}} \quad \underbrace{C_y \rightarrow y} _{\text {stage 3}}. \end{aligned}$$

(49)

In stage 1 and in stage 3, by the definition of ancestor and successor, x reaches $\widehat{C}_x$ and $C_y$ reaches y after at most $L-1$ forward moves. It remains to analyze the stage 2, for which we need the following lemmas.

Lemma 4

Assume $L>N\ge 3$. For any two configurations $x=\{x_1, \dots , x_N \}$ and $y=\{ y_1, \dots , y_N\}$, there exists a cyclic relabeling of y, denoted as $y'=\{y_1', \dots , y_N'\}$, satisfying

$$\begin{aligned} 1\le y_{m+1}'< y_{m+2}'< \dots< y_N'< y_1'<\dots <y_m' \le L \end{aligned}$$

(50)

with an integer $m\in [0, N]$, such that

(51)

(52)

Lemma 5

Assume $L>N\ge 3$. Let x and y be two arbitrary configurations, with $\widehat{C}_x=\{\tilde{x}_1, \dots , \tilde{x}_N\}$ a successor of x (with foremost active particle) and $C_y=\{\tilde{y}_1, \dots , \tilde{y}_N\}$ an ancestor (with backmost active particle). Suppose that $\widehat{C}_x=\{\tilde{x}_1, \dots , \tilde{x}_N\}$ and the cyclically relabeled configuration $C_y'=\{\tilde{y}_1', \dots , \tilde{y}_N'\}$ satisfy the conditions Eqs. (50) and (52) of Lemma 4 with an integer $m\in [0,N]$. Then we have that

$$\begin{aligned} d(\widehat{C}_x, C_y') \le \sum _{i=1}^N D(\tilde{x}_i, \tilde{y}_i') + \mathcal {O}\left( L \right) . \end{aligned}$$

(53)

Now we use Lemmas 4 and 5 to complete the analysis of the stage 2 in Eq. (49). By applying Lemma 4 to $\widehat{C}_x$ and $C_y$, we obtain an m and a cyclically relabeled configuration $C_y'=\{\tilde{y}_1', \dots , \tilde{y}_N'\}$ such that Eqs. (50), (51) and  (52) are satisfied. With the same m and the cyclically relabeled sequence $C_y'$ for $C_y$, Lemma 5 then suggests

$$\begin{aligned} d(\widehat{C}_x, C_y') \le \sum _{i=1}^N D(\tilde{x}_i, \tilde{y}_i') + \mathcal {O}\left( L \right) \le N(L-N+2)+\mathcal {O}\left( L \right) , \end{aligned}$$

(54)

where the last inequality follows from Eq. (51).

Therefore, x reaches y in at most

$$\begin{aligned} 2(L-1)+N(L-N+2)+\mathcal {O}\left( L \right) = N(L-N)+\mathcal {O}\left( L \right) \end{aligned}$$

(55)

moves, which establishes Eq. (42). $\square$

We provide the proofs of Lemmas 4 and 5 in the appendix.

3 Discussion

The discussed diameter bounds are compatible with the proven [12, 13] or conjectured [7] mixing times for the Ssep and the lifted Tasep, respectively. In particular, the diameter of the lifted Tasep, which is independent of $\alpha$ for $0< \alpha < 1$, provides a first geometrical characteristic of its sample space. In particular, it sets a lower bound on its mixing time for all values of the pullback $\alpha$. For non-critical pullbacks, numerical simulations [7, 8, 14] indicate a mixing-time scaling as $N^{5/2}$, much larger than the diameter bound $t_{\text {mix}}\ge d/2$. However, for $\alpha = \alpha _\text {crit}$, numerical simulations for $2N = L$ [7] (see also [8]) are compatible with a mixing time $t_{\text {mix}}\rightarrow N^2$ (for $N \rightarrow \infty$), which would saturate the diameter bound up to a factor of two. An asymptotically sharp diameter bound (up to a constant factor), for $\alpha = \alpha _\text {crit}$, would be exceptional as diameter bounds are in general very weak [11]. Given the importance of the model, it would be interesting to obtain other geometrical characteristics, as the $\alpha$-dependent conductance of the underlying graph. It appears also possible to obtain the mixing time of the lifted Tasep rigorously, given that this was achieved for the Ssep  [12, 13], where it is $\sim N^3 \log ~{N}$ and for the Tasep  [15], where it is $\sim N^{5/2}$. At present, the inverse-gap scaling for the lifted Tasep is known only from the Bethe ansatz, and it shows a pronounced dependence on $\alpha$. It will be fascinating to understand whether this $\alpha$ dependence is reflected in the basic geometry of the sample space and whether it can be obtained rigorously.

A Supporting Proofs

We provide proofs of Lemmas 4 and 5.

Proof of Lemma 4

We provide the following Algorithm 1 that inputs configurations x and y and returns the cyclic relabeling $y'$ characterized by an integer m and satisfying Eqs. (50), (51) and (52).

Algorithm 1

Find $y'$ and m in the proof of Lemma 4

Clearly, if Algorithm 1 exits through Line 14, the output satisfies Eqs. (50) and (52). If Algorithm 1 exits through Line 10, its output satisfies Eq. (52) due to Line 9 and satisfies Eq. (50) due to the assignment in Lines 3-8.

Now we show that the output of Algorithm 1 also satisfies Eq. (51). First suppose that Algorithm 1 terminates with $m=N$. Since $x_i \ge i$, $y_i' \le L-(N-i)$ and $y_i'\ge x_i +2$ it then holds that

$$\begin{aligned} D(x_i, y_i') = y_i' -x_i \le L-(N-i) -i = L-N. \end{aligned}$$

(56)

As Eq. (56) holds for $i=1,\dots ,N$, the case $m = N$ has thus been handled.

Second, we may suppose that Algorithm 1 terminates with $m<N$. Since Algorithm 1 does not satisfy Eq. (52) for $m+1$, one of two following conditions are satisfied (still for $m<N$):

• (i) $y_N' = y_{N-m}< x_1 +2$,

• (ii) There exists $i\le m$ such that $y_i' = y_{N-m+i} < x_{i+1} + 2$.

Under the case (i), we have

$$\begin{aligned} x_1 + (L-y_N') > x_1 + (L - x_1 - 2) = L-2 \end{aligned}$$

(57)

For any $j \in [1,m]$, since $x_j < y_j' \le L$, it holds that

$$\begin{aligned} D(x_j, y_j') \le L-(x_j + (L-y_j')) = L - (x_1 + (L-y_N')) +(x_1 - x_j) + (y_j' - y_N'). \nonumber \\ \end{aligned}$$

(58)

It follows from Eqs. (57) and (58) that

$$\begin{aligned} D(x_j, y_j') < 2 - (j - 1) + [L - (N-j)] = L-N+3. \end{aligned}$$

(59)

For $j\in [m+1, N]$, $x_j$ reaches $y_j'$ across the periodic boundary. By an analogous computation, we also have

$$\begin{aligned} D(x_j, y_j')&\le y_j' + (L - x_j) \le y_N' - (N-j) + (L - x_j) \end{aligned}$$

(60)

$$\begin{aligned}&< (x_1 + 2) + (L - x_j) - (N - j) \end{aligned}$$

(61)

$$\begin{aligned}&\le L+2-(j-1) - (N-j) = L-N+3. \end{aligned}$$

(62)

Next we consider the case (ii). For $j\in [1,m]$, we have

$$\begin{aligned} D(x_j, y_j')&\le L - (x_j + (L - y_j')) \end{aligned}$$

(63)

$$\begin{aligned}&= L - (x_{i+1} + (L - y_i')) + (x_{i+1} - x_j) + (y_j' - y_i') \end{aligned}$$

(64)

$$\begin{aligned}&< 2 + (x_{i+1} - x_j) + (y_j' - y_i'), \end{aligned}$$

(65)

where Eq. (65) follows from (ii). If $j \ge i+1$, then $x_{i+1} - x_j \le i+1-j$ and $y_j' - y_i' \le L -N + j -i$, so we obtain

$$\begin{aligned} 2 + (x_{i+1} - x_j) + (y_j' - y_i') \le 2+ (i+ 1 -j) + (L-N+j-i) = L-N+3.\nonumber \\ \end{aligned}$$

(66)

If $j\le i$, then $x_{i+1} - x_j \le L-N+(i+1)-j$ and $y_j' -y_i' \le j-i$ so again we obtain

$$\begin{aligned} 2 + (x_{i+1} - x_j) + (y_j' - y_i') \le 2 + (L - N +(i+1)-j)+ (j-i) = L-N+3. \nonumber \\ \end{aligned}$$

(67)

Combining inequalities Eqs. (63) and (67), we establish that $D(x_j, y_j') < L-N+3$. For $j \in [m+1, N]$, it holds that

$$\begin{aligned} D(x_j, y_j')\le y_j' + (L-x_j) \le y_i' - (i + N - j) + (L-x_j). \end{aligned}$$

(68)

By (ii), we have

$$\begin{aligned} y_i' - (i + N - j) + (L-x_j)&< x_{i+1} + 2 +L-N -x_j - (i-j)\end{aligned}$$

(69)

$$\begin{aligned}&= L - N +2 + (x_{i+1} - x_j) - (i-j) \end{aligned}$$

(70)

$$\begin{aligned}&\le L - N + 2 + (i + 1 -j) - (i-j) \end{aligned}$$

(71)

$$\begin{aligned}&= L - N +3. \end{aligned}$$

(72)

The inequalities Eqs. (68) and (72) imply that $D(x_j, y_j') < L-N+3$.

In both cases we have shown that $D(x_j, y_j') < L - N +3$ for all $j=1,\dots , N$, and Eq. (51) follows as $D(x_j, y_j')$ is an integer. $\square$

Proof of Lemma 5

Since configurations x and y are inconsequential to this proof, to simplify the notations, instead of writing $\widehat{C}_x=\{\tilde{x}_1, \dots , \tilde{x}_N\}$ for the successor of x and $C_{y}'=\{\tilde{y}_1', \dots , \tilde{y}_N'\}$ for the cyclic relabeling of the ancestor $C_{y}$ of y, we write $\widehat{C}_x=\{x_1, \dots , x_N\}$ and $C_y'=\{y_1, \dots , y_N\}$. Recall that configuration $\widehat{C}_x$ is an ordered N-tuple, so we could refer to the particle at $x_i$ as the particle i for each $i=1,\dots ,N$.

We first discuss two simple cases. If $m=N$, we can directly move each particle i to $y_i$ in the order of $i=N,\dots , 1$; in this case $d(\widehat{C}_x, C_y') = \sum _i D(x_i, y_i)$. If $m=N-1$, we just move the particle N across the periodic boundary to position 1 (first pushing any blocking particles forward by executing Lines 2-4 of Algorithm 2 if $x_1= 1$), then successfully move particles $N-1, \dots , 1$ to $y_{N-1}, \dots , y_1$ in the order of $N-1, \dots , 1$, and finally move the particle N to $y_N$ if $y_N>1$. Reaching $C_y'$ from $\widehat{C}_x$ through these steps implies $d(\widehat{C}_x, C_y') \le \sum _i D(x_i, y_i) + O(N)$, where we spend additional O(N) steps for the need to push the blocking particles forward at the beginning.

In the rest of the proof, we assume $m\le N-2$. Note that this assumption together with (51) ensures that

$$\begin{aligned} D(x_i, y_i) \ge 2 \quad \text {for~~} i\in [m+1, N]. \end{aligned}$$

(73)

Now, given any pair of $(\widehat{C}_x, C_y')$, we provide the following Algorithm 2 that reaches $C_y'$ from $\widehat{C}_x$ through the lifted Tasep steps.

Algorithm 2

An algorithm to reach $C_y'$ from $\widehat{C}_x$ in Lemma 5

Algorithm 3

CLEANUP subroutine used in Line 22 of Algorithm 2

We first verify the validity of Algorithm 2 in scenarios where the steps might be unclear. In Lines 8, 13 and 17, the attempted moves for the particle i could be blocked by the particle $i+1$, but at least in all these cases, a single pullback move could still take place due to Eqs. (73) and (51), and the pointer always successfully transfers to the particle $i-1$. Thus, operations in Lines 7-14 are always valid moves of the lifted Tasep. In addition, we need to verify that an infinite loop never takes place in Lines 6-15: since particles keep moving forward, the algorithm will eventually break out the repeat-until loop, and hence terminate in finite time.

To see the correctness of Algorithm 2, we make several useful observations. Observe that in Lines 7-11, if any particle i successfully reaches $y_i-1$, then the particle i is unable to block particle ${i-1}$ in the upcoming iteration of $i-1$. Consequently, all particles ${i-1}, \dots , {m+1}$ reach $y_{i-1}, \dots , y_{m+1}$ successfully in Line 8. Similarly, in Lines 12-14, if any particle i successfully reaches $y_i$ then all particles ${i-1}, \dots , 1$ reach their assigned destinations in Line 13. Hence, when the Algorithm 2 breaks out the repeat-until loop, either the particle 1 has arrived at $y_1$ or the particle ${m+1}$ has arrived at $y_{m+1} - 1$.

Case 1: particle 1 has arrived at $y_1$. Since $y_1> y_N> \dots > y_{m+1}$ by assumption, in Lines 16-18, all attempts will be successful. Next we consider the two cases in Line 19. By the previous observation, if particle m has arrived at $y_m$, which can only happen in Line 13, then each particle i has arrived at $y_i$ for $i\in [1,m]$. Hence if the algorithm reaches Line 20, the only unfinished particle is the particle $m+1$, which is then sent to $y_{m+1}$. Alternatively, if particle m is not at $y_m$ in Line 19, then we enter the CLEANUP subroutine in Algorithm 3. In Lines 2-5 of Algorithm 3, for each $i\in [m+1, l_1+1]$, since particle ${i+1}$ has been at position $y_{i} + 1$, these steps in Lines 2-5 will not be blocked by $i+1$ and thus they execute successfully. By the assumption of case 1, we have $l_1>1$, so we enter the else branch in Line 18. For each $i\in [l_1,m]$, from our earlier discussions, the particle $i+1$ has been staying at $y_i + 1$, so moving each particle i to $y_i$ would not get blocked by $i+1$; after Line 20 succeeds, particles i and ${i+1}$ are adjacent, so the forward move in Line 21 would also be justified. So far all particles except $m+1$ have arrived at their destinations. Finally, particle $m+1$ arrives at $y_{m+1}$ in Line 24. Therefore, the final configuration equals to $C_y'$, and we conclude the case 1.

Case 2: particle 1 has not arrived at $y_1$ but particle ${m+1}$ arrives at $y_{m+1}-1$. If $y_{m+1} \ne 1$, then in the last iteration of the repeat-until loop, all attempts in Line 13 of Algorithm 2 will be successful since particle $m+1$ has crossed the periodic boundary and will not able to block any of the movements in Lines 12-14. Then particle 1 would have arrived at $y_1$ but this contradicts our assumption. Thus, the only possibility that Case 2 could happen is $y_{m+1} = 1$, $y_m = L, \dots , y_1 = L-m$. Moreover, just before the execution of Line 16 of Algorithm 2, particle 1 is at $L-m-1$, particle 2 is at $L-m$,..., and particle ${m+1}$ is at L. Following this, Lines 16-18 ensure that there exists $l_2\in [m+2, N]$ such that particle i is blocked for $N\ge i\ge l_2$ while particle i is at $y_i$ for $m+2 \le i < l_2$. As in this case particle m is not at $y_m$, we enter the CLEANUP subroutine. In Lines 3-4 of Algorithm 3, we will send particle ${m+1}$ to $y_m+1=1$. If particle N has been at $y_N$, the rest of proof follows analogous arguments as in Case 1. If particle N has not been at $y_N$, additional steps in Lines 7-17 of Algorithm 3 are needed to make sure both the final positions of particles ${l_2}, \dots , N$ and the location of the pointer are correct. Noticing that the particles ${l_2}, \dots , N, 1, \dots , {m+1}$ are all adjacent to each other, the validity of these steps are readily verified.

Lastly, we count the total number of lifted Tasep steps used in Algorithm 2. Each particle i travels a distance $D(x_i, y_i)$ through a combination of forward and pullback moves; in addition, in Lines 2-4 of Algorithm 2 and in Lines 16, 21 of Algorithm 3, we use a total of $\mathcal {O}\left( L \right)$ forward moves to transfer the pointers without moving any particles. Therefore, the number of steps required to reach $C_y'$ from $\widehat{C}_x$ is at most

$$\begin{aligned} \sum _{i=1}^N D(x_i, y_i) + \mathcal {O}\left( L \right) , \end{aligned}$$

(74)

so we establish Eq. (53). $\square$