1 Introduction

Random sequential adsorption (RSA) is a protocol utilized to generate loose random packings [1]. A packing is constructed iteratively by adding one object after another by repeating the following steps. The position and orientation of a virtual particle are randomly selected, usually using the uniform probability distribution of places and orientations. The virtual shape is then tested to check if it overlaps with any of the objects that have already been added to the packing. If not, the virtual shape is placed in the packing and remains in its position and orientation indefinitely. Otherwise, the virtual shape is removed and abandoned. Particles can be added to a packing until it becomes saturated, meaning that there is no further space to place the next object. Although a similar approach was used for the first time by Flory to model the attachment of substituents to a vinyl polymer [2], RSA owes its popularity to Feder, who observed that the configuration of particles in such packings resembles the structure of adsorption monolayers obtained in irreversible adsorption experiments [3, 4]. Since then, RSA has become a valuable tool for interpreting a variety of adsorption experiments [5, 6], and a standalone field of theoretical studies. It is considered one of the simplest protocols for generating random configurations of arbitrary objects, taking into account the excluded volume effects [7]. Interestingly, some results obtained for RSA packings are similar to those observed for significantly different random close packings that model granular media in which neighboring particles touch themselves. For example, for both types of packings, slightly anisotropic shapes form denser configurations compared to more symmetric ones [8,9,10,11,12,13].

In this study, we examine the kinetics of RSA packing growth. For the majority of shapes, close to the saturation limit, the kinetics is given by Feder’s law:

$$\begin{aligned} \theta - \theta (t) \sim t^{-\frac{1}{d}}, \end{aligned}$$
(1)

where \(\theta \) represents the packing fraction at saturation, \(\theta (t)\) denotes the packing fraction after t RSA iterations, i.e. the number of random attempts to add the next particle to the packing, and d is some parameter. For RSA of hyperballs in a flat and continuous hyperspace, it has been proven analytically that d corresponds to the dimension of the packing [14, 15]. On the other hand, simulations show that \(d=3\), for randomly oriented anisotropic objects positioned on a continuous, flat, two-dimensional plane [12, 16, 17]. Thus, it is generally believed that d equals the number of degrees of freedom of the particle [18], but there are exceptions to this rule [19,20,21], and one of them is the RSA packing built of squares (or rectangles), aligned in parallel. Here:

$$\begin{aligned} \theta - \theta (t) \sim \frac{\log t}{t}. \end{aligned}$$
(2)

This result was obtained analytically [15] and was also confirmed numerically in multiple studies [22, 23]. It should be noted that the randomly oriented squares or rectangles comply with the general rule given by equation (1) with \(d=3\) [24, 25]. However, a recent study demonstrated that the kinetics of RSA of rectangles, which are permitted to align in only two perpendicular orientations conforms to the logarithmic law (2) [23]. This finding prompts fundamental inquiries as to how is the RSA kinetics influenced by the number of potential discrete orientations? Is the power law (1) recovered at some finite number of orientations or in the limit of infinite possible orientations? What is the effect of the number of orientations on other properties of generated packings? This study aims to address all these inquiries. Although our focus is on the properties of RSA protocol, it is important to note that during adsorption processes, a molecular docking process may occur as the adsorbate approaches a surface or an interface, aligning the particle on the surface. This process restricts the continuous spectrum of possible adsorbate orientations, and therefore, our study’s findings could have implications for related physical experiments. On the other hand, it is crucial to recognize that the amount of RSA iterations does not increase proportionally with the actual time of an adsorption experiment. In addition to the decreasing probability of adsorption due to surface filling, which can be determined through numerical RSA simulations, the transport mechanism that carries molecules from a bulk phase to the vicinity of a surface must also be considered. Examples of such calculations can be found in Refs. [6, 26,27,28].

In addition to squares and rectangles, we conducted the same study for ellipses and discorectangles of various width-to-height ratios. Here, in the limit of the low orientation number, the kinetics should be controlled by (1) with \(d=2\) [3, 18]. Therefore, in this instance, the previously posed questions pertain to the shifts between the power-law kinetics depicted by \(d=2\) and \(d=3\).

2 Model and Numerical Details

We generated saturated RSA packings consisting of rectangles, ellipses, and discorectangles (flat spherocylinders). The possible orientations of the particles in a single packing were given by \(k\pi / n\) for \(k=0,\dots ,n-1\), and the parameter n varied from 1 to \(2 \cdot 10^4\). We also investigated the effect of particle anisotropy on the results using shapes with an aspect ratio f of 1 (for rectangles only), 2, and 5. For every combination of (n, f) parameters, and of examined shapes, we generated 100 separated saturated configurations of shapes in a square with a surface area \(S = 10^6\), with each individual shape having a surface area of \(S_p = 1\). To mitigate the influence of finite-size effects, periodic boundary conditions were applied [29]. RSA iterations were measured in dimensionless time units, whereby one unit corresponds to \(S/S_p\) iterations. Note that such linear rescaling has no impact on the asymptotic laws (1) and (2).

To generate saturated packings, we employed the region tracing technique which identifies the areas where particles potentially can be inserted, see, e.g. [30, 31]. In brief, the sampling of possible locations is restricted exclusively to these zones, which significantly speeds up packing generation. The positioning of each particle reduces the size of these regions, which goes to zero at the point of saturation. Thus, if no such regions exist, the packing is saturated, making further attempts to add shapes unnecessary. Detailed instructions on implementing this method for RSA of rectangles, ellipses, and spherocylinders can be found in Refs. [32, 33].

3 Results

Example Fig. 1 displays saturated RSA packings constructed using rectangles, ellipses, and discorectangles.

Fig. 1
figure 1

Example saturated random packings built of rectangles (top row), ellipses (middle row), and discorectangles (bottom row) of 1 (left column), 3, (middle column) and 10 (right column) possible orientations. The packings have a surface area of \(20\times 20\) and the surface area of a single shape is 1. The width-to-height ratio in all cases is \(f=2\)

Full size image

Larger packings, measuring 1000 \(\times \) 1000, were created and analyzed to yield the results described below.

3.1 Kinetics of Packing Growth

The example dependence of the difference between the saturated packing fraction and the packing fraction after a certain number of iterations for squares with varying numbers of orientations is shown in the left panel of Fig. 2.

Fig. 2
figure 2

The dependence of the difference between the saturated packing fraction and the packing fraction after a specified number of iterations (left panel), and the dependence of the fitted value of parameter d on iteration (right panel) for squares of different numbers of allowed orientations

Full size image

Each line represents distinct kinetics, which will be thoroughly examined in the following subsections.

3.1.1 Kinetics Near Saturation

The kinetics of packing growth is analyzed using the parameter d from the power-law (1). To eliminate the parameter \(\theta \), which may depend on the number of permitted orientations, this relationship can be reformulated as

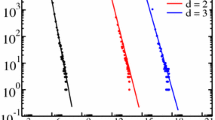
$$\begin{aligned} \frac{d}{dt} \theta (t) \sim \frac{1}{d} \,\, t^{-\frac{d+1}{d}}, \end{aligned}$$
(3)

which leads to \(\ln \frac{d}{dt} \theta (t) \sim -\frac{d+1}{d} \ln t\). Thus, the parameter d can be determined by the least squares fitting of the data \((\ln \frac{d}{dt} \theta (t), \ln t)\) obtained from the numerical experiment with respect to the aforementioned relationship. To perform this fitting we averaged the dependence of \(\theta (t)\) over 100 independent, saturated packings. Although the slopes in Fig. 2 appear straight, the estimated value of d varies over time, as demonstrated in the right panel of Fig. 2. Here, d(t) was obtained by fitting equation (1) to the data within the range \([0.01\, t, t]\). Nonetheless, we are interested in a value of d close to the saturation limit as the laws (1) and (2) are valid asymptotically, thus, the fitting should be performed as close to the saturation as possible. However, generated packings saturate after different numbers of iterations. Therefore, to minimize deviation from the saturation limit and preserve statistical accuracy, we determined the minimum saturation time \(t^{sat}_{min}\) and performed fitting on the data within the range of \([0.01 \, t^{sat}_{min}, t^{sat}_{min}]\). For packings generated during this study the value of \(t^{sat}_{min}\) was typically of the order of \(10^{20}\) iterations. Please note that while there are differences between kinetics (1) and (2), in practice, the second one closely follows Feder’s law with an exponent d slightly larger than 1 (see case \(n=1\) in Fig. 2). Therefore, we only used the relation (1) to the data in all cases. The results we obtained for the RSA packing made of rectangles can be seen in Fig. 3, while Fig. 4 shows the results of the packings built of ellipses and discorectangles.

Fig. 3
figure 3

The dependence of the parameter d on the number of possible orientations of packed rectangles for several different rectangle’s width-to-height ratios f

Full size image

For rectangles with one or two possible orientations, we get \(d\approx 1.2\) from the power-law fit. It is because in this case, the kinetics of packing growth is governed by the logarithmic law (2), which has been analytically predicted for \(n=1\) [14, 15], and previously observed for \(n=2\) [23]. When \(n=3\) we note a sudden change to \(d=2\), which is typical for RSA of disks, and other anisotropic shapes aligned in parallel [18]. The rapid change observed here is attributed to the shape of the regions, where subsequent objects are deposited. Close to saturation, they are rectangular for \(n=2\) and triangular for \(n\ge 3\), resulting in diverse asymptotic kinetics [15]. To test this hypothesis we generated several random packings built of rectangles of various aspect ratios \(f \in {1, 2, 5, 10}\) and only two allowable orientations of \(0^\circ \) and \(45^\circ \). The kinetics of packing growth for all these cases were described by the exponent \(d \approx 2\) that supports the aforementioned reasoning.

For a larger number of possible orientations n, this value remains unchanged until \(n\approx 500\). Then the parameter d starts to grow and for \(n\approx 2500\) it almost reaches a plateau at \(d\approx 3\), which is typical for most unoriented anisotropic objects [16, 24, 25]. The transition between \(d=2\) and \(d=3\) occurs for a slightly larger n when the width-to-height ratio of the rectangle increases. As discussed previously [20, 34, 35] such a transition is a result of mixing two behaviors: some packings are filled according to a power law with larger exponent d while others follow if with a smaller one. Here, for larger anisotropies of packed shapes, more systems are described by \(d=2\) than by \(d=3\). This means that the more systems approach saturation slower i.e. available sites for shape placement are filled at a slower rate. For larger anisotropies of packed objects, near saturation, particles are placed in parallel to their neighbors [24], and such parallel alignment may be more difficult to achieve, which could explain the results.

These observations were also confirmed by RSA packing of ellipses and discorectangles, as shown in Fig. 4.

Fig. 4
figure 4

The dependence of the parameter d on the number of possible orientations of packed ellipses and discorectangles for several different width-to-height ratios f

Full size image

Here, though, we do not see the logarithmic rule (2) since for \(f=1\) these shapes are two-dimensional disks for which the power law (1) is applicable.

3.1.2 Finite Size Effects

The numerically obtained results for kinetics at saturation may be sensitive to packing size [34]. Therefore, we investigated the variability of the above-presented results for RSA of squares to other packing sizes. Here, we utilized packing of size \(S \in \{10^4, 10^5, 10^6, 10^7 \}\). To have a comparable number of packed objects, we generated a different number of independent packing for each size. For instance, there were \(10^4\) packings for \(S=10^4\) and only 10 packings for \(S=10^7\). The results are presented in Fig. 5.

Fig. 5
figure 5

The dependence of the parameter d on the number of possible orientations of packed squares for several different packing sizes S

Full size image

The transition from \(d=2\) to \(d=3\) commences at a later stage for larger packings. A comparable outcome has been observed for more anisotropic shapes. To understand this result, it is crucial to acknowledge that statistically, the later the object is placed, the tighter the spot it occupies [36]. Accordingly, for larger packings, there are more such tight spots, and consequently, the kinetics decelerates and favors smaller values of d. Therefore, it is possible that the growth kinetics of packing consisting of nonparallel squares is governed by \(d=2\) for infinitely large packings given that the number of allowed orientations is finite.

The above observations are confirmed by the results from RSA of ellipses and discorectangles of \(f=2\), presented in Fig. 6.

Fig. 6
figure 6

The dependence of the parameter d on the number of possible orientations of packed ellipses (left panel) and discorectangles (right panel) for several different packing sizes S

Full size image

The results are qualitatively the same with the only difference corresponding to the lack of the case \(d\approx 1\), as for \(n=1\) the kinetics of packing growth is the same as for packings of disks, having two degrees of freedom. It is noteworthy that even with \(n=10^5\) possible orientations, the largest investigated packing of \(S=10^7\) did not achieve \(d=3\), which is observed for arbitrarily oriented shapes.

3.1.3 Kinetics at Low Packing Fraction

The kinetics of RSA can also be studied at a low coverage limit [37, 38] using the available surface function (ASF), which describes the relationship between the probability of the successful placement of a new shape in the packing and the packing density. For low coverage, the ASF can be expanded in the Taylor series:

$$\begin{aligned} \textrm{ASF}(\theta ) = 1 - C_1 \theta + C_2 \theta ^2 + ... \, , \end{aligned}$$
(4)

where \(\theta \) denotes a packing fraction and \(C_1\), \(C_2\) are the expansion coefficients. The coefficient \(C_1\) has a straightforward physical interpretation as it quantifies the mean surface area blocked by a single shape of a unit surface area. For instance, if the packing includes a solitary disk of radius r, the center of the next disk cannot be located within a circle with a radius of 2r around the first disk’s center. Therefore, the area blocked by the first disk is 4 times larger than its own surface area, and \(C_1=4\). The coefficient \(C_2\) denotes the mean intersection area of the blocked area of two deposited shapes [37, 39]. It is important to mention that the parameters \(C_1\) and \(C_2\) are in close relation with the parameters \(B_2\), \(B_3\) of virial expansion used for approximating a state equation of a system at thermodynamic equilibrium:

$$\begin{aligned} \frac{pV}{N k_\textrm{B} T} = 1 + B_2\rho + B_3 \rho ^2 + ... \, , \end{aligned}$$
(5)

where p is a pressure, V is a volume, T is an absolute temperature, N the number of particles, \(k_\textrm{B}\) the Boltzmann constant, and \(\rho \) a density of the system. For these expansions \(C_1 = 2B_2\) and \(C_2 = 2B_2^2-\frac{3}{2}B_3\) [38].

To determine the coefficients \(C_1\) and \(C_2\), we numerically estimated \(\textrm{ASF}(\theta )\) for \(\theta <0.1\) and then fitted a parabola to the data in this range using the least squares method. The dependence of the coefficient \(C_1\) on the number of orientations allowed n for the packings studied is shown in Fig. 7.

Fig. 7
figure 7

The dependence of the coefficient \(C_1\) on the number of allowed orientations n for squares and rectangles (left panel), and ellipses and discorectangles (right panel). Dots are data from numerical simulations, the solid lines are to guide the eye

Full size image

When there is only one orientation available, \(C_1\approx 4\), and then the value increases rapidly with n. Its limiting value is reached for \(n<10\) and, as expected, depends on the particle anisotropy f – the larger f is, the more space is blocked. A similar behavior is observed for the coefficient \(C_2\), see Fig. 8.

Fig. 8
figure 8

The dependence of the coefficient \(C_2\) on the number of allowed orientations n for squares and rectangles (left panel), and ellipses and discorectangles (right panel). Dots are data from numerical simulations, the solid lines are to guide the eye

Full size image

To conclude, the packing growth kinetics at low packing fractions is indistinguishable from the kinetics of unoriented particles when the number of allowed orientations is three orders of magnitude smaller than in the case of the kinetics near saturation, where \(n\ge 10^4\). This behavior is identical for all shapes studied.

3.2 Saturated Packing Fraction

The most fundamental property of a random packing is its mean density. The density is different for aligned and randomly oriented objects. For example, for RSA packing built of parallel squares or rectangles, it is \(0.5620219 \pm 0.0000072\) [22, 35], and for arbitrarily oriented ones, it is \(0.527640 \pm 0.000018\) [24, 32, 40]. Additionally, the highest density is reached for slightly anisotropic shapes [11, 12, 41]. The results for rectangles, ellipses, and discorectangles studied here are shown in Fig. 9.

Fig. 9
figure 9

The dependence of the saturated packing fraction \(\theta \) on the number of allowed orientations n for squares and rectangles (left panel), and ellipses and discorectangles (right panel). Dots are data from numerical simulations, the solid lines are to guide the eye

Full size image

In general, the packing fraction reaches its limit value for randomly oriented shapes when the number of allowed orientations exceeds \(n=100\), however, this threshold is slightly lower in the case of rectangles and slightly higher for ellipses end discorectangles. For a smaller number of allowed orientations, the packing fraction is strongly dependent on the specific shape of the particles. For rectangles of small to medium anisotropy f, we observe the maximum at \(n=2\) and then decrease to the limiting density. Different scenarios are observed for ellipses. For identical orientations (\(n=1\)), regardless of f, the packing fraction is identical as for disks, which is expected, since all of these systems are identical up to scaling in the direction of one of the semiaxes. Then, for small anisotropy f we observe monotonic growth of \(\theta \) with n. However, for \(f=5\) the packing fraction decreases with n and reaches a minimum at \(n=4\) well below the asymptotic value and then slowly increases. For discorectangles, the dependence seems to be monotonic for all width-to-length ratios studied.

3.3 Density Autocorrelation Function

The density autocorrelation function gives us information on the microstructural properties of the packing. The density autocorrelation function is proportional to the probability density function of finding two shapes at a given distance between their centers.

$$\begin{aligned} G(r) = \lim _{\textrm{d}r \rightarrow 0}\frac{N(r, r+\textrm{d}r)}{ 2\pi r \textrm{d}r \theta }, \end{aligned}$$
(6)

where \(N(r, r+\textrm{d}r)\) is the mean number of neighbors of a given shape whose centers are at a distance between r and \(r+\textrm{d}r\). The packing fraction \(\theta \) in the denominator is due to normalization \(G(r\rightarrow \infty ) = 1\). The density autocorrelation function in RSA packings is known to have a superexponential decay at large r [42]. Here, we estimate the function G(r) numerically using \(\textrm{d}r=0.01\). The results for the shapes studied are shown in Fig. 10.

Fig. 10
figure 10

Density autocorrelation function for rectangles, ellipses, and discorectangles of anisotropy \(f=2\) and various numbers of allowed orientations n

Full size image

As expected, the density autocorrelation function is sensitive to the number of orientations allowed, and therefore at small distances (\(r<1.5\)), we can observe a fine structure of local minima and maxima that correspond to specific orientations. However, the graphs are smooth for \(n=100\), suggesting that such packings are practically indistinguishable from those containing unoriented objects. This observation agrees with the results for packing fractions. Thus, the local and global properties of RSA packings built of unoriented shapes are the same as for shapes of discrete orientations if their number is large enough. For larger r and \(n \ge 3\), autocorrelations are generally difficult to distinguish. The only exception is observed for shapes aligned in parallel (\(n=1\)) because there the G(r) differs significantly from other correlation functions up to \(r=3\).

4 Conclusion

The number of discrete orientations allowed for shapes in RSA packings has an impact on all properties of the packings that were considered. The most interesting behavior is observed for the kinetics of packing growth near saturation. The number of orientations allowed must be greater than \(n=10^4\) to obtain numerically the same results as for arbitrarily oriented shapes, at least for \(S=10^6\). For larger packings, more allowed orientations can be needed. It is in line with other results, where the kinetics at the jamming limit was the most sensitive observable for detecting particle anisotropy [43], irregularities in its shape [20, 34] or in the space where objects were deposited [44]. The transition between these two universality classes of kinetics occurs for \(n \in [400, 4000]\) for rectangles and \(n \in [1000, 20 000]\) for ellipses and discorectangles. For rectangles, there is also a special case for \(n =1\) where the kinetics is governed by a logarithmic law (2). There, the regions in an almost saturated packing, where the center of the next particle can be successfully placed, are rectangular instead of triangular – see the reasoning in Ref. [15], and thus we observe there the difference in kinetics near saturation. The same is valid for \(n=2\) as long as the angles allowed are perpendicular to each other. Otherwise, kinetics is governed by the power law (1 with the exponent \(d=2\). For larger n, where the kinetics (1) and (2) are mixed, the asymptotic behavior is governed by the one, which decays slower, thus, for sufficiently large packings, law (1) is observed [20, 34, 35]. In the low packing fraction regime, the kinetics of packing growth varies only when \(n<10\). For a larger number of allowed orientations, it is the same as for arbitrarily oriented particles, regardless of the shape. The transition between limits for parallelly and arbitrarily oriented shapes can also be observed in the mean density and microstructural properties of the generated packings. However, their values become indistinguishable for \(n>100\), which is much earlier than in the case of packing growth kinetics at saturation.