1 Introduction

The dynamics of growth of bacteria and other microbes treated with antibiotic drugs is complex and multifaced. For a recent study see [1], in which the authors used a compartmental model to explore three scenarios by which bacteria develop antimicrobial resistance: point mutations, plasmid mediated horizontal gene transfer via conjugation, and either mutation or horizontal gene transfer resulting in resistance to the same class of antibiotic, using examples motivated by a study of Escherichia coli. Other studies can be found in [2, 3]. Authors of [2] characterized and built a model of the inoculum effect in E. coli cultures using a large variety of antimicrobials, where the outcome of a antibiotic treatment on the growth capacity of bacteria is largely dependent on the inoculum effect. In [3], the authors used a theoretical model to predict the dynamical response of a bacterial cell to a time-dependent dose of ribosome-targeting antibiotic.

Besides, it was found that bactericidal drugs induce demographic and environmental stochasticity, and thus the population size fluctuates over time [4, 5]. Authors of [4] used the Markovian birth-and-death model to demonstrate the stochastic nature of eradicating bacteria with antibiotics. In [5], stochastic response of bacterial cells to antibiotics was justified and its mechanisms and implications for population and evolutionary dynamics were shown. Also, in [6], the emergence of drug resistance both in bacterial colonies and in malignant tumors was discussed. Particularly, it was shown that individual resistant mutants emerge randomly during the birth events of an exponentially growing sensitive population. Overall, many factors can affect bacterial susceptibility to antibiotics such as cell-to-cell heterogeneity as well as mutations, which lead to the stochastic growth and stochastic fluctuations in population size. These fluctuations have important implications for the extinction and persistence of bacterial cells. Also, stochastic influences were justified in various population growth models. Some examples can be found in [7,8,9,10,11,12,13,14,15,16,17,18]. With such different models, the effect of the stochastic noise in the growth dynamics has been studied analytically and numerically. In such models, the stochastic characters have been found and discussed, such as the stationary probability distribution, mean first passage time, resonant activation, noise enhanced stability, stochastic resonance. Also, other stochastic growth models can be found in [19, 20].

In this paper, we study a stochastic bacterial population growth model under the influence of random fluctuations. Such a model is a simplified form of the model presented in [1] and describes the growth dynamics of bacterial population with antibiotic resistance. We mainly investigate the effect of multiplicative random noise on the growth dynamics especially extinction and persistence of bacterial cells. Similar models have also been considered by different authors can be found in [21,22,23]. Authors of [21] formulated continuous time Markov chain models using ODE models and analyzed the extinction probability for a cancer cell. They also used computer simulations to examine the effect of chemotherapy when applied to the different growth models. In [22] the authors derived and analyzed the time-dependent probability density function for the number of individuals in a population at a given time in a general logistic population model with harvesting effort using the Fokker–Planck equation. Authors of [23] studied the stochastic logistic-harvest population model with and without the Allee effect. With the help of the associated Fokker–Planck equation, they analyzed the population extinction probability and the probability of reaching a large population size and studied analytically and numerically the impact of the harvest rate, noise intensity, and the Allee effect on population evolution. In the case considered here we focus on long time behavior of the process solution.

The significance and novelty of this research work are follows.

  • We proposed this stochastic model based on the deterministic within-host model [1] of antibiotic resistance, which consists of the two/three equations for the strains of bacteria.

  • This simple model is able to capture the stochastic dynamics of bacterial population with antimicrobial resistance. Also, of that mentioned above, it is different from that for instance in [4] where the Markovian birth-and-death model has been used to demonstrate the stochastic nature of eradicating bacteria with antibiotics using the master equation.

  • Here, we studied the longtime behavior to obtain a threshold for extinction and persistence of bacterial cells.

The advantages of this model are (i) it demonstrate the stochastic effect of eradicating bacteria with antibiotics and (ii) it has significant implications for the prediction of treatment outcomes.

In practice, the results obtained enable us to understand the stochastic dynamics of the bacterial cells and effects of the anti-microbial treatments, which also gives us insights on how to eliminate bacterial cells. As a result, for instance we obtain a threshold which depends on the intrinsic growth rate, the antimicrobial rate and the noise intensity rate. Regarding the threshold, we find that decreasing the intrinsic growth rate of bacterial cells or increasing the noise intensity rate or the antimicrobial rate lead to the elimination of bacterial cells.

The rest of this paper is organized as follows. In Sect. 2, we introduce the stochastic differential equation model. In Sect. 3, we analyze the steady probability distribution. In Sect. 4, we analyze the extinction and persistence of bacterial cells. In Sect. 5 we verify and illustrate the model behavior by computer simulations. Section 6 contains a conclusion.

2 The Stochastic Differential Equation Model

In this section we introduce a stochastic model for bacterial growth with antibiotics. Different deterministic differential equation models for bacterial growth have been proposed and studied. Commonly used are logistic type growth models

$$\begin{aligned} \frac{d x}{d t}=\left( \alpha - \beta x \right) x, \end{aligned}$$
(1)

where x denotes the bacterial population density at time t, \(\alpha \) is the per capita maximum fertility rate of population, \(\beta \) denotes the strength of intra-competition of population. During antimicrobial resistance the bacterial growth kinetics is perturbed by the antibiotic drug, which can be described by a loss term \(-\gamma x\), where \(\gamma \) is the antimicrobial rate. Taking into account the effect of antimicrobial resistance leads to the model

$$\begin{aligned} \frac{d x}{d t}=\left( \alpha - \beta x \right) x-\gamma x. \end{aligned}$$
(2)

To study the bacterial evolution in stochastic environment, we assume that random fluctuations, such as rapid environmental changes, affect the system through external parameters. In this case, we suppose that, as random perturbations, the intrinsic growth parameter \(\alpha \) in model (2) is regarded as a random variable in the form

$$\begin{aligned} \tilde{\alpha }=\alpha +\sigma \xi (t), \end{aligned}$$
(3)

where \(\alpha \) is the mean intrinsic growth rate, \(\xi \) is Gaussian white noise, and \(\sigma \) is the intensity of the noise. Then, equation (2) is replaced by stochastic differential equation for the random process X in the form

$$\begin{aligned} d X=\left( \left( \alpha -\beta X \right) X-\gamma X\right) dt+\sigma X d W(t), X(0)=x_0, \end{aligned}$$
(4)

where \(dW(t)=\xi (t)dt\). Here, W is defined on complete probability space \((\Omega , \mathcal {F}, P)\) equipped with the natural filtration \((\mathcal {F}_t)_{t\ge 0}\) associated to the Wiener process. It is assumed that the variable x is dimensionless, i.e., the equation describes changes in relative bacterial population size.

3 Analysis for Steady Probability Distribution

In this section we analyze the steady state probability density of bacterial cells. First, we observe that the deterministic model can be written

$$\begin{aligned} \frac{dx}{dt}=-\frac{\partial V}{\partial x}, \end{aligned}$$

where V is the potential function defined by

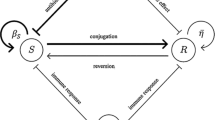
$$\begin{aligned} V(x)= -\frac{\eta }{2} x^2+\frac{\beta }{3} x^3, \end{aligned}$$

where \(\eta =\alpha -\gamma \), see Fig. 1. The potential function has a local minimum corresponding to the stable equilibrium and a local maximum at \(x=0\), which is an unstable equilibrium if \(\alpha -\gamma >0\). For \(\alpha -\gamma >0\), the bacterial population converges to the stable equilibrium \(x_s=(\alpha -\gamma )/\beta \). We observe that the population x(t) tends to 0, the state of extinction, namely there is not bacterial cells, if and only if \(\alpha /\gamma \le 1\); while in the stable state \(\alpha /\gamma > 1\), namely the bacterial cells exist and stay at a certain level. Thus, the system is bistable and the bistable feature of system depends on the parameter \(\gamma \).

Fig. 1
figure 1

Plot of the effective potential V as a function of the population size x, where a \(\alpha =1.0, \beta =0.1\), b \(\alpha =0.50, \beta =0.05\), c \(\alpha =0.1, \beta =0.01\), d \(\alpha =0.05, \beta =0.005\) and \(\gamma =0.02\)

Full size image

Now, the transitional probability density P(x, t) satisfies the corresponding Fokker-Planck equation

$$\begin{aligned} \frac{\partial P(x,t)}{\partial t}=-\frac{\partial }{\partial x} f(x) P(x,t)+\frac{\sigma ^2}{2} x^2 P(x,t), \end{aligned}$$
(5)

where \(f(x)=(\eta -\beta x)x \). Then, the steady state probability \(P_s(x)\) density can be obtained from (5) as in [24] and can be written as

$$\begin{aligned} P_s(x)= N_s x^{2\left( (\alpha -\gamma )/\sigma ^2-1\right) } \exp \left( -\frac{2\beta x}{\sigma ^2 }\right) , \end{aligned}$$
(6)

where \(N_s\) is a normalizing constant. Note that the probability density (6) is normalized for \(\eta => \sigma ^2/2\). At \(\sigma ^2/2<\eta <\sigma ^2\) the probability density is divergent at \(x=0\), and we have a nose induced phase transition at the point \(\eta =\sigma ^2\), see Fig. 2.

Next, we simulate the steady-state probability \(P_s(x)\) density of bacterial cells for different noise intensities \(\sigma ^2\) and antimicrobial parameter \(\gamma \). In Fig. 2, we plot the steady-state probability \(P_s(x)\) density for given parameters \(\alpha ,\beta , \gamma \) and different noise intensities \(\sigma ^2\). In Fig. 3, we plot the steady-state probability \(P_s(x)\) density varying with antimicrobial parameter and fixed \(\sigma ^2\). Clearly, the extinction of bacterial cells increases with increase of \(\gamma \) and is the more probable for large \(\sigma ^2\).

Fig. 2
figure 2

This figure shows the steady probability probability \(P_s(x)\) density of bacterial cells X(t) for \(\alpha =0.05, \beta =0.005, \gamma =0.02\) and different values of \(\sigma ^2\): a \(\sigma ^2=0.002\), b \(\sigma ^2=0.005\), c \(\sigma ^2=0.01\), and d \(\sigma ^2=0.04\)

Full size image
Fig. 3
figure 3

This figure shows the steady probability probability \(P_s(x)\) density of bacterial cells X(t) for the same parameters in figure 1 except \(\sigma ^2=0.004\) and different values of \(\gamma \): a \(\gamma =0.01\), b \(\gamma =0.02\), c \(\gamma =0.03\), and d \(\gamma =0.047\)

Full size image

4 Analysis for Extinction and Persistence

In this section we analyze longtime behavior using methods in [25] and present analytical results concerning the extinction and persistence for the model Eq. (4).

4.1 Extinction

In this subsection we will discus the extinction of the system (4).

Theorem 1

If

$$\begin{aligned} \frac{\alpha }{\gamma }-\frac{\sigma ^2}{2\gamma }<1 \,\,\,and \,\,\,\sigma ^2\le \alpha , \end{aligned}$$
(7)

then for any given initial values \(X(0)=X_0 \in (0,\alpha )\), the solution of the model (2) obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\log (X(t))\le \alpha -\gamma -\frac{\sigma ^2}{2}<0 \,\,\, a.s, \end{aligned}$$
(8)

namely, X(t) tends to zero exponentially almost surely.

Proof

From the Ito formula, we have

$$\begin{aligned} \log (X(t))=\log (X_0)+\int _0^t f(X(s))ds+\int _0^t\sigma d W(s), \end{aligned}$$
(9)

where \(f:\mathbb {R}\rightarrow \mathbb {R}\) is defined by

$$\begin{aligned} f(x)=\alpha -\gamma -\beta x-\frac{\sigma ^2}{2}. \end{aligned}$$
(10)

However, under condition (7), we have

$$\begin{aligned} \begin{aligned} f(X(s))&=\alpha -\gamma -\frac{\sigma ^2}{2}-\beta X(s) \\&\le \alpha -\gamma -\frac{\sigma ^2}{2}, \end{aligned} \end{aligned}$$

for \(X(s)\in (0,\alpha )\). It then follows from (9) that

$$\begin{aligned} \log (X(t))\le \log (X_0)+\left( \alpha -\gamma -\frac{\sigma ^2}{2}\right) t +\int _0^t\sigma d W(s). \end{aligned}$$
(11)

This implies

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} \log (X(t))\le \alpha -\gamma -\frac{\sigma ^2}{2} +\limsup _{t\rightarrow \infty } \frac{1}{t}\int _0^t\sigma d W(s) \,\,\,a.s. \end{aligned}$$
(12)

But by the larger number theorem for martingales, we have

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t}\int _0^t\sigma d W(s)=0 \,\,\,a.s. \end{aligned}$$

We therefore obtain the desired assertion (8) from (12).

The following theorem cover the case when \(\sigma ^2>2(\alpha -\gamma )\). \(\square \)

Theorem 2

If

$$\begin{aligned} \sigma ^2>2(\alpha -\gamma ), \end{aligned}$$
(13)

then for any given initial values \(X(0)=X_0 \in (0,\alpha )\), the solution of the model (2) obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} \log (X(t))\le \alpha -\gamma -\frac{\sigma ^2}{2}<0 \,\,\, a.s, \end{aligned}$$
(14)

namely, X(t) tends to zero exponentially almost surely.

Proof

From the Ito formula, we have

$$\begin{aligned} \log (X(t))=\log (X_0)+\int _0^t f(X(s))ds+\int _0^t\sigma d W(s), \end{aligned}$$
(15)

It then follows that

$$\begin{aligned} \log (X(t))\le \log (X_0)+\left( \alpha -\gamma -\frac{\sigma ^2}{2}\right) t +\int _0^t\sigma d W(s). \end{aligned}$$
(16)

In the same way as in the proof of Theorem 1, this implies that

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} \log (X(t))\le \alpha -\gamma -\frac{\sigma ^2}{2} \,\,\,a.s., \end{aligned}$$
(17)

Hence, the proof is complete. \(\square \)

4.2 Persistence

In this subsection we will discus the persistence of the model system (4).

Theorem 3

If

$$\begin{aligned} \frac{\alpha }{\gamma }-\frac{\sigma ^2}{2\gamma }>1, \end{aligned}$$
(18)

then for any given initial values \(X(0)=X_0 \in (0,\alpha )\), the solution of the model (2) obeys

$$\begin{aligned} \limsup _{t\rightarrow \infty } X(t)\ge \xi \,\,\, a.s., \end{aligned}$$
(19)

and

$$\begin{aligned} \liminf _{t\rightarrow \infty } X(t)\le \xi \,\,\, a.s., \end{aligned}$$
(20)

where

$$\begin{aligned} \xi =\frac{2(\alpha -\gamma )-\sigma ^2}{2\beta }, \end{aligned}$$
(21)

which is the unique root in \((0,\alpha )\) of

$$\begin{aligned} \alpha -\gamma -\beta x-\frac{\sigma ^2}{2}=0. \end{aligned}$$
(22)

That is, X(t) will rise to or above the level \(\xi \) infinitely often with probability one.

Fig. 4
figure 4

This figure shows computer simulation of the sample path X(t) for the model equation (4) (cyan) and its corresponding deterministic model Eq. (2) (red) with given parameters, using initial values in the left \(X(0)=0.5\) and in the right \(X(0)=5\)

Full size image
Fig. 5
figure 5

This figure shows computer simulation of the sample path X(t) for the model equation (4) (cyan) and its corresponding deterministic model Eq. (2) (red) with given parameters, using initial values in the left \(X(0)=0.5\) and in the right \(X(0)=5\)

Full size image
Fig. 6
figure 6

This figure shows computer simulation of the sample path X(t) for the model equation (4) (cyan) and its corresponding deterministic model Eq. (2) (red) with given parameters, using initial values in the left \(X(0)=0.5\) and in the right \(X(0)=5\)

Full size image
Fig. 7
figure 7

This figure shows computer simulation of the sample path X(t) for the model equation (4) (cyan) and its corresponding deterministic model Eq. (2) (red) with given parameters, using initial values in the left \(X(0)=0.5\) and in the right \(X(0)=5\)

Full size image
Fig. 8
figure 8

This figure shows histograms of the values of the path X(t) for given parameter values with \(X(0)=0.5\), and different values of \(\sigma \)

Full size image

Proof

We begin to prove assertion (19). If it is not true, then there is a sufficiently small \(\epsilon \in (0,1)\) such that

$$\begin{aligned} \mathbb {P}(\Omega _1)>\epsilon , \end{aligned}$$
(23)

where \(\Omega _1=\left\{ \limsup _{t\rightarrow \infty } X(t)\le \xi -2\epsilon \right\} \). Hence, for every \(\omega \in \Omega _1\), there is a \(T=T(\omega )>0\) such that

$$\begin{aligned} X(t,\omega )\le \xi -\epsilon \,\,\, whenever \,\,\, t\ge T(\omega ). \end{aligned}$$
(24)

It therefore follows from (24) that

$$\begin{aligned} f(X(t,\omega ))\ge f(\xi -\epsilon ) \,\,\, whenever \,\,\, t\ge T(\omega ). \end{aligned}$$
(25)

Moreover, by the large number theorem for martingales, there is a \(\Omega _2\subset \Omega \) with \(\mathbb {P}(\Omega _2)=1\) such that for every \(\omega \in \Omega _2\),

$$\begin{aligned} \lim _{t\rightarrow \infty }\frac{1}{t}\int _0^t \sigma dW(s,\omega )=0. \end{aligned}$$
(26)

Now, fix any \(\omega \in \Omega _1\cap \Omega _2\). It then follows from the Ito formula and (25) that, for \(t\ge T(\omega )\),

$$\begin{aligned} \begin{aligned} \log (X(t,\omega ))&\ge \log (X_0)+\int _0^{T(\omega )} f(X(s,\omega ))ds +f (\xi -\epsilon )(t-T(\omega )) \\&\quad +\int _0^t \sigma dW(s,\omega ). \end{aligned} \end{aligned}$$
(27)

This yields

$$\begin{aligned} \liminf _{t\rightarrow \infty } \frac{1}{t} \log (X(t,\omega ))\ge f(\xi -\epsilon )>0, \end{aligned}$$

whence

$$\begin{aligned} \lim _{t\rightarrow \infty } X(t,\omega )=\infty . \end{aligned}$$

But this contradicts (24). We therefore must have the desired assertion (19).

Next we prove assertion (20). If it is not true, then there is a sufficiently small \(\delta \in (0,1)\) such that

$$\begin{aligned} \mathbb {P}(\Omega _3)>\delta , \end{aligned}$$
(28)

where \(\Omega _3=\left\{ \liminf _{t\rightarrow \infty } X(t)\ge \xi +2\delta \right\} \). Hence, for every \(\omega \in \Omega _3\), there is a \(\tau =\tau (\omega )>0\) such that

$$\begin{aligned} X(t,\omega )\ge \xi +\delta \,\,\, whenever \,\,\, t\ge \tau (\omega ). \end{aligned}$$
(29)

Now, fix any \(\omega \in \Omega _3\cap \Omega _2\). It then follows from the Ito formula that, for \(t\ge \tau (\omega )\),

$$\begin{aligned} \begin{aligned} \log (X(t,\omega ))\le&\log (X_0)+\int _0^{\tau (\omega )} f(X(s,\omega ))ds +f (\xi +\delta )(t-\tau (\omega )) \\&\quad +\int _0^t \sigma _i dW(s,\omega ). \end{aligned} \end{aligned}$$
(30)

This, together with (26), yields

$$\begin{aligned} \limsup _{t\rightarrow \infty } \frac{1}{t} \log (X(t,\omega ))\le f(\xi +\delta )<0, \end{aligned}$$

whence

$$\begin{aligned} \lim _{t\rightarrow \infty } X(t,\omega )=0. \end{aligned}$$

But this contradicts (28). We therefore obtain the desired assertion (20). Hence, the proof is complete. \(\square \)

5 Computer Simulations

In this section we use the Euler-Maruyama method [26] with the time step \(10^{-2}\) and present computer simulations in order to illustrate the model behavior particularly for the extinction and persistence of the bacterial cells. According to the conditions in Theorems 1, 2 and 3, the extinction and persistence of bacterial cells rely on the parameter space \(\sigma \) and \(\gamma \). Figure 4 shows the extinction of bacterial cells according to the conditions in Theorem 1 for the parameters \(\alpha =0.05, \beta =0.004, \gamma =0.035\) and \(\sigma =0.2\). Figure 5 shows the same result according to the conditions in Theorem 2, with keeping the parameters the same but let \(\sigma =0.4\).

To illustrate the result in Theorem 3, we keep the same parameter values except \(\sigma \) is reduced to 0.15 from 0.2. The computer simulation in Fig. 6 shows this result, showing clearly fluctuation around the level \(\zeta =0.9375\). To further illustrate the effect of the noise intensity, we keep all the parameter values unchanged but reduce \(\sigma \) to \(\sigma =0.04\). In Fig. 7, we show the resulting computation simulation, illustrating clearly the increase of the level \(\zeta =3.55\) and persistence. Figure 8 shows a computer simulation of the distribution of the solution X(t) in the persistent case for higher and lower \(\sigma \). In this figure we plot histograms, showing the distribution of X(t) in the case of \(\sigma =0.15, 0.1, 0.05\) and 0.025.

6 Conclusion

In this paper, based on the deterministic model equations in [1], we have considered a stochastic model for the dynamics of bacterial population with antimicrobial resistance under the influence of random fluctuations. We have used the technique of parameter perturbation and investigated the effect of multiplicative noise on the evolutionary dynamics. We first have evaluated the steady state probability density of bacterial cells for different noise intensities and antimicrobial intensities. Then, we have studied the longtime behavior and obtained necessary conditions (a threshold) for extinction and persistence of bacterial cells. Further, the model behaviors ware illustrated by computer simulations. The obtained results demonstrate the growth dynamics of the bacterial population which was controlled by the antimicrobial rate and the noise strength rate. Regarding the results of the threshold, it can be used to analyze the drug resistance observed in evolving and variable bacterial cell population.

Overall, the principal theoretical implication of this study is that the stochastic model is capable to define the macroscale properties of the dynamics of bacteria with antimicrobial resistance, capturing stochastic growth, and identifying the specific response to antibiotic treatment. This may be important for the use of therapeutic purposes.