The Lorentz Gas with a Nearly Periodic Distribution of Scatterers

Abstract

We consider the Lorentz gas in a distribution of scatterers which microscopically converges to a periodic distribution, and prove that the Lorentz gas in the low density limit satisfies a linear Boltzmann equation. This is in contrast with the periodic Lorentz gas, which does not satisfy the Boltzmann equation in the limit.

1 Introduction

The Lorentz gas was introduced in [14] to give a new understanding of phenomena such as electric resistivity and the Hall effect. Lorentz introduced many simplifications to admit “rigorously exact solutions” to some questions, which has made the model very attractive in the mathematical community.

The Lorentz gas can be described as follows: Let ${\mathcal X}$ be a point set in $\mathbb {R}^2$ (actually most of what is said in this paper could equally well have been set in $\mathbb {R}^n$ with $n\ge 2$). The point set can be expressed as a locally finite counting measure,

$$\begin{aligned} {\mathcal X}(A) = \text {{\char "0023}}\{ X_i\in A\}, \end{aligned}$$

(1)

i.e. the number of points in the set A, or the empirical measure

$$\begin{aligned} {\mathcal X}= \sum \delta _{X_j}, \end{aligned}$$

(2)

Examples of interest are the periodic set ${\mathcal X}=\mathbb {Z}^2$, or random point processes such as a Poisson distribution. The Lorentz process is the motion of a point particle with constant speed in the plane, colliding elastically with the obstacles, which are circular of a fixed radius r and situated at each point $X\in {\mathcal X}$. Given an initial position and velocity of the point particle, $(x_0,v_0)\in \mathbb {R}^2\times S^1$, its position at time t is given by

$$\begin{aligned} (x(t),v(t))&= T^t_{{\mathcal X},r}( (x_0,v_0)) = \left( x_0 + \sum _{j=1}^M (t_j-t_{j-1}) v_{j-1} + (t-t_M) v_M, v_M\right) , \end{aligned}$$

(3)

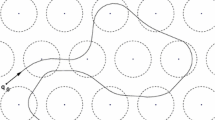
where $t_0=0$, and $\{t_1,\ldots ,t_M\}$ is the set of times where the trajectory of the point particle hits an obstacle, and where $v_j$ is the new velocity that results from a specular reflection on the obstacle. We also set $x_j=x(t_j)$. The notation is clarified in Fig. 1. For a general point set ${\mathcal X}$ it may happen that obstacles touch or overlap, and then a particle could be trapped or at least experience an infinite number of collisions in a finite time interval, and then (3) may fail to be valid. Adding further constraints on the obstacle configurations one may ensure that (3) is always valid, or fail only for a set of initial conditions of measue zero. This is true, for example, if the point set is a Delone set, and hence satisfies bounds on the minimal distance between the points as well as on the density of points. If ${\mathcal X}$ is deterministic, or if one considers a fixed realization of a random point process, this is a deterministic motion. Then $T^t_{{\mathcal X},r}$ forms a group of maps, and $(x,v)\mapsto T^t_{{\mathcal X},r}(x,v)$ is continuous in the interior of $\mathcal {M}:= \left( \mathbb {R}^2{\setminus } \cup _{{ x}\in {\mathcal X}} \bar{B}_{r}({ x})\right) \times S^1$, where $B_{r}( x)$ is the open disk of radius r and center at x, except at points (x, v, t) such that $T^t_{{\mathcal X},r}({ x},v)$ belongs to the boundary of $\mathcal {M}$. On this boundary, where the collisions take place, v jumps, and it is natural to identify ingoing and outgoing velocities, i.e. points (y, v) and $({ y},v')$ such that $|{ y}-{ x}| =r$ and $({ y}-{ x})\cdot (v + v')=0$ for some $x\in {\mathcal X}$; one may then chose to represent this point by the outgoing velocity to make $T^t_{{\mathcal X},r}(x,v)$ well-defined for all x, v and t.

Fig. 1

A trajectory of the Lorentz process

For a given point set ${\mathcal X}$ we also consider the rescaled set ${\mathcal X}_{\epsilon }=\sqrt{\epsilon } {\mathcal X}$, so that for any set $A\subset \mathbb {R}^2$

$$\begin{aligned} {\mathcal X}_{\epsilon }(A) = {\mathcal X}\left( \frac{A}{\sqrt{\epsilon }}\right) . \end{aligned}$$

(4)

We think of ${\mathcal X}$ as describing the domain of the Lorentz gas at a microscopic scale, and ${\mathcal X}_{\epsilon }$ as the macroscopic scale. Expressed in the macroscopic scale, we assume that for any open set $A\subset \mathbb {R}^2$

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \epsilon \; \text {{\char "0023}}\{ x\in {{\mathcal X}}_{\epsilon }\cap A\} = c m(A), \end{aligned}$$

(5)

where m(A) is the Lebesgue measure of the set A and c is a positive constant.

For the rest of the paper the obstacle radius is fixed to be equal to $\epsilon$ in the macroscopic scaling, and therefore $\sqrt{\epsilon }$ in the microscopic scaling.

In the macroscopic scale, the time $t_1$ of the first encounter with an obstacle for a typical trajectory $T_{{\mathcal X}_{\epsilon }, \epsilon }^t(x_0,v_0)$ satisfies $t_1 =\mathcal {O}(1/c)$, i.e. the mean free path-length of a typical trajectory is of the order 1/c. This is known as the low density limit, or the Boltzmann-Grad limit.

Consider next an initial density of point particles, i.e. a non-negative function $f_0\in L^1(\mathbb {R}^2\times S^1)$, and its evolution under the Lorentz process. For a fixed pointset ${\mathcal X}$ the density at a later time is given by $f_{\epsilon ,t}=f_{\epsilon }(x,v,t) = f_0(T^{-t}_{{\mathcal X}_{\epsilon },\epsilon }(x,v))$, which is well-defined when (3) holds for almost all $(x_0,v_0)$, because the map $T^{-t}_{{\mathcal X}_{\epsilon },\epsilon }$ is both invertible and measure preserving. One may now study the limit of $f_0(T^{-t}_{{\mathcal X}_{\epsilon },\epsilon }(x,v))$ for a given realization of ${\mathcal X}$; this is known as the quenched limit, as opposed to the annealed limit (see [1]), where the object of study is the expectation over all realizations of ${\mathcal X}$, $f_{\epsilon }(x,v,t) = \mathbb {E}[f_0(T^{-t}_{{\mathcal X}_{\epsilon },\epsilon }(x,v))]$ (see [15]). Here the expectation is taken with respect to the probability distribution of the point set ${\mathcal X}$. Of course there is no difference when ${\mathcal X}$ is deterministic.

Equivalently the evolution $f_{\epsilon ,t}$ in the annealed setting is defined as the function that satisfies, for each $g\in C_0(\mathbb {R}^2\times S^1)$

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f_{\epsilon }(x,v,t) g(x,v) \,dx dv = \int _{\mathbb {R}^2\times S^1} f_0(x,v) \mathbb {E}\left[ g\left( T^t_{{\mathcal X}_{\epsilon },\epsilon }(x,v)\right) \right] \,dx dv. \end{aligned}$$

(6)

Gallavotti [8, 9] proved that when ${\mathcal X}$ is a Poisson process with unit intensity, and $\epsilon$ converges to zero, then $f_{\epsilon ,t}$ converges to a density $f_t$ which satisfies the linear Boltzmann equation:

$$\begin{aligned} \partial _t f(x,v,t) + v\cdot \nabla _x f(x,v,t) = -2 f(x,v,t) + \int _{S^1_-} f(x,v',t) \vert v\cdot \omega \vert \,d\omega . \end{aligned}$$

(7)

Here $S^1_- =S^1_-(v) = \{\omega \in S^1\;\vert \; v\cdot \omega <0 \}$ and $v'= v-2(\omega ,v)\omega$. Spohn has proven a related, and more general, result in [27]. Both the results by Gallavotti and Spohn concern the annealed setting. Boldrighini, Bunimovich and Sinai [1] proved the same result in the quenched setting, i.e. taking the limit in (6) for a typical realization of ${\mathcal X}$, and not for the expectation over ${\mathcal X}$.

On the other hand, it is also known that when ${\mathcal X}=\mathbb {Z}^2$ (or for that matter many other regular point sets, such as quasi crystals), then the Lorentz process is not Markovian in the limit and therefore (6) does not hold, see [2, 11]. For a periodic distribution of scatterers, in dimension two and higher, Marklov and Strömbergsson have proven that there is a limiting kinetic equation in an enlarged phase space [16, 17]. Caglioti and Golse [5] obtained similar results, strictly in dimension two, using different methods.

Marklof and Strömbergsson have studied this problem in several papers [18,19,20,21]. Working in the quenched setting, they present in [22] a very general theorem concering the Boltzmann-Grad limit of the Lorentz process, where they give a concise set of conditions for a point set ${\mathcal X}$, such that the Lorentz process $T^t_{{\mathcal X}_{\epsilon },\epsilon }(x,v)$ converges to a random flight process. Their theorem and its relation to the results of this paper is discussed in some more detail in Sect. 2 below.

The problem studied in this paper is the following: Let ${\mathcal X}$ be the periodic point set that has one point at the center of each cell of the euclidean lattice, and let ${\mathcal Y}_{\epsilon }$ be a random point set that also has one point in each lattice cell, but in a random position, and we assume that ${\mathcal Y}_{\epsilon }$ converges to ${\mathcal X}$ in the sense that all points of ${\mathcal Y}_{\epsilon }$ converge to the corresponding point of ${\mathcal X}$ when $\epsilon \rightarrow 0$, uniformly over ${\mathcal X}$. This convergence is thus assumed to take place at the microscopic level. To study this in the Boltzmann-Grad limit, we set

$$\begin{aligned} {\mathcal Y}_{\epsilon ,\epsilon }= \sqrt{\epsilon }{\mathcal Y}_{\epsilon }\qquad \hbox {and}\qquad {\mathcal X}_{\epsilon }=\sqrt{\epsilon } {\mathcal X}. \end{aligned}$$

(8)

We are then interested in comparing the limits of the corresponding Lorentz processes, $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ and $T_{{\mathcal X}_{\epsilon }}^t$, assuming that the obstacle radius is $\epsilon$. The main result of the paper is the construction of a family of point sets ${\mathcal Y}_{\epsilon }$ that converges to the periodic distribution, and yet the Lorentz process $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$ converges to the free flight process generated by the linear Boltzmann equation (6), contrary to the limit of $T_{{\mathcal X}_{\epsilon }}^t(x,v)$. It is in a sense a non-stability result for the periodic Lorentz gas, and while not proven in this paper it seems very likely that if ${\mathcal X}$ is a Poisson process with constant intensity, (almost) any approximation ${\mathcal Y}_{\epsilon }$ would result in convergence of the two Lorentz processes to the same limit. The proof follows quite closely the construction in [6, 26], and consists in constructing a third process, ${\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ which can be proven to be path-wise close to the free flight process, and also to the Lorentz process. The full statement of the result, together with the main steps of the proof are given in Sect. 2. Section 3 gives the somewhat technical proof that ${\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ converges to the Boltzmann process, and Sect. 4 contains a proof that the probability that an orbit of $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ crosses itself near an obstacle is negligible in the limit as $\epsilon \rightarrow 0$, which is then used to prove that ${\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ and $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t$ with large probability are path-wise close.

The scaling studied here for the Lorentz process is not the only one studied in literature. A more challenging problem is the long time limit, where the process is studied over a time interval of $[0,t_\epsilon [$, where $t_\epsilon \rightarrow \infty$ when $\epsilon \rightarrow 0$. Recent results of this kind have been obtained in [15]. It would be intersting to try to adapt the techniques in [15] to the present sitution, but we leave that to a future study. And Marklof and Tóth prove a superdiffusive central limit theorem for the displacement of a particle at a finite time t [23].

In a different direction, there are many results concering the ergodic properties of the Lorentz gas with a fixed configuration of scatterers, as opposed to the small scatterer limit that is setting of the present work. Early results are due to Bunimovich and Sinai, [3, 4], and a recent example is [25]. Typically these works deal with periodic configurations of scatterers, but there are also results on non-periodic configurations for example by Lenci and coworkers, see [12, 13].

2 The Main Result and the Principal Steps of Its Proof

Let ${\mathcal X}=\mathbb {Z}^2$ and define ${\mathcal Y}_{\epsilon }$ as a perturbation of ${\mathcal X}$ in the following way: Let $\phi$ be a rotationally symmetric probability density supported in $\vert x\vert < 1$, fix $\nu \in ]1/2,1[$, set

$$\begin{aligned} {\mathcal Y}_{\epsilon }= \left\{ (j,k) +\epsilon ^{1-\nu } \xi _{j,k}\;\vert \; (j,k)\in \mathbb {Z}^2, \xi _{j,k} \;\hbox {i.i.d. with density}\; \phi \right\} , \end{aligned}$$

(9)

and let

$$\begin{aligned} {\mathcal Y}_{\epsilon ,\epsilon }= \sqrt{\epsilon }{\mathcal Y}_{\epsilon }. \end{aligned}$$

(10)

Thus each obstacle has its center in a disk of radius $\epsilon ^{1-\nu }$ centered at an integer coordinate, (j, k). This disk will be called the obstacle patch below. The obstacle itself reaches at most a distance $\epsilon ^{1-\nu } + \epsilon ^{1/2}$ from the same integer coordinate; this larger disk will be called an obstacle range below. The ratio of the obstacle range and the support of the center distribution is thus $1+\epsilon ^{\nu -1/2}$, which converges to 1 when $\epsilon \rightarrow 0$, and to simplify some notation the radius of the obstacle patch will be used instead of the radius of the obstacle range, and the difference will be accounted for with a constant in the estimates. In order to avoid cumbersome notation, the parameter $\nu$ is not indicated in the symbol ${\mathcal Y}_{\epsilon }$, but it is important to remember that the obstacle distribution also depends on $\nu$.

Clearly ${\mathcal Y}_{\epsilon }$ converges in law to the periodic distribution in $\mathbb {R}^2$. Nevertheless we have the following theorem:

Theorem 2.1

Fix $\nu \in ]1/2,1[$ and let $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$ be the Lorentz process obtained by placing a circular obstacle of radius $\epsilon$ at each point of ${\mathcal Y}_{\epsilon ,\epsilon }$. Let $\bar{t}>0$, and let $f_0(x,v)$ be a probability density in $\mathbb {R}^2\times S^1$. Define $f_{\epsilon }(x,v,t)$ as the function such that for all $t\in [0, \bar{t}]$ and all bounded functions $g\in C(\mathbb {R}^2\times S^1)$,

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f_{\epsilon }(x,v,t) g(x,v)\,dx dv = \int _{\mathbb {R}^2\times S^1} f_0(x,v) \mathbb {E}\left[ g\left( T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)\right) \right] \,dxdv, \end{aligned}$$

(11)

where $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$ is defined in Eq. (3). Then there is a density $f(x,v,t)\in C\left( [0,\bar{t}],L^1(\mathbb {R}^2\times S^1)\right)$ such that for all $t\le \bar{t}$, $f_\epsilon (x,v,t)\rightarrow f(x,v,t)$ in $L^1(\mathbb {R}^2\times S^1)$ when $\epsilon \rightarrow 0$, and such that f(x, v, t) satisfies the linear Boltzmann equation

$$\begin{aligned} \partial _t f(x,v,t) + v\cdot \nabla _x f(x,v,t) = \kappa \left( \int _{S^1_-} f(x,v',t) \vert v\cdot \omega \vert \,d\omega - 2 f(x,v,t) \right) . \end{aligned}$$

(12)

The constant $\kappa$ depends on $\phi$ and $S^1_-$ and $v'$ are defined as in Eq. (7).

Remark 2.2

To simplify notation, point particles are allowed to start inside obstacles, and to cross the obstacle boundary from the inside without any change of velocity.

Both the statement in this theorem and the proof are very similar to the main results of [6, 26], but the distribution of scatterers is quite different, and this leads to new questions on the relation between limits of the scatterer distribution and limits of the Lorentz process. In those papers the point processes ${\mathcal Y}_{\epsilon }$ are constructed as the thinning of a periodic point set:

$$\begin{aligned} {\mathcal Y}_{\epsilon }= \left\{ \epsilon ^{\nu }(j,k)\; \vert \; \eta _{j,k}=1, \; \eta _{j,k} \;\hbox {i.i.d. Bernoulli with } \mathbb {P}[\eta _{j,k}=1]=\epsilon ^{2\nu -1}\right\} . \end{aligned}$$

(13)

Here it is clear that this ${\mathcal Y}_{\epsilon }$ converges in law to the Poisson process with intensity one, and therefore it is perhaps not surprising that the limit of the Lorentz process is the same as for the Lorentz process generated by a Poisson distribution of the obstacles. Theorem 2.1 in the present paper states that the limit of the Lorentz process is the free flight process of the Boltzmann equation in some cases also if the limiting obstacle density is periodic, and raises the question as to which point processes ${\mathcal X}$ are stable to perturbation when it comes to the low density limit of the corresponding Lorentz processes.

Some understanding of this result can be drawn from the very heuristic argument used to derive the scaling of the Boltzmann–Grad limit: if a point particle is to move a distance L without hitting an obstacle of size $\epsilon$, it is required that a cylinder of radius $\epsilon$ and length $L=\mathcal {O}(1)$ around the particle path is free from obstacle centres. Or, what is the same, for any direction v, each obstacle is the origin of a cylinder of forbidden initial points $x_0$ for trajectories starting at $x_0$ in the direction of v, and with a free path of at least L. In the two dimensional case the cylinders are simply strips of width $2\epsilon$ and one finds that in order to have an average mean free path of order one, one needs to have a density of obstacles equal to $\mathcal {O}\left( \epsilon ^{-1}\right)$. If the obstacle centers are distributed one per each lattice cell as in our setting, then the lattice cell must be of order $\epsilon ^{1/2}$, which motivates the scaling in (10). However, the heuristic argument indicates that one needs to consider the point process at different scales along the path of a point particle and orthogonal to the path. This is expressed in a very precise form in [22] as the condition $[{\mathrm P2}]$ on the particle distribution ${\mathcal X}$. In a simplified form, restricted to our two-dimensinal case, it says the following: Writing points ${x} \in {\mathcal X}$ as row vectors, let R(v) be the orthogonal matrix that rotates the coordinate system so that $v\in S^1$ is in the direction of the first coordinate. Let $D_{\epsilon }$ be the diagonal matrix with entries $(\epsilon ^{1/2},\epsilon ^{-1/2})$. Let $\lambda (v)$ be a probability density on $S^1$, and let v be a random vector with distribution $\lambda$. For any fixed ${ x }\in {\mathcal X}$ (possibly excluding a small fraction of points of ${\mathcal X}$) consider the point set

$$\begin{aligned} \Xi _{\epsilon }=\left( {\mathcal X}-{ x}\right) R(v)D_{\epsilon }. \end{aligned}$$

(14)

This is a random point set, and the assumption $[{\mathrm P2}]$ is that $\Xi _{\epsilon }$ converges in distribution to a point process $\Xi$, independent of x and $\lambda$. Intuitively this says that starting from any point in ${\mathcal X}$ the point set looks the same, if it is expanded with a factor $\epsilon ^{-1/2}$ in the direction orthogonal to v, to make the obstacle size equal to $\mathcal {O}(1)$ in that direction, and compressed with a factor $\epsilon ^{1/2}$ in the direction along v. If ${\mathcal X}$ is a Poisson process with intensity one, then so is $\Xi _{\epsilon }$ for all $\epsilon >0$, and although this is not proven here, it seems likely that if $\Xi _{\epsilon }$ is defined starting with ${\mathcal Y}_{\epsilon }$ as defined in (8) then $\Xi$ will also be a Poisson process. This is due to the fact that when $\nu >1/2$, the points are randomly spread out around over a distance $\epsilon ^{1-\nu }$, which is much larger than the width of the strip. Figure 2 shows an example of this, where to the left there is a part of the perturbed periodic point set, with $\epsilon ^{1-\nu }\sim 10^{-4}$, so that by eye it is difficult to distinguish from a periodic distribution. The middle figure shows a realization of $\Xi _{\epsilon }$ for a random choice of v and with $\epsilon \sim 10^{-8}$, to be with compared with the image to the right which is the same $\Xi _{\epsilon }$ but starting from a periodic ${\mathcal X}$.

Fig. 2

Left: A perturbed periodic distribution. Mid: The corresponding $\Xi _{\epsilon }$ as defined by Eq. (14). Right: $\Xi _{\epsilon }$ computed from a periodic distribution. In all cases, the obstacle radius $\sqrt{\epsilon }$ is $10^{-4}$ and the diameter of the obstacle patch is $\mathcal {O}(10^{-2})$. The direction v is drawn from the uniform distribution on $S^1$

If $\nu <1/2$, the points in ${\mathcal Y}_{\epsilon }$ are spread out over a small patch small also after the rescaling with $D_{\epsilon }$, and therefore one would expect exactly the same behaviour in the limit as for the strictly periodic distribution ${\mathcal X}$. When $\nu =1/2$ the centres of the scatterers are distributed in a ball essentially of the same size as the obstacle. In Fig. 2 one would see an image as the one to the right, but where the points would be spread in an narrow ellipsis with a minor axis of order one in the vertical direction, and $\epsilon$ in the horizontal direction. As proven in [24], the distribution of free path lengths is then asymptotically the same as for the periodic case, and therfore the the particle density $f_{\epsilon }$ would not converge to the solution of a linear Boltzmann equation. However, the distribution of scattering angles could be quite different from the periodic case, and it could be of interest to study this in more detail, in particular in the long time limit as in [15].¹

The general results from [22] states that when $[\hbox {D2}]$ and some other conditions are satisfied, then the Lorentz process converges to a free flight process, which in general is not Markovian, except in a larger phase space. It is only in case the distribution of free path lenghts is exponential that one can derive a linear Boltzmann equation like Eq. (12).

Before presenting the proof of Theorem 2.1 two more remarks are relevant. First, the main theorem in [22] is very general, and it seems likely that the results presented here, and also the results from [6, 26] could be concluded from their results. However, the results in [22] are proven under the hypothesis $[{\mathrm P2}]$ described above, stating that the $\Xi _{\epsilon }$ from Eq. (14) converge for a fixed ${\mathcal X}$; here we have a family of distributions ${\mathcal Y}_{\epsilon }$ depending on $\epsilon$. The proof in [22] seems to be robust enough to cover also this case, but it would need to be checked. The second remark concerns the distinction between the quenched and annealed limits. In  [1, 22], the meaning of quenched is that you fix once and for all a realization of the point process ${\mathcal X}$, and the limits are obtained from a rescaling of this process. In this paper the distribution of scatters depends on $\epsilon$ also at a microscopic level, and so one cannot just simply take one fixed realization of ${\mathcal Y}_{\epsilon }$ and rescale. With ${\mathcal Y}_{\epsilon }$ defined as in (9) a natural way of viewing a quenched limit would be to take one fixed realization of the $\xi _{i,j}$, but with ${\mathcal Y}_{\epsilon }$ defined as in (13) there seems to be no unique way of defining a quenched limit. One could possibly define the $\eta _{i,j}$ as (independent) 0, 1-valued random processes $\epsilon \mapsto \eta _{i,j,\epsilon }$ with $\epsilon$ as a decreasing parameter, and with a transition rate $1\rightarrow 0$ defined so as to obtain the correct density of ${\mathcal Y}_{\epsilon }$ for all values of $\epsilon$. One could then define the quenched limit as the one obtained from one fixed realization of this process. The results in this paper concern the annealed limit, and then the difference is not important.

In the proof of Theorem 2.1 we consider three processes: The Lorentz process $T_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$, the free flight process $T_B^t(x,v)$ generated by the Boltzmann equation (11), and an auxiliary Markovian Lorentz process, ${\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$.

The Boltzmann process is the random flight process $(x(t),v(t))=T^t_B(x,v)$ generated by Eq. (1). Let $0=t_0<t_1<,\ldots ,t_n<t$ be a sequence of times generated by independent, exponentially distributed increments $t_j-t_{j-1}$ with intensity 2, let $v_0=v$ define $v_j=v_{j-1}-2 (\omega _j\cdot v_{j-1})\,\omega _j$, where the $\omega _j\in S^1$ are independent and uniformly distributed. Finally set

$$\begin{aligned} x(t)&= x_n(t) = x+t_1 v+ (t_2-t_1)v_1+\cdots + (t_n-t_{n-1})v_{n-1} + (t-t_n)v_n \nonumber \\ v(t)&= v_n\,. \end{aligned}$$

(15)

Of course the number n in the sum is then Poisson distributed. The solution of Eq. (1) may be defined weakly by

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f_0(x,v) g(x,v,t)\,dx dv = \int _{\mathbb {R}^2\times S^1}f(x,v,t) g(x,v)\,dx dv. \end{aligned}$$

(16)

The function g(x, v, t) can then be expanded as a sum of terms, each representing the paths with a fixed number of jumps:

$$\begin{aligned} g(x,v,t) = V^t g(x,v) = \sum _{n=0}^{\infty } g_n(x,v,t), \end{aligned}$$

(17)

with

$$\begin{aligned} g_n(x,v,t) = (V^tg)_n(x,v)&= e^{-2 t} \int _{0}^{t}\int _{t_1}^t\cdots \int _{t_{n-1}}^t dt_1\cdots dt_n \nonumber \\&\quad \times \int _{ {(S^1_{-})}^n}d\omega _1\cdots d\omega _n \prod _{k=1}^n \vert \omega _k\cdot v_{k-1}\vert g(x_n(t), v_n)\,. \end{aligned}$$

(18)

The Markovian Lorentz process here is similar to the corresponding process in [6, 26], in the way that re-collisions, i.e. the event that a particle trajectory meets the same obstacle a second time, are eliminated. The construction is explained in Fig. 3. The red thin circles mark the support of the distribution of obstacle center in each cell, and the blue circle indicates the reach of an obstacle, the obstacle range. In each cell there is an obstacle, fixed from the start in the Lorentz model, but changing in the Markovian Lorentz model. Note that the size of both the obstacle radius and the obstacle support are very small, and decreasing to zero with $\epsilon$, but drawn large here, for clarity. The path meets the same obstacle patch twice in the boxed cell. In the Lorentz case, the orbit simply traverses the cell the second time, because it misses the obstacle. In the Markovian case the obstacle is at a new, random position, drawn in blue color, the second time the orbit enters the support, and there is a positive probability that the path collides with the obstacle, as shown with the blue trajectory. In both cases the trajectory is surely well defined, but the probability of realizing an orbit is different.

Fig. 3

Trajectories for the Lorentz process and the Markovian Lorentz process. The obstacle size and the support for the probability distributions are exaggerated

The process can be defined as in Eq. (16), with the function g(x, v, t) replaced by

$$\begin{aligned} {\tilde{g}}_{\epsilon }(x,v,t)&= \mathbb {E}\left[ g({\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v))\right] = \sum _{n=0}^{\infty }{\tilde{g}}_{\epsilon ,n}(x,v,t)\,, \end{aligned}$$

(19)

$$\begin{aligned} \left( {\widetilde{V}}^t_{\epsilon ,n}\right) g(x,v)&= \mathbb {E}\left[ g({\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v))\mathbbm {1}_{n \; \tiny {\hbox { jumps}}} \right] ={\tilde{g}}_{\epsilon ,n}(x,v,t)\,, \end{aligned}$$

(20)

where ${\tilde{g}}_{\epsilon ,n}(x,v,t)$ is the contribution of trajectories having exactly n velocity jumps in the interval [0, t]. All these terms can be computed rather explicitly by counting the number of times a trajectory crosses the obstacle range of one cell.

The operators $V^t$ and $\tilde{V}^t_{\epsilon }$ are both well-defined operators $C(\mathbb {R}^2\times S^1)\rightarrow C(\mathbb {R}^2\times S^1)$, and contractions in $L^{\infty }$ because for the Boltzmann process as well as the Markovian Lorentz process we have with probability one a finite number of velocity jumps in a finite time interval, and for each n, the terms Eqs. (18) and (20) are continuous. Because $v\in S^1$, both $V^t$ and $\tilde{V}^t_{\epsilon }$ are maps $C_0(\mathbb {R}^2\times S^1) \rightarrow C_0(\mathbb {R}^2\times S^1)$, i.e. functions of compact support are mapped to functions of compact support, but this latter property is not needed here.

To simplify notation these three processes are hereafter denoted $z_{\epsilon }(t)$, z(t) and $\tilde{z}_{\epsilon }(t)$. As described in [6, 26] all these processes belong with probability one to the Skorokhod space $D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1)$ of càdlàg functions on $\mathbb {R}^2\times S^1$ equipped with the distance

$$\begin{aligned} d_S(x,y) = \inf _{\lambda \in \Lambda }\left\{ \sup _{t\in [0,\bar{t}]}\Vert x(t)-y(\lambda (t))\Vert _{\mathbb {R}^2\times S^1}+ \sup _{t\in [0,\bar{t}]}\vert t-\lambda (t)\vert \right\} , \end{aligned}$$

(21)

where

$$\begin{aligned} \Lambda =\{\lambda \in C([0,\bar{t}]): t>s \implies \lambda (t)>\lambda (s), \lambda (0)=0, \lambda (\bar{t})=\bar{t}\}. \end{aligned}$$

(22)

Any $z\in C(D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1))$ induces a measure $\mu$ on $D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1)$ which is first defined on cylindrical continuous functions F, i.e. functions $F\in C(D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1))$ of the form $F(z) = F_n(z(t_1),z(t_2),\ldots ,z(t_n))$ where $F_n\in C( (\mathbb {R}^2\times S^1)^n)$ and $0\le t_1<t_2<\cdots <t_n\le \bar{t}$. For such functions $\mu$ is defined by

$$\begin{aligned} \int F(z) \mu (dz) = \int f_0(z) P_{t_n,\ldots ,t_1,0}(z_1,z_2,\ldots ,z_n\vert z_0)dz_0 dz_1 \ldots dz_n, \end{aligned}$$

(23)

where $P_{t_n,\ldots ,t_1,0}(z_1,z_2,\ldots ,z_n\vert z_0)$ is the joint probability density of $z(t_1),z(t_2),\ldots ,z(t_n)$ given the starting point $z_0$. For a Markov process, such as the Boltzmann process, this is

$$\begin{aligned} \int F(z) \mu (dz) = \int f_0(z) P_{t_1,0}(z_1\vert z_0)P_{t_2,t_1}(z_2\vert z_1)\ldots P_{t_n,t_{n-1}}(z_n\vert z_{n-1})dz_0 dz_1 \ldots dz_n,\nonumber \\ \end{aligned}$$

(24)

where $P_{t_j,t_{j-1}}(z_j \vert z_{j-1})$ is the transition probability of going from state $z_{j-1}$ to state $z_j$ in the time interval from $t_{j-1}$ to $t_j$. Then by a density argument the measure $\mu$ is defined for all $F\in C(D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1))$.

(Proof of Theorem 2.1)

Let $\mu$, $\mu _{\epsilon }$ and $\tilde{\mu }_{\epsilon }$ be the measures induced by z(t), $z_{\epsilon }(t)$ and $\tilde{z}_{\epsilon }(t)$. Just like in [26], one may prove that for every F

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \int F(z) \tilde{\mu }_{\epsilon }(dz) = \int F(z) \mu (dz). \end{aligned}$$

(25)

The argument uses a theorem from Gikhman and Shorokhod (1974) [10], and relies on an equicontinuity condition and on the convergence of the marginal distributions of $\tilde{z}_{\epsilon }(t)$. Both the equicontinuity condition and the convergence of the marginal distributions are consequences of Proposition 3.5 which shows that the number of jumps of $z_{\epsilon }$ in small time intervals is not too large, and Theorem 3.1, which states that the one-dimensional marginals of $\tilde{z}_{\epsilon }(t)$ converge to the marginals of z(t). $\square$

The next step is to prove that $(\mu _{\varepsilon }-\tilde{\mu }_{\epsilon } )\rightharpoonup 0$ when $\epsilon \rightarrow 0$, i.e.

$$\begin{aligned} \left| \int F(z) \mu _{\epsilon }(dz) - \int F(z) \tilde{\mu }_{\epsilon }(dz)\right| \rightarrow 0 \end{aligned}$$

(26)

when $\epsilon \rightarrow 0$, and this is done by a coupling argument. Given that $z_{\epsilon }(0)=\tilde{z}_{\epsilon }(0)$, the two processes have the same marginal distributions up to the first time $t_*$ where $z_{\epsilon }(t)=\tilde{z}_{\epsilon }(t)$ returns to an obstacle range it already visited. For the process $z_{\epsilon }(t)$, the position of the obstacle within its support is then fixed, whereas for the process $\tilde{z}_{\epsilon }(t)$ a new random position of the obstacle is chosen when the trajectory arrives. Hence

$$\begin{aligned} \left| \int F(z) \mu _{\epsilon }(dz) - \int F(z) \tilde{\mu }_{\epsilon }(dz)\right|&= \left| \int _{K_{\epsilon }} F(z) \mu _{\epsilon }(dz) - \int _{K_{\epsilon }} F(z) \tilde{\mu }_{\epsilon }(dz)\right| \nonumber \\&\le \sup \vert F\vert \left( \mu _{\epsilon }(K_{\epsilon }) + \tilde{\mu }_{\epsilon }(K_{\epsilon })\right) \,, \end{aligned}$$

(27)

where $K_{\epsilon }\subset D_{[0,\bar{t}]}(\mathbb {R}^2\times S^1)$ is the set of trajectories that contain at least one such re-encounter for $t\le \bar{t}$. Proposition 4.1 states that the righthand side of (27) converges to zero when $\epsilon \rightarrow 0$. This together with (25) implies that

$$\begin{aligned} \mu _{\epsilon }\rightarrow \mu \end{aligned}$$

(28)

weakly when $\epsilon \rightarrow 0$, and this concludes the proof of Theorem 2.1. $\square$

We end the section with a comment on the propagation of chaos for these processes. For the Boltzmann process z(t) and for the process $\tilde{z}(t)$ it is clear that if a pair of initial conditions $(z^1(0),z^2(0))$ are chosen with joint density $f_0^1(x^1,v^1) f_0^2(x^2,v^2)$, then the joint densities of $(z^1(t),z^2(t))$ and $(\tilde{z}_{\epsilon }^1(t),\tilde{z}_{\epsilon }^2(t))$ also factorize: a chaotic initial state is propagated by the flow, because the two paths are independent, they never interact. The same is not true for $(z_{\epsilon }^1(t),z_{\epsilon }^2(t))$, because there is a positive probability that the two paths will meet in the obstacle density support of one obstacle, which creates correlations. However, the same kind of estimates as the ones used to prove that the probability of re-encounters for one trajectory becomes negligible when $\epsilon \rightarrow 0$ can be used to prove that also the probability that two different trajectories meet inside an obstacle range becomes small, and such estimates could be performed for any finite number of trajectories. The calculations are carried out in some detail in Sect. 4, and formulated as Theorem 4.2.

3 The Markovian Lorentz Process

The Markovian process may be described using the underlying periodic structure. Over a time interval [0, t], the particle traverses $\mathcal {O}\left( \epsilon ^{-1/2}\right)$ lattice cells, and when the path is sufficiently close to the cell center to cross the obstacle range, there is a positive probability that it is reflected by an obstacle. Because the obstacle position is chosen independently each time the trajectory enters a cell, this may all be computed rather explicitly.

We write

$$\begin{aligned} {\tilde{g}}_{\epsilon }(x,v,t) = \mathbb {E}\left[ g\left( {\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)\right) \right] = \widetilde{V}_{\epsilon }^tg(x,v) = \sum _{n=0}^{\infty } (\widetilde{V}_{\epsilon })_n^tg(x,v). \end{aligned}$$

(29)

This is the test function evaluated along the path of a point particle. It defines a semigroup $\widetilde{V}_{\epsilon }^t$ acting on the test function, and the terms in the sum express the contribution to this semigroup from paths with exactly n velocity jumps. Obviously these terms are not semigroups in their own right.

Theorem 3.1

Take $\nu \in ]1/2,1[$ and let ${\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)$ be the corresponding Markovian Lorentz process as defined above. Fix $\bar{t}>0$. For any density $f_0(x,v)$ in $\mathbb {R}^2\times S^1$, let $\tilde{f}_{\epsilon }(x,v,t)$ be the unique function such that

$$\begin{aligned} \int _{R^2\times S^1} \tilde{f}_{\epsilon }(x,v,t) g(x,v)\,dxdv = \int _{R^2\times S^1} f_0(x,v) \mathbb {E}\left[ g\left( {\widetilde{T}}_{{\mathcal Y}_{\epsilon ,\epsilon }}^t(x,v)\right) \right] \,dxdv, \end{aligned}$$

(30)

for all $t\in [0,\bar{t}]$, and any bounded $g(x,v)\in C(\mathbb {R}^2\times S^1)$. The expectation in (30) is taken with respect to the distribution of ${\mathcal Y}_{\epsilon }$. Then there is a function f(x, v, t) such that for all t

$$\begin{aligned} \tilde{f}_{\epsilon }(x,v,t)\rightarrow f(x,v,t), \end{aligned}$$

(31)

and f(x, v, t) satisfies the linear Boltzmann equation, Eq. (7).

Proof

Take any bounded function $g\in C_0(\mathbb {R}^2\times S^1)$, and $t<\bar{t}$. We must prove that

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} \left( \tilde{f}_{\epsilon }(x,v,t)-f(x,v,t)\right) g(x,v)\,dxdv\rightarrow 0\quad \hbox {when} \quad \epsilon \rightarrow 0, \end{aligned}$$

(32)

or, equivalently,

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f_0(x,v) \left( V^tg(x,v)-\tilde{V}_{\epsilon }^tg(x,v)\right) \,dxdv \rightarrow 0. \end{aligned}$$

(33)

The expression in (33) is bounded by

$$\begin{aligned} \Vert g\Vert _{L^{\infty }} \int _{\mathbb {R}^2\times S^1} f_0\left( \mathbbm {1}_{f_0>\lambda } + \mathbbm {1}_{\vert x\vert \ge M}\right) \, dxdv + \lambda \Vert (V^tg-\tilde{V}_{\epsilon }^t g) \mathbbm {1}_{\vert x\vert < M}\Vert _{L^1}, \end{aligned}$$

(34)

and choosing $\lambda$ and M large enough, depending on $f_0$, the first term can be made arbitrarily small, smaller than $\varepsilon _0/2$, say, where $\varepsilon _0$ is taken arbitrarily small. It then remains to show that the second term can be made smaller than $\varepsilon _0/2$ by choosing $\epsilon$ small enough. Both $V^t$ and ${\widetilde{V}}_{\epsilon }^t$ are bounded semigroups, and therefore, after dividing the interval [0, t] into N equal sub-intervals, $[j t/N,(j+1) t/N]$ one gets

$$\begin{aligned} V^tg(x,v) - {\widetilde{V}}_{\epsilon }^tg(x,v) = \sum _{j=0}^{N-1} {\widetilde{V}}_{\epsilon }^{j t/N} \left( V^{t/N}-{\widetilde{V}}_{\epsilon }^{t/N}\right) V^{(N-1-j)t/N}g(x,v). \end{aligned}$$

(35)

As noted in [6], the underlying Hamiltonian structure implies that he two semigroups are contractions in $L^1\cap L^{\infty }$, and therefore it is enough to prove that for $N=N_{\epsilon }$ appropriately chosen

$$\begin{aligned} N_{\epsilon } \left\| V^{t/N_{\epsilon }}g-{\widetilde{V}}_{\epsilon }^{t/N_{\epsilon }}g \right\| _{L^1}\rightarrow 0 \end{aligned}$$

(36)

when $\epsilon \rightarrow 0$. Setting $N_{\epsilon }=t/{\tau _{\epsilon }}$ for a suitable ${\tau _{\epsilon }}$, we find

$$\begin{aligned} \left| V^{{\tau _{\epsilon }}}g(x,v) - {\widetilde{V}}_{\epsilon }^{{\tau _{\epsilon }}}g(x,v) \right|&= \left| \sum _{k=0}^{\infty }\left( {(V^{{\tau _{\epsilon }}})}_{k} g(x,v) - {({\widetilde{V}}_{\epsilon }^{{\tau _{\epsilon }}})}_{k} g(x,v)\right) \right| \nonumber \\&\le \left| (V^{{\tau _{\epsilon }}})_0 g(x,v) - ({\widetilde{V}}_{\epsilon }^{{\tau _{\epsilon }}})_0 g(x,v) \right| + \left| (V^{{\tau _{\epsilon }}})_1g(x,v) - {({\widetilde{V}}_{\epsilon }^{{\tau _{\epsilon }}})}_1g(x,v) \right| \nonumber \\&\quad + \left| \sum _{k=2}^{\infty } (V^{{\tau _{\epsilon }}})_{k} g(x,v) \right| + \left| \sum _{k=2}^{\infty } {({\widetilde{V}}_{\epsilon }^{{\tau _{\epsilon }}})}_{k} g(x,v)\right| \,. \end{aligned}$$

(37)

Denote the four terms in the right-hand side by $R_{I}, R_{II}, R_{III}$, and $R_{IV}$, and set $r_{\epsilon }=\epsilon ^{(2\nu -1)/2}\left( 1+\log (t/\sqrt{\epsilon })\right)$. From Proposition 3.4 it follows that the first term, accounting for paths with no jump in the given interval, satisfies

$$\begin{aligned} N_{\epsilon }\int _{\mathbb {R}^2\times S^1} R_I(x,v)\, dxdv \le \frac{t}{\tau _{\epsilon }} C M^2 r_{\epsilon }^{1/2}, \end{aligned}$$

(38)

which converges to zero with $\epsilon$ if $r_{\epsilon }^{1/2}/\tau _{\epsilon }$ does. The second term accounts for paths with exactly one jump, and according to Proposition 3.6,

$$\begin{aligned} N_{\epsilon }\int _{\mathbb {R}^2\times S^1} R_{II}(x,v)\, dxdv \le C M^2 \left( \omega (\tau _{\epsilon },g) + r_{\epsilon } + \Vert g\Vert _{\infty } \sqrt{r_{\epsilon }} + \Vert g\Vert _{\infty } r_{\epsilon } /\tau _{\epsilon }\right) . \end{aligned}$$

(39)

Here $\omega (\tau _{\epsilon },g)$ is the modulus of continuity for g. For this term it is enough that $r_{\epsilon }/\tau _{\epsilon }$ converges to zero, but the rate of convergence may depend on the modulus of continuity of the test function g.

We also have that if $\tau _{\epsilon } > r_{\epsilon }^{1/2}$

$$\begin{aligned} N_{\epsilon }\int _{\mathbb {R}^2\times S^1} \left( R_{III}(x,v)+R_{IV}(x,v)\right) \, dxdv \le C M^2 \Vert g\Vert _{\infty } t \tau _{\epsilon }. \end{aligned}$$

(40)

This follows because for the Boltzmann process, the probability of having more than two jumps in an interval of length $\tau _{\epsilon }$ is of the order $\tau _{\epsilon }^2$, and Proposition 3.5 states that the same is true for the Markovian Lorentz process. Therefore, in conclusion, the convergence stated in eq. (32) holds with a rate depending on $f_0$ but which can be controlled by entropy and moments, and on the modulus of continuity of the test function g. $\square$

The expressions (35) and (36) imply that it is enough to study the processes in short intervals, and Proposition 3.5 below shows that it is then enough to consider two cases: a particle path starting at $(x,v)\in \mathbb {R}^2\times S^1$, i.e. with position $x\in \mathbb {R}^2$ in the direction v, moves without changing velocity during the whole interval, or hits an obstacle at some point $x'$ and continues from there in the new direction $v'$, but suffers no more collisions. The three propositions used in the proof of Theorem 3.1 all depend on Lemma 3.2 below, where the underlying periodic structure is used to analyze the particle paths in detail up to and just after the first collision with an obstacle. To set the notation for the following results, we consider a path starting in the direction v from a point x in the direction of v. It is sometimes convenient to denote the velocity $v\in S^1$ by an angle $\beta \in [0,2\pi [$, and both notations are used below without further comment. When a collision takes place, the new velocity $v'$ depends on v and on the impact parameter r as shown in Fig. 5, where $r\in [-1,1]$ when scaled with respect to the obstacle radius. In this scaling, $dr = \cos (\beta '/2)\,d\beta '/2$, when $\beta '$ is given as the change of direction.

Without loss of generality we may assume that the path is in the upward direction with an angle $\beta \in [0,\pi /4]$ to the vertical axis as in Fig. 4, because all other cases can be treated in the same way just by a finite number of rotations and reflections of the physical domain. Let $y_1$ be the first time the path enters the lower boundary of the lattice cell, and then let $y_j= y_1+(j-1) \tan (\beta ) \mod 1$ be the consecutive points of entry to the lattice cell. Setting $y_0=-\tan (\beta )/2$, the signed distance between the particle path through the cell and the cell center is $\rho _j=(y_j-y_0)\cos \beta$, and the probability that the path is reflected at the j-th passage and given the sequence $\rho _j$, the events of scattering in cell passage nr j are independent.

Define

$$\begin{aligned} p_0(x,v,t) = \mathbb {P}\Big [&\hbox { no collision in the interval } [0,t[ \nonumber \\&\qquad \qquad \hbox { for a path starting at } (x,v)\in \mathbb {R}^2\times S^1 \Big ]\,. \end{aligned}$$

(41)

The probability that a scattering event takes place in the j-passage of a lattice cell is a function of the distance from the path to the centre of the cell, $\rho _j$, and is zero outside $\vert \rho _j\vert <\epsilon ^{1-\nu } + \epsilon ^{1/2}$. This probability will be denoted $p_j=p_j(x,v)$, and depends only on the initial position x and the direction v. Given that a scattering event takes place, the outcome of this event depends on the scattering parameter, i.e. the distance between the path and the (random) center of the obstacle. Let $A_{x,v,t}$ be any event that depends on a position x and direction v of a path segment of length t. Then the probability that $A=A_{x',v',t'}$ is realized after the first collision can be computed as

$$\begin{aligned} \mathbb {P}[A] = \sum _{j=1}^n p_0(x,v,t_{j-})p_j(x,v) \mathbb {P}[ A_{x',v',t'} \; \vert \; j]\,. \end{aligned}$$

(42)

Here $\mathbb {P}[ A_{x',v',t'} \; \vert \; j\;]$ denotes the conditional probability of the event $A_{x',v',t'}$ given that the collision takes place when the particle crosses cell number j along the path, and this also depends on the x and v. The time when the path enters cell number j is denoted $t_{j-}$, and the terms in the sum contains a factor $p_0(x,v,t_{j-})$ for the probability that no collision has taken place earlier. Similarly $t_{j+}$ denotes the time when the trajectory leaves the cell; that is a random number, but we always have $0< t_{j+}-t_{j-1} < 2\sqrt{\epsilon }$.

In (42), $(x',v',t')$ are random, so $\mathbb {P}[A]$ involves also an integral over these variables, and the notation $\mathbb {P}[ A_{x',v',t'} \; \vert \; j]$ is intended to include this integration. The expectation $\mathbb {E}[\psi ]$ of some function $\psi$ is computed in the same way with $\mathbb {P}[ A_{x',v',t'} \; \vert \; j]$ replaced by $\mathbb {E}[ A_{x',v',t'} \; \vert \; j]$ .

Given the density $\phi$ for the position of the obstacle define

$$\begin{aligned} \varphi _0(x_1)=\int _{\mathbb {R}} \phi _0(x_1,x_2)\,dx_2, \end{aligned}$$

(43)

where $(x_1,x_2)$ is an arbitrary coordinate system in $\mathbb {R}^2$. Because $\phi$ is assumed to be rotationally symmetric, the resulting function $\varphi _0$ is independent of the orientation of this coordinate system. It is a smooth probability density with support in $[-1,1]$, and then $\varphi _{\epsilon }(r) \equiv \epsilon ^{\nu -1} \varphi _0( \epsilon ^{\nu -1}r)$ is also a smooth probability density with support in $\vert r\vert \le \epsilon ^{1-\nu }$.

For each k the obstacle center is chosen randomly inside a circle of radius $\epsilon ^{1-\nu }$ around the cell center, and one can then compute the probability that the path is reflected at step k.

Lemma 3.2

Consider a lattice cell in the microscopic scale, so that the cell side has length one, and assume that there is an obstacle of radius $\epsilon ^{1/2}$ with center distributed with a density of the form $\phi (x)=\epsilon ^{2\nu -2} \phi _0( \epsilon ^{\nu -1}x )$, where $\phi _0\in C^{\infty }(\mathbb {R}^2)$ has support in the unit ball of $\mathbb {R}^2$. Let $\varphi _{\epsilon }$ be defined as in Eq. (43) and rescaled with $\epsilon$. Let $\psi _0\in L^1(\mathbb {R})$ with $\psi _0(x)=0$ for $\vert x\vert >1$, and set $\psi _{\epsilon }(x) = \psi _0(x/\sqrt{\epsilon })$. Consider a particle path traversing the cell n times with an angle $\beta \in [0,\pi /4]$ to the vertical cell sides, and set $y_1,\ldots ,y_n$ to be the consecutive points at the lower edge of the cell. We have $y_1\in [-1/2,1/2[$ and $y_k=-1/2 + ( 1/2 + (k-1)\tan (\beta )) \mod \; 1$. Then

$$\begin{aligned} p[\psi _{\epsilon }](y,\beta ) = \int _{\mathbb {R}} \psi _{\epsilon }(x_1 ) \phi _{\epsilon }(y\cos (\beta ) +x_1)\,dx_1 \end{aligned}$$

(44)

satisfies

$$\begin{aligned} \sum _{k=1}^n p[\psi _{\epsilon }](y_k,\beta ) = \frac{\sqrt{\epsilon } \,n}{\cos (\beta )} \int _{-1}^{1} \psi _0(x)\,dx + R_a(y_1,\beta ). \end{aligned}$$

(45)

The remainder term $R_a$ also depends on n and $\epsilon$. It is bounded by a function $\bar{R}_A(\beta )$, that depends on $\phi$, n and $\epsilon$ but not on $\psi$, and that satisfies

$$\begin{aligned} \left| R_a(n,\epsilon , y_1,\beta )\right|&\le \Vert \psi _0\Vert _{L^1} \bar{R}_A(\beta ) \qquad \hbox {where} \end{aligned}$$

(46)

$$\begin{aligned} \int \bar{R}_A(\beta ) \, d\beta&\le C \epsilon ^{\nu -1/2} (1+\log n)\,. \end{aligned}$$

(47)

Proof

The result is a small extension of the corresponding proposition in [26], and also the proof follows closely that paper. For any fixed $\beta$, the expression $p[\psi _{\epsilon }](y,\beta )$ has support in an interval of length $2( \epsilon ^{1-\nu } + \epsilon ^{1/2})/\cos (\beta )$. Extend this function to be a one-periodic function of y. For simplicity we assume that n is odd, and set $n=2m+1$. With n large, this assumption would only make a very small contribution from adding one extra term to the sum in case n were even. Then

$$\begin{aligned} \sum _{j=1}^n p[\psi _{\epsilon }](y_j,\beta )&= \sum _{j=-m}^m p[\psi _{\epsilon }](y_1+ (j+m-1)\tan (\beta ),\beta )\nonumber \\&= \sum _{k=-\infty }^{\infty } {\hat{p}}_k \sum _{j=-m}^m e^{2\pi i k (y_1+(j+m-1)\tan (\beta ))}\nonumber \\&= \sum _{k=-\infty }^{\infty } {\hat{p}}_k e^{2\pi i k (y_1+(m-1)\tan (\beta ))} \sum _{j=-m}^m e^{2\pi i k j\tan (\beta )}\,. \end{aligned}$$

(48)

In this expression ${\hat{p}}_k$ is the k-th Fourier coefficient of the periodic function $p[\psi _{\epsilon }](\cdot ,\beta )$, and the sum to the right can be evaluated as the Dirichlet kernel of order m with argument $k\tan (\beta )$:

$$\begin{aligned} D_m(x) = \frac{\sin ((2m+1) \pi x)}{\sin (\pi x)}. \end{aligned}$$

(49)

Therefore

$$\begin{aligned} \sum _{j=1}^n p[\psi _{\epsilon }](y_j,\beta ) = (2m+1) {\hat{p}}_0 + R_a, \end{aligned}$$

(50)

where

$$\begin{aligned} R_a = \sum _{k\ne 0} {\hat{p}}_k e^{2\pi i k (y_1+(m-1)\tan (\beta ))} D_m(k\tan {\beta }). \end{aligned}$$

(51)

The Fourier coefficients ${\hat{p}}_k$ can be computed as the Fourier transform of $p[\psi _{\epsilon }](\cdot ,\beta )$ evaluated at the integer points k,

$$\begin{aligned} {\hat{p}}_k = \int _{-\infty }^{\infty } e^{-2\pi i k y} p[\psi _{\epsilon }](y,\beta )\,dy = \frac{\sqrt{\epsilon }}{\cos (\beta )}\widehat{\psi }_0\left( -\sqrt{\epsilon }k\right) \widehat{\varphi }_0\left( \epsilon ^{1-\nu }k\right) . \end{aligned}$$

(52)

Here $\widehat{\varphi }_0$ and $\widehat{\psi }_0$ are the Fourier transforms of $\varphi _0$ and $\psi _0$. Note the factor $\sqrt{\epsilon }$ which is due to the definition of $\psi _{\epsilon }$, which is not rescaled to preserve the $L^1$-norm. We have

$$\begin{aligned} {\hat{p}}_0 = \frac{\sqrt{\epsilon }}{\cos (\beta )}\int \psi _0(x)dx, \end{aligned}$$

(53)

and because $\psi _0\in L^1$ and $\varphi _0$ is smooth, the coefficients ${\hat{p}}_k$ decay rapidly: For any $a>0$ there is a constant $c_a$ depending on $\varphi _0$ such that

$$\begin{aligned} \vert {\hat{p}}_k\vert \le \sqrt{\epsilon } \Vert \psi _0\Vert _{L^1} \frac{c_a}{1+ \left| \epsilon ^{1-\nu }k\right| ^a}. \end{aligned}$$

(54)

Because $\beta \in [0,\pi ]$, the dependence on $\beta$ can be absorbed into the constant $c_a$. Let

$$\begin{aligned} \bar{R}_A(\beta ) = \sum _{k\ne 0} \frac{c_a\sqrt{\epsilon }}{1+\left| \epsilon ^{1-\nu }k\right| ^a} \left| D_m(k\tan \beta )\right| \end{aligned}$$

(55)

The remainder term $R_a=R_a(n,\epsilon , y_1,\beta )$ is therefore bounded by

$$\begin{aligned} \left| R_a\right| \le \Vert \psi _0\Vert _{L^1} \bar{R}_A(\beta ). \end{aligned}$$

(56)

Using a standard estimate of the $L^1$-norm of the Dirichlet kernel,

$$\begin{aligned} \int _{0}^{\pi /4} \vert D_m(k \tan \beta ) \vert \,d\beta&= \int _{0}^{1} \frac{\left| D_m( k \xi )\right| }{1+\xi ^2}\,d\xi \nonumber \\&\le \frac{1}{k}\int _{0}^{k}\left| D_m(\xi )\right| \,d\xi \,\le \, C(1+\log m). \end{aligned}$$

(57)

Therefore these integrals are independent of k, and so

$$\begin{aligned} \int \left| \bar{R}_A(\beta )\right| \,d\beta&\le C \sqrt{\epsilon } (1+\log (m)) \sum _{k\ne 0}\frac{c_a \Vert \psi _0\Vert _{L^1}}{1+ \left| \epsilon ^{1-\nu }k\right| ^a} \nonumber \\&\le C \Vert \psi _0\Vert _{L^1} \epsilon ^{\nu -1/2} (1+\log (n) )\,, \end{aligned}$$

(58)

because the sum is bounded by $C\int _{0}^{\infty } (1+ (\epsilon ^{1-\nu }x)^a)^{-1}\,dx$, and replacing $\log (m)$ by $\log (n)$ only modifies the constant. This concludes the proof. $\square$

Remark 3.3

The assumption that $\psi _0\in L^1$ is actually stronger than needed. The proof works equally well as long as the Fourier transform of $\psi _0$ is not increasing too fast, and a Dirac mass with support in $]-1,1[$, for example, would give the same kind of error estimate.

Proposition 3.4

The terms $(V^t)_0 g (x,v)$ and $({\widetilde{V}}^t_{\epsilon })_0 g(x,v)$ are given by

$$\begin{aligned} {(V^t)}_0 g (x,v)&= e^{-2t} g(x+vt,v)\qquad \hbox {and}\end{aligned}$$

(59)

$$\begin{aligned} {({\widetilde{V}}^t_{\epsilon })}_0 g(x,v)&= p_0(x,v,t) g(x+vt,v)\,. \end{aligned}$$

(60)

where $p_0(x,v,t)$ is the probability that a trajectory starting at $x\in \mathbb {R}^2$ in direction v does not hit an obstacle in the interval [0, t]; this can be computed explicitly. The function $p_0(x,v,t)$ satisfies $p_0(x,v,t)-e^{-2t} = R_b(x,v,t)$ with

$$\begin{aligned} \vert R_b(x,v,t)\vert&\le \bar{R}_B(\beta ) \end{aligned}$$

(61)

for a function $\bar{R}_B(\beta )$ that satisfies

$$\begin{aligned} \int _{S_1} \bar{R}_B(\beta ) \, dv&\le C \epsilon ^{(2\nu -1)/4}\sqrt{1+\log (t/\sqrt{\epsilon })}\,, \end{aligned}$$

(62)

and consequently, for any bounded $g\in C\left( \mathbb {R}^2\times S^1\right)$ with support in $\vert x\vert \le M$,

$$\begin{aligned} \left\| {(V^t)}_0 g - {({\widetilde{V}}^t_{\epsilon })}_0 g\right\| _{L^1(\mathbb {R}^2\times S^1)}\le C M^2 \Vert g\Vert _{L^{\infty }} \epsilon ^{(2\nu -1)/4}\sqrt{1+\log (t/\sqrt{\epsilon })}. \end{aligned}$$

(63)

Fig. 4

A particle path traversing the lattice cells. The cell size, diameter of the distribution of the obstacle center and obstacle size are given in the macroscopic scale to the left and microscopic scale to the right

Fig. 5

The figure illustrates a collision with an obstacle and the notation used to describe this

Proof

Consider a path starting at $x\in \mathbb {R}^2$ in the direction of v. There is no restriction in assuming that the direction v is clockwise rotated with an angle $\beta$ as illustrated in Fig. 4, which shows one lattice cell, with an obstacle patch indicated with a red circle, and a blue circle indicating the maximal range for an obstacle, and the red solid disk shows one possible position of the obstacle. In the macroscopic scale, the lattice size is $\epsilon ^{1/2}$, the obstacle has radius $\epsilon$, and the obstacle patch has radius $\epsilon ^{3/2-\nu }$. These values are indicated within parenthesis, and the microsopic scale, in which the lattice size is 1 is indicated to the left. When $\epsilon \rightarrow 0$ the obstacle patch in microscopic scale shrinks to a point, but is is drawn large in the image for clarity. The path under consideration enters a new lattice cell for the first time at $y_1$, and enters the second lattice cell at $y_2$, drawn in the same image. A path of length t in macroscopic scale will traverse a number n of lattice cells in the vertical direction. We set $m =\lfloor \frac{t \cos \beta }{2\epsilon ^{1/2}}\rfloor$. Then

$$\begin{aligned} n = 2m+1 = \frac{t \cos \beta }{\epsilon ^{1/2}} + \zeta , \end{aligned}$$

(64)

where $\zeta \in ]-1,1]$, and depending on whether where the path starts and ends, the path may touch one additional cell. The error due to the exact position of the start and end points in a lattice cell can be taken into account by allowing $\zeta \in [-2,2]$. Then

$$\begin{aligned} p_0(x,v,t)&=\mathbb {P}[\;\hbox {no collision in the interval }\; [0,t[\;] \nonumber \\&= \prod _{j=1}^n (1-p(y_j,\beta )) = \exp \left( \sum _{j=1}^n \log (1-p(y_j,\beta ))\right) \end{aligned}$$

(65)

where $p(y,\beta )$ is the probability that a trajectory entering a lattice cell at y with angle $\beta$ along the lower cell boundary meets an obstacle before leaving the cell on the top. Because $p(y_j,\beta )< c\epsilon ^{\nu -1/2}\rightarrow 0$ when $\epsilon \rightarrow 0$ we may assume that $p(y_j,\beta )<1/2$, and therefore

$$\begin{aligned} -(1+c \epsilon ^{\nu -1/2}) p(y_j,\beta )< \log (1-p(y_j,\beta )) < -p(y_j,\beta ), \end{aligned}$$

(66)

which provides an asymptotic expression for $p_0(x,v,t)$ once the sum $\sum _{j=1}^n p(y_j,\beta )$ has been evaluated. That $(V^t)_0 g(x,v)$ has the form (59) is evident, and hence it remains to prove the estimate (63). From (66) we get

$$\begin{aligned}&\left| e^{-2t}-p_0(x,v,t)\right| \nonumber \\&\qquad \le \left| e^{-2t} -e^{\sum _{j=1}^n p(y_1\beta ) }\right| + \left| e^{-(1+c\epsilon ^{\nu -1/2})\sum _{j=1}^n p(y_1,\beta )}-e^{-\sum _{j=1}^n p(y_j,\beta )}\right| \nonumber \\&\qquad \le \left| e^{-2t} -e^{-\sum _{j=1}^n p(y_1,\beta ) }\right| + c\epsilon ^{\nu -1/2}\,. \end{aligned}$$

(67)

Referring to the notation in Lemma 3.2 the probability $p(y_j,\beta )$ can be computed as

$$\begin{aligned} p(y_j,\beta ) = p[\mathbbm {1}_{\epsilon }](y,\beta ), \end{aligned}$$

(68)

that is, $\psi _0$ is set to one in the interval $[-1,1]$ and zero outside this interval. The same lemma then gives

$$\begin{aligned} \sum _{j=1}^n p(y_1,\beta ) = \frac{2\sqrt{\epsilon }n}{\cos (\beta )} + R_a(n,\epsilon ,y_1,\beta ) = 2 t + {\hat{R}}_a, \end{aligned}$$

(69)

where $R_a$ satisfies the estimate (47), and $\vert {\widehat{R}}_a-R_a\vert \le 2 \sqrt{\epsilon }$. Hence $\vert {\hat{R}}_a(n,\epsilon ,y_1,\beta )\vert \le C \bar{R}_A(\beta )$ for some constant C, and Markov’s inequality says that for any $\lambda >0$, the inequality $m( \{v\in S^1 \,\vert \, \bar{R}_A>\lambda \}) \le \frac{C}{\lambda } \epsilon ^{\nu -1/2}(1+\log (t/\sqrt{\epsilon }))$ holds. Therefore

$$\begin{aligned} \int _{S_1}&\left\| e^{-2t}-p_0(\cdot ,v,t)\right\| _{L^{\infty }}\,dv \le \int _{S^1} \left\| e^{-2t} -e^{-2t + {\hat{R}}_3 }\right\| _{L^{\infty }}\,dv + 2\pi c \epsilon ^{\nu -1/2}\nonumber \\&\le C \left( m( \{v\in S^1 \,\vert \, \bar{R}_A >\lambda \}) + \lambda + \epsilon ^{\nu -1/2}\right) \nonumber \\&\le C \frac{\epsilon ^{\nu -1/2}(1+\log (t/\sqrt{\epsilon }))}{\lambda }+C \lambda + C \epsilon ^{\nu -1/2} \le C \epsilon ^{(2\nu -1)/4} \sqrt{ 1+\log (t/\sqrt{\epsilon })}\,.\nonumber \\ \end{aligned}$$

(70)

where the norms inside the integrals are taken with respect to the variable x. Then (63) follows after integrating the expression over $\mathbb {R}^2$ because

$$\begin{aligned} \left\| {(V^t)}_0 g - {({\widetilde{V}}^t_{\epsilon })}_0 g\right\| _{L^{1}(\mathbb {R}^2\times S^1)} \le \Vert g\Vert _{L^{\infty }(\mathbb {R}^2\times S^1)} \pi M^2 \int _{S^1}\left\| p_0(\cdot ,v,t) - e^{-2t}\right\| _{L^{\infty }}\,dv, \end{aligned}$$

(71)

when $g=0$ for $\vert x\vert >M$. $\square$

Proposition 3.5

Let $t>\epsilon ^a$ with $a<(2\nu -1)/4$. Then if $g=0$ for $\vert x\vert >M$,

$$\begin{aligned} \left\| \sum _{k=2}^{\infty } {({\widetilde{V}}_{\epsilon }^{t})}_{k}g \right\| _{L^1(\mathbb {R}^2\times S^1)}\, \le C \Vert g\Vert _{L^{\infty }} M^2 t^2. \end{aligned}$$

(72)

Proof

Let $B_M$ be the ball of radius M in $\mathbb {R}^2$, and consider a path starting at $(x,v)\in B_M \times S^1$, and set $J_k=J_k(x,v,t)$ be the event that this path has exactly k velocity jumps in the time interval [0, t]. Similarly, let $J_{k+}$ denote the same for the case of at least k jumps. Then

$$\begin{aligned} \left\| \sum _{k=2}^{\infty } {({\widetilde{V}}_{\epsilon }^{t})}_{k}g \right\| _{L^{1}(\mathbb {R}^2\times S^1)} \le \Vert g\Vert _{L^{\infty }(\mathbb {R}^2\times S^1)} \int _{B_M \times S^1} \mathbb {P}[J_{2+} \; \vert \; (x,v)]\,dx dv, \end{aligned}$$

(73)

that is, the conditional probability that a path has at least two velocity jumps given the initial position and velocity (x, v) is integrated over x and v. Considering $J_{2+}(x,v,t)$ for one octant of $S^1$ at a time, we may represent v by an angle $\beta \in [0,\pi /4]$ as in the proof of Lemma 3.2. A path in the direction of $\beta$ starting at x will traverse $n = \lfloor t \cos (\beta )/\sqrt{\epsilon }\rfloor \pm 1$ lattice cells if it is not reflected on an obstacle along the way, and so

$$\begin{aligned} \mathbb {P}[J_{2+} \; \vert \; (x,v)]&= \sum _{j=1}^{n} p_0(c,v,t_{j-}) p_j \mathbb {P}[ J_{1+}(x',v',t-t_{j+})\; \vert \; (j,x',v') ] \end{aligned}$$

(74)

that is, as a sum of terms conditioned on the event that the first jump takes place at the j-th passage of a lattice cell. Clearly

$$\begin{aligned} \mathbb {P}[J_{2+} \; \vert \; (x,v)]&\le \sum _{j=1}^{n} p_j \mathbb {P}[ J_{1+}(x',v',t)\; \vert \; (j,x',v') ]\,, \end{aligned}$$

(75)

and the terms $p_j \mathbb {P}[ J_{1+}(x',v',t)\; \vert \; (j,x',v') ]$ can be expressed as $p[\psi _{\epsilon }](y,\beta )$ with

$$\begin{aligned} \psi _{\epsilon } = \Big (1-p_0(x',v'(r/\epsilon ))\Big )\mathbbm {1}_{\vert r\vert \le \epsilon } \end{aligned}$$

(76)

in Lemma 3.2; $p_0(x',v'(r/\epsilon ),t)$ is the probability that there is no collision in a path of length t starting at $x'$ in the direction of $v'$, and this direction is given as the outcome of a collision with an obstacle with impact parameter $r/\epsilon$. Using Proposition 3.4 we find that $\left| p_0(x',v'(r/\epsilon ),t)- e^{-2t}\right| \le \bar{R}_B(\beta '(r/\epsilon ))$, where $\beta '$ is the angular direction corresponding to $v'$. Rescaling $\psi _{\epsilon }$ gives

$$\begin{aligned} \left| \int _{-1}^1 \psi _{0} \,dr - 2 \left( 1-e^{-2t}\right) \right|&\le \int _{-1}^1 \bar{R}_B( v'(r),t)\,dr \nonumber \\&= \int _{S^1} \bar{R}_B(\epsilon ,v') \frac{\cos (\beta '/2)}{2}\,dv'\,, \end{aligned}$$

(77)

where $\beta '$ is the scattering angle of $v'$ with respect to the velocity before scattering, v. It follows that

$$\begin{aligned} \Vert \psi _{0} \Vert _{L^1} \le 2 (1-e^{-2t}) + C \epsilon ^{(2\nu -1)/4} \sqrt{1+\log (t/\sqrt{\epsilon })}. \end{aligned}$$

(78)

Therefore, using Lemma 3.2, the righthand side of Eq. 74 is bounded by

$$\begin{aligned} \frac{\sqrt{\epsilon } n }{\cos (\beta )}\Vert \psi _0\Vert _{L^1} + C \Vert \psi _0\Vert _{L^1}\bar{R}_A(\beta ), \end{aligned}$$

(79)

and integrating with respect to v over $S^1$ and then x over $B_M$, gives

$$\begin{aligned} \Vert g\Vert _{L^{\infty }} M^2 C&\left( 1-e^{-2t} + r_{\epsilon }^{1/2}\right) \left( \frac{\sqrt{\epsilon }n}{\cos (\beta )}+ r_{\epsilon } \right) \nonumber \\&\le \Vert g\Vert _{L^{\infty }} M^2C \left( t^2 +t (r_{\epsilon }^{1/2}+r(t,\epsilon )) + r_{\epsilon }^{3/2}\right) \end{aligned}$$

(80)

as a bound for the right hand side of Eq. (73). Here $r_{\epsilon }= \epsilon ^{(2\nu -1)/2} (1+\log (t/\sqrt{\epsilon })$, and t is assumed to be small. The proof is concluded by comparing the terms when $t>\epsilon ^{a}$ with $a< (2\nu -1)/4$. $\square$

The following proposition concerns the terms ${\left( V^t\right) }_1g(x,v)$ and ${\left( {\widetilde{V}}_{\epsilon }^t\right) }_1g(x,v)$ defined by

$$\begin{aligned} {\left( V^t\right) }_1g(x,v) = e^{-2t}\int _{0}^{t} \int _{S^1_-} g(x+\tau v + (t-\tau )v',v')\vert v\cdot \omega \vert \,d\omega \,d\tau \end{aligned}$$

(81)

and

$$\begin{aligned} {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1 g(x,v) = \mathbb {E}\left[ g(x+\tilde{\tau }v+(t-\tilde{\tau }) v',v') \mathbbm {1}_{J_1(x,v,t)} \right] , \end{aligned}$$

(82)

where as before, $J_1(x,v,t))$ is the event that there is exactly one jump on the trajectory starting at x in the direction of v. The $\tilde{\tau }\in ]0,t[$ and $v'\in S^1$ are the random jump time and velocity of the particle after the jump.

Proposition 3.6

Let $\omega (\delta ,g)$ be the modulus of continuity for g, i.e. a function such that $\vert g(x,v)-g(x_1,v_1)\vert \le \omega (\vert x-x_1\vert +\vert v-v_1\vert ,g)$. Then

$$\begin{aligned}&\left\| {\left( V^t\right) }_1g- {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1 g \right\| _{L^1(\mathbb {R}^2\times S^1)} \nonumber \\&\qquad \qquad \le C M^2 \left( t\omega (t,g) +r_{\epsilon }\omega (t,g) + \Vert g\Vert _{L^{\infty } } r_{\epsilon } + \Vert g\Vert _{L^{\infty } } t r_{\epsilon }^{1/2} \right) \end{aligned}$$

(83)

where the support of g is contained in $\{ (x,v)\,\vert \,\vert x\vert <M\}$ and $r_{\epsilon } =\epsilon ^{\nu -1/2}(1+\log n)$.

Proof

First, because g is assumed to have compact support, the modulus of continuity exists, and $\omega (\delta ,g)\rightarrow 0$ when $\delta \rightarrow 0$. Define $g_x(v)=g(x,v)$, i.e. a function depending only on v but with x regarded as a parameter. Because $\vert v\vert =\vert v'\vert =1$, we then have $\vert g_x(v')-g(x+\tau v + (t-\tau )v',v')\vert \le \omega (t,g)$, and therefore

$$\begin{aligned} \left| {\left( V^t\right) }_1g_x- {\left( V^t\right) }_1g\right| \le t \omega (t,g), \end{aligned}$$

(84)

where the factor t multiplying $\omega (t,g)$ comes from the integral in the definition of $V^t_1$. Similarly

$$\begin{aligned} \left| {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1g_x- {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1g\right| \le (1- p_0(x,v,t)) \omega (t,g) \le \left( 1-e^{-2t} + \bar{R}_A(\beta ) \right) \omega (t,g), \end{aligned}$$

(85)

where $p_0$ and $\bar{R}_A$ are defined as above. It remains to compare

$$\begin{aligned} {\left( V^t\right) }_1g_x(v) = t e^{-2t} \int _{S^1_-} g_x(v') \vert v\cdot \omega \vert \,d\omega \end{aligned}$$

(86)

and

$$\begin{aligned} {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1g_x(v) = \mathbb {E}\left[ g_x(v') \mathbbm {1}_{J_1(]x,v,t)}\right] . \end{aligned}$$

(87)

The operators ${\left( V^t\right) }_1$ and ${\left( {\widetilde{V}}^t_{\epsilon }\right) }_1$ act only on the variable v of $g_x$, x being considered as a parameter, and it is possible to use Lemma 3.2. By conditioning on the event that a velocity jump takes place in the j-the passage of a cell,

$$\begin{aligned} \mathbb {E}\left[ g_x(v') \mathbbm {1}_{J_1(x,v,t)}\right]&= \sum _{j=1}^n p_j \mathbb {E}\left[ g(v') p_0(x,v,t_{j-}) p_0(x_j,v',t-t_{j+})\big \vert j\right] \end{aligned}$$

(88)

where $t_{j-}$ and $t_{j+}$ denote the time points when the trajectory enters and leaves cell number j along the path, $x_j$ is the (random) point of reflection of the trajectory inside cell j, $v'$ the random new velocity, and finally, $\mathbb {E}[ f \vert j ]$ is shorthand for the expectation of f subject to the event that the jump takes place in cell number j along the path. Then

$$\begin{aligned} \mathbb {E}\left[ g_x(v') \mathbbm {1}_{J_1(x,v,t)}\right]&= e^{-2t} \sum _{j=1}^n p_j \mathbb {E}\left[ g(v')\big \vert j\, \right] \nonumber \\&\quad + \sum _{j=1}^n p_j \mathbb {E}\left[ g(v') p_0(x,v,t_{j-1}) \left( p_0(x_j,v',t-t_{j-})- e^{-2(t-t_{j+})} \right) \big \vert j\right] \nonumber \\&\quad + \sum _{j=1}^n p_j \mathbb {E}\left[ g(v') \left( p_0(x,v,t_{j-1})- e^{-2t_{j-}}\right) e^{-2(t-t_{j+})}\big \vert j\right] \nonumber \\&\quad + e^{-2t} \sum _{j=1}^n p_j \mathbb {E}\left[ g(v') \left( e^{2(t_{j+}-t_{j-})}-1)\right) \big \vert j\right] . \end{aligned}$$

(89)

Using Lemma 3.2 with $\psi _0(r)= g_x(v'(r))\mathbbm {1}_{\vert r\vert \le 1}$ one finds that the first term is

$$\begin{aligned} t \int _{-1}^1 g_x(v'(r))\,dr + R_a(n,\epsilon ,x,\beta ), \end{aligned}$$

(90)

with $R_a$ bounded by $\Vert g\Vert _{L^{\infty }}\bar{R}_A(\beta )$ and $\int _{S^1} \bar{R}_A(\beta ) \,dv'\le C \epsilon ^{\nu -1/2} (1+\log (t/\sqrt{\epsilon }))$. The second term is bounded by

$$\begin{aligned} \Vert g\Vert _{L^{\infty }} \sum _{j=1}^n p_j \mathbb {E}\left[ \bar{R}_B(\beta '(r/\epsilon )) \big \vert j\right] = \Vert g\Vert _{L^{\infty }} t \Vert \bar{R}_B(\beta (\cdot ) \Vert _{L^1} + \Vert g\Vert _{L^{\infty }} R_b(n,\epsilon ,x,v), \end{aligned}$$

(91)

where, in the same way as before, $\left| R_b\right| \le \Vert \bar{R}_B(\beta (\cdot ) \Vert _{L^1} \bar{R}_A(\beta )$ . Similarly the third term is bounded by

$$\begin{aligned} \Vert g\Vert _{L^{\infty }}&\sum _{j=1}^n \left| p_0(x,v,t_{j-1})- e^{-2t_{j-}}\right| p_j \le C \Vert g\Vert _{L^{\infty }} \bar{R}_B(\beta )\left( t+ C \bar{R}_A(\beta )\right) \,, \nonumber \\&\le C\Vert g\Vert _{L^{\infty }} \, t \bar{R}_B(\beta ) + C \Vert g\Vert _{L^{\infty }} \, \bar{R}_A(\beta )\,, \end{aligned}$$

(92)

and the last term by

$$\begin{aligned} C \sqrt{\epsilon } \left( t+ \bar{R}_A(\beta )\right) . \end{aligned}$$

(93)

Adding the error estimates from (84), (85), (90), (91), (92),and (93) and integrating over $\beta$ gives

$$\begin{aligned}&\int _{S^1}\left| {\left( V^t\right) }_1g(x,v)- {\left( {\widetilde{V}}^t_{\epsilon }\right) }_1 g(x,v) \right| \,dv \nonumber \\&\qquad \le C \left( t\omega (t,g) +r_{\epsilon } \omega (t,g) + \Vert g\Vert _{L^{\infty } } r_{\epsilon } + \Vert g\Vert _{L^{\infty } } t \,r_{\epsilon }^{1/2} \right) \,, \end{aligned}$$

(94)

again writing $r_{\epsilon }$ for the expression $\epsilon ^{\nu -1/2} (1+\log n)$. This concludes the proof, because the integration over the support of g in x is trivial. $\square$

4 Equivalence of Processes and Propagation of Chaos

The Lorentz process and the Markovian Lorentz process are equivalent in the set of trajectories that don’t return to the same obstacle patch, and the purpose of this section is to prove that the probability that a path in the Markovian process returns to the same patch vanishes in the limit as $\epsilon \rightarrow 0$. This is a geometrical construction which consists in estimating the measure of the set $B_{\epsilon }\subset \mathbb {R}^2\times S^1$ of initial values that result in a path returning to the same obstacle patch. This subset depends on the realization of the obstacle positions, but the estimates of the measure $m(B_{\epsilon })$ of this set do not, and $m(B_{\epsilon })\rightarrow 0$ when $\epsilon \rightarrow 0$. A very similar calculation is then made to prove that the probability that a pair of trajectories i the Markovian process meet in an obstacle range also converges to zero when $\epsilon$ does. The same calculation could be repeated for any number of simultaneous trajectories, and from that one can conclude that propagation of chaos holds for this system.

Consider then a path passing through an obstacle range, and then returning to the same patch. All such paths can be enumerated by giving the relative (integer) coordinates of the lattice cells where the path changes direction, that is $\xi _j\in \mathbb {Z}^2$ denotes the difference of the integer coordinates of the end point and starting point of a straight line segment of the path. This is illustrated in Fig. 6, where the starting point p of the loop is indicated with a black dot in cell nr. 0, which in this case is a point where the path is reflected, but in most cases it would not be. The point is not the starting point of the particle path, which may have a long history before entering this particular loop. For a loop with n collisions, we therefore have

$$\begin{aligned} \xi _1+\xi _2 +\cdots + \xi _{n+1} = 0 \in \mathbb {Z}^2. \end{aligned}$$

(95)

For a given time interval $t\in [0,\bar{t}[$, we must have

$$\begin{aligned} \vert \xi _i\vert + \vert \xi _2\vert + \cdots + \vert \xi _{n+1}\vert \le \bar{t}\epsilon ^{-1/2}, \end{aligned}$$

(96)

because the size of a lattice cell is $\sqrt{\epsilon }$ in the scaling we are considering here. The notation is indicated in Fig. 6, where the first few and the last segment of a loop are indicated with a solid line, the segments joining the lattice centers with dashed lines, and angles $\beta _j$ of the path segments, as well as the integer coordinates.

Fig. 6

A path making a loop by returning to the same obstacle range in the lattice cell that here is indexed by $0\in \mathbb {Z}^2$

When $\epsilon$ is small, the path segments are almost parallel to the corresponding segment joining the lattice cell centers, and the same holds for the segment lengths. In the worst case, with a segment joining two neighboring cells, the relative error at most of order $\mathcal {O}(\epsilon ^{1-\nu })$. In the following computation, all lengths are expressed in terms of the integer coordinates, and the error coming from this approximation is taken into account by a constant denoted c.

A loop returning to the same obstacle range is not uniquely determined by the integer sequence $\xi _1,\ldots ,\xi _{n+1}$, because there is some freedom in setting the initial position and angle of the path. The last angle $\beta _{n+1}$ must belong to an interval of width $\Delta \beta _{n+1}$ that satisfies

$$\begin{aligned} \Delta \beta _{n+1} \le c \frac{\epsilon ^{3/2-\nu }}{\sqrt{\epsilon } \vert \xi _{n+1}\vert }\, \end{aligned}$$

(97)

where the enumerator is the diameter of the obstacle range, and $\sqrt{\epsilon } \vert \xi _{n+1}\vert$ is the length of the last segment. And it is an easy argument to see that then the angle of the n-th segment must belong to an interval of width smaller than

$$\begin{aligned} \Delta \beta _{n} \le c \frac{\epsilon }{\sqrt{\epsilon } \vert \xi _n\vert } \Delta \beta _{n+1}. \end{aligned}$$

(98)

Following the path backwards gives

$$\begin{aligned} \Delta \beta _1 \le c^n \frac{\epsilon ^{n/2}}{\vert \xi _1\vert \vert \xi _2\vert \cdot \dots \cdot \vert \xi _n\vert }\Delta \beta _{n+1} \le c^{n+1} \frac{\epsilon ^{n/2}}{\vert \xi _1\vert \vert \xi _2\vert \cdot \dots \cdot \vert \xi _n\vert } \frac{\epsilon ^{1-\nu }}{\vert \xi _{n+1}\vert } . \end{aligned}$$

(99)

The history of the path leading up to the point p is at most $\bar{t}$, and hence the phase space volume spanned by the possible histories leading to a loop indexed by a sequence $(\xi _1,\ldots ,\xi _n)$ is bounded by $\bar{t}c \epsilon ^{3/2-\nu } \Delta \beta _1$, the length of the path times the diameter of of the obstacle range times the angular interval. The constant c is there to account for the difference between the diameter of the obstacle range and obstacle patch, and can be taken as close to 1 as one wishes. Of course the history is not likely to be one straight line segment, but different histories leading a particular loop may be very different, with none or many reflections. However, it is well-known that the so called billiard map is measure preserving. Let $\partial \Omega =\bigcup _{z \in \sqrt{\epsilon } \mathbb {Z}^2 } \{ x\in \mathbb {R}^2\;\vert \; x-z = \epsilon ^{3/2-\nu }\}$, i.e. the union of all obstacle boundaries. If $(x,v)\in \partial \Omega \times S^1_+$, a point on the boundary of an obstacle, with velocity pointing out from the obstacle, then the billiard map is the map $(x,v) \mapsto (x_1,v_1)$ where $(x_1,v_1)$ are the position and outgoing velocity after the trajectory hits the next obstacle. This map preserves the measure $\vert n \cdot v\vert dx_{\parallel }dv$, where n is the normal point out from the obstacle at x and $d x_{\parallel }$ is the length mesure of the obstacle boundary, see e.g. [7]. This means that even if the set of histories leading leading to the loop indexed by $(\xi _1,\ldots ,\xi _n)$ splits into a complicated form, the phase space volume in the full space still satisfies the same bound. Because the loop is indexed with coordinates relative to the starting point, all periodic translates of a point of the history maps into a loop of with the same index sequence, the fraction of points $(x,v)\in B\times S^1$, where B is any one lattice cell, that leads to a loop with the given index is bounded by

$$\begin{aligned} \bar{t}c \epsilon ^{3/2-\nu } \Delta \beta _1 m(B)^{-1}&\le \bar{t}c \epsilon ^{3/2-\nu } c^{n+1} \frac{\epsilon ^{n/2}}{\vert \xi _1\vert \vert \xi _2\vert \cdot \dots \cdot \vert \xi _n\vert } \frac{\epsilon ^{1-\nu }}{\vert \xi _{n+1}\vert } \epsilon ^{-1}\nonumber \\&=\bar{t}c c^{n+1} \epsilon ^{2(1-\nu ) + (n-1)/2} \frac{1}{\vert \xi _1\vert \vert \xi _1\vert \cdots \vert \xi _{n+1}\vert } \,. \end{aligned}$$

(100)

To compute an estimate of the fraction of $(x,v)\in B\times S^1$ that leads to any loop with $n+1$ segments it is enough to sum this expression over the set of $(\xi _1,\ldots ,\xi _n,\xi _{n+1})$ satisfying

$$\begin{aligned}&\xi _1+\xi _2+ \cdots + \xi _{n+1}=0;,\quad \xi _j\ne 0\,, \\&\vert \xi _1\vert +\vert \xi _2\vert + \cdots + \vert \xi _{n+1}\vert \le \bar{t}/\sqrt{\epsilon }. \end{aligned}$$

Using $\vert \xi _1\vert ^{-1}\vert \xi _{n+1}\vert ^{-1}\le \frac{1}{2} \left( \vert \xi _1\vert ^{-2}+\vert \xi _{n+1}\vert ^{-2}\right)$, we find that the sum is bounded by

$$\begin{aligned}&\sum \frac{1}{\vert \xi _1\vert ^2\vert \xi _2\vert \cdots \vert \xi _{n}\vert } \nonumber \\&\quad \le C \int _{\vert x_1\vert \le \bar{t}/\sqrt{\epsilon }}\frac{1}{\vert x_1\vert ^2} dx_1\int _{\vert x_2\vert +\cdots +\vert x_n\vert \le \bar{t}/\sqrt{\epsilon }-\vert x_1\vert } \frac{1}{\vert x_2\vert \cdots \vert x_{n+1}\vert } dx_2\ldots dx_n \nonumber \\&\quad \le C (2\pi )^n\int _1^{\bar{t}/\sqrt{\epsilon }} \frac{1}{s}\,ds \;\frac{(\bar{t}/\sqrt{\epsilon })^{n-1}}{(n-1)!} = C (2\pi )^n \log (\bar{t}/\sqrt{\epsilon }) \frac{\bar{t}^{n-1}}{(n-1)!\epsilon ^{(n-1)/2}}. \end{aligned}$$

(101)

The last line has been obtained by changing to polar coordinates in $\mathbb {R}^2$, and taking the simplex in the inner integral to span over the full length $T/\sqrt{\epsilon }$. Therefore, summing the estimate in (100) first over the loops of length $n+1$ and then over $n=1\cdots \infty$ the following estimate for the fraction of initial points in phase space that result in a loop along the path:

$$\begin{aligned} \bar{t}C e^{c \bar{t}} \log \left( \bar{t}/\sqrt{\epsilon }\right) \; \epsilon ^{2(\nu -1)} . \end{aligned}$$

(102)

This calculation may be summarized as a proposition:

Proposition 4.1

Let $T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t$ be the Lorentz process as in Theorem 2.1. Denote the event that there is a loop along the path of length $\bar{t}$ starting at (x, v) by $\mathcal {L}(x,v)$. Then

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f_0 (x,v) \mathbb {E}\left[ g(T^t_{\mathcal {Y}_{\epsilon ,\epsilon }}(x,v)) \mathbbm {1}_{\mathcal {L}(x,v)}\right] \,dx dv \rightarrow 0 \end{aligned}$$

(103)

when $\epsilon \rightarrow 0$.

Proof

It is enough to see that the integral is bounded by

$$\begin{aligned} \Vert g \Vert _{\infty }\int _{B_M\times S^1}f_0(x,v) \mathbbm {1}_{\mathcal {L}(x,v)}\,dxdv\, \end{aligned}$$

(104)

where $B_M$ is the ball of radius M in $\mathbb {R}^2$, and assumed to contain the support of g. This is bounded by

$$\begin{aligned}&\Vert g \Vert _{\infty }\int _{B_M \times S^1}f_0(x,v) \mathbbm {1}_{\{f_0>\lambda \}}\,dxdv\, + \Vert g \Vert _{\infty }\lambda \int _{B_M \times S^1}\mathbbm {1}_{\mathcal {L}(x,v)\cup \{ f<\lambda \} }\,dxdv\, \nonumber \\&\quad \le \Vert g \Vert _{\infty }\int _{B_M \times S^1}f_0(x,v) \mathbbm {1}_{\{f_0>\lambda \}}\,dxdv + \Vert g\Vert _{\infty } \lambda \bar{t}C e^{c \bar{t}} \log (\bar{t}/\sqrt{\epsilon }) \; \epsilon ^{2(\nu -1)}. \end{aligned}$$

(105)

This expression can be made arbitrarily small by first choosing $\lambda$ large enough to make the first term as one wishes, and then the second term can be made equally small by choosing $\epsilon$ sufficiently small. All this is uniform in the random positions of the obstacles. $\square$

The proof of propagation of chaos is similar in many ways. Consider two paths of the Markovian Lorentz model with independent initial conditions (x, v) and $(x',v')$. Because there is no interaction between the two particles, the particles remain independent until they meet the same obstacle range, if ever. As in the previous calculation, take a fixed realization of the random configuration of obstacles in each obstacle range. Let A(x, z) be the set of angles $v\in S^1$ such that there is a possible path from the point $x\in \mathbb {R}^2$ to the obstacle range with center at $z\in \sqrt{\epsilon }\mathbb {Z}^2$. The set of angles such that the path reaches the patch before hitting an obstacle is bounded by $\epsilon ^{3/2-\nu } /\vert x-z\vert$, and the measure of angles v such that the path meets the obstacle patch after at least one collision with an obstacle can be computed as above. The result is that

$$\begin{aligned} m(A(x,z)) \le C \epsilon ^{3/2-\nu } \left( \frac{1}{\vert x-z\vert } + e^{C\bar{t}}\log (\bar{t}/\sqrt{\epsilon }) \right) , \end{aligned}$$

(106)

and the set of angles v and $v'$ such that both the path $T^t(x,v)$ and $T^t(x',v')$ meet the same obstacle range is bounded by

$$\begin{aligned}&m\left( \left\{ (v,v')\in (S^1)^2 \; \vert \; v\in A(x,z), v'\in A(x',z) \right\} \right) \nonumber \\&\qquad \le C \epsilon ^{3-2\nu }\left( \frac{1}{\vert x-z\vert }+ e^{C\bar{t}} \log (\bar{t}/\sqrt{\epsilon })\right) \left( \frac{1}{\vert x'-z\vert }+ e^{C\bar{t}} \log (\bar{t}/\sqrt{\epsilon })\right) \,. \end{aligned}$$

(107)

This expression should now be summed over all possible $z\in \sqrt{\epsilon } \mathbb {Z}^2$, and because the speed of a particle is equal to one, these z belong to a ball of diameter $\bar{t}$. As above we find, after rescaling,

$$\begin{aligned} \sum _{z\in \mathbb {Z}^2, \vert z\vert<\bar{t}/\sqrt{\epsilon }} \frac{1}{\vert x'-z\vert }\frac{1}{\vert x-z\vert }&\le \frac{1}{2}\sum _{z\in \mathbb {Z}^2, \vert z\vert <\bar{t}/\sqrt{\epsilon }} \left( \frac{1}{\vert x-z\vert ^2}+\frac{1}{\vert x'-z\vert ^2}\right) \nonumber \\&\le C \log (\bar{t}/\sqrt{\epsilon })\,, \end{aligned}$$

(108)

and

$$\begin{aligned} \sum _{z\in \mathbb {Z}^2, \vert z\vert <\bar{t}/\sqrt{\epsilon }} \left( \frac{1}{\vert x'-z\vert }+\frac{1}{\vert x-z\vert }\right)&\le C \bar{t}/\sqrt{\epsilon }\,. \end{aligned}$$

(109)

The dominating term when summing the expression in (107) comes from the part that does not depend on z. We get

$$\begin{aligned} \sum _{z\in \mathbb {Z}^2, \vert z\vert <\bar{t}/\sqrt{\epsilon }}&m\left( \left\{ (v,v')\in (S^1)^2 \; \vert \; v\in A(x,z), v'\in A(x',z) \right\} \right) \nonumber \\&\qquad \qquad \qquad \le C(1+\bar{t}^2) e^{C \bar{t}} \log (\bar{t}/\sqrt{\epsilon }) \epsilon ^{2(1-\nu )}\,, \end{aligned}$$

(110)

which again decreases to zero when $\epsilon$ does. The maps $T_{{\mathcal Y}_{\epsilon }}^t$ and ${\widetilde{T}}_{{\mathcal Y}_{\epsilon }}^t$ extend to pairs of particles in a natural way, so that

$$\begin{aligned} (x(t),v(t),x'(t),v'(t))&= T_{{\mathcal Y}_{\epsilon }}^t\left( x_0,v_0,x'_0,v'_0\right) \;\hbox {and}\nonumber \\ (\tilde{x}(t),\tilde{v}(t),\tilde{x}'(t),\tilde{v}'(t))&= {\widetilde{T}}_{{\mathcal Y}_{\epsilon }}^t\left( x_0,v_0,x'_0,v'_0\right) \end{aligned}$$

(111)

denote the position in phase space of a pair of particles evolving with the Lorentz process and the Markovian Lorentz process respectively. In the latter case the obstacle position inside an obstacle patch is determined independently for the two particles, and every time a path meets an obstacle range, and therefore

$$\begin{aligned} {\widetilde{T}}_{{\mathcal Y}_{\epsilon }}^t\left( x_0,v_0,x'_0,v'_0\right) = \left( {\widetilde{T}}_{{\mathcal Y}_{\epsilon }}^t( x_0,v_0), {\widetilde{T}}_{{\mathcal Y}_{\epsilon }}^t(x'_0,v'_0)\right) . \end{aligned}$$

(112)

In the Lorentz evolution this breaks down as soon as there is a loop for one of the particle paths, or when the two particle paths meet in one and the same obstacle range. However, the computation above leads to the following theorem:

Theorem 4.2

Let $T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t$ be the Lorentz process as in Theorem 2.1. Then for $g_1, g_2\in C(B_M\times S^1)$

$$\begin{aligned} \lim _{\epsilon \rightarrow 0} \int _{(\mathbb {R}^2\times S^1)^2} f_0(x,v)&f_0(x',v') \Big ( \mathbb {E}\left[ g_1\otimes g_2 ( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x,v,x',v')) \right] - \nonumber \\&\mathbb {E}\left[ g_1( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x,v)) \right] \mathbb {E}\left[ g_2( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x',v')) \right] \Big ) \,dx dv dx' dv' = 0\,. \end{aligned}$$

(113)

This says that the evolution of two particles in the Lorentz gas become independent in the limit as $\epsilon \rightarrow 0$.

Proof

Let $\mathcal {L}_2(x,v,x',v')$ denote the event that the two particle paths starting at (x, v) and $(x',v')$ and evolving in the same random obstacle configuration meet in an obstacle range. Then

$$\begin{aligned}&\mathbb {E}\left[ g_1\otimes g_2 \left( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x,v,x',v')\right) (1-\mathbbm {1}_{\mathcal {L}_2(x,v,x',v')}) \right] \nonumber \\&\qquad \qquad = \mathbb {E}\left[ g_1\left( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x,v)\right) g_2 \left( T_{\mathcal {Y}_{\epsilon ,\epsilon }}^t(x',v')\right) \left( 1-\mathbbm {1}_{\mathcal {L}_2(x,v,x',v')}\right) \right] . \end{aligned}$$

(114)

Therefore the integral in  (113) is bounded by

$$\begin{aligned} \Vert g_1\Vert _{\infty } \Vert g_2\Vert _{\infty } \mathbb {E}\left[ \int _{(\mathbb {R}^2\times S^1)^2} f(x,v) f(x',v') \mathbbm {1}_{B(x,v,x',v')},dxdvdx'dv'\right] . \end{aligned}$$

(115)

Fix $\varepsilon >0$ arbitrary, and take $M>0$ and $\lambda >0$ so large that

$$\begin{aligned} \int _{\mathbb {R}^2\times S^1} f(x,v) (\mathbbm {1}_{\vert x\vert>M}+ \mathbbm {1}_{f>\lambda })\,dxdv < \varepsilon . \end{aligned}$$

(116)

We find that (113) is bounded by

$$\begin{aligned} \Vert g_1\Vert _{\infty } \Vert g_2\Vert _{\infty } 2 \varepsilon + C(\bar{t}) \lambda _2 R^2 \log (\bar{t}/\sqrt{\epsilon }) \epsilon ^{2(1-\nu )}, \end{aligned}$$

(117)

which can be made smaller then $2\varepsilon$ by choosing $\epsilon$ sufficiently small. Here $C(\bar{t})$ is a $\bar{t}$ depending constant coming from the expression (110). This concludes the proof because $\varepsilon$ was arbitrarily small. $\square$

Theorem 4.2 could have been proven for tensor products of any order with exactly the same kind of computations, and therefore this is a proof that propagation of chaos holds. The rate of convergence in the theorem depends on the density $f_0$, and also on the time interval. The dependence of f could have been replaced by bounds of the moments and entropy. The dependence of the time interval is much more difficult to get passed, but could maybe be addressed as in [15] which deals with the Lorentz gas in a Poisson setting.