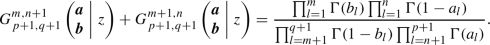Abstract
An exact map was established by Lacroix-A-Chez-Toine et al. in (Phys Rev A 99(2):021602, 2019) between the N complex eigenvalues of complex non-Hermitian random matrices from the Ginibre ensemble, and the positions of N non-interacting Fermions in a rotating trap in the ground state. An important quantity is the statistics of the number of Fermions \(\mathcal {N}_a\) in a disc of radius a. Extending the work (Lacroix-A-Chez-Toine et al., in Phys Rev A 99(2):021602, 2019) covering Gaussian and rotationally invariant potentials Q, we present a rigorous analysis in planar complex and symplectic ensembles, which both represent 2D Coulomb gases. We show that the variance of \(\mathcal {N}_a\) is universal in the large-N limit, when measured in units of the mean density proportional to \(\Delta Q\), which itself is non-universal. This holds in the large-N limit in the bulk and at the edge, when a finite fraction or almost all Fermions are inside the disc. In contrast, at the origin, when few eigenvalues are contained, it is the singularity of the potential that determines the universality class. We present three explicit examples from the Mittag-Leffler ensemble, products of Ginibre matrices, and truncated unitary random matrices. Our proofs exploit the integrable structure of the underlying determinantal respectively Pfaffian point processes and a simple representation of the variance in terms of truncated moments at finite-N.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and Discussion of Main Results
There are many applications for random matrices with complex eigenvalues nowadays, for instance, in open quantum systems or quantum field theory with finite baryon chemical potential, and we refer to [31] for a comprehensive review. Our main motivation comes from a recent physical realisation of the N complex eigenvalues of the complex Ginibre ensemble which is Gaussian. In [45] an exact map was constructed to the positions of N non-interacting Fermions in two dimensions in the ground state, confined by a harmonic trap that is rotating with a particular frequency. It is also equivalent to N free electrons in a perpendicular magnetic field in the lowest Landau level [29, Sect. 15.2]. The first map was extended to higher order levels [52] and may allow for a direct comparison to experiments on cold atoms in such a setup, cf. [22]. For a review of the extensive literature on the existence of such a map in one dimension to Hermitian ensembles, including finite temperature, we refer to [24].
One of the key quantities computed in [45] was the expected number of Fermions in a disc of radius a and its variance. We will investigate if the variance obtained there is universal, that is, if it holds for a much larger class of non-Gaussian ensembles. This question was already initiated in [45] for more general rotationally invariant potentials, where also the entanglement entropy and all moments of the cumulant generating function were determined, which yields the variance as a special case. Three different limits were identified in [45] where few, a finite fraction or almost all Fermions are contained in the disc. We will denote these by origin, bulk and edge limit, to be discussed in more detail below. We mention in passing that the intermediate and large deviations for the largest eigenvalue have been studied as well, see [23, 43] and references therein.
The computation of the number of eigenvalues in a disc has a long history in non-Hermitian random matrix theory, including [28, 35, 38, 47]. Perhaps surprisingly, it is much easier than in Hermitian ensembles to compute the probability that a disc is empty (gap probability), contains or exceeds (overcrowding) a prescribed number of eigenvalues, at least in the rotationally invariant case. This is because the corresponding eigenvalues of the Fredholm determinant (or Pfaffian) are explicitly known, and we refer to [6] for a comprehensive study in complex and symplectic ensembles. (See also [15, 18, 32] and references therein for recent development in this direction.) Other quantities have been analysed as well, including the number of eigenvalues in a generic, non-rotational invariant domain [1, 2, 48] or the probability of overcrowding a domain [5, 7, 42].
Our goal is to extend the realm of universality of the number variance and test its limitations in a rigorous analysis. In the bulk limit, when a finite fraction of eigenvalues (Fermions) are contained in a disc of radius a, the variance grows linearly with a [45], when measured in units of the mean eigenvalue density at a—which is itself a non-universal quantity. In the edge case, when almost all eigenvalues are contained, a universal scaling function was given in [45] for planar complex ensembles. For the bulk and edge limit, we will show that in a completely different symmetry class, the symplectic Ginibre ensemble and its generalisation to rotationally invariant potentials, the same universal answer prevails. This is despite the breaking of rotational invariance on the level of the joint distribution of eigenvalues through the presence of complex conjugate eigenvalue pairs and a repulsion from the real axis [33]. These planar symplectic ensembles also represent a two-dimensional Coulomb gas [30, 41] and are interesting in their own right.
In contrast, in the origin limit the number variance becomes sensitive to the presence of singularities or zeros of the mean eigenvalue density. We will present three different ensembles with distinct behaviour at the origin: the Mittag–Leffler ensembles, products of m Ginibre matrices, and truncated unitary random matrices. In all three cases we consider the symmetry classes with complex and with symplectic matrix elements. The truncated ensembles are special as a limit of weak non-unitarity exists, where the eigenvalues converge to the unit circle. It was suggested in the limit of quantum systems with few open channels, see e.g. [31] and references therein. At strong non-unitarity, we are back to the Ginibre universality class, including the origin limit as we will show.
A third ensemble of real non-symmetric Gaussian random matrices was introduced by Ginibre [33]. While both the complex and symplectic Ginibre ensemble enjoy a simple integrable structure, yielding an almost identical result for the variance already at finite-N as we will see, the Pfaffian structure of the real Ginibre ensemble is much more intricate. It separates into sectors with a different number of real eigenvalues, compare [29]. Thus we can only speculate if the same universal answer for the number variance found here in the bulk and at the edge also holds there.
1.1 Basic Setup
We study the complex eigenvalues of two types of ensembles of random matrices with complex (\(\beta =2\)) or quaternion entries (\(\beta =4\)), whence the name planar ensembles. Furthermore, we will restrict ourselves to rotationally invariant potentials. In the Gaussian case these are represented by the complex respectively symplectic Ginibre ensemble. For higher order potentials with \(\beta =2\), we consider random normal matrices. We will label these two ensembles by the number of independent real degrees of freedom \(\beta \) per matrix element. Although both correspond to a two-dimensional Coulomb gas [29], \(\beta \) does not represent the inverse temperature for \(\beta =4\).
For the planar complex ensemble \((\beta =2)\) the joint probability distribution of points \(\{z_j\}_{j=1}^N\in {\mathbb {C}}^N\) is defined as
Here \(dA(z):=\frac{1}{\pi }d^2z\) is the normalised area measure, and the partition function reads
It contains the modulus square of the Vandermonde determinant, \(\Delta _N(z_1,\ldots , z_N)=\prod _{j>k}^N (z_j-z_k)=\det _{1\le j,k\le N}[z_j^{k-1}]\). The function \(Q_N:{\mathbb {C}}\rightarrow {\mathbb {R}}\) is called external potential and satisfies suitable conditions to guarantee its existence, see Def. 1.1 below. In particular, if \(Q_N\) is given by
the ensemble (1.1) reduces to the complex Ginibre ensemble [33]. Equation (1.1) represents a determinantal point process, see Sect. 2 and Eq. (2.2) for more details later. All its correlation functions can be expressed in terms of the kernel of planar orthogonal polynomials, which are monomials due to the rotational invariance here.
The map to the lowest Landau level of N free electrons in a magnetic field can be seen as follows, and we refer to [45] for more details. The single particle Hamiltonian in a two-dimensional harmonic trap with frequency \(\omega \), rotating at frequency \(\Omega \), is given by
Choosing units \(\hbar =m=\omega =1\) and restricting ourselves to \(0\le \Omega \le 1\) to have bound states, the energy eigenvalues of the N particle Hamilton operator \(\sum _{i=1}^NH(\hat{\textbf{p}}_i,\hat{\textbf{r}}_i)\) are given by
with \(n_1,n_2\in {\mathbb {N}}\). For \(n_2=0\) we are in the lowest Landau level, which for \(1-2/N<\Omega <1\) is non-degenerate. The N lowest eigenfunctions \(\phi _{n_1}\) are then proportional to
Consequently, the Slater determinant of the N particle wave-function \(\Psi _0(z_1,\ldots ,z_N) \sim \Delta _N(z_1,\ldots ,z_N)\) is proportionally to the Vandermonde determinant, and the amplitude \(|\Psi _0|^2\) is the joint density (1.1).
For the planar symplectic ensemble \((\beta =4)\) the joint probability distribution of points \(\{z_j\}_{j=1}^N\) has an additional complex conjugation symmetry, that is the eigenvalues come in complex conjugate pairs. The point process follows the law
with
Inserting (1.2) we obtain the symplectic Ginibre ensemble [33]. Equation (1.4) represents a Pfaffian point process, to be detailed in Sect. 2 Eq. (2.5) later. All its correlation functions can be expressed in terms of the pre-kernel of skew-orthogonal polynomials that will be introduced there. Although the joint density (1.4) is proportional to the Vandermonde \(\Delta _{2N}(z_1,\ldots , z_N, {\bar{z}}_1,\ldots ,{\bar{z}}_N)\) [39], we are currently lacking a map to the Slater determinant of N electrons in a rotating trap as in (1.3).
Below we consider a general radially symmetric potential for both classes of point processes,
which possibly depends on N. Such an N-dependence is useful to describe ensembles that lead to different universality classes, see (1.16), (1.21), and (1.26) below. If the potential does not depend on N, we drop the subscript N and simply write \(Q\equiv Q_N\), \(g \equiv g_N\).
Let us first discuss the macroscopic behaviour of these ensembles. For this purpose, we denote \(Q:=\lim _{N\rightarrow \infty } Q_N\) and \(g:=\lim _{N\rightarrow \infty } g_N\), which is always assumed to be well defined. Somewhat roughly speaking, the macroscopic behaviour of the ensembles depends only on Q. It is well known [13, 17, 36, 41] that the empirical measure converges to Frostman’s equilibrium measure [51] of the form
where \(\Delta := \partial {{\bar{\partial }}}=\frac{1}{4}(\partial _r^2+\frac{1}{r} \partial _r)\), S is a certain compact set called the droplet, and \(\mathbb {1}_S(z)\) is the indicator function on this set.
Let us formulate the following conditions.
Definition 1.1
A rotational invariant potential \(Q_N(z) =g_N(|z|)\) will be called suitable, if it satisfies the following conditions:
-
(1)
\(g_N(r) \gg \log r\) as \(r \rightarrow \infty \),
-
(2)
\(g_N \in C^2(0,1]\),
-
(3)
\(r g'_N(r)\) increases on \((0,\infty )\),
-
(4)
\(\lim _{r \rightarrow 0} r g'(r)=0\), and \(g'(1)=\beta \).
The first condition is required to guarantee \(Z_N^{(\beta )}<\infty .\) The second condition is made merely for convenience. Due to the last condition the support or droplet S of the limiting spectral distribution is given by the unit disc, see [51, Sect. IV.6], [36, Sect. 2.7] and [13, Theorem 2.1]. For the Gaussian potential (1.2), it corresponds to the circular law. Note that
Thus \(rg_N'(r)\) increases on \((0,\infty )\) if and only if \(\Delta Q_N(z) > 0\) for \(z \not = 0\), as formulated in the third condition.
For \(a > 0\), let us write \(\mathcal {N}_a^{(\beta )}\) for the number of eigenvalues in the disc of radius a centered around the origin, \(D_a=\{ z \in {\mathbb {C}}: |z|<a \}\). Here, \(\beta \) labels the respective ensemble. We denote by
the mean \(E_N^{(\beta )}\), respectively the number variance \(V_N^{(\beta )}\) of \(\mathcal {N}_a^{(\beta )}\). It is easy to derive the leading order asymptotic behaviour of \(E_N^{(\beta )}\), see Corollary 1.3 and details in its proof, Eq. (4.3). The primary purpose of this work is to derive closed formulas for \(V_N^{(\beta )}\) in both symmetry classes at finite-N and their asymptotic behaviour as \(N \rightarrow \infty \).
1.2 Number Variance in the Bulk and at the Edge
In this subsection, we introduce our main results, where we begin with finite-N. For a general radially symmetric potential (1.5), let us write
for the non-vanishing jth moments, which are at the same time the squared norms of planar orthogonal polynomials (monomials). We also write
for the truncated moments or squared norms. Note that \(h_j=h_{j,1}(a)+h_{j,2}(a).\) We then obtain the following.
Proposition 1.1
(Mean and number variance of the number \(\mathcal {N}_a^{(\beta )}\) at finite-N)
For each N, we have
and
This proposition plays a key role in proving our main result, Theorem 1.2 below. Notice that for \(\beta =4\) only the odd moments appear. Let us emphasise that for \(\beta =2\), the expressions (1.10) and (1.11) also follow from [44] using the cumulant generating function.
We turn to our main result for the number variance in different large-N limits.
Theorem 1.2
Let \(Q_N\) be a suitable potential according to Definition 1.1. Then the following holds.
-
(i)
(Bulk) For \(a\in (0,1)\) fixed, we have
$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{\beta }{ \sqrt{N \Delta Q(a)} } V_N^{(\beta )}(a) = \frac{2a}{\sqrt{\pi }} . \end{aligned}$$(1.12) -
(ii)
(Edge) For \(\mathcal {S}\in {\mathbb {R}}\), we have
$$\begin{aligned} \lim _{N \rightarrow \infty } \frac{ \beta }{ \sqrt{N \Delta Q(1) } } V_N^{(\beta )}\Big ( 1-\frac{ \mathcal {S}}{ \sqrt{ 2 \Delta Q(1) N} } \Big ) = \frac{2}{\sqrt{\pi }} \, f(\mathcal {S}), \end{aligned}$$(1.13)where
$$\begin{aligned} f(\mathcal {S}):= & {} \sqrt{ 2\pi } \int _{-\infty }^{\mathcal {S}} \frac{{\text {erfc}}(t){\text {erfc}}(- t)}{4} \,dt \nonumber \\= & {} \frac{{\text {erfc}}(-\sqrt{2}\mathcal {S})}{2} -\frac{ e^{-\mathcal {S}^2} }{ \sqrt{2} } {\text {erf}}(\mathcal {S}) + \sqrt{ \frac{\pi }{2} } \, \mathcal {S} \,\frac{{\text {erfc}}(\mathcal {S}){\text {erfc}}(-\mathcal {S})}{2} \end{aligned}$$(1.14)
Note that \(f(\mathcal {S}) \rightarrow 1\) as \(\mathcal {S}\rightarrow \infty \). Thus one can see that as \(\mathcal {S}\rightarrow \infty \), the right-hand side of (1.13) recovers that of (1.12) in the limit \(a\rightarrow 1\). We also remark that the Laplacian of Q in (1.12) and (1.13) corresponds to the macroscopic density \(\rho \) in the large-N limit, see (1.6). While \(\rho \) itself is clearly non-universal, as it depends explicitly on the potential Q, the right hand side of the variance measured in units \(N\Delta Q(a)\) is universal. To the best of our knowledge, Theorem 1.2 for \(\beta =4\) has not appeared in the literature before.
The number variance of the complex Ginibre ensemble at \(\beta =2\) was computed in [45] in these limits, and was argued to be universal for more general rotational invariant potentials [43], using a saddle point approximation. In [45] the limit (i) we call “bulk” in Theorem 1.2 was called “extended bulk”. It is a global quantity, as the disc of radius a contains a macroscopic, finite fraction of the eigenvalues. The edge regime (ii) (with the same name as in [45]) is a local quantity, as we zoom into the vicinity of the edge of the limiting support, normalised to the unit disc (as mentioned after Definition 1.1). A third limit called “deep bulk” was investigated in [45] for the complex Ginibre ensemble. It is again a local quantity, as the vicinity of the origin is zoomed into. Although the origin is not special in the complex Ginibre ensemble, the corresponding variance shows a nontrivial behaviour, interpolating between quadratic and the linear behaviour in a in the (extended) bulk. We will also investigate this local origin limit in the next Sect. 1.3, allowing for more general classes of potentials with singular behaviour at the origin. These will give rise to different universality classes.
As a consequence of Theorem 1.2, we obtain the convergence of the random variable \(\mathcal {N}_a\) in probability.
Corollary 1.3
Under the same assumptions of Theorem 1.2, we have that for any \(a \in (0,1]\),
as \(N\rightarrow \infty \), in probability.
1.3 Number Variance at the Origin
In this subsection we present the asymptotic behaviour of \(V_N^{(\beta )}(a)\) near the origin \(a = 0\). This is achieved by rescaling \(a={\mathcal {T}}/N^\delta \) with some power \(\delta >1\). It depends on the local nature of the ensemble at the origin, and we shall present two related examples for ensembles exhibiting a singular or vanishing behaviour.
Example
(Mittag–Leffler ensemble) This ensemble owes its name to the appearance of the two-parameter Mittag–Leffler function in its limiting kernel [11]. It is defined through the potential
which is suitable according to Definition 1.1. Such a model was studied in [18, 21] for \(\beta =2\) and [8] for \(\beta =4\). In particular, if \(b=1\), the model is known as induced Ginibre ensemble, cf. [27]. It reduces to the standard Ginibre ensembles when also setting \(c=0\). The macroscopic density of the Mittag-Leffler ensemble is given by
Thus for \(b <1(>1)\), the density reveals a singular (vanishing) behaviour at the origin on a macroscopic scale. Furthermore, the insertion of a point charge c at the origin in (1.16) gives rise to a conical type singularity on a local scale.
When a is away from the origin, the number variance follows as a specific case of Theorem 1.2. For \(\beta =2\) this result was obtained by Charlier in [19, Corollary 1.4] in an expansion including higher order correction terms. (See [25] for an earlier work on the complex Ginibre ensemble.) Indeed, [19] contains precise large-N expansions of all higher cumulants of \(\mathcal {N}_a\) for the complex Mittag-Leffler ensemble. We also refer to [16, 20] for a generalisation involving circular-root and merging type singularities.
Recall that the (regularised) incomplete gamma functions P(a, z) and Q(a, z) are given by
see e.g. [49, Chapter 8].
Proposition 1.4
(Expected number and variance of the Mittag–Leffler ensemble at the origin) Let \(Q_N=Q_N^{ML }\). After rescaling \(a=\mathcal {T}/N^{\frac{1}{2b}}\) with \(\mathcal {T}>0\) fixed, we have
When setting \(b=1\) and \(c=0\), we obtain the result for the Ginibre ensembles, reproducing the findings of [45] for \(\beta =2\) in what was called the deep bulk there. As it was also discussed there, let us look at the small argument limit \(\mathcal {T}\rightarrow 0\) of (1.18) and (1.19). It is not difficult to see that using the expansion [49, Eq.(8.7.1)]
together with \(Q(\alpha ,z)=1-P(\alpha ,z)\), we obtain for both quantities for small \(\mathcal {T}\)
The leading order contribution comes from the summand at \(j=1\) and in fact holds already at finite-N. The fact that mean and variance agree indicates an underlying Poisson distribution - if we could show this for all cumulants, as it was done for the Ginibre ensemble at \(\beta =2\) in [45]. The large argument limit \(\mathcal {T}\) should match the linear behaviour found in Theorem 1.2 in the bulk limit as \(Q^{\textrm{ML}}\) satisfies the suitability conditions.
Example
(Product ensemble) When considering the product of \(m \in {\mathbb {N}}_+\) complex or quaternionic Ginibre matrices, the complex eigenvalues of the product matrix form a determinantal respectively Pfaffian point process , see [3] for \(\beta =2\) and [37] for \(\beta =4\). The corresponding potential is given by a Meijer G-function

see e.g. [49, Chapter 16] and Appendix A for its definition. Here \(\varvec{0}=(0,\ldots ,0)\) denotes a row vector of length m. This potential satisfies the suitability conditions in Definition 1.1. For instance, if \(m=1\), it follows from

that \(Q_N^{(m=1)}(z)=Q^{Gin }(z)\). More general products have been studied, e.g. rectangular or truncated unitary random matrices, see [4] for a review.
The density (top line) and variance (\(\beta =2\) middle and \(\beta =4\) bottom line) in the bulk and at the edge is shown for the product of \(m=1,3\) and 10 Ginibre matrices (left, middle, right column). A–C display the corresponding density (1.22) which is singular at the origin for \(m>1\). In D–F the variance \(\frac{\beta }{ \sqrt{N \Delta Q(a)} } V_N^{(\beta )}(a)\) is shown as a function of radius a for the corresponding ensemble at \(\beta =2\) with \(N = 500\) (red line), and the comparison with the analytic results in Theorem 1.2. Here, the full line corresponds to the linear prediction (i) in the bulk (1.12), whereas the dotted line corresponds to the prediction (ii) for the edge (1.13). The blue stars show the variance obtained via 10,000 random samples. G–I display the same figures at \(\beta =4\), with \(N = 250\)
The macroscopic density follows the “Halloween hat” lawFootnote 1
as shown in [14, 34, 50], see Fig. 1 top line. Note that as \(N\rightarrow \infty \), we have the following large argument asymptotic [26] of (1.21): as \(N\rightarrow \infty ,\)
Thus asymptotically the potential (1.21) corresponds to (1.16) with \(m=1/b\) and \(c = (1-m)/2m\). One can also see the relation \(m=1/b\) by comparing (1.17) and (1.22).
Proposition 1.5
(Expected number and variance of the product of m Ginibre matrices at the origin) Let \(Q_N=Q_N^{(m)}\). When rescaling \(a=\mathcal {T}/N^{m/2}\) with \(\mathcal {T}>0\), we have


Once again we denote by \(\varvec{ j} = (j,\ldots ,j)\) a row vector of lengths m. Note that for \(m=1\) we have

Thus one can notice that then Eq. (1.24) corresponds to Eq. (1.19) with \(b=1,c=0\).
As before, we look at the small argument limit \(\mathcal {T}\rightarrow 0\) of (1.23) and (1.24). Using Proposition A.2 we have

Combining this with the identity (4.4), we obtain that for small \(\mathcal {T}\),
where the leading order contribution again comes from the summand at \(j=1\). In particular, one can readily see that the asymptotic formula (1.25) for \(m=1\) agrees with (1.20) for \(b=1,c=0\).
Figure 1 illustrates Thm. 1.2 for products of Ginibre matrices. Because we use only the bulk scaling in this figure for the entire range of a, the bulk prediction given by the straight line remains the same for all plots, whereas the edge curve (1.13) changes slightly in this scaling. Recall that \(m = 1\) corresponds to the Ginibre ensembles. The quadratic or quartic behaviour close to \(a=0\) can be barely seen on this scale, compare Fig. 1G.
1.4 Truncated Unitary Ensembles
In this subsection we present the truncated unitary and truncated symplectic unitary ensembles, [53] and [40] respectively. The reason is that they possess a further large-N limit called weak non-unitarity, which is not covered by Theorem 1.2. It will be introduced below. For \(\beta = 2\) the ensemble is given by the joint eigenvalue distribution of the top-left corner \(N \times N\) sub-matrix of a random unitary \((N + c + 1) \times (N + c + 1)\) matrix, with \(c\in {\mathbb {N}}_+\) integer. In the \(\beta = 4\) case we consider the complex eigenvalues of a \((2 N + c + 1) \times (2 N + c + 1)\) random matrix from the compact symplectic group truncated to size \(2N\times 2N\). Note that here c must be odd, see [40, Section 2] for details. These truncations lead to the following potential, in contrast to the flat Haar measure without truncation:
From now on we also allow for a real valued c. If \(c \rightarrow -1\), this model degenerates to the circular unitary ensembles with a flat measure, where all eigenvalues lie on the unit circle, see e.g. [29].
Let us first consider the weak non-unitarity limit where \(c>-1\) remains fixed as \(N \rightarrow \infty \). Here, the vast majority of the eigenvalues live on the unit circle, where the global density localises. The potential (1.26) is not in the general class of suitable potentials we consider above, cf. Def. 1.1. Hence the bulk and edge behaviour differ from Theorem 1.2. Recall that the incomplete (regularised) beta function \(I_x(\alpha ,b)\) is given by
where \(B(\alpha ,b)=\frac{\Gamma (\alpha )\Gamma (b)}{\Gamma (\alpha +b)}\) is the beta function, see [49, Chapter 8]. The identity follows from simply changing variables \(t\rightarrow 1-t\) in the integral.
Proposition 1.6
(Number variance of truncated ensembles at weak non-unitarity) Let \(Q_N=Q_N^{trunc,w }\) with \(c>-1\) fixed. Then we have the following.
-
(i)
(Bulk) For a fixed \(a \in (0,1)\), we have
$$\begin{aligned} \lim _{N \rightarrow \infty } V_N^{(\beta )}(a)=\sum _{j=1}^\infty I_{a^2}\Big (\frac{\beta j}{2},c+1\Big ) I_{1-a^2}\Big (c+1,\frac{\beta j}{2}\Big ). \end{aligned}$$(1.27) -
(ii)
(Edge) For \(\mathcal {S}\ge 0\), we have
$$\begin{aligned} \lim _{N\rightarrow \infty } \frac{ \beta }{ N\beta } V_N^{(\beta )}\Big (1-\frac{\mathcal {S}}{N\beta }\Big )= \frac{1}{\mathcal {S}} \int \limits _0^{\mathcal {S}} P(c+1,u)Q(c+1,u)\,du. \end{aligned}$$(1.28)
Note that both in (1.27) and (1.28), the right hand sides vanish when \(c \rightarrow -1.\) This is intuitively obvious since for \(c=-1\) we recover the circular ensembles, where all eigenvalues are on the unit circle.
Because the density is zero at the origin, we omit the analysis there. We keep the terminology “bulk” limit for fixed a, although somewhat misleading here. This is because the spectrum is concentrated on the unit circle, and only of the order O(1) eigenvalues are inside. This follows from
which is of order unity, as in the origin limit in the previous example. This also explains why the variance is not rescaled with a power of N. It satisfies \(E^{(\beta )}(a)\sim a^2/B(\beta /2,c+1)\) for small argument. Thus from what we find in (1.27), the bulk limit at weak non-unitarity corresponds to an “extended” origin limit compared to the previous examples, with a replaced by \(\mathcal {T}\).
The edge behaviour from Prop. 1.6 is illustrated in Fig. 2.
Truncated ensembles at weak non-unitarity (edge): A–C in the top row display the graphs of \(V_N^{(2)}(a)/N\) (red line) at \(\beta =2\) and \(c=1,5,15\), where \(N = 500\). The comparisons with Proposition 1.6 (dashed black line) lie almost on top of each other. The blue stars show the variance obtained via 10,000 random samples. Note that the chosen values for the radius are in the vicinity of the unit circle, \(a \in [0.95, 1]\), i.e. here we only show the behaviour close to the edge. The figures in the bottom row D–F show the same quantities for \(\beta =4\): \(V_N^{(4)}(a)/N\), \(N = 250\). Note that for large c we begin to enter the regime of strong non-unitarity, compare Fig. 3
Let us now consider the limit at strong non-unitarity when c grows with N, keeping \({\tilde{c}}=\frac{2c}{\beta N}>0\) fixed. In the convention of [53], at \(\beta =2\) this corresponds to parametrising \(\mu =1/(1+{\tilde{c}})\) with fixed \(\mu <1\) (not too close to 1). There it was shown, that the complex eigenvalues condense onto a droplet of radius \(\sqrt{\mu }\). The corresponding potential then reads
This can be viewed as the potential (1.26) with \(c=\frac{\beta }{2}{\tilde{c}}N\) and fixed \({\tilde{c}}\), after the scaling \(z \rightarrow z/\sqrt{1+{\tilde{c}} }\). This rescaling is made so that the resulting droplet is the unit disc. The potential \(Q^{trunc,s }\) is a one-parameter generalisation of \(Q^{Gin }\), in the sense that \(\lim \limits _{ {\tilde{c}} \rightarrow \infty } Q^{trunc,s } = Q^{Gin }.\) Note that the macroscopic density is given by
That is unlike \(Q_N^{trunc,w }\), the potential \(Q^{trunc,s }\) is contained in the class of suitable potentials we consider above. Hence Theorem 1.2 applies to the bulk and at the edge here. This is illustrated as another example in Fig. 3.
Truncated ensembles at strong non-unitarity: The figures in the top row A–C show the limiting density (1.30). For large values of \({\tilde{c}}\) we approach the flat density of the Ginibre ensemble, see Fig. 1A. The middle row D–F displays the graphs of \(\frac{2}{\sqrt{N \Delta Q(a)}} V_N^{(2)}(a)\) (red line) where \(N = 500\), and their comparisons with the bulk limit (full line) and edge limit (dashed line) from Theorem 1.2. The blue stars show the variance obtained via 1000 random samples (eigenvalues rescaled by \(\sqrt{1+{\tilde{c}}}\)). The figures in the bottom row G–I show the same quantities for \(\frac{4}{\sqrt{N \Delta Q(a)}} V_N^{(4)}(a)\), \(N = 250\). Here, the deviation from the linear behaviour at the origin is more pronounced. Note that for \({\tilde{c}} \rightarrow \infty \) we recover the Ginibre case
For comparison let us also consider the origin limit at strong non-unitarity.
Proposition 1.7
(Number variance of truncated ensembles at strongly non-unitarity at the origin) Let \(Q=Q^{trunc,s }\), \({\tilde{c}}>0\). When rescaling \(a=\sqrt{ \frac{1+{\tilde{c}}}{ N{\tilde{c}} }} \mathcal {T}\) with \(\mathcal {T}>0\) fixed, we have
Note that the right-hand side of (1.31), (1.32) is same as that of (1.18), (1.19) when choosing \(b=1\), \(c=0\) there, as well as (1.23), (1.24) with \(m=1\). In that sense also the origin limit of the Ginibre ensembles is universal.
The remainder of this paper is organised as follows. In the following Sect. 2 we recall the determinantal and Pfaffian structure of our planar complex and symplectic ensembles. We then prove Proposition 1.1 giving the expected number and variance for general rotationally symmetric potentials at finite-N. In Sect. 3 the results for the Ginibre ensembles are discussed in preparation of the general case. This includes both finite- and large-N formulae for the expected number and variance for the complex and symplectic ensemble. In Sect. 4 we prove our main Theorem 1.2 about the bulk and edge limit of the variance for general rotationally invariant potentials. The proofs for the three examples for a singular behaviour at the origin, given in Propositions 1.4–1.7 are presented here as well. Appendix A contains the derivation of a general identity for Meijer G-functions, that is needed in a special case in the proof of Proposition 1.5, and the asymptotic at the origin.
2 Analysis of the Expected Number and Number Variance at Finite-N
In this section, we give a brief exposition of the integrable structures of the ensembles we consider and derive Proposition 1.1.
2.1 Correlation Kernels
By definition, the k-point function \(R_{N,k}^{(\beta )}\) is given by
When \(\beta =2\) the point process (1.1) is determinantal and the k-point correlation function \(R_{N,k}^{(2)}\) has the form
where \(K_N(z,w)\) is the correlation kernel of planar orthogonal polynomials. Examples for the 1- and 2-point function are given in (2.9). For the rotationally invariant potentials \(Q_N(z)=g_N(|z|)\) we consider here, these orthogonal polynomials are simply given by the monomials, and (2.2) reads [47]
where \(h_j\) is given by (1.8), the squared norms of these polynomials.
Example
(Complex Ginibre ensemble) Let us consider the potential \(Q^{\textrm{Gin}}(z)=|z|^2\). Then the correlation kernel \(K_N\) of the Ginibre ensemble is given by [47]
We refer to [10, Sect. 2] for a recent work on a detailed analysis of \(K_N\).
At \(\beta =4\), the point process (1.4) is of Pfaffian type and k-point function \(R_{N,k}^{(4)}\) has a Pfaffian structure [39]
where \(\kappa _N\) is called the (skew) pre-kernel. Examples for the 1- and 2-point function are given in (2.10). The skew-kernel \(\kappa _N\) in (2.5) can be constructed explicitly in terms of skew-orthogonal polynomials \(q_k\) and their skew-norms \(s_k\) for a general rotationally invariant potential [39]. Namely, we have
see e.g. [9, 37]. Then we have
where
Let us define
Then one can write
It is obvious but noteworthy that
Example
(Symplectic Ginibre ensemble) Let us consider the potential \(Q^{\textrm{Gin}}(z)=2|z|^2\). It then holds that
Therefore we have
2.2 Proof of Proposition 1.1
In this subsection, we determine the mean number and variance for general rotationally symmetric potentials at finite-N.
Proof of Proposition 1.1
By definition (1.7), we have
It is also well known that \(V_N^{(\beta )}\) is given by
see e.g. [47, Sect. 16.7]. For the second identity, we have used the reproducing property and normalisation,
which follow from the definition (2.1).
We first show the \(\beta =2\) case. For the determinantal Coulomb gas ensemble (1.1), by (2.2), we have
By (2.3), we have
Thus the expression \(E_N^{(2)}\) in (1.10) follows from the definition (1.9).
For the variance, by (2.3) and (2.9), we have
The rotationally invariant domain and potential project onto the diagonal component,
and likewise
By (1.9), this completes the proof for \(\beta =2\).
Next, we compute \(V_N^{(4)}(a)\) for \(\beta =4\). For the planar symplectic ensemble (1.4), by (2.5), we have
Note here that
Thus we have
which leads to (1.10).
For the variance we have
where we have used the symmetry \(w\rightarrow {\bar{w}}\) under the second integral for the second identity. Note that
Notice that the expression (2.6) for \(G_N(z,w)\) contains only odd powers of z and even powers of w. Therefore, the terms involving
do not contribute to the integral due to the angular integration. Furthermore, by the change of the variable \(z \mapsto {\bar{z}}\), \(w \mapsto {\bar{w}}\), we have
To analyse this expression, let us write
so that
We shall show that
which completes the proof.
Since
we have
Notice here that there is no set of indices that satisfies
Therefore we have \(V_{N,{\textrm{II}}}^{(4)}(a)=0.\) Similarly, we have
Therefore we obtain \(V_{N,{\textrm{III}}}^{(4)}(a)=V_{N,{\textrm{IV}}}^{(4)}(a)=0\) since there is no set of indices satisfying
or
We now compute \(V_{N,{\textrm{I}}}^{(4)}(a)\). For this, note that
Notice here that due to angular integration only the term
contributes to the integral. Thus by (2.7), we have
which completes the proof. \(\square \)
3 Ginibre Ensembles Revisited
Before proving our main result, we discuss \(E_N^{(\beta )}\) and \(V_N^{(\beta )}\) for the Ginibre ensembles as an application of Proposition 1.1.
3.1 Expected Number
Let \(b_k(\lambda )\)’s be the functions defined recursively by
We obtain the following.
Proposition 3.1
(Expected number for Ginibre ensembles) Let \(Q=Q^{Gin }\). Then the following holds.
-
(Finite-N expression) For each \(a>0\) and N, we have
$$\begin{aligned} \begin{aligned} E_N^{(2)}(a)&=\sum _{k=0}^{N-1} P(k+1,Na^2)= Na^2+N(1-a^2) \,P(N,Na^2)-\frac{ (Na^2)^N\, e^{-Na^2} }{ (N-1)! } \end{aligned}\nonumber \\ \end{aligned}$$(3.2)and
$$\begin{aligned} \begin{aligned} E_N^{(4)}(a)&= \sum _{k=0}^{N-1} P(2k+2,2Na^2) =\frac{1}{2} E_{2N}^{(2)}(a)- \frac{1}{2} \sum _{k=0}^{N-1} \frac{(2Na^2)^{2k+1} e^{-2Na^2} }{(2k+1)!} \\&= N a^2 +N(1-a^2) P(2N,2Na^2) -\frac{1}{2} \frac{ (2Na^2)^{2N}\, e^{-2Na^2} }{ (2N-1)! }\\&\quad - \frac{1}{2} \sum _{k=0}^{N-1} \frac{(2Na^2)^{2k+1} e^{-2Na^2} }{(2k+1)!}, \end{aligned} \end{aligned}$$(3.3)where \(P(a,z)=\gamma (a,z) / \Gamma (a)\) is the (regularised) incomplete gamma function.
-
(Large-N expansion) For a fixed \(a \in (0,1)\), we have
$$\begin{aligned} \begin{aligned} E_N^{(2)}(a)&\sim N a^2+ \frac{ (Na^2)^N\, e^{-Na^2} }{ (N-1)! } \sum _{k=1}^\infty \frac{ (-1)^k \, b_k(a^2) }{ (1-a^2)^{2k}} \frac{1}{N^{k}} \end{aligned} \end{aligned}$$(3.4)and
$$\begin{aligned} \begin{aligned} E_N^{(4)}(a)&\sim N a^2+\frac{1}{2} \frac{ (2Na^2)^N\, e^{-2Na^2} }{ (2N-1)! } \sum _{k=1}^\infty \frac{ (-1)^k \, b_k(a^2) }{ (1-a^2)^{2k}} \frac{1}{(2N)^{k}}\\&\quad - \frac{1}{2} \sum _{k=0}^{N-1} \frac{(2Na^2)^{2k+1} e^{-2Na^2} }{(2k+1)!}, \end{aligned} \end{aligned}$$(3.5)with \(b_k\)’s given by (3.1). Furthermore we have when rescaling \(Na^2=\mathcal {T}^2\) with \(\mathcal {T}\) fixed
$$\begin{aligned} E_N^{(2)}(\mathcal {T}/\sqrt{ N })\sim \mathcal {T}^2, \quad E_N^{(4)}(\mathcal {T}/\sqrt{ N }) \sim \mathcal {T}^2-\frac{1}{4}(1-e^{-4\mathcal {T}^2}). \end{aligned}$$(3.6)
See [6, 28] for some related statement.
Notice that by Stirling’s formula, we have
and we observe that \(2\log a+1-a^2<0\) for \(a \in (0,1)\).
Note also that for small \(\mathcal {T}\), we obtain a quartic behaviour \(E_N^{(4)}(\mathcal {T}/\sqrt{N})\sim 2\mathcal {T}^4+O(\mathcal {T}^6)\), in contrast to the quadratic behaviour at \(\beta =2\).
Proof of Proposition 3.1
Let us first show the finite-N expressions (3.2) and (3.3). Note that the first expressions
immediately follow from (1.2) and (1.10).
By [49, Eq. (8.4.10)] and (2.4), we have
Using integration by parts and properties of the incomplete gamma-functions one can show that
Thus we have
which gives (3.2). Furthermore, it follows from the recurrence relation [49, Eq. (8.8.5)] of the incomplete gamma function that
This gives (3.3).
We now show (3.4) and (3.5). For this, recall that for \(0<\lambda <1\)
see [49, Eq. (8.11.6)]. Using this, we have
which leads to (3.4). Moreover, (3.5) follows from the relation between (3.2) and (3.3).
It remains to show (3.6). By (3.7), we have
Integrating the following two elementary summations term wise on the left- and right-hand side,
we obtain the desired relations by applying the definition of the incomplete gamma function under the sum:
This gives (3.6). \(\square \)
3.2 Number Variance
It is instructive to derive Theorem 1.2 for the Ginibre ensembles with the potential (1.2) first, as this method will be generalised to prove Theorem 1.2 for a general potential. Note that for the complex case when \(\beta =2\), it was derived in [45] but we use a slightly different computation.
Proof of Theorem 1.2 for \(\mathbf{Q=Q}^{{\varvec{Gin}} }\)
It follows from Proposition 1.1 that
Let \(X \sim Poi ( \frac{\beta }{2} Na^2)\) be the Poisson random variable with intensity \( \frac{\beta }{2} Na^2\). Since Q(a, z) is the cumulative distribution function for Poisson random variables, we have
Furthermore, by the normal approximation of the Poisson random variable, we have
where Z is the standard normal distribution. Therefore if \(|j-Na^2|>M \sqrt{N}\) for a large M, the summand in (3.8) is exponentially small, i.e.
for some \(c>0.\) Thus we have
To analyse the main contribution (3.9), we write \(j=Na^2+2 \sqrt{ \frac{N}{\beta } } a \, t.\) Then we have
For the bulk case when \( a \in (0,1)\), by the Riemann sum approximation, we obtain
Here we have used
after integration by parts and upon applying [49, Eq. (7.14.3)]. Together with \(\Delta Q^\textrm{Gin}(z)=\frac{\beta }{2}\) we obtain \(\lim _{N\rightarrow \infty }\frac{\beta }{\sqrt{N\beta /2}}V_N^{(\beta )}(a) =2a/\sqrt{\pi }\) in the bulk.
For the near edge case, it follows from rescaling \(a=1-\frac{\mathcal {S}}{\sqrt{N\beta }}\) and
that we have
As stated in (1.14), the supplement of [45] gives a second form for this integral without derivationFootnote 2. It is obtained as follows
upon integrating by parts twice and using the definition of the error function. Now the proof is complete for the Ginibre ensembles. \(\square \)
4 Number Variance for General Radially Symmetric Potentials at Large-N
In this section, we prove our main result. For simplicity we shall drop the subscript in the potential \(Q_N\) and \(g_N\) here.
4.1 Proof of Theorem 1.2
For the proof, we shall use the standard Laplace method to derive the asymptotic of \(h_{j, 1}(a) / h_j\).
Proof of Theorem 1.2
We first consider the case \(\beta =2\). By Proposition 1.1, the case \(\beta =4\) follows along the same lines; the only difference comes from the step size when applying the Riemann sum approximation.
Write
Thus
Since \(\Delta =\frac{1}{4}(\partial _r^2+\frac{1}{r} \partial _r)\), the function \(f(r):=rg_N'(r)\) satisfies \(f'(r)>0\), according to our assumptions for a suitable potential. Therefore
has a unique critical point \(r_j,\) i.e.
Notice that
Thus we have as \(r\rightarrow r_j,\)
Using the change of variable
this gives
Let us turn to \(h_{j,1}(a)\) and \(h_{j,2}(a)\). We denote \(j_* = \frac{1}{2}(N a g'(a) - 1)\). Due to (4.1), we have \(r_{j*}=a\). By the Laplace method, for j such that \(|j-j_*|> M \sqrt{N}\) for a large M,
Therefore by Proposition 1.1, we have
To analyse the main contributions, let
Then we have
which leads to
Using the change of variable
we have
Using \(h_{j,2}(a)=h_j-h_{j,1}(a)\) we have thus shown that
For \(a \in (0,1)\), by (3.10), we obtain
On the other hand, for the edge we define
and obtain
This completes the proof. \(\square \)
We now prove Corollary 1.3.
Proof of Corollary 1.3
It is well known [13, 36] that the empirical measures converge to Frostman’s equilibrium measure [51]. As a consequence, as \(N \rightarrow \infty \), we have
By (2.8) and (4.2), we have that for \(a \in (0,1]\),
as \(N \rightarrow \infty \). Now (1.15) follows from Theorem 1.2 and (4.3). \(\square \)
4.2 Proof of Propositions 1.4 and 1.5
Proof of Proposition 1.4
For the potential (1.16) with \(\beta =2\), we have
Similarly,
Thus by Proposition 1.1, we have
Similarly, we have
The rescaling \(a=\mathcal {T}/N^{\frac{1}{2b}}\) removes the N-dependence inside the normalised incomplete Gamma-functions. The existence of the limiting sums can be seen for example using the quotient criterion. Combined with the large first argument asymptotic [49, Eq. (8.11.5)]
together with \(Q(\alpha ,z)=1-P(\alpha ,z)\), this completes the proof. \(\square \)
We now prove Proposition 1.5.
Proof of Proposition 1.5
Let \(\beta =2\). Note that by (1.21), we have

It can be shown that
see e.g. [3, Sect. 4.1]. On the other hand, we have

upon change of variables \(u = N^m r^2\), and the integral can be found in [12, 20.5.(1)] This yields our first result

leading to the expected number at \(\beta =2\). For \(h_{j,2}(a)\) we may use Proposition A.1, to see that

which yields

In summary, this leads to the variance

For \(\beta =4\) a simple shift \(N\rightarrow 2N\) and \(j\rightarrow 2j+1\) results into

and thus to the claimed expressions for the expected number and variance for \(\beta =4\).
In the microscopic regime we set \(N^m a^2 = \mathcal {T}^2\), to obtain

and likewise for the other quantities. This completes the proof. \(\square \)
4.3 Proof of Propositions 1.6 and 1.7
We first prove Proposition 1.6 which is at weak non-unitarity.
Proof of Proposition 1.6
For \(a \le 1\), we have
where \(X \sim B(j+c+1,1-a^2).\) Here B is the binomial distribution.
We present the proof for \(\beta =2\). Then \(\beta =4\) follows along the same lines. Note that if \(a\in (0,1)\) is fixed, we have for the bulk limit
On the other hand, for the edge limit with rescaling
the binomial distribution X tends to Poisson distribution with intensity \(\lambda =\mathcal {S}t\). Thus we have
Therefore we obtain
which completes the proof. \(\square \)
Now we prove Proposition 1.7 which is at strong non-unitarity.
Proof of Propositions 1.7
Note that for Q given by (1.29),
Thus for \(a \le \sqrt{1+{\tilde{c}}},\) we have
Then, due to the Poisson approximation of the binomial distribution, we have that for j fixed
after parametrising \(a=\sqrt{\frac{1+{\tilde{c}}}{N{\tilde{c}}}}\mathcal {T}\). Thus we obtain
which completes the proof.
Data Availability
The numerical data generated for part of the figures are merely an illustration of our entirely theoretical findings. These data are available upon request from the authors.
Notes
This name was proposed by V.L. Girko.
Notice a typo in the sign of the second term there.
References
Adhikari, K.: Hole probabilities for \(\beta \)-ensembles and determinantal point processes in the complex plane. Electron. J. Probab. 23, 1–21 (2018)
Adhikari, K., Reddy, N.K.: Hole probabilities for finite and infinite Ginibre ensembles. Int. Math. Res. Not. 21, 6694–6730 (2016)
Akemann, G., Burda, Z.: Universal microscopic correlation functions for products of independent Ginibre matrices. J. Phys. A 45(46), 465201, 18 (2012)
Akemann, G., Ipsen, J.: Recent exact and asymptotic results for products of independent random matrices. Acta Phys. Pol. B 46(9), 1747–1784 (2015)
Akemann, G., Strahov, E.: Hole probabilities and overcrowding estimates for products of complex Gaussian matrices. J. Stat. Phys. 151(6), 987–1003 (2013)
Akemann, G., Phillips, M.J., Shifrin, L.: Gap probabilities in non-Hermitian random matrix theory. J. Math. Phys. 50(6), 063504, 32 (2009)
Akemann, G., Ipsen, J.R., Strahov, E.: Permanental processes from products of complex and quaternionic induced Ginibre ensembles. Random Matrices Theory Appl. 3(04), 1450014 (2014)
Akemann, G., Byun, S.-S., Kang, N.-G.: Scaling limits of planar symplectic ensembles. SIGMA Symmetry Integr. Geom. Methods Appl. 18(007), 40 (2022)
Akemann, G., Ebke, M., Parra, I.: Skew-orthogonal polynomials in the complex plane and their Bergman-like kernels. Commun. Math. Phys. 389, 621–659 (2022)
Ameur, Y., Cronvall, J.: Szegö type asymptotics for the reproducing kernel in spaces of full-plane weighted polynomials. arXiv:2107.11148 (2021)
Ameur, Y., Kang, N.-G., Seo, S.-M.: The random normal matrix model: insertion of a point charge. Potential Anal. arXiv:1804.08587 (2021)
Bateman, H.: Tables of Integral Transforms [volume II], vol. 2. McGraw-Hill Book Company, New York (1954)
Benaych-Georges, F., Chapon, F.: Random right eigenvalues of Gaussian quaternionic matrices. Random Matrices Theory Appl. 1(2), 1150009, 18 (2012)
Burda, Z., Janik, R.A., Waclaw, B.: Spectrum of the product of independent random Gaussian matrices. Phys. Rev. E 81(4), 041132 (2010)
Byun, S.-S., Charlier, C.: On the almost-circular symplectic induced Ginibre ensemble. arXiv:2206.06021 (2022)
Byun, S.-S., Charlier, C.: On the characteristic polynomial of the eigenvalue moduli of random normal matrices. arXiv:2205.04298 (2022)
Chafaï, D., Gozlan, N., Zitt, P.-A.: First-order global asymptotics for confined particles with singular pair repulsion. Ann. Appl. Probab. 24(6), 2371–2413 (2014)
Charlier, C.: Large gap asymptotics on annuli in the random normal matrix model. arXiv:2110.06908 (2021)
Charlier, C.: Asymptotics of determinants with a rotation-invariant weight and discontinuities along circles. Adv. Math. 408, 108600 (2022)
Charlier, C., Lenells, J.: Exponential moments for disk counting statistics of random normal matrices in the critical regime. arXiv:2205.00721 (2022)
Chau, L.-L., Zaboronsky, O.: On the structure of correlation functions in the normal matrix model. Commun. Math. Phys. 196(1), 203–247 (1998)
Cooper, N.: Rapidly rotating atomic gases. Adv. Phys. 57(6), 539–616 (2008)
Cunden, F.D., Mezzadri, F., Vivo, P.: Large deviations of radial statistics in the two-dimensional one-component plasma. J. Stat. Phys. 164(5), 1062–1081 (2016)
Dean, D.S., Doussal, P.L., Majumdar, S.N., Schehr, G.: Noninteracting fermions in a trap and random matrix theory. J. Phys. A 52(14), 144006 (2019)
Fenzl, M., Lambert, G.: Precise deviations for disk counting statistics of invariant determinantal processes. Int. Math. Res. Not. 2022(10), 7420–7494 (2022)
Fields, J.L.: The asymptotic expansion of the Meijer G-function. Math. Comput. 26(119), 757–765 (1972)
Fischmann, J., Bruzda, W., Khoruzhenko, B.A., Sommers, H.-J., Życzkowski, K.: Induced Ginibre ensemble of random matrices and quantum operations. J. Phys. A 45(7), 075203, 31 (2012)
Forrester, P.J.: Some statistical properties of the eigenvalues of complex random matrices. Phys. Lett. A 169(1–2), 21–24 (1992)
Forrester, P.J.: Log-gases and Random Matrices (LMS-34). Princeton University Press, Princeton (2010)
Forrester, P.J.: Analogies between random matrix ensembles and the one-component plasma in two-dimensions. Nucl. Phys. B 904, 253–281 (2016)
Fyodorov, Y.V., Sommers, H.-J.: Random matrices close to hermitian or unitary: overview of methods and results. J. Phys. A 36(12), 3303–3347 (2003)
Ghosh, S., Nishry, A.: Point processes, hole events, and large deviations: random complex zeros and Coulomb gases. Constr. Approx. 48(1), 101–136 (2018)
Ginibre, J.: Statistical ensembles of complex, quaternion, and real matrices. J. Math. Phys. 6(3), 440–449 (1965)
Götze, F., Tikhomirov, A.: On the asymptotic spectrum of products of independent random matrices. arXiv:1012.2710 (2010)
Grobe, R., Haake, F., Sommers, H.-J.: Quantum distinction of regular and chaotic dissipative motion. Phys. Rev. Lett. 61, 1899–1902 (1988)
Hedenmalm, H., Makarov, N.: Coulomb gas ensembles and Laplacian growth. Proc. Lond. Math. Soc. (3) 106(4), 859–907 (2013)
Ipsen, J.R.: Products of independent quaternion Ginibre matrices and their correlation functions. J. Phys. A 46(26), 265201, 16 (2013)
Jancovici, B., Lebowitz, J.L., Manificat, G.: Large charge fluctuations in classical Coulomb systems. J. Stat. Phys. 72(3), 773–787 (1993)
Kanzieper, E.: Eigenvalue correlations in non-Hermitean symplectic random matrices. J. Phys. A 35(31), 6631–6644 (2002)
Khoruzhenko, B.A., Lysychkin, S.: Truncations of random symplectic unitary matrices. arXiv:2111.02381 (2021)
Kiessling, M.K.-H., Spohn, H.: A note on the eigenvalue density of random matrices. Commun. Math. Phys. 199(3), 683–695 (1999)
Krishnapur, M.: Overcrowding estimates for zeroes of planar and hyperbolic Gaussian analytic functions. J. Stat. Phys. 124(6), 1399–1423 (2006)
Lacroix-A-Chez-Toine, B., Grabsch, A., Majumdar, S.N., Schehr, G.: Extremes of 2d coulomb gas: universal intermediate deviation regime. J. Stat. Mech. 2018(1), 013203 (2018)
Lacroix-A-Chez-Toine, B., Garzón, J.A.M., Calva, C.S.H., Castillo, I.P., Kundu, A., Majumdar, S.N., Schehr, G.: Intermediate deviation regime for the full eigenvalue statistics in the complex Ginibre ensemble. Phys. Rev. E 100(1), 012137 (2019)
Lacroix-A-Chez-Toine, B., Majumdar, S.N., Schehr, G.: Rotating trapped fermions in two dimensions and the complex Ginibre ensemble: Exact results for the entanglement entropy and number variance. Phys. Rev. A 99(2), 021602 (2019)
Luke, Y.L.: The Special Functions and Their Approximations, vol. 53. Academic press, London (1969)
Mehta, M.L.: Random Matrices, volume 142 of Pure and Applied Mathematics (Amsterdam). Elsevier/Academic Press, Amsterdam (2004)
Nishry, A., Wennman, A.: The forbidden region for random zeros: appearance of quadrature domains. arXiv:2009.08774 (2020)
Olver, F.W., Lozier, D.W., Boisvert, R.F., Clark, C.W. (eds.): NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge (2010)
O’Rourke, S., Soshnikov, A.: Products of independent non-Hermitian random matrices. Electron. J. Probab. 16, 2219–2245 (2011)
Saff, E.B., Totik, V.: Logarithmic Potentials with External Fields. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 316. Springer-Verlag, Berlin (1997)
Smith, N.R., Doussal, P.L., Majumdar, S.N., Schehr, G.: Counting statistics for non-interacting fermions in a rotating trap. Phys. Rev. A 105, 043315 (2022)
Życzkowski, K., Sommers, H.-J.: Truncations of random unitary matrices. J. Phys. A 33(10), 2045–2057 (2000)
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have not disclosed any competing interests.
Additional information
Communicated by Paul Bourgade.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The work of Gernot Akemann was partly funded by the Deutsche Forschungsgemeinschaft (DFG) Grant SFB 1283/2 2021 – 317210226. Sung-Soo Byun was partially supported by Samsung Science and Technology Foundation (SSTFBA1401-51), by the National Research Foundation of Korea (NRF-2019R1A5A1028324) and by a KIAS Individual Grant (SP083201) via the Center for Mathematical Challenges at Korea Institute for Advanced Study. Markus Ebke was partially supported by the DFG grant IRTG 2235
Appendix A: An Identity for Meijer G-functions
Appendix A: An Identity for Meijer G-functions
The Meijer G-function is defined by the Mellin-Barnes integral representation

for \(p \ge n\ge 0\) and \(q \ge m \ge 0\). Here, the integration contour L in \({\mathbb {C}}\) depends on the poles of the gamma functions in the numerator, see e.g. [49, Chapter 16]. Using this representation we will prove the proposition below, that expresses a particular linear combination of Meijer G-functions in terms of a finite series. A special case of (A.2) is then used in the proof of Proposition 1.5.
Recall that the integration path L is chosen such that the poles of \(\Gamma (b_j - s)\) (\(j = 1, \dots , m\)) lie to the right of L, and those of \(\Gamma (1 - a_j + s)\) (\(j = 1, \dots , n\)) lie to the left, see e.g. [49, Section 16.17] for details. Since \(\Gamma (z)\) has (simple) poles at \(z = 0, -1, -2, \dots \), here we must consider the points \(s = b_j + n\) and \(s = a_j - 1 - n\) for \(n = 0, 1, 2, \dots \). Furthermore, we assume that the parameters of the Meijer G-function satisfy \(a_k - b_j \notin {\mathbb {N}}_{>0}\) for all \(k = 1, \dots , n\) and \(j = 1, \dots , m\), so that the poles of \(\Gamma (b_j - s)\) do not coincide with those of \(\Gamma (1 - a_j + s)\). In the proposition below there is one exception to this, for the last indices to satisfy \(a_{n+1} - b_{m+1} \in {\mathbb {N}}_{>0}\).
Proposition A.1
Let \(p \ge n\ge 0\), \(q \ge m\ge 0\) and \(\varvec{a} = \{ a_1, \dots , a_{p + 1} \}\) and \(\varvec{b} = \{ b_1, \dots , b_{q + 1} \}\) such that \(a_{n + 1} - b_{m + 1}=k\) is a positive integer, then

where the sum rums from \(c=b_{m+1}, b_{m+1}+1,\ldots ,a_{n+1}-1\) in integer steps.
Proof
First, note that the integrands of the two Meijer G-functions have the common factor
The factors that differ are \(\Gamma (1 - a_{n + 1} + s) / \Gamma (1 - b_{m + 1} + s)\) present in the first Meijer G-function \(G^{m , n + 1}_{p + 1, q + 1}\) with contour \(L_1\), and the factor \(\Gamma (b_{m + 1} - s) / \Gamma (a_{n + 1} - s)\) in the second Meijer G-function \(G^{m + 1, n}_{p + 1, q + 1}\) with contour \(L_2\). Due to the condition that \(a_{n + 1} - b_{m + 1}=k\in {\mathbb {N}}_{>0}\) is an integer, it is not difficult to see that these two ratios of Gamma-functions have only a finite number of poles, located at the very same positions,
because poles and zeros cancel otherwise. In fact these two ratios are proportional. To see this first notice that
Using the relation [49, Eq. (5.5.3)] for the Gamma function valid at non-integer argument, we thus obtain
Thus the two Meijer G-functions in (A.2) have the same integrand (up to a sign).
The integrals, however, do not simply add up, because their integration paths \(L_1\) and \(L_2\) are slightly different: following the definition (A.1), the poles (A.3) lie to the left of \(L_1\) in the first function in (A.2), but to the right of \(L_2\) in the second. Because all other factors and indices agree, the locations of all other poles with respect to \(L_1\) and \(L_2\) agree.
In order to determine the left-hand side of (A.2), we modify \(L_1\) by introducing clockwise contours around each pole (A.3) and adding appropriate lines to connect with \(L_{1}\). This new path \(L_{1}'\) can now be deformed continuously into \(L_{2}\) without crossing any other poles. We obtain

where we used (A.4) to cancel the two integrals over \(L_2\). The remaining sum is evaluated with the residue theorem. Note that the contours around the poles at \(s=c\) are clockwise, and that all factors except \(\Gamma (1 - a_{n + 1} + s)\), which has a simple pole at c, are smooth near \(s = c\).
Furthermore the residue of \(\Gamma (z)\) at \(z = - n\) is \((-1)^n / \Gamma (n + 1)\), see [49, 5.1(i)]. Thus for each summand we have
and merging the fractions by adjusting the indices in the denominator yields the summands in (A.2). \(\square \)
Remarks
We give some remarks on special cases of Proposition A.1.
-
(1)
If \(a_{n + 1} - b_{m + 1}\) is a negative integer or zero, then (A.2) still holds with the convention that the empty sum is zero. In this case no surgery of the integration path is necessary and it is clear from (A.4) that the end result must be zero. This case is known in the literature (e.g. [46, Sect. 5.3.2, Eq. (7)]).
-
(2)
In the proof of Proposition 1.5 we need the case \(b_{m + 1} = 0\), \(a_{n + 1} = 1\). Here the sum on the right-hand side consists of a single term with \(c = 0\) and thus it is independent of z:
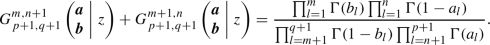 (A.5)
(A.5) -
(3)
In general, when \(a_{n+1}>b_{m+1}\ge 0\) are integers, the right hand side of (A.2) becomes a polynomial.
For the small argument limit \(\mathcal {T}\rightarrow 0\) of the results in Proposition 1.5 we need the following small argument asymptotic of the Meijer G-function.
Proposition A.2
Let \(m \ge 0\) and \(j \ge 1\). Then as \(z \rightarrow 0\) we have

Proof
By a similar computation in the proof of Proposition A.1, using the residue theorem, we have

where \(c \in \{j, j+1, \dots \}\) are the poles of the function \(\Gamma (j - s)\). It then follows from the generalised Leibniz rule for derivatives that
As \(z \rightarrow 0\), only the summand with \(r = l = k = m - 1\) contributes to the leading term. Thus we obtain that as \(z \rightarrow 0\),
Furthermore, the leading term in (A.6) comes from the \(c = j\) summand. Simplifying the resulting expression leads to the claimed asymptotic formula. Note that in the \(m = 1\) case the first subleading term is given by the \(c = j + 1\) summand. \(\square \)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Akemann, G., Byun, SS. & Ebke, M. Universality of the Number Variance in Rotational Invariant Two-Dimensional Coulomb Gases. J Stat Phys 190, 9 (2023). https://doi.org/10.1007/s10955-022-03005-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10955-022-03005-2